Joint Data Harmonization and Group Cardinality Constrained Classification

Abstract

To boost the power of classifiers, studies often increase the size of existing samples through the addition of independently collected data sets. Doing so requires harmonizing the data for demographic and acquisition differences based on a control cohort before performing disease specific classification. The initial harmonization often mitigates group differences negatively impacting classification accuracy. To preserve cohort separation, we propose the first model unifying linear regression for data harmonization with a logistic regression for disease classification. Learning to harmonize data is now an adaptive process taking both disease and control data into account. Solutions within that model are confined by group cardinality to reduce the risk of overfitting (via sparsity), to explicitly account for the impact of disease on the inter-dependency of regions (by grouping them), and to identify disease specific patterns (by enforcing sparsity via the l₀-‘norm’). We test those solutions in distinguishing HIV-Associated Neurocognitive Disorder from Mild Cognitive Impairment of two independently collected, neuroimage data sets; each contains controls and samples from one disease. Our classifier is impartial to acquisition difference between the data sets while being more accurate in diseases seperation than sequential learning of harmonization and classification parameters, and non-sparsity based logistic regressors.

1 Introduction

Popular for improving the power of classifiers is to expand application from a single data set (Fig. 1(a)) to multiple, independently collected sets of the same disease (Fig. 1(b)) [1]. To analyze across multiple sets, neuroimage studies generally first harmonize the data by, for example, regressing out demographic factors from MRI measurements and then train the classifier to distinguish disease from control samples [2]. However, harmonization might mitigate group differences making classification difficult (such as in Fig. 2). To improve classification accuracy, we propose the first approach to jointly learn how to harmonize MR image data and classify disease. Harmonization relies on both controls and disease cohorts to reduce differences in the image based measurements due to acquisition differences between sets while preserving the group separation investigated by the classifier. We evaluate our approach on the challenging task (Fig. 1(c)) of being trained on two data sets differing in their acquisition and diseases they sample, and tested on accurately distinguishing the two diseases while being impartial to acquisition differences, i.e., the controls of the two sets.

Fig. 1.

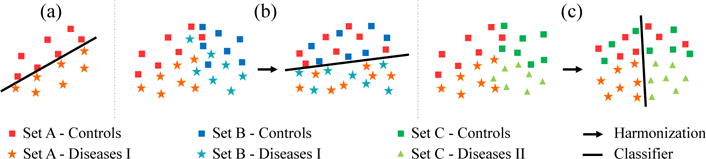
Examples for classifying data: (a) Classification based on a single set, (b) separating healthy and disease based on multiple sets requiring harmonization, and (c) part two disease groups based on harmonizing controls of disease specific data sets.

Fig. 2.

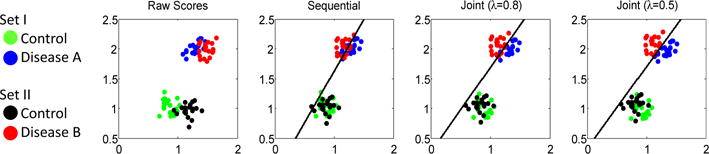
Impact of harmonization on classification (black line) of two synthetic sets. Compared to the raw scores, the Sequential approach mitigated differences between the two disease groups by ‘pushing’ them together. Our joint model with λ = 0.5 is the only approach that is indifferent to controls and correctly labels all disease cases.

Training of our approach is defined by an energy function that combines a linear harmonization model with a logistic regression classifier. Minimizing this function is confined to group cardinality constrained solutions, i.e., labeling is based on a small number of groups of image scores (counted via the l₀-‘norm’). Doing so reduces the risk of overfitting, accounts for inter-dependency between regions (e.g., bilateral impact of diseases), and identifies disease distinguishing patterns (defined by non-zero weights of classifiers) that avoid issues of solutions based on relaxed sparsity constraints [3]. Inspired by [4], our method uses block coordinate descent to find the optimal parameters for harmonizing the two data sets and correctly labeling disease samples while being indifferent to control cohorts (i.e., acquisition differences). During testing, we use those parameters to harmonize the image scores before performing classification ensuring that the data set associated with a subject is not part of the labeling decision.

Using 5-fold cross-validation, we measure the accuracy of our method on distinguishing HIV-Associated Neurocognitive Disorder (HAND) from Mild Cognitive Impairment (MCI) of two independently collected data sets; each set contains controls and samples of one disease only. Distinguishing HAND from MCI is clinically challenging due to similarity in symptoms and missing standard protocols for assessing neuropsychological deficits [5]. Not only is our classifier indifferent to the controls from both groups but is also significantly more accurate in distinguishing the two diseases than the conventional sequential harmonization and classification approach and non-sparsity based logistic regression methods.

2 Jointly Learning of Harmonization and Classification

Let a data set consists of set S_A of controls and samples with disease A, and an independently collected set S_B of controls and samples of disease B. The four subsets are matched with respect to demographic scores, such as age. Each sample s of the joint set is represented by a vector of image features x_s and a label y_s, where y_s = −1 if s ∈ S_A and y_s = +1 for s ∈ S_B. The acquisition differences between S_A and S_B are assumed to linearly impact the image features. To extract disease separating patterns from this joint set, we review the training of a sequential model for data harmonization and classification, and then propose to simultaneously parameterize both tasks by minimizing a single energy function.

2.1 Sequential Harmonization and Classification

Training the linear regression model for data harmonization results in parameterizing matrix U so that it minimizes the difference (with respect to the l₂-norm ‖·‖₂) between the inferred values U · [1 y_s]^⊤ (1 is the bias term of the linear model) and the raw image scores x_s across n_C controls of the joint data set, i.e.,

$$\widehat{U}:=\underset{U}{\text{arg}min}{h}_C(U)\mathrm{with}{h}_C(U):=\frac{1}{n_C}{\displaystyle \sum _{s=1}^{n_C}\Vert U\cdot {[1y_s]}^{\top }}-x_s{\Vert }_2^2.$$ (1)

A group sparsity constrained logistic regression classifier is trained on the residuals $r_s(\widehat{U}):=\widehat{U}\cdot {[1y_s]}^{\top }-x_s$, i.e., harmonized scores, across samples ‘s’ of two groups, which are n_D samples of the two disease cohorts. Note, classification based on the inferred values $\widehat{U}\cdot {[1y_s]}^{\top }$ is uninformative as all scores of a region are mapped to two values. Now, let the logistic function be θ(α) := log(1+exp(−α)), the weight vector w encode the importance of each score of r_s and v ∈ ℝ be the label offset, then the penalty (or label) function of the classifier is defined by

$$l_D(\widehat{U,}v,w):=\frac{1}{n_D}{\displaystyle \sum _{s=n_C+1}^{n_C+n_D}\theta }\left(y_s\cdot \left(w^{\top }\cdot r_s(\widehat{U})+v\right)\right).$$ (2)

The search for point $(\widehat{v},\widehat{w})$ minimizing $l_D(\widehat{U},\cdot ,\cdot )$ often has to be limited so that $\widehat{w}$ conforms to disease specific constraints, such as the bilateral impact of HAND or MCI on individual regions. These constraints can be modeled by group cardinality. Specifically, every entry of w is assigned to one of n_G groups $g_1(w),\dots ,g_{n_G}(w)$. The search space $𝕊$ is composed of weights where the number of groups with non-zero weight entries are below a certain threshold k ∈ ℕ, i.e., $𝕊:=\{w:{\displaystyle {\sum }_{i=1}^{n_G}\Vert \Vert g_i(w)}{\Vert }_2{\Vert }_0\le k\}$ with ‖·‖₀ being the l₀-‘norm’. Finally, the training of the classifier is fully described by the following minimization problem

$$(\widehat{v},\widehat{w}):=\arg \underset{v\in ℝ,w\in 𝕊}{min}{l}_D(\widehat{U},v,w),$$ (3)

which can be solved via penalty decomposition [4, 6]. Note, that Eq. (3) turns into a sparsity constrained problem if each group g_i is of size 1. Furthermore, setting ‘k = n_G’ turns Eq. (3) into a logistic regression problem. Finally, Eq. (3) can distinguish a single disease from controls by simply replacing y_s in Eq. (2) with a variable encoding assignment to cohorts instead of data sets.

2.2 Simultaneous Harmonization and Classification

We now determine $(\widehat{U},\widehat{v},\widehat{w})$ for a single minimization problem composed of the linear (harmonization) and logistic (classification) regression terms, i.e.,

$$(\widehat{U},\widehat{v},\widehat{w}):=\underset{U,v,w\in 𝕊}{\arg min}(1-\mathrm{\lambda })\cdot l_D(U,v,w)+\mathrm{\lambda }\cdot h_C(U),$$ (4)

Algorithm 1.

Joint Harmonization and Classification.

1:	Set ϱ = 0.1, $\sigma =\sqrt{10},{\epsilon }_B={\epsilon }_P={10}^{-3}$ (according to [4]) and U′ = 0, w′ = 0, q′ = 0, v′ = 1
2:	Repeat
3:	Repeat (Block Coordinate Descent)
4:	U″ ← U′, w″ ← w′, q″ ← q′, v″ v′
5:	U′ ←argminU (1 − λ)lD (U, v′, q′) + λhC (U) (via Gradient Descent)
6:	$(v^{\prime },q^{\prime })\leftarrow \text{arg}{min}_{v,q}(1-\mathrm{\lambda })l_D(U^{\prime },v,q)+\mathit{\varrho }\Vert w^{\prime }-q{\Vert }_2^2$ (via Gradient Descent)
7:	Update w′ by
	Sort groups gj(q′) so that $\Vert g_{j_1}(q^{\prime }){\Vert }_2\ge \Vert g_{j_2}(q^{\prime }){\Vert }_2\ge \dots \ge \Vert g_{j_{n_G}}(q^{\prime }){\Vert }_2$
	Define $𝕀$ to be the set of indices of q′ associated with groups $g_{j_1},\dots ,g_{j_k}{w}_i^{\prime }\leftarrow q_i^{\prime }$ if $q_i^{\prime }$ ∈ $𝕀$ and 0 otherwise.
8:	Until $max\{\frac{\Vert U\prime -U″{\Vert }_{max}}{max\{\Vert U\prime {\Vert }_{max},1\}},\frac{|v\prime -v″|}{max\left\{\right|v\prime |,1\}},\frac{\Vert w\prime -w″{\Vert }_{max}}{max\{\Vert w\prime {\Vert }_{max},1\}},\frac{\Vert q\prime -q″{\Vert }_{max}}{max\{\Vert q\prime {\Vert }_{max},1\}}\}<{\epsilon }_B,$
9:	ϱ ← σ · ϱ
10:	Until ‖w′ − q′ ‖max <εP.

where λ ∈ (0, 1). Note, the model fails to classify when λ = 1 ( $\widehat{v}$ and $\widehat{w}$ are undefined) or harmonize when λ = 0 (entries of $\widehat{U}$ are undefined). Motivated by [4], we simplify optimization by first parameterizing the classifier with respect to the ‘unconstrained’ vector q before determining the corresponding sparse solution $\widehat{w}$. The solution to Eq. (4) is estimated by iteratively increasing ϱ of

$$(U_{\mathit{\varrho }},v_{\mathit{\varrho }},w_{\mathit{\varrho }},q_{\mathit{\varrho }}):=\underset{U,v,w\in 𝕊,q}{\text{arg}min}(1-\mathrm{\lambda })\cdot l_D(U,v,q)+\mathrm{\lambda }\cdot h_C(U)+\mathit{\varrho }\cdot \Vert w-q{\Vert }_2^2$$ (5)

until the maximum of the absolute difference between elements of w_ϱ and q_ϱ is below a threshold, i.e., ‖w_ϱ−q_ϱ‖_max<ε_P. (U_ϱ,v_ϱ,w_ϱ,q_ϱ) are determined by block coordinate descent (BCD). As outlined in Alg. 1, let (U′, v′, w′, q′) be estimates of (U_ϱ, v_ϱ, w_ϱ, q_ϱ), then U′ is updated by solving Eq. (5) with fixed (v′, w′, q′):

$$U^{\prime }:=\underset{U}{\text{arg}min}\left(1-\mathrm{\lambda }\right)\cdot l_D(U,v^{\prime },q^{\prime })+\mathrm{\lambda }\cdot h_C(U).$$ (6)

As this minimization is over a convex and smooth function, Eq. (6) is solved via gradient descent. Note, that determining U′ is equivalent to increasing the separation between the two disease groups by minimizing l_D(·, v′, q′) while reducing the difference between the two control groups by minimizing h_C(·).

Next, BCD updates v′ and q′ by keeping (U′, w′) fixed in Eq. (5), i.e.,

$$(v^{\prime },q^{\prime }):=\underset{v,q}{\arg \min }(1-\mathrm{\lambda })\cdot l_D\left(U^{\prime },v,q\right)+\mathit{\varrho }\cdot \Vert w^{\prime }-q{\Vert }_2^2.$$ (7)

This minimization problem is defined by a smooth and convex function. Its solution is thus also estimated via gradient descent. Finally, w′ is updated by solving Eq. (5) with fixed (U′, v′, q′), i.e.,

$$w^{\prime }:=\underset{w\in 𝕊}{\text{arg}min}\Vert w-q\prime {\Vert }_2^2.$$ (8)

As shown in [4, 6], the closed form solution of Eq. (8) first computes ‖g_i(q′)‖₂ for each group i and then sets w′ to the entries of q′, who are assigned to the k groups with the highest norms. The remaining entries of w′ are set to 0. The procedures (6)~(8) are repeated until the relative changes of (U′, v′, w′, q′) between iterations are smaller than a threshold ε_B. (U_ϱ, v_ϱ, w_ϱ, q_ϱ) is updated with the converged (U′, v′, w′, q′), ϱ is increased and another BCD loop is initiated until w_ϱ and q_ϱ converge towards each other (see Alg. 1 for details).

Fig. 2 showcases the differences between sequential and joint harmonization and classification. Two synthetic data sets consist of a control and disease cohort, where the raw scores for each cohort are 20 random samples from a Gaussian distribution with the covariance being the identity matrix multiplied by 0.01. The mean of the Gaussian for Disease A of Set I (blue) is (1.3,2) resulting in samples that are somewhat separated from those of Disease B of Set II (mean=(1.5,2), red). The difference in data acquisition between the two sets is simulated by an even larger separation of the means between the two control groups (Set I: mean=(0.9,1), green; Set B: mean=(1.2,1), black). The Sequential method (see Sec. 2.1 without sparsity) harmonizes the scores so that the classifier assigns the controls to one set, i.e., the separating plane (black line) is impartial to acquisition differences. This plane fails to perfectly separate the two disease cohorts as the cohorts are ‘pushed’ together with the mean of Disease B being now to the right of the mean of Disease A. Higher accuracy in disease classification is achieved by our joint model (omitting sparsity) with λ = 0.8. Comparing this plot to the results with λ = 0.5 shows that as λ decreases the emphasis on separating the two disease increases as intended by Eq. (6). The classifier is still impartial to acquisition differences and perfectly labels the samples of the two disease cohort. In summary, the joint model enables data harmonization that preserves group differences, which was not the case for the sequential approach.

3 Distinguishing HAND from MCI

We tested our method on a joint set of two independently collected data sets: the ‘UHES’ set [7] contained cross-sectional MRIs of 15 HAND cases and 21 controls while the ‘ADNI’ set contained MRIs of 20 MCIs and 18 controls. The 4 groups were matched with respect to sex and age. Each MRI was acquired on a 3T Siemens scanner (with the two sets having different acquisition protocols) and was processed by [8] resulting in 102 regional volume scores. We assigned those scores to (n_G = 52) groups to account for the bilateral impact of MCI and HAND on both hemispheres. We now review our experimental setup and results highlighting that jointly learning harmonization and classification results in findings that are indifferent to the two control cohorts and more accurate in distinguishing the two disease groups compared to alternative learning models.

To measure the accuracy of our method, we used 5 fold-cross validation with each fold containing roughly 20% of each cohort. On the training sets, we used parameter exploration to determine the optimal group cardinality k ∈ {1, 2, …, 10} and weighing λ ∈ {0.1, 0.2, …, 0.9}. Across all folds and settings, our algorithm converged within 5 iterations while each BCD optimization converged within 500 iterations. For each setting, we then computed the disease accuracy of the classifier by separately computing the accuracy for each cohort (MCI and HAND) to be assigned to the right set (UHES or ADNI) and then averaging the scores to consider the imbalance of cohort sizes. We determined the control accuracy repeating those computations with respect to the two control groups. Since higher control accuracy infers worse harmonization, an unbiased control accuracy, i.e., around 50%, coupled with a high disease accuracy was viewed as preferable. Note, an unbiased control accuracy only qualifies the harmonization in that the remaining acquisition differences do not impact the separating plane (or weights $\widehat{w}$) of the classifier. For each training set, we then chose the setting (λ, k) with corresponding weights $\widehat{w}$ and harmonization parameters $\widehat{U}$ that produced the largest difference between the two accuracy scores. This criteria selected a unique setting for 2 folds, 2 settings for 2 folds, and 3 settings for 1 fold.

On the test set, we computed the harmonized scores (residuals) of all samples for each selected setting. We then hid the subjects’ data set associations from the ensemble of selected classifiers by applying the residuals to classifiers parameterized by the corresponding weight settings. Based on those results, we computed control and disease accuracy as well as the corresponding p-values via the Fisher exact test [9]. We viewed p < 0.05 as significantly more accurate than randomly assigning samples to the two sets. An ensemble of classifiers was viewed as informative, if separating HAND from MCI resulted in a significant p-value and a non-significant one for controls.

We repeated the above experiment for the sequential harmonization and classification approach of Section 2.1, called SeqGroup, to show the advantages of our joint learning approach, called JointGroup. To generalize our findings about joint learning of harmonization and classification parameters to non-sparsity constrained models, we also tested the approach omitting the group sparsity constraint, i.e., k = 52. JointNoGroup refers to the results of the corresponding joint method and SeqNoGroup to the sequential results.

Table 1 shows the accuracy scores and p-values of all implementations listed according to the difference between disease and control accuracy. The method with the smallest difference, SeqNoGroup, was the only approach recording a significant control accuracy score (68.4%, p = 0.024). The corresponding separating plane was thus not impartial to acquisition difference so that the relatively high disease accuracy (82.5%) was insignificant. The next approach, SegGroup, obtained non-significant accuracy scores for controls (64.6%) indicating that the group sparsity constrain improved generalizing the results from the relatively small training set to testing. The difference between control (52.8%) and disease accuracy (83.3%) almost doubled (30.5%) for the joint approach JointNoGroup. As reflected in Fig. 2, learning data harmonization separated from classification does not generalize as well as the joint approach, who harmonizes data so that differences between disease groups are preserved. Confirming all previous findings, the overall best approach (i.e., control and disease accuracy differ most) is our proposed JointGroup approach achieving a disease accuracy of 90%.

Table 1.

Implementations listed according to the difference between disease (MCI vs. HAND) and control (UHES controls vs. ADNI controls) accuracy. In bold are the findings that are statistically significant different from chance, i.e., p < 0.05. Our method, JointGroup, achieves the highest disease accuracy and largest spread in scores.

	Classification accuracy			p-value with ground truth
	Disease	Control	Difference	Disease	Control
SeqNoGroup	82.5	68.4	14.1	<0.001	0.024
SeqGroup	80.0	64.6	15.4	<0.001	0.073
JointNoGroup	83.3	52.8	30.5	<0.001	0.753
JointGroup	90.0	52.8	37.2	<0.001	0.753

The group sparsity constraint aided in separating diseases and identified patterns of regions (i.e., non-zero weights $\widehat{w}$) impacted by either MCI or HAND (or HIV). Each column of Fig. 3 shows the largest, unique pattern associated with a training set. For those training sets that selected multiple patterns (i.e., $\widehat{w}$ settings), patterns with less regions were always included in the largest pattern. The precentral gyrus, cerebellum VIII, and lateral ventricle were parts of all patterns. HIV is known to impact the cerebellum [10] and accelerated enlargement of ventricles is linked to both HIV [11] and MCI [12]. These findings indicate that the extracted patterns are informative with respect to MCI and HAND (and HIV), which requires an in-depth morphemic analysis for confirmation.

Fig. 3.

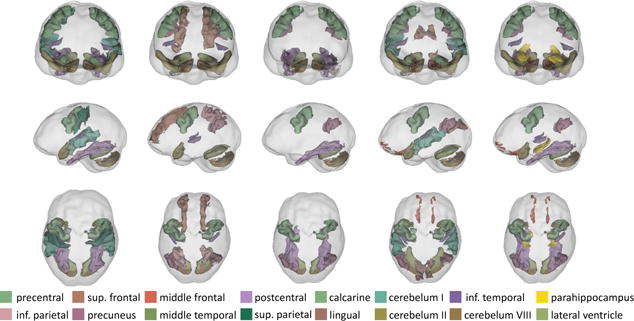
Each column shows the largest, unique pattern extracted by JointGroup on one of the 5 training sets. Identified regions are impacted by HAND, HIV, or MCI.

4 Conclusion

We proposed an approach that simultaneously learned the parameters for data harmonization and disease classification. The search for the optimal separating plane was confined by group cardinality to reduce the risk of overfitting, to explicitly account for the impact of disease on the inter-dependency of regions, and to identify disease specific patterns. On separating HAND from MCI samples of two disease specific data sets, our joint approach achieved better classification accuracy than the non-sparsity based model and sequential approaches.