An easily fabricated three-dimensional threaded lemniscate-shaped micromixer for a wide range of flow rates

Abstract

Mixing fluid samples or reactants is a paramount function in the fields of micro total analysis system (μTAS) and microchemical processing. However, rapid and efficient fluid mixing is difficult to achieve inside microchannels because of the difficulty of diffusive mass transfer in the laminar regime of the typical microfluidic flows. It has been well recorded that the mixing efficiency can be boosted by migrating from two-dimensional (2D) to three-dimensional (3D) geometries. Although several 3D chaotic mixers have been designed, most of them offer a high mixing efficiency only in a very limited range of Reynolds numbers (Re). In this work, we developed a 3D fine-threaded lemniscate-shaped micromixer whose maximum numerical and empirical efficiency is around 97% and 93%, respectively, and maintains its high performance (i.e., >90%) over a wide range of 1 < Re < 1000 which meets the requirements of both the μTAS and microchemical process applications. The 3D micromixer was designed based on two distinct mixing strategies, namely, the inducing of chaotic advection by the presence of Dean flow and diffusive mixing through thread-like grooves around the curved body of the mixers. First, a set of numerical simulations was performed to study the physics of the flow and to determine the essential geometrical parameters of the mixers. Second, a simple and cost-effective method was exploited to fabricate the convoluted structure of the micromixers through the removal of a 3D-printed wax structure from a block of cured polydimethylsiloxane. Finally, the fabricated mixers with different threads were tested using a fluorescent microscope demonstrating a good agreement with the results of the numerical simulation. We envisage that the strategy used in this work would expand the scope of the micromixer technology by broadening the range of efficient working flow rate and providing an easy way to the fabrication of 3D convoluted microstructures.

I. INTRODUCTION

Microfluidics, a technology characterised by the engineered manipulation of fluids at the micro/nanometre scale, is rapidly becoming a commonplace tool for basic and applied research. With inherent advantages such as small sample volume, high sensitivity, portability, low analysis time, and low power consumption, microfluidic devices are broadly applied in multiple domains including analytical chemistry, fundamental biological research, and materials synthesis.¹ Prime examples are in Lab-on-a-chip devices where biochemical assays are used for drug screening, organic synthesis, cell lysis, and cell staining. In all of those assays, mixing of two or more reagents is an inseparable part of sample handling and therefore a careful study of the microscale mixing phenomenon is necessary for the development of efficient micromixers to meet the individual needs.

In a micron scale, the laminar regime of the flow characterised by low Reynolds numbers (Re) entails a high momentum diffusion and a low momentum convection where viscous forces are dominant over inertial forces. Under this condition, mixing occurs mainly by molecular diffusion which is inherently slow and necessitates longer channels and extended retention time. To overcome these difficulties, research groups have proposed a considerable number of mixer designs, which classify micromixers into two broad categories of passive and active methods. Passive methods utilise smart channel geometries^2,3 to increase the interfacial contact area of the two mixing fluids whereas active methods employ an externally applied power source such as electro-osmotic,^4–7 magnetohydrodynamic,⁸ and ultrasonic forces.⁹ Although the active systems offer a superior flow manipulation, they are usually associated with complex operation protocols and require peripheral equipment. Passive methods, on the other hand, are more easily fabricated, readily accessible, and can be integrated with other microfluidic components.

2D passive micromixers are typically fabricated by photolithography which is a well-established microfabrication method. However, such systems fail to provide an efficient mixing within a short channel length. In 2D micromixers, the interfacial contact area of the fluids is limited by the two-dimensional structure of the microchannel, and thus, a high mixing efficiency (η) is only achievable within a certain range of Re and a mixing length in the order of several millimetres.¹⁰ Moreover, features like 2D static mixing elements,¹¹ which have been proven to increase η through chaotic advection, can only disturb the mixing interface in two dimensions.

3D micromixers have garnered the attention because they have the edge over conventional two-dimensional (2D) microchips. The addition of the third dimension can drastically affect the flow field by the introduction of 3D vortices¹² leading to a more disturbed contact surface and increased contact time. Furthermore, by extending the channel length in the third dimension, building a compact micromixer in a limited workspace will become possible.

3D passive micromixers can be categorised into two broad groups of Split and Recombination (SAR) mixers^13,14 and chaotic mixers.^15,16 Hossain and Kim¹⁴ compared a three-dimensional chaotic serpentine micromixer to a serpentine SAR micromixer at 1 < Re < 120. They stated that the serpentine micromixer equipped with SAR shows a stronger vortex which strengthens the transverse motion and leads to a higher mixing index. While SAR approaches have well-known working mechanisms, chaotic advection in 3D structures is involved in more sophisticated mixing techniques including interconnected multichannel networks,¹⁷ 3D spiral channels,¹⁸ 3D crossing manifold,¹⁹ and 3D periodic perturbation.²⁰ Although several 3D chaotic mixers have been designed, most of them offer a high mixing efficiency (i.e., η > 90%) only in a very limited range of Re. For instance, Yang et al.¹⁸ reported a 3D spiral micromixer with a maximum efficiency of 80% to 90% in the range of Re = 32 to 40, respectively. Also, a three-dimensional cross folding manifold micromixer was proposed by Lim et al.¹⁹ which achieves a maximum efficiency of 90% around Re = 1 only.

Based on the Reynolds number, the existing microfluidic mixing devices are divided into high (Re > 100), intermediate (10 < Re < 100), and low Reynolds numbers (Re < 10).²¹ Although the efficient mixing range of Re is limited to Re ≤ 10 for the applications of micro total analysis system (μTAS), the required Re for microchemical process applications is tens to hundreds.²⁰ Therefore, a versatile micromixer should demonstrate a high mixing performance in a relatively wide range of Re.

The traditional way of creating 3D microfluidic systems is to stack several polydimethylsiloxane-polymer (PDMS) layers fabricated using planar technologies (i.e., soft lithography using silicon or SU-8 master moulds) on top of each other. An extensive array of equipment and process steps are needed for photolithography to achieve some level of complexity while the design freedom still is severely limited.²² Besides, bonding multiple PDMS layers require tedious micro-scale alignments and surface treatment (oxygen plasma, adhesive, ultrasonic, etc.), which all render commercialization difficult.²³ More recently, femtosecond laser direct writing has shown to be a useful method to create 3D channels.^24,25 Although laser writing is a great promise to produce 3D structures, it still does not exclude the use of expensive machinery and is just limited to the glass and silicon.

Additive manufacturing, which refers to a process by which digital 3D design data is used to build up a component in layers by depositing material, is identified as a candidate to overcome the remaining obstacles.^26–29 3D printing has already been used for direct maskless fabrication of microfluidic devices from a variety of polymeric materials.^29,30 Nevertheless, these devices miss the advantages of versatile materials like PDMS which provide gas permeability and unmatched optical clarity for fluorescent microscopy and biological assays. There have been several attempts to combine the benefits of both PDMS and additive manufacturing.²³ In some of these efforts, aluminium moulds or clean room resources are replaced with 3D printed moulds resulting in planar chips.^31,32

Embedded template-assisted method is a relatively simple, but a promising approach for the fabrication of 3D microfluidic structures. This method has been successfully utilised for the fabrication of microvascular networks,³³ microfluidic channels,³⁴ and tissue engineering scaffolds³⁵ by using metal wires, polylactic acid (PLA), sugar,³⁶ acrylonitrile butadiene styrene (ABS),³⁷ and liquid metals³⁸ as a sacrificial (or template) material. In this approach, the embedded material is mainly used as a guiding template for the formation of the desired pattern inside a block of PDMS after its removal. Despite the great promise of this approach for the fabrication of complex 3D structures, some major obstacles such as inadequate resolution of templates (due to the low resolution of printers or materials such as sugar, chitosan, and ABS), distortion and collapse of PDMS block during the removal of the template (specially for the case of metal wires), utilization of harsh chemical (such as acetone), and residual of sacrificial layer in channel networks hinder their widespread adoption in the microfluidic community.³⁸

To address these fabrication issues, we utilised a simple technique by which PDMS microfluidic chips can be precisely made. This technique provides low-cost manufacturing of microchannels and structures with desired lengths, cross-sections, and directions. In this technique, a wax structure is printed by a high-resolution 3D printer to shape uncured PDMS in the desired form. After the PDMS is cured, the wax structure is removed to yield the finalised PDMS-made 3D micromixer.

In this paper, we designed a novel 3D micromixer which incorporates the curved and fine-threaded microchannels to induce the Dean flow and diffusive mixing, respectively. This versatile 3D micromixer exhibited the maximum η of 97.3% in the wide range of 1 < Re < 1000 while η always remained more than 90%. Obviously, the efficiency of the micromixer for Re < 1 is almost certainly 100% because of the extended retention time which provides the opportunity for the mixing fluids to diffuse perfectly and mingle with each other. Initially, a set of numerical simulations was performed to study the physics of the flow to determine the essential geometrical parameters of the mixers. Next, following the described fabrication technique, we used a 3D wax printer to fabricate the presented complex micromixers easily and then tested the performance of the mixers under a fluorescent microscope.

II. THEORY

The governing equations of the fluid flow in a micromixer are derived from the conservation of mass and momentum which are known as the continuity and Navier-Stokes equations, respectively. For incompressible Newtonian fluids, these equations can be expressed as

$$\nabla .\mathit{V}=0,$$ (1)

$$\frac{\partial \mathit{V}}{\partial t}+\rho \left(\mathit{V}.\nabla \right)\mathit{V}=-\nabla P+\mu {\nabla }^2\mathit{V},$$ (2)

where V is the velocity vector, ρ is the fluid density, μ is the dynamic viscosity of the fluid, and P is the thermostatic pressure. Furthermore, the conservation of chemical species is the principle law governing the transport of mixing fluids in a micromixer which is described by the so-called convection-diffusion equation

$$\frac{\partial c}{\partial t}+\left(\mathit{V}.\nabla \right)c=D\hspace{0.17em}{\nabla }^{2}c,$$ (3)

where c is the concentration of species, D is the diffusion coefficient of the species, and V is the velocity vector. The terms on the left-hand side of the above equation represent the accumulation and advection of species, and the right-hand side represents molecular diffusion. In order to find the distribution of the concentration of species, one needs first to solve the continuity and Navier-Stokes equations to obtain the velocity field V using which the convection-diffusion equation can be solved. Basically, there are two forms of mass transport which govern the mixing mechanism: molecular diffusion and advection. Molecular diffusion is caused by the random motion of molecules and is dependent on the interfacial area and the diffusion coefficient. Advection, on the other hand, is caused by fluid motion leading to the chaotic distribution of the mixed species.³⁹

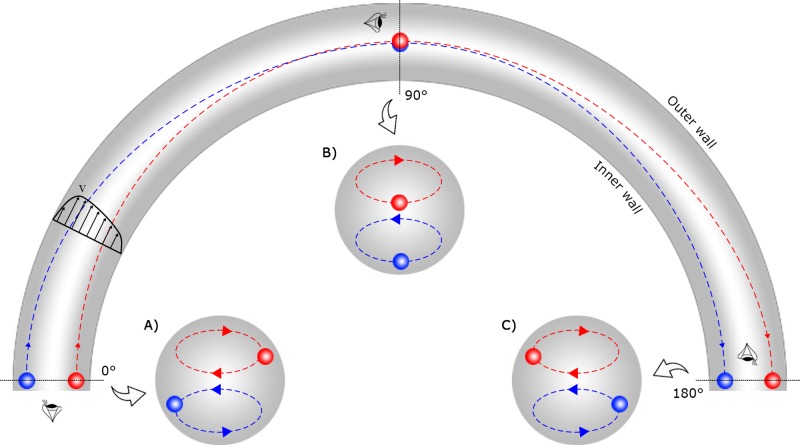
A chaotic flow can be induced by exploiting the Dean flow to enhance the mixing efficiency.⁴⁰ As can be seen in Fig. 1, the magnitude of the velocity of the main stream near the outer half of the channel is more than that of near the inner half because the fluid needs to travel a longer distance near the outer wall. The difference between the speed of the fluid near the inner and outer wall is followed by a pressure gradient along the radial direction which gives rise to a secondary flow driving the fluid from the inner wall to the outer wall of the channel. In addition, the continuity of the flow dictates a circulation which forms two counter-rotating vortices called Dean vortices.⁴¹

FIG. 1.

The physics of the Dean flow demonstrated in a curved channel from top-view as well as cross-sectional views at 0°, 90°, and 180°. (a) Two pseudoparticles, which reveal the fluid flow, are located near the inner and outer wall of the channel at 0°. (b) Following the Dean vortices, the pseudoparticles reach the centre of the channel at 90°. (c) At 180°, the pseudoparticles reach the opposite wall of the channel during a Dean half-cycle. Such a flow pattern, which is mostly independent of Re, can be exploited to induce chaotic mixing in a micromixer.

In order to quantitatively evaluate the mixing efficiency η of a micromixer, the intensity of mixing at any cross-section of the mixer is calculated as follows:⁴²

$$\eta =1-\sqrt{\frac{{\sigma }_m^2}{{\sigma }_{\mathit{m}\mathit{a}\mathit{x}}^2}},$$ (4)

where ${\sigma }_{\mathit{max}}^2$ is the maximum variance of mixture concentrations at the specified cross-section along the channel, and ${\sigma }_m^2$ is

$${\sigma }_m^2=\frac{1}{N}\sum _{i=1}^N{\left(c_i-\overline{c}\right)}^2,$$ (5)

where N is the total number of the cross-section mesh elements, c_i is the concentration of species for each of the mesh elements, and $\overline{c}$ is the average value of c_i calculated for the cross-section. ${\sigma }_{\mathit{max}}^2$ is calculated from the following equation:

$${\sigma }_{\mathit{m}\mathit{a}\mathit{x}}^2=\overline{c}\hspace{0.17em}(1-\overline{c}).$$ (6)

III. DESIGN OF 3D MICROMIXERS

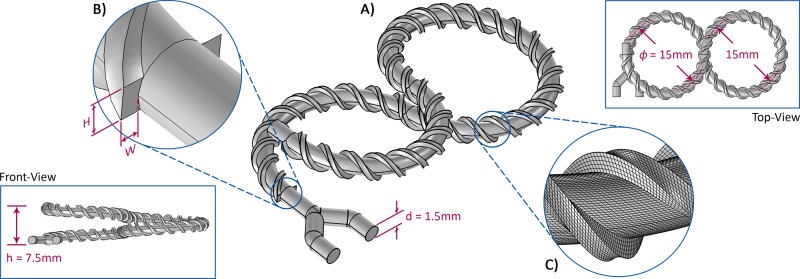
Although each mixing method, i.e., SAR and chaotic, offers a unique mechanism for splitting, folding and stretching of the fluid streams, an interesting question could be how to consolidate these methods to build a more complex 3D structure with a higher mixing efficiency and a shorter mixing length. Having this in mind, we designed a novel 3D micromixer (Fig. 2) which combines the two different mixing strategies followed by a set of numerical investigations to reveal the physics of the flow and specify the essential geometrical parameters of the micromixer shown in Table I.

FIG. 2.

The structure of the designed 3D micromixers. (a) The main channel consists of half a loop of a left-handed helix, one loop of a right-handed helix, and another half a loop of a left-handed helix all attached together. The total length of the channel is 98.84 mm. The threads twisted around the main structure are designed to improve the mixing efficiency. (b) The width W and height H of the threads winding around the curved structure of the mixer may vary for designing distinct mixers. Also, the turn number of the threads n can be different case-by-case. In this work, the rest of the geometrical parameters, including h, d, and φ shown in the figure remain constant. (c) A close-up of generated mesh around the threads for the numerical simulation of the micromixers.

TABLE I.

The design parameters of the proposed 3D micromixers.

Micromixer	Threads width W (mm)	Threads height H (mm)	Threads cross-sectional area A (mm2)	Turn number of threads n
I	0	0	0	N/A
II	0.36	0.72	0.26	10
III	0.36	0.72	0.26	20
IV	0.26	0.90	0.23	20
Va	0.18	0.36	0.06	20

^aAll dimensions of this micromixer are half of mixer III.

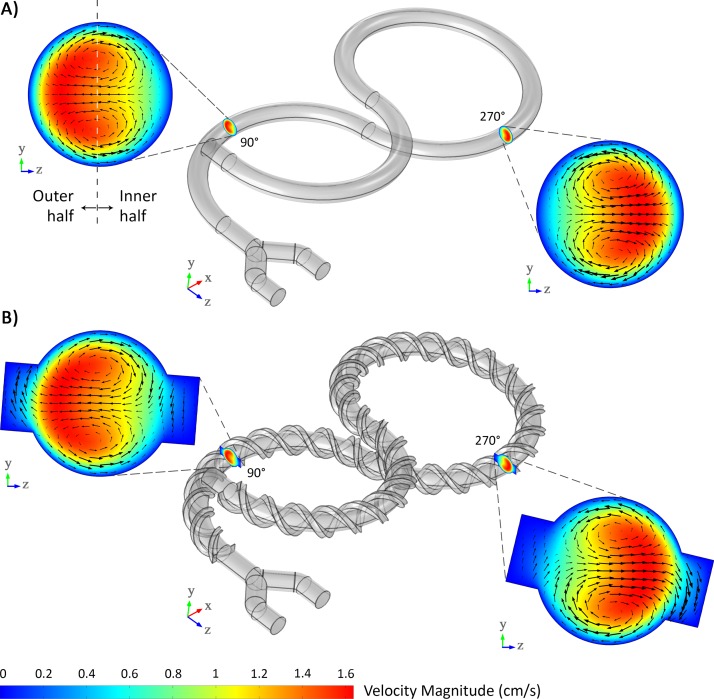
The first strategy is the continuous presence of the Dean flow occurring in curved channels throughout the 4 × 180° helix structures of the mixer. As can be seen at each cross-section of the channel in Fig. 3(a) corresponding to mixer I, the magnitude of the flow velocity is greater near the outer half of the channel. The Dean vortices are reversed by switching between the left and right-handed helices. Through this way, a chaotic flow is induced, which enhances the mixing efficiency.⁴⁰ In most of the previous passive mixers, where vortices play a key role in increasing the mixing efficiency, vortex regions were confined to a specific segment of the channel^43,44 while in the micromixers presented in this work, mixing process occurs throughout the structure. Moreover, in designs where the Dean vortices are responsible for increasing the efficiency, the channel length was normally limited due to the lack of fabrication space on a 2D plane.^45,46 The presented mixers in this work solved both of these issues by arranging consecutive helices on top of each other.

FIG. 3.

Simulation results showing Dean vortices in the lemniscate-shaped micromixers. (a) In the absence of the twisting threads, the Dean vortices, which signify the direction of the secondary flow in the channel, blend the fluids naturally. (b) The Dean vortices also affect the fluid being carried by the threads, which can increase the mixing efficiency.

The second mixing strategy used in the presented design is the introduction of two helical groove structures twisted along the channel wall (Fig. 3(b)). The use of grooves in the design of micromixers can create another type of secondary flow.^47,48 Although exploiting the grooves is not a new phenomenon, the new fabrication approach enabled us to wind the grooves like threads around the curved channel. As can be inferred from Fig. 3(b), the magnitude of the velocity of the fluid in the threads is very low. As a result, the fluid can stay for a relatively long distance in the threads and will come into direct contact with the fluid having a different concentration, which provides an opportunity for a more efficient diffusive mixing. Together with the mixing owing to diffusion, the Dean vortices penetrating into the threads establish the feasibility of mixing through chaotic advection, which enhances the mixing efficiency even more.

In this work, we designed four micromixers (mixer I–IV) to investigate the effect of the number and dimensions of the threads on η. The geometric parameters of these micromixers are all the same except for those of the threads expressed by W, H, and n. We also designed an extra micromixer (mixer V) whose dimensions including h, d, and φ shown in Fig. 2 are half of the other micromixers to evaluate the accuracy of the utilised fabrication technique further.

IV. MATERIALS AND METHODS

A. Fabrication process

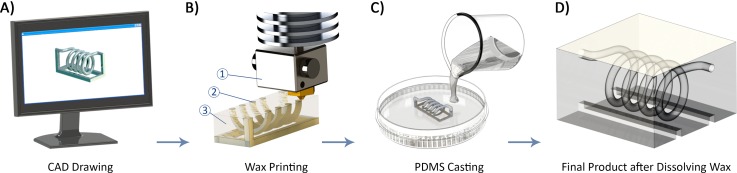
The workflow for the fabrication of a micromixer is shown in Fig. 4. First, the device is modelled using a computer aided design (CAD) software application (Fig. 4(a)); here, SolidWorks 2014 (Dassault Systèmes SolidWorks Corporation, Waltham, MA, USA). To support the main structure, a dummy stand can be designed to keep the channel intact during printing and post processing. The design needs to be exported to the stereolithography (STL) data so that the printer software can convert the geometry of the part to the machine language. The 3D printing process of the part is performed using a Solidscape^® MAX² printer (Solidscape, Inc., Merrimack, NH, USA). This printer uses a combination of additive and subtractive manufacturing to make an object by forming successive 2D layers. Each layer is created using a direct writing technique depositing molten wax droplets which solidify by cooling on impact. In this process, 3Z Model material (Solidscape, Inc.) is used for the object, and 3Z Support material (Solidscape, Inc.) is employed for voids and supporting overhanging structures. After completion of a layer, the wax is milled off to a set thickness. The substrate lowers one layer thickness, and the machine proceeds to the next cross-section (Fig. 4(b)). Once this process is finished, the support material is removed using a solvent. The completed product is then placed in a dish. Next, PDMS (Sylgard 184 Silicone Elastomer Kit, Dow Corning, MI, USA) mixed in a 10:1 ratio of the base and the curing agent is poured on the wax structure (Fig. 4(c)). The mixture is degassed in a vacuum chamber and then cured at the room temperature for 24 h. The cured PDMS, which now contains the wax model, is cut tangent to the inlets and outlets of the structure. Afterwards, the 3D printed mould is removed from the PDMS by melting the wax in an oven (melting temperature 95–115 °C) and flushing the channels with hot sunflower oil and water (50–60 °C) (Fig. 4(d)).

FIG. 4.

Workflow of PDMS microchannel fabrication. (a) Design of a 3D microfluidic channel using CAD software. (b) The design is printed using a high-resolution wax printer. The numbers 1, 2, and 3 denote the print head, build material, and support material, respectively. (c) PDMS is poured on the printed wax structure which is attached to a dish. (d) The cured PDMS is cut tangent to the inlets and outlets, and liquefied wax structure is drained after heat treatment and dissolution.

It would be extremely difficult or even impossible to build such 3D micromixers using conventional microfabrication techniques, but it is expected to be straightforward using the employed approach in this work. In order to evaluate the applied fabrication process, we decided to fabricate the micromixer with the finest features (mixer V), whose geometrical scale is half of the other micromixers. The design procedure explained in Section III has been done by means of the SolidWorks software and prepared for the fabrication process (Figs. 5(a) and 5(b)). At one side, two conical inlets are connected to the mixer via a Y-junction, and at another side, one conical outlet is added. These conical shaped channels facilitate the connection of the tubing without any adapter. The inlets and outlets are linked to each other by a bar which functions as a support structure.

FIG. 5.

(a) 3D schematic model of the novel proposed micromixer. (b) A close-up view showing the threads of the mixer. (c) Optical picture of 3D printed wax model. (d) A close-up view showing sharp edges of threads of the printed structure. (e) The wax model is attached to a petri dish using double-sided tape and PDMS is poured on the wax structure. (f) The final micromixer is obtained by removing the wax using heat treatment and flushing with a hot vegetable oil.

This model is printed using the Solidscape MAX² printer (Figs. 5(c) and 5(d)) with a slicing thickness of 0.0127 mm. The printer took 4.21 h to build the structure. After the completion of the printing process, the wax model was cleaned and attached to a petri dish using double-sided tape, and then the PDMS was added and degassed (Fig. 5(e)). After curing the PDMS at room temperature, the entire block of PDMS was released from the petri dish for subsequent wax removal. To remove the wax, the PDMS block containing the 3D printed model was placed inside an oven at 120 °C until the wax was softened. Wax residuals were removed by continuous flushing of channels using hot water and vegetable oil (Fig. 5(f)).

B. Mixing experiments

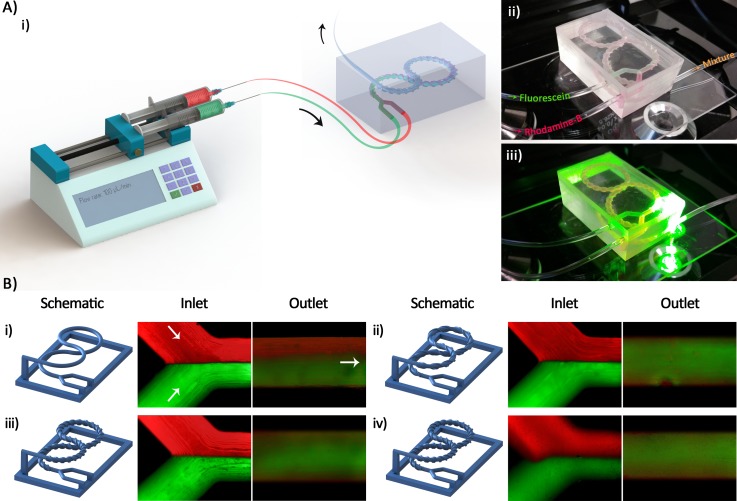
Having specified the geometrical parameters of the mixers by analysing numerical simulation results, we fabricated the 3D micromixers accordingly. Afterwards, fluid mixing experiments were performed to evaluate the mixing efficiency of the micromixers. In these experiments, the microchip was mounted on an inverted phase contrast/epifluorescence microscope (Olympus IX81, Olympus Inc., USA) equipped with a 12-bit EMCCD camera (iXonEM + 885, Andor Technology, USA). 1 μg/ml of Rhodamine-B (red) and 1 μg/ml of Fluorescein (green) powders were separately dissolved in MACS buffer consisting of 1× phosphate buffered saline (PBS), and 2 mM EDTA supplemented with 0.5% bovine serum albumin (BSA) (MiltenyiBiotec, Germany). BSA was used to prevent the nonspecific adhesion of the fluorescent solutions to the tubing and micromixer walls. The two aqueous solutions were simultaneously injected in the micromixer at the same flow rate of 100 μl/min (Re = 1.58) using a syringe pump. First, the images were separately taken from each solution, where proper fluorescent light illuminated the field under the microscope. Next, the images were composited to make a single picture showing the presence of both the fluorescent solutions in micromixer channels.

V. RESULTS AND DISCUSSION

A. Numerical simulation results

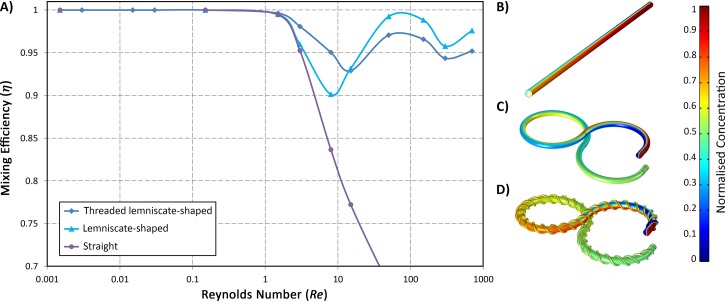
The numerical simulation of the laminar mixing of two incompressible fluids within the 3D micromixers was performed via solving the continuity and Navier-Stokes equations as well as the convection-diffusion equation using COMSOL Multiphysics. Before investigating the micromixers performance, the effect of turning a straight microchannel into a lemniscate-shaped one and also adding helical threads around it on the mixing efficiency η were studied over a wide range of Re. As can be seen in Fig. 6, For Re < 1, η is 100% regardless of the geometry of the mixer. In fact, at these low Reynolds numbers, the creeping regime of the flow facilitates the diffusive mixing.

FIG. 6.

(a) The numerical mixing efficiency of a straight, lemniscate-shaped, and threaded lemniscate-shaped micromixer in a wide range of Re. For Re < 1, η is almost certainly 100%. From Re = 1 to 15, the efficiency decreases due to less opportunity for diffusive mixing; however, the Dean flow with the aid of the threads can partially compensate the reduced diffusion. The distribution of the concentration of species in the (b) straight mixer, (c) lemniscate-shaped mixer, and (d) threaded lemniscate-shaped mixer.

By increasing Re from 1 to 15, the influence of diffusion diminishes gradually and is replaced by that of convection. Here, concerning the mixing is performed mostly due to the diffusion, one needs to find ways to compensate for the diminution of the diffusion effects. There are two remedies for this. One is the utilisation of Dean flow through curving the channel to induce convective diffusion. However, since the magnitude of the velocity of the secondary flow is proportional to Re^1.63, there is no significant difference between the efficiency of the straight and lemniscate-shaped channel at Re close to 1. Another remedy is to produce more diffusion via devising a geometrical shape like threads by which the mixing fluids can come more into contact with each other.

Raising the Reynolds number even more than 15, the effects of convection overcome that of diffusion. Hence, any geometric distortions which decrease the velocity of the fluid can adversely affect the mixing efficiency. This is why at high Re, the η of the threaded lemniscate-shaped mixer is less than that of the curved micromixer with no threads. In contrast to conventional passive micromixers whose efficient mixing merely occurs in a particular range of Re, the designed micromixer in this work can be effectively used in a wide range of Re while its efficiency always remains higher than 90%.

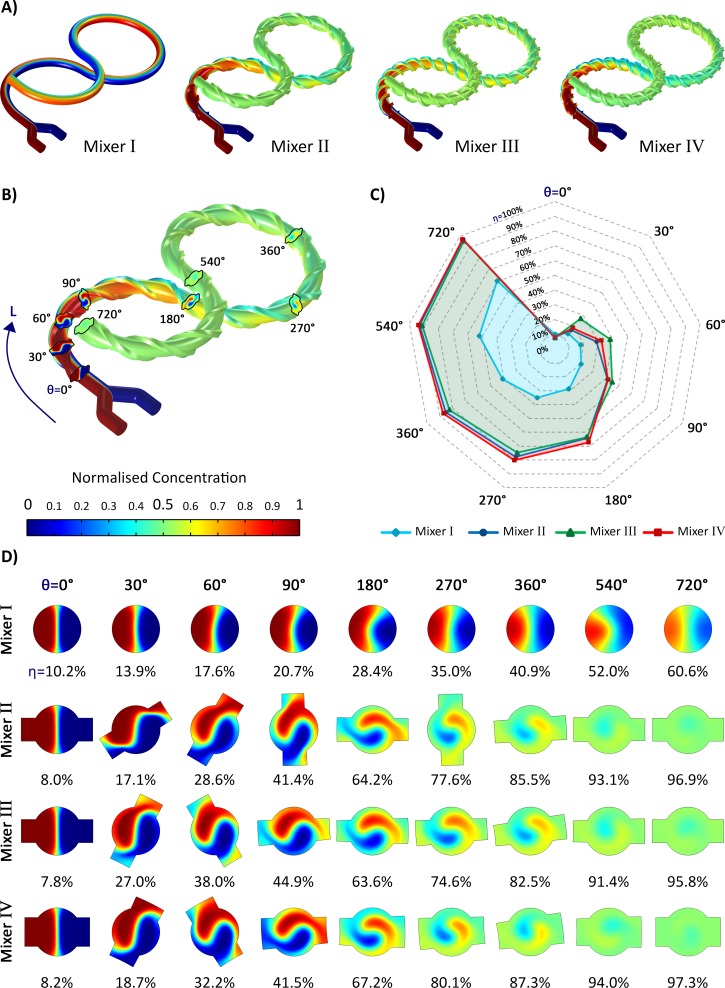
The simulation results of the 3D micromixers I, II, III, and IV at the flow rate of 100 μl/min (Re = 1.58) are demonstrated in Fig. 7. It can be seen that by adding threads to the bare structure of mixer I, as of the other mixers, the mixing efficiency is increased substantially.

FIG. 7.

The numerical simulation of the mixing process at the flow rate of 100 μl/min (Re = 1.58). (a) Distribution of normalised concentration as a result of the mixing. (b) The cross-sections identified by their absolute angle using which the progress of the mixing is investigated. The parameter L represents the mixing length. (c) The mixing efficiency η of all the micromixers, which expresses the rate of the mixing (i.e., η′ = Δη/ΔL) at the selective angles. Mixer I with no threads has always the lowest efficiency. In the beginning, mixer III shows the best performance while gradually lags behind mixer II due to the adverse effect of the threads during the second half of the mixing length. (d) The distribution of concentration at the selective cross-sections of all the mixers. Mixer IV has a higher overall η than that of mixer III because of its longer threads height H; however, its η values are less than those of mixer III during the first 90°, which is due to its smaller thread's cross-sectional area A.

The cross-sectional shape of the threads of mixer II and III are the same, but they differ in the number of turns (see Table I). Although adding more turns results in having a higher efficiency during the first 90° of the lemniscate-shaped microchannel, it is followed by a negative effect reducing the overall performance of the mixing (Fig. 7(d)). This revealed that raising the turn number of the threads does not necessarily improve the mixing efficiency. In fact, the optimum design of the threads which maximises the mixing efficiency can be expressed as a function of the rate of mixing (η′) defined as

$${{\eta }^{\prime }|}_{{\theta }_2-{\theta }_1}=\frac{\Delta \eta }{\Delta L}=\frac{{\eta }_{{\theta }_2}-{\eta }_{{\theta }_1}}{L_{{\theta }_2}-L_{{\theta }_1}},$$ (7)

where Δη is the increase of the mixing efficiency and ΔL is the mixing length between two arbitrary absolute angles θ₁ and θ₂ shown in Fig. 7(b). As can be deduced from Fig. 7(c), for all of the mixers, η′ has its maximum value at the beginning of the channel due to the utmost difference between the concentrations of the contacting fluids. In this stage, having more threads would help because the effect of the diffusive mixing is more than that of the chaotic mixing. Gradually, η′ decreases and the chaotic mixing becomes dominant. Here, the large number of the helical threads around the curved body of the mixer adversely reduces η′ as implied by the higher values of η′ belonging to mixer II in comparison with mixer III from 90° onwards. The reason is that the chaotic advection is disturbed by the sharp edges of the threads as the streamlines undergo low-speed areas inside the threads due to the presence of stagnation points at the corners.

The primary function of the threads is to carry one fluid from one side of the channel to its opposite side to be in contact with the other mixing fluid. Therefore, what mostly improves the effect of the threads on η are two factors. The first one is the contact surface area between the mainstream and the fluid flowing within the threads; the larger the contact surface, the more diffusion takes place. The second factor is the volume of the fluid being carried by the threads; the larger the volume, the more diffusion comes about because the bigger concentration difference remains between the contacting fluids in the same mixing length. As can be seen in Table I, the thread's cross-sectional area A of mixer IV is smaller than that of mixer III. Hence, although mixer IV which is equipped with the longest H has the highest overall η amongst all the mixers, the values of η for the first 90° of the channel belonging to mixer III are higher than those of mixer IV (Fig. 7(d)). It disclosed that the effect of the threads volume on mixing efficiency is greater than that of the contact surface.

B. Experimental results

The results of the experimental mixing using the fabricated micromixers are presented in this section. The schematic illustration of the experimental setup is shown in Fig. 8(a-i). Optical pictures of the device during operation and microscopy are also displayed in Figs. 8(a-ii) and 8(a-iii). The Rhodamine-B (red) and Fluorescein (green) solutions were used as dyed fluids to evaluate the mixing efficiency of different micromixers. Fig. 8(b) exhibits fluorescent composite images of the inlet and outlet of the micromixers during the mixing process.

FIG. 8.

(a-i) A schematic illustration of the experimental setup: Two syringes of the same size containing the Rhodamine-B and Fluorescein solutions are connected to the fabricated micromixer through two sets of tubing of the same length. The solutions are pumped into the mixer using a syringe pump at the flow rate of 100 μl/min (Re = 1.58). ((a-ii) and (a-iii)) An optical picture of a micromixer placed on the microscope stage under illumination showing the condition of data acquisition. (b) Schematic of 3D printed wax structures as well as the microscopic images of the inlet and outlet of (b-i) mixer I, (b-ii) mixer II, (b-iii) mixer III, and (b-iv) mixer IV. Rhodamine-B (red) and Fluorescein (green) solutions at the same concentration were used for all of the mixers.

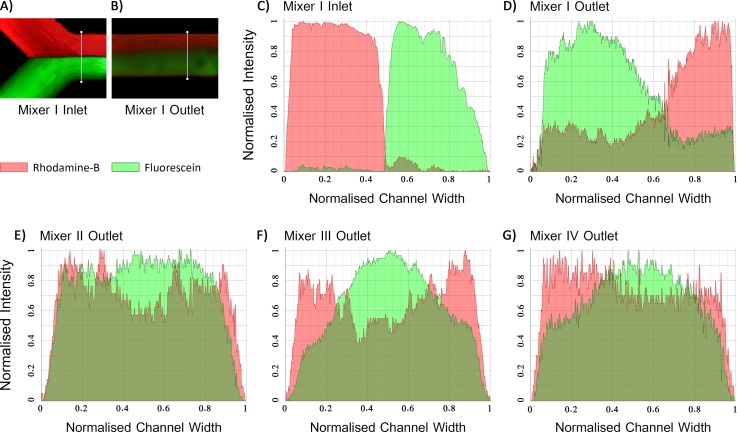
To further investigate the results of the mixing, the intensity profiles of both the solutions at the inlet and outlet of the mixers were generated. Fig. 9(a) displays a sampling line over which the intensity profiles of the solutions at the inlet of mixer I were calculated to demonstrate the distribution of the solutions before mixing (Fig. 9(c)). As can be seen in this figure, initially, the mixing fluids were separated completely. Besides, Fig. 9(d) shows the intensity profiles of the solutions at the outlet of the same mixer. These profiles were obtained based on the sampling line displayed in Fig. 9(b). Additionally, Figs. 9(e), 9(f), and 9(g) illustrate the intensity profiles at the outlet of mixer II, III, and IV, respectively. The area under the normalised intensity profile of the Rhodamine-B A_R and Fluorescein A_F represents the amount of that solution in the mixture.

FIG. 9.

(a) A sampling line drawn at the inlet of mixer I based on which the intensity profiles of Rhodamine-B and Fluorescein solutions were calculated. (b) A sampling line drawn at the outlet of mixer I over which the intensity profiles were calculated. (c) The intensity profiles of both the solutions obtained at the inlet of mixer I. The pixels over the sampling line shown in (a) used to compute the profiles. (d) The intensity profiles of the solutions at the outlet of mixer I computed based on the sampling line shown in (b). (e)–(g) The intensity profiles of the solutions at the outlet of (e) mixer II, (f) mixer III, and (g) mixer IV.

The percentage of the mixed area of the Rhodamine-B and Fluorescein solutions, calculated as ψ = mixed area/total area × 100, are denoted by ψ_R and ψ_F, respectively. Moreover, the empirical mixing efficiency ξ of a mixer is acquired by taking the weighted average of mixed areas of the solutions as below

$$\xi =\frac{A_R{\psi }_R+A_F{\psi }_F}{A_R+A_F}.$$ (8)

Table II presents the quantitative results obtained from the intensity profiles of the solutions. According to the obtained data, the outcomes of the experimental mixing are in good agreement with the predicted numerical simulation results. Fig. 9(d) discloses that mixer I combined almost half of the solutions only. In contrast, the other mixers equipped with the threads have remarkably a higher performance, which experimentally confirms that the threads enhanced the mixing efficiency.

TABLE II.

Mixing efficiency of the micromixers obtained from the experiments.

Mixer	Normalised area of Rhodamine-B (0 ≤ AR ≤ 1)	Normalised area of Fluorescein (0 ≤ AF ≤ 1)	Mixed area of Rhodamine-B ψR (%)	Mixed area of Fluorescein ψF (%)	Weighted average of Mixing ξ (%)
I	0.43	0.54	59.3	47.2	52.6
II	0.67	0.74	97.4	87.9	92.4
III	0.62	0.61	90.5	88.5	89.5
IV	0.69	0.62	87.8	98.5	92.8

VI. CONCLUSION

In this work, we designed the fine-threaded lemniscate-shaped micromixers based on two distinct mixing strategies, namely, the inducing of chaotic and diffusive mixing through the presence of Dean flow and thread-like grooves around the curved body of the mixers, respectively. First, a set of numerical simulations was performed to study the physics of the flow and to determine the essential geometrical parameters of the mixers. Second, we utilised a 3D wax printer to make the microstructure of the mixers and then flushed out the wax from cured PDMS slabs to obtain the finalised micromixer chips. The microfabrication technique consists of four major steps: (1) designing a microchannel using CAD software; (2) printing the design using a high-resolution wax printer; (3) pouring PDMS on the printed object, and (4) removing the wax model from the cured PDMS. This technique provides fast and cost-effective fabrication of microfluidic chips with arbitrary channel cross-sections and paths. Finally, we have conducted experiments using Rhodamine-B and Fluorescein under a fluorescent microscope to evaluate the empirical mixing efficiency of the mixers.

Having performed the numerical simulation of the mixers, we confirmed that adding the threads to the bare structure of a curved mixer can substantially increase the mixing efficiency. However, increasing the turn number of the threads does not necessarily improve the mixing efficiency. It was also revealed that the effect of diffusive mixing is much more than that of the chaotic mixing in the entrance of the mixer. Since the diffusive mixing becomes gradually weaker along the channel, the chaotic mixing becomes dominant, and the presence of the threads will have a less influence on the mixing performance. Next, we compared and contrasted the effects of both the volume and contact area of the mixing fluids to investigate which one is more effective. It was concluded that the effect of the threads volume on mixing efficiency is greater than that of the contact surface.

Investigating the effect of Re on the mixing efficiency, we concluded that the threaded lemniscate-shaped micromixer could maintain its high performance (i.e., η > 90%) over a wide range of flow rates. Therefore, it can be used for numerous applications in both the fields of μTAS and microchemical process applications. The experimental results were in good agreement with the results of the numerical simulation. We envisage that the strategy used in this work would expand the scope of the micromixer technology by broadening the range of efficient working flow rate and providing an easy way to the fabrication of 3D convoluted micromixers.