Abstract
Many viruses, including human norovirus and influenza, cause self-limiting diseases of short duration. However, infection by the same viruses in an immunocompromised host can result in prolonged illness in the absence of effective treatment. Such persistent infections are often characterized by increased genetic diversity with potentially elevated rates of evolution compared to acute infections, leading to suggestions that immunocompromised hosts represent an important reservoir for the emergence of novel viral variants. Here, we develop a mathematical model that combines epidemiological dynamics with within-host evolution to quantify the relative contribution of immunocompromised hosts to the overall rate of pathogen evolution. Using human norovirus as a case study we show that the majority of evolutionary substitutions are expected to occur in acute infections of immunocompetent hosts. Hence, despite their potential to generate a high level of diversity, infections of immunocompromised hosts likely contribute less to the evolution and emergence of new genetic variants at the epidemiological scale because such hosts are rare and tend to be isolated. This result is robust to variation in key parameters, including the proportion of the population immunocompromised, and provides a means to understand the adaptive significance of mutations that arise during chronic infections in immunocompromised hosts.
Keywords: virus evolution, epidemiology, modeling, substitution rate, immunocompromised host, norovirus
1. Introduction
Viral infections are typically described as being of either short (acute) or long (chronic) duration representing fundamentally different types of virus–host interaction. However, there is increasing evidence that individuals whose immune systems are compromised can shed what are normally considered acute viruses for far longer time periods. Important examples are provided by RNA viruses such as influenza A virus (Pinsky et al. 2010; van der Vries et al. 2013), rhinovirus (Kaiser et al. 2006), and poliovirus, where, remarkably, chronic infections of up to 28 years have been reported (Dunn et al. 2015). As well as its obvious clinical importance, such chronic shedding of normally acute viral infections may have major implications for virus evolution and emergence, including the generation of antigenic variation (McMinn et al. 1999; Debbink et al. 2014), drug resistance (Memoli et al. 2010; Rogers et al. 2015), and even novel emerging viruses (Weiss 2001).
Noroviruses (NoVs; family Caliciviridae) are also considered ‘acute’ pathogens that cause sporadic and epidemic gastrointestinal infections in humans (Siebenga et al. 2009). While the majority of NoV infections are mild and self-limiting with symptoms lasting for 1–3 days (Lopman et al. 2004), infection within an immunocompromised host can result in severe and prolonged illness, where the infection persists for months to years without intervention [reviewed in (Bok and Green 2012)]. Chronic NoV infections have been described in a range of clinical settings and immunodeficiency types including individuals with cancer (Ludwig et al. 2008; Capizzi et al. 2011; Ronchetti et al. 2014), HIV/AIDS (Cunningham et al. 1988; Cegielski et al. 1994; Wingfield et al. 2010), congenital conditions (Gallimore et al. 2004; Bull et al. 2012; Frange et al. 2012), and also deficiencies associated with immunosuppressive therapy in hematopoietic stem cell or solid organ transplant recipients (Lee et al. 2008; Roddie et al. 2009; Schorn et al. 2010; Boillat Blanco et al. 2011; Aulagnon et al. 2014; Salvador et al. 2014).
A common feature of prolonged NoV infections are high rates of evolution with exceptional viral diversity when compared to acute infections ( Nilsson et al. 2003; Carlsson et al. 2009; Bull et al. 2012; Hoffmann et al. 2012). This has led to suggestions that immunocompromised individuals with chronic NoV infections could act as reservoirs for the emergence of novel variants that have significantly diverged to escape herd immunity (Sukhrie et al. 2010; Vega et al. 2014; Karst and Baric 2015). Supporting this notion is that the genetically diverse variants produced during these chronic infections have been shown to be antigenically variable (Debbink et al. 2014). This is also the case for influenza virus, where antigenic variation generated within a chronically infected, immunocompromised host mimicked that observed in the wider-community of circulating strains at epidemiological scales (McMinn et al. 1999). Additionally, such patients have been a source for the rapid emergence of drug resistance variants (Memoli et al. 2010; Rogers et al. 2015). More generally, it has been proposed that because of their severely weakened immune systems, AIDS patients could be an important driver of the emergence of viruses in general, allowing novel pathogens to more easily acquire the suite of mutations necessary to adapt to a new human host (Weiss 2001).
Despite the potential importance of extended periods of replication in immunocompromised hosts to viral evolution and emergence, to date there has been no work to address these key issues quantitatively. Additionally, from a phylodynamics perspective (Grenfell et al. 2004), there is clearly a need to develop models that fully integrate the dynamics of evolutionary change at different scales. In particular, it is important not only to define pathogen evolution at the level of individual hosts (intra-host), and in multiple hosts at the epidemiological scale (inter-host), but also to link these scales in a quantitatively rigorous manner (Peck et al. 2015). Furthermore, phylodynamic models need to better account for the complexity of host factors, particularly immune status, that contribute to variation in the natural history of infection and ultimately to different trajectories of pathogen evolution. Indeed, as the immune response may be a major selective pressure shaping intra-host pathogen evolution, it is unsurprising that removing these selective barriers, as in immunocompromised hosts, would significantly impact the pattern and dynamics of pathogen evolution.
To determine how viral evolution in immunocompromised hosts may impact larger-scale viral evolution and emergence we developed a mathematical model based on the standard epidemiological categorization of susceptible, infected and recovered individuals (i.e. the SIRS model) (Anderson and May 1991) that, importantly, incorporates measures of pathogen evolution to reveal the relative contribution of immunocompromised hosts to the overall pathogen evolution. We apply this model to human NoV as a real data example, and demonstrate that despite the apparent capacity for immunocompromised hosts to generate significant diversity during infection, the relative isolation and rarity of such hosts in the community limits their impact on NoV evolution and epidemiology. This model provides a generalizable framework for estimating the influence and interactions across different scales of pathogen evolution.
2. Models and methods
To measure the contribution of rapidly evolving pathogens in chronically infected, immunocompromised hosts to the overall dynamics of pathogen evolution, we constructed a mathematical model with two major components. First, the between-host dynamics of the pathogen were modeled using a standard SIRS model of an epidemic in a closed population with a small proportion of immunocompromised hosts. The SIRS model determines the equilibrium numbers of new cases in immunocompromised and immunocompetent hosts per unit time as a function of the epidemiological parameters. Second, these infection rates were combined with the nucleotide substitution rate of the pathogen in each host subpopulation to determine the subpopulation-level nucleotide substitution rates. The ratio of these quantities was then used to measure the relative contribution of pathogen populations in each host subpopulation to the overall pathogen evolution.
2.1 The epidemiological model
We consider a population of constant size with a constant proportion of immunocompromised individuals where there are no births or deaths and infection does not kill hosts so that all cases recover, become immune and then susceptible to reinfection. For convenience, the complementary proportion is referred to as the ‘general’ subpopulation that we assume occupies the same area of constant size as the immunocompromised subpopulation. Let , be the numbers of susceptible, infectious, and recovered individuals, respectively, who are immunocompromised at time , and let be the corresponding numbers for the general subpopulation at time . Let , , and be the transmission, recovery, and loss of immunity rates for immunocompromised people who can become chronically infected with the pathogen, and let , , and be the transmission, recovery and loss of immunity rates for the general subpopulation. In the Supplementary Material, Part A, we also consider a single outbreak model where reinfection is not possible and so .
Importantly, within the context of this model, we define ‘immunocompromised hosts’ as those with more severe immunodeficienies, and hence that proportion of the population who are more likely to result in long-term chronic infections by typically acute pathogens. As many of these immunocompromised individuals will be isolated within the community or in a hospital, the model also considers the effects of ‘quarantining’ a proportion of immunocompromised individuals through reducing the infection rates in both the general and immunocompromised subpopulations.
The dynamics are governed by the following differential equations:
| (1a) |
| (1b) |
| (1c) |
| (1d) |
where and . From this model, the basic reproductive number was calculated using the next generation method (see the Supplementary Material, Part B) as
| (2) |
When this quantity is less than unity, the disease-free equilibrium is stable; otherwise at equilibrium the pathogen is endemic in the host population (van den Driessche and Watmough 2002). This model can be rescaled to:
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where , , , and . The initial conditions are , , and with all other variables set to zero.
From this, six dimensionless quantities were derived that are relevant to the dynamics of this epidemiological model: (1) the ratio of infection duration (), (2) the ratio of the initial susceptible fraction of hosts (), (3) the expected number of secondary cases in the general population due to an infected host in the general population (), (4) the expected number of secondary cases in the immunocompromised population due to an infected immunocompromised host (), (5) the ratio of duration of infection to the duration of immunity for the general (), and (6) immunocompromised populations ().
Finally, we let be the equilibrium number of immunocompromised people infected with, immune to and susceptible to being infected by the pathogen, respectively, and be the equilibrium numbers for all other people when the pathogen is endemic. These can be found by either solving the differential Equations (1) when , or by numerically solving the system of equations, and are functions of the six epidemiological parameters of the model (that is, , , , , , ). These determine the numbers of new infections per unit time at endemic equilibrium in the general and immunocompromised populations:
| (4a) |
| (4b) |
2.2 Incorporating rates of pathogen nucleotide substitution into the model
We next considered the evolution of the pathogen within this epidemiological system. To measure the relative contribution by each subpopulation (general and immunocompromised) to the overall evolution of the pathogen we determined a relative substitution rate (at the population level) at endemic equilibrium in the immunocompromised subpopulation when compared to the general subpopulation, . If this quantity is much less than unity (), then we can infer that persistently infected immunocompromised hosts do not make a significant contribution to pathogen evolution. In contrast, if this quantity is of the order of unity or above, then we can suppose that immunocompromised hosts play a key role in pathogen evolution. If and are the rates of pathogen nucleotide substitution per unit time within hosts in the general and immunocompromised subpopulations, respectively, then since the durations of infection are and for the two subpopulations, the population-level relative substitution rate at endemic equilibrium is:
| (5) |
This quantity is linearly dependent on the relative rate of nucleotide substitution (), as well as the number of hosts infected with the pathogen in the general and immunocompromised populations at endemic equilibrium ( and ). The analytical expressions of and are complex so we do not reproduce them here. However, they depend on the six epidemiological parameters of the model (that is, , , , , , and ). Importantly, this suggests the combinations of parameters to vary when considering the sensitivity of to uncertainty in parameters.
When the proportion of immunocompromised hosts is small () we can approximate by a Taylor expansion around the point (see the Supplementary Material, Part C) as
| (6) |
Hence, when the proportion of immunocompromised hosts is small, is proportional to . The quantity is also an increasing function of the duration of infection in immunocompromised hosts . The above equation shows that as parameters for immunocompromised hosts approach those of the general population approaches as expected.
Implicit in our modeling framework is that there is no selective advantage of novel genetic variants [i.e. they do not alter pathogen dynamics described by Equation (1)] and that immunocompromised hosts are just as likely as the general population to generate viable variants. While it may be more realistic that immunocompromised hosts have a reduced capacity to select for immune escape variants than hosts of the general population given that immune pressure is less, it is difficult to measure effects of individual mutations without considering their phylogenetic context. Therefore, for this particular model, we consider all the nucleotide substitutions that occur through the epidemic to be effectively neutral.
To calculate the population-level relative substitution rate under the single-outbreak model (described in the Supplementary Material, Part A) we used the final numbers of infections in the general and immunocompromised populations, and , in place of the numbers of new infections per unit time at endemic equilibrium so that:
| (7) |
These ‘attack rates’, and , can be found by numerically solving the system of differential Equations (1) with . We note that in a standard SIR model, if the attack rate () is known, then the basic reproductive number () can be estimated from the final size equation:
| (8) |
2.3 Application of model to NoV epidemiology and evolution
Next, as a case study, we apply our model to human NoV infections, and particularly, the GII.4 viruses, which are the predominant cause of acute gastroenteritis in both a sporadic and outbreak setting globally (Siebenga et al. 2009). Critical parameters such as , , ,, , and were estimated directly from the literature on NoV evolution and epidemiology. First, we can derive and from the average duration of illness (or infection). In a healthy host, NoV causes an infection with a symptomatic period of approximately two days (Lopman et al. 2004), although viral shedding will continue for a further two to four weeks (Tu et al. 2008; Aoki et al. 2010). Given that most transmission will occur when the host is symptomatic and the viral load is high, we used a value of seven days for the duration of infection () for the general population. In contrast, for an immunocompromised host, the infection will generally persist until the immune status has been restored, so that infections can last for months or even years ( Nilsson et al. 2003; Carlsson et al. 2009; Boillat Blanco et al. 2011). Consequently, the duration of infection in the immunocompromised population () is expected to be longer and more variable, and in our model we explored this parameter using values ranging from 7 days to twelve months.
For the basic reproductive number (), a previous model of NoV epidemiology used values of 1.64, 3.28, and 4.92 to represent low-, medium-, and high-transmission settings, respectively (Lopman et al. 2014). Here, we used the more conservative value of 1.64 (range: 1–4.5), which corresponds to a final attack rate of 67% [according to Equation (8)] as it is largely consistent with reported primary attack rates for NoV outbreaks (Matthews et al. 2012). In our model, we use to calculate the transmission rates for the general and immunocompromised populations by assuming that so that
[according to Equation (2)]. We explored the effects of varying the quarantine parameter () with values of 0.1, 0.5 and 0.9.
Third, for estimates of substitution rates, most studies of NoV evolution report population level (i.e. epidemiological scale) rates of between 2 and 4 × 10−3 nucleotide substitutions per site per year (subs/site/year) depending on the strain, gene, and method used for analysis (Bok et al. 2009; Bull et al. 2010). Therefore, we used a substitution rate for our general subpopulation () of 3 × 10−3 subs/site/year (range: 2–4 × 10−3 subs/site/year). In immunocompromised hosts, rates of NoV evolution are generally greatly elevated compared to a typical infection in a healthy host, with rates reported between 1.85 and 2.66 × 10−2 subs/site/year in the viral capsid gene (Nilsson et al. 2003; Carlsson et al. 2009; Hoffmann et al. 2012). However, in such hosts, pathogens are likely subject to weaker immune selection pressure such that it seems reasonable to expect that they will not commonly generate immune escape variants. Hence, we are interested in the case where immunocompromised hosts can conceivably generate epidemiologically important variants due to genetic drift, immune pressure operating at a low level, and high rates of viral evolution so that the within-host substitution-rate ratio () is non-zero. Accordingly, we explored this parameter using four values of 0.1, 1, 5, and 10, respectively.
Fourth, and can be derived from the average duration of immunity, which for NoV has not been well-defined. Early volunteer studies suggested protective immunity may last from 2 months to 2 years (Parrino et al. 1977). Using a NoV transmission modeling approach, it was estimated that the mean duration of immunity ranged from ≈4 to 8 years (Simmons et al. 2013). To bridge some of this uncertainty, we used a mean value of 3 years (range: 2.0–4.0 years) for the duration of immunity () for the general subpopulation. In contrast, the duration of immunity in the immunocompromised subpopulation () is likely to be much shorter and immunity may even be non-existent in these hosts. We explored these two scenarios by using the values of 2 years (to represent a short duration of immunity) and 3 days (to represent no immunity), respectively.
Finally, to estimate the proportion of the population that were severely immunocompromised (), we based our values on a review of data from the United States that measured the risk of serious influenza-associated complications in immunosuppressed populations; this estimated that there were approximately 3.5 million immunocompromised individuals present in the US, or ∼0.01 of the total population (Kunisaki and Janoff 2009). Importantly, this included many groups at risk of chronic NoV infections such as HIV/AIDS and transplant patients, as well as newly diagnosis case of hematological and invasive solid-organ cancers. Hence, this definition deliberately focuses on patients with more severe immune deficiencies, that are more likely to host the complex chronic infections with acute viruses described here (i.e. infections measured in months and years with significantly increased viral diversity), rather than simply any host with a weakened immune system such as the young, pregnant women and the elderly (Simon et al. 2015). Still, as this definition of immunocompromised is broad, we set this as the upper bound of our model and instead chose a middle value for of 0.001 (range: 0.0001–0.01). All of the key parameter values used for the analysis of NoV evolution are summarized in Table 1.
Table 1.
Model parameter estimates for NoV.
| Symbol | Parameter | Estimates considered | ||
|---|---|---|---|---|
| Infection duration, general | 7 days | |||
| Infection duration, immunocompromised | 7 days–12 months | |||
| Substitution rate ratio | 0.1, 1, 5, 10 | |||
| Immunity duration, immunocompromised | 3 days and 2 years | |||
| Quarantine parameter | 0.1, 0.5, and 0.9 | |||
| Population size | 106 | |||
| Symbol | Parameter | Mean/mode | Lower bound | Upper bound |
| Basic reproduction number | 1.64a | 1 | 4.5 | |
| Duration of immunity, general | 3 | 2 | 4 | |
| Substitution rate, general | 0.003 | 0.002 | 0.004 | |
| Proportion immunocompromised | 10−3 | 10−4 | 10−2 | |
Corresponds to an attack rate of 67%.
2.4 Sensitivity analysis
To determine how robust our results are to variation in parameter values, particularly those with the greatest uncertainty, a sensitivity analysis was performed by sampling 1,000 points in the parameter space using the Latin Hypercube Sampling method (Blower and Dowlatabadi 1994). Parameters were sampled from either a triangular, normal, or log normal distribution. Specifically, the basic reproductive number for the general population () was sampled from a triangular distribution with mode 1.64, lower bound 1, and upper bound 4.5; the proportion of the population immunocompromised () was sampled from a log normal distribution of base 10 with and ; the duration of immunity in the general population () was sampled from a triangular distribution with mode 3, lower bound 2, and upper bound 4; while the general population nucleotide substitution rate () was sampled from a normal distribution with mean 0.003 and standard deviation 0.0003. All other parameters were held constant (Table 1).
3. Results
3.1 Numerical results for model of NoV evolution in immunocompromised hosts
The mathematical model developed here suggests that there are seven key biological parameters that govern the contribution of immunocompromised hosts to the overall pathogen evolution. These are: (1) the ratio of the initial susceptible fraction of hosts (), (2) the ratio of infection duration (), (3) the expected number of secondary cases in the general population due to a host in the general population (), (4) the expected number of secondary cases in the immunocompromised population due to an immunocompromised host (), (5) the ratio of duration of infection to the duration of immunity for the general (), (6) immunocompromised populations (), and (7) the relative rate of nucleotide substitution (). Here, we have applied this model to the case study of human NoV infections.
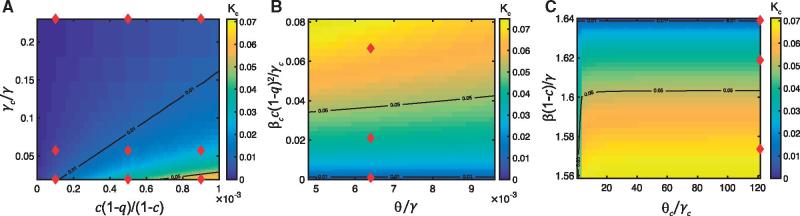
To investigate the effects of these parameters on the relative population-level substitution rate (), we plot as a function of model parameters (Fig. 1 and Supplementary Material, Fig. C1). In this analysis, we map two key parameters to the value of , while holding all other parameters constant with the best estimates for each of the key parameters identified with a red diamond. From this, it is clear that increases as the ratio of the initial fraction of susceptible hosts [] increases (Fig. 1a), the relative duration of infection () decreases (Fig. 1a), and the relative nucleotide substitution rate () increases (compare Fig. 1 where and Supplementary Material, Fig. D1 where ). Additionally, was found to increase when the expected number of secondary cases in the immunocompromised population due to a host in the immunocompromised population () increases (Fig. 1b), and the expected number of secondary cases in the general population due to a host in the general population () decreases (Fig. 1c). also increases as the ratio of duration of infection to the duration of immunity for the general population () decreases (Fig. 1b), although if the expected number of secondary cases in the immunocompromised population due to a host in the immunocompromised population () is very small, appears to have a minor effect on . Similarly, if the expected number of secondary cases in the general population due to a host in the general population () is small enough, increasing the ratio of duration of infection to the duration of immunity for the immunocompromised populations () acts to increase (Fig. 1c); otherwise appears to have a minor effect on . These results are reinforced by the linear approximation of around the point [Equation (6)].
Figure 1.
Model estimates for the contribution of immunocompromised hosts to NoV evolution. The relative substitution rate (at the population level) in the immunocompromised population versus the general population when and (a) , , , , , , and ; (b), , , , , , and ; (c) , , , , , , and . Red diamonds represent the best estimates of the parameters in the parameter space considered. The black lines correspond to the contours .
In sum, our model shows that the contribution of immunocompromised hosts to the overall evolution of NoV increases as the nucleotide substitution rate () increases, the level of their quarantining () decreases, their population fraction increases (), their duration of infection () increases, and their duration of immunity () decreases. Importantly, when we consider the best estimates of our model parameters, the relative population-level substitution rate in the immunocompromised subpopulation versus the general subpopulation is less than 0.07 when , indicating that immunocompromised hosts will have a limited impact on the overall evolution of NoV at epidemiological scales unless their within-host substitution rate is much larger than that in other hosts. Hence, our results suggest that the rarity and isolation of immunocompromised hosts prevents them from substantially contributing to pathogen spread and evolution despite their increased duration of infection, reduced duration of immunity, and increased rates of evolution (Fig. 2).
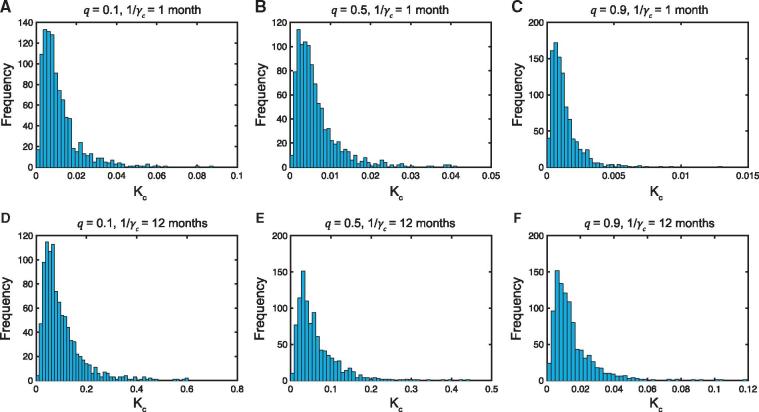
Figure 2.
Sensitivity analysis of model parameters. Frequency distributions of the relative nucleotide substitution rate at the population level in the immunocompromised population compared to the general population from sampling 1000 points of the parameter space using Latin Hypercube Sampling. Panels (a–c) 1 month; Panels (d–f) months. Panels (a,d) ; Panels (b,e) ; Panels (c,f) . In all cases, days, , , and .
3.2 Sensitivity analysis
To determine how robust our results are to any variation in key model parameters (,, , and ), we performed a sensitivity analysis, which outputs a frequency distribution rather than one outcome for the relative population-level substitution rate in the immunocompromised subpopulation versus the general subpopulation (. For each simulation, all other parameters were held constant as per the values shown in Table 1.
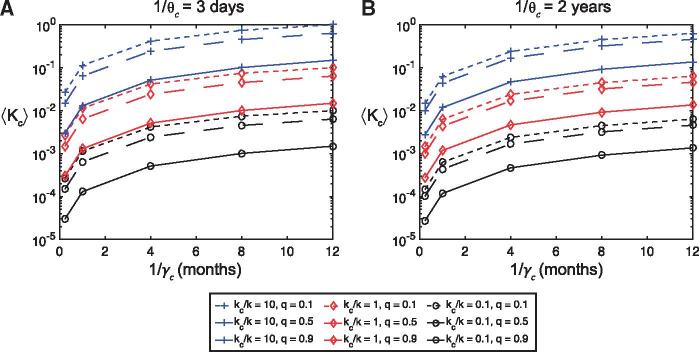
A selection of the resulting frequency distributions for , all of which are skewed to the right, are shown in Fig. 2 and Supplementary Material, Fig. E2 for given values of the quarantine parameter (), duration of infection for immunocompromised hosts (), and the relative nucleotide substitution rate (). The corresponding mean values () are shown as a function of , for , , and days and 2 years in Fig. 3 and Supplementary Material, Fig. E3. As expected, the ratio has a linear effect on the mean values , while the order of magnitude of ranges from 0.0003 to 0.1 when and days (Fig. 3a), and 0.0003–0.06 when and years (Fig. 3b). Hence, varying the four parameters ,, and does not appear to raise the order of magnitude of the mean relative population level substitution rate to unity or above if . In fact, this only occurred when we considered the extreme parameter values of , months, days and (Fig. 3a).
Figure 3.
Sensitivity analysis of model parameters. The mean relative nucleotide substitution rate at the population level in the immunocompromised population compared to the general population (from sampling 1000 points of the parameter space using Latin Hypercube Sampling) as a function of the duration of infection in immunocompromised hosts (), for a range of values of the quarantine parameter (), and the ratio of substitution rates (at the individual host level) (). (a) SIRS model with days and ; (b) SIRS model with years and . Blue lines with square markers indicate , red lines with diamond markers , and black lines with circle markers . Dotted lines indicate , dashed lines and solid lines . Here days.
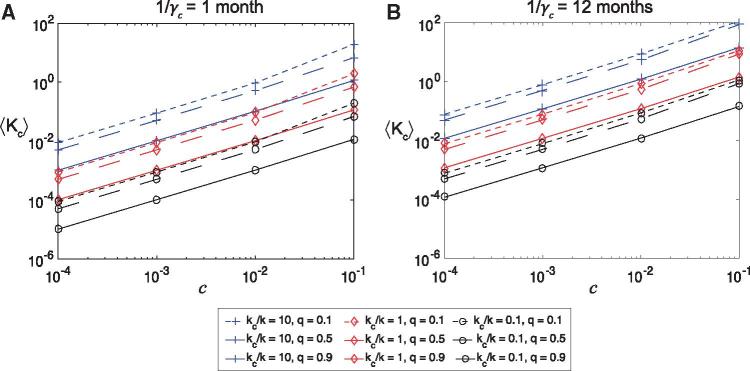
To determine how large the immunocompromised population needs to be to raise the mean relative population level substitution rate to unity or above, we performed additional sensitivity analyses holding the proportion of immunocompromised hosts () fixed at . The results are presented in Fig. 4 and show as a function of , for , , days, and 1 month and 12 months. These panels confirm robustness of the linear relationship between and as given by the Taylor series approximation in Equation (6). When 10, needs to be greater than to push , while if , needs to be greater than , and greater than if . If we restrict the results to those corresponding to high levels of quarantining of immunocompromised hosts (), or to those corresponding to a shorter duration of infection for immunocompromised hosts (1 month) then these limits increase by an order of magnitude. Considering a longer duration of immunity for immunocompromised hosts () further increases the value of needed to achieve (results not shown).
Figure 4.
Sensitivity analysis of model parameters. The mean relative nucleotide substitution rate at the population level in the immunocompromised population compared to the general population (from sampling 1000 points of the parameter space using Latin Hypercube Sampling) as a function of the proportion of immunocompromised hosts (), for a range of values of the quarantine parameter (), and the ratio of substitution rates (at the individual host level) (). (a) SIRS model with month and ; (b) SIRS model with year and . Blue lines with square markers indicate , red lines with diamond markers , and black lines with circle markers . Dotted lines indicate , dashed lines and solid lines . Here days and days.
In the Supplementary Material, Part D and E, we provide extended outputs for , as well as extra sensitivity analysis details and results including when . These results show that the SIRS model and SIR model behave similarly when the duration of immunity for the general and immunocompromised populations are both large.
4. Discussion
Understanding the epidemiological and evolutionary dynamics of pathogens requires analytical frameworks that account for the complexities of their interactions with hosts. Herein, we address one such interaction: how the extended replication of normally acute viral infections in immunocompromised hosts may impact viral evolution and emergence. We achieve this through the development of a mathematical model (presented as a graphical heuristic in Fig. 5) that incorporates nucleotide substitution rates to measure the relative contribution of subpopulations to the overall dynamics of pathogen evolution at the epidemiological scale.
Figure 5.
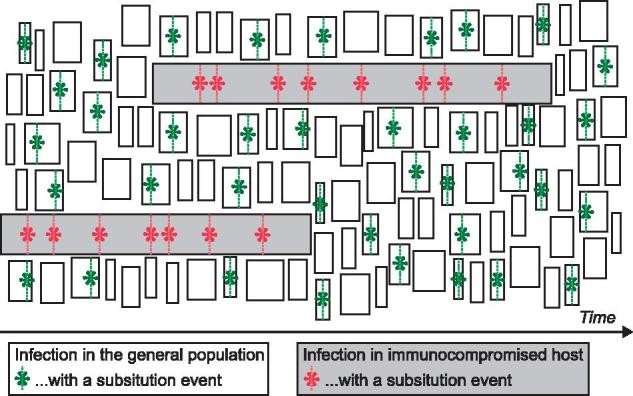
Heuristic representation of the model results. Due to the small size of the subpopulation, immunocompromised hosts do not significantly contribute to the evolution of the pathogen, despite their higher molecular-substitution rate and longer infection durations.
Using our model with the case study of human NoV infections we evaluated the impact of rapidly evolving, persistent viral populations in immunocompromised hosts to its overall evolutionary dynamics. At face value, the greatly elevated rate of nucleotide substitution of NoV within chronically infected immunocompromised hosts, combined with their characteristically long duration of infection, suggests that these hosts may be an important reservoir for novel viral variants (Sukhrie et al. 2010; Vega et al. 2014; Karst and Baric 2015). However, our numerical analysis using estimates derived from real data clearly shows that immunocompromised hosts do not significantly contribute to the overall rate of evolution for NoV at epidemiological scales, even when allowing for small quarantining effects, and with a variety of parameter values as reflected in the sensitivity analysis (Figs 2–4). Hence, despite an increased rate of nucleotide substitution and an extended duration of infection, the rarity of immunocompromised hosts in the population limits their influence to broader NoV dynamics, which are still dominated by the lower evolutionary rates apparent in the general population.
These results help resolve uncertainty with respect to the impact of these novel, chronic NoV infections in immunocompromised hosts to broader dynamics of a pathogen that otherwise cause an acute infection. The capacity for severely immunocompromised hosts to generate genetically complex and diverse viral populations does not necessarily exclude them as a reservoir population for the emergence of novel variants; however, our results suggest that their impact is much less in relative terms than the weight of typical acute infections in otherwise healthy hosts that dominate the infected population. Indeed, in the case of NoV, the perceived lack of evolutionary ‘intermediates’ in phylogenies of pandemic GII.4 viruses, which are characterized by the rapid emergence of genetically distinct (i.e. an average 5% amino acid divergence in the VP1 capsid protein) and antigenically novel viruses (Kroneman et al. 2013), has led to suggestions that immunocompromised hosts play a key role as a ‘source’ population. There is, however, no clear evidence to support this hypothesis, as no GII.4 lineages appear to have arisen and spread in the population from a chronically infected, immunocompromised host, although the available sample is admittedly small. In addition, the observed evolutionary pattern of NoV at epidemiological scales can be explained by other factors within the typical acutely infected, immune competent population. For example, the pace with which novel variants emerge could be dominated by the strong and rapid influence of positive selection for variants that carry mutations capable of escaping herd immunity. Similarly, the genetic ‘gaps’ between different GII.4 variants may be explained by widespread recombination among circulating lineages (Eden et al. 2013) and inadequate global sampling. Indeed, both rapid positive selection and recombination were central to the emergence of the most recent pandemic GII.4 variant, known as Sydney 2012 (Eden et al. 2014).
Although our model has been applied to the specific example of human NoV infection, with suitable virus-specific modifications it may be informative in measuring the relative contribution of subpopulations characterized by greatly different durations of infection and substitution rates to the epidemiological scale of pathogen evolution in other acute RNA viruses. Indeed, our sensitivity analysis reveals that this model is robust to the proportion of immunocompromised hosts and how they interact with the general population. In this context, it is important that our modeling set an upper limit of 1% for the proportion of immunocompromised hosts (), which may be conservative according to some broader definitions of ‘immunocompromised’ that include the whole spectrum of severity. However, there is still little data on those individuals with severe immunodeficiencies who are chronically infected with typically acute viruses that enable us to provide more precise model parameterization.
There are also obvious areas where our model could be improved and extended, and importantly, provide a means to further test the robustness of the NoV-specific conclusions presented here (Ganusov 2016). First, we assume that all substitutions that occur in both the general and immunocompromised populations are of equal fitness, and do not adapt over the time-scale of sampling so as to impact epidemiological parameters. Hence, the progress of an epidemic is not directly influenced by the substitutions that accumulate under our model. Similarly, we do not assess any competition between any variants that arise during our simulated epidemics, therefore cross-immunity is not considered. While it may be more realistic that adaptive, immune escape variants are less likely to emerge in immunocompromised hosts, it is impossible to weigh the effects of any adaptive substitutions in this model, and in our model we focus on the appearance of new genetic variants in a heterogeneous host population, but not on the subsequent dynamics of those new variants. Second, we do not account for detailed host population structures that do exist in an institutional setting like hospitals and nursing homes, and may act as hubs for transmissions between immunocompromised patients and subsequently increase their relative contribution. Instead, we assume population homogeneity with respect to transmission, for both healthy and immunocompromised hosts, and that contact rates are only influenced by any quarantining effects. Third, we assume equal underlying transmission rates for each of our subpopulations. Transmission rates may depend on within-host dynamics (Antia et al. 1994) but here we instead modify transmission through a parameter that measures quarantining effects. Future developments could extend the model by including details of within host dynamics and the relationship between pathogen load and transmission. Fourth, incorporating the dynamics of transmission and the effects of strong genetic bottlenecks on the passage of substitutions between hosts may be of importance, particularly in typical acute infections. For NoV, one study has suggested that only a single minor variant establishes infection at transmission; however, the sample of this study was very small and further work is needed to confirm if such a strong transmission bottleneck is commonplace in nature (Bull et al. 2012). Finally, we have only considered the evolutionary dynamics within a closed population. A more realistic model could incorporate the birth and death of hosts and perhaps mutations that affect the course of and future epidemics.
In conclusion, our model shows, at least in the case of human NoV infection, that despite the apparent capacity of immunocompromised hosts to generate significant diversity during infection through increased rates of evolution and duration of infection, the relative isolation and rarity of such hosts limits their impact on the broader evolution and epidemiology of pathogens. Although the study of viral evolution in immunocompromised hosts may help reveal key aspects of the intimate relationship between hosts and their pathogens, we suggest that such individuals play only a minor role in shaping large-scale evolutionary patterns and processes.
Author contributions
J.S.E. helped design the study, participated in formation of the model and drafted the manuscript. R.H.C. participated in formation and coding of the model, carried out data analysis and helped draft the manuscript. P.A.W. provided input with the study design and with R.A.B. provided critical feedback for both the model and manuscript. E.C.H. and M.M.T. co-ordinated and designed the study and participated in formation of the model and drafting of the manuscript. All authors gave their final approval for publication.
Funding
J.S.E. is supported through the Australian NHMRC with an Early Career Fellowship (1073466). E.C.H. is funded by an NHMRC Australia Fellowship (GNT1037231). M.M.T. is supported by an Australian Research Council grant (FT140100398).
Conflict of interest: We have no competing interests.
Supplementary data
Supplementary data are available at Virus Evolution online.
Supplementary Material
References
- Anderson R. M., May R. M.. 1991. Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxford University Press. [Google Scholar]
- Antia R., Levin B. R., May R. M. (1994) ‘Within-Host Population Dynamics and the Evolution and Maintenance of Microparasite Virulence’, The American Naturalist, 144: 457–72. [Google Scholar]
- Aoki Y. et al. (2010) ‘Duration of Norovirus Excretion and the Longitudinal Course of Viral Load in Norovirus-Infected Elderly Patients’, Journal of Hospital Infection, 75: 42–6. [DOI] [PubMed] [Google Scholar]
- Aulagnon F. et al. (2014) ‘Diarrhea after Kidney Transplantation: A New Look at a Frequent Symptom’, Transplantation, 98: 806–16. [DOI] [PubMed] [Google Scholar]
- Blower S. M., Dowlatabadi H. (1994) ‘Sensitivity and Uncertainty Analysis of Complex-Models of Disease Transmission—An HIV Model, as an Example’, International Statistical Review, 62: 229–43. [Google Scholar]
- Boillat Blanco N. et al. (2011) ‘Chronic Norovirus Gastroenteritis in a Double Hematopoietic Stem Cell and Lung Transplant Recipient’, Transplant Infectious Diseases, 13: 213–5. [DOI] [PubMed] [Google Scholar]
- Bok K. et al. (2009) ‘Evolutionary Dynamics of GII.4 Noroviruses Over a 34-Year Period’, Journal of Virology, 83: 11890–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bok K., Green K. Y. (2012) ‘Norovirus Gastroenteritis in Immunocompromised Patients’, New England Journal of Medicine, 367: 2126–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull R. A. et al. (2010) ‘Rapid Evolution of Pandemic Noroviruses of the GII.4 Lineage’, PLoS Pathogens, 6: e1000831.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull R. A. et al. (2012) ‘Contribution of Intra- and Interhost Dynamics to Norovirus Evolution’, Journal of Virology, 86: 3219–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capizzi T. et al. (2011) ‘Chronic Diarrhea Associated with Persistent Norovirus Excretion in Patients with Chronic Lymphocytic Leukemia: Report of Two Cases’, BMC Infectious Diseases, 11: 131.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlsson B. et al. (2009) ‘Quasispecies Dynamics and Molecular Evolution of Human Norovirus Capsid P Region During Chronic Infection’, Journal of General Virology, 90: 432–41. [DOI] [PubMed] [Google Scholar]
- Cegielski J. P., Msengi A. E., Miller S. E. (1994) ‘Enteric Viruses Associated with HIV Infection in Tanzanian Children with Chronic Diarrhea’, Pediatric AIDS HIV Infection, 5: 296–9. [PubMed] [Google Scholar]
- Cunningham A. L. et al. (1988) ‘Gastrointestinal Viral Infections in Homosexual Men Who Were Symptomatic and Seropositive for Human Immunodeficiency Virus’, Journal of Infectious Diseases, 158: 386–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debbink K. et al. (2014) ‘Within-Host Evolution Results in Antigenically Distinct GII.4 Noroviruses’, Journal of Virology, 88: 7244–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunn G. et al. (2015) ‘Twenty-Eight Years of Poliovirus Replication in an Immunodeficient Individual: Impact on the Global Polio Eradication Initiative’, PLoS Pathogens, 11: e1005114.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eden J. S. et al. (2013) ‘Recombination within the Pandemic Norovirus GII.4 Lineage’, Journal of Virology, 87: 6270–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eden J. S. et al. (2014) ‘The Emergence and Evolution of the Novel Epidemic Norovirus GII.4 Variant Sydney 2012’, Virology, 450–451: 106–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frange P. et al. (2012) ‘Prevalence and Clinical Impact of Norovirus Fecal Shedding in Children with Inherited Immune Deficiencies’, Journal of Infectious Diseases, 206: 1269–74. [DOI] [PubMed] [Google Scholar]
- Gallimore C. I. et al. (2004) ‘Chronic Excretion of a Norovirus in a Child with Cartilage Hair Hypoplasia (CHH)’, Journal of Clinical Virology, 30: 196–204. [DOI] [PubMed] [Google Scholar]
- Ganusov V. V. (2016) ‘Strong Inference in Mathematical Modeling: A Method for Robust Science in the Twenty-First Century’, Frontiers in Microbiology, 7: 1131.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenfell B. T. et al. (2004) ‘Unifying the Epidemiological and Evolutionary Dynamics of Pathogens’, Science, 303: 327–32. [DOI] [PubMed] [Google Scholar]
- Hoffmann D. et al. (2012) ‘Norovirus GII.4 and GII.7 Capsid Sequences Undergo Positive Selection in Chronically Infected Patients’, Infection, Genetics and Evolution, 12: 461–6. [DOI] [PubMed] [Google Scholar]
- Kaiser L. et al. (2006) ‘Chronic Rhinoviral Infection in Lung Transplant Recipients’, American Journal of Respiratory and Critical Care Medicine, 174: 1392–9. [DOI] [PubMed] [Google Scholar]
- Karst S. M., Baric R. S. (2015) ‘What is the Reservoir of Emergent Human Norovirus Strains? ’, Journal of Virology, 89: 5756–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroneman A. et al. (2013) ‘Proposal for a Unified Norovirus Nomenclature and Genotyping’, Archives of Virology, 158: 2059–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunisaki K. M., Janoff E. N. (2009) ‘Influenza in Immunosuppressed Populations: A Review of Infection Frequency, Morbidity, Mortality, and Vaccine Responses’, The Lancet Infectious Diseases, 9: 493–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee B. E. et al. (2008) ‘Chronic Norovirus and Adenovirus Infection in a Solid Organ Transplant Recipient’, The Pediatric Infectious Disease Journal, 27: 360–2. [DOI] [PubMed] [Google Scholar]
- Lopman B. A. et al. (2004) ‘Clinical Manifestation of Norovirus Gastroenteritis in Health Care Settings’, Clinical Infectious Diseases, 39: 318–24. [DOI] [PubMed] [Google Scholar]
- Lopman B. et al. (2014) ‘Epidemiologic Implications of Asymptomatic Reinfection: A Mathematical Modeling Study of Norovirus’, American Journal of Epidemiology, 179: 507–12. [DOI] [PubMed] [Google Scholar]
- Ludwig A. et al. (2008) ‘Quantitative Detection of Norovirus Excretion in Pediatric Patients with Cancer and Prolonged Gastroenteritis and Shedding of Norovirus’, Journal of Medical Virology, 80: 1461–7. [DOI] [PubMed] [Google Scholar]
- Matthews J. E. et al. (2012) ‘The Epidemiology of Published Norovirus Outbreaks: A Review of Risk Factors Associated with Attack Rate and Genogroup’, Epidemiological Infection, 140: 1161–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMinn P. et al. (1999) ‘Antigenic Drift of Influenza A (H3N2) Virus in a Persistently Infected Immunocompromised Host is Similar to that Occurring in the Community’, Clinical Infectious Diseases, 29: 456–8. [DOI] [PubMed] [Google Scholar]
- Memoli M. J. et al. (2010) ‘Rapid Selection of a Transmissible Multidrug-Resistant Influenza A/H3N2 Virus in an Immunocompromised Host’, Journal of Infectious Diseases, 201: 1397–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson M. et al. (2003) ‘Evolution of Human Calicivirus RNA In Vivo: Accumulation of Mutations in the Protruding P2 Domain of the Capsid Leads to Structural Changes and Possibly a New Phenotype’, Journal of Virology, 77: 13117–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parrino T. A. et al. (1977) ‘Clinical Immunity in Acute Gastroenteritis Caused by Norwalk Agent’, New England Journal of Medicine, 297: 86–9. [DOI] [PubMed] [Google Scholar]
- Peck K. M., Chan C. H. S., Tanaka M. M. (2015) ‘Connecting Within-Host Dynamics to the Rate of Viral Molecular Evolution’, Virus Evolution, 1: vev013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinsky B. A. et al. (2010) ‘Long-Term Shedding of Influenza A Virus in Stool of Immunocompromised Child’, Emerging Infectious Diseases, 16: 1165–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roddie C. et al. (2009) ‘Allogeneic Hematopoietic Stem Cell Transplantation and Norovirus Gastroenteritis: A Previously Unrecognized Cause of Morbidity’, Clinical Infectious Diseases, 49: 1061–8. [DOI] [PubMed] [Google Scholar]
- Rogers M. B. et al. (2015) ‘Intrahost Dynamics of Antiviral Resistance in Influenza A Virus Reflect Complex Patterns of Segment Linkage, Reassortment, and Natural Selection’, MBio, 6: e02464-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronchetti A. M. et al. (2014) ‘Norovirus-Related Chronic Diarrhea in a Patient Treated with Alemtuzumab for Chronic Lymphocytic Leukemia’, BMC Infectious Diseases, 14: 239.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvador C. et al. (2014) ‘Hemophagocytic Lymphohistiocytosis after Allogeneic Bone Marrow Transplantation During Chronic Norovirus Infection’, Hematology and Oncology, 32: 102–6. [DOI] [PubMed] [Google Scholar]
- Schorn R. et al. (2010) ‘Chronic Norovirus Infection after Kidney Transplantation: Molecular Evidence for Immune-Driven Viral Evolution’, Clinical Infectious Diseases, 51: 307–14. [DOI] [PubMed] [Google Scholar]
- Siebenga J. J. et al. (2009) ‘Norovirus Illness is a Global Problem: Emergence and Spread of Norovirus GII.4 Variants, 2001-2007’, Journal of Infectious Diseases, 200: 802–12. [DOI] [PubMed] [Google Scholar]
- Simmons K. et al. (2013) ‘Duration of Immunity to Norovirus Gastroenteritis’, Emerging Infectious Diseases, 19: 1260–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon A. K., Hollander G. A., McMichael A. (2015) ‘Evolution of the Immune System in Humans from Infancy to Old Age’, Proceedings Biological Sciences, 282: 20143085.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukhrie F. H. et al. (2010) ‘Chronic Shedders as Reservoir for Nosocomial Transmission of Norovirus’, Journal of Clinical Microbiology, 48: 4303–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu E. T. et al. (2008) ‘Norovirus Excretion in an Aged-Care Setting’, Journal of Clinical Microbiology, 46: 2119–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Driessche P., Watmough J. (2002) ‘Reproduction Numbers and Sub-threshold Endemic Equilibria for Compartmental Models of Disease Transmission’, Mathematical Biosciences, 180: 29–48. [DOI] [PubMed] [Google Scholar]
- van der Vries E. et al. (2013) ‘Prolonged Influenza Virus Shedding and Emergence of Antiviral Resistance in Immunocompromised Patients and Ferrets’, PLoS Pathogens, 9: e1003343.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vega E. et al. (2014) ‘RNA Populations in Immunocompromised Patients as Reservoirs for Novel Norovirus Variants’, Journal of Virology, 88: 14184–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss R. A. (2001) ‘The Leeuwenhoek Lecture 2001. Animal Origins of Human Infectious Disease’, Philosophical Transactions of the Royal Society of London Series B Biological Sciences, 356: 957–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wingfield T. et al. (2010) ‘Chronic Norovirus Infection in an HIV-Positive Patient with Persistent Diarrhoea: A Novel Cause’, Journal of Clinical Virology, 49: 219–22. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.