A New Sparse Representation Framework for Reconstruction of an Isotropic High Spatial Resolution MR Volume from Orthogonal Anisotropic Resolution Scans

Abstract

In magnetic resonance (MR), hardware limitations, scan time constraints, and patient movement often result in the acquisition of anisotropic 3D MR images with limited spatial resolution in the out-of-plane views. Our goal is to construct an isotropic high-resolution 3D MR image through upsampling and fusion of orthogonal anisotropic input scans. We propose a multi-frame super-resolution (SR) reconstruction technique based on sparse representation of MR images. Our proposed algorithm exploits the correspondence between the high-resolution slices and the low-resolution sections of the orthogonal input scans as well as the self-similarity of each input scan to train pairs of over-complete dictionaries that are used in a sparse land local model to upsample the input scans. The upsampled images are then combined using wavelet fusion and error back-projection to reconstruct an image. Features are learned from the data and no extra training set is needed. Qualitative and quantitative analyses were conducted to evaluate the proposed algorithm by using simulated and clinical MR scans. Experimental results show that the proposed algorithm achieves promising results in terms of peak signal to noise ratio, structural similarity image index, intensity profiles, and visualization of small structures obscured in the low-resolution imaging process due to partial volume effects. Our novel SR algorithm outperforms the non-local means (NLM) method using self-similarity, NLM method using self-similarity and image prior, self-training dictionary learning based SR method, averaging of upsampled scans and the wavelet fusion method. Our SR algorithm can reduce through-plane partial volume artifact by combining multiple orthogonal MR scans, and thus can potentially improve medical image analysis, research, and clinical diagnosis.

I. Introduction

Magnetic resonance imaging (MRI) plays a key role in non-invasive examination of various diseases. Fast MRI acquisitions are preferred to avoid motion artifacts and improve patient comfort; so many MRI scans are performed with relatively few slices and with rather large slice thickness to cover the imaged anatomy. As a result, highly anisotropic data sets are acquired that have higher resolution within the slices than in the slice-selection direction. Obviously, the spatial resolution of thick-slice rectangular voxels is not comparable to isotropic square voxels as the image is unequally resolved along the slice, frequency, and phase encoding axes [1]. Computer aided diagnosis, analysis, and research on disease demand high quality image data and particularly high spatial resolution data in 3D. Thus, reducing the voxel size and reconstructing isotropic 3D MR images with high spatial resolution is much desired.

Reducing the voxel size is challenging in MRI because the signal-to-noise ratio (SNR) is directly proportional to the voxel size and the square root of the number of averages. Decreasing the voxel size by a factor α (e.g. α = 8 to reduce the voxel size from 2×2×2 mm³ to 1×1×1 mm³) requires α² (e.g. 64) averages to ensure a similar SNR. A 5-min acquisition would become a 5-hour scan, which is not feasible in practice [2]. One solution to achieve higher resolution in MRI is to improve MRI scanner hardware. Higher magnetic fields, and stronger and faster gradients enable MR imaging with higher SNR; but these solutions require hardware upgrades, which are costly and often uneconomic.

Enhancing the resolution in MRI by post processing based on algorithms attracts widespread attention. Super-resolution (SR) techniques are among the popular methods that, because of their efficiency and satisfying results, can be combined with other methods to improve the efficacy of MRI [3], [4]. SR algorithms try to reconstruct a high-resolution (HR) image from a single low-resolution (LR) image (single-frame SR methods) [5], [6] or multiple LR images (multi-frame SR methods). Multi-frame SR methods usually use more information than single-frame SR methods thus may generate better results; but multi-frame acquisitions often require extra time and resources compared to a single frame acquisition. A combination of the two techniques for SR MRI can be very attractive and useful.

SR techniques were originally proposed as multi-frame SR algorithms for the reconstruction of HR images from a set of LR images in video sequences [7]. In 2001 and 2002, initial attempts were made to adopt SR algorithms from the computer vision field to medical imaging with a focus on MRI [8], [9]. Multiple MR images of the same subject with small shifts were obtained to reconstruct an HR image. The authors tried to reconstruct the HR MR image from a set of spatially subpixel shifted scans in the in-plane dimension in [8]. In-plane shifting, however, is equivalent to acquisition of the same points in k-space, which means they carry the same information, thus such techniques do not enable actual resolution enhancement in MRI. Greenspan [9] used Irani and Peleg’s IBP (Iterative Back Projection) method [7] to reconstruct HR isotropic MR image from subpixel shifted scans in the slice-selection dimension; the results of which showed that the proposed method did improve the resolution of MRI. Greenspan discussed these methods and the state-of-the-art in SR in medical imaging in [10].

Some of the modern applications of multi-frame SR reconstruction in MRI have been motion-robust fetal MRI [11], [12], [13], [14], SR cardiac MRI [15], [16], [17], [18], SR tongue and vocal tract MRI [19], [20] and SR diffusion-weighted (DW) MRI [2], [4], [21]. Gholipour et al. [11] developed a model-based SR technique that incorporated a model of subject motion, slice profile, and robust estimation, that enabled the reconstruction of a volumetric image from arbitrarily oriented slice acquisitions, a scenario that fit very well to fetal MRI. This framework was extended and used in attractive applications in various MR imaging applications affected by motion, such as cardiac MRI, vocal tract MRI and DW MRI. Rahman et al. employed a maximum a posteriori (MAP) based SR approach for computing a HR volume from two orthogonal short-axis and long-axis cardiac MR images [15]. The model-based SR algorithm was further extended to 4D image reconstructions in cardiac MRI [18]. Woo et al. introduced a framework to SR reconstruct an isotropic tongue volume using three orthogonal LR stacks [19]; and Zhou et al. also followed the model-based SR approach to SR reconstruct HR isotropic volume from three orthogonal LR vocal tract MR images [20]. Scherrer et al. [2], [21] proposed model-based SR methods, based on MAP estimation, to accelerate and reconstruct HR diffusion tensors and diffusion model compartments from multiple anisotropic orthogonal DW-MRI scans. Ning et al. [4] coupled compressed sensing with SR for accelerated HR DW-MRI.

For reviews of other super-resolution techniques in MRI we refer to [3], [10], [22], [23]. Inspired by the very interesting works on single image scale-up (or single frame SR) based on sparse representation [25], [26], several researchers developed single-frame SR methods in MRI. Jafari-Khouzani [5] used a feature-based approach to upsample a thick-slice MR image using another MR image of the same subject acquired with different contrast but at higher resolution, and compared it to an earlier work based on non-local means by Manjon et al. [24]. Rueda et al. [6] used HR MR images as examples to train a sparse model for single-frame SR. Jia et al. [22] proposed training a dictionary from HR in-plane data using K-SVD algorithm (K-Singular Value Decomposition) and obtained better results than non-local means approach. For a discussion of these methods and their relation to SR methods based on sparse representation we refer to [22].

To the best of our knowledge, there has not been any study that combines the information of multiple orthogonal anisotropic MR scans using sparse representation for SR image reconstruction. In this work, we propose a novel algorithm to reconstruct isotropic HR MRI by upsampling and fusing orthogonal anisotropic MR scans to increase the resolution by SR using sparse representation of images. This is different from single frame SR reconstruction in digital imaging [25], [26] and MRI [22]. To this end, we construct training sets based on the self-similarity and similarity between orthogonal LR 3D MR scans and combine them to achieve SR MRI. There is no need for extra training sets in this approach and the technique takes advantage of the data provided by multiple orthogonal acquisitions in two ways: 1) learning from data to reduce the effect of partial volume in anisotropic LR acquisitions for upsampling, and 2) fuse data that sample the 3D space of the anatomy in orthogonal complementary ways.

The remaining parts of this paper are organized as follows. The mathematical model behind the proposed method is discussed in Section II. The proposed methodology is described in Section III. In Section IV, experimental results and analysis are presented. Section V contains the conclusion.

II. Mathematical model behind the proposed method

The multi-frame SR problem can be formulated as follows:

$$Y_n=D_n{B}_n{G}_{n}X+V_n;n=1,\dots ,N$$ (1)

where Y_n is the nth LR image, N is the total number of LR images; X is the desired reconstructed HR image; D_n, B_n and G_n are the down-sampling, blurring and geometric transformation operators respectively; V_n is the additive noise in the nth LR image. With N = 1, (1) becomes a single-frame SR problem. To solve the above problem efficiently, we propose to decompose the multi-frame SR problem into three sub-problems presented as follows:

1) Upsampling LR images

We initiate the multi-frame SR problem by upsampling each of the LR images. The single image SR problem is expressed by:

$$Y_n=D_n{B}_n{G}_n{X}_n+V_n$$ (2)

Without loss of generality, (2) can be rewritten as:

$$Y_n=M_n{X}_n+V_n$$ (3)

where M_n=D_n B_nG_n. Upsampling is equivalent to finding X_n in equation (3) based on the acquired LR scans and the LR scans generative model. This is an under-determined inverse problem. We regularize and solve this problem using a sparse-land local model described in Section-III-A-1.

2) Initial HR image reconstruction

In this step, we fuse all the obtained HR images X _n from step 1 into one single HR image as the initial SR reconstructed result X⁰ in (1). While several techniques can be used for this [31], we choose to efficiently perform it through 3D wavelet decomposition of the upsampled images from step 1 and then fuse the wavelet decompositions to reconstruct X⁰ [32]. This process, which is based on [32], is discussed in Section-III-B-2.

3) Constrained reconstruction by error back-projection

The initial reconstructed HR image X⁰ is then refined by minimizing the error of estimating slices in the global generative model in (1). We perform this global reconstruction constrained by the projection of X⁰onto the solution space of (1) using:

$$X\ast =\mathit{arg}\underset{x}{min}{{\displaystyle {\sum }_n^N\Vert M_{n}X-Y_n\Vert }}^2+c{\Vert X-X^0\Vert }^2$$ (4)

where c balances the fidelity of the approximation of reconstructed LR MR scan and the difference between the solution and the initial value. The weighting coefficient c is set to be between 0.01 and 0.1 for regularization, but can be set to zero in a multi-frame SR problem with a relatively small SR factor (e.g. 2–3). The solution to the SR optimization problem can be numerically computed through iteration on the difference between the reconstructed and the original LR MR scans [6]. The update equation for the iterative optimization is:

$$X^{t+1}=X^t+\sigma [{\displaystyle {\sum }_n^N{M}_n^T\left(Y_n-M_n{X}^t\right)+c(X-X^0)}]$$ (5)

where X^t is the estimation of the HR image after the t-th iteration, and σ defines the step size.

III. Proposed methodology

The proposed algorithm aims to reconstruct an isotropic HR 3D MR image from orthogonal anisotropic scans. The proposed framework includes three steps: upsampling all the orthogonal scans based on sparse representation, orthogonal MR images fusion based on wavelet decomposition, and global reconstruction through error minimization, as shown in Fig. 1. The details of these three steps are discussed below.

Fig. 1.

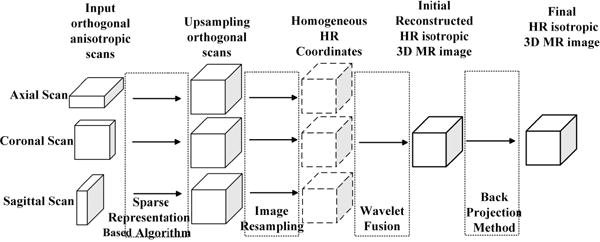
An overview of the proposed algorithm

A. Upsampling Orthogonal Scans

Orthogonal LR anisotropic MR scans include axial, coronal and sagittal scans with HR slices in the in-plane directions and LR slices in the slice-selection directions. In this step, our goal is upsampling the three LR anisotropic MR images to HR isotropic MR images respectively by the proposed algorithm based on sparse representation. This procedure includes training set construction, HR and LR dictionaries training, and HR MR image reconstruction.

1) Sparse-Land Local Model

The problem in the first step, as shown in (3), is ill-posed and has no unique solution, so we need regularizers to obtain a unique solution for this problem [27]. To regularize the solution using the sparsity of the MR image, we choose to introduce sparsity prior as the regularizer and work at the level of small 2D patches extracted from MR slices. We then compose the SR reconstructed patches into a 3D volume. The sparsity prior means the small patches can be represented as a sparse linear combination in the corresponding trained over-complete dictionaries. So (3) can be rewritten as:

$$y_k=M_k^{\#}{x}_k+{\upsilon }_k,k=1,\dots ,K$$ (6)

where $y_k=P_k^l\ast \left(F_l\ast Y_n\right),F_l$ is the feature extractor for the LR MR slice which extracts the high frequency information. The HR MR image loses its high frequency information through the acquisition process, and our task is to recover the high frequency information. That is why we use the high frequency features as the examples to consider the SR model and train dictionaries. In this paper, we utilize gradient and Laplacian image filters to extract features of the LR MR images. These two filters are simple and efficiently extract high frequency information from MR images. Besides, we get the HR feature vector by subtracting the low frequency from the HR slices. We use Principal Component Analysis (PCA) for dimensionality reduction on feature vectors to reduce computations and improve the reconstruction accuracy. In this formulation, $P_k^l$ is the overlapped 2D patch extractor from MR slices; y_k is the feature vector of 2D patch k; x_k is the corresponding feature vector extracted from the HR MR slice; $M_k^{\#}$ is the local down-sampling operator on patch k; v_k is the additive noise on patch k; and K is the total number of patches extracted from LR MR image Y_n. To be consistent, the patches are feature vectors extracted from the corresponding 2D patches in the following parts. The atoms of the dictionary are also feature vectors.

In this paper, we utilize the synthesis model to describe the sparse representation problem. The HR dictionary of the synthesis model D_X = [d₁, d₂, …, d_W] ∈ R^H×W, where H < W, that means the dictionary is over-complete, allows to represent a wide range of signal phenomena; where d_w ∈ R^H is one atom of the dictionary D_X. Vector x_k ∈ R^H can be expressed as a sparse linear combination of the atoms in the dictionary $D_X:x_k\approx D_X{\alpha }_k^X$, where ${\alpha }_k^X\in R^W$ is the coefficient of x_kover dictionary D_X. If the number of nonzero elements in ${\alpha }_k^X$ is $s(s\ll W),{\alpha }_k^X$ is s-sparse. Similarly, for the LR dictionary: $y_k\approx D_Y{\alpha }_k^Y$, where $D_Y=[d_1^{\prime },d_2^{\prime },\dots ,d_W^{\prime }]$ ∈ R^L×W. The over-complete dictionary ensures the coefficients ${\alpha }_k^X$ and ${\alpha }_k^Y$ of the patches are sparse. Furthermore, in the SR reconstruction problem, we assume ${\alpha }_k^X\approx {\alpha }_k^Y$ [26]. This means the LR patches and the corresponding HR patches share the same sparse representation. The problem of finding a sparse representation of y_k can be described as follow:

$$min\Vert {\alpha }_k^Y\Vert 0,s.t.{\Vert D_Y{\alpha }_k^Y-y_k\Vert }^2\le \epsilon$$ (7)

where l₀ is the number of non-zero elements.

Supported by the above theory, the SR method based on sparse representation and over-complete dictionary is defined in Fig. 2: Firstly, LR dictionary D_Y and HR dictionary D_X are trained from the training set by using a dictionary training algorithm. The dictionary training process will be discussed in the following section. Then the observed LR patch y_k is sparsely represented over the trained LR dictionary D_Y by utilizing sparse representation techniques, and the sparse coefficients ${\alpha }_k^Y$ are computed. As assumed above, the sparse representations of the LR and HR images are the same. So based on the obtained sparse representation ${\alpha }_k^X\approx {\alpha }_k^Y$ and the trained HR dictionary D_X, HR patch is reconstructed by $D_X{\alpha }_k^X$. After up-sampling each patch, the whole image is composed by all the overlapped patches. We describe the composition algorithm in Section 4. Test experiments show that the SR algorithm performing at overlapped patches lead to better reconstruction results than performing at non-overlapping patches, therefore we use overlapped patches here. The low-frequency information is then added to the composed HR image. The above model based on sparse representation can also be referred as local sparse-land. This model constructs a connection between HR patches and the corresponding LR patches, which is exploited to recover the HR image.

Fig. 2.

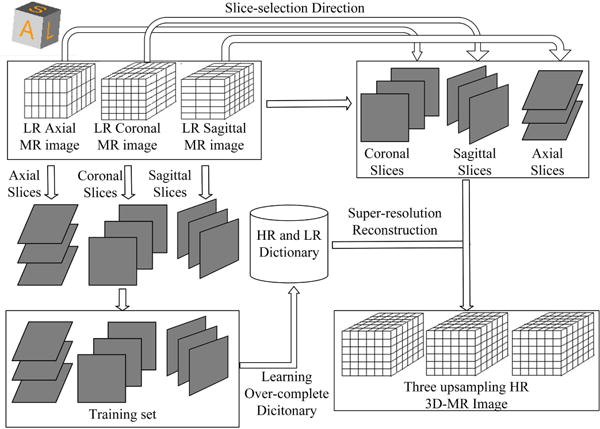
Upsampling orthogonal scans based on sparse representation. OMP stands for the orthogonal matching pursuit algorithm.

2) Training set construction

Based on the SR method described in Fig. 2, the first step of SR algorithm is constructing the training set to train the LR dictionary D_Y and the corresponding HR dictionary D_X, respectively. The training set includes HR patches and the corresponding LR patches which are produced through the observed model by the HR patches. It means the LR training examples are the down-sampled, blurred, transformed and noisy version of the corresponding HR training examples. The upsampled results depend on whether the trained dictionary matches the observed LR patches. Generally, the more similar the observed LR patches are to the training examples, better-trained dictionaries can be obtained. So in order to train dictionaries that closely resemble a sparse land model of the observed LR patches, it would cost much more time to select similar training examples from big datasets. Then we should consider the balance between accuracy and robustness of the dictionary, but there is no theoretical guidance. Furthermore, sometimes no extra training set is provided. To mitigate the above problems, here we propose to construct the training set from the orthogonal anisotropic MR scans themselves to utilize the similarity between the HR slices and the corresponding out-of-plane sections of the three orthogonal anisotropic MR scans, and the self-similarity of each of them.

In this paper, we train the dictionary based on all the HR in-plane slices extracted from the orthogonal anisotropic scans. The upsampling process of all the three orthogonal MR images shares the same dictionary. Then we upsample the LR slices containing the slice-selection direction (the out-of-plane slices) of each anisotropic scan. It is evident from k-space sampling in MRI and represented by the wavelet representation, these thick-slice 2D scans carry high-frequency information in two dimensions (phase encoding and frequency encoding dimensions) while not covering high frequencies in the third (slice select) dimension. So we trained the dictionary based on in-plane slices and performed the SR reconstruction process at the level of 2D patches rather than 3D patches. If we were using 3D patches, then the effect of the partial volume in the slice select direction could be problematic.

This is an efficient strategy to construct the training set. Firstly, the constructed training set is much more similar with the LR slices to be upsampled. Using axial scan as an example, the in-plane slices in the axial view is HR and our task is to upsample the out-of-plane slices. By analyzing the features of the three orthogonal anisotropic MR scans, the LR coronal and sagittal slices of the axial scan correspond to the HR in-plane slices of the coronal scan and the sagittal scan. So extracting the HR slices from coronal and sagittal scans to train the dictionary for the LR slices of the axial scan is an intuitive choice. Similarly, the HR slices in the axial scan can be utilized to train dictionary for the LR slices in coronal and sagittal scans. Furthermore, the local self-similarity of anatomical features occurs both within the same plane and across the planes. That means, for the same MR scan we can extract overlapping image patches from the in-plane direction that are similar to the out-of-plane patches. So the HR in-plane slices of the axial scan also could be utilized as the training examples for the reconstruction of the same scan. That means we could extract all the HR in-plane slices from the three orthogonal MR images to construct the training set. Secondly, the training set construction strategy is robust. For various MR scans, the constructed training set would always be similar with the LR slices to be upsampled, as the training set construction strategy utilizes the intrinsic similarity between the three orthogonal anisotropic MR scans and the self-similarity of each MR scan.

Based on the above analysis, this paper extracts the HR slices from the in-plane direction from all the orthogonal scans to construct the training set; and the same trained dictionary is used to upsample the LR slices of the orthogonal scans respectively.

3) Dictionary Training

The key step of the SR algorithm is dictionary training, including LR dictionary training and the corresponding HR dictionary training. Yang et al. [25] proposed jointly training HR and LR dictionaries for the HR and LR image patches, to enforce the similarity of sparse representation between the LR and HR image pairs based on their own dictionaries. This method, however, is very time consuming. To solve this problem, Zeyde et al. [26] simplified the overall process both in terms of computational complexity and the algorithm architecture. Meanwhile, the reconstruction results were also improved. We utilized Zeyde’s algorithm to train the HR and LR dictionary pair in this paper. They firstly trained the LR dictionary using K-SVD (K-Singular Value Decomposition) [28] algorithm based on LR training examples, and obtained the sparse representation; then the HR dictionary was learned based on the sparse representation and HR training examples. The details of the dictionary training algorithm are shown in the online Supplementary Material.

4) Orthogonal MR image SR reconstruction

Based on the trained HR and LR dictionary, we SR reconstruct all the orthogonal MR images. For each orthogonal MR image, we upsample the LR slices in the slice-selection direction. In our proposed sparsity-based SR reconstruction algorithm, we process small 2D patches. Firstly, feature extraction and dimensionality reduction are performed again over the LR slices of orthogonal MR images similar to the dictionary training phase. The next step is reconstruction. For each 2D patch extracted from the LR slices in out-of-plane directions, we get the sparse code by OMP (orthogonal matching pursuit) method [29], [30] using the trained LR dictionary D_Y. Because HR patches and the corresponding LR patches share the same sparse representation, we get the HR patches by multiplying the sparse code and the trained HR dictionary D_X.

As mentioned above, we process small 2D patches rather than the whole volume. So the reconstructed overlapped small 2D patches should be composed to reconstruct the HR slices; then HR slices are composed to the whole HR volume. The final HR slices are constructed by solving the following minimization problem with respect to x_k:

$$X_h=\mathit{arg}\underset{X_h}{min}{{\displaystyle {\sum }_k\Vert P_k^h\left(X_h-X_l\right)-x_k\Vert }}_2^2$$ (8)

where $P_k^h$ means an extractor to extract patches at location k from high frequency resulting image (X_h − X_l), where X_l is the low frequency part of X_h. The extracted patches should be as close as possible to the reconstructed patches x_k. This problem can be solved by the following equation:

$$X_h=X_l+{[{\displaystyle {\sum }_k{(P_k^h)}^T{P}_k^h}]}^{-1}{\displaystyle {\sum }_k{(P_k^h)}^T{P}_k^h}$$ (9)

It is equivalent to putting x_k in their proper location, averaging the overlap regions, and adding the low frequency content of X_l to generate the final image X_h. Then the HR slices are composed to reconstruct the HR volumes.

B. 3D Wavelet Fusion

1) Image Resampling

Orthogonal MR scans acquired from a subject often do not have the same origin, spacing, direction, and number of voxels; so in order to fuse orthogonal scans, we first resample them to match their geometry. For scans acquired in the same scan session, if the subject does not move between scans, an identity transformation is used for resampling. Alternatively, image registration may be used to correct for possible subject motion or misalignment between scans. The main component of resampling is interpolation. Classic interpolation algorithms like nearest neighbor, linear, cubic, B-spline, or Kaiser-Bessel windowed Sinc may be used. We used cubic interpolation as it provides good practical estimations of the ideal Sinc interpolator.

2) Wavelet fusion

The simplest method to fuse resampled images from orthogonal scans is averaging. Averaging is simple but does not take into account the physics of MRI slice acquisitions thus results in artificial blurring. SR MRI reconstruction accounts for MRI physics and can be done in the image, frequency, or wavelet domains [31]. Here, we adopt a wavelet-based approach [32] to combine the orthogonal scans as it is fast and efficient and performs nearly as good as the frequency and image domain approaches. Wavelet fusion approach intends to construct a high spatial resolution image, containing a wide range of spatial frequencies (from low to high) in each axis, derived from input MR scans that contain high spatial frequency information in the in-plane axes only. This is an important contribution because the ability to acquire directly high spatial frequency data in all three axes is restricted, both by acquisition time, by signal-to-noise ratio, and by the decay times of MRI contrast parameters T1 and T2. To this end, the wavelet fusion algorithm combined all the meaningful information from the input MR images, including the low frequencies and in-plane high frequencies; while discarding the parts without useful information, i.e. missing high frequencies in the slice-selection direction. The procedure is described below.

The 3D wavelet transform of an MR image (with “XYZ” coordinates) has eight blocks, often denoted as “LLL”, “LLH”, “LHL”, “LHH”, “HLL”, “HLH”, “HHL”, “HHH”, where, for instance, LHH stands for the block containing low-, high-, and high-frequency information in the X, Y, and Z directions, respectively. The sagittal scan, for example, has useful information in its L## blocks, but virtually no information in its H## blocks (“#” stands for both H and L). Similarly, the informative blocks of the coronal and axial scans would be the #L# and the ##L blocks, respectively. Following [32], we used Haar wavelets for wavelet transform.

Wavelet fusion uses as many informative blocks as possible from the three orthogonal scans to reconstruct the desired HR image. For example, the reconstructed LLL block will be the average of the LLL blocks of all the three scans, the LLH will be the average of the LLH blocks of the coronal and sagittal scans, and the LHH will be the LHH of the sagittal scan. The fusion rule is shown in Fig. 3. The HHH block is the only one missing in all the three scans, which is handled by zero padding. Performing an inverse wavelet transform will then produce an isotropic-voxel HR image, combining the useful information of the three available scans.

Fig. 3.

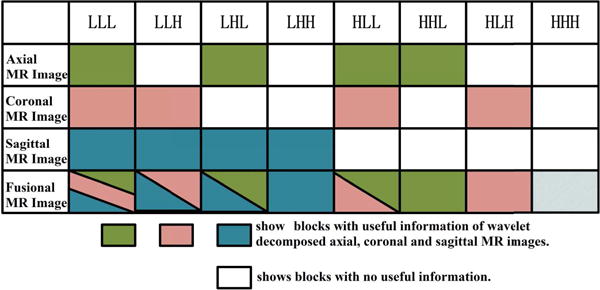
The rule of image fusion based on wavelet decomposition

C. Global Reconstruction

As a last step, we solve the global reconstruction problem (5) formulated in Section II. In the previous steps, we upsampled the three orthogonal input LR scans independently even though they shared the same training set and trained dictionary that were based on the similarity between them and their self-similarity. Through this last step, we refine the reconstructed image based on (1). This helps mainly because in upsampling each input LR scan based on sparse representation, we did not demand exact equality between the LR patches and the reconstructions $D_y{\alpha }^Y$, and we did not impose strict constraints to ensure α^X =α^Y in the dictionary training part. Besides, we worked at the level of patches and solved the reconstruction problem locally. Global reconstruction ensures the continuity between patches after composing the small patches into a final isotropic HR image.

IV. Experiments and analysis

To validate the efficacy of the proposed algorithm we conducted abundant experiments. This section includes four parts. The first part presents the implementation details and parameters selection. The second part gives a brief description of the MR data utilized in the experiment. In the third part, we test the proposed method over MR images with different features (different slice thickness, different noise power, with or without sclerosis), and also test the influence of number of input LR images over reconstructed results. In the fourth part, we compared our proposed method with single-frame SR and multi-frame SR algorithms over bigger datasets, including simulated MR images and clinical MR images.

A. Implementation Details and Parameters Selection

All algorithms were implemented in MATLAB R2014a, running on a Windows machine with two 3.10 GHZ Intel Core i5 CPUs and 4.00 GB of RAM. To quantitatively and qualitatively evaluate the performance of the proposed method over different MR data sets, we introduce 4 different methods in this section for two scenarios, including PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Image Metric) [34], visual inspection and intensity profile (The details of these four methods are provided in the online Supplementary Material). We ran several preliminary experiments with different parameters, to provide a good tradeoff between accuracy and efficiency. Based on these testing experiments we chose the patch size equal to 3×3, number of iterations of dictionary training algorithm = 40, overlapped region for patches = 1, number of dictionary atoms = 521 and the maximum sparsity = 3. Besides, we used cubic interpolation for the initial upsampling. The step size of gradient descent in the global reconstruction stage was set to $\frac{1}{3}$, and the maximum number of iterations of the error minimization in the global reconstruction algorithm was 40.

B. Experimental Data Acquisition

Experiments were conducted on the simulated T2-weighted (T2w) MR scans from the Brainweb database [33], T2w turbo spin echo (TSE) clinical MR scans of the brain, and T2w single slab 3D TSE with slab selective, variable excitation pulse (T2 SPACE) knee MRI scans. The simulated data included normal and pathologic (multiple sclerosis) MR images, with and without noise. The details of the datasets are shown in Table I. To simulate the down-sampled version of HR MR images, adjacent slices were averaged to produce different slice thicknesses. This simulates the Partial Volume Effect (PVE). PVE increases as the slice thickness increases. Orthogonal scans were generated by down-sampling different directions of the HR MR images.

Table I.

The detailed information of the MR scans utilized in the experiments

3D Images	#of slices	Matrix size	Voxel Size (mm)
T2w HR brain MR image	181	181×216	1×1×1
TSE T2w axial brain scan	80	512×408	0.5×0.5×2
TSE T2w coronal brain scan	80	408×512	0.5×2×0.5
TSE T2w sagittal brain scan	83	512×512	2×0.5×0.5
C00l T2w knee MR image	192	256×256	0.625×0.625×0.63
C002 T2w knee MR image	256	320×320	0.5×0.5×0.5
C003 T2w knee MR image	224	320×320	0.5×0.5×0.5
C004 T2w knee MR image	208	320×320	0.5×0.5×0.5
C005 T2w knee MR image	192	256×256	0.6×0.6×0.6
C006 T2w knee MR image	256	320×320	0.5×0.5×0.5
C007 T2w knee MR image	256	320×320	0.5×0.5×0.5
C008 T2w knee MR image	288	320×320	0.5×0.5×0.5
C009 T2w knee MR image	224	320×320	0.5×0.5×0.5
C010 T2w knee MR image	208	320×320	0.5×0.5×0.5

C. Tests on the proposed method

We performed experiments on the simulated T2w scans and clinical T2w knee MR scans to evaluate the efficacy of the proposed method. Simulated orthogonal scans with different thickness, different levels of noise, and cases with multiple sclerosis were utilized to produce HR isotropic 3D MR images. To show the efficacy of the proposed method in different situations, we compared with Cub-Ave and Cub-Wav. Cub-Ave indicates the traditional averaging method. Cub-Wav means interpolating those three orthogonal LR MR scans by cubic interpolation and combining the upsampled scans by wavelet fusion approach [32]. In Section D, we compare with more SR reconstruction algorithms over bigger datasets.

1) Influence of slice thickness

As mentioned in Section B, in order to simulate PVE, we constructed down-sampled MR images by averaging adjacent slices. In particular, the PVE is stronger as the slice thickness increases. To study the effect of slice thickness on the proposed method, we respectively produced three orthogonal LR down-sampled MR images with slice thickness of 2mm, 3mm, 4mm, 5mm, 6mm, and 7mm from simulated T2w brain MR image. We reconstructed T2w brain HR volume with voxel size 1mm × 1mm × 1mm from three simulated LR orthogonal brain MR images. Table II shows that the proposed algorithm generated the best results in terms of both PSNR and SSIM values. For example, the PSNR/SSIM values obtained from the proposed method were 42.78dB/0.999 in 2 mm and 36.68dB/0.995 in 3 mm, while the results of the other two algorithms were much worse. This indicates major improvements over Cub-Ave and Cub-Wav method. The PSNR/SSIM values dropped as the slice thickness increased.

Table II.

Accuracy of reconstructed images under the influence of slice thickness on simulated T2w brain MR image

Slice thickness (mm)		2	3	4	5	6	7
Cub-Ave	PSNR(dB)	31.61	27.01	24.52	22.97	21.86	20.90
	SSIM	0.986	0.958	0.916	0.877	0.832	0.7890
Cub-Wav	PSNR(dB)	37.45	28.17	25.35	23.59	22.35	21.30
	SSIM	0.996	0.968	0.931	0.893	0.849	0.808
Proposed Method	PSNR(dB)	42.78	36.68	3237	29.47	27.42	26.10
	SSIM	0.999	0.995	0.987	0.974	0.956	0.937

We tested the effect of slice thickness on the proposed method over knee MR scans and observed similar trends. For HR knee MRI reconstruction, the PSNR/SSIM values obtained from the proposed method were 47.26dB/0.996 for 2mm thick-slice LR images, while the results of the other two algorithms were 37.09dB/0.974 and 43.56dB/0.994, respectively. The PSNR and SSIM values of the knee reconstruction results are shown in the online Supplementary Material. Again, the proposed algorithm generated the best results in terms of both PSNR and SSIM values.

Similarly, the PSNR/SSIM values dropped as the slice thickness increased. The reason for the influence is that the upsampling factor increases as the slice becomes thicker. The limitation of most SR algorithms is that their performance deteriorates quickly when the magnification factor becomes moderately large.

Besides, we displayed several slices of the reconstructed knee MR image when slice thickness is 3mm in Fig. 4. Details are blurred in thick-slice scans due to PVE, but we obtained satisfactory results by our method. For example, the structure highlighted by the red rectangle in the coronal view of (a) could be observed clearly, but were very blurry in the coronal view of (b) and (d).

Fig. 4.

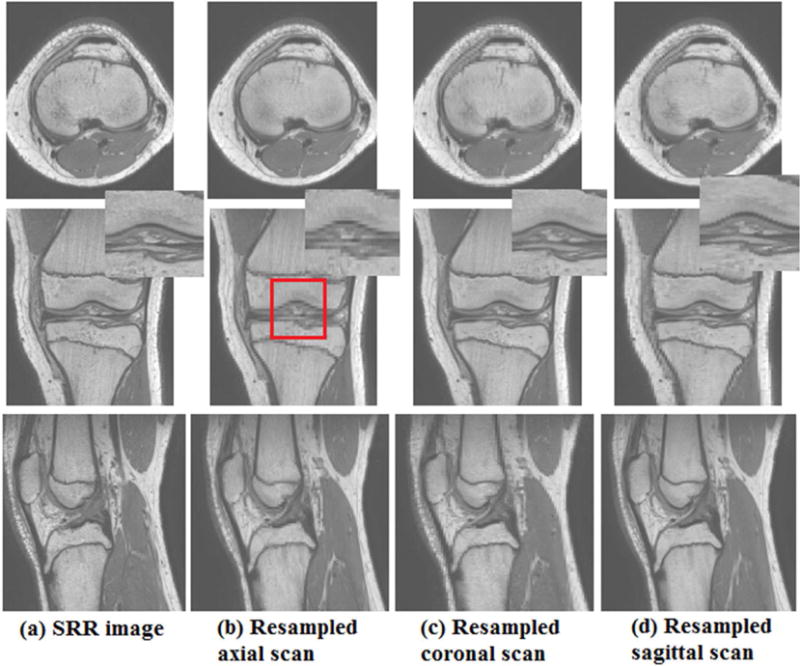
From top to bottom, this figure shows axial, coronal and sagittal views on (a) SRR knee image by our proposed method, (b) resampled knee axial scan, (c) resampled knee coronal scan and (d) resampled knee sagittal scan. The rectangle highlights some details.

2) Influence of noise power

The intension in our particular MR application is to reconstruct an HR isotropic 3D MR image from orthogonal clinical scans based on the SR algorithm, but without exposing the patient to longer acquisitions. So we did not consider and were not specifically focused on improving the reconstructed image by removing noise; however, it was important to evaluate the impact of the noise in the proposed algorithm. To do so, three orthogonal LR brain T2w MR scans with 2mm slice thickness were respectively produced. Different percentage noise (1%, 3%, 5%, 7%, and 9%) levels were used to investigate the noise influence. It is well known that the magnitude MR noise follows a Rician distribution. So we added Rician noise to the simulated LR orthogonal brain MR scans. Firstly, those three LR noisy MR scans were denoised using ODCT3D and PRI-NLM3D methods [35], which take advantage of two intrinsic properties of MR images: sparseness and self-similarity. Then, the proposed algorithm was applied to the denoised LR orthogonal scans.

Table III presents the reconstruction accuracy values in terms of PSNR and SSIM on simulated T2w brain MR image. The proposed method obtained the best results in all cases. In Table III, the PSNR/SSIM values dropped as the noise level increased. For example, the PSNR/SSIM value of the reconstructed T2w brain MR image was 39.78dB/0.993 when the noise power was 1%, while the PSNR/SSIM value was 35.71dB/0.974 when the noise power was 3%. We observed similar trends in the impact of noise in the proposed algorithm on knee MR data with 3mm slice thickness. The PSNR/SSIM values of the reconstructed results can be found in the online Supplementary Material. The results showed that the proposed method obtained the best results in most cases; and the PSNR/SSIM values dropped as the noise level increased.

Table III.

Accuracy of reconstructed images under the influence of noise power on simulated T2w brain MR image

Noise power		0%	1%	3%	5%	7%	9%
Cub-Ave	PSNR(dB)	31.61	31.50	30.91	30.06	29.10	28.13
	SSIM	0.986	0.982	0.963	0.938	0.910	0.883
Cub-Wav	PSNR(dB)	37.45	37.44	34.91	32.92	31.24	29.79
	SSIM	0.996	0.990	0.969	0.942	0.912	0.881
Proposed Method	PSNR(dB)	42.78	39.78	35.71	3336	31.64	30.16
	SSIM	0.999	0.993	0.974	0.949	0.922	0.894

The efficacy of the denoising method affects the SR reconstruction results. As the noise power increased, the difference between the results obtained by various algorithms became smaller. This is explained as follow: when the noise power becomes increasingly large, the results mostly depend on the denoising method and the SR reconstruction algorithms that use intrinsic image features perform less satisfactorily.

3) Influence of pathology

To test whether the proposed method could keep the details of the LR orthogonal scans, we applied the proposed algorithm to simulated pathologic scans and tested the accuracy of the reconstruction on MR scans with multiple sclerosis. As shown in Table IV, the PSNR/SSIM values obtained by the proposed method over three LR orthogonal pathologic brain T2w MR scans with 2mm slice thickness were 43.92dB/0.999, while the PSNR/SSIM values obtained by Cub-Ave and Cub-Wav were 32.69dB/0.987 and 38.64dB/0.997 respectively. Besides, we present the reconstruction results over orthogonal pathologic brain T2w MR scans with 4mm slice thickness in Fig. 5. Thin structures (sclerosis) are easily obscured and blurred in thick-slice scans due to PVE, but were reconstructed satisfactorily by the proposed method. For example, the sclerosis highlighted by the top red circle in the axial view of (a) could be observed clearly, but were obscured in the axial view of (c) and (d).

Table IV.

Reconstruction results over simulated pathologic brain MR scans

Slice thickness	2mm		3mm
	PSNR(dB)	SSIM	PSNR(dB)	SSIM
Proposed method	43.92	0.999	37.78	0.995
Cub-Ave	32.69	0.987	27.97	0.958
Cub-Wav	38.64	0.997	29.12	0.968

Fig. 5.

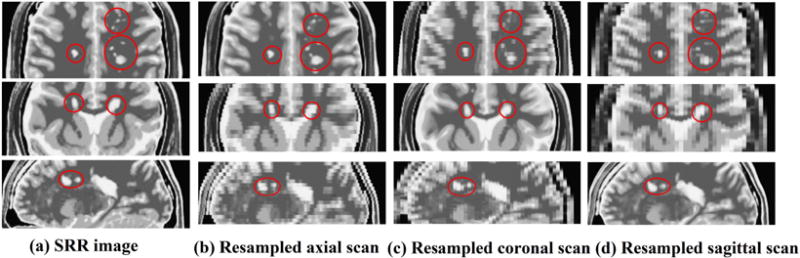
From top to bottom, this figure shows axial, coronal and sagittal views on (a) SRR pathologic brain image by our proposed method, (b) resampled pathologic axial brain scan, (c) resampled pathologic coronal brain scan and (d) resampled pathologic sagittal brain scan. The circles and ellipse highlight some sclerosis regions with differences.

4) Influence of the number of input LR MR images

To evaluate the additional benefit of SR reconstruction from three orthogonal scans compared to two scans and a single scan, we applied the proposed method to any pairs of the three simulated non-noisy LR orthogonal T2w brain scans with 2–7 mm slice thickness. Furthermore, we compared the proposed method with our previous work on single-frame MR SR reconstruction [22]. Table V presents the PSNR and SSIM values of the reconstruction results over various situations. The results show that SR reconstruction using three orthogonal scans provided much better results than SR reconstruction using two scans, and SR reconstruction using two scans outperformed single-frame SR. For example, when the slice thickness was 2mm, the PSNR/SSIM value of the reconstructed image from three LR MR scans was 42.78dB/0.999, but the average PSNR/SSIM value of the reconstructed images from two orthogonal MR scans and single scans were 38.45dB/0.997 and 30.92dB/0.983, respectively. This indicates that multi-frame SR has clear advantages over single-frame SR as it combines information from multiple MR scans. In fact, single-frame SR can be considered as an upsampling technique that uses prior information based on the sparsity of images to improve conventional interpolation; whereas multi-frame SR indeed fuses high-frequency image information in an efficient manner.

Table V.

Reconstruction results based on single MR scan, two orthogonal MR scans, and three orthogonal MR scans

Thickness (mm)		2	3	4	5	6	7
A	PSNR(dB)	31.75	26.87	24.40	22.83	21.70	20.67
	SSIM	0.985	0.954	0.916	0.876	0.837	0.792
C	PSNR(dB)	31.48	26.00	23.14	21.48	20.41	19.47
	SSIM	0.987	0.951	0.899	0.845	0.796	0.742
S	PSNR(dB)	29.54	24.86	22.57	21.12	20.08	18.89
	SSIM	0.978	0.932	0.878	0.824	0.774	0.717
A+C	PSNR(dB)	39.18	32.79	29.08	26.72	24.98	23.77
	SSIM	0.998	0.989	0.973	0.952	0.924	0.895
A+S	PSNR(dB)	38.57	32.16	28.70	26.49	24.79	23.79
	SSIM	0.997	0.987	0.970	0.947	0.918	0.892
C+S	PSNR(dB)	37.59	31.27	27.63	25.36	23.70	22.53
	SSIM	0.997	0.985	0.963	0.933	0.896	0.861
A+C+S	PSNR(dB)	42.78	36.68	3237	29.47	27.42	26.10
	SSIM	0.999	0.995	0.987	0.974	0.956	0.937

A, C and S stand for Axial, Coronal and Sagittal view scan respectively.

The quality of the reconstructed image improves as a larger number of LR MR images are fused. But the computational time also increases proportional with the number of LR MR images. When the slice thickness was 3mm, the average computational time of the single-frame SR reconstruction, two-frame SR reconstruction, and three-frame SR reconstruction were 3.59, 7.28, and 10.79 minutes, respectively. As the slice thickness increased, the computational time decreased. The computational time of the different scenarios in Table V can be found in the online Supplementary Material.

D. Comparison with other approaches

To identify the advantages and improvements of the proposed algorithm, we compared the proposed method with single-frame SR algorithms and multi-frame SR algorithms on simulated MR images and clinical MR images.

1) Comparison with single-frame SR algorithms

To compare the efficacy of our proposed algorithm over single-frame SR algorithms, we compare the proposed method with reconstructions based on the popular single MR image NLM SR [36], NLMp [24] and stDL algorithms [22] over simulated T2w brain MR images with various slice thickness and noise power. The reconstructions were made by averaging the upsampled orthogonal MR scans by each of the single-frame SR algorithms. Table VI presents the PNSR/SSIM values of reconstructed results over simulated T2w brain MR image with slice thicknesses changing from 2mm to 7mm. The proposed algorithm achieved the best results in all situations, and outperformed over the other three single-frame SR algorithms. For example, when the slice thickness was 2mm, the PSNR/SSIM value of the reconstructed results using the proposed method was 42.78dB/0.999, but the PSNR/SSIM values of the reconstructed results using the single-frame SR algorithms were 37.36dB/0.996, 36.90dB/0.996 and 34.71dB/0.993, respectively. Table VII shows the PNSR/SSIM values of reconstructed results over simulated T2w brain MR image with noise power changing from 0% to 9% when the slice thickness was 2mm. The proposed algorithm generated the best results in most situations compared to the single-frame SR algorithms. For example, when the noise power was 1%, the PSNR/SSIM value of the reconstructed result using the proposed method was 39.78dB/0.993, but the PSNR/SSIM values of the reconstructed results using the single-frame SR algorithms were 36.99dB/0.992, 36.43dB/0.991, and 34.38dB/0.989, respectively. It is noteworthy that while the NLMp algorithm utilized a HR T1w MR image as reference for upsampling, the proposed method generated better results at lower noise powers even though it only utilized the features of the input LR MR images. For high noise power (i.e. 5%, 7% and 9%), on the other hand, the PSNR/SSIM values of the reconstruction results by the proposed method were slightly lower than the PSNR/SSIM values of the results obtained by the NLMp method. The above results showed that our proposed multi-frame SR algorithm generated better results than the state-of-the-art single-frame SR and averaging combination algorithms.

Table VI.

Accuracy of reconstructed images using single-frame algorithms and the proposed algorithm over simulated brain Mr images with different slice thickness

Slice thickness (mm)	2		3		4		5		6		7
	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR N(dB)	SSIM
NLMp approach	37.36	0.996	32.87	0.990	29.83	0.975	27.90	0.961	26.30	0.937	25.02	0.916
NLM approach	36.90	0.996	30.50	0.979	26.93	0.948	24.70	0.900	23.24	0.858	22.00	0.804
stDL approach	34.71	0.993	29.07	0.974	26.17	0.945	24.20	0.908	22.79	0.866	21.86	0.826
Proposed approach	42.78	0.999	36.68	0.995	32.37	0.987	29.47	0.974	27.42	0.956	26.10	0.937

Table VII.

Accuracy of reconstructed images using iingle-frame algorithms and the proposed algorithm over simulated brain Mr images with different noise power

Noise power	0%		1%		3%		5%		7%		9%
	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM	PSNR (dB)	SSIM
NLMp approach	37.36	0.996	36.99	0.992	35.44	0.974	33.67	0.950	31.96	0.922	30.41	0.896
NLM approach	36.90	0.996	36.43	0.991	34.72	0.972	32.99	0.947	31.40	0.921	29.93	0.893
stDL approach	34.71	0.993	34.38	0.989	33.20	0.971	31.83	0.946	30.49	0.921	29.22	0.892
Proposed approach	42.78	0.999	39.78	0.993	35.71	0.974	33.36	0.949	31.64	0.922	30.16	0.894

2) Comparison with multi-frame SR algorithms

To further evaluate the efficacy of the proposed method over Cub-Ave and Cub-Wav, we compared those three multi-frame SR algorithms over bigger datasets, including the simulated T2w brain MR image, 10 clinical T2w knee MR images and 3 clinical T2W brain MR images. For the simulated T2w brain MR image and 10 clinical T2w knee MR images, we produced non-noisy LR orthogonal MR images by averaging 3 adjacent slices in three orthogonal directions. That corresponded to an upsampling factor of 3 in our experiments. Table VIII shows the reconstructed results. The performance of the proposed method was the best. For example, in the experiment over C004 knee MR image, the PSNR/SSIM value of the reconstructed result obtained by the proposed method was 46.87dB/0.993, while the PSNR/SSIM values of the reconstructed results using Cub-Ave and Cub-Wav were 39.76dB/0.953 and 41.05dB/0.967, respectively.

Table VIII.

Reconstructed results using multi-frame SR algorithms over 11 MR images

Dataset		T2w brain MRI	C001 knee MRI	C002 knee MRI	C003 knee MRI	C004 knee MRI	C005 knee MRI	C006 knee MRI	C007 knee MRI	C008 knee MRI	C009 knee MRI	C010 knee MRI
Cub-Ave	PSNR(dB)	27.01	33.65	37.07	33.83	39.76	34.29	34.45	35.60	37.93	36.85	33.34
	SSIM	0.958	0.959	0.943	0.964	0.953	0.942	0.943	0.957	0.961	0.942	0.959
Cub-Wav	PSNR(dB)	28.17	35.03	38.34	35.07	41.05	35.71	35.71	36.78	39.11	38.07	34.54
	SSIM	0.968	0.970	0.959	0.974	0.967	0.958	0.958	0.968	0.971	0.958	0.970
Proposed method	PSNR(dB)	36.68	40.78	44.04	40.47	46.87	41.52	41.29	41.76	44.24	4331	39.73
	SSIM	0.995	0.986	0.991	0.986	0.993	0.988	0.987	0.986	0.989	0.991	0.986

To test the efficacy of the proposed method in a clinical MRI exam setting, we reconstructed HR isotropic MR scans based on three orthogonal clinical TSE T2w anisotropic scans, and SR reconstructed HR volume with voxel size 0.5mm × 0.5mm × 0.5mm. The detail information of the clinical scans has been shown in Section B. The results are displayed in Fig. 6. We selected several slices from axial view, coronal view and sagittal view to compare the reconstruction results. Ellipses in this figure highlight the structures that were visualized with anatomic details on the SR reconstruction by the proposed method but were blurred or obscured in the axial scan. Similarly, the structures marked by ellipses in the coronal view were severely blurred in both axial and sagittal scans, while could be clearly visualized on the SR reconstructed image. The squares mark the structures that were visualized on the SR by the proposed method but blurred and obscured in both coronal and sagittal scans. Rectangles show the structures that were visualized on the SR reconstruction by the proposed method but were blurred in the sagittal scan. Even though the averaging method and wavelet fusion approach improved the input scans, the reconstructed results showed visually inferior quality to the SR reconstruction by the proposed method. For example, the structures marked by the squares in the axial view in the SR image by the proposed method were better visualized than the ones in the averaging result and the SR image by the wavelet fusion approach. Besides, we selected three lines from axial view, coronal view and sagittal view to evaluate image intensity profiles on the thick-slice scans and the reconstructed results by different methods, as shown in Fig. 7. These lines show that the reconstruction results by the proposed method always had the sharpest changes in intensity profile over the image edges. As observed in this figure, some lines are not following the same shapes, it is because the small structures are obscured in thick-slice scans. This analysis shows that our proposed method generates better results with better details, and intensity profiles show better delineation of image edge features than averaging and the state-of-the-art wavelet fusion method.

Fig. 6.

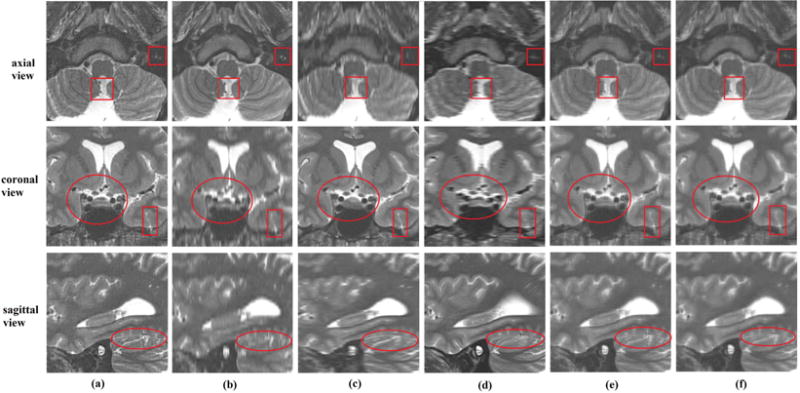
Reconstruction results over clinical orthogonal brain scans; (a) is the reconstructed image by the proposed method; (b), (c) and (d) are the resampled axial, coronal and sagittal scans by cubic interpolation method, respectively; (e) is the averaging of the resampled input orthogonal scans; and (f) is the reconstructed results by wavelet fusion approach.

Fig. 7.

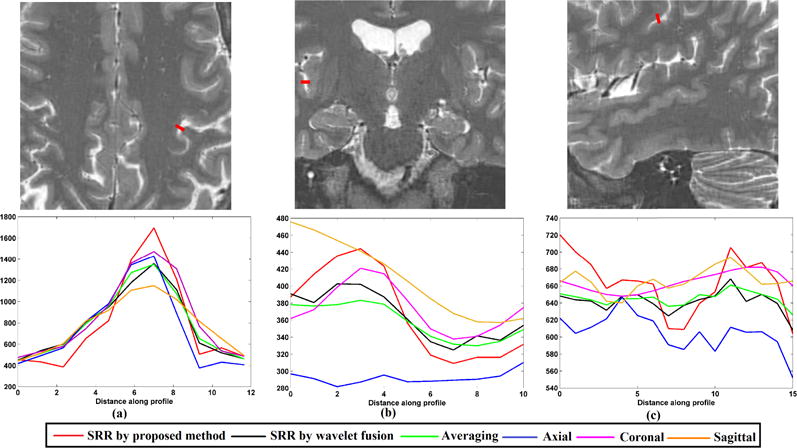
Intensity profiles of the selected lines shown in the upper row on multi-frame SRR and original brain scans.

V. Conclusions

This work proposed a novel super-resolution algorithm based on sparse representation for the reconstruction of an HR isotropic MR image from three MR scans acquired in orthogonal planes with anisotropic spatial resolution. The proposed algorithm decomposes the super-resolution reconstruction problem into three sub-problems, including upsampling thick-slice scans, super-resolution fusion based on wavelet decomposition, and global reconstruction. The proposed method exploits the similarity between the three orthogonal scans and the self-similarity of each scan at the same time. We examined and showed the superiority of our method by abundant experiments over simulated and clinical MR scans, and compared the results with three popular and efficient single MR image SR algorithms, including NLM algorithm, NLMp algorithm, and stDL algorithm. The results show that our algorithm outperformed the above three algorithms. Furthermore, we compared the proposed method with other multi-frame SR algorithms. The results show that the proposed technique outperforms the traditional averaging method and the classic wavelet fusion approach; and reconstructs small structures that are obscured in the thick-slice scan acquisition due to partial volume effects. The reconstruction results by the proposed method can provide HR MR image for clinical applications and facilitate computer-aided analysis, diagnosis, and research.