A cross-scale trophic cascade from large predatory fish to algae in coastal ecosystems

Abstract

Trophic cascades occur in many ecosystems, but the factors regulating them are still elusive. We suggest that an overlooked factor is that trophic interactions (TIs) are often scale-dependent and possibly interact across spatial scales. To explore the role of spatial scale for trophic cascades, and particularly the occurrence of cross-scale interactions (CSIs), we collected and analysed food-web data from 139 stations across 32 bays in the Baltic Sea. We found evidence of a four-level trophic cascade linking TIs across two spatial scales: at bay scale, piscivores (perch and pike) controlled mesopredators (three-spined stickleback), which in turn negatively affected epifaunal grazers. At station scale (within bays), grazers on average suppressed epiphytic algae, and indirectly benefitted habitat-forming vegetation. Moreover, the direction and strength of the grazer–algae relationship at station scale depended on the piscivore biomass at bay scale, indicating a cross-scale interaction effect, potentially caused by a shift in grazer assemblage composition. In summary, the trophic cascade from piscivores to algae appears to involve TIs that occur at, but also interact across, different spatial scales. Considering scale-dependence in general, and CSIs in particular, could therefore enhance our understanding of trophic cascades.

1. Introduction

Globally, many populations of large predators are declining due to overharvest, habitat loss and climate change [1,2]. These losses often trigger trophic cascades (indirect effects of predators on non-adjacent trophic levels) with far-reaching effects on ecosystem functions and processes, including diversity, atmosphere composition and biogeochemical cycling [3,4]. However, even though the existence of trophic cascades is supported by unequivocal evidence [2,4], their ubiquity is still highly debated. While some studies fail to detect cascading effects of predators [5,6], others have begun to disclose the manifold factors that influence the occurrence and magnitude of trophic cascades. Global drivers of variation in trophic cascade strength include temperature, precipitation [7,8], diversity and degree of omnivory [8,9]. At smaller scales, strong context-dependence of top-down and bottom-up control is known to depend on factors such as seasonality [10], nutrient loads [11], consumer behavioural responses [12], habitat complexity [13] and functional traits of both predators [14,15] and prey [16].

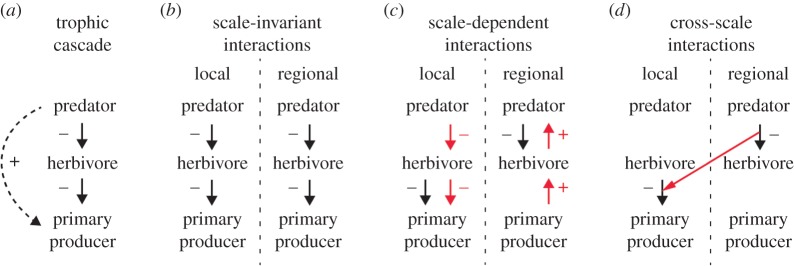
Here, we argue that an overlooked factor that may hinder our ability to detect trophic cascades and assess their strength is the explicit consideration of the multiple spatial scales at which trophic interactions (TIs) occur. Spatial scale is well known to affect functional responses of predators to prey density and, more generally, consumer–resource dynamics (e.g. [17–20]). Meanwhile, we suggest that studies on trophic cascades have so far addressed the role of spatial scale from just a few out of several possible perspectives. Particularly, the literature does not take into account that trophic cascades may consist of multiple TIs that not only occur at different scales (scale-dependence), but also interact across scales. To explain our reasoning, we contrast three scenarios (figure 1b–d) of how a simple trophic cascade (predator–herbivore–primary producer, figure 1a) could play out across spatial scales. In the first scenario (figure 1b), TIs and cascading effects are scale invariant (i.e. the same relationships re-appear at different scales). Such fractal-like ecosystem properties are generally understudied, but have been found in spatial and temporal patterns in macro-ecology [21], biological networks [22,23] and recently also in pelagic microbial food webs [24].

Figure 1.

Conceptual model depicting a trophic cascade, where predators indirectly facilitate primary producers (dashed line) by controlling herbivore populations (a), across spatial scales in three different scenarios (b–d). (b) Interactions between trophic levels are scale invariant (i.e. in fractal-like systems); they do not depend upon, or interact, across scales. (c) Interactions between trophic levels are scale-dependent; they change in intensity (black arrows) and/or direction (red arrows) across spatial scales. For example, predators control over grazers acts at larger scales, while grazer control over primary producers acts at smaller scales. (d) CSIs; TIs are not only scale-dependent but interact across scales. For example, effects of predators at one scale may influence (strengthen or weaken) TIs at another scale.

In the more commonly studied scenario (figure 1c), TIs are scale-dependent (i.e. they change in strength and/or direction with scale). Organisms from different trophic levels typically differ in size and mobility, and therefore experience and use habitats at different spatial scales [25,26]. Consequently, scale-dependent patterns can arise, where different drivers dominate at different ‘process resolution’ (i.e. the smallest scale of spatial variation in a driving variable that affects the outcome of the process, sensu [27]), and TIs vary in intensity and even direction with scale [28,29]. Scale-dependence is pervasive in ecology, and can strongly influence consumer–resource dynamics (e.g. [20,29]). For example, predator–prey relationships can be positive at large scales (e.g. across productivity gradients) but negative at small scales (due to top-down control) [30,31].

In the arguably least explored scenario (figure 1d), we propose that TIs may not only be scale-dependent, but that TIs at one scale can interact with (influence) TIs at another scale: a cross-scale interaction (CSI). CSIs are defined as processes at one spatial or temporal scale that interact with (strengthen or weaken) processes at another scale, and often result in emergent system properties such as nonlinear threshold dynamics [32,33]. CSIs have been found to explain, for example, spatial patterns in biodiversity [34], spread of wildfire [35], and the effect of wetlands on lake nutrient concentrations [33]. To the best of our knowledge, their potential role for trophic cascades remains unexplored until now.

Given the large consequences of trophic cascades, and the potential for threshold dynamics resulting from CSIs, we suggest that assessing explicitly the role of spatial scale in general, and the potential for CSIs in particular, will benefit the understanding of trophic cascades. Consequently, we studied the role of spatial scale for trophic cascades using food webs in shallow coastal bays of the Baltic Sea as a model. There, fish exclusion experiments suggest that piscivorous fish (perch, Perca fluviatilis; pike, Esox lucius) generate trophic cascades that reduce the biomass of epiphytic, filamentous algae by feeding on mesopredatory fish (three-spined sticklebacks, Gasterosteus aculeatus) and thereby facilitating algal-feeding epifaunal grazers [36–38]. However, mechanisms detected in small-scale and short-term experiments (e.g. trophic cascades) may not translate to large-scale processes, due to scale-dependence [19,20,30] and the innate complexity and spatio-temporal heterogeneity of natural ecosystems [39].

To investigate cascading effects across spatial scales, and the potential for cross-scale interactions (CSIs), we conducted a field survey at 139 stations spread across 32 bays. We sampled the main components of the food web (piscivorous fish, mesopredatory fish, epifaunal grazers, epiphytic algae, habitat-forming vegetation) and key abiotic factors. As fish mobility encompasses the between-bay scale, but herbivore–algae–plant interactions should manifest at finer scales [40], we explicitly included two spatial scales in the analyses: a larger ‘bay scale’ (across bays, km²), and a smaller ‘station scale’ (nested within bays, m²). We then tested alternative hypotheses about top-down and bottom-up regulation using piecewise path analysis, a form of structural equation modelling with the ability to solve complex multivariate relationships among interrelated variables [41,42] and incorporate multiple spatial scales within the same causal framework [43,44]. To support the hypotheses of key TIs, we also analysed the presence of the mesopredator three-spined stickleback in the stomachs of piscivorous fish, and assessed predation intensity on grazers using a tethering experiment.

To investigate the occurrence of CSIs, we specifically tested whether bay-level piscivorous fish biomass (a key driver at bay scale) affected the station-scale relationship between grazers and epiphytic algae.

2. Material and methods

(a). Study area

The Baltic Sea is one of the largest bodies of brackish water on the Earth, hosting species of marine, brackish and freshwater origin. Strong latitudinal and offshore–inshore gradients in salinity, temperature and wave exposure, combined with vast rocky archipelagos, result in a high diversity of communities and habitats. Shallow bays host diverse communities of aquatic vegetation (macroalgae, charophytes and angiosperms) and associated macro-invertebrates [45], and function as important spawning and recruitment areas for many coastal fish species, including Eurasian perch (Perca fluviatilis), northern pike (Esox lucius) and three-spined stickleback (Gasterosteus aculeatus) [46].

(b). Field survey

The field survey was conducted in May–June 2014 and covered 32 shallow bays situated along a 360 km stretch of the central Swedish Baltic Sea coast (figure 2). The bays were situated more than 10 km apart (water distance), and encompassed gradients in (i) topographic openness to the sea, (ii) wave exposure, (iii) distance from the open sea and (iv) nutrient loading.

Figure 2.

Map of the Swedish central Baltic Sea coast, showing the locations of the 32 sampled bays (black dots). Axis labels are latitude and longitude.

Fish communities were surveyed using Nordic survey gillnets (European Union standardized method EN 14757: 2005). Four to five gillnets were set out in each bay overnight (between 16.00–19.00 and 7.00–10.00). All fish caught were identified to species (electronic supplementary material, appendix A), measured (total length, cm) and counted. Individual biomass was calculated using length : weight conversion factors (Swedish national database for coastal fish, http://www.slu.se/kul). Catch per unit effort (CPUE) was calculated as biomass (kg) per net and night of piscivores (perch and pike pooled), three-spined stickleback (the dominant mesopredator in the system, with the potential to control macroalgal grazers [38,47]) and roach (Rutilus rutilus), another common mesopredator feeding mainly on gastropods [37]. Stomachs of perch (n = 634) and pike (n = 34) were dissected and the relative contribution (percentage volume) of three-spined stickleback to total stomach content was estimated visually [48]. In half of the bays, we also used a tethering experiment to estimate predation intensity on Gammarus spp., a commonly occurring grazer taxon (see the electronic supplementary material, appendix B for detailed methods and results).

Vegetation cover and biomass, and biomass of epifauna and epiphytic algae, were surveyed at three to six stations per bay, defined as 5 m-diameter areas of sea-bottom at 0.5–3 m depth, placed greater than or equal to 30 m apart. The percentage cover of macroscopic vegetation (excluding ephemeral macroalgae, see the electronic supplementary material, appendix C) was visually estimated by a snorkeller, within three randomly placed 0.5 × 0.5 m frames. Vegetation, algae and epifauna were collected within a randomly placed 0.2 × 0.2 m frame attached to a 1 mm-mesh bag. In the laboratory, vegetation and epiphytic algae were identified (electronic supplementary material, appendix C) and their dry biomass determined (60°C for 48 h). Epifaunal macroalgal grazers were identified (electronic supplementary material, appendix D), measured (body length, mm), and their biomass estimated as gram ash-free dry mass using taxon-specific length : AFDM correlations [49].

To estimate the influence of environmental forcing on different trophic levels, nine abiotic factors known to affect bay biota were quantified. At each station, water temperature and salinity were measured using a Multi 340i voltmeter (WTW, Germany). Thereafter, a water sample was collected at 0.5 m depth between 16.00 and 19.00, filtered through a 0.45 µm glass-fibre filter (Sarstedt, Germany), and frozen. Concentrations of total and dissolved nitrogen and phosphorus (µg l⁻¹) were later measured using segmented flow colorimetric analysis [50] with the Alpkem FlowSolution IV system from OI Analytical.

Bay topographic openness (Ea, dimensionless) was estimated as Ea = 100 At/a, where At is the smallest cross-sectional area connected to the sea (calculated from field measurements of inlet depth and width) and a is the bay surface area, estimated from Google Earth satellite images [51]. Surface wave exposure (m² s⁻¹) was estimated at station and bay level using a simplified wave model (25 m resolution), combining fetch calculations with wind conditions while accounting for diffraction effects [52]. Finally, distance from the open sea (a proxy for offshore influence) was calculated as the shortest water distance (m) from the baseline (the starting point for defining territorial sea, found as straight lines between the outermost islands in nautical charts) to the opening of each bay (using a 25 m resolution cost distance technique in GIS).

(c). Path analysis

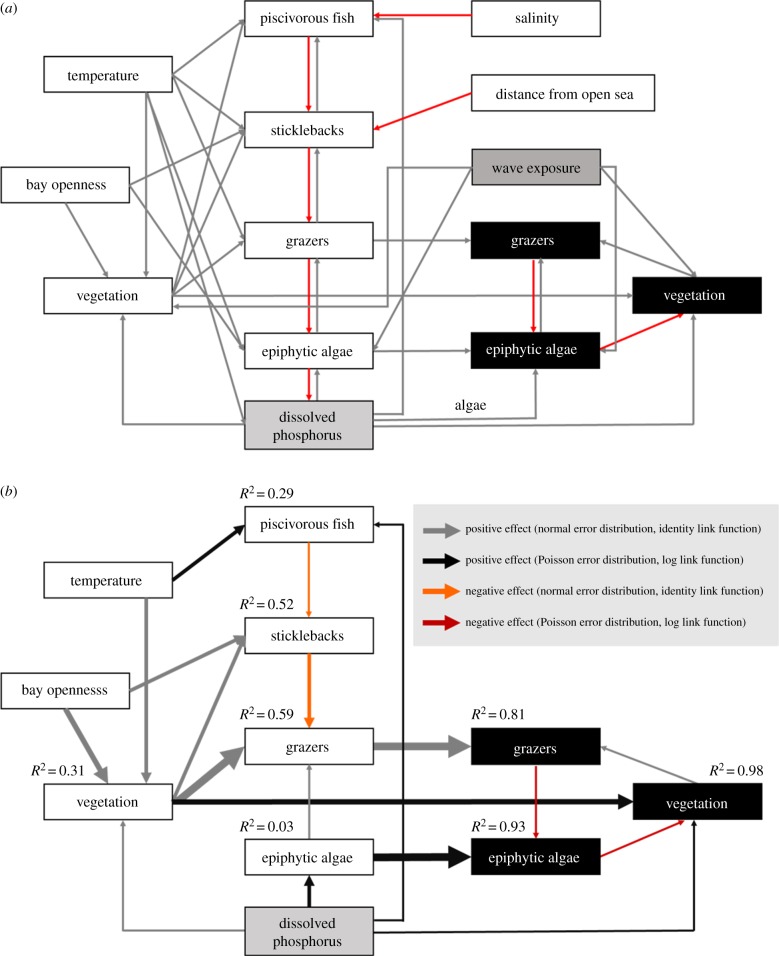
To explore the importance of trophic cascades, and how these propagate within or across spatial scales, we first formulated alternative hypotheses about the integrated functioning of the ecosystem (figure 3a). We hypothesized that (i) temperature affects all trophic levels (metabolic theory of ecology [53]), (ii) high salinity negatively affects the freshwater perch and pike [54], (iii) topographic openness and wave exposure increases biomass of stickleback [47], total vegetation and epiphytic algae [55], (iv) stickleback biomass decreases with distance from the open sea (longer migration distance [47]), (v) nutrient load increases piscivore biomass (exploitation ecosystem hypothesis [56]) and benefit algae and plants [57], (vi) vegetation facilitates piscivorous fish, sticklebacks and grazers by providing substrate and shelter [13], and (vii) epiphytic algae negatively affect habitat-forming vegetation by competing for light and nutrients [58]. We also tested the hypotheses that (viii) predation effects are influenced by habitat complexity [59,60], by incorporating interactive effects of vegetation cover and piscivore biomass on sticklebacks, and of vegetation cover and stickleback biomass on grazers. Finally, we hypothesized that (ix) trophic levels are top-down versus bottom-up regulated, resulting in negative or positive collinearity between adjacent trophic levels, respectively.

Figure 3.

(a) Schematic of all variables and paths included in the models. White, black and grey boxes indicate variables estimated at bay, station and both scales, respectively. Grey arrows represent positive effects, and red arrows are negative effects. (b) Best-supported structural equation models representing significant relationships between trophic levels and environmental factors at bay and station scale. Arrow widths are proportional to the standardized path coefficients. Marginal R²-values are shown for endogenous variables.

After formulating the conceptual model, we used path analysis to test the significance of specific combinations of paths corresponding to each hypothesis. Models included six exogenous variables: (i) water temperature, (ii) salinity, (iii) topographic openness (log-transformed to reduce skewness), (iv) wave exposure (log-transformed), (v) distance from the open sea and (vi) dissolved phosphorus (which explained more of the variability in the response variables than dissolved nitrogen, total phosphorus and total nitrogen). Endogenous variables included biomass of (i) piscivorous fish (perch and pike pooled), (ii) three-spined stickleback (the dominant mesopredator), (iii) grazers and (iv) epiphytic algae (percentage of total above-ground vegetation biomass), and (v) percentage cover of total vegetation (excluding epiphytic algae). As preliminary analyses did not show any significant relationships between roach and grazer biomass, roach biomass was excluded.

Our design yielded data at two hierarchical levels; three to six stations nested within each of 32 bays (139 stations in total). Multi-level relations were incorporated in our models by allowing station-level observations to depend on bay-level parameters (following [44]). First, we sought to explain variation in the endogenous variables measured at bay level according to our hypotheses, following [43]. Next, we fitted a station-level model including all observations at station level, and bay averages of all trophic levels as exogenous predictors. Owing to the hierarchical nature of our data and the distributional properties of our variables, we ran the path analyses (a linked set of generalized linear mixed models) using the piecewiseSEM package, v. 1.1.1 [42] in Rv. 3.2.3 (R Development Core Team, 2015).

Prior to model fitting, we graphically examined distributional properties of all variables. When normality assumptions were violated, a Poisson or a negative binomial error distribution with log-link function was applied. To assure independence, the random factor ‘bay’ (32 levels) was included in the station-level analysis. Collinearity in each component model was checked by calculating the variance inflation factor (VIF) for each predictor. As temperature and salinity were collinear (VIF ≥ 2), they were included in separate models.

Finally, we compared the relative fit of alternative piecewise models to the data, first using the test of directional separation [61], which produces a χ²-distributed Fisher's C statistic, where p-values of more than 0.05 indicate adequate fit, and second, through comparison of AIC values [62]. For the best-fitting (final) models, we calculated standardized path coefficients (scaled by mean and variance) to compare the relative importance of predictors [41]. Marginal R²-values for endogenous variables in the station-level model were estimated following [63]. Model validation was performed visually by plotting residuals versus fitted values for each component model.

(d). Cross-scale interaction

We investigated the presence of CSIs by statistically assessing whether piscivore biomass—a key ecosystem driver at the bay scale (see ‘Results’)—influenced the station-scale relationship between grazers and epiphytic algae (see [33] for a similar approach). We did so by testing the effects of the interaction between bay-level piscivore biomass and station-level grazer biomass (VIF values of less than or equal to 2) on station-level epiphytic algae biomass, using a generalized linear mixed model with Poisson error distribution, log-link function and ‘bay’ as random factor.

(e). Effects of piscivores on grazer assemblage composition

Our CSI analysis showed that effects of grazer biomass on algae at station scale depended on piscivore biomass (see ‘Cross-scale interaction’ below). To investigate whether a shift in grazer assemblage composition (e.g. from dominance of inefficient to efficient grazer taxa) could help explain the CSI effect (e.g. [63]), we used a permutated multivariate analysis of variance (PERMANOVA), and tested whether grazer composition (percentage of each taxon to total grazer biomass) was influenced by piscivore biomass, including three covariates: plant cover, salinity and bay openness (for detailed methods and results, see the electronic supplementary material, appendix E).

3. Results

(a). Path analysis: trophic cascade across spatial scales

Our path analyses suggest that high biomass of piscivores had cascading effects down the food web through scale-dependent TIs, which ultimately reduced algal biomass. Our best-supported bay- and station-scale models fitted the data well (bay scale: Fisher's C = 27.57, p = 0.120; station scale: Fisher's C = 14.87, p = 0.387; figure 3b). At the bay scale, piscivore biomass negatively affected stickleback biomass, which in turn reduced grazer biomass (table 1 and figure 3b). Moreover, these TIs were well supported by (i) the significant contribution of stickleback to piscivore stomach content (electronic supplementary material, appendix F) and (ii) the tethering experiment, where bay-level stickleback biomass alone explained predation rates on tethered grazers (electronic supplementary material, appendix B). As a consequence of these linked interactions, high piscivore biomass indirectly increased bay-level grazer biomass. Furthermore, bay-level algal biomass increased with stickleback biomass (table 1), a link included in the model as a correlated error, given the lack of theoretical support for a direct causal relationship. At the bay level, this relationship did not appear to be mediated by reduced grazing pressure on epiphytic algae. Instead, grazer biomass increased with epiphytic algae at the bay scale. At the station scale, however, grazer biomass suppressed epiphytic algae. Also, epiphytic algae negatively affected vegetation cover, a link that was not significant at bay scale, but decreased the model AIC value from 79.6 to 73.6 when modelled as correlated error (table 1 and figure 3b). In summary, the strength and the direction of some paths was scale-dependent, suggesting that TIs perform differently at different scales.

Table 1.

Path coefficients (single-headed arrow) and correlated errors (double-headed arrow) from the best-supported structural equation model (figure 3a). The last column shows the link function for each component model (see ‘Material and methods’ for details).

	unstandardized coefficients		standardized coefficients
effects	estimate	s.e.	estimate	s.e.	p-value	link function
bay scale
temperature → piscivorous fish	0.12	0.02	0.37	0.05	<0.001	log
dissolved phosphorus (bay) → piscivorous fish	3.19	0.75	0.23	0.05	<0.001	log
bay openness (log-transformed) → sticklebacks	0.07	0.01	0.32	0.06	<0.001	identity
top predators → sticklebacks	−0.07	0.01	−0.20	0.03	<0.001	identity
vegetation (bay) → sticklebacks	4 × 10−3	1 × 10−3	0.29	0.08	<0.001	identity
epiphytic algae (bay) ↔ sticklebacks	0.79	0.40	0.26	0.13	0.045	identity
dissolved phosphorus (bay) ↔ sticklebacks	0.63	0.27	0.14	0.06	0.023	identity
sticklebacks → grazers (bay)	−0.03	0.01	−0.27	0.06	<0.001	identity
vegetation (bay) → grazers (bay)	1 × 10−3	9 × 10−5	0.86	0.06	<0.001	identity
epiphytic algae (bay) → grazers (bay)	3 × 10−4	1 × 10−4	0.01	4 × 10−3	0.010	identity
dissolved phosphorus (bay) → epiphytic algae (bay)	4.71	1.85	0.34	0.13	0.011	log
bay openness (log-transformed) → vegetation (bay)	8.69	1.20	0.55	0.08	<0.001	identity
temperature → vegetation (bay)	3.22	0.68	0.38	0.08	<0.001	identity
dissolved phosphorus (bay) → vegetation (bay)	69.21	26.08	0.20	0.08	0.009	identity
epiphytic algae (bay) ↔ vegetation (bay)	−0.21	0.11	−0.01	5 × 10−3	0.065	identity
station scale
grazers (bay) → grazer (station)	0.99	0.06	0.76	0.04	<0.001	identity
vegetation (station) → grazers (station)	8 × 10−6	2 × 10−6	2 × 10−4	3 × 10−5	<0.001	identity
epiphytic algae (bay) → epiphytic algae (station)	0.09	0.01	1.46	0.17	<0.001	log
grazers (station) → epiphytic algae (station)	−2.76	0.91	−0.13	0.04	0.002	log
dissolved phosphorus (station) ↔ epiphytic algae (station)	−7.21	0.75	−0.69	0.07	<0.001	log
vegetation (station) → vegetation (station)	0.04	0.01	0.95	0.18	<0.001	log
dissolved phosphorus (station) → vegetation (station)	0.78	0.20	0.08	0.02	<0.001	log
epiphytic algae (station) → vegetation (station)	−0.01	1 × 10−3	−0.01	1 × 10−3	<0.001	log

(b). Path analysis: environmental forcing

As expected, water temperature increased piscivore biomass and vegetation cover (table 1 and figure 3b), while topographic openness increased vegetation cover and stickleback biomass (table 1 and figure 3b). Contrary to predictions, salinity did not affect piscivore biomass, and although we found a significant negative effect of distance from open sea on stickleback biomass, the model including this path fitted the data poorly (Fisher's C = 58.4, p = 0.001), and had considerably higher AIC than the best model (106.4 versus 73.57, respectively). Dissolved phosphorus increased vegetation cover at both bay and station scales, and epiphytic algae and piscivore biomass at bay scale (table 1 and figure 3b). Furthermore, the best-supported model contained correlated errors between dissolved phosphorus and (i) stickleback biomass, a positive correlation most probably reflecting covariation with unmeasured forcing variables, and (ii) station-level algae biomass (negative correlation), suggesting local depletion of nutrients around areas with high algal biomass (table 1). Finally, wave exposure had no influence (significant paths) at bay or station scale.

(c). Path analysis: the role of vegetation as habitat

Contrary to expectations, vegetation cover did not influence piscivore biomass, but increased both stickleback and grazer biomass (table 1 and figure 3b), most probably by providing habitat and shelter. The vegetation effect on grazers was among the strongest found at bay scale, and was also observed at station scale. Combined with the negative effect of grazers on epiphytic algae, and the negative effect of epiphytic algae on vegetation, these paths suggest a mutual facilitation (positive feedback) between grazers and vegetation. Finally, the hypothesis that habitat complexity mediates (interacts with) predation was not supported, as no significant interaction effects between vegetation cover and piscivore or stickleback biomass were found.

(d). Cross-scale interaction

The station-scale path model showed that the relationship between grazers and epiphytic algae was on average negative (see above). However, the additional cross-scale analysis revealed that the grazer–algae relationship actually shifted from positive to negative with increasing piscivore biomass (interaction effect between grazer and piscivore biomass: likelihood ratio test statistic = 129.76, p < 0.001; figure 4). Below a piscivore biomass of around 2 kg CPUE, grazer biomass increased with epiphytic algae biomass (indicating bottom-up regulation). However, above this apparent biomass threshold, the grazer–algae relationship turned increasingly negative (indicating top-down control) with increasing piscivore biomass. This suggests that high grazer biomass at the station scale more effectively controlled algae in bays with higher rather than lower piscivore biomass: a cross-scale interaction.

Figure 4.

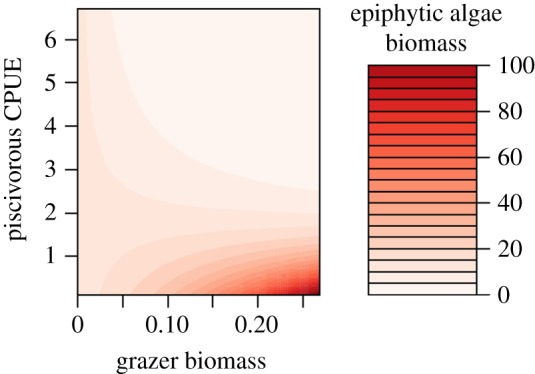
Relationship between station-level epiphytic algae (% biomass of total above-ground vegetation) and grazer biomass (g AFDW), and piscivore biomass (CPUE, kg per net night). When piscivore biomass is greater than 2, epiphytic algae biomass decreases steeply with increasing grazer biomass (indicative of top-down control). When piscivorous biomass is less than 2, epiphytic algae and grazer biomass instead correlate positively (bottom-up control).

(e). Effects of piscivores on grazer assemblage composition

Results from the PERMANOVA analysis showed a shift in the grazer assemblage composition with increasing piscivore biomass (electronic supplementary material, appendix E). In bays with low piscivore biomass, Idotea spp. and Gammarus spp. dominated, while in bays with high piscivore biomass, the assemblages were instead dominated by a mix of freshwater grazers, including Asellus aquaticus (Isopoda, Crustacea), Hydroptila sp. larvae (Trichoptera) and chironomid larvae.

4. Discussion

By combining (i) an extensive food-web survey along gradients of multiple abiotic factors, (ii) the assessments of two key TIs and (iii) causal inference, we assessed the strength of trophic cascades across two spatial scales, and the occurrence of CSIs, in shallow bay ecosystems. Our results support the occurrence of a four-level trophic cascade (from piscivorous fish to epiphytic algae) that results from scale-dependent TIs and, possibly, a cross-scale interaction between piscivore biomass at bay scale, and grazer control over algal biomass at station scale. At bay scale, high biomass of perch and pike regulated three-spined stickleback, a major mesopredator in these ecosystems [47], which in turn regulated predation intensity on, and biomass of, algal grazers. At bay scale, grazer biomass increased, albeit weakly, with algal biomass. Meanwhile, at station scale, grazers reduced algal biomass and facilitated vegetation, which in turn had positive effects on grazers. Moreover, the station-scale relationship between grazer and epiphytic algae changed direction and strength with increasing biomass of piscivorous fish, indicating the presence of a cross-scale interaction.

Small-scale experimental exclusion of predatory fish has been shown to increase stickleback abundance, reduce grazer biomass and boost algal biomass [36,38,39]. Our results not only show that these mechanisms are strong enough to influence natural food webs and ecosystems along a highly heterogeneous coastline; they also suggest that these TIs are scale-dependent, and that they may interact across scales. Both theory [20] and empirical data [27] suggest that consumer–resource dynamics depend on the spatial scale of resources and species habitat use. While scale-dependent interactions are well recognized in the literature, CSIs have received much less interest, but could play a pivotal role by generating emergent properties like thresholds or ‘tipping points’. For example, the effect of wetland size on lake phosphorus can shift from positive to negative with changing levels of regional agricultural intensity [33], and rapid wildfire spread in forests can be explained by the interaction between local scale features and large-scale connectivity [35]. Here, we found that the station-scale biomass of epiphytic algae depended on an interaction between bay-level piscivore biomass and the station-scale biomass of grazers. To the best of our knowledge, our study is the first to suggest that CSIs can also affect TIs and trophic cascades, and determine a shift between top-down and bottom-up control. One potential mechanism behind this CSI could be the demonstrated shift in the grazer assemblage composition with increasing piscivore biomass, from relatively inefficient grazers such as Idotea spp. in bays with low piscivore biomass, to dominance of more efficient grazers of ephemeral algae (e.g. Asellus, Chironomidae) in bays with high piscivore biomass [64]. Another potential explanation could be non-consumptive effects of abundant mesopredatory stickleback at low piscivore biomass (landscape of fear) changing grazer behaviour from feeding to hiding, thus boosting algal biomass. Such behavioural effects are increasingly recognized to affect both green and brown food webs [65,66].

Environmental forcing also influenced shallow bay communities, particularly at the larger scale. Piscivore biomass increased with both temperature and nutrient loading, in line with theory [53,56] and empirical studies [54]. Bay openness increased stickleback biomass and was the strongest predictor of vegetation cover, followed by temperature and dissolved phosphorus (see also [46,53]). On the one hand, the strong environmental forcing supports the assumption that abiotic conditions determine spatial variation at large scales, while small-scale variation is predominantly driven by biotic interactions such as competition, predation and facilitation [67]. On the other hand, even after accounting for environmental forcing, we found clear evidence of top-down control from piscivorous fish down to grazers across the 32 bays, together covering considerable abiotic variability and a 360 km stretch of the coast. Consequently, biotic interactions involving piscivorous fish appear to fundamentally influence ecosystem structure and function also at large scales.

The results from our extensive field survey add to a growing body of evidence that piscivorous fish play a key role for coastal ecosystem health, by reducing biomass of ephemeral algae and, potentially, buffering effects of eutrophication [68–70]. Our study also suggests that these effects depend on a threshold piscivore biomass (here, around 2 kg per net night). Predatory fish are also important for commercial and recreational fisheries in the Baltic Sea and elsewhere [71]. Consequently, ecosystem-based management actions [72] that maintain or enhance their stocks could help maintain multiple ecosystem services and benefits to society [73].

Our finding that TIs not only occur at different scales (dictated by the scale at which the organisms function) but also appear to interact (in a statistical sense) across spatial scales is unlikely to be restricted to shallow bay ecosystems. Instead, we hypothesize that CSIs is a general phenomenon in food webs that link organisms acting at different scales, and that the explicit consideration of these interactions could help us better understand other well-known trophic cascades [4]. Consequently, where similar types of data are available for other ecosystems, our approach of explicitly including the spatial scale of the natural history of key species, and their potential interactions across those scales, could be applied to further refine the understanding of the processes at work and to design better monitoring programmes.

Going beyond trophic cascades, our study echoes the conceptual arguments of hierarchy theory and the discontinuity hypothesis, which emphasize the hierarchical organization of ecosystems across discrete spatio-temporal scales (see [74,75] for reviews). Even if different processes dominate at specific scales, effects and disturbances could propagate up or down the hierarchy. For instance, the disruption of the grazer–epiphyte–vegetation feedback loop at station scale (e.g. following nutrient enrichment or mesopredator release) may lead to an abrupt decline of foundation species (vegetation) at bay scale. From a management perspective, this translates into two imperatives: to monitor the right ecosystem components at the right spatial scales, and to identify and steer away from potential thresholds. In summary, a more explicit consideration of the hierarchical spatial dimension of food webs in general, and the potential for CSIs in particular, is a crucial step to better understand the processes at work, to forecast ecosystem dynamics, and to effectively monitor, manage and preserve natural ecosystems and the services they provide.

Ethics

The fish sampling procedures applied in the project were judged and approved by the Ethical Board on Animal Experiments of the County Court of Uppsala, Sweden, permit C 139/13.

Data accessibility

Data are available from the Dryad Digital Repository (http://dx.doi.org/10.5061/dryad.v726t) [76].

Author's contribution

S.D. and J.S.E. developed the idea, designed the study and drafted the paper. S.D. analysed the data. M.v.R., P.J. and Å.N.A. conducted the laboratory work. All authors collected the data and revised previous versions of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This study is a product of project Plant-Fish (www.plantfish.se) and was funded by Formas (2013-1074), HM Carl XVI Gustaf's Foundation for Science and Education (2014-0002), the Baltic Sea 2020 foundation, the Baltic Sea Centre (Askö grants) and in-kind support from Groningen University (The Netherlands).