Attention model of binocular rivalry

Significance

Binocular rivalry provides a unique opportunity to characterize intrinsic neural dynamics of cortical processing. A computational model was developed as a parsimonious explanation of the empirical phenomena of rivalry for which there was no previous explanation. The key idea in the model is that rivalry relies on interactions between sensory processing and attentional modulation with distinct dynamics and selectivity. Bifurcation theory was used to identify the parameter regime in which the behavior of the model was consistent with empirical findings. The model explained a wide range of phenomena, including (i) that binocular rivalry requires attention, (ii) that different perceptual states emerge when the two images are swapped between the eyes, and (iii) how dominance duration changes as a function of stimulus input strength.

Abstract

When the corresponding retinal locations in the two eyes are presented with incompatible images, a stable percept gives way to perceptual alternations in which the two images compete for perceptual dominance. As perceptual experience evolves dynamically under constant external inputs, binocular rivalry has been used for studying intrinsic cortical computations and for understanding how the brain regulates competing inputs. Converging behavioral and EEG results have shown that binocular rivalry and attention are intertwined: binocular rivalry ceases when attention is diverted away from the rivalry stimuli. In addition, the competing image in one eye suppresses the target in the other eye through a pattern of gain changes similar to those induced by attention. These results require a revision of the current computational theories of binocular rivalry, in which the role of attention is ignored. Here, we provide a computational model of binocular rivalry. In the model, competition between two images in rivalry is driven by both attentional modulation and mutual inhibition, which have distinct selectivity (feature vs. eye of origin) and dynamics (relatively slow vs. relatively fast). The proposed model explains a wide range of phenomena reported in rivalry, including the three hallmarks: (i) binocular rivalry requires attention; (ii) various perceptual states emerge when the two images are swapped between the eyes multiple times per second; (iii) the dominance duration as a function of input strength follows Levelt’s propositions. With a bifurcation analysis, we identified the parameter space in which the model’s behavior was consistent with experimental results.

Binocular rivalry is a visual phenomenon in which perception alternates between incompatible monocular images presented to the two eyes. During binocular rivalry, perceptual experience evolves dynamically while the external inputs are held constant. Binocular rivalry thereby provides an opportunity to gain insights about the intrinsic cortical computations underlying visual perception (1, 2).

In conventional models of binocular rivalry, the competition between two percepts has been characterized as mutual inhibition between two populations of neurons selective for each of the two stimuli (3–11). Notwithstanding the differences in their details, these models consider the neural processing underlying binocular rivalry to be an automatic process. These models predict, therefore, that the dynamics of binocular rivalry are influenced mainly by bottom-up sensory inputs.

Converging experimental evidence has shown, however, that binocular rivalry also depends on attention (for a review, see ref. 12). First, EEG has been used to measure a neural correlate of the perceptual alternations during binocular rivalry when observers pay attention to the rival stimuli (13). However, this rivalry-induced modulation of the EEG signal is largely or entirely eliminated when attention is diverted away from the stimuli (14). Second, behavioral experiments comparing the perceptual consequences induced by attended and unattended rival stimuli also support the notion that binocular competition in general, and binocular rivalry in particular, requires attention (15–18). These findings demonstrate that visual attention, the neural and cognitive process that selectively prioritizes information under natural viewing conditions, is critical for binocular rivalry.

Here, we propose a computational model of binocular rivalry in which there are two processes that drive perceptual competition: attention and mutual inhibition. (i) Attention: According to the model, the two rival stimuli compete for attentional resources. Attention is modeled as multiplicative gains (attention gain factors; ref. 19) that fluctuate between neural populations selective for the two rival stimuli. At a given moment, the stimulus associated with stronger sensory responses attracts a greater share of attention and reduces the attention allocated to the other stimulus. This stimulus-driven attentional modulation is presumed to be active when observers attend the stimuli, but silent when attention is diverted. (ii) Mutual inhibition: In the model, mutual inhibition is mediated through opponency neurons (20). The opponency neurons take conflicting information between two eyes as inputs and suppress the activity of monocular neurons that respond to one or the other eye.

We show that the model exhibits three experimental hallmarks of binocular rivalry: (i) Rivalry (i.e., response alternations between two competing neural representations) occurs for attended stimuli with interocular conflict, but not without interocular conflict and not for unattended stimuli (12, 14–16). (ii) When the stimuli are rapidly swapped back and forth between the two eyes, the simulated percept either follows one image across the swapping or it follows the stimuli in one eye, depending on the temporal characteristics of the stimuli (21–24). (iii) The simulated dominance duration changes as a function of stimulus strength, following Levelt’s propositions (25, 26). Bifurcation analysis was used to explore all of the possible behaviors of the model as a function of the strength of sensory inputs, the amount of attentional modulation, and the amount of mutual inhibition. We identify the parameter regime in which the behavior of the model was consistent with empirical findings. Finally, we show that previous computational models of bistable perception fall short of explaining this full suite of phenomena.

Methods

Model.

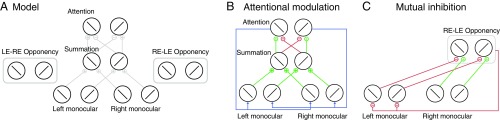
The model had three classes of neurons responsible for sensory representation, attentional modulation, and mutual inhibition, respectively (Fig. 1). The response of each individual neuron in the model is intended to represent the mean activity (instantaneous firing rate) of an ensemble of neurons with similar response properties. The responses of the neurons were computed by the same canonical motif, divisive normalization (27). The model is intended to characterize neural activity in visual cortex in terms of the signal-processing computations that are performed, not in terms of the underlying circuit, cellular, molecular, and biophysical mechanisms. For example, we do not intend for individual elements in the model to be interpreted as specific cell types, and the various model parameters (e.g., orientation selectivity, time constants) might emerge from a neural circuit rather than being intrinsic biophysical properties of individual neurons. See Table S1 for the values of all of the model parameters.

Fig. 1.

Model structure. (A) General structure of the model. For illustration, only some connections between neurons are depicted. The details of the attentional modulation and mutual inhibition are depicted in B and C. (B) Attentional modulation. There are two attention neurons selective for orthogonal orientations. Each attention neuron receives excitatory inputs from the binocular summation neuron that is selective for the same orientation, and suppressive inputs for different orientation. Monocular neurons selective for the same orientation receive the same attention gain factor (blue lines) determined by the response of the attention neuron with the same orientation preference. (C) Mutual inhibition. There are two groups of opponency neurons (RE–LE and LE–RE). Here, only the RE–LE opponency neurons are illustrated. Opponency neurons compute the response difference between the two eyes for a particular orientation. The left-eye (right-eye) monocular neurons are inhibited by the RE–LE (LE–RE) opponency neurons.

Table S1.

Parameter values

Parameter	Values for simulation	Description
$D$	0.5	Input strength
$n$	1 for monocular neurons; 2 for all of the other neurons	Exponent
$\sigma$	0.2 for attention neurons; 0.5 for all of the other neurons	Suppression constant
$\alpha$	2	Scaling factor of monocular neurons
${\tau }_s$	10 (ms)	Time constant of monocular and binocular summation neurons
${\tau }_a$	150 (ms)	Time constant of attention neurons
${\tau }_o$	20 (ms)	Time constant of opponency neurons
${\tau }_h$	2,000 (ms)	Time constant of adaptation
$w_a$	0.6	Weight of attentional modulation
$w_o$	0.65	Weight of mutual inhibition
$w_h$	2	Weight of adaptation

Sensory representations.

Sensory representations consisted of three populations: two monocular [left eye (LE) and right eye (RE)] populations and one binocular-summation population. Each population contained two neurons, each selective for one of two orthogonal orientations.

The response of the left-eye monocular neuron R_l1 selective for orientation 1 was computed as follows:

$$\begin{array}{l}{\tau }_s\frac{d}{dt}{R}_{l1}=-R_{l1}+\frac{\alpha E_{l1}}{S_m+H_{l1}^n+{\sigma }^n}\\ E_{l1}=[D_{l1}^n-w_o{O}_r{]}_{+}[1+w_a{R}_{a1}{]}_{+}\\ S_m={\displaystyle \sum _{k=\mathrm{1,2}}{E}_{lk}}+{\displaystyle \sum _{k=\mathrm{1,2}}{E}_{rk}}\\ {\tau }_h\frac{d}{dt}{H}_{l1}=-H_{l1}+w_h{R}_{l1}.\end{array}$$ [1]

The responses of all four monocular neurons (R_l1, R_l2, R_r1, R_r2) are characterized by similar expressions in which the subscripts l and r specify left eye and right eye, respectively, and the subscripts 1 and 2 specify the two orientations. The first line is an equation for calculating the response over time in terms of excitatory drive (E), suppressive drive (S), and adaptation (H). The subsequent lines provide expressions for the excitatory drive, suppressive drive, and adaptation, respectively. The excitatory drive (E) was determined by the input (D). The amplitude of the input was assumed to increase monotonically with stimulus contrast. The excitatory drive was modulated by two factors. First, the pooled responses of the opponency neurons (O_r) that responded to the opposite eye (Mutual inhibition) were subtracted from the input. Second, the resulting activity after this subtractive suppression was multiplied by an attention gain factor (1 + w_aR_a1), in which 1 was the baseline attention gain, and R_a1 was the response of the attention neuron that was selective for the same orientation (Attentional modulation). The values of w_o and w_a determined the amount of subtractive mutual inhibition and attentional modulation, respectively. The notation $[{]}_{+}$ represents half-wave rectification. The suppressive drive (S) of each monocular neuron was the sum of the excitatory drives of all of the monocular neurons. The values of n and $\sigma$ determined the slope and the contrast gain of the contrast-response functions of the neurons, and $\alpha$ was a scaling factor that determined the maximum response. The value of ${\mathit{\tau }}_s$ was the time constant of the monocular and binocular summation neurons. The sensory neurons slowly self-adapted through the adaptation term H with time constant ${\tau }_h$ and magnitude w_h.

The response of the binocular summation neuron R_b1 selective for orientation 1 was computed as follows:

$$\begin{array}{l}{\tau }_s\frac{d}{dt}{R}_{b1}=-R_{b1}+\frac{E_{b1}}{S_{b1}+H_{b1}^n+{\sigma }^n}\\ E_{b1}={\left(R_{l1}+R_{r1}\right)}^n\\ S_{b1}=E_{b1}\\ {\tau }_h\frac{d}{dt}{H}_{b1}=-H_{b1}+w_h{R}_{b1},\end{array}$$ [2]

where the responses of both binocular neurons (R_b1, R_b2) are characterized by similar expressions in which the subscript b specifies that it is a binocular neuron, and the subscripts 1 and 2 specify the two orientations. The excitatory drive (E) summed the responses of monocular neurons selective for the same orientation. The suppressive drive (S) was the same as the excitatory drive. Similar to monocular neurons, binocular summation neurons self-adapted through the adaptation term H. Unlike a previous model (4) that used mutual inhibition between binocular neurons to model a swapping experiment, there was no mutual inhibition between binocular neurons in our model. The functions of the binocular summation neurons in our model were only to represent sensory responses and provide inputs to neurons in the attention layer.

Attentional modulation.

According to the model, attention gain fluctuated between two sensory representations when observers attended to the rival stimuli. Whichever orientation had stronger sensory responses, at any moment, received a greater share of attention gain. We implemented the model in this way because a competing stimulus in one eye can suppress a target in the other eye by increasing the attention gain for the orientation of the competitor while decreasing the attention gain of the target (17, 18).

There were two neurons in the attention layer selective for orthogonal orientations (Fig. 1 A and B). The response of the attention neuron R_a1 that preferred orientation 1 was computed as follows:

$$\begin{array}{l}{\tau }_a\frac{d}{dt}{R}_{a1}=-R_{a1}+\frac{E_{a1}}{S_a+{\sigma }_a^n}\\ E_{a1}={\left(R_{b1}-R_{b2}\right)}^n\\ S_a={\displaystyle \sum _{k=\mathrm{1,2}}[E_{ak}{]}_{+}}.\end{array}$$ [3]

We used a similar expression to compute the responses of the other attention neuron R_a2. The excitatory drive (E_a1) was the difference between the responses of two binocular-summation neurons. The two orientation-selective neurons in the attention layer showed a trade-off. When the response of one neuron (e.g., R_a1) was positive, the response of the other neuron (R_a2) was negative, and vice versa. Hence, depending on their preferred orientation, monocular neurons in sensory layers received attention gain that fluctuated around a baseline value (Eq. 1). The negative responses of the attention neurons can be accommodated with complementary pairs of neurons that are each half-wave rectified, analogous to standard models of ON- and OFF-center retinal ganglion cells. ${\tau }_a$ (=150 ms) was the time constant of attentional modulation.

Mutual inhibition.

Mutual inhibition was mediated through opponency neurons (20). There were four opponency neurons in total: a pair of left-minus-right (LE-RE) opponency neurons and a pair of right-minus-left (RE-LE) opponency neurons, each with a pair of neurons selective for orthogonal orientations (Fig. 1 A and C). The response of the RE-LE opponency neuron R_or1 selective for orientation 1 was computed as follows:

$$\begin{array}{l}{\tau }_o\frac{d}{dt}{R}_{or1}=-R_{or1}+\frac{E_{or1}}{S_{or}+{\sigma }^n}\\ E_{or1}={\left[R_{r1}-R_{l1}\right]}_{+}^n\\ S_{or}={\displaystyle \sum _{k=\mathrm{1,2}}{E}_{ork}}\\ O_r={\displaystyle \sum _{k=\mathrm{1,2}}{R}_{ork}},\end{array}$$ [4]

where the subscript o denotes that it is an opponency neuron, the subscript r indicates that it is the RE-LE opponency neuron (not an LE-RE opponency neuron), and the subscript 1 specifies the orientation preference. We used a similar expression to compute the responses of the other opponency neurons (R_or2, R_ol1, R_ol2). The excitatory drive of the opponency neurons was the difference of the responses between LE and RE monocular neurons. The value of S_or was the suppressive drive of both RL opponency neurons. ${\tau }_o$ (=20 ms) was the time constant of the opponency neurons. The response of the two RL opponency neurons were pooled as O_r and subtracted from the left-eye monocular neurons (Eq. 1). The subtractive suppression ($-w_o{O}_r$ in Eq. 1) was analogous to mutual inhibition in previous models (3–8). However, previous models exhibited response alternations (in a magnitude similar to the response alternations for rivalry stimuli) for stationary, monocular-plaid stimuli (Fig. 2B), inconsistent with perceptual phenomena. Here, instead, the subtraction was mediated by the opponency neurons, which elicited mutual inhibition only when conflicting orientation information was present between the eyes (see details in ref. 20). These opponency neurons have been proposed to play a role in other perceptual functions outside the context of rivalry (e.g., ref. 28).

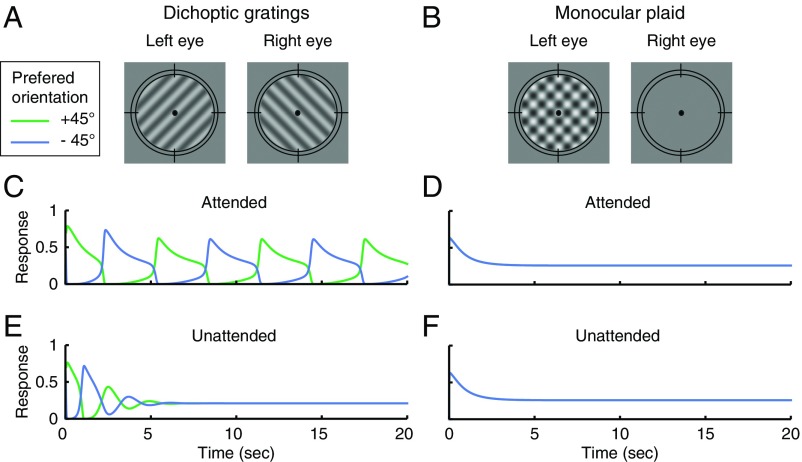
Fig. 2.

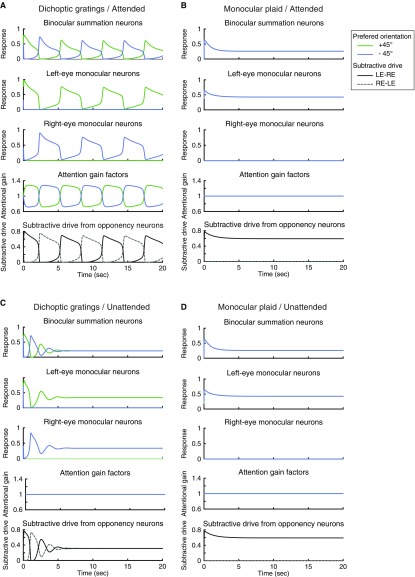
Simulated dynamics of binocular rivalry depends on attention. (A) Dichoptic gratings. (B) Monocular plaid. (C–F) The simulated responses of two binocular summation neurons. (C) Attended dichoptic gratings. (D) Attended monocular plaid. (E) Unattended dichoptic gratings. (F) Unattended monocular plaid. In D and F, the two summation neurons have the same responses so the blue and green curves overlap. The responses of neurons in monocular, attention, and opponency populations are illustrated in Fig. S2. The simulations for the binocular plaid condition are illustrated in Fig. S1C.

Noise.

A stochastic term, an Ornstein–Uhlenbeck process (8, 10), simulating neural noise, was added to the input drive for some of the simulations (Figs. 3A and 5B and Figs. S7 and S8): ${\tau }_n\frac{d}{dt}n=-n+\sigma \sqrt{2{\tau }_n}\xi \left(t\right)$, where ${\tau }_n=100\hspace{0.17em}\text{ms}$, $\sigma =0.02$, and $\xi \left(t\right)$ was a Gaussian white-noise process. We assumed that the EEG signal was a noisy version of the simulated neural responses. In addition to the neural noise, we simulated the EEG measurements (14) by adding low-pass–filtered Gaussian noise, representing measurement noise, to the responses of the binocular summation neurons (Fig. 3A).

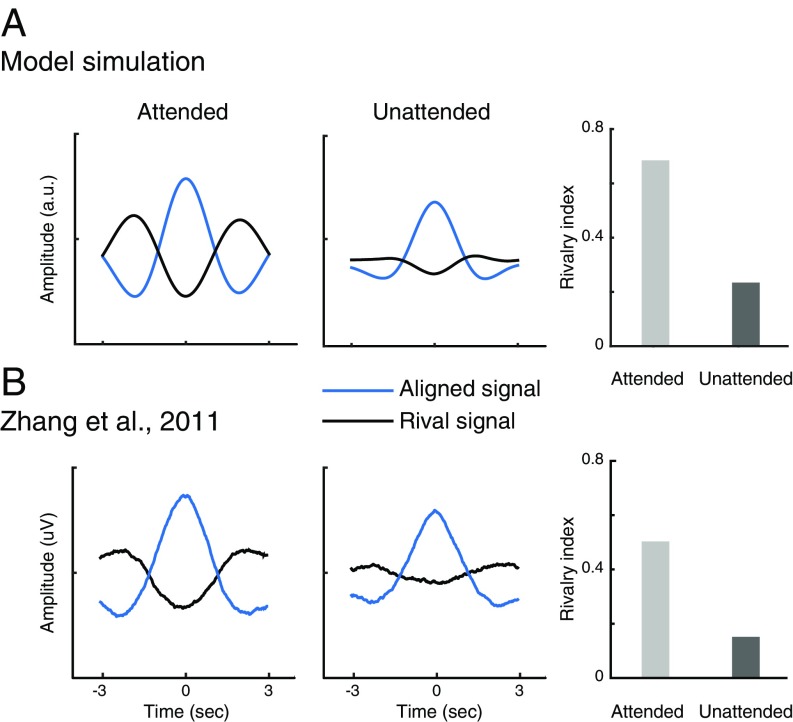
Fig. 3.

Dynamics of binocular rivalry depends on attention: EEG measurements and model simulation. (A) Simulated responses of binocular summation neurons. Blue curves, averaged neural responses aligned to the peak of the response of one of the binocular summation neurons. Black curves, averaged response of the other neuron in the same time window. Rivalry indices are computed by dividing the amplitude of the rival signal (black curve) by the amplitude of the corresponding aligned signal (blue curve). Light-gray bar, attended. Dark-gray bar, unattended. (B) Empirical results measured with EEG (replotted from ref. 14).

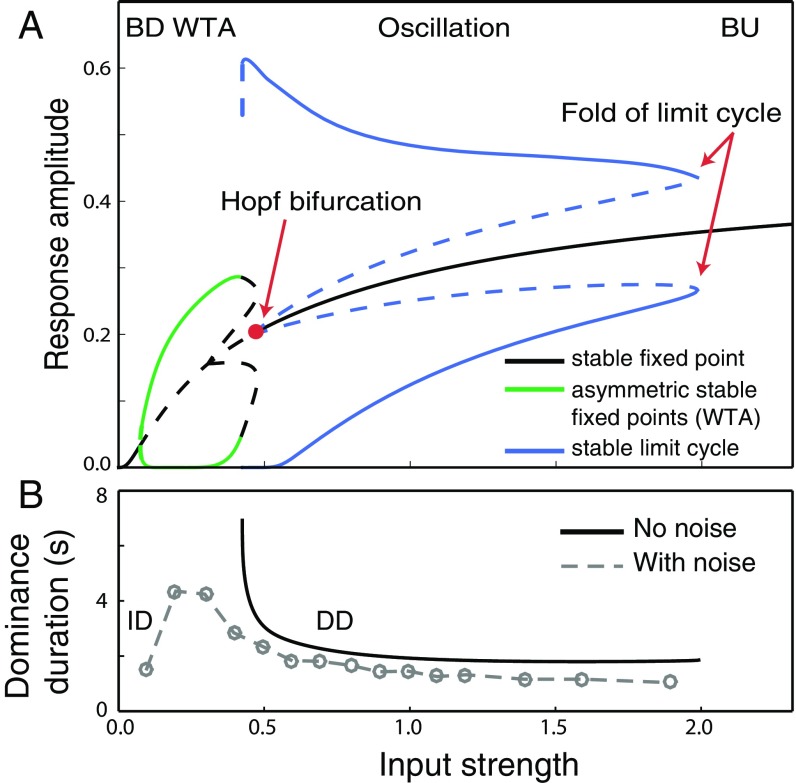
Fig. 5.

(A) Levelt’s proposition IV. The bifurcation diagram shows the response amplitude of binocular summation neurons as a function of input stimulus strength. Black solid curve, equal-activity regime [both-down (BD) and both-up (BU) regimes] in which the two summation neurons responded equally. Blue solid curves, stable oscillatory regime, in which the simulated neurons exhibited response alternations. Each neuron can be dominant (top branch) or suppressed (bottom branch) for a period, after which the responses of the two neurons alternate. Green solid curves, winner-take-all (WTA) regime, in which one of the two binocular summation neurons dominated with no alternations. Each neuron can be dominant (top branch) or suppressed (bottom branch) indefinitely, depending on the initial condition. Dashed curves, unstable (and physically unrealizable) solution states. (B) Black solid curve, dominance duration of the oscillation as a function of input strength. Gray dashed curve, simulated dominance duration in the presence of noise. ID (increasing duration), a regime in which dominance duration increases with input strength. DD (decreasing duration), a regime in which dominance duration decreases with input stimulus strength.

Fig. S7.

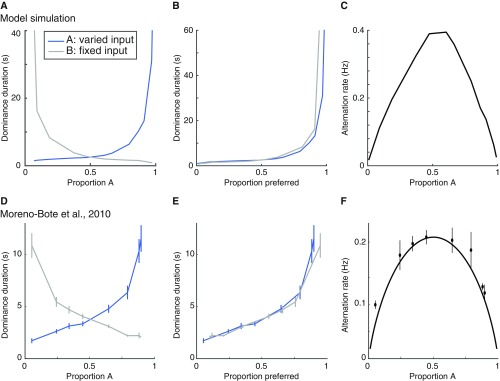
Levelt’s propositions I–III. (A) Dominance duration as a function of input stimulus strength. The strength of input B is fixed while input A is varied. Following ref. 10, we transformed the unit of the input strength of stimulus A to “Proportion A,” which was computed as follows: mean dominance duration A/(mean dominance duration A + mean dominance duration B). Blue curve, dominance duration of stimulus A, is the average period for which stimulus A is dominant. Gray curve, dominance duration of stimulus B. (B) Same as A, except that the gray curve is flipped vertically about the equidominance point (Proportion A = 0.5). (C) Alternation rate is highest when A and B have equal strength. (D–F) Empirical results replotted from ref. 10. The simulations for A–C are performed in the presence of neural noise (see SI Levelt’s Proposition and Methods, Noise).

Fig. S8.

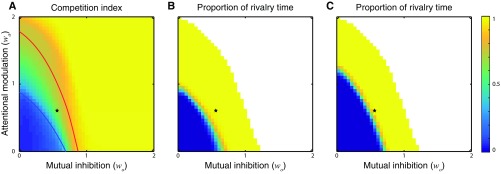
Effect of noise on system behavior. See SI Effect of Noise on Model Behavior for the details of the simulation with noise. (A) Competition index as a function of the attentional modulation (w_a) and the mutual inhibition (w_o), with fixed input strength (D = 0.5) and noise. The red and blue curves, copied from Fig. 6, were identified by bifurcation analysis of the noise-free system. Blue curve, boundary representing transitions from equal activity to oscillation. Red curve, boundary representing transitions from oscillation to WTA. (B) Proportion of time that rivalry was observed in the entire simulation (10-min duration). (C) Same as B, but with different criteria for defining rivalry responses (SI Effect of Noise on Model Behavior). In B and C, the parameter values at which one binocular summation neuron dominated over the other for the entire simulation were colored as white, representing WTA behavior. Black star, parameters used for simulations in Figs. 2–5.

Inputs.

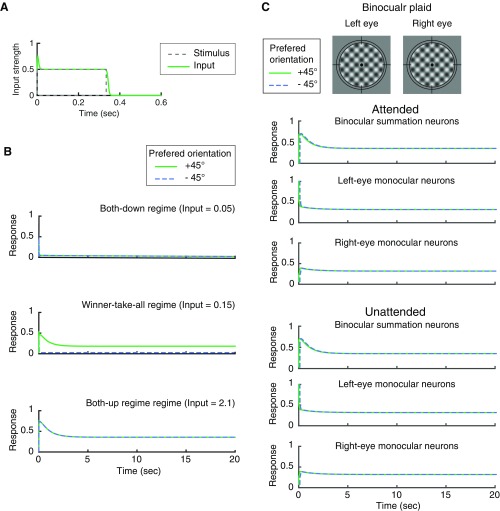
The inputs (D) to the model were assumed to be the responses of subcortical visual neurons. When the stimuli were swapped or flashed, the inputs exhibited an onset transient response [modeled by an α function $\left(t/{\tau }_{\alpha }\right)e^{\left(1-t/{\tau }_{\alpha }\right)}$, ${\tau }_{\alpha }=3\hspace{0.17em}\text{ms}$], which was 1.5 times greater than the designated sustained input strength (Fig. S1A). The transient response dropped rapidly to a sustained level of input strength. After stimulus offset, a decay was modeled by a hyperbolic tangent function with a half-life of 15 ms. The onset transient and the offset decay captured the delay and the time course of the responses of subcortical neurons (29, 30).

Fig. S1.

(A) Exemplary time course of the input strength. The dashed gray line represents the stimulus with duration of 333 ms. The green curve represents the input (D in Eq. 1) sent to the monocular neuron selective for the stimulus. The input is the same as the stimulus, except that a transient onset and offset decay are added to the input. (B) Exemplary time courses for different regimes. Responses of the binocular summation neurons are illustrated under different input strength for attended dichoptic gratings. The response amplitude corresponds to the steady-state response in Fig. 5A. From Top to Bottom: both-down regime, winner-take-all regime, and both-up regime. The neuronal responses in the oscillation regime are illustrated in Fig. 2A. (C) Example of binocular plaid stimuli (top row) and simulated neural responses in attended and unattended conditions. In all of the panels, the responses of two neurons selective for orthogonal orientations are overlapped.

Simulations.

The model can be simulated as a system of 18 ordinary differential equations (four monocular variables and two binocular variables, each with an intrinsic adaptation variable, two attention variables, and four opponency variables). Neural responses were simulated in MATLAB using forward Euler’s method with a time step of 1 ms. Further reducing the time step did not change the results. Parameter values are listed in Table S1.

Rivalry Index.

We followed the procedure in a previous EEG study (14) to simulate the rivalry index. The simulated responses of two binocular summation neurons (with neural and measurement noise; Methods, Noise) were first low-pass filtered with a Gaussian kernel (1.2-s SD). We then searched for local peaks in the time course of the neural responses. We segmented the time course into 6-s epochs, centered at the local peaks. For each epoch, the time course of the neuron associated with stronger responses (with the local peak) was defined as the “aligned signal,” and the response of the other neuron (with weaker response) was defined as the “rival signal.” The aligned signals were averaged across all epochs. The rival signals were also averaged across epochs. The rivalry index was computed by the amplitude (distance between the peak and trough) of the averaged aligned signal divided by the amplitude of the averaged rival signal.

Bifurcation Analysis.

We used bifurcation analysis to investigate the dynamics of the model, as a function of the strength of input, the weight of attentional modulation, and the weight of mutual inhibition. The steady-state responses were tracked as the model parameters were varied, and the boundaries where the system’s steady state changed qualitatively (bifurcations) were identified. This approach produced phase diagrams showing parameter values for which the model exhibited qualitatively different dynamical behaviors. Bifurcation analysis was performed using the freely available software AUTO-07p (31).

Results

Binocular Rivalry Requires Attention.

We simulated neural responses under two attention conditions, attended and unattended. In the attended condition, attention gain fluctuated between monocular neurons selective for different orientations. In the unattended condition, the attention gain of all of the monocular neurons stayed at baseline (=1). This was accomplished by setting the weight of attention feedback (w_a) to 0. The simulations were performed for two types of stimuli: dichoptic gratings (a pair of stationary, orthogonal gratings, presented in different eyes; Fig. 2A) and plaids (a pair of stationary, orthogonal gratings, presented simultaneously to one or both eyes; Fig. 2B and Fig. S1C).

The simulated responses of the binocular summation neurons and monocular neurons exhibited response alternations over time, consistent with perceptual alternations (Fig. 2C and Fig. S2A), when the stimuli were dichoptic gratings and were attended. For unattended dichoptic gratings, the responses alternated only briefly following stimulus onset, after which the competing neurons (the two binocular summation neurons or the two monocular neurons receiving inputs) exhibited responses that converged to the same steady-state level (Fig. 2E and Fig. S2). The initial phase of response alternations (Fig. 2E) is consistent with a psychophysical study reporting that withdrawing attention does not eliminate onset rivalry (32), even though withdrawing attention is effective in abolishing ongoing rivalry.

Fig. S2.

Dynamics of binocular rivalry depends on attention. (A) Attended dichoptic gratings. (B) Attended monocular plaid. (C) Unattended dichoptic gratings. (D) Unattended monocular plaid. The results shown here are the same as those in Fig. 2 of the main text, except that the responses of all of the sensory neurons, the attentional gains, and the mutual inhibition are presented.

Neither monocular plaids (Fig. 2 D and F) nor binocular plaids (Fig. S1C) exhibited response alternations regardless of the attention condition. For these stimuli, the model is in line with measurements of cross-orientation suppression (reviewed in ref. 27). Specifically, the steady-state response of a neuron selective for the target is given by Eq. 1, which reduces to E_l1/(S_m + σⁿ) in the absence of mutual inhibition and attentional modulation. Adding a cross-orientation mask suppresses the target through an increment of the normalization pool (S_m), which is computed as the summed excitatory drive across orientations and eyes (Eq. 1).

In the model, attention and mutual inhibition both facilitated competition, but their effects interacted nonlinearly. The attention gain was found to fluctuate only for attended dichoptic gratings, not for attended monocular plaids (Fig. S2 A and B). That is, the initiation of attentional modulation required an imbalance between the two orientations that was triggered by mutual inhibition. In addition, when the orientations presented to the two eyes were different, the presence of attention amplified the responses of the opponency neurons. The attention-dependent dynamics depicted in Fig. 2 was robust with respect to changes in the time constants: The model exhibited similar results (only attended dichoptic gratings generated ongoing rivalry) when τ_s, τ_a, and τ_o were independently adjusted to be nearly instantaneous (1 ms), or when τ_a and τ_o were changed to be double their original values. The values of the time constants were further constrained when simulating the eye-swapping experiments. In Operating Regime for Binocular Rivalry, we fully characterize how the strength of attentional modulation and mutual inhibition determined the dynamics of binocular rivalry in the model.

The model simulated human EEG measurements of neural activity when rival stimuli were attended and unattended (Fig. 3). To simulate the empirical EEG results (14), we added both neural noise to the input drive and measurement noise to the responses of the binocular summation neurons (Methods, Noise). We then analyzed the noisy responses of the binocular summation neurons using the same analysis as the EEG study. Specifically, we computed a rivalry index that quantified the amplitude of competition in rivalry (Methods, Rivalry Index, and ref. 14 for details). In the attended condition, the peak of the response of one binocular summation neuron (Fig. 3A, aligned signal) was accompanied by the trough of response of the other neuron (Fig. 3A, rival signal). This counter phase time-course represented a neural signature of binocular rivalry. This pattern was greatly reduced in the unattended condition and resulted in substantially smaller rivalry index (Fig. 3A, Middle and Right). The simulated attended and unattended responses resemble the empirical findings (Fig. 3B). Following the empirical study by Zhang et al. (14), we also simulated a replay condition, in which the two stimuli physically alternated irregularly to simulate rivalry. Consistent with that study, the simulated counter phase time-courses were not influenced by attention in the replay condition.

Mutual Inhibition Supports Eye Dominance and Attention Stabilizes Perceptual State.

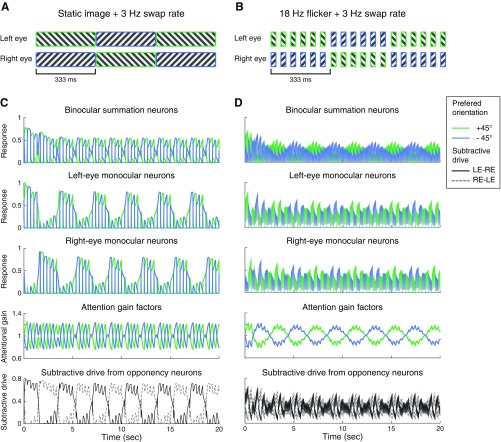
Swapping the stimuli between the two eyes rapidly and repetitively (Fig. 4) has been used to dissect the neural processing contributing to binocular rivalry (21–24). Two types of percept have been reported under these conditions. In fast alternation (FA), one eye dominates for a period, and observers report perceiving a rapid alternation between two images at a frequency equal to the swap rate. In slow alternation (SA), the perceptual dominance of one stimulus persists across swapping, and observers report seeing one image for a few seconds similar to conventional binocular rivalry. SA has been taken as evidence that binocular rivalry cannot be explained simply by mutual inhibition between neurons that respond selectively to each of the two eyes. The proportion of time that observers experience FA and SA depends on the temporal characteristics of the stimuli. If the stimuli are static images, presented to alternate eyes immediately when swapped (Fig. 4A), then observers report FA most of the time. Using flickering images (Fig. 4B), with an on-off flicker rate higher than the swap rate, increases the proportion of SA (21–24).

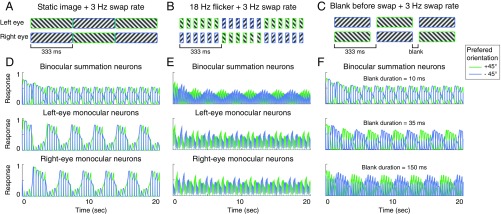
Fig. 4.

Stimuli and simulated neural responses in swapping experiment. In A–C, the eye of origin of the dichoptic gratings are swapped every 333 ms (3-Hz swap rate). (A) Stimuli are static images. (B) Stimuli are on–off flicker with 18 Hz flickering rate. (C) Similar to A, but a blank interval is inserted before the eye of origin of the gratings is swapped. (D–F) Simulated neural responses corresponding to the conditions from A to C, respectively. Blue and green curves, responses of neurons selective for each of the two orientations (+45° and −45° from vertical). In D and E, the responses of binocular summation neurons and monocular neurons are illustrated. In F, the responses of binocular summation neurons are presented for three conditions using different blank duration.

Neural responses simulated with our model exhibited slow alternations (SA) for some stimulus conditions and fast alternations (FA) for other stimulus conditions, consistent with empirical results. We simulated the eye-swapping experiment with a swap rate of 3.3 Hz, and with flicker rates of either 18 or 0 Hz (i.e., static). For static stimuli, the simulated percept followed the stimuli in one eye for a few seconds, such that the orientation “perceived” by the model changed rapidly with each swap (Fig. 4D, top row, alternating blue and green peaks). For flickering stimuli, the “perceived” orientation was maintained across swapping (Fig. 4E, top row, extended periods during which the green curve is above the blue curve and vice versa), resembling the SA percept. During simulated SA, the dominant orientation can be observed in both binocular-summation neurons (Fig. 4E, top row), and in monocular neurons (Fig. 4E, second and third rows). This result was consistent with the empirical findings that monocular populations are involved in the maintenance of the dominant percept in SA (33).

According to the model, the temporal dependence of FA and SA resulted from the different temporal characteristics of mutual inhibition and attention. The opponency neurons (mutual inhibition), when activated, suppressed the weaker eye regardless of the preferred orientations of the monocular neurons. This process captured the feature-invariant component in rivalry (34), and thereby supported FA. The attentional modulation, on the other hand, supported SA because the attention neurons were selective for orientation but not for eye-of-origin. The responses of the opponency neurons had a short time-constant, and thus mutual inhibition decayed rapidly after stimulus offset. The attention neurons had a comparatively long time-constant. For flicker stimuli, there was a gap before the swap, which allowed the eye-specific suppression from the opponency neurons to decay, while the activity of the attention neurons was sustained. So the alternations were primarily controlled by the attentional modulation under these conditions (Fig. S3D, fourth row), simulating SA. With static stimuli and no gap, the alternations were dominated by the activity of the opponency neurons (Fig. S3C, bottom row), simulating FA.

Fig. S3.

Stimuli and simulated neural responses in swapping experiment with static image (A and C) and flicker image (B and D). The results shown here are the same as those in Fig. 4 of the main text, except that the responses of all the sensory neurons, the attention gains, and the mutual inhibition are presented.

Due to the temporal dynamics described above, using static stimuli with a short blank before the swap could also induce SA (Fig. 4C). Our model showed SA for a range of blank durations from 35 ms to 150 ms, with a fixed swap rate (Fig. 4F). This result is consistent with previous studies reporting that blank duration around 100–150 ms gave rise to the greatest proportion of SA; blank durations longer than about 200 ms resulted in plaid percepts (22, 23).

Perceptual states in the swapping experiments depend on the timing of the stimuli, so the empirical results from these experiments constrain the time constants in the model. The results in Fig. 4 held when τ_s was ≤10 ms, and when the time constant of attentional modulation (τ_a) was doubled, but the response alternations in the 150-ms-blank-only condition (Fig. 4C) disappeared if ${\tau }_a$ dropped below 70 ms. The time constant of opponency neurons (${\tau }_o$) had to be shorter than the time constant of attentional modulation, as explained above. However, for the condition with a static image and 3.3-Hz swap rate, if ${\tau }_o$ was too short (<10 ms), the dominant eye in FA remained dominant for only one swap, rather than over a few seconds as in Fig. 4D (second and third rows).

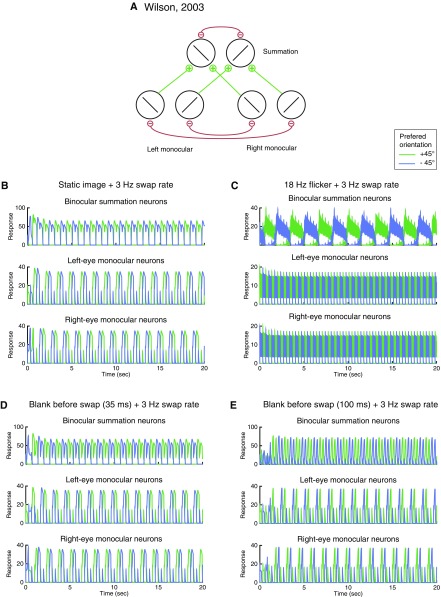
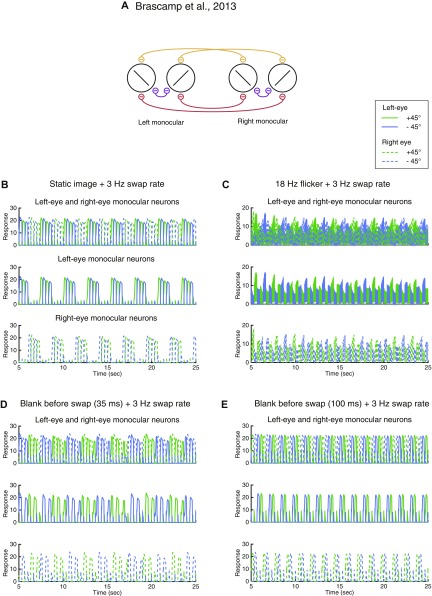
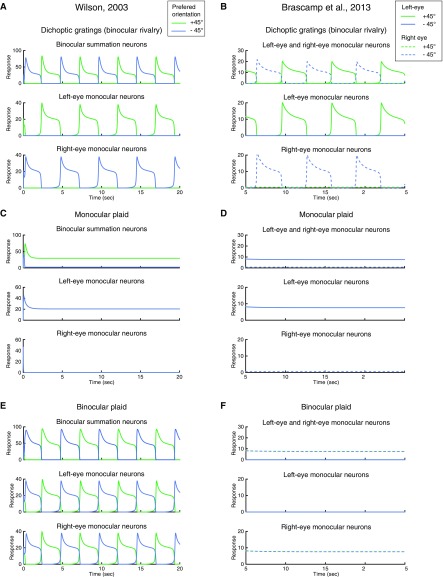
Two previous models (4, 33) also aimed to explain perception in swapping experiments. We found that they were able to capture the perceptual dynamics in some, but not all, of the conditions demonstrated here. Specifically, Wilson’s model (4) generated SA with flicker stimuli, but did not generate FA with static images. Instead, the model predicted that the “perceived” orientation alternated with a frequency half of, but not equal to, the swap rate (Fig. S4 A–C). With blank intervals inserted before each swap, the model did not exhibit SA for either short or long blank duration (Fig. S4 D and E). The model proposed by Brascamp et al. correctly predicted FA with static images (Fig. S5B) and SA with 18-Hz flicker (Fig. S5C). However, their model generated SA only when the blank was short (35 ms in Fig. S5D), not when the blank duration was lengthened (100 ms in Fig. S5E). In contrast, empirical studies have reported that SA increases with longer blank durations (22, 23). In addition, these two models exhibited strong competition for stationary plaid stimuli. Specifically, in response to monocular plaids, Wilson’s model exhibited behavior in which one of the gratings suppressed the other indefinitely (Fig. S6C). For binocular plaids, Wilson’s model exhibited response alternations, similar to dichoptic gratings (Fig. S6E), and Brascamp’s model exhibited behavior in which the representation of the plaid in one eye suppressed the plaid in the other eye indefinitely (Fig. S6F). These results are inconsistent with empirical observations that rivalry does not occur when the images in the two eyes are compatible (35, 36). See details of the simulations and results on these two models in Supporting Information.

Fig. S4.

Wilson’s model, swapping experiments. (A) Model structure. Reprinted with permission from ref. 4. (B–E) Simulations of four conditions. For all four conditions, the two orthogonal gratings were swapped between eyes every 333 ms. (B) Static images with no blank. (C) Flickering images. (D) Blank before swap (35-ms blank duration). (E) Blank before swap (100-ms blank duration).

Fig. S5.

Brascamp et al.’s model, swapping experiments. (A) Model structure. Reprinted with permission from ref. 33. (B–E) Simulations of four conditions. For all four conditions, the two orthogonal gratings were swapped between eyes every 333 ms. (B) Static images with no blank. (C) Flickering images. (D) Blank before swap (35-ms blank duration). (E) Blank before swap (100-ms blank duration).

Fig. S6.

(A, C, and E) Wilson’s model. Reprinted with permission from ref. 4. Simulations of three conditions: (A) Dichoptic gratings, conventional binocular rivalry. (C) Monocular plaid. In the middle row (left-eye monocular neurons), the two neurons selective for orthogonal orientations have the same response amplitude, and thus the green and blue curves overlap. (E) Binocular plaid. (B, D, and F) Brascamp et al.’s model. Reprinted with permission from ref. 33. Simulations of three conditions: (B) Dichoptic gratings, conventional binocular rivalry. (D) Monocular plaid. Here, the two left-eye monocular neurons selective for orthogonal orientations have the same response amplitude, and thus the solid green curve and the solid blue curve overlap. (F) Binocular plaid. Here, the two right-eye monocular neurons selective for orthogonal orientations have the same response amplitude, and thus the dashed green curve and the dashed blue curve overlap. The left-eye monocular neurons are suppressed throughout the simulation.

Levelt’s Propositions.

Levelt’s four propositions characterize how dominance durations (average duration of all of the individual periods for which one of the rivalry stimuli dominates) depend on stimulus contrast (25). We investigated the range of input strength (D) for which our model exhibited Levelt’s propositions. We used the updated version of Levelt’s propositions (26) as the standard. Levelt’s first three propositions (LI–LIII) describe how dominance durations change when the contrasts of the stimuli in two eyes vary independently of one another. In Supporting Information, we show that the model exhibited dominance durations consistent with LI–LIII (SI Levelt’s Propositions and Fig. S7). Here, we focus on model behavior as the inputs in both eyes are varied simultaneously.

Levelt’s Proposition IV (L-IV). Increasing stimulus strength in both eyes while keeping it equal between eyes will generally increase the perceptual alternation rate, but this effect may reverse at near-threshold stimulus strengths.

We performed bifurcation analysis to characterize the steady-state responses of the binocular summation neurons as a function of input strength (D). The model exhibited three types of behavior (regimes) when the input strength was varied. (i) At the lowest and the highest input strength, the two binocular summation neurons maintained at equal activity [black solid curves, labeled as both-down (BD) and both-up (BU) in Fig. 5A; also see Fig. S1B]. (ii) The BD state became unstable when input strength increased through a critical value (∼0.15), and a winner-take-all (WTA) state emerged—a so-called steady-state bifurcation (37). In the WTA regime, depending on the initial conditions, one binocular summation neuron dominated over the other indefinitely (green curves in Fig. 5A; also see Fig. S1B). (iii) There was an oscillatory regime in which the responses of two summation neurons alternated, resembling the perceptual alternations in rivalry (solid blue curves, labeled as “Oscillation” in Fig. 5A; also see Fig. 2C). In more detail, the BU state became unstable as input strength decreased through a critical value (Hopf bifurcation in Fig. 5A). Here, the dynamic response, locally near the BU state, changed from damped to growing oscillations and a small-amplitude oscillation state emerged—a so-called Hopf bifurcation (37). In this case, the emergent oscillation was unstable (dashed blue curves). It merged with the stable large-amplitude oscillation regime at a higher input strength (fold of limit cycles in Fig. 5A), defining the upper boundary of the oscillation region.

Critically, in the oscillation regime where the model exhibited rivalry-like response alternations, the dominance duration decreased with increasing input strength [Fig. 5A, blue solid curves, and Fig. 5B, black solid curve labeled as decreasing duration (DD)], consistent with L-IV.

Adding noise to the model resulted in the following effects (Fig. 5B, gray dashed line): First, noise eliminated the WTA regime, as the noise prevented indefinite dominance by either of the two binocular summation neurons. Second, noise reduced the dominance duration. Third, a new regime emerged in which dominance duration increased with input strength [labeled as increasing dominance (ID) in Fig. 5B]. This corresponded to the lower part of the WTA regime with no noise. We suggest that input strengths corresponding to this short ID branch were below the threshold for visibility (Operating Regime for Binocular Rivalry).

Operating Regime for Binocular Rivalry.

Bifurcation analysis over a wide range of parameter values allowed us to explore all possible behaviors of the model. We characterized the dynamics of the model as a function of three parameters that controlled input strength (D), attentional modulation (w_a), and mutual inhibition (w_o). In a subspace of the 3D volume defined by these three parameters, the behavior of the model was consistent with empirical findings. Here, we illustrate this subspace by depicting 2D slices of the parameter space, and by indicating the boundaries that differentiate distinct model behaviors.

We defined a boundary between different regimes in the parameter space as follows. In some cases, one regime turned into the other through loss of stability of one state and emergence via bifurcation to a stable state of a different type (e.g., the transition from BD to WTA in Fig. 5A) or to oscillatory responses [e.g., the transition from WTA to DD, the Hopf bifurcation (HB), in Fig. 5A]. We traced the bifurcation points and plotted them as boundaries in Figs. 6 and 7. In some cases, the stable oscillatory response of the neurons in the oscillatory region was not directly connected to the steady-state response of the equal-activity regime at the transition (e.g., the transition from oscillation to BU regimes in Fig. 5A). We identified such boundaries by tracing the outermost bound of the oscillatory responses (fold of limit cycles in Fig. 5A; blue curves in Figs. 6 and 7). In other cases, for example close to HB in Fig. 5A, bifurcations on several branches occurred within a small parameter range. This remained true along the Hopf bifurcation boundaries in Figs. 6 and 7. In the interest of parsimony, we plot only the Hopf curves, while noting that the explicit bifurcation mechanism for the transition between different regions can also involve other bifurcations.

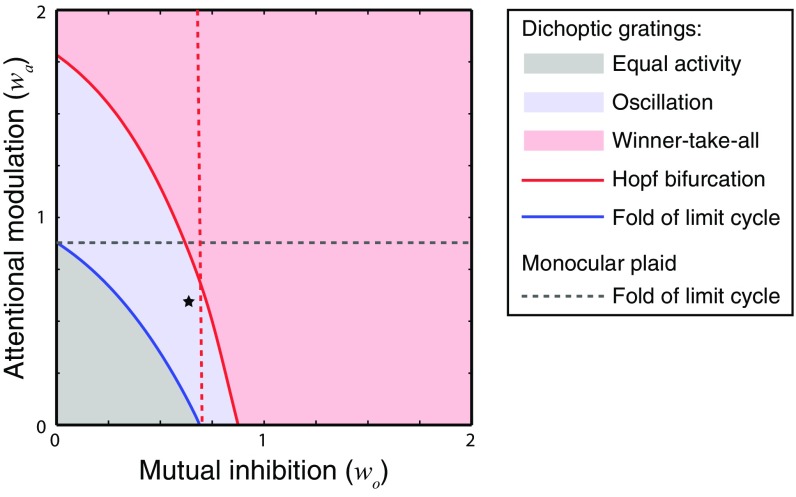
Fig. 6.

Bifurcation analysis as a function of the attentional modulation (w_a) and the mutual inhibition (w_o), with fixed input strength (D = 0.5). All of the elements in the figure depict the model behavior for dichoptic gratings, except the gray dashed lines. The areas in three different colors represent three regimes: equal activity, oscillation, and winner-take-all. Solid curves, boundaries between the different regimes. The red dashed line is positioned where the blue curve intersects the x axis. Left of this boundary, rivalry is absent when attention is diverted (w_a = 0). The gray dashed line indicates the boundary of the oscillatory regime (i.e., response alternations) for monocular and binocular plaids. For values of w_a above this curve, the model exhibits response alternations with plaids. Black star, parameters used for simulations in Figs. 2–5.

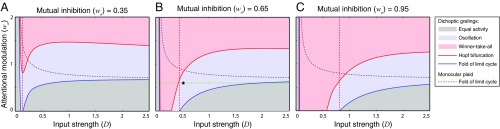
Fig. 7.

Bifurcation analysis as a function of input stimulus strength (D), attentional modulation (w_a), and mutual inhibition (w_o). The results are illustrated as 2D (D vs. w_a) bifurcation diagrams. Each panel (from A to C) corresponds to a different value of mutual inhibition (w_o). All of the elements in the figure depict the model behavior for dichoptic gratings, except the gray dashed curves. The areas in three different colors represent three regimes: equal activity (Left gray area corresponds to the both-down regime, and Right gray area to both-up regime), oscillation, and winner-take-all. Solid curves, boundaries between the different regimes. The red dashed line is positioned where the blue curve intersects the x axis. Right of this boundary, rivalry is absent when attention is diverted (w_a = 0). The gray dashed curve indicates the boundary of the oscillatory regime (i.e., response alternations) for monocular and binocular plaids. For values of w_a above this curve, the model exhibits response alterations with plaids. The green dashed line indicates the domain corresponding to the 1D bifurcation analysis in Fig. 5A. Black star, parameters used for simulations in Figs. 2–5. The solid blue curve and the solid red curve, extending vertically near the Left of B and C, are very close together. These solid blue and red curves are continuations of the same boundaries indicated in A. The blue curve is the boundary between the gray region and the blue region. The red curve is the boundary between the blue region and the pink region. The pink region in B and C, unlike in A, descends below the horizontal axis. Only the boundaries that are critical for defining different regimes are illustrated.

Under a fixed input strength (D = 0.5, same as in the simulations in Figs. 2–4), the binocular summation neurons responded equally, and there were no response alternations when the attentional modulation and mutual inhibition were both weak (Fig. 6, gray zone). The model exhibited oscillations or WTA as the weight of attentional modulation or mutual inhibition increased (Fig. 6, blue and red zones). The boundary between these regimes had a negative slope, indicating that attention and mutual inhibition both facilitate competition in rivalry, and jointly determined the model’s behavior.

The shapes of these regimes also depended on input strength (Fig. 7). The WTA and oscillatory regimes extended to larger input strengths with increasing mutual inhibition (from Fig. 7A to Fig. 7C) or attentional modulation (within each panel). There were two distinct equal-activity regimes. When the input strength was low, the binocular summation neurons responded equally with small responses (BD, gray strip on the Left of each panel in Fig. 7). When the input strength was high, and when attentional modulation was small, the binocular summation neurons exhibited equally large responses (BU, gray region at the bottom of each panel in Fig. 7).

There was a 3D region within the parameter space for which the model exhibited the critical phenomenology of binocular rivalry (Figs. 6 and 7, in which the black star corresponds to the parameters used for the simulation results in Figs. 2–5). First, the weight of attentional modulation (w_a) was chosen so that the model did not exhibit oscillations for monocular or binocular plaids (Figs. 6 and 7B, black star below dashed gray boundaries). Second, the weight of mutual inhibition (w_o) was chosen so that there were no response alternations for unattended dichoptic gratings (Fig. 6, black star to the Left of red dashed line, so as to be in an equal-activity regime when w_a = 0 directly below the black star). Third, there was a lower bound on the input strength to avoid responses alternations for unattended stimuli (Fig. 7B, black star to the Right of the red dashed line, so as to be in an equal-activity regime when w_a = 0 directly below the black star). Input strengths below this level were assumed to be below the threshold for visibility. Fourth, within the volume defined by the previous three criteria, we chose a combination of attentional modulation and mutual inhibition (black star in Figs. 6 and 7), so the model exhibited distinctly different behaviors corresponding to the FA and SA percepts in the swapping experiment. We found that to fulfill this criterion the model had to operate close to the boundary between oscillatory and WTA regimes (Figs. 6 and 7, black star near solid red curve). Fifth, binocular rivalry has been reported up to the highest contrast level testable, imposing an upper bound of the input strength (Fig. 7B, input strength increases along the green dashed line but cannot exceed the value where the green dashed line intersects the blue curve). Input strengths above this level were presumed to be physically unrealizable.

In summary, when the rival stimuli were attended, the model operated close to the boundary between oscillatory and WTA regimes (Figs. 6 and 7B, black star). A previous study, in which the authors independently varied the strength of adaptation and noise to fit the statistics of dominance durations (9), also led to a similar conclusion. When attention was diverted, the model moved to an equal-activity regime that was near the boundary of an oscillatory regime. We only specified the relative position of this volume and did not aim to illustrate its size and shape. The phases and regimes in the bifurcation diagram stretch or squeeze depending on the other parameters in the model including the exponent (n) and suppression constant ($\sigma$). For example, we assumed that the input to the neurons increased monotonically with stimulus intensity. Changing the mapping between stimulus intensity (e.g., contrast) and neural input strength would scale and/or warp the x axis in Figs. 5 and 7 (38, 39).

SI Levelt’s Propositions

Levelt’s Propositions I–III.

L-I. Increasing stimulus strength for one eye will increase the perceptual predominance of that eye’s stimulus. L-II. Increasing the difference in stimulus strength between the two eyes will primarily act to increase the average perceptual dominance duration of the stronger stimulus. L-III. Increasing the difference in stimulus strength between the two eyes will reduce the perceptual alternation rate (25, 26).

Levelt’s propositions I–III can be summarized in an experiment in which dominance duration is measured when the contrast of the stimulus in one eye is fixed, while the contrast of the stimulus in the other eye varies across a range, encompassing contrasts both lower and higher than the fixed-contrast image (10, 26).

We simulated such an experiment by varying the input strength of a stimulus in one eye from 0.2 to 0.9 (stimulus A) while fixing the input strength of the stimulus in the other eye at 0.5 (stimulus B). We added noise to the simulated neural responses, and computed the mean dominance durations of A and B. We plotted the dominance duration of stimulus A and stimulus B as a function of their input strength. Following Moreno-Bote et al. (10), we transformed the input strength of stimulus A to “Proportion A” (see the legend of Fig. S7).

Consistent with L-I, increasing the strength of A increased the proportion of time that A was “perceived” by the model and lengthened the mean dominance duration of A (Fig. S7). In agreement with L-II, the change in dominance duration was more pronounced for the image with the higher contrast. That is, the change of A’s dominance duration was more pronounced right of the equidominance point (fraction A = 0.5), and the change of B’s dominance duration was more pronounced left of the equidominance point. We also observed that the dominance durations of A and B were approximately symmetric around the equidominance point (Fig. S7 A and B). This symmetry relied on normalization, due to the suppressive drive of the monocular neurons in the model (Eq. 1), similar to the “input normalization” in a previous model (10). In accordance with L-III (Fig. S7C), the mean alternation rate was fastest at the equidominance point. All of these simulation results resemble previous experimental results (10) (Fig. S7 D–F).

In the absence of noise, response alternations were constrained to a narrow range of input strengths (input A = 0.45–0.55). The model exhibited WTA behavior outside this range. This occurred because the model operated close to the boundary between an oscillator (adaptation-driven) and an attractor (noise-driven), as shown in the main text (Results, Operating Regime for Binocular Rivalry).

Levelt’s Proposition IV.

Some previous conventional mutual inhibition models of binocular rivalry predict an increased duration (ID) regime; ID corresponds to oscillatory behavior in which dominance duration increases with input, in violation of Levelt’s proposition IV (reviewed in ref. 6). Although ID is absent in Fig. 5A, we found ID in a very limited parameter space in the present model. For example, in Fig. 7A, if one takes a horizontal slice at w_a = 1, the WTA regime is flanked by two oscillatory regimes. The very small oscillatory regime to the left of the WTA regime, exhibited ID. The other, a large oscillatory regime to the right of the WTA regime, exhibited DD. We found that increasing the strength of attention reduced ID. This might be related to previous findings that recurrent positive feedback (from attention in our case) could reduce ID (38, 39). In addition, we also found that changing the slope and threshold of the neural response functions (by manipulating n and $\sigma$) changed the relative sizes of the different regimes. These results are consistent with observations suggesting that ID may depend on which stimulus dimension is manipulated in an experiment (95, 96) and how one specifies the mapping between stimulus intensity and neural inputs in the model (38, 39).

At the lower end of the input strength, the model had a WTA regime (Fig. 5A). There are two potential interpretations of this regime. First, in the presence of noise, WTA does not occur because the noise will cause the percept to alternate eventually (6, 8). Second, in the absence of noise, the WTA regime offers a possible explanation for the so-called “rivalry memory” (97). Neurons exhibit nonzero resting-state firing rate (the background activity) in the absence of sensory input. After stimulus offset, the background activity might correspond to the WTA regime such that the dominant percept before stimulus offset would remain dominant (at a low overall firing rate) after stimuli offset, and become dominant again when the rival stimuli reappear.

Discussion

We propose a computational model of rivalry, in which perceptual competition is driven by both attentional modulation and mutual inhibition. Attention (with a relatively slow time constant) recurrently amplifies the imbalance between the two rival stimuli triggered by the mutual inhibition (with a relatively fast time constant). This model captures three signatures of binocular rivalry simultaneously. (i) Diverting attention greatly reduces or eliminates response alternations (14–16). The model exhibits this phenomenon because of the recurrent amplification from attention. (ii) When rival stimuli are swapped rapidly between the two eyes, the dominant percept either follows the same eye or the same image, depending on the temporal characteristics of the stimuli (21–24). The model exhibits these phenomena because of the different temporal dynamics of mutual inhibition and attention. (iii) The relationship between dominance duration and input strength follows Levelt’s propositions (10, 25, 26). These propositions are satisfied because of a combination of competition (from attentional modulation and mutual inhibition), recurrent excitation (from attentional modulation), and slow adaptation (6, 38, 39). Levelt’s proposition IV, in particular, depends on having some degree of recurrent excitation (38, 39).

Attentional Modulation.

In our model, attentional modulation depends on the sensory responses, a form of stimulus-driven attention. Reducing stimulus-driven attention mimics the effect of diverting attention away from the rival stimuli. This is consistent with findings that an attention-demanding task diminishes the stimulus-driven attention triggered by the stimuli outside the focus of attention (40–42). The notion that bottom-up inputs strongly influence the deployment of attention in rivalry may explain why binocular rivalry is only weakly biased by instructions [e.g., attend to the left-tilted grating (43)].

Attentional modulation in the model is selective for orientation but not for eye of origin. In previous psychophysical experiments, we measured how a competing image in one eye modulated the discriminability of a target image in the other eye. We found that a model with feature-selective attention, not eye-based attention, best explained the data (18). Some behavioral studies have suggested that attention can modulate eye-specific information (44, 45). However, these studies placed different stimuli not only in different eyes but also in different retinal locations. This is different from binocular rivalry in which conflicting information is presented in corresponding retinal locations. Moreover, with such experimental conditions, an apparent attention effect might be the result of a combination of spatial attention and interocular divisive normalization (46–49).

The present model extends the normalization model of attention (19) to a dynamical system. The time constant of the attentional modulation chosen here (∼150 ms) is consistent with the temporal dynamics of stimulus-driven attention measured in psychophysical experiments. Stimulus-driven attention peaks around 100–120 ms after a trigger stimulus, whereas goal-driven attention requires more time (∼300 ms) to be deployed (50–52). The speed of stimulus-driven attention in rivalry could be slower than that typically measured in studies of exogenous attention, because the changes in neural activity during rivalry are less abrupt than those evoked by a high-contrast brief cue typically used to summon attention. In any case, the temporal dynamics of attention are much slower than the speed of the mutual inhibition [<50 ms in the present and previous models (reviewed in ref. 6)]. Because the attentional modulation is computed recurrently (via feedback) with a time constant longer than the sensory responses, the model is in line with neurophysiological findings that stimulus-driven attentional modulation has little or no impact on the early transient part of the response evoked by stimulus onset (53).

The simulation results indicated that the prevalence of two types of percepts (FA vs. SA) in swapping experiments depends on the balance between attention and mutual inhibition. This idea may explain two additional aspects of phenomenology observed in swapping experiments. First, observers usually report that the perceptual state fluctuates between FA and SA during a single trial, even when the stimuli are optimized for one particular percept (22, 23, 54). This might result from fluctuations in the strength of attention and arousal. Attention and arousal are known to vary over time during an experiment (55, 56). Increasing the strength of attention would amplify SA and reduce FA, and vice versa. Second, the depth of suppression is weaker (57, 58), and the dominance durations are shorter (54) in swapping experiments compared with conventional binocular rivalry. Likewise in our simulations, SA responses had shorter dominance durations than conventional rivalry responses, indicating a weaker competition in SA (Figs. 2C and 4E).

Future work might extend the current model to explain empirical observations regarding the deployment of endogenous attention in rivalry. Manipulating observers’ endogenous attention by asking observers to “hold on” to one of the two images can bias the percept in ongoing rivalry (43, 59, 60). However, the effects of biasing endogenous attention (to one of the rivalry stimuli) are not as pronounced as those of withdrawing attention, which can abolish ongoing rivalry (14–16). This difference in the magnitude of attentional effect might result from the differences in experimental designs: First, the perceptual report when observers are instructed to hold on to one percept has been usually compared with a neutral condition (in which observers are not instructed to hold on). It has been assumed that observers’ voluntary attention is equally deployed to the two images in this neutral condition, but this might not be the case. Given the stochastic nature of the perceptual alternations in rivalry, voluntary attention may participate when observers attempt to track and report their percept. Consequently, the effect of endogenous attention could be underestimated. Second, in the hold-on condition, the to-be-attended image went through a period in which it was less visible than the to-be-ignored image presented at the same location (43, 59, 60). In contrast, in the withdraw-attention procedure the to-be-ignored rivalry stimuli were presented at other locations (14–16). Thus, the withdraw-attention procedure, involving spatial and feature-based attention, could be stronger than the hold-on condition, involving only feature-based attention.

Extensions and Limitations of the Model.

By modeling neurons selective for dimensions other than orientation (e.g., motion), one can extend the current model to investigate other forms of bistable phenomena, such as motion-plaid rivalry (10, 61–63) and ambiguous structure from motion (64). The strength of mutual inhibition might vary across different bistable stimuli. If the mutual inhibition is strong enough, response alternations and thus bistable percepts can exist without attention (Fig. 6). This may explain why some bistable phenomena, such as motion-induced blindness and ambiguous structure from motion, persist when attention is diverted or withdrawn (64, 65).

For a stationary plaid (Fig. 2B), observers can sometimes experience weak perceptual alternations [monocular rivalry (66)]. The model can capture this effect by adjusting the strength of attention to a value above the gray dashed lines in Figs. 6 and 7. In that regime, attentional modulation alone induces response alternations for a plaid stimulus.

We remain agnostic as to the mechanism contributing to the stochastic characteristics of binocular rivalry. Similar to previous oscillator models (3–6), we focused primarily on characterizing the deterministic response alternations exhibited by our model. Adding noise to this type of system generates a gamma-like distribution of dominance durations (7, 9). One could finely tune the strength of adaptation and the amplitude of the noise to reproduce the dominance duration statistics found in behavioral data. Alternatively, a mechanism based on assemblies of stochastic, bistable neurons can generate gamma-like distributions of dominance durations and can account for the scaling properties (i.e., constant skewness and coefficient of variation) of the dominance durations observed across input strengths and across different bistable phenomena (67).

Introducing noise to the model does not change the qualitative organization of the bifurcation diagrams: In general, noise induces small fluctuations in the equal-activity regime, response alternations in the WTA regimes [if sufficiently close to the oscillation regime (9)], and some variability to the alternations in the oscillatory regime. Simulations with noise showed that withdrawing attention reduced the strength of competition and the probability (proportion of time) that rivalry was observed (Fig. S8 and SI Effect of Noise on Model Behavior).

The current model only assumes that withdrawing attention abolishes the fluctuations of attention gain, but distributing attention can also lead to a decrease of effective or perceived contrast (68). Because our model follows Levelt’s fourth proposition, one can extend the model—for example, by reducing the baseline of attention gain or input drive (69) while still allowing the attention neurons to be active—to simulate the finding that adding a concurrent task could slow down the reported perceptual switches (70).

Neural Mechanisms.

In the present model, the neurons in the attention layer were selective for orientation, and their inputs were linear combinations of the responses of the early sensory neurons. Visual neurons in areas downstream from V1 (e.g., V2–V4 and LO) could be responsible for such computations. Stimulus-driven attention in the model might reflect enhanced communication between early and late visual cortical areas. This idea is supported by studies that demonstrated greater interarea correlations of activity between visual areas with attention (71–73). An alternative, but not mutually exclusive, hypothesis is that attentional modulation is mediated by neural signals from frontoparietal cortices (74, 75). Neurons in frontoparietal regions not only exhibit control signals but also feature-selective representations (76, 77). However, whether the frontoparietal cortices are directly involved in binocular rivalry is controversial (78, 79).

Neural activity in visual cortex, measured with single-cell electrophysiology, exhibits rivalry-like alternations (80, 81), and neural responses in visual cortex also exhibit interocular suppression (82, 83). However, some of these experiments were performed with anesthetized animals. One should be careful about comparing these results with those from human neuroimaging and psychophysics because responses of neurons in visual cortex depend on brain state (84–86). The dynamics of our model depend on multiple factors, stimulus strength, attentional modulation, and mutual inhibition (Fig. 7), which could have very different effects under anesthesia.

Binocular Rivalry as a Gateway for Understanding Perceptual Inference.

Perception is unconscious inference (87). Sensory stimuli are inherently ambiguous so there are multiple (often infinite) possible interpretations of a sensory stimulus. Multistable phenomena (e.g., binocular rivalry) can be used to probe the intrinsic neural dynamics of cortical processing and the neural processes underlying perceptual inference (88–90), and neural networks with mutual inhibition as the main ingredient have been designed to perform perceptual inference (89). The present model adds attentional modulation as a critical component, not only to explain a large body of literature on the phenomenon of binocular rivalry but also toward developing a neural-based computational theory of perceptual inference.

Binocular rivalry is rare in everyday visual experience. Outside the laboratory, discrepancies between monocular images from the two eyes often occur when a foreground object occludes the background of a visual scene, leaving some regions of the background visible to only one eye and other regions visible to only the other eye. At corresponding retinal locations with conflicting inputs in the two eyes, the retinal image with lower strength (e.g., contrast) is usually suppressed for a prolonged period. Even though perceptual alternations are rarely experienced in this case, the interocular suppression might arise from the same processes that drive the suppression in binocular rivalry (91).

SI Effect of Noise on Model Behavior

We investigated how the presence of noise changed the general organization of the (w_a − w_o) bifurcation diagram. Neural noise was modeled as an Ornstein–Uhlenbeck process and added to the input drive (Methods, Noise). We varied the strength of attentional modulation (w_a) and mutual inhibition (w_o) from 0 to 2 in steps of 0.05. For each combination of w_a and w_o, we simulated neural responses using dichoptic gratings as the inputs (Fig. 2A) with a duration of 10 min. Two approaches were used to quantify the model behavior: (i) We computed a competition index to represent the magnitude of competition observed in the simulated neural responses. The competition index was computed as follows:

$$\text{Competition}\hspace{0.17em}\text{index}=\frac{\mathrm{\Delta }t}{T}{\displaystyle \sum _{j=1}^N\frac{\left|R_{b1}-R_{b2}\right|}{R_{b1}+R_{b2}}},$$

where R_b1 and R_b2 were the responses of the two binocular summation neurons, T was the total simulation duration, $\mathrm{\Delta }t$ was the duration of a time step, N was the total number of time steps, and j indexed the time steps. The value of the competition index was bounded between 0 and 1, with a larger value indicating a stronger competition between two neural populations. (ii) We used the switches of R_b1 and R_b2 (R_b1 > R_b2 and R_b1 < R_b2) to segment the simulated responses into epochs. We computed the duration and competition index for individual epochs. We defined an epoch exhibiting rivalry to be an epoch with a duration longer than 300 ms (10) and a competition index larger than a criterion (competition index > 0.3 in Fig. S8B and competition index > 0.5 in Fig. S8C). We computed the proportion of rivalry time by summing the durations of all of the epochs that exhibited rivalry based on these criteria, and divided the summed duration by the total simulation duration (10 min).

The general organization of the bifurcation diagram was preserved in the presence of noise (Fig. S8). The change of competition index was generally parallel to the boundaries identified through bifurcation analysis in a no-noise system (compare the change of color and the two curves in Fig. S8A). Both attention and mutual inhibition enhanced the competition and increased the competition index. With the w_a = 0.6 and w_o = 0.55, values chosen for the simulations in the no-noise system, the simulated responses had a competition index of 0.63 (black star in Fig. S8A) and a proportion of rivalry time of 97% or 96% depending on the criteria (Fig. S8 B and C). When w_a and w_o were set to 0 and 0.55, respectively (withdrawing attention), the competition index dropped to 0.19, and the proportion of rivalry time decreased to 10% or 0% depending on the criteria.

Conclusions

Attention has long been known to affect binocular rivalry (59, 92). However, not until recently was it recognized that attention is necessary for rivalry (14–18). These findings require a revision of the computational framework for binocular rivalry. In the model we propose here, attention plays a role that amplifies visual competition by biasing attention gain toward one of the rival stimuli. This is similar to the role of attention in natural viewing: attention regulates competing information and allocates limited neural resources (93, 94).

Our model exhibited attention-dependent dynamics and captured the dynamics of binocular rivalry in a wide range of experimental conditions. The computations in the model (divisive normalization, mutual inhibition, and attentional modulation) have been hypothesized to be canonical motifs underlying information processing at multiple stages of the visual processing hierarchy (19, 27, 38). Consequently, this framework can be extended to understand the spatiotemporal dynamics of interactions between attention and perception in conditions other than binocular rivalry.

SI Previous Models for Swapping Experiments

Wilson’s Model.

There were two populations of monocular neurons and one population of binocular summation neurons in Wilson’s model (4). Each population had a pair of neurons tuned to orthogonal orientations (Fig. S4A). There were two types of mutual inhibition. First, monocular neurons selective for different eyes and orthogonal orientations suppressed each other (Fig. S4A, red connections at Bottom). Second, two binocular summation neurons inhibited each other (Fig. S4A, red connections at Top). The neural responses were as follows:

$$\begin{array}{l}\tau \frac{d}{dt}{E}_{l1}=-E_{l1}+\frac{100{\left[V_{l1}-g{I}_{r2}\right]}_{+}^2}{{(10+H_{l1})}^2+{\left[V_{l1}-g{I}_{r2}\right]}_{+}^2}\\ {\tau }_I\frac{d}{dt}{I}_{l1}=-I_{l1}+E_{l1}\\ {\tau }_H\frac{d}{dt}{H}_{l1}=-H_{l1}+h{E}_{l1}.\end{array}$$

The asymptotic firing rate of the excitatory neurons was computed according to a Naka–Ruston function. E_l1 was the firing rate of the excitatory neuron selective for the left eye l and orientation 1. The excitatory neuron received input V_l1, and subtractive drive I_r2 as inhibition from the neuron selective for the orthogonal orientation 2 and for the right eye r. g determined the strength of mutual inhibition. This excitatory neuron drove an inhibitory neuron I_l1. H_l1 described the slow self-adaptation of this neuron.

The binocular summation neuron selective for orientation 1 was computed as follows:

$$\begin{array}{l}\tau \frac{d}{dt}{E}_{b1}=-E_{b1}+\frac{100{\left[\alpha E_{l1}+\alpha E_{r1}-g{I}_{b2}\right]}_{+}^2}{{\left(10+H_{b1}\right)}^2+{\left[\alpha E_{l1}+\alpha E_{r1}-g{I}_{b2}\right]}_{+}^2}\\ {\tau }_I\frac{d}{dt}{I}_{b1}=-I_{b1}+E_{b1}\\ {\tau }_H\frac{d}{dt}{H}_{b1}=-H_{b1}+h{E}_{b1}.\end{array}$$

These computations were similar to the monocular neurons, except that the inputs to the binocular summation neurons were the responses (weighted by $\alpha$) of the two monocular neurons selective for the same orientation.

We used the parameter values reported by Wilson (4): input V = 10 when the stimulus was presented, inhibitory weight g = 0.45 (we assumed that the g = 45 reported in ref. 4 was a typo) for monocular neurons and 1.53g for the binocular neurons, adaptation strength h = 0.47, excitatory input gain monocular to binocular neurons $\alpha$ = 0.75, time constant for monocular and binocular excitatory neurons $\tau$ = 20 ms, time constant for inhibitory neurons ${\tau }_{\mathit{I}}$ = 11 ms, and time constant of adaptation ${\tau }_h$ = 900 ms.

We replicated the findings from Wilson (4) demonstrating that this model exhibited SA in the flickering image condition (Fig. S4C). In this condition, the mutual inhibition between monocular neurons was too weak to produce suppression; SA was achieved by the mutual inhibition between two binocular neurons.

The model did not exhibit FA for static images. The dominant orientation changed every 666 ms (Fig. S4B, top row, alternations of blue and green curves). That is, the simulated neural activity alternated every other swap (i.e., every 666 ms), not in pace with the swap rate (every 333 ms). This is different from what has been found empirically; observer’s perceived the image in one eye for a prolonged period with static images (22, 23, 32). There were several reasons leading to this failure: First, the mutual inhibition between monocular neurons was only between orthogonal orientations across eyes. Thus, if orientation 1 was dominant in the left eye (R_l1) at one particular moment and orientation 2 was suppressed in the right eye (R_l2), then there was no mechanism to determine which one of the neurons, R_l2 and R_r1, should win after the two images were swapped. Second, the simulated neural activity was forced to alternate every 666 ms. If R_l1 was dominant during one interval (e.g., 0–333 ms), then the same orientation 1 was presented to the left eye again after the second swap (666–999 ms). In this interval (666–999 ms), the same orientation 1 had to be suppressed because the adaptation term H_l1 (or H_b1) was stronger than H_r2 (or H_b2; due to the most recent dominance phase of R_l1 during 0–333 ms). Which neuron would be dominant between 333–666 ms, in this case, depended on the initial condition. In some cases (not shown here), the two orientations in this period maintained an equal low level of activity.

With blank intervals inserted before each swap, the model showed responses similar to those in the static image condition, except that the responses dropped at the time of blank (Fig. S4 D and E; also see Fig. 4C for the stimulus). These results were not consistent with studies reporting a high proportion of SA in the presence of the blank (22, 23).

The model generated winner-take-all behavior for monocular plaids as one orientation dominated over the other indefinitely (Fig. S6C). In addition, the model exhibited response alternations for binocular plaids with the same amplitude as the response alternations to dichoptic gratings (Fig. S6E). These results were not consistent with the perceptual phenomena of rivalry: strong alternations for dichoptic gratings and weak or no alternations for stationary monocular and binocular plaids.

Brascamp et al.’s Model.

This model had two populations of monocular (Fig. S5A) and no binocular neurons (33). The formulation of this model was very similar to Wilson’s model, except that each monocular neuron drove three types of inhibitory neurons and also received three types of inhibition:

$$\begin{array}{l}\tau \frac{d}{dt}{E}_{l1}=-E_{l1}+\frac{100{\left[V_{l1}-g_{xx}{I}_{r2xx}-g_{xs}{I}_{r1xs}-g_{sx}{I}_{l2sx}\right]}_{+}^2}{{(10+H_{l1})}^2+{\left[V_{l1}-g_{xx}{I}_{r2xx}-g_{xs}{I}_{r1xs}-g_{sx}{I}_{l2sx}\right]}_{+}^2}\\ {\tau }_{xx}\frac{d}{dt}{I}_{l1xx}=-I_{l1xx}+E_{l1}\\ {\tau }_{xs}\frac{d}{dt}{I}_{l1xs}=-I_{l1xs}+E_{l1}\\ {\tau }_{sx}\frac{d}{dt}{I}_{l1sx}=-I_{l1sx}+E_{l1}\\ {\tau }_H\frac{d}{dt}{H}_{l1}=-H_{l1}+h{E}_{l1}.\end{array}$$

For the neuron selective for left eye l and orientation 1, there were three sources of inhibition: First, there was inhibition from the neuron selective for the right eye r and orientation 2. The weight of this inhibition was g_xx (in which xx represented cross-eye and cross-orientation; Fig. S5A, red curves). Second, there was inhibition from the neuron selective for the right eye r and orientation 1. The weight of this inhibition was g_xs (in which xs represented cross-eye and same-orientation; Fig. S5A, orange curves). Third, there was inhibition from the neuron selective for the left eye l and orientation 2. The weight of this inhibition was g_sx (in which sx represented same-eye and cross-orientation; Fig. S5A, purple curves).

We used the parameter values reported by Brascamp et al. (33): input V = 10 when the stimulus was presented; cross-eye–cross-orientation inhibition had a weight g_xx = 0.9 and time constant ${\tau }_{xx}$ = 11 ms; cross-eye–same-orientation inhibition had a weight g_xs = 0.55 and time constant ${\tau }_{xs}$ = 4 ms; same-eye–cross-orientation inhibition had a weight g_sx = 0.25 and time constant ${\tau }_{sx}$ = 26 ms; adaptation term had a gain of h = 2.4, and time constant ${\tau }_H$ = 4 s. We used the Euler method with a 0.2-ms time step for the simulations [Brascamp et al. (33) used a time step of 0.25 ms]. Further reducing the time step did not change the results. We plotted the responses of the left- and right-eye monocular neurons separately (Fig. S5 B–E, second and third row) and overlaid (Fig. S5 B–E, top row)

We replicated the findings reported by Brascamp et al. (33), demonstrating that this model exhibited SA for flickering images (Fig. S5C). The dominant orientation can be observed in the responses of the monocular neurons (instead of only in binocular neurons in Wilson’s model), consistent with psychophysical results (33). The model also correctly predicted FA for static images (Fig. S5B).

The distinction between SA and FA depended on two types of inhibition in the model. Because of cross-eye–same-orientation inhibition (g_xs), the simulated percept tended to stay within the same eye when the images were swapped. Because of same-eye–cross-orientation inhibition (g_sx), the orientation of the percept tended to be maintained when swapping. The value of g_xs was larger than g_sx so when there was no blank (static image condition), the dominant percept stayed in one eye supporting FA. However, cross-eye–same-orientation inhibition had a very short time constant (4 ms). Hence, cross-eye–same-orientation inhibition decayed when there was a blank before the swap (e.g., the blank resulted from flicker), allowing the same-eye–cross-orientation inhibition to take over, resulting in SA (see details in ref. 33). Consequently, the model also exhibited SA when a short blank was inserted before the swap (Fig. S5D; also see Fig. 4C for the stimulus).

One drawback of the model was that it exhibited SA only for blank durations less than 72 ms. For blank duration longer than that (e.g., 100 ms in Fig. S5E), the model did not predict the prevalence of SA. This was inconsistent with empirical findings that the proportion of SA was higher than FA up to 200-ms blank duration (22, 23). One possible remedy for the model was to let the decay of same-eye–cross-orientation inhibition (${\tau }_{sx}$) to be even slower so that SA could exist for longer blank durations. However, when we gradually increased the value of ${\tau }_{sx}$, we found that ${\tau }_{sx}$ could not be set longer than 32 ms. If ${\tau }_{sx}$ was longer than 32 ms, FA did not occur with the static image condition. The reason behind this observation might be that if ${\tau }_{sx}$ was too slow, the mutual inhibition (between the two orientations) accumulated within one eye would prevent a single eye from being dominant for longer than two swaps. This resulted in a percept in which the dominant orientation switched every 666 ms (similar to the simulation results with Wilson’s model; Fig. S4 D and E). Constraining the value of τ_sx ≤ 32 ms, Brascamp et al.’s model exhibited SA up to 90 ms.

For monocular plaids, the model exhibited equal activity for both orientations (Fig. S6D). Thus, even though the two monocular neurons in a single eye had mutual inhibitory connections, its weight g_sx was too small to generate response alternations. For binocular plaids, the model exhibited winner-take-all behavior as the plaid in one eye suppressed the plaid in the other eye indefinitely (Fig. S6F). This can be understood as two populations (two left-eye monocular neurons vs. two right-eye monocular neurons) competing with each other through the combination of two mutual inhibition processes: cross-eye–cross-orientation and cross-eye–same-orientation. The competition here was stronger than that from dichoptic plaids (binocular rivalry) in which only one mutual inhibition process (cross-eye–cross-orientation) was involved. These results with binocular plaids were not consistent with the empirical findings that binocular competition does not occur when the both eyes are presented with compatible images (35, 36).