Accurate age estimation in small-scale societies

Significance

Understanding demographic and evolutionary processes shaping human life history diversity depends on precise age estimations. Inferring age is a challenge in small-scale societies, and especially in those societies that do not follow a calendar year. Our method opens possibilities in demographic and life history studies allowing cross-sectional data to be incorporated in cross-cultural comparisons and a better understanding of the adaptive importance of human life history variation.

Abstract

Precise estimation of age is essential in evolutionary anthropology, especially to infer population age structures and understand the evolution of human life history diversity. However, in small-scale societies, such as hunter-gatherer populations, time is often not referred to in calendar years, and accurate age estimation remains a challenge. We address this issue by proposing a Bayesian approach that accounts for age uncertainty inherent to fieldwork data. We developed a Gibbs sampling Markov chain Monte Carlo algorithm that produces posterior distributions of ages for each individual, based on a ranking order of individuals from youngest to oldest and age ranges for each individual. We first validate our method on 65 Agta foragers from the Philippines with known ages, and show that our method generates age estimations that are superior to previously published regression-based approaches. We then use data on 587 Agta collected during recent fieldwork to demonstrate how multiple partial age ranks coming from multiple camps of hunter-gatherers can be integrated. Finally, we exemplify how the distributions generated by our method can be used to estimate important demographic parameters in small-scale societies: here, age-specific fertility patterns. Our flexible Bayesian approach will be especially useful to improve cross-cultural life history datasets for small-scale societies for which reliable age records are difficult to acquire.

Accurate estimation of the age of individuals is essential in evolutionary anthropology. Major questions in the field require an accurate inference of the timing of life history events, such as age at menarche, age at first reproduction, age at cessation of reproduction, interbirth intervals, and death. Age is also essential when assessing infant growth or developmental trajectories and when estimating age structure properties of a population (e.g., the potential for population growth or decline, recovering signatures of epidemics, assessing vulnerability to ecological perturbations). Humans have important derived life history features, such as shorter interbirth intervals, longer life span, extended postreproductive longevity, and childhood dependence (1). These life history traits vary across species in the slow/fast continuum (2), and they likely vary within humans in response to differences in ecology, such as differential mortality rates (3) and energetics (4). However, due to unreliable age estimations, very few studies have highlighted variability in life history traits in traditional societies (3, 5, 6). The challenge of estimating ages is particularly problematic for populations where individuals do not relate their age to calendar years, as is the case among many hunter-gatherer and other small-scale societies (7, 8). Although longitudinal studies (7, 9) are an ideal approach to address questions about variation in life history traits in small-scale populations, these studies are rare. There is consequently a need for methods to estimate ages based on cross-sectional data from these populations.

A few approaches have been proposed to estimate ages in small-scale societies (reviewed in 7). The simplest one is visual inspection and approximate clustering into age cohorts (e.g., infant, child, teen, adult, old age). A clear disadvantage of this method is its lack of precision, because establishing life history strategies requires a refined age structure. Furthermore, differences in physical appearance trajectories in forager populations in comparison to Western counterparts are likely to cause misattribution of ages. For instance, forager infants are often small and underdeveloped, appearing younger than their Western peers, whereas older individuals may appear older compared with Western individuals of the same age. An alternative class of approaches is exemplified by indirect demographic models developed in the field of human demography (10), which are characterized by model parameters that are estimated based on actual population data. For example, Howell (8) applied a “steady-state model” approach to the Dobe !Kung foragers. This method assumes a stable population structure, ascertains a relative age list of all individuals, and estimates the death and fertility rates of the population. This approach permits an approximation of the population age structure by mapping these rates onto different life tables (e.g., in which 80% live to the age of 1 y, 75% live to the age of 2 y, etc.) and selecting the life table with the best correspondence. Given that these life tables are created from very different populations, caveats of this approach include the difficulty in finding matching life tables, particularly for growing or declining populations for which these rates are unknown (7). Crucially, stable population models fix the proportion of individuals who live up to a certain age, which may obscure differences in life history adaptations and demography.

To overcome these problems, Hill and Hurtado (ref. 7, but ref. 11 for the Hadza) designed an alternative method to estimate the ages of Ache hunter-gatherers that did not assume a stable population. It is based on a relative age list, including all individuals, with absolute ages for a subset of individuals. The relative age list was constructed by first dividing the population into age cohorts containing individuals of approximately the same age. Each individual ranked all others within their cohort, as well as those individuals in the cohorts above and below them (i.e., either older or younger than themselves). These relative lists were combined into cohorts, and then a master population list, by selecting the rankings with the smaller number of contradictions. The absolute ages of some of the individuals were obtained from birth certificates, estimated from known events, or estimated by an “age-difference chain” (individuals were questioned about their age at the time a younger individual was born by picking an individual of a known age and matching their age at the time of birth of the younger individual) (7). Given these absolute ages and the relative age list, a fifth-order polynomial curve was fitted with relative age rank as the independent variable and age as the dependent variable. Finally, the ages of the remaining individuals were estimated as the value of the polynomial curve at the corresponding rank.

Despite improving upon previous methods, this approach still presents several drawbacks. First, the choice of a fifth-order polynomial is arbitrary. Previous investigators (11) have, for example, used third-order polynomials. Some ages may be fitted poorly by a polynomial, whereas overfitting may also be an issue, especially for datasets with few known ages. In addition, the uncertainty associated with any age estimation is not taken into account. This issue is particularly problematic in age-difference chains because the error is cumulative, leading to high uncertainty, especially for older individuals. For example, for the Ache with known ages, Hill and Hurtado (7) have shown that the error in age estimations using this age-difference chain is approximately +0.5 y (SD = 1.2) for each 12.5-y interval. Although relatively small, with the oldest individuals potentially overestimated in age by an average of ∼2 y, this method does not control for the concomitant increase in error with age. Based on SDs, this concomitant increase would be between +8.6 y and −3.4 y for the oldest individuals based on their predicted age from the regression model. This error has particular relevance for the estimation of age at some important life history events in later life, such as age at last reproduction and menopause.

Here, we present a Bayesian method for age estimation improving upon previous approaches. Bayesian approaches have previously been designed and successfully applied in, for example, paleodemography (12, 13) and radiocarbon dating in archaeology (14); however, they are not readily applied to data typically collected in anthropological fieldwork on small-scale societies. Our method requires two inputs: first, a single ranking or multiple partial rankings of individuals by age obtained from interviewing members of the population, and, second, an arbitrary a priori age distribution per individual chosen by the researchers familiar with the population, which can be based on accurate measures or on “eyeballing.” These two pieces of information are combined using a statistical inference technique called Gibbs sampling, generating a posterior age distribution for each individual. This posterior distribution represents all that can be known about the age of that individual, given the age ranks and prior age distributions. We show that our method generates more accurate age estimations than regression-based approaches on 65 individuals from a hunter-gatherer society with known ages. As further empirical validation, and to show the flexibility of our method for actual fieldwork, we present a case study on Agta foragers from Palanan, the Philippines. Finally, we analyze age-specific fertility patterns in the Agta, fully integrating the uncertainties in the estimated ages of a mother and her offspring. This case study demonstrates how the posterior distributions produced by our method can be reliably used for estimating important demographic parameters in small-scale societies for which precise dates of birth do not exist. Our method opens new possibilities in demographic and life history studies, allowing cross-sectional data to be incorporated in cross-cultural comparisons.

Results

Validation and Benchmarking: Bayesian Outperforms Regression-Based Approaches to Age Estimation.

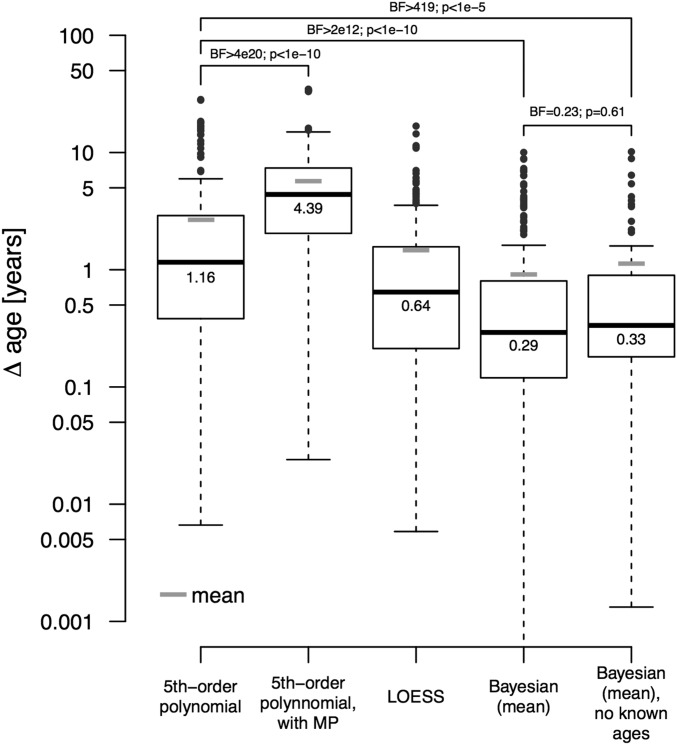
First, we assess how well our Bayesian approach estimates ages compared with regression methods. We apply fivefold cross-validation (CV) [i.e., we randomly partition 65 Agta with known ages (obtained from ref. 15) into five groups of 13 individuals, consider the ages of the individuals in each group in turn as known, and estimate the ages of the remaining individuals]. For each of the five partitions, this procedure yields 52 estimations that are then compared with the true known ages (details are provided in Materials and Methods). The results are summarized in Fig. 1 and SI Appendix, Table S1. The distribution of differences between known age and mean age estimated by our method across all five CV partitions shows that the median error of the differences per individual is about 0.29 y (i.e., 4 mo) and the mean is 0.91 y (i.e., 11 mo). Estimation accuracy becomes worse for older individuals, whose ages are inherently more difficult to estimate due to wider prior age brackets and larger age differences between the individuals (SI Appendix, Table S1). Interestingly, similar results are achieved even when no age is considered known and ages are estimated based on rank and age brackets alone. The near-equivalence of the Bayesian method with and without known ages is also supported by statistical comparison of the two distributions of error: a Bayesian t test finds no evidence for different means, whereas a nonparametric two-sided Kolmogorov–Smirnov (KS) test reports no significant differences between the two distributions [Bayes factor (BF) = 0.23, P = 0.61; Fig. 1].

Fig. 1.

Validation and benchmarking of the Bayesian approach. Box plots of absolute differences between estimated and known ages for all 65 individuals in all five partitions from the Headland database of Agta (15) are shown (also Fig. 2) for five different methods of estimation (i.e., fifth-order polynomial, fifth-order polynomial with midpoint age estimations, LOESS, Bayesian posteriors approximated by the mean, and Bayesian posteriors computed without taking into account known ages approximated by the mean). Note that the latter distribution without known ages only comprises 65 differences because no multiple partitions exist. Statistical comparisons are performed with Bayesian t tests quantifying the strength of evidence for different means of the logged distributions via BFs (BF > 3 is considered as positive evidence; BF > 150 is considered as strong evidence) and two-sided nonparametrical KS tests assessing difference between distributions (all pairwise comparisons are provided in SI Appendix, Table S2). The y axis is in log-scale to highlight the majority of differences that are below 10 (raw values are provided in SI Appendix, Fig. S6).

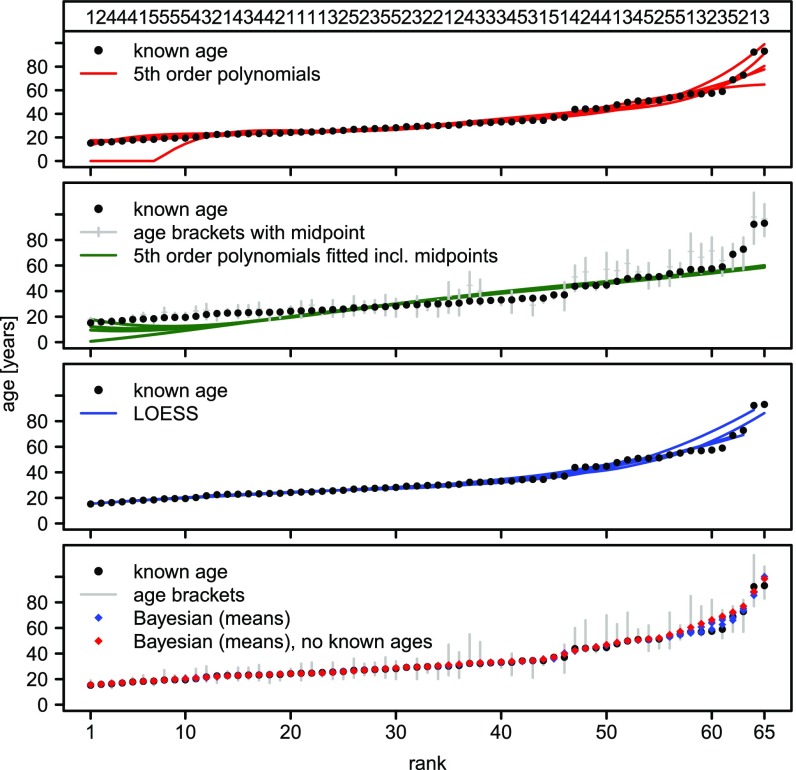
In comparison to the Bayesian approach, polynomial regression has a higher median error of the differences per individual of around 1.16 y (14 mo) and a high mean of 2.66 y (32 mo). The latter is the result of multiple outliers in the error distribution caused by high estimation errors for very young or very old individuals, especially when the closest individual with known age is far from these individuals. For example, the first individual with known age in the third partition (Fig. 2) has a rank of 12. Counterintuitively, regressing on both known ages and midpoints of the age brackets does not improve the estimation (the rationale behind including the midpoints is provided in Materials and Methods). The mean error for polynomial regression fitted with midpoints of the age brackets is 52 mo, and comparing it with the distribution without midpoints via a Bayesian t test and KS test yields very strong evidence for greater error in the model using midpoints (BF > 4 × 10²⁰, P < 1 × 10⁻¹⁰; Fig. 1). We also tested a third approach based on local regression (LOESS) (16), which drops the requirement for the data to fit a fifth-order polynomial and allows for more flexible curves. LOESS shows intermediate performance with a median error of 0.64 y (7 mo). P values and BFs of all pairwise comparisons of error distributions, including LOESS, are shown in SI Appendix, Table S2.

Fig. 2.

Experimental setup and results of validation and benchmark of the Bayesian approach. We show the results of four different ways to estimate age, including the Bayesian approach presented here. We performed fivefold CV; that is, we randomly partitioned the 65 Agta with known ages in the Headland database (15) into five groups of 13 individuals each (groups given at the top of the first panel) and used each group as the basis to estimate the age of the remaining individuals. Each panel shows the results for the five CV partitions (Top to Bottom): fifth-order polynomials; fifth-order polynomials fitted on 13 known ages and midpoints of the age brackets for the remaining individuals (age brackets are the lower and upper age limits inferred by the authors from photographs of the individuals); LOESS (16); and, finally, the Bayesian method, including the results of a sixth run where no ages are considered known.

We tested the influence of the number of known ages, using twofold to 13-fold CV. The performance of the Bayesian approach is not significantly influenced by the number of known ages. Such is not the case for the polynomial regression, for which large differences are observed, especially when fewer ages are known, mostly reducing the accuracy (details are provided in SI Appendix). Furthermore, we asked how robust the approaches are to errors in known ages and ranking order. SI Appendix, Fig. S4 shows that our Bayesian method is not influenced by slight errors in known ages, whereas polynomial regression and, to a lesser extent, LOESS follow a trend toward worse performance. Errors in ranking order cannot be tested independent of errors in known ages for regression approaches. We therefore only assessed our Bayesian approach, and find a clear impact of errors in ranking order on the estimation accuracy, as shown in SI Appendix, Fig. S5. However, even with 40% errors in the ranking order, the estimation accuracy is comparable to the estimation accuracy of polynomial regression when supplying the correct order. Finally, we explored how well the resulting posterior distributions quantify the estimation uncertainty. To be useful as quantification, a 95% credible interval, for example, should contain the true age in 95% of the individuals whose age is being estimated, whereas a 50% credible interval only in half of the individuals. We tested if highest posterior densities (HPDs) fulfill this requirement, and confirmed that HPDs closely mirror estimation uncertainty (SI Appendix, Fig. S2).

In summary, we observe that our Bayesian approach outperforms both LOESS and polynomial regression. It achieves this accuracy nearly independent of the availability of known ages and correctly quantifies estimation uncertainty. Finally, it is robust to errors in known ages and, to some extent, in rank order.

Palanan Agta Case Study: A Flexible Method for Fieldwork Data.

After testing the data in a longitudinal dataset with known ages, we applied our aging methodology to an anthropological cross-sectional case study on Agta foragers from the Philippines, for whom most ages are unknown. In particular, we highlight two key aspects of our approach: first, the flexibility of our method in dealing with fieldwork data by allowing for multiple partial ranks in age estimation, and, second, exemplifying how the uncertainties in age estimations can be integrated into subsequent analyses, such as estimating age-specific fertility patterns, which requires the estimation of the age of both mother and child, potentially increasing estimation errors.

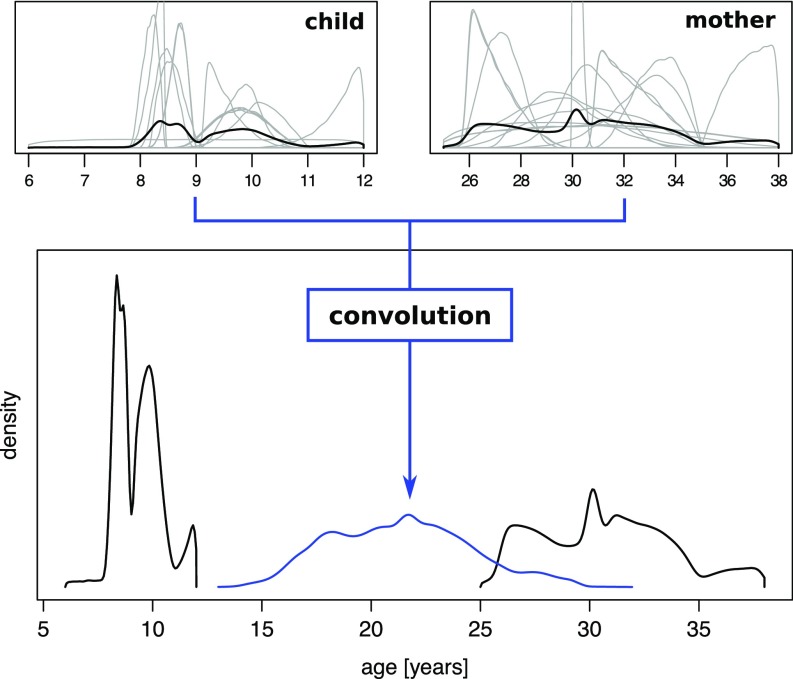
A key difficulty with small-scale societies, including the Agta, is that individuals living in geographically distant camps rarely know each other well enough to rank each other’s ages accurately. As a result, this loose pattern of familiarity among individuals precludes the assembly of a single age rank. Rather, multiple partial ranks are generated, 266 partial ranks in our case, that include different, yet overlapping, subsets of individuals, but never the entire population. One of the great flexibilities of our Bayesian approach is that this situation can be accommodated intuitively. We present our approach to multiple partial ranks informally here, and give more details in SI Appendix. In the first step, consistent partial ranks are merged. For example, $(\text{A},\text{B},\text{C})$ and $(\text{B},\text{C},\text{D})$ are consistent and can be merged to yield $(\text{A},\text{B},\text{C},\text{D})$. In contrast, $(\text{A},\text{B},\text{C})$ and $(\text{B},\text{A},\text{D})$ are not consistent, and therefore kept separate. Longer ranking orders that result from merging tend to impose stronger constraints on the prior age distributions, especially for individuals otherwise at either end of the partial rank, which results in narrower posterior distributions and, consequently, more accurate age estimations. Together with the priors on the individuals’ ages, all partial ranks resulting from this merging step are then used as input for separate runs of the Gibbs sampler, where a run produces distributions of ages for each individual contained in the partial rank. At this stage, one has multiple results from independent applications of our Bayesian approach to different partial ranks and the same age priors. The last step is to merge all distributions that belong to the same individual, generating a final age distribution per individual. To this end, the different distributions are combined to form a weighted mixture density, which can be thought of as simply adding up the various distributions and rescaling them to integrate to one. In this way, ranking orders that have been frequently reported by multiple individuals are naturally weighted more than ranking orders reported once or only a few times. Fig. 3 (Upper) demonstrates this procedure for two Agta.

Fig. 3.

Integrating uncertainties to estimate the mother’s age at parturition. (Upper) illustrations of how distinct partial rankings of individuals are combined by averaging the resulting age distributions (gray density curves) to give an overall age distribution (black density curves) per individual. The pair of individuals was chosen to be mother [Right Upper; right distribution (Lower)] and child [Left Upper; left distribution (Lower)], allowing us to “convolve” (Materials and Methods) the age distributions and obtain the posterior distribution of the mother’s age (Lower, blue density curve) at parturition.

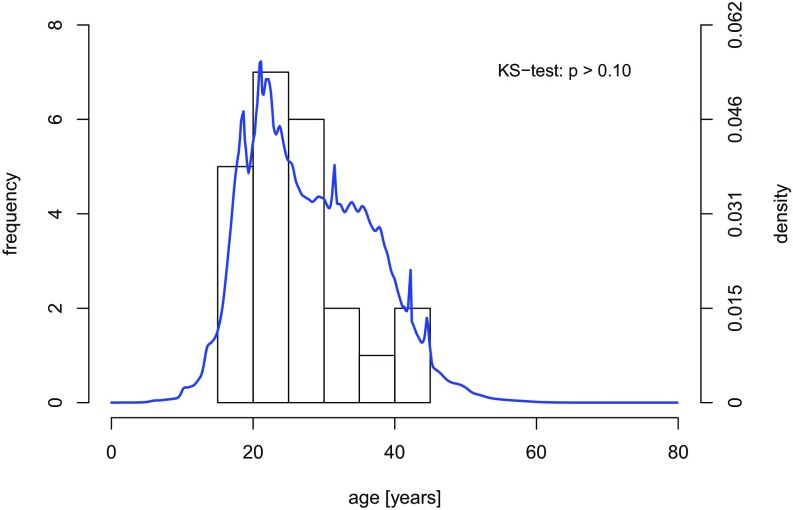
Besides its flexibility to deal with multiple partial ranks, a distinctive feature of the Bayesian approach presented here is that it produces full posterior age distributions that quantify uncertainty, rather than mere point estimates. Figs. 3 and 4 illustrate how the full information in the posterior age estimates can be integrated into subsequent analyses, age-specific fertility here. Computing the age at parturition is trivial when the ages of both mother and child are known exactly: Simply calculate the difference. However, if the age of the mother, the child, or both is uncertain, and therefore described by a distribution, the solution becomes less obvious. Our age estimation procedure faces this problem because it results in distributions that capture the uncertainty in the age estimation. In Fig. 3, we use convolution to derive the distribution of age at parturition for a mother (the definition of convolution is provided in Materials and Methods), which explicitly considers the uncertainty about maternal and child ages. This analysis was performed on all mother and child pairs, forming the mixture of the resulting distributions [think of as “averaged” (i.e., stacked and normalized)] to obtain the overall distribution of age at parturition in the Agta population. Fig. 4 depicts this posterior distribution of age at parturition separately for cases where both the mother’s and the child’s ages are known exactly from birth certificates (histogram) and for all other cases (density curve). Although we do not necessarily expect the distributions to be the same, because fewer precise ages are available for older individuals (SI Appendix, Table S3), we nonetheless fail to reject the null hypothesis that both are sampled from the same distribution (KS test, P > 0.10). We interpreted this failure to reject as an internal check validating our approach and results.

Fig. 4.

Overall distribution of age at parturition for the Palanan Agta. The overall distribution of the age at parturition in the Agta is obtained by averaging the age distributions obtained by the procedure depicted in Fig. 5 for all pairs of mother and child in our Palanan Agta dataset (blue density). This overall age distribution excludes 23 pairs for which the ages of both the mother and child are precisely known, which are shown separately (histogram).

Discussion

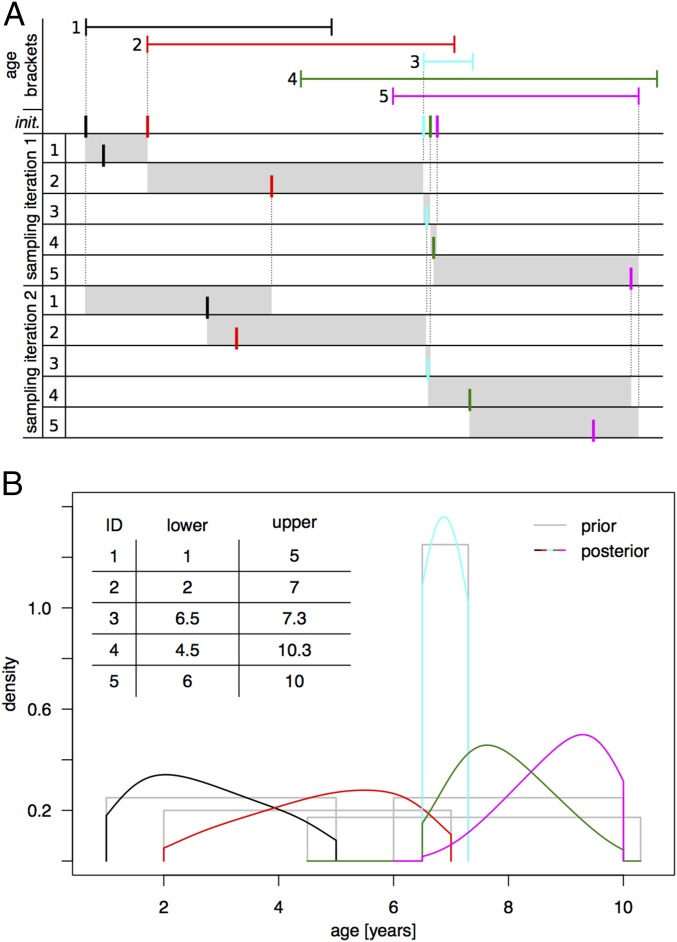
This study introduced a Bayesian approach to estimate ages in a fully probabilistic framework. Its strengths are high accuracy and great flexibility. Initial age ranges or prior distributions can be chosen from a wide spectrum of distributions to reflect the level of confidence in the a priori age estimation for each individual: from point masses when date of birth is known to wide uniform distributions when ages are vaguely estimated and lie in a poorly informed range. The second type of input data that is required is a ranking of individuals by age. However, our approach can also work on multiple partial ranks, a common difficulty when aging small-scale societies. Fig. 5B exemplifies how these two data types are integrated to produce posterior distributions that fully capture and quantify the uncertainty in the resulting age estimations.

Fig. 5.

Gibbs sampling of ages under ranking constraint (A) and exemplary input data and output of the Bayesian approach (B). (A) Illustration of how the iterative sampling of ages works. Given age brackets, the age of each individual is initialized (init.) to the smallest possible value so that, together, the ages respect the ordering constraint (here, 1 in black, 2 in red, 3 in cyan, 4 in green, and 5 in purple). Considering each individual in turn, a new age is sampled at random so that the ranking order remains valid at any time (admissible regions shaded in gray). A full mathematical description of the procedure is provided in SI Appendix. (B) Numerical example corresponding to individuals and age brackets from A and assuming uniform prior age distributions (in gray). The posterior distributions (same color code as in A, kernel-smoothed here) generated by the iterative Gibbs sampling procedure described above are shown.

By comparing our method with regression-based approaches, we have demonstrated that the Bayesian approach outperforms all regression methods considered, and furthermore correctly quantifies estimation uncertainty. Notably, this finding is true even when no known dates of birth are provided, a situation where regression-based approaches cannot be applied. Hence, our approach can also work when absolute ages for all or most individuals are not available. However, we caution that the number of individuals and the density with which they cover the range of ages are critical for the accuracy of estimated ages. No accurate estimation is possible with only a few individuals of very different ages. Nonetheless, the necessary data can be obtained in short field trips, which should make age estimations for various small-scale societies readily available, facilitating future studies on the evolution of human adaptive variation.

The Agta case study demonstrated that our method performs well in typical fieldwork conditions and challenges. The large geographical area of Agta camps made it impossible to compile a single complete age rank; therefore, we extended our basic Bayesian framework to deal with partial ranks (Fig. 3). This extension demonstrates that specific social organizations with particular traits can be integrated into our approach with relative ease, making our method widely applicable in diverse fieldwork conditions.

Finally, we analyzed the results we generated for the Agta to illustrate how the posterior age distributions produced by our method can be used in subsequent analysis. Age-specific fertility patterns are a fundamental aspect of population structure and are necessary to understand demographic and model population processes (17). Figs. 3 and 4 show how the uncertainties in the posterior age estimations can be propagated through the different steps of the analysis and integrated into the final result. In contrast, approaches based on summary statistics (e.g., mean and median, which, by definition, do not capture the full information contained in the data) or binning point estimations into arbitrary age classes may distort and inflate confidence in final results, and do not allow comparisons at the individual level.

The example above illustrates the importance for future work to derive statistical methods that use the posterior age distributions directly, and therefore the full information content of the data. In these cases, the potential of our probabilistic approach can be fully reached, although we show in Fig. 1 that point estimations (mean age of the posterior distribution) generated by our method already improve accuracy. Even though no generic solutions exist for analyses involving ages, standard approaches, such as resampling from the posterior distribution, can be implemented on top of the output produced by our method. It should be noted that, as with all Markov chain Monte Carlo (MCMC)-based Bayesian approaches, the MCMC chain, once mixed, is a sample from the posterior, making such approaches easy to implement.

In summary, our Bayesian approach has the potential to increase the utility of cross-cultural life history datasets for hunter-gatherers and small-scale societies living in various environments, and to enable robust and powerful statistical comparisons between human population groups to shed light on the adaptive processes shaping variability in human life history.

Materials and Methods

Bayesian Estimation of Age.

In contrast to previous approaches, we address age estimation in a fully probabilistic framework. For a set of individuals, two types of input data are required: (i) a ranking or ordering of all individuals by age of type A is younger than type B, is younger than type C, etc., and (ii) an a priori age distribution per individual. For example, in the simplest case, the a priori distributions may be uniform, that is, given by hard bounds on the plausible age of the individual of the type not younger than $l$ and not older than $u$, with all ages in-between equally probable. We also refer to the interval $[l,u]$ as the age bracket. We require rank order and age brackets to be compatible; that is, a combination of ages must exist that has nonzero prior probability and satisfies the ranking order. Note that in the main text we relax the requirement of a single ranking including all individuals, and allow multiple partial rankings. Ranking and prior age distributions are processed to generate a probability distribution of age per individual. If an individual is not included in any ranking order, the a priori age distribution and age bracket are all that can be known about the individual’s age.

In the following, we describe how these age distributions are generated by Gibbs sampling; the mathematical definitions can be found in SI Appendix. The heart of the procedure is iterative sampling of random numbers, which is constrained in a way to approach the desired age distributions gradually. Convergence to the correct distribution is certain and can be mathematically proven. As an example, Fig. 5A illustrates the initialization and two sampling steps for five hypothetical individuals. Say the ranking of the individuals is reflected by their label (i.e., 1 is younger than 2, is younger than 3, etc.) and their ages have been bounded a priori as shown by the age brackets. As a starting point for the sampling, we initialize the age of each individual to be the smallest possible value that satisfies both the constraints imposed by the ranking and the age brackets. In our example, doing so is achieved by choosing the left bound of the age bracket for individuals 1, 2, and 3; however, individuals 4 and 5 must be older than individual 3, and therefore appear in immediate succession after individual 3. Note that this configuration is only one of many possible starting configurations; however, as long as the ordering and age range constraints are satisfied, the actual starting point is irrelevant and all yield equal results. After setting the initial values, each individual is considered, in turn, from the youngest to the oldest and assigned a new age by random sampling. The essential requirement for Gibbs sampling to work is that the ranking constraints and age brackets are not violated. This requirement means that an appropriate range to sample a new age from has to be chosen at each step (e.g., marked by gray shading in Fig. 5A), which can be derived as follows. The youngest possible age is the higher value out of the preceding individual’s sampled age and the lower bound of the current individual’s age bracket. The oldest possible age is the lowest value out of the following: the upper bound of the current individual, the upper bound of all succeeding individuals, and the next individual’s age sampled in the previous iteration. If sampling is repeated often enough, this procedure results in individual age distributions that combine the information contained in both the age brackets and the age ranking. For the individuals introduced in Fig. 5A and uniform prior distributions, the effect is shown in Fig. 5B. Intuitively, one can think of the age ranking information as “distorting” the prior distributions. Note that the approach accommodates arbitrarily small age brackets, even containing only a single value in the extreme. Hence, if the age of certain individuals is known with certainty, this information is fully used without any change to the sampling scheme described above.

The results represent all that is known about the age of the individuals, and are a combination of all of the information already contained in the input; no information has been discarded or added based on additional assumptions. Hence, if the age brackets or the ranking contains errors, so will the output of our method. However, as we show in Results, we are able to extend our method to work with multiple partial ranks, which allows us to avoid making choices and potentially introduce ranking errors in cases where rank order is unclear. A fundamental advantage of our method is that its output is a distribution. This distribution allows subsequent analyses to incorporate the full uncertainty associated with point estimations (e.g., by confidence intervals around the mean age) or, in the best case, to use the full age distribution of an individual directly (e.g., age at parturition estimation), and therefore the entirety of the available information.

Validation and Benchmarking.

We validate our approach on 65 Agta hunter-gatherers from Casiguran (the Philippines), whose exact dates of birth are known (15) and can be directly compared with the estimations generated by our Bayesian approach. Ideally, we would have validated our method on multiple samples from populations with different age structures. However, we are not aware of any other public dataset providing both pictures and exact ages, which we require to run our method. As with any validation, we therefore caution that our performance results do not necessarily generalize beyond the dataset we used. However, because we do not make any assumption about the population, including a specific age structure, we are confident that the performance results we present extrapolate well.

As input data, we derived a relative ranking from the known dates of birth, and three of the authors (D.S., A.E.P. and M.D.) assigned upper and lower age bounds to these individuals based solely on visual inspection of the accompanying pictures (done before knowing the actual dates of birth). Because photographs were taken in different years (between 1972 and 2010), all ages and age estimations were adjusted to the year 2015; hence, the youngest age is 15 y and the oldest is 93 y. To make the results comparable, we summarized each posterior distribution by its mean, which can then easily be compared with the known age of the individual by calculating the difference between the two.

Besides validating our results against the known true ages, we also compare the quality of our inference against two alternative methods: the regression approach fitting a fifth-order polynomial (7) and a nonparametric alternative based on local regression with LOESS (18).

We implement a fivefold CV strategy. We randomly split the data into five groups of 13 individuals and consider each group in turn. For each group, we estimate the regression equation and use it to deduce the ages of the remaining individuals. Within the Bayesian framework, known ages are taken into account by choosing discrete probability masses as priors for the age of an individual rather than uniform densities over an age interval. Fig. 2 sums up our setup: the random partitioning of the individuals in five groups (numbers above first panel), the known ages and the lower and upper limits (i.e., age brackets) derived from the individuals’ pictures, and the regression curves. The lower and upper age limits vary between individuals, with older individuals tending to have wider ranges because their age is generally associated with more uncertainty. Note that the regression approaches do not accommodate information on the age ranges provided by the age brackets, whereas our Bayesian approach does. We therefore also test a fifth-order polynomial regression fitted not only on the known ages of 13 individuals for a given CV partition but on the middle values of the age brackets for all other individuals as well. As far as the differences between the method presented here and regression allow, this inclusion ensures a fair comparison because both approaches are provided with equivalent input. Finally, to test how our method would work in a situation where exact ages are impossible to obtain, we also apply our approach entirely without known ages (i.e., solely relying on the information from the age brackets and the ranking of individuals).

Case Study: Palanan Agta.

We apply our age estimation method to data we collected on the Palanan Agta, a hunter-gatherer population from northeastern Luzon, north of the Casiguran Agta, to demonstrate the application and flexibility of our method. We give a detailed description of the collection procedure we devised for the two types of data required as input, the ranking orders, and the age brackets for all individuals in SI Appendix, Sup. Materials and Methods. Ethical approval for this project was granted by the University College London Ethics Committee (UCL Ethics code 3086/003) and carried out with permission from local government and tribal leaders in Palanan. Informed consent was obtained from all participants, and parents signed the informed consents for their children (after group and individual consultation and explanation of the research objectives in the Agta language).

Estimated Age at Parturition Based on Age Distributions of Mother and Child.

Let the age of mother and child be modeled by random variables $M$ and $C$, respectively. Analogous to the case where ages are known exactly, the age at parturition, say $P$, is then described by the difference between the two random variables, $P=M-C$. Because $M$ and $C$ are both defined by distributions, so is $P$, and the full probabilistic description of the age at parturition we seek is given by the probability density function (pdf) of $P$, say $f_P\left(x\right)$. It can be derived from the pdfs of $M$ and $C$ by a mathematical operation called “convolution”: Let $f_M\left(x\right)$ and $f_C\left(x\right)$ be the pdfs of $M$ and $C$, respectively; then

$$f_P\left(x\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{f}_M\left(\tau \right)f_C\left(\tau -x\right)d\tau .$$

Convolution can therefore be thought of as an operation transforming two distributions into one, as illustrated in Fig. 3.

Implementation and Statistical Analyses.

The Gibbs sampler has been implemented in Python 2.7 (19) and can be downloaded from our website at www.ucl.ac.uk/mace-lab/resources/software. Detailed information, including burn-in, thinning, and various diagnostic statistics, is provided in SI Appendix.

All analyses and plotting were implemented in the statistical analysis programming language R, version 3.1.3 (20). Regression analyses were performed using the functions “lm” (chapter 4 in ref. 16) and “loess” (chapter 8 in ref. 16), KS statistical tests with “ks.test,” and convolution with the function “convolve,” all from the R library “stats.” Bayesian t tests were computed by the function “ttestBF” (21) from the “BayesFactor” library. The KS test in Fig. 4 is performed by rejecting the null hypothesis at level $\alpha$ if the KS statistic $D_{n,n\text{'}}$ is greater than the critical value approximated by $c\left(\alpha \right){\left(\frac{n+n\text{'}}{nn\text{'}}\right)}^{1/2}$, with $c\left(0.1\right)=1.22$ (tables 54 and 55 in ref. 22) and $n$ and $n\text{'}$ being the sample sizes: here, 23 exact ages at parturition (summarized in the histogram) versus a distribution derived from 324 mother/child pairs.