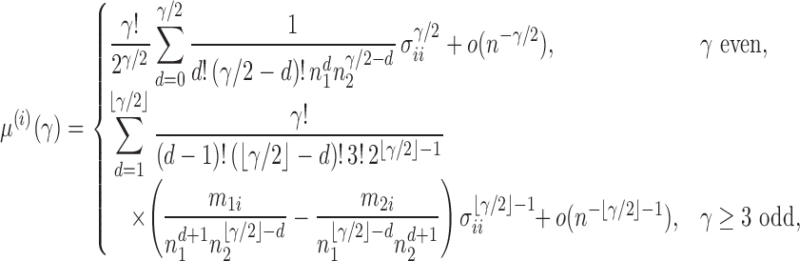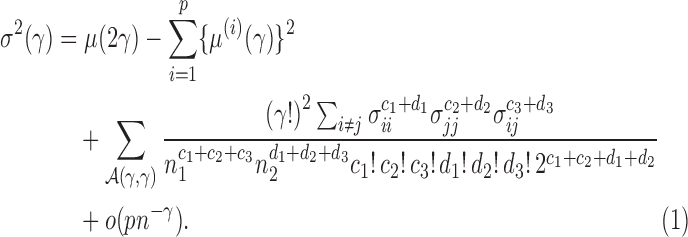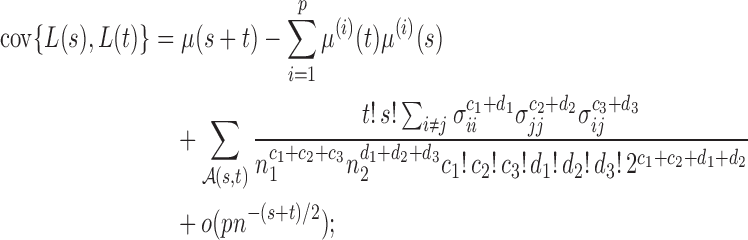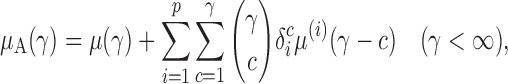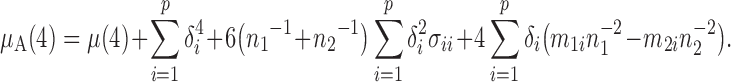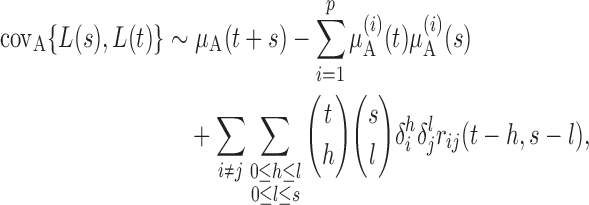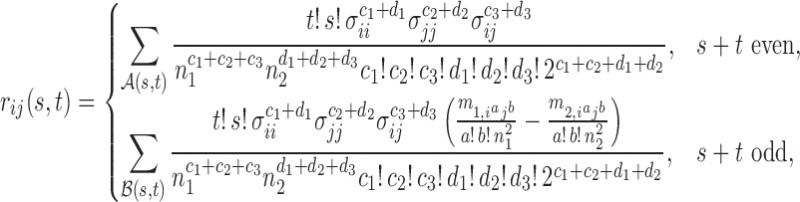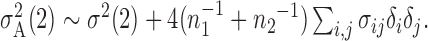SUMMARY
Several two-sample tests for high-dimensional data have been proposed recently, but they are powerful only against certain alternative hypotheses. In practice, since the true alternative hypothesis is unknown, it is unclear how to choose a powerful test. We propose an adaptive test that maintains high power across a wide range of situations and study its asymptotic properties. Its finite-sample performance is compared with that of existing tests. We apply it and other tests to detect possible associations between bipolar disease and a large number of single nucleotide polymorphisms on each chromosome based on data from a genome-wide association study. Numerical studies demonstrate the superior performance and high power of the proposed test across a wide spectrum of applications.
Keywords: Genome-wide association study, Single nucleotide polymorphism, Sum-of-powers test
1. Introduction
Two-sample testing on the equality of two high-dimensional means is common in genomics and genetics. For instance, Chen & Qin (2010) considered analysis of differential expressions for gene sets based on microarray data. In our motivating example and other genome-wide association studies (The International Schizophrenia Consortium, 2009), polygenic testing is of interest: one would like to test whether there is any association between a disease and a large number of genetic variants, mostly single nucleotide polymorphisms. In these applications, the dimension of the data, 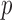 , is often much larger than the sample size
, is often much larger than the sample size 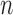 . Traditional multivariate two-sample tests, such as the
. Traditional multivariate two-sample tests, such as the 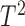 -test of Hotelling (1931), either cannot be directly applied or have too low power. As shown theoretically in Fan (1996), as the dimension
-test of Hotelling (1931), either cannot be directly applied or have too low power. As shown theoretically in Fan (1996), as the dimension 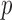 increases, even for simple one-sample testing on the mean of a normal distribution with a known covariance matrix
increases, even for simple one-sample testing on the mean of a normal distribution with a known covariance matrix 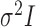 , the standard Wald, score or likelihood ratio tests may have power that decreases to the Type I error rate as the departure from the null hypothesis increases. Several two-sample tests for high-dimensional data have been proposed (Bai & Saranadasa, 1996; Srivastava & Du, 2008; Chen & Qin, 2010; Cai et al., 2014; Gregory et al., 2015; Srivastava et al., 2015). There are two common types of testing approach when
, the standard Wald, score or likelihood ratio tests may have power that decreases to the Type I error rate as the departure from the null hypothesis increases. Several two-sample tests for high-dimensional data have been proposed (Bai & Saranadasa, 1996; Srivastava & Du, 2008; Chen & Qin, 2010; Cai et al., 2014; Gregory et al., 2015; Srivastava et al., 2015). There are two common types of testing approach when 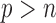 : one based on the sum-of-squares of the sample mean differences and the other based on the maximum componentwise sample mean difference. The two types of tests are powerful against different alternatives: if the true mean differences are dense in the sense that there is a large proportion of small to moderate componentwise differences, then the former type is more powerful; in contrast, if the true mean differences are sparse in the sense that there are only few but large nonzero componentwise differences, the latter type of test is more powerful. In practice, however, it is unclear which should be applied. Furthermore, as will be shown in the simulation study, there are denser and intermediate situations in which neither type of test is powerful.
: one based on the sum-of-squares of the sample mean differences and the other based on the maximum componentwise sample mean difference. The two types of tests are powerful against different alternatives: if the true mean differences are dense in the sense that there is a large proportion of small to moderate componentwise differences, then the former type is more powerful; in contrast, if the true mean differences are sparse in the sense that there are only few but large nonzero componentwise differences, the latter type of test is more powerful. In practice, however, it is unclear which should be applied. Furthermore, as will be shown in the simulation study, there are denser and intermediate situations in which neither type of test is powerful.
In this paper, we develop an adaptive testing procedure which yields high testing power against various alternative hypotheses in the high-dimensional setting. This is achieved through combining information across a class of sum-of-powers tests, including tests based on the sum-of-squares of the mean differences and the supremum mean difference. The main idea is to incorporate multiple tests in the procedure so that at least one of them would yield a high power for a particular application with unknown truth. The proposed adaptive sum-of-powers test then selects the most powerful of the candidate tests. To perform the proposed test, we establish the asymptotic null distribution of the adaptive test statistic. In particular, we derive the joint asymptotic distribution for a set of the sum-of-powers test statistics. The marginal distributions of the test statistics converge to the normal distribution or the extreme value distribution, depending on the power parameters. Based on the theoretical results, we develop a new way to calculate asymptotic 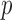 -values for the adaptive test.
-values for the adaptive test.
We further demonstrate the superior performance of the proposed adaptive test in the context of large 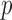 and small
and small 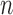 . We compare its performance with several existing tests which have not yet been applied to single nucleotide polymorphism data. Due to the discrete nature of single nucleotide polymorphism data, normal-based parametric tests are not suitable. In addition, although the sparsity assumption has been so widely adopted, the nonzero differences in single nucleotide polymorphism data may not be sparse, as predicted by the polygenic theory of Fisher (1918). The problem of nonsparse signals has begun to attract the attention of statisticians (e.g., Hall et al., 2014). It is highly relevant here because the performance of a test, especially a nonadaptive one, may depend on how sparse the signals are, as illustrated in the real-data analysis. An R (R Development Core Team, 2016) package highmean that implements the tests studied here is available from the Comprehensive R Archive Network, CRAN.
. We compare its performance with several existing tests which have not yet been applied to single nucleotide polymorphism data. Due to the discrete nature of single nucleotide polymorphism data, normal-based parametric tests are not suitable. In addition, although the sparsity assumption has been so widely adopted, the nonzero differences in single nucleotide polymorphism data may not be sparse, as predicted by the polygenic theory of Fisher (1918). The problem of nonsparse signals has begun to attract the attention of statisticians (e.g., Hall et al., 2014). It is highly relevant here because the performance of a test, especially a nonadaptive one, may depend on how sparse the signals are, as illustrated in the real-data analysis. An R (R Development Core Team, 2016) package highmean that implements the tests studied here is available from the Comprehensive R Archive Network, CRAN.
2. Some existing tests
Suppose that we observe two groups of 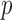 -dimensional independent and identically distributed samples
-dimensional independent and identically distributed samples 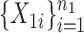 and
and 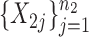 ; we consider high-dimensional data with
; we consider high-dimensional data with 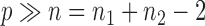 . Let
. Let 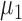 and
and 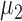 denote the true mean vectors of the groups, and assume throughout that the two groups share a common covariance matrix
denote the true mean vectors of the groups, and assume throughout that the two groups share a common covariance matrix 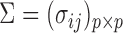 . Our primary object is to test
. Our primary object is to test 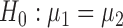 versus
versus 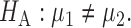 In this section, we review existing two-sample tests for high-dimensional data. For
In this section, we review existing two-sample tests for high-dimensional data. For 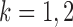 let
let 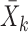 be the sample mean for group
be the sample mean for group 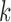 , and let
, and let 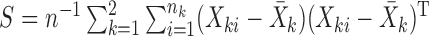 be the pooled sample covariance matrix. The precision matrix, i.e., the inverse of the covariance matrix, is written as
be the pooled sample covariance matrix. The precision matrix, i.e., the inverse of the covariance matrix, is written as 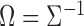 . Moreover, for a vector
. Moreover, for a vector 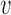 , we denote by
, we denote by 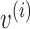 its
its 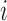 th element.
th element.
The best-known two-sample test for low-dimensional data is the 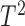 -test of Hotelling (1931), which is a generalization of the two-sample
-test of Hotelling (1931), which is a generalization of the two-sample 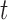 -test for
-test for  to multivariate data with
to multivariate data with 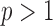 but
but 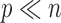 :
: 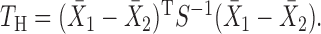 The
The 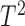 -test, however, is not applicable to high-dimensional data because
-test, however, is not applicable to high-dimensional data because 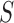 is singular. Accordingly, some modifications have been proposed in which
is singular. Accordingly, some modifications have been proposed in which 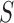 is replaced by a known quantity or another estimate. A straightforward procedure is to substitute an identity matrix
is replaced by a known quantity or another estimate. A straightforward procedure is to substitute an identity matrix 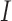 for
for 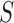 , forming a sum-of-squares-type test, which is directly based on the
, forming a sum-of-squares-type test, which is directly based on the 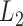 -norm of the sample mean differences,
-norm of the sample mean differences, 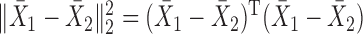 , or its weighted version (Bai & Saranadasa, 1996; Srivastava & Du, 2008; Chen & Qin, 2010). Bai & Saranadasa (1996) proposed a test statistic
, or its weighted version (Bai & Saranadasa, 1996; Srivastava & Du, 2008; Chen & Qin, 2010). Bai & Saranadasa (1996) proposed a test statistic
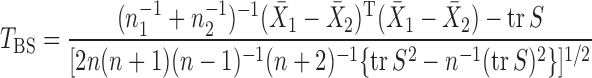 |
and established its asymptotic normal null distribution. Chen & Qin (2010) noticed some theoretical difficulties due to the presence of the cross-product terms 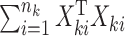 in
in 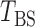 , and proposed removing them to obtain a new test statistic
, and proposed removing them to obtain a new test statistic
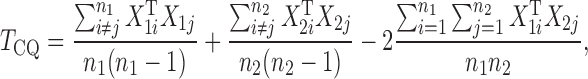 |
whose asymptotic properties were established under much weaker conditions.
To account for possibly varying variances of the components of the data, one may replace 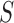 by a diagonal version
by a diagonal version 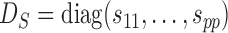 , where
, where 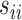 are the diagonal elements of
are the diagonal elements of 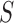 ; the matrix
; the matrix 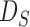 is in general nonsingular. Srivastava & Du (2008) introduced such a weighted version of the sum-of-squares-type test of Bai & Saranadasa (1996):
is in general nonsingular. Srivastava & Du (2008) introduced such a weighted version of the sum-of-squares-type test of Bai & Saranadasa (1996):
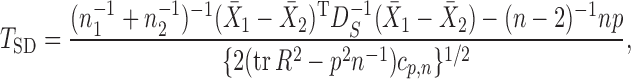 |
where 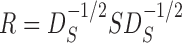 is the sample correlation matrix and
is the sample correlation matrix and 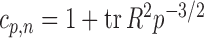 .
.
All of the above sum-of-squares-type test statistics are asymptotically distributed as normal under 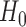 . These tests are usually powerful against moderately dense alternative hypotheses, where there is a large proportion of nonzero components in the true mean differences
. These tests are usually powerful against moderately dense alternative hypotheses, where there is a large proportion of nonzero components in the true mean differences  . However, if the nonzero signals are sparse, these tests lose substantial power (Cai et al., 2014). Accordingly, Cai et al. (2014) proposed a supremum-type statistic using the
. However, if the nonzero signals are sparse, these tests lose substantial power (Cai et al., 2014). Accordingly, Cai et al. (2014) proposed a supremum-type statistic using the 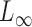 -norm of the sample mean differences, i.e.,
-norm of the sample mean differences, i.e.,
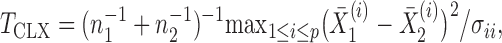 |
where 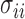 are the diagonal elements of the covariance matrix
are the diagonal elements of the covariance matrix 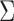 . In practice, we use the sample variances
. In practice, we use the sample variances 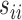 to estimate the
to estimate the 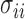 .
.
A supremum-type statistic and a sum-of-squares-type statistic represent two extremes: the former uses only a single component as evidence against the null hypothesis, while the latter uses all of the components. Neither of the statistics will be uniformly better; they are more powerful for sparse and dense nonzero signals, respectively (Gregory et al., 2015). However, for more dense or only weakly dense nonzero signals, neither may be powerful: there may not be a single component to represent a strong departure from 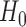 , whereas a sum-of-squares statistic may accumulate too much noise through summing over the zero components. To boost the power when nonzero signals are neither too dense nor too sparse, Chen et al. (2014) proposed removing estimated zero components through thresholding; since zero components are expected to give small squared sample mean differences, those smaller than a given threshold would be ignored, leading to a test statistic
, whereas a sum-of-squares statistic may accumulate too much noise through summing over the zero components. To boost the power when nonzero signals are neither too dense nor too sparse, Chen et al. (2014) proposed removing estimated zero components through thresholding; since zero components are expected to give small squared sample mean differences, those smaller than a given threshold would be ignored, leading to a test statistic
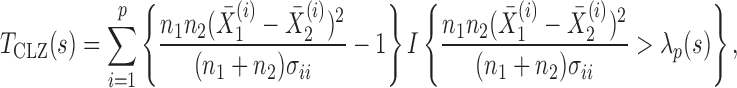 |
where the threshold level is 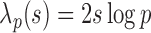 and
and 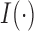 is the indicator function. Since an optimal choice of the threshold is unknown, Chen et al. (2014) proposed trying all possible threshold values and then choosing the most significant one as the final test statistic:
is the indicator function. Since an optimal choice of the threshold is unknown, Chen et al. (2014) proposed trying all possible threshold values and then choosing the most significant one as the final test statistic:
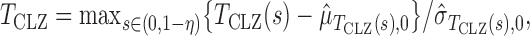 |
where 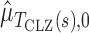 and
and 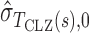 are estimates of the mean and standard deviation of
are estimates of the mean and standard deviation of 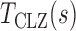 under the null hypothesis. The asymptotic null distribution of
under the null hypothesis. The asymptotic null distribution of 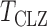 is an extreme value distribution. Because of the slow convergence to the asymptotic null distribution, Chen et al. (2014) proposed using the parametric bootstrap to calculate its
is an extreme value distribution. Because of the slow convergence to the asymptotic null distribution, Chen et al. (2014) proposed using the parametric bootstrap to calculate its 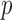 -values. The test
-values. The test 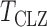 can be regarded as an adaptive test: it uses thresholding to adapt to unknown signal sparsity. It is closely related to another adaptive test for association analysis of rare variants in genetics (Pan & Shen, 2011).
can be regarded as an adaptive test: it uses thresholding to adapt to unknown signal sparsity. It is closely related to another adaptive test for association analysis of rare variants in genetics (Pan & Shen, 2011).
Remark 1. —
Sum-of-squares-type tests and supremum-type tests have also been used in analyses of genome-wide association studies with large
and small
. For example, in the framework of generalized linear models, the sum-of-squared-score test in Pan (2009) for association analysis of multiple single nucleotide polymorphisms can be regarded as a sum-of-squares-type test, while another widely used test in single nucleotide polymorphism analysis is similar to the supremum-type test of Cai et al. (2014). As shown in Pan (2011), the sum-of-squared-score test is equivalent to the variance-component-score test with a linear kernel (Wu et al., 2010) and a nonparametric multivariate analysis of variance (Wessel & Schork, 2006), both used in genetics, as well as to an empirical Bayes test for high-dimensional data (Goeman et al., 2006).
Remark 2. —
Cai et al. (2014) also introduced test statistics based on linearly transformed sample mean differences. Although they discussed the transformation only for their supremum-type statistic, the same transformation can be applied to other test statistics (Chen et al., 2014). However, the transformation may not work for very dense signals; for example, in some cases with more than
nonzero signals for
, a test using the precision matrix transformation could be outperformed by that without transformation (Cai et al., 2014). Furthermore, conducting the
-transformation requires an estimate of the
precision matrix, which is time-consuming for large
(Gregory et al., 2015). More importantly, any test can be conducted on either the original or the transformed data, which is not a focus here. Therefore, this article does not consider data transformations.
3. Main results
3.1. Test statistics
We first propose a family of sum-of-powers tests, indexed by a positive integer 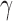 . For any
. For any 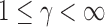 , we define a sum-of-powers test statistic with power index
, we define a sum-of-powers test statistic with power index 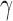 as
as
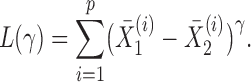 |
When 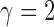 , this yields a sum-of-squares-type test statistic equivalent to that of Bai & Saranadasa (1996). Since, as an even
, this yields a sum-of-squares-type test statistic equivalent to that of Bai & Saranadasa (1996). Since, as an even 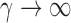 ,
,
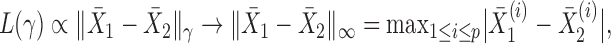 |
following the supremum-type test statistic in Cai et al. (2014) we define
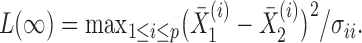 |
Thus, the class of the sum-of-powers tests includes both a sum-of-squares test and a supremum-type test as special cases. Furthermore, 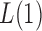 is like a burden test widely studied in genetic association analysis of rare variants for large
is like a burden test widely studied in genetic association analysis of rare variants for large 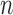 and small
and small 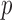 (Pan & Shen, 2011; Lee et al., 2012). If nonzero signals are extremely dense with almost the same sign, then a burden test like
(Pan & Shen, 2011; Lee et al., 2012). If nonzero signals are extremely dense with almost the same sign, then a burden test like 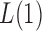 can be more powerful than both the sum-of-squares and the supremum-type tests; see our numerical examples and § 3.3. Similarly, there are situations with only weakly dense signals, in which an
can be more powerful than both the sum-of-squares and the supremum-type tests; see our numerical examples and § 3.3. Similarly, there are situations with only weakly dense signals, in which an 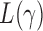 test with
test with 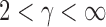 may be more powerful than both the sum-of-squares and the supremum-type tests.
may be more powerful than both the sum-of-squares and the supremum-type tests.
Which 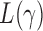 is most powerful depends on the unknown pattern of nonzero signals, such as sparsity and signal strength. Hence, we propose the following adaptive test to combine the sum-of-powers tests and improve the test power:
is most powerful depends on the unknown pattern of nonzero signals, such as sparsity and signal strength. Hence, we propose the following adaptive test to combine the sum-of-powers tests and improve the test power:
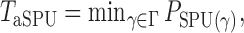 |
(1) |
where 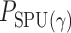 is the
is the 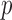 -value of
-value of 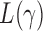 test. The idea of taking the minimum
test. The idea of taking the minimum 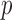 -value to approximate the maximum power has been widely used (e.g., Yu et al., 2009), but
-value to approximate the maximum power has been widely used (e.g., Yu et al., 2009), but 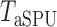 is no longer a genuine
is no longer a genuine 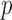 -value. In order to perform the proposed adaptive test, in the next section we derive the asymptotic distribution. In practice, one has to decide what candidate values of
-value. In order to perform the proposed adaptive test, in the next section we derive the asymptotic distribution. In practice, one has to decide what candidate values of  are to be used. From the theoretical power study in § 3.3 and the simulation study, we suggest using
are to be used. From the theoretical power study in § 3.3 and the simulation study, we suggest using 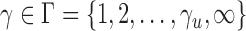 with
with 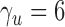 or a little bigger for a larger
or a little bigger for a larger 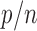 ratio.
ratio.
Remark 3. —
Our tests for small
and large
are in the same spirit as those proposed for analysis of rare variants with large
and small
(Pan et al., 2014). Specifically, Pan et al. (2014) defined spu
, where
is the score vector for a parameter, say
, in a generalized linear model under a null hypothesis
. The spu
test can be regarded as a weighted score test (Lin & Tang, 2011) with weights
. In the current context, the score
becomes the sample mean difference, so we use the same name and denote the adaptive test statistic by
in (1). Apart from, the difference between the small
large
and large
small
scenarios, asymptotic results for the adaptive test have not yet been described in the literature. In this paper we derive asymptotics of the test statistics
in the high-dimensional setting, based on which we can calculate the asymptotic
-values of
and
.
3.2. Asymptotic theory
For simplicity, we present our results under the assumption of a common covariance matrix 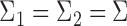 , although our derivations and proofs in the Supplementary Material are established without this assumption. In the following we write
, although our derivations and proofs in the Supplementary Material are established without this assumption. In the following we write 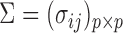 . Under
. Under 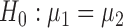 , we first derive asymptotic approximations to the mean and variance of
, we first derive asymptotic approximations to the mean and variance of 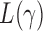 for
for 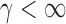 , denoted by
, denoted by 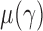 and
and 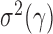 , respectively. We assume that
, respectively. We assume that 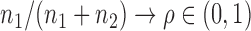 as
as 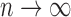 . We write
. We write 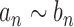 if
if 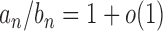 and let
and let 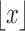 denote the largest integer not greater than
denote the largest integer not greater than 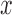 .
.
We need the following assumptions.
Condition 1 (Covariance assumption). —
There exists some constant
such that
where
and
denote the minimum and maximum eigenvalues of the covariance matrix
. In addition, all correlations are bounded away from
and 1, i.e.,
for some
.
Condition 2 (Mixing assumption). —
For a set of multivariate random vectors
and integers
, let
be the
-algebra generated by
. For each
, define the
-mixing coefficient
We assume that
is
-mixing for
and that
, where
and
is some constant.
Condition 3 (Moment assumption). —
We assume that
and max1≤i≤pE[exp{h(X(i)k1−μ(i)k)2}]<∞ for
and
.
Remark 4. —
Conditions 1 and 3 were also assumed in Cai et al. (2014), and they are needed to establish the weak convergence of
. When
, asymptotic normality can be established under weaker assumptions on the eigenvalues and correlations. However, in order to establish weak convergence of
for
, stronger moment assumptions may be needed than those in Chen & Qin (2010), whose test statistic is similar to
. Condition 2 imposes weak dependence on the data. A similar mixing condition is considered in Chen et al. (2014), and such weak dependence is also commonly assumed in time series and spatial statistics. Alternatively, we may consider the weak dependence structure introduced in Bai & Saranadasa (1996) and Chen & Qin (2010), where a factor-type model for
is assumed. Since the variables in the motivating genome-wide association studies have a local dependence structure, with their correlations often decaying to zero as their physical distances on a chromosome increase, we focus on mixing-type weak dependence in this paper.
We write 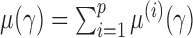 , where
, where 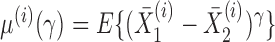 . Then the following approximation holds for
. Then the following approximation holds for  and
and  with
with 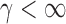 .
.
Proposition 1. —
Under
, we have
and
where
is the third central moment of the random variable in component
from group
, i.e.,
.
For any positive integers 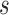 and
and 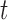 with
with 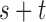 even, define a set
even, define a set 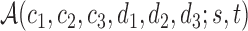 of integers
of integers 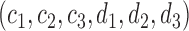 such that
such that 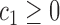 ,
, 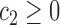 ,
, 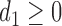 ,
, 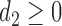 ,
, 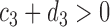 ,
, 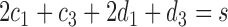 and
and 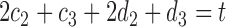 . For simplicity, we write the set as
. For simplicity, we write the set as 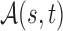 .
.
Proposition 2. —
Under Conditions 1–3 and
,
where
is a
vector whose elements are all 1, and, for
,
(2)
Because 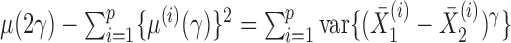 , we have that
, we have that 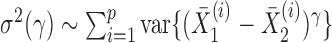 if
if 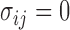 for any
for any 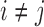 . Since the boundedness condition on the eigenvalues, Condition 1, implies the boundedness of the variances
. Since the boundedness condition on the eigenvalues, Condition 1, implies the boundedness of the variances 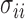 ,
, 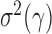 is of order
is of order 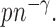
To derive the asymptotic joint distribution of the test statistics 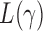 , we also need the following result to approximate their correlations:
, we also need the following result to approximate their correlations: 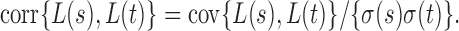
Proposition 3. —
Under Conditions 1–3 and
, for finite
, if
is even then
and if
is odd,
.
Now we are ready to introduce the asymptotic joint distributions for the test statistics 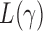 .
.
Theorem 1. —
Let
be a candidate set of
values containing
. Assume that
for
. Under Conditions 1–3 and the null hypothesis
, the following properties hold:
for the set
,
converges weakly to a normal distribution
, where
satisfies
for
and
for
. In particular,
when
is odd;
when
,
for any
, where
and
are asymptotically independent.
We can use Propositions 1–3 to approximate 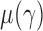 ,
, 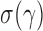 and
and 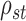 , respectively, and then calculate the
, respectively, and then calculate the 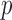 -value for the proposed adaptive test. Define
-value for the proposed adaptive test. Define 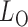 and
and 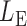 as the sets consisting of standardized
as the sets consisting of standardized 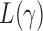 with
with 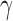 odd and even, respectively, i.e.,
odd and even, respectively, i.e., 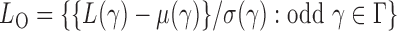 and
and 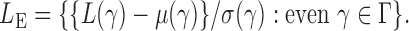 By Theorem 1,
By Theorem 1, 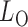 and
and 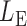 are asymptotically independent, and each is asymptotically independent of
are asymptotically independent, and each is asymptotically independent of 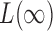 . Thus we can obtain the
. Thus we can obtain the 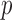 -value of the adaptive test from these three sets of statistics. Consider the realizations of the test statistics,
-value of the adaptive test from these three sets of statistics. Consider the realizations of the test statistics, 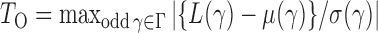 and
and 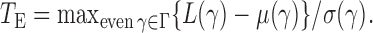 We calculate the
We calculate the 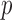 -values for
-values for 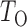 and
and 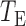 as
as 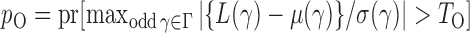 and
and 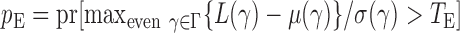 . We use the function pmvnorm in the R package mvtnorm to calculate the multivariate normal tail probabilities
. We use the function pmvnorm in the R package mvtnorm to calculate the multivariate normal tail probabilities 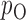 and
and 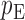 (R Development Core Team, 2016). Finally, we take the minimum
(R Development Core Team, 2016). Finally, we take the minimum 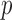 -value from the odd, even and infinity tests, i.e.,
-value from the odd, even and infinity tests, i.e., 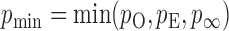 ; then, by the asymptotic independence of
; then, by the asymptotic independence of 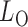 ,
, 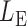 and
and 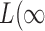 ), the asymptotic
), the asymptotic 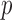 -value for the adaptive test is
-value for the adaptive test is 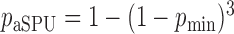 .
.
The above discussion focuses on the case where the covariance matrix 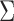 is known. In practice,
is known. In practice, 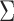 must be estimated. We can apply existing methods, such as banding and thresholding techniques, to estimate a high-dimensional sparse covariance matrix (Bickel & Levina, 2008; Rothman et al., 2010; Cai & Liu, 2011; Xue et al., 2012). In the simulation study and real-data analysis, we used the banding approach of Bickel & Levina (2008): for a sample covariance matrix
must be estimated. We can apply existing methods, such as banding and thresholding techniques, to estimate a high-dimensional sparse covariance matrix (Bickel & Levina, 2008; Rothman et al., 2010; Cai & Liu, 2011; Xue et al., 2012). In the simulation study and real-data analysis, we used the banding approach of Bickel & Levina (2008): for a sample covariance matrix 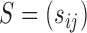 , the banded matrix with bandwidth
, the banded matrix with bandwidth 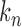 is defined as
is defined as 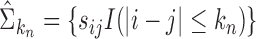 . Theoretical properties of
. Theoretical properties of 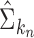 have been studied in Bickel & Levina (2008). We used five-fold crossvalidation to select an optimal bandwidth in our simulations and real-data analysis (Bickel & Levina, 2008; Cai & Liu, 2011). Under the conditions in Theorem 1, we can show that
have been studied in Bickel & Levina (2008). We used five-fold crossvalidation to select an optimal bandwidth in our simulations and real-data analysis (Bickel & Levina, 2008; Cai & Liu, 2011). Under the conditions in Theorem 1, we can show that 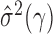 estimated based on the banded matrix
estimated based on the banded matrix 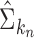 satisfies
satisfies 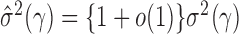 for properly chosen
for properly chosen 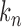 . Consider the approximation of
. Consider the approximation of 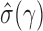 in (2). Under the weak dependence condition, Condition 2, for any
in (2). Under the weak dependence condition, Condition 2, for any 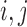 and
and 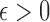 , there is a constant
, there is a constant 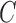 such that
such that 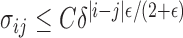 (see, e.g., Guyon, 1995). Therefore, for
(see, e.g., Guyon, 1995). Therefore, for  as
as 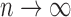 , the sum of terms with
, the sum of terms with 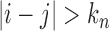 , i.e.,
, i.e., 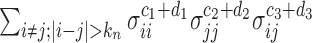 , is ignorable. On the other hand, in
, is ignorable. On the other hand, in 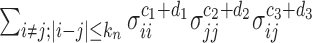 there are
there are 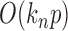 summands in total. Since
summands in total. Since 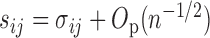 , we can obtain
, we can obtain 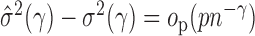 if
if 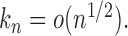 By the result that
By the result that 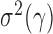 is of order
is of order 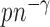 , we obtain
, we obtain 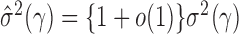 . Similarly, we can show that
. Similarly, we can show that 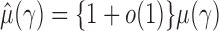 and the estimators of the correlations are consistent.
and the estimators of the correlations are consistent.
In applications, the components of the observations may be measured on different scales. Therefore, we could consider an inverse variance weighted test statistic 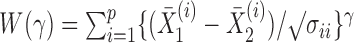 (
(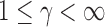 ). For
). For 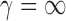 ,
, 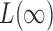 is already weighted by the inverse variances and we let
is already weighted by the inverse variances and we let 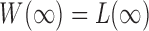 . To calculate the
. To calculate the 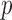 -values for
-values for 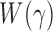 and the corresponding adaptive test, it is straightforward to use the asymptotic properties on the weighted samples
and the corresponding adaptive test, it is straightforward to use the asymptotic properties on the weighted samples 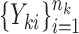 , where
, where 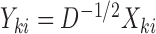 and
and 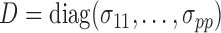 . In practice, we replace the unknown
. In practice, we replace the unknown 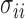 with the sample variances
with the sample variances 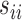 . Results similar to Theorem 1 can be established.
. Results similar to Theorem 1 can be established.
Remark 5. —
For simplicity, this paper focuses on the case where two groups of samples share a common covariance matrix. More generally, the two groups may have different covariance matrices,
. In this situation, one may apply a two-sample test without assuming a common covariance matrix: the definitions of the tests remain the same, while for the weighted tests, the weights for the sample mean differences become the reciprocals of the diagonal elements in
. The asymptotic properties of the proposed tests are still valid in this situation; see the Supplementary Material.
Remark 6. —
The asymptotic independence of the sum-of-squares- and supremum-type statistics has been studied in Hsing (1995) for weakly dependent observations. Under the sparse signal alternative with
, similar tests to the proposed
and
have also been studied in Zhong et al. (2013) with an additional higher criticism thresholding of the means; the asymptotic independence between the sum-of-squares-type statistics and a screening statistic by higher criticism thresholding has been studied in Fan et al. (2015). However, our study differs from theirs in several respects. First, our proposed method is adaptive and powerful for both sparse and dense signal alternatives, as shown by the theoretical and numerical results, whereas Zhong et al. (2013) and Fan et al. (2015) focus on sparse alternatives. As illustrated in the simulation, when the signals are dense, the proposed test performs better than the thresholding-type test in Chen et al. (2014). Second, we theoretically study a family of power statistics
with different finite and infinite values of
and establish their joint distribution; Zhong et al. (2013), on the other hand, focused on
- and
-type statistics and studied their performance separately, while Fan et al. (2015) considered the limiting behaviour of the summation of a sum-of-squares-type statistic and a screening statistic by higher criticism thresholding.
3.3. Asymptotic power analysis
In this section, we analyse the asymptotic power of the proposed adaptive test. Under the alternative 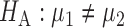 , we first derive approximations for the mean, variance and covariance functions for
, we first derive approximations for the mean, variance and covariance functions for 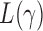 with
with 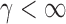 , denoted respectively by
, denoted respectively by 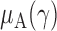 ,
, 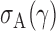 and
and 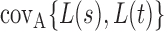 for
for 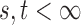 . We write
. We write 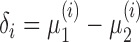 (
(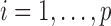 ).
).
Proposition 4. —
Under the regularity conditions in Theorem 1 and
,
where approximations for
and
are given in Proposition 1. In particular,
,
,
, and
Proposition 5. —
Under the conditions in Theorem 1 and
,
where for
or
,
, and for
and
,
where
for
and
is the set of nonnegative integers
such that
,
,
and
or
.
The variance function is
. In particular,
and
We now analyse the power of the test. For the testing statistic in (1), let 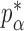 be the critical threshold under
be the critical threshold under 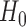 with significance level
with significance level 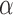 . The test power under
. The test power under 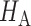 then satisfies
then satisfies 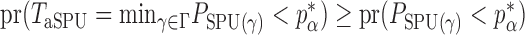 for any
for any 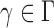 . Therefore, the asymptotic power of the proposed adaptive test is 1 if there exists
. Therefore, the asymptotic power of the proposed adaptive test is 1 if there exists 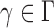 such that
such that 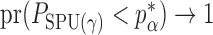 , that is, if
, that is, if 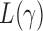 has asymptotic power equal to 1. Hence, to study the asymptotic power of the adaptive test, we only need to focus on the power of
has asymptotic power equal to 1. Hence, to study the asymptotic power of the adaptive test, we only need to focus on the power of 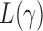 for
for 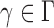 .
.
Under the alternative, we denote the set of locations of the signals by 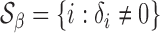 and the cardinality of
and the cardinality of 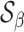 by
by 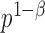 , where
, where 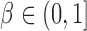 is the sparsity parameter. In the following, we consider two cases: the dense signal case with
is the sparsity parameter. In the following, we consider two cases: the dense signal case with 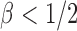 and the sparse signal case with
and the sparse signal case with 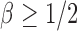 .
.
Case 1: 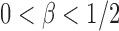 . To study the asymptotic power, we consider the local alternative with small
. To study the asymptotic power, we consider the local alternative with small 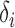 . Consider the set
. Consider the set 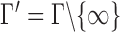 , and for any finite
, and for any finite 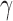 define the corresponding average standardized signal as
define the corresponding average standardized signal as 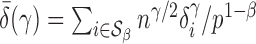 . If
. If 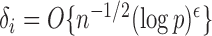 with
with 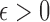 , then
, then 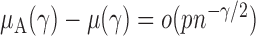 and
and 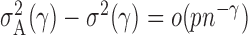 . A proof similar to that of Theorem 1 gives the following result.
. A proof similar to that of Theorem 1 gives the following result.
Theorem 2. —
Under the conditions in Theorem 1 and the alternative
with
and
for
,
converges weakly to a multivariate normal distribution with mean zero and covariance matrix
given in Proposition 5.
Theorem 2 gives the asymptotic test power of 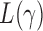 at significance level
at significance level 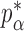 as
as
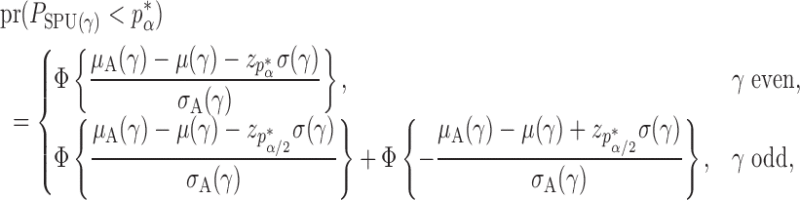 |
where 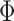 is the standard normal cumulative distribution function and
is the standard normal cumulative distribution function and 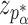 is its
is its 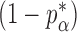 th quantile. Since
th quantile. Since 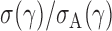 is bounded under the alternative considered, the asymptotic power is mainly dominated by
is bounded under the alternative considered, the asymptotic power is mainly dominated by 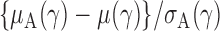 . In addition,
. In addition, 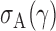 is of order
is of order 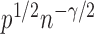 and therefore the power goes to 1 if
and therefore the power goes to 1 if 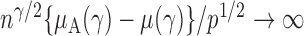 . Intuitively speaking, the power of the adaptive test converges to 1 if some of the average standardized signals are of order higher than
. Intuitively speaking, the power of the adaptive test converges to 1 if some of the average standardized signals are of order higher than 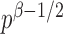 , which is
, which is 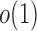 . For example, when
. For example, when 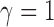 or 2, from the derivations in Proposition 4 we have that the asymptotic power of
or 2, from the derivations in Proposition 4 we have that the asymptotic power of 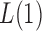 or
or 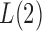 goes to 1 if
goes to 1 if 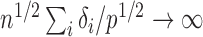 or
or 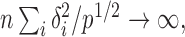 that is, if
that is, if 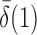 or
or 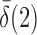 is of order higher than
is of order higher than 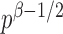 .
.
For different values of 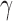 , the test statistic
, the test statistic 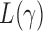 that achieves the highest power depends on the specific dense alternative. To further study the power of different test statistics
that achieves the highest power depends on the specific dense alternative. To further study the power of different test statistics  and how to choose the set
and how to choose the set 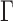 , we consider a special case where the signal strength is fixed at the same level,
, we consider a special case where the signal strength is fixed at the same level, 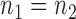 ,
, 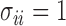 and
and 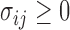 . In this case, we show in the Supplementary Material that under the alternative hypothesis with small
. In this case, we show in the Supplementary Material that under the alternative hypothesis with small 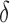 , the
, the 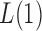 test is asymptotically more powerful than the other
test is asymptotically more powerful than the other 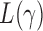 tests. On the other hand, because of the slow convergence rate to the asymptotic distribution, which depends on the value of
tests. On the other hand, because of the slow convergence rate to the asymptotic distribution, which depends on the value of 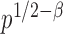 , the performance of
, the performance of 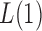 for a finite sample may not be as good as that of
for a finite sample may not be as good as that of 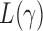 tests with
tests with 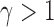 , especially when the sparsity parameter
, especially when the sparsity parameter 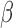 is close to
is close to 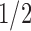 and
and 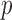 is not large enough; see the Supplementary Material. Similarly, we can show that
is not large enough; see the Supplementary Material. Similarly, we can show that 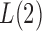 is asymptotically more powerful if the absolute values of the
is asymptotically more powerful if the absolute values of the 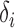 have the same level but the signs are random with about half being positive.
have the same level but the signs are random with about half being positive.
Case 2: 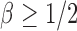 . The result in Case 1 implies that when
. The result in Case 1 implies that when 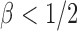 and
and 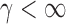 , the test power of
, the test power of 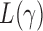 goes to 1 if
goes to 1 if 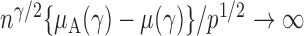 , which is satisfied in most cases if some average standardized signal is of order higher than
, which is satisfied in most cases if some average standardized signal is of order higher than 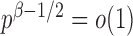 . However, in the sparse setting with
. However, in the sparse setting with 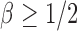 and
and 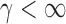 ,
, 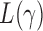 loses power. To illustrate this, take
loses power. To illustrate this, take 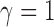 and 2. For any
and 2. For any 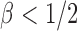 , the powers of
, the powers of 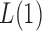 and
and 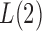 converge to 1 if
converge to 1 if 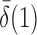 and
and 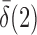 are of order higher than
are of order higher than 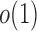 . However, when
. However, when 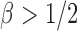 ,
, 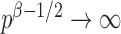 and the asymptotic powers of
and the asymptotic powers of 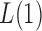 and
and 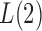 are strictly less than 1 even if
are strictly less than 1 even if 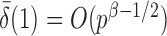 and
and 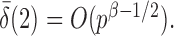
On the other hand, 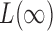 is known to be powerful against sparse alternatives; therefore, the proposed adaptive sum-of-powers test still has asymptotic power equal to 1 if that of
is known to be powerful against sparse alternatives; therefore, the proposed adaptive sum-of-powers test still has asymptotic power equal to 1 if that of 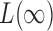 converges to 1. The asymptotic power of
converges to 1. The asymptotic power of 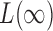 has been studied in Cai et al. (2014); from their Theorem 2, the power of
has been studied in Cai et al. (2014); from their Theorem 2, the power of 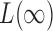 converges to 1 if
converges to 1 if 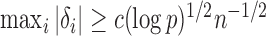 for a certain constant
for a certain constant 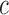 and if the nonzero
and if the nonzero 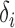 are randomly uniformly sampled with sparsity level
are randomly uniformly sampled with sparsity level 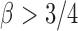 . The condition that
. The condition that 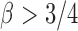 was assumed by the authors because of the technical difficulty in proving the asymptotic results. It is expected that the asymptotic power is still 1 for
was assumed by the authors because of the technical difficulty in proving the asymptotic results. It is expected that the asymptotic power is still 1 for 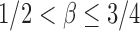 but the proof would be more challenging (Cai et al., 2014).
but the proof would be more challenging (Cai et al., 2014).
Combining the above theoretical arguments and simulation results, we recommend including small 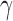 values such as
values such as 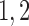 and medium
and medium 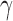 values such as
values such as 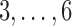 in
in 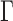 to achieve balance between the asymptotic and finite-sample performances when the signals are dense; in addition, we also recommend including
to achieve balance between the asymptotic and finite-sample performances when the signals are dense; in addition, we also recommend including 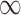 in
in 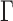 , as
, as 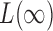 is more powerful when the signals are sparse. See the Supplementary Material for more details and simulation studies.
is more powerful when the signals are sparse. See the Supplementary Material for more details and simulation studies.
Remark 7. —
When the signal is dense,
, the
test performs similarly to the tests in Bai & Saranadasa (1996) and Chen & Qin (2010). As discussed above, there are alternatives under which
is not as powerful as other
tests, and therefore in these dense signal cases, the proposed test is more powerful than those of Bai & Saranadasa (1996) and Chen & Qin (2010), as illustrated by the simulation study. When the signal is sparse,
, the
test is equivalent to the supremum test in Cai et al. (2013), so the proposed adaptive test would perform similarly to that of Cai et al. (2013). On the other hand, under certain sparse alternatives, the
test may not be as powerful as the thresholding tests in the literature, such as the test proposed in Chen et al. (2014). To illustrate this, consider the oracle case, where the signal set
is known and has order
with
. Suppose that the
are independent standard normal and signals are at the same level
for some large constant
. Then, the oracle test statistic with power index
, namely
, has test power going to 1 if
. In particular, the log of the Type II error is of the order of
For the
test, the log of the Type II error is of the order of
Therefore, in this ideal case, the
test, which excludes nonsignal locations, is more powerful than the supremum-type test
.
4. Simulations
In this section we compare, through simulations, the performance of the proposed adaptive method and the existing tests described in §2. The candidate set of 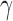 for the sum-of-powers tests
for the sum-of-powers tests 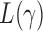 was taken to be
was taken to be  . We generated two groups of random samples,
. We generated two groups of random samples, 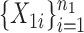 and
and 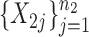 , with sample sizes
, with sample sizes 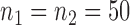 , from two multivariate normal distributions of dimension
, from two multivariate normal distributions of dimension 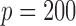 , so
, so 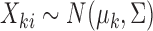 for
for 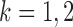 . Without loss of generality, we let
. Without loss of generality, we let 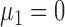 . Under the null hypothesis,
. Under the null hypothesis, 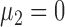 ; under the alternative hypothesis,
; under the alternative hypothesis, 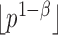 elements in
elements in 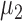 were set to nonzero values, where
were set to nonzero values, where 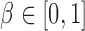 controls the signal sparsity. In our simulations we used
controls the signal sparsity. In our simulations we used 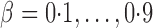 , covering very dense signals for an alternative hypothesis at
, covering very dense signals for an alternative hypothesis at 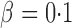 , to dense and then only moderately dense signals at
, to dense and then only moderately dense signals at 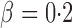 and
and 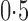 , and finally to moderately sparse and very sparse signals at
, and finally to moderately sparse and very sparse signals at 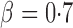 and
and 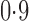 , respectively. The nonzero elements of
, respectively. The nonzero elements of 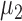 were assumed to be uniformly distributed in
were assumed to be uniformly distributed in 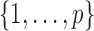 , and their values were constant at
, and their values were constant at 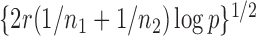 , where
, where 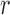 controls the signal strength. The common covariance matrix is
controls the signal strength. The common covariance matrix is 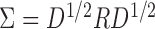 , where
, where 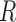 is the correlation matrix and the diagonal matrix
is the correlation matrix and the diagonal matrix 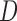 contains the variances. We considered various structures of
contains the variances. We considered various structures of 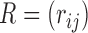 and
and 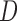 , as detailed in the Supplementary Material. To save space, here we only show results for a first-order autoregressive correlation matrix
, as detailed in the Supplementary Material. To save space, here we only show results for a first-order autoregressive correlation matrix 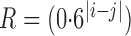 and an equal-variance case with
and an equal-variance case with 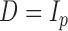 . Although this covariance matrix is only approximately bandable, we applied the banding estimator of Bickel & Levina (2008) to show the robustness of the proposed tests. For each setting, 1000 replicates were simulated to calculate the empirical Type I error and power of each test. The
. Although this covariance matrix is only approximately bandable, we applied the banding estimator of Bickel & Levina (2008) to show the robustness of the proposed tests. For each setting, 1000 replicates were simulated to calculate the empirical Type I error and power of each test. The 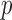 -values were calculated based on both the asymptotic distributions of the tests and the permutation method with
-values were calculated based on both the asymptotic distributions of the tests and the permutation method with 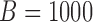 iterations. The nominal significance level was set to
iterations. The nominal significance level was set to 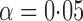 .
.
Table 1 presents empirical Type I error rates and powers for 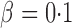 . The results of most tests based on the asymptotics are very close to those based on permutations. This validates the results in Theorem 1. The Type I error rate and power of the thresholding test
. The results of most tests based on the asymptotics are very close to those based on permutations. This validates the results in Theorem 1. The Type I error rate and power of the thresholding test 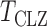 were overestimated by the corresponding asymptotic approximation, probably due to the slow convergence to its asymptotic distribution.
were overestimated by the corresponding asymptotic approximation, probably due to the slow convergence to its asymptotic distribution.
Table 1.
Empirical Type I errors and powers 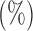 of various tests for normal samples with
of various tests for normal samples with 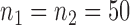 ,
, 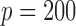 and covariance matrix
and covariance matrix 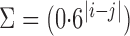 . Zero signal strength
. Zero signal strength 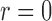 represents Type I errors, while
represents Type I errors, while 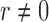 represents powers; the results outside and inside parentheses were calculated from asymptotics- and permutation-based
represents powers; the results outside and inside parentheses were calculated from asymptotics- and permutation-based 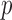 -values, respectively. The sparsity parameter was
-values, respectively. The sparsity parameter was  , leading to 117 nonzero elements in
, leading to 117 nonzero elements in 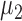 with a constant value of
with a constant value of 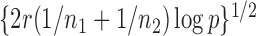
| Test | 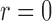 |
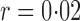 |
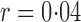 |
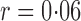 |
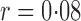 |
|---|---|---|---|---|---|
| SPU(1) | 5 (5) | 50 (46) | 78 (76) | 92 (91) | 98 (97) |
| SPU(2) | 5 (5) | 22 (20) | 47 (46) | 69 (67) | 87 (85) |
| SPU(3) | 4 (4) | 40 (40) | 71 (70) | 88 (89) | 97 (97) |
| SPU(4) | 5 (5) | 19 (18) | 38 (37) | 61 (60) | 79 (78) |
| SPU(5) | 4 (5) | 24 (25) | 47 (49) | 70 (72) | 84 (86) |
| SPU(6) | 4 (4) | 13 (14) | 26 (29) | 42 (45) | 60 (64) |
SPU(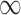 ) ) |
6 (5) | 12 (9) | 18 (15) | 25 (21) | 35 (28) |
| aSPU | 6 (5) | 33 (34) | 66 (66) | 85 (85) | 94 (94) |
| CLZ | 12 (5) | 33 (15) | 56 (34) | 77 (57) | 91 (76) |
| CLX | 6 (5) | 12 (9) | 18 (15) | 25 (21) | 35 (28) |
| BS | 6 (5) | 23 (20) | 48 (46) | 70 (67) | 88 (85) |
| CQ | 6 (5) | 23 (20) | 48 (46) | 70 (67) | 88 (85) |
| SD | 4 (5) | 19 (19) | 43 (45) | 67 (68) | 85 (86) |
SPU, the proposed sum-of-powers tests with different values of 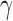 ; aSPU, the
adaptive sum-of-powers test; CLZ, test of Chen et al. (2014); CLX, test of
Cai et al. (2014); BS, test of Bai & Saranadasa (1996); CQ, test of Chen &
Qin (2010); SD, test of Srivastava & Du (2008).
; aSPU, the
adaptive sum-of-powers test; CLZ, test of Chen et al. (2014); CLX, test of
Cai et al. (2014); BS, test of Bai & Saranadasa (1996); CQ, test of Chen &
Qin (2010); SD, test of Srivastava & Du (2008).
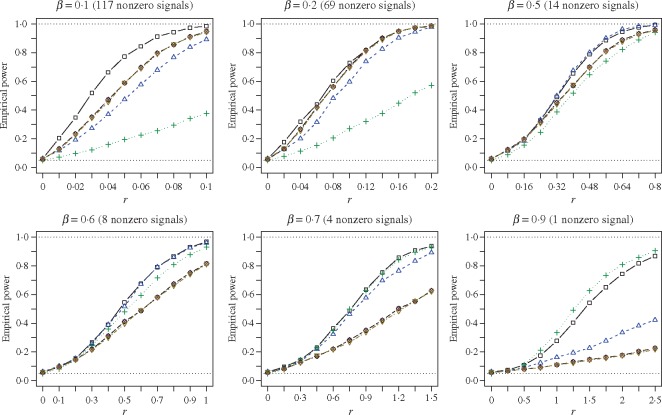
Since the Type I error rates of all the tests were well controlled by their permutation-based 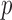 -values, we present the permutation-based powers in Fig. 1 to offer a fair comparison between the tests. The proposed adaptive sum-of-powers test
-values, we present the permutation-based powers in Fig. 1 to offer a fair comparison between the tests. The proposed adaptive sum-of-powers test 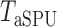 was much more powerful than the other tests when the signals were highly dense, with
was much more powerful than the other tests when the signals were highly dense, with 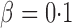 . When the signal sparsity increased from
. When the signal sparsity increased from 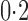 to
to 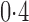 , the adaptive sum-of-powers test performed similarly to the sum-of-squares-type tests in Bai & Saranadasa (1996), Srivastava & Du (2008) and Chen & Qin (2010), and it was slightly more powerful than the thresholding test in Chen et al. (2014) and much more powerful than the supremum-type test in Cai et al. (2014). As the signals became less dense at
, the adaptive sum-of-powers test performed similarly to the sum-of-squares-type tests in Bai & Saranadasa (1996), Srivastava & Du (2008) and Chen & Qin (2010), and it was slightly more powerful than the thresholding test in Chen et al. (2014) and much more powerful than the supremum-type test in Cai et al. (2014). As the signals became less dense at 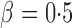 , the adaptive sum-of-powers and thresholding tests were the most powerful, closely followed by the sum-of-squares-type tests and then the supremum-type test. At
, the adaptive sum-of-powers and thresholding tests were the most powerful, closely followed by the sum-of-squares-type tests and then the supremum-type test. At 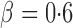 , although the adaptive sum-of-powers and thresholding tests remained the winners, the supremum-type test was more powerful than the sum-of-squares-type tests. When the signals were moderately sparse at
, although the adaptive sum-of-powers and thresholding tests remained the winners, the supremum-type test was more powerful than the sum-of-squares-type tests. When the signals were moderately sparse at 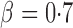 , the adaptive sum-of-powers and supremum-type tests were the most powerful, closely followed by the thresholding test; they were much more powerful than the sum-of-squares-type tests. When the signals were highly sparse at
, the adaptive sum-of-powers and supremum-type tests were the most powerful, closely followed by the thresholding test; they were much more powerful than the sum-of-squares-type tests. When the signals were highly sparse at 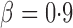 , as expected, the supremum-type test became the sole winner, and the powers of the sum-of-squares-type and thresholding tests dropped substantially; however, the power of the adaptive sum-of-powers test remained high, close to that of the winner, the supremum-type test.
, as expected, the supremum-type test became the sole winner, and the powers of the sum-of-squares-type and thresholding tests dropped substantially; however, the power of the adaptive sum-of-powers test remained high, close to that of the winner, the supremum-type test.
Fig. 1.
Empirical powers of the adaptive sum-of-powers test (squares) and the tests of Chen et al. (2014) (triangles point up), Cai et al. (2014) (plus signs), Bai & Saranadasa (1996) (crosses), Chen & Qin (2010) (diamonds), and Srivastava & Du (2008) (triangles point down). The signal sparsity parameter 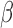 varies from
varies from 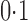 to
to 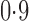 .
.
We obtained similar results for other simulation settings, including a more extreme case with a compound symmetric 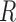 and unequal variances
and unequal variances 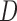 for multivariate normal data, and for simulated single nucleotide polymorphism data; see the Supplementary Material. In summary, owing to its adaptivity, the adaptive sum-of-powers test either achieved the highest power or had power close to that of the winner in any setting; it performed consistently well across all the situations. The banding estimator performed well, although occasionally the asymptotic adaptive sum-of-powers test would have slightly inflated Type I error rates when the assumptions in §3.2 were severely violated.
for multivariate normal data, and for simulated single nucleotide polymorphism data; see the Supplementary Material. In summary, owing to its adaptivity, the adaptive sum-of-powers test either achieved the highest power or had power close to that of the winner in any setting; it performed consistently well across all the situations. The banding estimator performed well, although occasionally the asymptotic adaptive sum-of-powers test would have slightly inflated Type I error rates when the assumptions in §3.2 were severely violated.
5. Real-data analysis
We applied the various tests to the bipolar disorder dataset from a genome-wide association study collected by The Wellcome Trust Case Control Consortium (2007). We used their quality control procedure to screen the subjects and obtained 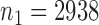 controls and
controls and 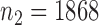 cases. We filtered out all the single nucleotide polymorphisms with minor allele frequency lower than
cases. We filtered out all the single nucleotide polymorphisms with minor allele frequency lower than 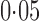 and those with Hardy–Weinberg equilibrium test
and those with Hardy–Weinberg equilibrium test 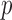 -value less than
-value less than 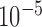 in either cases or controls, giving 354 796 variables in total. To obtain a set of single nucleotide polymorphisms in approximate linkage equilibrium, as in the work of The International Schizophrenia Consortium (2009), we used the software plink (Purcell et al., 2007) to prune them with a criterion of linkage disequilibrium
in either cases or controls, giving 354 796 variables in total. To obtain a set of single nucleotide polymorphisms in approximate linkage equilibrium, as in the work of The International Schizophrenia Consortium (2009), we used the software plink (Purcell et al., 2007) to prune them with a criterion of linkage disequilibrium 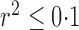 , a sliding window covering 200 single nucleotide polymorphisms, and a moving step of 20; this yielded 42 092 remaining single nucleotide polymorphisms. As The International Schizophrenia Consortium (2009) has shown that for bipolar disorder there is strong evidence of polygenic effects, we applied the various tests to the single nucleotide polymorphisms in each of the 22 autosomes separately to better demonstrate the possible power differences between the tests. The familywise nominal significance level was set at
, a sliding window covering 200 single nucleotide polymorphisms, and a moving step of 20; this yielded 42 092 remaining single nucleotide polymorphisms. As The International Schizophrenia Consortium (2009) has shown that for bipolar disorder there is strong evidence of polygenic effects, we applied the various tests to the single nucleotide polymorphisms in each of the 22 autosomes separately to better demonstrate the possible power differences between the tests. The familywise nominal significance level was set at 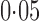 , and it would be
, and it would be  for each chromosome after Bonferroni adjustment. This indicates that 10 000 permutations should be sufficient to yield a possibly significant
for each chromosome after Bonferroni adjustment. This indicates that 10 000 permutations should be sufficient to yield a possibly significant 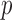 -value to reject the null hypothesis.
-value to reject the null hypothesis.
We calculated both asymptotics- and permutation-based 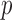 -values for each test. To save space, Table 2 shows only some representative results. Most of the asymptotics-based
-values for each test. To save space, Table 2 shows only some representative results. Most of the asymptotics-based 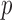 -values of the proposed sum-of-powers and adaptive tests were similar to their permutation-based ones, indicating good approximations. Again, the thresholding test
-values of the proposed sum-of-powers and adaptive tests were similar to their permutation-based ones, indicating good approximations. Again, the thresholding test 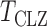 produced asymptotics-based
produced asymptotics-based 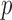 -values that were far more significant than the permutation-based ones for most chromosomes, indicating its poor approximation. The test of Srivastava & Du (2008) also performed poorly; it always gave asymptotic
-values that were far more significant than the permutation-based ones for most chromosomes, indicating its poor approximation. The test of Srivastava & Du (2008) also performed poorly; it always gave asymptotic 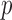 -values less than
-values less than 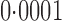 . To avoid potentially poor asymptotic approximations, we use the permutation-based
. To avoid potentially poor asymptotic approximations, we use the permutation-based 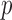 -values to compare the various tests. In chromosomes 1, 2, 3, 6, 7, 9, 14, 15 and 16, both the sum-of-squares-type tests and the adaptive sum-of-powers test gave
-values to compare the various tests. In chromosomes 1, 2, 3, 6, 7, 9, 14, 15 and 16, both the sum-of-squares-type tests and the adaptive sum-of-powers test gave 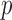 -values less than
-values less than  . In contrast, the thresholding test yielded significant
. In contrast, the thresholding test yielded significant 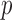 -values for only five of those chromosomes, while the supremum-type test was not significant for any chromosome. These results were presumably due to dense signals in these chromosomes, thus favouring the sum-of-squares-type tests. However, in other situations the sum-of-squares-type tests might not perform well. For example, for chromosome 13, only the sum-of-powers test
-values for only five of those chromosomes, while the supremum-type test was not significant for any chromosome. These results were presumably due to dense signals in these chromosomes, thus favouring the sum-of-squares-type tests. However, in other situations the sum-of-squares-type tests might not perform well. For example, for chromosome 13, only the sum-of-powers test 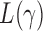 with
with 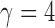 gave a significant
gave a significant 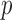 -value. Another example is chromosome 18: perhaps due to sparse signals, the supremum-type test gave the most significant
-value. Another example is chromosome 18: perhaps due to sparse signals, the supremum-type test gave the most significant 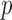 -value, but none of the sum-of-squares-type tests yielded even marginal significance; borrowing strength from the supremum-type test, i.e.,
-value, but none of the sum-of-squares-type tests yielded even marginal significance; borrowing strength from the supremum-type test, i.e., 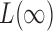 , the
, the 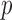 -value of the adaptive sum-of-powers test was marginally significant. In summary, owing to its adaptivity, the proposed adaptive test retained high power across various chromosomes with varying association patterns.
-value of the adaptive sum-of-powers test was marginally significant. In summary, owing to its adaptivity, the proposed adaptive test retained high power across various chromosomes with varying association patterns.
Table 2.
The 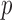 -values
-values 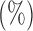 of various tests applied to the Wellcome Trust Case Control Consortium bipolar disease data; the
of various tests applied to the Wellcome Trust Case Control Consortium bipolar disease data; the 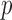 -values outside parentheses were calculated from asymptotic distributions, and those inside parentheses were based on permutations
-values outside parentheses were calculated from asymptotic distributions, and those inside parentheses were based on permutations
| Chromosome (number of single nucleotide polymorphisms) | |||||
|---|---|---|---|---|---|
| Test | 1 (3340) | 2 (3194) | 4 (2617) | 13 (1592) | 18 (1421) |
| SPU(1) | 63 6 (64 6 (64 3) 3) |
17 0 (17 0 (17 8) 8) |
0 2 (0 2 (0 2) 2) |
3 7 (3 7 (3 7) 7) |
33 0 (32 0 (32 3) 3) |
| SPU(2) |
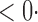 1 ( 1 (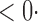 1) 1) |
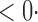 1 ( 1 (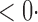 1) 1) |
1 5 (1 5 (1 7) 7) |
2 7 (2 7 (2 9) 9) |
28 9 (28 9 (28 7) 7) |
| SPU(3) | 73 8 (74 8 (74 5) 5) |
0 6 (0 6 (0 7) 7) |
3 1 (3 1 (3 1) 1) |
12 9 (12 9 (12 6) 6) |
18 7 (17 7 (17 4) 4) |
| SPU(4) |
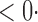 1 ( 1 (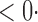 1) 1) |
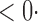 1 ( 1 (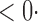 1) 1) |
2 0 (2 0 (2 7) 7) |
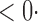 1 (0 1 (0 2) 2) |
35 3 (33 3 (33 1) 1) |
| SPU(5) | 74 2 (73 2 (73 2) 2) |
0 2 (0 2 (0 3) 3) |
37 5 (36 5 (36 1) 1) |
39 4 (37 4 (37 1) 1) |
25 9 (23 9 (23 4) 4) |
| SPU(6) |
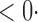 1 ( 1 (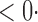 1) 1) |
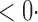 1 (0 1 (0 1) 1) |
2 7 (4 7 (4 1) 1) |
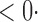 1 (0 1 (0 4) 4) |
44 8 (38 8 (38 6) 6) |
SPU(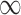 ) ) |
13 1 (11 1 (11 8) 8) |
4 5 (4 5 (4 3) 3) |
12 1 (11 1 (11 9) 9) |
8 8 (8 8 (8 0) 0) |
0 5 (0 5 (0 4) 4) |
| aSPU |
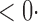 1 ( 1 (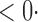 1) 1) |
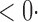 1 ( 1 (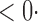 1) 1) |
1 0 (1 0 (1 2) 2) |
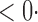 1 (1 1 (1 3) 3) |
1 4 (1 4 (1 9) 9) |
| CLZ |
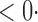 1 ( 1 (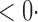 1) 1) |
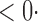 1 (0 1 (0 3) 3) |
9 6 (10 6 (10 2) 2) |
0 2 (0 2 (0 5) 5) |
5 6 (6 6 (6 6) 6) |
| CLX | 13 1 (11 1 (11 8) 8) |
4 5 (4 5 (4 3) 3) |
12 1 (11 1 (11 9) 9) |
8 8 (8 8 (8 0) 0) |
0 5 (0 5 (0 4) 4) |
| BS |
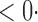 1 ( 1 (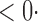 1) 1) |
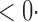 1 ( 1 (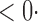 1) 1) |
1 5 (1 5 (1 7) 7) |
2 6 (2 6 (2 9) 9) |
28 8 (28 8 (28 7) 7) |
| CQ |
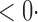 1 ( 1 (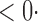 1) 1) |
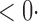 1 ( 1 (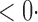 1) 1) |
1 5 (1 5 (1 7) 7) |
2 7 (2 7 (2 9) 9) |
29 0 (28 0 (28 7) 7) |
| SD |
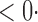 1 ( 1 (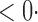 1) 1) |
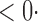 1 ( 1 (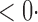 1) 1) |
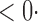 1 (1 1 (1 0) 0) |
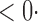 1 (11 1 (11 4) 4) |
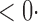 1 (9 1 (9 7) 7) |
SPU, the proposed sum-of-powers tests with different values of 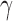 ; aSPU, the
adaptive sum-of-powers test; CLZ, test of Chen et al. (2014); CLX, test of
Cai et al. (2014); BS, test of Bai & Saranadasa (1996); CQ, test of Chen &
Qin (2010); SD, test of Srivastava & Du (2008).
; aSPU, the
adaptive sum-of-powers test; CLZ, test of Chen et al. (2014); CLX, test of
Cai et al. (2014); BS, test of Bai & Saranadasa (1996); CQ, test of Chen &
Qin (2010); SD, test of Srivastava & Du (2008).
Supplementary material
Supplementary material available at Biometrika online includes additional numerical results and proofs of the main theoretical results.
Supplementary Material
Acknowledgments
We thank the editor, an associate editor and two reviewers for many helpful and constructive comments. This research was supported by the U.S. National Institutes of Health. This study makes use of data generated by The Wellcome Trust Case Control Consortium. A full list of the investigators who contributed to the generation of the data is available at www.wtccc.org.uk. Funding for the project was provided by the Wellcome Trust. Peng Wei is also affiliated with the Human Genetics Center at the University of Texas.
References
- Bai Z. D. & Saranadasa H. (1996). Effect of high dimension: By an example of a two sample problem. Statist. Sinica 6, 311–29. [Google Scholar]
- Bickel P. J. & Levina E. (2008). Regularized estimation of large covariance matrices. Ann. Statist. 36, 199–227. [Google Scholar]
- Cai T. T. & Liu W. (2011). Adaptive thresholding for sparse covariance matrix estimation. J. Am. Statist. Assoc. 106, 672–84. [Google Scholar]
- Cai T. T., Liu W. & Xia Y. (2013). Two-sample covariance matrix testing and support recovery in high-dimensional and sparse settings. J. Am. Statist. Assoc. 108, 265–77. [Google Scholar]
- Cai T. T., Liu W. & Xia Y. (2014). Two-sample test of high dimensional means under dependence. J. R. Statist. Soc. B 76, 349–72. [Google Scholar]
- Chen S. X., Li J. & Zhong P.-S. (2014). Two-sample tests for high dimensional means with thresholding and data transformation. arXiv:1410.2848.
- Chen S. X. & Qin Y.-L. (2010). A two-sample test for high-dimensional data with applications to gene-set testing. Ann. Statist. 38, 808–35. [Google Scholar]
- Fan J. (1996). Test of significance based on wavelet thresholding and Neyman's truncation. J. Am. Statist. Assoc. 91, 674–88. [Google Scholar]
- Fan J., Liao Y. & Yao J. (2015). Power enhancement in high-dimensional cross-sectional tests. Econometrica 83, 1497–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R. A. (1918). The correlation between relatives on the supposition of Mendelian inheritance. Trans. R. Soc. Edin. 52, 399–433. [Google Scholar]
- Goeman J. J., van de Geer S. A. & van Houwelingen H. C. (2006). Testing against a high dimensional alternative. J. R. Statist. Soc. B 68, 477–93. [Google Scholar]
- Gregory K. B., Carroll R. J., Baladandayuthapani V. & Lahiri S. N. (2015). A two-sample test for equality of means in high dimension. J. Am. Statist. Assoc. 110, 837–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyon X. (1995). Random Fields on a Network: Modeling, Statistics, and Applications. New York: Springer. [Google Scholar]
- Hall P., Jin J. & Miller H. (2014). Feature selection when there are many influential features. Bernoulli 20, 1647–71. [Google Scholar]
- Hotelling H. (1931). The generalization of Student's ratio. Ann. Math. Statist. 2, 360–78. [Google Scholar]
- Hsing T. (1995). A note on the asymptotic independence of the sum and maximum of strongly mixing stationary random variables. Ann. Prob. 23, 938–47. [Google Scholar]
- Lee S., Emond M. J., Bamshad M. J., Barnes K. C., Rieder M. J., Nickerson D. A., NHLBI GO Exome Sequencing Project ESP Lung Project Team, Christiani D. C., Wurfel M. M. & Lin X. (2012). Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am. J. Hum. Genet. 91, 224–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D.-Y. & Tang Z.-Z. (2011). A general framework for detecting disease associations with rare variants in sequencing studies. Am. J. Hum. Genet. 89, 354–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. (2009). Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genet. Epidemiol. 33, 497–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. (2011). Relationship between genomic distance-based regression and kernel machine regression for multi-marker association testing. Genet. Epidemiol. 35, 211–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W., Kim J., Zhang Y., Shen X. & Wei P. (2014). A powerful and adaptive association test for rare variants. Genetics 197, 1081–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. & Shen X. (2011). Adaptive tests for association analysis of rare variants. Genet. Epidemiol. 35, 381–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M. A. R., Bender D., Maller J., Sklar P., deBakker P. I. W. & Daly M. J.. et al (2007). PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team (2016). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. http://www.R-project.org.
- Rothman A. J., Levina E. & Zhu J. (2010). A new approach to Cholesky-based covariance regularization in high dimensions. Biometrika 97, 539–50. [Google Scholar]
- Srivastava M. S. & Du M. (2008). A test for the mean vector with fewer observations than the dimension. J. Mult. Anal. 99, 386–402. [Google Scholar]
- Srivastava R., Li P. & Ruppert D. (2015). RAPTT: An exact two-sample test in high dimensions using random projections. J. Comp. Graph. Statist. 25, 954–70. [Google Scholar]
- The International Schizophrenia Consortium (2009). Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460, 748–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Wellcome Trust Case Control Consortium (2007). Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 447, 661–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessel J. & Schork N. J. (2006). Generalized genomic distance-based regression methodology for multilocus association analysis. Am. J. Hum. Genet. 79, 792–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M. C., Kraft P., Epstein M. P., Taylor D. M., Chanock S. J., Hunter D. J. & Lin X. (2010). Powerful SNP-set analysis for case-control genome-wide association studies. Am. J. Hum. Genet. 86, 929–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Xue L., Ma S. & Zou H. (2012). Positive-definite
 -penalized estimation of large covariance matrices. J. Am. Statist. Assoc. 107, 1480–91. [Google Scholar]
-penalized estimation of large covariance matrices. J. Am. Statist. Assoc. 107, 1480–91. [Google Scholar] -
Yu K., Li Q., Bergen A. W., Pfeiffer R. M., Rosenberg P. S., Caporaso N., Kraft P. & Chatterjee N. (2009). Pathway analysis by adaptive combination of
 -values. Genet. Epidemiol. 33, 700–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
-values. Genet. Epidemiol. 33, 700–9. [DOI] [PMC free article] [PubMed] [Google Scholar] - Zhong P.-S., Chen S. X. & Xu M. (2013). Tests alternative to higher criticism for high-dimensional means under sparsity and column-wise dependence. Ann. Statist. 41, 2820–51. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.