Periodic perturbations in Shaker K⁺ channel gating kinetics by deletions in the S3–S4 linker

Abstract

Upon depolarization positive charges contained in the transmembrane segment S4 of voltage-dependent channels are displaced from the cytoplasmic to the external milieu. This charge movement leads to channel opening. In Shaker K⁺ channels four positively charged arginines in the S4 domain are transferred from the internal to the external side of the channel during activation. The distance traveled by the S4 segment during activation is unknown, but large movements should be constrained by the S3–S4 linker. Constructing deletion mutants, we show that the activation time constant and the midpoint of the voltage activation curve of the Shaker K⁺ channel macroscopic currents becomes a periodic function of the S3–S4 linker length for linkers shorter than 7 aa residues. The periodicity is that typical of α-helices. Moreover, a linker containing only 3 aa is enough to recover the wild-type phenotype. The deletion method revealed the importance of the S3–S4 linker in determining the channel gating kinetics and indicated that the α-helical nature of S4 extends toward its N terminus. These results support the notion that a small displacement of the S4 segment suffices to displace the four gating charges involved in channel opening.

Voltage-gated ion channels are essential for information to flow without attenuation across the nervous system. These molecular sensors of transmembrane electric field changes are proteins made up of four homologous domains or subunits, each of which contain six transmembrane segments (1). The fourth segment (S4) contains several positively charged residues every third or fourth position and its displacement driven by the electric field initiates the events leading to channel opening (refs. 2–15; for reviews see refs. 16 and 17). Mutant Shaker K⁺ channels in which arginines have been replaced by histidines display a passive proton transport across the membrane concomitant with channel activation (11). These experiments demonstrate that the charges contained in the S4 domain are relocated from the internal to the external aqueous environment of the channel during activation. The histidine mutagenesis results are consistent with a picture in which narrow vestibules line the S4 segment (11).

According to some models, the S4 segment moves during channel activation across the membrane as a sliding helix (18, 19). In these models the helical screw movement is normal to the lipid bilayer. Assuming that the S4 segment is α-helical, the transfer of 10 aa residues in Shaker K⁺ channel requires a displacement of 15 Å. On the other hand, several investigators have proposed that the electric field can be focused in a region of the membrane much narrower than the bilayer thickness. If this is the case, only small conformational changes of the voltage sensor would be necessary to translocate the gating charges through the entire electric field (e.g., ref. 16). Indeed, spectroscopic measurements indicate that voltage-dependent changes in intersubunit distance during channel activation are not larger than 4 Å (5, 7). The voltage-dependent distance changes are in almost perfect correlation with the changes in the amount of gating charge displaced by voltage (5). This finding is inconsistent with models that assume large displacements of S4 perpendicular to the plane of the membrane. However, recent results aimed to localize the position of the extracellular end and the voltage-dependent movements of S4 were explained in terms of a large outward translation of the S4 (6, 20).

We previously reported that deletions of segments of the Shaker protein contained between domains S3 and S4 have profound effects on Shaker K⁺ channel gating kinetics (21, 22). In that study the linker was defined as the stretch of amino acid contained between residues 330 and 360 (see ref. 23 and Discussion). We showed that although the number of gating charges per channel remains unmodified even in Shaker mutant channels containing S3–S4 linkers as short as 5 aa, the channel activation kinetics are 2 orders of magnitude slower (21). The successful expression of a mutant in which a stretch of 31 aa, ShakerH4Δ(6–46)Δ(330–360), between S3 and S4 was removed is utterly inconsistent with models that proposed large displacements of the S4 domain (e.g., ref. 6). Because the boundaries of the transmembrane segments and loops are poorly defined, the linker definition we used (21) should be considered as purely operational. It is one of the aims of the present work to set approximate limits to N and C terminus of the S3–S4 linker.

In the present study, we investigate in detail the role of the protein segment comprised between valine 330 and isoleucine 360 by deleting this protein region and restoring one by one both from the N and the C terminus the deleted amino acid residues. The deletion method we used here unveiled a periodicity in the activation time constants and in the half activation voltages of the mutant channels consistent with a α-helical structure of the N terminus of the S4 domain. The results also show that a very short amino acid domain suffices to recover the gating kinetics and voltage-dependent characteristic of the parent ShakerH4Δ(6–46) K⁺ channel. We conclude that a small movement of the voltage sensor can account for the full displacement of the gating charges across the electric field.

Methods

Deletion Mutants.

According to Wallner et al. (23) the S3–S4 linker is the protein domain comprised of between amino acid valine 330 and isoleucine 360. Based on this definition we constructed the deletion mutants listed below (Table 1). The mutants were named by the remaining amino acids in the S3–S4 linker as indicated in the second column of Table 1.

Table 1.

Properties of S3–S4 linker deletion mutants

Mutant	Amino acids remaining in deletion zone	τact (0)* (ms)	τdeact (0) (ms)	V1/2† (mV)	zδ†	N
ShakerΔ	VVAEEEDTLNLPKAPV
	SPQDKSSNQAMSLAI	3.2  ± 0.8	12.1  ± 1.3	−52  ± 9	1.9  ± 0.9	5
C-terminal side of the deleted region
ShakerΔΔ(330–360)	None	141.0  ± 6.1	96.7  ± 11.7	−28  ± 3	0.9  ± 0.1	10
ShakerΔΔ(330–359)	I	535.1  ± 9.2	—	−7  ± 1	0.8  ± 0.1	6
ShakerΔΔ(330–358)	AI	692.1  ± 107.0	22.7  ± 8.2	−46  ± 11	2.1  ± 0.9	5
ShakerΔΔ(330–357)	LAI	5.7  ± 0.1	161.6  ± 15.4	−41  ± 9	1.6  ± 0.9	5
ShakerΔΔ(330–356)	SLAI	89.1  ± 2.1	8.3  ± 1.1	7  ± 2	1.7  ± 0.7	5
ShakerΔΔ(330–355)	MSLAI	458.9  ± 9.8	80.9  ± 10.7	−23  ± 5	1.7  ± 1.0	7
ShakerΔΔ(330–354)	AMSLAI	13.2  ± 1.9	29.5  ± 8.9	−39  ± 9	2.8  ± 1.0	10
ShakerΔΔ(330–353)	QAMSLAI	6.4  ± 0.5	120.0  ± 48.4	−25  ± 7	2.8  ± 1.1	6
ShakerΔΔ(330–352)	NQAMSLAI	7.5  ± 2.5	42.0  ± 6.6	−23  ± 7	4.2  ± 1.1	5
ShakerΔΔ(330–350)	SSNQAMSLAI	4.5  ± 0.3	49.6  ± 6.9	−46  ± 8	2.3  ± 0.8	10
N-terminal side of the deleted region
ShakerΔΔ(331–360)	V	23.8  ± 0.3	76.2  ± 7.8	38  ± 10	2.9  ± 1.0	5
ShakerΔΔ(332–360)	VV	3.3  ± 0.2	13.1  ± 0.9	−40  ± 8	1.4  ± 0.9	5
ShakerΔΔ(333–360)	VVA	22.9  ± 8.0	220.0  ± 66.3	−77  ± 7	3.4  ± 1.0	6
Other deletion mutants
ShakerΔΔ(332–357)	VVLAI	44.1  ± 1.2	—	46  ± 7	1.2  ± 0.2	5
ShakerΔΔ(330–355)	MSLVV	1,484.0  ± 311.1	—	−2  ± 1	1.2  ± 0.2	5
A359VI360V
ShakerΔΔ(332–355)	VVMSLAI	13.4  ± 1.4	—	−42  ± 5	2.6  ± 0.5	5

ShakerΔ is the control channel ShakerH4Δ(6–46). 

^*The activation time constant at zero voltage was obtained by simple interpolation of the τ_act vs. voltage data in those cases that measurements of τ_act could be done for positive and negative voltages or by extrapolation of the data to 0 mV when the τ_act data were only obtained for positive voltages (solid lines in Fig. 2A). 

^† Parameters calculated by fitting the voltage activation data to Eq. 5. N is the number of different cell-attached patches used to measure macroscopic currents induced by ShakerΔ and S3–S4 linker mutants. 

Molecular Biology.

Constructs were prepared on n-type inactivation removed ShakerH4Δ(6–46) (ShakerΔ). The ShakerΔ K⁺ channel cDNA was originally cloned into an engineered version of the pBSTA vector. The S3–S4 deletion mutants were prepared by PCR-based mutagenesis (Expand Hi Fidelity PCR System, Roche Molecular Biochemicals; or Pfu DNA polymerase, Stratagene). Primer design, purification of the PCR products, transformation of the DH5 α or XLI blue competent Escherichia coli cells, colony selection, DNA sequencing, subcloning, and transcription to cRNA were as in Gonzalez et al. (21).

Electrophysiology.

Xenopus oocytes were injected with 50 nl of cRNA solution (0.1–0.2 μg/μl). Two to five days after cRNA injection, currents elicited by the different mutants were recorded in cell-attached macropatches of oocyte membrane. Patch pipettes of 10–30 μm had a resistance of ≈1 MΩ. Bath and pipette solutions contained 110 mM potassium methanesulfonate, 10 mM Hepes, and 2 mM CaCl₂, pH 7.2. The acquisition and basic analysis of the data were performed with PCLAMP 6.0 software (Axon Instruments, Foster City, CA) driving a 12-bit analogue interface card (labmaster dma, Scientific Solutions, Solon, OH and with our own software, analysis).

For macroscopic current analysis, pulse protocols used a holding potential of −100 mV, a test pulse between −90 and +180 mV in 3- to 10-mV increments, followed by a tail pulse at −60. The duration of the test pulse was modified according to the kinetic properties of individual mutants. Voltage-activation curves were calculated by using standard tail-current analysis (e.g., ref. 21). Activation kinetics were compared among various mutants by fitting the upper 50% of the rising phase of the current to an exponential function. The time course of channel activation was I(t) = 0 for t < d and for t > d it was fitted to:

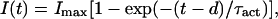1

where d is the delay and τ_act the time constant of the exponential. In a sequential model, 1/τ_act is a good estimate of the rate-limiting rate constant of the process (24). Deactivation kinetics parameters were obtained by fitting the early decay of the tail current to a sum of two exponential decays. The fastest time constant of the decay of the tail currents was used as an estimation of the rate constant for closing.

Variance Analysis and Limiting Slope Analysis.

To estimate the maximum probability of opening we collected 256–1,024 current records during activation of the channels by a depolarizing voltage step. Ensemble average current (<I>) and its variance (σ²) on each isochrone was computed as described (25). The variance (σ²) as a function of the ensemble mean current (I) data were fitted by the equation:

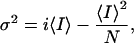2

where i is the open channel unitary current and N the number of channels in the patch (25, 26). The maximum open probability P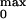 was obtained according to the relation:

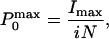3

where I_max is the maximum mean current measured in the experiment. The effective gating charge coupled to channel opening was obtained from the limiting slope analysis (27, 28). The ionic current recorded during a voltage ramp was subtracted off-line from the linear leakage and subsequently converted into conductance [g(V)] by dividing the ionic current by its driving force. The value for the effective charges per channel (z_lim) was obtained from the relationship

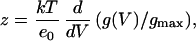4

where k is the Boltzmann constant, T the absolute temperature, g_max the maximum conductance, and e_o the charge of the electron. In the limit of large negative voltages, z will asymptotically approach a constant value equal to the total number of charges per channel, z_lim.

Evaluation of Periodicity.

For the sake of simplicity we assume that channel opening involves four independent and identical conformational changes of the subunits forming the Shaker K⁺ channel. In this model P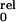 would be described by the fourth power of a Boltzmann distribution (31):

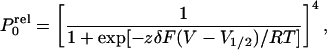5

where zδ is the equivalent charge, V_1/2 is the voltage where half of the independent and identical conformational changes have occurred, and F is Faraday's constant, R the universal gas constant and T the absolute temperature. The relative open probability can be rewritten as (31): P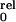 = [1 + K₀exp(−zδV/RT)]⁻⁴ where K₀ = exp(zδFV_1/2/RT) represents the voltage-dependent equilibrium constant in the absence of any applied voltage for the activation of each voltage sensor. The change in free energy caused by each deletion (ΔΔG^o) was calculated according to the relation:

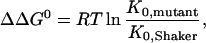6

where K_0,mutant and K_0,Shaker are the equilibrium constants for the mutants and the wild type, respectively.

The change in free energy of activation (ΔΔG*) caused by the mutations was obtained from the relation

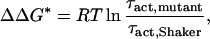7

where τ_act,mutant and τ_act,Shaker are the activation time constants determined at 0 mV for the deletion mutant and the ShakerΔ K⁺ channel, respectively.

Preliminary evaluation of the periodicity of the free energy changes as a function of the number of amino acid residues was done by fitting trigonometric functions of the form

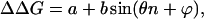8

where n is the number of amino acids remaining in the deletion region, θ is an angular frequency related to the number of amino acid residues in a period, and a, b, and ϕ are constants. Best values of a, b, θ, and ϕ were searched for by using a least-square curve-fitting procedure (solver, Microsoft excel).

Fourier transform methods (29, 37) were used to evaluate further the periodicity of the changes in Gibbs free energy between closed and open states as well as the changes in activation energy. The Fourier transform power spectrum of ΔΔG* or ΔΔG^o, P(ω), were calculated as described by Cornette et al. (29). P(ω) as a function of angular frequency ω was used to calculate the periodicity of the changes in free energy for the various mutations.

To evaluate the α-helical character from power spectra, the α-periodicity index (α) at 100^o was calculated with:

9

An ideal α-helix should give a peak in the power spectrum at ω = 100. α values >2 have been considered indicative of α-helical structure (29, 37).

Results

Deletions at the Carboxyl-Terminal End of the S3–S4 Linker.

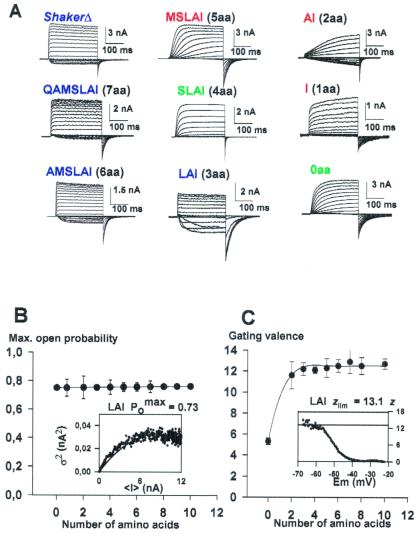
In previous studies we showed that complete removal of the region comprised between amino acid residues 330 and 360 (0-aa mutant) dramatically slowed down the ShakerΔ K⁺ channel gating kinetics (21). In view of these results, we carried out a systematic study of a series of S3–S4 linker deletion mutant channels to define the minimal linker necessary to recover the gating characteristics of the control channel. Deletion mutants constructed yield strong K⁺ currents when expressed in Xenopus laevis oocytes (Fig. 1A). The exception was the I mutant (Table 1), which expressed poorly and in many batches of oocytes we were unable to detect K⁺ currents.

Figure 1.

(A) Functional expression of deletion mutants in Xenopus oocytes. The holding potential was −100 mV, and the membrane was pulsed to voltages between −100 to +125 mV in 10-mV increments followed by a step to −60 mV. (B) Variance analysis for the deletion mutants. The solid line represents the mean P among the different linker mutants. (Inset) The mean current induced by the LAI mutant was obtained from 256 current traces recorded with the patch technique from a holding voltage of −100 mV to a test potential of 120 mV. Variance (σ²) versus mean current (<I>) was fitted to a parabola (solid line, Eq. 2) where the single channel amplitude, i, and the number of channels, N, was left as free parameters. P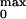 was obtained by using the relation I_max/iN. The maximum P_o was 0.73. (C) Limiting slope analysis in S3–S4 linker mutant channels. The number of charges, z, as a function of voltage was obtained by using a voltage ramp and recording the ionic current. The speed of the ramp was such to ensure steady-state conditions (1.2 mV/s), and the result was the same when ramping in the positive and the negative direction. The number of charges per channel was obtained by using Eq. 4 as illustrated in the Inset where z is plotted against applied voltage. The solid line indicates the asymptotic value of z at very hyperpolarizing voltages, z_lim. Blue, green, and red letters indicate fast, intermediate, and slow activation kinetics mutants, respectively.

Number of Equivalent Gating Charges (z_lim) per Channel and Maximum Open Probability (P).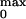

For all mutants tested, we determined the number of gating charges per channel, z_lim and maximum open probability, P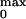. These two parameters help us to determine whether or not the deletions were affecting the charge displacement and/or the coupling of the voltage sensor movement to the pore opening (Fig. 1 B and C). P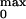 of the opening for the ShakerΔ K⁺ and the linker mutant channels was determined by using nonstationary fluctuation analysis (25, 26, 30). As an example, in Fig. 1B Inset we show the variance-mean current plot obtained for the LAI mutant. The maximum open probability was obtained by using Eq. 3 and was 0.73. We found that P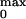 was, within experimental error, the same for the ShakerΔ K⁺ and for all of the mutants channels studied here (Fig. 1B). Τhe average maximum open probability was 0.75 (solid line, Fig. 1B).

To calculate the number of effective charges per channel (z_lim), we applied the limiting slope method. In this case, the number of charges per channel is only obtained when the probability of opening approaches zero. For all mutants we determined the slope of the logarithm of the conductance-voltage curve at low open probabilities and z at different voltages (see Eq. 4, Methods). z plotted as a function of voltage should reach a plateau that is equal to the actual value of the limiting slope, z_lim (see Fig. 1C Inset). Complete removal of the linker results in a channel with a gating valence reduced to one-half as measured by using the limiting slope method (21). For all other mutants studied the limiting slope is consistent with a gating charge of 12–13 electron charges, which is also the charge observed for the ShakerΔ (Fig. 1C).

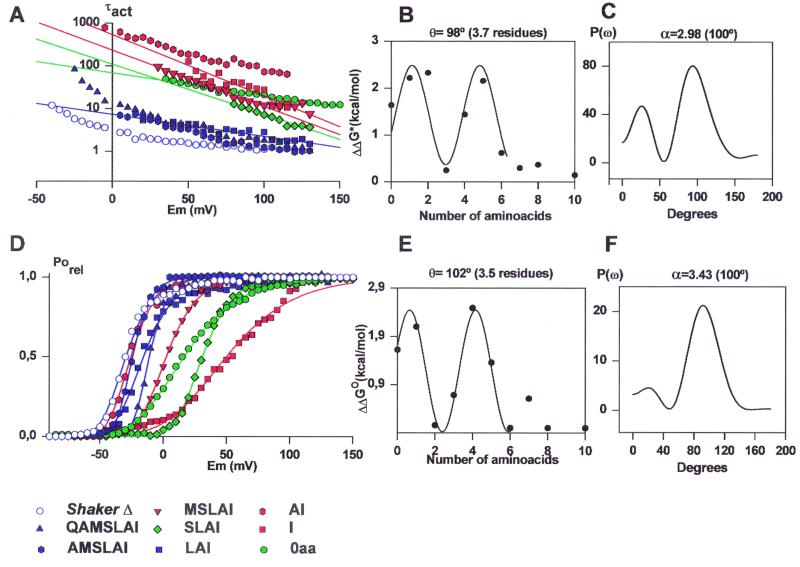
Activation Time Constants Are a Periodic Function of the Number of Amino Acids in the S3–S4 Linker.

Activation time constants (τ_act) measured as a function of voltage and the number of amino acids left on the C-terminal side of the linker are plotted on Fig. 2A. Our naive expectation was that the zero voltage activation time constant would decrease monotonically as amino acids are added to the linker, reaching a value close to the ShakerΔ when the linker is large enough. Experimental observation contradicted this expectation because the AI mutant (Table 1), instead of increasing the activation time constant with respect to the 0-aa mutant, has the effect of decreasing it. Adding a third amino acid (LAI mutant) restored the time constant value to that of the ShakerΔ. Linkers with 4 or 5 aa exhibited again activation time constants that are 28 and 143 times longer at 0 mV than the ShakerΔ activation time constant, respectively (Fig. 2A; Table 1). Mutants with S3–S4 linkers with 7, 8, or 10 aa have activation time constants similar to that obtained for ShakerΔ (Fig. 2 A and B; Table 1).

Figure 2.

(A) Voltage dependence of the activation kinetics in ShakerΔ and deletions mutants at the carboxyl-terminal end of the S3–S4 linker. 0 aa, green circles; I, red squares; AI, red hexagon; LAI, blue squares; SLAI, green diamond; MSLAI, red inverted triangles; AMSLAI, blue hexagons; QAMSLAI, blue triangles; ShakerΔ, blue open circles. The solid lines are fits to the data by using an equation of the form τ_act = A exp(−ZFV/RT) where A is a constant and Z defines the voltage dependence of τ_act. (B) Changes in activation free energy of the limiting rate of channel opening at 0 mV (ΔΔG*) induced by deletions in the protein region between S3 and S4. ΔΔG* was calculated from Eq. 7: Activation time constant data for the ShakerΔ and deletion mutant channels are from Table 1. The data are fitted to Eq. 8 with θ = 98°. (C) The power spectrum of the ΔΔG* values considering up to the value of the 7-aa deletion mutant. The maximum α periodicity index, α value (2.98) was obtained at 100°. (D) Effects on the voltage activation induced by deletions at the carboxyl-terminal end of the S3–S4 linker. Symbols are as in A. Each point is the average of determinations on 5–10 separate patches. Solid lines were drawn by using the parameters in Table 1 and Eq. 5. (E) Distribution of free energy perturbations (ΔΔG^o) in channel gating. Changes in activation free energy ΔΔG^o caused by each mutant were calculated from V_1/2 and zδ as described in Methods (Eq. 6). The data are fitted by Eq. 8 with θ = 102°. (F) Power spectrum of the ΔΔG^o values considering up to the value of the 7-aa deletion mutant. The maximum α value of 3.43 was obtained at 100°.

The change in free energy of activation (ΔΔG*) due to the mutations was obtained from the activation time constants by using Eq. 7. The ΔΔG* data, if only linker mutants containing 0–6 aa are considered, is well described by a sine function (Eq. 8) with an angle θ = 98° (Fig. 2B). This angle implies a period of 3.7 aa residues per revolution (Fig. 2B). This periodicity in the variation of the activation rate constant is consistent with a model in which the amino acids of the linker adopt some form of helical secondary structure. The Fourier transform power spectrum using the ΔΔG* values computed from the activation time constants for the linker mutants between Gln-354 and Ile-360 is shown in Fig. 2C. The strongest peak occurs at 100^o, a frequency within the characteristic range for a α-helix (29). The α-periodicity index (Eq. 9) calculated from the spectrum in Fig. 2C is 2.98.

Deactivation Time Constants.

Although the deactivation time constants also are affected by the deletions performed in the S3–S4 linker, they did not show periodicity (Table 1) and will be not discussed further in this article.

Effects on the Voltage Activation Induced by Deletions at the Carboxyl-Terminal End of the S3–S4 Linker.

Conductance versus voltage curves for the control and mutant channels were obtained directly by plotting the peak tail current amplitude at a constant postpulse potential (−60 mV). Responses to families of depolarizing pulses are shown in Fig. 1A for the ShakerΔ and 7-, 6-, 5-, 4-, 3-, 2-, 1-, and 0-aa S3-S4 linker mutants. Fig. 2D shows that mutants with activation kinetics close to that of ShakerΔ K⁺ channel have voltage activation curves qualitatively similar (compare ShakerΔ and the 7-, 6-, and 3-aa linker mutants in Fig. 2D). However, the amount of shifting to the right in the voltage activation curves is not proportional to the linker length (Table 1) and shows periodicity (see Fig. 2E). Assuming that the movement of each subunit follows a simple two-state model in which they can be in either a resting or in a permissive state, the conductance-voltage data were fit by using a Boltzmann to the fourth power (Eq. 5 in Methods). The voltage-dependent equilibrium constant in the absence of any applied voltage for the activation of each voltage sensor was calculated from the V_1/2 values obtained from fits to Eq. 5 by using the relationship K₀ = exp(zδFV_1/2/RT). The assumption of the two-state model is an oversimplification but convenient operationally to obtain the change in free energy due to the deletions, ΔΔG^o, by using Eq. 6.

Comparison of the K₀ values is meaningful because K₀ determines the equilibrium between active and resting conformation of subunits in both cases. The ΔΔG^o data are well fitted by using a sine function (Eq. 8) with θ = 102° (Fig. 2E). This angle implies a period of 3.5 aa residues, which is consistent with an α-helical structure. The power spectrum [P(ω)] shown in Fig. 2F shows a strong peak at 100° and α value of 3.43 (Eq. 9). This large α value strongly suggests that the stretch of amino acid considered, Ala-355 to Leu-361, has a α-helical structure.

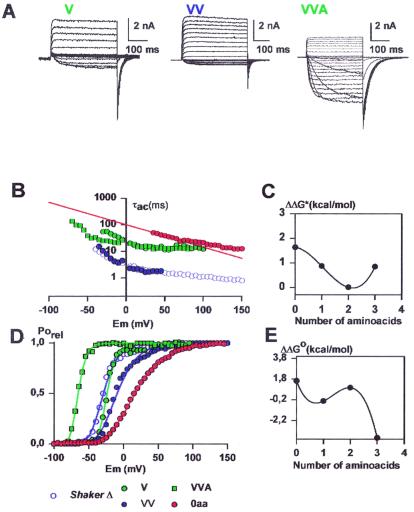
Deletions at the Amino-Terminal End of the S3–S4 Linker.

We examine now the effect of the linker length but this time by adding amino acids belonging to the N-terminal side of the linker. Ionic currents induced by the V, VV, and VVA mutants are shown in Fig. 3A. The three mutants studied have maximum probability of opening with an average value of 0.75. The number of gating charges per channel was measured by using the limiting slope method only for the VV mutant channel, and it was 12.5. The V mutant channel proved to be 7.4-fold slower than the wild-type ShakerΔ channel, and its voltage-activation curve is right-shifted by 14 mV (Fig. 3 B and D and Table 1). The voltage-activation curve for the VV mutant is right-shifted by 7 mV and its activation time constant at 0 mV (3.3 ms) is almost identical to that of the ShakerΔ K⁺ channel (Fig. 3 B and D and Table 1). The activation time constant at 0 mV for the VVA mutant is similar to that of the V mutant but its voltage-activation curve is left-shifted in 40 mV with respect to the ShakerΔ K⁺ channel (Fig. 3 B and E and Table 1). The changes in activation time constant and V_1/2 as those found on the N-terminal side of the linker exhibit a nonmonotonous behavior (Fig. 3 C and E). However, given the scarce number of mutants studied it is not possible to determine the degree of periodicity of τ_act or V_1/2. Surprisingly, the gating kinetics of the VV mutant channel is more that 2 orders of magnitude faster than the 2-aa linker mutant AI. We do not have an explanation for this paradox, but apparently not only the number, but also the type of amino acids contained in the zone that put in contact the S3 and S4 segments determines the activation kinetics. This contention is supported by the fact that the mutant MSLAI is slow but the mutant VVLAI has activation kinetics 10-fold faster and the mutant MSLVV is again very slow (Table 1).

Figure 3.

(A) Functional expression of deletion mutants at the amino terminal end of the S3–S4 linker. The holding potential was −100 mV and the membrane was pulsed to voltages between −70 mV to 125 mV in 10-mV increments followed by a step to −60 mV for the V and VV mutants. For the holding voltage of VVA mutant was −100 mV, and the membrane was pulsed between −100 mV and 125 mV in 10-mV increments followed by a step to −100 mV. (B) Voltage dependence of the activation kinetics of the deletion mutants shown in A. Time constants were determined as described in Methods. V, green diamonds; VV, blue triangles; VVA, green squares. For comparison the results for 0 aa (red circles) and the ShakerΔ (blue circles) are shown. (C) Changes in activation free energy of the rate limiting step of channel opening at 0 mV (ΔΔG*) induced by deletions in the S3–S4 linker region. ΔΔG* was calculated as described in Results. Activation time constant data were obtained from Table 1. (D) Voltage-activation curves in deletion mutants at the amino-terminal end of the S3–S4 Linker. Symbols as in A. Each point is the average of determinations on 5–10 separate patches. Solid lines were drawn by using the parameters in Table 1 and Eq. 5. (E) Distribution of free energy perturbations (ΔΔG^o) in channel activation. Changes in activation free energy ΔΔG^o caused by each mutant were calculated from V_1/2 and zδ as described in Methods. For more details see legend of Fig. 2.

Discussion

The general conclusion of this work is that the reduction of the linker does not prevent channel gating. In fact, the linker can be shortened drastically and the channel still opens with the same open probability, indicating that the conformational change of the S4 segment is still as complete as in the wild type. In the extreme case, when the linker is reduced to 0 aa, the kinetics of opening are slowed down but the open probability is still normal. In this mutant the total gating charge is reduced, suggesting that at least one of the charges are not moving in the electric field. The model developed below predicts this effect. The kinetics are normal when the linker contains two valines. This means that a channel with a very short linker is still gating normally, implying that, unless S3 moves along with S4, the movement of the S4 is relatively small. Certainly the movement of 15 Å as implied by models that require an extrusion of the S4 to expose the first four charged residues (6, 18, 19) now seem highly unlikely.

There are other important consequences of the results. First, from the C terminus of the linker region, the channel protein accommodates deletions with a periodicity reminiscent of a α-helical structure. This periodicity also reveals that a linker containing only 3 aa (LAI) is enough to have an activation gating kinetics and a displacement of the voltage sensor similar to the ShakerΔ K⁺ channel. Second, when the length of the restored region is 5 aa residues or less, the kinetics of activation gating and the voltage dependence of the channels are determined by the length and the type of amino acid comprising the region. Two striking cases are the pair of mutants MSLAI and VVLAI and the pair AI and VV. In both cases the mutant channels containing VV have fast activation kinetics (Table 1) whereas the mutants MSLAI and AI showed very slow activation. The position of the amino acids VV is also important because the mutant MSLVV is as slow as the MSLAI mutant. Third, introducing segments longer than 6 aa in the deletion zone between S3 and S4 induced channels with activation kinetics very similar to that of the unmodified channel. These results are most economically explained by assuming that in Shaker K⁺ channels S4 is a α-helix with the NH₂-terminal edge extending at least up to alanine 355.

S3–S4 Linker Definition.

There is no consensus about the extent of the S3–S4 linker. According to Wallner et al. (23) the S3–S4 linker is the protein domain comprised between amino acids Val-330 and Ile-360. However, Shih and Goldin (32) defined the S3–S4 loop as extending from at least Glu-333 to Met-356, but pointed out that the loop can extend further, because insertion of a Flag epitope after residue Val-363 does not disrupt channel function. Others have proposed the start of the linker in Gln-333 and the end in Ser-357 (33–35). According to this definition, elimination of the whole linker should not affect the activation kinetics much because it has amino acids residues VVASLAI in the deletion zone (Table 1). Moreover, both tryptophan substitution and alanine substitution in the S3 transmembrane domain fails to produce an orderly pattern of functional segregation, making it difficult to define the NH₂ terminal of this region of the protein (refs. 36 and 37, but see ref. 38).

Based on our observations we propose that the S3–S4 linker definition (23), starting at Val-330 and ending at Ile 360, includes some amino acids of the N terminus of S4. An S3–S4 linker consistent with our results starts at Glu-333 and ends at Ala-355 although the α-helical nature of the S4 region can be extended further into the S3–S4 linker (6). This result is of importance because although the alanine-substitution mutagenesis indicates that the C-terminal part of S4 is α-helical (37), the structure of the N terminus is uncertain. The periodicity in the activation time constants found with the deletion procedure is difficult to explain without assuming that the N terminus of S4 is α-helical in nature. It is of interest to note here that the proposal that the S4 domain undergoes a rotation during channel activation emerged from the observation that the site Ser-351, Ser-352, and Asn-353 move further from the pore, does not move, and moves closer to the pore, respectively (5). For this to happens these amino acid residues should be in a α-helical conformation. Our results are consistent with an S4 α-helix extending at least up to residue Ala-355. However, it is perfectly possible that Ser-351, Ser-352, and Asn-353 are also part of the S4 and that beyond Ala-355 the α-helix gets too slack to follow periodic changes in activation time constants or in the voltage-activation curves.

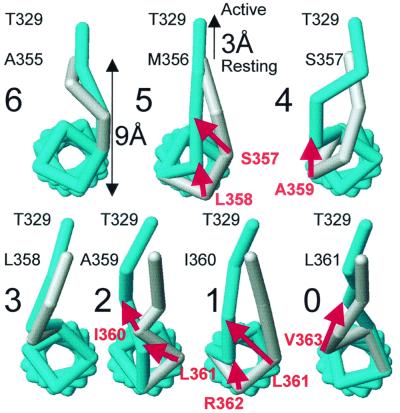
A Structural Model Describes the Periodical Distribution of Activation Time Constants.

An illustration of a possible mechanism able to explain the observed periodicity of the activation time constants and V_1/2 observed when we add amino acids to the C terminus of the linker is given in Fig. 4. We assume that the S4 segment has an α-helical secondary structure (37). Fig. 4 shows the positions of the α-carbons linked by sticks and the coordinates were calculated by assuming φ and ϕ dihedral angles of typical α-helix structure. The α-carbon of the last amino acid of S3 was located 9 Å away from the first amino acid of the S4 helix on the resting configuration of the voltage sensor (Fig. 4). A view of the S4 segment from the extracellular side is shown. Threonine 329, which appears on the top of each drawing, is the last residue of segment S3. The residue next to Thr-329 down in the primary structure is the first residue of the S3–S4 linker and it is labeled on each drawing e.g., Ala-355 for the six-residue deletion mutant. The voltage sensor activation was simulated by a 3-Å displacement of S3 away from S4. The rationale of this maneuver is that S4 α-helix rotates during channel activation (5, 7), and this displacement may be seen as a particular way of moving S4 away from S3. The 3-Å displacement was taken considering that when the channel moves into the open state there is a voltage-dependent movement of ≈3.2 Å between residues on contiguous subunits (5). The structure in the activated state is painted in blue, and in the resting state in gray. Transition from the resting to the activated state for the six residues and the three-residue deletion mutants is accomplished by changing the dihedral angles of the residues forming the linker. For other mutants activation involves the dissociation of one or two residues from the S4 α-helix. Those residues that get dissociated upon activation are labeled in red and a red arrow indicates their displacements. The model predicts a fast activation for the mutants with six- or three-residue deletion mutants. For the other mutants, the model predicts slower activation because some extra activation energy is needed to break the hydrogen bonds holding the amino acid residues in the α-helix structure. According to this model two hydrogen bonds are broken when five-, two-, and one-residue deletion mutants activate. Only one hydrogen bond breaks on the four- and zero-residue mutants. The number of hydrogen bonds compares well with the extra activation energy measured experimentally and listed in Table 1. The energy necessary to break a hydrogen bond in proteins is of the order of 1–2 kcal/mol. To compare the model predictions with our experimental data, we assume that ΔΔG* represents the energy necessary to break the hydrogen bonds in the α-helix. In reasonable agreement with the model, we concluded that the process of activation should involve the breakdown of about two hydrogen bonds for the MSLAI, AI, and I mutants, 1.3 hydrogen bonds for the SLAI, and 1.5 hydrogen bonds for the 0-aa mutant.

Figure 4.

A molecular model that reproduces the observed periodicity of the activation time constant and half activation voltages as a function of the number of amino acids in the C-terminus side of the S3–S4 linker. The figure represents a top view from the extracellular side of a trace connecting the α carbons of segment S4 and the S3–S4 linker for seven different deletion mutants, in both resting (gray) and activated (blue) states. Molecular models were created under Swiss-PDB viewer, released by Glaxo Welcome Experimental Research in Geneva (www.expasy.ch/spdbv/mainpage.html). Energy minimizations were done by using the GROMOS96 force field implementation of Swiss-PDB viewer. Structure renditions were prepared under weblab viewerpro released by Molecular Simulations, San Diego (www.msi.com). Energy minimizations were done by using a S4 α-helical model including the side chains of the amino acids.

The model we have developed provides a simple explanation to the decrease in the number of gating charges in the 0 linker mutant. In this case the charge residue R362 does not form part of S4. This charged amino acid is left in the external milieu when the whole linker is deleted and it will not contribute to the gating charge displacement. It is clear, therefore, that a very short linker still allows for the displacement of all of the gating charges albeit in some cases with very slow kinetics (e.g., AI mutant).

The Riddle of the N Terminus.

We have found that the kinetic properties of the deletion mutants with S3–S4 linkers containing 1, 2, or 3 aa of the N terminus, are dramatically different from the characteristics of the mutants with the same number of amino acids belonging to the C-terminus side of the S3–S4 linker. The molecular explanation constructed to explain the periodicity just does not work for these deletion mutants. Although the alanine and tryptophan scanning mutagenesis show an α-helical pattern up to Pro-322 of the S3 segment, the secondary structure of the last 8 aa, from I325 to A332, departs from helical periodicity (36). However, more recently the α-helical nature of the C terminus of the S3 domain was determined by monitoring the effects on channel gating and hanatoxin binding of lysine substitution in the drk1 K⁺ channel. This region of the S3 domain in the drk1 K⁺ channel interfaces with water and protein (38). In the lack of hard structural data it is difficult at present to emit an explanation for the results presented here. We can only say that there is something specific in the VV sequence of the N terminus of S3, because other amino acid pairs (e.g., AI) cannot replace it. One possible explanation for these results is that deletion mutants containing amino acids V, VV, and VVA as part of the S3–S4 linker disrupt the C terminus of the S3 α-helix to originate a linker long enough to allow normal kinetics for the movement of the S4.

In conclusion, the results presented here support the notion that the conformational change of the S4 segment upon voltage activation is small, perhaps of the order of 4 Å. This implies that to translocate all first four charges from the internal to the external medium upon depolarization, the S4 segment may rotate or change its tilt with minimal translation.