Efficient processing of fluorescence images using directional multiscale representations

Abstract

Recent advances in high-resolution fluorescence microscopy have enabled the systematic study of morphological changes in large populations of cells induced by chemical and genetic perturbations, facilitating the discovery of signaling pathways underlying diseases and the development of new pharmacological treatments. In these studies, though, due to the complexity of the data, quantification and analysis of morphological features are for the vast majority handled manually, slowing significantly data processing and limiting often the information gained to a descriptive level. Thus, there is an urgent need for developing highly efficient automated analysis and processing tools for fluorescent images. In this paper, we present the application of a method based on the shearlet representation for confocal image analysis of neurons. The shearlet representation is a newly emerged method designed to combine multiscale data analysis with superior directional sensitivity, making this approach particularly effective for the representation of objects defined over a wide range of scales and with highly anisotropic features. Here, we apply the shearlet representation to problems of soma detection of neurons in culture and extraction of geometrical features of neuronal processes in brain tissue, and propose it as a new framework for large-scale fluorescent image analysis of biomedical data.

1. Introduction

High-resolution fluorescence microscopy has emerged during the last decade as a fundamental tool for the study of molecular mechanisms in biological samples. Unlike traditional optical microscopy, fluorescence microscopy is based on the principle of absorption and subsequent reradiation of light emitted from fluorophores with separable spectral properties. Through chemical conjugation, these fluorophores can be linked with a high degree of specificity to single molecules and used as probes to track sub-cellular localization and expression pattern of any protein of interest. Hence, fluorescence microscopy can be invaluable to unravel structure-function properties at single cell level, in tissues or in whole organisms. Furthermore, combined with automated image acquisition and robotic handling, it can be applied for the systematic study of morphological changes within a large populations of cells under a variety of perturbations (e.g., drugs, compounds, gene silencing), so that automated fluorescence microscopy has become an essential technique for discovering new molecular pathways in diseases or new potential pharmacological treatments. However, the manual or semi-manual analysis of the large data sets acquired from these studies is very labor-intensive and there is a urgent need for automated methods which can rapidly and objectively process and analyze the image data. [24, 27]

The efficient analysis and processing of fluorescence images presents several additional challenges with respect to standard image processing problems. Fluorescence images are formed by detecting small amount of lights emitted by the fluorophores, a process which is affected by the randomness of photon emission, the spatial uncertainty inherent with the photon detection and photochemical reactions such as photobleaching, where a fluorophore loses its ability to fluoresce over time [28]. As a result, images acquired from fluorescent microscopy usually appear blurry and noisy. An additional difficulty stems from the complexity of the image data, which typically contain large variations in image contrast and object sizes, with features of interest varying from several tens of microns down to the resolution limit (~ 0.1 micron). Due to all these factors, standard image processing tools frequently perform poorly on fluorescent images and several specialized algorithms have been proposed in the literature, with different approaches often required to deal with different types of data [5, 22, 27].

Wavelets and multiscale methods, in particular, have been very successful in signal and image processing during the last decade, and several wavelet-based methods have been applied to fluorescent images for tasks such as image denoising, deblurring and segmentation (e.g., [3, 5, 38, 39]). Even though wavelets generally outperform Fourier-based and other traditional methods, they have serious limitations in multidimensional applications. This is due to the fact that the analyzing functions associated with the wavelet transform have poor directional sensitivity so that they are rather inefficient to represent edges and other anisotropic features which are frequently the most relevant objects in multidimensional data. To overcome this limitation, a new class of improved multiscale methods has emerged during the last decade, including most notably the shearlets and curvelets [2], which combine the advantages of multiscale analysis with the ability to efficiently encode directional information. Thanks to these properties, shearlets provide optimally sparse representations for 2D and 3D data containing edge discontinuities [2, 10, 21] and have been shown to perform very competitively for image denoising and enhancement, regularization and feature extraction [6, 20, 30, 44]. In particular, shearlet-based algorithms for denoising have been recently applied to fluorescent images in [7, 17], where they were shown to significantly outperform competing wavelet-based methods.

Motivated by the properties of directional multiscale representations, in this paper we present two algorithms which take advantage of the shearlet transform to efficiently and robustly extract the local geometry content from fluorescent imaging data. In particular, we will describe an algorithm for the automated identification of somas in neuronal cultures and an algorithm for the automated quantification of geometrical features of neurites in brain tissue.

The paper is organized as follows. In Section 2., we recall the basic properties of the shearlet transform. We next present the application of our shearlet-based approach to the identification of somas in neuronal cultures (Section 3.) and to the quantification of geometrical features of neurites in neuronal networks (Section 4.).

2. The Shearlet Transform

Before presenting the shearlet transform, let us briefly recall a few facts from the theory of wavelets.

2.1. The wavelet transform

Wavelets were introduced in the Eighties to provide efficient representations for functions with point discontinuities [25].

The basic idea at the core of this approach is to generate a family of waveforms ranging over several scales and locations through the actions of dilation and translation operators on a fixed ‘mother’ function. Hence, in the two-dimensional case, let G be a subgroup of the group GL₂(ℝ) of 2 × 2 invertible matrices. The affine systems generated by ψ ∈ L²(ℝ²) are the collections of functions of the form

$${\psi }_{M,t}(x)={|\det M|}^{-\frac{1}{2}}\psi (M^{-1}(x-t)),t\in {ℝ}^2,M\in G.$$ (2.1)

If there is an admissible function ψ so that any f ∈ L²(ℝ²) can be recovered via the reproducing formula

$$f={\displaystyle {\int }_{{ℝ}^n}{\displaystyle {\int }_G\langle f,{\psi }_{M,t}\rangle {\psi }_{M,t}d\lambda (M)dt,}}$$

where λ is a measure on G, then ψ is a continuous wavelet and the continuous wavelet transform is the mapping

$$f\to W_{\psi }f(M,t)=\langle f,{\psi }_{M,t}\rangle ,(M,t)\in G\times {ℝ}^2.$$ (2.2)

There are many examples of continuous wavelet transforms [41]. The simplest case is when the matrices M have the form a I, where a > 0 and I is the identity matrix, in which case the admissible ψ need to satisfy the simple condition

$${\displaystyle {\int }_{{ℝ}^2}{|\widehat{\psi }(a\xi )|}^2\frac{d\xi }{a^2}=1,\text{for a}.\mathrm{e}.\xi \in {ℝ}^2}.$$

In this situation, one obtains the ‘traditional’ continuous wavelet transform

$$W_{\psi }f(a,t)=a^{-1}{\displaystyle {\int }_{ℝ}f(x)\overline{\psi (a^{-1}(x-t))}dx,}$$ (2.3)

where the dilation factor is the same for all coordinate directions. Note that the classical discrete wavelet transform (in 2D) is obtained by discretizing (2.3) for a = 2^−j, t = 2^−jk, j ∈ ℤ, k ∈ ℤ².

One of the most useful properties of the continuous wavelet transform is its ability to identify the singularities of functions and distributions. Namely, if f is a function or distribution which is smooth apart from a discontinuity at a point x₀, then the continuous wavelet transform W_ψf(a, t) decays rapidly as a → 0, unless t = x₀ [15]. This property is critical to capture the local regularity and explains the ability of discrete wavelets to provide sparse approximations for functions with point singularities, which is one major reason for the success of wavelets in signal processing applications.

2.2. The shearlet transform

Despite its useful properties, the traditional continuous wavelet transform does not provide much information about the geometry of the singularities of a function or distribution. In many applications, edge-type discontinuities are frequently the most significant features and it is desirable not only to identify the their locations but also to capture their orientations. As shown by one of the authors and their collaborators in [11, 19], it is possible to combine multiscale analysis and improved geometric sensitivity by constructing a non-isotropic version of the continuous wavelet transform (2.2), called the continuous shearlet transform.

For appropriate admissible functions ψ^(h), ψ^(v) ∈ L²(ℝ²) and matrices

$$M_{as}=\left(\begin{array}{cc}a& -\sqrt{a}s\\ 0& \sqrt{a}\end{array}\right),N_{as}=\left(\begin{array}{cc}\sqrt{a}& 0\\ -\sqrt{a}s& a\end{array}\right),$$

we define the horizontal and vertical (continuous) shearlets by

$${\psi }_{a,s,t}^{(h)}(x)={|\det M_{as}|}^{-\frac{1}{2}}{\psi }^{(h)}(M_{as}^{-1}(x-t)),a>0,s\in ℝ,t\in {ℝ}^2,$$

and

$${\psi }_{a,s,t}^{(v)}(x)={|\det N_{as}|}^{-\frac{1}{2}}{\psi }^{(v)}(N_{as}^{-1}(x-t)),a>0,s\in ℝ,t\in {ℝ}^2,$$

respectively. The reason for choosing two systems of analyzing functions is to ensure a more uniform covering of the range of directions through the shearing variable s. Indeed, rather than using a single shearlet system where s ranges over ℝ, we will use the two systems of shearlets defined above and let s range over a finite interval only.

To define our admissible functions ψ^(h), ψ^(v), for ξ = (ξ₁, ξ₂) ∈ ℝ², let

$${\widehat{\psi }}^{(h)}({\xi }_1,{\xi }_2)={\widehat{\psi }}_1({\xi }_1){\widehat{\psi }}_2(\frac{{\xi }_2}{{\xi }_1}),{\widehat{\psi }}^{(v)}({\xi }_1,{\xi }_2)={\widehat{\psi }}_1({\xi }_2){\widehat{\psi }}_2(\frac{{\xi }_1}{{\xi }_2}),$$ (2.4)

where ${\widehat{\psi }}_1$, ${\widehat{\psi }}_2\in C^{\infty }(ℝ)$ and satisfy the following conditions:

$${\displaystyle {\int }_0^{\infty }{|{\widehat{\psi }}_1(a\omega )|}^2\frac{da}{a}=1,}\text{for a}.\mathrm{e}.\omega \in ℝ,\text{and supp}{\widehat{\psi }}_1\subset [-2,-\frac{1}{2}]\cup [\frac{1}{2},2];$$ (2.5)

$${\Vert {\psi }_2\Vert }_2=1\text{and supp}{\widehat{\psi }}_2\subset [-\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{4}].$$ (2.6)

Observe that, in the frequency domain, a shearlet ${\psi }_{a,s,t}^{(h)}$ has the form:

$${\widehat{\psi }}_{a,s,t}^{(h)}({\xi }_1,{\xi }_2)=a^{\frac{3}{4}}{\widehat{\psi }}_1(a{\xi }_1){\widehat{\psi }}_2(a^{-1/2}(\frac{{\xi }_2}{{\xi }_1}-s))e^{-2\pi i\xi \cdot t}.$$

This shows each function ${\widehat{\psi }}_{a,s,t}^{(h)}$ has the following support:

$$\text{supp}{\widehat{\psi }}_{a,s,t}^{(h)}\subset \{({\xi }_1,{\xi }_2):{\xi }_1\in [-\frac{2}{a},-\frac{1}{2a}]\cup [\frac{1}{2a},\frac{2}{a}],|\frac{{\xi }_2}{{\xi }_1}-s|\le \sqrt{a}\}.$$

That is, the frequency support of ${\widehat{\psi }}_{a,s,t}^{(h)}$ is a pair of trapezoids, symmetric with respect to the origin, oriented along a line of slope s.

The horizontal and vertical shearlets form a collection of functions ranging not only over various locations and scales, like the elements of a traditional wavelet system, but also over various orientations controlled by the variable s, and with frequency supports becoming highly anisotropic at fine scales (a → 0). In space domain, these functions are not compactly supported but their supports are essentially concentrated on orientable rectangles with side-lengths a, $\sqrt{a}$ and orientation controlled by s. The support becomes increasingly thin as a → 0. The frequency supports of some representative horizontal shearlets are illustrated in Figure 1.

Figure 1.

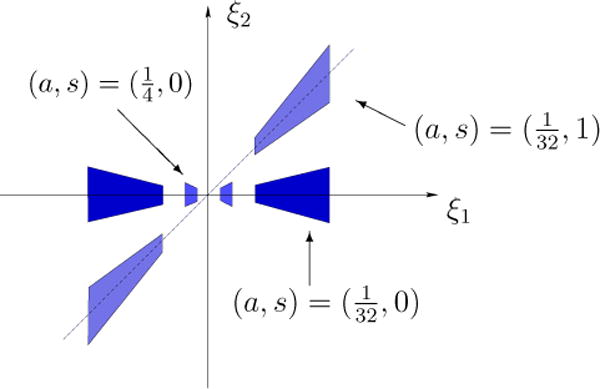
Frequency supports of the horizontal shearlets ${\widehat{\psi }}_{a,s,t}^{(h)}$ for different values of a and s.

For $0<a<\frac{1}{4}$ and $|s|\le \frac{3}{2}$, each system of continuous shearlets spans a subspace of L²(ℝ²) consisting of functions having frequency supports in one of the horizontal or vertical cones defined in the frequency domain by

$$\begin{array}{l}{\mathcal{P}}^{(h)}=\{({\xi }_1,{\xi }_2)\in {ℝ}^2:|{\xi }_1|\ge 2\text{and}|\frac{{\xi }_2}{{\xi }_1}|\le 1\}\\ {\mathcal{P}}^{(v)}=\{({\xi }_1,{\xi }_2)\in {ℝ}^2:|{\xi }_1|\ge 2\text{and}|\frac{{\xi }_2}{{\xi }_1}|>1\}.\end{array}$$

More precisely, the following proposition from [19] shows that the horizontal and vertical shearlets, with appropriate ranges for a, s, t, form continuous reproducing systems for the spaces of L² functions whose frequency supports are contained in ${\mathcal{P}}^{(h)}$ and ${\mathcal{P}}^{(v)}$, respectively.

Proposition 1

Let ψ^(h) and ψ^(v) be given by (2.4) with ${\widehat{\psi }}_1$ and ${\widehat{\psi }}_2$ satisfying (2.5) and (2.6). Let

$$L^2{\left({\mathcal{P}}^{(h)}\right)}^{\vee }=\{f\in L^2({ℝ}^2):\text{supp}\widehat{f}\subset {\mathcal{P}}^{(h)}\},$$

with a similar definition for $L^2{\left({\mathcal{P}}^{(v)}\right)}^{\vee }$. We have the following reproducing formulas.

1. For all $f\in L^2{\left({\mathcal{P}}^{(v)}\right)}^{\vee }$,

   $$f={\displaystyle {\int }_{{ℝ}^2}{\displaystyle {\int }_{-2}^2{\displaystyle {\int }_0^{\frac{1}{4}}\langle f,{\psi }_{\mathit{ast}}^{(h)}\rangle {\psi }_{a,s,t}^{(h)}\frac{da}{a^3}}dsdt,}}$$
2. For all $f\in L^2{\left({\mathcal{P}}^{(v)}\right)}^{\vee }$,

   $$f={\displaystyle {\int }_{{ℝ}^2}{\displaystyle {\int }_{-2}^2{\displaystyle {\int }_0^{\frac{1}{4}}\langle f,{\psi }_{\mathit{ast}}^{(v)}\rangle {\psi }_{a,s,t}^{(v)}\frac{da}{a^3}}dsdt,}}$$

where both identities hold in the weak topology of L²(ℝ²).

Using the horizontal and vertical shearlets, we define the (fine-scale) continuous shearlet transform on L²(ℝ²) as the mapping

$$f\in L^2{\left({ℝ}^2\backslash {[-2,2]}^2\right)}^{\vee }\to \mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t),a\in (0,\frac{1}{4}],s\in [-\infty ,\infty ],t\in {ℝ}^2,$$

given by

$$\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)=\{\begin{array}{ll}\mathcal{S}{\mathscr{H}}_{\psi }^{(h)}f(a,s,t)=\langle f,{\psi }_{a,s,t}^{(h)}\rangle ,\hfill & \text{if}|s|\le 1\hfill \\ \mathcal{S}{\mathscr{H}}_{\psi }^{(v)}f(a,\frac{1}{s},t)=\langle f,{\psi }_{a,\frac{1}{s},t}^{(v)}\rangle ,\hfill & \text{if}|s|>1.\hfill \end{array}$$ (2.7)

In the above expression we adopt the convention that the limit value of $\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)$ for s = ±∞ is set equal to $\mathcal{S}{\mathscr{H}}_{\psi }^{(v)}f(a,0,t)$.

The term fine-scale refers to the fact that the shearlet transform $\mathcal{S}{\mathscr{H}}_{\psi }f$, given by (2.7), is only defined for the “fine scales” scale variable a ∈ (0, 1/4]. In fact, as it is clear from Proposition 1, $\mathcal{S}{\mathscr{H}}_{\psi }f$ defines an isometry on L²(ℝ² \ [−2, 2]²)^˅, the subspace of L²(ℝ²) of functions with frequency support away from [−2, 2]² but not on L²(ℝ²). This is not a limitation since the geometric characterization of singularities only requires asymptotic estimates as a approaches 0.

Thanks to its directional sensitivity, the continuous shearlet transform is able to capture the geometry of edges precisely, going beyond the limitations of the traditional wavelet approach. If f is a cartoon-like image – a simplified model of natural images consisting of regular regions separated by smooth (or C^m regular, m ≥ 2) edges – then the shearlet transform of f provides a description of the location and orientations of the edges of f through its asymptotic decay at fine scales. In particular, we have he following theorem from [11].

Theorem 2

Let f = χ_S, where S ⊂ ℝ² is a compact set whose boundary ∂S is a simple smooth curve. Then we have the following.

1. If t ∉ ∂S, then

   $$\underset{a\to 0^{+}}{\lim }{a}^{-N}\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)=0,\mathit{\text{for}}\mathit{\text{all}}N>0.$$
2. If t ∈ ∂S and s does not correspond to the normal direction of ∂S at t, then

   $$\underset{a\to 0^{+}}{\lim }{a}^{-N}\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)=0,\mathit{\text{for}}\mathit{\text{all}}N>0.$$
3. If t ∈ ∂S and s corresponds to the normal direction of ∂S at t, then

   $$\underset{a\to 0^{+}}{\lim }{a}^{-\frac{3}{4}}\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)\ne 0.$$

In other words, the continuous shearlet transform of f = χ_S decays rapidly, asymptotically for a → 0, unless t is on the boundary of S and s corresponds to the normal direction of ∂S at t, in which case one observes the slow decay

$$\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)~O(a^{\frac{3}{4}}),\text{as}a\to 0.$$

This result can be extended to planar regions S whose boundaries contain corner points and even to more general functions which are not necessarily characteristic functions of sets [11, 12].

The discrete shearlet transform is obtained by sampling (2.7) at a = 2^−2j, s = 2^−jℓ, $t=B_{2^{-j}\ell }{A}_{2^{-2j}}k$, for j, ℓ ∈ ℤ, k ∈ ℤ² [14]. In this case, with an abuse of notation, we write the discrete shearlet transform as the mapping

$$f\to \mathcal{S}{\mathscr{H}}_{\psi }f(j,\ell ,k)=\langle f,{\psi }_{j,\ell ,k}\rangle ,j,\ell \in \mathbb{Z},k\in {\mathbb{Z}}^2.$$

This transform inherits some useful analytic properties from its continuous counterpart and can be implemented by fast wavelet-like algorithms. These efficient numerical implementations, combined with the property that discrete shearlet representations provide highly sparse approximations, make the discrete shearlet transform very useful for singularity detection and other image processing applications [20, 44].

3. Soma identification in fluorescent images of neuronal cultures

Recall that a neuron typically possesses two morphological structures: a round cell body called the soma and several branched processes called neurites, i.e., dendrites and axons. In many biological studies, it is often necessary to identify the individual neurons and their subcellular compartments, i.e., soma and neurites, in a culture or a brain tissue. For example, High Content Analysis applications for screening drugs normally require the extraction and quantification of several morphological features on large datasets for identifying compounds that cause phenotypic changes. Clearly, in these studies, traditional analysis methods such as manual segmentation or semi-automated segmentation with human intervention are highly impractical and automated methods for the quantification of morphological features are virtually necessary.

The automated extraction of the location and morphology of the somas in a neuronal network is essential for such applications and several ideas have been proposed in the literature. Some popular methods use intensity thresholding [37, 40], which is very effective in images acquired from phase-contrast microcopy where the somas often have higher contrast than the neurites. However, this approach is unreliable in fluorescent microscopy due to the inhomogeneity of the fluorescence intensity. Other more sophisticated methods from the literature use Laplacian-of-Gaussian and related filters [1, 32] to detect local maxima, but irregular intensity profiles inside the soma frequently lead to detect more than one soma candidate for each soma. Other more flexible methods include the use of morphological operators [37, 43].

In this paper, we propose a novel approach which takes advantage of the shearlet transform to accurately separate the somas from the neurites by classifying appropriate geometric descriptors extracted from the fluorescent image data. Our method is motivated by the properties of the shearlet transform presented in Sec. 2. in connection with the detection of the location and orientation of edges.

3.1. A shearlet-based Directional Ratio

Let us consider the cartoon-like image of a neuron f = χ_S in Figure 2, where S is a subset of ℝ² consisting of the union of a disk-shaped region and a thin and long solid rectangle. One might expect S to be compact but, to simplify the mathematical analysis, we assume that the thin and long rectangle extends to infinity. Moreover, we consider its centerline to be the y-axis and the disk-shaped area to be centered at the origin of the coordinate system and be attached to it, so that S is connected. The continuous shearlet transform provides a precise characterization of the boundaries ∂S of the region S since $\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)$ has rapid asymptotic decay, as a → 0, for all (s, t), except for t located on ∂S and for s associated with the normal orientation to ∂S at t. Clearly, the discrete version of the shearlet transform $\mathcal{S}{\mathscr{H}}_{\psi }f(j,\ell ,k)$ can only be computed up to a minimal but finite resolution level. In this case, we expect that, at “fine scales”, the largest shearlet coefficients in magnitude will be those located near the edges, with the values of the shear parameter corresponding to the normal orientation to the edges. In particular, as shown by one of the authors in [44], we can use this observation to distinguish points near the edges from points away from the edges. At the points near the edges, the local orientation of an edge remains constant and the shearlet coefficient $\mathcal{S}{\mathscr{H}}_{\psi }f(j,\ell ,k)$ corresponding to a directional subband parallel to this orientation will have a significant value. This is visible in Panel B in Fig. 3.1., showing the consistent directional sensitivity of the shearlet transform for a single scale a near the singularities. The panel illustrates that the response of the transform at higher scales is more consistent in thinner neurites, while in thicker ones the response of the shearlet transform is less consistent. The same phenomenon is observed in the interior of the neurite, where the orientations of maximum response appear to be distributed almost like white-noise, in stark contrast to the consistent strong responses shown at the boundaries of the neurite. However, at intermediate scales, depending on the relative thickness of a neurite as compared to its length (aspect ratio), the shearlet transform “sees” the entire neurite as a singularity spatially organized along its centerline. Then, the orientations of maximum response in the interior of the neurite and on its boundary become more consistent. This observation leads to the conclusion that tubular and non-tubular structures appear with different degrees of directional coherence at different scales in the shearlet transform domain.

Figure 2.

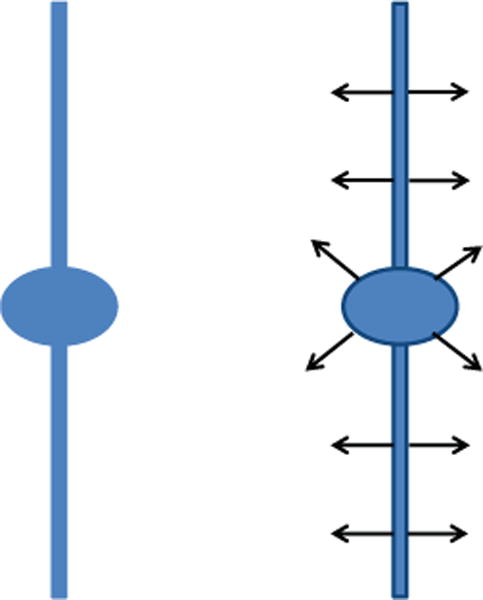
Left: Cartoon-like model of a neurite and a soma. Right: The continuous shearlet transform of the cartoon-like image has rapid asymptotic decay everywehere except at the boundaries, for values of the shear variable corresponding to the normal orientation.

Figure 3.

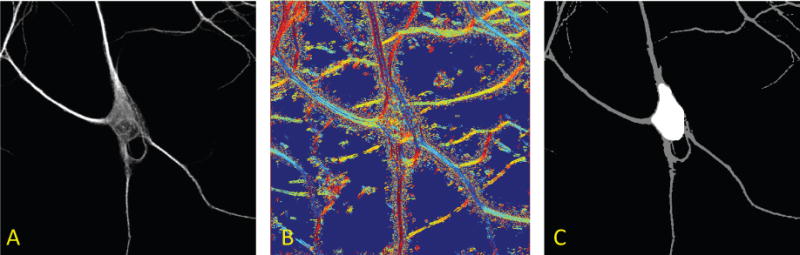
Automatic detection of the soma. Panel A shows the maximum projection of a neuron imaged from fluorescent microscopy. Panel B illustrates the maximum response orientation components of the image (directions are color-coded) computed using the continuous shearlet decomposition at a single scale. Note that similar or slowly-changing colors are located along the neurites, unlike the soma region where there are no dominant orientations, that is, directional components vary randomly creating a white noise pattern. Using the directional ratio, we can accurately segment the soma from the rest of the structure in the image (Panel C).

As a measure of directional coherence, we consider a notion of directional ratio with respect to the continuous shearlet transform, which we use as a shape descriptor to separate isotropic from anisotropic structures. This concept was originally introduced in [29] using another set of analysis atoms. Similar directional ratios can be defined using other classes of multiscale transforms induced by appropriate ‘directional’ atoms.

The shearlet-based Directional Ratio of f at scale a > 0 and location t ∈ ℝ³ is given by

$${\mathcal{D}}_{a}f(t)=\frac{{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)|\}}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)|\}},f\in L^2({ℝ}^2),$$ (3.1)

and measures the strength of directional information at scale a and location t. The next theorem predicts consistent responses of directional ratio on tubular structures in general and, thus, it formalizes the preceding discussion.

Theorem 3

Let f = χ_S be a cartoon-like image of a neuron, where S contains two disjoint subsets: A, a ball centered at the origin with radius R > 0 and B, the cylinder [−r, r]×[2R, + ∞), r > 0. Let the cylinder [−r, r] × [0, ∞) be contained in S. Moreover, assume that

1. the Fourier transforms of both ψ₁ and ψ₂ are C^∞ and even;

2. the wavelet function ψ₁ has two “plateaus” in the frequency domain: ${\widehat{\psi }}_1(\xi )=1$ for all 3/4 ≤ |ξ| ≤ 3/2;

3. the “bump” function ψ₂ satisfies ${\widehat{\psi }}_2(\xi )=c>0$ for all |ξ| ≤ 1/4 and that ${\displaystyle {\int }_{-R}^R{\psi }_2(x)dx>1}$.

Then, for 4r ≤ a ≤ 1/4, there exists a threshold τ such that the shearlet-based Directional Ratio of f, given by (3.1), satisfies:

$${\mathcal{D}}_{a}f(y)\le \tau y\in B.$$ (3.2)

On the other hand, if ε > 0 is an arbitrary positive number, then, for every y ∈ κ_εA, orientation s and sufficiently fine scale a, where 0 < κ_ε < 1, we have that $|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|<\epsilon$.

3.2. Proof of Theorem 3

Before starting the proof of the theorem we remark that the constant c above must exceed 1 because the support of ${\widehat{\psi }}_2$ is the interval $[-\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{4}]$ and ‖ψ₂‖₂ = 1. Also, with no loss of generality, we can assume that ${\widehat{\psi }}_2(0)=1$.

Proof

We begin by making clear that the sinc-function is given by

$$\text{sinc}(x):=\frac{\sin (2\pi x)}{\pi x}={\left({\chi }_{[-1,1]}\right)}^{\vee }(x)\text{with}x\in ℝ.$$

Let y = (y₁, y₂) be an arbitrary element in B which is contained in the rectangle C = [−r, r] × [y₂ − R, y₂ +R] ⊂ B. Since the length of the cylinder B is large enough, with no loss of generality we can shift the origin in order to have y₂ = 0. We have:

$$\begin{array}{l}{\mathcal{D}}_{a}f(y)=\frac{{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}\\ \le \frac{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,\infty ,y)|}{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,0,y)|}\\ =\frac{|\mathcal{S}{\mathscr{H}}_{\psi }{f}^{(v)}(a,0,y)|}{|\mathcal{S}{\mathscr{H}}_{\psi }{f}^{(h)}(a,0,y)|}\\ =\frac{|\langle f,{\psi }_{a,0,y}^{(v)}\rangle |}{|\langle f,{\psi }_{a,0,y}^{(h)}\rangle |}.\end{array}$$ (3.3)

The absolute integrability of the shearlet functions implies that, for any ε > 0, there exists a square with side of length 2R₀, such that

$${\displaystyle {\int }_{{\left([-R_0,R_0]\times [-R_0,R_0]\right)}^c}|{\psi }_{1,0,0}^{(v)}(x,y)|\mathit{dxdy}<\epsilon .}$$

A similar relation holds for ${\psi }_{1,0,0}^{(h)}$, with the roles of R₀ and r₀ reversed. For technical reasons, we will assume R₀ > 1/2. Later in the proof we will determine ε. The above inequality implies that, for both the vertical and horizontal shearlets, we have

$${\displaystyle {\int }_{{\left([-a^{1/2}{R}_0,a^{1/2}{R}_0]\times [-a{R}_0,a{R}_0]\right)}^c}|{\psi }_{a,0,0}^{(v)}(x,y)|\mathit{dxdy}<a^{3/4}\epsilon },$$ (3.4)

and

$${\displaystyle {\int }_{{\left([-a{R}_0,a{R}_0]\times [-a^{1/2}{R}_0,a^{1/2}{R}_0]\right)}^c}|{\psi }_{a,0,0}^{(h)}(x,y)|\mathit{dxdy}<a^{3/4}\epsilon }.$$

Our strategy is to show that the numerator in the fraction (3.3) is significantly smaller than the denominator. We begin by estimating the latter.

We stress that we have not specified the quantity ε yet, thus R₀ still needs to be determined. However, we postpone this task until the end of the analysis of the behavior of directional ratio on the tubular part of the cartoon-like neuron.

On the other hand, f = χ_S contains the rectangle [−r, r] × [−R, R] which, in turn, contains y. Once again, with no loss of generality, since S extends as long we wish toward the positive direction of the y-axis, we can assume R > R₀. Our assumptions on R₀ and on the scale a imply aR₀ ≥ 2r. Consequently, both rectangles −y + [−r, r] × [−R, R] and [−aR₀, aR₀] × [−a^1/2r₀, a^1/2r₀] are contained in the rectangle [−aR₀, aR₀] × [−R, R].

We observe that

$$\langle f,{\psi }_{a,0,y}^{(h)}\rangle =\langle T_{-y}f,{\chi }_{[-a{R}_0,a{R}_0]\times [-R,R]}{\psi }_{a,0,0}^{(h)}\rangle +\langle T_{-y}f,{\chi }_{{([-a{R}_0,a{R}_0]\times [-R,R])}^c}{\psi }_{a,0,0}^{(h)}\rangle ,$$

which, if combined with aR₀ ≥ 2r, allows us to take y₁ = 0 and to conclude that

$$|\langle f,{\psi }_{a,0,y}^{(h)}\rangle |>|\langle f{\chi }_{[-a{R}_0,a{R}_0]\times [-R,R]},{\psi }_{a,0,0}^{(h)}\rangle |-a^{3/4}\epsilon .$$

Thus,

$$|\langle f,{\psi }_{a,0,y}^{(h)}\rangle |>|\langle {\chi }_{[-r,r]\times [-R,R]},{\psi }_{a,0,0}^{(h)}\rangle |-a^{3/4}\epsilon .$$

We also observe that

$$\begin{array}{l}|\langle {\chi }_{[-r,r]\times [-R,R]},{\psi }_{a,0,0}^{(h)}\rangle |\\ =\left|{\displaystyle {\int }_{\frac{1}{2a}<|{\xi }_1|<\frac{2}{a}}{\displaystyle {\int }_{\frac{|{\xi }_2|}{|{\xi }_1|}<\frac{\sqrt{2a}}{4}}{a}^{3/4}rR\text{sinc}(r{\xi }_1)\text{sinc}(R{\xi }_2){\widehat{\psi }}_1(a{\xi }_1){\widehat{\psi }}_2}\left(\frac{{\xi }_2}{\sqrt{a}{\xi }_1}\right)d{\xi }_{2}d{\xi }_1}\right|\\ =2a^{3/4}\left|{\displaystyle {\int }_{\frac{1}{2a}<|{\xi }_1|<\frac{2}{a}}r\text{sinc}(r{\xi }_1){\widehat{\psi }}_1(a{\xi }_1)\left({\displaystyle {\int }_{\frac{|{\xi }_2|}{|{\xi }_1|}<\frac{\sqrt{2a}}{4}}R\text{sinc}(R{\xi }_2){\widehat{\psi }}_2}\left(\frac{{\xi }_2}{\sqrt{a}{\xi }_1}\right)d{\xi }_2\right)d{\xi }_1}\right|,\end{array}$$

where we drop the absolute value of ξ₁ due to the symmetry of the integrand with respect to the ξ₂-axis. First, we estimate the inner integral. To do so, we set $\eta =\frac{{\xi }_2}{\sqrt{a}{\xi }_1}$. Then we observe:

$${\displaystyle {\int }_{\frac{|{\xi }_2|}{{\xi }_1}<\frac{\sqrt{2a}}{4}}R\text{sinc}(R{\xi }_2){\widehat{\psi }}_2}\left(\frac{{\xi }_2}{\sqrt{a}{\xi }_1}\right)d{\xi }_2={\displaystyle {\int }_{|\eta |<\frac{\sqrt{2}}{4}}\sqrt{a}{\xi }_{1}R\text{sinc}(R\sqrt{a}{\xi }_1\eta ){\widehat{\psi }}_2(\eta )d\eta .}$$

Note that

$${\chi }_{[-R\sqrt{a}{\xi }_1,R\sqrt{a}{\xi }_1]}\ast {\psi }_2(0)={\displaystyle {\int }_{-R\sqrt{a}{\xi }_1}^{R\sqrt{a}{\xi }_1}{\psi }_2(x)dx}.$$

Since $c={\widehat{\psi }}_2(0)={\displaystyle {\int }_{-\infty }^{\infty }{\psi }_2(x)dx}$, the scale a does not exceed $\frac{1}{4}$ and $\frac{1}{2a}<{\xi }_1$, we conclude that both ${\displaystyle {\int }_{-R\sqrt{a}{\xi }_1}^{R\sqrt{a}{\xi }_1}{\psi }_2(x)dx}$ and ${\displaystyle {\int }_{-R}^R{\psi }_2(x)dx}$ are greater than 1. In conclusion,

$${\displaystyle {\int }_{\frac{|{\xi }_2|}{{\xi }_1}<\frac{\sqrt{2a}}{4}}R\text{sinc}(R{\xi }_2){\widehat{\psi }}_2}\left(\frac{{\xi }_2}{\sqrt{a}{\xi }_1}\right)d{\xi }_2>1.$$ (3.5)

Next, we examine the outer integral

$${\displaystyle {\int }_{\frac{1}{2a}}^{\frac{2}{a}}r\text{sinc}(r{\xi }_1){\widehat{\psi }}_1(a{\xi }_1)d{\xi }_1=}{\displaystyle {\int }_{\frac{1}{2}}^2\frac{r}{a}\text{sinc}}\left(\frac{r}{a}\xi \right){\widehat{\psi }}_1(\xi )d\xi .$$

The selection of the scale a implies $0\le \frac{r}{a}{\xi }_1\le \frac{1}{2}$ for every value of ξ₁ in the interval of integration. Since the sinc function takes positive values in the open interval $(-\frac{1}{2},\frac{1}{2})$ and ${\widehat{\psi }}_1(\xi )=1$ for all $\xi \in [\frac{3}{4},\frac{3}{2}]$, using (3.5) we finally conclude that

$$|\langle f,{\psi }_{a,0,y}^{(h)}\rangle |>2a^{3/4}\frac{3}{4}\frac{\sin (\frac{3r\pi }{a})}{\frac{3r\pi }{2a}}-a^{3/4}\epsilon \ge 2a^{3/4}\frac{3}{4}\frac{\sin (\frac{3\pi }{4})}{\frac{3\pi }{8}}-a^{3/4}\epsilon =a^{3/4}\frac{2\sqrt{2}}{\pi }-a^{3/4}\epsilon .$$ (3.6)

Now we turn our attention to the numerator of (3.3); we need to show that it is relatively much smaller than the denominator. We have that

$$\langle f,{\psi }_{a,0,y}^{(v)}\rangle =\langle T_{-y}(f{\chi }_{[-r,r]\times [-R,R]}),{\psi }_{a,0,0}^{(v)}\rangle +\langle T_{-y}(f{\chi }_{{([-r,r]\times [-R,R])}^2}),{\psi }_{a,0,0}^{(v)}\rangle .$$

Regardless of how y₁ varies between −r and r, the rectangle $[-\sqrt{a}{R}_0,\sqrt{a}{R}_0]\times [-a{R}_0,a{R}_0]$ always stays inside ℝ × [−R, R], so $|\langle T_{-y}(f{\chi }_{{\left([-r,r]\times [-R,R]\right)}^c}),{\psi }_{a,0,0}^{(v)}\rangle |\le a^{3/4}\epsilon$. Therefore, we have that

$$|\langle f,{\psi }_{a,0,y}^{(v)}\rangle |\le |\langle T_{-y}{\chi }_{[-r,r]\times [-R,R]},{\psi }_{a,0,0}^{(v)}\rangle |+a^{3/4}\epsilon .$$ (3.7)

Note that

$$\begin{array}{l}\langle T_{-y}{\chi }_{[-r,r]\times [-R,R]},{\psi }_{a,0,0}^{(v)}\rangle \\ =a^{3/4}{\displaystyle {\int }_{\frac{1}{2a}<|{\xi }_2|<\frac{2}{a}}{\displaystyle {\int }_{|\frac{{\xi }_1}{{\xi }_2}|<\frac{\sqrt{2a}}{4}}Rr\text{sinc}(r{\xi }_1)\text{sinc}(R{\xi }_2)e^{2\pi i{\xi }_1{y}_1}{\widehat{\psi }}_1(a{\xi }_2){\widehat{\psi }}_2}}\left(\frac{{\xi }_1}{\sqrt{a}{\xi }_2}\right)d{\xi }_{1}d{\xi }_2.\end{array}$$

Since ${\widehat{\psi }}_2$ is even, we obtain that the latter double integral is equal to

$$=a^{3/4}{\displaystyle {\int }_{\frac{1}{2a}<|{\xi }_2|<\frac{2}{a}}{\displaystyle {\int }_{\frac{-\sqrt{2a}|{\xi }_2|}{4}}^{\frac{\sqrt{2a}|{\xi }_2|}{4}}{\widehat{\psi }}_1(a{\xi }_2)R\text{sinc}(R{\xi }_2)e^{2\pi i{\xi }_1{y}_1}r\text{sinc}(r{\xi }_1){\widehat{\psi }}_2}}\left(\frac{{\xi }_1}{\sqrt{a}|{\xi }_2|}\right)d{\xi }_{1}d{\xi }_2.$$ (3.8)

We now estimate the inner integral. First, using the change the variable $\eta =\frac{{\xi }_1}{\sqrt{a}|{\xi }_2|}$, we obtain that the inner integral in (3.8) is equal to

$$\begin{gathered} {\displaystyle {\int }_{\frac{-\sqrt{2}}{4}}^{\frac{\sqrt{2}}{4}}{e}^{2\pi i\eta \sqrt{a}|{\xi }_2|y_1}r\sqrt{a}|{\xi }_2|\text{sinc}(r\sqrt{a}|{\xi }_2|\eta ){\widehat{\psi }}_2(\eta )d\eta \\ ={\chi }_{[-r\sqrt{a}|{\xi }_2|,r\sqrt{a}|{\xi }_2|]}\ast {\psi }_2(\sqrt{a}|{\xi }_2|y_1)}={\displaystyle {\int }_{\sqrt{a}|{\xi }_2|y_1-r\sqrt{a}|{\xi }_2|}^{\sqrt{a}|{\xi }_2|y_1+r\sqrt{a}|{\xi }_2|}{\psi }_2(x)dx}. \end{gathered}$$

By applying the Cauchy-Schwartz inequality to ψ₂, which has norm equal to 1, we deduce ${\Vert {\psi }_2\Vert }_{\infty }\le {\Vert {\widehat{\psi }}_2\Vert }_1<1$. Therefore, the inner integral in (3.8) is bounded above $2r\sqrt{a}|{\xi }_2|$. Thus, the absolute value of the integral in (3.8) is bounded above by

$$\begin{array}{l}{a}^{3/4}{\displaystyle {\int }_{\frac{1}{2a}<|{\xi }_2|<\frac{2}{a}}R|\text{sinc}(R{\xi }_2){\widehat{\psi }}_1(a{\xi }_2)|2r\sqrt{a}|{\xi }_2|d{\xi }_2}=2a^{3/4}{\displaystyle {\int }_{\frac{1}{2a}}^{\frac{2}{a}}R\frac{|\sin (2\pi R{\xi }_2)|}{\pi R{\xi }_2}}2r\sqrt{a}{\xi }_{2}d{\xi }_2\\ \le \frac{12r{a}^{3/4}}{2\pi \sqrt{a}}\le \frac{3\sqrt{a}{a}^{3/4}}{2\pi },\end{array}$$

where the last inequality follows from our assumption on the scale a. Using (3.7) and the last inequality, we obtain that

$$|\langle f,{\psi }_{a,0,y}^{(v)}\rangle |\le \frac{3\sqrt{a}{a}^{3/4}}{2\pi }+a^{3/4}\epsilon .$$

Next, using (3.6), we derive the following upper bound for ${\mathcal{D}}_{a}f(y)$:

$${\mathcal{D}}_{a}f(y)\le \frac{\frac{3\sqrt{a}}{2\pi }+\epsilon }{\frac{2\sqrt{2}}{\pi }-\epsilon }.$$

Taking $\epsilon =\frac{1}{10\pi }$, we get that ${\mathcal{D}}_{a}f(y)<\tau :=\frac{15\sqrt{a}+1}{20\sqrt{2}-1}<1/3$, for all y ∈ B.

To complete the proof we turn our attention to the isotropic part of the cartoon neuron, the ball A. Since A is centered at the origin and it is a ball, it is enough to prove the statement for horizontal shearlets only. As we did in the first part of the proof, for each arbitrary ε > 0, we can find a square with side of length 2R_0,ε such that

$${\displaystyle {\int }_{{\left([-R_{0,\epsilon },R_{0,\epsilon }]\times [-R_{0,\epsilon },R_{0,\epsilon }]\right)}^c}|{\psi }_{1,0,0}^{(h)}(x,y)|\mathit{dxdy}<\epsilon .}$$

The shearing parameter s varies between −1 and 1 and, as it does so, it “shears” the square Q := [−R_0,ε, R_0,ε] × [−R_0,ε, R_0,ε]. Therefore, if the scale is sufficiently fine, it is not hard to see that there exists 0 < κ_ε < 1 such that

$$y+M_{as}(Q)\subset A,$$

for every y ∈ κ_εA. Now, let −1 ≤ s ≤ 1. Then $|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|=|\langle f,{\psi }_{a,s,y}^{(h)}\rangle |$. However, ${\displaystyle {\int }_{ℝ}{\displaystyle {\int }_{ℝ}{\psi }_{a,s,y}^{(h)}}}=0$. Thus,

$$\langle f,{\psi }_{a,s,y}^{(h)}\rangle ={\displaystyle {\int }_{{ℝ}^2}(f-1)\overline{{\psi }_{a,s,y}^{(h)}}}={\displaystyle {\int }_{{\left(y+M_{as}(Q)\right)}^c}({\chi }_S-1)}\overline{{\psi }_{a,s,y}^{(h)}},$$

because y + M_as(Q) ⊆ A. Therefore, we conclude that

$$|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|<{\displaystyle {\int }_{{\left(y+M_{as}(C)\right)}^c}|f-1||{\psi }_{a,s,y}^{(h)}|}<2a^{3/4}\epsilon <\epsilon .$$

□

The last part of the proof of Theorem 3 illustrates the behavior of the shearlet transform in isotropic regions. We don’t have to take the ε very small because, as the scale becomes finer and finer, the quantity 2a^3/4ε decreases as well. In any case, the main implication of the second part of Theorem 3 is that the shearlet transform will attain very small values everywhere in the isotropic part of the cartoon-like neuron, as long as the location variable of the transform is away from the boundaries. As a result, the values of the Directional Ratio ${\mathcal{D}}_{a}f$ will vary wildly in isotropic regions (see Fig. 3.2.) and, consequently, the Directional Ratio is not useful to detect such regions. As we discuss in the next paragraph, there is a method to detect and segment isotropic regions such as somas.

To identify somas with respect to neurites, we will use Theorem 3, which predicts that there is a threshold below which, at appropriate scales, the directional ratio in the neurites does not exceed this threshold. The existence of such a threshold is numerically verifiable as one can see in Fig. 3.2.

Thus, given a segmented neuron, we can identify within this subvolume the grid points corresponding to somas. In fact, Proposition 4 below indicates that, in the interior of tubular structures modeling the (thin) neurites, the function ${\mathcal{D}}_a$ is weakly differentiable. This property can be used to circumscribe a boundary between a neurite and a soma via a level-set method. This method can be significantly more accurate than plain thresholding to locate this boundary.

Recall that level set methods propagate a surface or a curve which evolves until it coincides with a desired level set. In our case, this level set would be the boundary between a neurite and a soma. The gradient field required to evolve the interface curve to the desired level set can be defined by taking finite differences of the directional ratio, since this function is weakly differentiable. To initialize the evolution we can use the curve which is the boundary of the set of points inside the soma whose values of ${\mathcal{D}}_{a}f$, for a suitable a, are less than a threshold predicted by Theorem 3.2. In [29], we have proposed a similar method to segment somas in fluorescent images of neurons.

3.3. Weak differentiability

Let us now turn our attention to the weak differentiability of the directional ratio of f, where f is a cartoon-like neuron. To establish that ${\mathcal{D}}_{a}f$, given by the ratio (3.1), satisfies a Lipschitz condition, it is enough to verify this property for the numerator and the denominator of that ratio. To control how small the denominator can become, we assume that in an open set Ω there exists α > 0 such that $|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|>\alpha$ for all y ∈ Ω. Select y ∈ Ω and a vector h such that y + h ∈ Ω. Using the triangle inequality we have

$$|\langle f,T_{y+h}{\psi }_{a,s,0}^{(v)}\rangle |\le |\langle f,T_y{\psi }_{a,s,0}^{(v)}\rangle |+|\langle f,(T_h-I){\psi }_{a,s,0}^{(v)}\rangle |,$$

for every scale a and shear variable s. A similar inequality holds for horizontal shearlets. We will assume Ω to be convex. Since the Fourier transforms of ψ^(v) and ψ^(h) are C^∞ and compactly supported, the ψ^(v) and ψ^(h) are in the Schwartz space. Hence, all of their partial derivatives are uniformly bounded.

By applying the Mean Value Theorem of differential calculus we obtain that

$$\begin{array}{l}|\langle f,(T_h-I){\psi }_{a,s,0}^{(v)}\rangle |=\left|{\displaystyle {\int }_{{ℝ}^2}f(x)({\psi }_{a,s,0}^{(v)}(x-h)-{\psi }_{a,s,0}^{(v)}(x))dx}\right|\\ \le {\displaystyle {\int }_{{ℝ}^2}|f(x)||{\psi }_{a,s,0}^{(v)}(x-h)-{\psi }_{a,s,0}^{(v)}(x)|dx}\\ \le C{\Vert f\Vert }_1\Vert h\Vert ,\end{array}$$

where C is a constant derived by the L^∞-bounds of the partial derivatives of the horizontal and vertical shearlets. Since the shear variable s is taken in [−1, 1], the constant C holds uniformly in s. Therefore, for every s ∈ [−1, 1] we have that

$$|\langle f,T_{y+h}{\psi }_{a,s,0}^{(v)}\rangle |\le \underset{s}{\sup }\{|\langle f,T_y{\psi }_{a,s,0}^{(v)}\rangle |\}+C\Vert h\Vert \le \underset{s\in ℝ}{\sup }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}+C\Vert h\Vert .$$

By combining horizontal and vertical shearlets, we deduce that

$$\underset{s\in ℝ}{\sup }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}\le \underset{s\in ℝ}{\sup }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}+C\Vert h\Vert .$$

By swapping the points y and y + h in the previous inequality, we obtain that

$$|\underset{s}{\sup }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}-\underset{s}{\sup }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}|\le C\Vert h\Vert$$

On the other hand, a similar argument establishes that

$$|\underset{s}{\inf }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}-\underset{s}{\inf }\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}|\le C\Vert h\Vert$$

Combining these two observations we derive the following result.

$$\begin{array}{l}|{\mathcal{D}}_{a}f(y+h)-{\mathcal{D}}_{a}f(y)|\\ =\left|\frac{{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}}-\frac{{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}\right|\\ \le \frac{{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}-{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}}\\ +\frac{|{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}-{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}|}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y+h)|\}}\frac{{\inf }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}{{\sup }_s\{|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|\}}\\ \le \left(\frac{C}{\alpha }+\frac{C}{\alpha }\right)\Vert h\Vert .\end{array}$$

The above discussion yields the next statement:

Proposition 4

Assume that, for every point y in the open and convex set Ω ⊂ ℝ², there exists α > 0 such that $|\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,y)|>\alpha$. Then the shearlet-based Directional Ratio ${\mathcal{D}}_{a}f$, at scale a, restricted on Ω, satisfies a Lipschitz condition and, thus, it is weakly differentiable on Ω.

The weak differentiability of ${\mathcal{D}}_{a}f$ follows from the fact that ${\mathcal{D}}_{a}f$ is absolutely continuous since it satisfies a Lipschitz condition.

4. Quantitative measure of alteration in biological neural networks

Structural and morphological changes of neurites often precede functional deficits or neuronal death associated with many brain disorders and several methods have been proposed to quantify these phenotypes. Popular methods include the Sholl analysis [36, 23], the Schoenen Ramification Index [35] and the fractal analysis [26], which are used to measure the branching characteristics of neurons, and the tortuosity index, defined as the ratio of the arc length over the end-point distance of a curve, which is used to describe the degree of ‘straightness’ of a given neurite [31, 42]. While these methods are very effective at single neuron level and have been often used to classify neuron populations, they are unable to provide a quantitative measure of the structural properties of a biological neural network. Emerging evidence indicates that many brain disorders are associated with the disruption of the network of neurites in defined brain areas [4, 16]. Thus, the ability to quantify the loss of regularity and structural organization in these networks is potentially very helpful to unravel fundamental structure-function properties involved in the insurgence of brain disorders.

An example of the type of data for which we wish to provide a quantitative analysis is illustrated in Fig. 5, where axonal processes in a brain tissue derived from a control mouse (Fig. 5(a)) and from a transgenic mouse which models neurodegeneration (Fig. 5(b)) are visualized with confocal fluorescent microscopy. The figure shows that, while in the control specimen the axonal processes are rather straight and tend to run parallel to one another, in the transgenic animal neighbouring processes are not very aligned and tortuous, leading to an overall disrupted and chaotic pattern. To deal with these types of data, we introduce a new approach which models a network of neurites as a system of tubular structures. Our observation is that one can measure the overall structural organization and regularity of this system by estimating the statistical spread of orientations of the tubular structures sampled over the region they occupy.

Figure 5.

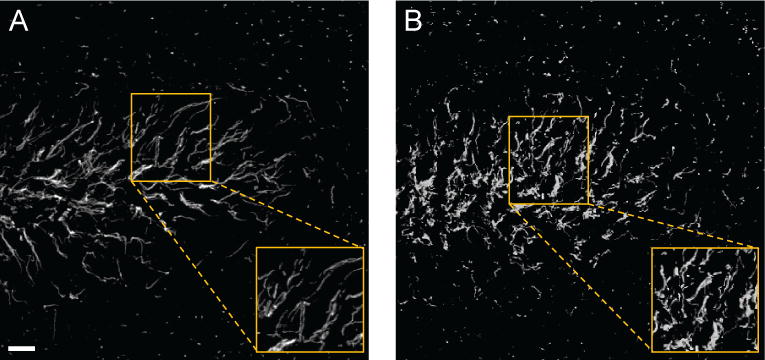
Representative confocal images of axonal processes in the dentate gyrus, a brain area important for cognitive function, in a control mouse (A) and in a transgenic mouse model of neurodegeneration (B). Axonal processes are labeled with an anti-beta-IV-spectrin antibody and visualized with an Alexa 488-conjugated secondary antibody. Note that the pattern distribution of beta-IV-spectrin is disrupted in the dentate gyrus of the transgenic animal. The boxed region is enlarged on the bottom right of each panel to highlight the orientation pattern of the axonal processes at a higher resolution. Scale bar = 10 μm.

A direct approach to measure the spread of orientations would require to extract the local directional information of the tubular structures and use the notion of circular variance from directional statistics [8]. In an ideal tubular structure, this can be obtained by detecting the edges and then estimating their orientations. However, in the case of fluorescent images, it is difficult to extract the edges reliably due to the presence of noise. Therefore, we introduce an alternative procedure which uses the shearlet transform to estimate the local directional content of an image. As illustrated in Section 2., the continuous shearlet transform maps a function f into the elements $\mathcal{S}{\mathscr{H}}_{\psi }f(a,s,t)$ measuring the energy content of f near t at scale and orientations associated with a and s, respectively. Hence, for a_j = 2^−2j and $t_k=B_s{A}_{2^{-2j}}k$ fixed, the functions $h_{j,k}(s)={|\mathcal{S}{\mathscr{H}}_{\psi }f(a_j,s,t_k)|}^2$ measure the distribution of the directional content of f at scale 2^−2j and location t_k. We will use these functions to build an histogram of the directional content of an image.

4.1. Shearlet-based histogram of directional content

To define an histogram of the directional content of an image I using the shearlet transform, we consider the functions $h_{j,k}(s)={|\mathcal{S}{\mathscr{H}}_{\psi }I(a_j,s,t_k)|}^2$ evaluated at the discrete directional values s(ℓ) = 2^−jℓ, ℓ ∈ N_j, where N_j is a finite set depending on j. We assume that the image is normalized so that ‖I‖₂ = 1. For each fixed scale j, we compute the quantities

$$H_j(\ell )={\displaystyle \sum _k{h}_{j,k}(s(\ell ))}={\displaystyle \sum _k{|\mathcal{S}{\mathscr{H}}_{\psi }I(j,\ell ,k)|}^2},$$

where $\mathcal{S}{\mathscr{H}}_{\psi }I(j,\ell ,k)$ is the discrete shearlet transform introduced in Sec. 2.. Hence, H_j describes the energy amount of I in each directional band indexed by ℓ.

Using the vectors H_j, we define a measure of the directional spread by computing a distance between the image I and an appropriate reference image I₀. That is, the image I₀ models the situation where all neurites are perfectly straight and parallel to one another, so that the corresponding feature vectors $H_j^{(0)}$ have all components equal to 0, except for one component (with ‖I₀‖₂ = 1). We define the directionality spread index as the quantity

$${\nu }_2(I)={\displaystyle \sum _j\underset{0\le d\le n_j}{\min }}{\displaystyle \sum _{\ell }{|H_j([\ell +d]n_j)-H_j^{(0)}(\ell )|}^2},$$ (4.1)

where [ℓ+d]_n(j) is the sum ℓ+d modulo n_j and is used to ensure that I₀ is compared to all possible rotated versions of I. That is, ν₂(I) is the rotation-invariant ℓ² distance between the feature vectors of I and I₀. Note that ν₂ ranges between ν₂(I) = 0, corresponding to the case where all neurites are perfectly straight and parallel to one another in the image I, and ν₂(I) ≈ 2, corresponding to the case of maximum misalignment, where the directional content is uniformly distributed among all directional bands.

However, while the use of the ℓ²-norm in (4.1) is a natural mathematical choice, it is not very ‘physical’ (the inadequacy of ℓ²-norm to measure distances between features in well-known in computer vision, e.g., [9, 34]). As a more effective alternative, we can consider the Earth Mover’s Distance (EMD), known in mathematics as the Wasserstein metric, which is based on a solution of the transportation problem and was originally proposed to provide a consistent measure of distance or dissimilarity between two distributions of mass [33, 34]. This metric is particularly appealing in our context. In fact, the histogram associated with the vector H_j can be viewed as the amount of directional content piled over the various directionals bins. The directionality spread index associated with the EMD gives a measure of the minimum cost of turning these piles into the single pile corresponding to $H_j^{(0)}$. In other words, it is measuring the cost of turning a network of possibly misaligned neurites into an ideal configuration where all neurites run parallel to one another. With respect to other notions of distances between histograms such as the information theoretic Kullback-Leibler divergence [18] and the entropy, which account only for the correspondence between bins with the same index and do not use information across bins, EMD is a cross-bin distance measure, is not affected by binning differences and meaningfully matches the physical notion of closeness.

To illustrate the use of our new definition, we have computed the directionality spread index ν₂ and its variants associated with the EMD and other types of distances on a set of confocal fluorescent images similar to those in Fig. 5 in order to compare the axonal processes in brain tissues from control mice versus transgenic mice. The values of the directionality spread index associated with the ℓ²-norm, EMD, Kullback-Leibler distance (KLD) and the entropy distance are reported in Table 1. For each population (control animal, i.e., wild type, vs. transgenic animal), the table shows the mean directionality spread index computed over 8 samples together with the standard deviation. Note that only the values of the directionality spread index associated with the EMD have passed the normality test. The numbers that we have obtained show that the difference between the directionality spread index of the two populations is statistically significant.

Table 1.

Mean tortuosity scores using different metrics. Data are in the form: mean ± SD; p < 0.0001. The values are obtained from 8 sample images for each population.

Sample tissue	EMD	KLD	ℓ2	ENTROPY
Wild type	28.1 ± 3.4	32.8 ± 3.4	1.9 ± 0.07	4.7 ± 0.11
Transgenic	37.3 ± 1.5	45.8 ± 1.9	1.5 ± 0.02	4.9 ± 0.01

5. Conclusion

In this paper, we have shown that directional multiscale representations and, in particular, the shearlet representation offer a powerful and flexible framework for the analysis and processing of fluorescent images of complex biomedical data. The power of the shearlet representation comes for its ability to combine multiscale data analysis and high directional sensitivity, making this approach particularly effective for the representation of objects defined over a wide range of scales and with highly anisotropic features, such as the somas and neurites which are the main morphological constituents of imaged neurons. We have applied the shearlet representation to detect somas in fluorescent images of neuronal cultures and extract geometrical features from complex networks of neuronal processes in brain tissue. Our theoretical observations and numerical results show that the shearlet approach offers a very competitive analytical and computational framework for the geometric quantification of morphological features from large-scale fluorescent images of neurons.

Figure 4.

Values of directional ratio (color-coded) computed at various discrete scales; from left to right: $a=2^{-4}{2}^{\frac{1}{4}}$, $a=2^{-3}{2}^{\frac{1}{4}}$, and $a=2^{-1}{2}^{\frac{1}{4}}$ according to the conventions of this paper. Using the convention of the discrete shearlet transform, from left to right we show the directional ratio at two, three and five scales below the resolution level of the original. As the scale becomes coarser, the values of the directional ratio in the interior of neurites become consistently more uniform and do not exceed a certain low threshold, whose existence is predicted by Theorem 3.2. In the interior of the soma and of thicker neurites, the values of directional ratio vary wildly, once again as predicted by Theorem 3.2.