Suppression of viral infectivity through lethal defection

Abstract

RNA viruses replicate with a very high error rate and give rise to heterogeneous, highly plastic populations able to adapt very rapidly to changing environments. Viral diseases are thus difficult to control because of the appearance of drug-resistant mutants, and it becomes essential to seek mechanisms able to force the extinction of the quasispecies before adaptation emerges. An alternative to the use of conventional drugs consists in increasing the replication error rate through the use of mutagens. Here, we report about persistent infections of lymphocytic choriomeningitis virus treated with fluorouracil, where a progressive debilitation of infectivity leading to eventual extinction occurs. The transition to extinction is accompanied by the production of large amounts of RNA, indicating that the replicative ability of the quasispecies is not strongly impaired by the mutagen. By means of experimental and theoretical approaches, we propose that a fraction of the RNA molecules synthesized can behave as a defective subpopulation able to drive the viable class extinct. Our results lead to the identification of two extinction pathways, one at high amounts of mutagen, where the quasispecies completely loses its ability to infect and replicate, and a second one, at lower amounts of mutagen, where replication continues while the infective class gets extinct because of the action of defectors. The results bear on a potential application of increased mutagenesis as an antiviral strategy in that low doses of a mutagenic agent may suffice to drive persistent virus to extinction.

Rates of spontaneous mutation per genome differ strikingly among species, indicating that this character is subjected to selection and evolutionary change. The optimal mutation rate results from the need to maintain an accurate enough level of genetic information while adapting fast to changes in the environment. Organisms living in constant environments usually display low mutation rates, whereas organisms thriving in fluctuating environments need to generate a high genetic diversity. In the latter case, a complex interaction between the structure of the heterogeneous population and the environment ensues (1).

The transmission cycle of RNA viruses in nature includes large fluctuations in the environment in which replication takes place: invasion of different organs and tissues, changes of host, presence of antibodies and molecules secreted by the immune system, and population bottlenecks, among others. It is believed that the high mutation rates characteristic of RNA viruses, together with their short replication time and large populations, favor their adaptation: rare variants that confer an advantage in a new environment can become rapidly amplified (2, 3). However, as described in molecular evolution theories applied to theoretical genome populations, the mutation rate has an upper limit set by the requirement of accurate transmission of the genetic information (4). When this threshold is crossed, disorganization of the mutant distribution of the quasispecies occurs, the genetic information is lost, and the population becomes extinct because of genetic meltdown. This phenomenon is known as error catastrophe. The high mutation rate of RNA viruses places viral quasispecies very close to the error threshold (5, 6), and it has been experimentally demonstrated that small increases of mutation rate through the use of mutagens can force the extinction of viral populations (6–15). Classical theories on error catastrophe equal fitness to replicative ability and explain extinction on the basis of the accumulation of many deleterious mutations in the viral genomes, so that they eventually fail to replicate themselves. However, if these theories are to be applied to viral quasispecies, it is necessary to take into account that fitness is not only determined by the replicative ability of the genomes but also that there are a number of phenotypic functions that are involved in the completion of the viral life cycle. The effect of mutations in all these functions adds extra complexity to the mechanisms driving viral populations to extinction through increased mutagenesis.

Within an infected cell, there are many viral genomes sharing the necessary resources for replication to take place. These genomes include cellular structures and viral proteins (i.e., polymerase and structural proteins of the capsid and envelope). Because of the high error rates of RNA viruses, even inside a single cell, the genetic diversity can be very large, because mutants with a reduced ability to replicate or encode functional proteins are continuously generated (12). However, as long as functional products that can act in trans are accessible for any genome in the cellular interior, there is nothing limiting their use by defective mutants unable to code for correct proteins themselves. This finding means that in a normal infection a variable amount of the viruses produced are necessarily noninfective. Inside the cell, the noninfective class can be regarded in practice as a parasite of the viable type, thus resulting in viable–defector interactions (16–18) that likely interfere in a deleterious way with the efficient replication of the altruistic, viable class (19). Under these circumstances, it seems plausible that many defective mutants can replicate as fast as viable particles. This finding is supported by observations made with poliovirus (7–9) and Hantaan virus (20) where decreases in infectivity preceded decreases in viral RNA levels. As far as the mutation rate is kept below a (virus-dependent) critical threshold, noninfective mutants maintain a dynamic equilibrium with fully viable genomes. Increases in the mutation rate force the appearance of larger amounts of genomes unable to code for functional proteins although able to replicate when these proteins are furnished by other viruses. If the amount of defective particles grows beyond a critical fraction, it is reasonable to suppose that a form of extinction where defective mutants exhaust functional resources produced by viable genomes might supervene.

Materials and Methods

Virus and Cells. The genome of lymphocytic choriomeningitis virus (LCMV) consists of two single-stranded RNA segments: small segment (S; 3,376 nt) and large segment (L; 7,220 nt) of negative polarity (21). Virus infections and maintenance of baby hamster kidney (BHK-21) and Vero cells were carried out as described (10). LCMV ARM 53b is a triple plaque-purified clone from ARM CA passaged four times in BHK-21 cells. Virus infectivity in supernatants and intracellular samples were determined by assay on Vero cell monolayers because the virus does not form lytic plaques on BHK-21 cells. Vero cells monolayers (1 × 10⁶ cells in six-well dishes, Falcon) were infected in duplicate with virus suspensions. After 1 h of adsorption, the virus was removed and cells were overlaid with 4 ml of DMEM supplemented with 0.7% FCS/2% l-glutamine/50 μg/ml gentamicin/0.25% agar. After 84 h, cells were stained with Neutral red in PBS at a final concentration of 0.25 mg/ml and incubated for 8 h, and viral plaques were counted.

RNA Amplification, Quantification of the L Genomic Segment, and Calculation of Mutation Frequencies. Total RNA from samples was extracted with TRIzol (Invitrogen) and reverse transcription of the genomic segment L (viral RNA polymerase) was performed with ThermoScript RT (Invitrogen) at 65°C for 60 min with primer L4252R (antisense). Amplification by PCR was performed with Pfu (Promega) with primers L3654F (sense) and L4252R. RNA corresponding to the L genomic segment was quantified by two-step RT-PCR with the Light Cycler Fast Start DNA Master SYBR green I kit (Roche Applied Science, Penzburg, Germany) in a Light Cycler instrument (Roche Applied Science). An LCMV RNA from nucleotides 3654 to 4252 was used as standard. DNA cloned into pGEM T Easy Vector (Promega) was transcribed with SP6 DNA polymerase and purified with RNA Easy minikit (Qiagen, Hilden, Germany). Molecular clones were obtained by cloning the region encompassing nucleotides 3654–4252 into pGEM T Easy Vector (Promega) and were sequenced with T7 and SP6 promoter primers. Mutation frequencies were calculated for each virus sample by comparing the sequences of individual clones with their corresponding consensus sequence.

Computational Model. Initially, a small number of particles infect an empty cell. Each virtual viral genome is characterized by two parameters, the replicative ability r, which takes continuous values between 1 and R, and the ability to encode viral proteins correctly, which is a Boolean variable (either yes or no). For simplicity, we call the genomes viable if the second variable is yes and defective otherwise. The number of copies produced by a genome is a random variable drawn from a Poisson distribution of average r. Replication of the genome, irrespectively of its type, takes place only if a second randomly chosen genome is of the viable type. This action mimics the fact that resources are shared by both types. The effect of the mutagen is represented through a parameter m, which stands for the average number of mutations per genome and replication. The actual number of mutations for each copy, k, is chosen from a Poisson distribution of average m. Each mutation has an independent effect (δr) on the replicative ability, with δr randomly chosen from an exponential distribution of average one. The effect of each individual mutation can be deleterious (δr < 0 with probability p), advantageous (δr > 0 with probability q), or neutral (δr = 0 with probability 1 – p – q). The total change Δr is finally calculated as the sum of k independent effects. The amount of mutagen also influences the transition rates between viable and defective types. The transition from viable to defective types takes place with probability w whenever Δr is negative; defective particles can become viable with probability w if Δr is positive. This last rule includes a reasonable correlation between the loss of replicative ability and a decrease in the capability to code for proteins correctly. Finally, at each replication cycle and for each genome, there is a probability d that the genome is eliminated from the system because of degradation. Once the cell is infected, error-prone replication proceeds, as described, until a maximal number of genomes N are reached. When genomes are in excess, they replace randomly chosen genomes that are eliminated, thus mimicking virus release by the host cell to the culture supernatant. For simplicity of the model, neither degradation nor the outgoing flux depends on the replicative ability or on the viability of the particles.

Results

To study the effect of increased mutagenesis in the production of noninfective genomes, we have carried out several in vitro experiments with the prototypic Arenavirus LCMV. We have monitored infective virus production and the amount of L RNA genomic molecules during a virological steady-state persistent infection of BHK-21 cells by LCMV in the absence and presence of 100 μg/ml of the mutagenic base analogue 5-fluorouracil (5-FU). The quantification of infective units and L RNA molecules was made separately in the cell culture supernatant (viruses released by the cell) and in the cellular monolayers. In the course of the infection, there is a clear increase in the number of genomic RNA molecules, both in the intracellular fraction and in supernatants of control and mutagenized virus (Fig. 1). However, in FU-treated virus cultures at ≈48 h after infection, infectivity declines and falls below detection, despite the high number of genomic RNA molecules attained. At 72 h after infection, there are ≈100 times more RNA molecules in the control than in the mutagenized sample (Table 1). Interestingly, the ratios are much more dramatic for the number of infective units. In the control sample (either in the intracellular fraction or in the supernatant), there is between 10⁵- and 10⁶-fold larger number of infectious units than in the mutagenized sample. The ratio between total RNA molecules and infective units grows almost exponentially when the population approaches extinction. These results indicate that, in the presence of 5-FU, replication of LCMV RNA molecules is affected to a much lower extent than infectivity, and clearly demonstrates that the relative production of nonviable particles dramatically raises with an increase in the mutation rate.

Fig. 1.

Quantification of the L genomic segment in the extinction of LCMV. Infectivity of virus in supernatants and cell fractions of LCMV incubated in the absence (A, control) or presence of 100 μg/ml 5-FU (B) were assayed on Vero cell monolayers. ic, intracellular; sn, supernatant. Total RNA from these samples was extracted with TRIzol (Invitrogen) and the RNA corresponding to the L genomic segment was quantified by two-step RT-PCR with the Fast Start DNA Master SYBR green I kit (Roche Applied Science) in a Light Cycler instrument (Roche Applied Science). Virus titers (circles) and RNA (squares) are expressed as total plaque-forming units and total molecules of L genomic RNA, respectively, for each sample. Error bars for selected points correspond to 1 SD from the average.

Table 1.

Ratios of RNA and plaque-forming unit abundance between the controls and the FU-treated samples (data are in Fig. 1).

Time after infection, h	Ratio of total RNA molecules (sn)	Ratio of total RNA molecules (ic)	Ratio of pfu (sn)	Ratio of pfu (ic)
0	—	0.232	0.39	0.14
24	29.4	2.441	2.88 × 103	2.24 × 103
48	264.7	129.4	2.19 × 105	2.85 × 104
72	60.9	56.74	5.50 × 106	6.33 × 105

sn, supernatant; ic, intracellular.

To analyze the effect of the mutagen on the error rate of viral replication, the accumulated number of mutations in 20 viral genomes at different times after infection was determined. To this end, we cloned and sequenced a region of the L gene both from intracellular and supernatant fractions in mutagenized and control populations (see Materials and Methods). For control viruses, mutation frequency values were in the range of 1.2 to 3.5 × 10^–4 substitutions per nucleotide. In 5-FU-treated samples, the mutation frequency varied between 1.0 × 10^–4 and 1.8 × 10^–3. Whereas in the intracellular fraction of mutagenized viruses, we find a statistically significant trend to increase the mutation frequency with the time of exposure to FU, the regression analysis does not show a significant positive trend in the supernatant fraction. This finding indicates that, at least within the cellular environment, the action of the mutagen keeps the system out of the mutation-selection equilibrium, eventually resulting in extinction of infectivity.

The representation of the number of infective units per RNA molecule as a function of the mutation frequency (Fig. 2) yields a curve with a sharp decay when the mutation frequency increases past a critical threshold (6). This sudden loss of infectivity takes place through a transition analogous to that predicted by error catastrophe theory. However, the unexpected outcome of the experiment is the presence of large numbers of RNA molecules, revealing that the replicative ability does not disappear simultaneously with the infectivity.

Fig. 2.

Relation between infectivity and mutation frequency for infections in the presence of 5-FU. Infectivity values (plaque-forming units per RNA molecule) were calculated by using the results of Fig. 1. The mutation frequency was determined after sequencing the region encompassing nucleotides 3654–4233. There is a critical mutation rate beyond which infectivity gets extinct. For the intracellular fraction of mutagenized samples, a number between 13 and 25 sequences was analyzed. The corresponding standard deviation for the mean number of mutations per sequence (SD) lies between 0.41 and 0.92. For supernatant fractions of mutagenized samples, the number of sequences analyzed varied between 7 and 15 (SD values between 0.38 and 1.20). In the control intracellular samples, we analyzed 13–15 sequences (SD values between 0.27 and 0.41). For control supernatant fractions, 20 sequences were analyzed at 24 h after infection in the intracellular fraction (SD = 0.31) and 19 sequences at 72 h after infection (SD = 0.54).

Our results so far seem to support the initial statement that an enhanced presence of defective replicators might cause the extinction of a viable (infective) class. Ideally, we would like to repeat the same experiment in the absence of defective genomes and with a mutagenic agent affecting only the replicative ability of the virus. This experiment cannot be carried out with real viruses because of the intrinsic impossibility of separating defective from infective genome populations. At this point, however, suitable in silico experiments can fill this gap and illustrate the qualitative behavior to be expected in such a situation (see Materials and Methods). With the goal of proving that, in the computational model, extinction is induced by the action of defective genomes, two different settings are considered. In the first one, both viable and defective particles are present (VD setting). In the second one, all genomes are viable and the mutagen only acts on their replicative ability, that is, on the number r of copies produced per genome (V setting).

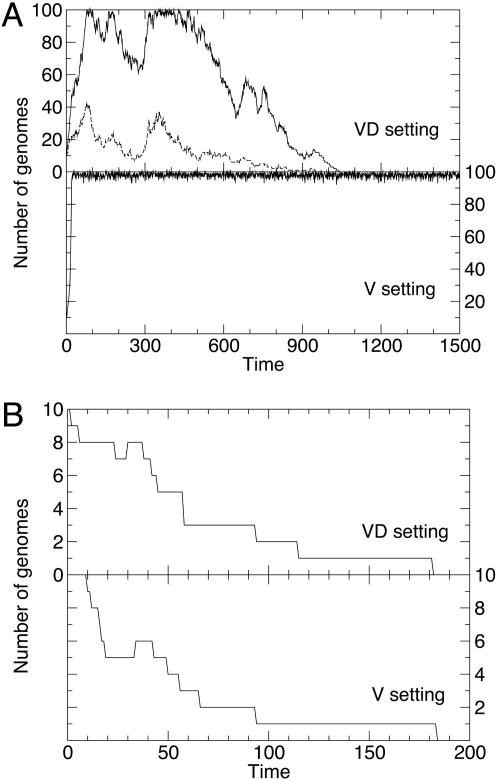
The dynamics of the process in both settings is represented in Fig. 3. The two settings, VD and V, display a qualitatively different dynamical behavior at low concentration of mutagen (Fig. 3A), whereas they behave similarly for high values of m (Fig. 3B). For relatively large amounts of mutagen, setting V or setting VD, experience the effect of mutagen in a similar way: replication is strongly impaired and the initial population goes readily extinct. In most computer simulations, defective particles with r > 0 never appeared. This scenario changes for lower amounts of mutagen, where a persistent coexistence of both types becomes possible in the VD setting. Then, the typical time required for disappearance of all viable particles increases many fold, although eventual extinction is unavoidable. This situation contrasts strongly with the dynamical behavior of setting V: for amounts of mutagen lower than the critical value forbidding replication (m_c), extinction of the population has never been observed. Thus, in the absence of defectors, extinction does not occur once the total number of particles becomes large enough. Taking m as independent variable, we have monitored the average behavior of several relevant quantities (Fig. 4). Whereas in the V setting extinction is possible only above the critical error threshold m_c, the two different dynamical regimes in the VD setting represent two different pathways to extinction: as in the V setting, extinction takes place when the error rate in replication is above the critical error rate (m > m_c), but a second pathway to extinction appears below that threshold because of lethal defection (m < m_c). In the presence of defective genomes, the system is doomed to extinction.

Fig. 3.

Dynamics of the model system at low and high amounts of mutagen m, illustrating the two different pathways to extinction. (A) Extinction due to the action of defectors. The curves show the number of genomes inside a model cell in the VD and V settings (with VD genomes or only V genomes, respectively), for m = 6 mutations per genome and replication cycle. In the VD setting, the total number of genomes (VD, full line) fluctuates broadly because of the decoupling between replicative ability and viability for each genome, which translates into a variable amount of V genomes (dashed line). Once V genomes disappear, replication is no longer possible, and the extinction of unviable (although replicative) genomes follows. In the V setting (lower plot), high numbers of viable genomes are maintained and extinction is not observed. (B) Extinction due to the loss of the replicative ability. At high amounts of mutagen (m = 20 in these plots), viability and replicative ability are simultaneously lost, extinction occurs readily, and no qualitative difference between the VD and V settings is observed. Time is measured in replication cycles. All simulations start with 10 viable particles of replicative ability r = 2. Other parameters values are P = 0.9, q = 0.05, R = 4, d = 0.02, and w = 0.5 for the setting VD.

Fig. 4.

Statistical behavior of the model system as a function of the average number of mutations per copy (m, horizontal axis). Two different regimes separated by the vertical dotted line at the critical amount of mutagen m_c = 15 can be distinguished. (A) Average time to extinction. Diamonds stand for the V setting (with viable genomes only), stars stand for the VD setting (with VD genomes). In the V setting, there is no extinction for m < m_c; in the VD setting, extinction occurs in finite time for any value of m. Above the critical value m_c, both settings behave similarly, and extinction takes place in a few hundred replication cycles. (B) Average number of genomes present until extinction supervenes. Open squares correspond to the V setting. There is a clear transition from a full system to only few genomes present at m > m_c. Solid symbols correspond to the VD setting. Defective (triangles) and V genomes (circles) coexist before extinction occurs in the phase m < m_c. Above the transition, the behavior is comparable to the system without defective genomes (V). (C) Average replicative ability of the genomes (symbols are as in B). In all cases, the replicative ability of the genomes decreases monotonously with the increase in the amount of mutagen. In the VD setting, and for m > m_c, defective genomes appear only rarely, and the average fitness of the viable genomes is just that of the initial population. The average replicative ability of the defective type lies always below that of the viable type, this being the result of the correlation between positive/negative changes in replicative ability and gain/loss of viability. In all images, each point represents an average over several thousand independent numerical simulations of the system. Parameter values are as in Fig. 3.

Discussion

The high sensitivity of LCMV to FU (10, 15) and the steady-state persistent infection that the virus establishes in BHK-21 cells (22) permits monitoring of intracellular and extracellular LCMV RNA and infectivity without confounding effects of cell killing and RNA release inherent to cytolytic infections or persistently infected, carrier cultures.

The empirical observations, together with the numerical results, suggest that, in the experiments, it is the presence of defectors which induces extinction at moderate concentrations of mutagen. An additional constraint is essential to observe extinction: that the system size be finite because, as N grows, the average time to extinction increases as well, and eventually diverges for an infinite system. Another difference between the settings V and VD is the nature of the transition between the two dynamical regimes. In the setting without defectors, there seems to be a discontinuity at m = m_c, where the time to extinction jumps from finite (and small) values to infinity. In contrast, the transition for VD seems to be continuous, with the extinction time growing smoothly once the amount of mutagen is low enough to permit the coexistence of viable and defective genomes. The qualitative behavior displayed in Figs. 3 and 4 is robust with respect to changes in the values of the parameters and rules of the model, as long as the separation of the effects of mutations in replication and viability is included.

The intrinsic dynamics of the process in the pathway to extinction because of the action of defectors (m < m_c) is highly fluctuating. This is because of the multiplicative nature of the replicative process and to the stochastic appearance of mutants.

The system is highly sensitive to the events occurring at the initial steps of growth, which can determine whether extinction occurs readily and before the number of particles is large enough to settle the system. Later, the number of viable particles, which determines the sustainability of the entire system, is hardly affected by the contingent appearance of defective mutants. As a consequence, it is not possible in practice to establish with a high degree of accuracy the moment at which extinction occurs, in agreement with previous experiments (10).

The position of the error threshold and the pathway leading to extinction are not only determined by the mutation rate. Virus infection comprises more processes than genome replication and, because these processes can also be affected by mutations, they must be taken into account (3, 6). This situation can become more complex when the error threshold at which genotypic information is lost differs from that at which phenotypic information disappears (23), or when phenotypic traits experiencing different selective pressures in two environments are coupled through fitness tradeoffs (24).

Our conceptual framework includes phenotypic characteristics, such as the ability to encode proteins, as a relevant fact affecting the dynamics and fate of heterogeneous populations. We have only distinguished between viable and defective genomes as those able or not to code for the functional proteins necessary for virus completion. However, in a viral infection it is expected to obtain genomes with different abilities to code for products or, in other words, viral particles with different degrees of infectivity. In a natural system, there will also be genomes that lack the signals for interacting with the polymerase or for encapsidation. These viruses will not further replicate and will be eliminated from the system. Taking into account these other properties, not explicitly considered in our model, implies that our numerical results probably underestimate the fraction of defective genomes present. In addition, it seems plausible that when fitness is separated in a number of essential traits that experience differential selection in a certain environment, there will be as many pathways to extinction (or extinction thresholds) as traits considered. If, moreover, the disappearance of one of the traits implies the extinction of a second one (as is the case here, where the extinction of viability forbids further replication), a cascade of effects triggered with the extinction of the first trait is to be expected. In practice, it might prove difficult to disentangle direct effects because of the action of external forces (like the mutagen) from indirect effects because of the disappearance of a particular but essential trait.

Another consequence of the mechanism just described is that a (potentially viable) population may contain infective genomes that are nevertheless unable to replicate just because of the interfering effect of deleterious mutants. In this sense, the occurrence of bottlenecks can be decisive to avoid extinction by aiding to isolate genomes that are able to initiate an infection (25, 26). From this point of view, bottleneck events would be a kind of positive selection operating against extinction caused by increases in the mutation rate. These results confer new and renewed biological implications to the defective viral genomes that coexist with viable counterparts, implications that faded after the studies with defective interfering particles three decades ago. This finding comes at a time in which error-prone replication, cellular and viral genome plasticity, and limited accuracies in cellular processes are becoming the rule rather than the exception. Finally, the results imply that a modest mutagenic activity to increase the level of viral genome defectors may be sufficient to effect viral extinction, thus facilitating a possible clinical application of viral extinction through lethal defection.