Generalized Bienenstock–Cooper–Munro rule for spiking neurons that maximizes information transmission

Abstract

Maximization of information transmission by a spiking-neuron model predicts changes of synaptic connections that depend on timing of pre- and postsynaptic spikes and on the postsynaptic membrane potential. Under the assumption of Poisson firing statistics, the synaptic update rule exhibits all of the features of the Bienenstock–Cooper–Munro rule, in particular, regimes of synaptic potentiation and depression separated by a sliding threshold. Moreover, the learning rule is also applicable to the more realistic case of neuron models with refractoriness, and is sensitive to correlations between input spikes, even in the absence of presynaptic rate modulation. The learning rule is found by maximizing the mutual information between presynaptic and postsynaptic spike trains under the constraint that the postsynaptic firing rate stays close to some target firing rate. An interpretation of the synaptic update rule in terms of homeostatic synaptic processes and spike-timing-dependent plasticity is discussed.

The efficacy of synaptic connections between neurons in the brain is not fixed, but it varies, depending on the firing frequency of presynaptic neurons (1, 2), the membrane potential of the postsynaptic neuron (3), spike timing (4–6), and intracellular parameters such as the calcium concentration; for a review see ref. 7. During the last decades, a large number of theoretical concepts and mathematical models have emerged that have helped to understand the functional consequences of synaptic modifications, in particular, long-term potentiation (LTP) and long-term depression (LTD) during development, learning, and memory; for reviews see (8–10). Apart from the work of Hebb (11), one of the most influential theoretical concepts has been the Bienenstock–Cooper–Munro (BCM) model originally developed to account for cortical organization and receptive field properties during development (12). The model predicted (i) regimes of both LTD and LTP, depending on the state of the postsynaptic neuron, and (ii) a sliding threshold that separates the two regimes. Both predictions i and ii have subsequently been confirmed experimentally (2, 13, 14).

In this paper, we construct a bridge between the BCM model and a seemingly unconnected line of research in theoretical neuroscience centered around the concept of optimality.

There are indications that several components of neural systems show close to optimal performance (15–17). Instead of looking at a specific implementation of synaptic changes, defined by a rule such as in the BCM model, we therefore ask what would be the optimal synaptic update rule so as to guarantee that a spiking neuron transmits as much information as possible? Information theoretic concepts have been used by several researchers because they allow to compare performance of neural systems with a fundamental theoretical limit (16, 17), but optimal synaptic update rules have so far been mostly restricted to a pure rate description (18–21). In the following, we apply the concept of information maximization to a spiking-neuron model with refractoriness. Mutual information is maximized under the constraint that the postsynaptic firing rate stays as close as possible to the neuron's typical target firing rate stabilized by homeostatic synaptic processes (22). In the special case of vanishing refractoriness, we find that the optimal update rule has the two BCM properties, i.e., regimes of potentiation and depression separated by a sliding threshold. In contrast to the optimality approach of Intrator and Cooper (23), the sliding threshold follows automatically from our formulation of the optimality problem. Moreover, our extension of the BCM rule to spiking neurons with refractoriness shows that synaptic changes should naturally depend on spike timing, spike frequency, and postsynaptic potential (PSP), which is in agreement with experimental results.

Methods and Models

Spiking-Neuron Model. We consider a stochastically spiking-neuron model with refractoriness. For simulations, and also for some parts of the theory, it is convenient to formulate the model in discrete time with step size Δt, i.e., t^k = kΔt. However, for the ease of interpretation and with respect to a comparison with biological neurons, it is more practical to turn to continuous time by taking Δt → 0. The continuous time limit is indicated in the following formulas by a right arrow (→). The postsynaptic neuron receives input at N synapses. A presynaptic spike train at synapse j is described in discrete time as a sequence 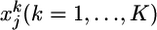of zeros (no spike) and ones (spike). The upper index k denotes time bin k. Thus, 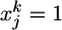indicates that a presynaptic spike arrived at synapse j at a time 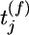with 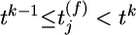. Each presynaptic spike evokes a PSP amplitude w_j and exponential time course 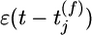with time constant τ_m = 10 ms. The membrane potential at time step t^k is denoted as u(t^k) and calculated as the total PSP

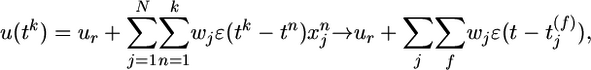[1]

where u_r = –70 mV is the resting potential. The probability ρ^k of firing in time step k is a function of the membrane potential u and the refractory state R of the neuron,

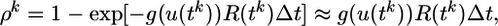[2]

where Δt is the time step and g is a smooth increasing function of u. Thus, the larger the membrane potential, the higher the firing probability. For Δt → 0, we may think of g(u)R(t) as the instantaneous firing rate, or hazard of firing, given knowledge about the previous firing history. We focus on nonadapting neurons where the refractoriness R depends only on the timing of the last postsynaptic spike, but the model can be easily generalized to include a dependence on earlier spikes as well. More specifically, we take for the simulations

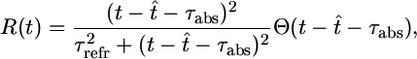[3]

where t̂ denotes the last firing time of the postsynaptic neuron, τ_abs = 3 ms is the absolute refractory time, and τ_refr = 10 ms is a parameter characterizing the duration of relative refractoriness. The Heaviside function Θ(x) takes a value of one for positive arguments and vanishes otherwise. With a function R(t) such as in Eq. 3 that depends only on the most recent postsynaptic spike, the above neuron model has renewal properties and can be mapped onto a spike-response model with escape noise (9). Except for Fig. 2, we take throughout the paper g(u) = r₀ log{1 + exp[(u – u₀)/Δu]} with u₀ = –65 mV, Δu = 2 mV, and r₀ = 11 Hz. This set of parameters corresponds to in vivo conditions with a spontaneous firing rate of ≈1 Hz. The function g(u) and the typical firing behavior of the neuron model are shown in Fig. 1A. For Fig. 2, we consider the case τ_abs = τ_refr = 0 and an instantaneous rate g₂(u) = {10 ms + [1/g(u)]}^–1 with g(u) as above i.e., the neuron model exhibits no refractoriness and is defined by an inhomogeneous Poisson process with maximum rate of 100 Hz; compare Fig. 1 A. Integration of all equations is performed in matlab on a standard personal computer by using a time step Δt = 1 ms.

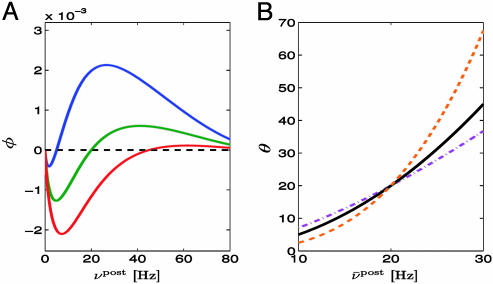
Fig. 2.

Relation to BCM rule. (A) The function φ(ν^post) of the BCM learning rule Eq. 16 derived from our model under assumption of Poisson firing statistics of the postsynaptic neuron. A value of φ(ν^post) > 0 for a given postsynaptic rate ν^post means that synapses are potentiated when stimulated presynaptically. The transition from depression to potentiation occurs at a value θ that depends on the average firing rate 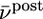of the postsynaptic neuron (blue 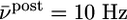; green 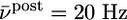; red 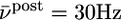). B. The threshold θ as a function of 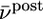for different choices of the parameter γ, i.e.,γ = 0.5 (purple); γ = 1 (black); γ = 2 (orange).

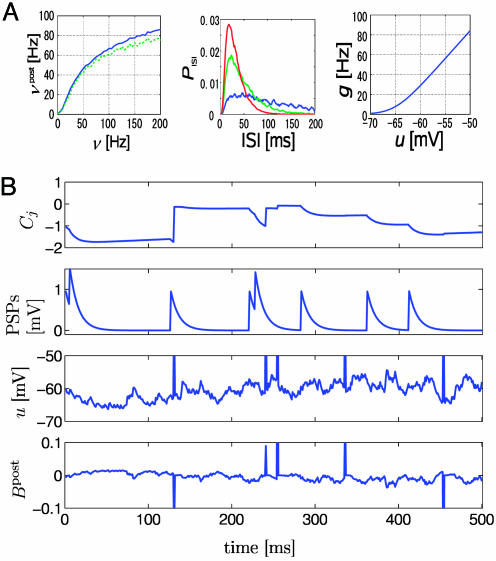
Fig. 1.

Neuron model. (A Left) Output rate ν^post of the model neuron (solid line, spiking neuron model used in Figs. 3, 4, 5; green dashed line, Poisson model used in Fig. 2) as a function of presynaptic spike arrival rate at n = 100 synapses. All synapses have the same efficacy w_j = 0.5, and are stimulated by independent Poisson trains at the same rate ν. (Center) Interspike interval distribution P_ISI of the spiking neuron model during firing at 10 (blue line), 20 (green line), or 30 Hz (red line). Firing is impossible during the absolute refractory time of τ_abs = 3 ms. (Right) The function g(u) used to generated action potentials (see Methods and Models for details). (B) From the first row to the fourth row (with the first row being at the top): The measure C_j that is sensitive to correlations between the state of the postsynaptic neuron and presynaptic spike arrival at synapse j, the PSPs caused by spike arrival at the same synapse j, the membrane potential u, and the postsynaptic factor B^post of Eq. 14 as a function of time. During postsynaptic action potentials, the postsynaptic factor B^post has marked peaks. Their amplitude and sign depend on the membrane potential at the moment of action potential firing. The coincidence measure C_j exhibits significant changes only during the duration of PSPs at synapse j.

Spike Trains. The output of the postsynaptic neuron at time step t^k is denoted by a variable y^k = 1 if a postsynaptic spike occurred between t^k–1 and t^k and 0 otherwise. A specific output spike train up to time bin k is denoted by uppercase letters Y^k = {y¹, y²,..., y^k}. Because spikes are generated by a random process, we distinguish the random variable Y^k by using boldface characters from a specific realization Y^k. Note that the lowercase variable y^k refers always to a specific time bin, whereas the uppercase variable Y^k refers to a whole spike train. Similar remarks hold for the input: X is the random variable characterizing the input at all synapse 1 ≤ j ≤ N; X^k is a specific realization of all input spike trains up to time t^k; X^k_j = {x¹_j, x²_j,..., x^k_j} a specific realization of an input spike train at synapse j, and x^k_j, its value in time bin k. For given presynaptic spike trains X^k and postsynaptic spike history Y^k–1, the probability of emitting a postsynaptic spike is described by the following binary distribution:

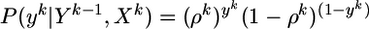[4]

since y^k ∈ {0, 1}. Analogously, we find the marginal probability of y^k given Y^k–1

[5]

where 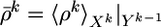and 〈·〉_X^k|Y^k–1 = ∑_X^k · P(X^k |Y^k–1).

From probability calculus, we obtain the conditional probability of the output spike train Y^k given the presynaptic spike trains X^k,

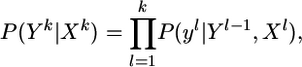[6]

and an analogous formula for the marginal probability distribution of P(Y^k). With Eqs. 4 and 6, we have an expression for the probabilistic relation between an output spike train and an ensemble of input spike trains.

Mutual Information Optimization. Transmission of information between an ensemble of presynaptic spike trains X^K of total duration KΔt and the output train Y^K of the postsynaptic neuron can be quantified by the mutual information (24)

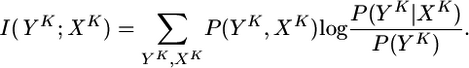[7]

While it is easier to transmit information if the postsynaptic neuron increases its firing rate, firing at high rates is costly from the point of view of energy consumption and also difficult to implement by the cells biophysical machinery. We therefore optimize information transmission under the condition that the firing statistics P(Y^K) of the postsynaptic neuron stays as close as possible to a target distribution P̃(Y^K). With a parameter γ (set to γ = 1 for the simulations), the quantity we maximize is therefore

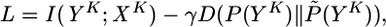[8]

where D(P(Y^K)||P̃(Y^K)) = ∑_Y^KP(Y^K)log(P(Y^K)/P̃(Y^K)) denotes the Kullback–Leibler divergence (24). The target distribution is that of a neuron with constant instantaneous rate g̃ (set to g̃ = 30 Hz throughout the paper except for Fig. 2) modulated by the refractory variable R(t), i.e., that of a renewal process.

The main idea of our approach is as follows. We assume that synaptic efficacies w_j can change within some bounds 0 ≤ w_j ≤ w_max so as to maximize information transmission under the constraint of a fixed target firing rate. To derive the optimal rule of synaptic update, we calculate the gradient of Eq. 8. Applying the chain rule of information theory (24) to both the mutual information I and the Kullback–Leibler divergence D, we can writ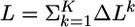e where

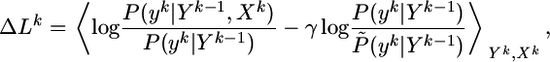[9]

with 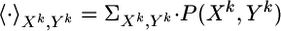. Assuming slow changes of synaptic weights, we apply a gradient ascent algorithm to maximize the objective function and change the synaptic efficacy w_j at each time step by 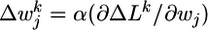with an appropriate learning rate α. Evaluation of the gradient (see Supporting Text, which is published as supporting information on the PNAS web site) yields

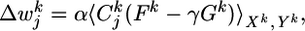[10]

with three functions C_j, F, and G, described in the following. First, with ρ′ denoting the derivative of ρ with respect to u, the quantity

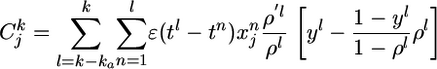[11]

is a measure that counts coincidences between postsynaptic spikes (y^l = 1) and the time course of PSPs generated by presynaptic spikes 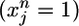at synapse j, normalized to an expected value. The time span k_a of the coincidence window is given by the width of the autocorrelation of the spike train of the postsynaptic neuron (see Supporting Text and Fig. 6 which are published as supporting information on the PNAS web site). The term

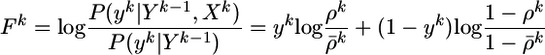[12]

compares the instantaneous firing probability ρ^k at time step k with the average probability, 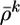and, analogously, the term G^k = log(P(y^k|Y^k–1)/P̃(y^k|Y^k–1)) compares the average probability with the target value 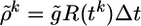. We note that both F and G are functions of the postsynaptic variables only. We therefore introduce a postsynaptic factor B^post by the definition B^post(t^k) = [F^k – γG^k]/Δt and take the limit Δt → 0. Under the assumption of small learning rate α (i.e., α = 10^–4 in our simulations), the expectations 〈〉_X,Y in Eq. 10 can be approximated by averaging over a single long trial that allows us to define an on-line rule (dw_j(t)/dt) = αC_j(t)B^post(t – δ) with a postsynaptic factor

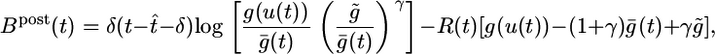[13]

where t̂ is the firing time of the last postsynaptic spike. The delay δ in the Dirac-δ function reflects the order of updates in a single time step of the numerical implementation, i.e., we first update the membrane potential, then the last firing time t̂, then the factors C_j and B, and finally the synaptic efficacy w_j; for the mathematical theory, we take δ → 0. The rate g ρ(t) = 〈g(u(t))〉_X|Y denotes an expectation over the input distribution given the recent firing history of the postsynaptic neuron. For a numerical implementation, it is convenient to estimate the expected rate g(t) by a running average with exponential time window (a time constant of 10 s). Similarly, we replace the rectangular coincidence count window in Eq. 11 by an exponential one (with a time constant of 1 s; see Supporting Text).

Results

We analyzed information transmission for a model neuron that receives input from 100 presynaptic neurons. A presynaptic spike that arrives at time 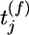at synapse j evokes an excitator PSP of time course 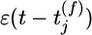. The amplitude w_j of the postsynaptic response is taken as a measure of synaptic efficacy and subject to synaptic dynamics. Firing of the postsynaptic neuron is more likely if the total PSP 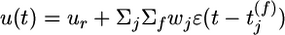is large; however, because of refractoriness firing is suppressed after a postsynaptic action potential at time t̂ by a factor R, which depends on the time since the last postsynaptic spike; see methods for details.

Maximizing the mutual information between several presynaptic spike trains and the output of the postsynaptic neuron can be achieved by a synaptic update rule that depends on the presynaptic spike arrival time 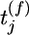, the postsynaptic membrane potential u, and the last postsynaptic firing timet̂. More precisely, the synaptic update rule can be written as

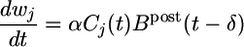[14]

where C_j is a measure sensitive to correlations between pre- and postsynaptic activity, and B ^post is a variable that characterizes the state of the postsynaptic neuron (see Methods and Models). α is a small learning parameter. We note that in standard formulations of Hebbian learning, changes of synaptic efficacies are driven by correlations between pre- and postsynaptic neurons, similar to the function C_j(t). The above update rule, however, augments these correlations by a further postsynaptic factor B^post.

This postsynaptic factor B^post depends on the firing time of the postsynaptic neuron, the refractory state of the neuron, its membrane potential u by means of the instantaneous firing intensity g(u), and on its past firing history by means of g ρ(t). The postsynaptic factor can be decomposed into two terms: the first term compares the instantaneous firing intensity g(u) with its running average g ρ(t) and the second term compares the running average with a target rate g̃. Thus, the first term of B^post measures momentary significance of the postsynaptic state, whereas its second term accounts for homeostatic processes; see Methods and Models for details.

The variable C_j measures correlations between the postsynaptic neuron and its presynaptic input at synapse j

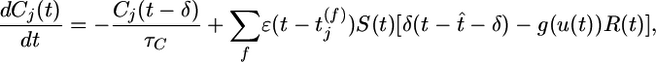[15]

with time constant τ_C = 1s. Here g(u(t))R(t) is the instantaneous firing rate modulated by the refractory function R(t), and S(t) = g′(u(t))/g(u(t)) is the sensitivity (the prime denoting the derivate with respect to u) of the neuron to a change of its membrane potential. The term with the Dirac δ-function δ(t –t̂– δ) induces a positive jump of C_j immediately (with short delay δ) after each postsynaptic spike. Between postsynaptic spikes, C_j evolves continuously. Significant changes of C_j are conditioned on the presence of a PSP 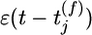caused by spike arrival at synapse j. In the absence of presynaptic input, the correlation estimate decays with time constant τ_C back to 0.

Both the correlation term C_j and the postsynaptic factor B^post can be estimated online (Fig. 1) and use only information that could, directly or indirectly, be available at the site of the synapse: information about postsynaptic spike firing could be conveyed by backpropagating action potentials; timing of presynaptic spike arrival is transmitted by neurotransmitter receptors; and the total PSP can be estimated, although not perfectly, from the local potential at the synapse. The direction of change of a synapse is determined by a subtle interplay between the correlation term C_j and the postsynaptic factor B^post, which can both be positive or negative.

To elucidate the balance between potentiation and depression of synapses, we first considered a simplified neuron model without refractoriness and firing rate ν^post = g₂(u). In this special case, the synaptic update rule Eq. 10 can be rewritten in the simpler form

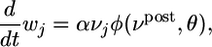[16]

where v_j is the instantaneous firing rate of the presynaptic neuron as estimated from the amplitude of the PSP. 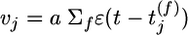generated at synapse j [If the potential is measured in millivolts and time in milliseconds, then the proportionality constant a has units 1/(mV ms)]. φ(ν^post, θ) = f(ν^post)log(ν^post/θ) is a function that depends on the instantaneous postsynaptic firing rate ν^post = g₂(u) and a parameter θ. The function f is proportional to the derivative of g₂, i.e., 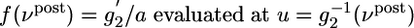. The parameter θ denotes the transition from a regime of potentiation to that of depression. It depends on the recent firing history of the neuron and is given by

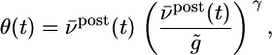[17]

where g̃ = 20 Hz denotes a target value of the postsynaptic rate implemented by homeostatic processes (22) and ν ρ ^post(t) is a running average of the postsynaptic rate. The function φ in Eq. 16 shown in Fig. 2 is characteristic for the BCM learning rule (12). Our approach by information maximization predicts a specific form of this function that can be plotted either as a function of the postsynaptic firing rate ν^post or as a function of the total PSP 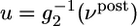, in close agreement with experiments (2, 13). Moreover, because information maximization was performed under the constraint of a fixed target firing rate, our approach yields automatically a sliding threshold of the form postulated in ref. 12, but on different grounds. Thus for neurons without refractoriness, i.e., a pure rate model, our update rule for synaptic plasticity reduces exactly to the BCM rule.

An application of rate models to stimulation paradigms that vary on a time scale of tens of milliseconds or less has often been questioned because an interpretation of rate is seen as problematic. Our synaptic update rule is based on a spiking-neuron model that includes refractoriness and that captures properties of much more detailed neuron models well (25). The learning rule for spiking neurons has a couple of remarkable properties that we explore now.

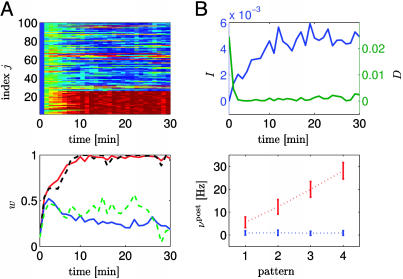
First, we consider a pattern discrimination task in a rate coding paradigm. Patterns are defined by the firing rate ν^pre of 25 presynaptic neurons (ν^pre = 2, 13, 25, and 40 Hz for patterns, 1–4, respectively) modeled as independent Poisson spike trains. The remaining 75 synapses received uncorrelated Poisson input at a constant rate of 20 Hz. Each second, a pattern was chosen stochastically and applied during 1 sec. Those synapses that received pattern-dependent input developed strong efficacies close to the maximal value w_max = 1, whereas most of the other 75 synapses developed weaker ones; compare Fig. 3. However, some of the weakly driven synapses also spontaneously increased their efficacy. This was necessary for the neuron to achieve a mean postsynaptic firing rate close to the target firing rate. Despite the fact that the mean firing rate approaches on a time scale of tens of seconds the target rate, the spike count in each 1-sec segment is strongly modulated by the input pattern and can be used to distinguish the patterns (Fig. 3B) with a misclassification error of <20%. (See Supporting Text and Fig. 7, which is published as supporting information on the PNAS web site.)

Fig. 3.

Pattern discrimination. The first 25 synapses 1 ≤ j ≤ 25 are stimulated by Poisson input with a rate ν^pre = 2, 13, 25, and 40 Hz that changes each second. The remaining 75 synapses receive Poisson input at a constant rate of 20 Hz. (A Upper) Evolution of all synaptic weights as a function of time (red; strong synapses, w_j ≈ 1; blue: depressed synapses, w_j ≈ 0). All synapses are initialized at the same value w_j = 0.1. (Lower) The evolution of the average efficacy of the 25 synapses that receive pattern-dependent input (red line) and that of the 75 other synapses (blue). Typical examples of individual traces (synapse 1: black and synapses 30: green) are given by the dashed lines. (B Upper) Evolution of the average mutual information I per bin (blue line and left scale) and of the average Kullback–Leibler distance D per bin as a function of time. Averages are calculated over segments of 1 min. (Lower) Output rate (spike count during 1 sec) as a function of pattern index before (blue bars) and after (red bars) learning.

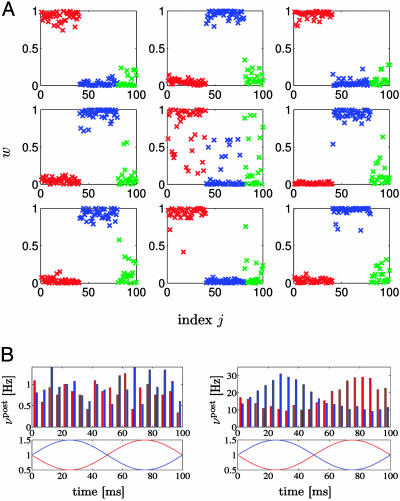
In a second set of simulation experiments, we again studied rate coding, but considered two groups of input defined by periodic modulation of the presynaptic firing rates. More precisely, 40 neurons received input spike trains generated by an inhomogeneous Poisson process with common rate modulation v(t) = v₀ + A sin (2π t/T) with amplitude A = 10 Hz and period T = 100 ms. Another group of 40 neurons received modulated input of the same amplitude and period, however, with a phase shift π. The remaining 20 synapses received Poisson input at a fixed rate v₀ = 20 Hz. All 100 inputs projected onto nine postsynaptic neurons. Synaptic weights were initialized randomly (between 0.10 and 0.12) and evolved according to the update rule Eq. 14. Of the nine postsynaptic neurons, four developed strong connections to the first group of correlated inputs, whereas five developed strong connections to the second group of correlated inputs (Fig. 4A). The rate of the output neurons reflects the modulation of their respective inputs (Fig. 4B). To summarize, the synaptic update rule derived from the principle of information maximization drives neurons to spontaneously detect and specialize for groups of coherent inputs. Just as in the standard BCM rule, several output neurons (with different specialization) are needed to account for the different features of the input.

Fig. 4.

Rate modulation. (A) Distribution of synaptic efficacies of nine postsynaptic neurons after 60 min of stimulation with identical inputs for all neurons. Synapses 1 ≤ j ≤ 40 (red symbols) received Poisson input with common rate modulation; the input at synapses 41 ≤ j ≤ 80 (blue symbols) was also rate-modulated but phase-shifted; and the input at the remaining 20 synapses was uncorrelated (green symbols). Four postsynaptic neurons (numbers 1, 3, 5, and 8) develop a spontaneous specialization for the first group of modulated input (red symbols close to the maximum efficacy of one) and five (numbers 2, 4, 6, 7, and 9) specialized for the second group. (B) Modulation of the output rate of the nine postsynaptic neurons before (Left) and after (Right) learning. Red/blue bars, neurons responding to the first/second group of input; Red/blue lines, modulation of the input of groups 1 and 2.

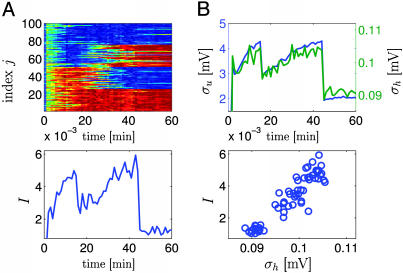
Whereas the two preceding paradigms focused on rate modulation, we now show that, even if all presynaptic neurons fire at the same mean rate, the presence of weak spike-spike correlations in the input is sufficient to bias the synaptic selection mechanism; compare Fig. 5. All synapses received spike input at the same rate of 20 Hz, but the spike trains of 50 synapses showed weak correlations (c = 0.1), whereas the remaining 50 synapses received uncorrelated input. Most of the 50 synapses that received a weakly correlated input increased their weights under application of the synaptic update rule (Fig. 5). If at a later stage the group of correlated inputs changes, the newly included synapses will be strengthened as well, whereas those that are no longer correlated decay. Moreover, the final distribution of synaptic efficacies persists, even if the input is switched to random spike arrival. Thus the synaptic update rule is sensitive to spike–spike correlations on a millisecond scale, which would be difficult to account for in a pure rate model. A biophysical signature of spike–spike correlations are systematic and large fluctuations of the membrane potential. If several postsynaptic neurons receive the same input, their outputs are again correlated and generate large fluctuations in the membrane potential of a readout neuron further down the processing chain (Fig. 5B). Thus, information that is potentially encoded in millisecond correlations in the input can be detected, enhanced, transmitted, and read out by other neurons.

Fig. 5.

Spike–spike correlations. The n = 100 synapses have been separated into four groups of 25 neurons each (group A, 1 ≤ j ≤ 25; group B, 26 ≤ j ≤ 50; group C, 51 ≤ j ≤ 75; group D, 76 ≤ j ≤ 100). All synapses were stimulated at the same rate of 20 Hz. However, during the first 15 min of simulated time, neurons in groups C and D were uncorrelated, whereas the spike trains of the remaining 50 neurons (groups A and B) had correlations of amplitude c = 0.1, i.e., 10% of the spike arrival times were identical between each pair of synapses. After 15 min, correlations changed so that group A became correlated with C, whereas B and D were uncorrelated. After 45 min of simulated time, correlations stopped, but stimulation continued at the same rate. (A Upper) Evolution of all 100 weights (red, potentiated; blue, depressed). (Lower) Average mutual information per bin as a function of time. In the absence of correlations (t > 45 min), mutual information is lower than before, but the distribution of synaptic weights remains stable. (B) Nine postsynaptic neurons 1 ≤ i ≤ 9 with membrane potential u_i(t) are stimulated as discussed in A and project to a readout unit with potential 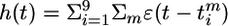where the sum runs over all output spikes m of all nine neurons. Mean membrane potentials are ū and h̄, respectively. The fluctuations σ_u =〈 (u_i(t) – u ρ)²〉^0.5 of the PSPs (blue line, top graph) and those of the readout potentials (σ_h = 〈(h(t) – h ρ)²〉^0.5, green line) are correlated (Lower) with the mutual information and can serve as neuronal signal.

Discussion

The synaptic update rule discussed in this paper relies on the maximization of the mutual information between an ensemble of presynaptic spike trains and the output of the postsynaptic neuron. As in all optimization approaches, optimization has to be performed under some constraint. Because information scales with the postsynaptic firing rate, but high firing rates cannot be sustained by the biophysical machinery of the cell over long times, we imposed that, on average, the postsynaptic firing rate should stay close to a desired firing rate. This idea is consistent with the widespread finding of homeostatic processes that tend to push a neuron always back into its preferred firing state (22). The implementation of this idea in our formalism gave naturally rise to a control mechanism that corresponds exactly to the sliding threshold in the original BCM model (12). While derivations of the BCM model from optimality concepts (23, 19) or statistical approaches (26) are not new, our approach gives another perspective on the concept of a sliding threshold.

Our derivation extends the BCM model, which was originally designed for rate models of neuronal activity to the case of spiking-neuron models with refractoriness. Spiking-neuron models of the integrate-and-fire type, such as the one presented here, can be used to account for a broad spectrum of neuronal firing behavior, including the role of spike–spike correlations, interspike interval distributions, coefficient of variations, and even timing of single spikes; for a review, see ref. 9. The essential ingredients of the spiking neuron model considered here were (i) PSPs generated by presynaptic spike arrival, (ii) a heuristic spiking probability that depends on the total PSP, and (iii) a phenomenological account of absolute or relative refractoriness. The synaptic update rule depends on all three of these quantities. While we do not imply that synaptic potentiation and depression of real neurons are implemented the way it is suggested by our update rule, the rule shows nevertheless some interesting features.

First, in contrast to pure Hebbian correlation driven learning, the update rule uses a correlation term modulated by an additional postsynaptic factor. Thus, presynaptic stimulation is combined with a highly nonlinear function of the postsynaptic state to determine the direction and amplitude of synaptic changes. The essence of the BCM rule (presynaptic gating combined with nonlinear postsynaptic term) is hence translated into a spike-based formulation.

Second, the spike-based formulation of a synaptic update rule should allow a connection to spike-timing-dependent plasticity (5, 6) and allow its interpretation in terms of optimal information transmission (27–29). Given the highly nonlinear involvement of postsynaptic spike times and PSP in the optimal synaptic update rule, a simple interpretation in terms of pairs or pre- and postsynaptic spikes as in many standard models of synaptic plasticity (30, 31) can only capture a small portion of synaptic plasticity phenomena. The optimal learning rule suggests that nonlinear phenomena (32–35) are potentially highly relevant.