Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer

Significance

We have revisited the 2D spectroscopy of the excitation energy transfer in the Fenna–Matthews–Olson (FMO) protein. Based on 2D spectroscopic signatures, the energy transfer dynamics in the FMO protein has been argued to be supported by long-lived electronic quantum coherence on timescales up to 1.5 ps. In contrast, our analysis, based on experimental data and confirmed by theoretical calculations, shows that the electronic decoherence occurs within 60 fs, in agreement with typical dephasing times in systems under these conditions. Given the relatively well-defined structure of the FMO protein, and comparative couplings between chlorophylls to other photosynthetic systems, the observed extremely fast decoherence should be viewed as general, bringing to question any significant quantum coherent transport contributions to photosynthesis.

Abstract

During the first steps of photosynthesis, the energy of impinging solar photons is transformed into electronic excitation energy of the light-harvesting biomolecular complexes. The subsequent energy transfer to the reaction center is commonly rationalized in terms of excitons moving on a grid of biomolecular chromophores on typical timescales $<$100 fs. Today’s understanding of the energy transfer includes the fact that the excitons are delocalized over a few neighboring sites, but the role of quantum coherence is considered as irrelevant for the transfer dynamics because it typically decays within a few tens of femtoseconds. This orthodox picture of incoherent energy transfer between clusters of a few pigments sharing delocalized excitons has been challenged by ultrafast optical spectroscopy experiments with the Fenna–Matthews–Olson protein, in which interference oscillatory signals up to 1.5 ps were reported and interpreted as direct evidence of exceptionally long-lived electronic quantum coherence. Here, we show that the optical 2D photon echo spectra of this complex at ambient temperature in aqueous solution do not provide evidence of any long-lived electronic quantum coherence, but confirm the orthodox view of rapidly decaying electronic quantum coherence on a timescale of 60 fs. Our results can be considered as generic and give no hint that electronic quantum coherence plays any biofunctional role in real photoactive biomolecular complexes. Because in this structurally well-defined protein the distances between bacteriochlorophylls are comparable to those of other light-harvesting complexes, we anticipate that this finding is general and directly applies to even larger photoactive biomolecular complexes.

The principle laws of physics undoubtedly also govern the principle mechanisms of biology. The animate world consists of macroscopic and dynamically slow structures with a huge number of degrees of freedom, such that the laws of statistical mechanics apply. Conversely, the fundamental theory of the microscopic building blocks is quantum mechanics. The physics and chemistry of large molecular complexes may be considered as a bridge between the molecular world and the formation of living matter. A fascinating question since the early days of quantum theory is on the borderline between the atomistic quantum world and the classical world of biology. Clearly, the conditions under which matter displays quantum features or biological functionality are contrarious. Quantum coherent features only become apparent when systems with a few degrees of freedom with a preserved quantum mechanical phase relation of a wave function are well shielded from environmental fluctuations that otherwise lead to rapid dephasing. This dephasing mechanism is very efficient at ambient temperatures, at which biological systems operate. Also, the function of biological macromolecular systems relies on their embedding in a “wet” and highly polar solvent environment, which is again hostile to any quantum coherence. Therefore, the common view of multichromophoric Förster resonance energy transfer has been developed in which excitons are quantum-mechanically delocalized over a few neighboring pigments (1, 2), but a quantum coherent phase relation between the clusters involved in any biologically relevant dynamical process is rapidly destroyed on a sub-$100$-fs timescale. The transport is dominated by dipolar coupling between the sites with different energies, such that it is spatially directed and naturally leads to energy relaxation and flow to the reaction center. The nature of any quantum coherence is short-lived and could, at most, only involve a few neighboring sites—a view that is distinctively different from that of a largely quantum coherent process as implied by very long-lived electronic coherence living as long as proposed (3–5).

In recent years, ultrafast nonlinear 2D optical spectroscopy (6–8) has made it possible to challenge the orthodox view of the energy transfer because it can provide direct access to the couplings between excitonic states. A prominent energy transfer complex, which is simple enough to provide clean experimental spectroscopic data, is the Fenna–Matthews–Olson (FMO) protein (9). In 2007, the oscillatory beatings observed in the off-diagonal signals of 2D optical spectra have been reported to survive for >$660$ fs at cryogenic temperatures at $77$ K (3). They were interpreted as signatures of long-lived electronic quantum coherent exciton dynamics in the FMO network. The same conclusion was also drawn from an experiment at higher temperatures up to $4^{\circ }$ C (4), and similar beatings have been reported for marine cryptophyte algae (5) as well. These experiments have triggered an enormous interest in a potential new field of “quantum biology” (10–14), with far-reaching consequences, even for the functionality of the human brain (15) and for technological applications (16). The cornerstone experiments (3–5) remained unconfirmed until recently, when a new effort was made to identify the excitonic energy transfer pathways (17) at $77$ K. However, observation of long-lived electronic coherences in the 2D off-diagonal signals was not mentioned in ref. 17.

Interesting conceptual studies on the possible constructive role of dephasing fluctuations on the efficiency of energy transfer in networks (18–23) were initiated subsequently. However, critical questions were also formulated (24–28), which remained largely unresolved up to present. Advanced dynamical simulations (29, 30) did not confirm long-lived electronic coherence and, as a consequence, wave-like energy transfer. An additional strong coupling of the excitonic to the nuclear degrees of freedom was also considered (31–39) as a possible driving source of coherence. Such a mechanism can yield longer-lived oscillations of the cross-peak amplitude (40, 41), yet, a strong vibronic coupling is required, and the oscillation amplitudes typically remain small. Moreover, in general, electronic coherence could only be enhanced by vibrational coherence if it lives at least as long as a single vibrational period lasts, an issue that has not been discussed.

Results

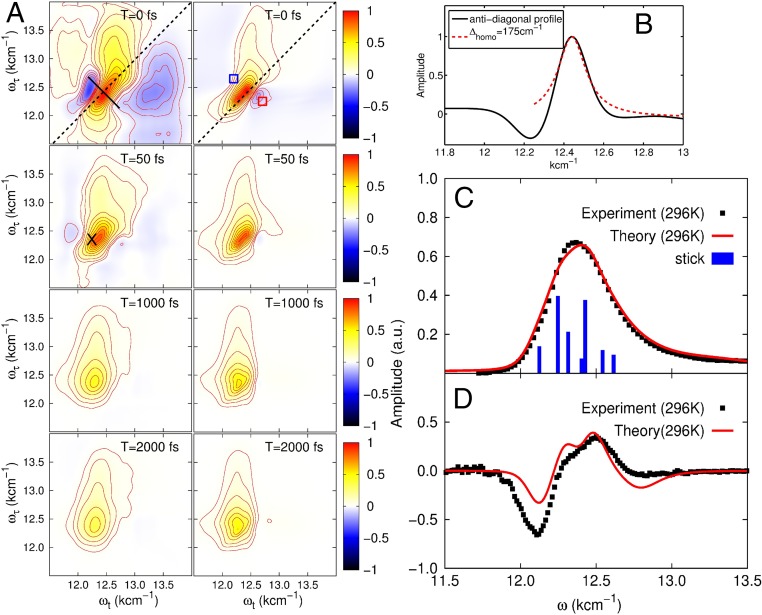
Motivated by the unsatisfactory lack of experimental confirmation of the long-lived electronic coherence at ambient temperatures, we have revisited this question in the present combined experimental and theoretical study, with the important distinction that we have conducted these studies under physiologically relevant conditions. We have measured a series of photon echo 2D optical spectra of the FMO trimer, extracted from green sulfur bacteria Chlorobium tepidum, at room temperature ($296$ K or ${23}^{\circ }$ C) and for different waiting times $T$. The 2D spectra for selected times between $T=0$ and $T=\mathrm{2,000}$ fs are shown in Fig. 1A. In addition, we have calculated the 2D spectra of the FMO monomer (see SI Appendix for details) and compared them to the experimental ones (Fig. 1A). In passing, we note that the calculated absorption spectrum shown in Fig. 1C coincides with that measured in ref. 42. The experimental and calculated 2D spectra for different waiting times agree well. At initial waiting time $T=0$, the 2D spectrum is stretched along the diagonal, which is a manifestation of a significant inhomogeneous broadening. With increasing waiting time, the inhomogeneous broadening is rapidly reduced and becomes undetectable beyond $T\sim \mathrm{1,000}$ fs. A central feature of 2D electronic spectroscopy is that the antidiagonal width uniquely reveals the electronic dephasing timescale. This property also holds when strong vibronic coupling is present (40). In Fig. 1B, we show the antidiagonal cut of the 2D spectrum measured at $T=0$ (indicated in Fig. 1A by the black line) with a fitted Lorentzian profile yielding a FWHM of ${\mathrm{\Delta }}_{\text{hom}}=175$ cm⁻¹, which corresponds to an electronic dephasing time of ${\tau }_{\text{hom}}={[\pi c{\mathrm{\Delta }}_{\text{hom}}]}^{-1}=60$ fs ($c$ is the speed of light). We note that the negative peaks in Fig. 1 A and B are due to a mixed photon echo signal with contributions from the solvent and the excited state absorption (6–8). The mixed photon echo signal gives $50$ counts (cts) for the solvated FMO, and, in the absence of FMO, we have detected $10$ cts. The solvent signal completely disappears for waiting times up to $20$–$30$ fs. Therefore, we estimate that the solvent (FMO excited state absorption) contribution to the negative peak is $\sim 20\%$ ($80\%$). Furthermore, the magnitude of the off-diagonal peaks in the upper left region of the 2D spectra remarkably increases for growing waiting times. The spectrum becomes strongly elongated along the ${\omega }_{\tau }$ coordinate and reveals an efficient energy transfer between the FMO pigments (6–8). The progressions ranging from the central peak at ${\omega }_{\tau }={\omega }_t=\mathrm{12,400}$ cm⁻¹ to the region ${\omega }_{\tau }=\mathrm{13,500}$ cm⁻¹, ${\omega }_t=\mathrm{12,400}$ cm⁻¹ indicate a vibrational relaxation of the localized vibrational modes of the bacteriochlorophylls. In addition, we clearly observe a fast decay of the central peak amplitude within the first $1-2$ ps, induced by thermally fluctuating electric fields from the polar protein environment.

Fig. 1.

(A) The 2D photon echo spectra for different waiting times $T$ taken at $296$ K. Shown is the real part. A, Left shows the experimental results, while A, Right displays the theoretically calculated spectra using the parameters obtained from the fits shown in C and D. The black solid line marks the antidiagonal along which the spectral signal is shown in B. It is used as a consistence check for the electronic dephasing time. The blue and red squares in the top right spectrum marks the spectral positions at which we evaluate the cross-peak time evolution shown in Fig. 3 A and B. In A, Left, the black cross in the second spectrum from the top marks the spectral position evaluated in Fig. 3C. (B) Spectral profile along the antidiagonal as extracted from the experimental data shown in A. We note that the negative amplitude part in the profile shows a mixed signal from the solvent and the excited state absorption at $T=0$ fs, which leads to a slight underestimation of the homogeneous line width. (C) Linear absorption spectrum at $296$ K. Black symbols indicate the measured data, and the red solid line marks the theoretically calculated result. The blue bars show the calculated stick spectrum. (D) Circular dichroism (CD) spectrum at $296$ K. Black symbols mark the measured data. The red solid lines show the theoretical result calculated with the same parameters as in C. a.u., arbitrary units.

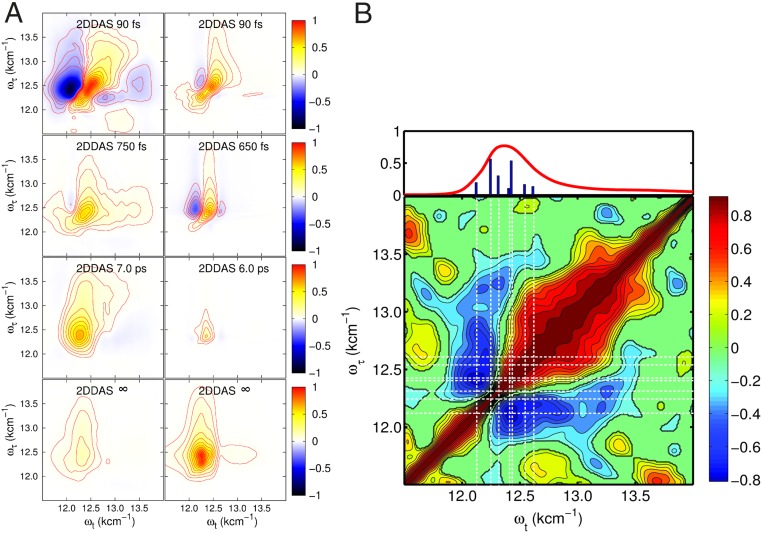
The energy transfer pathways and the associated timescales are revealed by a multidimensional global analysis (43) of consecutive 2D spectra at different waiting times $T$, arranged in a 3D array $S({\omega }_{\tau },{\omega }_t,T)$ (for a detailed description, see supporting information in ref. 44). This results in 2D decay-associated spectra (2DDAS) $A_i({\omega }_{\tau },{\omega }_t)$, which are shown in Fig. 2A (Left, analyzed experimental spectra; Right, analyzed theoretical data; see also SI Appendix for more details). We have resolved four different energy transfer timescales. The shortest decay time, ${\tau }_1=90$ fs, is mainly associated to the electronic dephasing of the diagonal peak at $12,500$ cm⁻¹. Furthermore, a strong negative off-diagonal peak at (${\omega }_{\tau }=\mathrm{12,500}$ cm⁻¹, ${\omega }_t=\mathrm{12,000}$ cm⁻¹) indicates a rapid loss of absorption in the 2D spectra. This feature illustrates contributions from the energy transfer process from the excitonic states located around $12,500$ cm⁻¹ to the lower ones at $12,000$ cm⁻¹. The second 2DDAS, associated with a lifetime of ${\tau }_2=750$ fs, displays a similar feature, but with slightly broader peaks and a noticeable extension to the blue spectral side. The third (${\tau }_3=7.0$ ps) and fourth (${\tau }_4=\mathrm{\infty }$) components of the 2DDAS only show one diagonal peak at the central position of $12,200$ cm⁻¹ with rather broad peaks. This observation indicates a thermal relaxation of the pigments inside the FMO protein. Our findings qualitatively agree with those in ref. 17, with all our dephasing times being shorter, which is due the difference in temperature between 77 K and the present studies under ambient conditions.

Fig. 2.

(A) The 2DDAS. A, Left shows the experimental results, and A, Right shows the theoretically calculated spectra. The four resulting associated decay times ${\tau }_{1,\mathrm{\dots },4}$ are indicated in the spectra. (B) The 2D correlation map of residuals obtained from the series of experimental spectra after subtracting the kinetics by the global fitting procedure. The red line on top is the measured absorption spectrum of the FMO trimer, and the blue bars mark the stick spectrum of the FMO model. The white dashed lines mark the exciton energies, which are used to overlap with the correlation map.

Next, we address the question of long-lived coherent oscillations in off-diagonal signals in the 2D spectra. We have analyzed the residuals obtained after removing the underlying slow kinetics from the 3D dataset $S({\omega }_{\tau },{\omega }_t,T)$. Their Fourier transform provides a 3D spectrum of the possible vibrations. The most intense of them, with the amplitudes above the noise threshold, are plotted in SI Appendix, Figs. S9 and S10. As a result of our model, all of the exciton states in the FMO complex are located in the frequency region of $12,123–12,615$ cm⁻¹. Hence, the largest oscillation frequency that can be expected from the beatings between them is $\sim 490$ cm⁻¹. However, the lowest oscillation frequency that we found in the residuals lies well above ($\sim 600$ cm⁻¹). Hence, we can safely conclude that the origin of these oscillations is not due to interference between the excitonic states.

A cross-correlation analysis (44) of the residuals across the diagonal ${\omega }_{\tau }={\omega }_t$ in a delay time window up to $2$ ps yields a 2D correlation spectrum shown in Fig. 2B, where the (negative) positive values indicate (anti)correlated residuals. We find two strong negative peaks, which proves on the basis of refs. 45 and 46 that the oscillations in this region are related to vibrational coherence. Moreover, we clearly observe two negative peaks at the frequencies $12,400$ cm⁻¹ and $13,300$ cm⁻¹. They can be associated to strong localized vibrational modes of the bacteriochlorophylls, which follows from the vibrational progression in the absorption spectrum (SI Appendix, Fig. S2A).

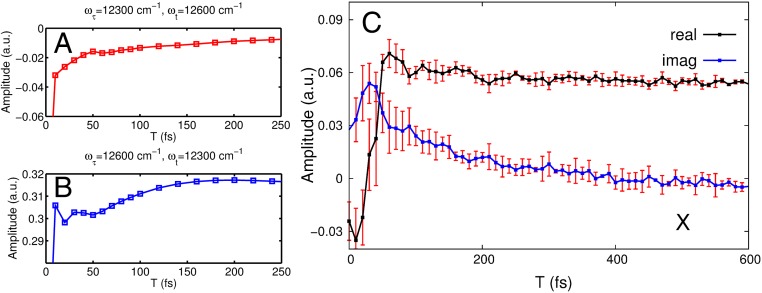
To underpin the vibrational origin of the oscillations with rather small amplitudes, we consider the time evolution of the two off-diagonal signals located at the pair of frequencies $12,300$ cm⁻¹ and $12,600$ cm⁻¹, marked by the red and blue squares in Fig. 1A. We consider the results of the theoretical modeling, which explicitly only includes an overdamped vibrational mode (with a vibrational lifetime of ${\tau }_{\mathrm{\Gamma }}=15$ fs; SI Appendix), but does not include underdamped vibrational states of the bacteriochlorophylls. Hence, any calculated oscillations occurring out to long time must originate from possible beatings of the electronic dynamics due to a coherent coupling between the excitonic states. This feature helps to uniquely determine the origin of the oscillations observed in the experimental spectra. The results shown in Fig. 3 A and B illustrate that any electronic coherence between excitonic states vanishes within a dephasing time window of $\sim 60$ fs. It is interesting to point out that this value of the dephasing time agrees with the time of the dephasing measured by the antidiagonal bandwidth of the 2D spectrum at $T=0$ fs. In fact, when the fluctuations are fast, the timescales of homogeneous and inhomogeneous broadening are well separated, and we are in the fast modulation or homogeneous limit. The resulting exciton dynamics is then Markovian, and, in this limit, the antidiagonal (or homogeneous) line width and the electronic dephasing time coincide (47, 48). The Markovian character of the exciton dynamics is revealed by the exponentially decaying frequency correlation function (48), which can be extracted by measuring the ellipse eccentricity (49) of the 2D spectra as a function of the waiting time (SI Appendix, Fig. S13). In addition, in the numerically exact calculation of ref. 50, the non-Markovianity measure of the FMO exciton dynamics has been calculated to be zero. Furthermore, the excellent agreement between the experimental and theoretical values of the antidiagonal bandwidth demonstrates the validity of our model to capture the damping induced by the thermal noise. In addition, our direct observation of the homogeneous linewidth in this fast modulation limit is in agreement with the independent FMO data of ref. 17 (SI Appendix, Fig. S6). This study finds an $\sim 100$ cm⁻¹ homogeneous line width estimated from the low-temperature data at $77$ K. The resulting electronic dephasing time can be calculated from our model with all of the parameters kept unchanged except the temperature. We find $110$ fs (SI Appendix, Fig. S7). In fact, if long-lived electronic coherence were operating on the $1$-ps timescale as claimed perviously (3), the electronic dephasing should be significantly reduced due to a weaker exciton–phonon interaction. The corresponding antidiagonal line width of the 2D spectrum would have to be on the order of $10$ cm⁻¹ (SI Appendix, Fig. S8) and would appear as an extremely (unrealistically) sharp ridge in the inhomogeneously broadened 2D spectrum. The lack of this feature conspicuously points to the misassignment of the long-lived features to long-lived electronic coherences, which, as now established in the present work, is due to weak vibrational coherences. The frequencies of these oscillations, their lifetimes, and amplitudes all match those expected for molecular modes (51, 52), and not long-lived electronic coherences.

Fig. 3.

(A and B) Time evolution of the real part of the calculated 2D photon echo signal at the spectral positions ${\omega }_{\tau }=\mathrm{12,300}$ cm⁻¹, ${\omega }_t=\mathrm{12,600}$ cm⁻¹ marked by a red square in Fig. 1A (A) and for ${\omega }_{\tau }=\mathrm{12,600}$ cm⁻¹, ${\omega }_t=\mathrm{12,300}$ cm⁻¹ marked by a blue square in Fig. 1A (B). It is apparent that a minimal amount of electronic coherence only survives up to $\sim 60$ fs. (C) The real (black) and imaginary (blue) part of the experimentally measured time trace at the same spectral position (black cross in Fig. 1A) ${\omega }_{\tau }=\mathrm{12,350}$ cm⁻¹, ${\omega }_t=\mathrm{12,200}$ cm⁻¹ as measured in ref. 4, however, measured here at $296$ K. The error bars indicate the SD obtained after averaging four datasets. The imaginary part is vertically shifted by $0.035$ for clarity. a.u., arbitrary units.

For a comparison with the previous experimental work [at the temperature $277$ K ($4^{\circ }$ C) of ref. 4], we have extracted from our measured 2D spectra the time evolution of the “cross-peak” located at ${\omega }_{\tau }=\mathrm{12,350}$ cm⁻¹, ${\omega }_t=\mathrm{12,200}$ cm⁻¹ (spectral position marked by a black cross in Fig. 1A). As follows from Fig. 3C (see also SI Appendix), no long-lived beatings and associated electronic coherence can be observed at this position in the measured 2D spectra. Within the available experimental signal-to-noise ratio, we can conclude that there are no oscillations with amplitudes >$5\%$ of the signal. They may be interpreted as weak vibrational coherence, consistent with earlier findings (41) for a much smaller excitonically coupled system (a dimer) with strong vibronic coupling.

Conclusion

The present work provides a full analysis of possible electronic state couplings, decay-associated spectra, signs/amplitudes of off-diagonal features, and, most telling, the directly determined homogeneous lineshape, and thus shows that the previous assignment of weak long-lived oscillatory signals in 2D spectra to long-lived electronic coherences is incorrect. There is no long-range coherent energy transport occurring in the FMO complex and, in all cases, is not needed to explain the overall efficiency of energy transfer. This finding constitutes the main result of our work and confirms the orthodox picture of rapidly decaying electronic coherence on a timescale of 60 fs in the exciton dynamics in the FMO protein complex at ambient temperature. In turn, contributions of quantum coherence to biological functionality under ambient conditions in natural light-harvesting units is extremely unlikely, a finding being in line with our previous study of the light-harvesting complex LHCII (44). Because the FMO complex is rather small and a structurally quite well-defined protein, with the distances between bacteriochlorophylls comparable to other natural light-harvesting systems, we anticipate that this finding is generic and also applies to even larger photoactive biomolecular complexes.

Materials and Methods

Experimental Setup.

Ultrashort coherent light pulses were generated by a home-built noncollinear optical parametric amplifier pumped by a commercial femtosecond laser Pharos (Light Conversion). A broadband spectrum with a FWHM of 100 nm was centered at the wavelength of 770 nm and overlapped the ${\mathrm{Q}}_y$ absorption band of the FMO antenna complex (SI Appendix, Fig. S2A). The laser pulses were compressed to the transform-limited with the pulse duration of $16$ fs FWHM by a combination of a prism compressor (F2) and a deformable mirror shaper (OKO Technologies). Their temporal profiles were characterized by means of the frequency-resolved optical gating (FROG) measured in situ by using a $1$-mm fused silica window. The measured FROG traces were analyzed by using a commercial program, FROG3 (Femtosecond Technologies). The 2D spectra were collected in an all-reflective 2D spectrometer based on a diffractive optic (Holoeye) with a phase stability of $\lambda /160$, whose configuration is described elsewhere (53), equipped with the Sciencetech spectrometer model 9055 and a high-sensitive CCD linear array camera (Entwicklungsbüro Stresing). To avoid possible annihilation of excitons in the FMO trimer, the excitation energy was kept at <$12$ nJ per beam. Under this excitation condition, the magnitude of the homodyne photon-echo signal was proportional to the third power of the incoming pulse energy, which confirms the regime of linear excitation (SI Appendix, Fig. S2B). The 2D spectra were collected at each fixed waiting time $T$ by scanning the delay $\tau =t_1-t_2$ in the range of $[-128$ fs,$128$ fs$]$ with a delay step of $1$ fs. At each delay point, $150$ spectra were averaged. The waiting time $T=t_3-t_2$ was linearly scanned within the range of $0-2$ ps in steps of $10$ fs and with logarithmically spaced delay time steps up to $10$ ps.

Sample Preparation and Measuring Condition.

The FMO protein was isolated from the green sulfur bacteria C. tepidum (see SI Appendix for details). Before each series of measurements, the sample was filtered with a $0.2\mu$m filter to reduce light scattering. The absorption spectrum was recorded by using a Shimadzu spectrometer (UV-2600) in a cell of $1$-mm optical path length. To avoid the influence of the sample degradation (see SI Appendix for details), the cell in the 2D setup was placed on a precise 2D translator and moved at a speed of $\sim 20$ cm/s in both directions. The excitation spot diameter on the sample was $\sim 80$ $\mu$m. In the experiments, we used a $1$-mm quartz cell (Starna). We did not detect any noticeable difference of the measured spectra when a $0.5$-mm cell was used.

Theoretical Model.

We considered a standard molecular model of the FMO monomer described by the Hamiltonian $H_{mol}$ and consisting of seven bacteriochlorophylls in the single-excitation subspace. Double excitation played no role at the considered weak spectroscopic field strengths. Recently, an eighth pigment in the FMO complex was found (54). However, its spatial distance from the other seven pigments is very large, and it is very likely that this pigment is removed in the majority of the complexes during the isolation procedure (17, 54). The model parameters (i.e., the site energies ${ϵ}_m$ and the electronic couplings $J_{n,m}$) were taken from ref. 55. The spectral density of the bath is given in SI Appendix. During the procedure of fitting the model to the measured absorption and CD spectra, we kept the electronic coupling elements unchanged and optimized the site energies. To fit the absorption and CD spectra simultaneously, we optimized the site energies and the inhomogeneous broadening, which accounts for the static disorder. In particular, we chose a Gaussian distribution with a FWHM of $90$ cm⁻¹, except for site $3$, for which we found that it was necessary to reduce the static disorder to 54 cm⁻¹ of FWHM to fit the absorption peak of $12,150$ cm⁻¹ at 77 K (the low-temperature calculations in comparison with the experimental spectra are shown in SI Appendix). To obtain converged results, $500$ calculated spectra were included in the average. The orientations of the transition dipole moments were taken from Protein Data Bank ID code 3ENI (56), and the magnitudes of the transition dipole moments were assumed to all be $4$ Debye. The modeling has been additionally verified (SI Appendix) by comparing the calculated results for the time-dependent FMO site populations with available exact numerical calculations (29).