Abstract
Objective
State-of-the-art techniques for surgical data analysis report promising results for automated skill assessment and action recognition. The contributions of many of these techniques, however, are limited to study-specific data and validation metrics, making assessment of progress across the field extremely challenging.
Methods
In this paper, we address two major problems for surgical data analysis: (1) lack of uniform shared datasets and benchmarks and (2) lack of consistent validation processes. We address the former by presenting the JHU-ISI Gesture and Skill Assessment Working Set (JIGSAWS), a public dataset we have created to support comparative research benchmarking. JIGSAWS contains synchronized video and kinematic data from multiple performances of robotic surgical tasks by operators of varying skill. We address the latter by presenting a well-documented evaluation methodology and reporting results for six techniques for automated segmentation and classification of time-series data on JIGSAWS. These techniques comprise four temporal approaches for joint segmentation and classification: Hidden Markov Model, Sparse HMM, Markov semi-Markov Conditional Random Field, and Skip-Chain CRF; and two feature-based ones that aim to classify fixed segments: Bag of spatiotemporal Features and Linear Dynamical Systems.
Results
Most methods recognize gesture activities with approximately 80% overall accuracy under both leave-one-super-trial-out and leave-one-user-out cross-validation settings.
Conclusion
Current methods show promising results on this shared dataset, but room for significant progress remains, particularly for consistent prediction of gesture activities across different surgeons.
Significance
The results reported in this paper provide the first systematic and uniform evaluation of surgical activity recognition techniques on the benchmark database.
Index Terms: Activity recognition, benchmark robotic dataset, kinematics and video, surgical motion
I. Introduction
In 1889, Dr. William Halsted, one of the early members of the Johns Hopkins Hospital, established the classical training program for medical residents [1]–[3]. His teaching philosophy of “see one, do one, teach one” is being practiced to this day. His philosophy follows the idea that a student reaches a required competency level by deliberately practicing and actively participating in mentored cases.
Faculty surgeons conventionally assess and report trainees’ performance by completing global and task-specific checklists [4], [5]. However, assessment based on checklists is observational and thus susceptible to inter-observer variability [6]. Furthermore, checklists require substantial faculty time to be feasible for routine use in surgical training curricula. The usability of checklists is especially challenging after 2002 when the Accreditation Council for Graduate Medical Education (ACGME) mandated that all medical residents be evaluated continuously (not merely periodically) by competency-based measures [7], [8]. Consequently, surgeons in many specialties have repeatedly advocated for less resource-intensive and more objective metrics of surgical skill [9]–[12].
An alternative to checklists is to measure surgical skill by collecting and assessing motion and video data from surgical activities using automated tools. Surgical simulators and the da Vinci surgical robot (Intuitive Surgical Inc. Sunnyvale, CA) are both examples of devices that support the capture of video and tool motion data on surgical performance. Given such data, one common approach to assessing and predicting surgical technical skill is to use overall performance statistics, such as time to completion [13], [14], speed and number of hand movements [13], distance travelled [14], and force and torque signatures [14]–[16].
Global methods are generally easy to implement, but they provide little to no insight on where a learning surgeon is deficient and requires additional training. An alternative pursued by our group and others [17]–[25] is to break down surgical task execution into smaller components, and to base the assessment of performance on both the quality of those components and/or the sequence of components themselves. The core hypothesis in these models is that surgical manipulative motion can be described by a relatively compact and general language of gestures. Given the many similarities between the structure of a surgical task and the structure of natural languages (where words, syllables, and phonemes correspond to gestures), the above approach to surgical skill assessment is known as the language of surgery. In this approach, fine-grained segmentation and labeling are thus necessary steps for surgical skill assessment. Recent studies [26]–[28] have shown that given the sequence of surgical gestures and their boundaries, one can predict the surgeon’s skill level with up to 90% accuracy for new trails of known (observed) surgeons or 75% accuracy for a new trails of unobserved surgeons.
A major limiting factor for research in this area is the lack of standardized benchmark databases. Nearly all state-of-the-art methods report prediction results for surgical gesture recognition using study-specific datasets, and are evaluated using different validation metrics. This makes assessment of progress in the field extremely challenging.
To address this issue we have created the JHU-ISI Gesture and Skill Assessment Working Set (JIGSAWS), which is the first public benchmark surgical activity dataset captured from the da Vinci robot. The JIGSAWS contains synchronized video and kinematic data from three standard surgical tasks performed by subjects with different skill levels. The dataset also contains a gesture vocabulary, gesture annotations for all trials, and a unified cross validation setup to evaluate the gesture prediction performance of the developed techniques.
In this paper, we describe the JIGSAWS dataset, and we report, using a consistent methodology, the prediction performance of six of our representative gesture recognition and segmentation techniques. We refer to the latter as “performance” which should not be confused with surgical performance of the surgeons. Our major contributions in this paper are:
The description of a freely shareable data set and associated meta-data that others can use for comparative performance analysis.
The description of a consistent methodology for performance assessment in this domain.
A detailed and consistent representation, comparison, and validation of six of our techniques using the proposed methodology.
In the remainder of the paper, we first introduce the elements of the JIGSAWS dataset and our evaluation methodology (Section III). We then present, in a consistent format, techniques to tackle joint segmentation and classification (Section IV) and only classification (Section V) of surgical gestures. The best performance of the techniques are discussed in Section VI. We close with a discussion about the shortcomings, strengths, and influential factors for each technique.
II. Background
Existing approaches to automatically and objectively assess surgical skill from tool motion data can be divided into two main categories: global performance statistics, and time-series-based analytical models.
Global statistical metrics [13]–[16] use overall measurements of a well-defined task to predict skill. Even though these methods are generally easy to implement, they effectively produce an average value for a specific measure, such as time of completion, over the entire task to which they are applied.
Broad application of a global metric cannot provide local feedback to the trainees on which parts of their performance require more practice. On a practical level, they are not able to reliably predict skill for multiple-surgeon cases where experts and novices switch roles during surgery, which is not uncommon in live surgery.
Developing more refined metrics depends on the ability to segment a surgery or surgical training task into logical and well-defined components. While such decompositions are increasingly well established in highly structured non-manipulative activities such as dance and gymnastics, very few studies have examined the notion of a language of motion in the context of manipulative surgical motion. Early work by Rosen and others [17], [18], [23] pioneered the idea that the Markov structure of a surgical task was an indicator of skill. Later work extended this to hidden Markov models (HMMs) learned from kinematic (hand-movement) data [19]–[21], [24], [25] using simple statistical models. Recent work [22]–[25], [29]–[33] extended basic HMM models in a variety of ways, and introduced conditional random fields as an alternative discriminative approach. These approaches all model each gesture as one or more latent variables. Their main difference is in how they model the observations within each gesture.
While most of the statistical techniques use only kinematic data, there are a few studies [32]–[43] that have used surgical video data for gesture recognition. For example, authors in [34]–[39], [41] focus on coarse-grained surgical activity recognition and model operating room workflows using video data. Other recent approaches [32], [33], [38]–[43] have focused on fine-grained activity recognition of surgical tools using both kinematic and video data. They suggest that combining kinematic and video data can improve the performance of automatic gesture recognition. The kinematic-based techniques are challenged by the lack of information about the composition of tissue and other external surgical objects in the scene such as needle and threads. The challenge of video-based action recognition techniques is to define an efficient and robust technique to model the semantic relationships in the presence of noise, occlusions and clutter, and variability of tool pose.
III. JIGSAWS: a Benchmark for Modeling Surgical Gestures
In this section, we first provide the description of the JIGSAWS dataset. We then specify a consistent framework for evaluating the performance of the state-of-the-art methods in automatic classification and segmentation of surgical time-series data. More detailed information about the JIGSAWS is available on our website [44].
A. Data Collection from the da Vinci Surgical Robot
The da Vinci robot can provide both kinematics and stereo video of a surgery. In the JIGSAWS dataset, the kinematic data contains variables of both master and slave’s left and right manipulators (76 motion variables collected at 30 frames per second: tooltip positions and orientation, linear and rotational velocities, and gripper angle). The stereo video is recorded at 30 frames per second with 640×480 pixel resolution.
Video and kinematic data carry relevant and complementary information. The kinematic data contains 3D trajectories and 3D velocities of the robot’s arms, not directly measurable in video, and the video data provides contextual and semantic information such as the interaction between tools and tissue, not directly available in kinematic data.
B. Dataset description
The JIGSAWS dataset contains surgical data collected from eight subjects (all right-handed) with different skill levels performing three different surgical tasks using the da Vinci surgical system. A trial is a part of the data that corresponds to one subject performing one instance of a specific task. All the trials performed consecutively by an individual user in one sitting are grouped together as a session. Each subject participated in 3 to 5 data collection sessions, in which they performed one trial of each task.
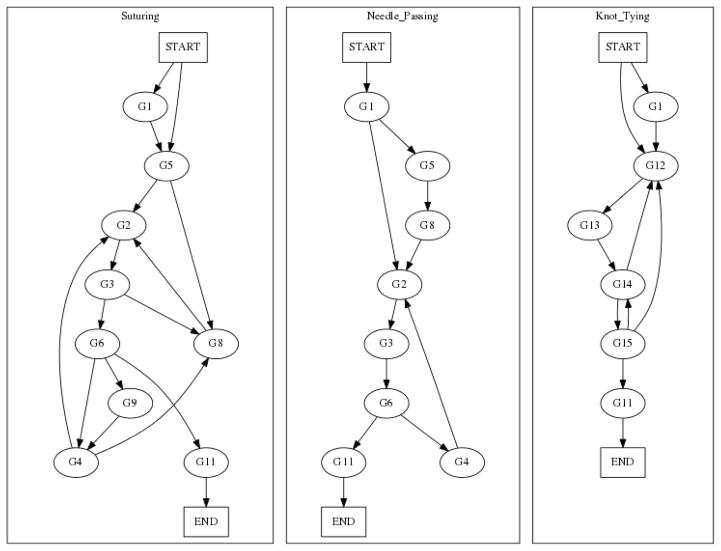
The tasks are 4-throw suturing (39 trials), needle-passing (26 trials), and knot-tying (36 trials) performed on benchtop training phantoms. The suturing phantom had needle insertion marker points and a line drawn on it as the wound line (Figure 1). In the needle-passing task, the users passed a needle through four small metal loops from right to left. In the knot-tying task, they tied a simple-loop knot around a plastic rod.
Fig. 1.
Snapshots of the three surgical tasks in the JIGSAWS (from left to right): suturing, needle-passing, knot-tying.
A surgical gesture is defined as an atomic action or single movement that finishes one small clearly identifiable step of the surgery. Gestures represent the lowest level of meaningful segments of a surgery and usually appear in some specific patterns, e.g., one gesture often follows another or several gestures appear close to each other. The surgical gestures used in JIGSAWS were defined by a group of faculty surgeons at the Johns Hopkins University. The gestures are:
(G1) Reaching for the needle with right hand.
(G2) Positioning the tip of the needle.
(G3) Pushing needle through the tissue.
(G4) Transferring needle from left to right.
(G5) Moving to center of workspace with needle in grip.
(G6) Pulling suture with left hand.
(G7) Pulling suture with right hand.
(G8) Orienting needle.
(G9) Using right hand to help tighten suture.
(G10) Loosening more suture.
(G11) Dropping suture and moving to end points.
(G12) Reaching for needle with left hand.
(G13) Making C loop around right hand.
(G14) Reaching for suture with right hand.
(G15) Pulling suture with both hands.
Each trial in the JIGSAWS dataset has been manually annotated with these surgical gesture definitions at the frame level.
Figure 2 represents the relationship, order, and flow of different gestures during the execution of each task. In the suturing task, gestures G1 to G11 excluding G7 are used. In needle-passing, G1 to G6, G8, and G11 are used. In knot-tying, G1 and G11 to G15 are used.
Fig. 2.
Grammar graph for Suturing (left), Needle-Passing (center), and Knot-Tying (right)
C. Evaluation Methodology
We employ two different cross-validation settings to evaluate modeling techniques: (1) Leave-One-User-Out (LOUO), and (2) Leave-One-Super-Trial-Out (LOSO). In the former, all of the trials performed by a single subject are left out as the test set and the remaining trials are used to train our models. In the latter, the ith trial of each subject are left out as the test set. These two cross-validation approaches will help to measure models’ generalization to new and unknown surgeons or new trials performed by a known surgeon. Please see Supplemental document for details on usage of the methodology.
For each cross-validation setting, the performance of each technique is reported using two sets of parameters: (1) Micro average accuracy, Macro average recall, and average Precision, and (2) the generalization power of each technique by fitting a Beta distribution to the results of the cross-validation tests.
The calculation of the Micro, Macro, and Precision averages is as follows: first, for each of the F cross-validation folds (of an n-way classification problem), a confusion matrix Cf (f = {1, 2, …, F}) of size n × n is computed as:
The complete confusion matrix, C, is the sum of all of the confusion matrices:
| (1) |
Given the complete confusion matrix, the Micro average is computed as the average of total correct predictions across all classes:
| (2) |
and the Macro average and std are the mean and standard deviation of true positive rates for each class:
| (3) |
| (4) |
Similarly, the Precision average and std are calculated as:
| (5) |
| (6) |
Note that for the skewed multi-class data (such as the one in JIGSAWS), these two average accuracies report two different aspects of the prediction performance: (1) overall prediction performance regardless of the number of samples available for training and testing (reflected in Micro average) and (2) sensitivity in modeling smaller classes (reflected in Macro average). For example, if one gesture class has many fewer samples and during the prediction phase they all are classified incorrectly (or correctly) then the Micro average will not change significantly. However, the Macro average will drop (or increase) drastically, properly reflecting the prediction accuracy of that particular class.
Beside reporting performance quality in terms of Micro and Macro averages, we also provide a probabilistic model for estimating the average and standard deviation of a classifier’s accuracy in LOSO and LOUO settings. Here, we explain the LOUO setting for concreteness. The LOSO follows identically.
First, suppose that we observe the per-user accuracies p1, p2, …, pF, for F users. One usually reports sample mean and variance, which gives the reader some idea of what the accuracy for a new user may be. The 95% confidence interval is another way of presenting the variance. But the sample mean and sample variance are somewhat misleading in this case, because accuracies are not Gaussian; they range between 0 and 1. A better assumption therefore is that the pi are Beta distributed with parameters A and B. In this case, we need to first fit the parameters A and B (both > 0) to the observed accuracies p1, …, pF, which can be done via maximum likelihood (ML). Once we do that, the mean (estimated accuracy for a new user) and variance (variance of the accuracy for a new user) are defined as:
| (7) |
| (8) |
Computing the ML estimates for A and B from p1, …, pF is trivial, but problem is that (with doing cross-validation) we do not observe p1, …, pF. Instead, we observe F pairs (k1, n1), (k2, n2), …, (kF, nF), which are respectively the number of correct predictions (kf) and number of test samples (nf) for each user (f):
| (9) |
| (10) |
In this case, we assume that the outcomes in the nf tests for user f are Bernoulli with probability of success pf. Assuming that nf is fixed and known, we can use the Beta-Binomial formula to write down the probability that the f-th user has kf correct predictions as:
| (11) |
where A and B (both > 0) are parameters of the Beta-Bernoulli distribution and Γ is the Gamma function. Therefore, the total log-likelihood of the observed data k1, …, kF is:
| (12) |
LogL is a function of (A,B) with fixed (kf, nf). The derivative of the LogL function is formulated as below:
where is the logarithmic derivative of the Gamma function. We find the values of A and B that maximize the LogL function numerically using both the LogL function and its derivative. After finding the optimum values of A and B parameters, we can calculate the mean μ and variance σ of the Beta distribution and report mean, variance, and the 95% confidence interval (CI) of the distribution.
Note that Beta μ and σ are comparable with Micro average values. The former computes a local Micro average in each fold (for local confusion matrices Ci) and report their mean and variance, whereas the latter reports a global Micro average operated on the summation of all confusion matrices C.
Methods developed in this paper were grouped based on their prediction goal: (1) gesture classification: These methods assume that the boundaries (start and end) of each gesture segment are known and the goal is to predict a surgical gesture for each data segment in the test set, and (2) joint segmentation and classification: These methods predict a surgical gesture for each frame in the test set. This problem is significantly more challenging than gesture classification since it requires solving simultaneously for both the boundaries and the labels. A candidate technique is expected to perform better in the easier case of gesture classification and extend well to the more challenging problem of joint segmentation and classification.
This entire process is automated in a common script to ensure that (1) all results are directly comparable across all the methods and (2) no test data are left out or treated differently (down to every frame of data) across different techniques.
The aforementioned parts of the JIGSAWS dataset including kinematics, videos, annotations, cross-validation setups, and evaluation script are accessible at https://cirl.lcsr.jhu.edu/research/hmm/datasets/jigsawsrelease/.
IV. Surgical Gesture Segmentation and Classification
In this section, we introduce a group of techniques that address the challenging problem of joint gesture segmentation and classification using two families of statistical models: Hidden Markov Models (HMMs) and Conditional Random Fields (CRFs). In these models the prediction of the gesture label is achieved at the frame level (no pre-segmentation of the data is assumed) and the temporal coherence of the predicted gesture labels are captured by transition probabilities.
HMMs and linear-chain CRFs are closely related. HMMs are generative learning methods that model the joint probability of the observation (feature) and gesture label. On the other hand, CRFs are discriminative models in which the posterior probability of the predicted gesture label given the observation is directly modeled. These models are applicable to both kinematic and video data. Aside from different computational complexities, one approach may perform better than the other for the dataset at hand [45].
In this paper, we describe several variations on both HMMs and CRFs: Gaussian Mixture Model Hidden Markov Model (GMM-HMM), Sparse HMM (S-HMM), Markov Semi-Markov Conditional Random Field (MsM-CRF), and Skip-Chain Conditional Random Field (SC-CRF). These techniques were previously validated on other surgical datasets. In this section, we first briefly introduce them using a consistent terminology, emphasizing their similarities and differences, and then validate them on the JIGSAWS dataset. Further technical details are available in the supplemental material.
The following list defines notation shared throughout this section.
m: number of training samples.
ot: frame-level observation at time t.
zt: gesture label at time frame t.
xt: latent variable at time frame t.
st: state at time frame t.
hi: segment-level observation at segment i.
li: frame index of the start of the ith segment.
𝒱: a given time series.
ψ, θ, γ: CRF potential functions.
p(o|s): emission probability, with p(xt|st) for GMM-HMM and p(ot|zt) in S-HMM.
q(s′|s) = qs′,s: transition probability between two hidden variables. We use q(s′|s) for GMM-HMM and q(z′|z) for S-HMM.
A. Gaussian Mixture Model-Hidden Markov Model: GMM-HMM
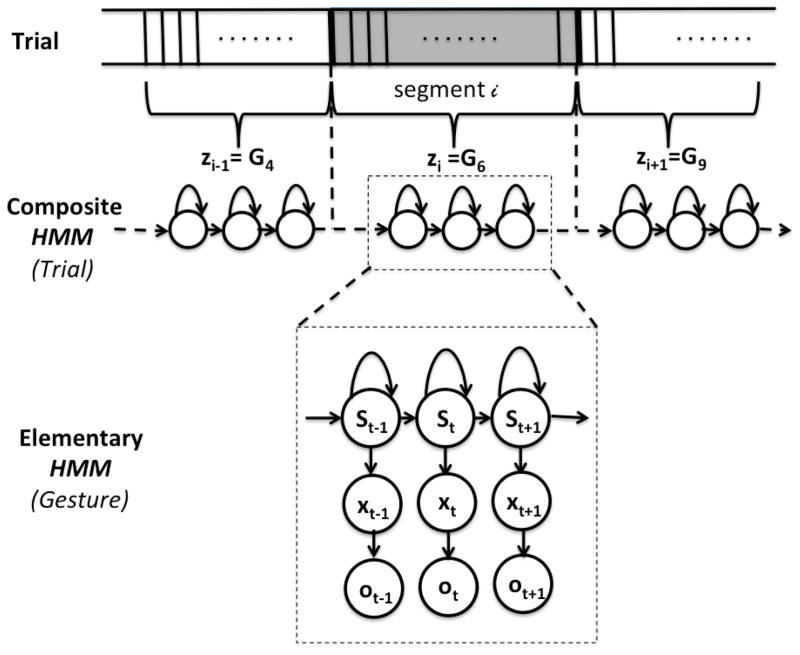
Following early published techniques [17], [18], [23], we employed a composite Hidden Markov Model (HMM) [46] to tackle the problem of surgical activity recognition. This technique models each gesture as an elementary HMM where each state corresponds to one Gaussian Mixture Model (GMM). By concatenating the elementary HMMs of different gestures together, a composite HMM is formed to model the entire trial. Figure 3 illustrates the GMM-HMM configuration.
Fig. 3.
Trial model and gesture model using composite HMM.
The frame-level observation vector ot ∈ ℛD can be the raw kinematic variables or features extracted from the robot’s kinematics or video images at time (frame) t. Let Z and S be the sets of all finite discrete indices for all possible gestures and states, respectively. Then at time t, zt ∈ Z represents the gesture label, xt ∈ ℛd a latent variable (e.g., a low-dimensional representation of ot), and st ∈ S the corresponding HMM state. The factor graph in Figure 3 shows the dependency between these variables. Since the raw observations ot generally have large dimension, the dimensionality of the data is reduced by performing Linear Discriminant Analysis (LDA) [47] prior to modeling. In this case, the low dimensional latent variable xt is computed from the observations ot and gesture label zt.
Learning
In the training procedure, the parameters for each elementary HMM are learnt separately using their corresponding labeled frames. In this configuration, each HMM has S states and each state is modeled by a mixture of M Gaussians. All the parameters that define the relationship between the states, observations, and gesture labels are learnt.
Let q(st|st−1) denote the transition probability between two consecutive states (based on the Markov assumption) and p(x|s) denote the emission probability. Then the sequence of low dimensional observations x1..T and states s1,..T are modeled as
| (13) |
where π(s0) is the distribution of the initial state. The emission probability of xt given st is
| (14) |
where the superscript st denotes that the GMM is associated with the state st, M is the number of mixture components, and wms are the mixture weights. The parameters of the composite HMM are estimated via the Baum-Welch [48] algorithm. Specifically, the GMM parameters can be estimated further from the first and second order statistics. After training, the GMM-HMM parameters and the LDA projection matrix are saved as the trained model.
Inference
In the decoding procedure, a gesture sequence is predicted for a given test trial constrained by a pre-defined gesture grammar. The grammar is represented by a directed graph where each node is a gesture and each edge permits a one directional transition between two gestures (Figure 2). The grammar graphs for three surgical tasks of the JIGSAWS dataset are shown in Figure 2.
In case of using only the GMM-HMM parameters, many sequences of gestures can be generated for the test trial. However, the decoder uses the grammar’s constraints to eliminate some of the sequences and constructs a composite HMM from all elementary HMMs. Using the grammar’s constraints, the Viterbi algorithm [49] is employed to infer the most likely state sequence for the test trial.
Implementation and Discussion
The following parameters can affect the performance of the GMM-HMM model: number of states for each elementary HMM (S), number of Gaussians per state and their configuration (M), LDA dimension (d), and choice of feature vector. A larger S and M requires training a larger set of parameters which might need more training data. On the other hand, more complex tasks are recommended to be modeled with more states or more Gaussian mixture components.
To validate the GMM-HMM technique on the JIGSAWS kinematic dataset, we tested a variety of parameter configurations: S from 1 to 15 and M from 1 to 5. We achieve the best performance with a medium complexity model of 3 states and one Gaussian per state.
To reduce the dimensionality of the input data, we observe that very large or very small values of d ≤ 𝒟 would cause a decrease in performance. We assume that for an n-way classification problem, there are at maximum n − 1 linearly independent dimensions. After testing a variation of values for d (range 5 to n−1), we chose d to be 9 for our application. For data collected with high sampling frequency, we can reshape the data using a splicing technique before applying LDA. Since the frame by frame variations of the data is relatively small in the JIGSAWS dataset, we can replace each frame with a longer frame constructed by concatenation of the frame with its neighboring frames [50]. This method provides more robust data for LDA.
To choose the feature vector, the following subsets of the robot kinematics were tested: (f1) all kinematics variables from master and slave robot arms, (f2) f1 excluding the tooltip position and orientation of the slave robot, (f3) only master robot kinematic data, and (f4) only slave robot kinematic data. Feature f1 on average performs 5% to 10% lower than other features. The last three features perform similarly on the suturing task. In most of the scenarios f4 performs 5% better for needle-passing, while f2 works 4% better for the knot-tying task. Considering this trade-off, we choose f4 to represent the robot’s kinematics since this type of kinematic information is consistent with what other generic robots can provide.
It is important to mention that figure 3 represents an example of the elementary HMM with a Simple Left-to-Right (SLR) topology which generated the best performance for activity recognition using the JIGSAWS dataset. In this topology, all connections between the elementary HMMs must be from the end-state of one elementary HMM to the start-state of another elementary HMM. In general, however, this technique [46] is able to learn any type of topologies with interconnected states.
This method can be easily used for gesture classification with known boundaries. The training phase remains the same as above, but in the inference phase a new grammar graph is used. This graph has no connections between gesture nodes; instead all the nodes are directly connected to both the start and end nodes.
B. Sparse Hidden Markov Model: S-HMM
To achieve a richer observation model, we investigated [30] a variation of the HMM called a Sparse-HMM (S-HMM). In this model, each observation is a sparse linear combination of a dictionary of atomic motions associated with a specific gesture.
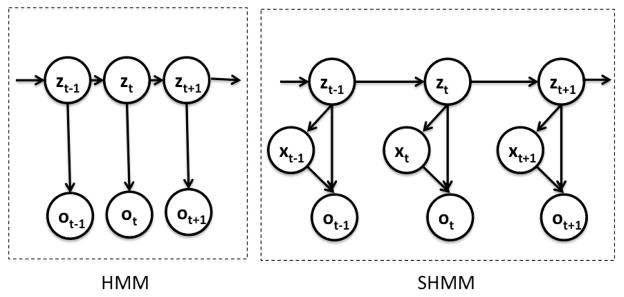
Similar to GMM-HMM, in S-HMM, the gesture label zt is the unobserved hidden state, and is modeled as a Markov process. This Markov process is characterized by the transition probability q(z′,z) = q(zt = z|zt−1 = z′). The observation ot (here, is the robot’s kinematics) is modeled as a sparse linear combination of elements from an overcomplete dictionary of surgical atomic motions. Therefore, the observation ot also depends on another latent hidden state, namely the sparse coefficient xt. Figure 4 illustrates, in a comparable fashion, graphical models for a typical HMM and the proposed S-HMM.
Fig. 4.
Graphical models for standard HMM (left) and the S-HMM with latent variables (right).
The sparse representation of the observation ot with respect to an overcomplete dictionary of motion words Dzt is modeled as follows:
| (15) |
where Dzt ∈ ℝD×N is an over-complete dictionary (D < N), μzt is the feature mean for class zt, xt ∈ ℝN is a sparse latent variable, i.e., it has only a few nonzero entries, and et is an independent Gaussian noise distributed as . As a result, the distribution of ot given the latent variables is
| (16) |
To have a sparse latent variable, we use a Laplace prior on the distribution of xt for each hidden state where
| (17) |
with a parameter λz > 0.
Learning
Given m training trials and their gesture labels , the parameters to be learned are the transition probabilities Q = {qz′,z}z,z′=1,…,Z and the parameters for each gesture model , for z = 1, …, Z.
Since the gesture labels are given, the transition probabilities can be directly computed from the frequency of gesture transitions, and the remaining parameters can be learned separately from data corresponding to each gesture z. To learn the other parameters, we adopt an EM-like algorithm to maximize the log-likelihood of the observations corresponding to gesture z, with respect to the parameters Θz. In the E-step the expectation of the complete log-likelihood with respect to the posterior of xt cannot be computed in closed form (due to the Laplacian prior), so we approximate the MAP estimate of xt as a delta function: , where . The E-Step reduces to the following ℓ1 minimization:
| (18) |
which can be solved using sparse coding algorithms such as Basis Pursuit. Thus the approximate expectation of the complete log-likelihood can be written as:
| (19) |
In the M-step, we need to maximize this expression with respect to the parameters Θz. Notice that the first two terms in equation (19) are similar to the standard sparse dictionary learning cost, and the feature mean μz is set to empirical mean , with Nz being the number of frames with label z. Interestingly, the approximate EM algorithm now involves an E-step where the MAP estimate of is calculated given D̂z (sparse coding) and an M-step where the dictionary Dz is updated based on . This is analogous to sparse dictionary learning techniques, which alternate between finding the sparse coefficients and updating the dictionary. In our proposed algorithm, we employ the KSVD algorithm for sparse dictionary learning, which uses the greedy Orthogonal Matching Pursuit (OMP) algorithm by solving the ℓ0-seminorm for sparse coding [51]. In particular λz and are not involved in KSVD, we set them to be equal across classes and compute them afterwards using a 2-fold cross-validation on the training set. We call this approximate learning method KSVD-S-HMM.
Inference
Given a trial and the S-HMM parameters, the sequence of gesture labels is inferred using a dynamic programming method similar to the Viterbi algorithm [49], where one maximizes the joint probability of the hidden states and the observations as
| (20) |
The technical details of the inference algorithm are described in the supplemental material.
Implementation and Discussion
To validate the S-HMM on the JIGSAWS dataset, we use the KSVD-S-HMM algorithm and only slave information in the kinematic data. The parameters that might affect the performance of KSVD-S-HMM are the sparsity level and the dictionary size.
For the validation, the sparsity level K is varied from 3 to 15. We observe that the performance of the algorithm is not sensitive to the choice of K under the LOSO setup, but a proper choice of K improves performance under the LOUO setup by 5%. In our application, choosing K to be 7 typically leads to the best performance.
Increasing the dictionary size improves the performance, but it saturates for larger dictionary sizes. Since larger dictionary sizes require larger computation power, a medium and computationally efficient dictionary of 200 words is chosen to validate the S-HMM technique on the JIGSAWS dataset.
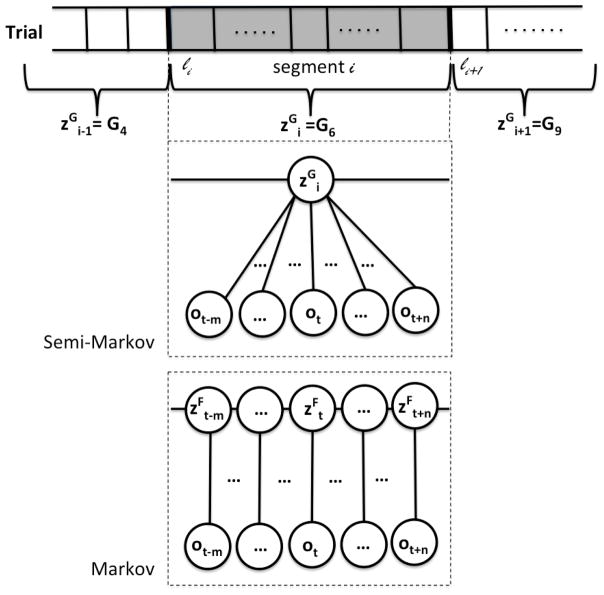
C. Markov Semi-Markov Conditional Random Field: MsM-CRF
As noted, there are generally two approaches for training a classifier: generative and discriminative. In the previous two sections, we described two variations of a generative model (HMM). In the following two sections, we employ variations of a discriminative statistical model called CRF for modeling the surgical gestures.
A standard linear-chain CRF shares the same Markov assumption as in the HMM where the label at the current frame is dependent only on the one from the previous frame. However, the frame-to-frame transitions are not representative of transitions among gestures which might last for a couple of seconds. In this section, we describe our Markov/semi-Markov Conditional Random Field (MsM-CRF) technique [31] (2013), which was developed to model gestures at two layers jointly: one at the level of frames (Markov CRF model) and another at the level of segments (semi-Markov CRF model). We then validate it on both kinematics and video data of the JIGSAWS dataset.
In this model, we represent a time series (kinematic or video data) 𝒱 with a graphical model 𝒢 = (𝒩F, ℰF, 𝒩G, ℰG). Each node denotes a frame It, hence |𝒩F| = T, while each node denotes a gesture segment with label , and , where Ili is the first frame of segment i = 1, …, L, and L = |𝒩G| is the number of segments in 𝒱. In this graphical model the edges ei ∈ ℰ denote the connection between two consecutive nodes Ni and Ni+1.
The conditional probability of the sequence of gesture labels 𝒵 = {zt} given a time series 𝒱 is modeled with a Gibbs distribution: p(𝒵|𝒱) ∝ exp(−E(𝒵, 𝒱)), where
| (21) |
is an energy function obtained as the dot product of a vector of potential functions Ψ = [ψFU,ψFP,ψGU,ψGP] and a vector of weights w = [λFU,λFP,λGU,λGP]. Here, ψFU and ψFP are the CRF unary and pairwise potentials, and ψGU and ψGP are the semi-CRF unary and pairwise potentials.
The CRF potential gives the score of assigning a gesture label to a single frame It. For kinematic data, the score is computed from the output of an SVM classifier, with RBF kernel on the kinematic data . For video data, this score is obtained from the output of an SVM classifier applied to the BoF histogram of features. Concretely, first each video frame is represented with a histogram of words extracted from a neighborhood around the frame t, and then these histograms are used to train an SVM classifier with a χ2-RBF kernel. In both kinematics and videos, the logarithm of the probability returned by regression of the SVM output is used as a unary score.
The semi-CRF unary potential gives the score of assigning a gesture label to a segment [li, li+1), thereby capturing global features related to the overall gesture. For video data, each segment is represented by the histogram of words accumulated over all the frames that correspond to the segment using the same dictionary of visual words described before. These histograms are then used to train a new SVM classifier with χ2-RBF kernel and the logarithm of the probability returned by regression on the SVM output as our unary term. In contrast with the approach in [31], we also adopt a BoF representation for kinematic data. A dictionary of kinematic data is used and each segment is then represented by a histogram.
The CRF pairwise and the semi-CRF pairwise are set as the logarithm of the transition frequency at frame-level and gesture-level, respectively, as in the S-HMM case.
Learning and Inference
Given m training time series and their corresponding labels , structured SVM [52] (a max-margin formulation) is used to train the parameters:
| (22) |
The intuition behind the first inequality is that we want the energy E at the ground truth labeling w⊤Ψ(𝒵̄i; 𝒱i) to be less than the energy of any incorrect labeling w⊤Ψ(𝒵; 𝒱i) by the loss ℓ(𝒵̄i, 𝒵), while still allowing some slack ξi. The loss function ℓ(𝒵̄i, 𝒵) measures the error in the labeling 𝒵 as the fraction of misclassified frames. Since the number of constraints is exponentially large, we use the cutting plane algorithm [53] to find w.
Given the MsM-CRF model parameters and a test time series 𝒱, we can perform joint gesture segmentation and recognition by solving the inference problem 𝒵* = arg min𝒵 E(𝒵, 𝒱), which can be written as an energy that depends only on the segment labels { }. Thus the resulting energy can be minimized using a Viterbi-like dynamic programming algorithm, as described in [54].
Implementation and Discussion
We use the MsM-CRF approach to perform gesture recognition using the robot’s kinematic and video data of the JIGSAWS dataset individually and in combination. For the kinematic data, we use all the master and slave information combined. For the spatiotemporal features in the video data, we use the dense features presented in [55], which are the concatenation of HOG, HOF, and histograms of motion boundaries and projected positions computed around dense trajectories. In [31], we show that the dense feature vector performs better than STIP features.
For the validation of the MSM-CRF technique on the JIGSAWS, the following combination of models and data are tested: (m1) kinematics to train Markov CRF potentials only (λGU = λGP = 0), (m2) kinematics to train both Markov CRF and semi-Markov CRF potentials, (m3) videos to train Markov CRF potentials, (m4) videos to train both Markov CRF and semi-Markov CRF potentials, (m5) videos to train Markov CRF and kinematics to train semi-Markov CRF potentials, and (m6) kinematics to train Markov CRF and videos to train semi-Markov CRF potentials.
Training both Markov CRF and semi-Markov CRF (m2 and m4) increase the performance about 5% as opposed to training only the Markov CRF potentials (m1 and m3). In the mixed models, m5 performs 5% to 10% better than m6. Finally, we observe similar performance for models trained only on kinematic or video features, while the mixed model m5 achieves 5% to 10% higher performance.
D. Semantic Image Model and Skip-Chain Conditional Random Field
As our fourth approach for gesture recognition, we employ [32], [33], an augmentation of the Skip Chain CRF (SC-CRF) [56] with the image semantic objects [57]. The former captures the transition between gestures and the latter models the deformable relationship between important objects in the scene. We use both kinematic and video data of the JIGSAWS as observations and predict a gesture label for each frame.
In HMM and linear-chain CRF methods, we assume that the label at the current frame is dependent only on the previous frame’s label and the data. In SC-CRF, we investigate a larger dependency between non-neighboring frames to capture higher-order transition between the gestures or the flow of the surgery.
We also extract information about the semantic objects in the video as opposed to using abstract features as in BoF and MsM-CRF methods. For example in the suturing task, where the relative geometry of the insertion points on the phantom are constrained, we can achieve better performance by modeling this semantic object information. The JIGSAWS dataset contains three dominant objects: a structured set of insertion points and the wound line (in suturing task), a set of metal loops (in needle-passing task), and a rod (in knot-tying task). Figure 6 shows examples of these objects.
Fig. 6.
Deformable Part Model for three surgical tasks: (top left) cartoon diagram of the suturing model, (top right) Suturing, (botom left) Needle-Passing, and (bottom right) Knot-Tying
Skip Chain CRF
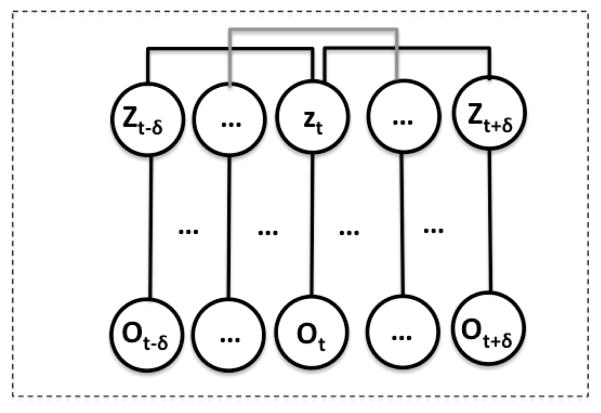
Following [33], we model the relationship between observations and labels at time t and time t − δ using a set of potential functions (Figure 7). Let ot be the observation (features extracted from video and kinematics) made at time t with gesture label zt, and let δ be the skip-chain length. We model P(Z|O) ∝ exp(−EC(Z, O)), where EC is the energy between a sequence of observations O = {o1, … oT} and corresponding labels Z = {z1, …, zT}. EC(Z, O) is modeled as
Fig. 7.
A Skip-Chain Conditional Random Field is used to capture state transitions over large periods of time. In this figure we show a skip-length of δ.
| (23) |
where the function Ψ(O, Z) represents unary, pairwise, and skip-length features:
| (24) |
and w = [wcu,wcp,wcs]T denotes the corresponding weight factors. The unary potential ϕC is defined to be a linear combination of the features. Therefore the vector wcu has L×F elements, where L is the number of gestures and F is the number of features. The pairwise potential ψC is defined to return a binary vector of size L2. This vector has only one element “1” where the index matches the transition zt−δ to zt. The length of wcp is L2 as well. The skip-length data potential γC function is defined to return a vector of size L×Fs, where Fs is the number of binary features (such as gripper angle status). For a given gesture index g and feature index i, γC is defined as a Dirac delta function: .
Learning and Inference
Similar to the MsM-CRF model, the parameters of the SC-CRF are learnt using the structural SVM proposed in [52] along with the Block Coordinate Frank Wolfe [58] optimizer. For inference, a modified version of Viterbi algorithm [57] is used.
Semantic Image Models and Features
We develop a deformable part model [57] to detect and localize the positions of the objects in the video. The part model has the form of a graph, with each object (i.e. insertion points in the suturing task) defined as a node. The edges act as springs that regulate the distance between objects (Figure 6).
After determining the object locations in the image, we compute two new semantic-driven features: (fd) absolute distance between the projection of the tooltip position and the closest object in the image, and (fo) the relative position between the projection of the tool and the closest object. Training the semantic model and extracting the semantic features are described in the supplemental material.
Implementation and Discussion
We validate the SC-CRF for gesture recognition using both video and kinematic data of the JIGSAWS dataset. We first evaluate the accuracy of the deformable part model on all three tasks (suturing, needle passing and knot-tying) using the labeled frames. To do so, we leave a group of frames out (under LOUO setup) during testing, learn the parameters (μij, Σij) from the training frames, and then evaluate the models on the test frames. The average error for the semantic part model is less than 5 pixels (95% accuracy).
For surgical gesture segmentation and classification, we test the model using several different parameter configurations: skip-length (δ from 1 to 100) and observation vectors O (subsets of kinematic features, subsets of video features, semantic features, and their combination). After computing the prediction sequence, we apply a median filter with width δ to smooth the results.
For the skip-length parameter δ, we observe that the performance of the system declines when δ is very small (δ ≤ 20) or very large (δ ≥ 50) and peaks at 30 ≤ δ ≤ 40. We choose δ to be 30 for our application. Notice that our video frequency is also 30 frames per second.
To select a subset of kinematic features for the observation vector, we test the following combination of features: (k1) all master data, (k2) all slave data, (k3) concatenation of k1 and k2, (k4) k3 excluding the positions, (k5) k3 excluding the linear velocities, (k6) k3 excluding the rotational velocities, and (k7) k3 excluding the gripper angles. We observe almost similar performance when using only master data, only slave data, or a combination of the two, which supports the conclusion that both the slave side and the master side carry almost the same information. However, we notice a slightly better performance for the data of the slave side (4%), which could be due to the fact that slave side is a more controlled environment in terms of noise canceling and tremor control. Features k4 to k6 show similar performance to the first three features, but when we remove the gripper angles their performance drops by 10%. We also observe that if we remove the depth information (z-axis) from k3, the performance drops by another 10%.
In the light of these experiments, we conclude that a combination of slave positions, velocities, and gripper angle is a fair representation of the kinematic data. This subset of features are more consistent with sensor readings from other robots that do not have a master side or cannot report their joint configurations. These conclusions are in agreement with the ones concluded from the HMM experiments.
To select a mix of kinematic and video features, we test the following combination of the features in the suturing task and measure the system performance with δ fixed at 30: (f1) only kinematic positions and velocities and gripper angle of both slaves, (f2) video projected positions and velocities, (f3) video projected positions and velocities concatenated with semantic feature fd, (f4) video projected positions and velocities concatenated with semantic feature fo, (f5) combination of f1 and fd, and (f6) mix of f1 and fo. Based on the results, the video features (f2 to f4) perform 15% lower than kinematic features, but when they are combined with the kinematic features in f5, they provide the best performance. Feature f6 performs only 2% lower than f5.
Even though the SC-CRF models are translatable directly to other surgical tasks or other human activities [59], [60], the semantic object models are highly dependent on a-priori knowledge about the structure of their environment (such as the wound line in the suturing task). However, it is important to mention that this particular semantic object model was specifically designed for the assessment of surgical skill (via activity detection) in virtual-reality simulators and bench-top tasks, where the structure of the environment is known a-priori.
V. Surgical Gesture Classification
The first four techniques introduced in this paper are designed to tackle the difficult problem of joint segmentation and classification of time-series data. Solving simultaneously for both the boundaries and the labels, they are able to predict a surgical gesture for each frame in the test set.
In this section, we present and validate two of representative methods for classifying surgical gestures: (1) Bag of Spatio-Temporal Features (BoF) and (2) Linear Dynamical System (LDS). In the classification problem, we assume the temporal boundaries (start and end) of each gesture segment are known and the goal is to predict a correct gesture label for the segment in the test set.
A. Bag of Spatio-Temporal Features: BoF
The bag of features approach was originally introduced for the object recognition problem in computer vision [61], [62] and was later applied to action recognition in videos [63]–[65].
Similarly, we developed the Bag of Spatio-Temporal Features approach for surgical gesture classification of presegmented video data [42], [43] (2013). In our version of the BoF technique, features are, however, extracted from the sequence of images in the video segment rather than from a single image, and consists of the following four steps:
Feature extraction
Features are extracted from multiple Space-Time Interest Points (STIP [63]) in each video segment. A STIP is a point (x, y, t) in the video that has high texture variations (e.g. large gradients) both spatially and temporally. It usually detects the motion in the video and ignores the static background. A 3D cuboid is centered around each extracted STIP at different spatio-temporal scales. Then local features are extracted from each cuboid: a 72-bin histogram of orientation gradients (HOG), and a 90-bin histogram of optical flow (HOF) [66]. In [43], we discuss the results obtained using these features individually or in combination, as well as the effect of a multichannel approach [67].
Clustering
After extracting the features, a codebook (a dictionary of spatio-temporal words) is built from all the locally computed features using a clustering technique such as K-means where each cluster of similar features is then represented by its cluster centroid. The clustering process is used to reduce the dimensionality of each video segment from a large feature set to a smaller set of representative features. In addition, it also provides some robustness against small variations in the features. Concretely, if G features of dimension D (F = [f1, … fG] ∈ ℝD×G) are extracted from a set of video segments used for training, they are then clustered into K centroid points v1, …, vK. We have tested two clustering techniques: K-means and Sparse Dictionary Learning (SDL) [68]. If we employ K-means for clustering, we would find the codebook, , that satisfies:
| (25) |
In SDL clustering technique [43], for each feature fg we compute its sparse representation yg with respect to the codebook V. Let Y = [y1, …, yG], then both V* and Y* are optimized as follows:
| (26) |
The SDL technique can be seen as a generalization of K-means where K-means provides hard assignments, the yg vectors (in absolute value) can be interpreted as soft assignments.
Encoding
The set of features extracted from each video segment can now be represented by a histogram of codebook words. To construct the histogram, we employ a variety of combinations of encoding schemes (hard, soft and hybrid assignments) and pooling (sum and max) methods [43].
The assignment decision can be viewed as the way each feature “votes” for the words of the codebook. In hard assignment, votes are binary (i.e., 1 or 0) and each feature is associated only with one word. In the case of soft assignment, a feature spreads its votes among all K words. A hybrid assignment is a combination of hard and soft assignments, such as the one proposed in [43].
Classification
At this stage, each video segment i is represented by its histogram hi. A one-vs-one multi-class SVM classifier is trained, using three different types of kernels: linear, intersection (KI), and 𝒳2 (K𝒳). For features computed with the multi-channel approach, a Radial Basis Function (RBF) (KRBF) is also employed for the SVM classifier. (see supplemental material for more details).
Implementation and Discussion
We employ the BoF technique for gesture classification on the video data of the JIGSAWS. The parameters that can affect BoF classification performance are: feature type, encoding method, dictionary size (number of spatio-temporal words), sparsity weights for dictionary learning, and choice of the kernel.
In [43], we tested the BoF using combination of choices among four features (HOG, HOF, and combinations of HOG and HOF using concatenation or a multi-channel approach), two clustering methods (K-means, SDL), different dictionary sizes (300 to 4000 words), six encoding approaches (combination of hard, soft, hybrid assignment, and max, sum-pooling), and three SVM kernels (intersection, 𝒳2, and RBF).
The HOG features extracted from the whole frame did not capture the differences between the surgical gestures due to the large constant background in the videos. On the other hand, HOG features extracted from STIP could successfully discard the constant background and capture the moving robot arms and hands. In addition, the HOG descriptors (capturing the shape and appearance of the objects) alone are more discriminative than HOF (capturing the object motion). As expected, their concatenation improved the results 5% to 10%. For BoF validation on the JIGSAWS, we use concatenation of HOF and HOG.
Independent of the type of the features, increasing the dictionary size in the tested range (300 to 4000 words) improved the performance. This improvement was however saturated for larger dictionary sizes. Since larger computation power is required for larger dictionary sizes, as suggested in [43], we choose a medium dictionary of size 2000 to validate the BoF technique on the JIGSAWS dataset.
For the encoding step, we tested all combinations of assignment techniques and pooling methods. Hybrid assignment performed just 1% lower than hard assignment, and combining soft assignment with max-pooling outperformed sum-pooling. We noticed that tuning parameters in soft and hybrid assignment is very important, and can improve the results by up to 25%. Finally, hard membership assignment combined with sum-pooling provided the best results. We use the same configuration to validate BoF on the JIGSAWS.
For clustering, SDL (SPAMS toolbox [69]) performance was robust to the choice of parameter λ and K-means performance was only 1–2% lower. In addition, 𝒳2 and intersection kernels performed equally well for SVM classification, independent of the choice of the clustering technique, while results obtained using a linear kernel were worse. Following these observations, to validate BoF on the JIGSAWS, we use K-means for clustering (computationally more efficient than SDL) and 𝒳2 for the SVM kernel.
B. Linear Dynamical System
Employing the idea of linear dynamical system, we also validate the LDS technique introduced in [42], [43] on the JIGSAWS dataset. This technique consists of the following three steps: (1) the kinematics data or image intensities of a video frames are modeled as the output of a LDS with Gaussian noise as an input, (2) After fitting LDS models to the manually segmented data, all the pairwise distances between LDSs are measured using Martin [70], Frobenius [71], Binet-Cauchy (BC) [72], and alingment [73] metrics, and finally, (3) a classifier (k-Nearest Neighbors (k-NN) or SVMs with RBF) is trained for classifying novel kinematics and/or video sequences. Below we discuss these steps in details:
Training the LDS
Let ot ∈ ℝd be either one image frame with d pixels from the video or one frame from the kinematic data. We assume that ot is the output of an LDS:
| (27) |
| (28) |
where xt ∈ Rn is the hidden state (with n ≪ d). Matrices A ∈ Rn×n, B ∈ Rn×d, and C ∈ Rd×n are the state transition, noise-coloring, and observation matrices, respectively. The stochastic processes ut ~ 𝒩(0, I) and wt ~ 𝒩(0, R) are assumed to be i.i.d. Gaussian and model the process and measurement noise, respectively.
For this LDS model, only ot is known and the parameters M = (A, B, C, R) need to be identified using the observations for each pre-segmented data in the training set. To identify the parameters of the LDS model, we employ a sub-optimal method based on Principal Component Analysis proposed in [74].
Comparing LDSs
One difficulty in assessing the similarity or distance between two LDS models is the fact that the identified representation is not unique because (A, B, C, R) and (PAP−1, PB, CP−1, R) are equivalent representations of the same LDS for all invertible n × n matrices P. To address this challenge, we use three different metrics in the space of dynamical systems: (1) metrics based on subspace angles between the observability subspaces of the dynamical models [70], [71], (2) metrics based on Binet-Cauchy kernels [72], and (3) alignment distance based on the equivalence of representation between models [73] (see supplemental material for the descriptions of these metrics).
Classification
After computing all the pairwise distances between the LDS models fitted to the segments of the data in training set, a classifier such as k-Nearest Neighbor (k-NN) or RBF-kernel SVM is trained to predict a gesture label for novel sequences of data. The RBF kernel [75] is defined as:
| (29) |
Where γ > 0 is a parameter and dX is one of the metric distances described above.
Implementation and Discussion
We validate the LDS technique on the JIGSAWS dataset for gesture classification from both video and kinematic data. The videos are downsampled to 320×240 pixel resolution and their raw pixel intensities are used as the input observation.
The order of the linear dynamical model (n), the choice of the distance metric, classifier type, and feature types can affect the classification performance of the LDS. Similar to [43], we again test the model with different orders (n = 5 to 21), distance metrics (Martin, Frobenius, BC, and alignment), classifiers (k-NN and SVM), and features (optical flow, pixel intensities in video, and kinematics).
The LDS is moderately sensitive to the choice of the order: a carefully chosen order would increase the performance by up to 10%. However, there are outliers to this conclusion, such as the unsuccessful combination of the BC-kernel metric and the SVM classifier. Other combinations of parameters performed well when n was chosen to be between 10 and 17.
Similar to the observations made in [43], among different distance metrics, there is no clear winner that performs well under both LOSO and LOUO setups for both kinematic and video data. Nonetheless, the metrics based on subspace angles (Martin and Frobenius) often perform better. In most scenarios, other metrics provide similar results. For a fixed dynamical order, one can improve the performance of the LDS model 5% to 10% by choosing an appropriate distance metric.
Slightly different from observations made in [43], we observe that different feature types performed differently depending on the choice of the model order, classifier and metric. For example, kinematic features achieve the highest performance when we choose the following combination: n = 15, SVM classifier, and BC metric. The video pixel features perform the best with n = 15, SVM, and alignment metric. [43] also tested for optical flow features (BoF), and observed that on average, they performed worse than pixel intensities and kinematic data. On average, the kinematic data perform the best, with the results from pixel intensities following very closely.
Between different choices of classifier, in general, the SVM classifier achieves the best performance.
VI. Results
The results reported in this section are generated using the JIGSAWS unified cross-validation setup, which ensures that they are directly comparable and that no test data are left out or treated differently across different methods.
Tables I, II, III, and IV summarize the best performance for the six techniques described in this paper. In their corresponding sections, we discussed details of the parameter configurations, their effects on classification performance, and the configurations that yielded the best overall results for each technique. All the parameter values described in this paper were found either by learning them in the validation phase (using the training set) or by consistently sweeping the parameter space in a reasonable range and not by manual tweaking.
TABLE I.
Best performance of joint segmentation and classification techniques validated on the JIGSAWS, for LOSO cross-validation. GMM-HMM (S = 3, M = 1, d = 1, feature f4), KSVD-S-HMM (K = 7, 200-word dictionary, feature slave arms), MsM-CRF (kinematic m2, video m4, video and kinematics m5), and SC-CRF (δ = 30, feature f5).
| Method (Data type) | Evaluation | Suturing | Needle-passing | Knot-tying |
|---|---|---|---|---|
| GMM-HMM (kin) | Micro | 82.22 | 70.55 | 80.95 |
| Macro±std | 70.99±22.67 | 66.10±14.19 | 79.27±13.06 | |
| Precision±std | 73.03±27.76 | 67.86±13.06 | 81.66±7.75 | |
| β (μ ± σ) | 82.98±0.13 | 70.56±0.05 | 80.59±0.18 | |
| β 95%CI | 75.20–89.56 | 65.70–75.20 | 71.40–88.37 | |
|
| ||||
| KSVD-SHMM (kin) | Micro | 83.40 | 73.09 | 83.54 |
| Macro±std | 73.05±28.03 | 68.51±19.28 | 82.13±4.62 | |
| Precision±std | 72.82±27.18 | 69.45±17.33 | 86.04±7.96 | |
| β (μ ± σ) | 83.89±0.09 | 74.01±0.59 | 83.23±0.23 | |
| β 95%CI | 77.45–89.43 | 57.56–87.55 | 72.71–91.58 | |
|
| ||||
| MsM-CRF (kin) | Micro | 81.99 | 72.44 | 79.26 |
| Macro±std | 72.56±26.70 | 67.73±16.93 | 79.05±7.62 | |
| Precision±std | 72.23±27.69 | 67.54±18.97 | 82.12±7.27 | |
| β (μ ± σ) | 83.04±0.24 | 73.24±0.29 | 79.19±0.14 | |
| β 95%CI | 72.29–91.57 | 62.075–83.09 | 71.15–86.22 | |
|
| ||||
| MsM-CRF (vid) | Micro | 84.43 | 74.54 | 82.84 |
| Macro±std | 71.77±28.09 | 66.76±19.08 | 81.17±6.85 | |
| Precision±std | 75.84±27.14 | 72.89±10.42 | 84.58±9.00 | |
| β (μ ± σ) | 84.78±0.03 | 75.27±0.28 | 82.80±0.02 | |
| β 95%CI | 80.96–88.24 | 64.06–84.98 | 79.90–85.52 | |
|
| ||||
| MsM-CRF (kin+vid) | Micro | 85.10 | 75.09 | 84.03 |
| Macro±std | 72.68±28.38 | 66.59±18.88 | 82.13±6.78 | |
| Precision±std | 75.79±27.06 | 74.42±10.00 | 85.85±7.56 | |
| β (μ ± σ) | 85.51±0.05 | 75.65±0.19 | 84.03±0.02 | |
| β 95%CI | 80.80–89.66 | 66.55–83.72 | 81.07–86.78 | |
|
| ||||
| SC-CRF (kin) | Micro | 85.18 | 77.30 | 80.72 |
| Macro±std | 74.19±28.14 | 71.34±17.20 | 79.75±9.76 | |
| Precision±std | 77.03±27.51 | 74.96±9.84 | 81.19±8.69 | |
| β (μ ± σ) | 85.87±0.15 | 78.27±0.36 | 80.66±0.12 | |
| β 95%CI | 77.25–92.71 | 65.39–88.83 | 73.35–87.04 | |
|
| ||||
| SC-CRF (kin+vid) | Micro | 85.04 | Not Available | Not Available |
| Macro±std | 74.52±28.44 | |||
| Precision±std | 76.88±27.48 | |||
| β (μ ± σ) | 85.86±0.18 | |||
| β 95%CI | 76.35–93.23 | |||
TABLE II.
Best performance of joint segmentation and classification techniques validated on the JIGSAWS, for LOUO cross-validation. GMM-HMM (S = 3, M = 1, d = 1, feature f4), KSVD-S-HMM (K = 7, 200-word dictionary, feature slave arms), MsM-CRF (kinematic m2, video m4, video and kinematics m5), and SC-CRF (δ = 30, feature f5).
| Method (Data type) | Evaluation | Suturing | Needle-passing | Knot-tying |
|---|---|---|---|---|
| GMM-HMM (kin) | Micro | 73.95 | 64.13 | 72.47 |
| Macro±std | 57.99±31.57 | 55.63±19.54 | 65.90±25.24 | |
| Precision±std | 61.75±29.93 | 57.97±18.26 | 70.71±15.95 | |
| β (μ ± σ) | 72.60±1.27 | 64.28±1.08 | 73.03±0.53 | |
| β 95%CI | 48.07–91.32 | 42.75–83.12 | 57.56–86.06 | |
|
| ||||
| KSVD-SHMM (kin) | Micro | 73.45 | 62.78 | 74.89 |
| Macro±std | 52.34±31.68 | 55.32±18.90 | 72.73±7.29 | |
| Precision±std | 66.45±25.69 | 58.81±21.61 | 76.41±11.29 | |
| β (μ ± σ) | 73.17±0.09 | 64.64±1.25 | 75.33±0.83 | |
| β 95%CI | 66.92–78.99 | 41.43–84.63 | 55.45–90.71 | |
|
| ||||
| MsM-CRF (kin) | Micro | 67.84 | 44.68 | 63.28 |
| Macro±std | 51.05±28.62 | 37.58±12.63 | 53.05±26.31 | |
| Precision±std | 54.27±32.20 | 47.43±27.12 | 57.95±31.66 | |
| β (μ ± σ) | 68.24±1.34 | 46.83±2.14 | 64.40±1.13 | |
| β 95%CI | 43.67–88.26 | 19.36–75.43 | 42.38–83.58 | |
|
| ||||
| MsM-CRF (vid) | Micro | 77.29 | 66.98 | 75.65 |
| Macro±std | 57.59±33.78 | 60.02±21.53 | 72.82±9.87 | |
| Precision±std | 61.83±33.83 | 65.08±16.69 | 80.3±14.56 | |
| β (μ ± σ) | 77.54±0.22 | 66.65±0.69 | 77.03±0.34 | |
| β 95%CI | 67.72–86.03 | 49.41–81.84 | 64.54–87.48 | |
|
| ||||
| MsM-CRF (kin+vid) | Micro | 78.98 | 65.871 | 77.319 |
| Macro±std | 59.26±34.14 | 56.34±20.09 | 72.66±14.83 | |
| Precision±std | 63.61±34.15 | 64.21±17.65 | 80.88±10.82 | |
| β (μ ± σ) | 79.10±0.28 | 65.51±0.69 | 77.97±0.34 | |
| β 95%CI | 67.80–88.49 | 48.42–80.75 | 65.50–88.28 | |
|
| ||||
| SC-CRF (kin) | Micro | 81.74 | 74.77 | 78.95 |
| Macro±std | 68.68±29.85 | 66.41±19.80 | 77.56±10.81 | |
| Precision±std | 70.22±26.91 | 71.33±13.71 | 76.25±14.05 | |
| β (μ ± σ) | 82.33±0.39 | 74.96±0.76 | 80.09±0.59 | |
| β 95%CI | 68.47–92.79 | 56.00–89.89 | 63.09–92.73 | |
|
| ||||
| SC-CRF (kin+vid) | Micro | 81.60 | Not Available | Not Available |
| Macro±std | 67.67±30.01 | |||
| Precision±std | 69.51±27.60 | |||
| β (μ ± σ) | 82.17±0.41 | |||
| β 95%CI | 67.86–92.91 | |||
TABLE III.
Best performance of classification techniques validated on the JIGSAWS, for LOSO cross-validation. BoF (2000-word dictionary, concatenation of HOG and HOF, hard encoding with sum-pooling, K-means clustering, 𝒳2 kernel SVM), LDS(n = 15, SVM classifier, BC metric for kinematics and align for video), and GMM-HMM (S = 3, M = 1, d = 1, feature f4).
| Method (Data type) | Evaluation | Suturing | Needle-passing | Knot-tying |
|---|---|---|---|---|
| BoF (vid) | Micro | 92.56 | 76.98 | 91.37 |
| Macro±std | 82.17±29.51 | 75.60±16.33 | 89.95±9.05 | |
| β (μ ± σ) | 81.12±29.37 | 75.17±13.60 | 92.7±7.71 | |
| β 95%CI | 92.95±0.19 | 76.99±0.01 | 91.34±0.007 | |
| 82.12–98.91 | 74.66–79.24 | 89.61–92.93 | ||
|
| ||||
| LDS (kin) | Micro | 84.61 | 59.768 | 81.67 |
| Macro±std | 63.87±30.82 | 46.55±25.81 | 74.51±23.73 | |
| Precision±std | 73.30±28.41 | 52.91±17.31 | 76.07±18.72 | |
| β (μ ± σ) | 84.77±0.06 | 59.78±0.01 | 81.67±0.016 | |
| β 95%CI | 79.36–89.49 | 57.42–62.12 | 79.12–84.09 | |
|
| ||||
| LDS (vid) | Micro | 90.29 | 67.12 | 89.49 |
| Macro±std | 74.73±29.64 | 56.82±23.29 | 87.61±7.99 | |
| Precision±std | 82.26±29.59 | 73.40±15.09 | 91.67±7.10 | |
| β (μ ± σ) | 90.58±0.10 | 67.12±0.014 | 89.45±0.008 | |
| β 95%CI | 83.26–95.96 | 64.72–69.49 | 87.58–91.18 | |
|
| ||||
| GMM-HMM (kin) | Micro | 92.56 | 75.68 | 89.76 |
| Macro±std | 79.66±29.85 | 72.36±16.99 | 87.29±12.76 | |
| Precision±std | 81.20±30.42 | 73.60±20.43 | 91.52±7.41 | |
| β (μ ± σ) | 92.76±0.07 | 75.66±0.01 | 89.71±0.43 | |
| β 95%CI | 86.38–97.234 | 73.31–77.941 | 73.72–98.556 | |
TABLE IV.
Best performance of classification techniques validated on the JIGSAWS, for LOUO cross-validation. BoF (2000-word dictionary, concatenation of HOG and HOF, hard encoding with sum-pooling, K-means clustering, 𝒳2 kernel SVM), LDS(n = 15, SVM classifier, BC metric for kinematics and align for video), and GMM-HMM (S = 3, M = 1, d = 1, feature f4).
| Method (Data type) | Evaluation | Suturing | Needle-passing | Knot-tying |
|---|---|---|---|---|
| BoF (vid) | Micro | 82.97 | 67.11 | 86.52 |
| Macro±std | 67.39±36.32 | 63.11±19.98 | 85.41±7.80 | |
| β (μ ± σ) | 63.47±36.05 | 64.34±22.39 | 88.42±10.88 | |
| β 95%CI | 83.18±0.80 | 68.32±1.15 | 86.40±0.09 | |
| 62.35–96.48 | 45.64–87.09 | 79.85–91.83 | ||
|
| ||||
| LDS (kin) | Micro | 73.64 | 47.96 | 71.42 |
| Macro±std | 51.75±32.91 | 32.59±29.74 | 63.99±24.51 | |
| Precision±std | 53.39±32.01 | 32.01±27.76 | 65.74±21.54 | |
| β (μ ± σ) | 73.80±0.30 | 45.68±1.45 | 71.44±0.15 | |
| β 95%CI | 62.31–83.84 | 22.92–69.44 | 63.31–78.93 | |
|
| ||||
| LDS (vid) | Micro | 79.32 | 56.48 | 82.75 |
| Macro±std | 58.53±34.73 | 45.53±25.14 | 81.11±11.35 | |
| Precision±std | 62.48±33.92 | 60.65±22.11 | 86.96±12.36 | |
| β (μ ± σ) | 79.47±0.47 | 56.62±0.21 | 82.57±0.18 | |
| β 95%CI | 64.44–91.16 | 47.48–65.53 | 73.45–90.10 | |
|
| ||||
| GMM-HMM (kin) | Micro | 80.83 | 66.22 | 78.44 |
| Macro±std | 65.03±33.07 | 62.70±16.38 | 72.68±21.31 | |
| Precision±std | 71.98±33.05 | 66.55±25.45 | 83.27±13.04 | |
| β (μ ± σ) | 81.31±1.32 | 69.19±2.97 | 78.16±0.58 | |
| β 95%CI | 54.16–97.47 | 31.31–95.59 | 61.47–91.07 | |
We report five non-probabilistic performance metrics for each technique: Micro, Macro, Macro variance, Precision, and Precision variance and three probabilistic metrics mean μ, variance σ, and 95% confidence interval of the Beta distribution.
As noted in the evaluation methodology section, we evaluate and report the performance of our techniques under two cross-validation techniques: LOUO (Leave-One-User-Out) and LOSO (Leave-One-Super-Trial-Out). These two cross-validation approaches help to measure the models’ generalization to new and unknown surgeons or to new trials performed by a known surgeon, respectively. We observe that all the techniques perform on average 10% lower on the harder test of LOUO. This deficiency is probably not due to the training sample size, because the size of the training pool (in all folds) for the LOUO test is equal to or larger than those in the LOSO test. The lower performance on the LOUO, therefore, suggests a higher inter-surgeon variability – for example, different novice surgeons make different mistakes and expert surgeons practice different styles.
The difference between surgeons’ styles could be due to the following two factors: (1) The JIGSAWS cross-validation tests combine the trials performed by both experts and novices. For example, if trials from a novice surgeon are left out for the test, their executions of the gestures may not resemble either those performed correctly by experts or wrongly (but differently) by other novices; and/or: (2) For dexterous and mentored tasks such as surgical activities, individual subjects develop certain styles, resembling their mentors. Therefore, activities performed by expert individuals may differ style-wise from those performed by other experts, a potential source of variability even across expert task executions.
The results in Table I show that our techniques can recognize the gesture activities with high accuracy (about 80%) when the human performer is observed beforehand (LOSO). For the case of predicting a gesture label for a surgery performed by an unobserved surgeon (LOUO reported in Table II), the prediction accuracy decreases on average 10% (range 4% to 30%).
There are three factors to notice when comparing the results: (1) the chance baseline for gesture recognition (micro average) is 10%, 12.5%, and 8.3% for the suturing, needle passing, and knot tying tasks, respectively. This shows that the described techniques perform 8× to 10× better than chance, (2) for the case of joint segmentation and classification, the granularity of the classifier is very fine at frame level which is about 0.03 second long, and (3) at this granularity, independent human annotators agree only on 75% to 80% of the frames [26], [27]. Therefore for a machine (trained to replicate manual labels) a performance of 80% is within the range of human labeling performance. These three factors should put into perspective the highest accuracies that a specific algorithm can be expected to achieve.
Since the introduced techniques are implemented with different programming language, a direct comparison between their run-time is not justifiable. For a fair comparison, and for the first time, we report and compare the time complexity of each algorithm both for the training phase and the decoding phase (note supplemental document).
The supplemental document also includes additional results useful to understand the strengths and limitations of the described techniques. Tables I, II, III, and IV report the best results for each technique achieved with chosen subsets of kinematic features: e.g. while MsM-CRF uses data from both slave and master arms, GMM-HMM and KSVD-S-HMM use only slave arms data, and SC-CRF uses a subset of slave arms data. Table I and II in the supplemental document present the performance of the described techniques when the same input features (both master and slave arms) are used. The results show that even though some of the techniques perform lower than the ones reported in Tables I and II, their order remains similar. In addition, Tables III and VI in the supplemental document report state-of-the-art results on skill assessment of the JIGSAWS database.
VII. Conclusion
Processing of surgical time-series data is challenging due to complexity of both the data and its purpose, ranging from surgical skill assessment to patient outcome prediction. The emerging field of surgical activity recognition aims to facilitate, and ultimately provide targeted feedback to improve, e.g., residents’ competency. This is becoming increasingly feasible thanks to the availability of methods for automated high-fidelity data collection (e.g. using surgical robots) and analysis.
In this paper, we first described the elements of the JIGSAWS dataset – the first public benchmark surgical activity dataset. We presented a unified framework supporting performance evaluation of state-of-the-art methods for automatic classification and segmentation of surgical time-series data. We then presented several methods for segmentation and classification using both kinematic and video data, with consistent evaluation of their performance using the JIGSAWS benchmark dataset. Note that this includes representing and re-evaluating several previously developed methods to be consistent with the methodology presented in this paper.
The data used for our research is structurally similar in many ways to that captured using other approaches, such as electromagnetic or visual trackers. Consequently, it is possible to exchange the data and the techniques introduced in this paper with those from activity recognition fields other than on surgical robots or simulators. Our recent publications demonstrate that the presented techniques are applicable to the broader category of human action recognition [59], [76]. Currently we are expanding them to more complex activities with data collected from other trackers which is noisier than robotic data, live patient data which is less structured than training tasks, and live patient surgical video data which lacks salient features due to the presence of blood.
The methodologies and the results published in this paper aim to provide a comparative baseline as well as a rich and insightful direction for future researchers in the emerging field of robotic surgery.
Supplementary Material
Fig. 5.
Graphical model for Markov semi-Markov Conditional Random Field.
Acknowledgments
This work was supported in part by NIH 1R01-DE025265, NSF 0534359, NSF IIS-0748338, NSF-OIA 0941362, NSFCSN 0931805, the Sloan Foundation, and the NSF Graduate Research Fellowship Program (CER). Dr. Béjar was supported in part by the Talentia Fellowship Program of the Andalusian Regional Ministry of Economy, Innovation and Science. Prof. Vidal was supported in part by European Research Council grant VideoWorld. Lea was supported in part by NSF grant DGE-1232825.
The authors would like to thank Dr. Grace Chen and Carol Reiley for their contribution to data collection and annotation. We appreciate Simon P. DiMaio and Intuitive Surgical Inc. for their help in data collection and Balazs P. Vagvolgyi for his contribution to the data collection software. We also thank Jonathan Jones, Amanda Edwards, and Dr. Austin Reiter for proofreading the manuscript.
Biographies
Narges Ahmidi received her Ph.D. in Computer Science from Johns Hopkins University (JHU) 2015, her B.S. in Computer Engineering and M.S. in Artificial Intelligence from Tehran Polytechnic University, Iran. Her research interest are surgical data science and clinical pathways analysis based on electronic medical records.
Lingling Tao is a Ph.D. student in Johns Hopkins University. She received the B.S. degree in Electronic Engineering from Tsinghua University, Beijing, China in 2010 and M.Se degree in JHU in 2013. Her research interests are computer vision and machine learning.
Shahin Sefati received his Ph.D. from JHU in 2014. He is currently a senior researcher at Comcast Labs in Washington DC, and a visiting scientist at JHU. His research interests are in machine learning and robotics.
Yixin Gao is a Ph.D. student at JHU. She received her B.S. and M.S. in electrical engineering from Xi’an Jiaotong University, and M.S. in computer science from JHU. Her research interests are machine learning and computer vision. She is a student member of the IEEE.
Colin Lea is a Ph.D. student at JHU where he works on human activity modeling. He received his B.S. at the University at Buffalo Honors College and was a graduate research fellow of both the National Science Foundation and Intuitive Surgical.
Benjamín Béjar Haro received his Ph.D. degree in Electrical Engineering from the Universidad Politécnica de Madrid in 2012. He received the best paper award of MICCAI 2012. He now works as a postdoctoral fellow in the Audiovisual Communications Laboratory at EPFL.
Luca Zappella received his Ph.D. at the University of Girona. He then worked at JHU as a post-doctoral fellow. Currently he is working as a CV/ML research engineer in the industry setting.
Sanjeev Khudanpur is an associate professor at the Department of Electrical and Computer Engineering. He received his B.Tech degree in Electrical Engineering from the Indian Institute of Technology, Bombay, in 1988, and the Ph.D. degree in Electrical and Computer Engineering from the University of Maryland, College Park, in 1997.
René Vidal is a professor of Biomedical Engineering, Computer Science, Mechanical Engineering, and Electrical and Computer Engineering at JHU. He is the director of the Vision Dynamics and Learning Lab, which is part of the Center for Imaging Science (CIS). He received the BS degree in electrical engineering (valedictorian) from the Pontificia Universidad Católica de Chile in 1997 and the MS and Ph.D. degrees in electrical engineering and computer sciences, University of California at Berkeley in 2000 and 2003, respectively.
Gregory D. Hager is the director of the Computational Interaction and Robotics Lab (CIRL) in the Laboratory for Computational Sensing and Robotics, and also deputy director of the NSF Engineering Research Center for Computer-Integrated Surgical Systems and Technology (CISST). He is also the director of the Malone Center for Engineering in Healthcare. He is a member of the Computing Community Consortium Council and the board of the International Federation of Robotics Research.
Contributor Information
Narges Ahmidi, Department of Computer Science, Johns Hopkins University, Baltimore, MD, 21218 USA.
Lingling Tao, Center for Imaging Science, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21218 USA.
Shahin Sefati, Center for Imaging Science, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21218 USA.
Yixin Gao, Department of Computer Science, Johns Hopkins University, Baltimore, MD, 21218 USA.
Colin Lea, Department of Computer Science, Johns Hopkins University, Baltimore, MD, 21218 USA.
Benjamín Béjar Haro, Center for Imaging Science, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21218 USA.
Luca Zappella, Center for Imaging Science, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21218 USA.
Sanjeev Khudanpur, Electrical and Computer Engineering, Johns Hopkins University, Baltimore, MD, 21218 USA, Johns Hopkins University, Baltimore, MD, 21218 USA.
René Vidal, Center for Imaging Science, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, 21218 USA.
Gregory D. Hager, Department of Computer Science, Johns Hopkins University, Baltimore, MD, 21218 USA.
References
- 1.Bass B. Fundamental changes in general surgery residency training. American Journal of Surgery. 2007;73:109–113. [PubMed] [Google Scholar]
- 2.Moller M, et al. Mentoring the modern surgeon. The American College of Surgeons. 2008:19–25. [PubMed] [Google Scholar]
- 3.Polavarapu H, et al. 100 years of surgical education: The past, present, and future. The American College of Surgeons. 2013 [PubMed] [Google Scholar]
- 4.Martin J, et al. Objective structured assessment of technical skill for surgical residents. British Journal of Surgery. 1997;84:273–278. doi: 10.1046/j.1365-2168.1997.02502.x. [DOI] [PubMed] [Google Scholar]
- 5.Goh A, et al. Global evaluative assessment of robotic skills: validation of a clinical assessment tool to measure robotic surgical skills. The Journal of urology. 2012;187:247–252. doi: 10.1016/j.juro.2011.09.032. [DOI] [PubMed] [Google Scholar]
- 6.Hatala R, et al. Constructing a validity argument for the objective structured assessment of technical skills (osats): a systematic review of validity evidence. Advances in Health Science Education: Theory and Practice. 2015:1149–1175. doi: 10.1007/s10459-015-9593-1. [DOI] [PubMed] [Google Scholar]
- 7.Kohn L, et al. To err is human: building a safer health system. National Academy Press. 2002 [PubMed] [Google Scholar]
- 8.Pellegrini C the acgme outcomes project. American Council for Graduate Medical Education. Surgery. 2002;131:214–215. doi: 10.1067/msy.2002.120666. [DOI] [PubMed] [Google Scholar]
- 9.Shah J, Darzi A. Surgical skills assessment: an ongoing debate. British Journal Urology International. 2001;88:655–660. doi: 10.1046/j.1464-4096.2001.02424.x. [DOI] [PubMed] [Google Scholar]
- 10.Hamstra S, Dubrowski A. Effective training and assessment of surgical skills, and the correlates of performance. Surgery Innovation. 2005;12:71–77. doi: 10.1177/155335060501200110. [DOI] [PubMed] [Google Scholar]
- 11.Fried G, Feldman L. Objective assessment of technical performance. World Journal of Surgery. 2008;32:156–160. doi: 10.1007/s00268-007-9143-y. [DOI] [PubMed] [Google Scholar]
- 12.Darzi A, Mackay S. Assessment of surgical competence. Quality of Health Care. 2001;10:ii64–ii69. doi: 10.1136/qhc.0100064... [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Datta V, et al. The use of electromagnetic motion tracking analysis to objectively measure open surgical skill in laboratory-based model. Journal of the American College of Surgery. 2001;193:479–485. doi: 10.1016/s1072-7515(01)01041-9. [DOI] [PubMed] [Google Scholar]
- 14.Judkins T, et al. Objective evaluation of expert and novice performance during robotic surgical training tasks. Surgical Endoscopy. 2008;1(4) doi: 10.1007/s00464-008-9933-9. [DOI] [PubMed] [Google Scholar]
- 15.Richards C, et al. Skills evaluation in minimally invasive surgery using force/torque signatures. Surgical Endoscopy. 2000;14:791–798. doi: 10.1007/s004640000230. [DOI] [PubMed] [Google Scholar]
- 16.Yamauchi Y, et al. Surgical skill evaluation by force data for endoscopic sinus surgery training system. Medical Image Computing and Computer-Assisted Intervention. 2002:44–51. [Google Scholar]
- 17.Rosen J, et al. Markov modeling of minimally invasive surgery based on tool/tissue interaction and force/torque signatures for evaluating surgical skills. IEEE Trans Biomedical Eng. 2001;48(5):579–591. doi: 10.1109/10.918597. [DOI] [PubMed] [Google Scholar]
- 18.McKenzie C, et al. Hierarchical decomposition of laparoscopic surgery: A human factors approach to investigating the operating room environment. Journal of Minimally Invasive Therapy and Allied Technologies. 2001;10(3):121–127. doi: 10.1080/136457001753192222. [DOI] [PubMed] [Google Scholar]
- 19.Lin HC, et al. Automatic detection and segmentation of robot-assisted surgical motions. Medical Image Computing and Computer-Assisted Intervention. 2005:802–810. doi: 10.1007/11566465_99. [DOI] [PubMed] [Google Scholar]
- 20.Lin HC, et al. Towards automatic skill evaluation: detection and segmentation of robot-assisted surgical motions. Computer Aided Surgery. 2006 doi: 10.3109/10929080600989189. [DOI] [PubMed] [Google Scholar]
- 21.Reiley CE, et al. Automatic recognition of surgical motions using statistical modeling for capturing variability. Medicine Meets Virtual Reality. 2008;132:396–401. [PubMed] [Google Scholar]
- 22.Dosis A, et al. Laparoscopic task recognition using hidden Markov models. Studies in Health Technology and Informatics. 2005;111:115–122. [PubMed] [Google Scholar]
- 23.Rosen J, et al. Task decomposition of laparoscopic surgery for objective evaluation of surgical residents’ learning curve using hidden Markov model. Computer Aided Surgery. 2002;7(1):49–61. doi: 10.1002/igs.10026. [DOI] [PubMed] [Google Scholar]
- 24.Leong J, et al. HMM assessment of quality of movement trajectory in laparoscopic surgery. Medical Image Computing and Computer-Assisted Intervention. 2006:752–759. doi: 10.1007/11866565_92. [DOI] [PubMed] [Google Scholar]
- 25.Reiley CE, Hager GD. Task versus subtask surgical skill evaluation of robotic minimally invasive surgery. Medical Image Computing and Computer-Assisted Intervention. 2009:435–442. doi: 10.1007/978-3-642-04268-3_54. [DOI] [PubMed] [Google Scholar]
- 26.Vedula SS, et al. Analysis of the structure of surgical activity for a suturing and knot-tying task. PLOS one. 2016 doi: 10.1371/journal.pone.0149174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ahmidi N, et al. String motif-based description of tool motion for detecting skill and gestures in robotic surgery. Medical Image Computing and Computer-Assisted Intervention. 2013 doi: 10.1007/978-3-642-40811-3_4. [DOI] [PubMed] [Google Scholar]
- 28.Ahmidi N, et al. Automated objective surgical skill assessment in the operating room from unstructured tool motion in septoplasty. International Journal of Computer Assisted Radiology and Surgery. 2015:981–991. doi: 10.1007/s11548-015-1194-1. [DOI] [PubMed] [Google Scholar]
- 29.Varadarajan B. dissertation. Johns Hopkins University; 2011. Learning and inference algorithms for dynamic system models of dextrous motion. [Google Scholar]
- 30.Tao L, et al. Sparse hidden markov models for surgical gesture classification and skill evaluation. Information Processing in Computer-Assisted Interventions. 2012;7330:167–177. [Google Scholar]
- 31.Tao L, et al. Surgical gesture segmentation and recognition. Medical Image Computing and Computer-Assisted Intervention. 2013 doi: 10.1007/978-3-642-40760-4_43. [DOI] [PubMed] [Google Scholar]
- 32.Lea C, et al. Using vision to improve activity recognition in surgical training tasks. The role of human sensorimotor control in surgical robotics workshop. 2014;61:55–79. [Google Scholar]
- 33.Lea C, et al. Improved modeling of fine grained activities with application to surgical training tasks. Applications of Computer Vision. 2014;61:55–79. [Google Scholar]
- 34.Miyawaki F, et al. Scrub nurse robot system - intraoperative motion analysis of a scrub nurse and timed-automata-based model for surgery. Transactions on Industrial Electronics. 2005;52(5):1227–1235. [Google Scholar]
- 35.Klank U, et al. Automatic feature generation in endoscopic images. International Journal for Computer Assisted Radiology and Surgery. 2008;3:331–339. [Google Scholar]
- 36.Padoy N, et al. A boosted segmentation method for surgical workflow analysis. Medical Image Computing and Computer-Assisted Intervention. 2007:102–109. doi: 10.1007/978-3-540-75757-3_13. [DOI] [PubMed] [Google Scholar]
- 37.Blum T, et al. Workflow mining for visualization and analysis of surgeries. International Journal of Computer Assisted Radiology and Surgery. 2008;3(5):379–386. [Google Scholar]
- 38.Padoy N, et al. Statistical modeling and recognition of surgical workflow. Medical Image Analysis. 2012;16(3):632–641. doi: 10.1016/j.media.2010.10.001. [DOI] [PubMed] [Google Scholar]
- 39.Lalys F, et al. Automatic knowledge-based recognition of low-level tasks in ophthalmological procedures. International Journal on Computer Assisted Radiology and Surgery. 2013;8(1):39–49. doi: 10.1007/s11548-012-0685-6. [DOI] [PubMed] [Google Scholar]
- 40.Lin HC. dissertation. Johns Hopkins University; 2010. Structure in surgical motion. [Google Scholar]
- 41.Lalys F, et al. An application-dependent framework for the recognition of high-level surgical tasks in the OR. Medical Image Computing and Computer-Assisted Intervention. 2011:331–338. doi: 10.1007/978-3-642-23623-5_42. [DOI] [PubMed] [Google Scholar]
- 42.Béjar B, et al. Surgical gesture classification from video data. Medical Image Computing and Computer-Assisted Intervention. 2012:34–41. doi: 10.1007/978-3-642-33415-3_5. [DOI] [PubMed] [Google Scholar]
- 43.Zappella L, et al. Surgical gesture classification from video and kinematic data. Medical Image Analysis. 2013;17:732–745. doi: 10.1016/j.media.2013.04.007. [DOI] [PubMed] [Google Scholar]
- 44.Gao Y, et al. Language of surgery: A surgical gesture dataset for human motion modeling. 2014 http://cirl.lcsr.jhu.edu/wpcontent/uploads/2015/11/JIGSAWS.pdf.
- 45.Ng AY, Jordan MI. On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes. Advances in neural information processing systems. 2002;14:841. [Google Scholar]
- 46.Varadarajan B, et al. Data-derived models for segmentation with application to surgical assessment and training. Medical Image Computing and Computer-Assisted Intervention. 2009:426–434. doi: 10.1007/978-3-642-04268-3_53. [DOI] [PubMed] [Google Scholar]
- 47.Belhumeur PN, et al. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection. IEEE Transaction on Pattern Analysis and Machine Intelligence. 1997;19(7):711–720. [Google Scholar]
- 48.Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE. 1989:257–286. [Google Scholar]
- 49.Forney G., Jr The Viterbi algorithm. Proceedings of the IEEE. 1973;61(3) [Google Scholar]
- 50.Gao Y, et al. Query-by-example surgical activity detection. International journal of computer assisted radiology and surgery. 2016:1–10. doi: 10.1007/s11548-016-1386-3. [DOI] [PubMed] [Google Scholar]
- 51.Aharon M, et al. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans on Signal Processing. 2006;54(11):4311–4322. [Google Scholar]
- 52.Tsochantaridis I, et al. Large margin methods for structured and interdependent output variables. J Mach Learn Res. 2005;6:1453–1484. [Google Scholar]
- 53.Joachims T, et al. Cutting-plane training of structural svms. Machine Learning. 2009;77(1):27–59. [Google Scholar]
- 54.Shi Q, et al. Human action segmentation and recognition using discriminative semi-markov models. International Journal of Computer Vision. 2011;93(1):22–32. [Google Scholar]
- 55.Wang H, et al. Action recognition by dense trajectories. IEEE Conference on Computer Vision and Pattern Recognition. 2011 [Google Scholar]
- 56.Sutton C, Mccallum A. Introduction to conditional random fields for relational learning. MIT Press. 2006 [Google Scholar]
- 57.Felzenszwalb P, Huttenlocher D. Pictorial structures for object recognition. International Journal of Computer Vision. 2005;61(1):55–79. [Google Scholar]
- 58.Lacoste-Julien S, Jaggi M. Block-coordinate frank-wolfe optimization for structural SVMs. International Conference on Machine Learning. 2013 [Google Scholar]
- 59.Lea C, et al. Learning convolutional action primitives for fine-grained action recognition. ICRA. 2016:1642–1649. [Google Scholar]
- 60.Rupprecht C, et al. Sensor substitution for video-based action recognition. IROS. 2016:1–8. [Google Scholar]
- 61.Csurka G, et al. Visual categorization with bags of keypoints. European Conference on Computer Vision. 2004 [Google Scholar]
- 62.Sivic J, Zisserman A. Video google: A text retrieval approach to object matching in videos. IEEE International Conference on Computer Vision. 2003:1470–1477. [Google Scholar]
- 63.Laptev I. On space-time interest points. International Journal of Computer Vision. 2005;64:107–123. [Google Scholar]
- 64.Willems G, et al. An efficient dense and scale-invariant spatio-temporal interest point detector. European Conference on Computer Vision. 2008 [Google Scholar]
- 65.Chaudhry R, et al. Histograms of oriented optical flow and binetcauchy kernels on nonlinear dynamical systems for the recognition of human actions. IEEE Conference on Computer Vision and Pattern Recognition. 2009 [Google Scholar]
- 66.Wang H, et al. Evaluation of local spatio-temporal features for action recognition. British Machine Vision Conference. 2009:1–11. [Google Scholar]
- 67.Zhang J, et al. Local features and kernels for classification of texture and object categories: A comprehensive study. International Journal of Computer Vision. 2007;73(2):213–238. [Google Scholar]
- 68.Yu JYK, et al. Linear spatial pyramid matching using sparse coding for image classification. IEEE Conference on Computer Vision and Pattern Recognition. 2009:1794–1801. [Google Scholar]
- 69.Mairal J, et al. Online dictionary learning for sparse coding. Proceedings of the 26th Annual International Conference on Machine Learning. 2009:689–696. [Google Scholar]
- 70.Martin A. A metric for ARMA processes. IEEE Trans on Signal Processing. 2000;48:1164–1170. [Google Scholar]
- 71.Cock K, Moor B. Subspace angles and distances between ARMA models. System and Control Letters. 2002;46:265–270. [Google Scholar]
- 72.Vishwanathan S, et al. Binet-Cauchy kernels on dynamical systems and its application to the analysis of dynamic scenes. International Journal of Computer Vision. 2007;73:95–119. [Google Scholar]
- 73.Afsari B, et al. Group action induced distances for averaging and clustering linear dynamical systems with applications to the analysis of dynamic visual scenes. IEEE Conference on Computer Vision and Pattern Recognition. 2012 [Google Scholar]
- 74.Doretto G, et al. Dynamic textures. International Journal of Computer Vision. 2003;51:91–109. [Google Scholar]
- 75.Scholkopf B, Smola A. Learning with kernels. MIT Press; 2002. [Google Scholar]
- 76.Lea C, et al. Segmental spatiotemporal cnns for fine-grained action segmentation. ECCV. 2016:36–52. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.