Global energy gradients and size in colonial organisms: Worker mass and worker number in ant colonies

Abstract

Body mass shapes processes from cell metabolism to community dynamics. Little is known, however, about how the average body mass of individuals varies among ecological communities. Ants alter colony mass by independently changing worker mass and/or worker number. In a survey of 49 ecosystems from tundra to tropical rainforest, average worker mass and worker number were uncorrelated (r_s = 0.2, P > 0.14) and varied 100-fold. Data supported the hypothesis that higher mean monthly temperatures, T, reduce worker mass by increasing metabolic costs during worker development. In contrast, worker number was unimodal over a 1,000-fold gradient of net primary productivity (NPP, g of carbon per m² per yr), a measure of organic carbon available to consumers. At the lowest levels of NPP colonies appeared to be carbon-limited; above 60 g of carbon per m² per yr average worker number decreased to a global low. This decline in worker number with increasing NPP supports the hypothesis that abundant carbon ameliorates the Achilles heel of small taxa in competition with large taxa: their relatively high metabolic demands. Higher predation rates in resource-rich environments may also play a role in limiting worker number. In all, about half the global variation in worker mass and number was accounted for by gradients of NPP and T. Changes in global temperature and rainfall may thus mold gradients of ectotherm size, with consequences for the structure and function of the ecosystems.

Body size can fundamentally shape an organism's ecological niche (1–6), a population's rate of evolution (7–10), and an ecological community's structure and function (4, 11–14). Given its role as a linchpin of functional biology, understanding how and why body size varies globally is a key challenge to ecology. Solar energy may shape gradients of body size by its effects on local temperature and net primary productivity† (16–20). Rising global temperatures (21, 22) give new import to understanding these effects. Progress toward that goal has been hampered by the lack of global size data from a set of communities experiencing the full range of solar energy.

Ants (family Formicidae) are colonial ectotherms that are important players in every terrestrial biome from tundra to rainforest (19, 23) and whose distribution thus spans global gradients of NPP and T. Studies of body size regulation in unitary organisms typically focus on the number and size of cells in an individual (18). Studies of size in colonial organisms such as bryozoans, corals, and the social insects, in contrast, focus on the mass and number of a colony's subunits (24, 25). Ant colonies have two life history options, under separate control, for increasing their mass: adding workers and increasing worker mass.

Here I quantify the average worker mass and worker number of colonies in 49 New World ant communities. I explore how four energy-based hypotheses that sometimes make opposite predictions account for geographical gradients in these two variables. The four hypotheses describe the harvesting of resources, developmental constraints on growth, and adaptive responses to a basic life history tradeoff.

On Fueling a Colonial Ectotherm

One limit to size is the rate at which an organism can harvest resources. Solar energy shapes the harvest rate of ectotherms in at least two ways (19). First, it colimits NPP [along with water supply (26)] to generate gradients of harvestable energy available for consumers. The resource-harvest hypothesis (27, 28) posits that an organism's maximum size is ultimately limited by this fundamental supply rate. For an ectotherm, however, ample resources are useless without warm temperatures that allow their harvest (29). In the temperature-harvest hypothesis (19, 30, 31), harvest rates increase with T and harvest rates limit size [i.e., the Q₁₀ (ratio of rates over a 10°C increase in temperature) for ant foraging is >0].

Combined, the harvest hypotheses suggest that the kinetic energy reflected by T provides access to the potential energy of NPP. They predict that the average size of an ectotherm should increase with ecosystem NPP, and for a given NPP, average size should increase with T. Within ant colonies, both worker mass (32, 33) and number (32, 34) have been shown to increase with food supply. Likewise, ants are thermophilic (19, 25, 35): colonies tend to send out more foragers with increases in biologically active temperature (≈10–35°C). However, local adaptation may erase such a trend at a geographic scale if, for example, high-latitude populations evolve to forage faster at a given T (36).

On Growing a Colonial Ectotherm

Solar energy can also constrain the way that ectotherms convert harvested resources into body mass. The temperature-growth hypothesis (17, 18, 37–39) operates at the cellular level, focusing on how the construction and breakdown of tissue varies during an ectotherm's ontogeny. von Bertalanffy (17) suggested in 1960 that high temperatures will cause individual ectotherms to mature at a smaller size if Q₁₀ for catabolism > Q₁₀ for anabolism; that is, if T enhances the metabolic release of heat energy faster than the anabolic buildup of new chemical bonds (17, 40). von Bertalanffy's hypothesis has been refined (38, 39) as evidence has accrued showing that the inequality “Q₁₀ catabolism > Q₁₀ anabolism” is more true late in ontogeny, effectively putting a “brake” on growth.

As the metabolic rate of ectotherms can vary 1,000-fold over biologically active temperatures (6) the temperature-growth hypothesis predicts that ectotherm size at maturity will vary inversely and commensurately. Within and across ant species, there is some evidence that the Q₁₀ values of catabolism and anabolism shape worker mass. For example, highly active high-metabolism species tend to produce smaller workers (41). Starved colonies of Solenopsis invicta appear to exploit the Q₁₀ inequality by moving brood to cooler parts of the nest so as to maintain worker mass (42). However, as before, the temperature-growth hypothesis extrapolated to global scales assumes that local adaptation does not alter the Q₁₀ of metabolism.

On When to Stop Growing and Start Reproducing

Another set of constraints predicts a shifting optimal size at maturity. The tradeoff hypothesis (43) contrasts the scaling of two fitness components. The scaling of resource harvest rate in excess of maintenance needs (= mass^0.75) favors large individuals; the rate at which harvested energy is converted to offspring (mass^–0.25) favors smaller individuals. Combined, the two scaling relationships predict an intermediate optimal size [= optimal reproductive power (43)] for a given taxon. Above the optimum, reproductive power is limited by the ability to convert harvested food into offspring; below the optimum, it is limited by the rate at which that food is harvested. Increasing NPP thus relaxes the fundamental constraint for a community's smallest individuals (i.e., resource acquisition rate) and enhances their competitive advantage over larger individuals (43). The tradeoff hypothesis makes the counterintuitive prediction that more food should decrease the average size of individuals in a community.

In colonial organisms the number of subunits is an excellent predictor of maximum reproductive output (24, 25) and is hence an appropriate size metric to evaluate the tradeoff hypothesis. However, the paucity of interspecific data on the scaling of growth and reproduction in ants currently bars testing the assumptions of the tradeoff hypothesis (44).

In sum, four hypotheses that describe the physiology of foraging, growth, and reproduction predict the body size of ectotherms as one moves through gradients of T and NPP. The temperature-growth hypothesis predicts gradients of worker mass; the tradeoff hypothesis predicts gradients of worker number; and both harvest hypotheses describe how resource availability and access constrain the building of more or bigger workers. I simultaneously test these hypotheses, quantifying biogeographic patterns of average worker mass and number/colony. As I shall demonstrate, these hypotheses are not mutually exclusive.

Methods

I sampled the soil ant communities from 49 sites, selecting sites to maximize coverage of the New World NPP gradient (45). Sites were sampled from 1994 through 1997 during seasons of peak ant activity. Ant colonies were counted by using a transect of 30 1-m² plots, spaced every 10 m (19, 46, 47). In each 1-m² plot, abundance was quantified by searching for nests in the soil and litter. Plots were then baited to search for cryptic nests. Workers from each colony in a plot were stored in 95% ethanol; whenever possible the entire colony was collected. I found a total of 434 species nesting across the 49 sites for a total of 665 site–species combinations (45). Vouchers are in the author's collection.

I used a dissecting microscope to measure head lengths of up to five pinned, randomly selected specimens for each species at each site. I estimated mass by using subfamily specific regressions (48). Major workers from dimorphic species, found in only 3 of 82 genera in this study, were not measured, given the scarcity of majors in most nest collections. Worker number (minors plus majors) was estimated when possible from harvested reproductive colonies. When these were not available, I used a value for that species from another site or from the literature (e.g., ref. 34). When no such colony data for that species were available, I used the mean of the log₁₀(worker number) for that genus.

All four hypotheses predict the size distribution of individual colonies. As species could vary more than 10-fold in abundance at a site (45), I calculated community averages of log₁₀ values that were weighted by each species' abundance. Mean monthly temperatures T for each site were calculated from site records or nearby airports. I estimated a site's aboveground NPP from its actual evapotranspiration (45, 49).

Results

Across the 49 ecosystems sampled, the average mass of an ant worker and the number of workers in a colony varied ≈100-fold. Maximal variation in both was found ≈35°N, across a span of ecosystems ranging from warm deserts, grasslands, and evergreen and deciduous forests.

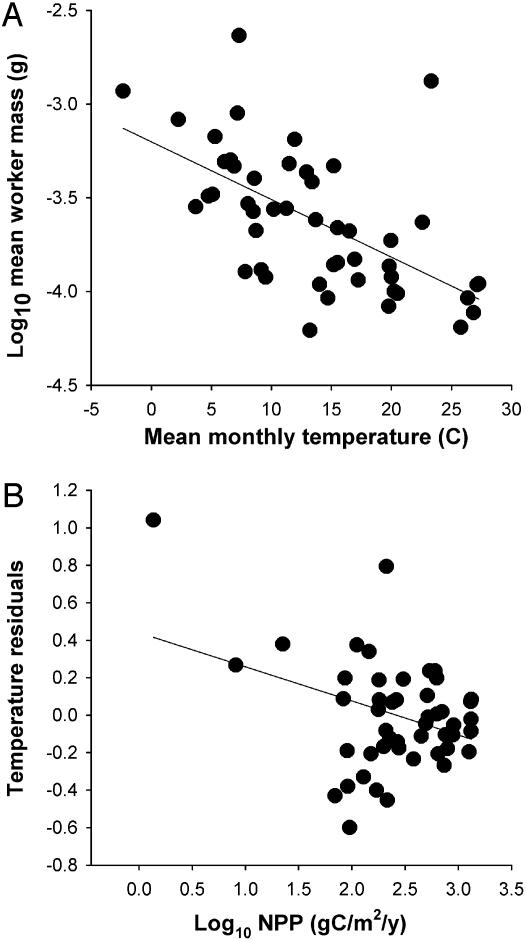
Worker Mass. Average worker mass ranged from 2.34 mg in a montane temperate forest to 0.06 mg in an upland desert. T better accounted for variation in worker mass than log₁₀NPP. log₁₀(worker mass) decreased with T (y = –3.2 – 0.0308x, F_1,48 = 26.24, P < 0.0001, r² = 0.36) as predicted by the temperature-growth hypothesis (Fig. 1A). log₁₀(worker mass) weakly decreased to the quarter power with NPP (y = 0.00098x^–0.251, F_1,48 = 8.29, P < 0.006) but NPP accounted for less than half the variance of T (r² = 0.15).

Fig. 1.

The biogeography of worker mass tracks kinetic and potential energy. (A) Average worker mass across 49 ant communities decreased (partial r² = 0.36) with ambient temperature T. (B) The temperature residuals further decreased (partial r² = 0.08) with NPP, the rate that organic carbon is made available to consumers.

I used a stepwise regression (50) to separate the effects of the two variables (Table 1). Consistent with the tradeoff hypothesis, the temperature residuals of worker mass decreased with NPP^–0.19. This decrease, however, was largely driven by the hypoproductive environments (Fig. 1B), which had larger workers than predicted by temperature alone. Combined, NPP and T accounted for 44% of the variation in worker mass across the New World soil ant communities.

Table 1. Stepwise multiple regressions contrasting the role that T and NPP play in shaping two size measures of an ant colony: the average size of an individual worker ant and the average number of workers per colony.

	Parameter	F	P	Partial r2
log10(worker mass)
Intercept	-2.78	230.7	0.0001
T	-0.03	23.9	0.0001	0.36
log10NPP	-0.19	6.75	0.0126	0.08
			Total r2	0.44
log10(worker number)
Intercept	1.13	0.61	0.0222
log10NPP2	-0.58	27.01	0.0001	0.32
log10NPP	1.79	17.14	0.0002	0.06
T	0.034	12.69	0.0009	0.14
			Total r2	0.52

A second multiple regression, in which community means were unweighted by abundance (i.e., each species' worker mass contributed equally) gave similar results. Worker mass was proportional to 0.23T (partial r² = 0.34), residuals scaled to NPP^–0.17 (partial r² = 0.09) with the model accounting for 43% of the variation in worker number.

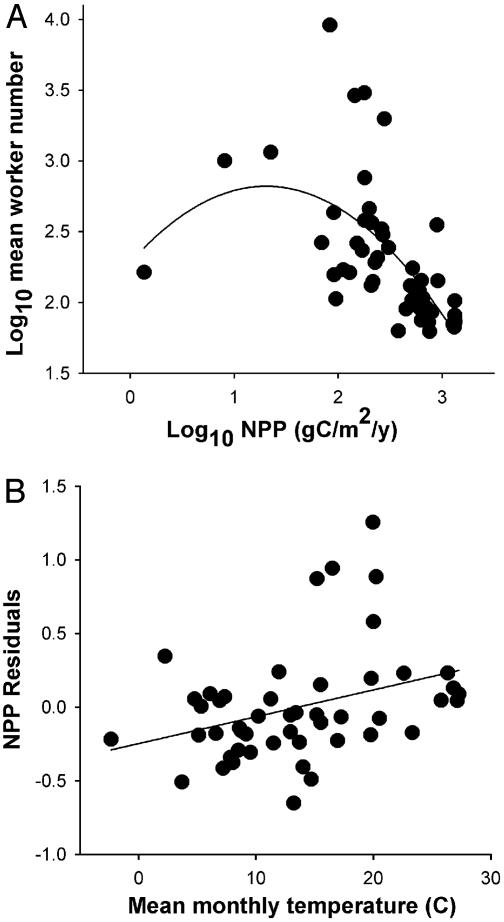
Worker Number. Average worker number varied from 63 workers in a cold temperate pine forest to 9,057 in a hot temperate desert (Fig. 2A). T alone failed to account for any variation in log₁₀(worker number) (r² = 0.01, y = 2.39 – 0.0049x_, P = 0.63, n = 49). The scatterplot of log₁₀(worker number) vs. NPP suggested a unimodal relationship. This possibility was verified by a multiple regression with linear and quadratic terms (Table 1 and Fig. 2 A). log₁₀(average worker number) increased with log₁₀NPP across the least productive deserts (<60 aboveground g of carbon per m² per yr). It decreased thereafter to values ⅕ of the low-NPP minimum (Fig. 2). Consistent with both the resource-harvest and tradeoff hypotheses, NPP first appeared to constrain worker number in the most depauperate environments, then relaxed the harvesting constraint on small colonies as NPP reached its maximum.

Fig. 2.

The biogeography of worker number tracks potential and kinetic energy. (A) Average worker number across 49 communities showed a unimodal relationship (partial r² = 0.39) with NPP, the rate that organic carbon is made available to consumers. (B) Residuals of this relationship increased (partial r² = 0.14) with ambient temperature T.

Furthermore, and consistent with the temperature-harvest hypothesis, the NPP residuals of log₁₀(worker number) increased with temperature (Fig. 2B and Table 1). In particular, a suite of warm shrub and grasslands had larger colonies than predicted by NPP (Fig. 2B). The combined regression model accounted for 52% of the variation in worker number across the New World soil ant communities.

As before, a second multiple regression using community means unweighted by abundance gave results similar to those of the weighted analysis (Table 1). Worker number [= NPP^1.79 – (NPP²)^–0.58, partial r² = 0.47] was a unimodal function of NPP and was further proportional to 0.04T (partial r² = 0.20). This model accounted for 67% of the variation.

Recall that in the absence of reliable worker number data for a species, I substituted worker number values from a congener. To evaluate this potential bias I deleted those species values from each community and recomputed community means. As before, worker number [= NPP^1.61 – (NPP²)^–0.58, partial r² = 0.60] was a unimodal function of log₁₀NPP and was proportional to 0.03T (partial r² = 0.11) with the model accounting for 71% of the variation.

Conclusions

Evidence mounts for climate's role in generating geographic gradients of abundance and diversity (19, 45, 51–53). Perhaps not surprisingly, a variety of mechanisms appeared to shape the two components of size in colonial organisms: the number of units, and their mass. T and NPP, operating through the constraints and tradeoffs experienced by organisms in the field, combine to account for 44–52% of the variation in size found across New World ecosystems (see also ref. 54). Warmer ecosystems were associated with larger colonies of smaller workers; the poorest and richest ecosystems yielded the smallest colonies.

This study takes a pattern already well known from the lab, that ectotherms mature at a smaller size in warmer environments (37), and suggests that it operates globally for ants. However, this pattern applied only to worker mass; the opposite trend appears for worker number. To see why, it is useful to view the temperature-harvest hypothesis as an expression of Q₁₀ of anabolism: higher temperatures allow the harvest of more food and the building of more tissue. When then does Q₁₀ of catabolism predominate in social insects, and when does Q₁₀ of anabolism?

These results suggest that as environments warm, the higher metabolic costs for a growing pupa exceed any benefits achieved from the colony's higher harvest rate. Instead, it appears that these increased resources go into provisioning the queen, whose egg production ultimately limits worker number (55). If this explanation is true, then Q₁₀ of catabolism > Q₁₀ of anabolism at the level of the growing individual, but Q₁₀ of anabolism > Q₁₀ of catabolism at the level of the colony. At present, such working hypotheses require a far better understanding of the role that temperature and resources play in the catabolism and anabolism of social insects, a currently small dataset that suggests many intriguing nonlinearities (32, 44, 55).

For unitary ectotherms, if warmer temperatures during ontogeny lead to a smaller size due to higher metabolic costs, warm temperatures after maturity may allow such individuals to forage more and lay in more reserves for survival and/or reproduction. This possibility suggests one reason why lab-reared Drosophila matured at a smaller size at higher temperatures but compensated with higher lifetime fecundity (56). The Q₁₀ of anabolism exceeded the Q₁₀ of metabolism at maturity.

I know of no other study that shows a unimodal size cline across the 1,000-fold terrestrial NPP gradient. In impoverished warm deserts NPP appears to limit worker number in a fashion shown by three studies of unitary organisms (27, 28, 57). The subsequent decline in worker number beyond 60 g of carbon per m² per yr is consistent with the tradeoff hypothesis of Brown, Marquet, and Taper (43). We focus here on one logical outcome of this hypothesis, that high NPP should ameliorate the cost small individuals pay because of their relatively high metabolism (34, 43), improving their odds in competition with larger taxa. This results, not in a single optimal taxon mass (58, 59), but in a site-specific optimum dependent on local T and NPP.

There is at least one other viable hypothesis for the decrease phase of the unimodal worker number–NPP curve. Predation risk may also increase in more productive ecosystems (60–63). If so, these data are also consistent with hypotheses predicting a smaller optimal size in the face of higher predation pressure (64). Respiration studies and field experiments combining food additions and predator exclosures will help resolve the role of these non-mutually exclusive hypotheses.

If NPP and T generate size gradients across other ectotherm communities, then ecology will have an important mechanism linking the abiotic environment to community structure and function (4, 11–13). For example, temperature increases of 1.4–5.8°C are likely over the next 90 years (65). Cautious extrapolation suggests that the average mass of ant workers in a community may decrease 9–31% through some combination of phenotypic plasticity, natural selection, and species sorting. Furthermore, as ant species with small workers appear to be particularly successful invasives (66), ant invasions, already destructive (5, 67), may be more common in a warming world.

Finally, the ubiquity and mechanisms of Bergmann's rule, the positive correlation between size and latitude, has generated heat but little consensus (16, 18, 19, 37, 38, 68–70). In this study, ant worker mass shows Bergmann's rule (r_Pearson = 0.60, P < 0.0001, n = 49) because (i) there is a mechanism for enhancing size (the temperature-growth hypothesis) and (ii) T and latitude are strongly correlated (r_s = –0.86 across the 49 sites). Worker number, in contrast, weakly expresses Bergmann's rule (r_Pearson = 0.26, P = 0.07) because NPP is only weakly correlated with latitude across our sites (r_s =–0.37) and because it is a unimodal relationship. Tests for clines in size absent hypotheses for their mechanism can lead to confusion (e.g., an investigator can find a positive, negative, or null relationship between NPP and worker number depending on the portion of the NPP gradient studied). Furthermore, perhaps the variety of results from the literature on the biogeography of size arises from the fact that temperature gradients can favor increases in one component of size and decreases in another. By testing multiple hypotheses incorporating multiple causal factors for multiple size components, perhaps we can move beyond the question “How prevalent is Bergmann's rule?” to the much more interesting “How and why do size gradients arise?” (14, 38, 71, 72).