Structure theorems and the dynamics of nitrogen catabolite repression in yeast

Abstract

By using current biological understanding, a conceptually simple, but mathematically complex, model is proposed for the dynamics of the gene circuit responsible for regulating nitrogen catabolite repression (NCR) in yeast. A variety of mathematical “structure” theorems are described that allow one to determine the asymptotic dynamics of complicated systems under very weak hypotheses. It is shown that these theorems apply to several subcircuits of the full NCR circuit, most importantly to the URE2–GLN3 subcircuit that is independent of the other constituents but governs the switching behavior of the full NCR circuit under changes in nitrogen source. Under hypotheses that are fully consistent with biological data, it is proven that the dynamics of this subcircuit is simple periodic behavior in synchrony with the cell cycle. Although the current mathematical structure theorems do not apply to the full NCR circuit, extensive simulations suggest that the dynamics is constrained in much the same way as that of the URE2–GLN3 subcircuit. This finding leads to the proposal that mathematicians study genetic circuits to find new geometries for which structure theorems may exist.

As microarray technology has brought systems biology to the theater, the desire to understand gene regulatory networks has brought mathematical modeling to center stage. Recent work has focused on two goals: the determination of recurring network motifs (1) followed by an understanding of their design significance through an analysis of their dynamics (2, 3). Thus, it is now a central objective in mathematics, neuroscience, molecular biology, and medicine to understand how and to what extent the structure of the connections between the components of a system determine its dynamic behavior. We refer to mathematical results that relate these two properties as structure theorems. Our impression is that this body of work has received insufficient attention from biologists, bioinformaticians, engineers, and physicists pursuing gene regulatory networks. The aim here is to demonstrate through an important example, the process of nitrogen catabolite repression (NCR) in yeast, the power of the theory, its current limitations, and some promising new directions.

Fig. 1 shows a circuit of five genes whose dynamics ultimately control NCR in yeast. Although much is known about the architecture of the NCR circuit and the interactions among its components, quantitative models do not exist, and neither a molecular-level nor a systems-level understanding is at hand.

Fig. 1.

The NCR circuit. Green arrows indicate up-regulation; blunted red arrows represent down-regulation at the level of transcription. Dashed lines indicate a weaker response. Blue lines indicate repression that is not at the transcriptional level. A subset of the connections are numbered, and these are referred to in the text. Arrow 10 indicates up-regulation of DEH1 by GAT1.

The power and promise of the structure theorem approach is to be able to infer dynamics from a (possibly annotated) graph of biological interactions, like that shown in Fig. 1. One of the earliest structure theories, called the chemical reaction network theory, was developed by M. Feinberg (4, 5). This theory provides a classification of the dynamics of chemical reaction networks based on the associated circuit diagram. This method is completely scalable because the results depend only on the possible reactions and not on the number of elements, nor on any particular assignment of reaction rates. Recent work indicates that the results of the theory can be obtained by using symbolic computations and computer algebra (6). What is gained by this approach is that the dynamics of extremely large chemical reaction systems is readily computable in a manner that completely avoids numerical simulation of the underlying differential equations. Unfortunately, the theory is based on mass action kinetics that are not sufficiently general for modeling signal transduction/gene regulatory circuits.

Feedback control is ubiquitous in biological systems and gene regulation and is clearly present in the NCR circuit of Fig. 1. Cyclic feedback systems represent an important class of models with nearest-neighbor interactions where the nodes lie around a circle. If these connections are unilateral and monotone, Mallet-Paret and Sell (7) have shown that all solutions converge to either an equilibrium or a periodic orbit. This theorem is the so-called Poincare–Bendixson theorem for monotone cyclic feedback systems. On a coarse level, the overall structure of the global dynamics of cyclic feedback systems is well understood, even if one relaxes the monotonicity assumption (8). However, in this case, chaotic dynamics are possible. The NCR circuit is not a cyclic feedback system, and results for this more general, but obviously important, circuit geometry are lacking.

By now it is well accepted that even simple dynamical systems can have extremely complicated or chaotic asymptotic states. Thus, it is of great interest to be able to understand whether such behavior is possible given a particular circuit topology. A class of systems, where almost all solutions converge to equilibria, are competitive and cooperative systems (9–12). These systems belong to the more general class of monotone systems (13),†† that include dynamical systems generated by parabolic partial differential equations (14, 15) and delay-differential equations. Although the full NCR circuit is not monotone, it contains subcircuits, such as that regulating the GLN3 gene product, Gln3p, that are. Notice that the URE2–GLN3 subcircuit is independent of the remainder of the NCR circuit. Thus, a reasonable first step is to understand the dynamic behavior of the GLN3 gene and the Ure2p-dependent gating mechanism.

These comments provide the motivation for the work described here. We introduce a biologically motivated, conceptually simple, but mathematically complex, model for the URE2–GLN3 subcircuit that governs the switching behavior of the circuit as a whole. This model is based on delay-differential equations and can be naturally scaled to describe the full NCR circuit. Furthermore, we explicitly state the qualitative mathematical assumptions that are necessary for the analysis of the URE2-GLN3 subcircuit and refer to experimental data that support these assumptions.

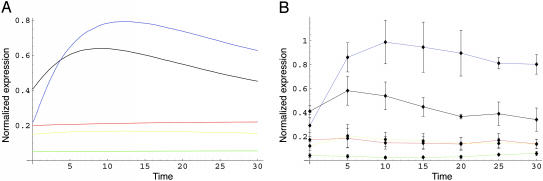
Our results contain a description of a rigorous mathematical analysis of the URE2-GLN3 subcircuit (the proofs of which appear in Supporting Appendix, which is published as supporting information on the PNAS web site). The main results, described in Theorems 1–4, show that if the time for nuclear transport is small compared with that of the cell cycle, then the dynamic behavior of both mRNA and protein species within this subcircuit will consist of periodic oscillations where the period is an integer multiple of the cell cycle. By using our model, we have numerically simulated the full NCR circuit and compared it with an experimental mRNA expression time-series for the same process (see Fig. 2). The strong qualitative and quantitative fit provides at least partial validation for our model.

Fig. 2.

mRNA expression from simulation of System 8 and from experiment with yeast strain BY4743, after a switch from good to poor nitrogen. Blue is Dal80, black is GAT1, red is GLN3, green is URE2, and yellow is DEH1. The time axis is in minutes. These data compare favorably; the key features are the relatively constant GLN3 levels, fast rise in the DAL80, and the crossing of the DAL80 and GAT1 curves in the first few minutes after the switch.

NCR and the URE2–Gln3 Subcircuit Model

All living organisms require nitrogen as a basic building block of biomolecules, such as proteins and nucleic acids. NCR is the physiological process by which Saccharomyces cerevisiae selectively uses good nitrogen sources (glutamine, asparagine, and ammonia in some strains) in preference to poor ones (allantoin, proline, and urea). NCR-sensitive gene expression is mediated by the regulatory circuit shown in Fig. 1 (16, 17). In the presence of excess nitrogen (a good nitrogen source in adequate supply), transcription of genes encoding the proteins needed to transport and degrade poor nitrogen sources occurs at only very low levels; it is, if you will, “repressed.” Conversely, when the amount of a good nitrogen source becomes limiting, or only poor nitrogen sources are available, the genes needed for their transport and catabolism are transcribed. Excellent supporting evidence for this fact is demonstrated in the work of Lee et al. (1), where that study failed to detect the NCR circuit, precisely because it was off under the experimental conditions of a rich nitrogen supply they used. The NCR circuit is a complex switch, much of whose sensitivity and range remains unexplored. To model the most basic nitrogen state dependency, we introduce a binary variable N = 0 in good nitrogen source and N = 1 in a poor nitrogen source that accounts only for the extreme on and off characteristics of the switch.

The transcription factors Gln3p, Gat1p, Dal80p, and Deh1p are all from the GATA family of zinc-finger DNA binding proteins, i.e., they recognize and bind GATA containing cis-acting elements. Because they all recognize similar or indistinguishable sequence motifs, it is proposed that they act in concert at the same promoter by competition (16, 17). A quantitative model of their joint gene regulatory interaction has not been described. It is known that the repressors DAL80 and presumably DEH1 bind both as homodimers and heterodimers, and it is believed that their affinity for the DNA is greater than for the monomeric activators GLN3 and presumably GAT1, but no clear measurements have been reported. Gln3p and Gat1p recognize individual cis-acting elements, whereas Dal80p requires two appropriately spaced and oriented cis-acting elements. As a first approximation to model the competition among the GATA factors at the relevant promoters that incorporates an excluded volume effect, we introduce the fraction of nuclear activators f(t) that is defined as the ratio of the sum concentrations of Gln3p and Gat1p over the sum of the concentration of all four transcription factors.

An important feature of NCR is the URE2-dependent gating mechanism that keeps the circuit repressed in a good nitrogen source, which is depicted by the blunted blue arrows labeled 1 and 2 in Fig. 1. There is convincing evidence (17–24) to suggest that Gln3p and, to a lesser extent, Gat1p are sequestered in the cytoplasm in complex with Ure2p, and it is hypothesized that the aggregation of the complex is driven by nitrogen state-dependent phosphorylation. Under conditions of excess nitrogen, the Gln3p and Gat1p proteins are suggested to be phosphorylated and are found to be bound to Ure2p in the cytoplasm, although the precise mechanism is not understood (17–24). There is good evidence supporting the direct physical interaction of Gln3p with Ure2p; there is less direct evidence of a complex with Gat1p. In a nitrogen-poor environment, or in rapamycin-treated cells, the cytoplasmic Gln3p and Gat1p proteins move into the nucleus where they activate transcription at the GAT1, DAL80, and DEH1 genes (17, 19–22). It is natural to model this process as a bimolecular interaction of Ure2p with Gln3p to form a protein–protein complex C, with rate constants that depend on the nitrogen state variable N. As a first approximation, we assume no back reaction in the two different nitrogen states. If N = 0, then

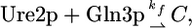and if N = 1, then

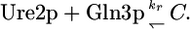Compartmentalization is a key feature of living organisms. The Ure2p-dependent gating of cytoplasmic Gln3p, but not nuclear Gln3p, demonstrates that a compartmental description is both natural and necessary. Because we are considering yeast, we include cytoplasmic and nuclear compartments and consider explicitly the transport of transcription factors and mRNA between them. We model transport with time delays rather than as convection or diffusion. The transport time delays reflect an average time spent in conveyance, in a compartment, between nucleus and cytoplasm. We begin with the assumption that this process can be modeled with a single time delay, τ, that may vary from protein to protein. Once the mass in transit has reached the nuclear pore complex, a well described mechanism involving karyopherins transports the cargo in or out. In our model, we denote by K_imp(·) and K_exp(·) a pair of concentration-dependent nuclear import and export rate functions.

There are two removal mechanisms operative on both mRNA and protein, dilution due to volume growth and degradation. Volumetric growth around a cell cycle has been measured (25, 26) in bacteria and budding yeast and is found to be exponential. The observed exponential growth rate means that the rate at which macromolecules are removed by dilution is accurately modeled by a linear decay term. Most of the experimental evidence of mRNA and protein decay is well described by single exponential decay (27, 28). There has been a growing appreciation for nontranscriptional control mechanisms. In the NCR circuit, an operative mechanism of control is nitrogen state-dependent control of degradation rates. The mechanism for enforcing this control is not understood, but its existence has been demonstrated (29). In the model, we let α, β, γ, θ, and κ represent degradation rate constants that may depend on the nitrogen state N.

The GLN3 and URE2 genes are believed to be constitutively expressed. We therefore let the parameters r_g, r_u denote the constitutive production rate of GLN3 and URE2 mRNA. Following Mahaffy (30), we introduce a function S(t) that takes into account the cell cycle: the continuous exponential growth in volume of the budding yeast, and discrete exponential increase in the genes due to replication of the DNA. It is well known that time delays are involved and important in both transcription and translation. Notice that because of the constitutive production rate, there is no apparent transcriptional time delay for these two genes. We denote by T(·) a concentration-dependent translation initiation rate function and denote by δ a delay that takes into account the elongation and folding of the nascent protein.

Letting x represent nuclear Gln3p, letting X and U represent GLN3 and URE2 mRNA, respectively, and finally letting ξ and μ represent cytoplasmic Gln3p and Ure2p, respectively, we formulate the following differential delay model for the URE2–GLN3 subcircuit:

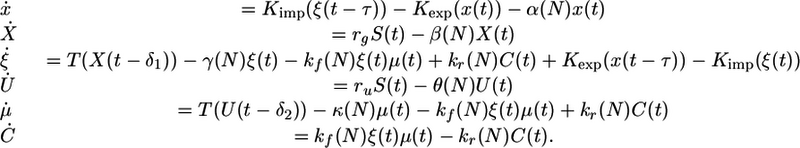[1]

The variables of our model, x, X, μ, etc., describe the concentrations of the relevant protein or mRNA species, not necessarily in a single cell but in a small aggregate of synchronously dividing cells. Although budding yeast can be synchronized by a variety of means, including the mating pheromone α-factor, this intervention is not absolutely necessary, because it can be observed by microscopy that a single yeast will induce a small clump of synchronously dividing cells for several generations, and thus the model predictions can be compared with experiment.

Qualitative Assumptions and Experimental Data

The results in Theorems 1–4 that describe the asymptotic dynamics of System 1 rest on a few simple assumptions that we now spell out explicitly. We want to emphasize that these assumptions are qualitative in nature and do not depend on the particular form of the functions involved, nor on the particular values of the parameters and constants. This consideration is extremely important in modeling a circuit where the quantitative values of many of the rate constant have not been established. However, as we argue below, there is ample evidence that our qualitative assumptions are valid.

1. The transport rate functions K_imp and K_exp are required to be positive and monotonically increasing functions that are bounded from above. The rate of the nuclear transport process as a function of concentration has been measured in vitro (31), and these data fit a simple model function K(a, b, c, x) = [ax(1 + bx)]/(c + x) with parameter values a = 60, b = 0.03, and c = 4 when the protein concentration variable x is expressed in micromoles. This function satisfies all of the assumptions save boundedness. These measurements were made in vitro, free of competitive intracellular clutter, and only over a finite concentration range; thus, it is not surprising that the rates were not observed to saturate. We are left to make the reasonable assumption that the transport rate is bounded from above; that is, given a large enough concentration of protein, the nuclear pore complex will reach a state at which it cannot translocate matter any faster.

2. The mass action kinetics term for the aggregation rate of the Gln3p–Ure2p complex, k_f(N)ξ(t)μ(t) can be of a more general functional form, k_f(N)g(ξ(t), μ(t)). The only requirement is that the partial derivatives of the rate function g(·, ·) are positive.

3. The translation initiation rate function T is required to be positive. Translation initiation rates as a function of concentration have been measured in vitro for yeast (32) and are well described by the function T(a, c, x) = ax²/(c + x) with the measured parameter values a = 0.1 and c = 0.26; x represents mRNA concentration expressed in micromoles.

4. The right-hand sides of System 1 need to be at least C¹. This restriction is a technical assumption that is biologically plausible. The only place that caution is required is in the cell-cycle function S(t) that might involve a discontinuity associated with the cell division. This discontinuity can be approximated arbitrarily well by a smooth function.

Results

Our main result guarantees that when the nitrogen source is switched from a good source to a poor one, or vice versa, the dynamics of the URE2–GLN3 subcircuit typically converges to a periodic solution that is in synchrony with the cell cycle. The solutions can be subharmonic, that is, periodic with a period that is a multiple of the cell cycle, but this multiple is bounded above by some integer m. By “typically,” we mean that such behavior occurs for an open and dense set of initial conditions. One consequence of these results is that chaotic dynamics and quasiperiodic dynamics, although possible, are unstable and thus will not be observed in real systems. To facilitate continuity of presentation, most of the technical details, including definitions and proofs, are compiled in Supporting Appendix.

The first observation is that one can solve explicitly for X(t) and U(t),

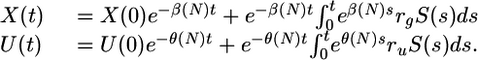[2]

Because S(t) is periodic in time, then X(t) → X̄(t) and U(t) → Ū(t) as t → ∞, where both X̄(t) and Ū(t) are periodic functions of time.

Switch from Good to Bad Nitrogen Source. First, consider the case when at t = 0 the system switches from a good nitrogen source to a poor nitrogen source (N → 1). In this case, System 1 reduces to the following nonautonomous system of delay differential equations:

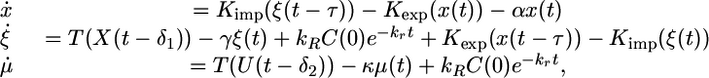[3]

where X(t), U(t) are as in System 2.

System 3 is an asymptotically periodic system of differential delay equations. Indeed, as t → ∞, this system asymptotically approaches the system

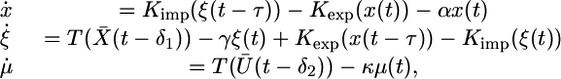[4]

where X̄(t) and Ū(t) are the periodic functions defined above.

Notice that the μ equation decouples from the first two equations and can be solved explicitly

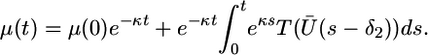Now we consider the remaining system,

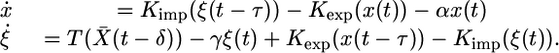[5]

Let r be the minimal period of the function S(t) that is also the minimal period of the functions X̄(t) and Ū(t). Then, System 5 is an r-periodic system of delay-differential equations. System 5 has the additional important property that if an initial condition has each of its components nonnegative, then this property will remain unchanged along the entire solution for all t ≥ 0. Therefore, we can restrict our phase space the biologically relevant to positive cone 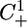of the Banach functions space of continuous from the interval [–τ, 0] to the plane R², denoted C([–τ, 0], R²), which is the relevant phase space for delay differential equations like System 5.

Let T(t, t₀, w₀) be the solution of System 5 with initial condition T(t₀, t₀, w₀) = w₀. Standard results guarantee existence and uniqueness (13, 33). One typical way to attack problems of this type is to consider the behavior of a map that is defined by looking at the value of a solution at regular time intervals. Let 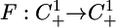be such a time r solution map of the System 5, i.e.,

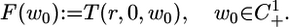The superscript in C¹₊ represents the fact that 5 is a system where N = 1. We can now state the result.

Theorem 1. Assume that the length of the period of the cell cycle is at least twice as long as the transport delay associated with nuclear import. Then, typically the solution to System 5 will converge to a periodic orbit with a period equal to a multiple of the cell-cycle period. More concisely, if r ≥ 2τ, then there exists a positive integer m and an open dense set of initial conditions 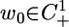, such that T(t, t₀, w₀) converges to a periodic orbit with period equal to sr for some integer s ≤ m.

Although we know of no direct experimental measurements of nuclear import/export time delays for the NCR-circuit genes, there are several indirect measurements to estimate τ. The mRNA expression profiles shown in Fig. 2 support the conclusion that τ ≤ 6. Furthermore, the data in figure 6 of ref. 23 show that the nuclear accumulation of a GLN3-GFP construct is no slower than 6 min. This value of τ is significantly smaller than half the cell cycle (72 min), and thus the physical systems satisfy the assumptions of the theorem.

This result holds not only for System 5 but also for System 4, because the explicit solution μ(t) can be appended to any solution x(t), ξ(t) of 5. We now extend the result for 4 to the full nonautonomous System 3.

Theorem 2. Consider 3 and assume that all of the invariant sets of 4 are hyperbolic. Then the set of points (t₀, w₀) 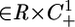such that T(t, t₀, w₀) converges to a single periodic orbit with a period sr, s ≤ m, contains an open and dense set.

Switch from Poor to Good Nitrogen Source. Now we consider the case when at t = 0, the system switches from a poor to a good nitrogen source (N: 1 → 0). In this case, we get the following nonautonomous system of delay differential equations:

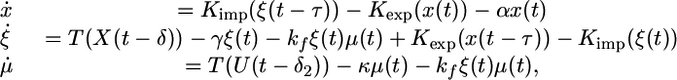[6]

where X(t) and U(t) are as in 2.

System 6 is again an asymptotically periodic system of differential delay equations. As t → ∞, this system asymptotically approaches a system

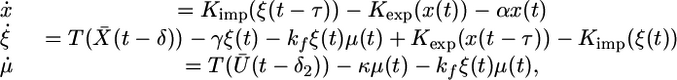[7]

where X̄(t) and Ū(t) are periodic functions as defined above. In this situation, the μ equation is coupled to the first two equations and cannot be solved independently. However, we can still use the same approach as before. System 7 admits a positively invariant positive cone C⁰₊ of the Banach space of continuous functions from the interval [–τ,0]to R³, denoted C([–τ, 0], R³), which is the relevant phase space for 7. Let U(t, t₀, w₀) denote the solution of System 7, consider the time r solution map of System 7 mapping 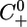into 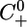. We have the following analogous results.

Theorem 3. Assume that the length of the period of the cell cycle is at least three times as long as the transport delay associated with nuclear import. Then, typically the solution to 5 will converge to a periodic orbit with period equal to a multiple of the cell-cycle period. More concisely, if r ≥ 3τ, then there is an open and dense set of initial conditions 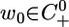such that U(t, t₀, w₀) converges to a single periodic orbit with period equal to a multiple of r.

Theorem 4. Consider the full System 6 and assume that all of the invariant sets of System 7 are hyperbolic. Then the set of points (t₀, w₀) 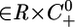, such that U(t, t₀, w₀) converges to a single periodic orbit with period equal to some multiple of r, contains an open and dense set.

Simulation and Experiment. A simple model for the full NCR circuit, which is a natural extension of System 1, is presented in Supporting Appendix. Given the specific choices of functional forms and parameter values described in the previous section and additional reaction terms for the action of the DAL80, GAT1, and DEH1 promoters that are described in Supporting Appendix, we have performed numerical simulations of the full system.

Fig. 2 describes the system after having been subjected to a change from a good to a poor nitrogen source at time t = 0. The units of time are minutes, and concentrations are in micromoles. Fig. 2 Left depicts the simulation of our model equations (see Supporting Appendix), and Fig. 2 Right shows the results of the experiment. Briefly, yeast strain BY4743 was grown in glucose–glutamine medium and switched to glucose–proline medium. Aliquots were taken every 5 min, and total RNA was isolated. mRNA levels of the five NCR genes plus ACT1 were measured by RNase protection assays. Gels were quantitated by phosphorimaging, and the data are reported as actin-normalized ratios. (Complete materials and methods appear in Supporting Appendix). Our simulation results compare very favorably with an experimentally measured mRNA expression profile, with regard to several key features: the rapid rise of DAL80, the crossing of the DAL80 and GAT1 curves inside of 5 min, and the near constancy of the remaining three species.

Discussion and Conclusion

Understanding the dynamics of genetic circuits, and in general understanding how nature engineers robustness in the face of complexity, is a central interdisciplinary challenge. We have proposed a conceptually simple, experimentally motivated mathematical model for the NCR circuit, in the yeast S. cerevisiae. We have been able to analyze the behavior of an important independent subcircuit that governs the switching behavior of the circuit as a whole. Our results predict that the behavior of the subcircuit will be oscillation of both mRNA and protein species that is in synchrony with the cell cycle. This oscillation will be harmonic or subharmonic to the cell-cycle oscillation. These results are based on very general, qualitative assumptions about the monotonicity of certain reaction terms and do not depend on particular parameter values nor on the specific functional forms used in the model. As such, this finding is a significant extension to earlier work by Mahaffy and coworkers (30, 34). Furthermore, simulations of the full system model agree well with mRNA expression data.

There are two immediate observations concerning the mathematical results. First, in a mammalian cell without cell division, the function S(t) would be constant. Under these conditions, our results show generic convergence to equilibria, which highlights an obvious distinction between constitutive gene expression in bacteria and yeast vs. mammalian tissue. Second, if the genes for the different species in the circuit are replicated at different times in the cell cycle, then the corresponding function S(t) for the different loci will still have the same period but will differ in phase. This modification also does not affect our results.

The role of thermal fluctuations and noise has received considerable attention (35–37). Some of the dispersion in expression that is commonly attributed to random fluctuations can in fact be explained by the inhomogeneous distribution of variables such as cell cycle or age (38). Nevertheless, it is clear that any structure theorems approach based on deterministic differential equations must be augmented with an analysis of the perturbing effects of random thermal fluctuations. However, because our results concern the behavior for a generic set of initial conditions, it is expected that these results will persist when subjected to small amounts of noise (39).

It is postulated (17) that after the switch to a poor nitrogen source, the NCR system quickly reaches an equilibrium. How rapidly the yeast nitrogen system can or should respond to fluctuations in nitrogen source is not understood, and, to our knowledge, no measurements have been reported. There are additional aspects of the NCR circuit that have proven to be difficult to measure, and a quantitative model such as ours may contribute new biological insight. For instance, it is not known whether Gln3p is degraded in the nucleus and/or whether it cycles into and out of the nucleus. Also, it is not clear whether and how GAT1 is gated by URE2. An analysis of experimental mRNA expression profiles (see Fig. 2) indicate that GAT1 and DAL80 mRNA rapidly increase to near-maximal levels within a few minutes of shifting from glutamine to proline medium. Under the same conditions, the mRNA levels of the remaining three genes remain nearly constant. It is interesting to look at data in Fig. 2 from the point of view of computational biology and ask whether it would be possible to algorithmically (40) reconstruct the graph of Fig. 1 from the data. Because the levels of GLN3 mRNA remain relatively constant, whereas the DAL80 and GAT1 levels rapidly rise, the answer is probably not. Even with proteomics data implicating a Ure2p–Gln3p interaction, it would be difficult to distinguish between the many different network structures that are compatible with Fig. 2B. This observation indicates the importance of both the detailed experimental investigation of the physiological process of NCR as well as the importance of quantitative modeling of the NCR circuit. These observations, coupled with the fact that large-scale network elucidations like those performed in ref. 1 have failed to find the NCR circuit diagram, indicate that the NCR circuit provides a demanding benchmark for those pursuing cellular network inference.

The full NCR circuit is not monotone and thus not currently amenable to the same sort of analysis as was successfully applied to the URE2–GLN3 subcircuit. However, numerical and biological observations indicate a lack of complicated dynamics. This conclusion is precisely what one expects for cyclic feedback systems. Although we cannot claim to understand the full system, several observations can be made that suggest promising directions of ongoing research.

The first observation is that both GLN3-GAT1 and GLN3-DAL80 subcircuits are monotone cyclic feedback systems, either positive (GAT1) or negative (DAL80). Existing mathematical results (7) imply the existence of an integer-valued Lyapunov function for the period map. In a system with constant S(t), this result implies that all solutions converge to either a periodic solution or a set of equilibria. The extension of this result to time periodic S(t) is an important question for mathematical research. A second observation concerns the GLN3-GAT1-DAL80 subcircuit. If we remove the autoregulatory interactions from the graph, then this system forms a single loop feedback system. The same results about the dynamics now apply to this negative monotone feedback system, and interesting questions arise as to the behavior of this subcircuit with weak autoregulatory interactions.

The perturbation provided by DEH1 is also both biologically and mathematically intriguing. It is known experimentally (17) that the interaction of DEH1 with the other components of the NCR circuit are an order of magnitude weaker and thus can be interpreted to represent a perturbation. We do not understand the biological or the mathematical reason for the inclusion of this particular interaction in the circuit. Speculating, one might suggest a noise-filtering mechanism; however, simulations of the full circuit vs. simulations of a DEH1-deleted circuit with and without Gaussian white noise are virtually indistinguishable. One of the intriguing postulates put forward in ref. 2 is that (auto)repression allows an organism to speed transcriptional response times by allowing the organism to couple a strong promoter with a mechanism to prevent overexpression. Therefore, it is interesting to observe that DEH1 down-regulates only DAL80 and that from our experimental measurements (Fig. 2B) it is clear that DAL80 has the fastest and largest transcriptional response in the circuit. Thus, it is possible that the introduction of additional DAL80-independent repression at the DAL80 locus has allowed that promoter strength to increase and increase the NCR response time. Because DEH1 is larger than DAL80, a final possibility that is not mutually exclusive of those above is that DEH1 provides additional combinatorial control. Because of the spacing requirements for DAl80 cis-acting elements, it is quite likely that the three distinct dimer species have different optima, which allows for finer control of downstream expression.

We believe that evolution has selected gene circuit structure so that the response of the circuit is predictable for a wide range of inputs and parameters. Therefore, an interplay between biological experiment and mathematical theory may lead to new network geometries to which monotone cyclic feedback results can be extended. In this very real sense, biology can provide the intuition that leads to the creation or discovery of new structure theorems, and we contend that the field of mathematics has as much to gain as the fields of biology and medicine from the study of genetic networks.