The contribution of GABA to glutamate/glutamine cycling and energy metabolism in the rat cortex in vivo

Abstract

Previous studies have shown that the glutamate/glutamine (Glu/Gln) neurotransmitter cycle and neuronal glucose oxidation are proportional (1:1), with increasing neuronal activity above isoelectricity. GABA, a product of Glu metabolism, is synthesized from astroglial Gln and contributes to total Glu/Gln neurotransmitter cycling, although the fraction contributed by GABA is unknown. In the present study, we used ¹³C NMR spectroscopy together with i.v. infusions of [1,6-¹³C₂]glucose and [2-¹³C]acetate to separately determine rates of Glu/Gln and GABA/Gln cycling and their respective tricarboxylic acid cycles in the rat cortex under conditions of halothane anesthesia and pentobarbital-induced isoelectricity. Under 1% halothane anesthesia, GABA/Gln cycle flux comprised 23% of total (Glu plus GABA) neurotransmitter cycling and 18% of total neuronal tricarboxylic acid cycle flux. In isoelectric cortex, glucose oxidation was reduced >3-fold in glutamatergic and GABAergic neurons, and neurotransmitter cycling was below detection. Hence, in both cell types, the primary energetic costs are associated with neurotransmission, which increase together as cortical activity is increased. The contribution of GABAergic neurons and inhibition to cortical energy metabolism has broad implications for the interpretation of functional imaging signals.

Glutamate (Glu) and GABA are the major excitatory and inhibitory neurotransmitters in the mature cerebral cortex and together account for ≈90% of total cortical synapses (1). Excitatory synapses outnumber inhibitory synapses ≈5:1 (2), suggesting that excitation plays an energetically dominant role in the cortex. The energetic cost of GABAergic neurotransmission remains an open question, however, because current methods used to assess cortical activity are based on changes in local blood flow or metabolism (e.g., glucose or oxygen consumption), which cannot differentiate glutamatergic from GABAergic neurons. Thus, the interpretation of changes in cortical activity in terms of the energetics of excitation and inhibition requires other methods that are sensitive to the synthesis of these neurotransmitters.

Glutamatergic neurotransmitter cycling flux and energy consumption have been reported for rat and human cortex by using ¹³C NMR spectroscopy during the i.v. infusion of ¹³C-labeled glucose (3–10). These studies show that the Glu/glutamine (Gln) cycling flux (V_cyc) is substantial, from ≈30% to 42% of neuronal tricarboxylic acid (TCA) cycle flux in anesthetized rats (V_TCAn) (4, 5, 8) to ≈38–50% of V_TCAn in resting awake rat and human cortex (7, 9, 10). In the cortex of anesthetized rats, changes in V_cyc and V_TCAn are proportional (≈1:1) over a large cortical activity range above isoelectricity (4, 8).

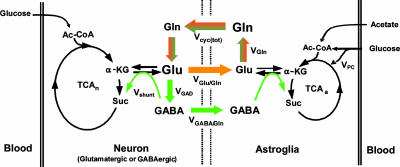
The determination of V_cyc from Gln and Glu ¹³C turnover, using [1-¹³C]glucose as tracer, includes contributions from GABA as well as Glu (4, 5, 11). This is because Gln is a common precursor, and ¹³C labeling of Gln-C4 during GABA catabolism in glia is indistinguishable from direct labeling by neuronal Glu-C4 in the Glu/Gln cycle (Fig. 1). Thus, the contribution of glial GABA catabolism to Gln labeling and V_cyc has not been distinguished previously. The contribution of GABAergic neurons to energetics is particularly important because of recurring suggestions from neuroimaging studies, which are responsive to energy consumption, that inhibitory processes may require either no energy or very little energy (12).

Fig. 1.

Schematic depiction of Glu/Gln and GABA/Gln cycling between glutamatergic (orange) and GABAergic (green) neurons and astroglia relevant to ¹³C NMR experiments using [1-¹³C]glucose or [2-¹³C]acetate as tracer. Metabolism of [1-¹³C]glucose through glycolysis and the TCA cycle labels neuronal Glu-C4 and GABA-C2 with label transfer to Gln-C4 by neurotransmitter cycling, V_cyc(tot) = V_Glu/Gln + V_GABA/Gln. [2-¹³C]acetate metabolism in astroglia labels Gln-C4 directly with label transfer to neuronal Glu-C4 and GABA-C2 by neurotransmitter cycling, V_cyc(tot). V_GAD, rate of GABA synthesis via Glu decarboxylase; V_shunt, rate of neuronal GABA catabolism; V_Gln, rate of Gln synthesis; and V_PC, rate of pyruvate carboxylation.

In this study, we evaluated the contributions of GABAergic and glutamatergic neurotransmitter fluxes and their respective rates of glucose oxidation using ¹³C and ¹H-[¹³C]NMR spectroscopy during i.v. infusions of either [1,6-¹³C₂]glucose or [2-¹³C]acetate. Whereas glucose is oxidized in both neurons and glia, acetate is metabolized almost exclusively in glia (13–16), providing a highly specific means of tagging the common glial Gln precursor of Glu and GABA. The steady-state fractional enrichments of Glu-C4, GABA-C2, and Gln-C4 attained during the infusion of [2-¹³C]acetate were used to compute the ratios V_cyc/V_TCAn for glutamatergic and GABAergic neurons. The ratios were then used as parameter constraints in fitting a three-compartment metabolic model to the time courses of ¹³C labeling of amino acids from [1,6-¹³C₂]glucose, yielding values of the absolute neurotransmitter and TCA cycle fluxes for each neuronal cell type.

We found that, compared with glutamatergic neurons, GABAergic neurons consume a sizable but smaller fraction of total energy and contribute a similar fraction to the total (Glu plus GABA) neurotransmitter flux. Furthermore, both glutamatergic and GABAergic neurotransmitter cycling and energy consumption increased with neuronal activity above an isoelectric baseline. Our findings lend in vivo support to recent electrophysiological studies in vitro of proportional (balanced) changes in excitatory and inhibitory ion conductance with increasing activity (17).

Materials and Methods

Animal Preparation. All experiments were performed under protocols approved by the Yale Animal Care and Use Committee. Male Sprague–Dawley rats, fasted overnight, were anesthetized with halothane (2%), tracheotomized, and ventilated on 68% N₂O/30% O₂. The left femoral artery and both femoral veins were cannulated for the continuous monitoring of arterial blood pressure and blood gases and for the i.v. infusion of glucose and acetate, respectively. After surgery, halothane was reduced to ≈1% (Group A) or was discontinued and anesthesia maintained with pentobarbital (Group B). Core temperature was maintained near 37°C with a heating pad and a temperature-regulated recirculating water bath.

Animals in Group A (halothane anesthesia) were infused with either [1,6-¹³C₂]glucose and unlabeled acetate (in vivo experiment) or [2-¹³C]acetate and unlabeled glucose (ex vivo experiment). The glucose infusion followed the schedule described previously (18). Acetate was administered by bolus-variable rate infusion over 2 h (3 M dissolved in water, pH adjusted to 7.0) at 1.25 mmol/min per kg (0–5 min), 0.625 mmol/min per kg (5–10 min), and 0.25 mmol/min per kg thereafter. The 2-h infusion time was sufficient for Glu-C4, GABA-C2, and Gln-C4 to attain their steady-state ¹³C enrichments. Additional bench experiments were conducted in which rats received [1,6-¹³C₂]glucose and unlabeled acetate for 7 and 20 min to assess GABA ¹³C turnover, which was too low in concentration to detect in vivo with sufficient sensitivity.

Animals in Group B (isoelectric) received sodium pentobarbital at a dose (120 mg/kg, i.p., with supplements of 10 mg/kg every 20 min) sufficient to induce and maintain isoelectricity as assessed by continuous electroencephalography (4). The rats in Group B received [1,6-¹³C₂]glucose and acetate for 20 min using the same infusion protocol as described for Group A. No attempt was made to measure steady-state labeling from [2-¹³C]acetate due to the very low metabolic rate. The high dose of pentobarbital (Group B) led to a decrease in mean arterial blood pressure to 50–60 mmHg (1 mmHg = 133 Pa).

Arterial blood gasses were maintained within normal physiological limits for rats in both groups. Arterial blood samples were taken periodically for the analysis of the concentration and ¹³C enrichments of plasma glucose and acetate. After each experiment, the brain was immediately frozen in situ with liquid N₂ while mechanical ventilation was continued (19).

In Vivo NMR Spectroscopy. In vivo NMR experiments were performed on a 7-T horizontal-bore NMR spectrometer/imager (Bruker AVANCE) operating at 75.50 MHz (¹³C) and 300.30 MHz (¹H). ¹³C NMR spectra were detected by using a circular surface coil of 14 mm diameter, whereas an outer butterfly coil was used for ¹H decoupling. Magnetic-field homogeneity was optimized by using fastmap (20). ¹H decoupled ¹³C NMR spectra were obtained from a localized volume (9 × 4 × 10 mm³) by using a polarization transfer pulse sequence in which the 90° and 180° pulses were replaced with adiabatic half- and full-passage pulses, respectively (9). Suppression of signals outside the localized volume was achieved by using outer volume suppression along the x, y, and z (axial) dimensions (21). ¹³C NMR spectra were acquired every 1.5 sec in blocks of 128 scans (≈4 min per spectrum).

Analysis of Plasma Glucose and Acetate. The concentration of glucose in plasma samples was determined by using a Beckman Glucose Analyzer II (Beckman Coulter). The ¹³C isotopic enrichment of plasma glucose and the concentration and ¹³C enrichment of plasma acetate were determined from filtered (10-kDa) samples at 11.74 T by using ¹H NMR (Bruker AVANCE AM500). ¹H-[¹³C]NMR spectra of plasma samples were also obtained at the conclusion of [2-¹³C]acetate infusions to assess potential ¹³C labeling in glucose.

Preparation of Tissue Extracts. Frozen tissue (150–200 mg) from frontoparietal cortex was ground with 0.1 M HCl/methanol (2:1 vol/wt) at –40°C followed by extraction with ice-cold ethanol (22). The supernatant was clarified by centrifugation, lyophilized, and resuspended in 500 μl of phosphate-buffered (100 mM, pH 7) D₂O (Cambridge Isotope Laboratories, Cambridge, MA) solution containing 3-trimethylsilyl[2,2,3,3-D₄]-propionate (0.5 mM). After the measurement of total amino acid concentrations in the extracts using ¹H-[¹³C]NMR, the amino acids were separated by using AG1-X8 anion exchange chromatography, as described (22).

NMR Spectroscopy of Plasma and Brain Tissue Extracts. ¹H NMR spectra of plasma and brain extracts were acquired at 11.74 T (Bruker AVANCE AM500) under fully relaxed pulsing conditions. The ¹³C enrichments of glucose-C1 (5.2 ppm) and acetate-C2 (1.9 ppm) in ¹H NMR spectra were calculated as the ratio of ¹³C satellites to the total resonance intensity. ¹H-[¹³C]NMR spectra of brain tissue extracts were acquired by using a pulse sequence incorporating adiabatic pulses for ¹H and ¹³C excitation (23). The concentrations of metabolites were determined relative to [2-¹³C]glycine added during tissue extraction. The isotopic ¹³C enrichments of Glu (C4,C3), Gln (C4,C3), and GABA (C2,C3) in the separated fractions were determined as the ratio of ¹³C-bound ¹H to total ¹H(¹²C+¹³C) for each carbon position.

Determination of the V_cyc/V_TCA During [2-¹³C]Acetate Infusion. The differential equations that describe the flow of ¹³C through the Glu/Gln and GABA/Gln cycles were solved analytically for the steady-state condition (see Derivation of flux ratios in Supporting Text, which is published as supporting information on the PNAS web site), which yielded the following relationships between V_cyc and V_TCA for glutamatergic (24) and GABAergic neurons:

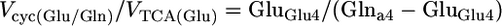[1]

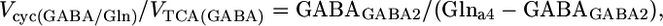[2]

where Glu_Glu4, GABA_GABA2, and Gln_a4 represent the steady-state ¹³C enrichments of amino acids during the infusion of [2-¹³C]acetate and unlabeled glucose in the neuronal or astroglial (a) compartment. GABA and Gln were assumed to be entirely neuronal and glial, respectively, whereas Glu-C4 was corrected for glial Glu assuming the latter to be 10% of total Glu with a steady-state ¹³C enrichment given by Gln-C4. The ¹³C enrichments were also corrected for the small amount of ¹³C labeling that appeared in blood glucose-C1 during the [2-¹³C]acetate infusion by subtraction of the ¹³C enrichment of lactate-C3 (3.5 ± 0.3%), the latter assumed to reflect pyruvate-C3.

Metabolic Modeling of ¹³C Time-Course Data. The metabolic fluxes were determined by fitting the three-compartment metabolic model [glutamatergic neuron, GABAergic neuron, and astroglia; (25)] depicted in Fig. 1 to the time courses of ¹³C enrichments of Glu-C4, Glu-C3, and Gln-C4 measured in vivo, and Glu-C4, Glu-C3, GABA-C2, GABA-C3, Gln-C4, and Gln-C3 measured ex vivo during the [1,6-¹³C₂]glucose and acetate infusions. The values of the ratios V_cyc(Glu/Gln)/V_TCA(Glu) and V_{cyc(GABA/Gln)}/V_TCA(GABA) (Eqs. 1 and 2) were fixed as model constraints. Mass and ¹³C isotope flows from [1,6-¹³C₂]glucose into neuronal and glial Glu and Gln pools were written as coupled differential equations (see Mass and isotope balance equations in Supporting Text) within the cwave software package running in matlab (26). The equations were solved by using a first-/second-order Runge–Kutta algorithm, and fitting was done by using a Levenburg–Marquardt algorithm. Total Gln and GABA pools were assigned to the glial and GABAergic neuronal compartments, respectively, whereas Glu was divided between glutamatergic neurons (88%), glia (10%), and GABAergic neurons (2%) (27, 28). Pyruvate carboxylase flux (V_PC) was assumed to be 20% of the rate of total Gln synthesis (5, 29). Astroglial TCA cycle flux was assumed to be 15% of total TCA cycle flux (24). The cerebral metabolic fluxes were determined from the best fits of the model to the time-course data sets by using a simulated annealing algorithm (30). Cerebral metabolic rates of glucose oxidation [CMR_glc(ox)] were calculated as ½V_TCA.

Determination of Cerebral Metabolic Fluxes During Pentobarbital-Induced Isoelectricity. For animals in Group B (isoelectric), the rates of glucose oxidation in glutamatergic and GABAergic neurons were calculated from the quantity of ¹³C trapped in amino acids after a 20-min infusion of [1,6-¹³C₂]glucose and acetate. Because of the slow rate of cerebral metabolism under these conditions, the rate of glucose oxidation in the two cell types was approximated from the initial rate of label accumulation in Glu and GABA according to:

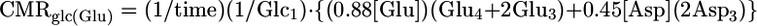[3]

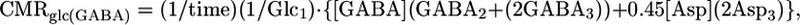[4]

where [Glu], [GABA], and [Asp] are the total tissue concentrations; Glc₁ is the percent ¹³C enrichment of plasma glucose-C1; and Glu_i, Asp_i, and GABA_i are the percent ¹³C enrichments at ith carbon. Tissue aspartate was assumed to be distributed between neurons (90%) and glia (10%), with equal percentages in glutamatergic (45%) and GABAergic (45%) neurons. Total neurotransmitter cycling [V_cyc(tot)] and V_PC were calculated by taking into account that Gln resulting from pyruvate carboxylase flux leads to equivalent contributions between Gln-(C3+C2) and Gln-C4, such that the excess labeling in Gln-C4 arises from neurotransmitter cycling with neuronal Glu-C4 as precursor.

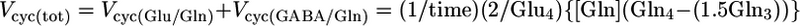[5]

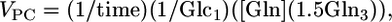[6]

where [Gln] and Gln_i are the Gln concentration and fractional enrichments, respectively. The factor of 1.5 arises from incomplete equilibration of OAA-C2 and OAA-C3 (5).

Results

Enrichment of Plasma Glucose and Acetate. The preinfusion concentrations of plasma glucose and acetate were similar in animals of both groups [Group A (halothane), glucose, 4.6 ± 0.9 mM, and acetate, 0.23 ± 0.10 mM; Group B (isoelectric), glucose, 5.2 ± 0.6 mM]. The infusion of [1,6-¹³C₂]glucose and acetate increased plasma glucose concentrations and percentage enrichments to similar levels in both groups within minutes, and these values remained relatively constant thereafter (Group A, 9.5 ± 0.8 mM, 53 ± 2%; Group B, 12.6 ± 0.1 mM, 47 ± 5%). The infusion of [2-¹³C]acetate/glucose in Group A increased plasma acetate concentration (15.8 ± 6.2 mM) and enrichments (>90%) to constant levels within the first 3–4 min of the infusion.

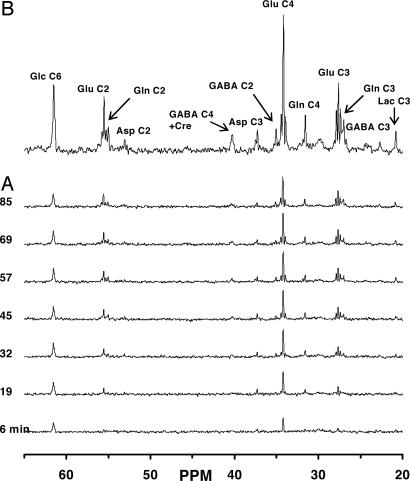
¹³C Labeling of Cerebral Amino Acids During [1,6-¹³C₂]Glucose and Acetate Infusion [Group A (Halothane)]. Fig. 2A depicts the time course of ¹³C labeling of cortical amino acids in spatially localized ¹H-decoupled ¹³C NMR spectra after infusion of [1,6-¹³C₂]glucose and acetate in vivo. The ¹³C spectrum (Fig. 2B) displays well resolved resonances and isotopomer splittings of Glu (C4, C3, and C2), Gln (C4, C3, and C2), GABA (C2, C3, and C4), aspartate (C3 and C2), and glucose C6 (C1 not shown). The concentrations and endpoint ¹³C enrichments of the amino acids were determined in cortical extracts (Table 1), which allowed normalization and quantitation of the ¹³C time courses.

Fig. 2.

Spatially localized ¹³C-[¹H]NMR spectrum of metabolites in the intact rat brain after infusion of [1,6-¹³C₂]glucose and acetate under halothane. Time courses of ¹³C-labeling of metabolites (A) and averaged spectrum over the last 30 min (60–90 min) of the 1.5-h [1,6-¹³C₂]glucose and acetate infusion (B). Peak label definitions: Asp, aspartate; Lac, lactate; Glc, glucose.

Table 1. Cortical amino acid concentrations and percentage ¹³C enrichments during [1,6-¹³C₂]glucose/acetate and [2-¹³C]acetate/glucose infusions in rats under halothane and pentobarbital (isoelectric) anesthesia.

	Glu		Gln		GABA		Aspartate
	C4	C3	C4	C3	C2	C3	C3
Group A (halothane)
Total concentration, μmol/g, n = 11	14.4 ± 1.3		6.8 ± 0.4		1.8 ± 0.5		4.3 ± 0.5
[1,6-13C2]Glucose/acetate, %Eep, n = 12	34.4 ± 1.0	24.5 ± 0.6	22.2 ± 1.8	17.3 ± 1.2	29.1 ± 1.1	13.3 ± 1.2	26.9 ± 4.5
[2-13C]Acetate/glucose, %Eep, n = 12	10.9 ± 0.3	9.3 ± 0.9	23.4 ± 3.6	12.0 ± 1.5	11.1 ± 1.2	10.2 ± 2.0	6.6 ± 2.8
Group B (pentobarbital),
Total concentration, μmol/g, n = 4	12.1 ± 1.5		8.3 ± 0.6		2.6 ± 0.2		3.1 ± 0.8
[1,6-13C2]Glucose/acetate, %E20, n = 4	14.1 ± 2.2	2.0 ± 0.5	1.6 ± 0.6	0.7 ± 0.4	9.0 ± 2.4	1.0 ± 0.7	7.3 ± 2.5

%E_ep, percent ¹³C enrichment at end of experiment; %E₂₀, percent ¹³C enrichment at 20 min of infusion. Values represent mean ± SD.

GABAergic and Glutamatergic Fluxes Under Halothane Anesthesia. The steady-state ¹³C enrichments of Glu-C4, Gln-C4, and GABA-C2 as measured in the [2-¹³C]acetate/glucose experiment (Table 1) were used to compute the ratio of neurotransmitter cycling to TCA cycle flux (V_cyc/V_TCA) for glutamatergic and GABAergic neurons for animals in Group A (halothane). Using the values in Table 1 with Eqs. 1 and 2 gave V_cyc/V_TCAn of 0.63 ± 0.10 (GABAergic) and 0.45 ± 0.09 (glutamatergic). The difference of the ratios was statistically significant (P < 0.001, n = 12).

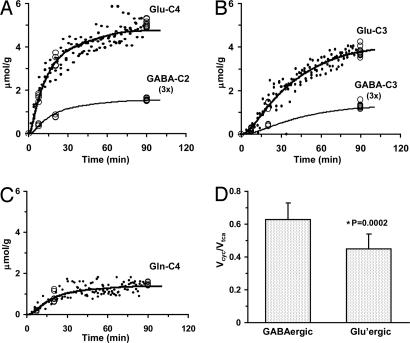
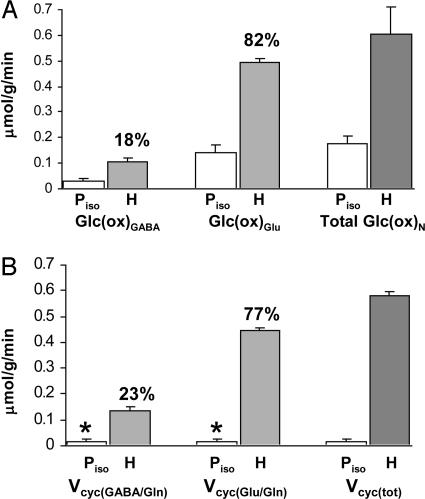
The values of V_TCAn and V_cyc for both GABAergic and glutamatergic neurons were determined by fitting the metabolic model (constrained by V_cyc/V_TCAn) to the ¹³C enrichment time courses of Glu-C4, Glu-C3, GABA-C2, GABA-C3, and Gln-C4 measured in vivo during the [1,6-¹³C₂]glucose and acetate infusion. The best fits of the metabolic model to the group-averaged time-course data are shown in Fig. 3 and best-fit parameter estimates in Fig. 4. Glucose oxidation in GABAergic and glutamatergic neurons was 18% and 82% of CMR_glc(tot)N, respectively (0.107 ± 0.012 vs. 0.495 ± 0.015 μmol/g per min), which includes both activity-dependent and independent contributions to the energetics. Neurotransmitter cycling in GABAergic and glutamatergic neurons was 23% and 77% of V_cyc(tot), respectively (0.135 ± 0.015 vs. 0.445 ± 0.013 μmol/g per min), which was similar to their contribution to energy consumption.

Fig. 3.

Fit of the metabolic model to experimental data. The in vivo time course of ¹³C labeling of Glu-C4 (A), Glu-C3 (B), and Gln-C4 (C) from [1,6-¹³C₂]glucose is depicted for all animals (data points). Ex vivo measurements at selected time points are depicted by open circles in (A) Glu-C4 and GABA-C2, (B) Glu-C3 and GABA-C3, and (C) Gln-C4. The best fit of the mathematical model to the experimental data is shown by the smooth curves. (D) Values of the ratio, V_cyc/V_TCA, in glutamatergic and GABAergic neurons calculated from steady-state fractional enrichments of Glu-C4, Gln-C4, and GABA-C2 during infusion of [2-¹³C]acetate and glucose (Table 1) used as constraints in the data fitting shown in A–C.

Fig. 4.

Contribution of GABAergic and glutamatergic neurons to neuronal glucose oxidation and neurotransmitter cycling. (A) Rates of glucose oxidation, Glc(ox), for GABAergic and glutamatergic neurons and their sum, total Glc(ox)_N. (B) Rates of GABA/Gln and Glu/Gln cycling and their sum, V_cyc(tot). P_iso, pentobarbital-induced isoelectricity; H, halothane/N₂0 anesthesia. *, maximum possible value for P_iso condition given by the measured value of V_cyc(tot) for isoelectricity. Percentages denote the contributions of GABAergic and glutamatergic neurons to the total fluxes given.

Metabolic Fluxes in GABAergic and Glutamatergic Neurons During Isoelectricity. The cerebral metabolic fluxes for animals in Group B [pentobarbital (isoelectric)] were calculated from the rate of ¹³C label accumulation into Glu, aspartate, GABA, and Gln during a 20-min [1,6-¹³C₂]glucose and acetate infusion (Table 1 and Eqs. 3–6). For the isoelectric cortex, V_cyc(tot) was negligible (0.015 ± 0.013 μmol/g per min), as shown by the very low ¹³C labeling of Gln-C4. Glucose oxidation in GABAergic neurons (0.030 ± 0.013 μmol/g per min) was ≈21% of that in glutamatergic neurons (0.143 ± 0.060 μmol/g per min) (Fig. 4). This finding is consistent with the 1:1 relationship for ΔV_cyc(tot) with ΔV_TCAn(tot) reported previously (4, 8). Comparison of the isoelectric (Group B) and more active halothane-anesthetized (Group A) animals showed that V_{cyc(GABA/Gln)} and V_cyc(Glu/Gln) had increased together with increased activity, as had their respective rates of glucose oxidation.

Discussion

Contribution of GABA to V_cyc(tot) and Glial Energetics. Unlike Glu, which can undergo direct conversion to Gln in astroglia, catabolism of GABA is indirect, involving transamination with α-ketoglutarate (α-KG) (the only known acceptor of GABA nitrogen) to produce Glu and succinic semialdehyde, the latter being oxidized to succinate that enters the TCA cycle (31). The Glu formed by transamination can proceed to Gln (Fig. 1; see also Fig. 5, which is published as supporting information on the PNAS web site). However, glial oxidation of [1-¹³C]glucose labels α-KG_C4 and, through transamination with GABA, labels Glu_C4 (and Gln_C4), rendering this pathway indistinguishable from glutamatergic cycling, V_cyc(Glu/Gln). Thus, V_cyc as calculated from the labeling of Gln_C4 in experiments using [1-¹³C]glucose represents the sum of Glu and GABA cycling fluxes, i.e., V_cyc(tot) (4, 5). Because transamination of GABA with α-KG requires a molar equivalent influx of acetylCoA, V_{cyc(GABA/Gln)} can be viewed as a lower limit of this flux and the glial TCA semicycle from succinate to α-KG. Thus, for each molecule of GABA metabolized to α-KG through glial respiration, 11 molecules of ATP would be formed (3 NADH₂ = 9 ATP, 1 FADH₂ = 2 ATP), which is ≈92% (11/12) of the ATP expected from the complete oxidation of acetylCoA in the glial TCA cycle. Glial TCA cycle flux is estimated to be 15–25% of total oxidative metabolism (6, 24), suggesting that astroglial GABA catabolism could account for a substantial fraction of glial oxidative metabolism.

Comparison of V_{cyc(GABA/Gln)} to Total GABA Synthesis. The rate of GABA synthesis catalyzed by Glu decarboxylase (GAD) in GABAergic neurons (V_GAD) at metabolic steady state (constant GABA level) must equal the sum of the catabolic fluxes in the GABA shunts of neurons and glia, given by V_shunt and V_{cyc(GABA/Gln)}, respectively (Fig. 1). Thus, V_{cyc(GABA/Gln)} < V_GAD. V_GAD can be estimated if the shunt flux in GABAergic neurons is known. In a ¹³C NMR labeling study of mouse brain, Hassel et al. (32) reported that in GABAergic neurons, glucose oxidation in the pathway from α-KG to succinate is divided about equally between the TCA cycle and the GABA shunt. In our study, V_TCA(GABA) sums all pathways from α-KG to succinate, which includes the GABA shunt in GABAergic neurons (25). Thus, an estimate of V_GAD using this information yields V_TCA(GABA)/2 + V_{cyc(GABA/gln)} = 0.11 + 0.14 = 0.25 μmol/g per min. Although this value is 1.3- to 2.0-fold higher than the range in V_GAD previously reported for rat cortex under α-chloralose anesthesia (25), energy metabolism was also ≈2× higher under halothane, which might explain this difference [V_TCAn(tot) of 1.2 μmol/g per min vs. 0.5 μmol/g per min].

Neuronal Reuptake vs. Glial Clearance of Extracellular GABA. Astroglia play a dominant role in the clearance of Glu after synaptic release (33), but the clearance of GABA involves neuronal and glial transport (33–36), and both processes are highly regulated (35, 37). It is generally believed that GABA reuptake dominates clearance because of the higher density of GABA transporters in neurons than glia (33), although quantitative information on reuptake in vivo does not yet exist. Although the present findings relate only to GABA synthesis from Gln and not to reuptake per se, the results do provide an estimate of the maximum potential reuptake flux. If we assume that depolarization-related GABA release, which includes Ca²⁺-dependent (exocytosis) and -independent (transporter reversal) release, is coupled to GABA synthesis (V_GAD), then an upper estimate of reuptake is given by the neuronal shunt flux, V_shunt, which is the difference between V_GAD and V_{cyc(GABA/Gln)} (Figs. 1 and 5). As discussed above, V_shunt is comparable in magnitude to V_{cyc(GABA/Gln)}, so to the extent that GABA reuptake occurs, it will add to GABA release and thus influence extracellular levels and inhibition; however, the rate of steady-state GABA release should neither exceed V_GAD nor influence the measured value of cycling from glial Gln to GABAergic neurons, V_{cyc(Gln/GABA)}. Thus, V_{cyc(Gln/GABA)} will underestimate the rate of GABA release to the extent GABA is cleared by reuptake, whereas both processes would be included in the measured value of CMR_glc(ox), which includes all pathways of release coupled to GABA synthesis.

In the scheme depicted in Fig. 1, V_{cyc(GABA/Gln)} returns Gln-derived carbon to the glia and therefore does not require anaplerosis (V_PC) to maintain this flux. On the other hand, to the extent that GABA synthesized from Gln did not return to glia, anaplerosis (V_PC) would be expected to balance this flow such that V_{cyc(Gln/GABA)} = V_{cyc(GABA/Gln)} + V_PC(GABA). In either case, ¹³C labeling of αKG_C4 (and Gln_C4) would be the same, as would the value of V_{cyc(Gln/GABA)}. The only difference would be that V_{cyc(Gln/GABA)} now contains a portion of flux arising from V_PC, as described for V_cyc(Glu/Gln) (38). A recent study by Oz et al. (7) suggests that V_PC increases with total neuronal activity, supporting a role in neurotransmitter cycling. However, questions remain as to the total fraction of V_PC devoted to replacing lost Glu or GABA and dependence on activity. For example, the finding that V_PC did not increase acutely with V_cyc(tot) during bicuculline seizures (29), which is known to increase GABAergic and glutamatergic activity (8, 39), suggests that V_PC may not be immediately responsive to large changes in neuronal activity.

Relationship of GABAergic Fluxes to Cortical Activity. V_cyc(tot) in isoelectric cortex was only 3% of that under halothane and just 11% and <4% of V_{cyc(GABA/Gln)} and V_cyc(Glu/Gln), respectively. The low value of V_cyc(tot) for isoelectric cortex (0.015 μmol/g per min) is consistent with findings in previous studies (4, 40) for the activity-independent or “housekeeping” oxidative metabolism of neurons. Thus, both neurotransmitter fluxes had increased with the higher state of cortical activity associated with halothane. Evidence that GABAergic inhibitory pathways are more active during increased activity has been reported. Persistent network activity in vitro is associated with increased spiking rates of both glutamatergic pyramidal neurons and fast-spiking GABAergic interneurons (17, 41). In ferret-brain slices, persistent recurrent activity, which is characteristic of anesthetized and certain sleep states, involves nearly balanced and proportional increases in both excitatory and inhibitory synaptic currents (17). A theoretical study using a cortical network model predicted a linear relationship between inhibitory and excitatory conductances, with slopes ranging from 1:1 to 1:5 (42). During seizures, the rate of GABA synthesis is substantially increased (39) when total glucose and oxygen consumption is increased (43), as well as V_cyc(tot) and CMR_glc(ox)N (8). Direct afferent stimulation of cerebellar inhibitory neurons has also been shown to increase cerebral blood flow (44), consistent with known mechanisms of energy metabolism and its coupling to hemodynamics.

Contribution of GABAergic Neurons to Cortical Oxidative Metabolism. In the neocortex, excitatory (glutamatergic) pyramidal neurons and inhibitory (GABAergic) interneurons are estimated to be 70–85% and 15–30% of total neurons (45, 46), respectively. Inhibitory synapses account for ≈14–17% of total neocortical synapses (2). In the present study, GABAergic neurons accounted for 18% of neuronal oxidative metabolism (Fig. 4) or 13–15% of the total oxidative metabolism of neurons and glia, assuming that glia contributes 15–25% of total TCA cycle flux (6, 24). Remarkably, the relative fluxes appear similar to their relative synaptic densities. This value is near the range (15–25%) reported for the GABAergic TCA cycle flux based on cortical GABA-C2 turnover during [1-¹³C]glucose infusion (25) but is substantially greater than estimates (1–2%) based on rates of cortical GABA synthesis after GABA-transaminase inhibition (47), which is likely to underestimate the absolute rate of GABA synthesis and its contribution to total oxidative metabolism. In whole brain of awake mice, GABAergic TCA cycle flux was reported to be ≈34% of total oxidation based on ¹³C labeling of amino acids from [1-¹³C]glucose and [2-¹³C]acetate (32), although measurement of whole brain may emphasize higher GABAergic fluxes in subcortical structures (e.g., substantia nigra), and the cortex could be lower.

Implications of GABAergic Activity in Functional Neuroimaging. Neuronal activation in functional imaging studies is traditionally concerned with excitatory synapses (48, 49). The basic mechanisms coupling cellular activity to energy demand, however, are likely to be similar at excitatory and inhibitory synapses (50, 51). In vivo studies showing increased ¹⁴C-2-deoxyglucose uptake in areas densely populated by inhibitory synapses during selective stimulation of inhibitory pathways are consistent with this idea (52, 53). In cerebellum, stimulation of inhibitory parallel fibers simultaneously with excitatory climbing fibers increases the total local field potential and cerebral blood flow (44, 54). Thus, reduced activity at excitatory synapses could arise directly from decreased afferent stimulation or by activation of GABAergic interneurons (55). Therefore, the interpretation of the functional neuroimaging signal in terms of excitation is limited by the unknown contribution of inhibitory and excitatory pathways to energy consumption. Waldvogel et al. (12) recently concluded that excitatory synaptic activity contributed to the blood oxygenation level dependent signal, whereas synaptic inhibition was less metabolically demanding than excitation. Although the present study shows that GABAergic activity contributes quantitatively less than glutamatergic activity, energy consumption increased in both cell types as activity increased, suggesting that GABAergic inhibition is of energetic importance during activation.