Water Multilayers on TiO₂ (101) Anatase Surface: Assessment of a DFTB-Based Method

Abstract

A water/(101) anatase TiO₂ interface has been investigated with the DFT-based self-consistent-charge density functional tight-binding theory (SCC-DFTB). By comparison of the computed structural, energetic, and dynamical properties with standard DFT-GGA and experimental data, we assess the accuracy of SCC-DFTB for this prototypical solid–liquid interface. We tested different available SCC-DFTB parameters for Ti-containing compounds and, accordingly, combined them to improve the reliability of the method. To better describe water energetics, we have also introduced a modified hydrogen-bond-damping function (HBD). With this correction, equilibrium structures and adsorption energies of water on (101) anatase both for low (0.25 ML) and full (1 ML) coverages are in excellent agreement with those obtained with a higher level of theory (DFT-GGA). Furthermore, Born–Oppenheimer molecular dynamics (MD) simulations for mono-, bi-, and trilayers of water on the surface, as computed with SCC-DFTB, evidence similar ordering and energetics as DFT-GGA Car–Parrinello MD results. Finally, we have evaluated the energy barrier for the dissociation of a water molecule on the anatase (101) surface. Overall, the combined set of parameters with the HBD correction (SCC-DFTB+HBD) is shown to provide a description of the water/water/titania interface, which is very close to that obtained by standard DFT-GGA, with a remarkably reduced computational cost. Hence, this study opens the way to the future investigations on much more extended and realistic TiO₂/liquid water systems, which are extremely relevant for many modern technological applications.

1. Introduction

The titanium dioxide interaction with water is relevant for many TiO₂-based technologies,¹ ranging from traditional uses in pigments and coatings to advanced applications in photocatalytic processes, such as fuel generation² from carbon dioxide³ or water^4,5 and environmental decontamination,⁶ which are normally performed in an aqueous medium or humid environments. Recently, TiO₂ nanoparticles photoactivity and redox chemistry have attracted growing interest for biomedical applications.⁷ In this field, knowledge of the properties of this solid–liquid interface is of key importance since the interaction with biomolecules and polymer coatings is competitive with water adsorption or even mediated by it.⁸⁻¹¹ Rutile is the most stable bulk TiO₂ phase at normal conditions; however, sub-20 nm TiO₂ nanoparticles prefer the anatase phase.¹²

In recent years, the structure of water layers on the most exposed (101) anatase surface has been elucidated by several works based on ab initio Car–Parrinello molecular dynamics.¹³⁻¹⁵ These studies evidenced that water adsorption and its ordering are governed by a complex and delicate interplay of many factors, such as the topology and roughness of the surface and the relative strength of water–water and water–titania interactions. The molecular mode of water adsorption was always computed to be favored with respect to the dissociated one on the stoichiometric anatase (101) surface, in line with experimental findings.¹⁶⁻²¹

However, most of the above-mentioned modern technological applications involve the use TiO₂ nanoparticles, as fundamental building blocks. These low-dimensional titania materials (4–20 nm) may present peculiar wetting properties due to size and shape effects and to characteristic surface and defect structures.²²⁻²⁴ Nonetheless, the dynamical study of nanoparticle models of realistic size in a complex environment, with an appropriate time scale, is not feasible by means of density-functional theory (DFT) calculations.

Self-consistent-charge density functional tight-binding (SCC-DFTB) is an efficient quantum mechanical method based on DFT, from which it retains much of the physics at a significantly lower computational cost.^25,26 It can be seen as an approximate Kohn–Sham DFT scheme,²⁷ where the Hamiltonian matrix includes only one- and two-center contributions. Part of the computational efficiency of this procedure originates from the use of tabulated Hamiltonian and overlap matrix elements as a function of the distance between atomic pairs. In the self-consistent charge (SCC) extension, DFTB is augmented by a self-consistency treatment based on individual atomic charges, which describe also charge transfer effects of the system. It has been shown that this method is 2–3 orders of magnitude faster than standard DFT with a medium-sized basis set,²⁸⁻³⁰ without any significant loss of accuracy in many biochemistry/biophysics, organic, and inorganic materials chemistry cases.^{25,29,31−36} This means that this approximate method can handle systems up to some thousands of atoms.³⁷ Additionally, DFTB is also capable, being a DFT-based method, to describe chemical reaction processes. Most of the molecular mechanics (MM) methods are not, except the reactive force field (reaxFF).³⁸ However, the latter one cannot compute electronic properties, whereas with DFTB it is possible to obtain electronic structure and optical and infrared spectra, in analogy with DFT.^{25,29,30,37,39,40}

The parametrization of SCC-DFTB consists of a small number of element and element-pair parameters. Although they are meant to be transferable within different contexts (bio or organic molecules, material science, solids, surfaces, etc.), the accuracy of the results is not universal and depends on the system. To this end, it is important to evaluate the applicability of a certain parametrization scheme before exploiting it for larger and more complex models.

Currently, two sets of parameters are available⁴¹ for the study of Ti-containing compounds: (1) “mio-1-1/tiorg-0-1”⁴² and (2) “matsci-0-3”.⁴³ The “tiorg-0-1” is an extension to introduce Ti-X pairs in the “mio-1-1” set²⁵ that was developed for the main group elements and largely benchmarked for organic molecules^31,33,44 and biological systems.^30,45,46 Results from this set were found to be in good agreement with DFT and experimental data for small titania-like molecules, bulk properties, surface energies, and water adsorption on specific low index surfaces of both anatase and rutile.^42,47−50 However, to the best of our knowledge, no clear assessment of this set of parameters for the (101) anatase surface has been published yet. On the other hand, the “matsci-0-3” set has been specifically parametrized from the very beginning for materials science and solid-state simulations. Its reliability for bulk TiO₂ structures and chemical reactivity of (101) anatase and (110) rutile surfaces toward isolate or monolayers of water and organic molecules has been previously demonstrated.^43,51

Nevertheless, the description of multilayer water adsorption and dynamics on an oxide surface requires also a proper modeling of liquid water and hydrogen bonding. The above-mentioned “mio-1-1” set²⁵ for main group elements was extensively tested for water or solvated models.⁵²⁻⁵⁵ Its ability to reproduce the geometries of large water clusters is remarkable, although it systematically underestimates hydrogen bonding distances and energies. Considerable improvements on the energetics and the dynamic structure have been obtained with a priori or empirical modifications of the original SCC-DFTB scheme.⁵⁶⁻⁶⁰ Contrarily, the “matsci-0-3” set was not conceived for describing the water/water interactions, and an assessment on its performance is still missing.

In this work, we present a comparative study on the static and dynamic behavior of the water/titania interface by the two sets of DFTB parameters mentioned above, with respect to DFT results already reported in the literature.^13,14,17,61 From this comparative analysis, it has been possible to determine the successes and failures of both sets and, as a next step, to define a new set of parameters (called hereafter “matorg”), where the best of both is combined (for details on the procedure, see Section 2.2): the “matsci-0-3” set is found to better describe the titania/water interaction, whereas the “mio-1-1” set gives a more accurate evaluation of the water/water interaction. The new set has been further improved by including an empirical correction⁵⁶ for a finer description of the hydrogen bonding (“matorg+HBD”).

The composed new set of parameters provides an impressive performance for the description of the water interaction with the (101) anatase TiO₂ surface, if compared with high-level DFT-GGA calculations, but at an extremely reduced computational cost. Thus, with this work, we have set up a reliable tool for the static and dynamic study of realistic TiO₂-based nanosystems of large size in an explicit aqueous medium, which is an extremely relevant (nano)solid/liquid interface for technological applications.

The paper is organized according to the following scheme: in Section 2, we provide the computational details on the SCC-DFTB method (Section 2.1), on the procedure to obtain the new set of parameters as a combination of the two existing ones (Section 2.2), on the setup for the molecular dynamics calculations (Section 2.3), and for the transition state search (Section 2.4). In Section 3, we present our results, first, on the single components of the interface (i.e., water, Section 3.1, and bulk TiO₂, Section 3.2), second, on the static (Section 3.3) and dynamic (Section 3.4 and 3.5) behavior of the water/titania interface. Finally, in Section 4, we summarize the results and draw some relevant conclusions on the proper description of this complex interface by less sophisticated but still rather accurate DFTB methods.

2. Computational Methodology

2.1. SCC-DFTB Method

In the following, we present only a brief overview of the self-consistent charge DFTB (SCC-DFTB) method. For more details on the derivation and the underlying approximations, see refs (25, 28), and (62).

The SCC-DFTB method is based on a second-order expansion of the Kohn–Sham total energy with respect to the charge density fluctuations. The total energy for a SCC-DFTB calculation is defined as

1

where H⁰_μν are the elements of the Hamiltonian matrix, which contains only two-centers terms and are evaluated using a minimal basis set of Slater-type (pseudo)atomic orbitals, c_μⁱ and c_ν are the wave function expansion coefficients, Δq_α and Δq_β are the charge fluctuation terms for atoms α and β, respectively, and E_rep is an approximation of the short-range repulsion term.

In the original formulation of the SCC-DFTB method, the γ_αβ function consists of two terms

2

where r_αβ is the interatomic distance between α and β and S_αβ is an exponentially decaying short-range correction term between the two nuclei.

Later, it was shown that this function plays a crucial role in the correct description of hydrogen-bonded systems.^46,56 To deal with this peculiar case, a modified hydrogen bonding damping (HBD) function γ_αH was introduced only for the interaction between an atom α and a hydrogen atom

3

where U_α and U_H are the atomic Hubbard parameters, which are linked to the chemical hardness of atom α and the corresponding hydrogen, respectively. The parameter ζ is generally determined by fitting to hydrogen-bonding energies from high level ab initio calculations. As a result, γ_αH becomes more positive in the short range, leading to stronger polarization for the atoms forming H-bonds, thus increasing the accuracy of describing hydrogen bonds.

2.2. Electronic Structure Calculations

The SCC-DFTB calculations of the water/TiO₂ surface interface were performed with the DFTB+ simulation package.⁶³ We initially employed the publicly available parameter sets contained in the so-called Slater–Koster files, “mio-1-1/tiorg-0-1” (TIORG)⁴² and “matsci-0-3” (MATSCI)⁴³ for Ti-containing compounds. Subsequently, we have properly combined the two parametrization sets in what we called the “matorg” (MATORG) set: the MATSCI set of parameters was used for Ti–O and Ti–Ti interactions and the “mio-1-1” (MIO)²⁵ for O–O, O–H, and H–H interactions (the phases of the O–H integrals, H⁰_μν in eq 1, from the MIO set were checked to be equal to the ones from MATSCI as a function of the interatomic distance or changed accordingly). In addition, we made use of the HBD modified γ function, in which a ζ = 4 parameter has been used.⁵⁶ In this work, we refer to this combined Slater–Koster file set, HBD modified, as “matorg+HBD” (MATORG+HBD).

For bulk anatase calculations, we used a 4 × 4 × 4 Monkhorst–Pack grid for k-point sampling. The optimal lattice parameters of the unit cell were obtained using the lattice optimization algorithm, as implemented in DFTB+.

The (101) anatase surface has been modeled with a three-triatomic-layer slab, and the bottom layer was kept fixed to the optimized bulk positions during the geometry optimization. To investigate the binding energies and equilibrium geometries of water on the surface, we used a 1 × 2 supercell model (72 atoms) and 2 × 2 × 1 Monkhorst–Pack k-point mesh grid. Periodic replicas were separated by 20 Å of vacuum in the direction perpendicular to the surface to avoid interactions between images.

DFT calculations were carried out by means of the Quantum ESPRESSO simulation package⁶⁴ within the generalized gradient approximation (GGA) using the PBE functional.⁶⁵ The models were generated using the same strategy used for the tight-binding approach. Electron–ion interactions were described by ultrasoft pseudopotential; the plane-wave basis set cut off was kept to 30 Ry (300 Ry for the charge density) and the Monkhorst–Pack k-point mesh grid to 2 × 2 × 1. Forces were relaxed to less than 0.005 eV/Å.

In the 1 × 2 (101) anatase slab model we have used, there are four active sites for water adsorption, corresponding to the 5-fold coordinated cationic Ti (Ti_5c) atoms of the surface. Also, the superficial 2-fold coordinated O (O_2c) atoms, connecting surface Ti atoms, are involved in the interaction with the water molecules, generally forming H-bonds or accepting the protons of the dissociated water molecules.

The total adsorption energy is defined as

4

where E_slab+nmol is the energy of the whole system, E_slab the energy of the surface slab alone, n_mol the number of water molecules adsorbed, and E_mol the energy of a single water molecule in the gas phase. In order to compare results for different water coverages, we defined also an adsorption energy per molecule ΔE_ads^mol

5

Finally, the absolute error (ε) of each calculated DFTB value (ν) with respect to the reference DFT one (ν_ref) was evaluated

6

2.3. Molecular Dynamics Setup

For the simulation of bulk water, we have created a box containing 113 water molecules and then performed a Born–Oppenheimer molecular dynamics simulation in the NPT ensemble in order to determine the correct volume of the box. The Newton’s equations of motion were integrated with the Velocity Verlet algorithm, and a relative small time step of 1.0 fs was used to ensure reversibility. The simulation was run at 1 atm and the temperature kept at 300 K by means of a Nosé–Hoover thermostat. This pre-equilibration simulation was run for 10 ps and results in a box of 1.49 nm³ and a corresponding density of water of 1.004 g/cm³. By means of a Born–Oppenheimer molecular dynamics simulation, the system has been further equilibrated (within the NVT ensemble) at 300 K for 20 ps and then let to evolve in the NVE ensemble for other 20 ps to calculate the radial distribution functions (RDF).

A larger 1 × 3 supercell slab model (108 atoms) for the (101) anatase surface was used for the molecular dynamics simulations of the water/surface interface. A Monkhorst–Pack k-point mesh of 2 × 2 × 1 ensured the convergence of the electronic structure, and the forces were relaxed to less than 10^–4 au.

We have studied a monolayer (ML), a bilayer (BL), and a trilayer (TL) of water, composed of 6, 12, and 18 water molecules, respectively. The Newton’s equations of motion were integrated with the Velocity Verlet algorithm, and a relative small time step of 0.5 fs was used to ensure reversibility. A Nosé–Hoover thermostat ensured a constant low value temperature (160 K) to avoid the desorption of superficial water molecules. After 5 ps of equilibration, the systems were allowed to evolve for other 20 ps.

2.4. Transition State Search

The transition state structure for a single water molecule dissociation on the 1 × 2 model has been evaluated with the NEB method,⁶⁶ as implemented in the Atomic Simulation Environment (ASE).⁶⁷ This toolkit is a driver, which interfaces an internal NEB algorithm with an external total energy calculator (the DFTB+ program in this case). The NEB procedure was carried out employing 20 intermediate images. Successively, we have calculated the Hessian matrix for the transition structure to confirm it was a saddle point on the potential energy surface. The reaction barrier for the dissociation process is defined as

7

where E_TS is the energy of the transition state geometry and E_slab+mol the total energy of the optimized geometry of molecular water adsorbed on the titania surface.

3. Results and Discussion

3.1. Testing DFTB sets on Water Dimer and Bulk Water Properties

Aiming for a correct description of the water/TiO₂ (101) anatase surface interface, the methods must adequately describe the two components separately. Here, we focus the attention on the liquid component: water.

First, we use the water dimer binding energy as a measure of the strength of a single hydrogen bond (ΔE_H-bond). In Table 1, we report the ΔE_H-bond values and the equilibrium oxygen–oxygen distance (R_O–O) as obtained with the MATSCI, the MIO, and the combined MATORG+HBD sets. For comparison, we show the corresponding values obtained with the post-HF CCSD⁶⁸ and standard and hybrid DFT⁶⁹ methods, together with the experimental values, determined by velocity map imaging (for ΔE_H-bond)⁷⁰ and molecular beam electric resonance spectroscopy (for R_O–O).⁷¹

Table 1. Binding Energy (ΔE_H-bond) and Oxygen–Oxygen Distance (R_O–O) of a Water Dimer, as Obtained with SCC-DFTB Methods (MATSCI, MIO, and MATORG+HBD), with High Level Wavefunction and Density Functional Methods (CCSD, PBE, and B3LYP), and with Velocity Map Imaging (for ΔE_H-bond) and Molecular Beam Electric Resonance Spectroscopy (for R_O–O) Experiments^a.

method	ref	ΔEH-bond (eV)	RO–O (Å)
DFTB-MATSCI	this work	0.084 (−0.152)	2.863 (−0.109)
DFTB-MIO	this work	0.144 (−0.092)	2.862 (−0.110)
DFTB-MATORG+HBD	this work	0.199 (−0.037)	2.815 (−0.157)
CCSD	ref (68)	0.218	2.912
DFT-PBE	ref (69)	0.222	2.889
DFT-B3LYP	ref (69)	0.198	2.926
exp.	refs 70 and 71	0.236	2.972

^aThe absolute error with respect to the experimental values is reported in parentheses.

Not surprisingly, the MATSCI set presents the poorest description of the H-bond since it was not conceived to describe this type of system. The H-bond energy obtained with the MIO set is in better agreement with data in the literature but still significantly underestimated. With the inclusion of the hydrogen-bond damping function (HBD),⁵⁶ the underestimation is greatly healed, and the binding energy is closer to the ab initio references and the experiment (see MATORG+HBD value). However, the HBD correction causes a slight shortening of the oxygen–oxygen distance (∼0.05 Å), so hydrogen bonds are expected to be somewhat too short.

The second crucial point in the description of water systems is the correct evaluation of the radial distribution function (RDF) of oxygen–oxygen (O_w–O_w) and hydrogen–hydrogen (H_w–H_w) atoms in bulk water. The RDF obtained with the DFTB methods together with the experimental reference are shown in Figure 1. The first intermolecular peaks of r(O_w–O_w) and r(H_w–H_w) in the experiment are located at 2.77 and 2.31 Å, respectively. In the MATSCI RDFs, these two intermolecular peaks are located at ∼2.92 and 2.96 Å, respectively. For r(O_w–O_w), we observe a significant shift of ∼0.3 Å, which indicates that water molecules of the first solvation shell are too far apart. Additionally, the first water density depletion is very shallow, and its minimum is located at large distances, approximately where the second solvation shell peaks in the experimental RDF. This implies an overcoordination in the first water solvation shell and a poor description of the long-range structure. Moreover, the shape of the H_w–H_w RDF is completely different from the experiment, and the first intermolecular peak is shifted by ∼0.6 Å with respect to the experiment.

Figure 1.

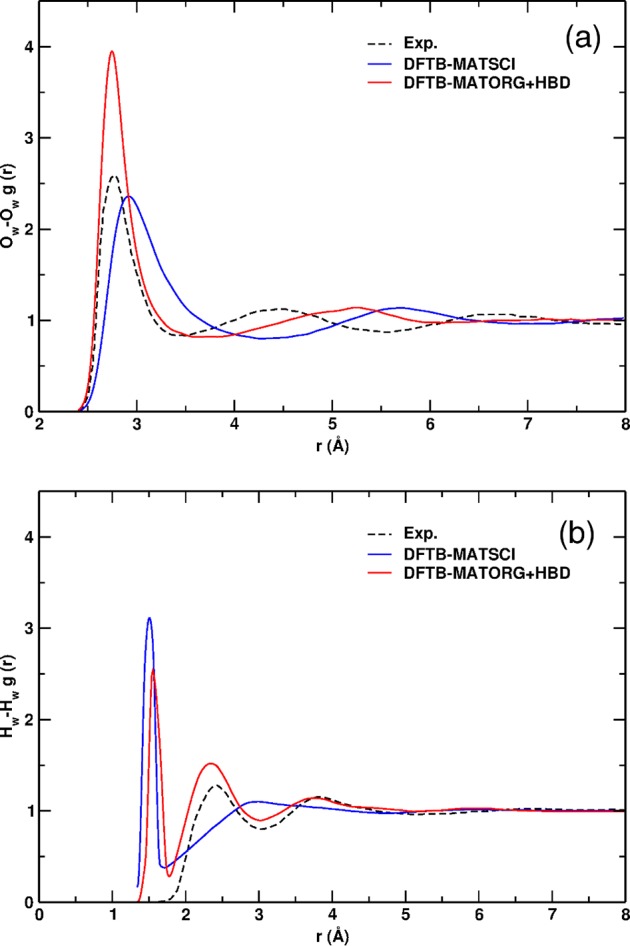
Comparison of the oxygen–oxygen (O_w–O_w, a) and hydrogen–hydrogen (H_w–H_w, b) radial distribution functions (RDF): dashed black line, experimental measurement; blue line, DFTB-MATSCI; red line, DFTB-MATORG+HBD with the modified γ function for the H-bond.

On the contrary, as previously reported,⁵⁶ using the MIO set and introducing the corrected γ function by the MATORG+HBD method, there is a significant improvement of the O_w–O_w radial distribution function, shown in Figure 1a: even if the first peak is too high, its position is shifted back to 2.75 Å. Thus, the RDF function partially overlaps with the experimental curve for distances lower than 3.30 Å; the density depletion zone is found within a range of distances closer to the experiment; the second intermolecular peak at 5.25 Å is closer to the experimental data (4.55 Å). Additionally, the experimental H_w–H_w radial distribution function in Figure 1b is better reproduced by MATORG+HBD, with the first intermolecular peak located at 2.34 Å, in very good agreement with experiments. We have also considered the effect of the dispersion corrections (D3), as proposed by Grimme,³⁴ on the evaluation of the bulk water RDF (Figure S1, Supporting Information). The position of the first two intermolecular peaks in the distribution functions r(O_w–O_w) and r(H_w–H_w) is found to be unaffected. We only observe a slight increase in their relative peaks height.

In addition, we have calculated the normalized velocity autocorrelation functions (C_vv) for oxygen and hydrogen (Figure S2, Supporting Information) and compared them with Car–Parrinello (PBE) molecular dynamics data (CPMD).⁷² DFTB autocorrelation functions decay approximately to zero within 500 fs. However, the DFTB O and H C_vv are different from CPMD ones in the first 200 fs where they decay more quickly. As previously pointed out,⁵⁷ this is related to the fact that the MATORG+HBD approach gives weaker H-bonds (Table 1) with respect to the DFT-PBE and experiment. This also leads to a higher DFTB water self-diffusion coefficient (0.65 ± 0.02 Ų/ps) that is, however, still comparable to the experimental (0.23 ± 0.04 Ų/ps)⁷³ and CPMD (0.1 Ų/ps) ones.

Concluding this section, we showed that the MATORG+HBD set presented in this work overcomes the limits of the MATSCI set, providing reasonable results both for the H-bond energy in water dimers and for the bulk water structure.

3.2. Testing DFTB Sets on Bulk Anatase TiO₂

In this section, we compare bulk anatase structural parameters from DFTB approaches with DFT and experimental values, as detailed in Table 2.

Table 2. Bulk TiO₂ Anatase a and c Parameters and Their c/a Ratio as Computed with DFTB and DFT Methods, Compared with the Experimental Values^a.

method	ref	α (Å)	c (Å)	c/a (Å)
DFTB-TIORG	this work	3.848 (+0.066)	9.355 (−0.147)	2.431 (−0.081)
DFTB-MATSCI	this work	3.810 (+0.028)	9.732 (+0.230)	2.554 (+0.042)
DFTB-MATORG+HBD	this work	3.796 (+0.014)	9.790 (+0.288)	2.579 (+0.067)
DFT-PBE	this work	3.789 (+0.007)	9.612 (+0.110)	2.537 (+0.025)
DFT-PBE	ref (74)	3.786 (+0.004)	9.737 (+0.235)	2.572 (+0.060)
DFT-B3LYP	ref (75)	3.783 (+0.001)	9.805 (+0.303)	2.592 (+0.080)
exp.	ref (76)	3.782	9.502	2.512

^aThe absolute errors (in parentheses) refer to the experimental data.

In general, DFTB values are in excellent agreement with both DFT and experimental data. The MATSCI set gives a very good a value but overestimates the lattice parameter c and consequently the c/a ratio, although less than the DFT-B3LYP method. Only the TIORG parametrization results in a small underestimation of the c lattice vector, giving a consequently lower c/a ratio. We recall that the MATORG+HBD set differs from the MATSCI set for the O on-site and pair interactions since they are taken from the MIO set. Nonetheless, bulk parameters from MATORG+HBD are as good as those from MATSCI. It is important to underline that the HBD correction does not act here since no H atoms are present.

3.3. Water Adsorption on TiO₂ Anatase (101) Surface

3.3.1. Adsorption Energy

In this section, we analyze adsorption energy per molecule (ΔE_ads^mol) for different water coverages on the anatase TiO₂ (101) surface in both the molecular and dissociated state, i.e., when all the water molecules in the model are undissociated or dissociated, respectively. DFTB values for all the parametrization schemes are compared to DFT-PBE results and experimental data in Table 3.

Table 3. Adsorption Energies Per Molecule (ΔE_ads^mol) of Water on the (101) Anatase Slab in Molecular (H₂O) and Dissociated (OH,H) States at Low (θ = 0.25) and Full (θ = 1) Coverage, as Obtained with DFT and DFTB Methods^a.

method	ref	coverage, θ	ΔEadsmol, H2O (eV)	ΔEadsmol, OH, H (eV)
DFTB-TIORG	this work	0.25	–0.86 (–0.19)	–0.83 (–0.51)
		1	–0.80 (–0.18)	–0.98 (–0.55)
DFTB-MATSCI	this work	0.25	–0.79 (–0.12)	–0.34 (–0.02)
		1	–0.70 (–0.08)	–0.38 (+0.05)
DFTB-MATORG	this work	0.25	–1.08 (–0.41)	–0.54 (–0.22)
		1	–0.96 (–0.34)	–0.58 (–0.15)
DFTB-MATORG+HBD	this work	0.25	–0.80 (–0.13)	–0.31 (+0.01)
		1	–0.71 (–0.09)	–0.40 (+0.03)
DFT-PBE	this work	0.25	–0.67	–0.32
		1	–0.62	–0.43
DFT-PBE	ref (17)	0.25	–0.74	–0.23
		1	–0.72	–0.44
exp.	TPD, refs 18 and 19	1	–0.5/–0.7

^aThe experimental range of adsorption energy of the water monolayer on the (101) surface is also given. The absolute error reported in parentheses for DFTB data is calculated with respect to the PBE values from this work.

Only with the TIORG set are binding energies for the water adsorption on the (101) surface overestimated, and at high coverage, water dissociation is even favored, at odds with several experimental reports^16,18−20 and previously reported DFT values.^17,21 With all the other sets, this crucial qualitative feature is always well reproduced. Given these results, we refrained from further investigating the applicability of the TIORG set for this specific water/TiO₂ benchmark system.

We note that with all DFTB methods, as the water coverage increases, the binding energy per molecule decreases for the molecular state, whereas it slightly increases for the dissociated one, in line with DFT calculations.

However, molecular adsorption energies are, in general, overestimated by DFTB methods, particularly in the case of MATORG, with errors up to 0.41 eV. The inclusion of the HBD modified γ function (MATORG+HBD) corrects this serious issue, reducing the errors to less than 0.13 eV, in line with MATSCI results.

Therefore, both MATSCI and MATORG+HBD are expected to provide an accurate description of the water monolayer/anatase surface dynamical behavior. Nonetheless, the MATORG+HBD set should outperform MATSCI when two or more layers of water molecules are present over the surface slab since water/water interactions are much better described by MATORG+HBD.

3.3.2. Equilibrium Geometries

The equilibrium structure of the molecular and dissociated water molecule on the (101) anatase surface, as computed with DFT-PBE in the low coverage regime (θ = 0.25), is shown in Figure 2. In Table 4, bond distances and α angle values (as defined in Figure S3 in the Supporting Information) are reported as obtained with different theoretical methods.

Figure 2.

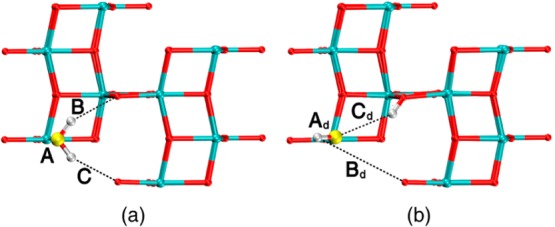
Molecular, H₂O (a) and dissociated, OH, H (b) equilibrium structure in the low coverage regime, θ = 0.25, as obtained with DFT-PBE calculations. Values of bond distances are reported in the Table 4.

Table 4. Relevant Interatomic Distances (in Å) of Equilibrium Structures of H₂O (Molecular Adsorption, top panel) and OH, H (Dissociative Adsorption, bottom panel) on the (101) TiO₂ Anatase Slab, in the Low Coverage Regime (θ = 0.25) as Obtained with DFTB and DFT Methods^a.

molecular adsorption
method	ref	Ti5c–OH2 A (Å)	H···O2c B = C (Å)	α (deg)
DFTB-MATSCI	this work	2.37 (+0.06)	2.33 (−0.01)	101.6°
DFTB-MATORG+HBD	this work	2.31 (+0.00)	2.26 (−0.08)	105.5°
DFT-PBE	this work	2.31	2.34	96.2°
DFT-PBE	ref (17)	2.28	1.96

dissociative adsorption
method	ref	Ti5c–OH Ad (Å)	H···O2c Bd (Å)	H*···OH Cd (Å)
DFTB-MATSCI	this work	1.90 (+0.07)	4.14 (−0.17)	2.80 (+0.14)
DFTB-MATORG+HBD	this work	1.89 (+0.06)	3.92 (−0.39)	2.92 (+0.26)
DFT-PBE	this work	1.83	4.31	2.66
DFT-PBE	ref (17)	1.85	–	2.39

^aH is the hydrogen atom of the OH group bound to the Ti atom, whereas H* is the hydrogen atom bound to the bridging O_2c atom. These geometrical parameters are graphically defined in Figure 2 and Figure S3. The absolute error reported in parentheses for DFTB data is calculated with respect to the PBE values from this work.

The undissociated water molecule binds to the 5-fold coordinated titanium atom with a bond length of about 2.3 Å (defined as A in Figure 2a and Table 4). Hydrogen atoms establish two identical H-bonds, with a length of about 2.3 Å (defined as B and C in Figure 2a and Table 4), with the neighboring bridging O_2c atoms. Analyzing the data in Table 4, one can clearly conclude that both DFTB sets correctly describe the geometry of a single water molecule adsorbed on the TiO₂ (101) anatase surface, with the MATORG+HBD being better for Ti–OH₂ equilibrium distance. However, the bond angle α (defined as the angle between the oxygen atom of the water molecule, the Ti surface atom, bonded to H₂O, and its nearest O_2c atom, H₂O–Ti–O_2c, see Figure S3) is wider for both the DFTB methods than the DFT value. Since Ti–OH₂ bond lengths are about the same, we must conclude that with DFTB methods the water molecule is closer to the surface with respect to what computed with DFT.

In the case of the dissociated water molecule (Figure 2b and bottom panels of Table 4), one of the hydrogen atoms of the water molecules is adsorbed at the bridging oxygen site (O_2c), whereas the residual OH binds to the Ti_5c site. The Ti–OH equilibrium distance (A_d in Table 4 and Figure 2b) is only slightly overestimated by the two DFTB methods, whereas the two distances describing the H-bonds (B_d and C_d in Table 4 and Figure 2b) are in qualitative agreement with the DFT reference.

Similar considerations can be drawn at the full coverage regime (θ = 1), whose geometrical parameters of molecular and dissociated water molecules on the anatase surface are given in Figure S4 and Table S1 in the Supporting Information.

3.4. Molecular Dynamics of Water Layers on TiO₂ Anatase (101) Surface

In this section, we present the results obtained by performing molecular dynamics (MD) simulations with the MATORG+HBD set, which we proved to have an accuracy comparable to DFT in describing the water adsorption on the TiO₂ anatase (101) surface in the previous section. We compare them with previous studies based on Car–Parrinello (PBE) MD simulations¹⁴ and other DFT (PBE) structural investigations.⁶¹

3.4.1. Monolayer

The most stable, fully undissociated configuration of the water monolayer (ML) was considered, as shown in Figure 3.

Figure 3.

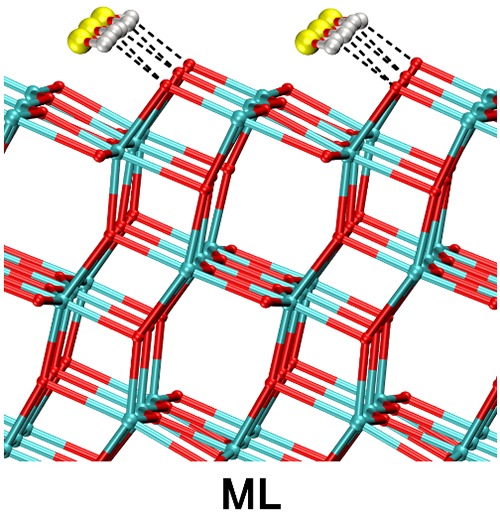
MATORG+HBD structure of a monolayer of water on the (101) TiO₂ anatase surface. Dashed lines correspond to H-bonds. The structure corresponds to the 0 K geometry optimization of the last snapshot of the molecular dynamics trajectory.

From the MD simulation run, we extracted the distribution p(z) of the vertical distances between the O atoms of the H₂O molecules and the Ti_5c plane of the surface, together with their time evolution, z(t) (Figure 4). In this case, the agreement with the Car–Parrinello (PBE) molecular dynamics data¹⁴ is satisfactory: the width of the p(z) distribution is very similar to the reference, and the peak is shifted by only 0.1 Å to shorter values. This is because, as already mentioned for static calculations in Section 3.3.2, the Ti–OH₂ bond distance is perfectly reproduced by DFTB, whereas a broader α angle (H₂O–Ti–O_2c, see Figure S3) is computed: 108.7° with MATORG+HBD vs 93.0° with PBE, with tiny oscillations around this value during the simulation. This tilting effect is further confirmed by the good overlap of the DFT and DFTB distributions of the Euclidean Ti–OH₂ distances p(d) in place of the perpendicular distances p(z), as shown in Figure S5 of the Supporting Information.

Figure 4.

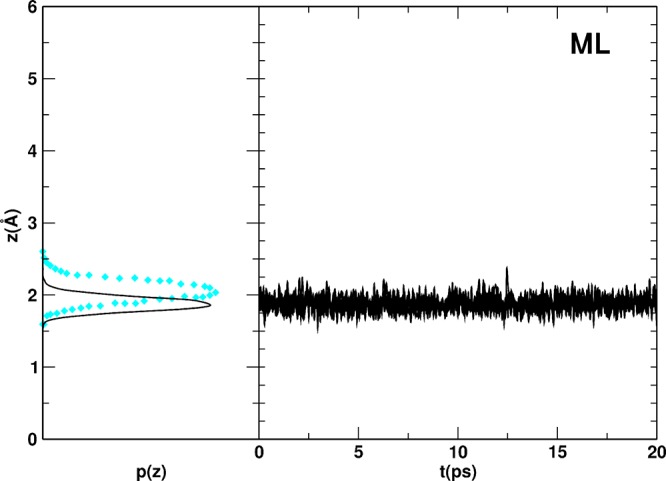
MATORG+HBD distribution p(z) and time evolution z(t) of the distances between the water molecules (O atoms) of the water monolayer and the titania surface (Ti_5c atoms). The DFT Car–Parrinello corresponding distribution p(z) is reported in cyan diamonds.¹⁴

During the MD simulation, we observe that each molecule librates around its equilibrium site, as it can be seen in the time evolution of perpendicular distances (see right side of Figure 4).

Furthermore, the adsorption energy per molecule (ΔE_ads^mol in Table 5), as computed with the MATORG+HBD method for the water monolayer (ML), is 0.70 eV and shows a very good quantitative agreement with the PBE references.¹³

Table 5. Binding Energy Per Molecule (ΔE_ads^mol) of the Water Monolayer (ML), Bilayer (BL1 and BL2), and Trilayer (TL1 and TL2) on the (101) TiO₂ Anatase 1 × 3 Slab Model, as Obtained with DFT and DFTB Methods after an Optimization Run of the Last Snapshot of the MD Simulation^a.

	ΔEadsmol (eV)
water configuration	DFTB-MATORG+HBD	DFT-PBEb	DFT-PBEc
ML	–0.70	–0.62	–0.69
BL1	–0.73	–0.67	–0.65
BL2	–0.84	–0.66	-
TL1	–0.53	–0.53	–0.56
TL2	–0.51	–0.45	-

^aThe binding energy has been calculated as the total energy difference between the equilibrium structure of the water/titania interface and the isolated systems, i.e., six isolated water molecules and the optimized slab with one water layer less.

^bThis work.

^cFrom ref (13).

3.4.2. Bilayer

The situation is more complicated for the water bilayer (BL). Here, two different configurations have been considered, in line with previous works.^13,14,61 We label them BL1 and BL2, as reported in Figure 5. In the BL1 configuration, each molecule of the first water layer is bound to Ti_5c atoms and forms two H-bonds with two molecules of the second layer. The second layer molecules have only one H-bond with an O_2c of the TiO₂ surface, with the other H atom pointing upward. In the BL2 configuration, the first layer water molecules are still bound to the Ti_5c atom of the surface, but each one presents only one H-bond with the second layer molecules, which, in turn, establish two H-bonds with the surface O_2c. Overall, the number of H-bonds is the same in the two cases. Indeed, with our DFT-PBE setup, we found that the two configurations are essentially isoenergetic: the absorption energy of the second layer for the BL1 case is −0.67 eV per molecule, whereas it is −0.66 eV for the BL2 (Table 5). Similar results are reported in ref (13).

Figure 5.

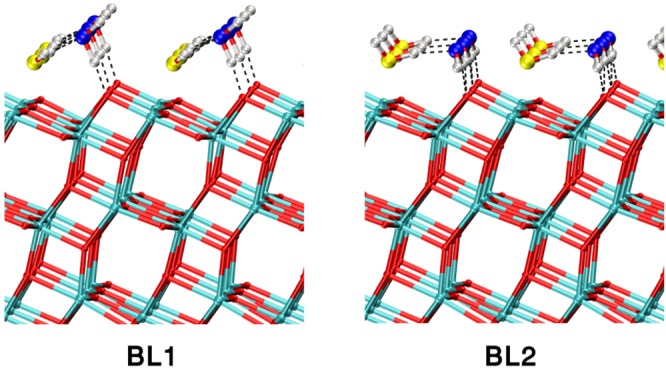
MATORG+HBD structures of different models of water bilayers on the (101) anatase titania surface, BL1 and BL2. Dashed lines correspond to H-bonds. The structure corresponds to the 0 K geometry optimization of the last snapshot of the molecular dynamics trajectory.

For completeness, we performed molecular dynamics simulations starting from both configurations. The p(z) distribution and z(t) time evolution of the vertical (z) component of the distance between the O atoms of the H₂O molecules, and the Ti_5c atoms of the surface are compared to PBE simulations in Figure 6.

Figure 6.

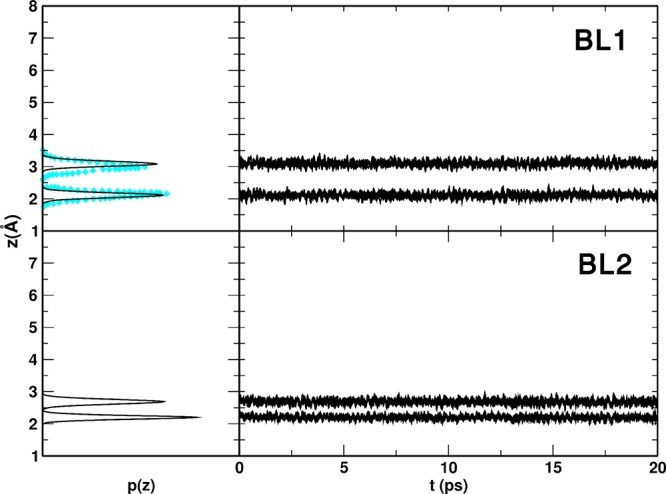
MATORG+HBD distribution p(z) and time evolution z(t) of the distances between the water molecules (O atoms) of the two water bilayer configurations, defined in Figure 5, and the titania surface (Ti_5c atoms). The DFT Car–Parrinello corresponding distribution p(z) for BL1 (top panel) is reported in cyan diamonds.¹⁴

Focusing on the BL1 plots, there is a very good match between the DFT and DFTB p(z) distribution, both for the position of the peaks and for their broadening: with PBE, the first layer is at 2.15 Å and the second one at 2.98 Å, whereas with MATORG+HBD, the first group of distances is peaked at 2.11 Å and the second at 3.08 Å. The α angle (H₂O–Ti–O_2c) of first layer water molecules with the slab, as defined in Figure S3, is around 90° for both DFTB and DFT.

In the case of BL2 plots in Figure 6, we can see that distance distributions are strongly peaked at 2.20 and 2.69 Å for DFTB, indicating a good stability for this kind of configuration, where the water molecules of the second layer are closer to the surface.

Although the bilayer structures and dynamics are well-reproduced by DFTB with respect to DFT, the adsorption energies per molecule (ΔE_ads^mol) for both configurations are slightly overestimated, and BL2 is computed to be favored with respect to BL1, in contrast with DFT results where they are isoenergetic (Table 5). This effect may be explained by a greater stability of the water molecules in the second layer of BL2 when using DFTB with respect to DFT-PBE. In fact, these water molecules establish stronger and shorter H-bonds with the bridging oxygen atoms of the surface, as clearly shown for a single water molecule in Figure S6 in the Supporting Information.

Although there are some little differences between DFTB and DFT results, the qualitative picture is similar, i.e., the first two layers are vertically ordered and adapt to the TiO₂ surface periodic structure.

3.4.3. Trilayer

The water trilayer (TL) cannot be uniquely defined since the third layer of water is too mobile. However, we devised two different starting configurations based on what observed above for the water bilayers. Thus, we set up the TL1 and TL2 configurations, where the first two water layers are in the same conformation of the BL1 and BL2 models, respectively. The geometries of both structures, as obtained with MATORG+HBD, are shown in Figure 7.

Figure 7.

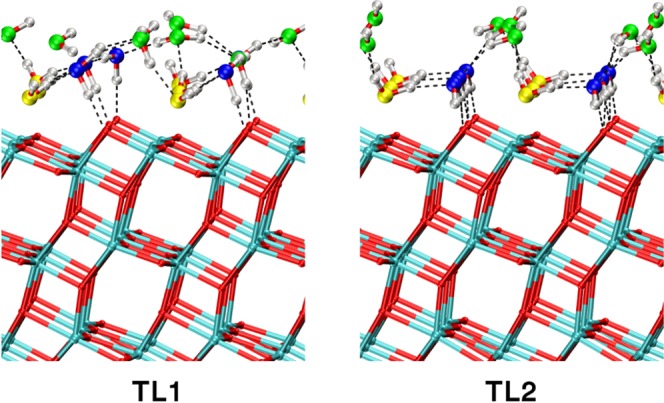
MATORG+HBD structures of different models of water trilayers on the (101) anatase titania surface, TL1 and TL2. Dashed lines correspond to H-bonds. The structure corresponds to the 0 K geometry optimization of the last snapshot of the molecular dynamics trajectory.

In Figure 8, we report the results of the MD run, i.e., the distribution p(z) of the distances along the z coordinate and their evolution in time, z(t), for the two configurations and compare them to the available DFT reference.¹⁴ The agreement is rather good.

Figure 8.

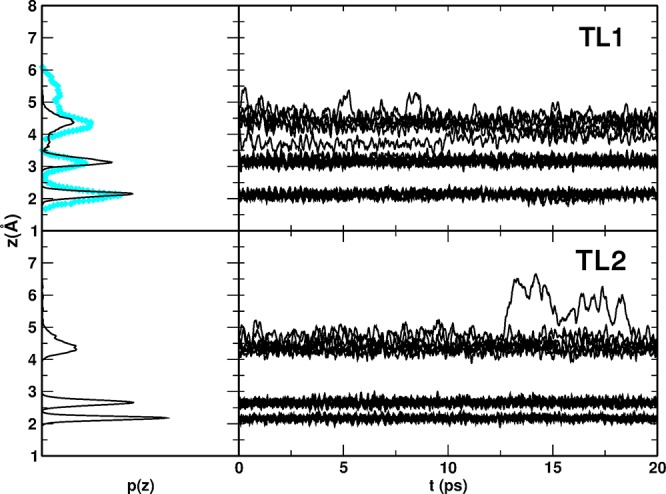
MATORG+HBD distribution p(z) and time evolution z(t) of the distances between the water molecules (O atoms) of the two water trilayer configuration and the titania surface (Ti_5c atoms). The DFT Car–Parrinello corresponding distribution p(z) for TL1 configuration (top panel) is reported in cyan diamonds.¹⁴

The p(z) distribution of the TL1 configuration, in the top panel of Figure 8, shows a good match between the DFT and DFTB curves: the first two layers in the DFTB MD simulation are vertically ordered in a fixed position and never interact during the whole simulation, whereas the third layer is more mobile and interacts with the second layer water molecules. The range of vertical distances for the third layer is between 3.6 < z < 5.1 Å with DFTB; thus, it is closer to the surface than with DFT.

The adsorption energies per molecule (ΔE_ads^mol) for the TL1 and TL2 configurations (Table 5) match the values obtained with DFT-PBE. Additionally, the TL1 structure is found to be more energetically favorable with both approaches.

In Figures S7–S9 of the Supporting Information, the analogous p(z) and z(t) for the ML, BLs, and TLs as obtained from the molecular dynamics simulations with the MATSCI set of parameters are given. We observe a very good match with the DFT reference only for the monolayer configuration (Figure S7), whereas there is a poor overlap for the bilayer and trilayer cases (Figures S8 and S9) because the water/water interactions, which are underestimated by MATSCI, become more important.

From this analysis, we can extract the main factors governing the water/titania interface, which are correctly addressed by DFTB. First of all, it is clear that the balance between water/surface and water/water interactions is the key aspect in the multilayer water adsorption. The water/water interaction is found to be always weaker than the water/surface one, in accordance with a previous DFT work.¹³ Furthermore, while the water molecules are always vertically ordered in all the situations considered (ML, BLs, TLs), the in-plane order is present only for the first two layers since the third one is found to be very mobile, in agreement with another DFT work.¹⁴ The in-plane order is related to the strong coordination of the first layer water molecules with the Ti_5c atoms of the surface, which keeps the molecules far from the others and prevents interactions. This still holds for the second layer water molecules, which are H-bonded to the surface bridging O atoms, but not for the third layer that does not directly interact with surface atoms. Finally, we observed that the binding strength of the first water layer increases at coverages higher than 1 ML, as also reported in ref (14). This effect can be assessed from the decreasing Ti_5c–water average distance (ML= 2.43 Å, BL = 2.29 Å, TL = 2.28 Å), as extracted from the DFTB MD simulations.

To conclude this section, one can summarize that the use of a corrected hydrogen bonding damping function (HBD) in the combined MATORG set allows for a punctual description of the balance between water/water and water/titania interactions, which results in a good agreement with the DFT reference for the p(z) distributions in Figures 4, 6, and 8 and ΔE_ads^mol values in Table 5. We have also tested the effect of the additional inclusion of the dispersion corrections (D3) proposed by Grimme.³⁴ The result is that binding energies systematically increase by about 0.2 eV, but no qualitative improvement in the description of the water/titania interface is observed. For instance, the issue regarding the relative stability between BL1 and BL2 bilayers still persists.

3.5. Energy Barrier for Water Dissociation on the TiO₂ Anatase (101) surface

In this section, we compare the energy barrier associated with the dissociation of a single molecule of water on a Ti_5c site of the anatase TiO₂ (101) surface (coverage θ = 0.25) as obtained with DFTB and DFT methods (Table 6).

Table 6. Energy Barrier for Water Dissociation on the Anatase TiO₂ 1 × 2 Model (ΔE_diss^‡) and Total Energy Difference between Molecular and Dissociated Water Adsorption (ΔE_diss).

method	ref	ΔEdiss‡	ΔEdiss
MATSCI	this work	1.12	0.41
MATORG+HBD	this work	0.96	0.49
DFT-PBE+U	ref (77)	0.52	0.40
DFT-B3LYP-D*	refs 78 and 79	0.81	0.36

The barrier for this reaction is generally overestimated by all DFTB methods, in particular, with the MATSCI set. However, the MATORG set, after the introduction of the HBD correction, gives results in better agreement with the references. Additionally, one should mention that the reaction barrier for water dissociation, as found with DFT-B3LYP-D*,^78,79 is higher than the PBE+U reference, with a barrier closer to the one obtained with DFTB. In any case, we note that such high barriers would not allow observing spontaneous water dissociation processes in a reasonably long MD simulation time. In Figure S10 and Table S2 in the Supporting Information, transition state structure and its geometrical parameters are reported. With the HBD correction, the transition structure is also decently reproduced, with absolute errors lower than 0.2 Å. Specifically, the transition state is predicted to be to some extent later than with DFT-B3LYP-D*, i.e., the distance between the oxygen atom of the water and the leaving hydrogen atom is longer with MATORG+HBD.

4. Summary and Conclusions

Titanium dioxide systems have been extensively investigated with DFT-based methods, but the simulation of large TiO₂ models and their interaction with an aqueous medium is yet not feasible, especially if one aims at studying dynamical properties. SCC-DFTB is a fast approximated quantum mechanical method, which has been successfully applied to a wide range of systems in (bio)chemistry and materials science. Since the computational effort within SCC-DFTB is significantly lower than in DFT, it is capable of performing simulation of large models with thousands of atoms. However, the accuracy of the method is related to the DFTB approximations as outlined above and described in detail in, e.g., refs (25, 28, and 62).

In this work, we have demonstrated the applicability of SCC-DFTB to the study of the structural, energetic, and dynamical properties of the titania/water-multilayers interface when a proper combination of the already existing DFTB sets of parameters and corrections for water systems are employed. Specifically, we combined the parameters generally used for solid-state systems (“matsci-0-3”, MATSCI) with the ones largely benchmarked for water and organic systems (“mio-1-1”, MIO) in a novel DFTB-based approach, which we have called the MATORG+HBD method.

On the basis of this new technique, we have first separately studied the two components of the interface to test the ability in describing the water/water interaction, and we evaluated the water dimer H-bond energy and the bulk water radial distribution function, whereas for bulk TiO₂ the lattice parameters of the unit cell have been reproduced. The agreement with DFT and experimental references is very satisfactory with an absolute error of 0.04 eV for water dimer energy, root-mean-square error of 0.17 Å for the position of the first two peaks of the O and H RDF, and 0.14 Å for the bulk TiO₂ lattice parameters. Regarding the interface, we obtained a correct static description of the water adsorption on the (101) anatase surface both from a structural and energetic point of view. Therefore, given this good balance between water/water and water/titania interactions, the method was found to be successful also for the dynamic description of the interface, when compared with previous DFT-based MD calculations (Car–Parrinello). In addition, the MATORG+HBD method was also found to give a correct description of the transition barrier for water dissociation, even though the activation energy is slightly overestimated with respect to hybrid DFT calculations. Overall, we found that our combined approach describes better this specific interface (anatase (101) TiO₂/water-multilayers) with respect to the other pre-existing DFTB sets.

In conclusion, with the set of parameters presented in this work (MATORG+HBD), we are able to reproduce the main features of the titania/water-multilayers interface with an accuracy comparable to DFT methods at a particularly low computational cost. On the basis of the proven reliability of SCC-DFTB for water/water/titania interactions, computationally efficient simulations of TiO₂ in an aqueous environment are justified: larger and realistic models of TiO₂ nanosystems into a solvent surroundings, as well as long-time molecular dynamics, can be successfully devised and performed.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b00479.

• Water radial distribution function obtained with D3 dispersion corrections; water normalized velocity autocorrelation functions; graphical definition of the α angle; water monolayer equilibrium structures and geometrical parameters; distribution of Euclidean distances d(t) between the water monolayer and the Ti_5c of the slab; geometry of a single water molecule of the second layer of the bilayer; distribution functions z(t) as obtained with MATSCI for the ML, BLs, and TLs; and structure and bond lengths for the water dissociation transition state. (PDF)

Author Contributions

D.S. and G. F. have equally contributed to this work.

The authors declare no competing financial interest.