On the conservative nature of intragenic recombination

Abstract

Intragenic recombination rapidly creates protein sequence diversity compared with random mutation, but little is known about the relative effects of recombination and mutation on protein function. Here, we compare recombination of the distantly related β-lactamases PSE-4 and TEM-1 to mutation of PSE-4. We show that, among β-lactamase variants containing the same number of amino acid substitutions, variants created by recombination retain function with a significantly higher probability than those generated by random mutagenesis. We present a simple model that accurately captures the differing effects of mutation and recombination in real and simulated proteins with only four parameters: (i) the amino acid sequence distance between parents, (ii) the number of substitutions, (iii) the average probability that random substitutions will preserve function, and (iv) the average probability that substitutions generated by recombination will preserve function. Our results expose a fundamental functional enrichment in regions of protein sequence space accessible by recombination and provide a framework for evaluating whether the relative rates of mutation and recombination observed in nature reflect the underlying imbalance in their effects on protein function.

A major goal in understanding the molecular basis of evolution is to quantitatively describe how effectively mutation and recombination traverse protein sequence space to create new functional proteins (1). Protein sequence distance (measured by counting the number of amino acid substitutions, m, separating two sequences) is a fundamental metric of evolutionary rate and relationships (2), diversity of structure and function (3), and a key variable in protein engineering (4, 5), whereas mutation and recombination are its biochemical cause. Genetic studies (6, 7) and algorithmic inferences from biological sequence data (8–10) have revealed that recombination can occur preferentially within coding sequences, at times with a higher frequency than mutation (11, 12). When sequences encoding divergent but related proteins recombine, large distances may be traveled in sequence space relative to random mutation (13–16) without disturbing function and/or structure. However, a complete understanding of the underlying relative efficiency of mutation and recombination in accessing nearby or distant regions of sequence space cannot be gained from genomic sequences because these become available only after natural selection has acted.

Laboratory (17) and in silico (18) evolution experiments, in contrast, can be used to quantitatively differentiate the effects of mutation or recombination on protein structure and function. By screening or selecting libraries of proteins for retention of parental function and determining the sequences of functional and nonfunctional proteins, one can determine how the retention of function or structure depends on m, the sequence distance. This type of analysis has been used to determine the effects of random mutation on the function of subtilisin (19), DNA polymerase, HIV reverse transcriptase (20), antibody fragments (5), lysozyme (21), DNA repair enzymes (22), β-lactamase, and lattice proteins (23). These studies have revealed a strikingly consistent exponential decline in the proportion of variants retaining function with increasing distance from wild type. This exponential dependence occurs because a random amino acid substitution preserves protein function with some average probability (19, 22), referred to as mutational tolerance or neutrality, ν. Multiple independent substitutions lead to an exponential decline in the probability of retaining protein function P_f, i.e., P_f(m) = ν^m (23).

Effects of recombination on protein function have not been similarly characterized, although anecdotal and qualitative studies abound. Structurally related polypeptides have been swapped among homologous single-domain proteins to create functional chimeras with substitution levels much higher than in random mutation experiments (24–30). The more conservative nature of recombination is likely to arise at least in part because the individual amino acid substitutions created by recombination, having proved compatible with a similar structure, are less likely to be incompatible in the homolog structure than substitutions created by mutation. Whether differences in residue–structure compatibility alone are sufficient to explain the conservative nature of recombination relative to mutation has remained unclear.

Here we attempt to answer the following related questions. What is the relationship between retention of function and the number of amino acid substitutions, m, introduced by homologous recombination? How does this relationship compare to random mutation, and how is it influenced by neutrality and homolog sequence identity? To set the stage, we derive a simple model comparing retention of protein function after m amino acid substitutions generated by random mutation or recombination. We show that under the simple assumption that protein function depends on compatibility of residues with the protein backbone and with each other, recombination benefits from fundamental advantages over mutation. To test our model's predictions, we measured the effects of random mutation and recombination on the function of β-lactamases. Detailed tests using in silico evolution of lattice proteins confirm the generality of the model predictions and demonstrate that recombinational tolerance depends on the neutrality of the parental structures.

Methods

Materials. Escherichia coli XL1-Blue was from Stratagene. Enzymes for DNA manipulations were obtained from New England Biolabs or Roche Molecular Biochemicals. Synthetic oligonucleotides were obtained from Invitrogen. DNA purification kits were from Zymo Research (Orange, CA) and Qiagen (Valencia, CA), and other reagents were from Sigma.

Functional Conservation and Recombination. In a previous study, we recombined PSE-4 and TEM-1 to create a well defined library of chimeras (28) and selected for those that allowed E. coli XL1-Blue to grow on 20 μg/ml ampicillin. Approximately 100 colonies were observed, and sequencing fifty of these clones identified 23 unique functional chimeras. Sequencing of the remaining clones revealed an additional eight sequences for a total of 31 unique functional chimeras (see Table 1, which is published as supporting information on the PNAS web site). Although no point mutations were found in the newly characterized chimeras, one of those previously identified as functional has two adjacent amino acid substitutions (28). Sequencing of unselected chimeras showed that nine of 13 (69%) contained frameshifts introduced during oligonucleotide synthesis. To calculate the fraction of functional chimeras at each amino acid substitution level m, we divided the number of functional chimeras by the number of possible chimeras at each m. At many substitution levels, no functional chimeras were found despite large sample sizes. To determine the average effects of recombining PSE-4 and TEM-1 over all possible substitution levels, we partitioned all chimeras into bins of substitution levels containing at least one functional chimera. The number of unique synthesized chimeras in each bin sets an upper bound on the denominator of the fraction of functional chimeras; because of the possibilities that frameshifts inactivated some chimeras and that certain fragments were overrepresented because of biases in library construction (28), it is unlikely that this upper bound was reached. The calculated fraction of functional chimeras therefore represents a lower bound on the true fraction functional at each m.

Creation and Functional Analysis of Random Mutants. PCR under mutagenic conditions was used to create libraries of PSE-4 variants with a range of amino acid substitutions. An initial library was created by amplifying 1 ng of the PSE-4 gene (100-μl total volume) in the presence of 0.5 mM MnCl₂/0.2 mM dATP/0.2 mM dGTP/1.0 mM dCTP/1.0 mM dTTP/7 mM MgCl₂/50 pmol of each primer (with restriction sites for cloning)/5 units of AmpliTaq polymerase. The temperature cycling scheme was 95°C for 5 min, followed by 13 cycles of 95°C for 30 s, 50°C for 30 s, and 72°C for 30 s. PCR products (≈0.9 kb) were purified by using a 1% agarose gel and a Zymoclean gel purification kit (Zymo Research). Libraries with increasing levels of mutation were generated by sequentially mutating 1 ng of product from each previous reaction. Each round of PCR resulted in ≈0.5 μg of a 0.9-kb amplified fragment, corresponding to nine doublings. This procedure is expected to produce an exponential decline in the fraction of functional variants at increasing library mutation levels, simplifying analysis (31).

The gene products from each library were digested with HindIII and SacI, purified by using a Zymo DNA Clean and Concentrator kit (Zymo Research), and ligated into pMon-1A2 as in a previous study (28). E. coli XL1-Blue was transformed with plasmids containing each library as recommended by the manufacturer and plated on three or more nonselective (10 μg/ml kanamycin) and selective (20 μg/ml ampicillin/10 μg/ml kanamycin) plates. The fraction of functional variants in each library P_f(〈m_nt〉) was determined by dividing the average number of colonies on selective medium by the average number on nonselective medium; all fractions reported are ± SE. The fraction of functional clones in the control populations created by cloning the PSE-4 gene into pMon-1A2 was 1.05 ± 0.06.

To determine the average mutation level 〈m_nt〉 for each library, 6,000–8,000 bp of unselected clones were sequenced. Error-prone PCR by the multiround method used here produces a known distribution of nucleotide mutations in the resulting gene library and is expected to produce an exponential decline in the fraction functional with increasing average library nucleotide mutation level 〈m_nt〉. To calculate ν, we must first take into account the fraction of nonsynonymous nucleotide mutations, p_ns; the probability of truncated/frameshifted and, thus, inactive gene products because of deletions and stop codons, p_tr; and the physical process of DNA amplification by error-prone PCR with n_cyc thermal cycles per round and PCR efficiency λ (31). The resulting experimentally observed fractions functional can be fitted with a model incorporating all these factors to obtain a value for ν:

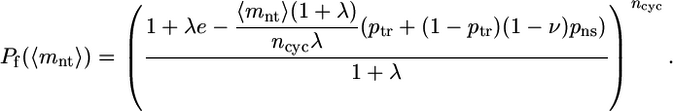[1]

See Supporting Text and Table 2, which are published as supporting information on the PNAS web site, and ref. 31 for the derivation of Eq. 1.

Lattice Protein Simulations. We implemented a 5 × 5 two-dimensional lattice model (32, 33) in which simulated polypeptide chains of length L = 25 residues fold into a maximally compact structure representing one of 1,081 self-avoiding compact walks not related by symmetry. Residues were one of 20 amino acids, contact energies between nonbonded neighboring residues were computed by using published values (table 3 of ref. 34), and conformational energy was the sum of all contact energies for that conformation.

Each simulation run began with an arbitrarily chosen wild-type conformation and a minimum stability (maximum free energy, –5.0 kT). Lattice proteins were defined as functional if their lowest free energy conformation was the wild-type conformation with free energy at or below the maximum value. An initial DNA sequence 75 nt long and encoding a functional lattice protein was found by an adaptive walk equilibrated for 10⁶ generations and used to seed two populations of 500 DNA sequences. In each generation, sequences coding for functional lattice proteins were randomly chosen to reproduce with a nucleotide mutation rate of 0.0002 per site until the new population contained 500 sequences. Evolution continued until the two populations had diverged by D amino acid substitutions. From these populations, two homologous DNA sequences were chosen, and the encoded lattice proteins designated the parental homologs. The DNA sequences were no longer considered. Site-directed amino acid recombination between these parental homologs was carried out at seven randomly chosen protein crossover points (equivalent to gene-level recombination constrained to codon boundaries) to make 512 chimeras. The number of chimeras retaining function that differed from a given parent at m residues was tabulated. Random amino acid substitutions were made to each parental sequence; all 475 1-mutants and 10,000 each of 2-mutants, 3-mutants, and so on were generated, evaluated for function, and tabulated. The fraction functional at each level of substitution is the number of functional lattice proteins divided by the number generated. This process was repeated 50 times with the same initial DNA sequence to obtain means and variances. Error analysis and fitting procedures are described in Supporting Text.

Results

A Model Comparing Mutation and Recombination. We want to answer the question, What is the probability that a protein will retain fold after m amino acid substitutions, generated by mutation or recombination? We analyzed retention of fold rather than attempted to explicitly model function for two reasons. First, the definition of function depends strongly on the particular assay or selective environment used (e.g., the precise concentration of antibiotic), whereas fold does not and is thus more tractable. Second, function requires that the protein be folded, so results for conservation of fold create an upper bound on functional conservation.

For mutation, probability of retaining fold declines exponentially with the number of substitutions,

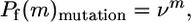[2]

where ν is the neutrality and the exponential relationship results from the approximate independence of random substitutions (23). For recombination, the exponential relationship cannot hold. Consider recombination of two protein sequences that fold into the same structure. A chimera is formed, in essence, by taking m residues from one protein and placing them at the corresponding positions in the other protein. Two proteins differing at D amino acids can produce chimeras with at most D–1 substitutions, and P_f(0) = P_f(D) = 1. Moreover, for parental proteins with similar properties, the probability of retaining fold will be symmetrical, P_f(m) = P_f(D–m), because the choice of which homolog is at m = 0 and m = D is arbitrary.

Let us assume that chimeras fold if all their residues are compatible with the native structure (e.g., have a hydrophobicity consistent with the structure's hydropathic pattern) and compatible with all other residues (e.g., not in steric clash). As in previous work (23), we suppose that each incompatibility on average reduces the stability, in some cases enough to disrupt folding. For proteins that share a structure, all residues must be compatible with that structure, so only pairwise interactions enter into P_f(m).

Each of the m substitutions in a chimera come from one parental protein and are thus compatible with each other. The only possible incompatibilities result from interactions between the m substitutions and the (D–m) remaining residues that are not identical between the homologs (all but D residues are the same). The number of possible pairwise incompatibilities resulting from these interactions is m(D–m).

If each interaction has an independent probability, q, of not disrupting folding, then a chimera with m substitutions [and thus m(D–m) possible incompatibilities] will have a probability P_f(m) = q^m(D–m) of retaining fold. (If only local interactions in the folded structure can create incompatibilities, larger proteins will have a higher apparent q than smaller proteins; we did not attempt to distinguish these effects in this analysis.) Notably, this simple expression satisfies the symmetry and end-point considerations introduced above. Because we wish to directly compare mutation and recombination, we write the probability as

[3]

so that P_f(1)_{recombination} = ρ and P_f(1)_mutation = ν.

We have now formulated P_f(m) in terms of two unknown parameters that allow us to compare mutation and recombination in a simple way: ν (the neutrality) represents the average probability that a random residue substitution will preserve fold, and ρ (the recombinational tolerance) measures the average probability that a substitution coming from a homolog via recombination will preserve fold. ν < ρ indicates that substitutions created by recombination are more conservative than random substitutions, and ν > ρ indicates the opposite. See Supporting Text for a more rigorous derivation of Eqs. 2 and 3.

Lactamase Evolution Supports Model Predictions. Our model predicts that substitutions created by recombination should have distinct effects on protein function from those created randomly. The logarithm of the fraction of functional chimeras is predicted to have a parabolic shape with the vertex center at the maximal substitution level. We also expect ν < ρ when recombining structurally related proteins, because recombination incorporates substitutions that have been preselected for compatibility with the structures being recombined.

To investigate these qualitative predictions, we took advantage of a previously reported library of lactamase chimeras in which the related PSE-4 and TEM-1 β-lactamases (43% amino acid identity and 0.98-Å backbone rms deviation) were divided into 14 fragments, which were then synthesized as oligonucleotides and combinatorially ligated to produce a maximum of 2¹⁴ (= 16,384) unique chimeric sequences (28). This construction protocol allowed us precise knowledge of the maximum number of chimeric sequences at each substitution level m, where m = 0 for PSE-4 and m = 150 for TEM-1. The structural conservation of these chimeras was assessed by selecting the library for variants that enabled E. coli growth on an ampicillin concentration that is approximately two orders of magnitude lower than the minimal inhibitory concentrations for cells expressing TEM-1 and PSE-4 (28).

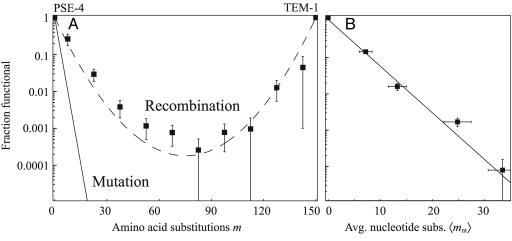
A total of 31 functional chimeras were identified upon sequencing the lactamase genes obtained from the functional selection. Of the 136 substitution levels sampled by the library, 27 contained at least one functional chimera. We calculated the fraction of chimeras that retained β-lactamase activity over all substitution levels by partitioning all possible chimeras in our library into 10 bins and dividing the number of functional chimeras by the number of total chimeras in each bin. These data represent a lower bound on the fraction of functional chimeras. Fig. 1A shows that the minimum fraction of chimeras retaining function does not decrease exponentially as it does for random amino acid substitution (5, 19–21). Rather, the logarithm of the minimum fraction of functional chimeras has a parabolic shape with its vertex found near the substitution level farthest from both parents (m = 75), as predicted by Eq. 3. A fit of Eq. 3 to the recombination data yielded ρ = 0.79 ± 0.02 (P << 0.0001) (asymptotic standard error), indicating that at least 79% of the substitutions generated by recombination preserve function. We believe that this minimum ρ is not larger than what would be found on average in other PSE-4 and TEM-1 chimeric libraries (see Supporting Text and Fig. 5, which are published as supporting information on the PNAS web site).

Fig. 1.

Effects of recombination and mutation on lactamase function. (A) Recombination results in a higher fraction of functional lactamase variants than mutation. The (minimum) fractions of functional chimeras (▪) in each bin of substitution levels m are shown relative to PSE-4 (m = 0) and TEM-1 (m = 150) (see Methods). Eq. 3 using the best-fit value ρ = 0.79 ± 0.02 (dashed line) agrees well with these data. Mutation produces a lower fraction of functional variants (Eq. 2 with a best-fit value of ν, solid line) than recombination at all values of m. (B) Error-prone PCR mutagenesis of PSE-4 results in exponentially declining retention of lactamase function with increasing substitutions. The fractions of functional PSE-4 random mutants in each of four libraries and a no-mutation control (▪) are plotted against each library's average nucleotide mutation level 〈m_nt〉± SE. The exponential best-fit of the random mutation data to Eq. 1 yields ν = 0.54 ± 0.03 (solid line).

To determine the effects of mutation on lactamase function, we mutated the PSE-4 gene by using error-prone PCR and analyzed the fractions functional in the resulting libraries. Four libraries were created, and nine or 10 unselected variants from each library were sequenced and used to calculate the average nucleotide mutation level in each library, 〈m_nt〉. Fig. 1B shows that, as observed with other proteins (5, 19–21), increasing mutations cause an exponential decrease in PSE-4 function. A fit of Eq. 1 to our experimental data revealed that the neutrality for random single amino acid substitutions is ν = 0.54 ± 0.03 (P < 0.0001) (asymptotic standard error) (see Supporting Text). Thus the individual amino acid substitutions created by error-prone PCR are tolerated 54% of the time versus at least 79% for substitutions created by recombination. We plotted ν^m for random mutation along with the recombination data in Fig. 1 A to compare the effects on function of multiple substitutions created by mutation and recombination. Extrapolation of random mutation effects to the highest substitution level accessible by recombination (m = 75) suggests that recombination is at least 16 orders of magnitude more effective than random mutation at creating the most highly substituted chimeras.

The Effects of Parental Sequence and Structure on ρ. We wanted to know to what extent the value of ρ depends on the sequence identity of parents recombined and on parental structure. To approach this question, we evaluated the effects of mutation and recombination on lattice proteins, simple simulated polymers that that have been used to rapidly assess the general features of protein sequence space (18, 32, 35).

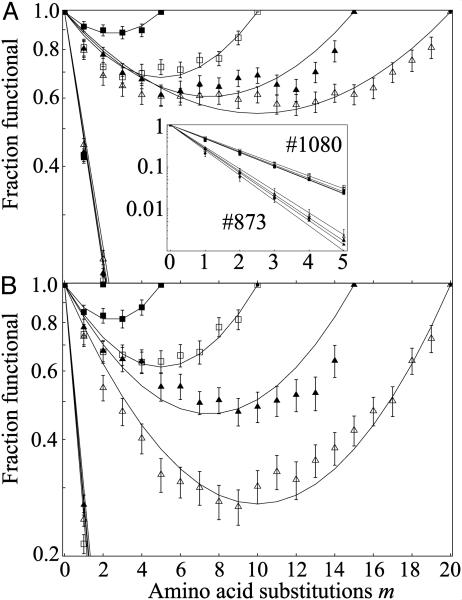
In initial experiments, libraries of chimeras were created by recombining structurally related proteins exhibiting a range of sequence identities (20–80%), and the fraction of all functional mutants (see Methods) that differed by one to five substitutions from the parents was calculated. Fig. 2 A and B shows the results from recombination experiments using distinct protein structures exhibiting high and low neutrality, respectively. For both structures, the results mirrored those from the lactamase experiments. Recombination produced proteins with parent-like structures at a rate that is orders of magnitude higher than random substitution of the same structure. The logarithm of the fraction of folded chimeras at each m is parabolic as predicted by our model, regardless of parental sequence identity or the neutrality of the proteins recombined.

Fig. 2.

Lattice protein results mirror experimental findings. Shown are average fractions of functional chimeras over 50 replicates using parents sharing 20–80% sequence identity (D = 20, 15, 10, or 5) for a high-ν structure, #1080 (A), and a low-ν structure, #873 (B) (see Supporting Text). Independent fits for ρ and ν are plotted. (Inset) Mutation data for each structure collected from homologs used to construct A and B. Curves show four independent best fits to Eqs. 2 and 3 (see Methods); error bars are ±1 SE.

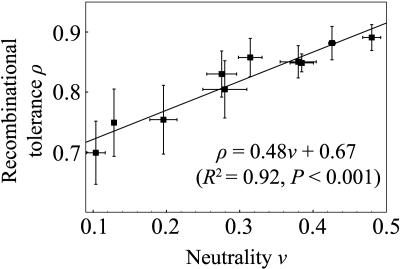
Comparable mutation and recombination data were collected for 10 distinct structures. The four trials for each structure correspond to the results from mutating and recombining four pairs of structural homologs with sequence identities of 20%, 40%, 60%, and 80%. Fig. 3 shows that recombination was more conservative than random substitution (ν < ρ) for all structures examined and that ρ correlates strongly with ν, as anticipated (see Supporting Text and Tables 3 and 4, which are published as supporting information on the PNAS web site). We fit our model to the 50-run average for each trial independently and found that fits to each data set were highly significant for ρ and ν (P < 0.0001 in all cases). Although ν varied several-fold, ρ varied less (Fig. 3). The standard deviation in ν and ρ across differing choices of homolog sequence identity was <15% of the average values, suggesting that neutrality and recombinational tolerance are determined primarily by protein structure. The values of ρ anticorrelated with sequence distance D with high significance but low variation (mean R² = 0.75; mean slope, –0.002).

Fig. 3.

Neutrality ν is correlated with recombinational tolerance ρ for lattice proteins. Results are from 10 different structures. Error bars show SD of averages of ν and ρ taken at four values of sequence identity (20%, 40%, 60%, and 80%, as in Fig. 2). For the two lowest-neutrality structures, error bars reflect two and three sequence identities, respectively, because no highly diverged homologs were found.

Discussion

We have directly demonstrated that recombination of structurally related proteins preserves function with a higher probability than does random mutation. A simple model captures the interplay of amino acid substitutions (m), parental sequence divergence (D), neutrality (ν), and recombinational tolerance (ρ) to a high degree of accuracy: Retention of function declines exponentially as ν^m after random mutation but curves symmetrically and log-parabolically as ρ^{m(d–m)/(d–1)} after recombination. For a pair of β-lactamases, we find that recombination is significantly more conservative than mutation (ν < ρ), as predicted. Notably, this finding is true even though mutations were generated by error-prone PCR, which creates less deleterious changes than truly random substitution would because of the conservative nature of the genetic code.

Computational work using lattice proteins reinforces our experimental findings and allows us to explore consequences of the model that point out potentially general phenomena and suggest future experiments. For these simulated proteins, we find that mutationally tolerant proteins are likely to be recombinationally tolerant as well (Fig. 3). The neutrality ν reflects the connectivity of function or fold networks in sequence space and has been studied as a key measure of mutational tolerance in proteins (23, 35) and RNA sequences (36, 37); our results demonstrate its importance for recombination through the correlation of recombinational tolerance ρ with neutrality. We find that the proportion of functional sequences after homologous recombination is a simple function of sequence identity and the recombinational tolerance ρ for homologs sharing 80% to as little as 20% of their primary sequence, in support of the idea that, at least for these simulated proteins, recombinational tolerance is a property of the structure.

The negative correlation between recombinational tolerance and parental sequence divergence may be explained by considering the line of descent. As two proteins diverge from a common ancestor, they accumulate substitutions at different sites. Substitutions along these lines of descent, not the total number of substitutions separating the homologs, define the potential pair-wise incompatibilities considered in our model. Our model thus undercounts substitutions and incompatibilities for highly diverged homologs, decreasing the estimate of recombinational tolerance relative to less-diverged homologs.

Specific physical observations motivate our model. Our assumptions that protein folding can be modeled by considering single (residue–backbone) and pairwise (residue–residue) interactions and that residue–backbone incompatibility is more deleterious than residue–residue incompatibility are inspired in part by a plausible source of such interactions and incompatibilities, the hydrophobic and mixing energies (38) contributing to the free energy of folding. The hydrophobic force, a residue–backbone contribution, is a dominant force in protein folding (38). Our finding that retention of function after homologous recombination can be modeled by consideration of pairwise interactions alone is consistent with the findings that proteins sharing >40% sequence identity are likely to have a shared structure (39) and that model proteins undergoing homologous recombination are overwhelmingly likely to retain the parental structure (40), thus conserving pairwise spatial relationships.

Our finding that ν < ρ is consistent with the idea that substitutions generated by recombination have been pretested for structural compatibility (25). The preservation of hydrophobic-polar patterning via recombination of similarly patterned sequences (TEM-1 and PSE-4 have 76% hydrophobic-polar identity) is one likely source of this pretesting (40). Conserved residue charge and side-chain volume may also improve the odds that recombination preserves fold and/or function (26).

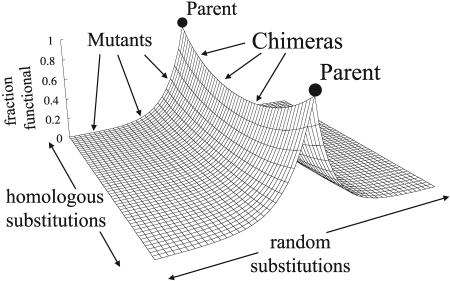
The qualitative difference between the effects of substitutions generated by random mutation and homologous recombination also has an intuitive basis: Whereas random substitutions move variant proteins away from all functional sequences on average, substitutions from homologs always move chimeras toward at least one functional sequence. Fig. 4 illustrates this fundamental difference schematically by compressing sequence space into a landscape with the average probability of retaining parental function represented by height. Although random mutants fall down exponentially sloped hills, chimeras traverse a ridge connecting the two parental sequences. Pure mutants and chimeras occupy the axes, and mutated chimeras fill the landscape. Under the assumption that the two parents and their chimeras have the same structure, mutation of these chimeras must produce the same exponential slope on average as the schematic suggests.

Fig. 4.

Chimeras occupy a functionally enriched ridge in sequence space. Surface height, the product of Eqs. 2 and 3 (see text), represents the probability of retaining parental function given independent random and homologous substitutions. Mutants lie along the near and far edges (slope determined by ν), chimeras lie on the ridge (slope determined by ρ), and mutated chimeras lie on the hillsides.

Various methods have been described that attempt to anticipate the effects of recombination on protein structure and function using sequence and structural information. Among sequence-based measures, number of crossovers (25) and crossover position (26) have been shown to affect the likelihood that recombination will preserve protein function. Our results suggest that, on average, the number of substitutions that result from a set of crossovers is the more important underlying variable. The choice of a particular structure-based measure used to anticipate chimera folding, the number of broken residue–residue contacts (SCHEMA disruption) (27, 28, 41), is supported by the present work, because these residue–residue interactions are predicted to be the dominant contributors to retention of chimera fold. For mutation, residue–backbone interactions dominate, and our work suggests that strategies to reduce these conflicts (e.g., by preserving side-chain volume and avoiding proline residues) should play a correspondingly larger role.

Our simple analytical model integrates the effects of a variety of other design parameters of interest in protein engineering (mutational tolerance, substitution level, and parental sequence divergence), providing a basis for optimizing the design of a recombination library and some general rules for obtaining libraries with a higher fraction of folded sequences (28). When sequence diversity (folded sequences with high values of m) is a goal, choosing parents with the minimum divergence necessary to achieve that goal will maximize the yield of functional proteins, all else being equal. We recently showed that mutational tolerance depends on thermodynamic stability (23), suggesting that another way to increase the efficiency of recombination for a particular structure is to choose parents with high stability. Many important questions, e.g., regarding recombination effectiveness at or between domain boundaries (24), must go beyond our average metric, but our findings create a null-model baseline for evaluating recombination strategies. Our model is limited to studying retention of function or fold by using homologs of similar structure. Furthermore, we have neglected the effects of mutations on expression, e.g., through changes in mRNA half life or secondary structure, because TEM-1 and PSE-4 are low-expression proteins for which effects on expression are unlikely to be significant relative to the inactivating effects of amino acid substitutions. The effect of mutations on expression determinants remains an important open question.

One question raised by our observations is whether relative rates of intragenic mutation and recombination reflect the underlying imbalance in their effects on protein function. This question can be partly answered. In both natural and laboratory evolution, recombination allows creation of broad sequence diversity with relatively low cost in loss of function compared to mutation. Pathogens under immune surveillance wage combinatorial warfare with their hosts, recombining homologous surface proteins to create folded proteins with diverse epitopes to escape immune responses (13, 42). In the laboratory, gene shuffling (25) and site-directed recombination (27) have proven useful in evolving new enzyme functions by generating diversity while preserving overall fold. By contrast, mutation allows access to only narrow regions of sequence space because of its deleterious effects, although it can be used to search exhaustively for local optima inaccessible by recombination. Our results may explain why recombination is so strongly favored when diversity is the goal: Intragenic recombination efficiently creates protein sequence diversity while conserving structure via preservation of interactions (24), symmetry, and conservatively chosen substitutions. Conservation of fold allows exploration of function.