Abstract
An individual’s genes may influence the phenotype of neighboring conspecifics. Such indirect genetic effects (IGEs) are important as they can affect the apparent total heritable variance in a population, and thus the response to selection. We studied these effects in a large, pedigreed population of Eucalyptus globulus using variance component analyses of Mycosphearella leaf disease, diameter growth at age 2 years, and post-infection diameter growth at ages 4 and 8 years. In a novel approach, we initially modeled IGEs using a factor analytic (FA) structure to identify the most influential neighbor positions, with the FA loadings being position-specific regressions on the IGEs. This involved sequentially comparing FA models for the variance–covariance matrices of the direct and indirect effects of each neighbor. We then modeled IGEs as a distance-based, combined effect of the most influential neighbors. This often increased the magnitude and significance of indirect genetic variance estimates relative to using all neighbors. The extension of a univariate IGEs model to bivariate analyses also provided insights into the genetic architecture of this population, revealing that: (1) IGEs arising from increased probability of neighbor infection were not associated with reduced growth of neighbors, despite adverse fitness effects being evident at the direct genetic level; and (2) the strong, genetic-based competitive interactions for growth, established early in stand development, were highly positively correlated over time. Our results highlight the complexities of genetic-based interactions at the multi-trait level due to (co)variances associated with IGEs, and the marked discrepancy occurring between direct and total heritable variances.
Introduction
Recent developments in quantitative genetics suggest that interactions among conspecifics may change the understanding of the inheritance and response to selection for polygenic traits (Bijma, 2011). Classical quantitative genetic models have overlooked the fact that an individual’s genes may also influence the phenotype of neighboring conspecifics. Such indirect genetic effects (IGEs; Griffing, 1967; Moore et al., 1997; Wolf et al., 1998; Bijma, 2014) may occur by, for example, competitive interactions (Muir, 2005; Bijma et al., 2007; Muir et al., 2013; Wilson, 2014), as well as exposure to disease infection (Lipschutz-Powell et al., 2012; Anche et al., 2014), with both recently reported among trees in a plantation (Costa e Silva et al., 2013). As with direct genetic effects, IGEs are dynamic and may change with age (Moorad and Nussey, 2016), sex (Wilson et al., 2011) and environment (Camerlink et al., 2015), and they may arise from multiple genetic causes (Wolf et al., 2011; Bailey and Hoskins, 2014). IGEs underlie many ‘social’ interactions in plants and animals (Bijma, 2014; Wilson, 2014), may vary across a species range (Bailey et al., 2014) and, at the interspecific level (IIGEs), structure biological communities (Shuster et al., 2006).
Within a univariate variance-component framework, a quantitative genetic model including IGEs seeks to estimate the covariance between direct and indirect genetic effects. This is a key determinant of the impact of indirect genetic effects on the heritable variation available at the population level for a trait affected by interactions among conspecifics (Griffing, 1967; Bijma et al., 2007; Bijma, 2011). However, as selection operates on complex phenotypes involving several correlated traits, it is important to also consider covariances among traits for direct and indirect genetic effects to better understand and predict genetic responses to selection (McGlothlin et al., 2010). Under either a variance-component or a trait-based modeling of IGEs (McGlothlin and Brodie, 2009; Bijma, 2014), recent studies have used multivariate approaches to address direct and indirect genetic relationships among traits in animals (for example, Peeters et al., 2012; Bailey and Hoskins, 2014) and in plants (for example, Mutic and Wolf, 2007; Wolf et al., 2011) but, to our knowledge, no such multivariate studies have yet been reported in forest trees.
Previous univariate models evaluating the genetic basis of interactions among trees have assumed that the indirect breeding values of all the surviving immediate neighbors impacted on the focal individual’s phenotype (Cappa and Cantet, 2008; Costa e Silva and Kerr, 2013; Costa e Silva et al., 2013; Cappa et al., 2015). They devised weights based on distance to each neighbor to integrate the neighbor effects into a modeling of IGEs as a combined effect. However, it begs the question whether the weights are optimal, and whether cardinal direction or cultural operations may moderate the position effect. For example, the neighbor effect could be moderated by prevailing wind direction, by slope and aspect and dominant direction of sunlight. In forest genetic trials, identifying the neighbor positions contributing most to IGEs is important because: (1) it may enable better detection of IGEs under a variance-component framework; and (2) it has implications for the accurate estimation of the total heritable variance determining potential response to selection.
Using a large pedigreed population of the forest tree Eucalyptus globulus, the present study aims to:
develop an approach to identify the neighbor positions contributing most to IGEs for Mycosphearella leaf disease and diameter growth;
follow over time the estimates of direct and indirect additive genetic (co)variance parameters and total heritable variance obtained for diameter growth; and
extend univariate models to the multivariate level to assess the magnitude and significance of correlations among direct and/or indirect additive genetic effects between traits (leaf disease and post-infection growth) and ages.
Materials and methods
Plant material, crossing design, field experiment and trait measurements
The plant material was generated by combining crosses from both diallel and factorial mating schemes, and evaluated in a field trial located in Western Australia (latitude 34°13′34′′ S, longitude 116°8′37′′E). Both mating schemes were unbalanced. A total of 570 full-sib families were planted, generated from 51 parents in the diallel crosses and 110 parents in the factorial crosses. The diallel scheme incorporated reciprocal mating but no self crosses. The factorial crosses were included to provide genetic links with previous breeding and research trials. The E. globulus trees used as parents in the crosses were in general selected from first-generation breeding trials, with the base population parents belonging to three races (Furneaux, Strzelecki Ranges and Otways; for Otways, all are from the Western Otways except one which was from the proximal Eastern Otways) and eight races (Furneaux, King Island, North- and South-eastern Tasmania, Southern Tasmania, Strzelecki Ranges, Eastern and Western Otways) for the diallel and factorial schemes, respectively. The numbers of parents and crosses in the diallel differed slightly from those reported by Costa e Silva et al. (2013), as some parents were re-allocated to the factorial to improve the number of families per parent and geographic focus of the parents in the diallel. The base population parents were assumed to be unrelated and non-inbred due to widely spaced sampling.
The field experiment was designed as a resolvable row–column design (John and Williams, 1995) with 15 replicates. One seedling per full-sib family was randomly planted as a single-tree plot within each replicate, and the tree spacing was 2.125 and 5.0 m within and between planting rows, respectively. There were 9450 trees originally planted in an incomplete rectangular grid of 72 rows by 161 columns. For spatial modeling purposes (see below), coordinates with missing values were added to complete the planting grid, which is a standard practice in spatial analysis of field trials with an irregular shape (Gilmour et al., 2015).
There was an outbreak of Mycosphaerella leaf disease (MLD) 2 years after planting. Each tree was then assessed for the percentage of the juvenile foliage affected by MLD, following the method described by Milgate et al. (2005). Over-bark diameter at breast height (DBH) was measured at 2, 4 and 8 years from planting, with the later age corresponding to about half the harvest age of E. globulus plantations. The MLD mean was 23% (s.d.=11%), and the DBH means increased from 98 mm (s.d.=16 mm) at age 2 to 175 mm (s.d.=37 mm) at age 8 years. The mean tree survival was high, dropping from 96% at age 2 to 93% at age 8 years.
The sequence and rationale of the analytic steps followed to model our data are depicted in Figure 1, and further details are given below and in Supplementary Information.
Figure 1.
Sequence of analyses followed to model indirect effects at the heritable and non-heritable levels for the MLD and DBH data measured in a forest genetic trial of Eucalyptus globulus.
Univariate data analysis
Definition of the general statistical model
For each trait at a given age, the following univariate general linear mixed model was fitted:
where y is a vector of individual tree observations, b is a vector of fixed effects, ua is a vector of random additive genetic effects, us is a vector of random full-sib family effects, um is a vector of random maternal effects in the diallel, ur is a vector of random reciprocal effects in the diallel, uo is a vector of additional random effects, e is a vector of random residual effects and X, Za, Zs, Zm, Zr and Zo are incidence matrices linking a tree’s phenotype to the fixed and random effects. The vector b included the overall trait mean and a term to account for the race effects within each cross type (that is, diallel or factorial). The vector ua was composed of sub-vectors comprising direct and indirect additive genetic effects. The vector us contained full-sib family effects for each cross type. The vector uo included effects for the different experimental design features such as replicates, and rows and columns within replicates. The residual term e was partitioned into e=ξ+η, with the elements in vector ξ following a spatial autoregressive process and the elements in vector η being distributed independently of each other and of those in ξ. Vectors b and uo also included terms to remove non-stationarity from ξ.
Under the general mixed model specified in Equation (1), the joint distribution of the random terms was assumed to be multivariate normal with a zero-mean vector and a block-diagonal variance matrix, specified as a direct sum of variance–covariance matrices related to the effects in ua, us, um, ur, uo and e. The form of the variance–covariance matrices for effects in uo and e depended on the analysis that was carried out for modeling the interactions between a focal tree and its immediate neighbors, as described below. An arcsine transformation 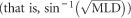 was applied for the MLD data, as preliminary analysis of this trait indicated that the distribution of the model residuals was slightly skewed.
was applied for the MLD data, as preliminary analysis of this trait indicated that the distribution of the model residuals was slightly skewed.
Modeling individual neighbor effects
In forest genetic trials, trees are usually planted in a rectangular or square grid indexed by row and column numbers, and so a focal tree has up to eight immediate neighbors (Figure 2). We jointly modeled the covariance of a focal tree with its eight immediate neighbors with the aim of identifying the positions impacting most on IGEs. For this purpose, we considered three basic models as follows:
indirect effects at both the heritable (that is, additive genetic) and non-heritable (that is, independent residual) levels, using all eight neighbors (hereafter called model FN_1);
indirect effects at the additive genetic level only, using all eight neighbors (hereafter called model FN_2); and
indirect effects at the additive genetic level only, using a subset of the neighbor positions (hereafter called model RN).
Figure 2.
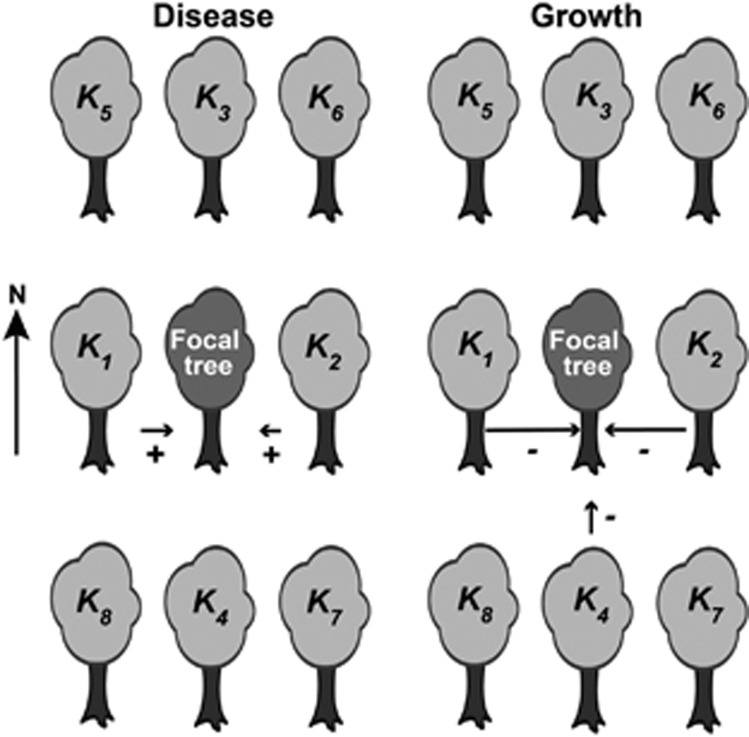
Neighborhood consisting of a focal tree and its eight immediate neighbors, and the neighbors contributing most to IGEs for Mycosphearella leaf disease (MLD) and breast-height stem diameter (DBH) growth at ages 2 and 4 years, respectively. The same-row neighbors are denoted as K1 and K2; the same-column neighbors are denoted as K3 and K4; and the diagonal neighbors are denoted as K5, K6, K7 and K8. The inter-column (within row) spacing corresponds to a distance between the focal tree and K1 or K2 of 2.125 m, and the inter-row spacing corresponds to a distance between the focal tree and K3 or K4 of 5 m. The direction to the north is also depicted. The arrows indicate the neighbors contributing most to IGEs, as detected when modeling IGEs as individual neighbor effects by using a factor analytic structure with one factor (FA1). In this context, the arrow length is proportional to the parameter estimate/standard error ratio of a neighbor’s loading on the common factor, standardized by the maximum value observed for this ratio across the two illustrated cases. The sign of the direct–indirect genetic covariance between the focal tree and each of its influential neighbors is also shown. The FA1 model for MLD had a generally positive correlation between direct and indirect genetic effects, which reflects the infection process; the FA1 model for DBH had a generally negative correlation between direct and indirect genetic effects, reflecting competitive interactions (see Supplementary Table S1 and its footnotes for further details).
In models FN_1 and FN_2, 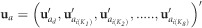 with the related incidence matrix given by
with the related incidence matrix given by 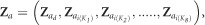 where the subscripts d and i denote direct and indirect effects, respectively, the subscripts K1 to K8 denote the neighbor positions (Figure 2), and the superscript ′ refers to the transpose operation.
where the subscripts d and i denote direct and indirect effects, respectively, the subscripts K1 to K8 denote the neighbor positions (Figure 2), and the superscript ′ refers to the transpose operation. 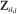 relates the phenotype of a focal tree to its own direct additive genetic effect, and
relates the phenotype of a focal tree to its own direct additive genetic effect, and 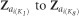 relate the phenotype of a focal tree to the indirect additive genetic effect of each of its eight immediate neighbors (that is, from K1 to K8). For the indirect genetic effects under model RN, ua and Za pertained to a reduced set of neighbors. To model the IGEs as a common effect across positions except for scale, we used a constrained factor analytic structure with one factor, hereafter denoted as FA1, for the genetic effects in ua. A common indirect effect was modeled by setting the specific variances (representing variation that is not explained by the factor) associated with the neighbor effects to zero, so that the correlations between the indirect effects of K1 to K8 and the direct effect are the same except for sign, and the correlations among the indirect effects of K1 to K8 are all one or minus one. Thus, the ‘factor’ represents the common indirect effect, and the loading for a given neighbor represents the size (scale) of the effect in that direction. This constrained FA1 matrix with 10 parameters was used in models FN_1 and FN_2. A reduced form, obtained by deleting certain neighbor positions, was used in model RN. Further details on modeling effects in ua are given in Supplementary Note S1 (Supplementary Information).
relate the phenotype of a focal tree to the indirect additive genetic effect of each of its eight immediate neighbors (that is, from K1 to K8). For the indirect genetic effects under model RN, ua and Za pertained to a reduced set of neighbors. To model the IGEs as a common effect across positions except for scale, we used a constrained factor analytic structure with one factor, hereafter denoted as FA1, for the genetic effects in ua. A common indirect effect was modeled by setting the specific variances (representing variation that is not explained by the factor) associated with the neighbor effects to zero, so that the correlations between the indirect effects of K1 to K8 and the direct effect are the same except for sign, and the correlations among the indirect effects of K1 to K8 are all one or minus one. Thus, the ‘factor’ represents the common indirect effect, and the loading for a given neighbor represents the size (scale) of the effect in that direction. This constrained FA1 matrix with 10 parameters was used in models FN_1 and FN_2. A reduced form, obtained by deleting certain neighbor positions, was used in model RN. Further details on modeling effects in ua are given in Supplementary Note S1 (Supplementary Information).
In these three models, the spatially correlated residuals in ξ were modeled by a variance–covariance structure based on a separable autoregressive process in the row and column directions of the field layout, and thus 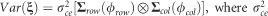 is the variance of the trend (correlated residual) process, and Σrow and Σcol are autoregressive correlation matrices with autocorrelation parameters ϕrow and ϕcol for row and column directions, respectively. In addition, under model FN_1, we explicitly modeled direct and indirect (co)variances pertaining to non-heritable effects that may cause interactions between a focal tree and its immediate neighbors, and distributed independently of the correlated residuals in ξ. In this sense, and akin to effects in ua, we used a FA1 structure to model the variance–covariance matrix for the independent residuals in η. For models FN_2 and RN, the residuals in η were assumed to represent direct non-heritable effects only. Further details on the modeling of effects in ξ and η are provided in Supplementary Note S2 (Supplementary Information).
is the variance of the trend (correlated residual) process, and Σrow and Σcol are autoregressive correlation matrices with autocorrelation parameters ϕrow and ϕcol for row and column directions, respectively. In addition, under model FN_1, we explicitly modeled direct and indirect (co)variances pertaining to non-heritable effects that may cause interactions between a focal tree and its immediate neighbors, and distributed independently of the correlated residuals in ξ. In this sense, and akin to effects in ua, we used a FA1 structure to model the variance–covariance matrix for the independent residuals in η. For models FN_2 and RN, the residuals in η were assumed to represent direct non-heritable effects only. Further details on the modeling of effects in ξ and η are provided in Supplementary Note S2 (Supplementary Information).
We used the Akaike’s (AIC; Akaike, 1974) and Schwarz’s Bayesian (BIC; Schwarz, 1978) information criteria (see Supplementary Note S3 in Supplementary Information) to successively compare the models. The comparison of model FN_2 to model FN_1 assessed whether there was important non-heritable indirect effects after allowing for indirect effects at the genetic level. Then, assuming that FN_2 was a plausible model, several RN models were compared to the model FN_2 to assess whether all eight neighbor positions were necessary for modeling IGEs. Differences (Δ) in AIC or BIC values were computed with respect to the more parsimonious model (that is, FN_2 and RN in the first and second comparisons described above, respectively). Supplementary Note S4 (Supplementary Information) describes the procedure used to compare RN and FN_2 models for identifying those neighbor positions with the greatest influence on the expression of IGEs for a given trait and age.
Modeling a combined indirect effect
The preceding models used a FA1 structure to define an underlying factor for indirect effects, and the loadings provided the regression or weighting of this factor with respect to the various neighbor positions. Thus, the underlying factor in the FA1 model represents a common indirect effect. Alternatively, one can calculate a combined indirect effect using a sum of weighted neighbor design matrices, where the weights are calculated as ‘intensity of interaction factors’ based on neighbor distance, as done by earlier authors (for example, Cappa and Cantet, 2008; Costa e Silva and Kerr, 2013). In the present case, we used both approaches in a complementary manner, by first applying the FA1 structure to identify the neighbor positions contributing most to IGEs, and then using these influential neighbors to model a combined indirect effect (Figure 1). Supplementary Note S5 (Supplementary Information) describes the methodological details in regard to the modeling of a combined indirect effect under univariate data analysis.
Bivariate data analysis
To study the genetic relationships between pairs of traits or ages, we extended the univariate approach that modeled IGEs as a combined effect using the most influential neighbors and intensity of interaction factors to obtain a bivariate linear mixed model which, following a reformulation of Equation (1), can be represented as:
where 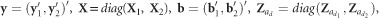
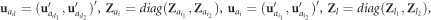
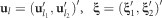 and
and 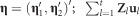 includes each of the terms defined under Equation (1) for full-sib family, maternal, reciprocal and additional random effects; the subscripts 1 and 2 refer to a pair of traits or ages.
includes each of the terms defined under Equation (1) for full-sib family, maternal, reciprocal and additional random effects; the subscripts 1 and 2 refer to a pair of traits or ages.
The vector b included a mean term, as well as other fixed effects fitted as required for each trait or age. For all the random terms defined under Equation (2), the description of the corresponding variance–covariance matrices is provided in Supplementary Note S6 (Supplementary Information).
Parameter estimation
Restricted maximum likelihood (REML) estimates of (co)variance parameters were obtained by using the Average Information REML algorithm developed by Gilmour et al. (1995), and implemented in the ASReml software (Gilmour et al., 2015). The phenotypic variance for a trait at a given age was calculated as described by Costa e Silva et al. (2013). On the basis of the REML estimates of additive genetic (co)variances obtained by modeling IGEs as a combined effect, direct–indirect genetic correlations were calculated for a trait at a given age under the univariate analysis, and between traits or ages under the bivariate analysis. In addition, the correlation between the total breeding values of two traits or ages 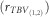 was computed as described in Supplementary Note S7 (Supplementary Information).
was computed as described in Supplementary Note S7 (Supplementary Information).
Taylor series expansion was used to obtain approximate standard errors for the (co)variance parameters estimated from the linear mixed model, as well as for derived linear combinations or ratios of the (co)variance estimates (Lynch and Walsh, 1998; Gilmour et al., 2015). Because of the computational time required to fit more complex models, no attempts were made to formally test the significance of the genetic correlations estimated under the bivariate analysis, although REML likelihood-ratio tests were used to test the significance of (co)variance parameters estimated under simpler (univariate) models fitted for a given trait and age. Consequently, where adequate, the significance of a genetic correlation (that is, deviation from zero) was judged by a conservative approach based on the ratio of the parameter estimate relative to its approximate standard error (that is, a statistically significant outcome at the 5% level occurs when the ratio is⩾1.96, assuming that it is asymptotically normally distributed).
Results
Univariate data analysis
Modeling individual neighbor effects
Table 1 presents the results obtained from comparing model FN_2 to FN_1, and model RN to FN_2, by using the AIC and BIC information criteria. In general, the AIC and BIC tended to agree on the preferred model, although the magnitude of the differences in ΔAIC were considerably smaller than those in ΔBIC, reflecting the larger weight placed on the penalty for model complexity in the BIC relative to AIC (see Supplementary Note S3).
Table 1. Modeling indirect effects at the non-heritable (that is, independent residual) and/or heritable (that is, additive genetic) levels as individual neighbor effects on a focal tree: model comparison using the AIC and BIC information criteriaa , b , c , d , e.
| Trait (age) |
FN_1 |
FN_2 |
RN |
Comparing FN_2 to FN_1 |
Comparing RN to FN_2 |
Neighbors kept in RN |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | ΔAIC(FN_2, FN_1) | ΔBIC(FN_2, FN_1) | ΔAIC(RN, FN_2) | ΔBIC(RN, FN_2) | Using AIC | Using BIC | |
| MLD (2 years) | 55265.3 | 55471.6 | 55266.8 | 55409.1 | 55264.7 | 55364.3 | 1.5 | −62.5 | −2.1 | −44.8 | K1, K2 | K1, K2 |
| DBH (2 years) | 57772.9 | 57972.1 | 57769.2 | 57911.5 | 57764.4 | 57864.0 | −3.7 | −60.6 | −4.8 | −47.5 | K1, K2 | K1, K2 |
| DBH (4 years) | 63371.0 | 63569.6 | 63368.4 | 63510.3 | 63367.5 | 63437.9 | −2.6 | −59.3 | −0.9 | −72.4 | K1, K2, K4 | K1, K2, K4 |
| DBH (8 years) | 70238.6 | 70443.8 | 70235.2 | 70376.8 | 70236.4 | 70342.5 | −3.4 | −67.0 | 1.2 | −34.3 | K1, K2, K4 | K1, K2, K4 |
Abbreviations: AIC and BIC refer to the Akaike's (1974) and Schwarz's (1978) information criteria, respectively; FN and RN represent full and reduced neighborhoods, respectively; DBH and MLD denote stem diameter at breast-height and Mycosphearella leaf disease, respectively.
The models compared correspond to: FN_1, modeling indirect effects at both the heritable and non-heritable levels, using all eight immediate neighbors of a focal tree; FN_2, modeling indirect effects at the heritable level only, using all eight immediate neighbors of a focal tree; and RN, modeling indirect effects at the heritable level only, using a subset of the neighbor positions.
Differences (Δ) between models in AIC or BIC values were computed with respect to the more parsimonious model, that is: FN_2, when comparing FN_2 to FN_1, and thus ΔAIC(FN_2, FN_1)=AIC(FN_2) – AIC(FN_1) and ΔBIC(FN_2, FN_1)=BIC(FN_2) – BIC(FN_1); and RN, when comparing RN to FN_2, and thus ΔAIC(RN, FN_2)=AIC(RN) – AIC(FN_2) and ΔBIC(RN, FN_2)=BIC(RN) – BIC(FN_2).
The neighbors kept in the RN model pertain to a reduced set of neighbor positions that were identified as having the greatest influence on the expression of IGEs (for more details on the comparison of the FN_2 and RN models, see Supplementary Note S4 in Supplementary Information).
For either AIC or BIC values, there was a difference of nine fitted parameters when comparing the FN_1 and FN_2 models; for the RN/FN_2 model comparisons, the difference in the number of fitted parameters depended on the number of neighbor positions kept in the RN model (that is, the FN_2 and RN models differed in either five or six fitted parameters).
An arcsine transformation was applied for the MLD data (see the Materials and methods section). To avoid convergence problems, which may occur when trait variances are very small, the transformed MLD data were then rescaled by multiplying the observations by 100. Thus, for MLD, the results tabulated above refer to the (arcsine) transformed and rescaled observations.
As a model for these data, FN_2 provided in general a better compromise between model fit and complexity than FN_1. For DBH, the negative values of ΔAIC(FN_2, FN_1) and ΔBIC(FN_2, FN_1) indicated that both information criteria preferred FN_2 over FN_1. For MLD, model FN_2 was clearly supported by the BIC only. However, despite its positive value (which would favor model FN_1), the magnitude of ΔAIC(FN_2, FN_1) for MLD was ⩽2 which, according to the guidelines proposed by Burnham and Anderson (2002; page 70), indicates a substantial level of empirical support for FN_2. Hence, based on the AIC, model FN_2 was essentially as good as FN_1 for MLD, as the increase in REML log-likelihood obtained from FN_1 did not justify the extra model complexity. Under these circumstances, and as suggested by Kuha (2004), ‘playing safe’ and preferring the simpler, more parsimonious model is the best decision. Selection of an overly complex model is more likely when the true effect of a measured factor is relatively weak (Richards, 2008). This could be the case of MLD, as suggested by the estimate/standard error ratios of FA1 loadings estimated for indirect additive genetic effects being in general weaker for MLD than for DBH (see Supplementary Table S1 in Supplementary Information). Consequently, when compared with FN_1, modeling indirect effects at the additive genetic level only under FN_2 was preferred to FN_1 for these traits and ages.
In the sequential approach followed for comparing model RN to FN_2, the AIC and BIC preferred the same RN model for all the pairs of RN/FN_2 comparisons. For MLD and DBH at age 2 years, the RN model indicated by AIC included neighbor positions K1 and K2 only, but position K4 was also included for DBH at ages 4 and 8 years. In all cases, the change in BIC from adding an extra neighbor position was >2, indicating empirical evidence against a more complex RN model (Kass and Raftery, 1995). Figure 2 illustrates the neighbors contributing most to IGEs for MLD and DBH at ages 2 and 4 years, respectively.
Modeling a combined indirect effect
Table 2 shows the genetic (co)variance parameters estimated by modeling IGEs as a combined effect, using either the full set (hereafter called FS) of eight immediate neighbors or a reduced set (hereafter called RS) comprising the most influential neighbors that were identified under model RN. Figure 3 and Supplementary Table S4 (Supplementary Information) present estimates over time for the total heritable variance [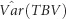 , where TBV denotes total breeding value] underlying potential response to selection, including the components of
, where TBV denotes total breeding value] underlying potential response to selection, including the components of 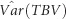 due to direct and indirect genetic effects.
due to direct and indirect genetic effects.
Table 2. Additive genetic (co)variance components (±standard errors) estimated from a univariate model in which IGEs were modeled as a combined effect, using either full or reduced sets of neighbor positionsa , b , c , d , e , f.
| Trait (age) |
All eight neighbor positions |
Reduced set of neighbor positions |
||||
|---|---|---|---|---|---|---|
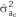 |
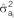 |
 |
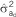 |
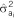 |
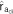 |
|
| MLD (2 years) | 78.18±13.81 (5.7) | 1.63±0.65 (2.5) | 0.82±0.13 (6.3) | 82.96±14.45 (5.7) | 1.50±0.62 (2.4) | 0.83±0.13 (6.4) |
| DBH (2 years) | 91.27±16.18 (5.6) | 6.08±1.50 (4.0) | −0.92±0.06 (−15.3) | 90.32±15.26 (5.9) | 6.78±1.49 (4.6) | −0.90±0.06 (−15.0) |
| DBH (4 years) | 218.12±29.60 (7.4) | 32.27±5.18 (6.2) | −0.96±0.03 (−32.0) | 218.29±28.68 (7.6) | 36.34±5.10 (7.1) | −0.95±0.03 (−31.7) |
| DBH (8 years) | 708.05±72.62 (9.7) | 116.74±14.13 (8.3) | −0.97±0.02 (−48.5) | 643.50±68.90 (9.3) | 149.96±16.61 (9.0) | −0.95±0.03 (−31.7) |
Abbreviations: IGEs signifies indirect genetic effects; DBH and MLD denote stem diameter at breast-height and Mycosphearella leaf disease, respectively.
The tabulated (co)variance parameter estimates refer to: 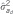 =direct additive genetic variance;
=direct additive genetic variance; 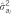 =indirect additive genetic variance; and
=indirect additive genetic variance; and 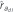 =direct–indirect additive genetic correlation. The ratio of the parameter estimate relative to its standard error is given in parenthesis.
=direct–indirect additive genetic correlation. The ratio of the parameter estimate relative to its standard error is given in parenthesis.
Modeling IGEs as a combined effect used either all eight immediate neighbors of a focal tree (Figure 2) or a subset of the neighbor positions that were found to contribute most to IGEs (that is, see ‘Neighbors kept in RN’ in Table 1).
Results obtained from modeling IGEs as a combined effect by using all eight immediate neighbors were previously reported by Costa e Silva et al. (2013) for MLD at age 2 years, and DBH at ages 2 and 4 years. However, the results provided above for all neighbor positions differ slightly to those reported in Costa e Silva et al. (2013), as some parents have been subsequently re-allocated to the factorial to improve the number of families per parent and geographic focus of the parents in the diallel (see the Materials and methods section).
For MLD, the parameter estimates refer to the (arcsine) transformed and rescaled observations (for more details, see footnote e of Table 1).
A univariate model that ignored additive genetic terms involving IGEs was used as a base model to assess the statistical significance of the direct additive genetic variance via a one-tailed likelihood-ratio test (Stram and Lee, 1994). In this sense, a nested model constraining the estimate of the direct additive genetic variance to be zero was compared with the base model. For all traits and ages, the estimate of the direct additive genetic variance was found to be always highly significant (P<0.001).
The complete univariate model that estimated both direct and indirect additive genetic (co)variances (providing the results tabulated above) was compared with a nested model that fitted only direct additive genetic effects, in order to carry out a joint test of significance for the variance and covariance parameter estimates involving IGEs. Using a two-tailed likelihood-ratio test, highly significant (P<0.001) results were detected for all traits and ages.
Figure 3.
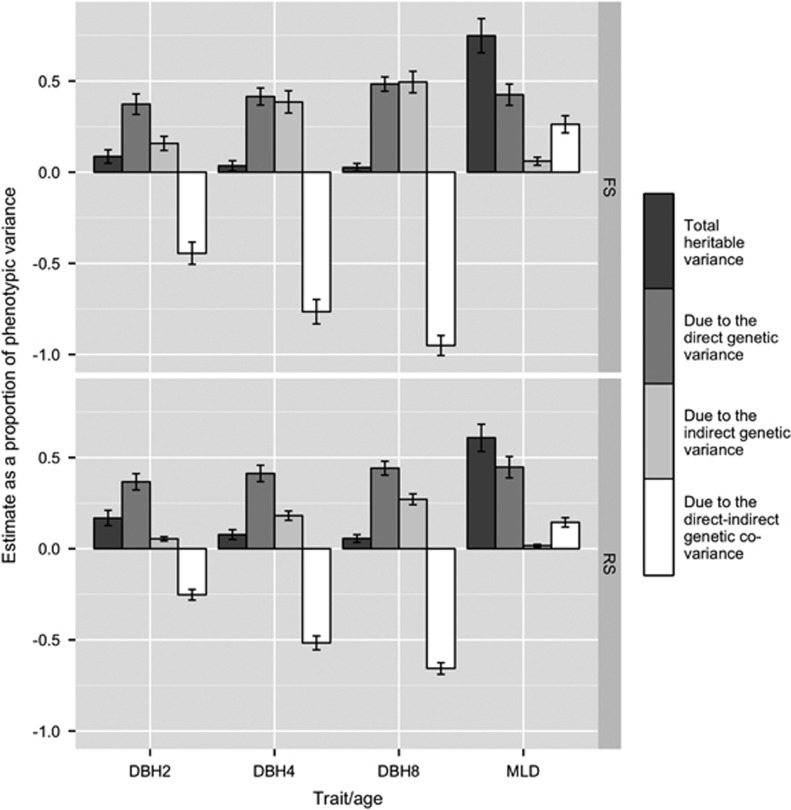
Relative contributions (that is, as a proportion of the phenotypic variance) to the total heritable variance due to the variances associated with direct and indirect genetic effects, and to their covariance, for breast-height stem diameter (DBH) growth at ages 2, 4 and 8 years, and for a damage due to a transient outbreak of Mycosphearella leaf disease (MLD) occurring at age 2 years, estimated using the full (FS) and reduced (RS) sets of neighbor positions. There is a marked contrast of the impact of IGEs on disease damage compared with growth: for MLD, the positive direct–indirect covariance (indicative of infection) significantly increased the total heritable variance in the population compared with the direct genetic variance; conversely, for DBH, the negative direct–indirect covariance (indicative of competition) resulted in a substantial decrease of the total heritable variance. For DBH, the relative magnitude of the indirect genetic variance and the direct–indirect genetic covariance increased more with age than the direct genetic variance did, but less between ages 4 and 8 years than between ages 2 and 4 years, leading to a stabilization of the impact of competitive interactions on the heritable variance at the later age. Further details on these results are provided in Supplementary Table S4 (Supplementary Information).
The 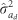 estimate was found to be always highly significant (P<0.001), according to a one-tailed likelihood-ratio test; in addition, highly significant (P<0.001) outcomes were also always obtained by a two-tailed likelihood-ratio test of the overall significance of IGEs, and involving a joint test of both of the parameter estimates
estimate was found to be always highly significant (P<0.001), according to a one-tailed likelihood-ratio test; in addition, highly significant (P<0.001) outcomes were also always obtained by a two-tailed likelihood-ratio test of the overall significance of IGEs, and involving a joint test of both of the parameter estimates 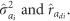 In general, no major changes were detected between the FS and RS neighborhoods for
In general, no major changes were detected between the FS and RS neighborhoods for 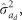 a trend that was also observed for
a trend that was also observed for 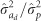 ratios (that is, ordinary heritability; Figure 3 and Supplementary Table S4), as well as for the
ratios (that is, ordinary heritability; Figure 3 and Supplementary Table S4), as well as for the 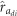 estimates which are consistent with neighbor infection (MLD) and strong competition (DBH) (Table 2). However, while remaining virtually unchanged for MLD, the magnitude and significance (as indicated by the ratio of the parameter estimate relative to its standard error) of
estimates which are consistent with neighbor infection (MLD) and strong competition (DBH) (Table 2). However, while remaining virtually unchanged for MLD, the magnitude and significance (as indicated by the ratio of the parameter estimate relative to its standard error) of 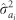 values for DBH increased under the RS analysis compared with those under the FS analysis, with the relative improvement in the magnitude of
values for DBH increased under the RS analysis compared with those under the FS analysis, with the relative improvement in the magnitude of 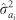 being accentuated with age (Table 2). These results were reflected in the ΔAIC obtained from comparing the RS and FS analyses for a given trait/age (not shown).
being accentuated with age (Table 2). These results were reflected in the ΔAIC obtained from comparing the RS and FS analyses for a given trait/age (not shown).
The contributions of IGEs to 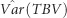 differed between the FS and RS analyses for a given trait/age, reflecting a lower value under the RS neighborhood for the quantity
differed between the FS and RS analyses for a given trait/age, reflecting a lower value under the RS neighborhood for the quantity 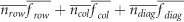 in the equation used to calculate
in the equation used to calculate 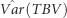 (Costa e Silva and Kerr, 2013). For MLD under the RS, the reduction of the contribution of the indirect genetic variance, coupled with a lower positive contribution due to the direct–indirect genetic covariance, resulted in a decrease of
(Costa e Silva and Kerr, 2013). For MLD under the RS, the reduction of the contribution of the indirect genetic variance, coupled with a lower positive contribution due to the direct–indirect genetic covariance, resulted in a decrease of 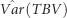 when compared with the FS (Figure 3). For DBH under the RS, and despite the increases observed in
when compared with the FS (Figure 3). For DBH under the RS, and despite the increases observed in 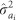 (Table 2), there was also a reduction at all ages of the contribution of the indirect genetic variance when compared with the FS; yet, the lower value for
(Table 2), there was also a reduction at all ages of the contribution of the indirect genetic variance when compared with the FS; yet, the lower value for 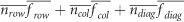 under the RS led to a less negative contribution due to the direct–indirect genetic covariance, which resulted in a net increase of
under the RS led to a less negative contribution due to the direct–indirect genetic covariance, which resulted in a net increase of 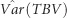 relative to the FS (Figure 3).
relative to the FS (Figure 3).
The contributions of IGEs to the total heritable variance also differed among traits/ages. When compared with 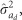 IGEs increased
IGEs increased 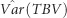 for MLD by 76 and 36% under the FS and RS, respectively, leading to corresponding
for MLD by 76 and 36% under the FS and RS, respectively, leading to corresponding 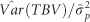 ratios of 0.75 and 0.61, and thus were noticeably greater than the
ratios of 0.75 and 0.61, and thus were noticeably greater than the 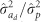 ratios of ≈ 0.4 (Supplementary Table S4). The IGEs reduced substantially
ratios of ≈ 0.4 (Supplementary Table S4). The IGEs reduced substantially 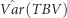 for DBH at all ages when compared with
for DBH at all ages when compared with 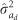 (Figure 3): the percentage decreases under the FS were 77, 92 and 95%, and those under the RS were 54, 81 and 87%, at ages 2, 4 and 8 years, respectively; this led to corresponding
(Figure 3): the percentage decreases under the FS were 77, 92 and 95%, and those under the RS were 54, 81 and 87%, at ages 2, 4 and 8 years, respectively; this led to corresponding 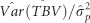 ratios of 0.09, 0.04 and 0.03 under the FS, and 0.17, 0.08 and 0.06 under the RS (Supplementary Table S4). All of these
ratios of 0.09, 0.04 and 0.03 under the FS, and 0.17, 0.08 and 0.06 under the RS (Supplementary Table S4). All of these 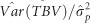 ratios were considerably lower than the
ratios were considerably lower than the 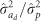 ratios (varying from 0.37 to 0.48), indicating that the heritable competition expressed in DBH growth will substantially limit the potential for response to selection. Yet, these results over time suggest that the impact of competitive interactions among individuals on the heritable variance of DBH tended to stabilize at age 8 years (as also observed for
ratios (varying from 0.37 to 0.48), indicating that the heritable competition expressed in DBH growth will substantially limit the potential for response to selection. Yet, these results over time suggest that the impact of competitive interactions among individuals on the heritable variance of DBH tended to stabilize at age 8 years (as also observed for 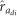 in Table 2). Indeed, although the component of
in Table 2). Indeed, although the component of 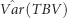 due to the direct–indirect genetic covariance was increasingly negative with age for DBH, the relative difference between ages 2 and 4 years was much greater than that between 4 and 8 years (Figure 3). These results clearly indicate a marked change in the competitive environment between ages 2 and 4 years, an interval usually associated with canopy closure.
due to the direct–indirect genetic covariance was increasingly negative with age for DBH, the relative difference between ages 2 and 4 years was much greater than that between 4 and 8 years (Figure 3). These results clearly indicate a marked change in the competitive environment between ages 2 and 4 years, an interval usually associated with canopy closure.
Bivariate data analysis
On the basis of data analyses using a bivariate linear mixed model, estimates of genetic correlations—that is, correlations comprising the direct (ad) and/or indirect (ai) additive genetic effects, plus those involving TBV—are given in Table 3 for relationships between MLD measured at the age of infection (2 years) and post-infection DBH growth at ages 4 and 8 years, and in Table 4 for relationships between DBH measured at early (2 and 4 years) and late (8 years) ages. Preliminary analysis that used a simpler bivariate model fitting direct genetic effects only indicated a non-significant genetic correlation estimate (−0.03±0.16) between MLD and DBH measured at age 2 years; no correlation is expected since DBH at this age effectively reflects growth before infection by Mycosphaerella. Thus, a more complex variance–covariance matrix (as defined in Equation [S_6] see Supplementary Note S6) to estimate direct–indirect and indirect–indirect genetic correlations between these traits at age 2 years was not attempted.
Table 3. Genetic correlations (with standard errors in parenthesis) estimated between MLD measured at the age of infection (2 years) and post-infection DBH growth (ages 4 and 8 years)a , b.
|
DBH (4 years) |
DBH (8 years) |
|||||
|---|---|---|---|---|---|---|
| ad | ai | TBV | ad | ai | TBV | |
| MLD (2 years) | ||||||
| ad | −0.44 (±0.11) | 0.42 (±0.10) | — | −0.31 (±0.11) | 0.36 (±0.09) | — |
| ai | −0.34 (±0.22) | 0.41 (±0.24) | — | −0.07 (±0.24) | 0.24 (±0.25) | — |
| TBV | — | — | −0.37 (±0.18) | — | — | 0.01 (±0.21) |
Abbreviations: IGEs signifies indirect genetic effects; DBH and MLD denote stem diameter at breast-height and Mycosphearella leaf disease, respectively.
Additive genetic (co)variance components were estimated from a bivariate model in which IGEs were modeled as a combined effect, using a subset of the neighbor positions that were found to contribute most to IGEs (that is, see ‘Neighbors kept in RN’ in Table 1). The estimated (co)variances were used to derive genetic correlations between: the direct genetic effects (ad) for the two traits; the ad for one trait and the indirect genetic effect (ai) for another, and vice versa; the ai for the two traits; and the total breeding values (TBV) for the two traits.
For MLD, the parameter estimates refer to the (arcsine) transformed and rescaled observations (for more details, see footnote e of Table 1).
Table 4. Genetic correlations (with standard errors in parenthesis) estimated between DBH growth measured at late (8 years) and early ages (2 and 4 years)a.
|
DBH (4 years) |
DBH (2 years) |
|||||
|---|---|---|---|---|---|---|
| ad | ai | TBV | ad | ai | TBV | |
| DBH (8 years) | ||||||
| ad | 0.93 (±0.02) | −0.99 (±0.01) | — | 0.79 (±0.05) | −0.94 (±0.03) | — |
| ai | −0.94 (±0.02) | 0.99 (±0.01) | — | −0.80 (±0.05) | 0.95 (±0.03) | — |
| TBV | — | — | 0.73 (±0.14) | — | — | 0.60 (±0.15) |
Abbreviations: IGEs, indirect genetic effects; DBH, stem diameter at breast-height.
Additive genetic (co)variance components were estimated from a bivariate model in which IGEs were modeled as a combined effect, using a subset of the neighbor positions that were found to contribute most to IGEs (that is, see ‘Neighbors kept in RN’ in Table 1). The estimated (co)variances were used to derive genetic correlations between: the direct genetic effects (ad) for the two traits; the ad for one trait and the indirect genetic effect (ai) for another, and vice versa; the ai for the two traits; and the total breeding values (TBV) for the two traits.
The direction of the genetic correlations involving ad and/or ai effects was stable between MLD and post-infection DBH, but the magnitude and significance of the estimates decreased over time (Table 3). Negative genetic correlation estimates indicated an adverse impact of MLD assessed at age 2 years on the ad effects for later growth. This appeared mainly at the direct genetic level, as genotypes with higher ad effects for damage by MLD were significantly associated with lower DBH in the focal tree 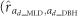 =−0.44±0.11 and −0.31±0.11 for DBH measured at ages 4 and 8 years, respectively) but did not reduce the growth of its neighbors. Rather, the ad effects for MLD were significantly positively correlated with the ai effects for DBH measured at ages 4 and 8 years
=−0.44±0.11 and −0.31±0.11 for DBH measured at ages 4 and 8 years, respectively) but did not reduce the growth of its neighbors. Rather, the ad effects for MLD were significantly positively correlated with the ai effects for DBH measured at ages 4 and 8 years 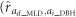 =0.42±0.10 and 0.36±0.09). In addition, despite a highly positive
=0.42±0.10 and 0.36±0.09). In addition, despite a highly positive 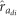 for MLD (Table 2), the estimated correlations between the ai effects for MLD and the ad effects for DBH did not appear to differ significantly from zero
for MLD (Table 2), the estimated correlations between the ai effects for MLD and the ad effects for DBH did not appear to differ significantly from zero  =−0.34±0.22 and −0.07±0.24). These outcomes could be explained by the following: (1) a focal tree performing poorly for growth (a lower ad effect for DBH) due to disease damage (a higher ad effect for MLD) will compete less with its neighbors (a less negative, or even positive ai effect for DBH), as indicated by the strong negative
=−0.34±0.22 and −0.07±0.24). These outcomes could be explained by the following: (1) a focal tree performing poorly for growth (a lower ad effect for DBH) due to disease damage (a higher ad effect for MLD) will compete less with its neighbors (a less negative, or even positive ai effect for DBH), as indicated by the strong negative 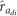 (Table 2) estimate for DBH; and (2) this reduced competitive environment of the neighborhood as a whole could result in a favorable effect by countering any adverse impact that the increased risk of neighbor infection (a higher ai effect for MLD, reflecting a strong positive
(Table 2) estimate for DBH; and (2) this reduced competitive environment of the neighborhood as a whole could result in a favorable effect by countering any adverse impact that the increased risk of neighbor infection (a higher ai effect for MLD, reflecting a strong positive 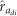 estimate; Table 2) would have on the DBH growth of neighboring trees. These putative explanations are also mirrored in the positive relationships between MLD and DBH for ai effects, although the estimated genetic correlations did not appear to be significant particularly for DBH at age 8 years
estimate; Table 2) would have on the DBH growth of neighboring trees. These putative explanations are also mirrored in the positive relationships between MLD and DBH for ai effects, although the estimated genetic correlations did not appear to be significant particularly for DBH at age 8 years 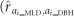 =0.24±0.25). When the direct and indirect genetic effects were combined (as in Equations [S_9] and [S_10] see Supplementary Note S7), a significant adverse overall association was obtained between MLD and post-infection DBH at age 4 years
=0.24±0.25). When the direct and indirect genetic effects were combined (as in Equations [S_9] and [S_10] see Supplementary Note S7), a significant adverse overall association was obtained between MLD and post-infection DBH at age 4 years 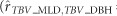 =−0.37±0.18), but was virtually zero for later growth
=−0.37±0.18), but was virtually zero for later growth 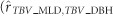 =0.01±0.21) (Table 3).
=0.01±0.21) (Table 3).
The results in Table 4 show that the direct–direct genetic correlations between DBH at ages 2 or 4 years and at age 8 years were positive and significant, although lower for age 2 (0.79±0.05) than for age 4 (0.93±0.02), a pattern also observed for the total breeding values (that is, 0.60±0.15 versus 0.73±0.14). The direct–indirect genetic correlations were all negative and significant among the early-late DBH relationships: the correlation between the ad effects at age 2 years and the ai effects at age 8 years (−0.80±0.05) indicated that a genotype growing rapidly at an early stage will have (on average) a substantial negative heritable effect on the later growth of its neighbors; in addition, the correlation between the ai effects at age 2 years and the ad effects at age 8 years (−0.94±0.03) is consistent with an early onset of competitive interactions for growth between a focal tree and its neighbors. For the ai effects, the significant correlation estimates for DBH over time indicated that heritable competition effects were highly positively correlated between early and late growth stages.
Discussion
A new approach to identify the most influential neighbors
A novel application using a factor analytic (FA) model enabled the modeling of indirect effects, at the non-heritable and/or heritable levels, as individual neighbor effects on a focal tree. For a given trait and age, a sequential approach comparing factor analytic models allowed the identification of a subset of neighbor positions with the greatest influence on the expression of IGEs. Although factor analytic models have been commonly applied for studying genotype by environment interaction (Smith et al., 2001; Meyer, 2009), including forest trees (for example, Costa e Silva and Graudal, 2008; Cullis et al., 2014), we are unaware of any studies where they have been used to study the interactions between neighbors at the genetic or non-genetic levels. However, structural equation modeling, which combines path and factor analyses, has been used to study phenotypic interactions underlying IGEs in plants (Wolf et al., 2011) and animals (Santostefano et al., 2016).
The application of the factor analytic model has the advantage that it allows for: (i) an initial testing of whether interaction effects can be partitioned into a genetic and non-genetic component; and (ii) directionality of the interaction effects to be empirically detected. In allowing for asymmetry, the factor analytic model enables the identification of the most influential neighbor positions, and these alone can subsequently be used to model a combined indirect effect. Our results also indicated that the relative importance of the contribution of each neighbor to IGEs was associated with the significance of the corresponding loading in the factor analytic model. When compared with all eight immediate neighbors, modeling IGEs as a combined effect of the most influential neighbors often resulted in increases in the magnitude and significance of the estimated indirect genetic variance, while estimates of narrow-sense heritability remained virtually unchanged. Forest genetics trials are generally smaller than that used in the present study, and IGEs may go unnoticed unless the most influential neighbors are identified. We have indeed observed this in other field trial analyses, in which a significant indirect genetic variance estimate has been detected after considering only a subset of neighbor positions (unpublished results). Thus, in forest trees, we suggest that quantitative genetic studies involving interactions among conspecifics commence with the identification of the neighbors contributing most to indirect effects (see Supplementary Figure S1 in Supplementary Information, and also the Discussion section in Costa e Silva and Kerr, 2013).
In the present study, the FA1 model was fitted to individual neighbor positions to explicitly investigate their influence on IGEs depending on directionality. If our interest had been focused mainly on distance, the FA1 model could have been fitted to distance categories (that is, in our case, three classes resulting from collapsing same-row, same-column or same-diagonal neighbors together). However, using a FA approach for the analysis of IGEs in animal systems will be limited by the fact that there is usually no positional basis for giving differential weights to individuals. Nevertheless, an application of the FA model in both farmed and wild animal systems could be possible where categories of interacting individuals can be identified, for example, based on the time the animals interact within a given pen/cage (Cantet and Cappa, 2008). In this sense, the length of time the animals share a pen could be used to collapse all pen mates onto a specified number of categories (for example, akin to collapsing neighboring trees onto distance classes), and then the FA model could be applied using these categories as a positional basis.
The most proximal trees are the most influential
The most influential neighbors varied with trait and age, but in all cases the same-row positions were identified as impacting most on IGEs. These trees were the spatially closest neighbors to the focal tree, and these results are consistent with the well-documented distance-related competition demonstrated in E. globulus (Soares and Tomé, 1999). Nevertheless, given that the same-row positions were also in the direction of cultivation and ripping, below-ground intra-row interactions may have been further facilitated by greater ease of root growth within rows due to less compacted soils (Misra and Gibbons, 1996). Although our results indicated that diagonal neighbors could be effectively ignored, the same-column (inter-row) neighbors were sometimes important depending on trait and age. Weaker competition effects of diagonal neighbors have also been reported for growth in eucalypt clones (Resende et al., 2016) and Douglas-fir progenies (Cappa et al., 2016). The present study found asymmetry in the effect of the same-column neighbor positions on the DBH growth of a focal tree. Specifically, only the southern same-column neighbor position (that is, K4; Figure 2) was identified as contributing most to IGEs, and this did not become apparent until after canopy closure (age 4 years). In forest trees, asymmetric competition is expected with respect to size (Boyden et al., 2008) and species (Canham et al., 2004; Boyden et al., 2005), but there is a paucity of reports of spatial asymmetry as we have observed. In the present case, the greater influence of the southern than the northern same-column position is not consistent with a shading effect, as in the southern hemisphere this position is the one which would be shaded by the focal tree and not the opposite. However, with E. globulus exhibiting a strong positive relationship between above-ground biomass and below-ground fine root surface and biomass (O’Grady et al., 2006), E. globulus fine roots reported to start occupying inter-row planting space by 14 months of age (O’Grady et al., 2005) and root systems of forest trees being often markedly asymmetric (Coutts et al., 1999), there is a possibility that the asymmetry we have observed in DBH for the same-column positions after age 2 years reflects some form of below-ground root competition (Schenk, 2006). In this case, competition for water is the most likely below-ground factor in this Mediterranean climate, although nutrient competition alone or in combination with water stress cannot be dismissed (White et al., 2009).
Age trends in genetic parameters estimated for DBH growth
Consistent with Costa e Silva et al. (2013), our results suggest that predictions of response to selection based on quantitative genetic models ignoring IGEs may be overestimated for growth and underestimated for disease susceptibility. This conclusion holds regardless of whether modeling IGEs as a combined effect was undertaken with the full neighborhood or with just the most influential neighbors. In particular, the significant variance due to IGEs and strong negative correlation between direct and indirect genetic effects observed in the latest 8-year DBH measurement were consistent with earlier-age estimates, and they demonstrate strong genetic-based competitive interactions for growth. Other studies with forest trees have also reported such heritable competition for diameter growth (Resende et al., 2005; Cappa and Cantet, 2008; Brotherstone et al., 2011; Cappa et al., 2015, 2016). Heritable competition is of particular concern in selection experiments, as strong competitors will appear better and poor competitors worse than they would in a production environment where genotypes are more similar in their competitive ability (Muir, 2005; Bijma et al., 2007; Muir et al., 2013). The competition observed among neighbor trees is akin to the negative effects of social interactions in animals (Ellen et al., 2014; Wilson, 2014), demonstrating the constraints imposed by the ‘social environment’ on response to selection. High negative correlations between direct and indirect genetic effects were reported for growth in Japanese quail (Muir, 2005) and for survival time in crossbreed laying hens (Peeters et al., 2012). Strong negative social interactions were also observed in deer mice (Wilson et al., 2009), red deer (Wilson et al., 2011) and fighting cows (Sartori and Mantovani, 2013).
Competition is positively related to neighbor tree size in E. globulus (Soares and Tomé, 1999), and it is expected to increase with age. Although the results for DBH showed a marked impact of competitive interactions on the heritable variance, this tended to stabilize after canopy closure as indicated by diminishing rates of change in genetic parameters associated with IGEs. Nevertheless, the total heritable variance for DBH was still declining between ages 4 and 8 years due to the increasingly negative direct–indirect genetic covariance, although both indirect and direct genetic variances increased with stand development. This dynamic interplay between increasing expression of genetic effects with age being countered by competition has analogies in classical heritability studies of E. globulus (Stackpole et al., 2010).
Genetic correlations
A multivariate approach is important to allow the identification of the interacting phenotypes responsible for the IGEs affecting the expression of a given trait (Wolf et al., 2011; Bailey and Hoskins, 2014). For example, in a QTL study where the same (standard) neighbor plant genotype was interacting with different focal genotypes from a set of Arabidopsis recombinant inbred lines, Mutic and Wolf (2007) and Wolf et al. (2011) showed that not only did the QTL have pleiotropic direct effects on multiple traits in the focal plant phenotype, but also ‘pleiotropic indirect’ effects on traits expressed in neighboring individuals. These effects were reported for size and developmental traits. Mutic and Wolf (2007) recognized both non-reciprocal and reciprocal pleiotropic interactions, to differentiate cases where, respectively: (i) the expression of a trait in an individual is influenced by another trait in another individual, but the second trait is not affected by the interaction; and (ii) a trait expression in an individual is affected by a second trait in another individual and vice versa (see also Moore et al., 1997). Wolf et al. (2011) further differentiated cases of identified and unidentified pleiotropy, where there is and there is not a functional/causal connection between the direct genetic effect on one trait and the IGE on a different trait, respectively. In the latter case, correlations between a direct genetic effect on one trait and the IGE on another trait can arise through pleiotropic direct genetic effects involving an unmeasured trait, which provides the mechanistic pathway for the IGE. Bailey and Hoskins (2014) similarly identified such interactions as cryptic IGEs in a study of Drosophila melanogaster, where the direct and indirect genetic effects for the same trait (male leg-tapping) were uncorrelated.
In the present study, a greater complexity to neighbor interactions was revealed by the bivariate models involving disease damage and diameter growth at various ages. For each trait, there were significant correlations between direct and indirect genetic effects, with IGEs reflecting an increased probability of neighbor infection and strong competition (consistent with Costa e Silva et al., 2013). Although the high direct–indirect correlation observed for MLD damage (that is, 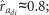 Table 2) suggests that these IGEs simply reflect variation in neighbor disease exposure arising from genetic variation in focal tree susceptibility, the possibility of genetic variation in infectivity per se cannot be dismissed (Lipschutz-Powell et al., 2012; Anche et al., 2014). At the time of infection (age 2 years), no significant direct genetic correlation was observed between MLD damage and DBH growth. However, later-age growth measurements revealed a significant adverse, direct genetic correlation between MLD damage and subsequent growth. For E. globulus, such genetic signatures of MLD damage on subsequent growth have been reported previously (Milgate et al., 2005), and are no doubt a pleiotropic direct effect of QTL affecting disease susceptibility (Freeman et al., 2008). While the initial MLD infection may favor faster growing plants in some cases (Milgate et al., 2005), this was not evident in the present study, and all evidence suggests that the direct, post-infection genetic correlations between these two traits reflect an adverse, non-reciprocal pleiotropic effect of disease damage on later-age growth. This functional conclusion follows from the well-documented adverse effects of pests and diseases on the growth of plantation-grown eucalypts (Eyles et al., 2013). MLD infection can lead to varying levels of premature leaf defoliation in E. globulus (Carnigie and Ades, 2003; Pinkard and Mohammed, 2006). Diameter growth of E. globulus is reduced following canopy defoliation (Carnegie and Ades, 2003; Quentin et al., 2011). In addition, leaves retained after MLD infection exhibit reduced photosynthetic capacity (Pinkard and Mohammed, 2006).
Table 2) suggests that these IGEs simply reflect variation in neighbor disease exposure arising from genetic variation in focal tree susceptibility, the possibility of genetic variation in infectivity per se cannot be dismissed (Lipschutz-Powell et al., 2012; Anche et al., 2014). At the time of infection (age 2 years), no significant direct genetic correlation was observed between MLD damage and DBH growth. However, later-age growth measurements revealed a significant adverse, direct genetic correlation between MLD damage and subsequent growth. For E. globulus, such genetic signatures of MLD damage on subsequent growth have been reported previously (Milgate et al., 2005), and are no doubt a pleiotropic direct effect of QTL affecting disease susceptibility (Freeman et al., 2008). While the initial MLD infection may favor faster growing plants in some cases (Milgate et al., 2005), this was not evident in the present study, and all evidence suggests that the direct, post-infection genetic correlations between these two traits reflect an adverse, non-reciprocal pleiotropic effect of disease damage on later-age growth. This functional conclusion follows from the well-documented adverse effects of pests and diseases on the growth of plantation-grown eucalypts (Eyles et al., 2013). MLD infection can lead to varying levels of premature leaf defoliation in E. globulus (Carnigie and Ades, 2003; Pinkard and Mohammed, 2006). Diameter growth of E. globulus is reduced following canopy defoliation (Carnegie and Ades, 2003; Quentin et al., 2011). In addition, leaves retained after MLD infection exhibit reduced photosynthetic capacity (Pinkard and Mohammed, 2006).
Despite adverse pleiotropic effects of disease damage on productivity at the direct genetic level, the IGEs arising from disease damage were not associated with a reduction in the growth of neighbors. Rather, increased disease damage on a focal tree (direct genetic effect) was associated with increased neighbor growth (indirect genetic effect) at a population level, despite the higher risk of neighbor infection. The reduced IGEs due to competition from slower-growing focal trees damaged by MLD thus appear to have over-ridden any adverse effects on growth of the increased risk of disease infection in the neighbors. This countering effect of IGEs for growth is sufficiently strong to result by age 8 years in: (i) a positive but non-significant correlation between the IGEs of MLD damage and growth; and (ii) a negligible correlation between the total breeding values of MLD damage and growth. The transient effect of the MLD damage on growth observed for the total breeding values was not evident for the direct breeding values, and no doubt will depend on the level of infection and strength of the adverse direct genetic effects of disease damage on growth. For example, a more enduring impact may be expected in outbreaks such as those reported by Milgate et al. (2005), where the average level of disease infection was higher (that is, 34% leaf area damaged compared with 23% observed in the present study) and the adverse direct genetic correlation with growth was stronger (that is, −0.77 versus our estimate of −0.44 at age 4 years).
Regardless of the dynamics associated with the interaction of IGEs for disease damage and growth, for growth itself the correlations involving indirect genetic effects remained relatively stable across ages. At the phenotypic level, the onset of competition in E. globulus plantings has been reported to occur between 21 and 31 months, depending on factors such as spacing and site productivity, with a shift from symmetric to asymmetric competition, as smaller trees become suppressed with age (Soares and Tomé, 1996). As indicated from univariate analyses of DBH, the increase in the relative importance of IGEs observed between ages 2 and 4 years, and attributed to increasing competition associated with canopy closure, appeared to stabilize at 8 years. In addition, the bivariate analyses of DBH across ages revealed that IGEs established at age 2 years remained stable through stand development. This is indicated by the age-to-age correlations between the IGEs not differing significantly from one, and even being higher than the genetic correlations between the direct genetic effects. Although strong age-to-age genetic correlations for direct genetic effects on growth are well established for forest trees (Stackpole et al., 2010), this is the first report for IGEs. Our declining age-to-age correlations for direct genetic effects and total breeding values are consistent with the tendency generally observed with increasing age difference. However, the absence of such an obvious decline for correlations involving IGEs is noteworthy, and may reflect either a time lag in their diminution or an inherent stability in competitive effects. Such stability may arise from an inherent greater susceptibility of smaller trees to competition reducing growth (Boyden et al., 2008), thus buffering changes in genetic-based competition with age.
Implications for wild populations
Although IGEs are clearly an important part of a tree’s environment in plantations, the extent to which the observed IGEs impact the eco-evolutionary dynamics of wild populations can only be inferred (Costa e Silva et al., 2013). As with heritability (Andrew et al., 2005), studies of IGEs in wild populations are rare (Wilson et al., 2011), but increasingly possible using large-scale pedigree reconstruction with molecular markers. Understanding the mechanisms, including interaction feedbacks, by which IGEs manifest (Trubenová et al., 2015) and the demographic dynamics of IGEs (Wilson et al., 2011) will be important. While some forest tree species grow in pure stands and regenerate en masse, creating even-aged monospecific cohorts similar to our planted population, in others recruitment is more continuous (Ashton, 2000). In these cases, the strongest interactions are likely across cohorts with pre-established, often related, phenotypes. The extent to which indirect genetic effects at the intraspecific level (IGEs) constitute a significant component of the biotic environment in the wild must also be assessed against the multitude of interspecific interactions (IIGEs) occurring at diverse trophic levels, from microbes to predators (Whitham et al., 2008). Such studies are basic for our understanding of the role of indirect genetic effects in shaping natural patterns of genetic diversity and response to environmental change (Bailey et al., 2014).
Data archiving
The trials and germplasm studied are being used for commercial tree-breeding purposes. The raw data used for this study are subject to pre-existing agreements and cannot be made public. The raw data have been archived on the long-term data management system of the Southern Tree Breeding Association Inc. (STBA; Mount Gambier, Australia). The authors should be contacted if there is interest in use of these data for collaborative research purposes.
Acknowledgments
The financial support given to João Costa e Silva by Fundação para a Ciência e a Tecnologia (Lisboa, Portugal), through the Programa Operacional Potencial Humano and the European Social Fund, is gratefully acknowledged. The trial was established by the Southern Tree Breeding Association Inc. (STBA) on a site provided by WAPRES. Data collection were coordinated by David Pilbeam (STBA), and supported by Australian Research Council Grants (LP0884001 and LP140100506), seedEnergy Pty Ltd, STBA and CRC for Forestry. We thank David Pilbeam and Greg Dutkowski for their discussion over the course of this study.
Footnotes
Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)
The authors declare no conflict of interest.
Supplementary Material
References
- Akaike H. (1974). A new look at the statistical model identification. IEEE Trans Autom Control 19: 716–723. [Google Scholar]
- Anche MT, de Jong MCM, Bijma P. (2014). On the definition and utilization of heritable variation among hosts in reproduction ratio R-0 for infectious diseases. Heredity 113: 364–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrew RL, Peakall R, Wallis IR, Wood JT, Knight EJ, Foley WJ. (2005). Marker-based quantitative genetics in the wild?: the heritability and genetic correlation of chemical defenses in Eucalyptus. Genetics 171: 1989–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashton DH (2000). Ecology of eucalypt regeneration. In: Keane PJ, Kile GA, Podger FD, Brown BN (eds). Diseases and Pathogens of Eucalypts. CSIRO Publishing: Collingwood, pp 35–46. [Google Scholar]
- Bailey JK, Genung MA, Ware I, Gorman C, Van Nuland ME, Long H et al. (2014). Indirect genetic effects: an evolutionary mechanism linking feedbacks, genotypic diversity and coadaptation in a climate change context. Funct Ecol 28: 87–95. [Google Scholar]
- Bailey NW, Hoskins JL. (2014). Detecting cryptic indirect genetic effects. Evolution 68: 1871–1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijma P. (2011). A general definition of the heritable variation that determines the potential of a population to respond to selection. Genetics 189: 1347–1359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijma P. (2014). The quantitative genetics of indirect genetic effects: a selective review of modelling issues. Heredity 112: 61–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bijma P, Muir WA, Van Arendonk JAM. (2007). Multilevel selection 1: quantitative genetics of inheritance and response to selection. Genetics 175: 277–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyden S, Binkley D, Senock R. (2005). Competition and facilitation between Eucalyptus and nitrogen-fixing Falcataria in relation to soil fertility. Ecology 86: 992–1001. [Google Scholar]
- Boyden S, Binkley D, Stape JL. (2008). Competition among Eucalyptus trees depends on genetic variation and resource supply. Ecology 89: 2850–2859. [DOI] [PubMed] [Google Scholar]
- Brotherstone S, White IMS, Sykes R, Thompson R, Connolly T, Lee S et al. (2011). Competition effects in a young Sitka spruce (Picea sitchensis, Bong. Carr) clonal trial. Silvae Genet 60: 149–155. [Google Scholar]
- Burnham KP, Anderson DR. (2002) Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Springer-Verlag: New York, NY, USA. [Google Scholar]
- Camerlink I, Ursinus WW, Bijma P, Kemp B, Bolhuis JE. (2015). Indirect genetic effects for growth rate in domestic pigs alter aggressive and manipulative biting behaviour. Behav Genet 45: 117–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canham CD, LePage PT, Coates KD. (2004). A neighborhood analysis of canopy tree competition: effects of shading versus crowding. Can J Forest Res 34: 778–787. [Google Scholar]
- Cantet RJC, Cappa EP. (2008). On identifiability of (co)variance components in animal models with competition effects. J Anim Breed Genet 125: 371–381. [DOI] [PubMed] [Google Scholar]
- Cappa EP, Cantet RJC. (2008). Direct and competition additive effects in tree breeding: Bayesian estimation from an individual tree mixed model. Silvae Genet 57: 45–56. [Google Scholar]
- Cappa EP, Muñoz F, Sanchez L, Cantet RJC. (2015). A novel individual-tree mixed model to account for competition and environmental heterogeneity: a Bayesian approach. Tree Genet Genomes 11: 120. [Google Scholar]
- Cappa EP, Stoehr MU, Xie CY, Yanchuk AD. (2016). Identification and joint modelling of competition effects and environmental heterogeneity in three Douglas-fir (Pseudotsuga menziesii var. menziesii trials. Tree Genet Genomes 12: 102. [Google Scholar]
- Carnegie AJ, Ades PK. (2003). Mycosphaerella leaf disease reduces growth of plantation-grown Eucalyptus globulus. Aust For 66: 113–119. [Google Scholar]
- Costa e Silva J, Graudal L. (2008). Evaluation of an international series of Pinus kesiya provenance trials for growth and wood quality traits. Forest Ecol Manag 255: 3477–3488. [Google Scholar]
- Costa e Silva J, Kerr RJ. (2013). Accounting for competition in genetic analysis, with particular emphasis on forest genetic trials. Tree Genet Genomes 9: 1–17. [Google Scholar]
- Costa e Silva J, Potts BM, Bijma P, Kerr RJ, Pilbeam DJ. (2013). Genetic control of interactions amongst individuals: Contrasting outcomes of indirect genetic effects arising from neighbour disease infection and competition in a forest tree. New Phytol 197: 631–641. [DOI] [PubMed] [Google Scholar]
- Coutts MP, Nielsen CCN, Nicoll BC. (1999). The development of symmetry, rigidity and anchorage in the structural root system of conifers. Plant Soil 217: 1–15. [Google Scholar]
- Cullis BR, Jefferson P, Thompson R, Smith AB. (2014). Factor analytic and reduced animal models for the investigation of additive genotype-by-environment interaction in outcrossing plant species with application to a Pinus radiata breeding programme. Theor Appl Genet 127: 2193–2210. [DOI] [PubMed] [Google Scholar]
- Ellen ED, Bas Rodenburg T, Albers GAA, Bolhuis JE, Camerlink I, Duijvesteijn N et al. (2014). The prospects of selection for social genetic effects to improve welfare and productivity in livestock. Front Genet 5: 377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyles A, Barry KM, Quentin A, Pinkard EA. (2013). Impact of defoliation in temperate eucalypt plantations: Physiological perspectives and management implications. Forest Ecol Manag 304: 49–64. [Google Scholar]
- Freeman JS, Potts BM, Vaillancourt RE. (2008). Few Mendelian genes underlie the quantitative response of a forest tree, Eucalyptus globulus, to a natural fungal epidemic. Genetics 178: 563–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour AR, Thompson R, Cullis BR. (1995). Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51: 1440–1450. [Google Scholar]
- Gilmour AR, Gogel BJ, Cullis BR, Welham SJ, Thompson R. (2015) ASReml User Guide Release 4.1. VSN International Ltd: Hemel Hempstead, HP1 1ES, UK. [Google Scholar]
- Griffing B. (1967). Selection in reference to biological groups. I. Individual and group selection applied to populations of unordered groups. Aust J Biol Sci 20: 127–139. [PubMed] [Google Scholar]
- John JA, Williams ER. (1995) Cyclic and Computer Generated Designs. Chapman and Hall: London, UK. [Google Scholar]
- Kass RE, Raftery AE. (1995). Bayes factors. J Am Stat Assoc 90: 773–795. [Google Scholar]
- Kuha J. (2004). AIC and BIC: comparisons of assumptions and performance. Soc Methods Res 33: 188–229. [Google Scholar]
- Lipschutz-Powell D, Woolliams JA, Bijma P, Doeschl-Wilson AB. (2012). Indirect genetic effects and the spread of infectious disease: are we capturing the full heritable variation underlying disease prevalence? PLoS ONE 7: e39551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B. (1998) Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland: MA, USA. [Google Scholar]
- McGlothlin JW, Brodie EDIII. (2009). How to measure indirect genetic effects: the congruence of trait-based and variance-partitioning approaches. Evolution 63: 1785–1795. [DOI] [PubMed] [Google Scholar]
- McGlothlin JW, Moore AJ, Wolf JB, Brodie EDIII. (2010). Interacting phenotypes and the evolutionary process. III. Social Evolution. Evolution 64: 2558–2574. [DOI] [PubMed] [Google Scholar]
- Meyer K. (2009). Factor-analytic models for genotype x environment type problems and structured covariance matrices. Genet Sel Evol 41: 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milgate AW, Potts BM, Joyce K, Mohammed C, Vaillancourt RE. (2005). Genetic variation in Eucalyptus globulus for susceptibility to Mycosphaerella nubilosa and its association with tree growth. Australas Plant Pathol 34: 11–18. [Google Scholar]
- Misra RK, Gibbons AK. (1996). Growth and morphology of eucalypt seedling-roots, in relation to soil strength arising from compaction. Plant Soil 182: 1–11. [Google Scholar]
- Moorad JA, Nussey DH. (2016). Evolution of maternal effect senescence. Proc Natl Acad Sci USA 113: 362–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore AJ, Brodie EDIII, Wolf JB. (1997). Interacting phenotypes and the evolutionary process. 1. Direct and indirect genetic effects of social interactions. Evolution 51: 1352–1362. [DOI] [PubMed] [Google Scholar]
- Muir WM. (2005). Incorporation of competitive effects in forest tree or animal breeding programs. Genetics 170: 1247–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muir WM, Bijma P, Schinckel A. (2013). Multilevel selection with kin and non-kin groups, experimental results with Japanese quail (Coturnix japonica. Evolution 67: 1598–1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutic JJ, Wolf JB. (2007). Indirect genetic effects from ecological interactions in Arabidopsis thaliana. Mol Ecol 16: 2371–2381. [DOI] [PubMed] [Google Scholar]
- O’Grady AP, Worledge D, Battaglia M. (2005). Temporal and spatial changes in fine root distributions in a young Eucalyptus globulus stand in southern Tasmania. Forest Ecol Manag 214: 373–383. [Google Scholar]
- O’Grady AP, Worledge D, Battaglia M. (2006). Above- and below-ground relationships, with particular reference to fine roots, in a young Eucalyptus globulus (Labill.) stand in southern Tasmania. Trees 20: 531–538. [Google Scholar]
- Peeters K, Eppink T, Ellen ED, Visscher J, Bijma P. (2012). Indirect genetic effects for survival in domestic chicken (Gallus gallus are magnified in crossbred genotypes and show a parent-of-origin effect. Genetics 192: 705–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinkard EA, Mohammed CL. (2006). Photosynthesis of Eucalyptus globulus with Mycosphaerella leaf disease. New Phytol 170: 119–127. [DOI] [PubMed] [Google Scholar]
- Quentin AG, Beadle CL, O’Grady AP, Pinkard EA. (2011). Effects of partial defoliation on closed canopy Eucalyptus globulus Labilladiere: Growth, biomass allocation and carbohydrates. Forest Ecol Manag 261: 695–702. [Google Scholar]
- Resende MDV, Stringer JK, Cullis BR, Thompson R. (2005). Joint modelling of competition and spatial variability in forest field trials. Rev Mat Estat 23: 7–22. [Google Scholar]
- Resende RT, Marcatti GE, Pinto DS, Takahashi EK, Cruz CD, Resende MDV. (2016). Intra-genotypic competition of Eucalyptus clones generated by environmental heterogeneity can optimize productivity in forest stands. Forest Ecol Manag 380: 50–58. [Google Scholar]
- Richards SA. (2008). Dealing with overdispersed count data in applied ecology. J Appl Ecol 45: 218–227. [Google Scholar]
- Santostefano F, Wilson AJ, Araya-Ajoy YG, Dingemanse NJ. (2016). Interacting with the enemy: indirect effects of personality on conspecific aggression in crickets. Behav Ecol 27: 1235–1246. [Google Scholar]
- Sartori C, Mantovani R. (2013). Indirect genetic effects and the genetic bases of social dominance: evidence from cattle. Heredity 110: 3–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schenk HJ. (2006). Root competition: beyond resource depletion. J Ecol 94: 725–739. [Google Scholar]
- Schwarz G. (1978). Estimating the dimension of a model. Ann Stat 6: 461–464. [Google Scholar]
- Shuster SM, Lonsdorf EV, Wimp GM, Bailey JK, Whitham TG. (2006). Community heritability measures the evolutionary consequences of indirect genetic effects on community structure. Evolution 60: 991–1003. [PubMed] [Google Scholar]
- Soares P, Tomé M. (1996). Changes in eucalypt plantations structure, variability and relative growth rate pattern under different intraspecific competition gradients Skovsgaard JP, Johannsen VK (eds). Modelling Regeneration Success and Early Growth of Forest Stands Proceedings from the IUFRO Conference (Copenhagen, 10–13 June 1996) Danish Forest and Landscape Research Institute: Hørsholm, pp 270–284. [Google Scholar]
- Soares P, Tomé M. (1999). Distance-dependent competition measures for Eucalyptus plantations in Portugal. Ann Forest Sci 56: 307–319. [Google Scholar]
- Smith AB, Cullis BR, Thompson R. (2001). Analyzing variety by environment data using multiplicative mixed models and adjustments for spatial field trend. Biometrics 57: 1138–1147. [DOI] [PubMed] [Google Scholar]
- Stackpole DJ, Vaillancourt RE, Aguigar M, Potts BM. (2010). Age trends in genetic parameters for growth and wood density in Eucalyptus globulus. Tree Genet Genomes 6: 179–193. [Google Scholar]
- Stram DO, Lee JW. (1994). Variance components testing in the longitudinal mixed effects model. Biometrics 50: 1171–1177. [PubMed] [Google Scholar]
- Trubenová B, Novak S, Hager R. (2015). Indirect genetic effects and the dynamics of social interactions. PLoS ONE 10: e0126907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White DA, Crombie DS, Kinal J, Battaglia M, McGrath JF, Mendham DS et al. (2009). Managing productivity and drought risk in Eucalyptus globulus plantations in south-western Australia. Forest Ecol Manag 259: 33–44. [Google Scholar]
- Whitham TG, DiFazio SP, Schweitzer JA, Shuster SM, Allan GJ, Bailey JK et al. (2008). Extending genomics to natural communities and ecosystems. Science 320: 492–495. [DOI] [PubMed] [Google Scholar]
- Wilson AJ. (2014). Competition as a source of constraint on life history evolution in natural populations. Heredity 112: 70–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson AJ, Gelin U, Perron M-C, Réale D. (2009). Indirect genetic effects and the evolution of aggression in a vertebrate system. Proc R Soc B Biol Sci 276: 533–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson AJ, Morrissey MB, Adams MJ, Walling CA, Guinness FE, Pemberton JM et al. (2011). Indirect genetics effects and evolutionary constraint: an analysis of social dominance in red deer, Cervus elaphus. J Evol Biol 24: 772–783. [DOI] [PubMed] [Google Scholar]
- Wolf JB, Brodie EDIII, Cheverud JM, Moore AJ, Wade MJ. (1998). Evolutionary consequences of indirect genetic effects. Trends Ecol Evol 13: 64–69. [DOI] [PubMed] [Google Scholar]
- Wolf JB, Mutic JJ, Kover PX. (2011). Functional genetics of intraspecific ecological interactions in Arabidopsis thaliana. Philos Trans R Soc B Biol Sci 366: 1358–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.