Abstract
The self-incompatibility (SI) gene that is specifically expressed in pistils encodes the SI-associated ribonuclease (S-RNase), functioning as the female-specificity determinant of a gametophytic SI system. Despite extensive surveys in Malus domestica, the S-alleles have not been fully investigated for Malus sieversii, the primary wild ancestor of the domesticated apple. Here we screened the M. sieversii S-alleles via PCR amplification and sequencing, and identified 14 distinct alleles in this species. By contrast, nearly 40 are present in its close wild relative, Malus sylvestris. We further sequenced 8 nuclear genes to provide a neutral reference, and investigated the evolution of S-alleles via genealogical and population genetic analyses. Both shared ancestral polymorphism and an excess of non-synonymous substitution were detected in the S-RNases of the tribe Maleae in Rosaceae, indicating the action of long-term balancing selection. Approximate Bayesian Computations based on the reference neutral loci revealed a severe bottleneck in four of the six studied M. sieversii populations, suggesting that the low number of S-alleles found in this species is mainly the result of diversity loss due to a drastic population contraction. Such a bottleneck may lead to ambiguous footprints of ongoing balancing selection detected at the S-locus. This study not only elucidates the constituents and number of S-alleles in M. sieversii but also illustrates the potential utility of S-allele number shifts in demographic inference for self-incompatible plant species.
Introduction
Self-incompatibility (SI) is a genetic system for preventing self-fertilization in angiosperms, via the rejection of pollen expressing the same specificity as found in the pistil (Kao and Tsukamoto, 2004; Chen et al., 2010). Self-incompatibility is widely distributed throughout the angiosperm phylogeny, and distinct molecular mechanisms have evolved in different groups of plants (Castric and Vekemans, 2004; Iwano and Takayama, 2012). Classical genetic studies have classified SI into gametophytic (GSI) and sporophytic, depending on whether the pollen SI phenotype is determined by the S haplotype of haploid pollen or by the S haplotypes of the diploid pollen donor (Kao and Tsukamoto, 2004; Iwano and Takayama, 2012). However, in the Solanaceae and the subtribe Pyrinae of Rosaceae, a ‘collaborative non-self recognition’ model has been proposed, in which a single SI-associated ribonuclease (S-RNase) acts as the pistil-specificity determinant and multiple S-locus F-box proteins function collectively as the pollen-specificity determinants to recognize non-self S-RNases (Kubo et al. 2010, de Franceschi et al., 2012).
One important feature of the SI system is that the S-locus is subject to strong, negative, frequency-dependent selection, as rare S specificities lead to greater opportunities for compatible mating than more frequent specificities (Richman, 2000). Consequently, the S-locus is characterized by a number of features in evolution (see reviews in Richman, 2000; Castric and Vekemans, 2004; Charlesworth, 2006). First, a large number of alleles with relatively even frequencies should be maintained at this locus. Second, S-alleles segregating at the S-locus are highly diverged from each other, and positive selection is frequently involved in the S-RNases’ amino-acid substitutions. Third, the level of population differentiation at the S-locus should be significantly less than that at the neutral loci because differentiation via drift will be decelerated and the transfer of S-alleles among populations will be promoted. Finally, because of the extremely long average coalescence times required for S-locus polymorphisms relative to neutral variation, these alleles can provide insights into the genetic and demographic events that occurred long before the divergence of the extant species. These four theoretical predictions have been tested and supported by a range of empirical studies (Glemin et al., 2005; Raspe and Kohn, 2007; Edh et al., 2009; Dreesen et al., 2010).
In contrast to the genealogy of S-alleles, which records evolutionary events over millions of years, the number of S-alleles appears to have evolved relatively rapidly as a result of sensitivity to changes in population size (Richman, 2000). Thus, variations in the numbers of alleles may elucidate recent changes in the demographic history of the species. This has been corroborated by a number of studies that have inferred fluctuations in population size by detecting shifts in allele numbers at the S-locus (Brennan et al., 2002; Paape et al., 2008; Guo et al., 2009). However, to shed more light on the demographic history of a SI species, it would be better to analyse the S-locus polymorphism in conjunction with neutral genomic variation.
The wild apple Malus sieversii (Ldb.) Roem is known to be the primary progenitor of the domesticated apple, which is one of the most important fruit crops cultivated in temperate zones around the world (Cornille et al., 2014). M. sieversii is native to the mountainous regions of Central Asia, mainly along the Tian Shan Mountains, and is extremely variable in its growth habit, height, fruit size and quality, and nutritional constituents (Forsline et al., 2003). Under favourable growing conditions, M. sieversii can bear fruits with excellent characteristics, approaching the quality and size of commercial cultivars (Cornille et al., 2014). The gene pool of M. sieversii is rich in genetic resources that can be applied to enhance the breeding of apple cultivars (Forsline et al., 2003). However, although no bottleneck has been detected during apple domestication (Cornille et al., 2012), the genetic diversity of the cultivated apple has been heavily eroded over the twentieth century, as modern cultivars have been bred using just a few founding lineages, while only a couple of cultivars were used for commercial orchard production (Gross et al., 2014). Thus, M. sieversii represents a valuable germplasm resource that is used to broaden the genetic base of cultivated apple.
Owing to the important role of M. sieversii in apple breeding, this species has been studied in terms of its genetic diversity and population structure (Zhang et al., 2007; Richards et al., 2009), gene flow with Malus domestica (Cornille et al., 2013b), historical demography (Zhang et al., 2015) and molecular basis for abiotic resistance (Forsline et al., 2003). As to the S-alleles controlling cross-compatibility, few studies have investigated them in M. sieversii, however, such alleles have been extensively studied for apple cultivars and other fruit crops within Rosaceae (Broothaerts, 2003; Sanzol, 2009; Long et al., 2010) owing to the importance of SI to fruit production. The S-alleles of non-cultivated wild species in the Malus genus have also been studied. Li et al. (2012), for example, cloned S-alleles from wild Malus species and identified several novel ones that were absent from M. domestica, while Dreesen et al. (2010) explored the diversity of these alleles in Malus sylvestris, the secondary donor to the domesticated apple genome. Interestingly, the majority of the S-alleles present in M. domestica are also found in M. sylvestris, which is consistent with a close relationship between these two species (Cornille et al., 2012). In addition, evolutionary analysis of S-alleles from Rosaceae species has led to the identification of amino acids under positive selection and enabled an estimation of the number of S specificities maintained in the ancestral lineage of the tribe Maleae (Vieira et al., 2010). At present, natural populations of M. sieversii are steadily declining due to forest destruction, over grazing and other biotic stresses (Zhang et al., 2007). Thus, analysing S-alleles and S-genotypes in M. sieversii could facilitate the design of mating schemes to increase the reproductive success of this species and consequently enable the better protection of genetic resources, and the efficient utilization of germplasm (Broothaerts, 2003; Long et al., 2010). Furthermore, comparative analyses of S-alleles between closely related Malus species will contribute to the understanding of their evolutionary dynamics in different lineages.
In this study, we extensively surveyed the S-alleles in M. sieversii using three pairs of consensus primers that were designed based on the conserved regions of S-RNases from species within the tribe Maleae of the family Rosaceae. Phylogenetic and population genetic analyses were performed to evaluate the evolutionary dynamics of M. sieversii S-alleles. We further sequenced eight unlinked nuclear loci for use as a neutral reference, from which the pattern of polymorphisms and population demography were inferred and compared with S-alleles. The aims of this study were to determine the following: (1) the number of distinct S-alleles present in M. sieversii and their relationship with the S-alleles present in domesticated apple and M. sylvestris; (2) whether or not the S-alleles of M. sieversii display the characteristics of a GSI system that is controlled by negative frequency-dependent selection; and (3) whether new insights into the demographic history of M. sieversii can be gained by studying S-alleles and whether or not this history can be corroborated by analysing reference nuclear loci.
Materials and methods
Population sampling
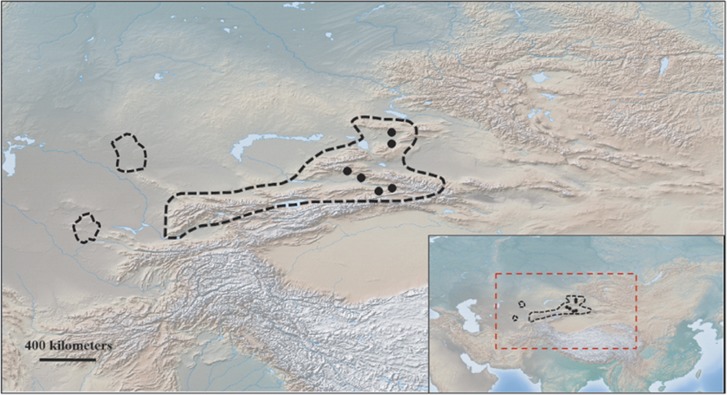
A total of 90 individuals from six M. sieversii populations were collected from the Xinjiang Uygur Autonomous Region of China (Figure 1). Of these, samples from four populations were gathered from the Yili valley in the Tian Shan Mountains, including Xinyuan, Mohe (MH), Daxigou and Yiling. Two other populations, Laofengkou and Eming, were sampled from sites in the western mountains of the Junggar Basin. All sampled trees were separated by a distance of at least 50 m, while young leaves were collected and immediately dried with silica gel. We deposited M. sieversii voucher specimens in the Herbarium of Hainan University, Haikou, China.
Figure 1.
Geographical distribution of M. sieversii and the localities of the populations sampled in this study. The broken black line indicates the geographic range of M. sieversii and solid circles represent the sampled populations of M. sieversii. Detailed information on these populations is provided in Supplementary Table S5.
Genomic DNA extraction, amplification, cloning and sequencing
We extracted genomic DNA from the silica gel-dried leaves using the cetyl trimethylammonium bromide method, as described by Zhang et al. (2015). All individuals are expected to be heterozygous at the S-locus in a GSI system because there is no dominance (Iwano and Takayama, 2012). The gene structure of rosaceous S-alleles is quite simple, with two exons and one intron in-between (Igic and Kohn, 2001). The consensus primers S-F and S-R1 were designed based on the conserved regions C1 (FTQQYQ) and C5 (FI(D/N)CP(H/R)) in Rosaceae S-RNases (Long et al., 2010), while primers S-R2 and S-R3 were designed in this study on the basis of highly conserved S-allele sequences from the tribe Maleae of the family Rosaceae. The primer pair S-F/S-R1 was initially used to amplify the S-allele genomic sequences from M. sieversii, but when just one S-allele was obtained using this approach, we further utilized S-F/S-R2 and S-F/S-R3 to amplify both alleles. Among the three primer pairs, the products of S-F/S-R1 and S-F/S-R2 almost encompass the whole gene region, while S-F/S-R3 only amplifies part of the first exon. DNA sequences representing the genomic background were obtained from eight nuclear loci located on eight different M. domestica chromosomes. Although one of the loci (C17) was distributed on the same chromosome as the S-locus, the long physical distance between the two loci (more than 2 × 104 base pairs, according to the genome sequences of the domesticated apple) indicates that they are essentially unlinked. Detailed information on the location, functional annotation and the primer sequences of these amplified regions is presented in Supplementary Table S1.
All PCR amplifications were performed in a total volume of 25 μl containing 5–50 ng of genomic DNA, 5.0 pM of each primer, 0.2 mM of each deoxyribonucleotide triphosphate, 2.0 mM of MgCl2 and 0.75 U exTaq DNA polymerase (TaKaRa, Shiga, Japan). The amplification of S-alleles was performed using a T gradient 96 U thermocycler (Biometra, Gotingen, Germany) as follows: 2 min at 94 °C, followed by 35 cycles of 30 s at 94 °C, 30 s at 52 °C, 90 s at 72 °C; and a final extension at 72 °C for 7 min. The products were examined in a 1.5% agarose gel stained with ethidium bromide, while the bands were incised and gel-purified using a DNA purification kit (Amersham Pharmacia Biotech, Piscataway, NJ, USA). If the PCR product obtained from an individual was separated into two clear-cut bands by agarose gel electrophoresis, the genomic sequences of the two S-alleles could be determined by separately sequencing the two bands. Otherwise, when only one band was detected, we first sequenced the PCR product directly to check whether two alleles were successfully amplified. PCR products containing two alleles were then cloned into pGEM-T Easy Vectors (Promega, Madison, WI, USA) and multiple clones were sequenced until both alleles were completely determined. For the PCR products containing just one allele, further amplifications using the two alternative primer pairs were conducted to try to obtain both S-alleles. PCR amplification was carried out for the eight nuclear loci following the same protocol as used for S-alleles. The amplified products were gel-purified and sequenced, either directly or after cloning into pGEM-T Easy Vectors, if dual peaks were identified due to the presence of heterozygous individuals. At least six cloned DNA fragments were sequenced in each case to retrieve both alleles at a locus. Previous studies showed that both Taq errors and interallelic PCR recombinants can be verified and removed using this multiclone sequencing strategy (Zhang and Ge, 2007). Sequencing was conducted using an ABI 3730 DNA sequencer (Applied Biosystems, Forster City, CA, USA).
Estimating the number of M. sieversii S-alleles
The total number of S-alleles present in the M. sieversii population was estimated using Paxman’s (1963) maximum likelihood (ML) method. For a GSI system, given that n alleles have been identified in a sample of r diploid individuals, the number of alleles (N) in the population can be estimated from
and the 95% confidence interval for this estimation was constructed following O’Donnell and Lawrence (1984).
Because Paxman (1963) assumed that S-alleles occurred at equal frequencies (that is, isoplethy) in a population, we tested this null hypothesis using the Mantel, 1974 statistic (Campbell and Lawrence, 1981b), which is defined as
where Cj refers to the number of times an allele occurs, n denotes the number of alleles identified and r is the number of diploid individuals sampled. We then further estimated the number of S-alleles present in the M. sieversii population using an improved ML method, that is, the E2 estimator proposed by O’Donnell and Lawrence (1984), which does not assume the presence of equal frequencies.
To facilitate comparisons between the numbers of M. sieversii alleles estimated here with earlier studies, we measured the thoroughness of sampling using the repeatability statistic, R (Campbell and Lawrence, 1981a), which is calculated as
where m denotes the number of alleles examined and n refers to the number of different alleles identified.
As the European crabapple M. sylvestris is a close relative of M. sieversii (Cornille et al., 2014), we estimated allele numbers for both species for comparison. The S-alleles collected from M. sylvestris by Dreesen et al. (2010) were used to estimate the allele number of this species. Mate availability was defined as the percentage of compatible crosses present in a given population (Campbell and Husband, 2007). Applying this definition, we estimated the mean mate availability for each M. sieversii population to examine whether mate limitation occurred in this species.
Retrieval and phylogenetic analysis of S-alleles from Maleae
We utilized the Basic Local Alignment Search Tool (BLAST) algorithm to retrieve all known S-RNases for the tribe Maleae from GenBank (Altschul et al., 1997). The S-RNases of M. domestica (Broothaerts, 2003; Long et al., 2010) and those of the European pear (Sanzol, 2009) were used as the initial queries; proteins from Rosaceae species in the GenBank non-redundant protein database were used as the subjects. We set the E-value threshold to 1 × e–5 and conducted the first BLAST search using the initial queries. Then, the retrieved sequences were used as new queries for the next BLAST search. Such searches were carried out iteratively until the number of S-RNases retrieved no longer increased. To provide cross-validation for our BLAST analyses, we implemented profile hidden Markov models using the hmmsearch software (Eddy, 2011). A profile hidden Markov model (PF00445.13) was searched against Maleae proteins retrieved from GenBank to identify S-RNases using hmmsearch with the default parameters.
The Maleae S-RNases were clustered using BLASTclust (Altschul et al., 1997) to remove redundant records from the retrieved sequences. In cases in which less than three amino-acid differences were seen between two S-RNases, the two hits were regarded as a single entity with identical specificity and placed into the same cluster (Vieira et al., 2008). The longest S-RNase in each cluster was chosen as the representative of that cluster, and the Maleae S-RNases were aligned using the ‘protein’ option in the Probabilistic Alignment Kit (PRANK) software, applying the default parameters (Loytynoja and Goldman, 2008). The best-fit model for the evolution of these proteins was evaluated using the software ProtTest 3 and applying three criteria: the Akaike information criterion; Bayesian information criterion; and corrected (second-order) Akaike Information Criterion (Darriba et al., 2011). The evolutionary history of Maleae S-RNases was then inferred using a best-fit substitution model in the Randomized Axelerated ML (RAxML) version 8. Topological robustness was assessed via 500 rapid bootstrapping searches implemented in RAxML (Stamatakis, 2014).
On the basis of the initial ML tree (Supplementary Figure S1), a trans-generic (TG) lineage was delimited as a strongly supported clade comprising S-RNases from more than one genus. We retained just one or two S-RNases from each genus of Malus, Pyrus, Sorbus, Crataegus and Eriobotrya to reduce the size of the TG lineages while, at the same time, preserving the inter-generic relationships among the S-alleles. These retained S-RNases, along with the 14 S-RNases identified from M. sieversii, were then subject to a second analysis in RAxML. The best-fit model was again determined using ProtTest 3, and an ML tree was inferred using the same search settings.
We assessed sequence divergence within and among the TG lineages that were identified by phylogenetic analyses. The amino-acid substitution mode JTT with a gamma distribution for the rate variation across sites was used to estimate genetic distance (Tamura et al., 2011). Moreover, we evaluated divergence among the 14 M. sieversii S-alleles based on three distance measures, that is, synonymous, non-synonymous and amino-acid substitutions. Synonymous and non-synonymous substitutions were calculated by MEGA5.2 (Tamura et al., 2011) using the Nei–Gojobori method (Nei and Gojobori, 1986) with the Jukes–Cantor correction (Jukes and Cantor, 1969), while amino-acid substitutions were calculated with the p-distance option implemented in MEGA5.2.
Molecular evolutionary analyses of the tribe Maleae S-alleles
We identified the coding sequences of M. sieversii S-alleles by aligning their genomic sequences to known examples from the tribe Maleae. The coding sequences of S-alleles used for detecting selection were then aligned in PRANK by applying the ‘codon’ option while setting the other parameters to default (Loytynoja and Goldman, 2008). Although alignment errors can lead to false inferences of positive selection (Fletcher and Yang, 2010; Jordan and Goldman, 2012), studies have shown that the ‘codon’ option in PRANK, which implements an empirical codon model to directly align the codon sequences, is the least error-prone method among the commonly applied approaches (Fletcher and Yang, 2010; Markova-Raina and Petrov, 2011; Jordan and Goldman, 2012).
The ratio between non-synonymous and synonymous substitution rates (ω) provides a measure of the selective pressure on protein-coding sequences. To test for selection and to identify positively selected codons within the sequences of Maleae S-alleles, we implemented a series of random-sites models in codeml using Phylogenetic Analysis by Maximum Likelihood software version 4.8 (Yang, 2007). M1a and M7 are two nearly neutral models, which use discrete site classes and a beta distribution, respectively, to model ω variation among codons (with the constraint ω⩽1), while M2a and M8 are two selection models, which take positive selection into account by adding an additional site class (with the constraint ω>1) to M1a and M7, respectively. We ran all these models three times while varying the initial values for κ and ω to avoid getting stuck at local optima when optimizing parameters.
We then used nested pairs of these models (M1a versus M2a and M7 versus M8) to formulate two likelihood ratio tests for positive selection (Yang, 2007). We compared twice of the log likelihood difference between the two compared models (2Δℓ) against a χ2 distribution with two degrees of freedom. If the selection model fit the data significantly better than the neutral model, positive selection was indicated. Bayes empirical Bayes inference was then used to calculate the posterior probability of being under selection for each codon (Yang, 2007).
We used the software omegaMap to account for the potential effects of recombination between S-alleles in our selection analyses (Vieira et al., 2010). This approach applies a population genetics approximation to the coalescent with recombination in order to identify codons that are probably under positive selection (Wilson and McVean, 2006). OmegaMap implements a reversible-jump Markov chain Monte Carlo (MCMC) to perform Bayesian inference on both the ω ratio and the recombination rate, allowing each to vary along the sequence. The MCMC chains were conducted for a total of 1 000 000 iterations and were sampled every 1000 iterations, with the first 25% of the samples discarded as burn-in. Ten random sequence orders were used to compute the product of approximate conditionals likelihood, while a block-like model was used to approximate the variation in ω and ρ along the sequence. The average length of a block was set at three for both parameters, and convergence of the MCMC algorithm was assessed by running two independent omegaMap analyses from different starting points.
Population genetic analyses
For the S-allelic genotype data, standard measures of genetic diversity, including the observed (Na) and effective number of alleles (Ne), gene diversity in terms of expected (He) and observed heterozygosity (Ho), as well as Shannon’s diversity index (I), were estimated using Genetic Analysis in Excel version 6.5 (Peakall and Smouse, 2012). In addition, we calculated the inbreeding coefficient FIS (an F-statistic that indicates the inbreeding coefficient of an individual relative to the subpopulation) and the allelic richness using FSTAT version 2.9.3.2 (Goudet, 1995). For the nucleotide sequences of the S-alleles and the reference loci, the number of segregating sites (S), number of haplotypes (h) and two parameters of nucleotide diversity, Nei’s π, the expected heterozygosity per nucleotide site (Nei, 1987), and Watterson’s θw, an estimate of the population mutation parameter 4Neμ (Watterson, 1975), were calculated using DNA Sequence Polymorphism (DnaSP) version 5.10 (Librado and Rozas, 2009). Nucleotide diversity estimates were calculated based on either the total sequences or the silent sites. We also estimated the minimum number of recombination events (Rm) for the reference loci via the four-gamete test (Hudson and Kaplan, 1985), which was also implemented in DnaSP.
To test for the neutral equilibrium evolutionary model, we calculated Tajima’s D (Tajima, 1989) and Fu and Li’s D* and F* (Fu and Li, 1993) statistics using the software DnaSP. Tajima’s D was based on the discrepancy between π and θw, while Fu and Li’s D* and F* use differences in the number of singletons and the total number of mutations, respectively. Negative values in both tests indicate an excess of low-frequency polymorphisms, while positive values indicate an excess of intermediate polymorphisms. Because selective forces generally act on a single locus while demography affects all genes within a genome, we further applied the multilocus Hudson–Kreitman–Aguadé (HKA) test (Hudson et al., 1987) across our eight reference loci, using HKA software (https://bio.cst.temple.edu/~hey/software/software.htm#HKA) to discriminate between the two effects. We used Malus kansuensis sequences as outgroups to conduct the HKA tests. In addition, to account for the demographic changes when testing for selection, we simulated 1 × 104 S-allele data sets for each population under the best-fit demographic model using the software ms (Hudson, 2002). Then, Tajima’s D, Fu and Li’s D* and F*, and two diversity measures (π and θw) were calculated. On the basis of the neutrality statistics estimated from the simulation, we determined the P-values for the observed S-allele data. The optimal demographic models were inferred by performing Approximate Bayesian Computations using the neutral reference loci (see below).
We used FST (an F-statistic that indicates the inbreeding coefficient of the subpopulation relative to the total population) to measure the extent of genetic differentiation at the S-locus and at the M. sieversii reference loci. We estimated the pairwise FST across our studied populations using the ‘Population comparisons’ algorithm in the software Arlequin 3.5 (Excoffier and Lischer, 2010) and plotted them with R (https://www.r-project.org/). The difference of pairwise FST between the S-locus and the reference loci was tested by an unequal variances t-test (Welch’s t-test).
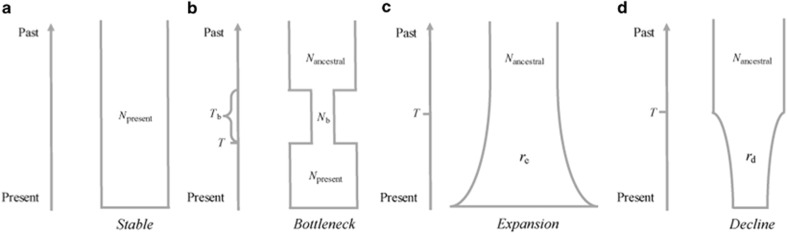
On the basis of neutrally evolving reference loci, we inferred the demographic histories of M. sieversii populations using coalescent simulation and Approximate Bayesian Computations. This approach bypasses exact likelihood calculations and has been widely used for parameter estimation and model selection analyses (Bertorelle et al., 2010; Csillery et al., 2010). Four demographic scenarios, indicating population stability, bottleneck, expansion and decline, were constructed (Figure 2). After several trial runs, prior distributions were specified (Supplementary Table S2). Priors were deliberately defined broadly as little prior information was available. Coalescent simulations were then performed for each population using the software fastsimcoal2 (version 2.5) (http://cmpg.unibe.ch/software/simcoal2/) with parameter values randomly drawn from the priors. For each scenario, 1 × 106 data sets were simulated, each comprising 6 unlinked genes sampled from 25 haploid individuals (that is, the average size of a population). As the differentiation across our studied populations is low (see Results on population genetic analyses), we simulated additional data sets for a ‘merged population’ that included all sampled accessions (that is, 148 haploid individuals). We calculated four summary statistics, π, S, Tajima’s D and Fu’s Fs, for both simulated and real data sets, using the software Arlequin 3.5 (Excoffier and Lischer, 2010). The R package abc (Csillery et al., 2012) was used to perform model selection, with the straightforward ‘rejection’ method (Beaumont et al., 2002) and the regression-based correction method ‘neuralnet’ (Blum and Francois, 2010) applied to the simulated data sets, both at a tolerance level of 0.001. However, as the rejection method is sensitive to the choice of tolerance level (Beaumont, 2010), a series of tolerance levels (that is, 0.01, 0.001, 0.0005 and 0.0002) were implemented to assess their impact on posterior probability estimates.
Figure 2.
Schematic representation of the four demographic scenarios tested on M. sieversii populations using the R package abc (Csillery et al., 2012). (a) Scenario 1 indicates a constant population size through time, (b) scenario 2 shows a population bottleneck, (c) scenario 3 involves population expansion and (d) scenario 4 indicates a population decline. ‘Npresent’ and ‘Nancestral’ are the effective population sizes for the present and ancestral populations, respectively. ‘Nb’ is the effective population size during a bottleneck. ‘Tb’ is the duration of the bottleneck. ‘T’ is the time for the latest demographic change (going backwards in time). re and rd are the growth and contraction rates for the expansion and decline scenarios, respectively. Times and effective population sizes are not to scale.
Results
Identification and estimation of M. sieversii S-alleles
Of the 90 individuals surveyed, we successfully identified both S-alleles in 68 individuals, among which 18 were obtained using the S-F/S-R1 primer pair, 52 using the S-F/S-R2 pair and 6 using the S-F/S-R3 pair (Supplementary Table S3). In the 22 cases in which the second S-allele was failed to retrieve, we randomly selected a few cases, cloned their PCR products into pGEM-T Easy Vectors and then sequenced up to 20 clones in an attempt to isolate this allele. However, unless a PCR product exhibited obvious signals for the presence of both S-alleles, simply cloning PCR products and sequencing large numbers of clones proved to be an ineffective approach for the identification of both alleles. We retrieved a total of 158 S-allele sequences, from which 14 distinct S-alleles were identified and numbered sequentially from S1 to S14. The best hits for the 14 M. sieversii S-alleles were determined using the protein BLAST searches available from the US National Center for Biotechnology Information (Supplementary Table S4). Divergence in the coding sequences among these S-alleles was measured using the Nei–Gojobori method and ranged between 0.037 and 0.267 for synonymous substitutions and between 0.022 and 0.285 for non-synonymous substitutions, while the divergence in amino-acid sequences ranged between 0.05 and 0.35.
We plotted the S-allele frequencies for our 6 M. sieversii populations (Supplementary Figure S2). Different populations have a nearly identical set of S-alleles; only a few alleles that occurred at low frequency differed among the populations. Because the S-allele frequency does not deviate from isoplethy in all populations, with the exception of MH (Table 1), the total number of S-alleles in each population can be estimated using the ML method of Paxman (1963). Our results show that the estimated allele numbers in each population are either identical, or nearly identical, to the corresponding observed numbers and that the confidence intervals on these estimates are narrow, with the exception of the Daxigou and Yiling populations (Table 1).
Table 1. The observed and estimated numbers of S-alleles (by the ML method of Paxman (1963) and the E 2 estimator of O’Donnell and Lawrence (1984)), 95% CI for the ML estimation, repeatability statistic R, MA and P-value of the isoplethy test for each M. sieversii population, and the combined populations for each of M. sieversii and M. sylvestris.
| Observed | ML method (95% CI) | E2 estimator | Repeatability statistic | MA (mean±s.d.) | Isoplethy | |
|---|---|---|---|---|---|---|
| EM | 8 | 9 (8.06–13.27) | 10 | 0.71 | 0.91±0.102 | 0.174 |
| FK | 10 | 10 (10.04–13.26) | 12 | 0.76 | 0.92±0.086 | 0.186 |
| XY | 9 | 10 (9.06–13.72) | 11 | 0.71 | 0.97±0.045 | 0.380 |
| MH | 9 | 9 (9.03–12.33) | 11 | 0.76 | 0.97±0.040 | 0.028 |
| DX | 10 | 12 (10.25–20.63) | 14 | 0.59 | 0.91±0.102 | 0.663 |
| YL | 8 | 12 (8.71–39.22) | 13 | 0.44 | 0.93±0.103 | 0.980 |
| M. sieversii | 14 | 14 (14.00–14.53) | 15 | 0.92 | NA | NA |
| M. sylvestrisa | 38 | 38 (38.00–38.57) | 39 | 0.91 | NA | NA |
Abbreviations: CI, confidence interval; DX, Daxigou; EM, Eming; FK, Laofengkou; MA, mate availability; MH, Mohe; ML, maximum likelihood; NA, not available; XY, Xinyuan; YL, Yiling.
Individuals with unidentified S-alleles were excluded from the analysis.
The allele number and repeatability statistic for M. sylvestris were estimated using the S-allele data from Table 2 in Dreesen et al. (2010).
We combined S-alleles from individual populations to infer the allele number at the species level. This analysis shows that the estimated allele numbers for both the M. sieversii and M. sylvestris species are equal to their observed values and are robust to sampling according to the R-values (Table 1). We further inferred the allele number using the improved ML method, that is, the E2 estimator of O’Donnell and Lawrence (1984) and obtained almost the same estimates as with the method of Paxman (1963) (Table 1). This result suggests that a potentially unequal allele frequency has little effect on the estimates of allele number. In addition, we identified 35 S-genotypes, which are about one-third of all possible S-genotypes (91) based on 14 distinct S-alleles (Supplementary Table S3). No mate limitation was detected, as the estimates for mate availability in all M. sieversii populations were close to 1 (Table 1).
Genealogical structure and molecular evolution of Maleae S-alleles
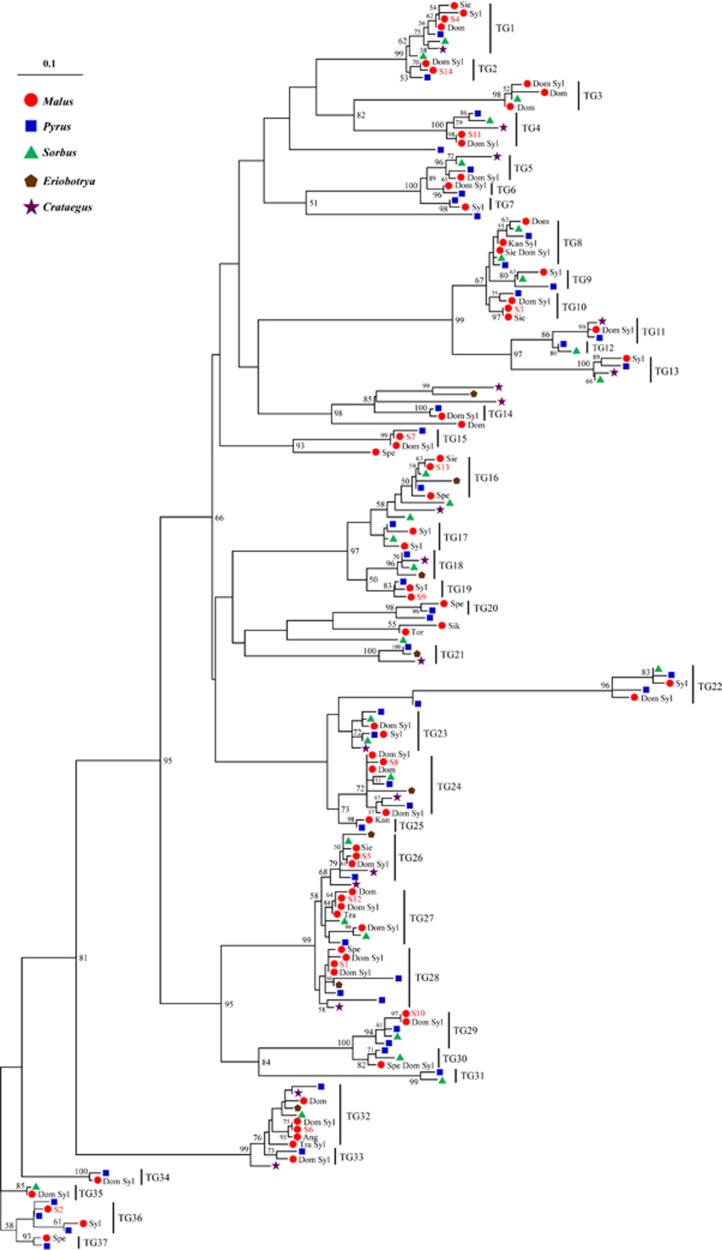
We retrieved 658 S-RNases for the tribe Maleae from GenBank using the protein BLAST procedure and identified the same set using hmmsearch analysis (Supplementary Table S5). Owing to the high level of redundancy of S-allele records in GenBank, we performed a two-step clustering procedure. The initial 658 Maleae S-RNases were reduced to 337 sequences via BLASTclust analysis and were further reduced to 159 sequences by phylogenetic analysis. After clustering, the redundant Maleae S-alleles were removed, while the TG evolution was preserved. The 159 Maleae S-alleles, together with the 14 M. sieversii S-alleles, were then subjected to ML analysis based on the best amino-acid substitution model HIVb+G selected by the software ProtTest.
On the basis of the topology and internal node support of the resultant ML tree, ~37 TG lineages can be identified (Figure 3). However, the true number of such lineages may be underestimated because of topological uncertainties in the ML tree and undiscovered Maleae S-alleles. The divergence of S-alleles among the TG lineages is much higher than within the lineages (Supplementary Figure S3), supporting delineation of the 37 TG lineages. A further important finding of our phylogenetic analyses is that the S-alleles from M. sieversii are absent in almost 40% of the TG lineages, whereas the S-alleles of M. sylvestris, M. domestica and Pyrus are generally present in these lineages (Figure 3). In addition, the TG lineages that lack M. sieversii S-alleles are randomly distributed across the tree (Figure 3). The contrasting genealogical structure of S-alleles between M. sieversii and M. sylvestris is more likely the result of allele losses from M. sieversii rather than gains in M. sylvestris, Pyrus and other Maleae genera.
Figure 3.
Genealogical history of the Maleae S-alleles inferred by ML analysis of 173 S-RNases from the tribe Maleae. The 14 S-RNases identified in M. sieversii are numbered from S1 to S14, and the 5 genera of Maleae are represented by 5 different shapes. Species of the genus Malus are denoted using three letters: Ang, M. angustifolia; Dom, M. domestica; Kan, M. kansuensis; Sie, M. sieversii; Sik, M. sikkimensis; Spe, M. spectabilis; Syl, M. sylvestris; Tor, M. toringoides; Tra, M. transitoria. In all, 37 TG evolved S lineages were recognized. There are 15 TG lineages lacking the M. sieversii S-alleles, they are TG3, 5, 6, 7, 9, 11, 13, 14, 17, 22, 23, 30, 33, 34 and 35. Numbers above the branches are bootstrap percentages, and bootstrap supports lower than 50% are not shown.
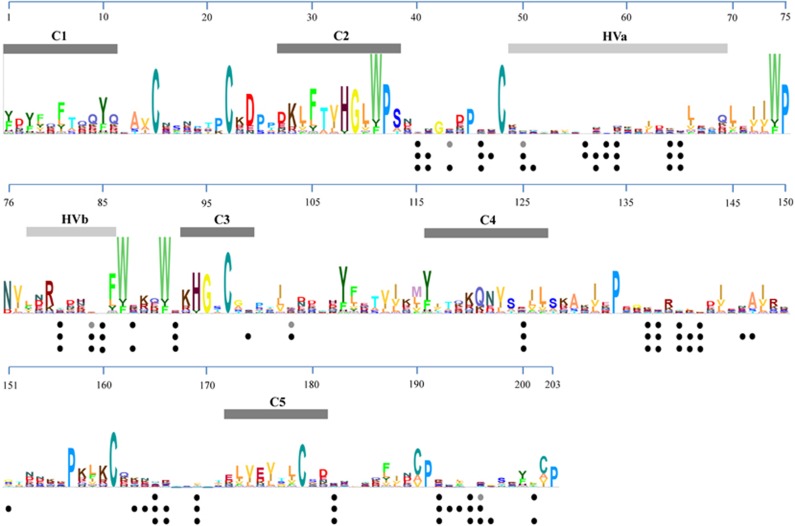
Analyses of random-sites models implemented using the codeml software suggest that the selection models M2a and M8 fit the S-allele data significantly better than the models of nearly neutral evolution (that is, M1a and M7; likelihood ratio test, χ2>241.01805 for M2a versus M1a, and χ2>183.07678 for M8 versus M7, P≪0.001 in both cases). The positively selected sites detected using the codeml and omegaMap software, as well as by Vieira et al. (2010), are essentially identical, with the exception of a few sites that were classified as under selection by only omegaMap (Figure 4). The amino-acid sites inferred to be under positive selection with more than one method were regarded as being confidently selected. We identified two hot spots of balancing selection within the Maleae S-RNases, which largely overlapped with the two hypervariable regions, HVa and HVb, that were recognized in previous studies (Sassa et al., 1996). The remaining positively selected sites occur in the latter regions of the S-RNases, outside of the conserved regions C4 and C5 (Figure 4).
Figure 4.
Positively selected amino-acid sites identified from the coding sequences of Maleae S-alleles. The profile hidden Markov model for Maleae S-alleles was created by skylign (http://skylign.org/). The height of a stack corresponds to the conservation at that position, and the height of a letter within a stack relies on the frequency of that letter occurred at that position. The five conserved (C1–C5) and two hypervariable regions (HVa and HVb) were highlighted following Long et al. (2010). Dots indicate amino acids identified as being under positive selection, with the first line by codeml, the second line by omegaMap and the third line by Vieira et al. (2010). For codeml analyses, the grey and black dots represent selection sites with posterior probability >0.95 and >0.99, respectively. For omegaMap analyses, the amino acids with posterior probability >0.95 were reported as positively selected sites.
Population genetic analyses
We used a suite of summary statistics to measure the variation in our S-allelic genotype data (Supplementary Table S6). In accordance with the prediction that a large number of alleles will be maintained at the S-locus, our results show that all the genetic diversity indices calculated from the S-allelic genotype data are much higher than genome-wide microsatellite data (OTable 2 in Zhang et al., 2007), while the negative FIS values indicate an excess of heterozygotes at the S-locus.
To compare the patterns of variation at the S-locus with the neutral reference sequences, we further sequenced 8 unlinked nuclear loci from 74 M. sieversii accessions. The length of these aligned sequences ranged between 435 and 936 bp for each locus, with a total concatenated length of 5268 bp, including 1963 bp of coding sequence and 3305 bp of noncoding sequence. A total of 87 single-nucleotide polymorphisms, and thus an average of 1 single-nucleotide polymorphism every 61 nucleotides, were found within M. sieversii, whereas no insertion–deletion polymorphisms were detected in the 8 nuclear gene sequences.
Standard statistics of sequence polymorphism for each locus were estimated (Table 2 and Supplementary Table S7). As expected, the reference loci were lower than the S-locus in nucleotide variation (mean πsil=0.0046 versus 0.1567). Levels of nucleotide diversity are heterogeneous among the reference loci, with C1 the least diverse (mean θsil=0.0020), while C11 was the most variable locus (mean θsil=0.0057). The minimum number of recombination events (Rm) at each locus was estimated using a four-gamete test for each population. The results show that recombination in M. sieversii was rare, as only a single Rm was observed at C15 in the MH population and one other was observed at C16 in the MH and Yiling populations.
Table 2. Summary of nucleotide polymorphisms and neutrality tests.
| Population | Locus a | S | h | θw | πall | πsil | D | D* | F* |
|---|---|---|---|---|---|---|---|---|---|
| EM (n=12) | Reference loci | 4.75±2.053 | 3.375±1.061 | 0.0020±0.001 | 0.0028±0.002 | 0.0039±0.002 | 0.7072±1.016 | 0.6693±0.726 | 0.7091±0.861 |
| S-locus | 168 | 8 | 0.1144 | 0.1870 | 0.1623 | 1.7215 | 0.6478 | 0.5381 | |
| FK (n=13) | Reference loci | 5±2.268 | 3.375±0.916 | 0.0021±0.001 | 0.0029±0.002 | 0.0040±0.002 | 0.8056±1.139 | 0.4579±1.140 | 0.6186±1.347 |
| S-locus | 205 | 10 | 0.1061 | 0.1689 | 0.1597 | 1.5458 | 0.3321 | 0.2466 | |
| XY (n=12) | Reference loci | 7±6.071 | 3.875±1.458 | 0.0027±0.002 | 0.0029±0.002 | 0.0042±0.003 | 0.2222±1.227 | −0.1497±1.454 | −0.1232±1.483 |
| S-locus | 180 | 9 | 0.1164 | 0.1969 | 0.1746 | 1.8464 | 1.3274** | 1.1046 | |
| MH (n=13) | Reference loci | 8.375±6.968 | 4.625±2.066 | 0.0033±0.002 | 0.0040±0.003 | 0.0053±0.003 | 0.6945±0.693 | 0.7704±0.378 | 0.8158±0.342 |
| S-locus | 194 | 9 | 0.1039 | 0.1554 | 0.1498 | 1.2544 | 0.1802 | 0.0482 | |
| DX (n=12) | Reference loci | 8.375±5.780 | 4.25±1.753 | 0.0034±0.002 | 0.0038±0.002 | 0.0049±0.002 | 0.074±1.263 | −0.0893±1.388 | −0.1080±1.565 |
| S-locus | 204 | 10 | 0.1176 | 0.1742 | 0.1472 | 1.2510 | 0.4561 | 0.2991 | |
| YL (n=12) | Reference loci | 9±5.928 | 4.375±1.506 | 0.0036±0.002 | 0.0038±0.002 | 0.0052±0.002 | 0.2836±0.819 | 0.3721±1.568 | 0.6237±1.376 |
| S-locus | 165 | 8 | 0.1292 | 0.1877 | 0.1468 | 1.2342 | 0.4530 | 0.2643 |
Abbreviations: DX, Daxigou; EM, Eming; FK, Laofengkou; MH, Mohe; XY, Xinyuan; YL, Yiling.
S, number of segregating sites;. h, number of haplotypes; θw, Watterson’s estimator of θ per base pair (Watterson, 1975), calculated based on the total number of polymorphic sites; πall and πsil, average number of pairwise nucleotide differences per site (Nei, 1987), calculated based on the total and silent number of polymorphic sites, respectively.
D and D*/F*, Tajima’s D (Tajima, 1989) and Fu and Li’s D* and F* (Fu and Li, 1993).
Summary statistics for the reference loci are denoted as the average calculated across the 8 loci ± standard deviation.
*P<0.05, **P<0.01. P-values for the reference loci were calculated by DnaSP, while P-values for the S-allele data were determined via coalescent simulation under the best-fit demographic models, which were inferred from Approximate Bayesian Computations using the neutral reference loci.
The values of Tajima’s D and Fu and Li’s D* and F* varied across the reference loci, and most of them were not significant (Supplementary Table S7). C11 deviated from the standard neutral model (P<0.05) in all populations, while neutrality was rejected for other loci (P <0.05) in either one (that is, C1, C12, C16 and C17) or two (that is, C15) populations. It is interesting to note that most of the significant examples either exhibited positive values for the Tajima’s D or positive values for Fu and Li’s D* and F*, a likely consequence of population contraction. Because a significant departure from neutrality at a specific locus may be the result of population structure and demography rather than selection (Ramos-Onsins and Rozas, 2002), we conducted a further multilocus HKA test encompassing the eight reference loci. Significant deviation from the standard neutral model was not detected in populations Eming, Laofengkou, Daxigou and Yiling, or in Xinyuan and MH after removing C12. Thus, loci C11 and C12 were excluded from subsequent Approximate Bayesian Computation analyses. Values of all three neutrality statistics were positive for the S-allele data (Table 2). To disentangle selection from demography at the S-locus, we performed a coalescent simulation for each population under the best-fit demographic model to determine the P-values for Tajima’s D and Fu and Li’s D* and F*. None of these statistics displayed a significant departure from the standard neutral model in any M. sieversii population, with the only exception of Fu and Li’s D* of the Xinyuan population (Table 2 and Supplementary Figure S4).
The results show that the population differentiation at the S-locus, as measured by a pairwise FST, is low, ranging between 0.0054 and 0.0548 (mean FST S-locus=0.0272). The degree of differentiation at the reference loci is about three times higher than that at the S-locus (mean FST reference=0.0877; Supplementary Figure S5), and a significant difference (P≪0.001) was detected between the pairwise FST estimated from the S-alleles and the reference loci using the unequal variance t-test.
The presence of a population bottleneck was revealed in four of the six sampled populations, while stable and declining models were slightly preferred in the Daxigou and Xinyuan populations, respectively (Supplementary Table S8). Owing to the weak differentiation among populations, we merged all six individual populations into one large population and conducted coalescent simulations and model selection using the same methods as before. The bottleneck model was again selected as the most likely demographic scenario for the merged population (Supplementary Table S8). We then assessed the severity of this bottleneck using the ratio of population size during and before a bottleneck (Table 3). The ratio ranged between 14.4 and 16.2% for individual populations, and it was 14.9% in the merged case. The bottleneck was estimated to last for ~20 000 years, ending roughly 17 000 years ago (Table 3).
Table 3. Estimates of the demographic parameters by Approximate Bayesian Computations under the bottleneck model.
| Population | Nancestral | Nb | Tb | T |
|---|---|---|---|---|
| EM | 4.00 × 105 | 0.58 × 105 | 20.6 | 16.35 |
| (2.13 × 105, 5.87 × 105) | (0.22 × 105, 0.97 × 105) | (6.10, 34.35) | (0.56, 84.83) | |
| FK | 3.93 × 105 | 0.59 × 105 | 20.42 | 16.84 |
| (2.13 × 105, 5.86 × 105) | (0.23 × 105, 0.97 × 105) | (5.81, 34.34) | (0.60, 88.17) | |
| MH | 4.01 × 105 | 0.63 × 105 | 18.97 | 17.62 |
| (2.16 × 105, 5.92 × 105) | (0.25 × 105, 0.97 × 105) | (5.81, 34.22) | (0.57, 86.63) | |
| YL | 4.06 × 105 | 0.66 × 105 | 18.32 | 18.21 |
| (2.14 × 105, 5.89 × 105) | (0.25 × 105, 0.98 × 105) | (5.55, 34.11) | (0.57, 85.31) | |
| Merged population | 3.48 × 105 | 0.52 × 105 | 22.69 | 17.35 |
| (2.05 × 105, 5.77 × 105) | (0.22 × 105, 0.96 × 105) | (6.81, 34.50) | (0.57, 86.91) |
Abbreviations: EM, Eming; FK, Laofengkou; MH, Mohe; YL, Yiling.
Estimation is based on 0.1% of the closest simulated data sets.
Nancestral, the effective population size of the ancestral population; Nb, the effective population size during the bottleneck; Tb, the duration of the bottleneck; T, the time that the bottleneck ended (going backwards in time).
The two numbers in parentheses are the 2.5 and 97.5% quantiles of the posterior distributions for parameter estimation.
The time unit is thousands of years.
Previous studies have suggested that the posterior probabilities estimated by Approximate Bayesian Computations may be sensitive to both the ranges of priors and tolerance levels (see reviews in Beaumont, 2010). We assessed these impacts on model selection by implementing three additional priors with wide ranges (Supplementary Table S9) and four increasingly strict tolerance levels in this study. The bottleneck model was selected as the best demographic scenario in 76.8% or 72.3% of all the model selection analyses (by the ‘rejection’ or ‘neuralnet’ method, respectively; Supplementary Table S10), suggesting the robustness of model selection to both priors and tolerance levels.
Discussion
M. sieversii has remarkably fewer S-alleles than other Rosaceae species
In this study, 14 distinct S-alleles and 35 S-genotypes were identified based on the 158 S-allele sequences obtained from 90 M. sieversii accessions. The 14 alleles are all heterozygous in the S-genotypes, indicating that they all function as unique S specificities. A complete diallel crossing among S-genotypes is the best way to accurately determine whether distinct S-alleles represent unique specificities or not. However, diallel crossing is usually impractical in empirical studies on trees (Raspe and Kohn, 2002; 2007,). As a result, other criteria have been proposed to define S specificities. Vieira et al. (2008; 2010) studied the molecular evolution and the number of S specificities for rosaceous plants. They suggested that S-alleles characterized by more than 5% amino-acid divergence represented different S specificities. In our study, the two S-alleles with the lowest genetic distance are S1 and S12, between which nine amino-acid differences (5.2%) were observed. Thus, the level of divergence between the 14 M. sieversii S-alleles suggests that each one of them represents a unique S specificity. Moreover, each M. sieversii S-allele occurs in a different TG lineage (Figure 3), which is a reflection of their ancient origin, further supporting the hypothesis that each M. sieversii S-allele corresponds to a unique S specificity (Raspe and Kohn, 2007; Fijarczyk and Babik, 2015).
By using the Paxman’s (1963) ML method and the E2 estimator of O’Donnell and Lawrence (1984), we estimated a total number of 14–15 alleles in the species M. sieversii, and the associated repeatability statistic (R=0.92) is remarkably higher than many other species (for example, Campbell and Lawrence, 1981a; Raspe and Kohn, 2002). This result suggested that the estimation of 14–15 S-alleles in M. sieversii should be an accurate estimate of the true allele number in this species. On the basis of the ML method of Paxman (1963), it was reported that there were ~40 S-alleles in flowering cherry Prunus lannesiana (Kato et al., 2007), 27 in one population of Crataegus monogyna (Raspe and Kohn, 2002) and 40 in Sorbus aucuparia (Raspe and Kohn, 2007). Using the allele data reported in Dreesen et al. (2010), M. sylvestris was estimated to possess nearly 40 S-alleles, and this estimation was robust to sampling (R=0.91). In addition, allele numbers inferred from phylogenetic analyses of the Maleae S-RNases are consistent with those obtained by analysing single Rosaceae species. On the basis of the inferred genealogy of S-RNases, we identified approximately 37 TG lineages that may correspond to 37 unique S specificities in the common ancestor of the tribe Maleae. It is noteworthy that while Vieira et al. (2010) estimated the specificity number using a different criterion, they nevertheless proposed the presence of 35 specificities in the ancestral lineage of the tribe Maleae. In conclusion, the number of S-alleles in M. sylvestris, Sorbus aucuparia and the common ancestor of the tribe Maleae are likely comparable at around 40, and this number of S-alleles is remarkably greater than the number seen in M. sieversii.
Demographic bottleneck accounts for the massive loss of S-alleles in M. sieversii
As noted above, the number of M. sieversii S-alleles is strikingly less than that of its close relative, M. sylvestris (Table 1). There may be several reasons for this, including (1) inaccurate estimation of the M. sieversii allele number due to insufficient sampling and/or unidentified S-alleles, (2) a significant increase in the number of M. sylvestris S-alleles owing to population subdivision and isolation and (3) a severe demographic bottleneck that occurred in M. sieversii. First, the R-values suggest a reasonably thorough species-level sampling (Table 1). In addition, Cornille et al. (2013b) assessed the genetic structure of M. sieversii using species-range sampling and revealed two well-defined genetic clusters. Of these, the larger cluster is spread across Central Asia, while the other smaller cluster comprises mostly individuals from the Tian Shan Mountains (Cornille et al., 2013b). Our sampling sites overlap with the geographic origins of both these genetic clusters; thus, our M. sieversii samples should adequately represent the species diversity. Therefore, we conclude that insufficient sampling alone is unlikely to have resulted in such a marked loss of M. sieversii S-alleles.
Null alleles are common in S-locus genotyping (for example, Holderegger et al., 2008; Dreesen et al., 2010) and may lead to underestimation of the true allele number. With this in mind, we conducted PCR amplification to retrieve the M. sieversii S-alleles using three pairs of consensus primers. The results of this study show that the proportion of null alleles (12%) was approximately half the number reported for M. sylvestris (that is, 21.6% Dreesen et al., 2010). Thus, even though the true allele number for M. sieversii may be underestimated in this study on account of the presence of unidentified S-alleles, our conclusion that there are fewer S-alleles in M. sieversii than in M. sylvestris is likely correct because an underestimation of the allele number due to null S-alleles is more severe for M. sylvestris than for M. sieversii.
Theoretical work has shown that more S-alleles may be maintained in a subdivided population compared to a panmictic one of similar size when the migration rate between subpopulations remains sufficiently low (Muirhead, 2001). Thus, if the higher allele number observed in M. sylvestris relative to M. sieversii is the result of subdivision and isolation, we would expect a strong population structure in the former species. However, Cornille et al. (2013a) detected only weak isolation by distance in M. sylvestris and suggested that high levels of gene flow might have occurred in this species. Therefore, the sharp increase in M. sylvestris S-alleles compared to that of M. sieversii could not be explained by strong isolation among subpopulations, leaving a demographic bottleneck as the most likely explanation for the massive loss of S-alleles in this species.
On the basis of the neutral reference loci, a severe demographic bottleneck was detected in four of the six sampled populations, and the ending of the bottleneck was approximately temporally consistent with the deglaciation of the Last Glacial Maximum (LGM) (Clark et al., 2009). The variance in Tajima’s D among the reference loci is also evidence of a recent bottleneck (Wright and Gaut, 2005). It is well known that climate oscillations in the Quaternary resulted in repeated and drastic climatic changes that profoundly shaped the distribution and genetic structure of many animals and plants across different latitudes (Hewitt, 2000). Although arid northwestern China did not experience major glaciations in the Quaternary, significant climatic oscillations did cause extreme aridity and the expansion of sandy deserts, which heavily impacted the evolution of the regional biota (Meng et al., 2015). When aridity intensified and deserts expanded, the M. sieversii populations declined, fragmented and retreated to either a small area in the Yili valley (Meng et al., 2015; Zhang et al., 2015) or to a small, more southwestern region of the Tian Shan Mountain in Kazakhstan (Richards et al., 2009; Cornille et al., 2013b). It is highly likely that M. sieversii may have experienced a severe demographic bottleneck during the LGM, and such a bottleneck may have caused the massive loss of S-alleles in M. sieversii.
Interestingly, M. sylvestris, a close relative of M. sieversii, maintained 38 distinct S-alleles, which is much greater than the number of S-alleles discovered in M. sieversii. Cornille et al. (2013a) demonstrated that M. sylvestris had experienced range contraction and fragmentation during the LGM as well. On the basis of microsatellite markers, three genetic clusters were detected from M. sylvestris, whereas two were revealed in M. sieversii (Cornille et al., 2013a, 2013b). Compared to M. sieversii, M. sylvestris has a relatively high level of genetic diversity, both at the genomic background and at the S-locus. This may result from more refugia for M. sylvestris than M. sieversii during the LGM. Three separate glacial refugia have been proposed for M. sylvestris (Cornille et al., 2013a), however, probably two at most were indicated for M. sieversii (Richards et al., 2009; Zhang et al., 2015). Although M. sieversii has fewer S-alleles than other Maleae species, no mate limitation has been detected. As a result, M. sieversii could survive naturally in the wild as long as no more S-allele loss occurs in this species.
Loss of diversity at the S-locus due to population bottlenecks has been observed in both sporophytic SI and GSI systems (Brennan et al., 2002; Paape et al., 2008; Guo et al., 2009). For example, in the family Solanaceae, characterized by GSI, an ancient bottleneck is known to have occurred within the lineage leading to the most recent common ancestor of the genera Physalis and Witheringia, as a result, only three S lineages persisted after the bottleneck (Paape et al., 2008).
Failure to reject the standard neutral model for the M. sieversii S-alleles on the basis of Tajima’s D and Fu and Li’s D* and F* statistics may also result from the confounding effects of the demographic bottleneck on selection detection. When a population size continues to decline, the impact of genetic drift would gradually increase and could eventually outweigh the effect of balancing selection. Consequently, the footprint of this selective force may be blurred or even undetectable. The severe bottleneck detected in M. sieversii can lead to strong random drift; as a result, the original signal of balancing selection may be overwritten, and the neutral evolution of the M. sieversii S-alleles could not be rejected. The inability to reject neutral evolution for loci under balancing selection has also been reported in the case of the major histocompatibility complex (MHC) in vertebrates. The MHC loci play important roles in pathogen resistance and, thus, are subject to strong balancing selection (Strand et al., 2012). However, neutral evolution of the MHC loci has been reported in situations in which the size of the populations under study sharply declined. In these bottlenecked situations, balancing selection does not seem to have been strong enough to counteract genetic drift, leading to the detection of the unusual pattern of neutral evolution (Ejsmond and Radwan, 2011; Strand et al., 2012; Grueber et al., 2013).
Molecular evolution of the M. sieversii S-alleles
Both shared ancestral polymorphism and an excess of non-synonymous substitution are evidence of long-term balancing selection (Charlesworth, 2006; Fijarczyk and Babik, 2015). The 14 M. sieversii S-alleles were recovered in separate clades in which S-alleles from other Maleae species were also presented (Figure 3). In addition, through phylogenetic and population genetic analyses, ~15% of the amino-acid sites from the aligned Maleae S-RNases were identified as positively selected (Figure 4). Thus, based on both shared polymorphism and a high proportion of non-synonymous substitution, we conclude that the M. sieversii S-alleles have evolved under long-term balancing selection.
The action of ongoing balancing selection is most apparent when the S-locus is compared with the neutral reference loci. First, the degree of population differentiation at the S-locus (FST=0.0272) is significantly lower than the genomic average measured at the reference loci (P≪0.001; Supplementary Figure S5). An S-locus subject to balancing selection is characterized by a weaker genetic structure relative to neutrally evolving genes (Glemin et al., 2005; Edh et al., 2009; Ganopoulos et al., 2012). This is because population differentiation via drift decelerates while the effective gene flow increases at the S-locus (Castric et al., 2008; Fijarczyk and Babik, 2015). In addition, a more even distribution of observed allele frequencies than would be expected under neutrality is a sign of recent balancing selection (Fijarczyk and Babik, 2015). We were unable to reject the null hypothesis of equal S-allele frequencies (isoplethy) for all populations, with the exception of the MH population (Table 2), supporting the operation of ongoing balancing selection at the S-locus in M. sieversii.
Conclusion
This is the first study to extensively survey S-allele diversity in the wild apple M. sieversii. Genealogical analyses revealed that M. domestica shared most of its S-alleles with M. sieversii and M. sylvestris, the primary and secondary donors of the domesticated apple genome, respectively. As expected, the evolution of the M. sieversii S-alleles is characterized by long-term balancing selection. Interestingly, M. sieversii has remarkably fewer S-alleles than its close relative M. sylvestris. A severe population bottleneck, probably induced by the LGM, was proposed as the main reason for the massive loss of S-alleles in M. sieversii, and such a bottleneck may also account for the ambiguous signature of ongoing balancing selection that was detected. Other potential causes, such as insufficient sampling, unidentified S-alleles and population structure, were less likely to result in large-scale S-allele loss in M. sieversii.
Data Archiving
Sequences of this study were submitted to GenBank under the accession numbers KX214331-KX214344 for S-alleles and KY676360-KY676417 for reference loci.
Acknowledgments
We are grateful to Zhi-yong Zhang (Jiangxi Agricultural University), Fu-min Zhang, Xin-hui Zou and Yu-su Du (Institute of Botany, CAS) for comments and technical assistance. We also thank Dun-yan Tan, Su-ying Chen and Yong-qiang Diao for help with collecting materials. We acknowledge the Nature language editing service for improving the English. This work was supported by the National Natural Science Foundation of China (31301747 and 41661010) and the Scientific Research Foundation of Hainan University (kyqd1613 and kyqd1617).
Footnotes
Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)
The authors declare no conflict of interest.
Supplementary Material
References
- Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W et al (1997). Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res 25: 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaumont MA (2010). Approximate Bayesian Computation in evolution and ecology. Annu Rev Ecol Evol Syst 41: 379–406. [Google Scholar]
- Beaumont MA, Zhang WY, Balding DJ (2002). Approximate Bayesian Computation in population genetics. Genetics 162: 2025–2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertorelle G, Benazzo A, Mona S (2010). ABC as a flexible framework to estimate demography over space and time: some cons, many pros. Mol Ecol 19: 2609–2625. [DOI] [PubMed] [Google Scholar]
- Blum MGB, Francois O (2010). Non-linear regression models for Approximate Bayesian Computation. Stat Comput 20: 63–73. [Google Scholar]
- Brennan AC, Harris SA, Tabah DA, Hiscock SJ (2002). The population genetics of sporophytic self-incompatibility in Senecio squalidus L. (Asteraceae) I: S allele diversity in a natural population. Heredity 89: 430–438. [DOI] [PubMed] [Google Scholar]
- Broothaerts W (2003). New findings in apple S-genotype analysis resolve previous confusion and request the re-numbering of some S-alleles. Theor Appl Genet 106: 703–714. [DOI] [PubMed] [Google Scholar]
- Campbell JM, Lawrence MJ (1981. a). The population genetics of the self-incompatibility polymorphism in Papaver rhoeas. I. The number and distribution of S-alleles in families from three localities. Heredity 46: 69–79. [Google Scholar]
- Campbell JM, Lawrence MJ (1981. b). The population genetics of the self-incompatibility polymorphism in Papaver rhoeas. II. The number and frequency of S-alleles in a natural population. Heredity 46: 81–90. [Google Scholar]
- Campbell LG, Husband BC (2007). Small populations are mate-poor but pollinator-rich in a rare, self-incompatible plant, Hymenoxys herbacea (Asteraceae). New Phytol 174: 915–925. [DOI] [PubMed] [Google Scholar]
- Castric V, Bechsgaard J, Schierup MH, Vekemans X (2008). Repeated adaptive introgression at a gene under multiallelic balancing selection. PLoS Genet 4: e1000168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castric V, Vekemans X (2004). Plant self-incompatibility in natural populations: a critical assessment of recent theoretical and empirical advances. Mol Ecol 13: 2873–2889. [DOI] [PubMed] [Google Scholar]
- Charlesworth D (2006). Balancing selection and its effects on sequences in nearby genome regions. PLoS Genet 2: e64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Zhang B, Zhao ZH, Sui ZH, Zhang H, Xue YB (2010). 'A life or death decision' for pollen tubes in S-RNase-based self-incompatibility. J Exp Bot 61: 2027–2037. [DOI] [PubMed] [Google Scholar]
- Clark PU, Dyke AS, Shakun JD, Carlson AE, Clark J, Wohlfarth B et al (2009). The Last Glacial Maximum. Science 325: 710–714. [DOI] [PubMed] [Google Scholar]
- Cornille A, Giraud T, Bellard C, Tellier A, Le Cam B, Smulders MJM et al (2013. a). Postglacial recolonization history of the European crabapple (Malus sylvestris Mill.), a wild contributor to the domesticated apple. Mol Ecol 22: 2249–2263. [DOI] [PubMed] [Google Scholar]
- Cornille A, Giraud T, Smulders MJM, Roldan-Ruiz I, Gladieux P (2014). The domestication and evolutionary ecology of apples. Trends Genet 30: 57–65. [DOI] [PubMed] [Google Scholar]
- Cornille A, Gladieux P, Giraud T (2013. b). Crop-to-wild gene flow and spatial genetic structure in the closest wild relatives of the cultivated apple. Evol Appl 6: 737–748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornille A, Gladieux P, Smulders MJM, Roldan-Ruiz I, Laurens F, Le Cam B et al (2012). New insight into the history of domesticated apple: secondary contribution of the European wild apple to the genome of cultivated varieties. PLoS Genet 8: 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csillery K, Blum MGB, Gaggiotti OE, Francois O (2010). Approximate Bayesian Computation (ABC) in practice. Trends Ecol Evol 25: 410–418. [DOI] [PubMed] [Google Scholar]
- Csillery K, Francois O, Blum MGB (2012). abc: an R package for approximate Bayesian computation (ABC). Methods Ecol Evol 3: 475–479. [Google Scholar]
- Darriba D, Taboada GL, Doallo R, Posada D (2011). ProtTest 3: fast selection of best-fit models of protein evolution. Bioinformatics 27: 1164–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Franceschi P, Dondini L, Sanzol J (2012). Molecular bases and evolutionary dynamics of self-incompatibility in the Pyrinae (Rosaceae). J Exp Bot 63: 4015–4032. [DOI] [PubMed] [Google Scholar]
- Dreesen RSG, Vanholme BTM, Luyten K, Van Wynsberghe L, Fazio G, Roldan-Ruiz I et al (2010). Analysis of Malus S-RNase gene diversity based on a comparative study of old and modern apple cultivars and European wild apple. Mol Breed 26: 693–709. [Google Scholar]
- Eddy SR (2011). Accelerated profile HMM searches. PLoS Comput Biol 7: e1002195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edh K, Widen B, Ceplitis A (2009). Molecular population genetics of the SRK and SCR self-incompatibility genes in the wild plant species Brassica cretica (Brassicaceae). Genetics 181: 985–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ejsmond MJ, Radwan J (2011). MHC diversity in bottlenecked populations: a simulation model. Conserv Genet 12: 129–137. [Google Scholar]
- Excoffier L, Lischer HEL (2010). Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour 10: 564–567. [DOI] [PubMed] [Google Scholar]
- Fijarczyk A, Babik W (2015). Detecting balancing selection in genomes: limits and prospects. Mol Ecol 24: 3529–3545. [DOI] [PubMed] [Google Scholar]
- Fletcher W, Yang ZH (2010). The effect of insertions, deletions, and alignment errors on the branch-site test of positive selection. Mol Biol Evol 27: 2257–2267. [DOI] [PubMed] [Google Scholar]
- Forsline PF, Aldwinckle HS, Dickson EE, Luby JJ, Hokanson S (2003). Collection, maintenance, characterization, and utilization of wild apples of Central Asia. Hort Rev 29: 1–61. [Google Scholar]
- Fu YX, Li WH (1993). Statistical tests of neutrality of mutations. Genetics 133: 693–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganopoulos I, Aravanopoulos F, Argiriou A, Tsaftaris A (2012). Genome and population dynamics under selection and neutrality: an example of S-allele diversity in wild cherry (Prunus avium L.). Tree Genet Genomes 8: 1181–1190. [Google Scholar]
- Glemin S, Gaude T, Guillemin ML, Lourmas M, Olivieri I, Mignot A (2005). Balancing selection in the wild: testing population genetics theory of self-incompatibility in the rare species Brassica insularis. Genetics 171: 279–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudet J (1995). FSTAT (version 1.2): A computer program to calculate F-statistics. J Hered 86: 485–486. [Google Scholar]
- Gross BL, Henk AD, Richards CM, Fazio G, Volk GM (2014). Genetic diversity in Malus × domestica (Rosaceae) through time in response to domestication. Am J Bot 101: 1770–1779. [DOI] [PubMed] [Google Scholar]
- Grueber CE, Wallis GP, Jamieson IG (2013). Genetic drift outweighs natural selection at toll-like receptor (TLR) immunity loci in a re-introduced population of a threatened species. Mol Ecol 22: 4470–4482. [DOI] [PubMed] [Google Scholar]
- Guo YL, Bechsgaard JS, Slotte T, Neuffer B, Lascoux M, Weigel D et al (2009). Recent speciation of Capsella rubella from Capsella grandiflora, associated with loss of self-incompatibility and an extreme bottleneck. Proc Natl Acad Sci USA 106: 5246–5251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hewitt G (2000). The genetic legacy of the Quaternary ice ages. Nature 405: 907–913. [DOI] [PubMed] [Google Scholar]
- Holderegger R, Haner R, Csencsics D, Angelone S, Hoebee SE (2008). S-allele diversity suggests no mate limitation in small populations of a self-incompatible plant. Evolution 62: 2922–2928. [DOI] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL (1985). Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111: 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kreitman M, Aguade M (1987). A test of neutral molecular evolution based on nucleotide data. Genetics 116: 153–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR (2002). Generating samples under a Wright-Fisher neutral model. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
- Igic B, Kohn JR (2001). Evolutionary relationships among self-incompatibility RNases. Proc Natl Acad Sci USA 98: 13167–13171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwano M, Takayama S (2012). Self/non-self discrimination in angiosperm self-incompatibility. Curr Opin Plant Biol 15: 78–83. [DOI] [PubMed] [Google Scholar]
- Jordan G, Goldman N (2012). The effects of alignment error and alignment filtering on the sitewise detection of positive selection. Mol Biol Evol 29: 1125–1139. [DOI] [PubMed] [Google Scholar]
- Jukes TH, Cantor CR (1969)Evolution of protein moleculesIn:Munro HN(ed) Mammalian Protein Metabolism vol. 3, Academic Press: New York, NY, USA. pp 21–132. [Google Scholar]
- Kao TH, Tsukamoto T (2004). The molecular and genetic bases of S-RNase-based self-incompatibility. Plant Cell 16: S72–S83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato S, Iwata H, Tsumura Y, Mukai Y (2007). Distribution of S-alleles in island populations of flowering cherry, Prunus lannesiana var. speciosa. Genes Genet Syst 82: 65–75. [DOI] [PubMed] [Google Scholar]
- Kubo K, Entani T, Takara A, Wang N, Fields AM, Hua ZH et al (2010). Collaborative non-self recognition system in S-RNase-based self-incompatibility. Science 330: 796–799. [DOI] [PubMed] [Google Scholar]
- Li TZ, Long SS, Li MF, Bai SL, Zhang W (2012). Determination S-genotypes and identification of five novel S-RNase alleles in wild Malus species. Plant Mol Biol Rep 30: 453–461. [Google Scholar]
- Librado P, Rozas J (2009). DnaSP v5: a software for comprehensive analysis of DNA polymorphism data. Bioinformatics 25: 1451–1452. [DOI] [PubMed] [Google Scholar]
- Long SS, Li MF, Han ZH, Wang K, Li TZ (2010). Characterization of three new S-alleles and development of an S-allele-specific PCR system for rapidly identifying the S-genotype in apple cultivars. Tree Genet Genomes 6: 161–168. [Google Scholar]
- Loytynoja A, Goldman N (2008). Phylogeny-aware gap placement prevents errors in sequence alignment and evolutionary analysis. Science 320: 1632–1635. [DOI] [PubMed] [Google Scholar]
- Mantel N (1974). Approaches to a health research occupancy problem. Biometrics 30: 355–362. [PubMed] [Google Scholar]
- Markova-Raina P, Petrov D (2011). High sensitivity to aligner and high rate of false positives in the estimates of positive selection in the 12 Drosophila genomes. Genome Res 21: 863–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng HH, Gao XY, Huang JF, Zhang ML (2015). Plant phylogeography in arid Northwest China: retrospectives and perspectives. J Syst Evol 53: 33–46. [Google Scholar]
- Muirhead CA (2001). Consequences of population structure on genes under balancing selection. Evolution 55: 1532–1541. [DOI] [PubMed] [Google Scholar]
- Nei M (1987)Molecular Evolutionary Genetics. Columbia University Press: New York, NY, USA. [Google Scholar]
- Nei M, Gojobori T (1986). Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Mol Biol Evol 3: 418–426. [DOI] [PubMed] [Google Scholar]
- O’Donnell S, Lawrence MJ (1984). The population genetics of the self-incompatibility polymorphism in Papaver rhoeas. IV. The estimation of the number of alleles in a population. Heredity 53: 495–507. [Google Scholar]
- Paape T, Igic B, Smith SD, Olmstead R, Bohs L, Kohn JR (2008). A 15-Myr-old genetic bottleneck. Mol Biol Evol 25: 655–663. [DOI] [PubMed] [Google Scholar]
- Paxman GJ (1963). The maximum likelihood estimation of the number of self-sterility alleles in a population. Genetics 48: 1029–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peakall R, Smouse PE (2012). GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research-an update. Bioinformatics 28: 2537–2539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos-Onsins SE, Rozas J (2002). Statistical properties of new neutrality tests against population growth. Mol Biol Evol 19: 2092–2100. [DOI] [PubMed] [Google Scholar]
- Raspe O, Kohn JR (2002). S-allele diversity in Sorbus aucuparia and Crataegus monogyna (Rosaceae: Maloideae). Heredity 88: 458–465. [DOI] [PubMed] [Google Scholar]
- Raspe O, Kohn JR (2007). Population structure at the S-locus of Sorbus aucuparia L. (Rosaceae: Maloideae). Mol Ecol 16: 1315–1325. [DOI] [PubMed] [Google Scholar]
- Richards CM, Volk GM, Reilley AA, Henk AD, Lockwood DR, Reeves PA et al (2009). Genetic diversity and population structure in Malus sieversii, a wild progenitor species of domesticated apple. Tree Genet Genomes 5: 339–347. [Google Scholar]
- Richman A (2000). Evolution of balanced genetic polymorphism. Mol Ecol 9: 1953–1963. [DOI] [PubMed] [Google Scholar]
- Sanzol J (2009). Genomic characterization of self-incompatibility ribonucleases (S-RNases) in European pear cultivars and development of PCR detection for 20 alleles. Tree Genet Genomes 5: 393–405. [Google Scholar]
- Sassa H, Nishio T, Kowyama Y, Hirano H, Koba T, Ikehashi H (1996). Self-incompatibility (S alleles of the Rosaceae encode members of a distinct class of the T2/S ribonuclease superfamily. Mol Gen Genet 250: 547–557. [DOI] [PubMed] [Google Scholar]
- Stamatakis A (2014). RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30: 1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strand TM, Segelbacher G, Quintela M, Xiao LY, Axelsson T, Hoglund J (2012). Can balancing selection on MHC loci counteract genetic drift in small fragmented populations of black grouse? Ecol Evol 2: 341–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima D (1989). Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura K, Peterson D, Peterson N, Stecher G, Nei M, Kumar S (2011)Mol Biol Evol 28: 2731–2739. [DOI] [PMC free article] [PubMed]
- Vieira J, Ferreira PG, Aguiar B, Fonseca NA, Vieira CP (2010). Evolutionary patterns at the RNase based gametophytic self-incompatibility system in two divergent Rosaceae groups (Maloideae and Prunus. BMC Evol Biol 10: 200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vieira J, Fonseca NA, Santos RAM, Habu T, Tao R, Vieira CP (2008). The number, age, sharing and relatedness of S-locus specificities in Prunus. Genet Res 90: 17–26. [DOI] [PubMed] [Google Scholar]
- Watterson GA (1975). On the number of segregating sites in genetical models without recombination. Theor Popul Biol 7: 256–276. [DOI] [PubMed] [Google Scholar]
- Wilson DJ, McVean G (2006). Estimating diversifying selection and functional constraint in the presence of recombination. Genetics 172: 1411–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright SI, Gaut BS (2005). Molecular population genetics and the search for adaptive evolution in plants. Mol Biol Evol 22: 506–519. [DOI] [PubMed] [Google Scholar]
- Yang ZH (2007). PAML 4: phylogenetic analysis by maximum likelihood. Mol Biol Evol 24: 1586–1591. [DOI] [PubMed] [Google Scholar]
- Zhang CY, Chen XS, He TM, Liu XL, Feng T, Yuan ZH (2007). Genetic structure of Malus sieversii population from Xinjiang, China, revealed by SSR markers. J Genet Genomics 34: 947–955. [DOI] [PubMed] [Google Scholar]
- Zhang HX, Zhang ML, Wang LN (2015). Genetic structure and historical demography of Malus sieversii in the Yili Valley and the western mountains of the Junggar Basin, Xinjiang, China. J Arid Land 7: 264–271. [Google Scholar]
- Zhang LB, Ge S (2007). Multilocus analysis of nucleotide variation and speciation in Oryza officinalis and its close relatives. Mol Biol Evol 24: 769–783. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.