Concurrent design of quasi-random photonic nanostructures

Significance

Quasi-random nanostructures with neither periodic nor fully disordered geometries have been used for photovoltaics and light-emitting diodes because the stochastic patterns can manipulate light over a broad range of wavelengths and over wide collection angles. Although serial processes such as electron-beam lithography can fabricate nanostructures, prototype manufacturing over large areas is not possible. Moreover, trial-and-error processing optimization cannot guarantee the fabrication feasibility of the designed structures. In this paper, we report wrinkle lithography, a wafer-scale fabrication procedure whose processing steps can be integrated with concurrent design of nanostructures and function. As a proof-of-concept demonstration, we rapidly optimized three-dimensional structures for light trapping in amorphous silicon and realized >160% enhancement in light absorption over the 800–1,200-nm wavelength range.

Abstract

Nanostructured surfaces with quasi-random geometries can manipulate light over broadband wavelengths and wide ranges of angles. Optimization and realization of stochastic patterns have typically relied on serial, direct-write fabrication methods combined with real-space design. However, this approach is not suitable for customizable features or scalable nanomanufacturing. Moreover, trial-and-error processing cannot guarantee fabrication feasibility because processing–structure relations are not included in conventional designs. Here, we report wrinkle lithography integrated with concurrent design to produce quasi-random nanostructures in amorphous silicon at wafer scales that achieved over 160% light absorption enhancement from 800 to 1,200 nm. The quasi-periodicity of patterns, materials filling ratio, and feature depths could be independently controlled. We statistically represented the quasi-random patterns by Fourier spectral density functions (SDFs) that could bridge the processing–structure and structure–performance relations. Iterative search of the optimal structure via the SDF representation enabled concurrent design of nanostructures and processing.

Quasi-random structures with neither periodic nor fully disordered geometries are useful in the design of superhydrophobic substrates (1, 2), stretchable electronics (3–6), and sensors (7, 8). In particular, these nanostructured systems support rich Fourier spectra that enable light manipulation over broadband wavelengths and over wide collection angles (9, 10). Independent control over the relative degree of order vs. disorder, materials filling ratio, and feature size is critical to generate patterns with a diverse range of optical responses (11). For example, quasi-random nanostructures in photonic materials such as amorphous silicon (a-Si) are being increasingly used in photovoltaics and light-emitting diodes (9, 12–18). To enhance device performance from the patterns, optimization of nanoscale structure is crucial. However, most efforts to control quasi-random patterns have relied on serial processes such as electron-beam lithography (9, 12, 16, 18, 19). Although such approaches enable precise pattern placement and maximum control over the nanostructured features, the tools are not scalable and are cost prohibitive for large-area fabrication (>1 cm²). Furthermore, most work has focused on the traditional, sequential strategy for pattern generation: (i) design nanostructures in real space for a target performance and then (ii) fabricate structures by trial-and-error processing optimization (9, 20). Without considering the fabrication conditions as part of the overall design strategy, however, conventional methods cannot ensure manufacturing feasibility of the optimized nanostructures. Trial-and-error experiments to achieve optimal designs are usually time-consuming. Hence, development of a concurrent design approach can establish the phase space of target quasi-random nanostructures and simultaneously consider the needed nanofabrication processing conditions.

Here, we show a design approach integrated with scalable nanomanufacturing that can optimize and fabricate quasi-random photonic nanostructures. We statistically represented the quasi-random patterns by Fourier spectral density functions (SDFs) (11, 21) that can bridge processing–structure and structure–performance relations because the SDF parameters have physical meanings closely associated with material formation procedures (22, 23). Hence, iterative searching of optimal structures via the SDF representation can enable concurrent design of both nanostructures and processing. To realize 3D structures, we developed wrinkle lithography, a procedure that can transfer quasi-random polymer wrinkles into inorganic materials with the same projected pattern. Wrinkle lithography enabled continuous and independent control over the quasi-periodicity of the patterns, materials filling ratio, and feature depth. As a proof-of-concept demonstration of our concurrent design approach, we optimized structural parameters for light trapping in an a-Si film and achieved ∼160% enhancement in light absorption over the 800–1,200-nm wavelength range.

Results

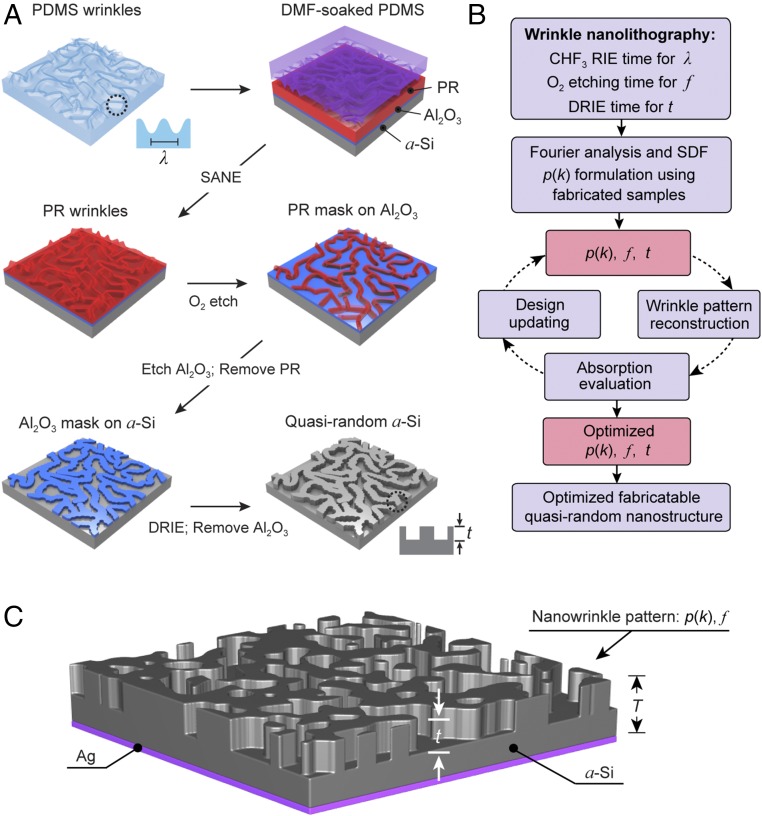
Fig. 1A summarizes how wrinkle lithography can pattern 3D quasi-random nanostructures in a-Si (SI Appendix, Methods). First, polymer nanowrinkles were generated by strain relief of a reactive ion etching (RIE) CHF₃-plasma treated polystyrene (PS) substrate (24–26). The 3D PS wrinkles functioned as a master, where poly(dimethysiloxane) (PDMS) was then cast against the pattern to produce a mold for solvent-assisted nanoscale embossing (SANE) (27). SANE transferred the 3D wrinkle patterns in PDMS into photoresist (PR) on an alumina (Al₂O₃)-coated a-Si substrate. Directional RIE of the PR pattern with an O₂ plasma resulted in a discontinuous pattern of PR that functioned as an alumina etch mask. Wet etching resulted in quasi-random 2D patterns of alumina (SI Appendix, Fig. S1) that were then transferred by deep RIE into a-Si.

Fig. 1.

Wrinkle lithography combined with concurrent design methodology for the fabrication of quasi-random nanostructures. (A) Process of wrinkle lithography to fabricate quasi-random nanostructures and (B) concurrent design approach to search the optimal structures for the broadband, light-trapping property. (C) A thin-film light-trapping photonic device with resulting pattern. A silver backing layer was used to prevent light from leaking.

Fig. 1B outlines the concurrent design approach to optimize broadband light trapping using nanopatterned a-Si as a model system (Fig. 1C). First, the processing–structure relation was defined by tuning the fabrication conditions to achieve nanostructures with distinct geometric characteristics, including wrinkle wavelength (λ), materials filling ratio (f), and feature depth (t). Then, the SDF [p(k), where k is the spatial frequency], the normalized radial average of the Fourier spectrum, was used to represent the fabricated structures (SI Appendix, Methods). The peak value of the p(k) was reciprocal to that of the wrinkle wavelength, allowing independent control of the processing conditions to achieve the desired structure. In the iterative search of optimal wrinkle patterns for light trapping at longer wavelengths (800–1,200 nm), we regarded p(k) and the two structural parameters (f and t) as independent design variables. For each iteration of light-trapping performance of the wrinkle patterns through structure–performance simulations, the nanostructures were reconstructed in real space from SDF representations using Gaussian random field (GRF) modeling (21). Rigorous coupled-wave analysis (28, 29) was then used to evaluate light absorption of the reconstructions (SI Appendix, Fig. S2). The structural design variables were updated in each optimization iteration using a genetic algorithm (GA) (30, 31) (SI Appendix, Methods). Once the optimal structure was obtained, the pattern was fabricated by wrinkle lithography based on the conditions from the processing–structure map (SI Appendix, Fig. S3).

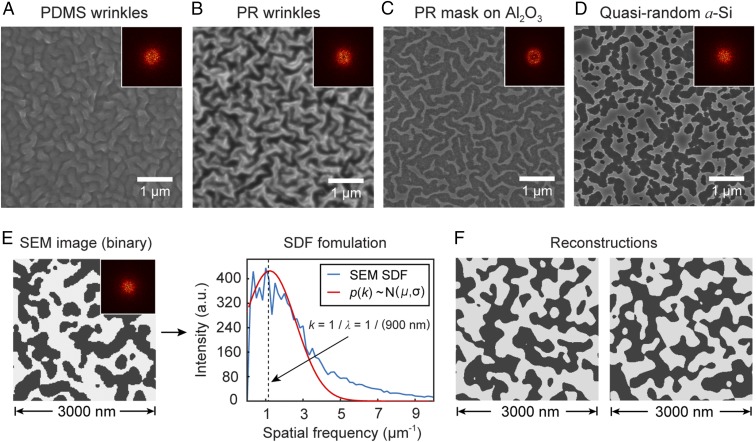
Fig. 2 summarizes SDF-based representations of quasi-random nanostructures produced by wrinkle lithography. We characterized the quasi-random nanostructures in each processing step by Fourier transformation of the SEM images (Fig. 2 A–D). Notably, we found that the structure of the PDMS wrinkles was preserved in the resulting a-Si patterns (SI Appendix, Fig. S4). Conventional approaches use a real-space representation, where the nanostructures are discretized into pixels to fully characterize the materials distribution at each location. Because each pixel requires one design variable (9, 11), this representation requires numerous variables to describe complex geometries, resulting in an optimization problem with large-design dimensionality (32). In contrast, we propose to use SDFs to model wrinkle structures in Fourier space, which significantly reduces the number of design variables. Whereas the stochastic features of quasi-random nanostructures over large areas are hard to represent by the deterministic pixilation method in real space (9), Fourier-space representation using SDF can be intrinsically tied to the wrinkle-lithography fabrication process. By analyzing a range of wrinkle patterns with wavelengths λ from 180 to 2,000 nm, we found that the profile of p(k) followed a truncated Gaussian distribution function (SI Appendix, Fig. S5). Using this SDF formulation, we identified the representative λ of the wrinkle features from the peak position of p(k). For example, SEM images of the wrinkle patterns followed p(k) with a peak around 900 nm in real space, which can be associated with λ of the quasi-random nanostructure (Fig. 2E). Based on the defined p(k) and f, multiple statistically equivalent nanowrinkle patterns that follow the same SDF were digitally reconstructed from Fourier space to real space (Fig. 2F) using GRF (21). Notably, our reconstruction process can be applied to a wide range of p(k) with different profiles (SI Appendix, Figs. S6 and S7). We also demonstrated that structures with different real-space geometries but the same SDF can achieve very similar light trapping performance (SI Appendix, Fig. S8).

Fig. 2.

Representation and reconstruction of quasi-random patterns using SDF. SEM images of (A) PDMS wrinkle stamp; (B) imprinted PR; (C) PR patterns after O₂ RIE etching; and (D) resulting quasi-random nanostructure in a-Si. (E and F) Representation and reconstruction of resulting quasi-random patterns in D using SDF. (A–E, Insets) Corresponding fast Fourier transform patterns.

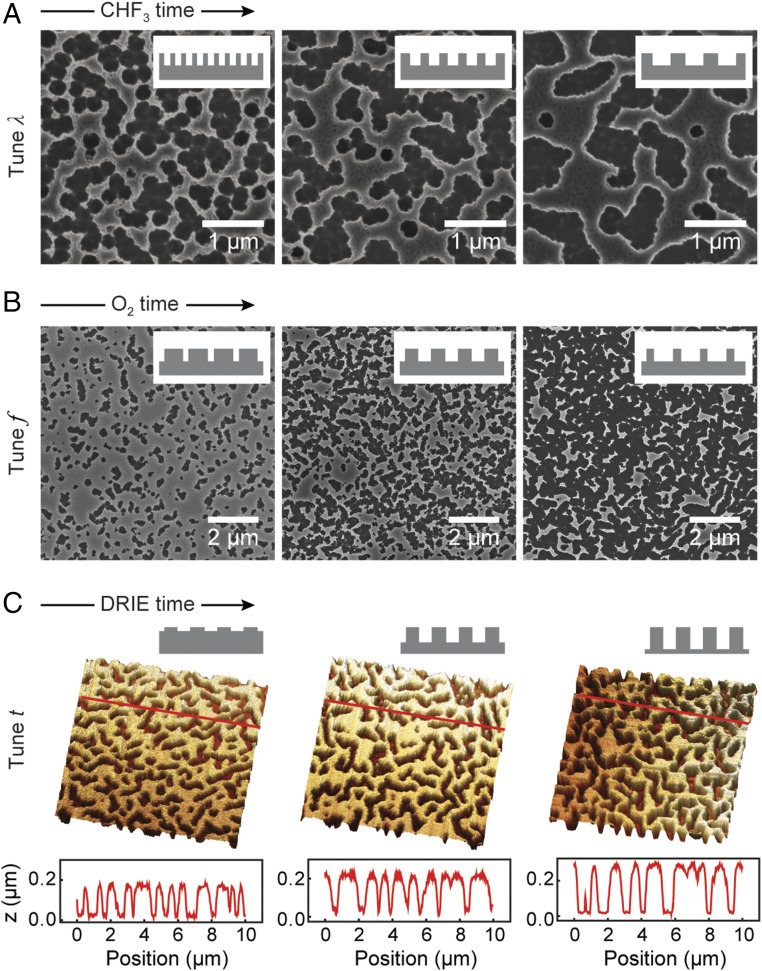
Using the SDF representation, we can describe the wrinkle-patterned surfaces by only three parameters: wavelength λ, material filling ratio f, and depth t. Fig. 3 highlights how wrinkle lithography can control independently these structural parameters for use as design variables. First, λ etched in a-Si can be continuously tuned by changing the CHF₃ RIE times needed to form PS wrinkle masters for the PDMS molds (24). Fig. 3A shows that a starting λ of ∼250 nm could increase linearly to 900 nm as CHF₃ time increases from 20 to 160 s with a fixed filling ratio (f ∼ 50%). Second, f could be tuned by changing O₂ treatment time of patterned PR wrinkles (Fig. 1C) before pattern transfer. For example, f from 30% to 50–73% was possible as O₂ time increased from 45 to 60 s at fixed λ (500 nm) (Fig. 3B). Third, t could be tuned by changing the deep-RIE (DRIE) time for etching the a-Si; t ∼ 165 nm increased to ∼290 nm as the etching time increased from 50 s to 90 s while keeping λ and f fixed at 600 nm and 50% (Fig. 3C). Because the wrinkle lithography processing conditions—CHF₃ treatment time (for λ), O₂ etching time (for f), DRIE time (for t)—can be continuously controlled, quasi-random patterns with nearly unlimited combinations of structural parameters can be realized.

Fig. 3.

Controlled structural parameters of quasi-random nanostructures using wrinkle lithography under different fabrication conditions. The wavelength (λ), filling ratio (f), and depth (t) of quasi-random nanostructures can be controlled by (A) CHF₃ treatment time on PS template, (B) O₂ plasma time on PR wrinkles, and (C) DRIE etching time of a-Si, respectively.

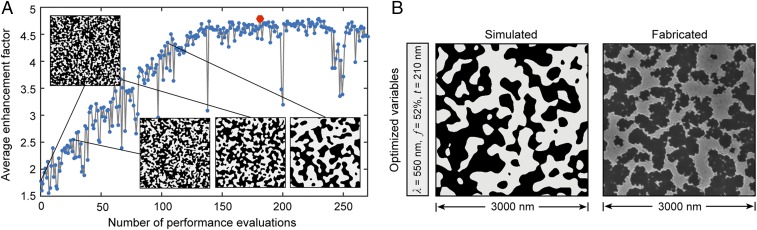
To validate the concurrent design approach in Fig. 1C, we optimized the wrinkle patterns for normal incidence light absorption over a range of wavelengths (Fig. 4). Broadband optimization maximized the average absorption enhancement factor over the weakly absorbing region of a-Si from 800 to 1200 nm (SI Appendix, Fig. S9), where the enhancement factor is defined as the ratio of the predicted light absorption and single-path absorption averaged over the wavelength spectrum (33, 34). The total thickness of the a-Si slab was set as T = 700 nm. Fig. 4A shows the optimization history of the predicted average enhancement factor versus number of performance evaluations. Initiated with a randomly generated design, the optimization of absorption enhancement factors increased linearly from ∼1.6 at the starting point and then started to converge as the number of evaluations increased above 130. We used a self-adaptive GA (31) to reduce the chance of the optimization being trapped at a low-performance local optimum. Fluctuations over the optimization history in Fig. 4A and the three design variables (SI Appendix, Fig. S10) are from self-adaptive mutation of the GA (SI Appendix, Methods).

Fig. 4.

Optimization of structural parameters in quasi-random nanostructures for broadband light trapping. (A) Optimization history of absorption enhancement factor in a light-trapping structure under normal incidence of 400–1,200-nm wavelength range. (B) Predicted and fabricated optimal nanowrinkle pattern in 3-μm × 3-μm window. Red point in A depicts the optimized point corresponding to the simulated image in B.

We identified an optimized solution of λ = 550 nm, f = 52%, t = 210 nm that showed an average enhancement factor up to 4.7 at the converged regime (number of evaluations = 186). This fast design exploration was made possible because the Fourier spectrum that largely determines the light-trapping performance of a structure was considered directly, and the SDF-based representation contained only three design variables for our structures. After applying a global, derivative-free search algorithm, such as GA, the nanostructure design with the highest performance was identified. Following a process–structure mapping (SI Appendix, Fig. S3), we identified the processing conditions and then fabricated an experimental sample using the identified conditions. The fabricated design compared with the real-space design reconstructed from the optimized SDF were in good agreement (Fig. 4B). Because the processing conditions were mapped to the structure design via the SDF, the fabricated nanopatterns were like those predicted computationally.

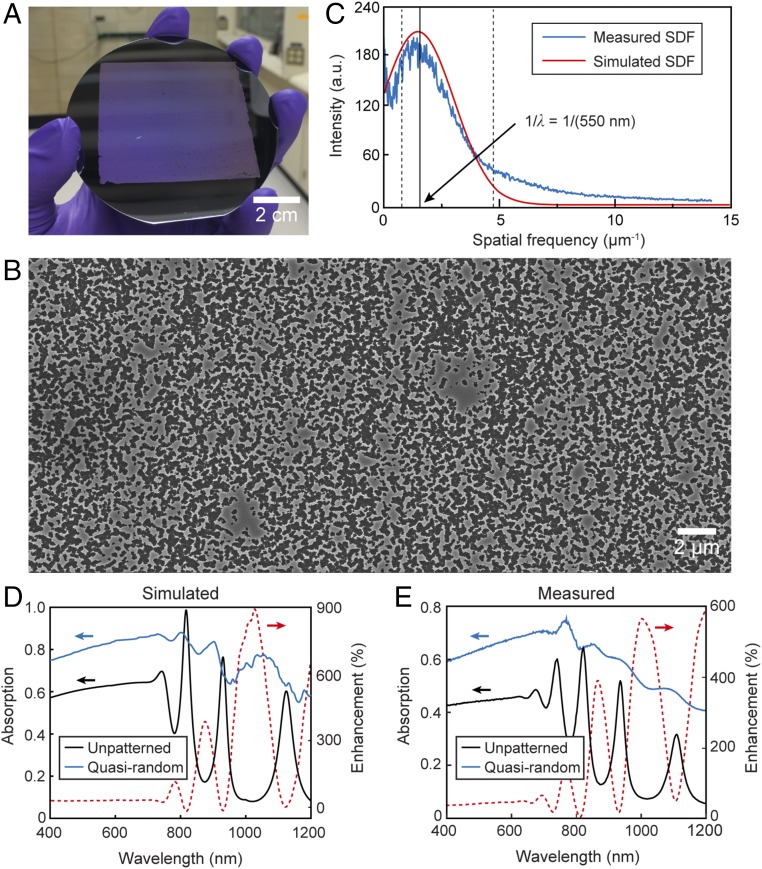
Fig. 5 shows a side-by-side comparison of the light-trapping characteristics of the designed and realized quasi-random nanostructures. The optimized structures were patterned over 3-inch a-Si wafers (Fig. 5 A and B). The SDF of the quasi-random nanopatterns from wrinkle lithography corresponded well with that from computation in Fig. 4B (Fig. 5C). Furthermore, we calculated the SDFs of five different local areas from the same sample with varying areas (SI Appendix, Fig. S11). Comparisons of the resulting SDFs confirmed that the SDFs from the different local patterns were consistent for two reasons. First, the SDF of the quasi-random nanostructure was determined by the formation process. The whole structure was manufactured via wrinkle nanolithography under the processing conditions mapped from the optimized SDF-based design. Therefore, for the same sample, the SDF should be consistent across different length scales and areas. Second, SDF represents a global characterization of the quasi-periodicity in the structures and is not significantly affected by local defects. Because the defects from wrinkle lithography are over relatively small areas and not periodic in nature, their impact on the overall broadband absorption performance of the entire quasi-random patterned structure was negligible.

Fig. 5.

Fabrication of broadband, light-trapping device over wafer scale. (A) Optimized light-trapping structure fabricated via wrinkle lithography in 3-inch wafer. (B) SEM image of the optimized light-trapping structure via wrinkle lithography. (C) SDFs of the simulated and fabricated patterns. (D) Simulated absorption spectrums of the optimized structure and unpatterned structure over the wavelength range from 400 to 1,200 nm. (E) Measured absorption spectrum of the fabricated optimal structure and unpatterned structure over the wavelength range from 400 to 1,200 nm.

Light trapping in silicon requires coupling of incident light into waveguide modes, which can be achieved by the diffraction from nanostructures with spatial frequencies that overlap with the wave vectors of the waveguide modes (11, 18). The two vertical dashed lines in Fig. 5C denote the lower (0.83 μm⁻¹) and upper (4.81 μm⁻¹) bounds of k over the weak absorbing spectrum of a-Si (11). The overlap between the SDFs and this range suggests that the light diffraction from the optimized pattern will couple with possible waveguide modes, resulting in broadband light trapping. Although previous work has used a Fourier-space representation to predict light-trapping structures with extraordinary absorption enhancement, the approaches usually involve a greater numbers of design variables without rigorously considering nanofabrication constraints (35, 36). Our method can achieve concurrent design of quasi-random photonic nanostructures over wafer-scale areas while considering their nanofabrication conditions at the same time.

Fig. 5D shows that the optimal design achieved an average light absorption 0.73 over the 800–1,200-nm spectrum, a 190% enhancement compared with the unpatterned (bare Si) case of 0.25. The averaged enhancement factor of the optimized design over the 800–1,200-nm spectrum was 4.7 (SI Appendix, Fig. S9). Similarly, the measured absorption spectrum on the quasi-random sample achieved an average of 0.53 over the same wavelength range, which is a 163% enhancement compared with the unpatterned case of 0.20 (Fig. 5E). We found that localized hot spots with high field intensity were distributed in a complex speckle pattern, which enabled superior light trapping with enhanced absorption (SI Appendix, Fig. S12). By considering that the interface between the a-Si and the Ag backing layer was flat, we found that any plasmonic mode effects were negligible. Over a larger wavelength range (400–1,200 nm), the nanofabricated sample achieved an average 0.60 light absorption, whereas the unpatterned sample was 0.32. We attribute high broadband absorption enhancement to the comprehensive design of the structural parameters. Simultaneous optimization of wrinkle wavelength, material filling ratio, and feature depth not only enables waveguide coupling but serves as a “natural” antireflection coating as well (37). Although the trends match, the absorption on fabricated samples compared with predications is slightly lower, which is likely attributed to undesired scattering from the surface roughness of features on a-Si (SI Appendix, Fig. S13). Overall, the close match of both structure and performance between predicted design and fabricated samples shows the effectiveness of the concurrent design approach. This first demonstration realized broadband light trapping with >100% enhancement over wafer scales using a parallel and highly flexible fabrication method.

Discussion

Wrinkle lithography is a parallel nanofabrication method that can rapidly transfer quasi-random geometries from soft templates into hard materials over wafer-scale areas. Independent, continuous control over structural parameters using this massively parallel manufacturing process can produce nearly unlimited topologies of nanostructures stochastically defined in 3D. The integration of concurrent design into wrinkle nanolithography allows extremely fast prototyping of quasi-ordered photonic systems and can avoid trial-and-error of fabrication processes. We expect that this approach can be readily generalizable to polymers, metals, oxides, and emerging 2D materials across all length scales. Our integrated processing–structure strategy can generate customizable libraries of quasi-random structures for various structure–performance applications, including biological imaging, random lasing, and photovoltaics.

Methods

Detailed information for the preparation of PS wrinkles, fabrication of PDMS wrinkle molds, procedure for wrinkle lithography, characterization of surface wrinkle pattern, SDF-based representation of quasi-random nanostructures, genetic algorithm for optimization search, and finite-difference time-domain simulation can be found in SI Appendix.