Time-resolved observation of protein allosteric communication

Significance

Allostery describes the puzzling phenomenon of long-range communication between distant protein sites. Representing the elementary process of cell signaling, allosteric interactions also provide prime targets in pharmaceutical research. Although a number of thermodynamic models have been proposed, the dynamic process of allosteric communication itself is still not well understood. Accounting for recent time-resolved infrared spectroscopy experiments, this study uses extensive all-atom molecular dynamics simulations that envision a real-time picture of the way allostery works. Mediated by the propagation of stress, allostery is found to trigger structural and dynamical changes in a nonlinear and nonlocal fashion. Similarly as found for downhill folding, the hierarchy and exceeding structural heterogeneity of the process gives rise to strongly nonexponential kinetics.

Abstract

Allostery represents a fundamental mechanism of biological regulation that is mediated via long-range communication between distant protein sites. Although little is known about the underlying dynamical process, recent time-resolved infrared spectroscopy experiments on a photoswitchable PDZ domain (PDZ2S) have indicated that the allosteric transition occurs on multiple timescales. Here, using extensive nonequilibrium molecular dynamics simulations, a time-dependent picture of the allosteric communication in PDZ2S is developed. The simulations reveal that allostery amounts to the propagation of structural and dynamical changes that are genuinely nonlinear and can occur in a nonlocal fashion. A dynamic network model is constructed that illustrates the hierarchy and exceeding structural heterogeneity of the process. In compelling agreement with experiment, three physically distinct phases of the time evolution are identified, describing elastic response ($\lesssim 0.1$ ns), inelastic reorganization ($\sim 100$ ns), and structural relaxation ($\gtrsim 1\mathrm{\mu }$s). Issues such as the similarity to downhill folding as well as the interpretation of allosteric pathways are discussed.

The function of many proteins is regulated through allostery, by which a binding event at one site of a protein affects the behavior of another distant site. Representing the elementary process of signal transduction, this long-range communication between protein sites has been intensively studied in experiment and computation (1–7). Although most studies on allostery have focused on thermodynamic properties such as substrate binding affinity, there is an increasing interest in the role of conformational dynamics. Known as “entropically driven” allostery, this notion commonly relates to the change of equilibrium fluctuations due to effector binding (8–14). On the other hand, the dynamic process of allosteric communication itself, also referred to as “allosteric transition” between the free and bound end states, has been rarely investigated (15–19); this is because of the experimental challenge of observing transition pathways and the timescale limitations of molecular dynamics simulations. Nonetheless, a number of theoretical models have been proposed that aim to predict the pathways of the intramolecular signal propagation (20–32). Compared with other biomolecular processes such as protein folding (33), however, it seems fair to say that the dynamical evolution of allosteric transitions is still not well understood.

As a new approach toward this end, Hamm and coworkers (34) recently performed time-resolved infrared experiments on a photoswitchable PDZ2 domain (Fig. 1A). PDZ2 is involved in the regulation of multiple receptor-coupled signal transduction processes, including apoptosis (35–37). Although various intramolecular pathways have been proposed (20–24), the nature of the allosteric interaction in PDZ2 remains a matter of debate. Showing that the removal of a short $\alpha$-helix at the C terminal reduces ligand affinity by a factor of 21, the NMR study of Petit et al. (36) revealed an allosteric communication between ligand binding and C-terminal dynamics. To observe this process in real time, Hamm and coworkers (34) covalently linked an azobenzene photoswitch across the binding groove and used a femtosecond laser pulse that effects cis$\mathrm{\to }$trans photoisomerization of azobenzene. The isomerization results in a photoinduced opening of the binding pocket, which mimics the free-bound transition of PDZ2. Using ultrafast time-resolved vibrational spectroscopy, they showed that the conformational rearrangement of the photoswitchable protein (referred to as PDZ2S) occurs on various timescales from picoseconds to microseconds in a highly nonexponential manner. In particular, the spectroscopic signals showed overshootings and “strange kinetics” (i.e., requiring stretched exponential fitting functions) as observed, e.g., in downhill folding (38–42).

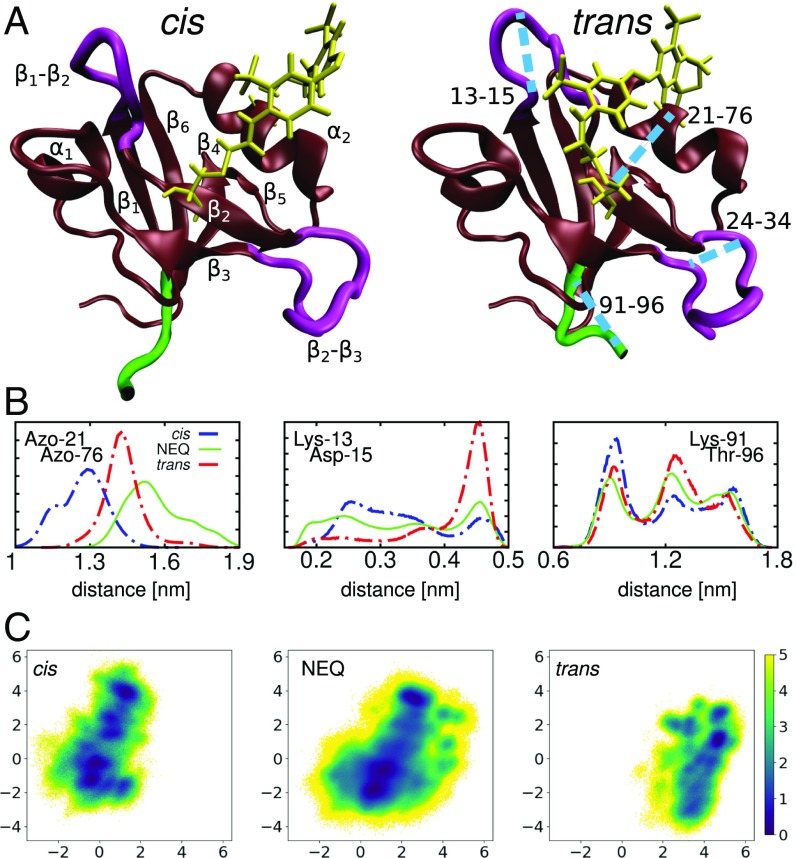
Fig. 1.

(A) Molecular dynamics snapshots of PDZ2S in cis (Left) and trans (Right) equilibrium states, showing $\alpha$-helices and $\beta$-sheets in brown, loop regions in purple, the C terminal in green, and the azobenzene photoswitch including linker atoms in yellow. Labels in Left indicate the regions ${\beta }_1$ (residues 6 to 12), ${\beta }_2$ (20 to 23), ${\beta }_3$ (35 to 40), ${\alpha }_1$ (45 to 49), ${\beta }_4$ (57 to 61), ${\beta }_5$ (64 to 65), ${\alpha }_2$ (73 to 80), and ${\beta }_6$ (84 to 90). Important loops connecting these regions include ${\beta }_1{\beta }_2$ (13 to 19), ${\beta }_2{\beta }_3$ (24 to 34), ${\beta }_3{\alpha }_1$ (41 to 44), and ${\alpha }_2{\beta }_6$ (81 to 83). The blue lines in Right indicate selected long-range distances that characterize the conformational transition following cis–trans photoisomerization of PDZ2S. (B) Distributions of three intramolecular distances that differ significantly in cis (blue) and trans (red) as well as in the NEQ simulations (green); see Materials and Methods. From left to right: C_α-distance between the anchor residues Cys-21 and Cys-76 of the photoswitch, contact distance $r_{13,15}$ between Lys-13 and Asp-15 in the ${\beta }_1{\beta }_2$-loop, and end-to-end distance $d_{91,96}$ of the C-terminal loop. (C) Free energy landscape $\mathrm{\Delta }G(x_1,x_2)$ (in units of $k_{\text{B}}T$) associated with the cis and trans equilibrium states as well as the NEQ evolution of PDZ2S, expressed by $-k_{\text{B}}T\ln P_{\text{NEQ}}(x_1,x_2)$ (Materials and Methods). Here $k_{\text{B}}$ is Boltzmann’s constant, T is the temperature, $x_1$ and $x_2$ denote the first two principal components of a dihedral angle PCA (Materials and Methods).

To aid the interpretation of these experiments, we first performed comprehensive all-atom molecular dynamics simulations that characterized the structural and dynamical differences of the cis and trans equilibrium states of PDZ2S (43). To study allosteric communication in PDZ2S in real time, in this work, we perform direct nonequilibrium (NEQ) molecular dynamics simulations of Hamm’s experiment. The extensive computer simulations reveal that the process is mediated by the propagation of stress, which triggers structural and dynamical changes that are genuinely nonlinear and may occur in a nonlocal fashion. By combination of principal component analysis (PCA) and clustering (44) methods, we construct a dynamic network model that illustrates the hierarchy and exceeding structural heterogeneity of the process. In excellent agreement with experiment, we identify three physically distinct phases of the time evolution (ranging from picoseconds to microseconds), and explain the peculiar overshooting of spectral observables. In light of the time-dependent picture, various commonly debated issues of allostery are addressed, including the role played by energy transfer, solvent dynamics, and allosteric pathways.

Results

Characterization of cis and trans Equilibrium States.

Following ref. 43, we extended our previous equilibrium simulations of PDZ2S and studied in detail structural changes following cis$\mathrm{\to }$trans photoisomerization (Fig. 1). In brief, we found that the relatively rigid $\alpha$-helices and $\beta$-sheets of PDZ2S undergo only small modifications (SI Appendix, Fig. S1), whereas the flexible loops of the system, in particular ${\beta }_1{\beta }_2$ and ${\beta }_2{\beta }_3$, exhibit significant changes of numerous residue–residue contacts (SI Appendix, Table S1) and backbone dihedral angles (SI Appendix, Table S2). To discuss some key observations of the conformational transition in PDZ2S, in the following, we consider distance coordinates (such as contact distances $r_{ij}$ and C$\alpha$ distances $d_{ij}$ between residues $i$ and $j$) describing local motions as well as collective coordinates (such as principal components) describing global motions (Materials and Methods).

As examples of local observables, Fig. 1B shows the distribution of three distances that characterize the cis and trans equilibrium states of PDZ2. (i) Monitoring the C_α-distance between the anchor residues Cys-21 and Cys-76 of the photoswitch, $d_{\mathrm{21,76}}$, directly exhibits the opening of the binding pocket due to $cis$–$trans$ photoisomerization. (ii) The contact distance $r_{\mathrm{13,15}}$ between Lys-13 and Asp-15 reflects the structural rearrangement of the ${\beta }_1{\beta }_2$-loop. (iii) The changes of the end-to-end distance $d_{\mathrm{91,96}}$ of the C-terminal loop reflect the stabilization of the C-terminal region due to newly formed contacts (SI Appendix, Table S1). In the absence of a specific binding partner at the distant site, we consider this change of the conformational distribution and dynamics of the C-terminal region as the “allosteric response” of the isolated PDZ domain (43). In fact, the allosteric communication between ligand binding and C-terminal dynamics in PDZ domain has been revealed in the NMR study of Petit et al. (36).

To obtain a global view of the conformational distribution of PDZ2S, we performed a dihedral angle PCA of the cis and trans equilibrium trajectories (Materials and Methods and SI Appendix, Fig. S2). Using the first two principal components $x_1$ and $x_2$, which reflect the largest variance of the dihedral angle motion, Fig. 1C, Left and Right show the resulting cis and trans free energy landscapes (45) $\mathrm{\Delta }G(x_1,x_2)$ (Eq. 2), respectively. We see that the cis and trans conformations are well separated along the first principal component. Analysis of the dihedral angles contributing to this component (mainly ${\varphi }_{15}$, ${\varphi }_{16}$, ${\psi }_{67}$, ${\varphi }_{68}$, and ${\psi }_{70}$) indeed reveals that $x_1$ predominantly accounts for the overall cis$\mathrm{\to }$trans rearrangement in the vicinity of the binding pocket. The second principal component (including mainly ${\varphi }_{15}$, ${\varphi }_{16}$, ${\psi }_{20}$, ${\varphi }_{21}$, ${\varphi }_{27}$, ${\psi }_{27}$, ${\psi }_{28}$, and ${\varphi }_{33}$) is found to account for the conformational heterogeneity of the ${\beta }_1{\beta }_2$- and ${\beta }_2{\beta }_3$-loops. The numerous minima of the free energy landscapes $\mathrm{\Delta }G(x_1,x_2)$ indicate metastable conformational states of PDZ2S (see below), which may be used to characterize the structural rearrangement. For example, we can use these states to quantify the overlap of cis and trans equilibrium conformations in the intermediate region, where $\sim 0.3\%$ cis-classified states were found in the trans region and $\sim 0.74\%$ trans-classified states were found in the cis region.

Propagation of Conformational Change.

To facilitate a direct simulation of the time-resolved experiment of Hamm and coworkers (34), we performed NEQ molecular dynamics simulations of the allosteric transition in PDZ2S. By mimicking the initial cis$\mathrm{\to }$trans photoisomerization of the azobenzene photoswitch via a potential-energy surface switching method (46), we generated 100 NEQ trajectories of 1-$\mathrm{\mu }$s length (of which 20 randomly selected were extended to $10$ $\mathrm{\mu }$s), and calculated time-dependent observables via an ensemble average (Materials and Methods). In what follows, we discuss the resulting photoinduced structural changes of PDZ2S, which appear to propagate from the anchor residues of the photoswitch via intermediate secondary structure segments to the C terminus (Fig. 2). Although Fig. 2 only shows a small selection of representative distance and angular coordinates, many more observables are discussed in ref. 47.

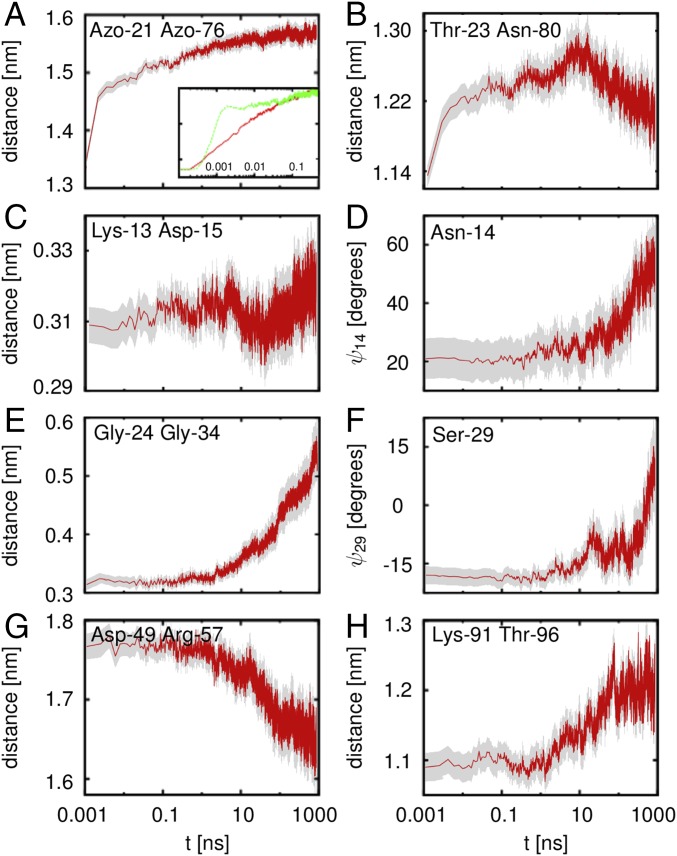
Fig. 2.

NEQ propagation of conformational change through PDZ2S, as revealed by the time evolution of the ensemble average of various local coordinates. The gray areas reflect the confidence intervals of the mean. The opening of the binding pocket is revealed by the C$\alpha$-distances between (A) the anchor residues Azo-21 and Azo-76 of the photoswitch and (B) residues Thr-23 and Asn-80 diagonally across the pocket. Inset of A zooms in at the short time evolution and compares to a simulation with reduced water mass ($m=m_0/100$, green line). Subsequent rearrangements of the ${\beta }_1{\beta }_2$-loop are monitored by (C) the contact distance between residues Lys-13 and Asp-15 and (D) the backbone dihedral angle $\psi$ of Asn-14. Rearrangements of the ${\beta }_2{\beta }_3$-loop are reflected by (E) the breaking of a contact between Gly-24 and Gly-34 and (F) the shift of backbone dihedral angle $\psi$ of Ser-29. (G) Rotation of the ${\alpha }_1$-helix results in a change of the C$\alpha$-distance between Asp-49 and Arg-57. (H) Long-range response of the C-terminal loop, monitored by its end-to-end distance $d_{91,96}$.

As for the equilibrium distributions in Fig. 1B, we begin again with the photoinduced opening of the binding pocket as described by the C_α-distance $d_{\mathrm{21,76}}$. Fig. 2A shows the evolution of the time-dependent average value $d_{\mathrm{21,76}}(t)$ (Eq. 1), which starts at the cis equilibrium value of about 1.3 nm and increases within 1 $\mathrm{\mu }$s to $\sim$1.6 nm in a highly nonexponential manner. (To better recognize the multiscale behavior of the dynamics, we use a logarithmic scale for the time axis throughout this paper.) Following the subpicosecond photoisomerization of the azobenzene photoswitch, the first half of the increase occurs within only 0.1 ns, whereas the second half takes about 100 ns before $d_{\mathrm{21,76}}(t)$ levels off. Analysis of interresidue contacts and backbone dihedral angles shows that the initial expansion of the binding pocket hardly involves conformational transitions including the crossing of free energy barriers. The first phase of the process for times $t\lesssim$ 0.1 ns therefore corresponds to an elastic response (i.e., the protein is expected to rapidly return to the initial state when we switch the azobenzene back to its cis configuration). Compared to a simulation using a reduced mass of the solvent water (48), Fig. 2A, Inset reveals that the response of $d_{\mathrm{21,76}}(t)$ depends on the solvent viscosity only for $t\lesssim$ 0.1 ns (see below). The elastic phase also features the dissipation of photoinduced excess kinetic energy (i.e., the cooling of PDZ2S to the solvent temperature), which typically occurs on a timescale of tens of picoseconds (48, 49).

The subsequent expansion of the binding pocket on a nanosecond timescale, on the other hand, does require inelastic rearrangements of the close-by residues. As a first indication of this effect, we consider the C_α-distance $d_{\mathrm{23,80}}$, which reaches diagonally across the binding pocket. Fig. 2B shows a steady increase of $d_{\mathrm{23,80}}(t)$ until $\sim$60 ns, when it suddenly starts to decrease again—a genuinely nonlinear behavior. A structural analysis of this somewhat surprising overshooting of $d_{\mathrm{23,80}}(t)$ reveals that the ${\beta }_2$-strand and the ${\alpha }_2$-helix first move apart parallel to the photoswitch, until, for $t\gtrsim$ 60 ns, it is apparently not possible any longer to expand the binding pocket in this direction. Hence ${\alpha }_2$ starts to move perpendicular to the photoswitch, which explains the decrease of $d_{\mathrm{23,80}}(t)$ (Fig. 1A). Facing the limits of the elastic expansion of the binding pocket, the photoinduced conformational stress extends to the surrounding residues. At the Azo-76 end of the photoswitch, this process eventually results in a stabilization of the ${\alpha }_2$-helix via the formation of three hydrogen bonds (SI Appendix, Table S1). The rigidity of the successive $\beta$-sheet, however, appears to hamper the direct propagation of the ${\alpha }_2$ conformational change to the C terminus. At the Azo-21 end, the stress propagates to the adjacent ${\beta }_1{\beta }_2$- and ${\beta }_2{\beta }_3$-loops. Being quite flexible, these relatively long loops may reorient the rather rigid $\beta$-sheets of PDZ2S toward the trans structure and thereby play a central role in the propagation of structural change.

In total, the ${\beta }_1{\beta }_2$-loop is found to change seven contacts (SI Appendix, Table S1) and five $(\varphi ,\psi )$ dihedral angle pairs (SI Appendix, Table S2), which, overall, leads to a stabilization of the loop. As representative examples, Fig. 2 C and D shows the time evolution of contact distance $r_{\mathrm{13,15}}$ as well as dihedral angle ${\psi }_{14}$. Interestingly, the destabilization of the contact between Lys-13 and Asp-15 results in a nonmonotonous behavior of $r_{\mathrm{13,15}}(t)$ with a minimum at $\sim$100 ns, quite similar to the overshooting found for $d_{\mathrm{23,80}}(t)$. The transition of Asn-14 from a 50/50 mixture of ${\alpha }_{\mathrm{R}}$-helical ($\sim -{30}^{\circ }$) and $\beta$-extended ($\sim {150}^{\circ }$) conformations to a mostly $\beta$-extended conformation (SI Appendix, Fig. S3) is reflected in a gradual increase of ${\psi }_{14}$ on a 100-ns timescale. In contrast to ${\beta }_1{\beta }_2$, the ${\beta }_2{\beta }_3$-loop at the other side of the binding pocket contains relatively few contacts. As a consequence, the loop exhibits a large conformational heterogeneity and resembles an intrinsically disordered system. As such, it undergoes structural changes in 8 (out of 11) $\varphi ,\psi$ dihedral angle pairs (SI Appendix, Table S2). As examples, Fig. 2 shows the breaking of the hydrogen bond between Gly-24 and Gly-34 (Fig. 2E) and the temporal evolution of the dihedral angle ${\psi }_{29}(t)$ (Fig. 2F). The latter reflects the gradual shift of the Ramachandran plot of Ser-29 toward more extended conformations (SI Appendix, Fig. S3).

To investigate how the structural changes of ${\beta }_1{\beta }_2$ and ${\beta }_2{\beta }_3$ extend to the distant C-terminal region, we again consider the end-to-end distance $d_{\mathrm{91,96}}$ of the C-terminal loop, which, in Fig. 1B, was shown to undergo a significant change. Fig. 2H reveals that the time evolution of $d_{\mathrm{91,96}}(t)$ remains constant until $\sim$10 ns, when it starts to increase on a 100-ns timescale to reach its trans value within 1 $\mathrm{\mu }$s. Structural analysis suggests that this response is a consequence of the stabilization of the C-terminal loop by several newly formed contacts with ${\beta }_2{\beta }_3$, ${\beta }_3$, and ${\alpha }_1{\beta }_4$ (SI Appendix, Table S1). For example, the two ${\alpha }_1{\beta }_4$-contacts are facilitated by a rotation of the ${\alpha }_1$-helix, which is reflected in a prominent decrease of the contact distance $r_{\mathrm{49,57}}(t)$ between residues Asp-49 and Arg-57 for $t\gtrsim$10 ns (Fig. 2G). To summarize, we conclude from Fig. 2 that the propagation of conformational change begins on a timescale of a few nanoseconds and leads to a significant structural reorganization of PDZ2S on a 100-ns timescale. Following the initial elastic phase ($t\lesssim$0.1 ns), this conformational rearrangement constitutes the second phase of the protein’s response.

NEQ Time Evolution on a Global Energy Landscape.

Although we have so far explained allosteric communication as a series of local structural changes, it is important to note that these changes do not necessarily occur in a directed sequence as in a falling row of dominoes. Given the similar timescales found in Fig. 2 for observables close to and far away from the effector site, the ensemble-averaged structural evolution rather seems to indicate that, on all timescales, numerous steps happen simultaneously! To test this presumption, we now change from a local to a global point of view and describe the structural changes in terms of collective coordinates, such as the principal components of PDZ2S. The first two principal components $x_1$ and $x_2$ have already been introduced above to represent the free energy landscape $\mathrm{\Delta }G(x_1,x_2)$ of the cis and trans equilibrium states (Fig. 1C). By calculating the probability distribution of all NEQ trajectories (Materials and Methods), we may furthermore define a free energy landscape associated with the NEQ evolution (50). Note that this “free energy” depends on the details of the NEQ process, such as the simulation length. Fig. 1C shows that this NEQ energy surface overlaps well with the landscapes of the cis and trans equilibrium states, which suggests that our (up to 10 $\mathrm{\mu }$s long) trajectories may be sufficient to cover a considerable part of the overall conformational transition.

Designed to account for the collective (and typically slowest) response of the system, the first principal components are particularly suited to describe the NEQ time evolution at long times. With this in mind, Fig. 3A shows the time evolution of expectation values $x_i(t)$ and standard deviations ${\sigma }_i(t)$ of the first two principal components. The overall appearance of these observables clearly shows that the structural reorganization of PDZ2S is not finished within 1 $\mathrm{\mu }$s. Rather, the qualitative changes of the time evolution for $t\gtrsim 1$ $\mathrm{\mu }$s seem to indicate a new phase of structural dynamics. This third and final phase of the allosteric response of PDZ2S is found to describe the relaxation of the NEQ conformational distribution toward the trans equilibrium state.

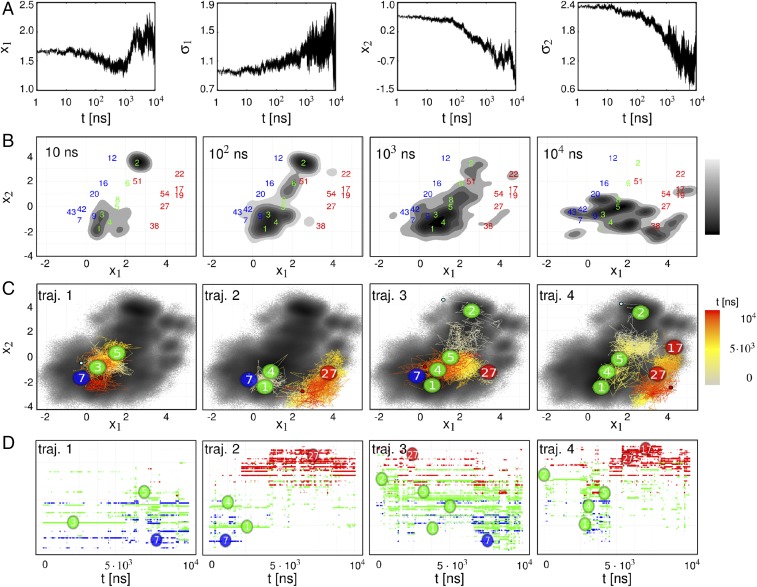
Fig. 3.

(A) From left to right: NEQ time evolution of mean $x_1(t)$ and ${\sigma }_1(t)$ of the first principal component, and the same for the second principal component. (B) Snapshots of the time evolution of the NEQ density $\rho (x_1,x_2,t)$. Numbers in blue, green, and red indicate the location of metastable conformational states of the cis, NEQ, and trans ensembles. States are labeled by decreasing population. (C) Time evolution of selected single NEQ trajectories as indicated by the color code, showing key metastable states visited. The background indicates the NEQ free energy landscape shown in Fig. 1C. (D) Corresponding time evolution in state space (using a linear time axis), with states ordered along the $y$ axis by their value of the first principal component.

The structural relaxation manifests itself through an intriguing correlation of the first two principal components. As explained above, $x_1$ describes the overall cis$\mathrm{\to }$trans rearrangement in the vicinity of the binding pocket, whereas $x_2$ reflects the conformational reorganization of the ${\beta }_1{\beta }_2$ and ${\beta }_2{\beta }_3$-loops. Interestingly, $x_1(t)$ shows a minimum around 1 $\mathrm{\mu }$s, before it moves toward its trans value for longer times. This process comes with an increase of ${\sigma }_1(t)$, indicating that individual trajectories of the ensemble evolve differently along $x_1$. On the other hand, the continuous decrease of $x_2(t)$ comes with a decay of ${\sigma }_2(t)$. This means that, with progressing structural reorganization of ${\beta }_1{\beta }_2$ and ${\beta }_2{\beta }_3$ (monitored by the decrease of $x_2$), the individual trajectories of the ensemble behave increasingly similarly along $x_2$. In this way, the structural reorganization accounts for a funnel of the free energy landscape (38, 45, 51) (when plotted as a function of the conformational entropy) that affects a decrease of the conformational heterogeneity.

Interestingly, Fig. 3A reveals a coincidence of the decrease of ${\sigma }_2(t)$ with the turning point of $x_1(t)$. This suggests that there are only a few specific conformations of the ${\beta }_1{\beta }_2$- and ${\beta }_2{\beta }_3$-loops that facilitate the transition to the trans equilibrium state. Recalling the timescale separation between the first and second principal components, we thus find that the relatively fast (100 ns) motion along $x_2$ represents a prerequisite of the slow (10 $\mathrm{\mu }$s) motion along $x_1$. Termed “hierarchical dynamics” (52, 53), the ubiquitous finding that fast fluctuations are required for slow functional motion represents a general dynamical mechanism to regulate function in biomolecules.

The hierarchical coupling of the motions described by $x_1$ and $x_2$ and the associated relation between the second and third phases of the allosteric response can be nicely observed in the time evolution of the NEQ density $\rho (x_1,x_2,t)$ shown in Fig. 3B (Materials and Methods). Following the initial elastic phase ($t\le$ 0.1 ns, not shown), the system starts in two separate regions at $t=10$ ns and gradually spreads over the large diagonal area of NEQ states. At the end of the inelastic phase ($t=1$ $\mathrm{\mu }$s), the population has significantly shifted to smaller values of $x_2$, which facilitates the onset of the relaxation phase. In the course of this relaxation, the density shifts to larger values of $x_1$ to approach the trans equilibrium state, which is only partly reached within $10$ $\mathrm{\mu }$s (Fig. 1C). It is noteworthy that the allosteric transition in PDZ2S is both enthalpically driven (via the initially applied conformational stress) and entropically driven. The latter is monitored by the time evolution of the width of the NEQ density, which generally increases during the reorganization phase and eventually decreases during the relaxation phase. In this way, the NEQ density indicates the spatial and temporal heterogeneity associated with the allosteric transition.

To reveal how this heterogeneity originates from the underlying single trajectories of the NEQ simulation, Fig. 3C shows the color-coded time evolution of some representative NEQ trajectories in $x_1$–$x_2$ space. Interestingly, we find that the four examples appear to be vastly different, indicating a substantial structural diversity of the allosteric transition. (In fact, all 100 NEQ trajectories behave differently!) Moreover, the overall appearance of the trajectories, with frequent changes and back-crossings between neighboring conformations, resembles a diffusive motion on the free energy landscape, similar to that discussed for protein folding (51). However, rather than the conventional picture of two-state folding with a dominant free energy barrier giving rise to single exponential kinetics, the structural rearrangements underlying allosteric communication resemble a “downhill folding” scenario (38–42). Proceeding from high-energy unfolded conformations to low-energy native states without passing major (say, $\gtrsim 3k_{\text{B}}T$) free energy barriers, downhill folders may exhibit numerous significantly populated conformational states that are connected by a large number of transition pathways. This structural and dynamical heterogeneity typically leads to highly nonexponential kinetics, which is just what we find for the allosteric communication in PDZ2S; see Figs. 2 and 3A. Starting from an ordered initial state, the allosteric system evolves (e.g., due to binding) into a disordered ensemble before it relaxes into an ordered final state. In this sense, allosteric communication may be considered as an “order–order” transition.

Metastable NEQ States Build up a Dynamic Network.

To characterize the structural evolution of the allosteric transition, we partitioned the NEQ trajectories into clusters of geometrically similar structures, the so-called microstates. Using density-based geometric clustering (44) (Materials and Methods), we obtained, in total, 207 microstates, which are [according to their (non)occurrence in the equilibrium simulations] 35 cis, 51 trans, and 121 NEQ states. That is, equilibrium trajectories, by definition, only sample cis and trans microstates, whereas NEQ trajectories may sample NEQ as well as cis and trans microstates. All 207 states are labeled by decreasing population. The free energy landscape in Fig. 3B indicates the seven highest populated states for cis, trans, and NEQ, showing cis states on the left in blue, trans states on the right in red, and NEQ states in the middle in green. Representative molecular structures of some prominent microstates are displayed in Fig. 4. Further characterization in terms of backbone dihedral angles and contact distances is provided in SI Appendix, Figs. S4 and S5, respectively.

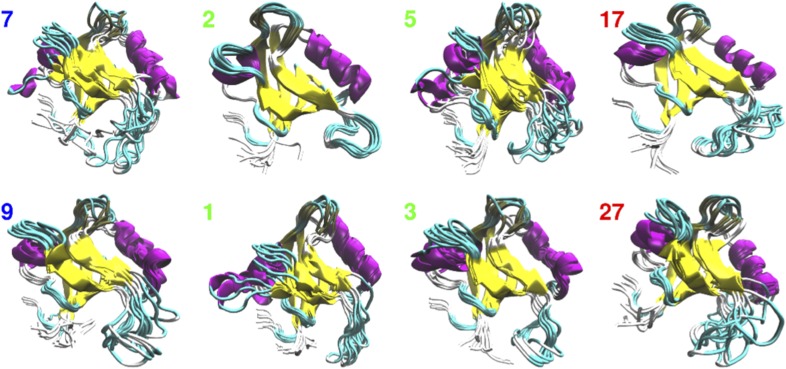
Fig. 4.

Representative molecular dynamics snapshots of some key microstates that illustrate the structural evolution of the allosteric transition in PDZ2S, processing from cis states 7, 9, via NEQ states 1 (hub), 2 (dead end), 3 (dynamic trap), and 5 (transition state), to trans states 17, 27.

To describe the NEQ dynamics of PDZ2S in state space, we first calculated the transition probabilities between all microstates. Due to NEQ initial conditions as well as insufficient sampling, these transition probabilities, in general, were found to change during the various phases of the NEQ process, which hampers a straightforward Markovian modeling that assumes constant transition rates (54). Nonetheless, subsequent dynamical clustering (55) revealed that the main microstates are indeed metastable (SI Appendix, Fig. S6). In this way, the microstates along with their connectivities (SI Appendix, Fig. S7) and resulting time-dependent population probabilities constitute a dynamic network (56). Focusing on some key states shown in Fig. 4, in the following, we use this network to illustrate the structural and dynamical evolution of the allosteric transition in PDZ2S.

During the elastic phase, we observe a rapid transition from initially populated cis states (e.g., 7 and 9) to various NEQ states, in particular 1, 2, and 3 (Fig. 3B). Among these, state 1 can be considered as a hub that interconnects numerous states of the network and is populated throughout the entire 10-$\mathrm{\mu }$s time evolution. State 2, on the other hand, is only highly populated at short times, before it decays on a 100-ns time scale. Although structurally quite similar to low-energy trans states, its slightly twisted ${\beta }_1{\beta }_2$-loop hampers a direct transition to the trans region, which renders it a “dead end.” Characterized by an overall stable structure, with the exception of a highly deformed ${\alpha }_2$-helix, state 3 represents a dynamic trap. That is, trajectories trapped in 3 (e.g., trajectory 1 in Fig. 3 C and D) tend to relax into that state until they are able to go back to the more flexible part of the NEQ region. During the second phase, we observe, along $x_2$, a downward shift of the population (Fig. 3A) to various intermediate NEQ states (mostly 4, 5, 6, and 8), which accounts for the structural reorganization of the ${\beta }_1{\beta }_2$- and ${\beta }_2{\beta }_3$-loops and small changes in the ${\alpha }_1{\beta }_4$-loop. In particular, state 5 is found to act as a “transition state,” which mediates the crucial conformational change from the NEQ region to the trans region (see, e.g., trajectory 4 in Fig. 3D for a successful transition, and see trajectory 1 for a rejected one). The structural change effected by state 5 (as well as a few other transition states such as 4) is mainly associated with the reorganization of the ${\beta }_1{\beta }_2$-loop, which marks the transition from the rearrangement phase to the relaxation phase around 1 $\mathrm{\mu }$s (Fig. 3A). During this phase, the first trans states are significantly populated, where 27 is an example of a short-lived state with a still-flexible ${\beta }_1{\beta }_2$-region, whereas 17 and 19 represent low-energy trans equilibrium states.

We note that, out of the four single trajectories shown in Fig. 3 C and D, only trajectory 4 makes it all of the way to the low-energy trans equilibrium region. Trajectory 1, for the most part, gets caught in the dynamical trap of state 3, trajectory 3 spends the full 10 $\mathrm{\mu }$s in the NEQ region searching for a premium spot to cross toward the trans region, and trajectory 2 only reaches high-energy trans states. Trajectories 1 and 3 are even seen to exhibit occasional back-crossings to cis state 7 at long times. As a common feature, all trajectories exhibit pronounced diffusive behavior in state space as well as in $x_1$–$x_2$ space. Although different force fields are known to predict different transition pathways (57), from the vast diversity of these paths, we expect that the overall picture is little affected by details of the force field.

The Quest for Allosteric Pathways.

The exceeding diversity found for the NEQ trajectories indicates a multitude of possible pathways of the allosteric transition. Furthermore, we note that these pathways do not necessarily correspond to a directed sequence of structural changes along certain residues. Instead, we find that even single trajectories may simultaneously undergo several structural changes. For example, trajectory 2 exhibits, at $t=1.6\mathrm{\mu }$s, a transition between two states that differ in the ${\beta }_1{\beta }_2$-loop and the ${\beta }_2{\beta }_3$-loop. Finally, the structural changes are not restricted to neighboring residues but may also occur nonlocally. That is, if a protein contains rather rigid segments (such as the $\beta$-barrel of PDZ domains), the initially applied conformational stress may directly propagate to distant sites and cause a structural change there. The feasibility of nonlocal and multiple simultaneous structural changes along a single trajectory together with the substantial heterogeneity found for different trajectories clearly suggest that the term “allosteric pathway” should not be taken literally as in a dominoes game. Given Hilser’s longstanding insight that an ensemble view of allostery hampers the concept of allosteric pathways (3, 58), this finding extends his notion to the realm of single trajectories.

Having said that, we acknowledge that the concept of allosteric pathways provides the basis for numerous network models that aim to predict intramolecular signaling (5–7). Here, typically, the protein residues are the “nodes” of the network, and the “edges” are some kind of interaction that mediates the signal propagation. This includes networks based on the statistical analysis of evolutionary conserved sequences (20), on vibrational energy flow (21, 24, 32) or residue–residue interaction energies (22), on the linear response to residue perturbation (23), on coupled side-chain fluctuations (31), on a force distribution analysis (30), and on information–theoretical approaches (27, 28). Due to different underlying assumptions, however, these models may yield quite different results. Attempting to identify “key residues” of the conformational transition of the native PDZ2 domain, for example, the predictions of various models were found to differ significantly (59).

Assuming that our direct simulation of the allosteric response in PDZ2S reveals the correct physical mechanisms, we may use this insight to develop new approximate methods for the identification of potential allosteric couplings. This process starts with the choice of appropriate coordinates, that is, intramolecular coordinates such as distances and dihedral angles rather than commonly used Cartesian coordinates, which suffer from mixing of intramolecular motion and global rotation (60). In the light of the fact that allostery manifests itself in a nonlinear manner (Fig. 2), it is interesting to study to what extent the allosteric response can be approximated by equilibrium correlation functions of linear response theory (23). In a similar vein, one wants to compare the performance of available linear and nonlinear correlation measures (28).

Discussion

To begin with, we want to state that our computational study has been facilitated by the experimentally driven focus on a specific system (the relatively small allosteric protein PDZ2S), a specific initiation of the response (via a photoswitch that mimics the binding of an effector molecule), and the discussion of intramolecular structural dynamics (rather than some binding behavior). We are certainly aware of the limitations of our study, e.g., photoswitching represents only a rough model of binding (see ref. 43 for a discussion), and the considered structural rearrangement in a PDZ domain may only constitute a small part of the allosteric process in a multidomain protein. Nonetheless, it is this focus that makes it possible to develop a descriptive time-dependent picture of allosteric communication, which may shed light on several so far elusive aspects of the phenomenon. After a comparison with experiment, in the following, we discuss various commonly debated issues on the basis of our simulations; this includes (i) the relation between signal and energy transport, (ii) potential effects of the solvent on allostery, and (iii) an emerging dynamic picture of allosteric communication.

In their pioneering experiment, Hamm and coworkers (34) discussed three phases of the time-dependent response of PDZ2S: a picosecond initial response, a highly nonexponential second phase (fitted by a stretched exponential) occurring on a 100-ns timescale, and a slow exponential phase that was followed up to tens of microseconds. Furthermore, their time-resolved vibrational spectrum clearly shows overshootings on timescales of 100 ns (at $\sim \mathrm{1,640}$ cm⁻¹) and 10 $\mathrm{\mu }$s (at $\sim \mathrm{1,655}$ cm⁻¹). These findings, in particular timescales, nonexponential behavior, and overshootings, are in compelling agreement with the simulation results in Figs. 2 and 3. Our computational results also provide a microscopic interpretation of the experimental findings. That is, the strongly nonexponential kinetics found in experiment as well as in simulation is readily explained by the insight that the structural reorganization of PDZ2S is not determined by a single main barrier but occurs (as in a downhill folding scenario) along a multitude of pathways of different durations. Moreover, the experimental overshootings at 100 ns correlate directly with the calculated overshooting due to the rebuilding of the ${\beta }_1{\beta }_2$-loop (Fig. 2 B and C). The experimental overshootings at 10 $\mathrm{\mu }$s may be explained by the onset of the relaxation phase shown in Fig. 3A. As a note of caution, we mention that only explicit calculations of the transient infrared spectra (which are quite ambitious) would prove that these motions are directly linked to the observed spectral features (61).

A number of studies have discussed possible connections between allostery and vibrational energy transport (21, 24, 32, 62). From various experimental and theoretical studies, it is well established that the dissipation of excess kinetic energy (e.g., due to photoexcitation or a chemical reaction) occurs on a timescale of tens of picoseconds (48, 49). As the structural rearrangement underlying allostery was shown to take at least nanoseconds to evolve, it appears obvious that vibrational energy transport and the propagation of structural change are physically different phenomena. Nonetheless, it remains to be shown if pathways of effective vibrational energy flow [essentially via the protein backbone and via polar residue–residue contacts (63)] may also indicate preferred directions of allosteric communication.

As solvent effects are ubiquitous in biomolecular dynamics, the question arises to what extent the solvent water may affect the structural rearrangement underlying allostery (34, 64). Recalling that the particle masses of a simulation do not change the free energy landscape but only the kinetics of the system (48), we performed additional NEQ molecular dynamics simulations with a reduced mass ($m=m_0/100$) of the solvent water. Fig. 2A, Inset reveals that the reduced solvent viscosity affects the response of the binding pocket distance $d_{\mathrm{21,76}}(t)$ only for $t\lesssim$ 0.1 ns, i.e., during the elastic phase. (Similar results were found for all other considered observables.) That is, in the absence of intramolecular barrier crossings, the solvent represents the main resistance to the initial protein motion. Hence a reduction of the solvent friction accelerates this motion. The rate of the subsequent structural rearrangement in the second and third phases, on the other hand, is mainly determined by intramolecular energy barriers. The speed of the allosteric transition in PDZ2S is therefore mostly governed by the internal friction of the protein (65–68).

We finally conclude with some remarks on the overall picture of allosteric communication emerging from our computational study:

• i)The extensive simulations have shown that the allosteric transition in PDZ2S amounts to a propagation of conformational change, which is mainly effected by a change of atomic contacts and dihedral angles in the flexible loop regions of the system. In particular, this manifests itself in the transient overshooting of several observables (Fig. 2), which indicate, e.g., that, first, some contacts need to be broken, before dihedral angles can change and new contacts are formed. In this sense, allosteric communication is a genuinely inelastic and nonlinear process.
• ii)Overall, the allosteric transition in PDZ2S with its prominent structural and dynamical heterogeneity has been found to show a remarkable similarity to the structural dynamics observed in downhill folding (38–42). Moreover, several concepts discussed in folding, such as diffusive motion on a rugged free energy landscape (Fig. 3C) showing a funnel as a function of the conformational entropy (38, 51), as well as hierarchical dynamics (52, 53) and the associated entropic barrier when the system proceeds from the inelastic to the relaxation phase (Fig. 3A), also seem to apply for allostery. Rather than the order–disorder transition observed in folding, however, an allosteric system exhibits an order–order transition, as it starts from an ordered state and transiently evolves (e.g., due to binding) into a disordered ensemble, before it relaxes into an ordered final state. Another difference is that structural changes in allostery are typically much more subtle than in folding, which renders their detection much harder in experiment and simulation.
• iii)Revealing nonlocal and multiple simultaneous structural changes along a single trajectory together with the exceeding structural heterogeneity found for different trajectories, our study has shown that the notion of allosteric pathways should not be taken literally as a directed sequence of structural changes along certain residues. In the context of sequence evolution, the existence of many low-energy pathways may confer the robustness of the signaling process (42).

Materials and Methods

Molecular Dynamics Simulations.

In an extension of recent work (43), we first performed $7\times 2.5\mathrm{\mu }$s molecular dynamics simulations of cis and trans equilibrium states of PDZ2S (Protein Data Bank entries 2M0Z and 2M10) (34) at 300 K, using the Amber99sb^∗-ILDN force field (69–71), TIP3P water, and the azobenzene parameters of refs. 43 and 47. Selecting 200 statistically independent equilibrium structures of PDZ2S-cis as initial conditions and using a previously developed potential-energy surface switching approach (46), we subsequently ran NEQ molecular dynamics simulations of the photoinduced conformational transition of PDZ2S. Using Gromacs with a hybrid GPU-CPU acceleration scheme (72), we performed, in total, 100 NVT runs of 1-$\mathrm{\mu }$s length each, of which 20 randomly chosen were extended to $10\mathrm{\mu }$s. Using these NEQ trajectories, $R^{(k)}(t)$ ($R^{(k)}\in {ℝ}^{3N},k=1\mathrm{\dots }M$), the time-dependent average value of some observable $f$ (say, an interresidue distance), is calculated via an ensemble average over $M=100$ (or 20) NEQ trajectories,

$$f(t)=\frac{1}{M}\sum _{k=1}^{M}f(R^{(k)}(t)).$$ [1]

For the molecular dynamics simulations with reduced water mass (Fig. 2A), a reduced integration time step of 0.2 fs was used (48).

Definition of Reaction Coordinates.

To describe the structural dynamics of PDZ2S, we considered various intramolecular observables, including $({\varphi }_i,{\psi }_i)$ backbone dihedral angles and distance measures such as C_α-distances $d_{ij}$ between residues or residue–residue contacts $r_{ij}$. Here two residues $i$ and $j$ were considered to be in contact if the minimal distance $r_{ij}$ between any atom of $i$ and any atom of $j$ was smaller than 0.45 nm. To describe the global motions of PDZ2S, we used PCA on the backbone dihedral angles as well as of the N=N torsion angle of the azobenzene photoswitch, to properly describe the secondary structure—especially the flexible loops—without ambiguities arising from overall rotation in a Euclidean coordinate system (60). We used the recently developed dPCA+ method, which defines a circular mean $\overline{\varphi }$ as the angle with minimum squared distance to all observations ${\varphi }_n$ and constructs a covariance matrix using the inner arc distance of the unit circle between observations and mean angle as distance metric. We used the first two PCs $x_1$ and $x_2$ to represent the system’s free energy landscape

$$\mathrm{\Delta }G(x_1,x_2)=-k_{\text{B}}T\ln P(x_1,x_2),$$ [2]

where $P$ denotes the probability distribution along these coordinates. To represent the conformational distribution of all equilibrium and NEQ simulations in a consistent way, we used the PCA eigenvectors of the concatenated equilibrium trajectories of PDZ2S-cis and PDZ2S-trans as a common basis. In a similar way, we also defined an NEQ energy landscape (50) via the distribution $P_{\text{NEQ}}(x_1,x_2)=\int dt\rho (x_1,x_2,t)$, where the time-dependent density $\rho (x_1,x_2,t)$ was calculated via a combination of an ensemble average and a moving time average.

Definition of Microstates.

To construct a set of microstates, we applied a recently developed density-based clustering method (44) on the first seven dPCA+ components. The idea is to estimate a local density $P(𝐫)$ at a data point $𝐫$ by counting all neighboring data points of the trajectory, which lie inside a hypersphere of fixed radius around the point (here $R=0.2$). By flooding the resulting free energy landscape $\mathrm{\Delta }G(𝐫)=-k_{\text{B}}T\ln P(𝐫)$ from low to high free energies, we can detect local free energy barriers and assign the data points to cluster labels given to their respective energy basins. Using the first seven PCs of dPCA+, clustering was performed on cis and trans equilibrium as well as on the $100\times 1\mathrm{\mu }$s NEQ trajectories, respectively.