Myosin Clusters of Finite Size Develop Contractile Stress in 1D Random Actin Arrays

Abstract

Myosin-powered force generation and contraction in nonmuscle cells underlies many cell biological processes and is based on contractility of random actin arrays. This contractility must rely on a microscopic asymmetry, the precise mechanism of which is not completely clear. A number of models of mechanical and structural asymmetries in actomyosin contraction have been posited. Here, we examine a contraction mechanism based on a finite size of myosin clusters and anisotropy of force generation by myosin heads at the ends of the myosin clusters. We use agent-based numerical simulations to demonstrate that if average lengths of actin filaments and myosin clusters are similar, then the proposed microscopic asymmetry leads to effective contraction of random 1D actomyosin arrays. We discuss the model’s implication for mechanics of contractile rings and stress fibers.

Introduction

Myosin-powered contraction generated by stable sarcomere structure of the muscle cells is a fundamental and well-studied physiological process (1). Actomyosin contractility is equally important in producing forces and movements in nonmuscle cells in 1D structures, such as dynamic stress fibers (2), cytokinetic rings (3), 2D structures such as lamellipodia (4) and cell cortices (5), and 3D cytoskeletal networks in migrating cells (6). However, the microscopic nature of the actomyosin contractility is not clear, despite recent successes of in vitro reconstitutions of 1D ringlike contractile structures (7, 8) and of 2D cortices (9, 10).

The puzzle that has to be solved to achieve clarity is the following: in muscle sarcomere, actin filaments are arranged in a perfect crystalline array optimal for contraction: pointed ends of actin filaments are at the center, where myosin-II moves to the outward-pointing barbed ends, thereby pulling filaments inward (11). Importantly, the size of myosin-II assemblies and of actin filaments are carefully regulated in muscle cell to optimize the contraction (12, 13). In random actomyosin networks of nonmuscle cells, filament pairs’ overlapping ends could be either pointed or barbed. In the former case, myosin-II would generate tension and contraction, but in the latter case the filaments would be under compression, and expansion will result with a similar probability. Some kind of asymmetry is necessary for the net contraction to develop.

A few recent models have put forward hypotheses about the origins of such asymmetry (reviewed in (14)). Not surprisingly, one of those is the structural asymmetry in the actin array associated with the existence of mini-sarcomeres (for example, in the cytokinetic ring of a dividing fission yeast cell) (15). There are a number of possible mechanisms of self-organization of such arrays, as follows. First, actin filaments could be nucleated at formins anchored at the membrane and extend with their pointed ends outward until the pointed ends overlap and interact with myosin (16), or mini-sarcomeres could emerge when the myosins do not slide off the barbed ends, but instead hang onto them (17, 18). Second, there could be a mechanical asymmetry: actin filaments under compression in expanding pairs with overlapping barbed ends would buckle, whereas filaments under tension in contracting pairs with overlapping pointed ends are mechanically stable, so a net contraction develops (19), which was indeed observed in vitro (20). Third, actin filaments’ disassembly at the pointed ends together with elastic deformations of cross-links that hang on to the disassembling ends could lead to net contraction (21). Fourth, actin filaments’ treadmilling was shown theoretically to shift myosin motors to the pointed ends, and so effectively to favor actomyosin interactions with overlapping pointed ends that create a bias to contractile, rather than expanding, structures (22, 23). A number of models recently demonstrated that various combinations of these mechanisms in complex actomyosin networks result in effective actomyosin contractility (8, 23, 24).

One additional possible mechanism relies on the myosin finite length: in 2D or 3D actin networks, myosin tends to slide closer to barbed ends of the overlapping actin filament pair, thereby causing effective symmetry break between the barbed and pointed ends and leading to net contraction, effectively zippering the filaments together (25, 26, 27, 28). This mechanism requires myosin rotation. It is an open question whether the finite myosin length can lead to contraction in a random 1D network without myosin rotation.

In this study, we demonstrate that a subtle structural asymmetry of the microscopic actomyosin arrays can generate contractile stress and movement in dynamic random 1D actomyosin networks (Fig. 1, A and B). Myosin II is a dimer of trimers that contains two identical motor domains, or heads, at the N-terminus of each heavy chain and a long C-terminal tail; multiple tails bundle together due to ionic and hydrophobic interactions into a stiff rod, thus multiple myosin motors assemble into elongated thick filaments (28) (Fig. 1, B and C). The force-generating heads extend from two zones at the ends of the thick filament; the midzone of the thick filament is bare (devoid of heads). In this article, for brevity, we use term “myosin” for myosin-II, and myosin “clusters” instead of “filaments” to avoid confusion with actin filaments.

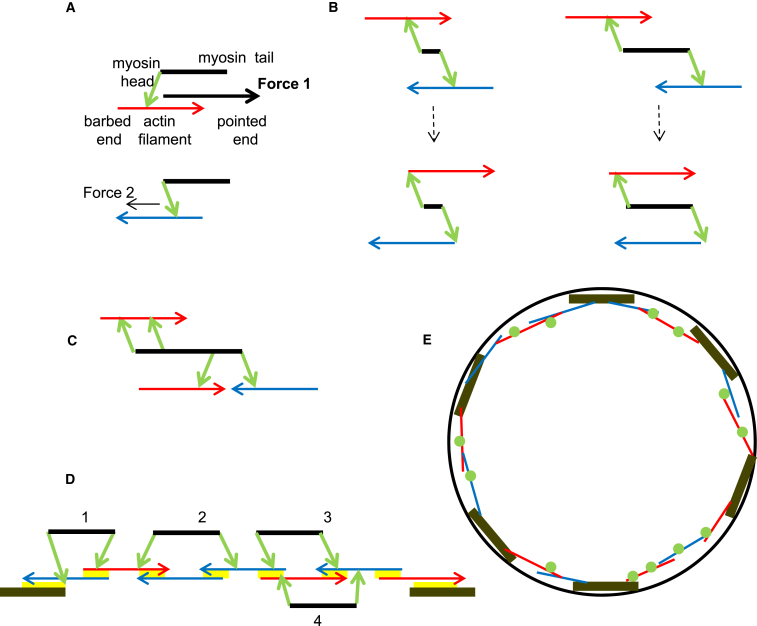
Figure 1.

Asymmetry of actomyosin contraction. Actin filaments are horizontal arrows; the arrow head/tail is the pointed/barbed end, respectively. Blue/red arrows mark filaments with barbed ends oriented to the right/left, respectively. The adhesive end segments are shown by brown rectangles. The myosin cluster backbone is shown by a black segment; heads attached to the actin filaments are shown by green arrows pointing to the filament. (A) Anisotropy of the force generation: myosin head from the cluster end oriented toward/away from the actin filament barbed end generates a significant/weak pulling force, respectively. (B) Effect of the finite length of the myosin cluster: a small cluster persistently sliding an antiparallel actin filament pair simply reshuffles the filaments (left), whereas the cluster where the length is comparable to that of the filaments generates contraction (right). (C) Multiple myosin heads per cluster enable the cluster to interact with more than two filaments at a time. (D) Given here is an example of a random actomyosin array. Cluster 1 is positioned such that neither of its two heads could interact with properly oriented filaments, so this cluster is detached. (Filament is oriented properly relative to a given head if, to reach the filament’s barbed end, the head has to walk away from the center of the cluster.) Both heads of clusters 2 and 4 interact with properly oriented filaments, and these clusters generate local contractions. Only one head of cluster 3 interacts with a properly oriented filament, and so this cluster glides to the barbed end of that filament without generating force. Yellow patches illustrate regions of cross-linking that generate effective friction. (E) Given here is a schematic illustration of the hypothetic contractile ring as independent contractile units in a periodic series. For simplicity, myosin clusters are shown with green circles, and arrowheads and cross-linking are not shown. Black circumference illustrates cell cortex to which the end segments adhere. To see this figure in color, go online.

Importantly, if a myosin cluster is aligned with an actin filament, there is a mechanical anisotropy: myosin heads point away from the cluster midzone and bind to the actin filament in a stereospecific way, so that heads that are extending toward the barbed end of the actin filament generate a significant pulling force, whereas heads that are extending toward the pointed end exert only very weak pushing force, perhaps because their necks have to bend into an unnatural direction (Fig. 1 A). Indeed, examination of actin filaments sliding over very long molluscan myosin clusters demonstrated that the actin filament, when moving toward the bare zone, went fast yet moved an order-of-magnitude slower if moving away from the bare zone (29). Use of actin filaments tethered to flexible microneedles showed that if the actin filament had the barbed end near the myosin heads extending from these long myosin clusters, then the generated force was significant. However, if the actin pointed end was near the myosin heads, the myosins did not generate significant force (30). Furthermore, use of the optical trap to examine the step size as a function of the angle that the actin filament makes relative to the myosin cluster resulted in a finding that steps of 10 nm were obtained at shallow angles between the pointed-to-barbed end vector and midzone-to-myosin-cluster-end vector. However, as the angle approached 180°, the step size decreased to 5 nm, and was 0 nm at a 90° angle (31).

A hypothesis that such force anisotropy could preferentially contract, but not expand, actin filament pairs was considered (32), but not explored in microscopic simulations. In fact, if the length of the myosin cluster was very small, this force anisotropy by itself would not generate net contraction (Fig. 1 B, left): when two antiparallel actin filaments slide, the filament pair eventually ends up in an expanded configuration. However, when the myosin cluster length, which is in fact ∼300 nm, is of the same order of magnitude as the actin filament length (Fig. 1 B, right), then sliding of the antiparallel actin filaments leads to the compacted configuration. In this study, we explore the hypothesis that the force anisotropy in myosin cluster together with the finite length of the myosin cluster can generate contraction in a 1D dynamic random actin array and use numerical simulations to confirm this hypothesis. We demonstrate that the contractile force becomes significant if average lengths of actin filaments and myosin clusters are similar. As there are multiple myosin heads per myosin cluster (33, 34), we investigate how the contractility depends on the number of heads per cluster and find that the contractility is insensitive to the number of heads per cluster. We show that rapid actin turnover is necessary for shortening of actomyosin units with dynamics similar to that of contractile rings in cytokinesis.

Methods

Structure of actomyosin arrays

A number of experimental studies recently led to the conclusion that actomyosin structures in cells consist of contractile modules that assemble and contract autonomously (33, 35, 36). Thus, in the model, we consider a 1D contractile unit with three main components (Fig. 1 D): N actin filaments, M myosin clusters with K motor heads each, and two adhesive segments at the end. We do two types of numerical experiments: in one, the end segments are immobile, and so the structure roughly resembles a stress fiber; we call this structure a stress fiber unit (SFU). In another, the segments are allowed to slide along the surface they are on against a friction specified below. In the latter case, the structure mimics a contractile unit of a hypothetical cytokinetic ring (Fig. 1 E); we call this structure a contractile unit (CU).

Actin filaments have lengths normally distributed around some prescribed value. Initially, the filaments are spread with random positions and polarities, so that each filament overlaps over finite distances with at least two neighbors, one at the right and another at the left. The end segments are positioned in such a manner that the left and right extreme points of the filament subsystem initially coincide with the corresponding points of the end segments of fixed size D. The myosin clusters of the fixed length are distributed randomly along the filament subsystem to maintain a constant total number m_tot of motor heads. The binding of a motor head to an actin filament is possible when a position of this head belongs to the interval determining position of the filament.

The ith filament is characterized by orientation (n(i) = ±1) of the barbed end, length L(i), and position of the ends (X(i) < Y(i)) along the straight line (Fig. S1 A). Each mth myosin cluster of the fixed size d is described by a position of its center c(m), attachment positions a(m,k) (relative to the center) of the kth motor head to the cluster, and binding position b(m,k) of every head to an actin filament. The positions a(m,k) of motor heads in the cluster are selected to have two motor heads at the end points (a(m,1) = d/2, a(m,2) = d/2), whereas the other heads are spread randomly along both ends with some characteristic distance between them in such a manner that the middle part of the cluster (the bare zone of length d₀ < d) remains devoid of motor heads (Fig. S1 B). The motor head attachment (to myosin cluster) position in the lab coordinate system is [a(m,k) + c(m)]. In the model, we assume that, irrespective of the filament orientation, the motor head cannot attach to the actin filament in such a way that the head’s attachment point to the filament is closer to the center of the cluster than the head attachment point to the cluster (mathematically, there is no attachment if [b(m,k) – (a[m,k] + c[m])] × sign(a[m,k]) < 0). Similarly, there is no attachment of the heads at the left/right end of the cluster to the ith actin filament with the barbed end at the right/left, respectively (mathematically, there is no attachment if [b(m,k) – (a[m,k] + c[m])] × sign(n[i]) < 0).

Forces and velocities

Following previous modeling studies (8, 34), we assume that the motor head is attached to the rigid backbone of myosin cluster by a linear spring with the zero rest length and spring constant κ. When attached to the ith actin filament, the kth head from the mth myosin cluster exerts a force on this filament equal to

$$F\left(m,k\right)=\kappa \left[b\left(m,k\right)-\left(a\left(m,k\right)+c\left(m\right)\right)\right],$$ (1)

providing the following condition is satisfied: the m^th cluster has at least two heads (say, k₁ and k₂) from the opposite ends of the cluster (mathematically, a(m,k₁) × a(m,k₂) < 0) bound to filaments. The position of each mth myosin cluster, provided that at least two such heads are attached to filaments, is determined by the condition that the sum of elastic forces from all attached myosin heads is equal to zero:

$$\sum _{k}F\left(m,k\right)=0,m=1\dots M.$$ (2)

If only one head on a cluster is attached to actin, the force is not generated, and this cluster translocates to the barbed end of a single filament to which it is bound with the free myosin gliding speed V_max (Fig. S1 C). Indeed, it was shown that if a myosin cluster interacts with a single actin filament, then the myosin heads facing the pointed end do not create a significant drag on the movement of the actin filament by the myosin heads facing the barbed end (37). When the number of heads is greater than two, it is possible that two, or more, heads at one end of the cluster bind different filaments, whereas there is no binding of the heads at the other end. Then, the cluster slides along several filaments.

Following previous modeling (23), we assume that dynamic cross-linking between ith and jth actin filaments causes effective friction force proportional to the filaments’ relative sliding velocity (v_i – v_j). This force is also proportional to the length of the overlap between this filament pair, A_ij, based on the assumption that there is a constant density of the cross-linking at each of the filament pair overlapping intervals. Thus, the drag force between the ith and jth actin filaments is F_ij = ζ_iA_ij(v_i – v_j), where ζ_l is the viscous drag coefficient (Fig. S1 D). We assume, similarly, that there is an effective viscous friction between the end segments and filaments overlapping with these segments proportional to the overlapping length, velocity of the filaments relative to the segments, and the viscous drag coefficient ζ_E. In the calculations, the coefficient ζ_E is of the same order of magnitude as parameter ζ_i; we vary both coefficients to understand their influence on the actin-myosin array’s mechanics. In the case of the mobile end segments (for the CU case), there is an additional effective viscous drag force between the end segment and the solid surface on which the segment can slide, ζ_E0. In the calculations, the coefficient ζ_E0 is of the same order of magnitude as parameter ζ_E; we vary these coefficients to understand their influence on the actin-myosin array’s mechanics.

The velocity V(m,k) of the myosin head attached to ith actin filament (the head has to be projected from the end of the cluster facing the barbed end) is found from the linear force-velocity relation (8, 23, 34):

$$F\left(m,k\right)=-F_{\max }\left[n\left(i\right)-\left(V\left[m,k\right]-v\left[i\right]\right)/V_{\max }\right],$$ (3)

where v(i) and n(i) indicates the filament’s velocity and polarity, respectively; F_max is the stall force; and V_max is the free myosin gliding speed. Note that there is no contradiction in the fact that both Eqs. 1 and 3 have the expression for the force on the left-hand side. Eq. 1 determines the elastic force exerted by a myosin head on an actin filament, and by Newton’s third law, the same force is applied from the filament to the head. Equation 3 is used as the force-velocity relation to compute the myosin head velocity at a given force calculated from Eq. 1. In other words, Eqs. 1 and 3 constitute the system of two equations for two variables—force and velocity. The myosin head position b(m,k) is updated at each computational step based on its movement, with rate V(m,k) calculated at each step from Eq. 3. At the moment of an initial myosin head’s attachment to an actin filament, b(m,k) = a(m,k). The linearity of the force-velocity relation is an approximation for the generally nonlinear relation observed in the experiments, but the nonlinearity for myosin is not great, and the approximation is generally believed to be adequate (8, 23, 34).

The force balance for each actin filament states that the sum of all forces exerted by all myosin motor heads bound to it is equal to the sum of all cross-linking friction forces applied to the filament:

$$\sum _{m,k}F\left(m,k\right)={\zeta }_l\sum _j{A}_{ij}\left(v_i-v_j\right)+{\zeta }_E{B}_i\left(v_i-v_e\right),i=1\dots N.$$ (4)

On the left-hand side, the summation includes all heads that are attached to the ith filament and all clusters from which these heads extend. The first term in the right-hand side describes the friction between all jth filaments overlapping with the ith filament, whereas the last term stands for the friction between the ith filament and one of the end segments having velocity v_e, if respective overlap length B_i is nonzero (v_e = 0 for SFU). For the CU, the sum of the friction forces between the end segment and the filaments overlapping it is balanced by the friction force between the segment and the surface:

$${\zeta }_E\sum _i{B}_i\left(v_i-v_e\right)={\zeta }_{E0}D{v}_e.$$ (5)

Actin filament turnover and disassembly

Instead of investigating the actin filament treadmilling that was done in Oelz et al. (23), we explore three types of actin dynamics. In the first one, the assumption is that a filament, after nucleation, elongates rapidly and then gets capped and keeps its constant length for a random time determined by processes of cooperative cofilin binding and rapid severing and disassembly (38). In this case, we neglect the short assembly and disassembly times, and so add a filament of a finite size to the array and then after a random time remove the whole filament. The average number of actin filaments is governed by

$$\frac{dN}{dt}=r_{\text{add}}-r_{\text{rem}}N,$$ (6)

which leads to the steady-state filament number N = r_add/r_rem. The rate of filament removal r_rem is constant; the rate of filament addition r_add is either kept constant or scaled with the CU length L, defined as the distance between the extreme points of the end segments, r_add(t) = r_addL(t)/L(0).

In the stochastic simulations, at each time step (duration of the step is Δt) we add a filament at random (with uniform random distribution) with probability r_addΔt and remove each existing filament with probability r_remΔt. When at any computational step no filaments overlap with one or both end segments, new filaments are added to the ends of the unit instantly. In the second type of dynamics, filaments are not added and removed, but rather shorten from the pointed end with the disassembly rate r_d. In this case, we first generate a random actin array, then, for some time interval, add, remove, and shorten filaments from the pointed ends until a steady length distribution of filaments is achieved. Only then do we switch off the filament turnover, leaving only pointed end depolymerization. Finally, in the third type of dynamics, we combine the addition, removal, and pointed end depolymerization.

Myosin clusters transport

When at least two heads of a myosin cluster generate force, the center-of-mass of the cluster is determined at each computational step by Eq. 2. If only one head on a cluster is attached to actin, this cluster translocates to the barbed end of a single filament to which it is bound with the free myosin gliding speed V_max. When all heads of a myosin cluster lose their binding to actin filaments, this cluster is assumed to diffuse and rebind rapidly and at random location in the array; in the simulations, this takes place within one computational step. The myosin head density (ρ) is in units of 1 per nanometer of actin length.

Simulation procedure

At each computational step, we solve (1), (2), (3), (4), (5), (6), as follows: 1) The velocity of each filament is calculated from the solution of the linear algebraic system of Eq. 4. 2) Each filament is shifted with the calculated velocity by distance v_iΔt. 3) All overlap lengths are recomputed. 4) Each myosin cluster is shifted to the position in which the total elastic force on the cluster is 0, according to Eq. 2. 5) Each attached myosin head is shifted to its respective barbed end by distance V(m,k)Δt, where the velocity is found from Eq. 3. 6) In the case of CU, the end segments are shifted by a distance v_eΔt, where the velocity is found from Eq. 5. 7) Each myosin cluster attached by only one head is shifted to the barbed end of the filament, to which the head is attached, as described above. 8) If any attached myosin head, at any time step, overshoots its respective barbed end, this head instantly detaches (at the next step, this head attaches to any filament at random that is available at this location such that the respective elastic force is 0, but if no such filament is available, the head remains unattached until such a filament becomes available). 9) Filaments are stochastically added and removed according to Eq. 6. 10) Unattached myosin clusters are shifted randomly and their heads “look for” attachments.

The time step duration was chosen to be short enough to avoid numerical instabilities and keep numerical errors of the Euler’s method for solving the mechanical problem below 1%. The major part of results’ variability comes from the stochastic actin turnover, not the numerical error. We made sure that reducing the time step did not change the amount of variability in the results. Simulations were performed using the software Mathematica (https://www.wolfram.com/mathematica/).

Model parameters

We gather the values of the parameters in Table S1. In the table, we marked parameters that are, and those that are not, varied between the simulations. Values of the varied parameters are described in the figure legends. The small scale of the contractile unit in the model is chosen for computational efficiency; however, it was also argued that this scale, a few microns, characterizes effective contractile units in actin-myosin networks (25). Myosin cluster length d, as well as the length of the bare zone d₀ in the middle of the cluster, were measured in the literature (39, 40, 41). The characteristic number of the myosin heads per cluster was measured to be 28 in Niederman and Pollard (41). In the model, one head corresponds to ∼20 real, physical myosin heads, because the duty ratio of myosin II is low, and out of ∼20 heads approximately one is developing a power stroke at any given time (34). Thus, two heads per cluster in the model approximately correspond to the measurement in Niederman and Pollard (41); increasing the number of heads per cluster in the simulation corresponds to a higher number of heads in muscle myosin (34). The total number of the myosin clusters $M$ and motor heads m_tot is of the same order of magnitude as that reported in Wu and Pollard (42). The motor head spring constant, κ, is of the same order of magnitude as that reported in Veigel et al. (43). The stall force F_max and free myosin gliding speed V_max were widely reported to be of the same order of magnitude as used in this article (40). Effective viscous drag coefficient ζl was not measured directly, but estimated many times based on the protein friction theory; we use the same order of magnitude for this parameter as that used previously in Oelz et al. (23). For parameters ζ_E and ζ_E0, we use the same order of magnitude as that for ζ_l. The length of the adhesive segment, D, is of the same order of magnitude as the observed size of small adhesion complexes (44).

Three measurements of the actin filament lengths in the contractile rings give values varying from hundreds of nanometers in Schizosaccharomyces pombe contractile rings to ∼100 nm in Dictyostelium cleavage furrows to tens of nanometers in the cleavage furrows of HeLa cells (45, 46, 47). In addition, the filament length in actin fibers was indirectly estimated by measuring track lengths of processive myosin motors in Tee et al. (48); this study reports hundreds of nanometers. In the simulations, we use the value $L$∼700 nm. Actin turnover time was reported to be on the order of 10 s in cytokinetic cortex (49) and stress fibers (50); we used this order of magnitude to choose the slower limit for parameter r_rem and vary this parameter to investigate the role of the actin turnover. Parameter r_add was varied proportionally to keep a sufficient number of filaments in the array (on the order of tens, to ensure that each filament overlaps with other filaments; a greater filament number slows down the simulations). Finally, the order of magnitude of the disassembly rate at pointed ends, r_d, is of the same order as that reported in the in vitro studies (51). Orders of magnitude of most of the model parameters were also discussed and used in other recent studies (8, 23, 33, 34).

Results

We first tested whether the combination of the force anisotropy in the myosin cluster with the finite size of the cluster leads to contractile force generation. To do that, we simulated the isometric SFU (Fig. 2 A), in which the actin filaments at the ends of the unit slide, with viscouslike friction, relative to the immobile adhesive segments, and recorded the generated force. Positive sign corresponds to the contractile force pulling the adhesive end segments of the SFU inward.

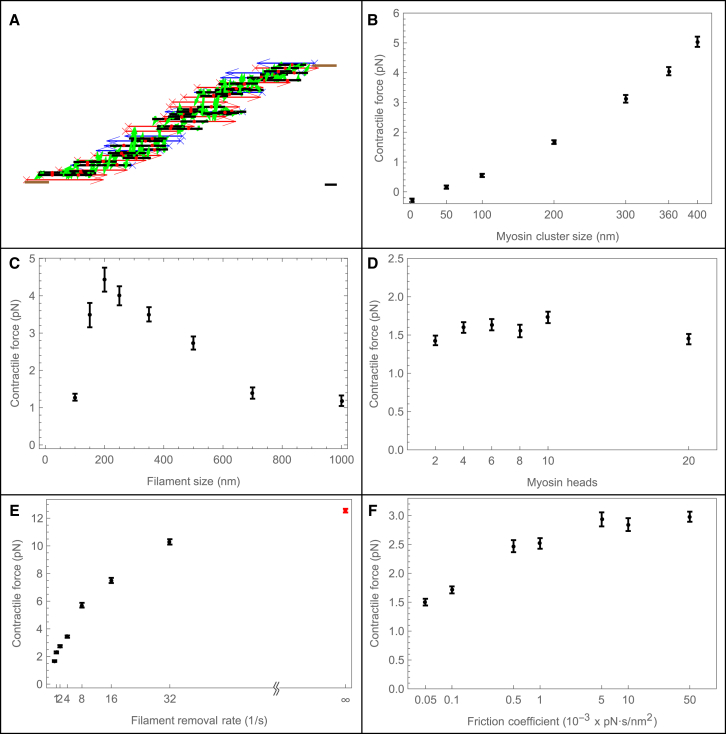
Figure 2.

Contractile force is maximized by similar myosin and actin length, high actin turnover, and high cross-linking. The basic parameter set for the simulations is: K = 2, L = 700 nm, r_add = 10 fil/s, r_rem = 0.5/s, ρ = 0.01/nm, $\overline{L}$ = 2 μm, d = 220 nm, and ζ_i = 10⁻⁴ pN × s/nm². For each parameter set, simulations were repeated 40 times; each simulation was done for 60 s of physical time. The results are shown as the mean ± SE. (A) Snapshot from the simulation of the isometric SFU, in which filaments were removed and added randomly; there was no change in filament length during the time interval of the filament existence. The arrowhead/cross is the pointed/barbed end, respectively. Blue/red arrows mark filaments with barbed ends oriented to the right/left, respectively. The adhesive end segments are shown by brown rectangles. The myosin cluster backbone is shown by a black segment; heads attached to the actin filaments are shown by green arrows pointing to the filament. Bar: 100 nm. (B) Contractile force for various sizes of myosin clusters (d = 10–400 nm). (C) Contractile force for various sizes of actin filament (L = 100–1000 nm). The SFU length was scaled with the filament size; L = 700 nm corresponded to $\overline{L}$ = 2 μm. (D) Contractile force given for various numbers of heads per myosin cluster (K = 2–20) of the fixed length. The total number of myosin heads per stress fiber is constant. (E) Contractile force is given as a function of the turnover rate. The rate of filament addition varied proportionally to the rate of removal r_rem = (0.5–16) × 1/s, so that the average number of filaments in the array was 20 in all simulations. Red marks the data corresponding to the maximally random turnover (see the text). (F) Contractile force is given as a function of the effective cross-linking drag between the actin filaments, ζ_l = (0.5–500) = 10⁻⁴ pN × s/nm². To see this figure in color, go online.

Contractile stress is maximized when myosin cluster and actin filaments lengths are similar

As expected, we found that the generated force was too small to detect when the myosin length was small, 0–50 nm, or for any myosin length without the force anisotropy in the myosin cluster. Noticeable contractile force emerged when myosin cluster length became on the order of 100 nm and increased significantly when the myosin cluster length increased to roughly half the size of the actin filament (Fig. 2 B). We expect maximal contractile force when the lengths of the actin filament and myosin cluster are similar, because in this case the centers of two antiparallel filaments converge to the same position after the myosin heads at the opposite ends of a cluster reach the barbed ends of the respective filaments (Fig. 1 B, right). On the other hand, if actin filament length is much less than that of the myosin cluster, myosin heads can slide the short filaments by no more than their lengths, and so the contractile effect would be too small. If actin filament length is much greater than that of the myosin cluster, then, as we illustrate in Fig. 1 B (left), the actin filaments are expected to be simply reshuffled (they exchange places after the myosin heads reach respective barbed ends), also leading to a small contractile effect. We confirmed this intuition by performing numerical experiments with myosin clusters of fixed size (220 nm) and varying average filament length from 100 to 1 μm. The simulations confirmed the intuition: the dependence of the average contractile force on the filament length is biphasic, growing when the filament length increases from 100 to 200–250 nm, and decreasing for longer filaments (Fig. 2 C). As expected, the maximal force is achieved with roughly similar lengths of filaments and clusters.

Contractile stress is not sensitive to the number of myosin heads per cluster

Myosin clusters are assembled from bundling together of multiple myosin molecules, so tens to hundreds of myosin heads are localized to each cluster. Therefore, we wanted to test how the contractile force depends on the number of heads per cluster (34). We ran simulations with the total number of heads m_tot = 200 conserved for the numbers of heads per cluster K = 2, 4, 10, 20 (respectively the cluster number is M = 100, 50, 20, 10). This likely corresponds to a few tens to a few hundred real, physical myosin heads per cluster. We found that the contractile force was not sensitive to the number of myosin heads per cluster (Fig. 2 D). Interestingly, the contractile force increased slightly when the number of heads per cluster increased from 2 to 4 and decreased a little when the number of heads per cluster increased from 10 to 20 (Fig. 2 D), but these changes were not statistically significant.

Contractility is maximized by actin array randomization through rapid turnover

Previous models highlighted the need for actin filament turnover and cross-linking for proper filaments self-organization and force production (23, 52). Initially random actomyosin arrays tend to become less random with time because of a positive feedback: myosin tends to aggregate toward the barbed ends, creating polarity sorting of actin filaments in space, and this emerging polarity guides more myosin to the aggregates (23). This pattern formation worsens the force generation (20) because in the pattern, myosin is biased to the barbed ends, not to the pointed ends where the contraction is effective. We tested the dependence of the contractile force on the actin turnover rate and indeed found that faster turnover, which randomizes the array, corresponds to the stronger contractile force (Fig. 2 E). In agreement with earlier models, the force is strongest when the actin array is maximally random—when all filaments undergo a maximally random turnover. (In corresponding simulations, after each computational step in which the forces were computed, all actin filaments were deleted and equal numbers of filaments were added at random positions—effectively, the filaments were reshuffled at random at each time step.)

Contractility requires cross-linking

A certain amount of cross-linking is necessary for actomyosin contraction (8, 21, 23, 24, 52), and from theoretical consideration, lower friction between filaments dampens the contractile force (23) for two reasons: 1) faster sliding of filaments diminishes the force per myosin head due to the myosin force-velocity relation; and 2) faster sliding of filaments leads to faster polarity sorting and pattern formation, which also attenuates the force. Expectedly, we found that contractile force is an increasing function of the effective cross-linking drag coefficient; at large values of the drag, the force saturates to a constant (Fig. 2 E). We also found that at very low friction, the filaments slide so fast that gaps in the actin array develop, at which point the contractile unit becomes disconnected. We also varied the friction between the filaments at the actin array’s edges and the immobile adhesive segments, and found that the centripetal velocities of the actin filaments are not sensitive to the segments’ adhesiveness. The reason is that the combined internal forces in the actin-myosin array are much greater than the boundary forces. The resulting contractile force, which is the product of the centripetal velocities of the actin filaments and the segments’ adhesive strength, scales with the friction coefficient between the filaments and adhesive segments. For example, when parameter ζ_E was decreased twice from ζ_E = 2ζ_l to ζ_E = ζ_l, the contractile force decreased from 1.63±0.07 pN (mean±SE for 40 runs) to 0.90±0.04 pN (mean±SE for 40 runs).

Actin disassembly promotes effective contraction of the random actomyosin array

So far, we described simulations of the contractile stress generation in the isometric SFU. We turn now to investigating myosin-powered shortening of the CU. The difference between SFU and CU is that in the former, the adhesive segments at the end of the contractile array are immobile, and in the latter, the adhesive segments are able to slide against effective viscous drag (Fig. S1; Methods). Considering that experimental data points out that actomyosin structures in cells consist of semiautonomous contractile modules (36), one possible assumption would be that some contractile rings consist of such contractile units in series, with the “adhesive segments” shared between ends of the adjacent contractile units and in physical contact with cell cortex (Fig. 1 E). The contraction rate of the unit would then determine the contraction rate of the whole ring.

The contraction rate of the cytokinetic ring has been actively researched recently in a number of experimental studies using model systems from fission yeast, to Caenorhabditis elegans, to filamentous fungus Neurospora crassa. These studies established that actin and myosin are turning over in cytokinetic rings (21, 35, 42, 53). In fission yeast, it was found that actin filaments shorten as the ring contracts (46), whereas in C. elegans embryos the width and the thickness of the constriction ring remain constant during contraction (35), also implying that there is a net actin disassembly in the ring.

To find out conditions under which a random actin-myosin array can robustly and steadily shorten, we first simulated the CU without any actin dynamics, with neither removal/addition of the filaments nor pointed end depolymerization. This did not result in a significant contraction: in a sample simulation shown in Fig. S1 A, the CU contracted <10%, and then started to expand. Multiple simulations showed also that any movement stopped soon after initialization because the array became disconnected; there was usually as much expansion as contraction due to filament polarity sorting. Similar conclusions were reached earlier in Vavylonis et al. (52).

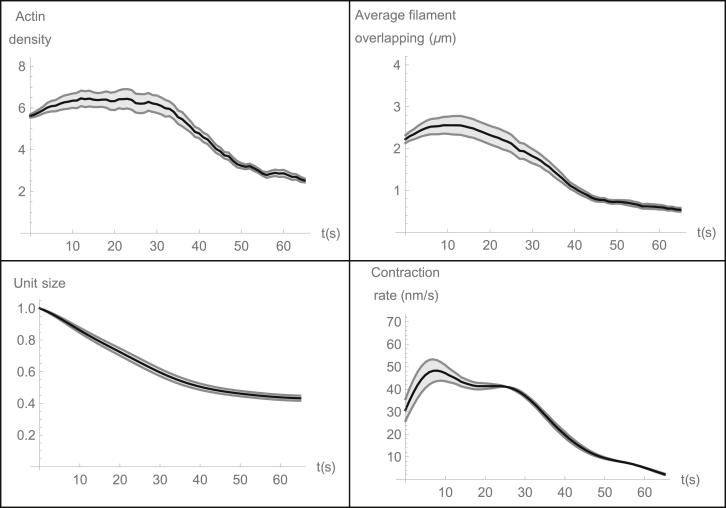
Then, we introduced pointed end depolymerization, while keeping removal/addition of the filaments switched off, and observed the sustained CU contraction (Fig. 3). In the course of the contraction, the actin and myosin densities, as well as the total actin overlap length, first increased slightly, and then decreased. The rate of contraction started from being significant and peaked very soon after initialization. In the middle of contraction, the rate of contraction plateaued, and then started to decline because of the polarity sorting pattern formation. In the simulations, the CUs contracted to ∼40% of their initial length. The reason is that in the simulations the contraction stopped when the array became short enough to be just approximately two filaments long, and we started the simulations when the CU is five filaments long. We tested how far would the contraction proceed in CUs with longer initial length (and proportionally higher initial number of filaments). The longest simulations, corresponding to the initial CU length ∼7 μm, proceeded until the final length was approximately two filaments long, so the simulation reproduces the contraction to ∼20% of the initial length, similar to the observations in C. elegans embryo (37). Note also that we increased the average number of the actin filaments in the cross section of the array (and respective number of the myosin clusters) 2–3-fold, and found that the contraction proceeded with similar rates.

Figure 3.

Actin disassembly promotes effective contraction of the random actomyosin array. In all cases, actin density, average total length of filaments’ overlap, CU length, and contraction rate are shown as functions of time; CU length is normalized to the initial length $\overline{L}$ = 3.5 μm. Myosin density is proportional to the actin density and not shown. In the simulations, the initial actin filament size is L = 700 nm, d = 220 nm, K = 6, ζ_l = 10⁻⁴ pN × s/nm²; ρ = 0.01/nm, r_d = 15 nm/s. Actin density is in units of total filament length divided by the CU length. Before the SFU simulation starts, the contractile unit without length change undergoes filament turnover and pointed end depolymerization for some time to achieve a characteristic random equilibrium state. After that, the end segments can slide, and there is no addition/removal of the filaments. For each parameter set, simulations were repeated 15 times; each simulation was done for 65 s of physical time. Solid curves are for the average, shaded curves are for average mean ± SE.

We varied the depolymerization rate a few-fold and found, expectedly, that slower depolymerization led to slower contraction. For many parameter choices, in the middle of contraction, the rate of contraction plateaued. The rate of contraction was proportional to the depolymerization rate if the viscous drag coefficient was simultaneously graded inversely proportionally to the depolymerization rate. When the depolymerization rate became too fast (twice higher than the base rate in the simulations reported in Fig. 3), we observed steady contraction at first, which, however, stopped short (Fig. S2 B), because in this case a hole appeared in the actin array, and the array became disconnected (Fig. S2 C).

The contraction rate was observed to remain approximately constant during most of the contraction process in a number of experimental systems (21, 35, 42, 53). However, recent measurements of the contraction rate in cytokinetic ring in C. elegans embryos showed, in fact, that the contraction rate was more or less constant only for a short time in the middle of the contraction process, whereas in the beginning of the contraction the rate increased, and then decreased steadily in the second half of the process (37) (Fig. S3), closely resembling the prediction from the model simulations (Fig. 3). Indeed, consider that our model predicts that the characteristic contraction timescale is inversely proportional to the pointed end depolymerization rate, and take into account that the rate of shortening of a chain of CUs connected in series (as depicted in Fig. 1 E) is proportional to the number of the CUs in this chain. Then, if we connect 30 CUs, 2-μm-long each, in series into a 60-μm-long ring (approximately the same as the cytokinetic ring’s length in C. elegans embryo (37)), decrease the pointed end depolymerization rate fivefold and increase the viscous drag coefficient fivefold, the model predicts the contraction rate as a function of time that is a very good approximation to the observation in C. elegans embryo (Fig. S3). Note that in the simulations the contraction stopped when the ring contracted to ∼40% of its initial length, whereas in the experiment the ring contracted to ∼20% of its initial length, so we are not claiming an accurate fit to the data. Mechanics of the C. elegans cytokinetic ring, no doubt, has features much more complex than what our simple model can accommodate. Rather, the goodness of the fit reflects on the qualitative validity of the model.

We also explored two cases: 1) the pointed end depolymerization is switched off, but the filaments are removed at a constant rate and added with addition rate scaled as current CU length; and 2) the removal/addition of the filaments is combined with the pointed end actin depolymerization. Simulations revealed the robust CU contraction in these cases with kinetics similar to those in the case with the pointed end depolymerization and without removal/addition of the filaments. In all these simulations, we kept the constant density of myosin clusters/heads, proportional to the actin density, based on the observations reporting a constant myosin linear density in C. elegans and budding yeast (21, 35). However, in fission yeast and filamentous fungus, total myosin pool is retained during cytokinesis, resulting in an increase of its concentration as the actin-myosin ring contracts (42, 53). We repeated model simulations by changing the conditions for myosin, namely, keeping the total myosin pool constant. We also checked what happens if the rate of addition of the actin filaments is constant, not scaled by the shortening CU length. We found that in both cases, changes in the contraction rate were very slight. We also varied effective friction between the filaments at the CU ends and the adhesive segments, and between the segments and the surface, and found that the contractile rate is insensitive to the values of the friction in wide ranges, because internal cross-linking resistance in the CU is the dominant factor balancing the contraction. All this indicates the robustness of the proposed contraction mechanism.

Discussion

In this study, we explored computationally the idea that the force anisotropy of the myosin heads at two opposite ends of the myosin cluster, together with the cluster’s finite length, can generate contraction in a 1D dynamic random actin array. A similar hypothesis was proposed in (32) to justify the assumptions of a continuous model of contraction, but the effect of the finite myosin length and other mechanical and kinetic parameters were not investigated in(32) in microscopic simulations. The idea that the myosin finite size can be crucial in generating contraction in 2D has been proposed in (25). We demonstrated that if average lengths of the actin filaments and the myosin clusters are similar, then myosin clusters, on average, pull antiparallel filaments closer together (Fig. 1 B), and the contractile force becomes significant. The measurements of the actin filament lengths in the contractile rings in S. pombe, Dictyostelium, and HeLa cells, indeed, reported filament lengths in the range of hundreds of nanometers (45, 46, 47), similar to the myosin cluster length (34). This generates a nontrivial prediction for the future experiments with 1D contractile arrays if the actin filament lengths can be measured and controlled.

In a way, the mechanism we propose belongs to the class of models that posit self-organization of mini-sarcomeres in the random actomyosin array. Indeed, the force anisotropy in conjunction with the finite cluster size favors force- and movement generations for microscopic actomyosin structures that have the sarcomere-like configuration, but the specific mechanism of this self-organization that we propose is different from the previous models. Mechanical effectiveness of the contraction mechanism proposed in this study can be estimated as follows. In the simulations that were done to produce Fig. 2 D of this study, ∼25 actin filaments 0.7-μm long each constituted the 3.5-μm-long actin array. If these filaments were distributed in a perfect alternating polarity array, there would be effectively ∼3 mini-sarcomere-like structures in series. If ∼200 myosin heads used in the simulations were distributed uniformly, and no force was lost to the effective viscous drag, then (200/2)/3 ∼35 myosin heads in parallel would contract each effective mini-sarcomere in each direction, so the net contractile force would be ∼35 pN. The predicted force is ∼5 pN, so the proposed mechanism utilizes ∼15% of the maximal possible force, which is a reasonable efficiency. The rest is lost due to nonoptimal actin array architecture, nonhomogeneity of myosin distribution, and cross-linking viscous dissipation. In fact, for the maximally fast actin turnover, we predict the force as high as ∼12.5 pN (Fig. 2 E). Respective efficiency ∼30% is probably as high as possible in random arrays.

Our model shows, in agreement with previous results (52, 54), that a sufficient cross-linking and actin turnover and/or depolymerization improves the force generation and shortening of actomyosin units. The force generation in the model is insensitive to the number of myosin heads per myosin cluster. We found that the model predicts the contraction rate that behaves in time similarly to the measured contraction rate in the C. elegans contractile ring (36). We emphasize that the actin dynamics per se is not necessary for the contraction in the mechanism that we consider, unlike in some previous models (16, 23). The actin turnover is necessary for randomizing the actin array, without which the pattern formation and actin polarity sorting ensues and dampens the contraction. Many actomyosin structures do indeed require cytoskeletal turnover, but some, such as the rings isolated from fission yeast protoplasts, constrict without turnover of ring components (55), so obviously cells are able to deploy multiple mechanisms of the force generation.

Our model, of course, does not deal with the tremendous complexity of the actin-myosin interactions and multiple mechanisms of cytokinesis (14). We did not consider actual mechanochemical cycles, complex microscopic geometry, and collective effects of multiple myosin heads interacting with actin filament (34, 56) or mechanosensing phenomena (34, 57). We did not take into account elastic and thermal fluctuation mechanics in actin networks (58), interactions of the actomyosin arrays with curved cell surfaces (32), delicate aspects of architecture and connectivity in actin networks (8), nonlinear mechanical properties of actin network, or of myosin kinetics and mechanics (24, 34, 59). Similarly, we did not simulate stereospecific aggregation of the myosin clusters in stress fibers reported in one recent study (60). Above all, we did not yet expand the agent-based model to 2D and 3D networks, where effects of filament alignment are predicted to change the contraction mechanics drastically (61, 62). The model’s simplicity has one simple purpose: to illustrate that the force anisotropy and finite myosin length generate contractility of 1D random arrays of short actin filaments even in the absence of more complex mechanisms. At this point, experimental evidence is insufficient to definitively identify microscopic mechanisms of the actomyosin contraction in disordered cytoskeletal arrays; therefore, it is important to use theory to make an inventory of all such possible mechanisms. Our model adds one more hypothetic mechanism to this growing inventory.

Conclusions

Effective contraction is developed in 1D random actin-myosin arrays, providing anisotropy of force generation and finite length of myosin clusters. Specifically, the anisotropy means that myosin heads extending outward from the myosin cluster center generate a significant pulling force, whereas heads that are walking inward to the cluster center exert a weak pushing force. The contractile force is significant if lengths of the myosin clusters and actin filaments are similar, if cross-linking is sufficient, and if actin turnover randomizes the actin array.

Author Contributions

B.Y.R. and A.M. designed research, analyzed data, and wrote the article. B.Y.R. performed research and contributed analytic tools.

Editor: David Odde.