Abstract
In many important cellular processes, including mRNA translation, gene transcription, phosphotransfer, and intracellular transport, biological “particles” move along some kind of “tracks”. The motion of these particles can be modeled as a one-dimensional movement along an ordered sequence of sites. The biological particles (e.g., ribosomes or RNAPs) have volume and cannot surpass one another. In some cases, there is a preferred direction of movement along the track, but in general the movement may be bidirectional, and furthermore the particles may attach or detach from various regions along the tracks. We derive a new deterministic mathematical model for such transport phenomena that may be interpreted as a dynamic mean-field approximation of an important model from mechanical statistics called the asymmetric simple exclusion process (ASEP) with Langmuir kinetics. Using tools from the theory of monotone dynamical systems and contraction theory we show that the model admits a unique steady-state, and that every solution converges to this steady-state. Furthermore, we show that the model entrains (or phase locks) to periodic excitations in any of its forward, backward, attachment, or detachment rates. We demonstrate an application of this phenomenological transport model for analyzing ribosome drop off in mRNA translation.
Introduction
Movement is essential for cell function. Cargoes like organelles and vesicles must be carried between different locations in the cells. The information encoded in DNA and mRNA molecules must be decoded by “biological machines” (RNA polymerases and ribosomes) that move along these molecules sequentially.
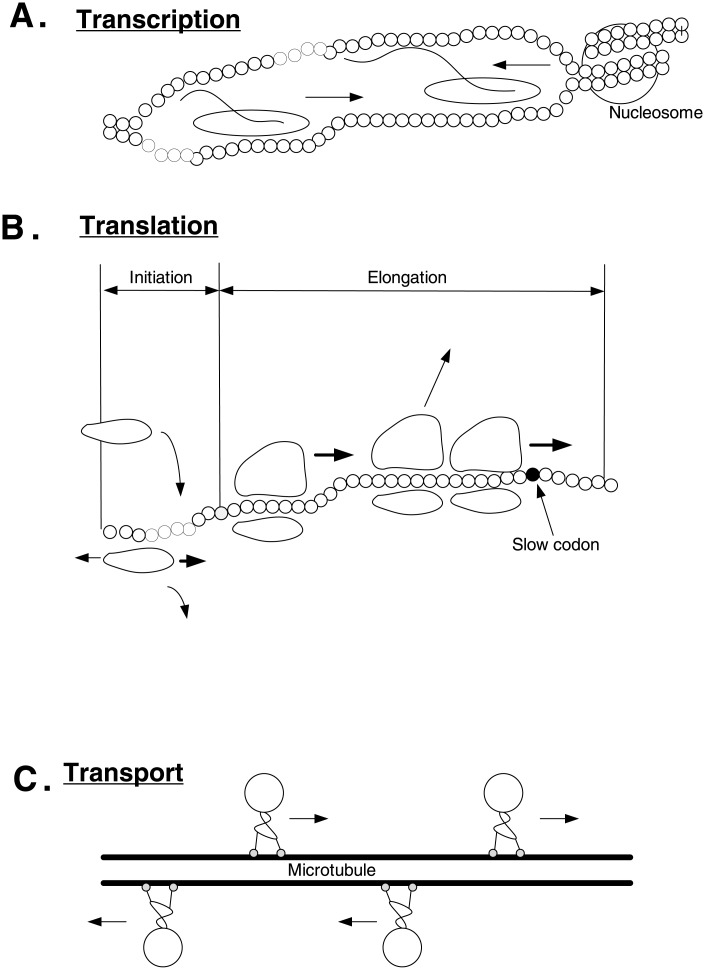
Many of these important biological transport processes are modeled as the movement of particles along an ordered chain of sites. In the context of intracellular transport, the particles are motor proteins and the chain models actin filaments or microtubules. In transcription, the particles are RNAPs moving along the DNA molecule, and in translation the particles are ribosomes moving along the mRNA molecule (see Fig 1).
Fig 1. Biological processes that can be studied using the model derived in this paper.
A—transcription of a DNA gene into messenger RNA (mRNA) by RNA polymerase. B—mRNA translation by macromolecules called ribosomes. C—intracellular transport by motor proteins.
The movement in such processes may be unidirectional, as in mRNA translation elongation, or bidirectional, as in transcription or translation initiation. Indeed, the normal forward flow of the RNAP may be interrupted, due to transcription errors and various obstacles such as nucleosomes, in which case the RNAP tracks back a few nucleotides and then resumes its normal forward flow [1–4]. Translation initiation in eukaryotes usually includes diffusion from the 5’end of the transcript towards the start codon [5]. This diffusion process is believed to be bidirectional, but with a preference to the 5’→3’ direction. The movement of motor proteins like kinesin and dynein along microtubules is typically unidirectional, but can be bidirectional as well [5].
To increase efficiency, many particles may move simultaneously along the same track thus pipelining the production process. For example, to increase translation yield, a number of ribosomes may act simultaneously as polymerases on the same mRNA molecule [6, 7].
The moving biological particles have volume and usually cannot overtake a particle in front of them. This means that a slowly moving particle may lead to the formation of a traffic jam behind it. For example, Leduc et al. [8] have studied Kip3, a yeast kinesin-8 family motor, and demonstrated that motor protein traffic jams can exist, given the right conditions. Other studies have suggested that traffic jams of RNAP [ribosomes] may evolve during transcription [translation] [7, 9, 10].
In some of these biological transport processes the biological machines may either attach or detach at various sites along the tracks. For example, ribosomes may detach from the mRNA molecule before reaching the stop codon due to traffic jams and ribosome-ribosome interactions or due to depletion in the concentration of tRNAs [11–13]. Also, it is known that kinesin-family motor proteins are more susceptible to dissociation when their path is blocked [14, 15]. Defects in these transport processes may lead to severe diseases or may even be lethal. For example, [16] lists the implications of malfunctions of protein motors in disease and developmental defects.
Developing a better understanding of these dynamical biological processes by combining mathematical modeling and biological experiments will have far reaching implications to basic science in fields such as molecular evolution and functional genomics, as well as applications in synthetic biology, biotechnology, human health, and more. Mathematical or computational modeling is especially important in developing approaches for manipulating and controlling these processes, e.g. in order to optimize various goals in biotechnology.
A standard model for such transport processes is the asymmetric simple exclusion process (ASEP) [17, 18]. This is a stochastic model describing particles that hop along an ordered lattice of sites. Each site can be either empty or occupied by a single particle, and a particle can only hop to an empty site. This simple exclusion principle represents the fact that the particles have volume and cannot overtake one another. Simple exclusion generates an indirect coupling between the particles. In particular, traffic jams may develop behind a slow-moving particle.
The motion is bidirectional i.e. a particle may hop to any of the two neighboring sites (but only if they are free) and asymmetric, that is, there may be a preferred direction of motion. Typically, a particle can attach to the lattice in one of its ends and detach from the other end. When particles can also attach or detach at internal sites along the lattice, the model is referred to as ASEP with Langmuir kinetics. In the special case where the hops are unidirectional, ASEP is sometimes referred to as the totally asymmetric simple exclusion process (TASEP). A TASEP-like system with Langmuir kinetics has been used to model limit order markets in [19], and is often used in modeling molecular motor traffic [20–24]. For TASEP with open boundary conditions (i.e. when the two sides of the lattice are connected to two particle reservoirs, as assumed in this paper) and with Langmuir kinetics, no exact solutions are known. The phase diagram and the shock formation of the homogeneous TASEP (i.e. where all the internal hopping rates are assumed to be equal) with Langmuir kinetics in the thermodynamical limit, that is as the number of lattice sites goes to infinity, was analyzed in [20, 21, 25] using a mean-field approximation. It was shown that the phase diagram is much richer than that of TASEP because phase coexistence becomes possible due to the Langmuir kinetics. Homogeneous TASEP with periodic boundary conditions (i.e. when the lattice forms a ring) and with Langmuir kinetics was analyzed in [24–26].
More generally, ASEP has become a fundamental model in non-equilibrium statistical mechanics, and has been applied to model numerous natural and artificial processes including traffic and pedestrian flow, the movement of ants, evacuation dynamics, and more [27].
In this paper, we introduce a deterministic mathematical model that may be interpreted as a dynamic mean-field approximation of ASEP with Langmuir kinetics (MFALK) [25]. We analyze the MFALK using tools from systems and control theory. In particular, we apply some recent developments in contraction theory to prove that the model is globally asymptotically stable, and that it entrains to periodic excitations in the transition/attachment/detachment rates. In other words, if these rates change periodically in time with some common period T then all the state-variables in the MFALK converge to a periodic solution with period T. This is important because many biological processes are excited by periodic signals (e.g. the 24h solar day or the periodic cell-division process), and proper functioning requires phase-locking or entrainment to these excitations.
Our work is motivated by the analysis of a model for mRNA translation called the ribosome flow model (RFM) [28]. This is a mean-field approximation of the unidirectional TASEP without Langmuir kinetics (see, e.g., section 4.9.7 in [27] and p. R345 in [29]). Recently, the RFM has been studied extensively using tools from systems and control theory [30–40]. The analysis is motivated by implications to many important biological questions. For example, the sensitivity of the protein production rate to the initiation and elongation rates along the mRNA molecule [36], maximization of protein production rate [35], the effect of ribosome recycling [33, 37], and the consequences of competition for ribosomes on large-scale simultaneous mRNA translation in the cell [41] (see also [42, 43] for some related models).
The MFALK presented here is much more general than the RFM, and can thus be used to model and analyze many transport phenomena, including all the biological processes mentioned above, that cannot be captured using the RFM. We demonstrate this by using the MFALK to model and analyze mRNA translation with ribosome drop off—an important feature that cannot be modeled using the RFM.
Ribosome drop off is a fundamental phenomena that has received considerable attention (see, e.g., [12, 13, 44–51]). In many cases, ribosome drop off is deleterious to the cell since translation is the most energetically consuming process in the cell and, furthermore, drop off yields truncated, non-functional proteins. Thus, transcripts undergo selection to minimize drop off or its energetic cost [12, 48, 49, 51–53]. There are various hypotheses on the biological advantages of ribosome drop off. For example, Zaher and Green [54] have suggested that ribosome drop off is related to proof reading. One may perhaps expect that another advantage is that drop off from a jammed site may increase the total flow by reducing congestion. Our analysis of the MFALK shows that this is not true. Drop off has a substantial effect on the flow, yet it always leads to a reduction in the steady-state protein production rate.
The remainder of this paper is organized as follows. The next section describes the new mathematical model. Section 2 presents our main analysis results. Section 3 describes the application of the MFALK to model mRNA translation with ribosome drop off. The final section concludes and describes possible directions for further research. To streamline the presentation, all the proofs are placed in the S1 File.
1 The model
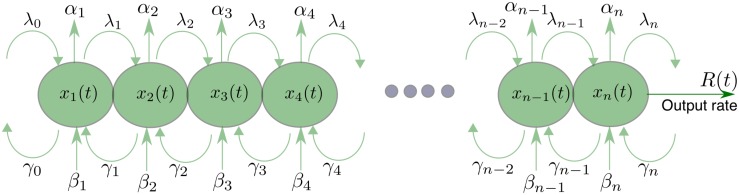
The MFALK is a set of n first-order nonlinear differential equations, where n denotes the number of compartments or sites along the track. Each site is associated with a state variable xi(t) ∈ [0, 1] describing the normalized “level of occupancy” (or density) at site i at time t, with xi(t) = 0 [xi(t) = 1] representing that site i is completely free [full] at time t. Since xi(t) ∈ [0, 1] for all t, it may also be interpreted as the probability that site i is occupied at time t.
The MFALK contains four sets of non-negative parameters:
λi, i = 0, …, n, controls the forward transition rate from site i to site i + 1,
γi, i = 0, …, n, controls the backward transition rate from site i + 1 to site i,
βi, i = 1, …, n, controls the attachment rate to site i,
αi, i = 1, …, n, controls the detachment rate from site i,
where we arbitrarily refer to left-to-right flow along the chain as forward flow, and to flow in the other direction as backward flow. Each parameter λi, γi, αi and βi has units of 1/time.
The dynamical equations describing the MFALK are:
| (1) |
To explain these equations, consider for example the equation for the change in the occupancy in site 2, namely,
The term λ1x1(1 − x2) represents the flow from site 1 to site 2. This increases with the occupancy in site 1, and decreases with the occupancy in site 2. In particular, this term becomes zero when x2 = 1, i.e. when site 2 is completely full. This is a “soft” version of the hard exclusion principle in ASEP: the effective entry rate into a site decreases as it becomes fuller. Note that the constant λ1 ≥ 0 describes the maximal possible transition rate from site 1 to site 2. Similarly, the term λ2x2(1 − x3) represents the flow from site 2 to site 3. The term γ2x3(1 − x2) [γ1x2(1 − x1)] represents the backward flow from site 3 to site 2 [site 2 to site 1]. Note that these terms also model soft exclusion. The term β2(1 − x2) represents attachment of particles from the environment to site 2, whereas α2x2 represents detachment of particles from site 2 to the environment (see Fig 2). The other equations can be explained similarly.
Fig 2. Topology of the MFALK.
The state variable xi(t) ∈ [0, 1] describes the density of site i at time t. The parameter λi [γi] controls the transition rate from site i [i + 1] to site i + 1 [i]. The parameter αi [βi] controls the detachment [attachment] rate from [to] site i. R(t) denotes the output rate at time t.
The MFALK is a compartmental model [55, 56], as every state-variable describes the occupancy in a compartment (e.g., a site along the mRNA, gene, microtubule), and the dynamical equations describe the flow between these compartments and also with the environment. Compartmental models play an important role in pharmacokinetics, enzyme kinetics, basic nutritional processes, cellular growth, and pathological processes, such as tumourigenesis and atherosclerosis (see, e.g., [55, 57] and the references therein). More specifically, the MFALK is a nonlinear tridiagonal compartmental model, as every directly depends on xi−1, xi, and xi+1 only.
Note also that
| (2) |
The term on the right-hand side of the first [second] line here represents the change in x0 [xn] due to the flow between the environment and site 1 [site n], whereas the term on the third line represents the flow between internal sites and the environment.
The output rate from site n at time t is the total flow from this site to the environment:
| (3) |
Note that R(t) may be positive, zero, or negative.
In the particular case where αi = βi = γi = 0 for all i the MFALK becomes the RFM, i.e. a dynamic mean-field approximation of the unidirectional TASEP with open boundary conditions and without Langmuir kinetics.
Let x(t, a) denote the solution of Eq (1) at time t ≥ 0 for the initial condition x(0) = a. Since the state-variables correspond to normalized occupancy levels, we always assume that a belongs to the closed n-dimensional unit cube:
Let int(Cn) denote the interior of Cn, and let ∂Cn denote the boundary of Cn. The next section analyzes the MFALK defined in Eq (1).
2 Main results
For notational convenience, let α0 ≔ 0, γ0 ≔ 0, αn+1 ≔ 0, and βn+1 ≔ 0. Recall that all the proofs are placed in S1 File.
2.1 Invariance and persistence
It is straightforward to show that Cn is an invariant set for the dynamics of the MFALK, that is, if a ∈ Cn then x(t, a) ∈ Cn for all t ≥ 0. The following result shows that a stronger property holds.
Proposition 1 Suppose that at least one of the following two conditions holds:
| (4) |
or
| (5) |
Then for any τ > 0 there exists d = d(τ) ∈ (0, 1/2] such that
| (6) |
for all a ∈ Cn, all i ∈ {1, …, n}, and all t ≥ 0.
This means in particular that trajectories that emanate from the boundary of Cn “immediately” enter Cn, and also that every occupancy is “immediately” uniformly separated from zero and from one. This result is useful because as we will see below on the boundary of Cn the MFALK loses some important properties. For example, the Jacobian matrix of the dynamics Eq (1) is irreducible on int(Cn), but becomes reducible at some points on the boundary of Cn.
2.2 Contraction
Differential analysis and in particular contraction theory proved to be a powerful tool for analyzing nonlinear dynamical systems. In a contractive system, trajectories that emanate from different initial conditions contract to each other at an exponential rate [58–60]. Let denote the L1 norm, i.e. for , |z|1 = |z1| + ⋯ + |zn|.
Proposition 2 Let
Note that η ≤ 0. For any a, b ∈ Cn and any t ≥ 0,
| (7) |
This means the following. Consider two ribosomal densities a, b ∈ Cn. Define the distance between densities using the L1 distance: |a − b|1 = |a1 − b1| + ⋯ + |an − bn|, i.e. the sum of the absolute differences at each site. Consider two time evolutions of the MFALK x(t, a) and x(t, b), i.e. the solution at time t when initialized with x(0) = a and with x(0) = b. Then the difference between x(t, a) and x(t, b) decreases with time with an exponential rate η. Thus, as time progresses the MFALK “quickly forgets” the initial condition and, as we will see below, the density always converges to the same steady-state density.
The value η depends on the MFALK parameters and increasing all the sums αi + βi, i = 1, …, n, makes the system “more contractive”. Indeed, these parameters have a direct stabilizing effect on the dynamics of site i, whereas the other parameters affect the site indirectly via the coupling to the two adjacent sites.
When η = 0, Eq (7) only implies that the L1 distance between trajectories does not increase. This is not strong enough to prove the asymptotic properties described in the subsections below. Indeed, in this case it is possible that the MFALK will not be contractive with respect to any fixed norm. Fortunately, a certain generalization of contraction turns out to hold in this case.
Consider the time-varying dynamical system
| (8) |
whose trajectories evolve on a compact and convex set . Let x(t, t0, a) denote the solution of Eq (8) at time t for the initial condition x(t0) = a. System (8) is said to be contractive after a small overshoot (SO) [61] on Ω with respect to (w.r.t.) a norm if for any ε > 0 there exists ℓ = ℓ(ε) > 0 such that
for all a, b ∈ Ω and all t ≥ t0 ≥ 0. Intuitively speaking, this means contraction with an exponential rate, but with an arbitrarily small overshoot of 1 + ε. The next result shows that the MFALK satisfies this generalization of contraction.
Proposition 3 Suppose that
| (9) |
and that at least one of the two conditions (4) and (5) holds. Then the MFALK is SO on Cn w.r.t. the L1 norm, that is, for any ε > 0 there exists ℓ = ℓ(ε) > 0 such that
| (10) |
for all a, b ∈ Cn and all t ≥ 0.
Note that if λi + γi = 0 for some i ∈ {1, …, n − 1}, that is λi = γi = 0, then the MFALK decouples into two separate MFALKs: one containing sites 1, …, i, and the other containing sites i+1, …, n. Thus, assuming Eq (9) incurs no loss of generality.
There is an important difference between Propositions 2 and 3. If η < 0 then Proposition 2 provides an explicit exponential contraction rate. If η = 0 then Proposition 3 can be used to deduce SO, but in this result the contraction rate ℓ depends on ε and is not given explicitly.
The contraction results above imply that the MFALK satisfies several important and useful asymptotic properties. These are described in the following subsections.
2.3 Global asymptotic stability
Since the compact and convex set Cn is an invariant set of the dynamics, it contains a steady-state point e. By Proposition 1, e ∈ int(Cn). Applying Eq (10) with b = e yields the following result.
Corollary 1 Suppose that the conditions in Proposition 3 hold. Then the MFALK admits a unique steady-state e ∈ int(Cn) that is globally asymptotically stable, i.e. limt → ∞ x(t, a) = e, for all a ∈ Cn.
This means that the rates determine a unique density profile along the lattice, and that all trajectories emanating from different initial conditions in Cn asymptotically converge to this density. Thus, any set of rate values λi, γi, αi, and βi is associated with a unique steady-state density and any solution of the MFALK converges to this density, regardless of the initial density. In addition, perturbations in the occupancy levels along the sites will not change this asymptotic behavior of the dynamics. This also means that various numerical solvers of ODEs will work well for the MFALK (see e.g. [62]).
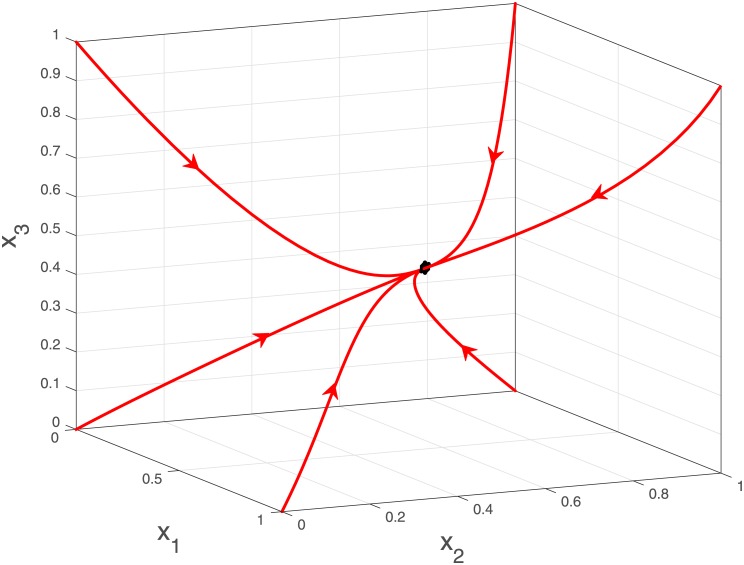
Example 1 Fig 3 depicts the trajectories of a MFALK with n = 3, λ0 = 1.0, λ1 = 1.2, λ2 = 0.8, λ3 = 0.9, γi = λi − 0.3, i = 0, …, 3, α1 = 0, α2 = 0.1, α3 = 0, β1 = 0, β2 = 0.2, β3 = 0, for six initial conditions in Cn. It may be seen that all trajectories converge to the same steady-state e ∈ int(C3).
Fig 3. Trajectories of the MFALK in Example 1 for six initial conditions in C3.
The MFALK Eq (1) can be written as
| (11) |
where
| (12) |
At steady-state, i.e. for x = e, the left-hand side of all the equations in Eq (11) is zero, so
| (13) |
Let denote the vector of parameters of the MFALK. It follows from Eq (13) that if we multiply all these parameters by c > 0 then e will not change, that is, e(cv) = e(v). Let
| (14) |
denote the steady-state output rate. Then R(cv) = cR(v), for all c > 0, that is, the steady-state production rate is homogeneous of order one w.r.t. the parameters. By Eq (13),
| (15) |
This yields the following set of recursive equations relating the steady-state occupancy levels and output rate in the MFALK:
| (16) |
For a given v, this is a set of n + 1 equations in the n + 1 unknowns: e1, …, en, R.
Example 2 Consider the MFALK with dimension n = 2. Then Eq (16) becomes
| (17) |
This yields the polynomial equation a2R2 + a1R + a0 = 0, where
with z1 ≔ λ0 + γ0 + α1 + β1 and z2 ≔ λ2 + γ2 + α2 + β2.
The polynomial equation admits several solutions for R, but only one solution corresponds to the unique steady-state e ∈ C2. For example, for λi = 1, γi = 2, βi = 3, and αi = 4 for all i the polynomial equation becomes −R2 − 131R − 40 = 0. This admits two solutions R1 ≔ (−3s − 131)/2 and R2 ≔ (3s − 131)/2, with . Substituting R1 in Eq (17) yields e = [e1 e2]′, with e2 < 0, so this is not a feasible solution. Substituting R2 in Eq (17) yields (all numbers are to four digit accuracy) e = [0.4305 0.4695]′ ∈ C2, which is the unique feasible solution. Thus, the steady-state output rate is R2 = −0.3046.
In general, Eq (16) can be transformed into a polynomial equation for R. The next result shows that the degree of this polynomial equation grows quickly with n.
Proposition 4 Consider the MFALK with dimension n and with λi ≠ γi, αi ≠ 0, βi ≠ 0, for all i. Then generically Eq (16) may be written as w(R) = 0, where w is a polynomial of degree , and with coefficients that are algebraic functions of the rates.
We note that this exponential increase in the degree of the polynomial equation is a feature of the MFALK that does not take place in the RFM. Indeed, in the RFM the degree of the polynomial equation for the steady-state production rate grows linearly with n.
Let denote the sign function, i.e.
An interesting question is how does sgn(R) depend on the parameters. Indeed, if R > 0 [R < 0] then there is a net steady-state flow from left to right [right to left]. The next subsection describes a special case where this question can be answered rigorously.
2.3.1 Bidirectional flow with no Langmuir kinetics
When βi = αi = 0, i = 1, …, n, i.e. a system with no internal attachments and detachments, Eq (15) becomes
| (18) |
Proposition 5 Consider the case where αi = βi = 0, i = 1, …, n, and suppose that Eq (9) holds. Then
| (19) |
In particular, if then R = 0, and for any i,
| (20) |
Eq (19) means that in the case of no Langmuir kinetics the steady-state output from the right hand-side of the chain will be positive [negative] if the product of the forward rates is larger [smaller] than the product of the backward rates. In transcription and translation the steady-state flow from the right hand-side of the chain should always be positive, but in other cases, e.g. transport along microtubules, the steady state flow may be either positive or negative.
Eq (20) is also quite intuitive. It considers the case of no Langmuir kinetics and when the product of all the forward rates equals the product of all the backward rates, i.e. . In this case the steady-state flow is zero, and the steady-state density at site i is the product of all the forward rates up to i, that is, λ0λ1 … λi−1 normalized by the sum of two terms: the product of all the forward rates up to i and the product of all the backward rates up to i.
2.4 Entrainment
Assume now that some or all the rates are time-varying periodic functions with the same period T. This may be interpreted as a periodic excitation feeding the MFALK. Many biological processes are affected by such excitations due for example to the periodic 24h solar day or the periodic cell-cycle division process. For example, translation elongation factors, tRNAs, translation and transcription initiation factors, ATP levels, and more may change in a periodic manner and this may be modeled using periodic rates in the MFALK.
A natural question is: will the state-variables of the MFALK converge to a periodic pattern with period T? We will show that this is indeed so, i.e. the MFALK entrains to a periodic excitation in the rates. In order to understand what this means, consider a different setting, namely, using the MFALK to model traffic flow. Then the rates may correspond to traffic lights, changing in a periodic manner, and the state-variables are the density of the moving particles (cars) along different sections of the road, so entrainment corresponds to what is known as the “green wave” (see e.g. [63] and the references therein).
We say that a function f is T-periodic if f(t + T) = f(t) for all t. Assume that the λis, γis, αis and βis are uniformly bounded, non-negative, time-varying functions satisfying:
there exists a (minimal) T > 0 such that all the λi(t)s, γi(t)s, αi(t)s, and βi(t)s are T-periodic.
- there exist c1, c2 > 0 such that at least one of the following two conditions holds for all time t
(21) (22) - there exists c3 > 0 such that
(23)
We refer to this model as the Periodic MFALK (PMFALK).
Theorem 1 Consider the PMFALK with dimension n. There exists a unique function , that is T-periodic, and for any a ∈ Cn the trajectory x(t, a) converges to ϕ as t → ∞.
Thus, the PMFALK entrains (or phase-locks) to the periodic excitation in the parameters. In particular, this means that the output rate R(t) in Eq (3) converges to the unique T-periodic function:
Note that since a constant function is a periodic function for all T ≥ 0, Theorem 1 implies that entrainment holds also in the particular case where a single parameter is oscillating (with period T > 0), while all other parameters are constant. Note also that Corollary 1 follows from Theorem 1.
Example 3 Consider the MFALK with dimension n = 3, parameters: λ0(t) ≡ 1.0, λ1(t) ≡ 1.2, λ2(t) = 1 + 0.5sin(πt/4), λ3(t) ≡ 0.9, γ0(t) ≡ 0.4, γ1(t) = 0.4(1 + sin((πt/4) + 1/2)), γ2(t) ≡ 0.25, γ3(t) ≡ 0.45, α1(t) ≡ 0, α2(t) ≡ 0.05, α3(t) ≡ 0, β1(t) ≡ 0, β2(t) = 0.05(1 + sin((πt/2) + 1/4)), β3(t) ≡ 0, and initial condition x(0) = [0.8 0.8 0.8]′. Note that all the rates here are periodic, with a minimal common period T = 8. Fig 4 depicts xi(t), i = 1, 2, 3, as a function of t. It may be seen that each state variable converges to a periodic function with period T = 8.
Fig 4. State variables x1(t) [solid line]; x2(t) [dashed line]; and x3(t) [dotted line] as a function of t in Example 3.
Note that each state variable converges to a periodic function with a period T = 8.
Since the MFALK is a mean-field approximation of ASEP with Langmuir kinetics, a natural question is does ASEP with Langmuir kinetics entrains as well (in some stochastic manner)? The following example addresses this question using Monte Carlo simulations.
Example 4 Consider ASEP with Langmuir kinetics with N = 8 sites and hopping rates:
, and , for all i ≠ 1,
γi(t)≡0, i = 0, …, 8,
αi(t)≡0, i = 1, …, 8,
, and βi(t) ≡ 0, i ≠ 6,
where T = 1E7. Note that all these rates are periodic with a common minimal period T. When simulating ASEP with Langmuir kinetics, these rates are used to determine the next event time (i.e., in this example, the next forward hopping event or the next attachment event). Given a corresponding rate r(t) at time t, the next event time is t + p(r(t)), where p(r(t)) is a random variable drawn from the exponential distribution with mean r(t).
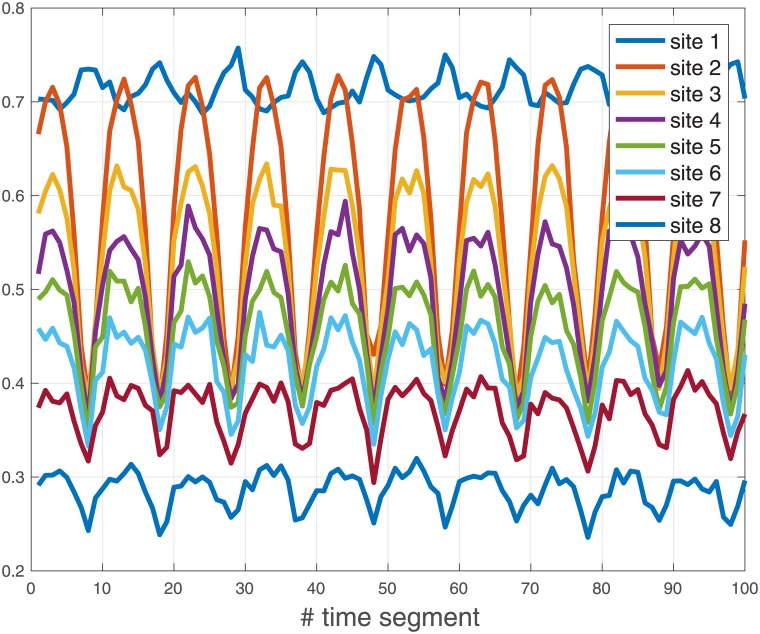
We ran MATLAB simulations of this process for 1E8 time ticks. Fig 5 depicts the average occupancies per site. Each data point in the figure (i.e. each segment) is the average over 1E6 consecutive occupancies (here of course the occupancies are either 0 or 1). For example, the value depicted at time segment 1 is the average occupancy in the time interval [0, 999999]. Note that since T = 1E7 time ticks, the period T is equal to 10 segments. It may be seen that all the average occupancies indeed entrain to the periodic excitation. In particular, they are periodic (up to the noise induced by the stochastic process) with a period of 10 segments. Thus, our simulations do suggest that some form of entrainment also takes place in ASEP with Langmuir Kinetics.
Fig 5. The average occupancies of ASEP with Langmuir kinetics in Example 4.
Note that each average occupancy converges to a periodic function with a period T = 10 segments.
2.5 Strong monotonicity
Recall that a proper cone defines a partial ordering in as follows. For two vectors , we write a ≤ b if (b − a) ∈ K; a < b if a ≤ b and a ≠ b; and a ≪ b if (b − a) ∈ int(K). The system is called monotone if a ≤ b implies that y(t, a) ≤ y(t, b) for all t ≥ 0. In other words, the flow preserves the partial ordering [64]. It is called strongly monotone if a < b implies that y(t, a) ≪ y(t, b) for all t > 0.
From here on we consider the particular case where the cone is . Then a ≤ b if ai ≤ bi for all i, and a ≪ b if ai < bi for all i. A system that is monotone with respect to this partial ordering is called cooperative.
Proposition 6 For any a, b ∈ Cn, with a ≤ b, the solutions of the MFALK satisfy
| (24) |
Furthermore, if Eq (9) holds then for any a < b
| (25) |
To explain this, consider two initial densities a and b with ai ≤ bi for all i, that is, b corresponds to a larger or equal density at each site. Then the trajectories x(t, a) and x(t, b) emanating from these initial conditions continue to satisfy the same relationship between the densities, namely, xi(t, a) ≤ xi(t, b), for all i and for all time t ≥ 0.
The MFALK is thus a strongly cooperative tridiagonal system (SCTS) on int(Cn). Some of the properties deduced above using contraction theory can also be deduced using this property [65].
Remark 1 Suppose that we augment the MFALK into a model of n + 1 ODEs in n + 1 state-variables by adding to it the equation:
that is, (see Eq (2) ). Let denote the vector of the n + 1 state-variables. Clearly, this augmented model admits a first integral , i.e. a property that is preserved for all t ≥ 0. Also, for any initial condition in , all the state-variables remain bounded, as the first n state-variables remain in Cn and for all t ≥ 0. It is straightforward to verify that the augmented system is a cooperative system, and that if Eq (9) holds then it is a SCTS. SCTSs that admit a non-trivial first integral have many desirable properties (see, e.g. [66]).
2.6 Effect of attachment and detachment
One may perhaps expect that detachment from a jammed site may increase the total flow by reducing congestion. The next result shows that this is not so. Detachment always decreases the steady-state output rate R. Similarly, attachment always increases R.
Proposition 7 Consider a MFALK with dimension n. Suppose that the conditions in Proposition 3 hold. Then , and , for all i, j. Also, , and for all j = 0, 1, …, n − 1.
This means that an increase in any of the detachment [attachment] rates decreases [increases] the steady-state density in all the sites. Also, an increase in any of the internal detachment [attachment] rates decreases [increases] the steady-state output rate. The next example demonstrates this.
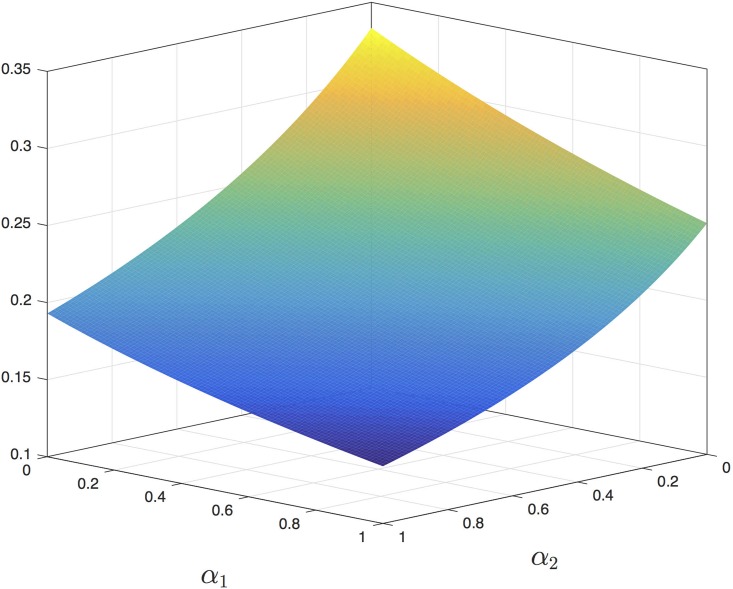
Example 5 Consider the MFALK with n = 3, λi = 1, γi = 0, i = 0, 1, 2, 3, βi = α3 = 0, i = 1, 2, 3. Fig 6 depicts R as a function of α1 ∈ [0, 1] and α2 ∈ [0, 1]. It may be seen that R decreases with both α1 and α2.
Fig 6. R as a function of α1 ∈ [0, 1] and α2 ∈ [0, 1] for the MFALK in Example 5.
It may be seen that R decreases with both α1 and α2.
We note that the analytical results in Proposition 7 agree well with the simulation results obtained using a TASEP model for translation that included alternative initiation along the mRNA and ribosome drop-off [67].
The next section describes an application of the MFALK to a biological process.
3 An application: Modeling mRNA translation with ribosome drop off
It is believed that during mRNA translation ribosome movement is unidirectional from the 5’ end to the 3’ end, and that ribosomes do not enter in the middle of the coding regions. However, ribosomes can detach from various sites along the mRNA molecule due to collisions between ribosomes, for example. This is known as ribosome drop off.
As mentioned in the introduction, ribosome drop off has been the topic of numerous studies [12, 13, 44–51, 68]. It was suggested that in some cases ribosome drop off is important for proof reading [54], and also that ribosome stalling/abortion plays a role in translational regulation (e.g. see [67, 69]).
It is clear that ribosome abortion has drawbacks. Indeed, translation is the most energetically consuming process in the cell, and abortion results in truncated, non-functional and possibly deleterious proteins. It is believed that transcripts undergo evolutionary selection to minimize abortion and/or its energetic cost [12, 48, 49, 51–53]. Nevertheless, there seems to be a certain minimal abortion rate even in non-stressed conditions [13, 68]. This basal value was estimated (see more details below) to be of the order or 10−4 − 10−3 abortion events per codon in E. coli. In other words, at each codon one out of 1,000–10,000 decoding ribosomes aborts. This value is non-negligible. If we consider a drop-off rate of 4 × 10−4 per codon along a coding region of 300 codons (approximately the average coding region length in E. coli) then on average, around 10 out of every 100 ribosomes will fail to complete translation of the mRNA.
To model translation with ribosome drop off, we use the MFALK with γi = 0 (i.e. no backwards motion) and βi = 0 (i.e. no attachment to internal sites along the chain) for all i. Changing the values of the αis allows to model and analyze the effect of ribosome drop off at different sites along the mRNA molecule. We assume that
| (26) |
as otherwise the chain decouples into two smaller, disconnected chains. Note that Eq (26) implies that the conditions in Proposition 3 hold, so the model is SO on Cn w.r.t. the L1 norm, and thus admits a unique globally asymptotically stable steady-state e ∈ int(Cn).
We study the effect of ribosome drop off on the steady-state protein production rate and the steady-state ribosome density using real biological data. To this end, we first considered 10 S. cerevisiae genes (see Figs 7 and 8) with various mRNA levels (all genes were sorted according to their mRNA levels and 10 genes were uniformly sampled from the list). Similarly to the approach used in [28], we divided the mRNAs related to these genes to non-overlapping pieces. The first piece includes the first 9 codons that are related to various stages of initiation [53]. The other pieces include 10 non-overlapping codons each, except for the last one that includes between 5 and 15 codons.
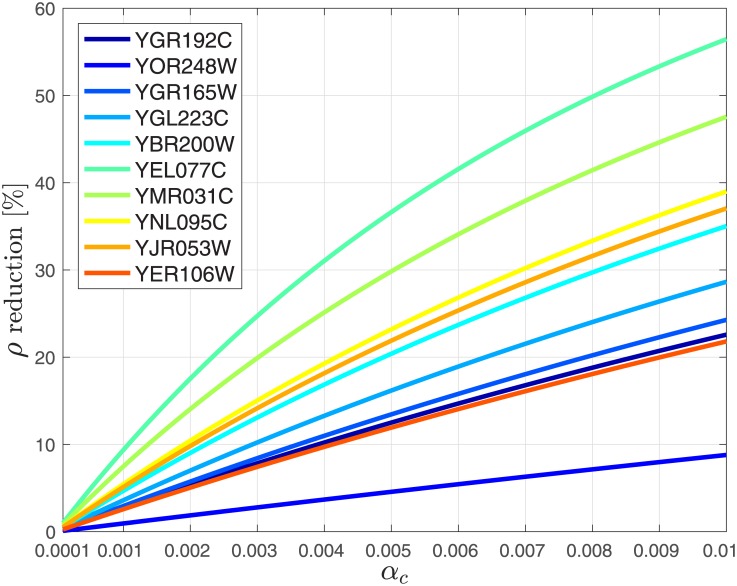
Fig 7. Reduction in percent in the steady-state mean density ρ as a function of αc ∈ [10−4, 10−2] for 10 S. cerevisiae genes.
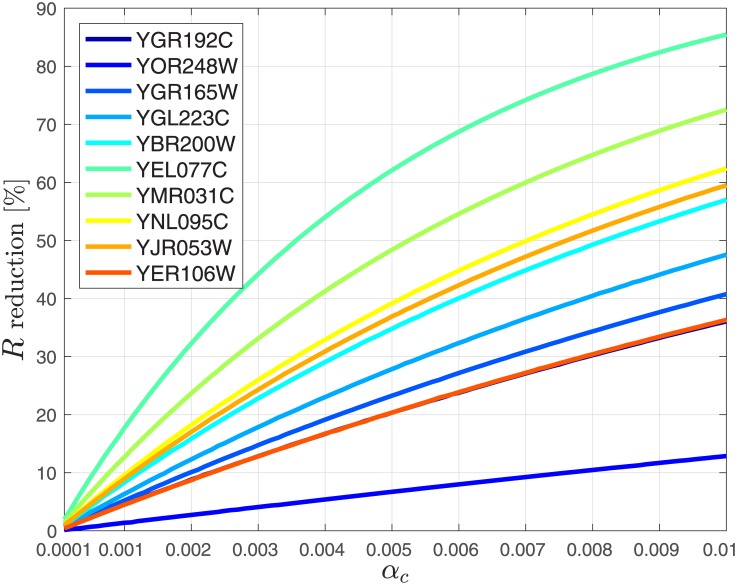
Fig 8. Reduction in percent in the steady-state output rate (production rate) R as a function of αc ∈ [10−4, 10−2] for 10 S. cerevisiae genes.
To model translation dynamics in these mRNAs using MFALK, we model every piece of mRNA as a site. We estimated the elongation rates λi at each site using ribo-seq data for the codon decoding rates [70], normalized so that the median elongation rate of all S. cerevisiae mRNAs becomes 6.4 codons per second [71]. We first applied a filter that considers the biases and traffic jams in ribo-seq to infer for each of the 61 codons a typical decoding time; these times are normalized to get an elongation rate of 6.4 codons/sec [71]. The site rate is (site time)−1, where site time is the sum over the decoding times of all the codons in the piece of mRNA corresponding to this site. These rates thus depend on various factors including availability of tRNA molecules, amino acids, Aminoacyl tRNA synthetase activity and concentration, and local mRNA folding [5, 53, 70].
The initiation rate λ0 (corresponding to the first piece) was inferred based on the fact that the ribosome density (and the translation rate) is proportional to the initiation rate when it is rate limiting [28, 30]. Thus, since in endogenous genes initiation is typically rate limiting the ribosome density should roughly be proportional to the initiation rate. We then normalized the initiation rates such that their mean match the measured/known initiation rate (0.8 initiations per second) [10].
We analyzed the effect of uniform ribosome drop off with a rate in the range of 10−5 to 10−3 per codon. This corresponds to α1 = ⋯ = αn ≔ αc, i.e., all the αis are equal, and αc denotes their common value. Since we assumed 10 codons per site, αc values range from 10−4 to 10−2 (ten times the rate associated with a single codon). This makes sense as in the MFALK the level of occupancy in a site may also be interpreted as the probability to see a ribosome in this site.
Let
denote the steady-state mean ribosomal density. Figs 7 and 8 depict the reduction in percentage in ρ and R, respectively, as a function of αc ∈ [10−4, 10−2]. In these figures the genes in the legends are sorted according to their expression levels: the gene at the top (YGR192C) has the highest mRNA levels while the gene at the bottom (YER106W) has the lowest levels. It may be seen that as the drop off (detachment) rate αc increases from 10−4 to 10−2, ρ decreases by about 30%, and R decreases by about 50%. This demonstrates the significant ramifications that ribosomal drop off is expected to have on translation and the importance of modeling drop off. It may also be observed that in general for mRNAs with higher expression levels (i.e. mRNAs with higher copy number in the cell) the reduction in both the steady-state production rate and mean density due to drop off is lower as compared to the reduction for mRNAs with low copy number.
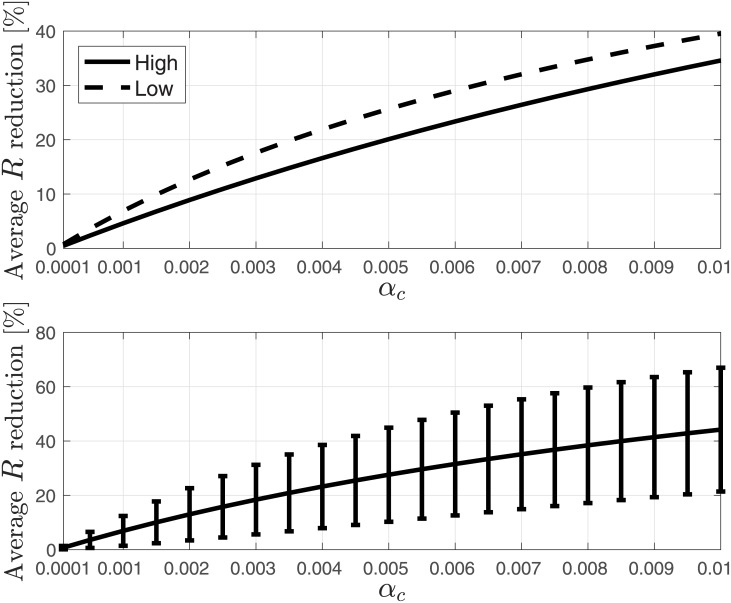
We next evaluated the reduction due to drop off over: 1) all 6310 protein-encoding S. cerevisiae genes; 2) most expressed S. cerevisiae genes (top 20%); and 3) least expressed S. cerevisiae genes (bottom 20%). The average reduction in R and ρ over these three sets of genes are depicted in Figs 9 and 10, respectively. It may be noticed that the average reduction over the highly expressed genes is lower than the average reduction over the lowly expressed genes. It is possible that this is related to stronger evolutionary selection for lower drop off rates in genes with higher mRNA levels. Indeed, highly expressed genes “consume” more ribosomes (due to higher mRNA levels), so a given (per-mRNA) drop off rate is expected to be more deleterious to the cell, and a mutation which decreases the drop off rate in such genes has a higher probability of fixation.
Fig 9. Average reduction in percent in the steady-state output rate (production rate) R as a function of αc ∈ [10−4, 10−2].
Upper figure: reduction over most expressed (top 20%) S. cerevisiae genes (solid-line), and over least expressed (bottom 20%) S. cerevisiae genes (dashed-line). Lower figure: reduction over all S. cerevisiae genes. Also shown are the variances as error bars.
Fig 10. Average reduction in percent in the steady-state mean density ρ as a function of αc ∈ [10−4, 10−2].
Upper figure: reduction over most expressed (top 20%) S. cerevisiae genes (solid-line), and over least expressed (bottom 20%) S. cerevisiae genes (dashed-line). Lower figure: reduction over all S. cerevisiae genes. Also shown are the variances as error bars.
4 Discussion
In many important processes biological “particles” move along some kind of a one-dimensional “track”. Examples include gene transcription and translation, cellular transport, and more. The flow can be either bidirectional (as in the case of transcription) or unidirectional (as in the case of translation elongation), with the possibility of both attachment and detachment of particles at different sites along the track. For example, motor proteins like kinesin and dynein that move along a certain microtubule may detach and attach to an overlapping microtubule.
To rigorously model and analyze such processes, we introduced a new deterministic mathematical model that can be derived as a dynamic mean-field approximation of ASEP with Langmuir kinetics, called the MFALK. Our main results show that the MFALK is a monotone and contractive dynamical system. This implies that it admits a globally asymptotically unique steady-state, and that it entrains to periodic excitations (with a common period T > 0) in any of its rates, i.e. the densities along the chain, as well as the output rate, converge to a unique period solutions with period T.
It is important to note that several known models are special cases of the MFALK. These include for example the RFM [28], the model used in [72] for DNA transcription, the model used in [73] for the various hydrolysis products of a molecular motor, and the model of phosphorelays in [74] (although in the latter model the occupancy levels are normalized differently).
Topics for further research include the following. In the RFM, it has been shown that the steady-state production rate is related to the maximal eigenvalue of a certain non-negative, symmetric tridiagonal matrix with elements that are functions of the RFM rates, i.e. the λis [35]. This implies that the mapping (λ0, …, λn) → R is strictly concave, and that sensitivity analysis of R is an eigenvalue sensitivity problem [36]. Similar results have also been derived for the ribosome flow model on a ring (RFMR) [75] which is a mean-field approximation of TASEP with periodic boundary conditions. An interesting research topic is whether R = R(λ0, …, λn, γ0, …, γn, α1, …, αn, β1, …, βn) in the MFALK can also be described using such a linear-algebraic approach.
The application of the MFALK to model ribosome drop off suggests an interesting direction for further study, namely, how to design genes that minimize the drop off rate.
Another research direction is motivated by the fact that many of the transport phenomena that can be modeled using the MFALK do not take place in isolation. For example, many mRNA molecules are translated in parallel in the cell. Thus, a natural next step is to study networks of interconnected MFALKs. In this context, ribosome drop off may perhaps increase the total production rate in the entire system, as it allows ribosomes to detach from slow sites, enter the pool of free ribosomes, and then attach to the initiation sites of other, less crowded, mRNA molecules. However, drop off still incurs the biological “cost” associated with the synthesis of a chain of amino-acids that is only a part of the desired protein. The fact that the MFALK is contractive may prove useful in analyzing networks of MFALKs, as there exist interesting results proving the overall contractivity of a network based on contractivity of the subsystems and their couplings (see, e.g. [76, 77]).
Finally, another interesting topic for further research is studying the effect of controlled detachment rates on the formation of traffic jams. Indeed, it is known that kinesin-family motor proteins are more susceptible to dissociation when their path is blocked [14, 15].
Supporting information
This file includes the proofs of all the theorems in the paper.
(PDF)
Acknowledgments
We are grateful to the anonymous referee for comments that greatly helped in improving this paper. The research of YZ is partially supported by the Edmond J. Safra Center for Bioinformatics at Tel Aviv University. The research of MM and TT is partially supported by research grants from the Israeli Ministry of Science and Technology, and the US-Israel Binational Science Foundation. The research of MM is also supported by a research grant from the Israel Science Foundation.
Data Availability
All relevant data are within the paper.
Funding Statement
MM and TT are partially supported by research grants from the Israeli Ministry of Science, Technology, and Space, and the Binational Science Foundation. YZ is partially supported by a fellowship from the Edmond J. Safra Center for Bioinformatics at Tel Aviv University. The research of MM is also supported by a research grant from the Israel Science Foundation. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Shaevitz JW, Abbondanzieri EA, Landick R, Block SM. Backtracking by single RNA polymerase molecules observed at near-base-pair resolution. Nature. 2003;426(6967):684–687. 10.1038/nature02191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Nudler E. RNA Polymerase Backtracking in Gene Regulation and Genome Instability. Cell. 2015;149(7):1438–1445. 10.1016/j.cell.2012.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Cheung ACM, Cramer P. Structural basis of RNA polymerase II backtracking, arrest and reactivation. Nature. 2011;471(7337):249–253. 10.1038/nature09785 [DOI] [PubMed] [Google Scholar]
- 4. Churchman LS, Weissman JS. Nascent transcript sequencing visualizes transcription at nucleotide resolution. Nature. 2011;469(7330):368–373. 10.1038/nature09652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. New York: Garland Science; 2008. [Google Scholar]
- 6. Yonath A. Ribosomes: ribozymes that survived evolution pressures but is paralyzed by tiny antibiotics In: Carrondo AM, Spadon P, editors. Macromolecular Crystallography: Deciphering the Structure, Function and Dynamics of Biological Molecules. Dordrecht: Springer Netherlands; 2012. p. 195–208. [Google Scholar]
- 7. Arava Y, Wang Y, Storey JD, Liu CL, Brown PO, Herschlag D. Genome-wide analysis of mRNA translation profiles in Saccharomyces cerevisiae. Proceedings of the National Academy of Sciences. 2003;100(7):3889–3894. 10.1073/pnas.0635171100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Leduc C, Padberg-Gehle K, Varga V, Helbing D, Diez S, Howard J. Molecular crowding creates traffic jams of kinesin motors on microtubules. Proceedings of the National Academy of Sciences. 2012;109:6100–6105. 10.1073/pnas.1107281109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Klumpp S, Hwa T. Traffic patrol in the transcription of ribosomal RNA. RNA Biol. 2009;6(4):392–4. 10.4161/rna.6.4.8952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Chu D, Kazana E, Bellanger N, Singh T, Tuite MF, von der Haar T. Translation elongation can control translation initiation on eukaryotic mRNAs. EMBO J. 2014;33(1):21–34. 10.1002/embj.201385651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Zhang G, Fedyunin I, Miekley O, Valleriani A, Moura A, Ignatova Z. Global and local depletion of ternary complex limits translational elongation. Nucleic Acids Res. 2010;38(14):4778–4787. 10.1093/nar/gkq196 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Kurland CG. Translational accuracy and the fitness of bacteria. Ann Rev Genet. 1992;26:29–50. 10.1146/annurev.ge.26.120192.000333 [DOI] [PubMed] [Google Scholar]
- 13. Sin C, Chiarugi D, Valleriani A. Quantitative assessment of ribosome drop-off in E. coli. Nucleic Acids Res. 2016;44(6):2528–37. 10.1093/nar/gkw137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Dixit R, Ross JL, Goldman YE, Holzbaur EL. Differential regulation of dynein and kinesin motor proteins by tau. Science. 2008;319:1086–1089. 10.1126/science.1152993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Telley IA, Bieling P, Surrey T. Obstacles on the microtubule reduce the processivity of Kinesin-1 in a minimal in vitro system and in cell extract. Biophys J. 2009;96:3341–3353. 10.1016/j.bpj.2009.01.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Schliwa M, Woehlke G. Molecular motors. Nature. 2003;422:759–765. 10.1038/nature01601 [DOI] [PubMed] [Google Scholar]
- 17. Shaw LB, Zia RKP, Lee KH. Totally asymmetric exclusion process with extended objects: a model for protein synthesis. Phys Rev E. 2003;68:021910 10.1103/PhysRevE.68.021910 [DOI] [PubMed] [Google Scholar]
- 18. Zia RKP, Dong J, Schmittmann B. Modeling Translation in Protein Synthesis with TASEP: A Tutorial and Recent Developments. J Statistical Physics. 2011;144:405–428. 10.1007/s10955-011-0183-1 [DOI] [Google Scholar]
- 19. Willmann R, Schütz G, Challet D. Exact Hurst exponent and crossover behavior in a limit order market model. Physica A: Statistical Mechanics and its Applications. 2002;316(1):430–440. 10.1016/S0378-4371(02)01217-7 [DOI] [Google Scholar]
- 20. Parmeggiani A, Franosch T, Frey E. Phase Coexistence in Driven One-Dimensional Transport. Phys Rev Lett. 2003;90:086601 10.1103/PhysRevLett.90.086601 [DOI] [PubMed] [Google Scholar]
- 21. Parmeggiani A, Franosch T, Frey E. Totally asymmetric simple exclusion process with Langmuir kinetics. Phys Rev E. 2004;70:046101 10.1103/PhysRevE.70.046101 [DOI] [PubMed] [Google Scholar]
- 22. Lipowsky R, Klumpp S. Life is motion: multiscale motility of molecular motors. Physica A: Statistical Mechanics and its Applications. 2005;352(1):53–112. 10.1016/j.physa.2004.12.034. [DOI] [Google Scholar]
- 23. Lipowsky R, Klumpp S, Nieuwenhuizen TM. Random walks of cytoskeletal motors in open and closed compartments. Phys Rev Lett. 2001;87(10):108101 10.1103/PhysRevLett.87.108101 [DOI] [PubMed] [Google Scholar]
- 24. Ezaki T, Nishinari K. Exact stationary distribution of an asymmetric simple exclusion process with Langmuir kinetics and memory reservoirs. Journal of Physics A: Mathematical and Theoretical. 2012;45(18):185002 10.1088/1751-8113/45/18/185002 [DOI] [Google Scholar]
- 25. Evans M, Juhasz R, Santen L. Shock formation in an exclusion process with creation and annihilation. Physical Review E. 2003;68(2):026117 10.1103/PhysRevE.68.026117 [DOI] [PubMed] [Google Scholar]
- 26. Klumpp S, Lipowsky R. Traffic of Molecular Motors Through Tube-Like Compartments. J Statistical Physics. 2003;113:233–268. 10.1023/A:1025778922620 [DOI] [Google Scholar]
- 27. Schadschneider A, Chowdhury D, Nishinari K. Stochastic Transport in Complex Systems: From Molecules to Vehicles. Elsevier; 2011. [Google Scholar]
- 28. Reuveni S, Meilijson I, Kupiec M, Ruppin E, Tuller T. Genome-Scale Analysis of Translation Elongation with a Ribosome Flow Model. PLOS Computational Biology. 2011;7:e1002127 10.1371/journal.pcbi.1002127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Blythe RA, Evans MR. Nonequilibrium steady states of matrix-product form: a solver’s guide. J Phys A: Math Gen. 2007;40(46):R333–R441. 10.1088/1751-8113/40/46/R01 [DOI] [Google Scholar]
- 30. Margaliot M, Tuller T. On the steady-state distribution in the homogeneous ribosome flow model. IEEE/ACM Trans Computational Biology and Bioinformatics. 2012;9:1724–1736. 10.1109/TCBB.2012.120 [DOI] [PubMed] [Google Scholar]
- 31. Zarai Y, Margaliot M, Tuller T. Explicit expression for the steady-state translation rate in the infinite-dimensional homogeneous ribosome flow model. IEEE/ACM Trans Computational Biology and Bioinformatics. 2013;10:1322–1328. 10.1109/TCBB.2013.120 [DOI] [PubMed] [Google Scholar]
- 32. Margaliot M, Tuller T. Stability analysis of the ribosome flow model. IEEE/ACM Trans Computational Biology and Bioinformatics. 2012;9:1545–1552. 10.1109/TCBB.2012.88 [DOI] [PubMed] [Google Scholar]
- 33. Margaliot M, Tuller T. Ribosome Flow Model with Positive Feedback. J Royal Society Interface. 2013;10:20130267 10.1098/rsif.2013.0267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Margaliot M, Sontag ED, Tuller T. Entrainment to Periodic Initiation and Transition Rates in a Computational Model for Gene Translation. PLoS ONE. 2014;9(5):e96039 10.1371/journal.pone.0096039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Poker G, Zarai Y, Margaliot M, Tuller T. Maximizing protein translation rate in the nonhomogeneous ribosome flow model: a convex optimization approach. J Royal Society Interface. 2014;11(100). 10.1098/rsif.2014.0713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Poker G, Margaliot M, Tuller T. Sensitivity of mRNA translation. Sci Rep. 2015;5:12795 10.1038/srep12795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Raveh A, Zarai Y, Margaliot M, Tuller T. Ribosome Flow Model on a Ring. IEEE/ACM Trans Computational Biology and Bioinformatics. 2015;12(6):1429–1439. 10.1109/TCBB.2015.2418782 [DOI] [PubMed] [Google Scholar]
- 38. Zarai Y, Margaliot M, Sontag ED, Tuller T. Controllability analysis and control synthesis for the ribosome flow model. IEEE/ACM Trans Computational Biology and Bioinformatics. 2017;. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Zarai Y, Margaliot M, Tuller T. On the ribosomal density that maximizes protein translation rate. PLOS ONE. 2016;11(11):1–26. 10.1371/journal.pone.0166481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Zarai Y, Margaliot M, Tuller T. Optimal down regulation of mRNA translation. Sci Rep. 2017;7(41243). 10.1038/srep41243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Raveh A, Margaliot M, Sontag ED, Tuller T. A model for competition for ribosomes in the cell. J Royal Society Interface. 2016;116(20151062). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Heldt FS, Brackley CA, Grebogi C, Thiel M. Community control in cellular protein production: consequences for amino acid starvation. Philosophical Trans Royal Society of London A: Mathematical, Physical and Engineering Sciences. 2015;373 (2056). 10.1098/rsta.2015.0107 [DOI] [PubMed] [Google Scholar]
- 43.Algar RJR, Ellis T, Stan GB. Modelling essential interactions between synthetic genes and their chassis cell. In: Proc. 53rd IEEE Conference Decision and Control. LA; 2014. p. 5437–5444.
- 44. Keiler KC, Waller PR, Sauer RT. Role of a peptide tagging system in degradation of proteins synthesised from damaged messenger RNA. Science. 1996;271:990–993. 10.1126/science.271.5251.990 [DOI] [PubMed] [Google Scholar]
- 45. Keiler KC. Mechanisms of ribosome rescue in bacteria. Nat Rev Microbiol. 2015;13:285–297. 10.1038/nrmicro3438 [DOI] [PubMed] [Google Scholar]
- 46. Zaher HS, Green R. A primary role for elastase factor 3 in quality control during translation elongation in Escherichia coli. Cell. 2011;147:396–408. 10.1016/j.cell.2011.08.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Chadani Y, Ono K, Ozawa S, Takahashy Y, Takay K, Nanamiya H, et al. Ribosome rescue by Escherichia Coli Arf-A (YhdL) in the absence of trans-translation systems. Mol Microbiol. 2010;78:796–808. 10.1111/j.1365-2958.2010.07375.x [DOI] [PubMed] [Google Scholar]
- 48. Subramaniam AR, Zid BM, O’Shea EK. An integrated approach reveals regulatory controls on bacterial translation elongation. Cell. 2014;159(5):1200–11. 10.1016/j.cell.2014.10.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Gilchrist MA, Wagner A. A model of protein translation including codon bias, nonsense errors, and ribosome recycling. J Theoretical Biology. 2006;239(4):417–34. 10.1016/j.jtbi.2005.08.007 [DOI] [PubMed] [Google Scholar]
- 50. Jorgensen F, Kurland CG. Processivity errors of gene expression in Escherichia coli. J Mol Biol. 1990;215:511–521. 10.1016/S0022-2836(05)80164-0 [DOI] [PubMed] [Google Scholar]
- 51. Hooper SD, Berg OG. Gradients in nucleotide and codon usage along Escherichia coli genes. Nucleic Acids Res. 2000;28:3517–3523. 10.1093/nar/28.18.3517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Zafrir Z, Zur H, Tuller T. Selection for reduced translation costs at the intronic 5’ end in fungi. DNA Res. 2016;23(4):377–94. 10.1093/dnares/dsw019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Tuller T, Zur H. Multiple roles of the coding sequence 5’ end in gene expression regulation. Nucleic Acids Res. 2015;43(1):13–28. 10.1093/nar/gku1313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Zaher SA, Green R. Quality control by the ribosome following peptide bond formation. Nature. 2009;457:161–166. 10.1038/nature07582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Jacquez JA, Simon CP. Qualitative theory of compartmental systems. SIAM Review. 1993;35(1):43–79. 10.1137/1035003 [DOI] [PubMed] [Google Scholar]
- 56. Sandberg IW. On the mathematical foundations of compartmental analysis in biology, medicine, and ecology. IEEE Trans Circuits and Systems. 1978;25(5):273–279. 10.1109/TCS.1978.1084473 [DOI] [Google Scholar]
- 57. Garca-Meseguer MJ, de Labra JAV, Garcia-Moreno M, Garca-Canovas F, Havsteen BH, Varon R. Mean residence times in linear compartmental systems. Symbolic formulae for their direct evaluation. Bull Math Biol. 2003;65:279–308. [DOI] [PubMed] [Google Scholar]
- 58. Lohmiller W, Slotine JJE. On Contraction Analysis for Non-linear Systems. Automatica. 1998;34:683–696. 10.1016/S0005-1098(98)00019-3 [DOI] [Google Scholar]
- 59. Russo G, di Bernardo M, Sontag ED. Global entrainment of transcriptional systems to periodic inputs. PLOS Computational Biology. 2010;6:e1000739 10.1371/journal.pcbi.1000739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Aminzare Z, Sontag ED. Contraction methods for nonlinear systems: A brief introduction and some open problems. In: Proc. 53rd IEEE Conf. on Decision and Control. Los Angeles, CA; 2014. p. 3835–3847.
- 61. Margaliot M, Sontag ED, Tuller T. Contraction after small transients. Automatica. 2016;67:178–184. 10.1016/j.automatica.2016.01.018 [DOI] [Google Scholar]
- 62. Desoer C, Haneda H. The measure of a matrix as a tool to analyze computer algorithms for circuit analysis. IEEE Trans Circuit Theory. 1972;19:480–486. 10.1109/TCT.1972.1083507 [DOI] [Google Scholar]
- 63. Kerner BS. The physics of green-wave breakdown in a city. Europhysics Letters. 2013;102(2):28010 10.1209/0295-5075/102/28010 [DOI] [Google Scholar]
- 64. Smith HL. Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems vol. 41 of Mathematical Surveys and Monographs. Providence, RI: Amer. Math. Soc.; 1995. [Google Scholar]
- 65. Smillie J. Competitive and cooperative tridiagonal systems of differential equations. SIAM J Mathematical Analysis. 1984;15:530–534. 10.1137/0515040 [DOI] [Google Scholar]
- 66. Mierczynski J. A class of strongly cooperative systems without compactness. Colloq Math. 1991;62:43–47. [Google Scholar]
- 67. Zupanic A, Meplan C, Grellscheid SM, Mathers JC, Kirkwood TBL, Hesketh JE, et al. Detecting translational regulation by change point analysis of ribosome profiling data sets. RNA. 2014;20(10):1507–1518. 10.1261/rna.045286.114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Kurland CG, Mikkola R. The impact of nutritional state on the microevolution of ribosomes In: Kjelleberg S, editor. Starvation in Bacteria. NY: Plenum Press; 1993. p. 225–238. [Google Scholar]
- 69. Shoemaker CJ, Eyler DE, Green R. Dom34:Hbs1 promotes subunit dissociation and peptidyl-tRNA drop-off to initiate no-go decay. Science. 2010;330(6002):369–72. 10.1126/science.1192430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Dana A, Tuller T. Mean of the typical decoding rates: a new translation efficiency index based on the analysis of ribosome profiling data. G3. 2014;5(1):73–80. 10.1534/g3.114.015099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Karpinets TV, Greenwood DJ, Sams CE, Ammons JT. RNA: protein ratio of the unicellular organism as a characteristic of phosphorous and nitrogen stoichiometry and of the cellular requirement of ribosomes for protein synthesis. BMC Biol. 2006;4(30):274–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Edri S, Gazit E, Cohen E, Tuller T. The RNA polymerase flow model of gene transcription. IEEE Trans Biomedical Circuits and Systems. 2014;8(1):54–64. 10.1109/TBCAS.2013.2290063 [DOI] [PubMed] [Google Scholar]
- 73. Fisher ME, Kolomeisky AB. The force exerted by a molecular motor. Proceedings of the National Academy of Sciences. 1999;96(12):6597–6602. 10.1073/pnas.96.12.6597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Csikasz-Nagy A, Cardelli L, Soyer OS. Response dynamics of phosphorelays suggest their potential utility in cell signaling. J Royal Society Interface. 2011;8:480–488. 10.1098/rsif.2010.0336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zarai Y, Ovseevich A, Margaliot M. Optimal Translation Along a Circular mRNA. ArXiv e-prints. 2017;. [DOI] [PMC free article] [PubMed]
- 76. Arcak M. Certifying spatially uniform behavior in reaction-diffusion PDE and compartmental ODE systems. Automatica. 2011;47(6):1219–1229. 10.1016/j.automatica.2011.01.010 [DOI] [Google Scholar]
- 77. Russo G, di Bernardo M, Sontag ED. A Contraction Approach to the Hierarchical Analysis and Design of Networked Systems. IEEE Trans Automat Control. 2013;58(5):1328–1331. 10.1109/TAC.2012.2223355 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
This file includes the proofs of all the theorems in the paper.
(PDF)
Data Availability Statement
All relevant data are within the paper.