Abstract
While interactions between the thalamus and cortex are critical for cognitive function1–3, the exact contribution of the thalamus to these interactions is often unclear. Recent studies have shown diverse connectivity patterns across the thalamus 4,5, but whether this diversity translates to thalamic functions beyond relaying information to or between cortical regions6 is unknown. Here, by investigating prefrontal cortical (PFC) representation of two rules used to guide attention, we find that the mediodorsal thalamus (MD) sustains these representations without relaying categorical information. Specifically, MD input amplifies local PFC connectivity, enabling rule-specific neural sequences to emerge and thereby maintain rule representations. Consistent with this notion, broadly enhancing PFC excitability diminishes rule specificity and behavioral performance, while enhancing MD excitability improves both. Overall, our results define a previously unknown principle in neuroscience; thalamic control of functional cortical connectivity. This function indicates that the thalamus plays much more central roles in cognition than previously thought.
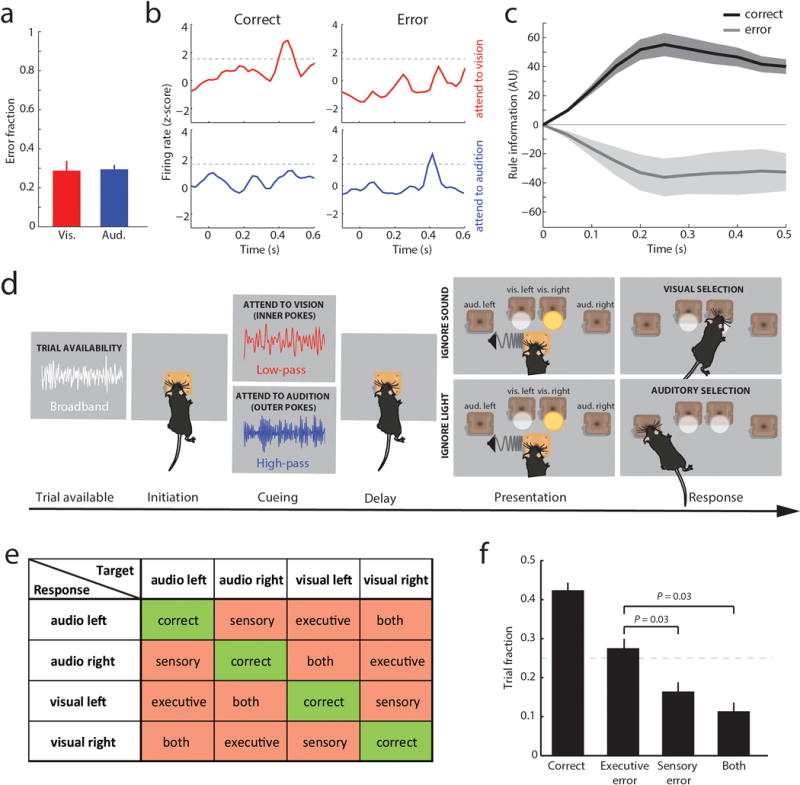
We recorded PFC ensembles in a two-alternative forced choice (2AFC) task, in which a freely behaving mouse selected between conflicting visual and auditory stimuli based on whether one of two rules was presented, and where rule presentation was varied on a trial-by-trial basis (Figure 1a). Broadband white noise was informative of trial availability, prompting trial initiation by snout-protrusion into a centrally located port. Subsequently, either high-pass (11 kHz) or low-pass (10 kHz) noise was presented for 100 ms to signal task rule (rule 1 [high-pass]: attend to vision; rule 2 [low-pass]: attend to audition), and following a brief delay where head position was stably maintanined, the animal selected between spatially conflicting visual and auditory stimuli to receive a reward. Animals achieved a balanced and robust performance across modalities (Extended Data Figure 1a) and no stereotypical behavior indicating a modality or location preference was observed during the delay. These findings suggest that animals were capable of holding the task rule ‘in mind’ and using it to map onto sensory targets.
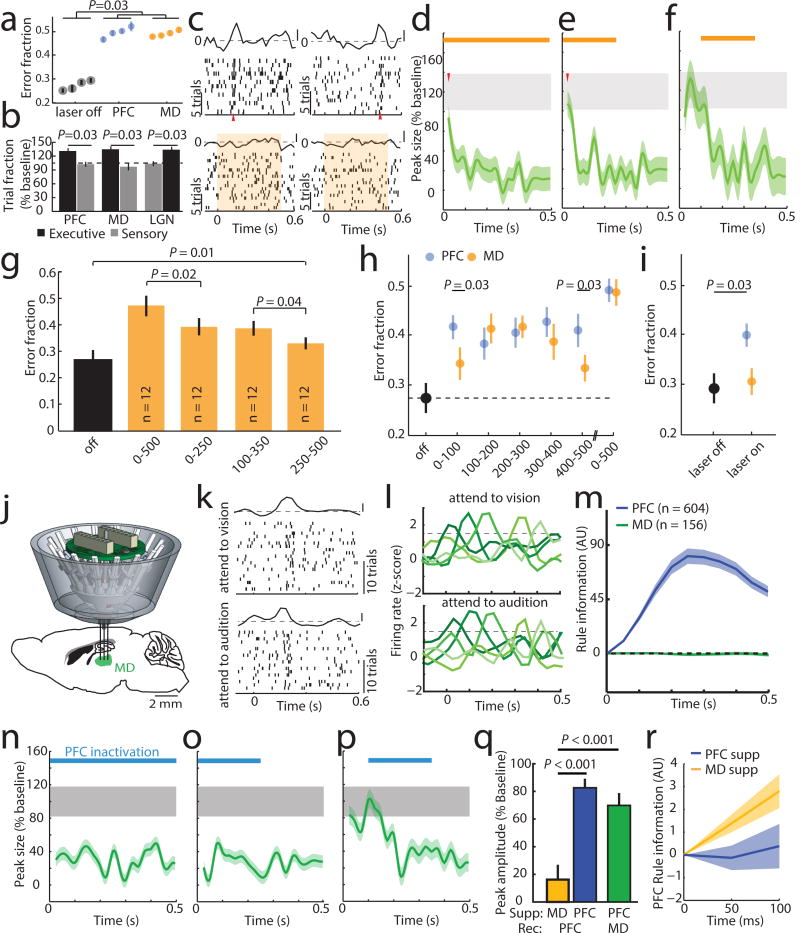
Figure 1. Task-specific sequential PFC activity maintains rule representation.
(a) Schematic of task design. (b) Example peri-stimulus time histogram (PSTH) and rasters for neurons tuned to either ‘attend to vision’ (red) or ‘attend to audition’ (blue) rules. (c) Examples of tuning peaks across multiple sessions. (d) Task-variable information, indicates that tuned neurons (n = 512 neurons from 4 mice) reflect rule information (top, green), but not movement (top, grey), but unturned neurons do not (n = 2727, bottom) (e) Example spike time cross-correlation between two neurons (50 μs bins), indicating a putative monosynaptic connection. (f) Putative monosynaptic connections in same rule tuned pairs showed a significantly larger average peak. Vertical ticks indicate peak times. (g) Cumulative plot showing cross-correlation values for each pair. (h) Same rule tuned pairs with putative monosynaptic connections had overlapping tuning peaks (i) Raster and PSTH examples showing diminished turning during optogenetic activation of inhibitory neurons (blue shading indicates laser). (j) Quantification of laser impact on peak sizes (n = 94 neurons, 3 mice; example in Extended Data Figure 3j). (k–l) Temporally-limited optogenetic manipulations (blue bars) indicate that later tuning depends on earlier activity. Shading indicates 95% confidence intervals.
Given that prelimbic cortex7 activity during the delay (referred to as prefrontal cortex (PFC)) is necessary for task performance8, we directly interrogated its neural substrates (Extended Data Figure 1b–d). We found that certain PFC neurons signaled task rule by an increase in spiking at a brief moment during the delay (Figure 1b). This temporal sparseness is analogous to that observed in primate dorsolateral PFC during task rule encoding/maintenance9. The majority of such neurons signaled only one rule, but a minority (17%) signaled both rules at different temporal offsets (Extended Data Figure 1e,f). Most tuned neurons exhibited regular spiking waveforms (RS: 82% of total tuned neurons; 19% of all recorded RS) consistent with them being pyramidal neurons. Only a minority were fast spiking (FS: 18% of total tuned neurons; 11 % of all FS; FStuned/FStotal vs RStuned/RStotal, P = 0.001, binomial test; Extended Data Figure 1g, Supplemental Note 1). Tuned peaks tiled the entire delay (Figure 1c), and tuning was independent of delay length (Extended Data Figure 1h).
Linear decoding10 showed that tuned neurons encoded task rule but not movement (Figure 1d; Supplemental Discussion 1). Rule information was exclusively represented by neurons we identified as tuned, because spike trains derived from the remaining neurons (untuned) did not contain rule information (or movement, Figure 1d bottom; Extended Data Figure 1i). As such, distinct PFC populations represent the two task rules used for sensory selection. The conclusion that these population codes reflect sensory selection rules, rather than ones directing the selection or avoidance of one sensory target, is supported by multiple findings. First, performance on trials with single target modality presentation was identical to that with sensory conflict (Extended Data Figure 2a). Second, in sessions with sufficient errors (> 20 trials), PFC neurons that were appropriately tuned to one rule displayed identical activity during error trials, indicating that inappropriate rule encoding was the major source of errors in this task (Extended Data Figure 2b, c). To fully test this idea, we developed a 4AFC task (Extended Data Figure 2d) in which animals separately indicated their choice for target modality type as well as its spatial location thereby distinguishing errors related to rule encoding (executive) from those related to target stimulus perception (sensory) (Extended Data Figure 2e). The largest source of 4AFC errors was executive (Extended data Figure 2f), consistent with our interpretation that similar misattribution of task rules explains most errors in the 2AFC task (Supplemental discussion 2).
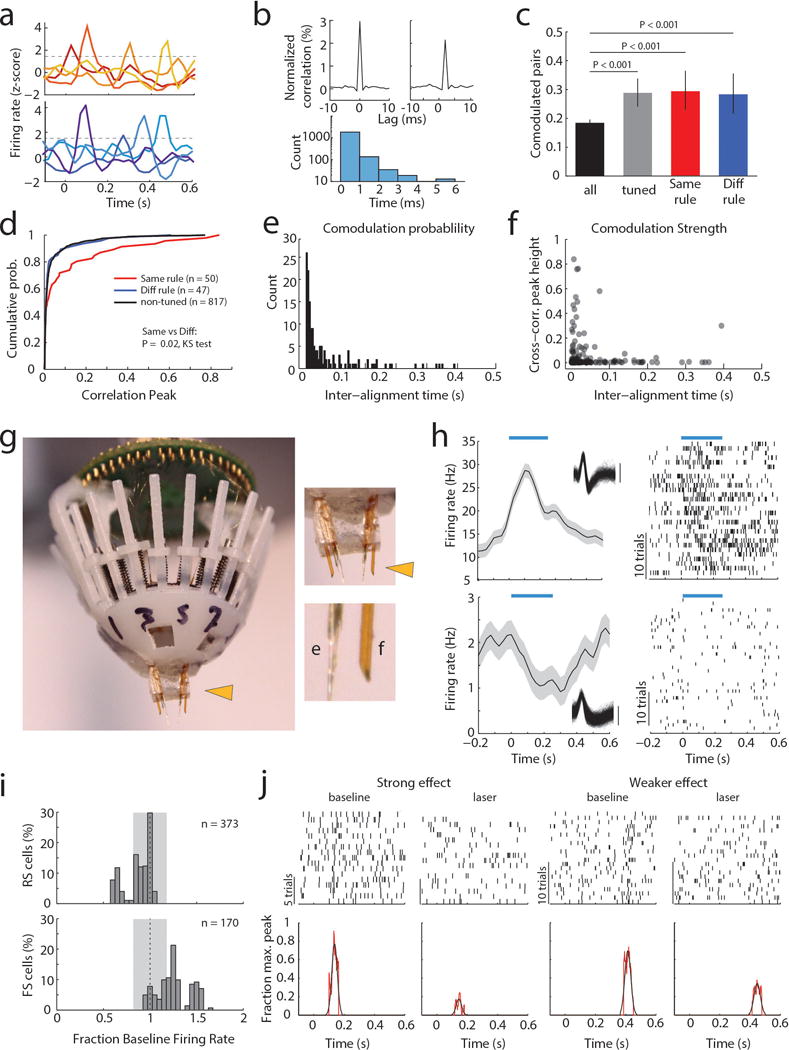
When multiple cells encoding the same rule were simultaneously recorded (Extended Data Figure 3a), their consistent temporal order indicated that a neural sequence maintained the relevant categorical representation over time11–15. Consistent with this notion, we found that many PFC neuronal pairs exhibited robust short-latency cross-correlations, indicating their co-modulation at synaptic timescales16,17. This co-modulation was related to similarity in both categorical and temporal tuning (Extended Data Figure 3b–f). Analysis at a higher temporal resolution required for inferring putative monosynaptic connections18,19 (example Figure 1e) showed significantly higher probability and strength among same-rule encoding pairs (Figure 1f, g) and was only observed among pairs with overlapping temporal fields (Figure 1h). As such, our data support a synaptic chain mechanism for categorical rule representation in PFC. This inferred relationship between connectivity and coding is reminiscent of the one directly demonstrated in mouse primary visual cortex, where neurons with similar orientation tuning are more likely to be synaptically connected20.
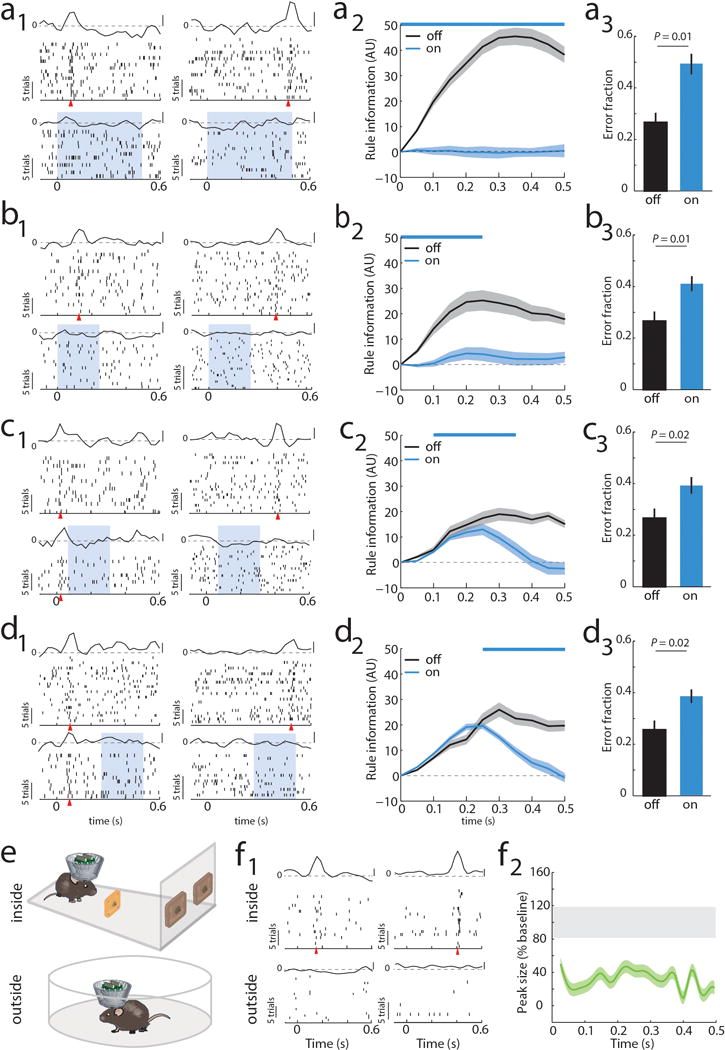
To causally test this synaptic chain model, we employed local optogenetic activation of inhibitory cortical neurons21 to produce temporally precise chain disruption (Extended data Figure 3g). For each mouse, we used the minimum light intensity that, when delivered specifically during the delay, was sufficient to render it incapable of appropriate sensory selection as previously shown8. Under those conditions, we found evidence for driving FS neurons, but overall, RS neurons were generally only slightly inhibited (Extended data Figure 3h, i). Nonetheless, laser delivery over the entire delay resulted in diminished rule tuning (Figure 1i,j; Extended Data Figure 3j, 4a1–a3). Temporally-limited manipulations revealed that early PFC manipulation diminished late task rule representation, even when the rule presentation period itself was spared (Figure 1k–l, Extended Data Figure 4b–d).
While synaptic PFC chains are likely necessary for sustaining rule representation, they are not sufficient; presenting the two rule-associated cues outside of the task did not generate PFC tuning (Extended Data Figure 2e, f). This indicated that additional factors are required for PFC populations to represent task rules. Given prior work showing a critical role for the mediodorsal thalamus (MD) in executive function2,22, and its heavy reciprocal connectivity with PFC23, we asked whether its interaction with PFC was one factor.
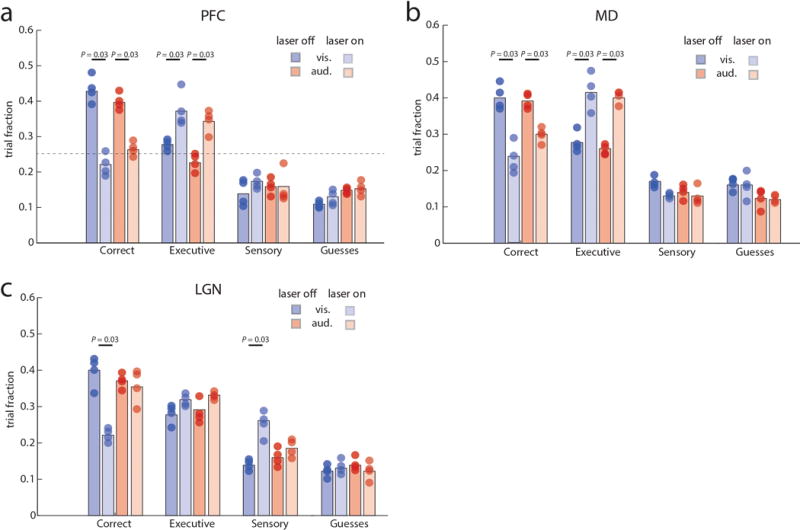
Bilateral optogenetic MD suppression during the delay rendered mice incapable of appropriate sensory selection in the 2AFC task (Figure 2a). Similar suppression in the 4AFC task resulted in identical error patterns to those resulting from PFC suppression (executive errors; Figure 2b; Extended data Figure 5a, b), and ones that were distinct from those resulting from visual thalamic suppression (LGN; lateral geniculate nucleus; Figure 2b; Extended data Figure 5c). Consistent with this behavioral dissociation, LGN suppression did not impact PFC rule-tuning (Extended Data Figure 6a), while MD suppression diminished its maintainence (Figure 2c–g, Extended Data Figure 6b–e) while largely sparing its initiation (first 100 ms, during rule presentation; Figures 2d, e). MD suppression limited to the latter half of the delay was less effective in eliminating population coding and behavior compared to an equivalent period of local PFC suppression (Extended Data Figure 6e). These differences indicate that MD activity is not required for initial rule encoding, and that MD may be recruited by the PFC to sustain rule representation in a manner that outlasts MD neuronal spiking. Consistent with this idea, optogenetic PFC suppression in 100 ms bins across the delay resulted in identical behavioral effects throughout, while corresponding MD suppression resulted in weaker impact at the earliest and latest bins (Figure 2h). Importantly, MD-dependence was linked to delay length (Figure 2i).
Figure 2. Categorically-free MD activity is required for PFC rule representation and task performance.
(a) Delay-limited PFC or MD inhibition diminishes task performance. (4 sessions, n = 4 mice each). (b) Delay-limited PFC or MD inhibition in the 4AFC task selectively increases executive errors while LGN suppression selectively increases sensory ones (n = 4 mice per group). (c) Raster and PSTH examples of PFC rule tuning with MD suppression (shading denotes laser). (d) Population quantification of c as in Figure 1j (n = 58 neurons). (e–f) Temporally-limited MD suppression effects on population tuning (e, n = 43 neurons; f, n = 46 neurons3 mice with 4 sessions per condition). (g) Comparison of behavioral performance with full and temporally limited MD suppression (n = 3 mice with 4 sessions each). (h) Effect of short duration (100 ms) suppression of PFC or MD across the delay on performance. (i) Effect of MD suppression with short delay (20 ms) trials. (j) MD recordings schematic. (k) Raster and PSTH example of an MD neuron showing similar peaks in both trial types. (l) Example PSTHs of five MD neurons showing consistent lack of rule-specificity. (m) Linear decoding fails to reveal rule information in MD neurons with peaks (PFC: n = 604 neurons, 6 mice, MD: n = 156 neurons, 3 mice). (n-p) MD peak elimination by PFC suppression, (full: n = 47 neurons, early: n = 34 neurons; middle: n = 36 neurons; 2 mice with 4–5 sessions each). (q) Effects of MD (yellow) and PFC (blue) suppression on the first 50 ms of PFC tuning. MD suppression produces a small effect on early PFC peaks (n = 101 neurons, 3 mice) relative to local PFC suppression (n = 146 neurons, 3 mice) while PFC suppression strongly reduced early MD tuning (green, n = 81 neurons, 2 mice). (r) Early rule information is preserved with MD, but not PFC suppression (decoding as in Figure 1. MD: n = 101 neurons, 3 mice; PFC: n = 146 neurons, 3 mice). Shading indicates 95% confidence intervals. Wilcoxon rank-sum test was used for all comparisons. Data is presented as mean ± SEM.
To understand how MD neurons sustained PFC representations, we recorded their spiking in the task (Figure 2j). Certain MD neurons displayed temporally-limited enhanced spiking during the task delay, but were non-selective to rule as the vast majority showed identical activity for both the ‘attend to vision’ and ‘attend to audition’ trials (Figure 2k,l; Extended Data Figure 7a; Supplemental Note 2). As such, it was not surprising that this MD population was uninformative of task rule (Figure 2m; Extended Data Figure 7b–e). Importantly, peaks were only encountered in the lateral MD (Extended Data Figure 7f), consistent with their reciprocal connectivity pattern with PFC24 (Extended Data Figure 7g,h). In fact, 58% of neurons recorded in the lateral MD showed rule non-selective peaks dependent on PFC activity (Figure 2n–p). However, in contrast to the impact of MD inactivation on PFC tuning, the very first MD peaks were eliminated by PFC suppression (Figure 2q,r). Overall, these data indicate that MD engagement in the delay is not to relay categorical rule information, but to rather sustain existing cortical representations. Consistent with this notion, neither overall spike rates nor tuning peaks were changed in error trials (Extended Data Figure 7i,j), confirming the conclusions that most errors in this task are due to rule misattribution and that this information is generated cortically. To our knowledge, this is the first direct mechanistic demonstration of a non-relay function of the thalamus.
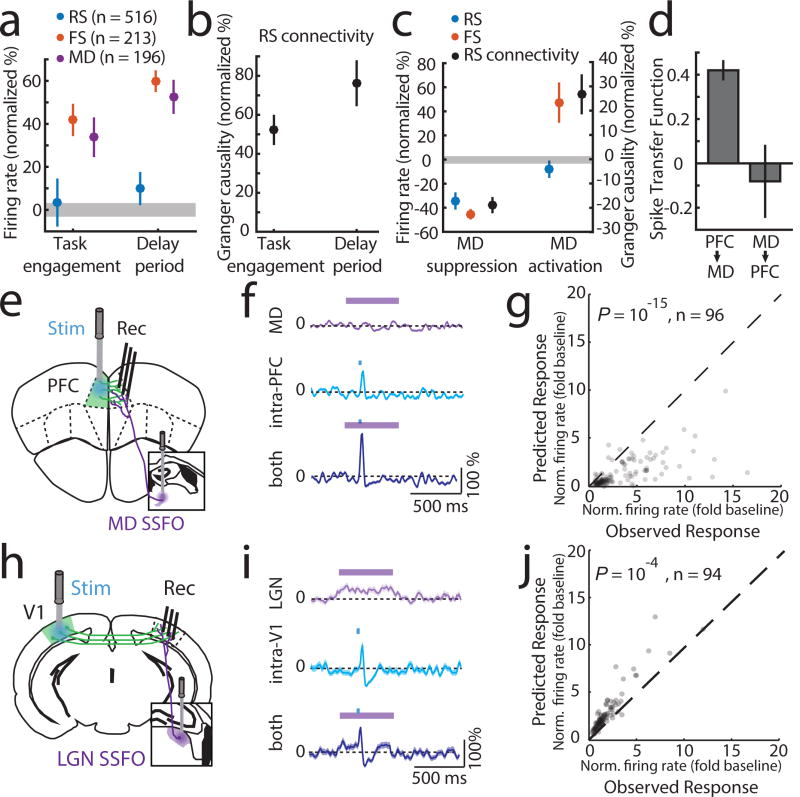
To gain mechanistic insight into how MD sustains categorical cortical representations, we performed multi-site recordings within the MD-PFC loop. We found that MD neurons increased spiking upon task engagement, but that only inhibitory cortical neurons (FS) not excitatory ones (RS) showed a similar increase (Figure 3a). This was also true for changes seen in the task delay; MD and cortical FS neurons showed additional spiking enhancement, while RS neural spike rates remained relatively unaltered (Figure 3a). What could maintain RS spike rates constant across these conditions that increase FS spiking? Because PFC neurons generate functional sequences following rule presentation, we suspected that their local connectivity might be enhanced by MD inputs, balancing increased inhibition. Consistent with this hypothesis, granger causality of cortical RS network spike trains, a proxy for functional connectivity25,26, increased upon task engagement and further during the task delay (Figure 3b). These findings suggested that RS firing rates became more dependent on local RS connections, and by extension MD inputs, as the animal engaged in the task. In agreement with this notion, optogenetic suppression of MD activity resulted in reduced RS spiking in but not outside the task (Figure 3c, Extended Data Figure 8a–c). Broadly enhancing MD excitability through stabilized step function opsin (SSFO) activation27 selectively increased FS spiking and augmented RS neuronal functional connectivity, but did not significantly change RS spike rates (Figure 3c, Extended Data Figure 8d–f). This finding indicated that MD activation enhanced local RS PFC connectivity without increasing their spiking. This modulatory MD→PFC input is quite different from the driving PFC→MD input we observe following SSFO-mediated activation of PFC (Figure 3d, Extended Data Figure 8g–i), and is consistent with the theoretical prediction that strong (driver-driver) thalamo-cortical loops are forbidden28. To further test that MD inputs enhance functional cortical connectivity, we examined the impact of MD activation on intra-cortical evoked responses (Figure 3e). In this context, an non-driving MD input significantly amplified an intracortical evoked response (Figure 3f). The supralinear nature of this amplification is evident by comparing the observed functional connection to the one predicted based on the arithmetic sum of its individual components (thalamic and cortical; Figure 3g). Critically, these results were different from the ones observed in the thalamo-cortical loop containing LGN and primary visual cortex (V1) (Figure 3h); LGN inputs drove robust spiking in ipsilateral V1 and combining this driving input with contralateral V1 stimulation led to sublinear responses (Figure 3i–j; Extended Data Figure 9a).
Figure 3. MD input amplifies local PFC connectivity.
(a) MD and cortical FS but not RS show increased firing rates upon task engagement and further increase during the delay (normalized to values outside of task; PFC, 6 mice, RS: 516 cells, FS: 213 cells, MD, 3 mice, 196 cells, grey shading indicates 95% CI of null distribution. (b) RS network connectivity, assessed by granger causality of spike trains.(normalized to values outside of task, n = 6 mice, 43 sessions; median 13 neurons/session). (c) Suppressing MD reduces cortical FS and RS firing rates during task delay (RS: 245, FS: 114, n = 2 mice), as well as RS connectivity (n = 2 mice, 19 sessions; median 13 neurons/session). Enhancing MD excitability increases cortical FS firing rates, connectivity among cortical RS neurons but not RS firing rates (RS: 303, FS: 131, n = 2 mice; RS connectivity [n = 17 sessions; median 18 neurons/session]). (d) Spike transfer function (methods) of PFC→MD is significantly higher compared to MD→PFC (n = 17 sessions, median 11 PFC and 10 MD neurons/session for PFC→MD, median 18 PFC and 15 MD neurons/sessions for MD→PFC, 2 mice per condition, error bars are 95% CI estimated per session). (e) Experimental setup for testing the impact of MD activation on local intra-PFC connectivity. (f) Example RS neuron responses (normalized PSTH, mean ± SEM) to MD activation alone, intra-PFC activation alone or the combination. (g) Comparison of the observed combined response with the arithmetic sum of its individual components shows supra-linearity (P < 10−15, sign-rank test). (h–i) As in e–g but for SSFO-mediated activation of LGN and recordings from V1. (j) Combined stimulation results in a sub-linearity (P < 10−4, sign-rank test).
To formalize our notion of this non-relay thalamic function, we built a data-driven spiking PFC-MD neural model (Extended Data Figure 9b–f; methods). Progressively increasing MD excitability to mimic task engagement enhanced correlated spiking among model PFC neurons, but resulted in rule-specific neural sequences only when co-tuned ‘starter’ neurons were synchronized by a common input (Extended Data Figure 9g,h). The theoretical prediction that a combinination of MD amplification of cortical connectivity with a specific input that drives initial synchrony is sufficient to generate a sequential categorical representation, was experimentally validated (Extended Data Figure 3i,j).
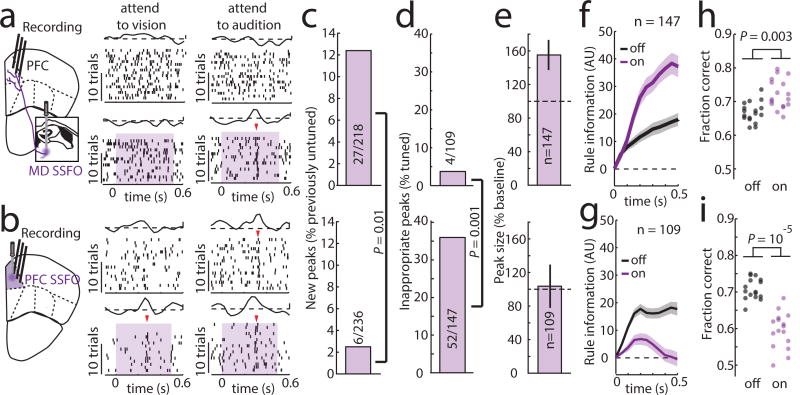
Our model showed that enhancing MD excitability increaseas PFC rule information content by improving tuning of individual cortical neurons, and by recruiting previously untuned ones (Extended Data Figure 9i). This enhancement comes in contrast to rule information reduction when PFC excitability itself is increased because of chain cross-talk (Extended Data Figure 9j). In agreement with the model, we found that SSFO-mediated enhancement of MD excitability led to increased PFC rule information (Figure 4a–f), while enhancing PFC excitability diminished it (Figure 4b–f). Changes in the neural code were also reflected in behavior; enhancing PFC excitability substantially diminished task performance, while boosting MD excitability improved it, with individual mice consistently performing at levels not typically observed in our cohorts absent manipulation (26% reduction in lapse rate, Figure 4h,i). Such enhancement was not found when primary auditory thalamus (medial geniculate body, MGB) activity was activated in the context of auditory discrimination (Extended Data Figure 10), highlighting the utility of the SSFO approach as a diagnostic test for categorical information encoding within neural circuits and the idea that in contrast to the MGB, the MD does not relay such information during attentional control. Even MD neurons that apparently signaled one rule showed emergenece of a peak in the oppsite trial type with local SSFO activation, confirming that such information is not used for task performance (Extended Data Figure 9k, j)
Figure 4. Enhancing MD excitability strengthens PFC rule representation and improves performance.
(a) Optogenetic MD activation causes tuning of previously unturned PFC neurons in the 2AFC delay period, while (b) Optogenetic PFC activation generates inappropriate PFC tuning peaks (shading indicates laser on). (c, d) Quantification of examples in a,b (binomial test). (e) Quantification of existing peak size change (data is mean ± CI) and (f, g) rule information within the PFC following MD or PFC activation (n = 2 mice). (h, i) Opposing performance effects of he two manipulations (n = 16 sessions each from 4 mice).). Shading indicates 95% confidence intervals (see methods). Behavioral data is presented as session averages and compared using Wilcoxon rank-sum test.
Overall, our study describes how a thalamic circuit amplifies local cortical connectivity to sustain attentional control. This function may be general to cognitive processes that require extended cortical representations in time (Supplemental Discussion 4 and 5). Because other thalamic circuits are thought to enhance connectivity between cortical areas1, the precise engagement of the thalamus in a cognitive process may determine which cortical regions process information locally and which ones are engaged when processing spans multiple cortical nodes. Future studies aimed at testing this idea will undoubtedly provide a new way of thinking about cognition where the thalamus forms a functional backbone that sustains, coordinates and switches distributed cortical computations.
Methods
Animals
A total of 43 male mice were used in this study and the figure contribution of each mouse is summarized in Supplemental table 1. All mice tested were between 2 and 12 month of age. C57Bl/6J (WT) mice were purchased from Taconic Biosciences and VGAT-ChR2 mice were obtained from the Jackson laboratories. VGAT-cre mice were backcrossed to C57Bl/6J mice for at least six generations. All mice were kept on a 12 h light-dark cycle. All animal experiments were performed according to the guidelines of the US National Institutes of Health and the Institutional Animal Care and Use Committee at the New York University Langone Medical Center.
Behavioral Training and Testing
Behavioral setup
Behavioral training and testing took place in grid-floor mounted, custom-built enclosures made of sheet metal covered with a thin layer of antistatic coating for electrical insulation (dimensions in cm: length: 15.2; width: 12.7; height: 24). All enclosures contained custom-designed operant ports, each of which was equipped with an IR LED/IR phototransistor pair (Digikey, Thief River Falls, MN) for nose-poke detection. Trial initiation was achieved through an ‘initiation port’ mounted on the grid floor 6 cm away from the ‘response ports’ located at the front of the chamber. Task rule cues and auditory sweeps were presented with millisecond precision through a ceiling mounted speaker controlled by an RX8 Multi I/O processing system (Tucker-Davis Technologies, Alachua, FL). Visual stimuli were presented via two dimmable, white light emitting diodes (Mouser, El Cajon, CA) mounted on each side of the initiation port and controlled by an Arduino Mega microcontroller (Ivrea, Italy). For the 2AFC and 4AFC tasks, two and four response ports were mounted at the angled front wall 7.5 or 5 cm apart, respectively. Response ports were separated by 1 cm divider walls and each was capable of delivering a milk reward (10μl evaporated milk delivered via a single-syringe pump (New Era Pump Systems, Farmingdale, NY) when a correct response was performed. For the auditory Go/NoGo task environment, response and reward ports were dissociated, with the reward port placed directly underneath the response port. In the 4 AFC, the two outermost ports were assigned for “select auditory” responses whereas the two innermost ports were assigned for “select visual” responses. Access to all response ports was restricted by vertical sliding gates which were controlled via a servo motor (Tower Hobbies, Champaign, IL). The TDT Rx8 sound production system (Tucker Davis Technologies, Alachua, FL) was triggered through MATLAB (MathWorks, Natick, MA), interfacing with a custom written software running on an Arduino Mega (Ivrea, Italy) for trial logic control.
Training
Prior to training, all mice were food restricted to and maintained at 85%–90% of their ad libitum body weight.
2AFC
Training was largely similar to our previously described approach8:
First, 10 µL of evaporated milk (reward) was delivered randomly to each reward port for shaping and reward habituation. Making response ports accessible signaled reward availability. Illumination of the LED at the spatially-congruent side was used to establish the association with visual targets on half of the trials. On the other half, association was established with the auditory targets where an upsweep (10–14 kHz, 500 ms) indicated a left and a downsweep (16–12 kHz, 500 ms) indicated a right reward. An individual trial was terminated 20 s after reward collection, and a new trial became available 5 s later.
Second, mice learned to poke in order to receive reward. All other parameters remained constant. An incorrect poke had no negative consequence. By the end of this training phase, all mice collected at least 20 rewards per 30 minute session.
Third, mice were trained to initiate trials. Initially, mice had to briefly (50 ms) break the infra-red beam in the initiation port to trigger target stimulus presentation and render reward ports accessible. Trial rule (‘attend to vision’ or ‘attend to audition’) was indicated by 10 kHz low-pass filtered white noise (vision) or 11 kHz high-pass filtered white noise (audition) sound cues. Stimuli were presented in blocks of 6 trials consisting of single-modality stimulus presentation (no conflict). An incorrect response immediately rendered the response port inaccessible. Rewards were available for 15 s following correct poking, followed by a 5 s inter-trial interval (ITI). Incorrect poking was punished with a time-out, which consisted of a 30 s ITI. During an ITI, mice could not initiate new trials.
Fourth, conflict trials were introduced, in which auditory and visual targets were co-presented indicating reward at opposing locations. Four different trial types were presented in repeating blocks: (1) three auditory-only trials, (2) three visual-only trials, (3) six conflict trials with auditory target, and (4) six conflict trials with visual target. The time that mice had to break the IR barrier in the initiation port was continuously increased over the course of this training stage (1–2 weeks) until it reached 0.5 s. At the same time, duration of the target stimuli was successively shortened to a final duration of 0.1 s. Once mice performed successfully on conflict trials, single-modality trials were removed and block length was reduced to three trials.
On the final stage of training, trial availability and task rule were dissociated. Broadband white noise indicated trial availability, which prompted a mouse to initiate a trial. Upon successful initiation, the white noise was immediately replaced by either low-pass or high-pass filtered noise for 0.1s to indicate the rule. This was followed by a delay period (variable, but for most experiments it was 0.4sec) prior to target stimuli presentation. All block structure was removed and trial type was randomized. Particular steps were taken throughout the training and testing periods to ensure that mice used the rules for sensory selection (see Supplemental Discussion 2).
4AFC
The first two training steps were identical to the 2AFC training, except that auditory stimuli consisted of tone clouds (interleaved pure tones (50 ms per tone over 200 ms, 36 tones total) spanning a frequency range of 1–15 kHz) directed to the left or right ear of the mouse to indicate the side of reward delivery. On the third training stage, after initiation training mice were trained to recognize the difference between visual and auditory response port positions, training on one modality occurred while access to the set of response ports for the other modality was blocked. All other parameters were as previously described in the 2AFC. Once mice successfully oriented to both target types (about 2 weeks), all four response ports were made available for subsequent training. Choosing a response port of the wrong modality was punished by a brief air puff delivered directly to the response port. Mice remained on this paradigm until they reached a performance criterion of 70% accuracy on both modalities.
On the fourth training stage, sensory conflict trials were introduced using the same parameters as in the 2AFC. Trial types and locations were randomized (spatial conflict was also random). Responses were scored as correct or one of three different error types (see confusion matrix Ext. Data Fig. 2e).
Auditory Go/No-Go
A total of 4 mice were trained. A pair of electrostatic speakers (Tucker Davis Technologies) producing the auditory stimuli were placed outside of the training apparatus and sound stimuli were conveyed via cylindrical tubes to apertures located at either side of the initiation port, allowing stereotypical delivery of stimuli across trials. Trial availability was indicated by a light positioned at the top of the box and trial initiation required a 200 ms continuous interruption of the IR beam in the initiation port to ensure that the animals head was properly positioned to hear the stimuli. Following trial initiation, a second port (the “response port”) was opened and a pure tone stimulus was played. A 20 kHz tone signaled a “Go” response, while frequencies above or below 20 kHz signaled a “No-Go” response. The pure tone stimuli were presented for 300 ms prior to response time, and were pseudo-randomly varied on a trial by trial basis, with trials divided between the “Go” stimulus (~40% of trials) and two “No-Go” stimuli (16 and 24 kHz, ~ 30% of trials per frequency). After stimulus presentation, the response port was made accessible for a 3 second period. In “Go” trials, correct poking within the trial period (“Hit”) rendered the reward port accessible, and reward was subsequently delivered upon poking. For a “Miss” in which the mouse failed to poke within the 3 second period, the reward port remained inaccessible. For a “correct rejection”, which involved withholding a response when “No-Go” stimuli were played, the reward port was made accessible at the end of the 3 second period. For a “False Alarm”, which involved a poke in the response port on a “No-Go” trial, the reward port remained accessible and the next trial was delayed by 15 second time-out, as opposed to the regular 10 second inter-trial interval.
Testing
For electrophysiological recordings and experiments with optical manipulation, testing conditions were equivalent to the final stage of training.
The first cohort of PFC recordings involving ‘manipulation free mice’ included 3 C57Bl6 wild-type mice and 1 VGAT-cre mouse. The VGAT-cre mouse in this cohort, which was also used for experiments involving PFC manipulations, was initially run for an equivalent number of laser-free sessions as the three wild-type mice prior to any manipulation. This design was employed to confirm equivalence in electrophysiological findings across genotypes, and to strengthen the overall conclusions drawn by using transgenic animals. Equivalence across genotypes can be readily appreciated by comparing the 4 PCA plots in Extended Data Figure 1j.
For laser sessions, laser pulses of either blue (473 nm for ChR2 activation) or yellow (560 nm for eNpHR3.0 activation) light at an intensity of 4–5mW (measured at tip of the optic fibers) were delivered pseudo-randomly on 50% of the trials. During most optogenetic experiments, laser stimulation occurred during the whole delay period (500 ms) of the task For temporal-specific manipulations concurrent with electrophysiological recordings (Figure 1k,l, Figure 2e,f, Extended Data Figure 4, Extended Data Figure 6), laser pulses were delivered for 250 ms either during the first half, after 100 ms (following cue presentation) or the latter half of the delay period. In the high resolution optogenetic inactivation experiment (Figure 2h) laser pulses were 100 ms long, dividing the 500 ms delay period equally into 5 periods. During a session, only one condition was tested. For step function opsin (SSFO, hChR2(C128S/D156A)) experiments (Figures 5, 6 and Extended Data Figure 8), a 50 ms pulse of blue (473 nm, 4 mW intensity) light at the beginning of the delay period was delivered to activate the opsins and a 50 ms pulse of red (603 nm, 8 mW intensity) light to terminate activation at the end of the delay period. Similarly, for MGB manipulations (Extended Data Figure 10), SSFO was activated by a 50 ms pulse blue (473 nm, 4 mW intensity) light prior to stimulus delivery and its activity was terminated by a 50 ms pulse of red (603 nm, 8 mW intensity) at stimulus offset. An Omicron-Laserage lighthub system (Dudenhofen, Germany) was used for all optogenetic manipulations.
Behavioral analysis
For all experiments with optogenetic manipulations only sessions where baseline performance was at ≥ 65% correct were included in the analysis. For all behavioral testing, single mouse statistics were initially used to evaluate significance and effect size followed by statistical comparisons across sessions. Performance on the auditory Go/No-Go task was assessed based on the number of correct responses to “Go” stimuli (hit rate) relative to “No-Go” stimuli (false alarm rate) and was considered sufficient if the overall discrimination index (d′ = Z(hit rate) – Z(false alarm rate)) was greater than 2 for the baseline condition. In cases where multiple groups were compared, Kruskal-Wallis one way analysis of variance (ANOVA) was used to assess variance across groups, followed by post-hoc testing. For pairwise comparisons Wilcoxon rank-sum test was used. Data is presented as mean ± sem and significance levels were set to p < 0.05.
Virus Injections
Injections were performed using a quintessential stereotactic injector (QSI, Stoelting, Wood Dale, IL). All viruses were obtained through UNC Chapel Hill, virus vector core. For prefrontal manipulation during electrophysiological recordings, 200 nL of AAV2-hsyn-DIO-ChR2 was injected bilaterally into the PFC of VGAT-cre mice. Bilateral injections of AAV1-hsyn-eNpHR3.0-eYFP (300 nL) were used for MD and LGN manipulations. For SSFO experiments, AAV1-CamKIIa-SSFO-GFP was injected bilateral either into PFC (200 nL) or MD (400 nL). To test the effect of MD activation on functional cortical connectivity we injected the MD with AAV1-CamKIIa-SSFO-GFP (400nL) ipsilateral and the PFC with AAV1-hsyn-ChR2-eYFP (200 nL) contralateral to the recording site. Following virus injection, animals were allowed to recover for at least 2 weeks for virus expression to take place before the start of behavioral testing or tissue collection.
Optic fiber implants for behavioral experiments
Mice were deeply anesthetized using 1% isoflurane. For each mouse, up to three pairs of optic fibers (Doric Lenses, Quebec, Canada) were used in behavioral optogenetic experiments and stereotactically inserted at the following coordinates (in mm from Bregma): PFC: A/P: 2.6, M/L: ±0.25, D/V: −1.25; MD: A/P: 1.4, M/L: ±0.6, D/V: −1.5; LGN: A/P: −2.2, M/L: 2.15 mm, D/V 2.6. Up to 3 stainless-steel screws were used to anchor the implant to the skull and everything was bonded together with dental cement. Mice were allowed to recover with ad libitum access to food and water for one week after which they were brought back to food regulation and behavioral training resumed. A 473nm laser was used for ChR2 activation while eNpHR3.0 activation was achieved with a laser of 561nm wavelength. Laser intensities were adjusted to be 4–5mW measured at the tip of the optic fiber which was generally the minimal intensity required to produce behavioral effects.
Multi-electrode array construction and implantation
Custom multi-electrode array scaffolds (drive bodies) were designed using 3D CAD software (SolidWorks, Concord, MA) and printed in Accura 55 plastic (American Precision Prototyping, Tulsa, OK) as described previously21. Prior to implantation each array scaffold was loaded with 12–18 independently movable microdrives carrying 12.5μm nichrome (California Fine Wire Company, Grove Beach, CA) stereotrodes or tetrodes. Electrodes were pinned to custom designed 96-channel electrode interface boards (EIB, Sunstone Circuits, Mulino, OR) along with a common reference wire (A-M systems, Carlsborg, WA). For combined optogenetic manipulations and electrophysiological recordings of PFC, optic fibers delivering the light beam lateral (45 degrees angled tips) were embedded adjacent to the electrodes (Extended Data Figure 3g). In the case of combined optogenetic PFC manipulations with MD recordings, the optic fiber was placed away from the electrodes at the appropriate spatial offset. For combined unilateral multi-site recordings of PFC and MD (4 mice) with SSFO manipulations, two targeting arrays (0.5 × 0.5 mm for PFC and 0.5 × 0.35 mm for MD) where separated by 3.2 mm in the A/P axis. For SSFO manipulations, optic fibers delivering a lateral light beam were implanted directly next to the array targeting either PFC or MD. To test the impact of MD activation on functional cortical connectivity, a single electrode array was targeted to the PFC unilaterally while a 400 μm core optic fiber (Doric Lenses, Quebec, Canada) was targeted to the contralateral PFC. In addition, a 200 μm core optic fiber was placed 2.8 mm behind the electrode array for activating SSFO in the ipsilateral MD. Similarly, to interrogate the same question in a sensory thalamocortical circuit, an electrode array was implanted unilaterally into V1 and an additional 400 μm core optic fiber (Doric Lenses, Quebec, Canada) was targeted to the contralateral V1. In addition, a 200 μm core optic fiber was placed 0.5 mm anterior to the electrode array for activating SSFO in the ipsilateral LGN. During implantation, mice were deeply anesthetized with 1% isofluorane and mounted on a stereotaxic frame. A craniotomy was drilled centered at A/P 2 mm, M/L 0.6 mm for PFC recordings (~1 × 2.5 mm), at A/P −3 mm, M/L 2.5 mm for V1 (1.5 × 1.5) or at A/P −1 mm, M/L 1.2 mm for MD recordings (~2 × 2 mm). The dura was carefully removed and the drive implant was lowered into the craniotomy using a stereotaxic arm until stereotrode tips touched the cortical surface. Surgilube (Savage Laboratories, Melville, NY) was applied around electrodes to guard against fixation through dental cement. Stainless steel screws were implanted into the skull to provide electrical and mechanical stability and the entire array was secured to the skull using dental cement.
Electrophysiological Recordings
Signals from stereotrodes (cortical recordings) or tetrodes (thalamic recordings) were acquired using a Neuralynx multiplexing digital recording system (Neuralynx, Bozeman MT) via a combination of 32- and 64-channel digital multiplexing headstages plugged to the 96 channel EIB of the implant. Signals from each electrode were amplified, filtered between 0.1 Hz and 9 kHz and digitized at 30 kHZ. For thalamic recordings, tetrodes were lowered from the cortex into MD −2.8 – −3.2 mm D/V over the course of 1–2 weeks. For PFC recordings, adjustments accounted for the change of depth of PL across the anterior-posterior axis. Thus, in anterior regions, unit recordings were obtained −1.2 – −1.7 mm D/V whereas for more posterior recordings electrodes were lowered −2 – −2.4 mm D/V. Following acquisition, spike sorting was performed offline based on relative spike amplitude and energy within electrode pairs using the MClust toolbox (http://redishlab.neuroscience.umn.edu/mclust/MClust.html). Units were divided into fast spiking (FS) and regular spiking (RS) based on waveform characteristics as previously described21. Briefly, peak to trough time was measured in all spike waveforms, and showed a distinct bimodal distribution (Hartigan’s dip test, p < 10–5). These distributions separated at 210 µs, and cells with peak to trough times above this threshold were considered RS and those with peak to trough times below FS cells (Extended data Figure 1g). The majority of cells (2727) in PFC recordings were categorized as RS while approximately one third (909) were categorized as FS.
Histology
For histological verification of electrode position, drive implanted mice were lightly anesthetized using isoflorane and small electrolytic lesions were generated by passing current (10 µA for 20 s) through the electrodes. All mice were then deeply anesthetized and transcardially perfused using phosphate buffered saline (PBS) followed by 4% paraformaldehyde. Brains were dissected and postfixed overnight at 4°C. Brain sections (50 µm) were cut using a vibratome (LEICA, Buffalo Grove, IL) and fluorescent images were obtained on a confocal microscope (LSM800, Zeiss, Thornwood, NY). Confocal images are shown as maximal projection of 10 confocal planes, 20 µm thick.
Analysis of Firing Rate
For all PFC and MD neurons, changes in firing rate associated task performance were assessed using peri-stimulus time histograms (PSTH). PSTHs were computed using 10 ms bin width for individual neurons in each recording session4 convolved with a Gaussian kernel (25 ms full width at half maximum) to create a spike density function (SDF30,31) which was then converted to z-score by subtracting the mean firing rate in the baseline (500 ms prior to event onset) and dividing by the variance over the same period. For comparison of overall firing rates across conditions, trial number and window size were matched between groups. Homogeneity of variance for firing rates across conditions was determined using Fligner and Killeen test of homoscedasticity32. For comparisons of multiple groups, Kruskal-Wallis one way analysis of variance (ANOVA) was used to assess variance across groups prior to pairwise comparisons.
Identification of peaks in task-modulated neurons
A total of 3444 single units were recorded within the PFC and 974 single units were recorded in the MD across animals. Overall assessment of firing rates during the task delay period showed that individual RS PFC neurons did not exhibit sustained increases in spiking relative to baseline (population shown in Extended Data Figure 1) and comparison of variance homoscedasticity (Fligner/Kileen test) did not reveal changes in variance. In a subset of cells, however, a brief enhancement of spiking timing consistency at a defined moment in the delay period was observed (Figure 1b). To formally identify these neurons we employed several steps:
First, periods of increased consistency in spike-timing across trials were identified using a Matching-Minimization algorithm33. This approach was used to determine the best moments of spike time alignment across trials (candidate tuning peaks). The number of these candidate tuning peaks (n) was based on firing rate values during the delay period for each neurons. n was obtained by minimizing the equation:
| (1) |
Where nk is the number of observed spikes in a trial k. As such, the initial (and maximum) number of candidate peaks is equal to the median number of spikes observed across trials.
With an initial number of candidate peaks in hand, their times were subsequently estimated. These times were initially placed randomly within the delay window, and iteratively adjusted to obtain the set of final candidate peak times. The result of this iterative process was the solution to the equation:
| (2) |
Where the set of final candidate peak times S is obtained by iteratively minimizing the temporal distance between candidate peak times (in each iteration) C and the observed spike times across trials Sk based on a penalty associated with increased temporal distance, computed across all trials k. In the first step, temporal adjustment for each candidate peak time was based on finding the local minimum of the temporal distance function, d2 (as described in33) after which spikes were adjusted by linear interpolation. Briefly, neighboring spike times across trials were sorted by their temporal offset to a given candidate peak time, and their linear fit was computed. Each candidate peak time was then moved to the midpoint of that fitted line, to achieve a local minimum. In a second step, cost minimization was jointly computed for all putative peaks using the Lagrange multiplier solution to the global minimization equation33 and intervals between peak times were adjusted based on this global minimum. Both the local and the global steps minimization steps were iterated until the spike time variance, defied as the sum of the squared distances between spikes across trials, converged and a set of final candidate peak times were determined.
Next, to identify genuine tuning peaks, we applied two further conditions. First, for 75% of the trials, at least one spike was required to fall within ± 25 ms of each final candidate peak time. This conservative threshold was based on the median firing rates observed during the delay (~10 Hz) predicting that inter-trial spike distances will be greater than 50 ms if spikes were randomly distributed, making it highly unlikely to fulfill this condition by chance. Second, these candidate peaks needed to exhibit z-score values of > 1.5 (equivalent to 1 sided test of significance) to be considered genuine tuning peaks. The z-score of spiking across trials during the delay was computed relative to the pre-delay 500 ms baseline (10 ms binning, convolved with a 25 ms full width at half-maximum gaussian kernel). Obtaining a genuine tuning peak identified a unit as task-modulated, which was subsequently used for most analyses in this study. The vast majority of units only exhibited a single tuning peak using this method. Independent validation of this method’s validity is discussed in Supplemental discussion 1.
Principle Component and Linear Regression Analysis of Population Code
To estimate the extent to which task modulated units differentially encode task rules, Principal Component (PC) analysis was first performed as described previously10. Next, linear regression was applied to define the two orthogonal, task related axes of rule type and movement direction. These analyses were performed on neural z-score time series, separately for each comparison (trials separated by rule type or movement direction). Briefly, a data matrix X of size Nunit × (Ncondition*T), was constructed in which columns corresponded to the z-scored population response vectors for a given task rule or movement direction at a particular time (T) within the 1 second window following task initiation. This window size was chosen to provide sufficient samples for analysis, but only the delay period data were examined for this study.
The contribution of each PC to the population response across time was quantified by projecting trial type-specific z-score time series (e.g. ‘attend to vision’ rule) onto individual PCs and computing the variance. The first PC was used for all subsequent analyses as subsequent PCs were found to be uninformative in initial analysis.
Multi-variable linear regression was applied to determine the contribution of task rule and subsequent movement to PC divergence across time for the corresponding trial type comparisons. Specifically, linear analysis related the response of unit i at time t to a linear combination of these two task variables using the following equation:
| (3) |
Where ri,t(k) is the z-score response for a neuron in trial set (k) for each task variable; movement and rule. The regression coefficients (β) were used to describe the extent to which z-score time series variation in the firing rate of unit at a given time point describes a particular task variable. This analysis was generally only applied to correct responses.
Regression coefficients were then used to identify dimensions in state space corresponding to variance across neural response data for the two task variables. Vectors of these coefficients across z-score time series matrices separated by trial types (e.g. rule1 vs. rule 2) were projected onto subspaces spanned by the previously identified PC.
We next constructed task-variable axes ( ) using QR-decomposition to identify PC separation associated with each task variable (v). To identify movement along these axes for each population response, their associated z-score time series were projected onto these axes across time as follows:
| (4) |
Where Xc is the population vector for trial type c. This projection resulted in two time-series vectors pv,c for each task variable that compared movement across trial types (rule1 vs. rule 2; right vs. left) on their corresponding axes. The difference between these two time-series was used as the main metric for information (task rule or movement) in this study. For evaluating rule information in error trials when their number permitted analysis (>20 error trials; based on empirical assessment of minimum trial numbers required for PC divergence), trial type axes obtained from correct trials were multiplied by −1 to reverse directionality. The significance bounds for all time-series were obtained using random subsampling and bootstrapping (~60% of total neurons per bootstrap, 200 replications). The 95% confidence bounds at each time point were then estimated based on the resulting distribution. To determine whether our inference that rule information was related to tuning peaks, task-modulated spike times were randomly jittered by 500ms and PC analysis repeated. This resulted in loss of rule information-related PC divergence, validating our inference.
Peak Strength Analysis
To obtain a quantitative estimate of peak fidelity across multiple trials, an internal neural synchrony measure34 modified for short-term synchrony associated with identified peaks. This approach was applied to spike trains associated with differing task conditions and responses. Each spike within the train was convolved with a gaussian kernel with a 9 ms half width. Trials were then summed and divided by the kernel peak size and trial number giving a maximum value (for perfect alignment) of 1 at any point. Convolution vector values around the tuning in the baseline condition were compared to the value within the same time window in the other condition.
Cross-Correlation Analysis
To compute cross-correlation histograms (cross-correlograms), the MATLAB function crosscorr was applied to whole-session spike trains from pairs of cells. Continuous traces at 1 kHz sampling rate were first generated based on spike times, with times at which spikes occurred set to one and all other times to zero. Crosscorr was then applied to trains from all possible cell pairs, using a maximum lag time of ± 50 ms.
The significance of a cross-correlogram was determined by randomly jittering all spike times independently and re-computing the cross-correlogram. Jitter values were drawn from a Gaussian distribution centered at zero with a standard deviation of 3 ms. This process was repeated 100 times for each pair, and if the observed peak cleared the 95% confidence bounds of all shuffled sets, the pair was determined to have a significant cross-correlation.
Pairs of cells were grouped as follows: the control group was composed of cells in which only the first cell was rule-tuned. The test group was composed of pairs in which both cells were tuned. This test group was further broken down into two subgroups: one in which both cells responded to the same rule and one in which the cells responded to different rules.
Within these groups, co-modulation was defined as the number of significant cross-correlograms divided by the total number of cross-correlograms. After overall group comparison using a chi-square test, proportion differences were statistically evaluated in a post-hoc pairwise fashion using the binomial proportion tests
To examine the effect of tuning to the same rule on co-modulation strength, the distributions of cross-correlogram peak heights were also compared for the groups of pairs described above. An empirical CDF was constructed using the peak heights of each group, and these distributions were compared using a sign-rank test.
Finally, the relationship between cross-correlogram peak height and inter-alignment time was explored. The inter-alignment times among neuronal pairs tuned to the same rule were calculated by taking difference in spike alignment times of each pair.
In order to more effectively assess putative monosynaptic connections, the significant cross-correlograms between tuned pairs were also re-computed at a 50 microsecond resolution. Significance thresholding at this resolution was repeated by determining whether a sequence of two or more successive bins of the adjusted trace which exceeded two standard deviations of the overall trace occurred within 10 ms of the center bin19. Cross-correlograms containing such outliers were further characterized based on their peak times. Those with peaks at 300 microseconds or later were categorized as putative monosynaptic connections18,19. Among these putative connections, the pairs were split into two groups: those that were tuned to the same rule, and those that were tuned to opposite rules. To compare peak strength, spike probability was estimated by subtracting a shuffled distribution of spike times with the same average firing rate as the postsynaptic neuron and dividing by the number of spikes in the presynaptic neuron17. The distributions of the resulting peak strengths among same rule and opposite rule putative monosynaptic connections were compared using the Kolmogorov-Smirnov test. Finally, the peak strengths of these pairs were plotted against their inter-alignment time. As in the above analysis, only same rule pairs were included.
Non-Linear Decoding Analysis
To further assess the degree of rule representation in the PFC and MD, we applied two population decoding approaches, the maximum correlation coefficient (MCC) and Poisson Naïve Bayes (PNB) classifiers as implemented in the neural decoding toolbox35. These analyses were applied to all tuned neurons recorded from either structure each of which were pooled into a pseudo-population for each structure (N = 604 PFC and N = 156 MD). For MCC decoding, firing rate response profiles in individual correct trials associated with each rule were preprocessed by converting them to Z-score using the mean and variance in the corresponding trial in order to prevent baseline spike-rate differences from impacting classification36. For PNB classification, neuron spiking activity was modeled as a Poisson random variable with each neuron’s activity assumed to be independent. Trial-specific Z-scores (MCC) or spike counts (PNB) from these pseudo-populations were then repeatedly and randomly subsampled (200 resampling runs) and divided into training and test subsets (6 training and 2 test trials per recording session across n = 360 PFC and n = 116 in MD sessions). For each subsampling, the classifier was trained using the training subset to produce a predictive mean response template ( ) for each rule (i). Templates were constructed separately for 100 ms overlapping windows across the trace (step size = 20 ms) and classifiers trained for each template. The windowed classifiers allowed us to estimate the temporal evolution of information in the population. In the cross-validation step, these templates were used to predict the class for each test trial in the test set (x*) by maximizing the correlation decision function ([ ]) in the case of MCC or the log likelihood decision function ([ ]) in the case of the PNB classifier37. Finally, we estimated the predictive strength of population activity at each time point, that is the extent to which activity in that time bin predicts the trial type, as the average of the correct predictions in the test-set. To determine the variability of this estimate, a bootstrapping procedure was applied in which 25% of neurons were subsampled from the overall population and the same procedure was repeated (50 resampling runs). The resulting traces were used to estimate the 95 % confidence intervals of the initial estimate from the full population.
Granger Causality Analysis
In order to determine the degree of causal connectivity in the ensemble of recorded neurons within the PFC or their counterpart in our simulated network, we employed Weiner-Granger vector autoregressive (VAR) causality analysis as implemented in the multivariate granger causality toolbox (MVGC)25. Spike train data from each recorded or simulated neuron within a session was converted to a continuous signal by binning at 1 ms increments38,39 and convolving the resulting signal with a Gaussian filter (half width 5 ms). For all neurons in individual sessions, this analysis used 500 ms segments either within the delay period (delay) or just prior (task engagement) along with an equal number of randomly selected segments recorded outside of the behavioral environment (out of task). For assessment of laser effects, a matched number of correct trials in the laser and non-laser condition were compared for each recording session across neurons. To improve stationarity in the signal, segments were adjusted by subtracting the mean and dividing by the standard deviation of each segment38,40 and stationarity was checked by determining whether the spectral radius of the estimated full model was less than one25. All models met this stationarity criteria. Model order was estimated empirically for each subset using Bayesian information criteria (BIC) after which VAR model parameters were determined for the selected model order. Based on the resulting parameters, time-domain conditional granger causality measures were calculated for each pair of cells across all trials. Causal density for a given condition in each session was taken as the mean pairwise-conditional causality25.
Connectivity Assay
To assess the impact of changes in thalamic excitability on cortical connection strength, we measured intra-cortical responses evoked by ChR2-mediated activation of the contralateral cortex for V1/LGN (94 neurons in 2 mice) and PFC/MD (96 neurons in 3 mice). Responses to either cortical stimulation alone (10 ms ChR2 activation to the contralateral cortex), thalamic activation alone (500 ms SSFO activation in ipsilateral LGN or MD) or the combination were recorded in V1 and PFC (100 interleaved trials per condition). For the combined condition, thalamic activation preceded cortical stimulation by 100 ms.
Computational Modeling
Network Structure and dynamics
We constructed a model that consisted of excitatory (RS) and inhibitory (FS) PFC neurons as well as MD neurons. Within the PFC, RS cells formed subnetworks representing each task rule consisting of multiple interconnected chains. Neurons in each of these chains were locally connected to their nearest neighbor within the chain as well as to other chains within the same subnetwork. While neurons representing different rules were connected, connections were made stronger within each subnetwork (e.g. among neurons representing the same rule) based on our cross-correlation experimental data. RS neurons of either rule sent overlapping projection to MD neurons and received reciprocal inputs from MD. MD inputs were modulatory with a longer time constant than PFC (1ms vs. 10ms), and resulted in increased FS spiking (direct synaptic drive: w = 0.6) while providing an amplifying input (factor: x1.6) to connections between RS neurons (regardless of rule tuning).
During Rule encoding, the arrival of input attributed to one rule simultaneously activated the starter neuron (first neuron in a chain) in chains encoding that rule, engaging MD neurons and enhancing their firing through synaptic convergence. In turn, MD neurons enabled signal propagation that was specific to that rule by amplifying currently active RS neuronal connections, while preventing irrelevant synchrony elsewhere through augmented inhibition.
Spiking neuron model
We employed the leaky integrate-and-fire (LIF) model to simulate both of the network paradigms described above. LIF is a simplified spiking neuron model that is frequently used to mathematically model neuron’s electrical activity. One can write the evolution of the membrane voltage of neuron j using LIF equation as follows:
| (5) |
where C is the membrane capacitance, Vj is the jth neuron’s membrane voltage, α is the leak conductance (α =0.95). Iext is an externally applied current with amplitude taken independently for each neuron from a uniform distribution (μ = 0.825, SD=0.25 for PFC and MD neurons). Ijsyn is the synaptic input to cell j, and it is defined as follows:
| (6) |
where ωij represents the strength of the connection between presynaptic cell i and the postsynaptic neuron j; Aij is the connectivity matrix that denotes the connectivity map. τ is the spike duration (1ms in our simulations) and the H(t) is a Heaviside function that is zero for negative values (t< τ) and one for positive values(t> τ). In this model the voltage across the cell membrane grows, and after it reaches a certain threshold (Vth=1), the cell fires an action potential, and its membrane potential is reset to the reset voltage. Here, the resting-potential (E) and reset-potential Vreset are set to zero. The neuron enters a refractory period (Tref=1.5 ms) immediately after it reaches the threshold (V=Vth) and spikes. To integrate the LIF equation, we employed the Euler method with step size of Δt=0.01ms. To reproduce the spontaneous activity of the network, we introduced a noise that arrives randomly at each cell with a predefined probability (fN =10Hz).
Code Availability
All computer code used for analysis and simulation in this study was implemented in MATLAB computing software (MathWorks, Natick, MA). Code will be made freely available to any party upon request. Requests should be directed to the corresponding author.
Statistical Analysis
For each statistical analysis provided in the manuscript, an appropriate statistical comparison was performed. For large sample sets Kolmogorov–Smirnov normality test was first performed on the data to determine whether parametric or non-parametric tests were required. Variance testing for analysis involving comparisons of firing rates under differing behavioral conditions and following optogenetic manipulations employed the Fligner/Killeen test of variance homoscedasticity. For small sample sizes (n < 5) non-parametric tests were used by default. Two different approaches were used to calculate the required sample size. For studies in which sufficient information on response variables could be estimated, power analyses were performed to determine the number of mice needed. For sample size estimation in which effect size could be estimated, the sample number needed was estimated using power analysis in MATLAB (sampsizepwr) with a β of 0.7 (70%). For studies in which the behavioral effect of the manipulation could not be pre-specified, including optogenetic experiments, we used a sequential stopping rule41. This method enables null-hypothesis tests to be used in sequential stages, by analyzing the data at several experimental points using non-parametric pairwise testing. In these cases, the experiment initially uses a small cohort of mice which are tested over multiple behavioral sessions. If the P value for the trial comparison across mice falls below 0.05, the effect is considered significant and the cohort size is not increased. If the P value is greater than 0.36 following four sessions that met criteria, the investigator stopped the experiment and retained the null hypothesis. Using this strategy, the required number of animals was determined to be between three and five animals per cohort across testing conditions. For multiple comparisons, non-parametric ANOVA (Kruskal-Wallis H-test) was performed followed by pairwise post-hoc analysis All post-hoc pairwise comparisons were two sided. No randomization or investigator blinding was done for experiments involving electrophysiology. Blinding was utilized for experiments involving SSFO and behavior (MD vs. PFC).
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Extended Data
Extended Data Figure 1. Behavioral and electrophysiological features reflected in the 2 AFC task.
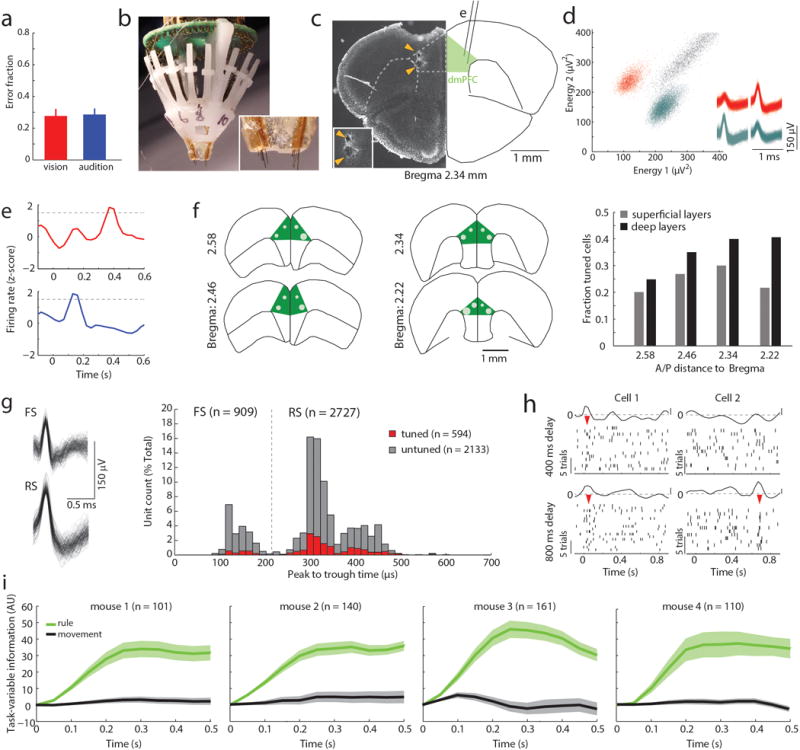
(a) Mice display equal performance across trial types (n = 4 mice, p = 0.52, Wilcoxon rank-sum). (b) Multi-electrode implant used for PFC neural recordings. Inset: magnification showing electrodes. (c) Postmortem histology in an example brain showing electrode tip locations (arrowheads). (d) Example of spike sorting in energy space to identify single units. Two identified clusters reflect two single units (color coded). Inset: Corresponding spike-waveforms. (e) In 17% of rule-tuned cells, tuning is observed for both task rules (example PSTHs shown), albeit with distinct temporal offsets during the delay. (f) Schematic showing electrode locations from which rule-tuned neurons (white dots) were recorded, illustrating that they are most frequently found in deeper layers. Dot sizes are scaled in proportion to the number of tuned neurons found at that location (n = 594 cells from 4 mice). (g) Fast spiking (FS) and regular spiking (RS) neurons are identified based on the peak to trough time of their spike waveform (left: example waveforms, right: peak to through time histogram, dashed line represents cut off for FS - RS classification21,29). (h) Example rasters and PSTHs for two cells during delay periods of either 400 or 800 ms, randomized within the same recording session. In the first, an early peak is present in both conditions (left) while in the other a late peak is only evident in the 800 ms condition (right). (i) Task-variable information for each mouse of our first cohort (‘manipulation free’). Task-variable information is based on PCA from the divergence of population activity of task modulated PFC neurons on the axis associated with each variable (see methods) and is highly informative for task rule (green) but contains no information about movement (side selection, grey). Shaded areas indicate the bootstrapped 95% confidence intervals.
Extended Data Figure 2. Behavioral errors are primarily driven by inappropriate rule encoding.
(a) Mice show comparable performance on trials with one target modality presented compared to performance in conflict trials (n = 4 mice, P = 0.81). (b) Example PSTHs of a neuron whose appropriate tuning to the ‘attend to vision’ rule is observed in error trials of the ‘attend to audition’ rule. (c) Rule information derived from PCA of sessions in which sufficient numbers of errors allowed for their analysis (93 neurons, 18 sessions from 4 mice) show that they contain information about the other rule; directionality of rule-related axis in error trials are along the same axis used in correct trials (see methods). Shaded areas indicate bootstrapped 95% CIs. (d) Schematic of the 4-alternative forced choice (4AFC) task developed to distinguish between errors related to rule encoding (executive) and those related to target cue perception (sensory, see methods). Visual and auditory targets are reported at different response port pairs (inner versus outer), making it possible to distinguish between outcomes in which the animal makes a selection based on prior cueing, the spatial location of sensory targets, both, only one or neither (e) 4AFC task outcomes illustrated in a confusion matrix showing outcomes conditional upon sensory target modality and location. Note that sensory conflict is not specified for these trials, as it can be either spatially congruent or in conflict with the appropriate target (f) Executive errors represent the majority of those observed, accounting for about 50% of all errors across mice (n = 4 mice). Dashed line represents chance performance (25%). All behavioral data was compared using Wilcoxon rank-sum test.
Extended Data Figure 3. Combining PFC recordings with local optogenetic control of inhibitory interneurons.
(a) Tuning peak examples of multiple PFC neurons simultaneously recorded in a single recording session. Tuning peaks associated with either rule occur at multiple times across the delay period in different neurons suggesting precisely timed, sequential activation. (b) Top: Two examples of a short-latency cross-correlation (shuffle corrected; see methods) observed between pairs of tuned neurons. Bottom: Histogram of cross-correlation peak times (n = 914 pairs). (c) Increased connection probability between tuned neurons (all: 914 pairs, tuned: 97 pairs, same rule: 50 pairs, diff rule: 47 pairs, comparison with binomial test). (d) Cross-correlation strength is significantly greater for neurons representing the same rule. (e) Co-modulation probability and (f) strength show dependence on temporal distance between tuning peaks among same rule-representing pairs (n = 138). (g) Photograph of a multi-electrode implant used to record from PFC with simultaneous optogenetic manipulation. Inset: top, enlargement of the drive component targeting bilateral PFC with optic fibers and electrodes; bottom, enlargement showing electrodes and optic fiber for one hemisphere. (h) Examples of an FS neuron that is driven (top) and an RS neuron that is inhibited (bottom) by exposure to blue light (blue bar, 473 nm). (i) Quantification of laser effects on FS and RS cell firing rate shows that this holds true at the population level (albeit with the population mean of RS being generally smaller than the example). Grey shading represents 95% CI of the no laser condition. (j) Top: example task-modulated spike rasters showing laser effect on tuning peak. Bottom: Visualization of peak strength measure for these examples (see methods).
Extended Data Figure 4. Causal evidence for task-specific sequential PFC activity maintaining rule representation.
(a) Impact of bilateral optogenetic enhancement of local inhibition on PFC rule tuning and behavior. (a1) Raster and PSTH examples of neurons tuned either early or late in the delay (blue shading indicates laser presentation), shows loss of tuning with minimal impact on overall spiking (see Extended Data Figure 3i for quantification of laser on spike rates). (a2) Laser impact on population tuning measured by averaged peak sizes over the delay (n = 94 neurons, 3 mice; example quantification in Extended Data Figure 3j; see method for peak quantification) (a3) Laser impact on population rule information from the same neurons in a2. (a4) Laser impact on behavior (n = 12 sessions; 4 from each mouse) (b-d) Temporally-limited optogenetic manipulations show that later PFC tuning is dependent on early tuning. (b) Manipulation limited to the first 250 ms is sufficient to mimic effect of full delay period suppression on neural tuning with a smaller impact on behavior likely due to a smaller laser dose and being close to the optical fibers (n = 52 neurons, 12 sessions). (c) Effect in b persists even when rule presentation period is spared (n = 46 neurons, 12 sessions). (d) Late laser only impacts late activity (n = 53 neurons, 12 sessions). (e) Cartoon of experimental comparison of the effect of sensory selection rule presentation inside and outside of the task. (f1) Example of two neurons that display tuning following rule-related cue presentation inside the task but not outside of it. (f2) Group quantification for population tuning in f1 (n = 52 neurons from 3 mice). For peak size, shaded error regions show the 95% CIs of the measure, while the gray bar denotes the subsampled bootstrapped 95% CIs for baseline error estimate. For rule information shaded areas indicate bootstrapped 95% CIs. Wilcoxon rank-sum test was used for all behavioral comparisons.
Extended Data Figure 5. Optogenetic dissection of error types in the 4AFC task.
(a) Inactivation of PFC in four VGAT-ChR2 mice during the delay period specifically increases executive errors while sensory errors remain comparable. (b) MD inhibition leads to a similar increase in executive errors. (c) In contrast, LGN inactivation specifically increases sensory errors in ‘attend to vision’ trials while executive errors remain comparable. Colored bars show median values and dots represent average performance of each mouse (4–5 sessions per mouse. Error bars were not included for visual clarity. Wilcoxon rank-sum test was used for all comparisons.
Extended Data Figure 6. MD recruitment by PFC is related to delay period length in the 2AFC task.
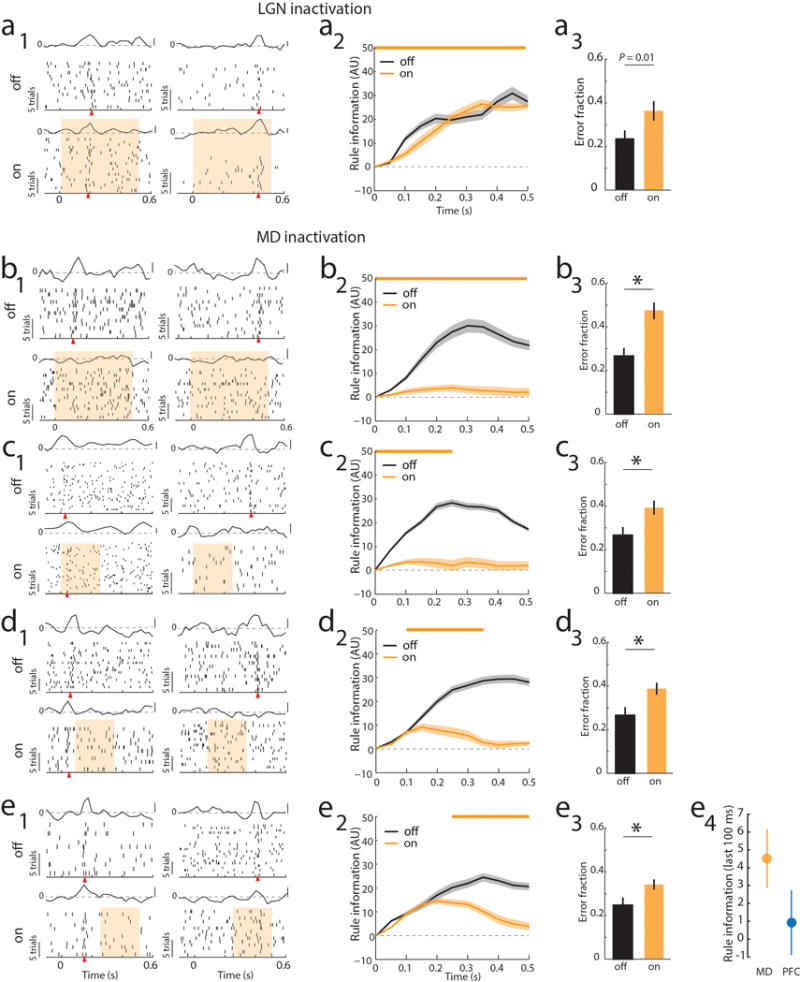
(a) Bilateral optogenetic LGN suppression through activation of NpHR3.0 (yellow bar) had no effect on PFC tuning during the delay period but did increase errors in the 2AFC task. (a1) Raster and PSTH examples of neurons tuned either early or late in the delay (yellow shading indicates laser presentation), shows that rule tuning persists during LGN inactivation. (a2) Laser impact on population rule information over the delay (n = 33 cells, 2 mice). (a3) Laser impact on behavior (n = 2 mice, 3 sessions each). (b–e) MD suppression using the same approach as in LGN leads to loss of tuning and disrupts behavioral performs. Data is presented as example units (b1-e1), followed by PCA for the laser on vs. off conditions (b2–e2) and behavioral impact (b3–e3). e4 shows the direct comparison between late PFC (Extended Data 4, d2) suppression and late MD suppression (e2) on PFC rule information in the last 100 ms (mean ± 95% CIs).
Extended Data Figure 7. Connectivity pattern and response profile of MD and PFC neurons.
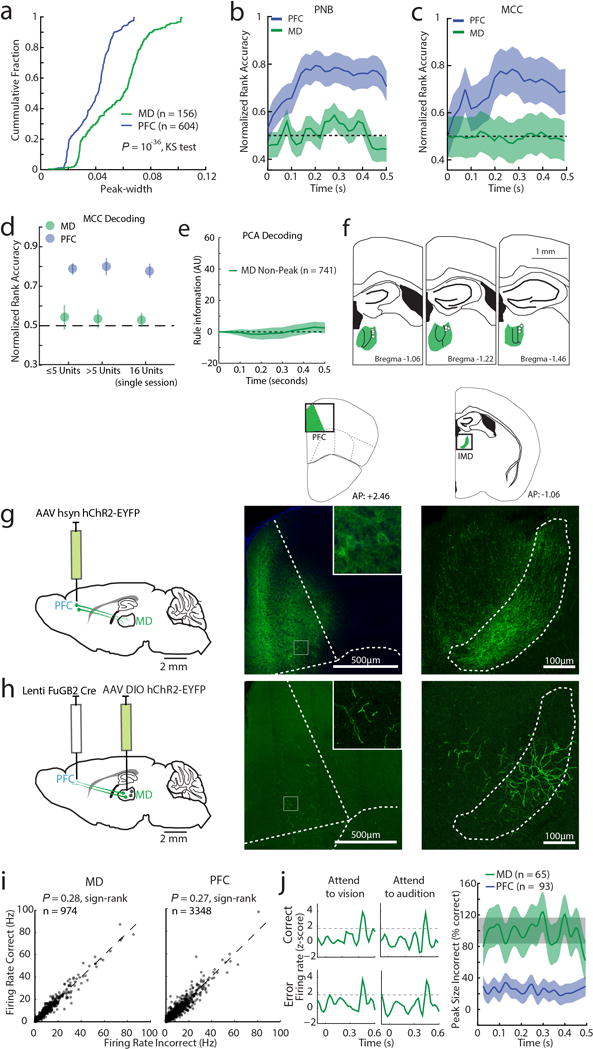
(a) Cumulative distributions of neuronal peak widths (measured as full width to half maximum, FWHM) for MD and PFC. Two non-linear decoding methods (b) Poisson Naïve Bayes (PNB) and (c) maximum correlation coefficient (MCC) fail to reveal rule information among tuned MD neurons (PFC: n = 604 neurons, 6 mice, MD: n = 156 neurons, 3 mice). (d) Rule information obtained from non-linear decoding does not depend on the number of simultaneously recorded neurons: Decoding of rule information among tuned MD and PFC neurons is similar in sessions containing 1–5 neurons (PFC: n = 318 neurons, 6 mice, MD: n = 73 neurons, 3 mice) and sessions containing greater than 5 neurons (PFC: n = 286 neurons, 6 mice, MD: n = 83 neurons, 3 mice). Similar results were obtained in single sessions with the highest population of simultaneously recorded MD neurons containing temporal peaks (n = 16), and an equivalent session containing the same number of simultaneously recorded tuned PFC neurons. Error bars are 95% CI. (e) Rule information is not encoded by MD neurons that do not show peaks. (f) Schematic diagram showing that tetrodes yielding MD neurons with peaks were located exclusively in lateral MD (white dots). (g) Anterograde labeling of PFC shows that their terminals are located in lateral MD. (h) Retrograde labeling from PFC identifies cells in lateral MD. Insets show enlarged view. (i) Firing rates are comparable in correct and incorrect trials for MD (left) or PFC (right) neurons. (j) Left: example PSTH of a single MD neuron in correct or error trials showing similar peaks across all conditions. Right: Quantification of peak size for the same rule in incorrect trials shows that MD peaks are retained while PFC peaks are diminished. Shade indicates 95% bootstrapped confidence intervals.
Extended Data Figure 8. MD→PFC and PFC→MD pathways are functionally asymmetric.
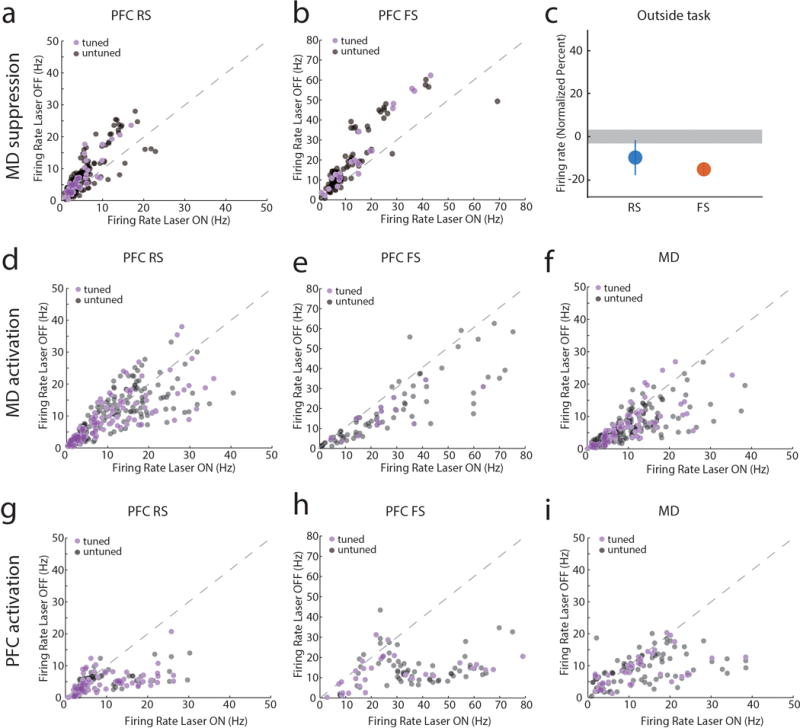
(a, b) Scatter plots comparing firing rates of PFC neurons during the delay period with and without MD suppression (each data point represents a neuron). (a) RS and (b) FS cells significantly show reduced firing when MD is optogenetically suppressed during the task delay period (P < 0.001). (c) In contrast, MD suppression outside of the task only reduces FS firing rates (RS: n = 245 neurons, FS: n = 114 neurons, data is presented as mean ± CI, grey shading indicates 95% CI of null distribution). (d) Increasing excitability in MD through activation of SSFOs has no effects on RS neuronal firing rate (n = 303 neurons, P > 0.05) but (e) significantly increases FS spiking (n = 131 neurons, P < 0.001) and (f) MD spiking (n = 254 neurons, P = 0.001). (g) The same manipulation in PFC increased firing rates in cortical RS neurons (n = 140 neurons, P < 0.001), (h) FS neurons (n = 91 neurons, P < 0.001) and (i) MD neurons (n = 111 neurons, P = 0.004). (j) All scatter plot data was compared using Wilcoxon signed-rank test. Other than panel c, the scatter plots are the raw data used for the normalized values in Figure 3.
Extended Data Figure 9. Experimental and modeling results clarifying the novel attributes of the MD/ PFC network.
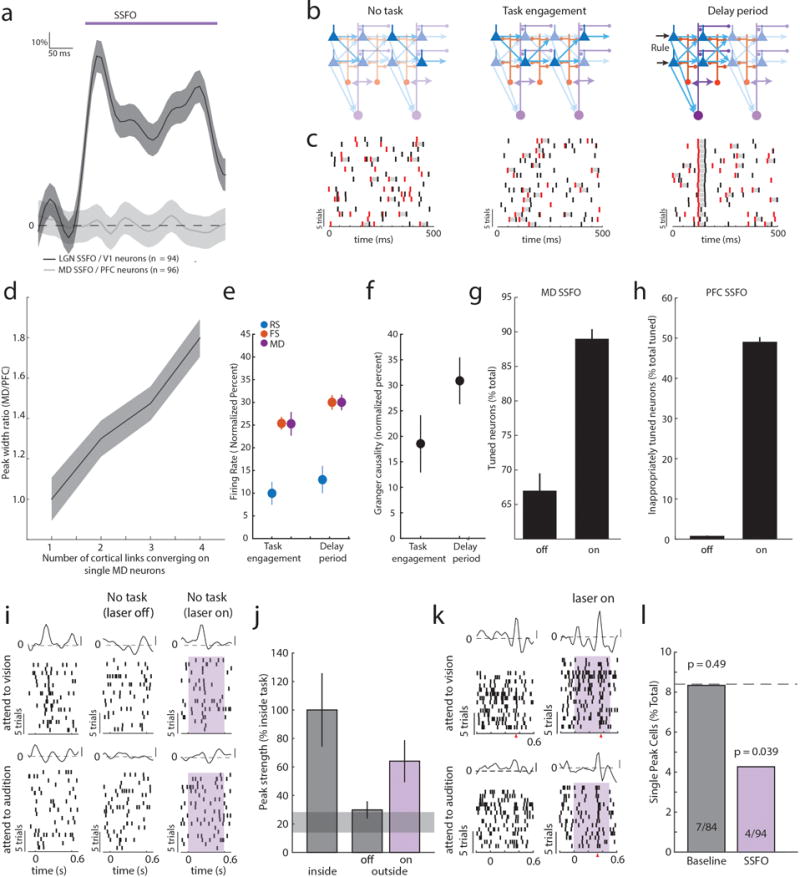
(a) While LGN activation drives spiking in V1, MD activation does not drive spiking in PFC. (b) Schematic of the conceptual model based on the data showing MD, cortical FS and RS neurons in the three different conditions: outside task, task engaged and during the delay period. Triangles represent PFC RS cells that are all tuned to a single rule, and send convergent input to MD neurons (purple). MD sends a modulatory like signal that enhances spiking in FS cells and amplifies connections among RS cells. Task engagement enhances MD activity and in turn FS neural activity. Rule information is simulated as synchronized input to starter RS neurons, which triggers convergent input onto one another, as well as that on MD, resulting in progression of the RS neural sequence in time. (c) Example data from spiking neural model capturing illustration in (b): spike rasters of two RS cells (red: cell 1 and black: cell 2) at different positions within a chain showing corresponding changes in activity during the three conditions. Note that overall spike rates don’t change, but coordinated spiking (gray shadings) increases. (d) Systematically exploring the degree of convergence in the MD/PFC model suggests that 3–4 links in the PFC chain converge onto individual MD neurons (n = 250 neurons, 3 simulations per condition). (e) The model captures the firing rate and (f) connectivity changes observed experimentally. (g) In the modeled MD/PFC network, enhancing excitability in MD neurons by 10% significantly increases the number of rule tuned cells in the PFC population (n = 250 neurons, 10 simulations, data is mean ± SEM, P = 0.002, Wilcoxon rank-sum). (h) Enhancing excitability in the PFC population by 8% drastically increased the proportion of neurons that show inappropriate tuning to both rules (n = 250 neurons, 10 simulation, P = 0.002, Wilcoxon rank-sum). (i) Example spike raster from a neuron tuned to one rule, showing that MD activation is sufficient to generate appropriate tuning outside the task. (j) Population data shows that MD activation is sufficient to partially generate tuning outside the task (n = 2 mice, 31 tuned neurons). Grey shading indicates 95% CI of null distribution. All data is presented as mean ± 95% CI, separation indicates P < 0.05. (k) Example of the effect of SSFO-based activation on an MD neuron containing only one peak showing the addition of a second peak at the same timepoint in the opposite trial type. (l) Relative to the population average (8.4%, dotted line), MD neurons showed significantly fewer single peaks in the SSFO condition despite the presence of an average number of single peaks in the same neurons without SSFO (cumulative binomial test vs population average, p values as shown).
Extended Data Figure 10. Behavioral effects of excitability changes in MGB.
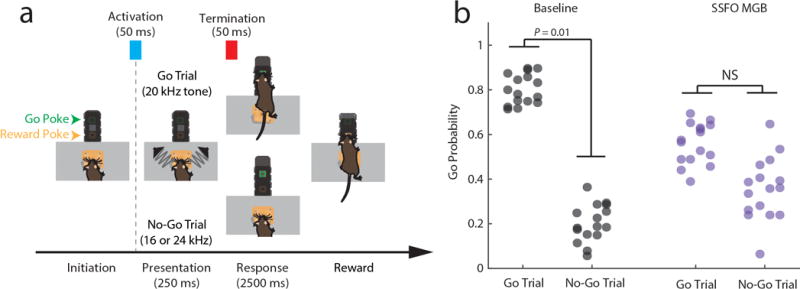
(a) Diagram showing task design and SSFO activation/termination timing in a Go/No-Go auditory discrimination task (see methods for task description). (b) Comparison showing the probability of a “Go” response after either “Go” or “No-Go” stimuli were presented across sessions (points) and mice (columns). NS: P = 0.52 non-significant, Wilcoxon signed-rank test.
Supplementary Material
Acknowledgments
We thank J.A. Movshon, D.J. Heeger, M.A. Wilson, C.D. Brody and E.K. Miller for helpful discussions. L.I.S is supported by a NARSAD young investigator award and R.D.W. by a fellowship from the Swiss National Science Foundation. M.N. is supported by a JSPS fellowship. M.M.H. is supported by grants from NIMH, NINDS, Brain and Behavior, Sloan and Klingenstein Foundations as well as the Human Frontiers Science Program.
Footnotes
Author Contributions
L.I.S. designed experiments, performed behavioral studies, analyzed the physiological data and contributed to writing the manuscript. R.D.W. designed the 4AFC task, performed the physiological recordings, analyzed behavioral data and contributed to writing the manuscript. M.N. validated viral tools, performed tracing studies and contributed to behavioral training. M.H. assisted L.I.S. with analysis. S.M. performed the modeling. M.M.H. conceived experiments and analyses, interpreted the data and wrote the manuscript.
Conflict of interest
The authors declare no conflict of interest.
References
- 1.Ito HT, Zhang SJ, Witter MP, Moser EI, Moser MB. A prefrontal-thalamo-hippocampal circuit for goal-directed spatial navigation. Nature. 2015;522:50–55. doi: 10.1038/nature14396. [DOI] [PubMed] [Google Scholar]
- 2.Parnaudeau S, et al. Inhibition of mediodorsal thalamus disrupts thalamofrontal connectivity and cognition. Neuron. 2013;77:1151–1162. doi: 10.1016/j.neuron.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Xu W, Sudhof TC. A neural circuit for memory specificity and generalization. Science. 2013;339:1290–1295. doi: 10.1126/science.1229534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kuramoto E, et al. Individual mediodorsal thalamic neurons project to multiple areas of the rat prefrontal cortex: A single neuron-tracing study using virus vectors. The Journal of comparative neurology. 2016 doi: 10.1002/cne.24054. [DOI] [PubMed] [Google Scholar]
- 5.Rubio-Garrido P, Perez-de-Manzo F, Porrero C, Galazo MJ, Clasca F. Thalamic input to distal apical dendrites in neocortical layer 1 is massive and highly convergent. Cerebral cortex. 2009;19:2380–2395. doi: 10.1093/cercor/bhn259. [DOI] [PubMed] [Google Scholar]
- 6.Sherman SM. Thalamus plays a central role in ongoing cortical functioning. Nature neuroscience. 2016;16:533–541. doi: 10.1038/nn.4269. [DOI] [PubMed] [Google Scholar]
- 7.Hoover WB, Vertes RP. Anatomical analysis of afferent projections to the medial prefrontal cortex in the rat. Brain structure & function. 2007;212:149–179. doi: 10.1007/s00429-007-0150-4. [DOI] [PubMed] [Google Scholar]
- 8.Wimmer RD, et al. Thalamic control of sensory selection in divided attention. Nature. 2015;526:705–709. doi: 10.1038/nature15398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lundqvist M, et al. Gamma and Beta Bursts Underlie Working Memory. Neuron. 2016 doi: 10.1016/j.neuron.2016.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature. 2013;503:78–84. doi: 10.1038/nature12742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Goldman MS. Memory without Feedback in a Neural Network. Neuron. 2009;61:621–634. doi: 10.1016/j.neuron.2008.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Harvey CD, Coen P, Tank DW. Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature. 2012;484:62–68. doi: 10.1038/nature10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ikegaya Y, et al. Synfire chains and cortical songs: temporal modules of cortical activity. Science. 2004;304:559–564. doi: 10.1126/science.1093173. [DOI] [PubMed] [Google Scholar]
- 14.Long MA, Jin DZ, Fee MS. Support for a synaptic chain model of neuronal sequence generation. Nature. 2010;468:394–399. doi: 10.1038/nature09514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rajan K, Harvey CD, Tank DW. Recurrent Network Models of Sequence Generation and Memory. Neuron. 2016;90:128–142. doi: 10.1016/j.neuron.2016.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bartho P, et al. Characterization of neocortical principal cells and interneurons by network interactions and extracellular features. Journal of neurophysiology. 2004;92:600–608. doi: 10.1152/jn.01170.2003. [DOI] [PubMed] [Google Scholar]
- 17.Csicsvari J, Hirase H, Czurko A, Buzsaki G. Reliability and state dependence of pyramidal cell-interneuron synapses in the hippocampus: an ensemble approach in the behaving rat. Neuron. 1998;21:179–189. doi: 10.1016/s0896-6273(00)80525-5. [DOI] [PubMed] [Google Scholar]
- 18.Hatsopoulos NG, Ojakangas CL, Paninski L, Donoghue JP. Information about movement direction obtained from synchronous activity of motor cortical neurons. Proceedings of the National Academy of Sciences of the United States of America. 1998;95:15706–15711. doi: 10.1073/pnas.95.26.15706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Young ED, Sachs MB. Auditory nerve inputs to cochlear nucleus neurons studied with cross-correlation. Neuroscience. 2008;154:127–138. doi: 10.1016/j.neuroscience.2008.01.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cossell L, et al. Functional organization of excitatory synaptic strength in primary visual cortex. Nature. 2015;518:399–403. doi: 10.1038/nature14182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Halassa MM, et al. State-dependent architecture of thalamic reticular subnetworks. Cell. 2014;158:808–821. doi: 10.1016/j.cell.2014.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Browning PG, Chakraborty S, Mitchell AS. Evidence for Mediodorsal Thalamus and Prefrontal Cortex Interactions during Cognition in Macaques. Cerebral cortex. 2015;25:4519–4534. doi: 10.1093/cercor/bhv093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Preuss TM, Goldman-Rakic PS. Crossed corticothalamic and thalamocortical connections of macaque prefrontal cortex. The Journal of comparative neurology. 1987;257:269–281. doi: 10.1002/cne.902570211. [DOI] [PubMed] [Google Scholar]
- 24.Alcaraz F, Marchand AR, Courtand G, Coutureau E, Wolff M. Parallel inputs from the mediodorsal thalamus to the prefrontal cortex in the rat. The European journal of neuroscience. 2016;44:1972–1986. doi: 10.1111/ejn.13316. [DOI] [PubMed] [Google Scholar]
- 25.Barnett L, Seth AK. The MVGC multivariate Granger causality toolbox: a new approach to Granger-causal inference. Journal of neuroscience methods. 2014;223:50–68. doi: 10.1016/j.jneumeth.2013.10.018. [DOI] [PubMed] [Google Scholar]
- 26.Kim S, Putrino D, Ghosh S, Brown ENA. Granger causality measure for point process models of ensemble neural spiking activity. PLoS computational biology. 2011;7:e1001110. doi: 10.1371/journal.pcbi.1001110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yizhar O, et al. Neocortical excitation/inhibition balance in information processing and social dysfunction. Nature. 2011;477:171–178. doi: 10.1038/nature10360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Crick F, Koch C. Constraints on cortical and thalamic projections: the no-strong-loops hypothesis. Nature. 1998;391:245–250. doi: 10.1038/34584. [DOI] [PubMed] [Google Scholar]
- 29.Gardner RJ, Hughes SW, Jones MW. Differential spike timing and phase dynamics of reticular thalamic and prefrontal cortical neuronal populations during sleep spindles. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2013;33:18469–18480. doi: 10.1523/JNEUROSCI.2197-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fries P, Neuenschwander S, Engel AK, Goebel R, Singer W. Rapid feature selective neuronal synchronization through correlated latency shifting. Nature neuroscience. 2001;4:194–200. doi: 10.1038/84032. [DOI] [PubMed] [Google Scholar]
- 31.Szucs A. Applications of the spike density function in analysis of neuronal firing patterns. Journal of neuroscience methods. 1998;81:159–167. doi: 10.1016/s0165-0270(98)00033-8. [DOI] [PubMed] [Google Scholar]
- 32.Wimmer K, Nykamp DQ, Constantinidis C, Compte A. Bump attractor dynamics in prefrontal cortex explains behavioral precision in spatial working memory. Nature neuroscience. 2014;17:431–439. doi: 10.1038/nn.3645. [DOI] [PubMed] [Google Scholar]
- 33.Wu W, Srivastava A. Towards statistical summaries of spike train data. Journal of neuroscience methods. 2011;195:107–110. doi: 10.1016/j.jneumeth.2010.11.012. [DOI] [PubMed] [Google Scholar]
- 34.Golomb D, Rinzel J. Dynamics of globally coupled inhibitory neurons with heterogeneity. Physical review. E, Statistical physics, plasmas, fluids, and related interdisciplinary topics. 1993;48:4810–4814. doi: 10.1103/physreve.48.4810. [DOI] [PubMed] [Google Scholar]
- 35.Meyers EM. The neural decoding toolbox. Frontiers in neuroinformatics. 2013;7:8. doi: 10.3389/fninf.2013.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang Y, et al. Object decoding with attention in inferior temporal cortex. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:8850–8855. doi: 10.1073/pnas.1100999108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Duda RO, Hart PE, Stork DG. Pattern Classification. Vol. 18. Wiley; 2001. [Google Scholar]
- 38.Cadotte AJ, DeMarse TB, He P, Ding M. Causal measures of structure and plasticity in simulated and living neural networks. PloS one. 2008;3:e3355. doi: 10.1371/journal.pone.0003355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zagha E, Ge X, McCormick DA. Competing Neural Ensembles in Motor Cortex Gate Goal-Directed Motor Output. Neuron. 2015;88:565–577. doi: 10.1016/j.neuron.2015.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ding M, Bressler SL, Yang W, Liang H. Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment. Biological cybernetics. 2000;83:35–45. doi: 10.1007/s004229900137. [DOI] [PubMed] [Google Scholar]
- 41.Dejean C, et al. Prefrontal neuronal assemblies temporally control fear behaviour. Nature. 2016;535:420–424. doi: 10.1038/nature18630. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.