SHAPE BASED IMAGE RECONSTRUCTION USING LINEARIZED DEFORMATIONS

Abstract

We introduce a reconstruction framework that can account for shape related a priori information in ill-posed linear inverse problems in imaging. It is a variational scheme that uses a shape functional defined using deformable templates machinery from shape theory. As proof of concept, we apply the proposed shape based reconstruction to 2D tomography with very sparse measurements, and demonstrate strong empirical results.

1. Introduction and motivation

It is well known that utilizing a priori information is critical in addressing inverse problems where data is very noisy or the problem is highly ill-posed, with the latter often due to inappropriate sampling of data. Regularization by providing an approximate inverse is far from the best choice for solving such challenging problems. Most current approaches focus on enforcing sparsity and/or regularity within a variational setting, see [33] for a survey.

Recognizing and interpreting shapes of structures in images is essential for translating images into knowledge. Furthermore, in many imaging problems the user has a priori information about what shapes to expect, whereas noise and reconstruction artifacts are less likely to fit into the a priori shape information. To illustrate this, consider electron tomography (ET) that uses an electron microscope to image the internal 3D structural arrangement at nano-scale of a specimen. Imaging by ET leads to a severely ill-posed inverse problem with incomplete and highly noisy data [27]. However, scientists often have an idea of the rough overall shape of the structures they seek to image in ET. As an example, consider a biological specimen containing antibodies that we seek to image. Here, one knows beforehand that antibodies are approximately “Y”-shaped. In a similar way, if the specimen contains virions that we seek to image, then often one has a priori shape information about these virions, e.g., they can be “near-spherical” with certain symmetry (like icosahedral) or they may form helical rod-like structures. This can often be seen in data.

To summarize, it makes sense to account for qualitative a priori shape information while performing the reconstruction in imaging. It is clear that enforcing an exact spatial match between sub-structures and a given template is asking for too much since realistic shape information is almost always approximate as in ET. More concretely, consider imaging near-spherical viruses embedded in aqueous buffer by ET. It would be erroneous to perform reconstruction in ET while enforcing that these sub-structures are spheres. Instead, a more natural approach is to perform reconstruction assuming the structures are ‘near-spherical” in some sense. This highlights the challenge associated with accounting for a priori shape information, namely to properly quantify shape similarity.

2. Survey of the field

The idea of accounting for shape information in reconstruction is gaining increasing interest within the inverse problems community. This is part of an ongoing development in which the reconstruction and feature extraction steps are combined when solving ill-posed inverse problems. Features are in this context specific structures in images relevant for the interpretation. Feature extraction is usually part of image analysis and powerful tools have been developed over the years to interpret images.

2.1. Joint segmentation and reconstruction

A step towards combined reconstruction and feature extraction is joint segmentation and reconstruction. One approach is to consider a level-set based approach where the true (unknown) image is assumed to be piecewise constant. In this setting one may consider joint segmentation and reconstruction by minimizing a Mumford–Shah like functional over the set of admissible contours and, given a fixed contour, over the space of piecewise constant densities which may be discontinuous across the contour within each level set [3]. This approach was applied to 2D inversion of the ray transform in [28] from complete data. A key step lies in the calculation of the “shape sensitivity” in order to find a descent direction for the cost functional, which in turn leads to an update formula for the contour in the level-set framework. Motivated in part by the inverse problem in ET, the approach was later generalized and applied to very noisy limited angle and region of interest tomography data in [16]. See also [15, 35] for further developments of the Mumford–Shah approach involving a variety of inverse problems in imaging. Another line of development is based on incorporating priors about the desired classes of the segmentation through a probabilistic model. Here, a hidden Markov measure field model has been used, see [26, 17, 29] for variants of this approach.

A drawback with these variational formulations is that they are computationally demanding. Furthermore, they also lead to non-convex problems, so there is always the issue of non-uniqueness. An entirely different approach for joint segmentation and reconstruction, that in part circumvents these problems, is provided in [19]. Here the approximate inverse method is extended to the setting where one recovers the features directly. It assumes the features in question can be extracted by applying an operator, which may be be a differential operator for calculating partial derivatives or the Laplacian, or it may be the solution operator for the heat equation for fixed time, or it may be a wavelet transform. The approach is however limited to features that can be extracted by applying a linear extraction operator on the image.

In general, the papers cited above demonstrate that joint reconstruction and segmentation typically leads to better results than performing the two steps successively, especially in inverse problems where there are high noise levels and/or data is incomplete.

2.2. Shape based reconstruction

The next natural step that follows joint segmentation and reconstruction is to consider the shape. A priori shape information often includes geometrical information about the structure in the image, so the reconstruction scheme has to capture such information.

One approach is based on describing such geometric information by means of invariants that carry geometrical information about the structures. Such invariants have been successfully used for shape based classification, see, e.g. [21, 1] and [40, Chapter 3]. There is in fact an axiomatic treatment for constructing invariant image features [18] useful for recognizing objects from different viewpoints and whose numerical values are equal or only moderately affected by basic image transformations. Returning to image reconstruction, [10] shows how such integral invariants can be used in reconstruction. The idea is to encode the a priori shape information in a variational setting by introducing the 2-norm of the difference between the invariant of the structure and the invariant of a prior. The main mathematical result is proof of existence of minimizers of the corresponding goal functional. The optimization is performed with a gradient descent approach that requires differentiating the goal functional and the actual numerical implementation is based on minimizing a smooth approximation functional, which converges (Γ–convergence) to the original functional.

Another approach for variational mage reconstruction that includes a priori shape information is given in [11]. Here, one constructs an energy functional based on local segmentation information obtained by segmentation and comparison with a known spatial model. The approach is demonstrated on tomography data from digital phantoms, simulated data, and experimental ET data of virus complexes.

An approach very similar to the one considered here is given in [2]. There, the authors propose a variational scheme for shape based reconstruction using a deformable template. The scheme is applied to emission tomography. Once a template is chosen, the activity map (the function describing the isotope intensity that one seeks to recover) is assumed to be a deformation of the template obtained through composition with various planar mappings together with a magnitude adjustment. Hence, just like we will do, they consider linear deformations of the form (5). On the other hand, in their approach the linear deformations are given by their wavelet coefficients whereas we will consider linear deformations given by vector fields in a reproducing kernel Hilbert spaces (RKHSs). Furthermore, [2] contains no analysis of existence or uniqueness.

3. Contribution of the paper

Our approach is heavily inspired by the deformable templates framework where shape is modeled as a deformation of a template. Shape based reconstruction can then be seen as an image matching problem in which a shape template in the image domain is matched against a given target representing indirect observations (data) in the imaging problem. There is by now a rich literature for variational methods for image matching, see, e.g., [5, 32, 31, 8]. Some parts of this theory is also used for reconstruction, most notably for spatiotemporal imaging as outlined in subsection 11.6. On the other hand, the usage for shape based reconstruction is yet to be explored more systematically.

This paper initiates such a study and the starting point is linearized deformations, which are among the simplest forms of deformations. Our main mathematical result is a proof of existence of minimizers. As with most other variational schemes for shape based reconstruction, we cannot expect uniqueness in general due to lack of convexity. We also explicitly calculate the shape derivatives of the functionals, both in the continuum setting and when the objective functional is discretized through finite span approximations of linearized deformations contained in a reproducing kernel Hilbert space. The latter can be of interest in actual numerical implementation since minimizers of objective functionals in the finite dimensional setting will in this case also give a minimizer to the objective functionals in the infinite dimensional setting (Remark 4). We also show the impact of using a priori shape information. The experiments strongly point to the improvement of using shape based information in reconstruction. Furthermore, they also show that the a priori shape information doesn’t have to be that accurate, which is important for the applications targeted by this paper. None of these claims are however proved formally by mathematical theorems. Finally, our variational framework for shape based reconstruction also extends to other deformation models that allow for large deformations, like the one suggested within the large deformation diffeomorphic metric mapping (LDDMM) framework [36, 6, 24, 13, 40, 37, 25] and variants based on relating the LDDMM to optimal transport for a better handling of grey scale values [20, 30]. These result in smooth deformations that preserve the topology and shape based reconstruction using such, more elaborate, deformation models left for future studies.

We conclude with a short overview of the paper. Section 4 introduces terminology and notation needed for variational reconstruction of inverse problems. Section 5 provides a brief introduction to shape theory based on the deformable templates framework, and in particular linearized deformations. Section 6 formulates the shape based reconstruction scheme and in section 7 we prove existence. section 8 contains the gradient calculations of the functionals involved in the variational formulation and section 9 is the corresponding gradients expressed when the linearized deformation is contained in a RKHS. section 10 shows some examples of how the shape based reconstruction scheme performs followed by conclusions given in section 11.

4. Inverse problems, ill-posedness and variational regularization

The goal in image reconstruction is to estimate some spatially distributed quantity (image) from indirect noisy observations (measured data). There are various ways to formalize such a statement and our starting point is the classical (non-statistical) viewpoint on inverse problems.

Image reconstruction as an inverse problem

Recover/reconstruct an image f_true ∈ 𝒳 from data g ∈ ℋ where

$$g=\mathcal{T}(f_{\text{true}})+e.$$ (1)

Here, 𝒳 (reconstruction space) is the vector space of all possible images, so it is a suitable Hilbert space of functions defined on a fixed domain Ω ⊂ ℝⁿ. Next, ℋ (data space) is the vector space of all possible data, which for digitized data is a subset of ℝ^m. Furthermore, 𝒯: 𝒳 → ℋ (forward operator ) models how a given image gives rise to data in absence of noise and measurement errors, and e ∈ ℋ (data noise component) is a sample of a ℋ –valued random element E whose probability distribution is (data noise model ) assumed to be known.

Ill-posedness

A naive approach at recovering the true (unknown) image f_true is to try to solve the equation 𝒯 (f) = g. Often there are no solutions to this equation since measured data is not in the range of 𝒯 for a variety of reasons (noise, modeling errors, e.t.c.). This is commonly addressed by relaxing the notion of a solution by considering

$$\underset{f\in \mathcal{X}}{min}\mathcal{D}(\mathcal{T}(f),g).$$ (2)

The mapping 𝒟: ℋ x ℋ → ℝ₊ (data discrepancy functional) quantifies the data misfit and a natural candidate is to choose it as a suitable affine transformation of the log likelihood of data. In such case, solving (2) amounts to finding maximum likelihood (ML) solutions.

The above approach works well when (2) has a unique solution (uniqueness) that depends continuously on data (stability). This is however not the case when (1) is ill-posed. These are the two main issues addressed by means of regularization, i.e.. to introduce uniqueness and stability by making use of a priori knowledge about f_true in the reconstruction.

Variational regularization

This is a class of regularization methods that have gained much attention lately, and especially so for imaging problems [33]. The idea is to add a penalization to (2):

$$\underset{f\in \mathcal{X}}{min}\mu \mathcal{R}(f)+\mathcal{D}(\mathcal{T}(f),g)\text{given}\mu \ge 0.$$ (3)

The functional ℛ: 𝒳 → ℝ₊ introduces well-posedness (uniqueness and stability) by encoding a priori information about f_true. It often encodes some a priori known regularity property of f_true, e.g., assuming 𝒳 ⊂ ℒ²(Ω,ℝ) and taking the ℒ²-norm of the gradient magnitude (Dirichlet energy) is known to produce smooth solutions whereas taking the ℒ¹-norm of the gradient magnitude (total variation) yields solutions that preserve edges while smooth variations may be suppressed.

5. Shape theory

Shape theory seeks to develop quantitative tools to study shapes and their variability. A key objective is to define a shape metric that quantifies the shape similarity between two objects/structures in the image.

There are a variety of mathematical approaches for modeling shapes, and the approach we consider is based on deformable templates. This approach, which traces back to work pursued in 1917 by D’Arcy Thompson [9], is based on the idea that shapes can be represented as a deformation of a template. A quantitative analysis of shape variability can then be based on quantifying the cost of the deformation. Grenander laid the foundations of pattern theory [12] that was necessary for a coherent mathematical and statistical theory for shape and shape variability based on the above idea of deformable templates. We here provide a very brief introduction to shape theory with emphasis on the linearized deformations framework.

The starting point is to define a set of deformable objects that represent the objects/structures whose shape we seek to analyze. We also define a set of deformations that can act on these deformable objects. In our case, a deformation is given as a diffeomorphic perturbation of the identity map (linearized deformation). Under certain conditions, the set of deformations becomes a group with a metric that can be used together with the group action to quantify the shape similarity between two deformable objects.

5.1. Set of deformable objects

We consider grey scale images as deformable objects, so the set ℳ of deformable objects are a vector space of real-valued functions defined on a fixed underlying image domain Ω ⊂ ℝⁿ (n = 2 for 2D images or n = 3 for 3D images), which we assume to be an open and bounded set. We furthermore assume that ℳ ⊂ ℒ²(Ω,ℝ).

5.2. Set of deformations – Linearized deformations

The set 𝒢_𝒱 of deformations will consist of transformations that map the image domain Ω ⊂ ℝⁿ into ℝⁿ. These “deform” elements in ℳ simply by transforming the underlying coordinate grid.

It is natural to be able to reverse and concatenate deformations, which amounts to requiring that 𝒢_𝒱 forms a group under the group law given by composition of functions and with the identity mapping as the identity element. The group structure also allows us to use the group action, which is a mapping 𝒢_𝒱 xℳ → ℳ formally denoted by (ϕ, f) ↦ ϕ.f, as a canonical way to define how a deformation in 𝒢_𝒱 transforms a deformable object in ℳ. Furthermore, alongside the group structure, we may also require that 𝒢_𝒱 is a vector space over ℝ where the vector space addition and scalar multiplication is given as

$$\begin{array}{l}(\varphi +\psi )(x):=\varphi (x)+\psi (x)\\ (\alpha \varphi )(x):=\alpha \varphi (x)\end{array}$$ (4)

for ϕ, ψ ∈ 𝒢_𝒱 and α ∈ ℝ.

We now consider linearized deformations that are given as

$${\varphi }^{\nu }:={\text{Id}}_{\mathrm{\Omega }}+\nu \text{for}\text{some}\nu \in \mathcal{V}.$$ (5)

Here, $\mathcal{V}\subset {\mathcal{C}}_0^1(\mathrm{\Omega },{ℝ}^n)$ is a fixed Hilbert space with norm ||·||_𝒱. The vector fields (deformation vector fields) in 𝒱 are supported in Ω and have a derivative that tends to zero as x tends to infinity.

Remark 1

The set ${\mathcal{C}}_0^1(\mathrm{\Omega },{ℝ}^n)$ is the Banach space of continuously differentiable vector fields on Ω ⊂ ℝⁿ that along with its derivative vanishes on ∂Ω and at infinity. Note also that these vector fields trivially extended to all of ℝⁿ simply by setting them to zero outside Ω.

Given the Hilbert space $\mathcal{V}\subset {\mathcal{C}}_0^1(\mathrm{\Omega },{ℝ}^n)$, define the set ${\mathcal{G}}_{\mathcal{V}}\subset {\mathcal{C}}_0^1(\mathrm{\Omega },{ℝ}^n)$ as

$${\mathcal{G}}_{\mathcal{V}}:=\left\{\varphi :\mathrm{\Omega }\to \mathrm{\Omega }:\varphi ={\varphi }^{\nu }\text{for}\text{some}\nu \in \mathcal{V}\text{and}{\varphi }^{\nu }\text{is}\text{given}\text{by}(5)\right\}.$$ (6)

If 𝒱 is a vector space closed under composition, then 𝒢_𝒱 is also closed under composition. Elements defined as (5) are however not necessarily invertible unless ν is sufficiently small and regular [40, Proposition 8.6]. In conclusion, 𝒢_𝒱 forms a group only when the linearized deformations in the vector space 𝒱 are small.

Remark 2

If one seeks to ensure that deformations in (5) do not create foldings or holes, then they need to preserve the topology. This naturally leads to the requirement that such deformations be diffeomorphisms. In our setting the issue is that deformations in (5) are not necessarily invertible. If they are, then 𝒢_𝒱 becomes a group of diffeomorphisms and elements in 𝒱 have to be small. To define deformations that are diffeomorphisms without necessarily being small requires considering alternative schemes for generating the deformations. One such approach is provided by LDDMM framework where deformations are generated by an ordinary differential equation with a time dependent velocity field that is contained in 𝒱 at each time point. If 𝒱 has some basic regularity properties, then 𝒢_𝒱 becomes a subgroup to the group of diffeomorphisms, see [40] for the details.

5.3. The deformation operator and shape similarity

Elements in 𝒢_𝒱 represent deformations that act on deformable objects, which in our case are grey scale images on Ω represented by square integrable functions f: Ω → ℝ. One way to let a deformation, i.e., element ϕ ∈ 𝒢_𝒱, act on a grey scale image f is by a group action, say ϕ.f:= f ∘ ϕ. Next, each element in 𝒢_𝒱 has a corresponding element in 𝒱, i.e., ϕ = ϕ^ν for some ν ∈ 𝒱. Hence, elements in 𝒱 acts on deformable objects by means of the deformation operator 𝒲_f: 𝒱 →𝒳 given as

$${\mathcal{W}}_f(\nu ):={\varphi }^{\nu }.f=f\circ {\varphi }^{\nu }\text{for}\nu \in \mathcal{V}$$ (7)

where ϕ^ν ∈ 𝒢_𝒱 is given by (5). The deformation operator models how a grey scale image is deformed by ϕ^ν.

The shape similarity between f and its deformed version 𝒲_f (ν) can now be quantified by ${\Vert \nu \Vert }_{\mathcal{V}}^2$. Note that it is zero only if the deformation is the identity mapping (no deformation) and a large value means ν is large, which in turn corresponds to a large deformation.

6. Shape based reconstruction

Consider the inverse problem in (1) where elements in 𝒳 represent grey scale images defined over some fixed image domain Ω ⊂ ℝⁿ, i.e., ℳ ⊂ 𝒳 ⊂ ℒ²(Ω,ℝ). Next, assume that the true image f_true is approximately a deformation of a known shape template I ∈ ℳ. As we shall see next, the shape functional in subsection 5.3 allows us to use such a priori shape information in the reconstruction of f_true in (1).

Here now assume the true (unknown) image f_true can be written as an admissible deformation of the shape template I, i.e.,

$$f_{\text{true}}={\mathcal{W}}_I(\nu )\text{on}\mathrm{\Omega }\text{for}\text{some}\nu \in \mathcal{V}.$$ (8)

To reconstruct f_true in (1), while accounting for a priori shape information given by (8), we formulate the following variational problem:

$$\underset{\nu \in \mathcal{V}}{inf}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+\mu \mathcal{R}({\mathcal{W}}_I(\nu ))+\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I(\nu )),g\right)\right].$$ (9)

Here, the mapping 𝒟: ℋ xℋ → ℝ₊ is the data discrepancy functional introduced in (2), ℛ: 𝒳 → ℝ₊ is the regularity functional that encodes regularity properties of f_true that are known before hand, and as already mentioned, ${\Vert \nu \Vert }_{\mathcal{V}}^2$ quantifies the shape similarity between the template I and its deformed variant 𝒲_I (ν). Finally, λ ≥ 0 regulates the influence of the a priori shape information and μ ≥ 0 regulates the influence of the a priori regularity properties that f_true might posses.

7. Mathematical analysis

The goal of a mathematical analysis of a reconstruction scheme is to assess if it is a regularization scheme with key formal properties. The first and most important property is whether the reconstruction scheme always has solutions (existence of solutions), since otherwise the scheme is not suitable for reconstruction. Two following properties are concerned with uniqueness and stability, i.e., whether the scheme renders a unique solution for given data and whether it is stable w.r.t. perturbations in data. Finally, the convergence properties of the scheme are concerned with whether the output from the scheme should converge to a (least-squares/maximum likelihood) solution of (2) when the data error (difference between measured data g and ideal data 𝒯 (f_true)) tends to zero in some norm while reconstruction parameters are chosen accordingly.

We will here only consider the key property of existence, and will follow this analysis by some remarks regarding uniqueness. The starting point is to reformulate the variational problem in (9) as an optimization over 𝒱. Then we prove existence of solutions for this latter equivalent optimization, which is now an optimization over 𝒱. The motivation for this approach is that variational problems over 𝒱 are much easier to analyze than those over the group 𝒢_𝒱, mainly due to the natural Hilbert space structure of 𝒱. This also has numerical consequences. It is also difficult to perform an optimization over 𝒢_𝒱 since it is difficult to parametrize elements in 𝒢_𝒱. As we shall see, elements in 𝒱 are more easy to parametrize, especially when 𝒱 is a RKHS.

7.1. Existence

Here we consider existence of solutions to the reconstruction method given by the variational problem in (9).

Theorem 1

Let 𝒱 be a Hilbert space and assume f ↦ 𝒟(𝒯 (f), g) and f ↦ ℛ(f) are both lower semi-continuous on 𝒳. Then, (9) has a solution in 𝒱.

Proof

Let ℰ: 𝒱 → ℝ₊ denote the goal functional in (9), i.e., for given λ, μ ≥ 0 and I ∈ 𝒳, it is defined as

$$\mathcal{E}(\nu ):=\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+\mu \mathcal{R}({\mathcal{W}}_I(\nu ))+\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I(v)),g\right)\text{with}\nu \in \mathcal{V}.$$ (10)

If we can prove that ℰ is lower semi-continuous on 𝒱, then (9) has solutions.

Let {ν_n}_n ⊂ 𝒱 be a minimizing sequence for (9) so ||ν_n||_𝒱 are bounded. 𝒱 is a Hilbert space, so it is in particular a complete metric space with respect to the distance function induced by the inner product. Hence, there is a subsequence, still denoted by {ν_n}_n, that converges weakly to some ν^* ∈ 𝒱 (see [40, Theorem A.16]). By [40, Proposition A.15] we then have

$${\Vert {\nu }^{\ast }\Vert }_{\mathcal{V}}\le \underset{n\to \infty }{liminf}{\Vert {\nu }_n\Vert }_{\mathcal{V}}.$$ (11)

Next, by (5) we get

$$\Vert {\varphi }^{{\nu }_n}(x)-{\varphi }^{{\nu }^{\ast }}(x)\Vert =\Vert {\nu }_n(x)-{\nu }^{\ast }(x)\Vert \text{for}x\in \mathrm{\Omega }.$$

Since ν ↦ ν(x) is a continuous linear form on 𝒱, we conclude that

$$\underset{x\in \mathrm{\Omega }}{limsup}\Vert {\varphi }^{{\nu }_n}(x)-{\varphi }^{{\nu }^{\ast }}(x)\Vert =0.$$

Thus, ϕ^ν is continuous in the weak topology of 𝒱. Furthermore, for every shape template I ∈ ℳ, using the result in the proof of [38, Theorem 2.5] gives us lim sup

$$\underset{x\in \mathrm{\Omega }}{limsup}\Vert {\mathcal{W}}_I({\nu }_n)(x)-{\mathcal{W}}_I({\nu }^{\ast })(x)\Vert =0.$$

Therefore, 𝒲_I is also continuous in the weak topology of 𝒱. Now, by assumption both f ↦ 𝒟(𝒯 (f), g) and f ↦ ℛ(f) are lower semi-continuous on 𝒳. Hence,

$$\mathcal{R}({\mathcal{W}}_I({\nu }^{\ast }))\le \underset{n\to \infty }{liminf}\mathcal{R}({\mathcal{W}}_I({\nu }_n)),$$ (12)

$$\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I({\nu }^{\ast })),g\right)\le \underset{n\to \infty }{liminf}\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I({\nu }_n)),g\right).$$ (13)

(11) together with (12)–(13) implies that ν^* is a solution for the variational problem (9) in 𝒱. This concludes the proof.

7.2. Uniqueness

Even though (9) always has a solution (Theorem 1), we do not have uniqueness. The problem is that there may be multiple solutions even when both

$$f\to \mathcal{R}(f)\text{and}f\to \mathcal{D}(\mathcal{T}(f),g)$$ (14)

are strictly convex. The reason is that the deformation operator 𝒲_f: 𝒱 →𝒳 in (7) introduces non-convexity. It is furthermore a non-trivial task to work out conditions on 𝒱 that would guarantee convexity.

8. Gradient calculations

Performing reconstruction following the scheme outlined in section 6 requires solving the optimization problem in (9). Most computationally feasible approaches make use of first order derivative information, so one central topic is to compute the gradient of the goal functional given in (10). The gradient is calculated w.r.t. the Hilbert structure of 𝒱, which is the natural inner-product space for this minimization. In computing the 𝒱-gradient of the mappings

$$\nu \mapsto \mathcal{R}({\mathcal{W}}_I(\nu ))\text{and}\nu \mapsto \mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I(\nu )),g\right),$$ (15)

we assume the mappings in (14) are both Gâtueaux differentiable and the template I is differentiable.

8.1. The deformation operator

We here provide an explicit expression for the Gâteaux derivative of the deformation operator defined in (7).

Proposition 2

Assume I ∈ 𝒳 is differentiable. Then, the deformation operator 𝒲_I: 𝒱 →𝒳 in (7) is Gâteaux differentiable at ν ∈ 𝒱 and its Gâteaux derivative is

$$\partial {\mathcal{W}}_I(\nu )(\eta )(x)={\langle \nabla I({\varphi }^{\nu }(x)),\eta (x)\rangle }_{{ℝ}^n}\mathit{for}x\in \mathrm{\Omega }\mathit{and}n\in \mathcal{V}.$$ (16)

Proof

The Gâteaux derivative is the linear mapping ∂𝒲_I (ν): 𝒱 →𝒳 defined as

$$\partial {\mathcal{W}}_I(\nu )(\eta ):={\frac{d}{d\epsilon }{\mathcal{W}}_I(\nu +\epsilon \eta )|}_{\epsilon =0}\text{for}\eta \in \mathcal{V}.$$

Hence, ∂𝒲_I (ν)(η): Ω → ℝ where

$$\partial {\mathcal{W}}_I(\nu )(\eta )(x):={\frac{d}{d\epsilon }{\mathcal{W}}_I(\nu +\epsilon \eta )(x)|}_{\epsilon =0}={\frac{d}{d\epsilon }(I\circ {\varphi }^{\nu +\epsilon \eta })(x)|}_{\epsilon =0}\text{for}x\in \mathrm{\Omega }.$$

Now, I ∈ 𝒳 ⊂ ℒ²(Ω,ℝ) is differentiable so the chain rule gives us

$$\partial {\mathcal{W}}_I(\nu )(\eta )(x)={\langle \nabla I({\varphi }^{\nu }(x)),{\frac{d}{d\epsilon }({\varphi }^{\nu +\epsilon \eta })|}_{\epsilon =0}(x)\rangle }_{{ℝ}^n}\text{for}x\in \mathrm{\Omega }.$$ (17)

The second term in the scalar product on the right hand side of (17) is the derivative of a deformation with respect to variations in the associated vector field.

Next, by (5) we have ϕ^ν+εη = Id_Ω +ν + εη, so

$${\frac{d}{d\epsilon }({\varphi }^{\nu +\epsilon \eta })|}_{\epsilon =0}(x)={\frac{d}{d\epsilon }\left(x+\nu (x)+\epsilon \eta (x)\right)|}_{\epsilon =0}=\eta (x).$$

Now, (16) follows from inserting the above into (17).

Remark 3

Unless derivatives are to be interpreted in the distribution sense, the template I ∈ 𝒳 has to be differentiable if the expression in (16) is to make sense.

8.2. The ${\Vert ·\Vert }_{\mathcal{V}}^2$-norm

The 𝒱-gradient of $\nu \mapsto {\Vert \nu \Vert }_{\mathcal{V}}^2$ is simply 2ν.

8.3. General matching functionals

Both of the functionals in (15) are of the form 𝒥_I: 𝒱 → ℝ₊ with

$${\mathcal{J}}_I(\nu ):=\mathcal{L}\circ {\mathcal{W}}_I(\nu )\text{for}\nu \in \mathcal{V},$$ (18)

where ℒ: 𝒳 → ℝ is a fixed functional on 𝒳 that is sufficiently regular, e.g., we require it to be Gâteaux differentiable.

We will here assume that $\mathcal{V}\subset {\mathcal{C}}_0^1(\mathrm{\Omega },{ℝ}^n)$ is admissible. In most cases it will be an RKHS with a continuous positive definite reproducing kernel 𝒦: ΩxΩ → ℒ(ℝⁿ,ℝⁿ) represented by the continuous positive definite function $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{n\times n}$, so

$${\langle \eta ,\nu \rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },{ℝ}^n)}={\langle \nu ,{\int }_{\mathrm{\Omega }}\mathcal{K}(·,x)(\eta (x))\mathrm{d}x\rangle }_{\mathcal{V}}.$$ (19)

Theorem 3

Assume ℒ: 𝒳 → ℝ is Gâteaux differentiable on 𝒳 and define 𝒥_I: 𝒱 → ℝ as in (18) where I ∈ ℒ²(Ω,ℝ) is differentiable. Then, the Gâtueaux derivative of 𝒥_I is given as

$$\partial {\mathcal{J}}_I(\nu )(\eta )=\partial \mathcal{L}({\mathcal{W}}_I(\nu ))\left({\langle \nabla I({\varphi }^v(x)),\eta (x)\rangle }_{{ℝ}^n}\right)\mathit{for}\nu ,\eta \in \mathcal{V}.$$ (20)

Furthermore, let 𝒳 ⊂ ℒ²(Ω,ℝ) and 𝒱 is a RKHS with a reproducing kernel represented by the symmetric and positive definite function $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{n\times n}$. Then

$$\nabla {\mathcal{J}}_I(\nu )(x)={\int }_{\mathrm{\Omega }}\nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(y)\mathrm{K}(x,y)·\nabla I({\varphi }^{\nu }(y))dy\mathit{for}x\in \mathrm{\Omega }.$$ (21)

Proof

The proof of (20) follows directly from the chain rule and Proposition 2. More precisely, by the chain rule we have

$$\partial {\mathcal{J}}_I(\nu )(\eta )=\partial \mathcal{L}({\mathcal{W}}_I(\nu ))(\partial {\mathcal{W}}_I(\nu )(\eta ))\text{for}\nu ,\eta \in \mathcal{V}.$$ (22)

Combining this with (16) gives us (20).

To prove (21) we need to use the assumption 𝒳 ⊂ ℒ²(Ω,ℝ). Then, the Riesz representation theorem allows us to define the gradient of ℒ as the mapping ∇ ℒ: 𝒳 → 𝒳 given implicitly by the relation

$$\partial \mathcal{L}(f)(h)={\langle \nabla \mathcal{L}(f),h\rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },ℝ)}\text{for}h\in \mathcal{X}.$$ (23)

Combining (22) with (23) gives

$$\partial {\mathcal{J}}_I(\nu )(\eta )={\langle \nabla \mathcal{L}({\mathcal{W}}_I(\nu )),\partial {\mathcal{W}}_I(\nu )(\eta )\rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },ℝ)}\text{for}\nu ,\eta \in \mathcal{V}.$$ (24)

Next, the expression in (16) can be inserted into (24):

$$\begin{array}{l}\partial {\mathcal{J}}_I(\nu )(\eta )={\langle \nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(·),{\langle \nabla I({\varphi }^{\nu }(·)),\eta (·)\rangle }_{{ℝ}^n}\rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },ℝ)}\\ ={\langle \nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(·),{\langle \nabla I({\varphi }^{\nu }(·)),\eta (·)\rangle }_{{ℝ}^n}\rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },ℝ)}\\ ={\langle \eta (·),\nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(·)\nabla I({\varphi }^{\nu }(·))\rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },{ℝ}^n)}.\end{array}$$

The last equality makes use of the fact that the inner product in ℒ²(Ω,ℝⁿ) (square integrable ℝⁿ-valued functions) is expressible as the inner product in ℝⁿ followed by the inner product in ℒ²(Ω,ℝ) (square integrable real valued functions). Note also that

$$x\mapsto \nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(x)\nabla I({\varphi }^{\nu }(x))\text{and}x\mapsto \eta (x)$$

are both mappings from Ω into ℝⁿ, so the ℒ²(Ω,ℝⁿ) inner product is well defined. Finally, we use the assumption that 𝒱 is a RKHS with reproducing kernel 𝒦: Ω×Ω → ℒ(ℝⁿ, ℝⁿ), so by (19) we have

$$\partial {\mathcal{J}}_I(\nu )(\eta )={\langle \eta (·),{\int }_{\mathrm{\Omega }}\mathcal{K}(·,x)(\stackrel{\sim }{\nu }(x))\mathrm{d}x\rangle }_{\mathcal{V}}$$

where ν̃: Ω → ℝⁿ is defined as

$$\stackrel{\sim }{\nu }(x):=\nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(x)\nabla I({\varphi }^{\nu }(x))\text{for}x\in \mathrm{\Omega }.$$

We can now read off the expression for the 𝒱-gradient of 𝒥_I and inserting the matrix valued function $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{n\times n}$ representing the reproducing kernel gives us

$$\nabla {\mathcal{J}}_1(\nu )(x)={\int }_{\mathrm{\Omega }}\mathcal{K}(x,y)(\stackrel{\sim }{\nu }(y))\mathrm{d}y={\int }_{\mathrm{\Omega }}\nabla \mathcal{L}({\mathcal{W}}_I(\nu ))(y)\mathrm{K}(x,y)·\nabla I({\varphi }^{\nu }(y))\mathrm{d}y.$$

The last equality is (21), so this concludes the proof of Theorem 3.

8.3.1. ℒ²–data discrepancy

Here we consider the special case when ℋ = ℒ²(Y, ℝ) with Y denoting some manifold that introduces coordinates for the measured data. If the data noise component e ∈ ℋ is a sample of a ℋ–valued Gaussian random element with mean zero and known co-variance operator, then a natural data discrepancy functional 𝒟: ℋ ×ℋ → ℝ in (9) is then given by

$$\mathcal{D}(u):={\Vert u-g\Vert }_{{\mathcal{L}}^2(Y,ℝ)}^2={\int }_Y{(u(y)-g(y))}^2\mathrm{d}y\text{for}u,g\in \mathscr{H}.$$ (25)

Define ℒ(f) := 𝒟(𝒯(f)) and consider 𝒥_I in (18), i.e.,

$${\mathcal{J}}_I(\nu ):=\mathcal{L}\circ {\mathcal{W}}_I(\nu )={\Vert \mathcal{T}(I\circ {\varphi }^{\nu })-g\Vert }_{{\mathcal{L}}^2(Y,ℝ)}^2.$$ (26)

We now seek the Gâteaux derivative of 𝒥_I in (26) assuming 𝒳 ⊂ ℒ²(Ω,ℝ) is a Hilbert space with the usual ℒ²–structure and the forward operator 𝒯: 𝒳 → ℋ in (9) is Gâteaux differentiable. First, the Gâteaux derivative of ℒ and its corresponding gradient are given as

$$\begin{array}{ll}\hfill \partial \mathcal{L}(f)(h)& =2{\langle \partial \mathcal{T}{(f)}^{\ast }(\mathcal{T}(f)-g),h\rangle }_{\mathcal{X}}\hfill \\ \hfill \nabla \mathcal{L}(f)& =2\partial \mathcal{T}{(f)}^{\ast }(\mathcal{T}(f)-g)\hfill \end{array}\text{for}f,h\in \mathcal{X}.$$ (27)

Here, “*” denotes the Hilbert space adjoint and ∂𝒯is the Gâteaux derivative of 𝒯. When 𝒯is linear, then ∂𝒯(f) = 𝒯, so (27) simplifies to

$$\begin{array}{ll}\hfill \partial \mathcal{L}(f)(h)& =2{\langle {\mathcal{T}}^{\ast }(\mathcal{T}(f)-g),h\rangle }_{\mathcal{X}}\hfill \\ \hfill \nabla \mathcal{L}(f)& =2{\mathcal{T}}^{\ast }(\mathcal{T}(f)-g).\hfill \end{array}$$ (28)

Corollary 4

Let the assumptions in Theorem 3 hold. Furthermore, assume that 𝒥_I : 𝒱 →ℝ is given as in (26) with 𝒯: 𝒳 → ℋ Gâteaux differentiable. Then

$$\partial {\mathcal{J}}_I(\nu )(\eta )=2{\langle \partial \mathcal{T}{({\mathcal{W}}_I(\nu ))}^{\ast }(\mathcal{T}({\mathcal{W}}_I(\nu )-g)(·)\nabla I({\varphi }^{\nu }(·)),\eta (·)\rangle }_{{\mathcal{L}}^2(\mathrm{\Omega },{ℝ}^n)}$$ (29)

for ν, η ∈ 𝒱. Furthermore, if 𝒳 ⊂ ℒ²(Ω,ℝ) and 𝒱 is a RKHS with a reproducing kernel represented by the symmetric and positive definite function $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{n\times n}$, then for x ∈ Ω we have

$$\nabla {\mathcal{J}}_I(\nu )(x)=2{\int }_{\mathrm{\Omega }}\partial \mathcal{T}{({\mathcal{W}}_I(v))}^{\ast }(\mathcal{T}({\mathcal{W}}_I(\nu )-g)(y)\mathrm{K}(x,y)·\nabla I({\varphi }^{\nu }(y))dy.$$ (30)

Proof

The proof of (29) follows directly from inserting the expression for ∂ℒ in (27) into (20). Similarly, (30) follows directly from inserting the expression for ∇ ℒ in (27) into (21).

8.4. Gradient of goal functional

It is common to make use of a gradient method in the actual minimization of the goal functional in (10). If we assume 𝒱 is a RKHS, then a general expression for its gradient ∇ ℰ: 𝒱 → 𝒱 can be obtained by combining the results in subsection 8.2 and (21). A common special case is however when μ = 0 and 𝒟 is given as in (25). Then, (30) gives an explicit expression for the gradient at x ∈ Ω as

$$\nabla \mathcal{E}(\nu )(x)=2\nu (x)+2{\int }_{\mathrm{\Omega }}\partial \mathcal{T}{({\mathcal{W}}_I(\nu ))}^{\ast }(\mathcal{T}({\mathcal{W}}_I(\nu )-g)(y)\mathrm{K}(x,y)·\nabla I({\varphi }^{\nu }(y))\mathrm{d}y.$$ (31)

9. Finite dimensional setting

𝒱 is in general an infinite dimensional Hilbert space of vector fields, so the variational problem in (9) is an optimization over an infinite dimensional Hilbert space. In a computational setting we can only minimize functionals over finite dimensional vector spaces. One approach is to formulate the optimization scheme for finding a local minima in the infinite dimensional setting. The explicit expressions for the gradient of the goal functional (section 8) can be used for this. One can then discretize this optimization scheme. Another approach is to look for “natural” finite dimensional formulations. In particular, elements in 𝒱 can only be evaluated at a finite number of points, so we need to consider suitable finite dimensional sub-spaces of 𝒱. It now turns out that there is such natural finite dimensional formulations when 𝒱 is a RKHS.

9.1. Finite span approximations of vector fields

If 𝒱 is an RKHS, then there is a natural way to construct admissible finite dimensional sub-spaces of vector fields by considering finite span approximations. Let $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{n\times n}$ denote the symmetric and positive definite function that represents the reproducing kernel of 𝒱. Next, define the (geometric) control points as the fixed set of points

$$\mathrm{\sum }:=\{x_1,\dots ,x_N\}\subset \mathrm{\Omega }\subset {ℝ}^n.$$

Given such a set, define the corresponding finite dimensional vector space as

$${\mathcal{V}}_{\mathrm{\sum }}:=\left\{\nu \in \mathcal{V}:\nu (x)=\sum _{j=1}^N\mathrm{K}(x,x_j)·{\alpha }_j\text{for}\text{some}{\alpha }_j\in {ℝ}^n\right\}.$$ (32)

Elements in 𝒱_Σ are called finite span approximations of elements in 𝒱.

Then 𝒱_Σ ⊂ 𝒱 is a finite dimensional RKHS with an inner product given by

$$\begin{array}{l}{\langle \nu ,\eta \rangle }_{{\mathcal{V}}_{\mathrm{\sum }}}:={\langle \sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j,\sum _{k=1}^N\mathrm{K}(·,x_k)·{\beta }_k\rangle }_{\mathcal{V}}\\ =\sum _{j,k=1}^N{\langle \mathrm{K}(·,x_j)·{\alpha }_j,\mathrm{K}(·,x_k)·{\beta }_k\rangle }_{\mathcal{V}}=\sum _{j,k=1}^N{\alpha }_j^{\top }·\mathrm{K}(x_j,x_k)·{\beta }_k\end{array}$$ (33)

for ν, η ∈ 𝒱_Σ given as

$$\nu =\sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j\text{and}\eta =\sum _{j=1}^N\mathrm{K}(·,x_j)·{\beta }_j.$$ (34)

Remark 4

Finite span approximations of the type in (32) are especially suitable for problems involving optimization over 𝒱. This is because minimizers of objective functionals that include typical loss-functions are expressible as finite span approximations. More precisely, representer theorems (like [40, Theorem 9.7], see also [34, 41]) show that

$${\nu }^{\ast }:=\underset{\nu \in \mathcal{V}}{argmin}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+\sum _{j=1}^{N}L(\nu (x_j))\right]\Rightarrow {\nu }^{\ast }\in {\mathcal{V}}_{\mathrm{\sum }}.$$ (35)

Here, L: ℝⁿ → ℝ is a given “loss” function, ${\Vert \nu \Vert }_{\mathcal{V}}^2:={\langle \nu ,\nu \rangle }_{\mathcal{V}}$ is the RKHS norm, and x_j ∈ Σ is a fixed set of N control points.

Before proceeding, we introduce some convenient vector/matrix notation. For each ν ∈ 𝒱_Σ there are unique α₁, … , α_N ∈ ℝⁿ such that

$$\nu (x)=\sum _{j=1}^N\mathrm{K}(x,x_j)·{\alpha }_j\text{for}x\in \mathrm{\Omega }.$$ (36)

Hence, each ν ∈ 𝒱_Σ corresponds uniquely to an Nn vector given by

$${\mathit{\alpha }}_{\nu }:=\text{vec}\left[(\begin{array}{lll}{\alpha }_1\hfill & \cdots \hfill & {\alpha }_N\hfill \end{array})\right]$$ (37)

where α₁, … , α_N ∈ ℝⁿ fulfill (36). Finally, define also K as the (Nn × Nn) kernel Gram matrix given as

$$\mathbf{K}={\left[\mathrm{K}(x_j,x_k)\right]}_{j,k=1,\dots ,N}.$$

The above notion allows us to express (33) as

$${\langle \nu ,\eta \rangle }_{{\mathcal{V}}_{\mathrm{\sum }}}={\mathit{\alpha }}_{\nu }^{\top }·\mathbf{K}·{\mathit{\beta }}_{\eta }.$$

9.2. The variational problem in the finite dimensional setting

We now consider the problem of minimizing the functional ℰ : 𝒱 → ℝ in (10). If data g ∈ ℋ is digitized, then this functional is similar to the “loss functional” in (35) (at least when μ = 0) and a minimizer of (9) should be contained in 𝒱_Σ ⊂ 𝒱. Hence, for finite data we can replace the (infinite dimensional) minimization in (9) with the following finite dimensional variational problem:

$$\underset{\nu \in {\mathcal{V}}_{\mathrm{\sum }}}{argmin}\mathcal{E}(\nu ).$$ (38)

Let us now consider (38) more closely. As already stated, to each ν ∈ 𝒱_Σ there are α₁, … , α_N ∈ ℝⁿ such that (34) holds. Hence, the values of ν at the control points in Σ ⊂ Ω is expressible through the following matrix equality:

$${(\begin{array}{lll}\nu (x_1)\hfill & \dots \hfill & \nu (x_N)\hfill \end{array})}^{\top }=\mathbf{K}·{\mathit{\alpha }}_{\nu }.$$

In particular, the RKHS norm of a deformation vector field ν ∈ 𝒱_Σ can be written as

$${\Vert \nu \Vert }_{\mathcal{V}}^2={\Vert \nu \Vert }_{{\mathcal{V}}_{\mathrm{\sum }}}^2={\langle \sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j,\sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j\rangle }_{{\mathcal{V}}_{\mathrm{\sum }}}={\mathit{\alpha }}_{\nu }^{\top }·\mathbf{K}·{\mathit{\alpha }}_{\nu }.$$ (39)

This motivates introducing the function

$$\mathrm{S}:{ℝ}^{N_n}\to {ℝ}_{+}\text{given}\text{as}\mathrm{S}(\mathit{\alpha }):={\mathit{\alpha }}^{\top }·\mathbf{K}·\mathit{\alpha }\text{for}\mathit{\alpha }\in {ℝ}^{Nn}.$$ (40)

Then, S above corresponds to the $\nu \mapsto {\Vert \nu \Vert }_{\mathcal{V}}^2$ term in (10) as shown in (39). Next, define W_I : ℝ^Nn → 𝒳 as

$${\mathrm{W}}_I(\mathit{\alpha }):=I\left(·+\sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j\right)\text{for}\mathit{\alpha }=\text{vec}[({\alpha }_1,\dots ,{\alpha }_N)]\in {ℝ}^{Nn}.$$ (41)

Then, W_I corresponds to the deformation operator 𝒲_I in (7), i.e., W_I (α_ν) = 𝒲_I (ν) whenever α_ν ∈ ℝ^Nn and ν ∈ 𝒱_Σ are related by (37). Finally, we define the functions R, J_I : ℝ^Nn → ℝ₊ as

$$\begin{array}{ll}\mathrm{R}(\mathit{\alpha })\hfill & :=\mathcal{R}({\mathrm{W}}_I(\mathit{\alpha }))\hfill \\ {\mathrm{J}}_I(\mathit{\alpha })\hfill & :=\mathcal{D}\left(\mathcal{T}({\mathrm{W}}_I(\mathit{\alpha })),g\right)\hfill \end{array}\text{for}\mathit{\alpha }\in {ℝ}^{Nn}.$$ (42)

As to be expected, R corresponds to ℛ in (15) and J_I corresponds to 𝒥_I in (18). Hence, solving (38) is equivalent to solving

$$\underset{\mathit{\alpha }\in {ℝ}^{Nn}}{min}\left[\lambda \mathrm{S}(\mathit{\alpha })+\mu \mathrm{R}(\mathit{\alpha })+{\mathrm{J}}_I(\mathit{\alpha })\right]\text{for}\text{fixed}\lambda >0.$$ (43)

If α^* denotes a solution to (43), then we can construct ν^* ∈ 𝒱_Σ from α^* by using the relations in (34) and (37):

$${\nu }^{\ast }:=\sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j^{\ast }$$

in which the n-vector ${\alpha }_j^{\ast }\in {ℝ}^n$ contains elements j to j+n−1 of α^*. The corresponding reconstruction f^* of f_true ∈ 𝒳 in (1) is then given by

$$f^{\ast }(x):={\mathrm{W}}_I({\nu }^{\ast })=I(x+{\nu }^{\ast }(x))\text{for}\text{all}x\in \mathrm{\Omega }.$$

Remark 5

The reconstruction f^* depends on a variety of choices. First are the functionals 𝒟: ℋ × ℋ → ℝ₊ and ℛ: 𝒳 → ℝ₊. How to choose these, and the (regularization) parameter μ ≥ 0, is a common topic in variational regularization. More precisely, the choice of 𝒟 is dictated by the data noise model and choice of μ ≥ 0 is governed by the “magnitude of the noise” in data. As an example, (25) is a natural choice for 𝒟 for additive Gaussian noise and if there is a reasonably accurate estimate of the noise level, then one may use the Morozov discrepancy principle to select μ. Furthermore, the choice of ℛ depends on what a priori regularity properties that one seeks to enforce on the reconstruction. The part in the scheme suggested here that differs from traditional variational regularization is the parts that controls the a priori shape information, which are the choice of template I ∈ 𝒳, kernel $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{n\times n}$, the control points Σ ⊂ Ω, and the (shape) regularization parameter λ ≥ 0.

9.3. Solving the finite dimensional minimization problem

We solve (43) using a gradient descent method, e.g., gradient descent. Such methods involves computing the gradients of

$$\mathit{\alpha }\mapsto \mathrm{S}(\mathit{\alpha }),\mathit{\alpha }\mapsto \mathrm{R}(\mathit{\alpha })\text{and}\mathit{\alpha }\mapsto {\mathrm{J}}_I(\mathit{\alpha }).$$

Computing gradients of the above functions amounts to calculating the partial derivative of them with respect to every element α_j,k (j = 1, … , N and k = 1, … , n) in the Nn vector α.

We will here present an example of such calculations in a special case. In doing so, we omit the regularization functional ℛ: 𝒳 → ℝ₊, i.e., we omit α ↦ R(α). Furthermore, we focus on the special case when ℋ = ℝ^m, i.e., there are m data points and 𝒯: 𝒳 → ℝ^m. The data discrepancy 𝒟: ℋ × ℋ → ℝ₊ is the corresponding finite dimensional version of (25):

$$\mathcal{D}(u):={\Vert u-g\Vert }_2^2=\sum _{\iota =1}^m{(u_{\iota }-g_{\iota })}^2\text{for}u,g\in \mathscr{H}.$$ (44)

9.3.1. The gradient of α ↦ S(α)

We know from (39) that

$$\mathrm{S}(\mathit{\alpha }):={\mathit{\alpha }}^{\top }·\mathbf{K}·\mathit{\alpha }={\Vert \nu \Vert }_{\mathcal{V}}^2\text{whenever}\mathit{\alpha }={\mathit{\alpha }}_{\nu }.$$

Hence, for j = 1, … , N and k = 1, … , n we get

$$\frac{\partial \mathrm{S}}{\partial {\alpha }_{j,k}}(\mathit{\alpha })=\frac{\partial }{\partial {\alpha }_{j,k}}\left[{\mathit{\alpha }}^{\top }·\mathbf{K}·\mathit{\alpha }\right]\Rightarrow \nabla \mathrm{S}(\mathit{\alpha })=2\mathbf{K}·\mathit{\alpha }\text{for}\mathit{\alpha }\in {ℝ}^{Nn}.$$

9.3.2. The gradient of α ↦ J_I (α)

When 𝒟: ℋ ×ℋ → ℝ₊ is given by (44), then J_I : ℝ^Nn → ℝ₊ defined in (42) becomes

$${\mathrm{J}}_I(\mathit{\alpha }):=\mathcal{D}\left(\mathcal{T}({\mathrm{W}}_I(\mathit{\alpha })),g\right)={\Vert \mathcal{T}({\mathrm{W}}_I(\mathit{\alpha }))-g\Vert }_2^2=\sum _{\iota =1}^m{\left(\mathrm{T}{(\mathit{\alpha })}_{\iota }-g_{\iota }\right)}^2$$ (45)

where T: ℝ^Nn → ℝ^m is defined as

$$\mathrm{T}(\mathit{\alpha }):=\mathcal{T}({\mathrm{W}}_I(\mathit{\alpha }))=\mathcal{T}\left(I\left(·+\sum _{j=1}^N\mathrm{K}(·,x_j)·{\alpha }_j\right)\right)\text{for}\alpha \in {ℝ}^{Nn}.$$ (46)

Then

$$\frac{\partial {\mathrm{J}}_I}{\partial {\alpha }_{j,k}}(\mathit{\alpha })=\frac{\partial }{\partial {\alpha }_{j,k}}\left[\sum _{\iota =1}^m{\left(\mathrm{T}{(\mathit{\alpha })}_{\iota }-g_{\iota }\right)}^2\right]=2\sum _{\iota =1}^m\left[\left(\mathrm{T}{(\mathit{\alpha })}_{\iota }-g_{\iota }\right)\frac{\partial }{\partial {\alpha }_{j,k}}\mathrm{T}{(\mathit{\alpha })}_{\iota }\right]$$

for j = 1, … , N and k = 1, … , n. A more explicit expression for the above partial derivatives requires one to calculate

$$\frac{\partial }{\partial {\alpha }_{j,k}}\mathrm{T}{(\mathit{\alpha })}_{\iota }:=\frac{\partial }{\partial {\alpha }_{j,k}}\left[\mathcal{T}{\left(I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right)}_{\iota }\right]$$

for j = 1, … , N, k = 1, … , n, and ι = 1, … , m. The above can be calculated through the chain rule and the resulting expression will involve derivatives of the forward model 𝒯 and the template I. Below, we do this calculation for linear forward operators.

Let 𝒯_ι: 𝒳 → ℝ denote the the ι:th coordinate of the forward operator 𝒯: 𝒳 → ℝ^m, which we now assume is linear. Then

$$\mathrm{T}{(\mathit{\alpha })}_{\iota }={\mathcal{T}}_{\iota }\left(I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right)\text{for}\mathit{\alpha }\in {ℝ}^{Nn}\text{and}\iota =1,\dots ,m.$$

For linear 𝒯_ι we get

$$\begin{array}{l}\frac{\partial }{\partial {\alpha }_{j,k}}\mathrm{T}{(\mathit{\alpha })}_{\iota }=\frac{\partial }{\partial {\alpha }_{j,k}}\left[{\mathcal{T}}_{\iota }\left(I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right)\right]\\ ={\mathcal{T}}_{\iota }\left(\frac{\partial }{\partial {\alpha }_{j,k}}\left[I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right]\right)\\ ={\mathcal{T}}_{\iota }\left(\nabla I{\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)}^{\top }·{(\mathrm{K}(·,x_j))}_k\right)\\ ={\mathcal{T}}_{\iota }\left({(\mathrm{K}(·,x_j))}_k^{\top }·\nabla I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right).\end{array}$$

Note that (K(· , x_j))_k is the k:th column of the matrix K(· , x_j ). Hence,

$$\nabla {\mathrm{J}}_I(\mathit{\alpha })=2\sum _{\iota =1}^m\left[(\mathrm{T}{(\mathit{\alpha })}_i-g_{\iota })\nabla \mathrm{T}{(\mathit{\alpha })}_{\iota }\right]$$

where

$$\begin{array}{l}\nabla \mathrm{T}{(\mathit{\alpha })}_{\iota }=\nabla \left[{\mathcal{T}}_{\iota }\left(I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right)\right]\\ ={\mathcal{T}}_{\iota }\left({(\begin{array}{lll}\mathrm{K}(·,x_1)\hfill & \dots \hfill & \mathrm{K}(·,x_N)\hfill \end{array})}^{\top }·\nabla I\left(·+\sum _{l=1}^N\mathrm{K}(·,x_l)·{\alpha }_l\right)\right).\end{array}$$

10. Results for 2D tomography

10.1. The inverse problem

In the continuum setting, image reconstruction in 2D tomography is the inverse problem of reconstructing f_true ∈ 𝒳 from (1) where data g = 𝒯(f) and 𝒯 is the 2D ray/Radon transform:

$$\mathcal{T}(f)(\ell ):={\int }_{\ell }f(x)\mathrm{d}{\mu }_{\ell }(x)\text{for}f\in \mathcal{X}\text{and}\ell \subset {ℝ}^2\text{is}\mathrm{a}\text{line.}$$

Here, dμ_ℓ is the 1-dimensional Lebesgue measure on the line ℓ.

𝒳 is some suitable Hilbert space of real valued functions defined on Ω ⊂ ℝ², for our purposes it is enough to require that $\mathcal{X}\subset {\mathcal{L}}_c^2(\mathrm{\Omega },ℝ)$. Moreover, in the continuum setting, tomographic data is a real-valued function g: Y → ℝ defined on some sub-manifold Y of lines in ℝ² that correspond to the tomographic data acquisition geometry.

It is possible to introduce explicit coordinates on the manifold Y. Any line ℓ in ℝ² can be described by a direction ω ∈ S¹ and a point x ∈ ω^⊥ that it passes through, i.e., ℓ : t ↦ tω+x. Since ω = (sinθ, cos θ) for some 0 ≤ θ ≤ π and x = p(−cos θ, sin θ) for some p ∈ ℝ, we can describe any line ℓ in ℝ² by a pair (θ, p) ∈ [0, π] × ℝ so that

$$\ell :t\mapsto t(sin\theta ,cos\theta )+p(-cos\theta ,sin\theta ).$$

Now, for parallel beam geometry data acquisition (i.e., all lines are parallel for a given angle θ), Y = Γ× ℝ for some subset Γ ⊂ [0, π] and

$$\mathcal{T}(f)(\theta ,p):={\int }_{-\infty }^{\infty }f\left(t(sin\theta ,cos\theta )+p(-cos\theta ,sin\theta )\right)\mathrm{d}t$$

for (θ, p) ∈ Y. Furthermore, we also have that

$$\partial \mathcal{T}{(u)}^{\ast }(g)(x)={\int }_{\mathrm{\Gamma }}g(\theta ,x·(-cos\theta ,sin\theta ))\mathrm{d}\theta \text{for}x\in \mathrm{\Omega }.$$

Remark 6

For digitized data, Y is a finite set of pairs (θ, p) where

$$\theta \in \{{\theta }_1,\dots ,{\theta }_k\}\subset [0,\pi ]\mathit{and}p\in \{p_1,\dots ,p_l\}\subset ℝ.$$

Hence, in this setting we would have k directions and l measurements for each direction, i.e., data is a vector g ∈ ℝ^m where m = kl is the total number of data points.

10.2. The reconstruction scheme

We will estimate f_true ∈ 𝒳 by shape based reconstruction, i.e., by minimizing ℰ : 𝒱 → ℝ in (10) with μ = 0 and 𝒟 as in (25), i.e.,

$$\underset{v\in \mathcal{V}}{min}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+{\Vert \mathcal{T}(I\circ {\varphi }^{\nu })-g\Vert }_{{\mathcal{L}}^2(Y,ℝ)}^2\right].$$ (47)

In the above, the shape template I ∈ 𝒳 and regularization parameter λ > 0 is fixed.

Next, the space of vector fields 𝒱 is chosen as the RKHS with a reproducing kernel represented by the following symmetric and positive definite Gaussian function $\mathrm{K}:\mathrm{\Omega }\times \mathrm{\Omega }\to {\mathbb{M}}_{+}^{2\times 2}$ that, for fixed σ > 0, is given as

$$\mathrm{K}(x,y):=exp\left(-\frac{1}{2{\sigma }^2}{\Vert x-y\Vert }_2\right)\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\text{for}x,y\in {ℝ}^2.$$ (48)

Considering finite span approximations of the type in (32) allows us to recast the minimization in (47) as the finite dimensional variational problem (43) with μ = 0 and J_I : ℝ^2N → ℝ₊ as in (45), i.e.,

$$\underset{\alpha \in {ℝ}^{2N}}{min}\left[\lambda ({\mathit{\alpha }}^{\top }·\mathbf{K}·\mathit{\alpha })+\sum _{i=1}^l\sum _{j=1}^k{\left(\mathrm{T}{(\mathit{\alpha })}_{i,j}-g_{i,j}\right)}^2\right]$$ (49)

where T: ℝ^2N → ℝ^m with m = lk is defined as

$$\mathrm{T}{(\mathit{\alpha })}_{i,j}={\int }_{-\infty }^{\infty }I[t(sin{\theta }_i,cos{\theta }_i)+p_j(-cos{\theta }_i,sin{\theta }_i)+\sum _{\tau =1}^N\mathrm{K}(t(sin{\theta }_i,cos{\theta }_i)+p_j(-cos{\theta }_i,sin{\theta }_i),x_{\tau })·{\alpha }_{\tau }]\mathrm{d}t$$

for i = 1, … , k and j = 1, … , l.

10.3. Results

This section illustrates some results of using shaped based reconstruction in 2D parallel beam tomography with very sparse data. Even though these tests are not exhaustive enough to constitute a formal validation study, they do give an indication of the impact of using a priori shape information.

10.3.1. Phantoms and data acquisition protocol

All phantoms reside in a fixed image domain given as Ω = [−2.5, 2.5] × [−2.5, 2.5] that is digitized into 101 × 101 pixels. Phantoms are either step functions or smoothed versions of step functions. The smoothing is done by applying a Gaussian kernel function. Hence, smoothed phantoms may present some grey-scale variations also in regions away from the edges, but in general the phantoms are rather homogenous and do not present any texture information.

Data is generated by evaluating the 2D parallel beam ray transform from equally distributed directions surrounding the aforementioned phantoms and then adding noise. All tests except for test suite 4 use three directions: 0°, 45° and 90°. In test suite 4 there are four directions. Each direction samples 151 parallel lines uniformly distributed and noise is additive Gaussian with varying noise levels. The noise level in data is quantified in terms of the signal-to-noise ratio (SNR) expressed using the logarithmic decibel (dB) scale:

$$\text{SNR}(g)=10{log}_{10}\left[\frac{{\sum }_{j=1}^m{\mid g_j^{\text{ideal}}-{\mu }_{\text{ideal}}\mid }^2}{{\sum }_{j=1}^m{\mid e_j-{\mu }_{\text{noise}}\mid }^2}\right].$$ (50)

Here, g = g^ideal + e in (1) where g^ideal ∈ ℝ^m is the noise-free component of data g and e is the noise component. Furthermore, μ_ideal is the arithmetic average of g^ideal and μ_noise is the arithmetic average of e. Note here that we assume one has access to the noise-free component of data.

10.3.2. Reconstruction protocol

Shape based reconstructions are obtained by solving (49) using a gradient descent method. Here, N = 2601 and kernel is as in (48) with σ² = 1 for all cases. Other reconstruction parameters, like value of λ and number of iterations, vary. Test suites 1 and 3 involve comparisons against filtered back projection (FBP), classical Tikhonov, and TV reconstruction.

• FBP reconstruction is obtained by applying the iRadon command to data. This is the implementation of FBP in the MATLAB Image Processing Tool-box [22, pp. 9–29–9–34] and we have used linear interpolation for the back projection and the Ram-Lak filter (full frequency range).

• Classical Tikhonov reconstruction is obtained by solving (3) with ℛ as the Dirichlet’s energy:

  $$\mathcal{R}(f):={\int }_{\mathrm{\Omega }}{\mid \nabla f(x)\mid }^2\mathrm{d}x.$$

  Gradient descent is used to solve the resulting quadratic optimization problem. Reconstruction parameters, like value of μ and number of iterations, vary.

• TV reconstruction is obtained by solving (3) with ℛ as the total variation functional:

  $$\mathcal{R}(f):={\int }_{\mathrm{\Omega }}\mid \nabla f(x)\mid \mathrm{d}x.$$

  The resulting non-smooth optimization problems is solved using a linearized split Bregman scheme [7]. Reconstruction parameters, like value of μ and number of iterations, vary.

10.3.3. Test suites

The test suites seek to illustrate different properties of the shape based reconstruction scheme. One is to investigates how the smoothness of the shape template influences the reconstruction. Another is to consider the sensitivity of the reconstruction scheme against the choice of regularization parameter λ. We also have tests for assessing the robustness against noise in data. Finally, we consider the impact of using a shape template with an erroneous topology.

Test suite 1: Smoothness of template

Here we seek to investigate how smoothness of the shape template influences the final reconstruction, so the test suite involves two phantoms and two shape templates with different regularity properties. One phantom is a disc with a sharp edge (Figure 1b) so it has a distinct singularity. The other phantom is a smoothed version of the first one (Figure 2b), i.e., it lacks singularities. Likewise, the two shape templates have different regularity properties. One template is a disc with a sharp edge centered at the origin with diameter equal to 1/4 of domain size (Figure 1f or Figure 2f). The other is a small square with a sharp edge and corners centered at the origin and rotated 45° (Figure 1g or Figure 2g). Data generated from these two phantoms has moderate noise level (SNR 13.7dB ), see Figure 1a and Figure 2a.

Fig. 1.

Test suite 1 – Smoothness of template. The phantom (b) is a disc with a sharp edge centered at the origin (diameter = 1/3 of domain). Reconstructions, obtained using different methods, are shown in (c)–(g). Shape based reconstructions clearly

Fig. 2.

Test suite 1 – Smoothness of template. The phantom, shown in (b), has smoothed edge and reconstructions, obtained using different methods, are shown in (c)–(g). Despite a phantom with smoothed edge, the shape based reconstructions have a sharp edge since the templates have those properties. To some extent the same also applies to corners.

The results are summarized in Figure 1 and Figure 2. We clearly see that shape based reconstructions inherit edge smoothness from the template. Likewise, corners in the template also leave traces in the reconstruction. This is to be expected since shape based reconstructions are given as a smooth deformation of a shape template, so the smoothness properties of the template is transferred to the reconstruction.

Test suite 2: Sensitivity w.r.t. regularization parameter

The parameter λ in (49) regulates the influence of the shape information, so in some sense it acts as a regularization and its choice should be dictated by the noise characteristics in data (noise level, statistical properties of noise, e.t.c.). A natural question is to empirically investigate the sensitivity of the reconstruction w.r.t. the choice of λ for data with fixed noise level. Hence, we consider a fixed phantom (Figure 3b) that is a smoothed concatenation of an ellipse and a rectangle and associated data (Figure 3a) is moderately noisy (SNR 13.7dB).

Fig. 3.

Test suite 2 – Sensitivity w.r.t. regularization parameter. Figures (d)–(j) show shape based reconstructions obtained from data in (a) after 400 iterations using shape template in (c) and different values for λ. The phantom is shown in (b). Reconstructions in (d) and (e) are clearly over-regularized, i.e., shape template has too much influence on the outcome. Once λ is small enough to allow for data to have an impact, it does not seem to influence the outcome that much.

The results are summarized in Figure 3 where reconstructions use the same shape template, a disc with a smoothed edge centered at the origin with diameter equal to 1/4 of domain size (Figure 3c). The shape based reconstructions for varying values of λ are shown in Figures 3d to 3j. It is clear that once λ is small enough to allow for data to have an impact, it does not seem to influence the outcome that much.

Test suite 3: Influence of noise

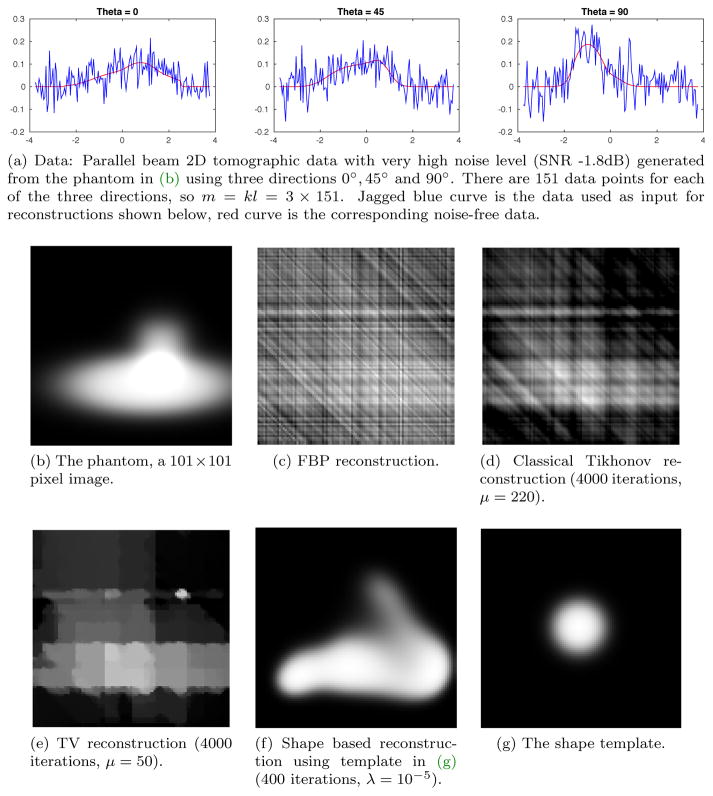
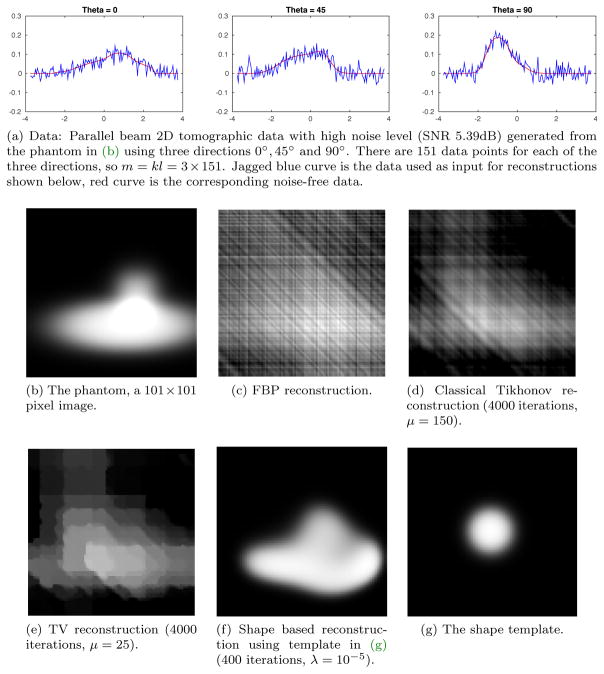
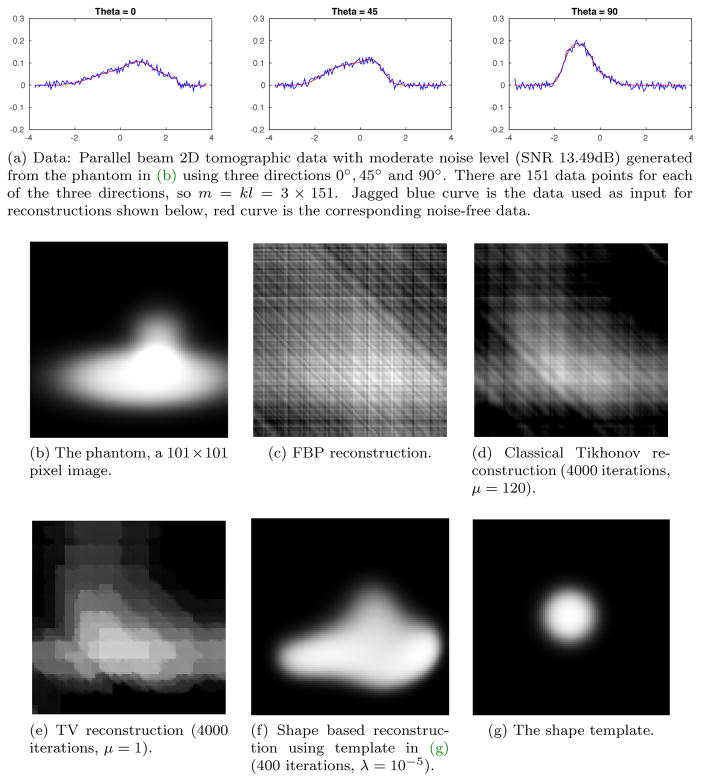
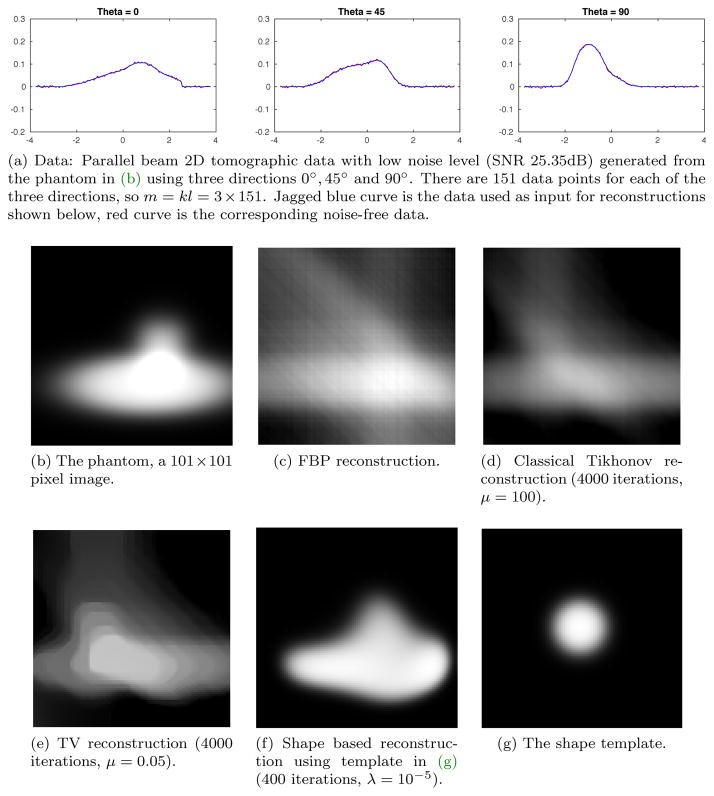
The tests here focus on robustness against noise in data, so there are four different data sets with noise levels ranging from very high (SNR −1.8dB) to low (SNR 25.35dB). All four data sets are generated using the same phantom (see, e.g., Figure 4b), which is a smoothed concatenation of an ellipse and a rectangle. The data sets are shown in Figure 4a, Figure 5a, Figure 6a, and Figure 7a.

Fig. 4.

Test suite 3 – Very high noise. Data, shown in (a), has very high noise (SNR − 1.8dB). The phantom is shown in (b) and reconstructions, obtained using different methods, are shown in (c)–(f). Only shape based reconstruction provides a result (f) that bears any similarities to the original phantom (b).

Fig. 5.

Test suite 3 – High noise. Data, shown in (a), has very high noise (SNR 5.39dB). The phantom is shown in (b) and reconstructions, obtained using different methods, are shown in (c)–(f). Only shape based reconstruction provides a result (f) that bears any similarities to the original phantom (b).

Fig. 6.

Test suite 3 – Moderate noise. Data, shown in (a), has very high noise (SNR 13.49dB). The phantom is shown in (b) and reconstructions, obtained using different methods, are shown in (c)–(f). Only shape based reconstruction provides a result (f) that bears any similarities to the original phantom (b).

Fig. 7.

Test suite 3 – Low noise. Data, shown in (a), has very high noise (SNR 25.35dB). The phantom is shown in (b) and reconstructions, obtained using different methods, are shown in (c)–(f). Only shape based reconstruction provides a result (f) that bears any similarities to the original phantom (b).

Shape based reconstructions are all based on the same shape template, a disc with smooth edge centered at the origin with diameter equal to 1/4 of domain size (see, e.g., Figure 4g). The results are summarized in Figures 4 to 7 and we see a rather remarkable robustness against noise. In fact, only shape based reconstruction provides a result that bears any similarity to the original phantom.

Test suite 4: The topology of the template

Here we seek to investigate the influence of topology of template. We have already seen in test suite 1 that smoothness properties of the template are essentially transferred to the reconstruction. The test suite involves two phantoms, one a disc with sharp edge centered at the origin with diameter equal to 1/3 of domain size (Figure 8b). The other is a U-shaped object (Figure 9b). Both are topologically equivalent, but the latter phantom has a more complex shape.

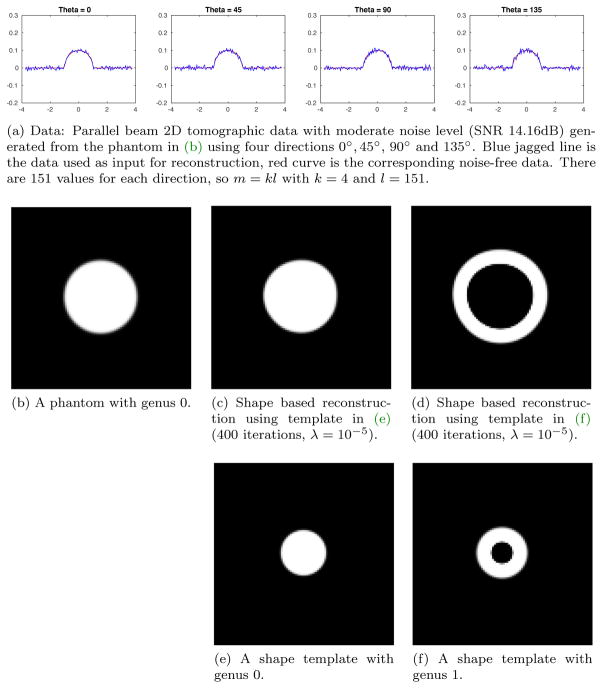
Fig. 8.

Test suite 4 – Topology of phantom. The phantom, shown in (b), is a 101×101 pixel image that is a “U”-shaped object with genus 0. The parallel beam data is shown in (a) and (c) and (d) show shape based reconstructions obtained using a template with genus 0 and 1, respectively. It is clear that the reconstruction inherits the topology of the template.

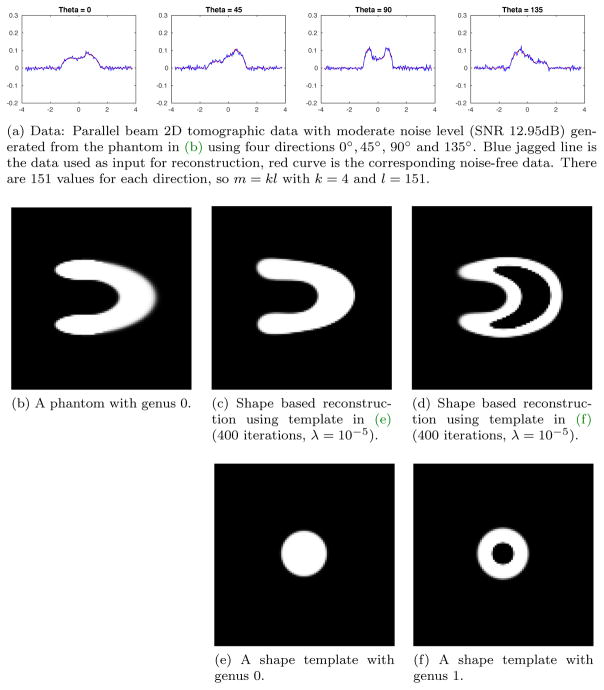
Fig. 9.

Test suite 4 – Topology of phantom. The phantom, shown in (b), is a 101×101 pixel image that is a “U”-shaped object with genus 0. The parallel beam data is shown in (a) and (c) and (d) show shape based reconstructions obtained using a template with genus 0 and 1, respectively. It is clear that the reconstruction inherits the topology of the template.

Next, there are two shape templates with different topologies. One is a disc with sharp edge centered at the origin with diameter equal to 1/4 of domain size (see, e.g., Figure 8e), so it has genus 0. The other an annulus centered at the origin (see, e.g., Figure 8f), so it has genus 1.

The results, summarized in Figure 8 and Figure 9, show that the topology of the template is transferred to the reconstruction. Again, this is to be expected since shape based reconstructions are given as a smooth deformation of a shape template, so the topology of the template is transferred to the reconstruction.

10.3.4. Conclusions

The tests clearly show that shape information is powerful in suppressing the streak artifacts that typically appears in reconstructions obtained from sparsely, or unevenly, sampled data. Furthermore, shape based reconstructions outperform other methods when the goal is to reconstruct “step-function like” objects. Test suites 1 and 4 show that apart from the topology, a priori shape information doesn’t have to be that accurate. This is a very important feature since a priori shape information is expected to be approximate at best. Furthermore, test suite 2 shows that reconstructions are not that sensitive to precise choice of λ. Finally, test suite 3 shows that shape based reconstructions are remarkably robust against noise in data. Taken together, these empirical observations clearly indicate that shape based reconstruction as suggested in (9), with its finite dimensional variant in (49), is an interesting approach for image reconstruction problems where texture is not of prime interest.

The tests in section 10 do however not constitute a proper validation and comparison study, which would include several components that are currently missing. Examples of such components are:

• Evaluation protocol: Define quantitative figures of merits for assessing reconstruction quality.

• Reconstruction protocol: Define schemes for selecting the “optimal” reconstruction parameters (like regularization parameter, choice of kernel function, number of iterates, e.t.c.) in reconstruction methods given different noise levels and sampling schemes (typically by training against a training set). The idea is to ensure a fair comparison between methods.

• Sensitivity: Asses sensitivity of reconstructions against variations in the reconstruction parameters and variations in the a priori assumptions (shape template).

Shape based reconstruction, as defined in (9), is applicable to a rather limited class of image reconstruction problems, see discussion in subsection 11.1. Hence, a proper validation as indicated above is probably not worth the effort. Time is better spent on addressing this shortcoming and thereby widen the applicability of the approach, at least so that it can be applied to some biomedical imaging problems of interest, like the one in ET. One can then conduct a proper validation and comparison study.

11. Discussion and remarks

11.1. Applicability

The reconstruction is a smooth deformation of a shape template in the scheme that is based on solving (9). Hence, only the texture present in the template will enter into the reconstruction, i.e., texture (intensity variations) not present in the template will not be accounted for during reconstruction. The suggested approach is therefore only feasible for image reconstruction problems where intensity variations are not important.

11.2. Optimization

As with all reconstruction methods that involve solving non-convex optimization problems, there is always the issue of getting stuck in local extrema. Empirical experience suggests that this risk is higher if the shape reconstruction includes a significant translation of the template. Hence, it is better to first centre the template, i.e., ensure its centre of gravity coincides reasonably well with the centre of gravity of the (unknown) image we seek to recover.

The shape based reconstructions in subsection 10.3 were obtained using a gradient descent method with a fixed step-length for solving (49). Convergence is slow and depends heavily on the fixed step size. More sophisticated approaches with better convergence properties are called for if one is to apply shape based reconstruction on larger problems. The expressions in section 8 for the gradient of a general regularization and discrepancy functionals in (9) can be used to derive alternative discretization schemes.

11.3. Regularity properties

We have seen that the regularity of I is preserved by the deformation operator (i.e., essentially any regularity preserved when composing with ν) will show up in the reconstruction. This can be used to derive reconstructions that are suited for specific tasks, e.g., one may consider using a sharp template if the reconstructed image is to be automatically segmented. In some cases knowledge about f_true may give an indication regarding the edge-smoothness of the shape template. As an example, in ET of a cryo-fixated aqueous specimen we expect to have isolated molecular assemblies embedded in ice. Here the shape template typically corresponds to the 3D electrostatic map of a molecular assembly with a shape similar to the structures being studied. The smoothness of this 3D electrostatic map is given by how the electrostatic potential behaves at the interface between the molecular assembly and the aqueous buffer. The blurriness of the edge is thus a consequence of the decay of the electrostatic potential as one moves from the molecule into the buffer, see [39, 27] for further details.

11.4. Extensions to handle intensity values

The influence of the shape template also poses a drawback regarding the handling of intensity values (texture). Assume f_true has texture but the shape template lacks texture, i.e., think of it as a set-function (with possibly smoothed edge). The reconstruction will lack texture as well since the only a priori information we make use of is shape related. Choosing an appropriate ℛ: 𝒳 → ℝ₊ and setting μ > 0 in (9) may have an impact since this makes it possible to account for intensity related regularity properties of f_true.

One approach to address this is to avoid enforcing the a priori assumption in (8) when defining the iterates that yield the reconstruction, e.g., by updating the template as well. The latter amounts to replacing (9) with

$$\underset{\nu \in \mathcal{V},I\in ℳ}{inf}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+\mu \mathcal{R}(I)+\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I(\nu )),g\right)\right].$$

An alternative, more feasible, formulation is to decouple the updating of the template from the updating of the deformation by considering the following intertwined recursive scheme:

$$\{\begin{array}{ll}{\nu }_n\hfill & :=\underset{\nu \in \mathcal{V}}{arginf}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_{I_{n-1}}(\nu )),g\right)\right]\hfill \\ I_n\hfill & :=\underset{I\in \mathcal{X}}{arginf}\left[\mu \mathcal{R}(I)+\mathcal{D}\left(\mathcal{T}({\mathcal{W}}_I({\nu }_n)),g\right)\right]\hfill \end{array}$$ (51)

Another approach would be to mimic the way metamorphosis extends the LDDMM framework to the case when the diffeomorphic deformations act simultaneously on both the shape and image intensity, see [40, Chapter 13] for further details on metamorphosis.

11.5. Deformation models

We consider linearized deformations, so each element in 𝒢_𝒱 is generated as in (5) by a smooth vector field in 𝒱. A drawback with this approach is that it becomes difficult to mathematically characterize those Hilbert spaces 𝒱 that ensure elements in 𝒢_𝒱 are invertible. A natural approach that addresses this is to generate deformations using the LDDMM approach (see Remark 2) instead of (5). Then, elements in 𝒢_𝒱 are diffeomorphisms if the Hilbert space 𝒱 fulfills a rather weak condition. Next, all of the analysis done here, including results in section 7, generalize to the LDDMM setting. The expressions for the gradients in section 8 do however become significantly more involved. Furthermore, the software implementation for shape based reconstruction used in section 10 is based on deformations generated as in (5). For these reasons, the theoretical and computational work using the LDDMM framework is part of a forthcoming paper. Finally, there are other deformation models that one may consider, e.g., see [23, 4] for an overview of various groups of diffeomorphisms that may act as deformation models.

11.6. Connection to spatiotemporal imaging

In spatiotemporal imaging, the image we seek to reconstruct will have a temporal and a spatial component, i.e., elements in the reconstruction space 𝒳 are functions f : [t₀, t₁] × Ω → ℝ where x ↦ f(t, x) ∈ ℒ²([t₀, t₁],ℝ) and t ↦ f(t, x) ∈ 𝒳₀, where 𝒳₀ is some suitable Hilbert space of functions defined on Ω. Hence, f(t, ·) is the image at time t ∈ [t₀, t₁] and f(·, x) is the time evolution of a image point x ∈ Ω. Now, it often it makes sense to explicitly separate the spatial and temporal components of f. Such a separation can be achieved by introducing a time evolution operator

$$\mathcal{W}:\mathcal{V}\times {\mathcal{X}}_0\to \mathcal{X}.$$ (52)

Here, 𝒱 is a fixed parameter set for the time evolution and 𝒳₀ is the reconstruction space for the spatial component. Spatiotemporal signals are now assumed to be of the form

$$f(t,x)=\mathcal{W}(\nu ,I)(t,x)\text{for}x\in \mathrm{\Omega }\text{and}t\in [t_0,t_1]\text{for}\text{given}\nu \in \mathcal{V}\text{and}I\in {\mathcal{X}}_0.$$

Here, I is the template, which is the time independent spatial component of the spatiotemporal signal. The evolution parameter ν ∈ 𝒱 governs the time evolution of the template I. In this setting, the spatiotemporal inverse problem is to estimate both the true template I* ∈ 𝒳₀ and the true evolution parameter ν* ∈ 𝒱 from data g(t, ·) ∈ ℋ where

$$g(t,·)=\mathcal{T}\left(\mathcal{W}({\nu }^{\ast },I^{\ast })(t,·)\right)+e(t,·)\text{for}t\in [t_0,t_1].$$ (53)

Note that 𝒳₀ is the reconstruction space for the spatial component of the spatiotemporal signals, ℋ is the data space, which is common for all data across time, 𝒯 : 𝒳₀ → ℋ is the Fréchet differentiable (spatial) forward operator, and 𝒲 in (52) is the time evolution operator modeling the evolution, governed by evolution parameter in 𝒱, across time. Finally, e(t, ·) ∈ ℋ are samples of independent (as t varies) ℋ–valued random process {E_t}_t.

Now, if 𝒱 is a normed space, then one scheme for solving the spatiotemporal inverse problem in (53) is to consider

$$\underset{\nu \in \mathcal{V},I\in {\mathcal{X}}_0}{inf}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+{\int }_{t_0}^{t_1}\left\{\mu \mathcal{R}(\mathcal{W}(\nu ,I)(t,·))+\mathcal{D}\left(\mathcal{T}(\mathcal{W}(\nu ,I)(t,·)),g(t,·)\right)\right\}\mathrm{d}t\right]$$ (54)

for fixed λ, μ ≥ 0 and given operators ℛ: 𝒳₀ → ℝ₊ and 𝒟: ℋ × ℋ → ℝ₊. The rationale for the above scheme is based on the following assumptions:

1. Regularity properties of image intensities can be encoded by the functional ℛ. These are assumed to be the same for all evolved templates 𝒲(ν, I)(t, ·) ∈ 𝒳₀ with t ∈ [t₀, t₁].

2. The stochastic process {E_t}_t modeling noise in data has elements that are independent and equally distributed so we may use the same data discrepancy functional 𝒟: ℋ × ℋ → ℝ₊.

Solving (54) is quite challenging. Similar to (51), it may be simpler to consider the following intertwined recursive scheme where the evolution model is updated separately from the template:

$$\{\begin{array}{ll}{\nu }^n\hfill & :=\underset{\nu \in \mathcal{V}}{arginf}\left[\lambda {\Vert \nu \Vert }_{\mathcal{V}}^2+{\int }_{t_0}^{t_1}\mathcal{D}\left(\mathcal{T}(\mathcal{W}(\nu ,I^{n-1})(t,·)),g(t,·)\right)\mathrm{d}t\right]\hfill \\ I^n\hfill & :=\underset{I\in {\mathcal{X}}_0}{arginf}\left[{\int }_{t_0}^{t_1}\left\{\mu \mathcal{R}(\mathcal{W}({\nu }^n,I)(t,·))+\mathcal{D}\left(\mathcal{T}(\mathcal{W}({\nu }^n,I)(t,·)),g(t,·)\right)\right\}\mathrm{d}t\right]\hfill \end{array}$$ (55)

The above is computationally more feasible, but it is unclear how these intertwined iterates relate to a solution of (54). Furthermore, it is highly non-trivial to understand whether (54), or (55), constitutes a regularization of the inverse problem in (53). As shown in [14], one may use the LDDMM framework (subsection 11.5) to define evolution operators with diffeomorphisms parametrized by admissible Hilbert spaces of vector fields $\mathcal{V}\subset {\mathcal{C}}_0^1(\mathrm{\Omega },{ℝ}^n)$.

Finally, the notion of “time” above does not have to correspond to physical time. It could be a mere parametrization of the evolution. The shape based reconstruction we considered in (3) is now a special case with only one dataset at say t₁ = 1 (stationary data) and known template I* ∈ 𝒳₀. In such case the time evolution operator 𝒲 models the (shape) deformation of the template and the goal is to estimate the evolution parameter ν ∈ 𝒱 from indirect noisy data.

Appendix A. Basic notation

ℝⁿ denotes the n-dimensional Euclidian space and 𝕄^n,m is the vector space of all (n×m) matrices. ${\mathbb{M}}_{+}^{n,m}$ will then refer to positive definite (n × m) matrices. Next, if 𝒳 and 𝒴 are two vector spaces, then ℒ(𝒳,𝒴) is the vector space of linear mappings defined on 𝒳 with values in 𝒴.

We also make use of the vec-operator that transforms a matrix into a (column) vector by stacking all the columns of the matrix one underneath the other. Hence, vec : 𝕄^n×m → ℝ^nm is defined as

$$\text{vec}[\mathbf{A}]:={(\begin{array}{ccccccc}{a}_{1,1}& \dots & a_{n,1}& \dots & a_{1,m}& \dots & a_{n,m}\end{array})}^{\top }$$

whenever A is an (n × m) matrix

$$\mathbf{A}:=\left(\begin{array}{cccc}{a}_{1,1}& a_{1,2}& \dots & a_{1,m}\\ a_{2,1}& a_{2,2}& \dots & a_{2,m}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n,1}& a_{n,2}& \dots & a_{n,m}\end{array}\right).$$