Sample Size Calculation for Testing Differences Between Cure Rates with the Optimal Log-rank Test

Abstract

In this article, sample size calculations are developed for use when the main interest is in the differences between the cure rates of two groups. Following the work of Ewell and Ibrahim, the asymptotic distribution of the weighted log-rank test is derived under the local alternative. The optimal log-rank test under the proportional distributions alternative is discussed, and sample size formulae for the optimal and standard log-rank tests are derived. Simulation results show that the proposed formulae provide adequate sample size estimation for trial designs and that the optimal log-rank test is more efficient than the standard log-rank test, particularly when both cure rates and percentages of censoring are small.

1 Introduction

When survival data include a portion of cured patients or long-term survivors, cure models are useful for analyzing the data and designing clinical trials. Recently, various parametric and semiparametric cure models have been proposed by Farewell (1982), Peng et al. (1998), and Kuk and Chen (1992). A maximum-likelihood expectation-maximization (EM) algorithm for parametric and semiparametric cure models has been proposed by Peng and Dear (2000) and Sy and Taylor (2000). A SAS macro PSPMCM, developed by Corbiere and Joly (2007), is available to fit both parametric and semiparametric cure models. Thus, survival data in which a portion of patients are cured can be analyzed using these methods for the purpose of designing clinical trials using the selected cure models.

In a cancer clinical trial in which a portion of patients experience long-term survival, the main interest is often in the differences between cure rates. Examples from the Children’s Cancer Group trials are given by Lee and Sather (1995). To develop an appropriate test for testing the differences between cure rates in a two-arm randomized trial, Gray and Tsiatis (1989) proposed a family of cure models with a proportional distributions alternative. The optimal log-rank test was discussed under the proportional distributions alternative, which has the form of a G^ρ test where ρ = −1 (Harrington and Fleming, 1982), and its efficacy relative to that of the standard log-rank test was also investigated. Ewell and Ibrahim (1997) extended the work of Gray and Tsiatis by deriving the large sample distribution of the weighted log-rank test under a more general sequence of local alternatives that allows for treatment effects on both short- and long-term survival. They also derived a power calculation for the weighted log-rank test assuming exponential failure times.

In this article, we focus on the situation where the main interest is in the differences between the cure rates of two groups. Following the work of Ewell and Ibrahim, sample size formulae are derived for both the standard log-rank test and the optimal weighted log-rank test. The relative efficacy of the two tests is also discussed.

The rest of the paper is organized as follows. A mixture cure model is introduced in Section 2. The sample size formula for the weighted log-rank test is derived in Section 3. The optimal log-rank test and its sample size formula are obtained in Section 4. In section 5, comparisons of the efficiency and robustness of the two tests are presented, and simulations are conducted to study the performance of the proposed sample size formulae. Section 6 illustrates clinical trial design using the proposed methods. Conclusions are presented in section 7.

2 Cure Models

The failure time, T^∗, is assumed to be vT +(1−v)∞, where v is an indicator of whether a subject will eventually (v = 1) or never (v = 0) experience treatment failure, and T denotes the failure time if the subject is not cured, with a survival distribution S(t), which is the conditional distribution for patients who will experience treatment failure and is often called the latency distribution. Thus, the unconditional survival distribution of T^∗ is a mixture model of a cure rate π = P(v = 0) and a latency distribution S(t) given by

$$S\ast (t)=\pi +(1-\pi )S(t).$$

Let λ^∗(t) and λ(t) be the hazard functions of T^∗ and T, respectively. We then have the following relation between the two hazard functions:

$$\mathrm{\lambda }\ast (t)=\frac{(1-\pi )S(t)}{\pi +(1-\pi )S(t)}\mathrm{\lambda }(t).$$

For a two-arm randomized survival trial, let $T_{ij}^{\ast }$ and C_ij denote the survival and censoring times, respectively, of patient i in the j^th group, where j = 1, 2 (1 for the control group and 2 for the treatment group). The observed data then consist of {X_ij; Δ_ij; i = 1, …, n_j, j = 1, 2}, where $X_{ij}=T_{ij}^{\ast }\wedge C_{ij}$ and ${\mathrm{\Delta }}_{ij}=I(T_{ij}^{\ast }\le C_{ij})$. It is commonly assumed that $\left\{T_{ij}^{\ast },C_{ij},i=1,\dots ,n_j\right\}$ are independent and identically distributed samples of (T_j, C_j) for control (j = 1) and treatment (j = 2) and that T_ij is independent of C_ij. Let $S_j^{\ast }(t)$ denote the unconditional survival distribution and let ${\mathrm{\lambda }}_j^{\ast }(t)$ denote its hazard function for the j^th group. When the main interest is in testing for differences between cure rates, it is reasonable to assume that the conditional survival distributions are the same for the two groups and are denoted by S(t), with the hazard function and cumulative hazard function being denoted by λ(t) and Λ(t), respectively. The cure rate for the j^th group is defined by π_j, where 0 ≤ π_j < 1. Then, the survival distribution of the mixture cure model for the j^th group is given by

$$S_j^{\ast }(t)={\pi }_j+(1-{\pi }_j)S(t),$$ (1)

and the hazard function for the j^th group is given by

$${\mathrm{\lambda }}_j^{\ast }(t)=\frac{(1-{\pi }_j)S(t)}{{\pi }_j+(1-{\pi }_j)S(t)}\mathrm{\lambda }(t).$$

We are interested in testing the following hypothesis:

$$H_0:{\pi }_1={\pi }_{2}vs.H_1:{\pi }_1\ne {\pi }_2.$$ (2)

Furthermore, we define the parameters γ and π₀ as follows:

$$\gamma =\frac{1}{2}\log \frac{1-{\pi }_2}{1-{\pi }_1},$$

$${\pi }_0=1-{\left[(1-{\pi }_1)(1-{\pi }_2)\right]}^{1/2},$$

where γ is the half-log ratio of the failure rates, and π₀ is the proportion of cured patients under the null hypothesis. Then, hypothesis (2) is equivalent to the following hypothesis:

$$H_0:\gamma =0vs.H_1:\gamma \ne 0.$$ (3)

The mixture cure model (1) can be written as

$$S_j^{\ast }(t)=1-e^{{(-1)}^j\gamma }(1-{\pi }_0)\left\{1-S(t)\right\},$$ (4)

and the corresponding hazard function is given by

$${\mathrm{\lambda }}_j^{\ast }(t)=\frac{e^{{(-1)}^j\gamma }(1-{\pi }_0)S(t)}{1-e^{{(-1)}^j\gamma }(1-{\pi }_0)+e^{{(-1)}^j\gamma }(1-{\pi }_0)S(t)}\mathrm{\lambda }(t).$$ (5)

This alternative implies that the unconditional failure distributions for two groups are proportional; it is called a proportional distributions alternative by Gray and Tsiatis (1989).

To test hypothesis (2) or (3), or the difference in the unconditional failure distributions, a weighted score test can be used, which is given by

$$U_w=n^{-1/2}{\displaystyle {\int }_0^{\infty }W(t)}\left\{\frac{Y_1(t)}{Y(t)}d{N}_2(t)-\frac{Y_2(t)}{Y(t)}d{N}_1(t)\right\},$$

where n = n₁ + n₂ is the total sample size of two groups, W(t) is a weight function that converges in probability to w(t), N_j(t) is the number of observed failures by time t, Y_j(t) is the number of subjects at risk just prior to t in groups j = 1, 2, and Y (t) = Y₁(t) + Y₂(t). By the martingale central limit theorem (Fleming and Harrington, 1991), under the null hypothesis, U_w converges in distribution to a normal variable with a mean of zero and variance

$${\sigma }_w^2=p(1-p)(1-{\pi }_0){\displaystyle {\int }_0^{\infty }{w}^2(t)G(t)S(t)d\mathrm{\Lambda }(t),}$$ (6)

where p = lim_n→∞ n₁/n, and G(t) is the common survival distribution of the censoring time of two groups (see appendix). The variance ${\sigma }_w^2$ in (6) can be estimated by

$${\widehat{\sigma }}_w^2=n^{-1}{\displaystyle {\int }_0^{\infty }{W}^2(t)}\frac{Y_1(t)Y_2(t)}{Y^2(t)}dN(t),$$

where N(t) = N₁(t) + N₂(t). Therefore, under the null hypothesis, the weighted log-rank test $L_w=U_w/{\widehat{\sigma }}_w$ is asymptotically standard normal distributed. Thus, given a significance level α, we reject the null hypothesis if |L_w| > z_1−α/2, where z_1−α/2 is the 100(1 − α/2)^th percentile of the standard normal distribution.

3 Sample Size Formula

To derive the sample size formula, we need to know the asymptotic distribution of the weighted log-rank test under the alternative hypothesis. Consider a sequence of local alternatives

$$S_j^{\ast (n)}(t)=1-e^{{(-1)}^j{\gamma }_n}(1-{\pi }_0)\left\{1-S(t)\right\},$$

where n^1/2γ_n = γ_a. Under the local alternatives, as shown in the appendix, the weighted log-rank test $L_w=U_w/{\widehat{\sigma }}_w$ converges in distribution to a normal variable with unit variance and mean μ(w, γ_a)/σ_w, where ${\sigma }_w^2$ is given by (6), and

$$\mu (w,{\gamma }_a)=2p(1-p)(1-{\pi }_0){\gamma }_a{\displaystyle {\int }_0^{\infty }w(t){\left\{S_0^{\ast }(t)\right\}}^{-1}G(t)S(t)d\mathrm{\Lambda }(t)},$$ (7)

for which $S_0^{\ast }(t)={\pi }_0+(1-{\pi }_0)S(t)$.

Therefore, on the basis of the limiting distribution of L_w under the local alternative, given a type I error of α, to achieve a power of 1 − β, the total sample size n of two groups must approximately satisfy the following equation:

$$1-\beta \simeq \mathrm{\Phi }\{\mu (w,{\gamma }_a)/{\sigma }_w-z_{1-\alpha /2}\}.$$

For a local alternative γ, we replace γ_a by n^1/2γ. Then, the sample size required to detect a local alternative γ can be determined by

$$n=\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2{\sigma }_w^2}{\mu {(w,\gamma )}^2}.$$ (8)

Substituting equations (6) and (7) into (8), the total sample size for the weighted log-rank test can be calculated by

$$n=\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2{\displaystyle {\int }_0^{\infty }{w}^2(t)G(t)S(t)d\mathrm{\Lambda }(t)}}{4p(1-p)(1-{\pi }_0){\gamma }^2{[{\displaystyle {\int }_0^{\infty }w(t)}{\left\{S_0^{\ast }(t)\right\}}^{-1}G(t)S(t)d\mathrm{\Lambda }(t)]}^2}.$$ (9)

4 Optimal Log-rank Test

It is well known that the log-rank test is optimal against the proportional hazards model. However, the cure model (1) does not satisfy the proportional hazards assumption; thus, the log-rank test is not an optimal test, and a study design based on the log-rank test is not fully efficient. Therefore, it is desirable to find an optimal test for the cure model (1) under the local proportional distributions alternative. As the mean of the weighted log-rank test is proportional to

$${\displaystyle {\int }_0^{\infty }w(t){\left\{S_0^{\ast }(t)\right\}}^{-1}h(t)dt,}$$

where h(t) = G(t)S(t)λ(t), by using the Cauchy-Schwartz inequality, we obtain the following inequality:

$${{\displaystyle {\int }_0^{\infty }w(t){\left\{S_0^{\ast }(t)\right\}}^{-1}h(t)dt\le \left\{{\displaystyle {\int }_0^{\infty }{w}^2(t)h(t)dt}{\displaystyle {\int }_0^{\infty }{\left\{S_0^{\ast }(t)\right\}}^{-2}h(t)dt}\right\}}}^{1/2},$$

with equality if only if w(t) is proportional to ${\left\{S_0^{\ast }(t)\right\}}^{-1}$. That is, the optimal weight function w(t) is proportional to ${\left\{S_0^{\ast }(t)\right\}}^{-1}$, which minimizes the sample size given by formula (9). Thus, taking the weight function W (t) = {K(t⁻)}⁻¹, where K(t⁻) is the left-continuous version of the Kaplan-Meier estimate computed from the pooled sample of two groups, gives the asymptotically optimal test for the proportional distributions alternative. Hence, by substituting $w(t)={\left\{S_0^{\ast }(t)\right\}}^{-1}$ into formula (9), the sample size for the optimal log-rank test L_K is given by

$$n_K=\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2}{4p(1-p)(1-{\pi }_0){\gamma }^2{\displaystyle {\int }_0^{\infty }{\left\{S_0^{\ast }(t)\right\}}^{-2}G(t)}S(t)d\mathrm{\Lambda }(t)},$$ (10)

and by substituting w(t) = 1 into formula (9), the sample size for the standard log-rank test L is given by

$$n=\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2{\displaystyle {\int }_0^{\infty }G(t)S(t)d\mathrm{\Lambda }(t)}}{4p(1-p)(1-{\pi }_0){\gamma }^2{[{\displaystyle {\int }_0^{\infty }{\{S_0^{\ast }(t)\}}^{-1}G(t)S(t)d\mathrm{\Lambda }(t)}]}^2}.$$ (11)

The asymptotic relative efficiency ρ = n/n_K (Randales and Wolfe, 1979) of the optimal test compared to the standard log-rank test is given by

$$\rho =\frac{{\displaystyle {\int }_0^{\infty }{\{S_0^{\ast }(t)\}}^{-2}G(t)S(t)d\mathrm{\Lambda }(t){\displaystyle {\int }_0^{\infty }G(t)S(t)d\mathrm{\Lambda }(t)}}}{{[{\displaystyle {\int }_0^{\infty }{\{S_0^{\ast }(t)\}}^{-1}G(t)S(t)d\mathrm{\Lambda }(t)}]}^2}.$$ (12)

In the special case when there is no censoring, that is, when G(t) = 1, the asymptotic relative efficiency ρ in (12) is reduced to

$$\rho =\frac{{(1-{\pi }_0)}^2}{{\pi }_0{[\log ({\pi }_0)]}^2}.$$

5 Comparison

We investigated three important issues. First, we studied the relative efficiency of the optimal log-rank test versus the standard log-rank test. Second, we evaluated the robustness of the optimal and standard log-rank tests when the hazard parameter was misspecified in the trial design. Third, we investigated the performance of the two sample size formulae under various design scenarios.

The relative efficiency ρ given in equation (12) was calculated for selected cure rates under the exponential cure model with an uncured hazard parameter λ = 1. Assume a uniform accrual over [0, τ] and no follow-up period, where τ is determined by the percentage of censoring ranging from 0% to 50%. The results (Table 1) showed that when the cure rate π₀ was at most 10% and there was no censoring, the gain in efficiency of the optimal log-rank test versus the standard log-rank test was more than 50%, whereas if the cure rate π₀ was at least 50%, the gain in efficiency was less than 5%. If the percentage of censoring was more than 50%, then the gain in efficiency was less than 10%, regardless of the cure rate. We also investigated the relative efficiency through the sample size calculations. Under the same assumptions, sample sizes were calculated under various combinations of the cure rates of two groups. Similarly, the largest gain in efficiency was achieved when both the cure rate and percentage of censoring were small (Table 2).

Table 1.

The relative efficiency ρ of the optimal log-rank test compared to the standard log-rank test under the exponential model with a hazard parameter λ = 1 and a uniform accrual over the interval [0, τ], where τ is determined by the percentage of censoring.

Cure rate π0
Cens	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
None	1.528	1.235	1.127	1.072	1.041	1.022	1.011	1.004	1.001
10%	1.490	1.221	1.120	1.068	1.039	1.021	1.010	1.004	1.001
20%	1.399	1.190	1.105	1.061	1.035	1.019	1.009	1.004	1.001
30%	1.272	1.144	1.084	1.050	1.029	1.016	1.008	1.003	1.001
40%	1.166	1.099	1.061	1.037	1.022	1.012	1.006	1.002	1.001
50%	1.095	1.061	1.040	1.026	1.016	1.009	1.005	1.002	1.000

Censoring time was uniformly distributed over [0, τ], with the value of τ being chosen so that the probability of the failure time being censored for a subject who was not cured was the specified censoring percentage. Abbreviation: Cens: censoring.

Table 2.

Sample sizes for the optimal and standard log-rank tests for various cure rates in two groups with a nominal type I error of 5% and power of 90%. Here, sample sizes were calculated under the exponential model, with a hazard parameter λ = 1 and a uniform accrual over the interval [0, τ], where τ is determined by the percentage of censoring.

Cure rate (π1, π2)
		(.05, .15)	(.05, .2)	(.1, .2)	(.1, .3)	(.2, .4)	(.3, .5)	(.4, .6)
Test	Cens			Sample size
L	None	598	301	738	217	257	279	281
	10%	766	379	916	263	304	323	321
	20%	1067	513	1218	338	375	388	379
	30%	1566	730	1697	453	481	483	460
	40%	2323	1058	2415	623	632	616	573
	50%	3479	1577	3509	881	860	813	740
LK	None	394	215	554	177	230	261	270
	10%	517	275	698	217	272	303	310
	20%	766	391	964	286	341	367	367
	30%	1233	597	1423	398	445	461	448
	40%	1993	926	2144	569	597	594	562
	50%	3180	1437	3262	831	828	794	729

Censoring time was uniformly distributed over [0, τ], with the value of τ being chosen so that the probability of the failure time being censored for a subject who was not cured was the specified censoring percentage. Abbreviations: Cens: censoring; L: standard log-rank test; L_K: optimal log-rank test.

To evaluate the robustness of the two tests, sample sizes (n) were calculated under exponential models with hazard parameters λ = 0.1 and 1. Cure rates were set to π₁ = 0.1 and ${\pi }_2={\pi }_1{e}^{{\gamma }_0}/(1-{\pi }_1+{\pi }_1{e}^{{\gamma }_0})$, where γ₀ ranged from 1.5 to 2.0, accrual time t_a = 1, and follow-up time t_f = 2. Sample sizes (n^∗) were also calculated under misspecification of the hazard parameter within a range of λ±20%λ. The %diff = 100(n^∗−n)/n was calculated for the evaluation of robustness. The results showed that both tests were sensitive to the misspecification of the hazard parameter. However, the %diff was similar for both tests, and the optimal test was slightly more sensitive than the standard log-rank test (Table 3).

Table 3.

Sample sizes for the exponential cure models under misspecification of the hazard parameter λ, with cure rates π₁ = 0.1 and π₂ = π₁e^γ0/(1−π₁ + π₁e^γ0), uniform accrual with accrual time t_a = 1 and follow-up time t_f = 2, and nominal type I error of 5% and power of 90%.

	True λ		Misspecified λ
		λ = 0.1	λ = 0.08		λ = 0.12
Test	γ0	n	n∗	%diff	n∗	%diff
L	1.5	2282	2885	26.4	1880	−17.6
	1.6	1873	2367	26.4	1545	−17.5
	1.7	1554	1963	26.3	1283	−17.4
	1.8	1302	1643	26.2	1075	−17.4
	1.9	1100	1387	26.1	909	−17.4
	2.0	938	1181	25.9	776	−17.3
LK	1.5	2274	2879	26.6	1872	−17.7
	1.6	1868	2363	26.5	1538	−17.7
	1.7	1550	1959	26.4	1278	−17.5
	1.8	1298	1640	26.3	1071	−17.5
	1.9	1097	1385	26.3	906	−17.4
	2.0	935	1179	26.1	773	−17.3

		λ = 1	λ = 0.8		λ = 1.2
Test	γ0	n	n∗	%diff	n∗	%diff
L	1.5	219	259	18.3	197	−10.0
	1.6	185	218	17.8	167	−9.7
	1.7	158	185	17.1	144	−8.9
	1.8	137	159	16.1	124	−9.5
	1.9	119	138	16.0	109	−8.4
	2.0	105	121	15.2	96	−8.6
LK	1.5	193	233	20.7	170	−11.9
	1.6	164	198	20.7	146	−11.0
	1.7	142	169	19.0	127	−10.6
	1.8	123	146	18.7	111	−9.8
	1.9	108	128	18.5	98	−9.3
	2.0	96	112	16.7	87	−9.4

%diff: change in sample size through misspecified hazard parameter λ, i.e., %diff =100 × (n^∗ − n)/n, where n is the sample size calculated under the true λ and n^∗ is the sample size calculated under the misspecified λ. Abbreviations: L: standard log-rank test; L_K: optimal log-rank test.

To investigate the performance of the sample size formulae for the optimal and standard log-rank tests, we calculated sample sizes under the cure model (1), where cure rates were set as in Table 3, and the conditional survival distribution was Weibull, $S(t)=e^{-\mathrm{\lambda }{t}^{\kappa }}$, or log-logistic, $S(t)=\frac{1}{1+\mathrm{\lambda }{t}^{\kappa }}$. The scale parameter λ was set to 0.4, and the shape parameter κ was set to 0.5, 1, or 2, reflecting a decreasing, constant, and increasing hazard function, respectively, for the Weibull distribution; and a decreasing and single-mode hazard function for the log-logistic distribution. We assumed that subjects were recruited with a uniform distribution over the accrual period t_a = 1, with a follow-up period t_f = 2. We further assumed that no subject was lost to follow-up during the study. Then, the censoring time was uniformly distributed over the interval [t_f, t_a + t_f], that is, the censoring survival distribution G(t) = 1 if t ≤ t_f; = (t_a + t_f − t)/t_a if t_f ≤ t ≤ t_a + t_f; = 0 otherwise. Therefore, given a two-sided nominal significance level of 0.05 and power of 90%, the required sample sizes were calculated for each design scenario under each distribution. The empirical type I errors and powers of the corresponding designs were simulated based on 100,000 runs. The simulation results presented in Table 4 can be summarized as follows. First, the empirical powers of both the optimal and standard log-rank tests were close to the nominal level of 90%. Thus, the sample sizes were adequately estimated. Second, the empirical type I errors of both tests were close to the nominal level of 5%. Thus, both tests preserved type I error well. Third, the sample sizes calculated from the optimal test were smaller than those calculated for the standard log-rank test.

Table 4.

Sample sizes (n) and corresponding simulated empirical type I errors $(\widehat{\alpha })$ and powers $(1-\widehat{\beta })$ for the optimal and standard log-rank tests under the Weibull and log-logistic distributions, with a scale parameter λ = 0.4, cure rates π₁ = 0.1 and ${\pi }_2={\pi }_1{e}^{{\gamma }_0}/(1-{\pi }_1+{\pi }_1{e}^{{\gamma }_0})$, nominal type I error of 0.05, power of 90%, and uniform accrual with accrual time t_a = 1 and follow-up time t_f = 2.

			κ = 0.5			κ=1			κ = 2
Dist	Test	γ0	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$	n	$\widehat{\alpha }$	$1-\widehat{\beta }$
WB	L	1.5	841	.048	.905	510	.053	.905	222	.052	.914
		1.6	695	.049	.900	424	.050	.899	188	.052	.914
		1.7	580	.051	.901	355	.045	.906	161	.050	.922
		1.8	488	.050	.903	301	.050	.906	139	.051	.924
		1.9	415	.049	.905	258	.048	.907	121	.052	.921
		2.0	356	.051	.907	222	.053	.906	106	.050	.925
	LK	1.5	827	.049	.901	490	.053	.904	195	.051	.919
		1.6	683	.045	.901	408	.048	.910	166	.055	.919
		1.7	571	.051	.902	343	.051	.902	143	.048	.925
		1.8	481	.049	.905	291	.050	.906	125	.052	.928
		1.9	410	.053	.904	250	.052	.909	110	.052	.926
		2.0	351	.052	.906	216	.047	.910	97	.052	.932
LG	L	1.5	1112	.048	.900	762	.052	.908	404	.048	.906
		1.6	916	.050	.907	630	.049	.903	337	.049	.908
		1.7	763	.047	.908	526	.053	.904	284	.051	.908
		1.8	641	.047	.905	443	.050	.907	241	.050	.916
		1.9	544	.049	.903	377	.050	.907	207	.049	.915
		2.0	465	.048	.900	324	.054	.907	180	.050	.912
	LK	1.5	1100	.048	.902	746	.051	.903	382	.053	.907
		1.6	907	.049	.906	617	.045	.897	319	.053	.909
		1.7	755	.050	.908	516	.052	.898	270	.051	.914
		1.8	635	.048	.903	436	.051	.906	230	.050	.911
		1.9	539	.049	.908	371	.056	.903	198	.051	.910
		2.0	461	.053	.904	319	.049	.910	172	.050	.916

Abbreviations: Cens: censoring; Dist: distribution; WB: Weibull; LG: log-logistic; L: standard log-rank test; L_K: optimal log-rank test.

Overall, the results showed that the derived sample size formulae provide adequate sample size estimation for trial design if the main interest is to detect the differences between the cure rates of two groups and that the optimal test is more efficient than the standard log-rank test, particular when both cure rates and percentage censoring are small.

6 Example

We illustrate study design under a parametric cure model by using the data from the Eastern Cooperative Oncology Group (ECOG) trial e1684. The ECOG trial e1684 was a two-arm phase III clinical trial to compare the relapse-free survival (RFS) of patients with melanoma who were treated with high-dose interferon alpha-2b or placebo as postoperative adjuvant therapy. The trial accrued patients between 1984 and 1990 and remained blinded under analysis until 1993 (Kirkwood, et al., 1996). Researchers have studied this dataset extensively using cure models (Corbiere and Joly, 2007). There were 92 deaths among the 146 patients in the treatment group. The SAS macro PSPMCM was applied to this data to fit the treatment arm data under the Weibull cure model (Figure 1), with an estimated shape parameter κ of 1.018, scale parameter λ of 0.836, and a cure rate of 35%. Suppose we wish to design a two-arm randomized phase III trial to detect a 20% difference between the cure rate in the arm that receives the new treatment and that in the control arm that receives the same therapy as the treatment arm of the ECOG trial, with a two-sided type I error of 0.05, power of 90% at the alternative, a uniform accrual with a 5-year accrual period and 5-year of follow-up, no loss to follow-up, and equal allocation between the two groups. Then, the required sample sizes calculated using formulae (10) and (11) under the Weibull cure model are 266 and 280 patients, respectively. The corresponding simulated empirical type I error and power are 0.05 and 91.4% for the optimal log-rank test, and 0.05 and 90.7% for the standard log-rank test. As the cure rate is relatively high, the gain in efficiency is only approximately 5% in this example.

Figure 1.

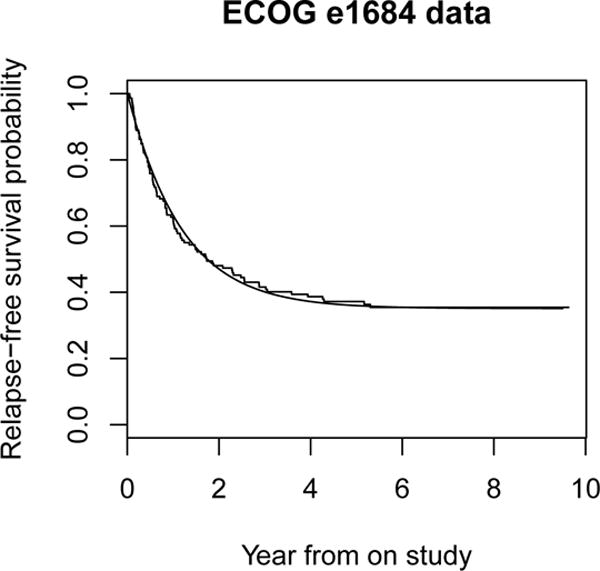
Relapse-free survival for ECOG e1864 data. The step function is the Kaplan-Meier survival curve. The solid curve is the fitted Weibull cure model.

7 Conclusion

For cancer clinical trials in which a portion of patients are cured, the main interest is in demonstrating the differences between the cure rates in the two treatment groups. In this article, sample size formulae are derived for both the optimal and standard log-rank tests. Because the proposed cure model is not a proportional hazards model, the standard log-rank test is not fully efficient. Thus, a sample size calculation derived under the optimal test can ensure the efficacy of the study design. The optimal log-rank test is implemented in the standard statistical software R by using the survdiff function with the option rho = −1. The simulation results demonstrated that the sample size formula for the optimal test provides adequate sample size estimation and is more efficient than the formula for the standard log-rank test. Finally, if trials are planned to include interim analyses to enable them to be halted early if futility or efficacy is demonstrated, then the group sequential methods developed by Lee and Sather (1995) can be used.

Appendix: Derivation of the asymptotic distribution of the weighted log-rank test

The weighted score test is given by

$$U_w=n^{-1/2}{\displaystyle {\int }_0^{\infty }W(t)}\left\{\frac{Y_1(t)}{Y(t)}d{N}_2(t)-\frac{Y_2(t)}{Y(t)}d{N}_1(t)\right\},$$

where n = n₁ + n₂ is the total sample size of two groups, W (t) is a weight function that converges in probability to w(t), N_j(t) is the number of observed failures by time t, Y_j(t) is the number of subjects at risk just prior to t in groups j = 1, 2, and Y (t) = Y₁(t) + Y₂(t). If we define martingale processes such that $M_j(t)=N_j(t)-{\displaystyle {\int }_0^t{\mathrm{\lambda }}_j^{\ast }}(t)Y_j(t)dt$, j = 1, 2, where ${\mathrm{\lambda }}_j^{\ast }(t)$ is given in equation (5), then the weighted score test can be written as

$$U_w=n^{-1/2}{\displaystyle {\int }_0^{\infty }W(t)}\left\{\frac{Y_1(t)}{Y(t)}d{M}_2(t)-\frac{Y_2(t)}{Y(t)}d{M}_1(t)\right\}+{\displaystyle {\int }_0^{\infty }W(t)}\frac{Y_1(t)Y_2(t)}{nY(t)}{n}^{1/2}\left\{{\mathrm{\lambda }}_2^{\ast }(t)-{\mathrm{\lambda }}_1^{\ast }(t)\right\}dt.$$

Under the null hypothesis H₀ : γ = 0, we have ${\mathrm{\lambda }}_1^{\ast }(t)={\mathrm{\lambda }}_2^{\ast }(t)={\mathrm{\lambda }}_0^{\ast }(t)$, where

$${\mathrm{\lambda }}_0^{\ast }(t)=\frac{(1-{\pi }_0)S(t)}{{\pi }_0+(1-{\pi }_0)S(t)}\mathrm{\lambda }(t).$$

Hence, by the martingale property, the mean of U_w is 0 and the variance of U_w is given by

$$\text{Var}(U_w)=n^{-1}E{\displaystyle {\int }_0^{\infty }{W}^2}(t)\frac{Y_1(t)Y_2(t)}{Y(t)}d{\mathrm{\Lambda }}_0^{\ast }(t),$$

where ${\mathrm{\Lambda }}_0^{\ast }(t)={\displaystyle {\int }_0^t{\mathrm{\lambda }}_0^{\ast }}(u)du$. As

$$n^{-1}\frac{Y_1(t)Y_2(t)}{Y(t)}=\frac{n_1{n}_2}{n^2}\frac{\left\{Y_1(t)/n_1\right\}\left\{Y_2(t)/n_2\right\}}{Y(t)/n}\to p(1-p)\frac{{\pi }_1(t){\pi }_2(t)}{\pi (t)},$$

where $p={{\text{lim}}_n}_{\to \infty }{n}_1/n,{\pi }_j(t)=P(T_{ij}^{\ast }>t)$ and π(t) = pπ₁(t) + (1 − p)π₂(t). Thus, by the martingale central limit theorem (Fleming and Harrington, 1991), $U_w\to N(0,{\sigma }_w^2)$, where

$${\sigma }_w^2=p(1-p){\displaystyle {\int }_0^{\infty }{w}^2}(t)G(t)S_0^{\ast }(t){\mathrm{\lambda }}_0^{\ast }(t)dt,$$

for which $S_0^{\ast }(t)={\pi }_0+(1-{\pi }_0)S(t)$ and G(t) is the common survival distribution of the censoring time of the two groups. By noting that $S_0^{\ast }(t){\mathrm{\lambda }}_0^{\ast }=(1-{\pi }_0)S(t)\mathrm{\lambda }(t)$, we have

$${\sigma }_w^2=p(1-p)(1-{\pi }_0){\displaystyle {\int }_0^{\infty }{w}^2}(t)G(t)S(t)\mathrm{\lambda }(t)dt.$$ (13)

The variance ${\sigma }_w^2$ can be estimated by

$${\widehat{\sigma }}_w^2=n^{-1}{\displaystyle {\int }_0^{\infty }{W}^2}(t)\frac{Y_1(t)Y_2(t)}{Y(t)}d{\widehat{\mathrm{\Lambda }}}_0^{\ast }(t),$$

where $d{\widehat{\mathrm{\Lambda }}}_0^{\ast }(t)=dN(t)/Y(t)$ and N(t) = N₁(t) + N₂(t). Therefore, the weighted log-rank test $L_w=U_w/{\widehat{\sigma }}_w$ is asymptotically standard normal distributed under the null hypothesis.

To derive the asymptotic distribution of the weighted log-rank test under the alternative, consider a sequence of local alternatives $H_1^{(n)}:S_j^{\ast (n)}(t)=1-e^{(-1)j_{\gamma n}}(1-{\pi }_0)\left\{1-S(t)\right\}$, or

$${\mathrm{\lambda }}_j^{\ast (n)}(t)=\frac{e^{(-1)j_{\gamma n}}(1-{\pi }_0)S(t)}{1-e^{(-1)j_{\gamma n}}(1-{\pi }_0)+e^{(-1)j_{\gamma n}}(1-{\pi }_0)S(t)}\mathrm{\lambda }(t),$$

where n^1/2γ_n = γ_a < ∞, and define martingale processes as $M_j^{(n)}(t)=N_j(t)-{\displaystyle {\int }_0^t{Y}_j(u){\mathrm{\lambda }}_j^{\ast (n)}(u)}du$_. Then, U_w = U_1w+U_1w+U_2w, where

$$U_{1w}=n^{-1/2}{\displaystyle {\int }_0^{\infty }W(t)}\left\{\frac{Y_2(t)}{Y(t)}d{M}_1^{(n)}(t)-\frac{Y_1(t)}{Y(t)}d{M}_2^{(n)}(t)\right\},$$

and

$$U_{2w}=n^{-1/2}{\displaystyle {\int }_0^{\infty }W(t)}\frac{Y_1(t)Y_2(t)}{Y(t)}\left\{{\mathrm{\lambda }}_1^{\ast (n)}(t)-{\mathrm{\lambda }}_2^{\ast (n)}(t)\right\}dt.$$

As γ_n → 0, $H_1^{(n)}\to H_0$ and, ${\mathrm{\lambda }}_j^{\ast (n)}(t)\to {\mathrm{\lambda }}_0^{\ast }(t)$, and by the martingale central limiting theorem, U_1w converges to a normal variable with mean EU_1w = 0 and variance

$$E{U}_{1w}^2=n^{-1}E{\displaystyle {\int }_0^{\infty }{W}^2(t)}\left\{\frac{Y_2^2(t)}{Y^2(t)}{Y}_1(t){\mathrm{\lambda }}_1^{\ast (n)}(t)+\frac{Y_1^2(t)}{Y^2(t)}{Y}_2(t){\mathrm{\lambda }}_2^{\ast (n)}(t)\right\}du\to p(1-p){\displaystyle {\int }_0^{\infty }{w}^2(t)}\left\{(1-p)\frac{{\pi }_2^2(t){\pi }_1(t)}{{\pi }^2(t)}{\mathrm{\lambda }}_0^{\ast }(t)+p\frac{{\pi }_1^2(t){\pi }_2(t)}{{\pi }^2(t)}{\mathrm{\lambda }}_0^{\ast }(t)\right\}dt=p(1-p){\displaystyle {\int }_0^{\infty }{w}^2(t)}\frac{{\pi }_1(t){\pi }_2(t)}{\pi (t)}{\mathrm{\lambda }}_0^{\ast }(t)du=p(1-p){\displaystyle {\int }_0^{\infty }{w}^2(t)}G(t)S_0^{\ast }(t){\mathrm{\lambda }}_0^{\ast }(t)dt={\sigma }_w^2.$$

By Taylor’s expansion of ${\mathrm{\lambda }}_j^{\ast }(t)$ at γ_n = 0, we have

$${\mathrm{\lambda }}_j^{\ast }(t)\simeq \frac{(1-{\pi }_0)S(t)}{{\pi }_0+(1-{\pi }_0)S(t)}\mathrm{\lambda }(t)+\frac{(1-{\pi }_0)S(t)}{{\left\{{\pi }_0+(1-{\pi }_0)S(t)\right\}}^2}\mathrm{\lambda }(t){(-1)}^j{\gamma }_n.$$

It then follows that

$$\underset{n\to \infty }{\lim }{n}^{1/2}\left\{{\mathrm{\lambda }}_2^{\ast }(t)-{\mathrm{\lambda }}_1^{\ast }(t)\right\}=\frac{2{\gamma }_a(1-{\pi }_0)S(t)\mathrm{\lambda }(t)}{{\left\{{\pi }_0+(1-{\pi }_0)S(t)\right\}}^2}.$$

By substituting this into U_2w, we have shown that U_2w converges in probability to μ(w, γ_a), where

$$\mu (w,{\gamma }_a)=2p(1-p)(1-{\pi }_0){\gamma }_a{\displaystyle {\int }_0^{\infty }w(t){\left\{S_0^{\ast }(t)\right\}}^{-1}G(t)S(t)\mathrm{\lambda }(t)dt}.$$

Thus, under the local alternatives $H_1^{(n)}$, the weighted log-rank test is asymptotically normal distributed with mean μ_w/σ_w and unit variance, that is,

$$L_w=U_w/{\widehat{\sigma }}_w\to N(\mu (w,{\gamma }_a)/{\sigma }_w,1).$$