Significance
Zika virus (ZIKV) continues to be a threat to countries with conditions suitable for transmission, namely adequate temperatures and the presence of competent mosquito vectors. Estimates of risk in other countries based on the sexual transmission of ZIKV may be underestimated because of inadequate surveillance. Here, we formulate random network models of sexual transmission of ZIKV with asymmetric transmission (men being infectious for longer than women) and show that, contrary to previous work, there exists two epidemic thresholds and that certain men who have sex with men communities could sustain transmission on their own. Our results also shed light on a class of processes on random networks by providing a complete analysis of dynamics with multiple critical points.
Keywords: phase transition, Zika virus, percolation, complex networks, mathematical epidemiology
Abstract
Zika virus (ZIKV) exhibits unique transmission dynamics in that it is concurrently spread by a mosquito vector and through sexual contact. Due to the highly asymmetric durations of infectiousness between males and females—it is estimated that males are infectious for periods up to 10 times longer than females—we show that this sexual component of ZIKV transmission behaves akin to an asymmetric percolation process on the network of sexual contacts. We exactly solve the properties of this asymmetric percolation on random sexual contact networks and show that this process exhibits two epidemic transitions corresponding to a core–periphery structure. This structure is not present in the underlying contact networks, which are not distinguishable from random networks, and emerges because of the asymmetric percolation. We provide an exact analytical description of this double transition and discuss the implications of our results in the context of ZIKV epidemics. Most importantly, our study suggests a bias in our current ZIKV surveillance, because the community most at risk is also one of the least likely to get tested.
Abstract modeling of epidemics on networks remains an active field, because some of the most basic features of epidemics are still misunderstood. The classic model is quite simple (1): disease spreads stochastically with a fixed transmission probability, , through contacts around a given patient zero. The outbreak dies quickly if is too small but spreads to a macroscopic fraction of the entire population if is larger than a threshold . At , most of the typical insights from phase transition theory are valuable. For instance, the sizes of microscopic outbreaks follow a power law distribution, such that the expected size of microscopic outbreaks, , indicates the position of a phase transition. Indeed, as increases, monotonically increases, diverges exactly at , and then monotonically goes down; meanwhile, the expected macroscopic epidemic size, , starts increasing monotonically at .
However, simple modifications to this model can dramatically alter its phenomenology. The epidemic threshold can vanish in networks with a scale-free degree distribution (2) or in growing networks (3). The phase transition can be discontinuous in the case of complex contagions with threshold exposition or reinforcement (4), interacting epidemics (5, 6), or adaptive networks (7–9). Recently, a unique phenomenon of double-phase transitions has also been observed numerically when networks have a very heterogeneous and clustered structure (10, 11).
The current Zika virus (ZIKV) epidemic exhibits two unique properties. First, while the main transmission pathway for ZIKV is through a mosquito vector [predominantly Aedes aegypti or Aedes albopictus (13, 14)], a feature which has its own type of well-studied model and behavior (14–16), it can also spread through sexual contacts (17, 18). Second, the probability of sexual transmission is highly asymmetric between males and females. Although this is also true for other sexually transmitted infections, such as HIV (19), it reaches an extreme level of asymmetry in the case of ZIKV. Indeed, males can be infectious for over 180 days (20), while females are infectious for less than 20 days (21). Assuming a symmetric risk of transmission per contact, males would be 10 times more likely to transmit to a partner than females. This is, however, a rather conservative estimate, since male-to-female transmissions tend to be more likely than the opposite (19, 22).
The dynamics of the ZIKV epidemic is well-understood in countries where the vector-borne pathway dominates (23). However, with travelers moving to and from endemic regions, the potential of ZIKV as an emerging sexually transmitted infection (STI) in regions without the mosquito vector remains to be fully assessed. Indeed, with only few reported cases of sexual transmission of ZIKV—including male to male, male to female, and female to male (18)—the scientific community still struggles to reach a consensus on the impact of sexual transmission of ZIKV (24, 25). It is, therefore, imperative to investigate the extent to which canonical knowledge about emerging infectious diseases applies to the threat assessment of ZIKV as an STI.
We model the ZIKV sexual transmission through asymmetric percolation on random sexual contact networks and solve it exactly using a multitype (multivariate) generating function formalism (26). We then show how the asymmetric percolation leads to a double transition. Interestingly, the formulation of our model allows us to provide a first analytic framework for the aforementioned numerical results on double transitions. More importantly, this allows us to identify two different thresholds for ZIKV to be endemic as an STI in regions where the mosquito vector is absent but where travelers to/from endemic regions can spark a sexual epidemic when they return/visit. We also find that, in the large interval of parameter space between those two thresholds, the asymmetric percolation creates a core–periphery structure in a system where there was none. Finally, we discuss the implications of this core–periphery structure for the surveillance and control of the ZIKV epidemic and provide policy guidelines.
Results
Inspired by the sexual transmission of ZIKV, we investigate the effect of asymmetry on bond percolation on networks and show that it yields outcomes akin to the double-phase transitions observed numerically in other contexts (10, 11). To isolate the effect of asymmetry alone and thus, provide a clear proof of concept, we consider a very simple model, in which nodes belong to one of six types based on their sex and sexual orientation (i.e., female/male and homo-/bi-/heterosexual). Each node is assigned a number of contacts, , independent of its type (i.e., all nodes have the same degree distribution ), and links are created randomly via a simple stub-matching scheme constrained by the sexual orientations (12, 26). For instance, bisexual males choose their partners randomly in the pools of heterosexual females, bisexual males and females, and homosexual males. This implies that there is no correlation between the type of a node and its number of contacts and consequently, no core–periphery structure. In fact, this model generates well-mixed contact networks that are indistinguishable from networks generated with the configuration model and the same degree distribution (SI Appendix).
Although these networks are originally undirected, asymmetric percolation implies that links can be more likely to exist (i.e., transmit) in one direction than in the other, thus inducing an effective semidirected structure to the networks (27). In other words, in general, with being the probability of transmission from a node of type to a node of type (hereafter, we denote as the set of the six possible types of nodes). In particular, we set for every except when corresponds to a female, in which case we set to enforce asymmetric probabilities of transmission (i.e., females are times less likely to transmit ZIKV than males).
We adapt the formalism presented in ref. 26 to compute the epidemic threshold and the expected final size of outbreaks in the limit of large networks. It is worth pointing out that, since asymmetric percolation (i.e., whenever ) induces an effective semidirected structure to the networks, the probability for the existence of an extensive connected component (i.e., an epidemic) does not equal to its relative size as for symmetric, traditional bond percolation (i.e., ). Here, we focus on the relative size for the sake of conciseness; we refer to SI Appendix for full details of the analysis and numerical validation.
To obtain the relative size of the extensive component, we define as the probability that a neighbor of type is not in the extensive component, which we solve by a self-consistent argument. If the neighbor of a node is not in the extensive component, then none of its other neighbors should be in it either. With the probability that the neighbor has a degree equal to being , with , this self-consistent argument can be written as
| [1] |
where is the probability that a neighbor of a node of type is of type (i.e., for any ). Solving this equation for every , the probability that a node of type is part of the extensive component, , corresponds to the probability that at least one of its neighbors is in it as well:
| [2] |
The relative size of the extensive component is then , where is the fraction of the nodes that are of type . Below the epidemic or percolation threshold, every is equal to one, since there is no extensive component. The percolation threshold corresponds to the point where the largest eigenvalue of the Jacobian matrix of Eq. 1 equals one.
The distribution of the composition of the small, nonextensive components can be computed in a similar fashion (full details are in SI Appendix). Let us define the probability-generating function (pgf) , with coefficients that correspond to the probability that a neighbor of type leads to a small component of a given composition (i.e., the number of nodes of type is given by the exponent of ). Invoking the same self-consistency argument as above, the pgfs are the solution of
| [3] |
where the extra has been added to account for the neighbor of type itself. Similarly, the small component that can be reached from a node of type is, therefore, given by
| [4] |
The distribution of the composition of the small components is . It is worth noting that, whenever , the distribution generated by is no longer normalized, , such that the average number of nodes of type in the small components is
| [5] |
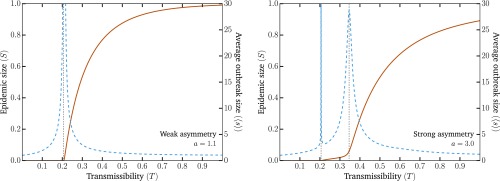
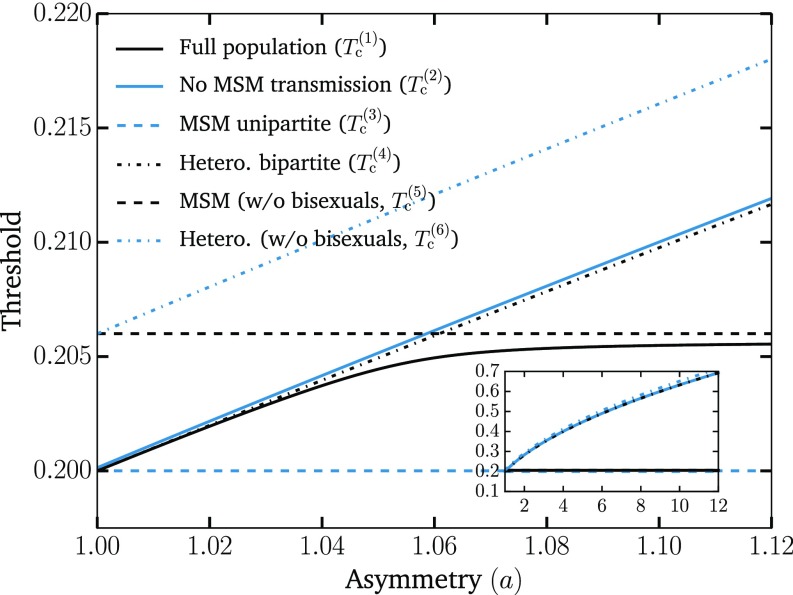
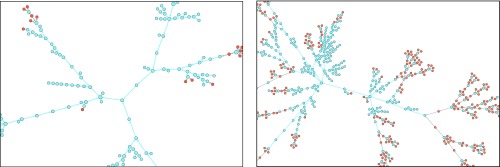
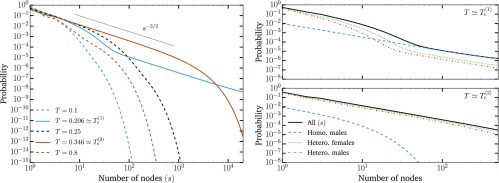
An example of the general phenomenology is shown in Fig. 1. Unlike the classic epidemic transition picture, where diverges at the epidemic threshold where the macroscopic epidemic emerges, we now find two peaks in . This double transition is similar to numerical results from ref. 10 but here observed without the need for either strong clustering or heterogeneity in degree distribution. In fact, we used the homogeneous Poisson degree to ensure that the asymmetry in the transmission is the only salient feature of the model. Interestingly, as shown in Fig. 2, and are virtually equal for small values of the asymmetry. As asymmetry increases, the peak separates, thus yielding a double transition corresponding to an effective core–periphery organization in the network of infections. The core then corresponds to the men having sex with men (MSM) population, where infections are more frequent than in the remaining population. Fig. 3 shows the network of who infected whom for two values of . For , the extensive component is mostly composed of one type of nodes, and any spillover in the other types quickly dies out. However, at , these spillovers now cause cascades into other types with truncated power law-distributed sizes (Fig. 4). For , the extensive component recovers the well-mixed structure of the original underlying network.
Fig. 1.
Emergence of the second transition as asymmetry increases. The solid lines show the expected fraction of the population in the extensive component (; left axis). The dashed lines show the average size of small nonextensive components (; right axis). The divergence of the average size of small components marks the phase transition after which the extensive components grow with the transmission probability . The vertical dotted black line shows the thresholds. (Left) With a small asymmetry between transmission values as a function of node types, we recover the classic epidemic transition. (Right) With a larger asymmetry, a second peak in the average size of small components appears. The first, , corresponds to the global epidemic threshold of the population. The second, , corresponds to the invasion of the large heterosexual subpopulation. The threshold corresponds to the value of , such that the largest eigenvalue of the Jacobian matrix of Eq. 1 equals one. The second threshold is obtained similarly but with the probability of transmission between homosexual males set to zero. The homo-/bi-/heterosexual subpopulations represent 5, 3, and 92%, respectively and are equally split between males and females. The degrees are distributed according to a Poisson distribution, , with an average degree, , equal to five. Additional details are in SI Appendix.
Fig. 2.
Separation of thresholds with increasing asymmetry. We show the two thresholds (critical points) and discussed in the text (solid lines) as well as the thresholds for different subpopulations (dotted lines), which can be easily calculated and further support our interpretation of the phenomenology. The first threshold, , corresponds to the epidemic threshold for the full population. The second threshold, , is computed by setting the transmission between MSM to zero. The MSM unipartite and Hetero. bipartite lines show the epidemic thresholds should the network be only populated with MSM or heterosexuals, respectively. They are defined as and , respectively, where is the average excess degree of the nodes (12). The last two thresholds correspond to the contributions to and that involve exclusively the homosexual male or heterosexual subpopulations, respectively. They are the solutions of and , respectively, where nodes of type zero, four, and five correspond to homosexual males, heterosexual males, and heterosexual females, respectively. These results, therefore, support the interpretation that the first threshold corresponds to the invasion of the MSM subpopulation [with and acting as lower and upper bounds, respectively] and that the second threshold is caused by the invasion of the remaining population [with and acting as lower and upper bounds, respectively]. Inset shows the growing separation of the two main thresholds as asymmetry increases to values close to what we expect for ZIKV. The same parameters as in Fig. 1 were used.
Fig. 3.
Composition of the components as the transmissibility increases. Nodes corresponding to males and females are shown in blue and orange, respectively, and arrows indicate who infected whom. The same parameters as for Fig. 1 have been used with asymmetry . (Left) At , the infection mostly follows the MSM subpopulation, with minimal and subcritical spillovers in the remaining population. (Right) At , the spillover causes cascades of power law-distributed sizes into the heterosexual population.
Fig. 4.
Distribution of the size and composition of small components. (Left) We find power law scaling of small outbreak sizes with scaling exponent , as expected from classic phase transition theory (12), at both and . However, unlike classic phase transitions, only the tail of the distribution follows a power law at , while at , we find a robust power law over many orders of magnitude before the distribution falls with the expected exponential cutoff. This cutoff goes to infinity when the size of the MSM community goes to zero, in which case now becomes the prominent critical point. Notice that the size of the components goes back to a homogeneous distribution in between the two epidemic thresholds. (Upper Right) At , the power law tail in the component size distribution is mainly caused by the critical core of homosexual males, while the exponential behavior is mainly caused by heterosexuals. The power law tail in the distributions of heterosexuals is caused by spillovers from the critical core. (Lower Right) At , the power law portion of the distribution is caused by heterosexuals now forming a critical core, while homosexual males, being already almost exclusively in the extensive component, do not contribute. All curves were obtained by solving Eq. 4 with asymmetry and the parameters given in the caption of Fig. 1.
Altogether, the second peak in the average size of outbreaks, , corresponds to a transition between subcritical and supercritical spillover in a less susceptible subpopulation but not to a second phase transition in the classic sense. Indeed, the analytical nature of our results allows us to confirm the null critical exponent observed in ref. 10 for the scaling of the height of the second susceptibility peak with regards to system size. Even in the infinite system considered by our calculations, the peak saturates, which is the only possible outcome for a system with an order parameter that is already nonzero. Interestingly, a critical power law-like behavior is nonetheless observed in the heterosexual population at both thresholds. Moreover, our results suggest that the asymmetry in transmission probability is reflected in the asymmetric prevalence within the male and female heterosexual populations, which is reminiscent of recent empirical results (28).
Based on our results, we can summarize the phase diagram of the ZIKV epidemic in three possible outcomes. First, with , all outbreaks are microscopic, quickly die out, and mostly infect MSM. Second, with , we now see a macroscopic epidemic within the network of homosexual contacts between males, with microscopic spillover into the rest of the population via bisexual males. Third, with , we now find a more classic epidemic scenario in the sense that it is of macroscopic scale in most of the population. It is also worth mentioning that this phenomenology is robust to the presence of multiple infectious seeds sparking outbreaks (SI Appendix). Our results are thus valid beyond ZIKV for any infections with asymmetry in probabilities of direct transmission, regardless of whether there is also vector transmission.
Discussion
We developed a network model of ZIKV transmission highlighting the importance of asymmetric sexual transmission between males and females. We find a double transition generated by a core group of MSM that could maintain ZIKV transmission without the presence of a viable mosquito vector, such as in regions where people may have brought back ZIKV with them after a trip to endemic regions. These results are unique, because previous models showing double transitions relied on the need for strong clustering and heterogeneity in degree distribution.
Our study carries important consequences for the ongoing ZIKV epidemic and stresses the large knowledge gap in the sexual transmission of ZIKV (25). The aim of our work is to present the epidemiological consequences of possible sustained sexual transmission. While there are many unknowns, recent work shows (i) multiple anecdotal cases of sexual transmission of ZIKV in humans (25, 29–31), (ii) multiple separate animal models showing sexual transmission (32–34), (iii) strong asymmetries between durations of ZIKV shedding in semen and vaginal secretions (20, 21), and (iv) differential risk between sexes for ZIKV infection in sexually active populations. Indeed, recent work has identified 90% more ZIKV infections in women between 15 and 65 years old than in men of the same age in Rio de Janeiro (28) adjusted for gender-related health-seeking behavior and pregnancy status. Importantly, this risk difference was not seen in women <15 or >65 years of age, indicating the potentially large impact of sexual transmission of ZIKV in a country with known ongoing vectored transmission of ZIKV. A similar situation has also been observed in Colombia (35) and the Dominican Republic (36). Although more research on the epidemiological impacts and basic biology of sexual ZIKV transmission is needed, there is compelling need to be prepared with epidemiological studies examining transmission on a population scale.
We showed that potential ZIKV persistence in MSM, even if barely critical within that subpopulation, could cause subcritical but dramatic spillover into the heterosexual community. ZIKV infections in adults are largely asymptomatic (37), and therefore, most testing occurs in the roughly of cases that are symptomatic or individuals seeking to have children (38). The vast majority of these individuals will be outside of the MSM community (38). This means that the community most at risk is also one of the least likely to get tested. To avoid underestimating the spread of ZIKV, it is, therefore, important for health officials and policymakers to keep its unique behavior and phenomenology in mind.
Given the extent of foreign travel to locations endemic with ZIKV, public health practitioners should be aware of the potential for infectious introduction into local MSM communities. Travel history as well as sexual history should be used when evaluating an occult fever. Cities which have a viable vector for ZIKV should be doubly aware of the potential transmission routes of ZIKV. As it stands, current estimates of the basic reproductive number, , of ZIKV may be too low, because they fail to account for sustained sexual transmission (17, 18, 39, 40). Important future work will be to accurately estimate of ZIKV across various settings with differing sexual practices and mosquito fauna.
Supplementary Material
Acknowledgments
A.A. acknowledges support from the Fonds de recherche du Québec–Nature et technologies. B.M.A. and L.H.-D. thank Bill and Melinda Gates for their support of this work and their sponsorship through the Global Good Fund. L.H.-D. acknowledges the Santa Fe Institute, the James S. McDonnell Foundation Postdoctoral Fellowship, and National Science Foundation Grant DMS-1622390. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1703073114/-/DCSupplemental.
References
- 1.Newman MEJ. Spread of epidemic disease on networks. Phys Rev E. 2002;66:016128. doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
- 2.Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Lett. 2001;86:3200–3203. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 3.Althouse BM, Hébert-Dufresne L. Epidemic cycles driven by host behaviour. J R Soc Interface. 2014;11:20140575. doi: 10.1098/rsif.2014.0575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dodds PS, Watts DJ. Universal behavior in a generalized model of contagion. Phys Rev Lett. 2004;92:218701. doi: 10.1103/PhysRevLett.92.218701. [DOI] [PubMed] [Google Scholar]
- 5.Hébert-Dufresne L, Althouse BM. Complex dynamics of synergistic coinfections on realistically clustered networks. Proc Natl Acad Sci USA. 2015;112:10551–10556. doi: 10.1073/pnas.1507820112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cai W, Chen L, Ghanbarnejad F, Grassberger P. Avalanche outbreaks emerging in cooperative contagions. Nat Phys. 2015;11:936–940. [Google Scholar]
- 7.Gross T, D’Lima CJD, Blasius B. Epidemic dynamics on an adaptive network. Phys Rev Lett. 2006;96:208701. doi: 10.1103/PhysRevLett.96.208701. [DOI] [PubMed] [Google Scholar]
- 8.Marceau V, Noël PA, Hébert-Dufresne L, Allard A, Dubé LJ. Adaptive networks: Coevolution of disease and topology. Phys Rev E. 2010;82:036116. doi: 10.1103/PhysRevE.82.036116. [DOI] [PubMed] [Google Scholar]
- 9.Scarpino SV, Allard A, Hébert-Dufresne L. The effect of a prudent adaptive behaviour on disease transmission. Nat Phys. 2016;12:1042–1046. [Google Scholar]
- 10.Colomer-de Simón P, Boguñá M. Double percolation phase transition in clustered complex networks. Phys Rev X. 2014;4:041020. [Google Scholar]
- 11.Bhat U, Shrestha M, Hébert-Dufresne L. Exotic phase transitions of k-cores in clustered networks. Phys Rev E. 2017;95:012314. doi: 10.1103/PhysRevE.95.012314. [DOI] [PubMed] [Google Scholar]
- 12.Newman MEJ, Strogatz SH, Watts DJ. Random graphs with arbitrary degree distributions and their applications. Phys Rev E. 2001;64:026118. doi: 10.1103/PhysRevE.64.026118. [DOI] [PubMed] [Google Scholar]
- 13.Althouse BM, et al. Potential for Zika virus to establish a sylvatic transmission cycle in the Americas. PLoS Negl Trop Dis. 2016;10:e0005055. doi: 10.1371/journal.pntd.0005055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Althouse BM, et al. Impact of climate and mosquito vector abundance on sylvatic arbovirus circulation dynamics in Senegal. Am J Trop Med Hyg. 2015;92:88–97. doi: 10.4269/ajtmh.13-0617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Smith DL, et al. Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012;8:e1002588. doi: 10.1371/journal.ppat.1002588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Althouse BM, et al. Synchrony of sylvatic dengue isolations: A multi-host, multi-vector SIR model of dengue virus transmission in Senegal. PLoS Negl Trop Dis. 2012;6:e1928. doi: 10.1371/journal.pntd.0001928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Althaus CL, Low N. How relevant is sexual transmission of Zika virus? PLoS Med. 2016;13:e1002157. doi: 10.1371/journal.pmed.1002157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yakob L, Kucharski A, Hue S, Edmunds WJ. Low risk of a sexually-transmitted Zika virus outbreak. Lancet Infect Dis. 2016;16:1100–1102. doi: 10.1016/S1473-3099(16)30324-3. [DOI] [PubMed] [Google Scholar]
- 19.Padian NS, Shiboski SC, Jewell NP. Female-to-male transmission of human immunodeficiency virus. JAMA. 1991;266:1664–1667. [PubMed] [Google Scholar]
- 20.Nicastri E, et al. Persistent detection of Zika virus RNA in semen for six months after symptom onset in a traveller returning from Haiti to Italy, February 2016. Euro Surveill. 2016;21:30314. doi: 10.2807/1560-7917.ES.2016.21.32.30314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Prisant N, et al. Zika virus in the female genital tract. Lancet Infect Dis. 2016;16:1000–1001. doi: 10.1016/S1473-3099(16)30193-1. [DOI] [PubMed] [Google Scholar]
- 22.Boily MC, et al. Heterosexual risk of HIV-1 infection per sexual act: Systematic review and meta-analysis of observational studies. Lancet Infect Dis. 2009;9:118–129. doi: 10.1016/S1473-3099(09)70021-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Q, et al. Spread of Zika virus in the Americas. Proc Natl Acad Sci USA. 2017;114:E4334–E4343. doi: 10.1073/pnas.1620161114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Folkers KM, Caplan AL, Igel LH. Zika, sexual transmission and prudent public health policy. Public Health. 2017;148:66–68. doi: 10.1016/j.puhe.2017.02.018. [DOI] [PubMed] [Google Scholar]
- 25.Moreira J, Peixoto TM, Siqueira AMd, Lamas CC. Sexually acquired Zika virus: A systematic review. Clin Microbiol Infect. 2017;23:296–305. doi: 10.1016/j.cmi.2016.12.027. [DOI] [PubMed] [Google Scholar]
- 26.Allard A, Hébert-Dufresne L, Young JG, Dubé LJ. General and exact approach to percolation on random graphs. Phys Rev E. 2015;92:062807. doi: 10.1103/PhysRevE.92.062807. [DOI] [PubMed] [Google Scholar]
- 27.Allard A, Noël PA, Dubé LJ, Pourbohloul B. Heterogeneous bond percolation on multitype networks with an application to epidemic dynamics. Phys Rev E. 2009;79:036113. doi: 10.1103/PhysRevE.79.036113. [DOI] [PubMed] [Google Scholar]
- 28.Coelho FC, et al. Higher incidence of Zika in adult women than adult men in Rio de Janeiro suggests a significant contribution of sexual transmission from men to women. Int J Infect Dis. 2016;51:128–132. doi: 10.1016/j.ijid.2016.08.023. [DOI] [PubMed] [Google Scholar]
- 29.Russell K, et al. Male-to-female sexual transmission of Zika virus—United States, January–April 2016. Clin Infect Dis. 2016;64:211–213. doi: 10.1093/cid/ciw692. [DOI] [PubMed] [Google Scholar]
- 30.Foy BD, et al. Probable non–vector-borne transmission of Zika virus, Colorado, USA. Emerg Infect Dis. 2011;17:880–882. doi: 10.3201/eid1705.101939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.D’Ortenzio E, et al. Evidence of sexual transmission of Zika virus. N Engl J Med. 2016;374:2195–2198. doi: 10.1056/NEJMc1604449. [DOI] [PubMed] [Google Scholar]
- 32.Morrison TE, Diamond MS. Animal models of Zika virus infection, pathogenesis, and immunity. J Virol. 2017;91:e00009–e00017. doi: 10.1128/JVI.00009-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Duggal NK, et al. Frequent Zika virus sexual transmission and prolonged viral rna shedding in an immunodeficient mouse model. Cell Rep. 2017;18:1751–1760. doi: 10.1016/j.celrep.2017.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yockey LJ, et al. Vaginal exposure to Zika virus during pregnancy leads to fetal brain infection. Cell. 2016;166:1247–1256. doi: 10.1016/j.cell.2016.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.PanAmericanHealth Organization/WHO . Zika—Epidemiological Report Colombia, March 2017. PAHO/WHO; Washington, DC: 2017. [Google Scholar]
- 36.Pan AmericanHealth Organization/WHO . Zika—Epidemiological Report Dominican Republic, March 2017. PAHO/WHO; Washington, DC: 2017. [Google Scholar]
- 37.Duffy MR, et al. Zika virus outbreak on Yap Island, Federated States of Micronesia. N Engl J Med. 2009;360:2536–2543. doi: 10.1056/NEJMoa0805715. [DOI] [PubMed] [Google Scholar]
- 38.Lessler J, et al. Times to key events in Zika virus infection and implications for blood donation: A systematic review. Bull World Health Organ. 2016;94:841–849. doi: 10.2471/BLT.16.174540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Allard A, Althouse BM, Hébert-Dufresne L, Scarpino SV. 2016. The risk of sustained sexual transmission of Zika is underestimated. bioRxiv:090324.
- 40.Miller JC. Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes. Infect Dis Model. 2017;2:35–55. doi: 10.1016/j.idm.2016.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.