Structure in neural population recordings: an expected byproduct of simpler phenomena?

Abstract

Neuroscientists increasingly analyze the joint activity of multi-neuron recordings to identify population-level structure that is believed to be significant and scientifically novel. Claims of significant population structure support hypotheses in many brain areas. However, these claims require first investigating the possibility that the population structure in question is an expected byproduct of simpler features known to exist in data. Classically, this critical examination can be either intuited or addressed with conventional controls. However, these approaches fail when considering population data, raising concerns about the scientific merit of population-level studies. Here we develop a framework to test the novelty of population-level findings against simpler features such as correlations across times, neurons and conditions. We apply this framework to test two recent population findings in prefrontal and motor cortices, providing essential context to those studies. More broadly, the methodologies we introduce provide a general neural population control for many population-level hypotheses.

A fundamental challenge of neuroscience is to understand how interconnected populations of neurons give rise to the remarkable computational abilities of our brains. To answer this challenge, advances in recording technologies have produced datasets containing the activity of large neural populations. Population-level analysis techniques have similarly proliferated^1–3 to draw scientific insight from this class of data, and as a result, researchers now generate and study hypotheses about structure in neural population activity. These population structures describe scientifically interesting findings at the population-level that elucidate properties or features of neural activity that, ostensibly, can neither be studied with traditional single-neuron analyses, nor be predicted by existing knowledge about single-neuron responses. Claims of significant population structures support results in many brain areas including the retina⁴, the olfactory system^{5, 6}, frontal cortex^{7, 8}, motor cortex^{9, 10}, parietal cortex^11–13, and more^{1, 3}.

While promising, these advances are also perilous. Population datasets are remarkably complex, and the population structures found in these data are often the result of novel data analysis methods with unclear behavior or guarantees. Specifically, many analysis techniques do not consider the very real concern that the observed population structure may be an expected byproduct of some simpler, already-known feature of single-neuron responses. Fig. 1 shows four examples of population structure from the literature, to demonstrate how this concern may arise. In rodent posterior parietal cortex (Fig. 1a), Raposo and colleagues¹¹ recorded single neurons tuned^{14, 15} to multiple task parameters (often called mixed selectivity¹⁶) – neural responses in a decision-making task modulated to both the choice and stimulus modality (auditory or visual). They used a machine learning algorithm to find individual readouts of the population that represented choice only and modality only (plotted against each other in Fig. 1a, right). However, one might ask: is this population structure truly a novel finding, or should we expect to find such readouts given our knowledge that single neurons are tuned to choice and modality? In primate prefrontal cortex, Murray and colleagues¹⁷ analyzed a neural population during a working memory task and found a readout that is more stable in time than the single neuron responses themselves (Fig. 1b). Again we may ask: is this stability significant, or expected as a byproduct of the temporal smoothness/correlations of single neuron responses? Population-level neural dynamics have also been studied: low dimensional projections of neural population responses seemingly evolve over time depending on their response history and initial conditions; examples include the locust antennal lobe¹⁸ (Fig. 1c) and primate motor cortex⁹ (Fig. 1d). Are these population findings novel signatures of dynamical systems^{19, 20}, or is this structure an expected byproduct of the temporal, neural and condition correlations of the neural data? This and the previous concerns of course depend on the subjective assumption that these simpler features are known a priori (i.e., not a consequence of the population structure, to which some researchers give primacy). Nonetheless, in the face of these concerns and a spate of prominent population-level results, the neuroscience community has begun to raise significant doubts about the extent to which population-level findings are an expected byproduct of simpler phenomena. This debate will remain unresolved in the absence of rigorous methodology for evaluating the novelty of population findings.

Figure 1. Population structure in systems neuroscience.

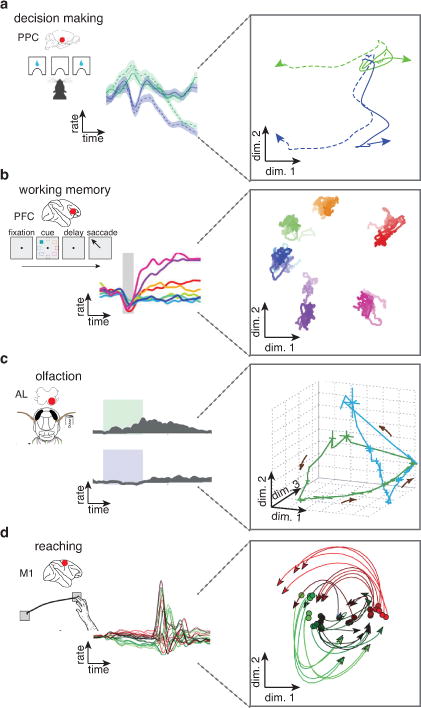
Examples from studies investigating structure at the level of the population. (a) Left panel shows an example firing rate response from a rat posterior parietal cortex neuron during a multi-modality decision-making task, adapted from Raposo et al.¹¹. The single-neuron responses show mixed selectivity to cue modality (blue: visual cue; green: auditory cue) and decision (dashed lines, right lick port; solid lines, left lick port). Right panel shows a two-dimensional projection of the population response, where choice information is separated along dimension 1 (horizontal) from the modality information, which is separated along dimension 2 (vertical). (b) Left panel shows an example firing rate response from a primate prefrontal cortex neuron during a working memory task, adapted from Murray et al.¹⁷. The single-neuron responses at the six stimuli (illustrated by different colors) show temporal dynamics. Right panel shows a two-dimensional projection of the population where stimulus information is stably represented across time. (c) Left panel shows an example firing rate response from a locust antennal lobe projection neuron responding to two odors, adapted from Broome et al.¹⁸. Right panel shows a three-dimensional projection of the population data with neural trajectories corresponding to the two odor stimuli. (d) Left panel shows an example firing rate response from a primate motor cortex neuron during a delayed-reach task, adapted from Churchland et al.⁹. Right panel shows a two-dimensional projection of the population data with neural trajectories corresponding to each reaching condition.

To address this challenge, we developed a methodological framework – the neural population control – to test whether or not a given population structure is an expected byproduct of a set of primary features: the tuning of single neurons^{14, 15}, temporal correlations of firing rates (regardless of whether one views that temporal correlation as fundamental or a result of smoothing^21–23), and signal correlations across neurons^{24, 25} (also called the low dimensionality of neural populations^{10, 26}). The central element of this neural population control is a set of algorithms that generate surrogate datasets that share the specified set of primary features with the original neural data, but are otherwise random. Accordingly, these surrogates will express any population structure to the extent expected by the specified primary features (since there is by definition no additional structure). We extended Fisher randomization and maximum entropy modeling to generate these surrogate datasets, and we chose the primary features to be the mean and covariance of the data across times, neurons, and experimental conditions. This choice is justified: the use of first¹⁵ and second^{24, 27} moments is standard in neuroscience, and further, these are the lowest order moments that can produce responses with qualitative similarity to real data in terms of temporal smoothness, low dimensionality, and tuning to conditions. These surrogate datasets formed the basis for a statistical test, giving a precise probability (a p-value) that a population structure is an expected byproduct of the specified primary features. Critically, careful inspection of this problem also revealed the inadequacy of typical statistical controls and validation techniques, and our results showed the extent to which ignoring such primary features can misstate statistical confidence, perhaps drastically, in a population-level result.

The neural population control can be applied to population structures and to datasets from almost any brain area. To show its utility, we used it to test two recent influential results. First, using data from macaque prefrontal cortex engaged in a working-memory task^{28, 29}, we found that the presence of strong stimulus-specific population readouts is expected from the robust tuning of single neurons. In contrast, we found that the decision-specific readouts are not expected. Second, using multi-electrode array recordings from the macaque motor cortex⁹, we found that population-level dynamical structure³⁰ is not an expected byproduct. The results of the neural population control framework contextualize and clarify these studies, quantitatively resolving skepticism and pointing to how this framework can be used throughout systems neuroscience.

RESULTS

Motivation for the neural population control

Consideration of conventional controls clarifies the need for the neural population control. Traditionally, one begins with a choice of a summary statistic, a number that quantifies the structure in question. In population studies, some common choices are variance explained¹¹ or a goodness-of-fit metric such as the coefficient of determination^{9, 13}. This statistic is calculated for the data and then compared to a null distribution, producing a p-value, which gives the likelihood of that statistic value (or greater) arising by chance under the null hypothesis. Critically, one requires a null distribution, and the most common approach is to shuffle the neural data so as to disrupt any special coordination that might have given rise to the population structure in question. Then, the summary statistic is calculated for each shuffled surrogate dataset, and the null distribution is built from the calculated statistics of many surrogate datasets. Should the summary statistic of the original data be likely under the null distribution, then, the argument goes, population structure was not surprisingly different than expected by chance. In principle, this procedure is appropriate only if the surrogate datasets conserve all the primary features of the original neural data, such that the surrogates remain a plausible comparison. However, often this essential requirement is not met, in which case one has a major problem of interpretation: is the difference in the summary statistic between the original and surrogate datasets due to disruption of the population structure itself, due to distortion of the primary features, or both?

Failure to account for known features presents a significant challenge, and can lead to misinterpreting results. To elucidate this pitfall and highlight what the neural population control offers, Fig. 2 presents two illustrative examples. Fig. 2a shows responses from two simulated neurons, each tuned to eight stimuli. Suppose a population-level analysis found a readout (shown as a black subspace in Fig. 2a) in which the data was well tuned to the stimulus, and further that this subspace accounted for a great deal of the population signal (99% of data variance captured, here). Of course (by construction) this finding is an expected byproduct of the fact that both neurons are well tuned to this stimulus. However, a standard shuffle (Fig. 2b, top) will corrupt tuning and suggest that population structure is in fact significant (variance of that tuned readout has dropped to 61%). Indeed, repeated shuffles produce a null distribution (Fig. 2c, gray) erroneously implying significance (with P<0.001). The neural population control, using algorithms we will shortly introduce, produces surrogates that maintain neural tuning and other primary features, leading to the correct conclusion both qualitatively (Fig. 2b, bottom) and quantitatively (Fig. 2c, brown): here the variance explained by this subspace is an expected byproduct of tuning, not a novel population-level result.

Figure 2. Motivation for the neural population control.

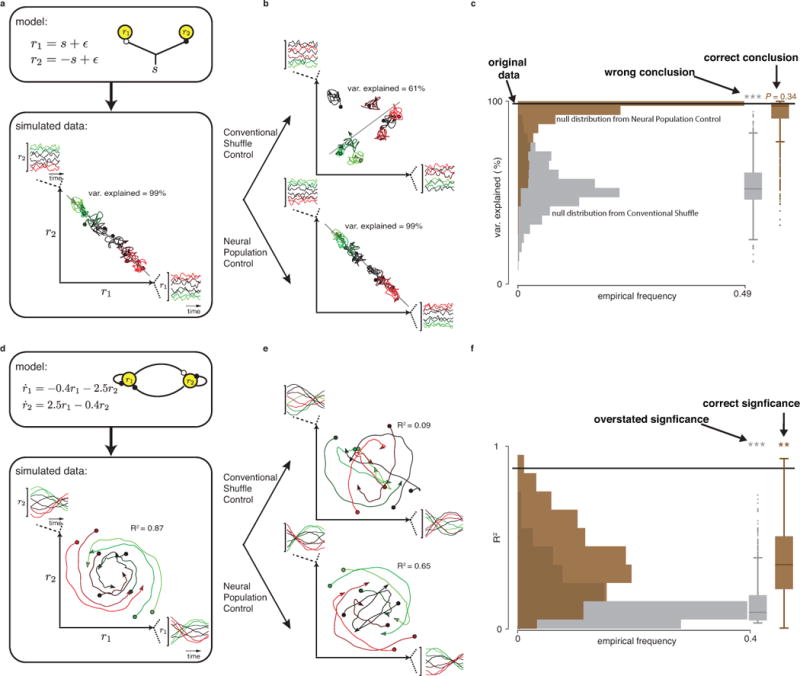
(a) Simulated firing rates from two neurons encoding a hypothetical stimulus at eight conditions (high, moderate, and low stimuli correspond to red, black, and green color shades, respectively) are shown, along with the corresponding neural trajectories in the population space (here two-dimensional). Black line illustrates a one-dimensional projection of the data that represents stimulus, identified by the target dimensionality reduction method from Mante et al.⁸. The data variance explained by this projection is shown (as a percentage). (b) Top panel shows shuffled surrogate data generated by shuffling the single neuron responses from panel a across conditions. The same data analysis method was then used to identify a one-dimensional projection of the data (black line) that represents the stimulus in the shuffled data. Bottom panel shows random surrogate data from the neural population control (Methods, to be described), and the identified projection that represents the stimulus (black line). (c) Distribution of variance-explained values from stimulus projections identified from 1000 surrogate datasets (gray) and another distribution of variance values from 1000 surrogate datasets from the neural population control (brown). Black line is the percentage variance explained from the neural data from panel a. Box-whisker plots summarize the two distributions (Tukey convention). (d) Firing rates for two neurons are solutions to the given differential equations (modeling an oscillator), with eight different initial conditions. The fit of these data to a linear system (R²) is shown. (e) Shuffled data (top) and surrogate data from the neural population control. (f) Distributions of R² values from 1000 shuffled datasets and 1000 surrogate datasets from the neural population control (same convention as panel c). Smoothed Gaussian noise was added to all simulated data.

Even when a population-level result is not an expected byproduct of simpler features, conventional controls can meaningfully misstate confidence. Fig. 2d shows two simulated neurons coupled as an oscillator, where eight stimuli set initial states of the given differential equations. Population-level neural responses thus evolve in time according to a dynamical flow field (Fig. 2d). Under standard shuffling (Fig. 2e, top), correlations across neurons and conditions change, and the consistency with the dynamical flow field is considerably reduced, both qualitatively (Fig. 2e, top) and quantitatively (using the coefficient of determination R², Fig. 2f, gray). The neural population control produces surrogate data with the appropriate primary features, producing the correct null distribution and confidence level (Fig. 2f, brown). Thus, the essential remaining challenge for rigorously testing the novelty of population-level results is to develop methods for producing random surrogate datasets (Fig. 2b bottom and Fig. 2e bottom) that match the primary features of the original data.

Corrected Fisher randomization and tensor maximum entropy

We need to generate surrogate datasets that share the primary features of the original neural data but are otherwise random. We developed two complementary methods that achieve that goal, termed corrected Fisher randomization (CFR) and tensor maximum entropy (TME). CFR adds an optimization step to traditional shuffling, in order to maintain the primary features, whereas TME samples random datasets from a probability distribution with the correct average primary features (Methods). The high-level mechanics of these methods are illustrated schematically in Supplementary Fig. 1. As in traditional shuffling, the first step of CFR is to randomly shuffle the responses of each neuron across experimental conditions. Because this standard shuffling step destroys the primary features of the original data, we then construct and apply an optimized neural readout, a matrix that reweighs the shuffled neural responses, to minimize the error between the primary features of the new shuffled responses and the primary features of the original neural data. The strength of CFR is that each surrogate dataset preserves the primary features of the original data (up to the optimization error, which is empirically quite minor; Supplementary Fig. 2 and Supplementary Fig. 3). However, as with most shuffling techniques, CFR is conservative as it operates on a finite dataset (i.e., it shuffles the finite set of recorded neural responses). Hence, some structures that are not stipulated by the null hypothesis may persist in shuffled data (e.g., if a neural trace is non-smooth at one time point, the trace after shuffling will still be non-smooth at this time point). Owing to this potential shortcoming, we also extended the maximum entropy principle (which has been widely used in neuroscience^{27, 31–33}) to develop the complementary TME method. We derived a probability distribution defined over random tensors (datasets) that maximizes Shannon entropy subject to the constraints that the expected primary features of the distribution are those of the original neural data (Methods). This distribution is a novel and nontrivial extension of classic maximum entropy distributions, both in terms of extending to tensor random variables and in terms of the computational techniques required to sample from this distribution. The primary strength of the maximum entropy principle is that higher-order structures in surrogate datasets are completely determined by the primary features (the distribution is by definition maximally unstructured beyond those primary feature constraints). On the other hand, since the constraints are enforced in expectation, variations in the primary features of each surrogate dataset will appear due to finite sampling. Thus, CFR and TME offer complementary and well-balanced techniques for generating surrogate datasets properly according to the null hypothesis.

To demonstrate the framework, we used CFR and TME to generate surrogate datasets based on neural responses recorded from primate prefrontal cortex during a working memory task (Fig. 3a). Fig. 3b shows the firing rates of one example neuron from the original neural data along with its primary covariance features. To illustrate the ability of CFR and TME to preserve the primary features, we generated three types of surrogate datasets (Methods). The first we term surrogate-T, which preserves only the primary features across time similar to the conventional shuffle control from Fig. 2. The second, surrogate-TN, preserves the primary features across both times and neurons. The third, surrogate-TNC, simultaneously preserves the primary features across times, neurons, and conditions. Qualitatively, single-neuron responses from the surrogate datasets appear realistic (Fig. 3c–e, Supplementary Fig. 4, and Supplementary Fig. 5). Quantitatively, the estimated covariances across times from all surrogate types were similar to the covariance across times of the original neural data ( ${\sum }_T$; Fig. 3c–e inset, Fig. 3b inset, Supplementary Fig. 2, and Supplementary Fig. 3). Additionally, the estimated covariances across neurons from surrogate-TN and surrogate-TNC were similar to the covariance across neurons of the original data ( ${\sum }_N$; Fig. 3c–e, Fig. 3b inset, Supplementary Fig. 2, and Supplementary Fig. 3). Finally, the estimated covariances across conditions from surrogate-TNC were also similar to the covariance across conditions of the original data ( ${\sum }_C$; Fig. 3c–e, Fig. 3b inset, Supplementary Fig. 2, and Supplementary Fig. 3). Thus, both CFR and TME successfully generated random surrogate data that preserved the specified primary features. These surrogate datasets are then appropriate for generating suitable null distributions for a statistical test of population structures.

Figure 3. CFR and TME surrogate datasets preserve the specified primary features.

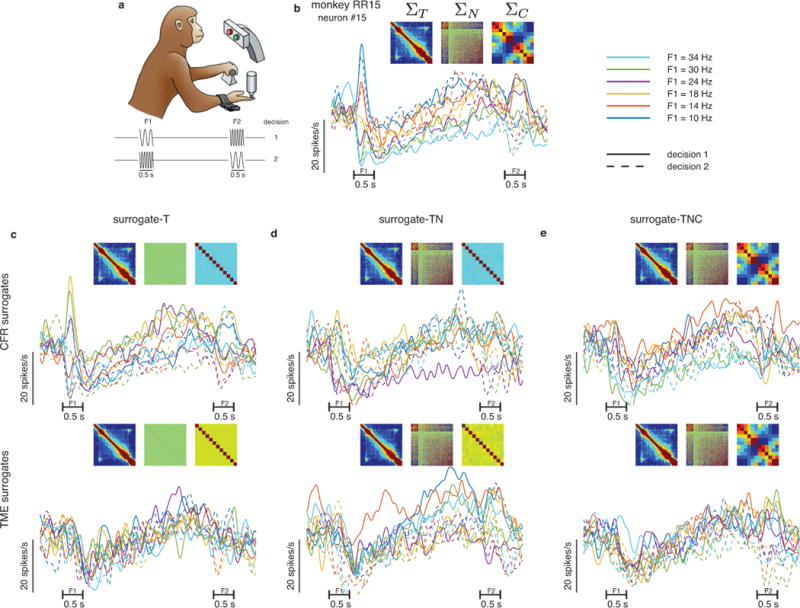
(a) Working memory task, adapted from Romo and Salinas³⁸. (b) Example neuron (neuron number 15 of 571 total) from prefrontal cortex. Each trace is the trial-averaged firing of the twelve task conditions (six stimuli and two decisions; one trace color and style for each). Horizontal bars denote the times of first (F1) and second (F2) vibrotactile stimuli. Heatmaps in the inset show three covariance matrices across times ( ${\sum }_T$), neurons ( ${\sum }_N)$and conditions $\left({\sum }_C\right)$ of all neurons in this dataset. (c-e) Example neurons from one surrogate-T, surrogate-TN, and surrogate-TNC dataset, respectively; with the same conventions as panel b. Top panels in c-e are surrogate datasets generated using the Corrected Fisher Randomization method (CFR) and bottom panels in c-e are surrogate datasets generated using the Tensor Maximum Entropy method (TME). The covariance matrices in the insets in c-e are obtained by averaging the primary features from 100 surrogate datasets.

In all that follows, we consider surrogate-TNC as the basis for the neural population control, as it addresses the full null hypothesis that temporal, neural, and condition means and covariances give rise to the population structures in question. That said, the inclusion of surrogate-T and surrogate-TN here remains important: first, surrogate-T connects to conventional shuffling and will demonstrate the inadequacies of that standard method. Second, surrogate-TN demonstrates an alternative null hypothesis that is appropriate in other settings³⁴, and it allows us to analyze empirically the benefits of adding each of the primary features to the null hypothesis. It is worth noting that other surrogate types such as surrogate-NC are easily generated (our software implementation accepts this choice as an input), but they appear visually implausible due to the standard of plotting responses over time.

Population representations and mixed selectivity in prefrontal cortex

Previous studies have demonstrated that neurons in a number of brain areas respond to multiple task parameters^{7, 11, 16, 29, 35, 36}. These mixed responses may obscure representation at the level of single neurons. Dimensionality reduction methods^{8, 37} are widely used to identify neural readouts (projections of the population) that separate the representation of each task parameter. Further, these readouts often are found to explain substantial data variance. Should we always expect such a finding from any collection of neurons that have these mixed responses? Not necessarily: one can produce toy examples where the representations fundamentally can not be separated, and other examples where separation would be possible but only with small variance explained (i.e., in the noise). The suggestion then typically follows that these robust readouts are thus evidence of a collective code in the population: neural responses are coordinated in such a way to produce these readouts, though that coordination is invisible at the level of single neurons. However, this line of reasoning misses the critical concern that these task-parameter-specific readouts may be an expected byproduct of simpler features in the data itself: tuning, temporal smoothness, and neural correlations. Asserting this claim of collective code requires the neural population control.

We tested recordings from prefrontal cortex (PFC) during a working memory task³⁸ (Fig. 3a). In this task, subjects received two vibrotactile stimuli with different frequencies. A delay period separated the presentation of the two stimuli, during which subjects were required to maintain a memory of the first stimulus. After the delay period, subjects reported whether the frequency of the first stimulus was higher or lower than the frequency of the second stimulus. Thus, the two relevant task parameters encoded by PFC are the decision and the first stimulus frequency.

Responses in PFC showed mixed selectivity to the two task parameters (Fig. 3b). We used demixed principal component analysis (dPCA)³⁷ to identify decision-specific and stimulus-specific population readouts in both the original neural dataset and our surrogate datasets. The projection of the population activity onto the decision (stimulus) readout reflects the population representation of the decision (stimulus). We then compared these projections to those found in surrogate datasets generated by CFR and TME. Qualitatively, the projections, from both the original and the surrogate-TNC datasets, appeared to be tuned to the decision and the stimulus (Fig. 4a–d). Quantitatively, we calculated the percentage variance explained by the decision and stimulus projections, which summarized the degree to which each projection accounts for the population response.

Figure 4. Decision (stimulus) readouts in PFC are not (are) an expected byproduct.

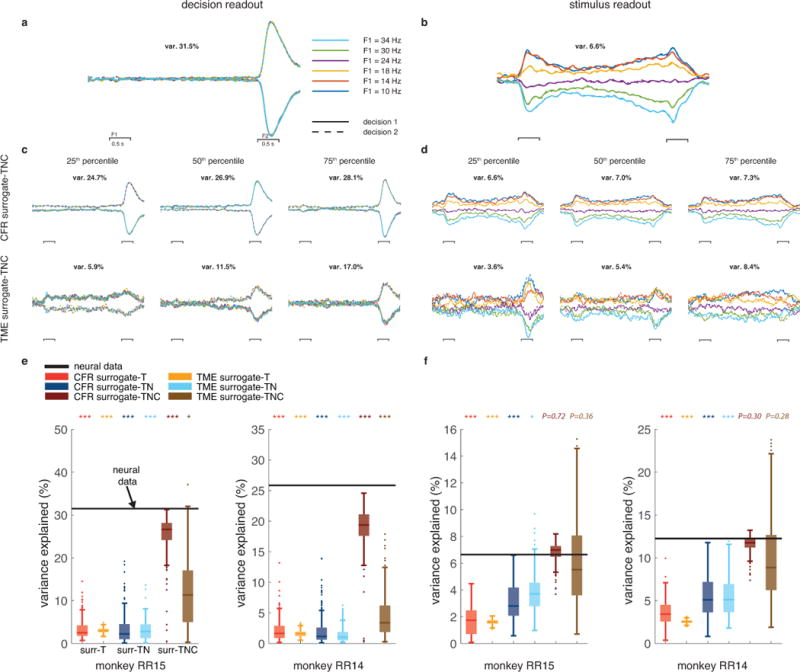
The population readouts for decision and stimulus were identified using demixed principle component analysis (dPCA). (a) Projections of the original population responses from monkey RR15 onto the top decision-specific readout. (b) Projections of neural responses from monkey RR15 onto the top stimulus-specific readout. The trace colors and style follows the same convention as those in Fig. 3b. (c) Same as a but for decision readouts from surrogate datasets generated by CFE (top) and TME (bottom). We show surrogates at various points in the distribution of variance explained (25^th, 50^th, and 75^th percentile, 200 surrogate datasets). (d) Same as b but for the surrogate datasets from CFE (top) and TME (bottom) methods; as in c the 25^th, 50^th, and 75^th percentile examples are shown (200 surrogate datasets). Scale bars and color scheme in b-d match the scale bars and color scheme in a. (e) Percent variance-explained of the population projection onto the top decision readout. Black lines show the percent variance explained from the original neural data, colored box-whisker plots show the variance explained distribution from 200 surrogate samples (same convention as Fig. 2 c,f; stars denote significantly high variance; upper-tail test). The variance of the decision projection is calculated during the decision epoch (100 ms after the second stimulus onset, until the second stimulus offset). (f) Same as e but for percent variance explained of the population projection onto the top stimulus readout. The variance of the stimulus projection is calculated during the stimulus epoch (100 ms after first stimulus onset, until the second stimulus onset).

Fig. 4e demonstrates that the variance captured by the decision projection from the original neural data is significantly higher than the variance captured by the decision projections from the surrogate datasets. This finding demonstrates that the population representation of the decision is not an expected byproduct of the primary features. However, the same procedure for the stimulus projection demonstrates that the population representation of the stimulus can not be distinguished from an expected byproduct of the primary features, as data generated with only those primary features displayed comparable population structure (Fig. 4f). The variance captured by the stimulus projection from the original neural data reaches significance only when compared to the variance captured to the stimulus projections from surrogate-T and surrogate-TN datasets, but not when compared to surrogate-TNC datasets. This result was similar when repeating the same analysis using another statistic (the explained variance metric used in Kobak et al.³⁷; Supplementary Fig. 6). This negative result contextualizes our understanding of population-level representations: sometimes, despite qualitative appearances of a collective population code, such a readout can exist simply because of a powerful algorithm and simpler known features in the data. Note that this result does not mean that the stimulus readout is absent or wrong in any way, but rather that it is expected, given the primary features of the data.

One advantage of this framework is that the contribution of each primary feature to the population structure can be quantified by studying the null distributions across different surrogate types. This inspection indicates that tuning across conditions is likely the feature giving rise to the stimulus readout. Although single neurons in PFC show mixed responses to the stimulus and decision, the tuning of the stimulus is prominent (Supplementary Fig. 7). Due to the task structure, neurons in PFC are responding to the first stimulus at all times of the task, except during the brief period starting at the second stimulus onset (Fig. 3a,b). Thus, the population representation of the stimulus arises from the prominent tuning of single neurons, as expressed by the mean and covariance across conditions. Unlike the stimulus, the neural responses to the decision are briefer (only after the second stimulus onset) and overlap with (and are dominated by) the neural responses to the stimulus (Fig. 3a,b; see Supplementary Fig. 7). Hence, the population representation of the decision is not an expected byproduct of the underlying primary features, and as such uncovers novel information about the representation of decision in PFC.

Population representations of task parameters are often useful to summarize large datasets, and novel and rigorous methods like dPCA are effective in finding those representations. The present result reminds us that care should be taken when interpreting the population representations found by these methods: in some cases, these representations may be significant indication of collective population codes hidden at the single-neuron level, while in other cases they may be simply a redescription of single-neuron tuning.

Primary features alone do not explain dynamical structure in motor cortex

To highlight the broad applicability of our framework, we next applied the neural population control to motor cortex responses during a delayed-reach task (Fig. 5a,b) to test the dynamical systems hypothesis^{9, 30}. Classical studies have assumed motor cortex activity represents movement kinematics¹⁵. Other studies have argued that the complexity of neural responses is beyond what is expected from coding models^39–41, and is more consistent with dynamical systems models^{9, 35}. In this view motor cortex generates simple dynamical patterns of activity that are initialized by preparatory activity^{39, 42, 43}, and these patterns are then combined to produce complex muscle activity^{39, 44}. As in Fig. 2d, a dynamical system implies a particular population structure, and recent studies have shown neural trajectories evolving (approximately) according to a low-dimensional linear dynamical system^{9, 35}. However, despite controls and comparisons with other hypotheses^{9, 39, 45}, the concern persists that this population structure may be an expected byproduct of simpler features in the data. That counterargument goes as follows: the temporal smoothness of neural responses in motor cortex data will give rise to temporally smooth neural trajectories, and correlated responses across neurons and conditions will give rise to low-dimensional neural trajectories that are also spatially smooth (in the sense that tuning implies that each neuron’s response changes smoothly from one condition to the next, and thus population trajectories must also change smoothly in neural space from one condition to the next). Together, it is quite reasonable to suppose that this population structure (low-dimensional linear dynamical system fit) will arise as an expected byproduct of primary features of data.

Figure 5. Motor cortex responses during a delayed-reach task.

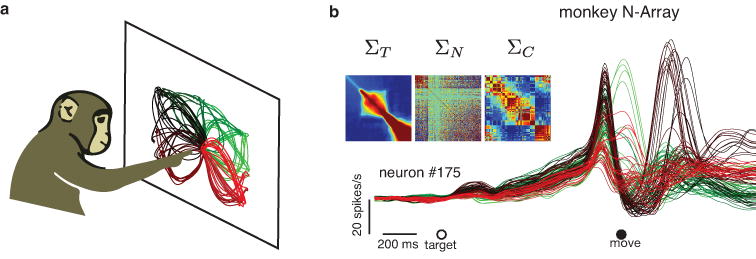
(a) Delayed-reach task. Monkeys performed straight and curved reaches to targets displayed on a frontoparallel screen. Trajectories represent the average hand position during each of 108 reaching conditions. (b) Example neuron (neuron number 175 of 218 total) recorded from the motor cortex of one monkey during the delayed-reach task. Each trace is the smoothed, trial-averaged firing rate during one of the reaching conditions. The trace color indicates the reach condition from panel a. Heatmaps in the inset represent three covariance matrices that quantify the primary features across time ( ${\sum }_T$), neurons ( ${\sum }_N)$and conditions $\left({\sum }_C\right)$ of the entire population dataset.

We fit low-dimensional linear dynamical systems to population responses from multiple monkeys (dimensionality was chosen by cross-validation; Supplementary Fig. 8), and quantified the quality of fit by the coefficient of determination R² (Methods). We then generated a null distribution of R² values by fitting surrogate datasets generated by CFR and TME to the same dynamical model. Our results show that the R² from the original neural data is significantly higher than the R² from every surrogate type (Fig. 6a; P<0.001). This result is consistent across different monkeys during different reaching tasks (Supplementary Fig. 9), and holds similarly for oscillatory linear dynamics (Supplementary Fig. 10). Our neural population control demonstrates that recently reported dynamical structure in motor cortical responses is not an expected byproduct of the specified primary features.

Figure 6. Population dynamics in motor cortex are not an expected byproduct.

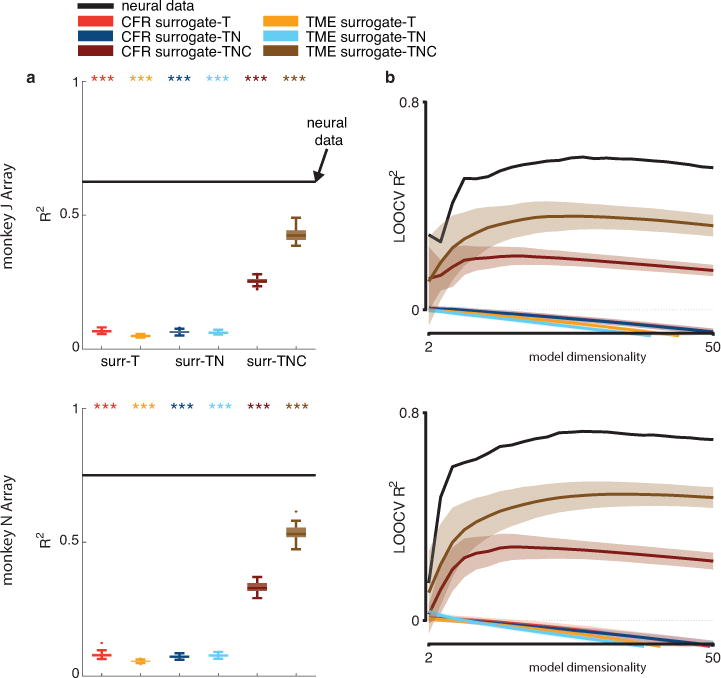
400 ms of movement-related neural activity in the motor cortex were projected on to the top principal components (PCs) and then fitted to a linear dynamical system. (a) Quality of fit (R²) of the original neural responses projected onto the top 28 PCs (determined by cross validation; Supplementary Fig. 8) to the dynamical system model. Black lines denote the R² from the original neural data. Colored box-whisker plots denote the R² distributions from 100 surrogate datasets from each surrogate type (same convention as Fig. 2 c,f). Stars denote significantly higher R² than the surrogates (P<0.001; upper-tail test). (b) Leave-one-condition-out cross-validation (LOOCV) for the R² measure of fitting data to a dynamical system model with different choices of model dimensionalities (number of PCs). Black trace denote the R² value from the original neural data and colored traces are the mean R² values from the surrogate datasets (same color convention as panel a. (Colored areas represent $\pm 2\mathrm{s}.\mathrm{d}.$

We can again use the different surrogate types (surrogate-T, -TN, and -TNC) to quantify the contribution of each primary feature. R² values from the surrogate-T and surrogate-TN datasets are similar, whereas the R² values from surrogate-TNC are much higher (Fig. 6a). The surrogate-TNC datasets are the only ones that preserve tuning (to experimental reach condition), from which we conclude that tuning contributes meaningfully to any appearance of dynamical structure in surrogate data (albeit significantly less than the original data). In other words, tuning inherently produces some degree of spatial smoothness that, if ignored, would have led to meaningful overstatement of the test significance of this dynamical structure.

To assess the sensitivity of this test result to model dimensionality, we performed leave-one-condition-out cross-validation and quantified R² of test conditions, both from the original neural data and the surrogate datasets, based on dynamical models with different dimensionalities. The same results hold: the R² value from the original neural data is still significantly higher than the R² values from all types of surrogate data, across a wide range of model dimensionalities (Fig. 6b). While a very low-dimensional model leads to low R² values in both the original neural data and the surrogate datasets, as model dimensionality increases, the R² value of the original neural dataset increases disproportionately, separating from the surrogate datasets.

The structure we investigated here is consistent with a simple class of dynamical systems^{19, 46}, but certainly the underlying mechanism generating population responses is more complex. It is essential to note that the present neural population control does not attempt to distinguish between linear dynamical models and other models (dynamical or otherwise); it specifically tests whether there is more linear dynamical structure than expected from the primary features in neural data.

DISCUSSION

Neural populations are increasingly studied, compelling the analysis of large neural datasets and the consideration of new scientific hypotheses. However, the future of these analyses hinges on our ability to reliably distinguish novel population-level findings from redescriptions of simpler features of the data. To that end, we developed a neural population control to statistically test if a population-level result is an expected byproduct of the primary features of temporal, neural, and condition correlations. The CFR and TME methods generate surrogate datasets that preserve the primary features but are otherwise random, and can thus be meaningfully compared to the original neural data. We applied the neural population control to data from PFC during a working memory task. We found that the presence of a neural readout that is specific to the decision is significant, and may be an interesting form of collective code, whereas the presence of a neural readout that is specific to the stimulus can be explained by the tuning of single-neurons. Further, we applied this framework to data from motor cortex during a reaching task, demonstrating that population-level dynamics are not an expected byproduct of primary features.

When applying the neural population control framework, interpretational precision is critical. Specifically, consider our finding that the presence of a stimulus readout in PFC is expected from single-neuron tuning. First, this finding does not assert that the stimulus readout is incorrect or absent, nor does it indicate any technical flaw in the analysis method, but rather that we can not rule out the possibility that the readout is merely a redescription of tuning, and thus that we should not necessarily infer evidence of a collective code. Second, and more subtly, any claim that a population-level readout is an expected byproduct is conditioned on the subjective belief that single-neuron tuning is known to be a fundamental feature that exists in data. Should one believe that, instead, the population-level readout of the stimulus is the fundamental feature, then one could instead ask if single-neuron tuning is an expected byproduct to that assumption (some indeed might quite sensibly argue this direction to be more scientifically plausible). Our framework makes no claims as to which features are fundamental, but rather quantifies the extent to which structure will appear at the level of the population as a result of a set of specified primary features. Indeed, our framework is conservative, as it assumes the existence of primary features without any mechanistic underpinning; in other words, we do not require the existence of a competing scientific model to produce data with these features (and finding such a model might be difficult). This assumption presents a high bar when compared to specific mechanistic models that correspond to the population structure in question.

At the broadest interpretational level, rejection of the null hypothesis does not prove the existence of a specific population structure. Instead, such a finding rules out a simpler explanation of observing that structure in data. We do not claim that a test that fails to reject this null hypothesis would somehow negate the scientific significance of a population structure. Indeed, these simpler explanations may themselves be scientifically interesting. For example, studies have demonstrated that minimal models of correlations among neurons provide accurate and non-trivial predictions of population activity patterns in primate^{32, 33} and other vertebrate²⁷ retina. Additionally, failing to reject this null hypothesis may simply imply that current data or the complexity of experimental behavior is inadequate to elucidate that structure².

At a technical level, the CFR and TME methods are complementary and exploit principles which have a long history in neuroscience^{27, 31–33}. These methods can be applied interchangeably, and their minor differences have little effect on the hypothesis being tested. That said, certainly each method possesses its advantages. CFR generally better preserves the primary features for each surrogate dataset, while TME has the exact primary features in expectation (Supplementary Fig. 2, 3). On the other hand, TME produces more thoroughly randomized surrogates than does CFR. By construction CFR operates on a finite set of original neural responses, which may allow structure to persist in the surrogate datasets even if it was not stipulated by the null hypothesis. In contrast, TME surrogate datasets are maximally random in the Shannon entropy sense and have no unintended structure. Thus, if it is most crucial to eliminate any structure beyond the primary features, TME is preferred. If it is most important that each surrogate dataset preserves the primary features of the original neural data as close as possible, CFR is preferred. For practical purposes, note also that CFR is more computationally expensive because it requires optimization for each surrogate dataset, whereas TME requires an optimization only once (Methods). On another technical point, in this work both the prefrontal and motor applications involved firing rates that were averaged across trials within a given condition. One natural technical question is how this framework works in the single trial setting. If one works with single trial time histograms (a single trial PSTH) or rate estimates (as is often done^47–49), then the neural population control works without further modification. Should one wish to work with spike trains directly, then further assumptions must be made so that means and covariances can be meaningfully calculated (as these features do not apply to point process data). A rate estimate is one choice; other non-rate choices such as a spike train metric⁵⁰ would require further development.

When studying population-level questions in neuroscience, it is important for our hypotheses to be consistent with existing, simpler features of neural data. Here we have found that it is equally important to quantitatively investigate whether these simpler features themselves reproduce the population structure being considered by that hypothesis. The neural population control may be applied to test a wide range of population hypotheses from essentially any brain area, and thus provides a general framework to rigorously resolve debates in the field about the novelty of population level results.

METHODS

Experimental design and recordings

Motor cortex data was recorded and described in previous work⁹. In brief, four male rhesus monkeys (J, N, A, and B) performed delayed reaches to radially arranged targets on a frontoparallel screen. Monkeys A and B performed straight reaches with different speeds and distances (28 reaching conditions); monkeys J and N performed both straight and curved reaches (108 reaching conditions). Recordings were made from primary motor and dorsal premotor cortices with single electrodes (datasets A, B, J1, J2, J3, J4, N) and chronically implanted 96-electrode arrays (datasets J-Array and N-Array). Large populations were recorded (64, 74, 50, 58, 55, 50, 170, 118, and 218 neurons for datasets A, B, J1, J2, J3, J4, J-Array, N, and N-Array, respectively). Firing rates were calculated by averaging spiking activity across trials for each reaching condition, smoothing with a 24 ms Gaussian kernel, and sampling the result at 10 ms intervals. See Churchland et al.⁹ for all further details about subjects and experiment. We further excluded one outlier neuron from monkey A, which had an unrealistically high firing rate.

Prefrontal cortex data was recorded and described in previous work (Romo et al.²⁸, Brody et al.²⁹). In brief, two male rhesus monkeys (RR15 and RR14) performed a working memory task. Two vibrotactile stimuli were delivered to one digit of the hand for 500 ms each, separated by an inter-stimulus delay period. Monkeys received a juice reward for discriminating and reporting the relative frequency of the two stimuli. Neural responses were recorded from the prefrontal cortex via an array of seven independent microelectrodes. See Romo et al.²⁸ and Brody et al.²⁹ for all further details about subjects and experiment. We followed the neuron selection criteria and firing rates computation method reported in Kobak et al.³⁷: first, we selected only the sessions where all six frequencies (10, 14, 18, 24, 30, 34 Hz) were used for the first stimulus and where the monkeys made the correct choice. Second, we included only neurons that had responses in all possible 12 conditions (all combination of 6 stimuli and 2 choices) with at least 5 trials per condition and firing rates less than 50 spikes per second (571, 217 neurons form monkey RR15, RR14, respectively). Third, firing rates were calculated by averaging spiking activity across trials for each stimulus condition, smoothing with a 50 ms Gaussian kernel, and sampling the result at 10 ms intervals.

For all datasets, the sample sizes were similar to those reported in the field and no randomization or blinding was used to assign subjects and conditions (see further details in Churchland et al.⁹, Romo et al.²⁸ and Brody et al.²⁹). We followed two further preprocessing steps used in previous work⁹. First, responses for each neuron were soft-normalized to approximately unity firing rate range (divided by a normalization factor equal to firing rate range+5 spikes per second). Second, responses for each neuron were mean-centered at each time by subtracting the mean activity across all conditions from each condition’s response because the analyses in this work focus on aspects of population responses that differ across conditions. In our statistical tests, no assumptions were made about the normality or other assumptions on the distribution of surrogate data (see additional information in the attached Life Sciences Reporting Summary).

Quantifying primary features across different modes of the data

Each dataset, processed as above, formed a tensor $X\in {ℝ}^{T\times N\times C}$ across T time points, C conditions, and N neurons. To quantify the primary temporal, neural, and condition features, we calculated the marginal mean and covariance across each of these three modes. Regarding the mean, we followed standard practice and, without loss of generality, centered the data to form a tensor $\overline{X}\in {ℝ}^{T\times N\times C}$, which had zero mean across the temporal mode ( $\frac{1}{NC}{\sum }_{n=1}^N{\sum }_{c=1}^C\overline{X}\left(:,n,c\right)=0$s), and similar for the neuron and condition modes. This mean-centering operation can be accomplished by sequentially calculating and subtracting the mean vectors across each mode (in any mode order), or equivalently calculating and subtracting the least-norm marginal mean tensor $M\in {ℝ}^{T\times N\times C}$, such that $\overline{X}=X-M$ (Supplementary Note 1).

With this zero-mean dataset $\overline{X}$, we then calculated the covariance matrices across times, neurons, and conditions, specifically:

$${\sum }_T=\sum _{n=1}^N\sum _{c=1}^C\overline{X}\left(:,n,c\right)\overline{X}{\left(:,n,c\right)}^{\top }\in {ℝ}^{T\times T}$$

$${\sum }_N=\sum _{t=1}^T\sum _{c=1}^C\overline{X}\left(t,:,c\right)\overline{X}{\left(t,:,c\right)}^{\top }\in {ℝ}^{N\times N}$$

$${\sum }_C=\sum _{t=1}^T\sum _{n=1}^N\overline{X}\left(t,n,:\right)\overline{X}{\left(t,n,:\right)}^{\top }\in {ℝ}^{C\times C}$$

The marginal mean tensor and covariance matrices quantify the basic univariate and pairwise structure of the data across each of the temporal, neural, and condition modes. As a technical point, note that other ways of estimating these moments can also be used without any change to the neural population control. For example, regularized covariance estimators are often computed to incorporate prior beliefs about these moments; should one use such a method, the null hypothesis of neural population control would embody the posterior belief of these moments, given the data.

Generating surrogate data with the corrected-Fisher-Randomization (CFR) method

Starting from the zero marginal mean data tensor $\overline{X}\in {ℝ}^{T\times N\times C},$we randomized the data by shuffling: we permute the condition labels for the responses of each neuron across time. The standard shuffling procedure was done independently across neurons, resulting in a shuffled tensor ${\overline{S}}_0\in {ℝ}^{T\times N\times C}$. Forming this tensor will also have destroyed the first-order and second-order features of the original neural data. To retain these primary features, we introduced a read-out weight matrix $K\in {ℝ}^{N\times N}$ such that the resulting surrogate tensor $S\in {ℝ}^{T\times N\times C}$ had the correct marginal means and covariances. That is, the surrogate tensor S is the read-out:

$$\overline{S}\left(:,:,c\right)={\overline{S}}_0\left(:,:,c\right)K\forall c\in \left[1,\dots .,C\right]$$

$$S=\overline{S}+M$$

where ${\overline{S}}_0\left(:,:,c\right)\in {ℝ}^{T\times N}$ is one condition of the shuffled tensor ${\overline{S}}_0$ corresponding to condition c and M is the marginal mean tensor. To ensure ${\overline{S}}_0$ has mean zero across all modes, we constrained K to have unit eigenvector with zero eigenvalue (Supplementary Note 2). This constraint ensures that the shuffled $\overline{S}$ has zero marginal mean across all the tensor modes. What remains is to optimize K such that the marginal covariances of the surrogate datasets are as matched as possible to those of the original data. We quantified the deviation of the original marginal covariances with the following three cost functions:

$$f_T=\frac{\Vert {\sum }_T-{\sum }_{c=1}^C{\overline{S}}_0\left(:,:,c\right)K{K}^{\top }{\overline{S}}_0{\left(:,:,c\right)}^{\top }\Vert {}_F^2}{{\sum }_{t=1}^T{e}_T\left(t\right)}$$

$$f_N=\frac{\Vert {\sum }_N-K^{\top }[{\sum }_{c=1}^C{\overline{S}}_0{\left(:,:,c\right)}^{\top }{\overline{S}}_0\left(:,:,c\right)]\Vert K_F^2}{{\sum }_{n=1}^N{e}_N\left(n\right)}$$

$$f_C=\frac{\Vert {\sum }_C-{\sum }_{t=1}^T{\overline{S}}_0{\left(t,:,:\right)}^{\top }K{K}^{\top }{\overline{S}}_0\left(t,:,:\right)\Vert {}_F^2}{{\sum }_{c=1}^C{e}_C\left(c\right)}$$

where ${\sum }_T,{\sum }_N$ and ${\sum }_C$ are the temporal, neural, and condition covariance matrices, respectively, with eigenvalue vectors $e_T,e_N$, and $e_C$. To find the desired linear read-out $\left(\widehat{K}\right)$, we solved:

$$\widehat{K}={\text{argmin}}_{K\in {ℝ}^{N\times N}}\left(f_T+f_N+f_C\right)\text{subject to }K\mathbf{1}\mathbf{=}\mathbf{0}$$

This objective can be optimized using any standard gradient descent package (we used the Manopt and LDR libraries^{51, 52}) and will result in a read-out matrix that retains the marginal covariance of the original neural data to the extent possible. The resulting surrogates will thus be random in the sense that population structure beyond these primary features should be absent, but constrained in the sense that the same primary features as the original neural are maintained (up to the minimum error achieved by the optimization). As an implementation note, we chose the read-out to be in the neural space because it is commonly used in systems neuroscience, but the above approach could be implemented similarly by reading out the condition or temporal modes (our software implementation takes that choice as an input). On a similar point of technical detail, above we chose to initially shuffle neurons across conditions as it is a standard choice (and one that agrees with the applications in prefrontal and motor cortices shown in the results), but again our software implementation takes the shuffle mode (conditions, neurons, or time) as an input.

Generating surrogate data with the tensor-maximum-entropy (TME) method

A complementary approach to generating surrogate datasets that preserve the primary features of the neural data is to follow the principle of maximum entropy modeling. In this context, that principle dictates that surrogate data should be drawn from the distribution which is maximally random (i.e., fewest additional assumptions), but for obeying the constraints of having the correct first-order and second-order marginal moments. Specifically, our maximum entropy objective was:

$$\widehat{p}\left(S\right)={\text{argmax}}_{p\left(S\right)}-\int p\left(S\right)\log \left(p\left(S\right)\right)dSs.t.\underset{}{\int }p\left(S\right)dS=1{\mathrm{E}}_p\left[S\right]=M\overline{S}=S-M$$

$${\mathrm{E}}_p\left[\sum _{n=1}^N\sum _{c=1}^C\overline{S}\left(:,n,c\right)\overline{S}{\left(:,n,c\right)}^{\top }\right]={\sum }_T$$

$${\mathrm{E}}_p\left[\sum _{t=1}^T\sum _{c=1}^C\overline{S}\left(t,:,c\right)\overline{S}{\left(t,:,c\right)}^{\top }\right]={\sum }_N$$

$${\mathrm{E}}_p\left[\sum _{t=1}^T\sum _{n=1}^N\overline{S}\left(t,n,:\right)\overline{S}{\left(t,n,:\right)}^{\top }\right]={\sum }_C$$

where $S\in {ℝ}^{T\times N\times C}$ is the surrogate random variable, and ${\mathrm{E}}_p[.]$ denotes expectation with respect to the distribution $p$. Intuitively, with first and second moment constraints, one expects this distribution to be Gaussian. While that is true, the solution is non-trivial (Supplementary Note 3,4). Using the standard Lagrangian method and Kronecker algebra, we derived the maximum entropy distribution:

$$\widehat{p}\left(\mathbf{v}\mathbf{e}\mathbf{c}\left(S\right)\right)=\mathcal{N}\left(\mathbf{v}\mathbf{e}\mathbf{c}\left(M\right),\Psi \right)$$

$$\Psi =\frac{1}{2}(Q_C\otimes Q_N\otimes Q_T){({\Lambda }_C\oplus {\Lambda }_N\oplus {\Lambda }_T)}^{-1}{(Q_C\otimes Q_N\otimes Q_T)}^{\top }$$

$$e_T\left(t\right)=\frac{1}{2}\sum _{n=1}^N\sum _{c=1}^C\frac{1}{{\lambda }_T\left(t\right)+{\lambda }_N\left(n\right)+{\lambda }_C\left(c\right)},\forall t\in \left[1,\dots ,T\right]$$

$$e_N\left(n\right)=\frac{1}{2}\sum _{t=1}^T\sum _{c=1}^C\frac{1}{{\lambda }_T\left(t\right)+{\lambda }_N\left(n\right)+{\lambda }_C\left(c\right)},\forall n\in \left[1,\dots ,N\right]$$

$$e_C\left(c\right)=\frac{1}{2}\sum _{t=1}^T\sum _{n=1}^N\frac{1}{{\lambda }_T\left(t\right)+{\lambda }_N\left(n\right)+{\lambda }_C\left(c\right)},\forall c\in \left[1,\dots ,C\right]$$

where $Q_T,Q_N$ and $Q_C$ are the known eigenvector matrices, and $e_T,e_N$and $e_C$ are the known eigenvalues of the true marginal covariance matrices ${\sum }_T,{\sum }_N$ and ${\sum }_C$, respectively. ${\Lambda }_T$, $\Lambda N$ and ${\Lambda }_C$ are diagonal matrices with diagonal elements ${\lambda }_T,{\lambda }_N$ and ${\lambda }_C$, respectively (the Lagrange multipliers). We numerically solved for the multiplier values in terms of the given eigenvalues and reached the exact solution (i.e., zero error, to machine precision). Note that this distribution is defined over a tensor variable, and thus its covariance matrix $\Psi \in {ℝ}^{\mathit{TNC}\times \mathit{TNC}}$ can easily be on the order of ${10}^6\times {10}^6$ for a modest dataset (e.g., a dataset with 100 neurons and 100 conditions recorded from 100 time points), which is prohibitively large for memory and runtime considerations. Left unaddressed, sampling surrogate data from this distribution would be infeasible. To address this challenge, we exploited the Kronecker structure⁵³ to efficiently operate with these matrices and exactly sample from this tensor distribution. It is worth noting that, in contrast to the CFR method, the samples from this maximum entropy distribution maintain the specified primary features in expectation (i.e., each individual surrogate sample will have differences in the primary features due to finite sampling along each mode). On the other hand, TME has the key virtue that, by construction, surrogates will have no structure beyond what is specified, whereas CFR only partially achieves this goal via shuffling.

Extensions to other surrogate types

The procedures described so far generate surrogate-TNC datasets that preserve the primary features across times, neurons and conditions. To constrain for only temporal features, or temporal and neural features, slight modifications were required. In CFR, the optimization objective was accordingly modified (surrogate-T: optimized only $f_T$and added only the temporal mean, surrogate-TN: optimized both $f_T$and $f_N$ and added the temporal and neural means). Similarly, in TME, the constraints were modified (surrogate-T: constrained only temporal covariance and added only the temporal mean, surrogate-TN: constrained both temporal and neural covariance and added both the temporal and neural means). This discussion also makes clear that both methods can be easily extended to other modes (and any number of modes) that might be available in other recording contexts, by a similar approach; our software implementation directly handles additional modes.

Quantifying structure in motor cortex – low-dimensional dynamical systems

Per standard practice, we analyzed data during the 400 ms duration reflecting the movement response ( $\underset{\_}{T}$), and projected the data onto the top $\underset{\_}{N}$ principal components (PCs) of the data to produce a reduced tensor $\underset{\_}{X}\in {ℝ}^{\underset{\_}{T}\times \underset{\_}{N}\times C}$, where $\underset{\_}{N}<N$obtained by cross validation (Supplementary Fig. 8). The linear dynamical system models the temporal evolution of these low-dimensional neural trajectories as fixed across conditions, namely:

$$\dot{\underset{\_}{X}}\left(:,:,c\right)\approx \underset{\_}{X}\left(:,:,c\right)J,\forall c\in \left[1,\dots ,C\right]$$

where $J\in {ℝ}^{\underset{\_}{N}\times \underset{\_}{N}}$ is the dynamics matrix determining the flow field. $\underset{\_}{N}$thus determines dimensionality of the model. We fit the model with:

$$\widehat{J}={\text{argmin}}_{J\in {ℝ}^{\underset{\_}{N}\times \underset{\_}{N}}}\frac{{\sum }_{c=1}^C\Vert \dot{\underset{\_}{X}}\left(:,:,c\right)-\underset{\_}{X}\left(:,:,c\right)\Vert J_F^2}{{\sum }_{c=1}^C\Vert \dot{\underset{\_}{X}}\left(:,:,c\right){\Vert }_F^2}$$

The solution of the above objective function can be analytically obtained by least squares, and the quality of the fit is quantified by the coefficient of determination (R²), which equals one minus the minimum normalized error achieved. We also quantified the generalization performance of the model by performing leave-one-condition-out cross-validation (LOOCV) on the reconstruction of $\dot{\underset{\_}{X}}\left(:,:,c_{\text{test}}\right)$ from $\widehat{J}$, which was appropriately estimated from data that did not include $c_{\text{test}}$. We repeated this procedure for $c_{\text{test}}=\left[1,\dots ,C\right]$, yielding a LOOCV R² statistic.

Quantifying structure in prefrontal cortex – identifying population read-outs

To identify stimulus and decision-specific population read-outs in PFC, we used demixed principle component analysis (dPCA). In brief, dPCA starts by performing different marginalization procedures of data to produce multiple datasets that each reflects one of the task parameters. Then, dPCA identifies dimensions (dPCs) that minimize the reconstruction error of each marginalization of data. Unlike principal component analysis, which maximizes variance, dPCA produces projections with high variance and good demixing of the specified covariates (see Kobak et al.³⁷ for dPCA details).

For the original data and each surrogate dataset, we allowed dPCA to find at most 30 dPCs, after which we selected the top component that represented the stimulus and the top component that represented the decision in each dataset. We projected the original and surrogate responses onto their top dPCs and quantified the variance captured by these projections during the relevant epochs. The stimulus projection variance was based on the epoch starting 100 ms after the first stimulus presentation and ending at the onset of the second stimulus. The decision-projection variance was based on the epoch starting 100 ms after the second stimulus presentation and ending at the second stimulus offset. In addition to the conventional percentage variance explained, we computed another variance statistic (the percentage reconstruction variance, as used in Kobak et al.³⁷), defined as:

$$\frac{\Vert X_N{\Vert }_F^2-\Vert X_N-\mathbf{v}{\mathbf{d}}^{\top }{X}_N{\Vert }_F^2}{\Vert X_N{\Vert }_F^2}\times 100\text{\%}$$

where $X_N\in {ℝ}^{N\times TC}$ is the data reshaped along the neuron mode, $\mathbf{d}\in {ℝ}^N$is the top dPC and $\mathbf{v}\in {ℝ}^N$ is the decoder vector mapping the projection ( ${\mathbf{d}}^{\top }{X}_N$) to the neural space (see Kobak et al.³⁷ for the encoder and decoder description).