Searching for the Pareto frontier in multi-objective protein design

Abstract

The goal of protein engineering and design is to identify sequences that adopt three-dimensional structures of desired function. Often, this is treated as a single-objective optimization problem, identifying the sequence–structure solution with the lowest computed free energy of folding. However, many design problems are multi-state, multi-specificity, or otherwise require concurrent optimization of multiple objectives. There may be tradeoffs among objectives, where improving one feature requires compromising another. The challenge lies in determining solutions that are part of the Pareto optimal set—designs where no further improvement can be achieved in any of the objectives without degrading one of the others. Pareto optimality problems are found in all areas of study, from economics to engineering to biology, and computational methods have been developed specifically to identify the Pareto frontier. We review progress in multi-objective protein design, the development of Pareto optimization methods, and present a specific case study using multi-objective optimization methods to model the tradeoff between three parameters, stability, specificity, and complexity, of a set of interacting synthetic collagen peptides.

Introduction

The ability to engineer proteins or design them from scratch holds the promise for the control of chemical and spatial properties of materials at the nanoscale. Despite a limited alphabet of 20 amino acids, living organisms have evolved proteins as highly efficient catalysts, materials with photonic properties, molecular nano-machines capable of converting between light, chemical, and mechanical energy, and sophisticated signaling and regulatory networks. Still, natural evolutionary processes have accessed only an infinitesimal slice of potential protein sequences (Povolotskaya and Kondrashov 2010), suggesting an immense expanse of undiscovered protein functionality waiting to be discovered.

The field is making forays into this unexplored territory, developing proteins as therapeutics to fight disease and infection, as materials for biomedical applications, and as catalysts for industrial or household use (Braxton and Wells 1992; Jiang et al. 2008; Röthlisberger et al. 2008; Whitehead et al. 2012). The computer has been an essential tool in these explorations, employing physical or statistical models of sequence–structure–function relationships in a high-throughput fashion, sampling large swaths of sequence space to identify promising candidates for characterization and development in the laboratory. The use of computational protein design is rapidly expanding, pushing the state-of-the-art in computational models that efficiently and accurately compute the quality of candidate sequences, and algorithmic or hardware advances that promote rapid sampling of sequence space.

To apply computational methods to a specific design problem, it is necessary to have a defined computable objective. In nearly all projects, the central objective is optimizing the thermodynamic stability of a unique folded state that is able to perform the desired function. Thermodynamic stability is computed using chemical models of various degrees of resolution from heuristic sequence-based scoring functions (Nautiyal et al. 1995; Summa et al. 2002) to high-accuracy but computationally expensive quantum mechanics calculations of energetics (Kiss et al. 2013). The majority of computational protein design platforms calculate energetics of interactions at the atomic level, emphasizing non-bonding interactions, i.e., van der Waals packing, hydrogen bonding, and electrostatics (Kuhlman et al. 2003). However, other objectives may be desirable: solubility, immunogenicity, toxicity, cell permeability, dynamics, or functional efficiency. Each requires an appropriate quantitative model relating the objective to protein sequence for it to be computationally optimizable. Tools for evaluating solubility (Sormanni et al. 2015) can be applied to optimize protein libraries for solubility and enhance the concentration and shelf life of protein formulations. Humanization of therapeutic antibodies using tools such as those by Choi et al. (2015) and Griswold and Bailey-Kellogg (2016) can be applied to minimize adverse immune responses during administration. At the end of this review, we discuss in some detail the specific problem of designing complex sets of specifically interacting molecules, focusing on collagen mimetic peptide studies from our laboratory.

There are a number of well-developed global search heuristics for addressing single-objective optimization problems. Effective approaches should converge on the same set of globally optimal solutions regardless of the starting point, although in practice, the degeneracy of solutions for a particular fold can be large, and, often, the practical goal is to identify solutions that are “good enough” instead of globally optimal. Simulated annealing (Hellinga and Richards 1994) and genetic algorithms (Voigt et al. 2000) are commonly used to sample high-barrier paths along a sequence trajectory between the starting point and a target solution.

Multi-objective protein design

In practice, protein design requires consideration of multiple objectives. This can complicate optimization if the quantitative measures of the multiple objectives are in different units, i.e., how would the stability of a therapeutic protein, measured in terms of free energy of folding, be compared with toxicity based on the maximum tolerated dose? Furthermore, objectives may be in conflict, resulting in a tradeoff where optimizing one compromises the other. For example, the objective of optimizing the stability of a target protein fold may be achieved by maximizing the number of favorable residue–residue interactions throughout the structure. However, this does not take into account the stability of that sequence in competing compact states that differ from the native fold, i.e., the specificity of a sequence for the unique target state. It was shown using lattice chain models of simple protein heteropolymers that the stability and specificity of folding are in fundamental conflict (Chan and Dill 1991). Introducing hydrophobic residues into a sequence will stabilize the native fold, but also increase the degeneracy of states it is likely to adopt (Handel et al. 1993). The conflict between stability and specificity also exists in protein–protein binding interactions. The signaling protein calmodulin interacts with hundreds of targets and achieves this multi-specificity at the expense of the stability of individual calmodulin–target interactions (Shifman and Mayo 2002; Fromer and Shifman 2009).

Stability is also often at odds with other desirable design objectives. Increasing hydrophobicity may affect solubility, expression yield, and complicate purification. In designing enzymes, enhancing stability may dampen protein dynamics that facilitate catalysis, a phenomenon seen in nature where thermophilic versions of enzymes are inactive at room temperature (Howell et al. 2014). Enhancing the stability of therapeutic proteins may improve pharmacokinetic properties such as in vivo half-life (Hall 2014), but may also increase their immunogenicity (Camacho et al. 2008). One can easily envision the need to simultaneously optimize several objectives from intrinsic stability and specificity of folding to cost and yield of production to therapeutic safety and efficacy.

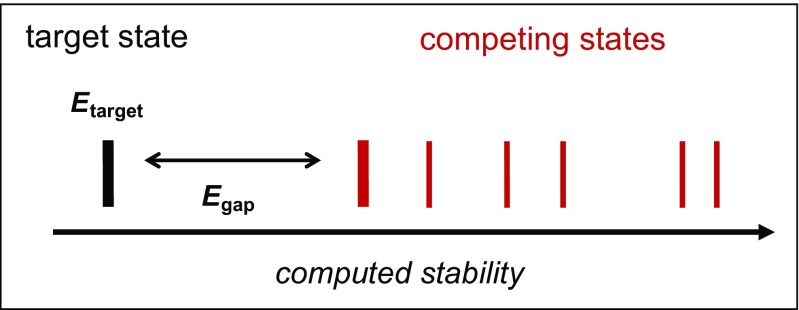
A number of strategies have emerged in the field for dealing with the inherent multi-objective nature of protein design problems. The simplest is to ignore alternate objectives and focus on one, such as stability. This is the nature of “forward design”, or positive design (Fleishman and Baker 2012), which seeks to optimize the stability of the target state. The key thermodynamic parameter that determines the probability a sequence will fold into the target state is the energy gap, i.e., the difference in stability between the target state and competing states (Fig. 1). Optimizing this gap is referred to as “negative design”. In forward design, the negative design problem is not explicitly considered under the assumption that improving the target stability will simultaneously improve the energy gap. This is often a reasonable approximation, particularly when the starting point for design is a natural protein, where much of negative design has been performed by evolution. On the other hand, there are examples where the positive design approach is ineffective, as seen in model systems (Yue et al. 1995), and in practical designs, such as the case of the development of collagen mimetic peptides (CMPs) presented later.

Fig. 1.

Computed stabilities of a series of states representing target and competing protein conformations or binding interactions can be represented as an energy level diagram. In positive design, the stability of the target state E_target is the only objective that is optimized. For negative design, the difference in stability between target and competing states is also included to optimize the sequence to both stably and specifically fold in the target conformation

An alternative in multi-state design is to explicitly consider a relevant subset of conformational states that a sequence may adopt. This may be accomplished by combining states into a single objective, such as the Boltzmann probability of forming the target over competing states (Seeman and Kallenbach 1983; Havranek and Harbury 2003; Stapleton et al. 2015). In the case where multiple target states are desired, summing the stabilities of the sequence mapped onto each target structure (Ambroggio and Kuhlman 2006) or by separating sequence optimization for a set of states while gradually enforcing coupling constraints to drive convergence to a single solution (Sevy et al. 2015). Algorithmic solutions to explicitly treating an arbitrary number of competing states was used to develop an interactome of α-helical oligomers (Grigoryan et al. 2009).

Multi-objective problems may also take the form of disparate properties that are not scored using the same scales, units, or computational methods. One approach would be to combine multiple objectives into a static cost function that weights them appropriately. For example, in the de novo design of a four-helix bundle porphyrin cofactor binding protein, there were multiple design objectives: optimizing metal binding, protein sequence, and topology of the bundle. Metal coordination is highly sensitive to bond lengths and angles and is most effectively modeled using quantum mechanics calculations. To simplify this calculation, coordination geometry was expressed as a series of harmonic constraints on key bond lengths and angles, and concurrently optimized with sequence and topology using standard atomistic force fields (Cochran et al. 2005). The other approach is to algorithmically separate the quantum mechanics optimization of the active site configuration, choice of scaffold, and sequence optimization into discrete steps, as has been done in the development of several artificial enzymes (Zanghellini et al. 2006; Jiang et al. 2008; Röthlisberger et al. 2008). Fleishman and colleagues have explored using fuzzy logic operators as a strategy for incorporating disparate variables into a single scoring function (Warszawski et al. 2014). Importantly, this aggregation approach has underlying mathematical limitations, such that it does not reach all available solutions in certain scenarios (Das and Dennis 1997).

Pareto optimality

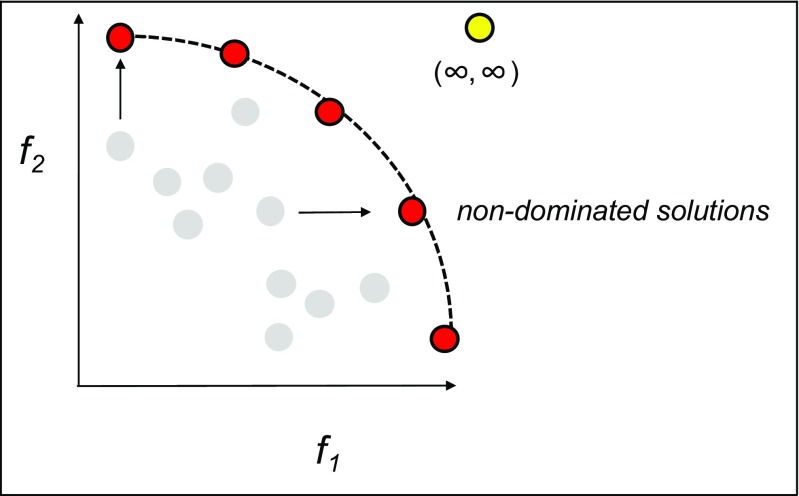
Multi-objective tradeoff problems are not limited to protein engineering, and are found in nearly all fields, from economics to engineering to biological evolution. Unifying these problems is the concept of finding solutions that satisfy the Pareto optimality criterion. These are the subset of solutions where the evaluation of one objective could not be improved without reducing another; for example, the distribution of a fixed number of goods between two parties (Fig. 2). Formal definitions of the Pareto optimal set with regard to protein design can be found in previous studies (Belure et al. 2017). Algorithms that search for Pareto optimal solutions have been applied across science from materials (Hartke 2004), nanotechnology (Wiecha et al. 2017), and protein folding (Cutello et al. 2006) to understanding constraints on animal evolution (Sheftel et al. 2013).

Fig. 2.

The Pareto optimal set is depicted for a bi-objective problem f₁, f₂, where non-dominated solutions (red) cannot be further improved for f₁ without degrading f₂ or vice versa. Other solutions (gray) may be improved along either objective without compromising the other

The Pareto non-dominated set, often called the Pareto frontier, are attractive targets for laboratory characterization, particularly if the relative significance of individual objectives to design success is a priori unknown. Thus, several groups have developed algorithms for identifying the Pareto frontier in protein design problems. Bailey-Kellogg and colleagues developed PEPFR (Protein Engineering Pareto Frontier), which uses dynamic programming to implement an efficient divide-and-conquer approach, and applied it to design problems in therapeutic protein deimmunization, characterizing interacting sets of bZIP helical oligomers and optimizing site-directed recombination protocols for generating diverse libraries that maintain stability and activity (He et al. 2012; Salvat et al. 2015). Pareto refinement methods have also been applied to the design of stabilizing mutations to proteins that minimally disrupt the native structure, concurrently optimizing energy and RMSD from the initial structure (Nivón et al. 2013). State-of-the-art multi-objective optimization evolutionary algorithms such as SMS-EMOA have been applied to the design of peptide ligands that bind with reasonable affinity and selectivity for a specific isoform of 14-3-3 proteins (Sanchez-Faddeev et al. 2012). In characterizing protein designs that are well distributed along a Pareto optimal set, one is able to evaluate the relative importance of objectives to design success. Below, we discuss how the analysis of Pareto optimality may help guide experiments in the design of a collagen peptide interactome.

Specific case study: collagen peptide interactome

We have been using CMPs as model systems for exploring the tradeoff between stability, specificity, and system complexity in oligomeric interactions. Inside of cells, thousands of proteins co-exist and function at very high concentrations without non-specifically aggregating. The same phenomenon occurs outside of cells in the extracellular matrix, where complex mixtures of fibrous proteins, proteoglycans, and other biopolymers co-assemble into a structurally controlled network. We have been using computationally designed mimics of one such extracellular protein, collagen, to understand how specificity is maintained under such complex conditions.

Natural fibrous collagen is composed of three chains that associate into a triple-stranded helix. Type 1 collagen (COL1), a major component of skin and bone connective tissue, exists as a heterotrimer, containing two strands coming from the COL1A1 gene and one from the COL1A2 gene. This heterospecificity is largely governed by interactions between globular pro-domains which are cleaved during protein maturation. However, peptide fragments of COL1 show preference for heterotrimer formation in the absence of pro-domains (Saccà et al. 2002) and it is possible to generate heterotrimers composed of chains with three different sequences using networks of complementary charge pair interactions (Gauba and Hartgerink 2007; Fallas et al. 2009).

Subsequently, we demonstrated that combining stability and energy gap specificity as separate steps in a Monte Carlo simulated annealing (MCSA) protocol could produce an abc heterotrimer where assembly of a folded triple-helix required the presence of all three peptides (Fig. 3) (Xu et al. 2010, 2011). The target abc was maintained by an extensive network of interchain electrostatic interactions. Competing states such as aaa, bbb, and ccc homotrimers, or aab, bbc … heterotrimers were disfavored by repulsive electrostatic interactions. Numerical simulations showed a clear tradeoff between heterotrimer stability and specificity. The most stable collagen peptide is rich in proline and hydroxyproline, cyclic sidechain amino acids that provide conformational stability to the collagen triple-helix. However, these lack the charge pair interactions that promote specificity.

Fig. 3.

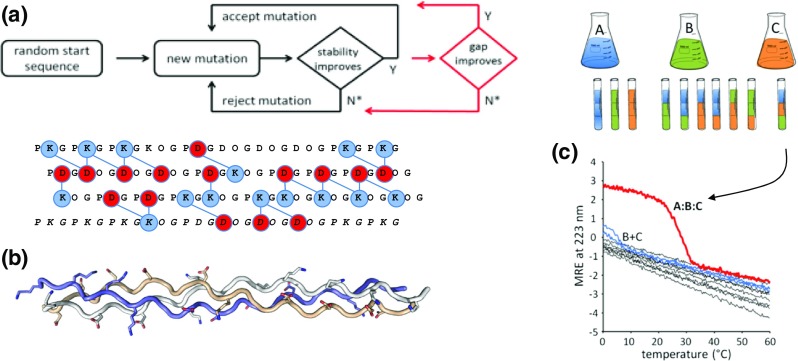
Multi-objective design of an abc collagen heterotrimer. a Monte Carlo simulated annealing (MCSA) algorithm for collagen sequence design splitting the objective across two tiers: evaluating the stability of the target (black) and evaluating the gap between the target and competing states (red). b Top: example of designed sequences for peptides a, b, and c highlighting favorable charge pair interactions between acidic (red) and basic (blue) amino acids. Bottom: three-dimensional model of that sequence on a collagen triple-helix. c Experimental evaluation of the design. Stock solutions of peptides a, b, and c are combined in various stoichiometric ratios. For a successful design, only a + b + c should form a triple-helix, where cooperative denaturation by circular dichroism spectroscopy (MRE: mean residue ellipticity) can be observed. Experimental details can be found in Xu et al. (2011)

Each run of the MCSA on abc heterotrimers yielded a unique design with similar values for the stability and specificity objectives. This high degeneracy in objective space led us to consider a third objective: could multiple abc-type heterotrimers assemble when present in the same solution, i.e., could the complexity of the system be optimized within the design constraints? Mimicking the natural process of protein circular permutation, we generated additional peptides e, f, and g, which, when combined with a, b, and c, formed two separate heterotrimers: abc + def (Xu et al. 2013). However, the specificity was notably affected, suggesting an emerging tradeoff between specificity and complexity.

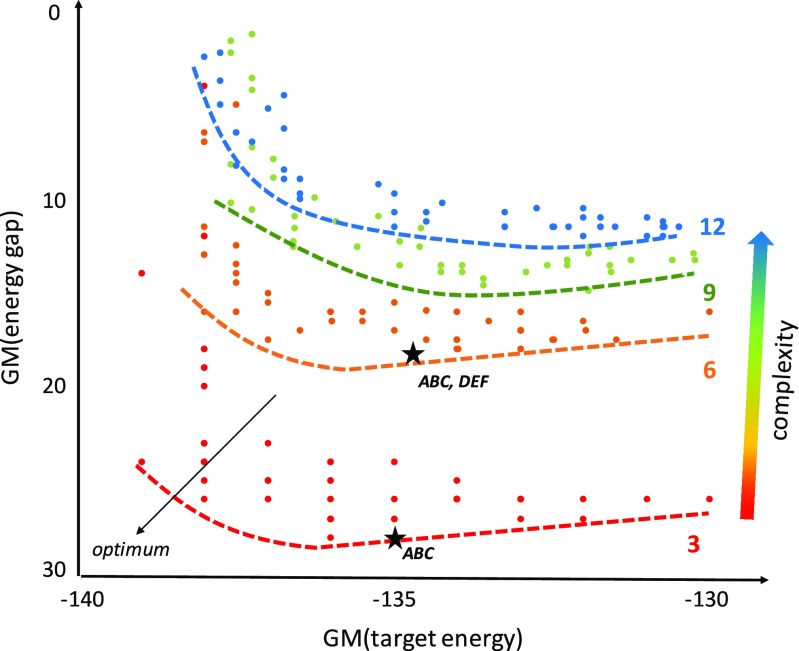
A systematic computational analysis of complexity, stability, and specificity demonstrates that complexity severely constrains the specificity of association (Fig. 4). The abc and abc + def designs lie on or near the apparent Pareto frontier, although the shallow dependence of energy gap and stability suggest that target stability could be increased without significant tradeoff for specificity. Increasing the number of peptides beyond six exhibits a significant tradeoff between complexity and specificity. Given that the number of states scales with the cube of the number of peptide types, the observed tradeoff is not surprising. Recently, we have applied a number of evolutionary and non-evolutionary algorithms to exploring the Pareto frontier for the 12-peptide system (Belure et al. 2017). Algorithms such as SMS-EMOA produce sets of non-dominated solutions, although replica exchange is also effective.

Fig. 4.

Solution sets for multiple runs of a replica exchange algorithm (see Belure et al. 2017 for method details) for four complexity levels: abc (red), abc + def (orange), abc + def + ghi (green), and abc + def + ghi + jkl (blue) collagen peptide interactome designs. Visually estimated Pareto frontiers are indicated with dotted lines. Target energies and gaps represent the geometric mean (GM) of individual target heterotrimers at each level of complexity. Experimentally characterized solutions for abc (Xu et al. 2011) and abc + def (Xu et al. 2013) are indicated by black stars

Conclusions

The collagen peptides provide a useful system for exploring tradeoffs among various objectives in designing an interactome of synthetic peptides. Notably, a similar constraint exists in natural proteomes, where complexity is limited by non-specific interactions between proteins (Tompa and Rose 2011), and measures of protein “stickiness” negatively correlate with expression levels (Levy et al. 2012). Nearly all protein design problems are either implicitly or explicitly multi-objective, and the development of efficient algorithms for producing a Pareto optimal set of sequences is an important goal. A practical approach for addressing multiple objectives in design would involve the synthesis and characterization of sequences that span a significant portion of the Pareto frontier in order to evaluate the relative importance of the multiple objectives. Subsequent design would then focus on libraries of solutions in a particular region of the frontier that represent an effective balance of the various objectives.

Compliance with ethical standards

Conflict of interest

Vikas Nanda declares that he has no conflict of interest. Sandeep V. Belure declares that he has no conflict of interest. Ofer M. Shir declares that he has no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.