Structural characterization of framework–gas interactions in the metal–organic framework Co₂(dobdc) by in situ single-crystal X-ray diffraction

In situ single-crystal X-ray diffraction experiments enable the direct observation of weak metal–gas interactions in a metal–organic framework.

Abstract

The crystallographic characterization of framework–guest interactions in metal–organic frameworks allows the location of guest binding sites and provides meaningful information on the nature of these interactions, enabling the correlation of structure with adsorption behavior. Here, techniques developed for in situ single-crystal X-ray diffraction experiments on porous crystals have enabled the direct observation of CO, CH₄, N₂, O₂, Ar, and P₄ adsorption in Co₂(dobdc) (dobdc^4– = 2,5-dioxido-1,4-benzenedicarboxylate), a metal–organic framework bearing coordinatively unsaturated cobalt(ii) sites. All these molecules exhibit such weak interactions with the high-spin cobalt(ii) sites in the framework that no analogous molecular structures exist, demonstrating the utility of metal–organic frameworks as crystalline matrices for the isolation and structural determination of unstable species. Notably, the Co–CH₄ and Co–Ar interactions observed in Co₂(dobdc) represent, to the best of our knowledge, the first single-crystal structure determination of a metal–CH₄ interaction and the first crystallographically characterized metal–Ar interaction. Analysis of low-pressure gas adsorption isotherms confirms that these gases exhibit mainly physisorptive interactions with the cobalt(ii) sites in Co₂(dobdc), with differential enthalpies of adsorption as weak as –17(1) kJ mol^–1 (for Ar). Moreover, the structures of Co₂(dobdc)·3.8N₂, Co₂(dobdc)·5.9O₂, and Co₂(dobdc)·2.0Ar reveal the location of secondary (N₂, O₂, and Ar) and tertiary (O₂) binding sites in Co₂(dobdc), while high-pressure CO₂, CO, CH₄, N₂, and Ar adsorption isotherms show that these binding sites become more relevant at elevated pressures.

Introduction

In situ X-ray diffraction using single crystals as solid-state matrices has emerged as a powerful approach toward the direct observation of molecules and their reactivity.^1–5 The crystal lattice acts to both stabilize and align molecular guests, enabling their isolation and subsequent structural determination by crystallography. Amid many significant advances over the past two decades, these systems have found promising applications in the study of weakly interacting species, such as adsorbed gases,^6–15 which have been traditionally difficult to characterize crystallographically. Considerable work in this area has focused on conducting in situ X-ray diffraction experiments to investigate host–guest interactions and guest reactivity in molecular flasks, macromolecular hosts designed to encapsulate molecular guests.^1,3 Recognition that the chemistry of these systems extends to the capture and confinement of gas molecules has led to the characterization of a series of small gases within a molecular cavitand.¹⁵ Recent work has featured single-crystal-to-single-crystal reactions of gas molecules with transition metal complexes. As particularly striking examples, this solid–gas reactivity has been leveraged to follow the exchange of small molecules (N₂, CO, NH₃, C₂H₄, H₂, and O₂) on an iridium pincer complex¹² and to isolate rhodium-alkane σ-complexes through the hydrogenation of their corresponding alkene complexes.^16–18 Although these reports reinforce the growing utility of molecular single-crystal matrices, their general applicability remains limited by the scarcity of structures that retain crystallinity upon binding and reaction of the molecular guests.² In addition, the tendency of molecules to pack closely in the crystalline state engenders only small or transient apertures in the crystal. This inability to support larger pore structures severely restricts the size of guests that can be incorporated.³ The need to develop new crystalline matrices to address these challenges outlines an opportunity for alternative materials to contribute to the advancement of the field.

Metal–organic frameworks are a class of materials composed of inorganic clusters or metal ions connected in three dimensions by organic linkers. These materials exhibit the ability to adopt highly porous crystalline structures with well-defined pore architectures,^19,20 leading to their extensive evaluation for applications in gas storage,^21,22 gas separations,^23,24 and catalysis.^25–28 In contrast to the non-covalent interactions in molecular crystals, the coordinate-covalent bonds linking the inorganic and organic units in metal–organic frameworks give rise to their inherently greater thermal and chemical stability. Consequently, these materials are capable of maintaining porous structures that accommodate the removal, inclusion, exchange, or reaction of a more diverse selection of molecular guests over a wider range of conditions compared to molecular assemblies. In particular, frameworks that exhibit permanent and open porosity are uniquely suited to the study of gaseous species. Furthermore, these materials can be designed to facilitate explicit framework–guest interactions through synthetic control over pore size, shape, and functionality.

Indeed, research on metal–organic frameworks has increasingly relied on in situ diffraction experiments to provide critical insight into the contribution of the pore structure to adsorption behavior and reactivity.^29–64 Such studies also complement and validate computational efforts focused on understanding and predicting the properties of these materials.^46,65–68 Despite the greater accessibility, simplicity, and precision associated with single-crystal X-ray diffraction, the majority of work involving gases has been accomplished using powder X-ray and neutron diffraction methods.^29–53,64 This primarily stems from the following challenges: (i) the difficulty in preparing single crystals of sufficient size and quality to be suitable for diffraction experiments, (ii) the tendency of some crystals to fracture under the evacuation or gas-dosing conditions, and (iii) the exceptionally high sensitivity to contaminants inherent to the small sample sizes used in single-crystal measurements (∼500 ng for a typical 200 μm wide single crystal). The third challenge is especially problematic in studying frameworks bearing metals with open coordination sites, due to the propensity of these sites to bind water over more weakly coordinating species. Nevertheless, several studies have proven to be successful in employing single-crystal X-ray diffraction experiments to observe framework–gas interactions.^{29,54,56,60–63,69}

The M₂(dobdc) series of metal–organic frameworks (M = Mg^II, Mn^II, Fe^II, Co^II, Ni^II, Cu^II, Zn^II, and Cd^II; dobdc^4– = 2,5-dioxido-1,4-benzenedicarboxylate; also referred to as M-MOF-74 or CPO-27(M)) have been intensely studied due to their high density of exposed metal(ii) sites, which can interact favorably with guest molecules.^{29–47,55,70,71} Much of the work evaluating the adsorption properties and reactivity of these materials has depended on powder X-ray or neutron diffraction for in situ characterization of gas binding.^29,31–47 Comparatively few studies have been performed using single-crystal X-ray diffraction^29,55 due to the intrinsic difficulty that accompanies in situ gas-dosing experiments on materials with open coordination sites and because only Co₂(dobdc) and Zn₂(dobdc) readily form single crystals. This work seeks to expand on these studies through techniques developed to dose gases into single crystals under rigorously air-free conditions. Herein, we report the direct structural characterization of CO, CH₄, N₂, O₂, Ar, and P₄ adsorption in single crystals of Co₂(dobdc) (Fig. 1). The resulting structures confirm that each gas binds first to the exposed cobalt(ii) site and allow the identification of secondary (for N₂, O₂, and Ar) and tertiary (for O₂) binding sites within the framework. Remarkably, further inspection of Co^II–gas distances reveals that binding occurs primarily through weak covalent (for CO) or non-covalent (for CH₄, N₂, O₂, and Ar) interactions, which have never been observed by single-crystal X-ray diffraction. Finally, a combination of low- and high-pressure gas adsorption isotherms are used to evaluate the relationship between structure and adsorption behavior.

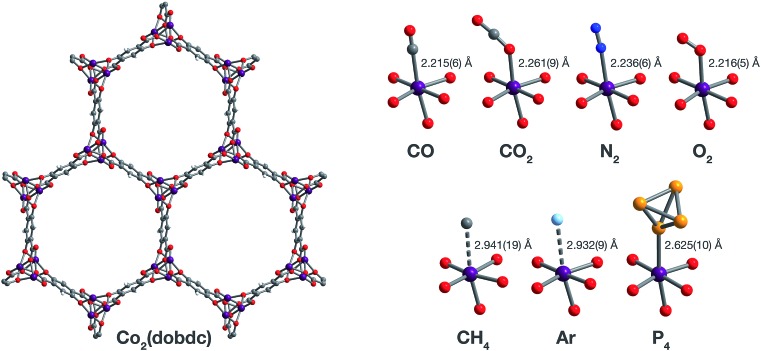
Fig. 1. Structures determined by single-crystal X-ray diffraction. (Left) A portion of the crystal structure of Co₂(dobdc) (dobdc^4– = 2,5-dioxido-1,4-benzenedicarboxylate) at 296 K viewed along the c axis. (Right) First coordination spheres for Co^II in the structures of CO, CO₂,²⁹ N₂, O₂, CH₄, Ar, and P₄ in Co₂(dobdc) (at 150 K for CO₂; at 100 K for N₂, O₂, CH₄, and P₄; at 90 K for CO and Ar); purple, red, gray, blue, light blue, light orange, and white spheres represent Co, O, C, N, Ar, P, and H atoms, respectively. Note that the O₂ molecules bound to the Co^II sites in Co₂(dobdc)·5.9O₂ were found to be disordered over two orientations with relative occupancies of 73(3)% and 27(3)% (Fig. S8†), but only one of these orientations (73(3)% occupancy) is shown for clarity. The structure of Co₂(dobdc)·2.9CO₂ has been reported previously²⁹ and is shown here to facilitate comparisons.

Experimental

Materials and methods

N,N-Dimethylformamide (DMF), ethanol, and methanol were obtained from commercial sources and used without further purification. Hexanes was deoxygenated by purging with Ar for 1 h and dried using a commercial solvent purification system designed by JC Meyer Solvent Systems. The compounds Co(NO₃)²·6H₂O and 2,5-dihydroxy-1,4-benzenedicarboxylic acid (H₄dobdc) were purchased from Sigma-Aldrich and used as received. White phosphorus (P₄) was prepared by heating red phosphorus under vacuum (∼80 μbar) in a flame-sealed borosilicate glass tube over a Bunsen burner flame. The crude white phosphorus was then purified by recrystallization from hexanes. Caution: white phosphorus is highly toxic and reacts violently with O ₂ in air. Single crystals of Co₂(dobdc) were synthesized using a slight modification to a previously published procedure.⁷¹ Briefly, a 100 mL Pyrex jar was charged with H₄dobdc (198 mg, 1.00 mmol), Co(NO₃)²·6H₂O (970 mg, 3.34 mmol), and a 1 : 1 : 1 (v/v/v) mixture of DMF/ethanol/water (80 mL), and was then sealed with a Teflon cap. The resulting mixture was sonicated until all reactants were fully dissolved to form a violet solution. The reaction mixture was then placed in an oven that was preheated to 100 °C and kept at this temperature for 24 h, yielding violet needle-shaped single crystals. The crystals were soaked three times in 80 mL of DMF for 24 h at 120 °C, followed by soaking three times in 80 mL of methanol at 60 °C. The crystals were then stored in methanol in a 20 mL PTFE-capped vial prior to use for single-crystal X-ray diffraction experiments or gas-adsorption measurements. The Langmuir surface area of the sample used for gas adsorption measurements was determined to be 1400 ± 2 m² g^–1.

Single-crystal X-ray diffraction

Gas dosing in the gas cell

For Co₂(dobdc), Co₂(dobdc)·0.58CO, Co₂(dobdc)·2.0CH₄, and Co₂(dobdc)·2.0Ar, a methanol-solvated crystal of Co₂(dobdc) was mounted on a MiTeGen loop using a minimal amount of epoxy to ensure that the crystal pores remained accessible. The sample was then placed in a custom-made gas cell equipped with a quartz capillary, an O-ring seal, and Beswick ball valves for gas-dosing (Fig. 2a). The cell was connected to a gas-dosing manifold using PTFE tubing, and was then evacuated under reduced pressure using a turbomolecular pump at an external temperature of 180 °C for 4–5 h to remove solvent molecules that fill the pores and coordinate to the exposed Co sites within the crystal. After obtaining the structure to confirm that the crystal was fully desolvated, the crystal was cooled to 25 °C and then dosed with the desired gas at a specified pressure (1.00 bar for CO and CH₄; 1.14 bar for Ar).

Fig. 2. (a) Diagram of the gas cell, which was designed and built at Advanced Light Source Beamline 11.3.1. (b) Diagram of a capillary-dosing assembly.

Gas dosing in capillaries

For Co₂(dobdc)·5.9O₂ and Co₂(dobdc)·3.8N₂, methanol-solvated crystals of Co₂(dobdc) were mounted on a borosilicate glass fiber using a minimal amount of epoxy, ensuring that the crystal pores remained accessible. The glass fiber was then inserted into a 1.0 mm borosilicate glass capillary, which was connected to a HiP Taper Seal valve using a Swagelok® Ultra-Torr vacuum fitting with a Viton® O-ring (Fig. 2b). The capillary-dosing assembly was then attached to a port on a Micromeretics ASAP 2020 instrument using a Cajon® VCO fitting. The capillary was evacuated under reduced pressure at 180 °C for 24 h to remove solvent molecules that fill the pores and coordinate to the exposed Co sites within the crystal. The capillary was dosed with a specific gas at a specified pressure (0.8 bar for N₂; 0.5 bar for O₂), and was then flame-sealed with a methane/oxygen torch.

Vapor dosing of P₄

For Co₂(dobdc)·1.3P₄, methanol-solvated Co₂(dobdc) crystals (∼20 mg) were desolvated in a glass tube under reduced pressure at 180 °C on a Micromeritics ASAP 2020 instrument. In an N₂-filled VAC Atmospheres glovebox, the desolvated crystals were transferred into a 4 mL vial, which was then placed in a 20 mL vial containing excess white phosphorus. Caution: white phosphorus is highly toxic and reacts violently with O ₂ in air. The 20 mL vial was sealed with a PTFE-lined cap then heated for 24 h at 80 °C. The P₄-dosed crystals were then coated with Paratone-N oil prior to use for single-crystal X-ray diffraction experiments.

Data collection and refinement

X-ray diffraction data for all samples were collected at Beamline 11.3.1 at the Advanced Light Source, Lawrence Berkeley National Laboratory using synchrotron radiation (λ = 0.7749 Å for Co₂(dobdc), Co₂(dobdc)·0.58CO, Co₂(dobdc)·1.19CO, Co₂(dobdc)·2.0CH₄, Co₂(dobdc)·5.9O₂, and Co₂(dobdc)·1.3P₄; λ = 0.6525 Å for Co₂(dobdc)·2.0Ar; λ = 0.6199 Å for Co₂(dobdc)·3.8N₂) with either a Bruker AXS APEX II CCD detector (Co₂(dobdc), Co₂(dobdc)·0.58CO, Co₂(dobdc)·1.2CO, Co₂(dobdc)·2.0CH₄, Co₂(dobdc)·3.8N₂, and Co₂(dobdc)·2.0Ar) or a Bruker PHOTON100 CMOS detector (Co₂(dobdc)·5.9O₂ and Co₂(dobdc)·1.3P₄) on a D8 diffractometer. The samples were cooled to a specified temperature (296 K for Co₂(dobdc); 100 K for Co₂(dobdc)·1.2CO, Co₂(dobdc)·2.0CH₄, Co₂(dobdc)·3.8N₂, Co₂(dobdc)·5.9O₂, and Co₂(dobdc)·1.3P₄; 90 K for Co₂(dobdc)·0.58CO and Co₂(dobdc)·2.0Ar) using an Oxford Cryosystems cryostream for data collection.

All crystals were found to be obverse/reverse twins based on analysis of their diffraction patterns. For each structure, CELL_NOW⁷² was used to determine the orientation matrices. Raw data for both twin matrices were integrated and corrected for Lorentz and polarization effects using Bruker AXS SAINT⁷³ software and corrected for absorption using TWINABS.⁷⁴ TWINABS was used to produce a merged HKLF4 file for structure solution and initial refinement and an HKLF5 file for final structure refinement. The structures were solved using direct methods with SHELXS^75,76 and refined using SHELXL^75,77 operated in the OLEX2 interface.⁷⁸ Thermal parameters were refined anisotropically for all non-hydrogen atoms. Disorder and thermal motion of the bound gas molecules required the use of displacement parameter (for Co₂(dobdc)·1.2CO, Co₂(dobdc)·5.9O₂, Co₂(dobdc)·3.8N₂ Co₂(dobdc)·2.0Ar, and Co₂(dobdc)·1.3P₄) and distance (for Co₂(dobdc)·5.9O₂, Co₂(dobdc)·3.8N₂, and Co₂(dobdc)·1.3P₄) restraints. All hydrogen atoms were refined using the riding model.

Gas adsorption

Low-pressure gas adsorption measurements

Pure-component gas adsorption isotherms for pressures in the range 0–1.2 bar were measured by a volumetric method using Micromeritics ASAP 2020 and ASAP 2420 instruments. UHP-grade gases (99.999% purity He, Ar, N₂, CO, CO₂, and CH₄; 99.998% purity CO₂; 99.993% purity O₂) were used for all measurements. A typical sample of 30–100 mg of Co₂(dobdc) was transferred to a pre-weighed analysis tube, which was capped with a Micromeretics TranSeal and evacuated by heating at either 180 °C, reached by ramping at a rate of 1 °C min^–1, under dynamic vacuum until an outgas rate of less than 3 μbar min^–1 was achieved. The evacuated analysis tube containing the degassed sample was then carefully transferred to an electronic balance and weighed again to determine the mass of sample. The tube was then transferred back to the analysis port of the gas adsorption instrument. The outgas rate was again confirmed to be less than 3 μbar min^–1. For all isotherms, warm and cold free space correction measurements were performed using ultra-high purity He gas. Nitrogen gas adsorption isotherms at 77 K were measured in liquid nitrogen using UHP-grade gas sources. Oil-free vacuum pumps and oil-free pressure regulators were used for all measurements to prevent contamination of the samples during the evacuation process or of the feed gases during the isotherm measurements. Langmuir surface areas were determined from N₂ adsorption data at 77 K using Micromeritics software, assuming a value of 16.2 Ų for the molecular cross-sectional area of N₂. Adsorption isotherms between 293 and 323 K were measured using a recirculating dewar connected to a Julabo F32-MC isothermal bath.

High-pressure gas adsorption measurements

High-pressure gas adsorption isotherms in the range of 0–100 bar were measured on an HPVA-II-100 from Particulate Systems, a Micromeritics company. In a typical measurement, 0.5–1.0 g of activated sample was loaded into a tared stainless steel sample holder inside a glovebox under a N₂ atmosphere. Prior to connecting the sample holder to the VCR fitting of the complete high-pressure assembly inside the glovebox, the sample holder was weighed to determine the sample mass. The sample holder was then transferred to the HPVA-II-100 instrument, connected to the instrument's analysis port via an OCR fitting, and evacuated at room temperature for at least 2 h. The sample holder was placed inside an aluminum recirculating Dewar connected to a Julabo FP89-HL isothermal bath filled with Julabo Thermal C2 fluid. The temperature stability of the isothermal bath is ±0.02 °C. Methods for accurately measuring the relevant sample free space, which involve the expansion of He from a calibrated volume at 0.7 bar and 25 °C to the evacuated sample holder, have been described in detail previously.²² Non-ideality corrections were performed using the compressibility factors tabulated in the NIST REFPROP database^79,80 at each measured temperature and pressure.

Adsorption isotherm fitting

Low-pressure Ar, N₂, and O₂ isotherms at 298, 308, and 318 K were fit with a single-site Langmuir equation, while low-pressure CH₄ isotherms at 293, 298, 303, 313, and 323 K were fit using a dual-site Langmuir equation (eqn (1)), where n is the total amount adsorbed in mmol g^–1, P is the pressure in bar, n _sat,i is the saturation capacity in mmol g^–1, and b _i is the Langmuir parameter in bar^–1.

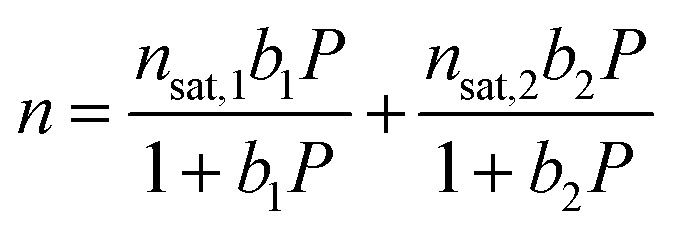1

b_i = e^–S_i/Re^E_i·1000/RT 2

The Langmuir parameter can be expressed using eqn (2), where S _i is the site-specific integral entropy of adsorption in J mol^–1 K^–1; E _i is the site-specific differential enthalpy of adsorption in kJ mol^–1, R is the gas constant in J mol^–1 K^–1, and T is the temperature in K. For all gases, isotherms were fit both independently for each temperature (Fig. S11, S13, S15, and S17†) and simultaneously for all temperatures (Fig. S12, S14, S16, and S18†).

Differential enthalpy of adsorption calculations

Using the Langmuir fits, the differential enthalpy of adsorption, Δh _ad, can be calculated as a function of the total amount of gas adsorbed, n, by using the Clausius–Clapeyron equation (eqn (3)), where R is the gas constant in J mol^–1 K^–1, T is the temperature in K, n is the total amount adsorbed in mmol g^–1, and P is the pressure in bar.

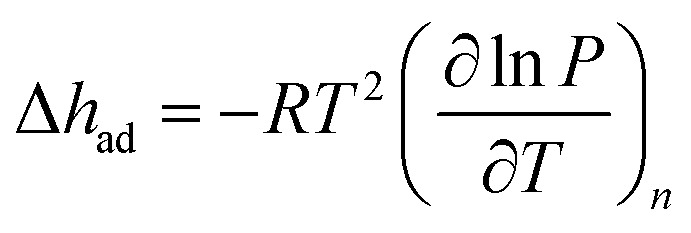3

The Langmuir fits for each gas (fit independently for each temperature) were used to obtain the exact pressures that correspond to specific loadings at different temperatures (298, 308, and 318 K for N₂, O₂, and Ar; 293, 298, 303, 313, and 323 K for CH₄). This was done at loading intervals of 0.05 mmol g^–1. At each loading, the slope of the best-fit line to ln(P) versus 1/T was calculated to obtain the differential enthalpy.

Results and discussion

Structural characterization

Two methods were developed for dosing gases into single crystals. The first involves using an environmental gas cell (Fig. 2a), which was designed and built at ALS beamline 11.3.1. Similar to other gas cells that have recently been developed,^81,82 the cell allows the collection of single-crystal X-ray diffraction data on samples under vacuum or dosed with a desired gas. With this method, the structure of the framework can be monitored throughout the evacuation and gas dosing of the crystal. This capability affords appreciable flexibility, as the temperature, gas pressure, and time can be changed at each stage of the experiment in response to structural data. As a result, the gas cell is especially useful for studying unfamiliar samples that still require experimental conditions to be optimized. Alternatively, a single crystal can be inserted into a borosilicate capillary, which is then heated under vacuum and subsequently dosed using a manifold or gas adsorption analyzer. The capillary is then flame-sealed with the crystal kept under a specified pressure of gas that is lower than 1 bar. Unlike the gas cell, using capillaries requires the evacuation time and temperature and the gas-dosing pressure to be determined prior to data collection. Although less versatile, the capillary method benefits from higher sample throughput compared to the gas cell because diffraction experiments are only conducted on gas-dosed samples. Consequently, this method can be preferable for samples that have established activation parameters and gas adsorption properties.

The metal–organic framework Co₂(dobdc) crystallizes in the space group R3, in which the special positions are exclusively situated along the one-dimensional helical chains of Co atoms, at the center of the organic linkers, and through the center of the hexagonal pores. This makes the framework particularly amenable to the crystallographic characterization of guest species as no crystallographic symmetry is enforced on sites above and within the vicinity of the coordinatively unsaturated cobalt(ii) centers. This is evident in the exceptionally ordered structures of gases within Co₂(dobdc) even in cases where the interactions are weak, as described previously^{29,33,40,55,68} and discussed below.

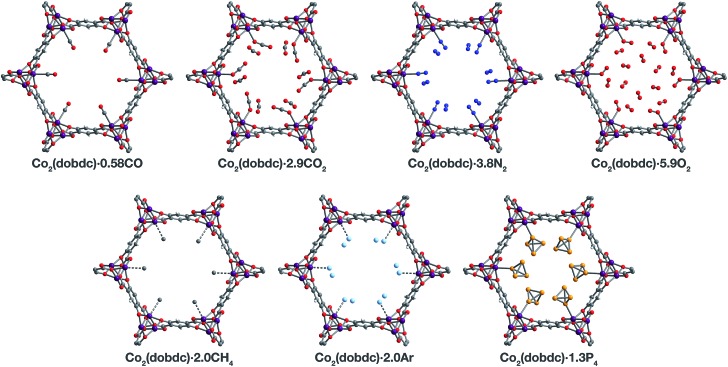
Inspection of the structures of Co₂(dobdc)·1.2CO, Co₂(dobdc)·0.58CO, and Co₂(dobdc)·2.0CH₄ (Fig. 3), where only a single adsorption site is populated, shows that CO and CH₄ first bind to the open coordination site of cobalt(ii), confirming that this site has the greatest contribution to the adsorption of these gases in the material. Multiple adsorption sites could be located in the structures of Co₂(dobdc)·3.8N₂, Co₂(dobdc)·5.9O₂, Co₂(dobdc)·2.0Ar, and Co₂(dobdc)·1.3P₄ (Fig. 3), which complicates the determination of the primary adsorption sites. Comparison of relative site occupancies, displacement parameters, and framework–guest distances, however, indicates that N₂, O₂, Ar, and P₄ also bind primarily to the cobalt(ii) sites. Remarkably, the secondary binding sites for N₂, O₂, and Ar were found to have nearly identical locations (Fig. S1 and S2†), close to the non-bridging carboxylate and phenoxide oxygen atoms of dobdc^4–. Previous reports also identify the same secondary binding site in structures of CO₂ (ref. 29) (Fig. 3) and H₂O⁶⁸ in Co₂(dobdc) (Fig. S1 and S2†). The similarity of these binding pockets likely arises from a slightly polarizing environment generated by the partial negative charges on surrounding linker oxygen atoms. In other metal–organic frameworks, the linker carboxylate oxygen atoms have been shown to facilitate similar weak interactions with gases.^52,54

Fig. 3. A portion of the crystal structures of Co₂(dobdc)·0.58CO at 90 K, Co₂(dobdc)·2.9CO₂ at 150 K,²⁹ Co₂(dobdc)·5.9O₂ at 100 K, Co₂(dobdc)·3.8N₂ at 100 K, Co₂(dobdc)·2.0CH₄ at 100 K, Co₂(dobdc)·2.0Ar, and Co₂(dobdc)·1.3P₄ at 100 K viewed along the c axis, as determined by single-crystal X-ray diffraction; purple, red, gray, blue, light blue, light orange, and white spheres represent Co, O, C, N, Ar, P, and H atoms, respectively. Note that the O₂ molecules bound to the Co^II sites in Co₂(dobdc)·5.9O₂ were found to be disordered over two orientations with relative occupancies of 73(3)% and 27(3)% (Fig. S8†), but only one of these orientations (73(3)% occupancy) is shown for clarity. In the structure of Co₂(dobdc)·1.3P₄, the P₄ molecules were found in two positions (Fig. S10†), one with P₄ molecules coordinated to the Co^II sites (45.5(10)% occupancy) and another 3.88(3) Å away from the Co^II sites centers (20.6(10)% occupancy), but only the coordinated P₄ molecules are shown for clarity. The structure of Co₂(dobdc)·2.9CO₂ has been reported previously²⁹ and is shown here to facilitate comparisons.

The structures of Co₂(dobdc)·1.2CO at 100 K and Co₂(dobdc)·0.58CO at 90 K (Fig. 3) were obtained under 1.00 bar of CO in the gas cell. In these structures, CO loading was found to be lower than one per cobalt(ii) site, which likely results from slow diffusion of CO as the crystals were rapidly cooled after CO dosing. Nevertheless, both structures display Co–C_CO distances of 2.215(6) Å (Fig. 1) and similar Co–C–O angles (175.7(12)° for Co₂(dobdc)·1.2CO and 178.0(11)° for Co₂(dobdc)·0.58CO). These distances and angles are comparable to those previously obtained from powder neutron diffraction at 10 K, Co–C_CO distance = 2.18(2) Å and Co–C–O angle = 171(2)°.⁴⁰ The long Co–C_CO distance and deviation of the Co–C–O angle from 180° are both consistent with a weak interaction between cobalt(ii) and CO with limited Co^II–CO π backbonding. This is further supported by larger CO oxygen displacement parameters compared to carbon, which suggests that the bound CO is free to bend out of the axis along the Co^II–CO bond. Surveying the Cambridge Crystal Structure Database (CCSD),⁸³ single-crystal structures of cobalt carbonyl complexes with Co–C_CO distances longer than 2.0 Å are unprecedented. Examples of cobalt(ii)–carbonyl complexes are exceedingly rare and all exhibit a low-spin configuration with Co–C_CO bond distances around 1.8 Å, which are typical to strong Co–CO bonds.⁸⁴ The weak-field dobdc^4– ligands in Co₂(dobdc) impose a high-spin configuration for cobalt(ii), which is maintained after binding CO.⁴⁰ Population of the anti-bonding cobalt(ii) orbitals makes the Co–CO σ interaction less favorable, lengthening the Co–C_CO distance. This diminishes Co^II–CO π back-donation by preventing overlap between the Co 3d and CO π* orbitals. Together, these interdependent effects manifest in the exceptionally weak and fully reversible M–CO interaction in Co₂(dobdc), which has been shown to be a major advantage of Co₂(dobdc) and its Mg^II, Mn^II, Fe^II, Ni^II, and Zn^II analogs as prospective materials for industrial CO separations.⁴⁰

X-ray analysis of a single crystal of Co₂(dobdc) under 0.8 bar N₂ at 100 K resulted in the structure of Co₂(dobdc)·3.8N₂ (Fig. 3). The structure shows that N₂ binds to cobalt(ii) through an end-on interaction with a Co–N_N2 distance of 2.236(6) Å (Fig. 1). This distance is comparable with the Fe–N_N2 distance of 2.30(1) Å obtained from the powder neutron diffraction structure of N₂ in Fe₂(dobdc).³⁵ Deviation of the Co–N–N angle (170.2(9)°) from 180° also suggests minimal π back-donation from Co^II to N₂. Of the cobalt dinitrogen complexes reported in the CCSD,⁸³ none have Co–N_N2 distances greater than 2.0 Å and only one of these features cobalt in its +2 oxidation state.⁸⁵ The long Co–N_N2 distance in Co₂(dobdc)·3.8N₂ indicates a much weaker interaction between N₂ and the high-spin cobalt(ii) centers in Co₂(dobdc) compared to the Co–N₂ bonds formed in typical cobalt dinitrogen complexes.^86–88 The Co–N₂ bonds in these complexes are strengthened by significant Co–N₂ π back-donation, whereas N₂ can be thought to interact mainly through σ donation to cobalt(ii) in Co₂(dobdc). The secondary N₂ binding sites in Co₂(dobdc)·3.8N₂ (Fig. 3 and S1†) display van der Waals interactions between N₂ and the oxygen atoms of dobdc^4–, with N···O contacts ranging from 3.44(2) to 3.771(2) Å (Fig. S2†). These sites are nearly identical to those located in the powder neutron diffraction structure of N₂ in Fe₂(dobdc).³⁵ Full population of both binding sites to give four N₂ molecules adsorbed per formula unit in Co₂(dobdc) corresponds surprisingly well to the estimated number of N₂ molecules adsorbed as a monolayer in the framework, which is ∼4.3 based on a Brunauer–Emmett–Teller (BET) fit to 77 K N₂ adsorption isotherm data.²⁹

To determine the structure of O₂ in Co₂(dobdc), data was collected on a single crystal dosed with 0.5 bar of O₂ in a sealed capillary at 100 K. In the structure of Co₂(dobdc)·5.9O₂ (Fig. 3), O₂ is found to bind end-on with a Co–O_O2 distance of 2.216(5) Å (Fig. 1). Disorder of the O₂ molecule results in two bent orientations with Co–O–O angles of 127.3(10)° and 128(3)° and relative occupancies of 73(3)% and 27(3)%, respectively (Fig. S8†). The Co–O_O2 distance in Co₂(dobdc)·5.9O₂ is unusually long. Structures of cobalt dioxygen complexes in the CCSD⁸³ and recently reported dioxygen adducts formed in other cobalt metal–organic frameworks,^60,62 all show Co–O_O2 distances that fall below 2.0 Å. This again suggests significant disparity between the Co–O₂ interaction in Co₂(dobdc) and those in molecular cobalt complexes, where O₂ binding is characterized by electron transfer from one or two cobalt(ii) centers to form superoxo or peroxo complexes, respectively.^89,90 In addition to the long Co–O_O2 distance, no significant difference in the average Co–O distances is apparent between cobalt(ii) and dobdc^4– in Co₂(dobdc) (2.035(5) Å) and in Co₂(dobdc)·5.9O₂ (2.036(5) Å). This further implies that partial oxidation of cobalt(ii) does not occur upon O₂ binding, which is in contrast to partial oxidation of the iron(ii) centers in Fe₂(dobdc) to form either iron-superoxo species at 211 K or iron-peroxo species at 298 K.³⁵ Like in Co₂(dobdc)·3.8N₂, the secondary bindings sites in Co₂(dobdc)·5.9O₂ feature O₂ interacting with the dobdc^4– oxygen atoms, with O···O contacts that range from 3.391(17) Å to 3.88(2) Å. Remarkably, tertiary binding sites for O₂ can also be identified in the structure, where O₂ interacts only with other O₂ molecules adsorbed on the primary and secondary sites. Similar sites were also observed by powder neutron diffraction in the structure of O₂ in Fe₂(dobdc).³⁵ Experimental observation of these sites is particularly helpful to computational efforts focused on understanding the contribution of gas–gas interactions to adsorption in metal–organic frameworks and other porous materials.^{46,65,68,91,92}

The structure of Co₂(dobdc)·2.0CH₄ (Fig. 3) was obtained by cooling a single crystal of Co₂(dobdc) under 1 bar of CH₄ to 100 K in the gas cell. Although methane hydrogen atoms could not be located in the structure due to disorder and the difficulty in locating hydrogen atoms by X-ray diffraction, electron density corresponding to a methane carbon atom could be distinctly resolved above the framework cobalt sites with a Co^II···C_CH4 distance of 2.941(19) Å (Fig. 1). Significantly, this is the first M–CH₄ interaction that has been characterized by single-crystal X-ray diffraction. The Co···C_CH4 distance is comparable to distances characterized for metal–methane interactions in other metal–organic frameworks, which are generally close to 3 Å. The most relevant of these are from structures determined by powder neutron diffraction for CD₄ in Fe₂(dobdc) (Fe···C_CD4 distance of 2.98(1) Å)⁶⁶ and in Mg₂(dobdc) (Mg···C_CD4 distance of 3.04 Å).⁹³ The long M···C_CH4 distances in all of these structures are indicative of weak non-covalent interactions that stem from polarization of CH₄ by the partial positive charge on the metal center. These distances contrast with the relatively short M···C distances (around 2.4–2.5 Å) in alkane σ-complexes, which involve donation from the alkane C–H σ bond to the metal center.^16–18 Although the Co^II–CH₄ interaction in Co₂(dobdc) and analogous noncovalent M–CH₄ interactions should clearly be distinguished from the bonds formed in true metal–alkane σ-complexes, characterization of such weak M–CH₄ interactions has become increasingly important in the evaluation of materials for natural gas storage.²²

The inherent chemical stability of the noble gases has been thoroughly exploited for maintaining an inert environment for highly reactive species. As a result of this stability, isolation of molecular metal–noble gas species is exceedingly difficult. While no molecular metal–noble gas species other than metal–Xe^94,95 have been characterized crystallographically, computational methods and experimental techniques such as photodissociation spectroscopy and mass spectrometry have been employed to study these species.^95–101 Encouraged by the preceding results, attempts were made to characterize metal–Ar interactions, which have never been crystallographically observed, in Co₂(dobdc). Under a pressure of 1.14 bar of Ar in the gas cell, no significant electron density could be observed over the cobalt(ii) sites in Co₂(dobdc) at 100 K. Upon cooling to 90 K, however, two binding sites for Ar were resolved, one directly above the metal center and another at a location similar to the secondary binding sites of N₂ and O₂ (Fig. 2 and S1†). It is highly improbable that Ar occupies these adjacent sites simultaneously, because the distance between Ar molecules in the two sites (2.71(3) Å) is much shorter than twice the van der Waals radius of Ar (3.76 Å). In agreement with this, refinement of the Ar site occupancies results in site occupancies of 60.6(1.3)% for Ar interacting with cobalt(ii) and 39.3(1.6)% for the second site, which give an overall formula of Co₂(dobdc)·2.0Ar. These observations suggest that both sites have comparable affinities for Ar, resulting in an equilibrium between the two. Similar adsorption behavior has been observed for Kr and Xe in Ni₂(dobdc) and Mg₂(dobdc).^43,47 The interaction of Ar with the cobalt(ii) centers in Co₂(dobdc) is characterized by a Co–Ar distance of 2.932(9) Å (Fig. 1), which represents the first metal–Ar interaction observed by crystallography. This distance compares well with M–Kr and M–Xe distances in Ni₂(dobdc) and Mg₂(dobdc) (Ni–Kr = 3.03(3) Å and 3.26(15) Å, Mg–Kr = 3.23(3) Å, Ni–Xe = 3.01(2) Å and 3.395(7) Å, Mg–Xe = 3.14(2) Å) obtained by powder X-ray diffraction.^43,47 The long distances between Ar, Kr, and Xe and the exposed metal sites in these frameworks is attributed to polarization induced by the partial positive charge on the metal centers. Like N₂ and O₂, Ar interacts with the dobdc^4– oxygen atoms in its second binding site (Fig. S2†). Interactions between Ar and other noble gases with the linker oxygen atoms in other metal–organic frameworks have also been observed by both single-crystal^10,54,69 and powder X-ray diffraction.^43,47

Motivated by previous work demonstrating the confinement of white phosphorus within a supramolecular cage¹⁰² and a coordination solid,¹⁰³ we envisioned that Co^II–P₄ species could be stabilized by leveraging the site-isolation of the open cobalt(ii) coordination sites in Co₂(dobdc). Heating activated single crystals of Co₂(dobdc) in the presence of white phosphorus in a sealed vial at 80 °C resulted in adsorption of P₄ molecules to give Co₂(dobdc)·1.3P₄ as determined by single-crystal X-ray diffraction. Initial refinement of the structure revealed clearly resolved P₄ tetrahedron exhibiting η¹-coordination to the cobalt(ii) sites of the framework, with a Co^II–P_P4 distance of ∼2.6 Å. The P₄ moiety, however, displayed highly prolate anisotropic displacement parameters and unusual P–P bond distances, long P_apical–P_basal bonds (∼2.6 Å) and short P_basal–P_basal bonds (∼2.0 Å), compared to the P–P bond distances in the crystal structure of P₄ (2.190(5)–2.212(5) Å).¹⁰⁴ Given the relatively long Co^II–P bond distance and large displacement parameters, the apparent distortion of the coordinated P₄ likely resulted from disorder of the P₄ molecule rather than activation by the cobalt(ii) center. Thus, the P₄ molecule was modelled to be disordered over two positions with all P–P distances restrained to be similar. The revised structure reveals that P₄ binds to only 45.5(10)% of the cobalt(ii) sites with a long Co^II–P_P4 distance of 2.625(10) Å (Fig. 1 and 3). The relative distance between P₄ molecules coordinated to adjacent cobalt(ii) sites suggests that P₄ cannot coordinate to each cobalt(ii) center because this would lead to P···P contacts (2.53(3) Å) that are much shorter than twice the van der Waals radius of P (3.90 Å). Consequently, the rest of the adsorbed P₄ populates a second site (20.6(10)% occupancy) 3.88 Å away from the cobalt(ii) center (Fig. S10†), where steric congestion prevents closer approach of the P₄ molecule to cobalt(ii). Although rare, several molecular η¹–P₄ complexes have been prepared by employing transition metal precursors with an agostic interaction or weakly coordinated ligand that can be displaced by P₄ under mild reaction conditions.^105,106 In contrast to the long Co^II–P_P4 distance in Co₂(dobdc)·1.3P₄, molecular η¹–P₄ complexes reported in the CCSD⁸³ possess much shorter metal–P_P4 distances that range from 2.1622(8)–2.464(3) Å and contain electron-rich metals capable of π backbonding to P₄. These comparisons imply that, similar to the Co^II–CO and Co^II–N₂ interactions characterized in Co₂(dobdc), the longer Co^II–P_P4 bond in Co₂(dobdc)·1.3P₄ arises from the inability of the high-spin cobalt(ii) centers to effectively support π back-donation to P₄. Notably, the weaker cobalt(ii)–P₄ complexes in Co₂(dobdc) can be prepared and remain stable at much higher temperatures whereas most molecular η¹–P₄ complexes readily decompose at room temperature.^105,106 This thermal stability is attributed to the site-isolation of these Co^II–P₄ species and their inability to decompose through oxidative addition of P₄, due to the high-spin state and coordinative saturation of the framework cobalt(ii) centers.

Gas adsorption

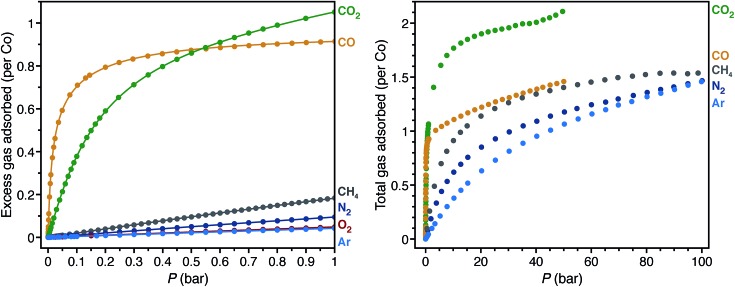
Low-pressure gas adsorption isotherms at different temperatures were collected for CH₄, N₂, O₂, and Ar, while the isotherms for CO and CO₂ were obtained from previous work^29,40 to relate the adsorption properties of these gases to the corresponding structures (Fig. 4 and S11–S18†). To provide a quantitative comparison, the differential enthalpies of adsorption (Δh _ad), a measure of the average binding energy for an adsorbate at a specific surface coverage, were calculated from isotherm data at low coverage of each gas (Table 1). In agreement with the crystal structures, the differential enthalpies of adsorption, which range from –48.8(2) (for CO) to –17(1) kJ mol^–1 (for Ar), indicate relatively weak Co–gas interactions compared to those characterized in molecular complexes. To place these values into context, –Δh _ad for CO in Co₂(dobdc) is about one third of the bond dissociation energy for the first CO in CpCo(CO)₂ (148(2) kJ mol^–1; Cp^– = cyclopentadienyl).¹⁰⁸

Fig. 4. Low-pressure gas adsorption isotherms for CO (yellow),⁴⁰ CO₂ (green),²⁹ CH₄ (gray), N₂ (dark blue), O₂ (red), and Ar (light blue) at 298 K (left). High-pressure gas adsorption isotherms for CO (yellow),⁴⁰ CO₂ (green), CH₄ (gray), N₂(dark blue), and Ar (light blue) at 298 K (right). The filled circles and solid lines represent experimental data and corresponding Langmuir fits, respectively.

Table 1. Co–X_gas distances and differential enthalpies of adsorption (Δh _ad) of CO, CO₂, CH₄, N₂, O₂, and Ar in Co₂(dobdc).

Gas	d(Co–Xgas) (Å)	Δd a (Å)	–Δh ad b (kJ mol–1)
CO	2.215(6) (Co–C)	–0.230(6)	48.8(2)40
CO2	2.261(9)29 (Co–O) c	–0.004(9)	33.6(1)29
N2	2.236(6) (Co–N)	–0.059(6)	20.3(6)
O2	2.216(5) (Co–O)	–0.049(5)	18.56(3)
CH4	2.941(19) (Co···C)	—	19.21(9)
Ar	2.932(9) (Co–Ar)	0.307(9)	17(1)

^aΔd = the Co–X_gas distance minus the sum of the ionic radius for high-spin cobalt(ii)¹⁰⁷ and the van der Waals radius of the coordinated atom. Δd was not calculated for CH₄ because the Co···C distance is between Co and the central atom of CH₄, not the coordinated hydrogen atoms, which makes it difficult to compare rigorously with the other gases.

^bLow-coverage differential enthalpies of adsorption were calculated at a loading of 0.5 mmol g^–1 using independent Langmuir fits to low-pressure adsorption isotherms.

^cAlthough the structure of CO₂ in Co₂(dobdc) was collected at a higher temperature (150 K) compared to the other structures (90 and 100 K), the Co–O_CO2 distance (2.23(4) Å) obtained at 10 K from powder neutron diffraction data shows that the Co–O_CO2 distance does not shorten significantly at lower temperatures.²⁹

The trend in –Δh _ad values, CO > CO₂ > N₂ > CH₄ > O₂ > Ar, shows no clear correlation with the Co–X_gas distances obtained by single-crystal X-ray diffraction. As an approximate method to account for differences in the van der Waals radii among coordinated atoms, the sum of the ionic radius for high-spin cobalt(ii) and the van der Waals radius of the coordinated atom can be subtracted from the Co–X_gas distances to give the parameter Δd. More negative values for Δd should correspond to stronger interactions. With the exception of CO₂ and CH₄, the trend in Δd is consistent with that of –Δh _ad. In the structure of CO₂ on Co₂(dobdc) (Fig. 1), CO₂ coordinated to the cobalt(ii) sites tilts towards one of the linker oxygen atoms to give a C_CO2···O distance of 3.29(7) Å.²⁹ This indicates that both direct interaction of CO₂ with the metal site and weak secondary interactions contribute to its enthalpy of adsorption. Conceivably, these additional interactions cause CO₂ to be an outlier in the trend between Δd and –Δh _ad. Care should be exercised, however, in inferring relative binding strengths by comparing crystallographic distances. Overall, these results show that multiple factors contribute to the binding energy of a molecule and that interaction distances alone cannot adequately represent all of these factors, especially when considering different molecules. More reliable correlations can be drawn if distances are compared between the same molecule interacting with the same metal center.

The high-pressure adsorption isotherms for CO, CO₂, CH₄, N₂, and Ar at 298 K (Fig. 4) show that secondary adsorption sites become relevant at higher pressures, as the uptake for all gases eventually exceeds one gas molecule per cobalt site with increasing pressure. Qualitative comparison of the isotherms suggests that the secondary adsorption sites for CO₂ have the highest binding affinity with an uptake of ∼2 CO₂ molecules per Co at 40 bar. This likely results from the favorable interaction between the partial positive charge on the CO₂ carbon atom with linker oxygen atoms in the framework and intermolecular interactions between neighboring CO₂ molecules (Fig. S2†). In contrast, CO, CH₄, N₂, and Ar have less pronounced adsorption at high pressures, with each showing an uptake of less than 1.5 molecules of gas per Co at 40 bar. Perhaps the most striking comparison lies between CO and CO₂. As a polar molecule, CO has a stronger interaction with the cobalt(ii) sites in the framework, which is clearly evident in its steeper low-pressure isotherm and more negative differential enthalpy of adsorption. At pressures beyond 0.55 bar, however, Co₂(dobdc) adsorbs significantly larger amounts of CO₂, demonstrating that distinct adsorption sites within a material can have considerably different selectivities depending on the nature of the gases adsorbed.

Conclusions

The foregoing results highlight the unique advantages of metal–organic frameworks as robust crystalline matrices that facilitate unhindered access of guest molecules, enabling for example the study of guest interactions with open metal coordination sites within the framework pores. Rigorously air-free gas-dosing methods were developed to overcome the challenges associated with studying weakly binding gases in single crystals. Through these methods, the interaction of CO, CH₄, N₂, O₂, Ar, and P₄ with the metal–organic framework Co₂(dobdc) were directly observed by single-crystal X-ray diffraction. The resulting structures reveal the location of the primary, secondary (for N₂, O₂, and Ar) and tertiary (for O₂) binding sites for these gases within the framework. Moreover, examination of the Co^II–gas distances shows that these Co^II–gas interactions are distinctly weak compared to those found in molecular complexes. These unique interactions arise from the square pyramidal coordination geometry and the high-spin electronic configuration enforced by the framework on cobalt(ii). As a result, this work represents the first report of the structural characterization of such species by single-crystal X-ray diffraction. Finally, differential enthalpies of adsorption determined from low-pressure gas adsorption isotherms corroborate the weak binding affinities inferred from the relatively long Co^II–gas distances observed in the single-crystal structures, while high-pressure gas adsorption isotherms at 298 K show significant contribution from secondary binding sites at pressures beyond 1 bar. Altogether, these results establish in situ single-crystal X-ray diffraction as a valuable technique, which imparts not only a practical understanding of gas adsorption in porous materials, but also new insights into the underlying interactions that give rise to their adsorption behavior.

Ongoing efforts are focused on developing in situ single-crystal X-ray diffraction methods that can be routinely employed in the evaluation of metal–organic frameworks for specific applications, such as gas separations and gas storage. In particular, techniques are being explored to enable (i) mounting crystals that decompose in air, (ii) systematic determination of the dependence of site occupancies for multiple binding sites on guest loading, (iii) collection of diffraction data at lower temperatures to lessen thermal disorder, and (iv) structural assessment of the absorptive properties of these materials in the presence of gas mixtures. Furthermore, it can be envisioned that these techniques can be used to isolate and observe reactive intermediates in metal–organic frameworks, providing a way to determine the structures of species that have only been amenable to characterization by spectroscopy.