Functional Joint Model for Longitudinal and Time-to-Event Data: An Application to Alzheimer’s Disease

Abstract

Functional data are increasingly collected in public health and medical studies to better understand many complex diseases. Besides the functional data, other clinical measures are often collected repeatedly. Investigating the association between these longitudinal data and time to a survival event is of great interest to these studies. In this article, we develop a functional joint model (FJM) to account for functional predictors in both longitudinal and survival submodels in the joint modeling framework. The parameters of FJM are estimated in a maximum likelihood framework via EM algorithm. The proposed FJM provides a flexible framework to incorporate many features both in joint modeling of longitudinal and survival data and in functional data analysis. The FJM is evaluated by a simulation study and is applied to the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study, a motivating clinical study testing whether serial brain imaging, clinical and neuropsychological assessments can be combined to measure the progression of Alzheimer’s disease.

1 Introduction

Modern technologies are currently producing increasingly large, complex, and high-dimensional data in medical research. One such type of data is functional data, whose units of observation are functions defined on certain continuous domains (e.g., time, space, or both) but sampled on discrete grids. These functions may be defined on a one-dimensional Euclidean domain, such as growth curve data, heart rate monitor (HRM) data, and electroencephalogram (EEG) data. A growing volume of functional data are also collected on higher dimensional domains such as magnetic resonance imaging (MRI), positron emission tomography (PET), and functional MRI (fMRI). Moreover, prospective cohort studies and clinical trials investigating neurodegenerative diseases such as Alzheimer’s disease (AD) and Huntington’s disease (HD) often collect repeated measurements of clinical variables, event history, and functional data, which induce complex correlation structures among the observations. The emergence of new data types and structures brings rich source of information but also poses new challenges in methodology development of functional data analysis (FDA).

Function regression, especially functional predictor regression (scalar-on-function regression, models the relationship between a scalar outcome and functional predictors), is an active area of FDA in the past 10 years. It was first introduced by Ramsay & Dalzell [1] and built up by Ramsay & Silverman [2]. There is a rich literature in functional predictor regression [e.g., 3–10], while most existing work deals only with cross-sectional data. Goldsmith et al. [11] first extended the penalized functional regression approach [10] to handle longitudinal measurements in both the response variable and functional predictors by incorporating scalar random effects. Gertheiss et al. [12] extended the functional principal component regression (PCR) to longitudinal functional data and allowed for different effects of subject-specific curves. More recently, Gellar et al. [13] extended the Cox proportional hazards model to incorporate functional predictors and estimated the parameters via penalized partial likelihood approach. Lee et al. [14] developed a Bayesian functional Cox regression model with both functional and scalar covariates, but used different regularization methods. To the best of our knowledge, there is no functional regression modeling attempts to simultaneously analyze the longitudinal measurements and time-to-event data under the joint modeling framework.

Joint models of longitudinal and time-to-event data were proposed by Faucett & Thomas [15] and Wulfsohn & Tsiatis [16]. The principle is to define two submodels (a mixed effects submodel for the longitudinal outcome and a Cox submodel for the survival outcome) and link them using a common latent structure. This modeling approach analyzes the two types of outcomes simultaneously and is able to reduce the bias of parameter estimates and improve the efficiency of statistical inference. Tsiatis and Davidian [17] and Proust-Lima et al. [18] gave excellent review of joint modeling research. However, current state-of-the-art joint models do not incorporate functional predictors.

The major objective of this article is to incorporate the growing volume of functional data in the longitudinal-survival setting. Specifically, we develop a functional joint model (FJM), where outcomes consist of a longitudinal measure and a time-to-event variable, and the exposure variables include both scalar covariates and functional predictors. The rest of the article is organized as follows. In Section 2, we describe a motivating clinical study and the data structure. In Section 3, we discuss the joint longitudinal-survival model with functional predictors, and the estimation procedure. In Section 4, we apply the proposed FJM to the motivating Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. In Section 5, we conduct a simulation study to examine the performance of the proposed FJM. Concluding remarks and discussion is presented in Section 6.

2 A Motivating Clinical Study

The methodology development is motivated by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. The ADNI study was launched in year 2003 with the primary goal of testing whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), cerebrospinal fluid (CSF) markers, and neuropsychological assessments can be combined to measure the progression of AD. The phase one of the ADNI study (ADNI-1) recruited more than 800 adults, of which about 200 cognitively normal individuals, 400 mild cognitive impairment (MCI) patients, and 200 early AD patients. Participants were reassessed at 6, 12, 18, 24 and 36 months, and additional follow-ups were conducted annually as part of ADNI-2. At each visit, various neuropsychological assessments, brain image, and clinical measures were collected. Detailed information about the ADNI study procedures, including participant inclusion and exclusion criteria and complete study protocol can be found at http://www.adni-info.org.

Because MCI is commonly considered as a transitional stage between normal cognition and Alzheimer’s disease, numerous recent studies are to assess various neuroimaging techniques and clinical markers to predict AD diagnosis among MCI patients [e.g., 19]. To this end, we select 355 MCI patients in ADNI-1 study without missing data in covariates of interests, and consider AD diagnosis to be the survival event of interest. Participants were followed up for a mean of 3.2 years (SD 2.6; range 0.4–9.3) before AD diagnosis or censoring. Among the 355 MCI patients, 180 patients were diagnosed with AD and 175 had stable MCI over a mean follow-up period of 2.3 years and 4.2 years, respectively.

Alzheimer Disease Assessment Scale-Cognitive (ADAS-Cog) score (with 11 items, referred to as ADAS-Cog 11) measures cognition functions and it is usually reported as a composite score of the 11 items and it ranges from 0 to 70 (or 85), with a higher score indicating poor cognitive function. Figure 1 displays the lowess smoothing curve [20] of ADAS-Cog 11 scores over time for the MCI patients, with follow-up time less than 3 years (203 patients, solid line), 3–6 years (82 patients, dotted line), and more than 3 years (70 patients, dashed line), in addition to 95% pointwise confidence intervals (shaded regions). Figure 1 suggests that the ADAS-Cog 11 scores of patients in all three groups increase with time (deteriorating cognitive functions). Moreover, patients with shorter follow-up time tend to have higher ADAS-Cog 11 scores, indicating that patients with more severe cognitive impairment were more likely to progress to AD. This phenomenon manifests strong correlation between the longitudinal ADAS-Cog 11 values and the time to AD diagnosis. Such a dependent terminal event time is often referred to as “dependent censoring” or “informative censoring” in the literature of joint modeling [21]. However, many studies [22, 23] designed to explore longitudinal measures for predicting future cognitive functions of MCI patients fail to account for such informative censoring, leading to biased inference.

Figure 1.

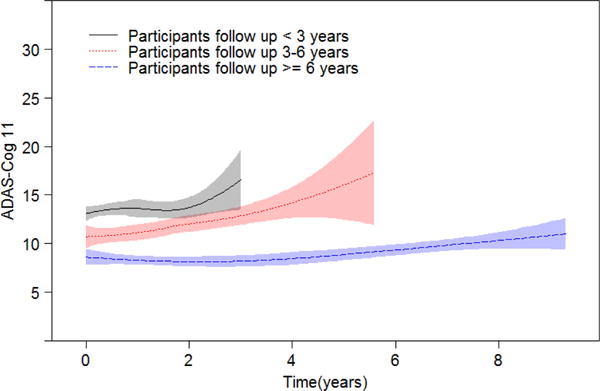
Smoothing curves of variable ADAS-Cog 11 over time for MCI patients with follow-up time less than 3 years (203 patients, solid line), 3–6 years (82 patients, dotted line), and more than 6 years (70 patients, dashed line). Shaded regions are 95% pointwise confidence intervals.

Moreover, degree of atrophy within the medial temporal lobe structures, especially within the hippocampus, was reported to be associated with the AD progression. Most of the current analysis was based on volumetric brain MRI data. For example, AD patients and MCI patients have been shown to have 27% and 11% smaller hippocampal volumes, respectively, as compared with normal age-matched elderly [24]. In the preliminary analysis, we fit regular joint models with baseline MRI imaging measure including bilateral hippocampal volume as a scalar covariate. The results (detailed in the Web Supplement) suggest that hippocampal volume has strong association with both cognitive function decline and time to AD diagnosis. Furthermore, some researches [25–28] demonstrated that the surface-based morphology analysis offers more advantages because these methods study patterns of hippocampal subfield atrophy and produce detailed pointwise correlation between atrophy and cognitive functions.

In this article, we propose a functional joint model (FJM) to examine the association between the longitudinal ADAS-Cog 11 score and the time to AD diagnosis, accounting for the clinical co-variates and MRI imaging measures. We include as a functional predictor the hippocampal radial distance (HRD) of each bilateral hippocampal surface point (referred to as vertex), which measures the distance from the medial core to each vertex on the surface and represents the hippocampal thickness. For image processing, we adopt a surface fluid registration package [29]. The left and right hippocampal surfaces are first conformally mapped to a two-dimensional (2D) rectangle plane, in the form of matrix, to form a feature image of the surface. After registering each feature image to a common template and calculating HRD for all vertexes, the 2D image matrices are vectorized into one-dimensional (1D) image vectors. The spatial information and image smoothing has been accounted for in part in the image preprocessing steps as described in Shi et al [29]. Our focus here is to propose methodology that is applicable to a wide variety of imaging and non-imaging functional data. To this end, the corresponding hippocampal radial distances of the vertexes are represented as a 1D functional data defined on domain S. Each point in the image vector retains a one-to-one relationship to the original vertex on the surface, which allows us to back-transform any functions defined on domain S to the hippocampal surfaces. The hippocampus image processing procedure is detailed in the Web Supplement.

3 Functional Joint Model

We introduce a general functional joint model (FJM) framework for a longitudinal process and a time-to-event process with time-invariant functional predictors. For the ease of illustration, we only incorporate a single time-invariant (baseline) functional predictor in both the longitudinal and survival submodels, while the FJM can readily accommodate multiple functional predictors.

3.1 Functional joint model framework

For each subject i (i = 1, …, I) at visit j (j = 1, …, J_i), we observe data $\{y_{ij},{\mathit{x}}_{ij},g_i^{(x)}(s)\}$, where y_ij = y_i(t_ij) is a scalar outcome recorded at time t_ij from the study onset. Vector x_ij is a p-dimensional covariate vector. Function $g_i^{(x)}(s)$ is a time-invariant functional predictor defined over a 1D domain s ∈ [0, S_max] = S. The longitudinal submodel is

$$y_i(t_{ij})=m_i(t_{ij})+{\epsilon }_{ij},\text{where }{m}_i(t_{ij})={\beta }_0+{\mathit{x}}_{ij}^{\top }\mathit{\beta }+{\displaystyle {\int }_{\mathit{S}}{g}_i^{(x)}(s)B^{(x)}(s)ds+z_{ij}^{\top }{\mathit{u}}_i}$$ (1)

is the unobserved true value of the longitudinal outcome at time t_ij, β₀ is the intercept, and β is the regression coefficient vector. Coefficient function B^(x)(s) (defined on the same domain as $g_i^{(x)}(s)$) determines a pointwise association between $g_i^{(x)}(s)$ and y_i(t_ij). Vector z_ij is a q dimensional covariates corresponding to random effects u_i, which is assumed to have u_i ~ N(0, Σ_u) to account for the within-subject correlation. The measurement error ${\epsilon }_{ij}~N(0,{\sigma }_{\epsilon }^2)$ is independent from u_i.

The event history is recorded for each subject i with observed event time $T_i=\mathit{\text{min}}(T_i^{\ast },C_i)$ and the event indicator ${\delta }_i=I(T_i^{\ast }\le C_i)$, where $T_i^{\ast }$ and C_i are the true event time and censoring time, respectively. The survival submodel is

$$h(t)=h_0(t)\text{exp}\{{\mathit{w}}_i^{\top }\gamma +{\displaystyle {\int }_{\mathit{S}}{g}_i^{(w)}(s)B^{(w)}(s)ds+\alpha m_i(t)}\},$$ (2)

where h₀(t) is the baseline hazard function, and w_i is a vector of time-independent covariates with regression coefficient vector γ. Functional predictor $g_i^{(w)}(s)$ may be the same or different from its counterpart $g_i^{(x)}(s)$ in model (1). Functional log hazard ratio B^(w)(s) measures the overall contribution of $g_i^{(w)}$ towards the event hazard. The association parameter α quantifies the strength of correlation between the unobserved true longitudinal function m_i(t) and the event hazard at the same time point. Models (1) and (2) consist of the functional joint model (FJM) framework.

3.2 Functional regression

To build the functional regression model, we follow the general strategy of functional principal component regression (FPCR; e.g., [4, 8]). We first express the time-invariant functional predictor $g_i^{(x)}(s)$ in model (1) using the Karhunen-Loève decomposition. Let μ^(x)(s) be the mean of $g_i^{(x)}(s)$ and ${\sum }^{(x)}(s,s^{\prime })=\mathit{\text{cov}}\{g_i^{(x)}(s),g_i^{(x)}(s^{\prime })\}$ be the covariance function between two locations (s and s′) of the functional predictor. The spectral decomposition of the covariance function is given by ${\sum }^{(x)}(s,s^{\prime })={\displaystyle {\sum }_{l=1}^{\infty }{\lambda }_l^{(x)}{\varphi }_l^{(x)}(s){\varphi }_l^{(x)}(s^{\prime })}$, where ${\lambda }_1^{(x)}\ge {\lambda }_2^{(x)}\ge \cdots \ge 0$ are non-increasing eigenvalues and ${\varphi }_l^{(x)}(s)’\mathrm{s}$ are the corresponding orthonormal eigenfunctions. The Karhunen-Loève expansion of $g_i^{(x)}(s)$ is

$$g_i^{(x)}(s)={\mu }^{(x)}(s)+{\displaystyle \sum _{l=1}^{\infty }{\xi }_{il}^{(x)}{\varphi }_l^{(x)}(s)},$$

where the functional principal component (FPC) scores ${\xi }_{il}^{(x)}={\displaystyle {\int }_{\mathit{S}}\{g_i^{(x)}(s)-{\mu }^{(x)}(s)\}{\varphi }_l^{(x)}(s)ds}$ are uncorrelated random variables with mean zero and variance ${\lambda }_l^{(x)}$. In practice, we adopt a truncated approximation for $g_i^{(x)}(s)$ given by $g_i^{(x)}(s)\approx {\mu }^{(x)}(s)+{\displaystyle {\sum }_{l=1}^{K_x}{\xi }_{il}^{(x)}{\varphi }_l^{(x)}(s)}$. The number of components K_x can be determined using the proportion of explained variance (PEV). Specifically, K_x may be chosen as the minimum number of functional principal components such that ${\displaystyle {\sum }_{l=1}^{K_x}{\widehat{\lambda }}_l^{(x)}}/{\displaystyle {\sum }_{l=1}^{\infty }{\widehat{\lambda }}_l^{(x)}}\ge L$, where L is a pre-specified PEV, e.g., L = 80%, 90%, or 95%.

In the second step, we use the first K_x eigenfunctions as the basis functions to expand the coefficient function B^(x)(s) in model (1) as $B^{(x)}(s)={\displaystyle {\sum }_{l=1}^{K_x}{B}_l^{(x)}{\varphi }_l^{(x)}(s)}$, where the coefficient $B_l^{(x)}={\displaystyle {\int }_{\mathit{S}}{B}^{(x)}}(s){\varphi }_l^{(x)}(s)ds$. We let vector of FPC scores ${\mathit{\xi }}_i^{(x)}={[{\xi }_{i1}^{(x)},\dots ,{\xi }_{i{K}_x}^{(x)}]}^{\top }$, vector of eigenfunctions ${\varphi }^{(x)}(s)={[{\varphi }_1^{(x)}(s),\dots ,{\varphi }_{K_x}^{(x)}(s)]}^{\top }$, and vector of coefficients ${\mathit{B}}^{(x)}={[B_1^{(x)},\dots ,B_{K_x}^{(x)}]}^{\top }$. Then we have

$$\begin{array}{l}{\displaystyle {\int }_{\mathit{S}}{g}_i^{(x)}(s)B^{(x)}ds}\approx {\displaystyle {\int }_{\mathit{S}}{\mu }^{(x)}(s)B^{(x)}(s)ds+{\displaystyle {\int }_{\mathit{S}}{({\mathit{\xi }}_i^{(x)})}^{\top }{\varphi }^{(x)}(s){\varphi }^{(x)}{(s)}^{\top }{\mathit{B}}^{(x)}ds}}\\ ={\displaystyle {\int }_{\mathit{S}}{\mu }^{(x)}(s)B^{(x)}(s)ds}+{({\mathit{\xi }}_i^{(x)})}^{\top }{\displaystyle {\int }_{\mathit{S}}{\varphi }^{(x)}(s){\varphi }^{(s)}{(s)}^{\top }ds{B}^{(x)}-{\displaystyle {\int }_{\mathit{S}}{\mu }^{(x)}(s)B^{(x)}(s)ds+{(B_i^{(x)})}^{\top }{\mathit{B}}^{(x)}}}.\end{array}$$

Note that ∫_S ϕ^(x)(s)ϕ^(x)(s)^⊤ds = I, where I is an identity matrix, because the eigenfunctions ${\varphi }_l^{(x)}(s)’\mathrm{s}$ are orthonormal.

Similarly, the functional predictor g^(w)(s) in model (2) can be expressed as $g_i^{(w)}(s)\approx {\mu }^{(w)}(s)+{\displaystyle {\sum }_{l=1}^{K_w}{\xi }_{il}^{(w)}{\varphi }_l^{(w)}(s)}$ and thus ${\displaystyle {\int }_{\mathit{S}}{g}^{(w)}(s)B^{(w)}(s)ds\approx {\displaystyle {\int }_{\mathit{S}}{\mu }^{(w)}(s)B^{(w)}(s)ds+{({\mathit{\xi }}_i^{(w)})}^{\top }{\mathit{B}}^{(w)}}}$, where μ^(w)(s), ${\xi }_{il}^{(w)}$, ${\varphi }_l^{(w)}(s)$, and B^(w) have the same meanings as μ^(x)(s), ${\xi }_{il}^{(w)}$, ${\varphi }_l^{(x)}(s)$ and B^(x), respectively. Thus, the FJM based on the FPC scores is

$$y_i(t)=m_i(t)+{\epsilon }_{ij},\text{where }{m}_i(t)={\beta }_0^{\prime }+{\mathit{x}}_{ij}^{\top }\mathit{\beta }+{({\mathit{\xi }}_i^{(x)})}^{\top }{\mathit{B}}^{(x)}+z_{ij}^{\top }{\mathit{u}}_i,$$ (3)

and

$$h(t)=h_0^{\ast }(t)\text{exp}\{{\mathit{w}}_i^{\top }\gamma +{({\mathit{\xi }}_i^{(w)})}^{\top }{\mathit{B}}^{(w)}+\alpha m_i(t)\},$$ (4)

where ${\beta }_0^{\prime }={\beta }_0+{\displaystyle {\int }_{\mathit{S}}{\mu }^{(x)}(s)B^{(x)}(s)ds}$ and $h_0^{\ast }(t)=h_0(t)\text{exp}\left\{{\displaystyle {\int }_{\mathit{S}}{\mu }^{(w)}(s)B^{(w)}(s)ds}\right\}$. For notational ease and without ambiguity, we replace the approximation sign (≈) by the equal sign. Note that models (3) and (4) are similar to a linear mixed model for the longitudinal scalar response variable and a Cox model for the survival outcome, respectively, in a standard joint model framework [16]. And FPC scores ${\mathit{\xi }}_i^{(x)}$ and ${\mathit{\xi }}_i^{(w)}$ can be treated as scalar covariates. Similar to mixed models, our FJM can readily handle unbalanced data in the longitudinal measurement of y_i(t).

Let $\mathit{\theta }={[{\mathit{\beta }}^{\top },{({\mathit{B}}^{(x)})}^{\top },\text{vech}{({\sum }_u)}^{\top },{\gamma }^{\top },{({\mathit{B}}^{(w)})}^{\top },\alpha ,{\sigma }_{\epsilon }^2,{\mathit{\theta }}_{h_0^{\ast }}^{\top }]}^{\top }$ be the parameter vector, where vech(Σ_u) is the vector being formed by vectorizing the lower triangular part of covariance matrix Σ_u, vector ${\mathit{\theta }}_{h_0^{\ast }}$ denotes the parameters in the baseline hazard function $h_0^{\ast }(·)$. The conditional likelihood from the longitudinal data ${\mathit{y}}_i={[y_{i1},\cdots ,y_{i{J}_i}]}^{\top }$ is

$$p({\mathit{y}}_i|\mathit{\theta },{\mathit{u}}_i)={(2\pi {\sigma }_{\epsilon }^2)}^{-J_i/2}\text{exp}\left\{-\frac{1}{2{\sigma }_{\epsilon }^2}{\displaystyle \sum _{j=1}^{J_i}{\left[y_{ij}-({\beta }_0^{\prime }+{\mathit{x}}_{ij}^{\top }\mathit{\beta }+{({\mathit{\xi }}_i^{(x)})}^{\top }{\mathit{B}}^{(x)}+z_{ij}^{\top }{\mathit{u}}_i)\right]}^2}\right\},$$

and the density function of the random effects u_i is $p({\mathit{u}}_i|\mathit{\theta })={(2\pi )}^{-q/2}{|{\sum }_u|}^{-1/2}\text{exp}(-\frac{1}{2}{\mathit{u}}_i^{\top }{\displaystyle {\sum }_u^{-1}{\mathit{u}}_i}),$ where q is the dimension of the covariance matrix Σ_u. The conditional likelihood from the survival data is

$$p(T_i,{\delta }_i,|\mathit{\theta },{\mathit{u}}_i)=h_i{(T_i|\mathit{\theta },{\mathit{u}}_i)}^{{\delta }_i}{S}_i(T_i|\mathit{\theta },{\mathit{u}}_i)=h_i{(T_i|\mathit{\theta },{\mathit{u}}_i)}^{{\delta }_i}\text{exp}\left[-{\displaystyle {\int }_0^{T_i}{h}_i(t|\mathit{\theta },{\mathit{u}}_i)dt}\right],$$

where $h_i(T_i|\mathit{\theta },{\mathit{u}}_i)=h_0^{\ast }(T_i)\text{exp}\{{\mathit{w}}_i^{\top }\mathit{\gamma }+{({\mathit{\xi }}_i^{(w)})}^{\top }{\mathit{B}}^{(w)}+\alpha m_i(T_i)\}$, and function $h_0^{\ast }(·)$ can be approximated by a piecewise-constant function or a B-spline function.

Under the local independence assumption (i.e., conditional on the random effects vector u_i, all components in y_i and T_i are independent), the joint likelihood function is

$$L(\mathit{\theta })={\displaystyle \prod _{i=1}^{I}p({\mathit{y}}_i,T_i,{\delta }_i|\mathit{\theta })={\displaystyle \prod _{i=1}^I{\displaystyle \int p({\mathit{y}}_i|\mathit{\theta },{\mathit{u}}_i)p(T_i,{\delta }_i,|\mathit{\theta },{\mathit{u}}_i)p({\mathit{u}}_i|\mathit{\theta })d{\mathit{u}}_i}}}.$$ (5)

3.3 Estimation and inference

In practice, the functional predictors such as $g_i^{(x)}(s)$ are measured over finite grids in domain S and often with error, i.e., the observed functional predictor $g_i^{(x^{\prime })}(s)=g_i^{(x)}(s)+{\epsilon }_i(s)$, where measurement error ${\epsilon }_i(s)~N(0,{\sigma }_{\epsilon }^2)$. The mean function μ^(x)(s) is estimated by ${\widehat{\mu }}^{(x)}(s)={\displaystyle {\sum }_{i=1}^I{g}_i^{(x^{\prime })}(s)/I}$, and the empirical covariance function is estimated by $$\begin{gathered} {\widehat{\sum }}^{(x)}(s,s^{\prime })={\sum }_{i=1}^I\{g_i^{(x^{\prime })}(s)-{\widehat{\mu }}^{(x)}(s)\} \\ \{g_i^{(x^{\prime })}(s^{\prime })-{\widehat{\mu }}^{(x)}(s^{\prime })\}/(I-1) \end{gathered}$$. We apply kernel smoothing to the off-diagonal elements of ${\widehat{\sum }}_x(s,s^{\prime })$ to remove the effects from measurement errors [30, 31]. Then the estimated eigenvalues ${\widehat{\lambda }}_l^{(x)}$ and the corresponding estimated eigenfunctions ${\widehat{\varphi }}_l^{(x)}(s)$, where l = 1, …, S_max, are calculated based on the decomposition of the smoothed covariance function. Finally, the estimated FPC scores for each subject are calculated as ${\widehat{\xi }}_{ij}^{(x)}={\displaystyle {\int }_{\mathit{S}}\{g_i^{(x^{\prime })}(s)-{\widehat{\mu }}^{(x)}(s)\}{\widehat{\varphi }}_l^{(x)}(s)ds}$, and the integral can be approximated by the Riemann sum. We choose the first K_x estimated eigenfunctions and FPC scores, and denote them as ${\widehat{\varphi }}^{(x)}(s)={[{\widehat{\varphi }}_1^{(x)}(s),\dots ,{\widehat{\varphi }}_{K_x}^{(x)}(s)]}^{\top }$ and ${\widehat{\mathit{\xi }}}_i^{(x)}={[{\widehat{\xi }}_{i1}^{(x)},\dots ,{\widehat{\xi }}_{i{K}_x}^{(x)}]}^{\top }$, respectively.

Maximization of the likelihood function in model (5) with respect to parameter vector θ can be performed using Expectation Maximization (EM) algorithm. More details regarding the EM algorithm implementation are given in the Web Supplement. Based on the estimated coefficient vector ${\widehat{\mathit{B}}}^{(x)}$, the estimated coefficient function is calculated by ${\widehat{B}}^{(x)}(s)={({\widehat{\mathit{B}}}^{(x)})}^{\top }{\widehat{\varphi }}^{(x)}(s)$. A pointwise 95% confidence interval for B^(x)(s) can be constructed based on D (e.g., D = 1,000) bootstrap samples [32], e.g., at location s, a 95% bootstrap confidence interval for B^(x)(s) can be $[{\widehat{q}}_{B,0.0025}(s),{\widehat{q}}_{B,0.975}(s)]$ where ${\widehat{q}}_{B,p}(s)$ is the p-quartile of the bootstrap samples ${\widehat{B}}_d^{(x)}(s)$, d = 1, ⋯, D. Alternatively, a Wald-type confidence interval based on the standard deviation of the bootstrap estimates, ${\widehat{s}}_B(s)$, is given by ${\widehat{B}}^{(x)}(s)\pm 1.96{\widehat{s}}_B(s)$. These two types of bootstrap confidence intervals give very similar results in our simulation study. Similarly, the estimated coefficient function ${\widehat{B}}^{(w)}(s)$ and its confidence interval can be obtained. For visualization in the ADNI study, we can map the coefficient function ${\widehat{B}}^{(x)}(s)$ back to the hippocampal surfaces, because there is an one-to-one relationship between the location s in domain S and the vertex on the hippocampal surfaces.

3.4 Implementation using software

An advantage of the proposed FJM is that its implementation can be done using available standard software. The first step is to conduct FPCA for functional predictors and to estimate the FPC eigenfunctions and scores, using fpca.sc function in the refund package [33] or fpca.mle and fpca.score functions in the FPCA package [34] in R. In the second step, FPC scores are used as scalar covariates in a standard joint model for longitudinal and survival data and their coefficients can be estimated using JM package [35] in R. The estimated coefficient function can be calculated as weighted sum of FPC eigenfunctions. In addition, we have fitted the proposed FJM via our own code and have obtained the estimation results very close to those from the aforementioned packages. To facilitate easy reading and implementation of the proposed FJM, we provide in the Web Supplement the R codes to conduct FPCA, and to fit the FJM using either the JM package or our estimation methods based on EM algorithm.

4 Application to the ADNI Study

We apply the proposed FJM to the motivating ADNI study. We include the following variables as scalar covariates: baseline age (bAge, mean: 74.4, SD: 7.3, range 55.1–89.3), gender (gender, 36.1% female), years of education (Edu, mean: 15.6, SD: 3.0, range 4–20), and presence of at least one apolipoprotein E allele (APOE–ε4, 56%), given their potential effects on AD progression [36–38]. To utilize the brain imaging information, we include baseline hippocampal volume (bHV) as a scalar covariate and the baseline hippocampal surfaces based on hippocampal radial distance (HRD) as a functional predictor. We follow the procedure in the Web Supplement to convert the 3D HRD to a 1D domain denoted by S.

The first model we consider is the regular joint model (refer to as model JM, identified in the preliminary analysis in Section 2), which incorporates variable bHV in both longitudinal and survival submodels. Additionally, we consider three FJMs, i.e., model FJM1 includes HRD only in the longitudinal submodel and model FJM2 includes HRD only in the survival submodel, while model FJM3 includes HRD in both submodels as

$$\begin{array}{l}\mathit{\text{ADAS}}-Co{g}_i(t_{ij})=m_i(t_{ij})+{\epsilon }_{ij}\\ m_i(t_{ij})={\beta }_0+{\beta }_1{t}_{ij}+{\beta }_2{\mathit{\text{gender}}}_i+{\beta }_{3}b{\mathit{\text{Age}}}_i+{\beta }_{4}Ed{u}_i+{\beta }_5\mathit{\text{APOE}}+{\beta }_{6}bH{V}_i\\ +{\displaystyle {\int }_{\mathit{S}}HR{D}_i(s)B^{(x)}(s)ds+u_{1i}+u_{2i}{t}_{ij}}\\ h(t)=h_0(t)\text{exp}\{{\gamma }_1{\mathit{\text{gender}}}_i+{\gamma }_{2}b{\mathit{\text{Age}}}_i+{\gamma }_{3}Ed{u}_i+{\gamma }_4\mathit{\text{APOE}}-\epsilon 4\\ +{\gamma }_{5}bH{V}_i+{\displaystyle {\int }_{S}HR{D}_i(s)B^{(w)}(s)ds+\alpha m_i(t)\}.}\end{array}$$

We perform functional principal component analysis (FPCA) on HRD and select the first 20 FPCs which explain 82.6% of the total variance in the hippocampus radial distance data. Baseline hazard function h₀(t) is approximated by a piecewise constant function. Specifically, the observed survival time is divided into M = 7 intervals by every 1/Mth quantiles. We have also explored other selections of M and obtained very similar results.

Table 1 displays the values of Akaike information criterion (AIC) from the four candidate models. The FJM1 and FJM3 have smaller AIC than model JM, suggesting that including HRD as a functional predictor in the longitudinal submodel may improve the model fit. Model FJM1 is selected as the final model because it has the smallest AIC value. This may indicate that after adjustment of hippocampal volume and other covariates, HRD remains an important functional predictor for the cognitive functions manifested by variable ADAS-Cog 11 among the MCI patients. The HRD may not be significantly associated with the time to AD diagnosis, because FJM2 has the largest AIC.

Table 1.

Akaike information criterion (AIC) from four candidate models in the ADNI study

	JM	FJM1	FJM2	FJM3
AIC	10211	10202	10217	10208

Parameter estimates from model FJM1 are presented in Table 2, while the estimated vector of coefficients ${\widehat{\mathit{B}}}^{(x)}$ (for a vector of 20 FPC scores ${\mathit{\xi }}_i^{(x)}$ as in model (3)) are presented in Web Table 3. ADAS-Cog 11 score increases (deteriorates) as time progresses, i.e., an average increase of 1.006 unit (95% CI: [0.881–1.131]) per year for MCI patients. Higher education, lack of APOE-ε4 allele(s), and larger hippocampal volume at baseline are associated with lower (better) ADAS-Cog 11 scores. Moreover, Web Table 3 suggests that the coefficients for eight FPC scores are significant (p < 0.05), indicating that the baseline hippocampal radial distance (HRD) is associated with the ADAS-Cog 11 score at all visits. In the survival submodel, the presence of APOE-ε4 allele(s) increases the hazard of AD diagnosis by 44%(exp(0.364) − 1, 95% CI: [4%–100%]), which is consistent with the literature [39]. Older age and larger hippocampal volume at baseline are associated with lower risk of AD diagnosis. Furthermore, larger ADAS-Cog 11 score increases the risk of AD diagnosis, i.e., one unit increase in ADAS-Cog 11 score increases the hazard of AD diagnosis by 11% (exp(0.107) − 1, 95% CI: [8%–15%]).

Table 2.

ADNI data analysis results from model FJM1.

	Parameters	MLE	SE	p
For longitudinal outcome
ADAS-Cog 11	Time (Years)	1.006	0.064	<0.001
	Female	−0.227	0.375	0.546
	bAge	−0.259	0.177	0.143
	Edu (years)	−0.248	0.051	<0.001
	APOE-ε4	1.090	0.278	<0.001
	bHV (mm3)	−0.954	0.201	<0.001
For survival process
MCI to AD	Female	−0.203	0.168	0.227
	bAge	−0.165	0.087	0.059
	Edu (years)	−0.002	0.026	0.951
	APOE-ε4	0.364	0.168	0.030
	bHV (mm3)	−0.300	0.091	<0.001
	α	0.107	0.015	<0.001

Table 3.

Parameter estimation in simulation Setting I.

	n=200, CR= 0.3					n=500, CR=0.3
	Bias	AMSE	SE	SD	CP	Bias	AMSE	SE	SD	CP
For longitudinal data
β1 = 0.78	<0.001	<0.001	0.002	0.002	0.970	<0.001	<0.001	0.001	0.002	0.940
B(x)(s) = 2 sin(πs/5)		0.008					0.003
${\sigma }_{\epsilon }^2=1$	<0.001	<0.001	0.030	0.028	0.965	0.007	<0.001	0.019	0.022	0.920
${\sigma }_u^2=1$	0.052	0.017	0.130	0.121	0.970	0.005	0.009	0.081	0.092	0.950
For survival data
γ1 = −1.75	0.077	0.060	0.219	0.233	0.930	0.012	0.027	0.152	0.163	0.940
α = 0.29	0.012	<0.001	0.021	0.022	0.940	0.003	<0.001	0.013	0.016	0.925
B(w)(s) = 1.2 sin(πs/4)		0.023					0.012
	n=200, CR=0.5					n=500, CR=0.5
	Bias	AMSE	SE	SD	CP	Bias	AMSE	SE	SD	CP
For longitudinal data
β1 = 0.78	<0.001	<0.001	0.002	0.002	0.930	<0.001	<0.001	0.001	0.001	0.985
B(x)(s) = 2 sin(πs/5)		0.007					0.003
${\sigma }_{\epsilon }^2=1$	0.002	0.001	0.030	0.030	0.955	<0.001	<0.001	0.019	0.017	0.960
${\sigma }_u^2=1$	0.044	0.019	0.130	0.130	0.955	0.016	0.007	0.081	0.083	0.940
For survival data
γ1 = −1.75	0.115	0.082	0.255	0.262	0.950	0.043	0.021	0.154	0.160	0.950
α = 0.29	0.019	0.001	0.024	0.025	0.920	0.008	<0.001	0.015	0.015	0.915
B(w)(s) = 1.2 sin(πs/4)		0.031					0.010

The coefficient function B^(x)(s) is estimated via ${\widehat{B}}^{(x)}(s)={\displaystyle {\sum }_{l=1}^{20}{\widehat{B}}_l^{(x)}}{\widehat{\varphi }}_l(s)$. For visualization purpose, each point in the 1D domain S, along with the coefficient function on that point, are mapped back to the corresponding vertex on the hippocampal surfaces (Figure 2). Due to the difficulty of displaying a 3D object on paper, Figure 2 only displays two views (from top and bottom) of left and right hippocampal surfaces. Panel (a) displays a schematic representation of the hippocampal subfields defined by Apostolova et al. [40], on the hippocampal surface template. Panel (b) displays the coefficient function ${\widehat{B}}^{(x)}(s)$ of the functional predictor HRD in the longitudinal submodel. Blue colors denote negative values of ${\widehat{B}}^{(x)}(s)$ in the regions. It suggests that the decrease of HRD (i.e., hippocampal atrophy) in the blue regions is associated with increasing ADAS-Cog 11 score and deteriorating cognitive functions. Most blue regions in Panel (b) are located in the CA1 subfield and subiculum (Sub) subfield displayed in Panel (a), suggesting that regional radial atrophy in these subfields may be a good predictor of AD progression among MCI patients. The similar point was made in the previous literature [40, 41].

Figure 2.

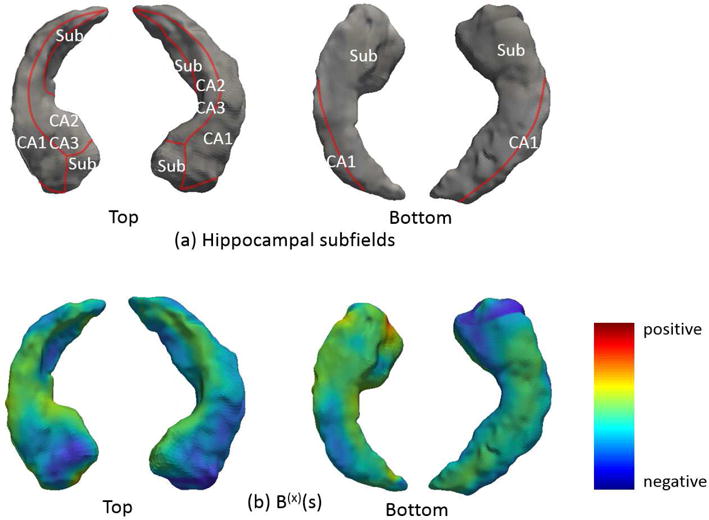
Hippocampal subfields mapped onto the hippocampal surfaces (Panel (a)) and the estimated coefficient function ${\widehat{B}}^{(x)}(s)$ from the longitudinal submodel, mapped onto the hippocampal surfaces (Panel (b)).

5 Simulation Study

In this section, we conduct a simulation study with two settings to evaluate the proposed FJM models. In Setting I, we include one functional predictor in both longitudinal and survival submodels, while in Setting II, we simulate a functional predictor and its coefficient which are similar to Section 4.

In Setting I, we select I = 200 or 500 subjects and each subject has J_i=4 measurements at time 0, 40, 80, and 120. The longitudinal submodel is

$$\begin{gathered} y_i(t_{ij})=m_i(t_{ij})+{\epsilon }_{ij}, \\ {m}_i(t_{ij})={\beta }_0+{\beta }_1{t}_{ij}+{\displaystyle {\int }_{\mathit{S}}{g}_i^{(x)}(s)B^{(x)}(s)ds+u_i}, \\ s\in [0,10]=\mathit{S}, \\ {g}_i^{(x)}(s)=u_{i1}+u_{i2}s \\ +{\displaystyle \sum _{k=1}^{10}\{{\nu }_{is1}\times \text{sin}(\frac{\pi k}{5}s)+{\nu }_{is2}\times \text{cos}(\frac{\pi k}{5}s)\}}, \end{gathered}$$

where j = 1, …, J_i, ${\epsilon }_{ij}~N(0,{\sigma }_{\epsilon }^2=1)$, $u_i~N(0,{\sigma }_u^2=1)$, u_i1 ~ U(0, 5), u_i2 ~ N(1, 0.2), and ν_is1, ν_is2 ~ N(0, 1/k²). The time-invariant functional predictor is defined on a 1D domain S = [0, 10], and it is observed on a discrete grid at location s = m/10, where m = 0, …, 100. The observed functional predictor $g_i^{(x^{\prime })}(s)=g_i^{(x)}(s)+{\epsilon }_i(s)$, where the measurement errors ε_i(s) ~ N(0, 0.1) across s. The coefficient function B^(x)(s) = 2 sin(πs/5). The survival submodel is

$$h(t)=h_0(t)\text{exp}\{{\gamma }_1{w}_1+{\displaystyle {\int }_{\mathit{S}}{g}_i^{(w)}(s)B^{(w)}(s)ds+\alpha m_i(t)}\}s\in [0,10]=\mathit{S},$$

where the baseline hazard function h₀(t) = 0.02, w₁ is simulated from Bernoulli distribution with probability being 0.5, and γ₁ = −1.75. Functional predictor $g_i^{(w)}(s)=g_i^{(x)}(s)$ and the observed functional predictor $g_i^{(w^{\prime })}(s)$ is generated in a similar fashion as $g_i^{(x^{\prime })}(s)$. The coefficient function B^(w)(s) = 1.2 sin(πs/4). Censoring times are independently simulated from a uniform distribution U(0, c), where c is chosen to achieve a desired censoring rate (CR) of 30% or 50%. Due to censoring, each subject has 2 to 3 repeated measurements. We perform FPCA to the simulated functional predictors $g_i^{(x^{\prime })}(s)$ and $g_i^{(w^{\prime })}(s)$, and choose the first 5 functional principal components which explain 95% of the total variance in the original data.

We generate 200 simulated datasets (denoted by subscript r) for each combination of sample sizes (I = 200 or 500) and censoring rates (30% or 50%). Table 3 presents the average mean squared error (AMSE) for the coefficient functions $\widehat{B}(·)$ and other parameters as $\mathit{\text{AMSE}}(\widehat{B}(.))=\frac{1}{200}{\displaystyle {\sum }_{r=1}^{200}{[{\widehat{B}}_r(s)-B(s)]}^2}$ and $\mathit{\text{AMSE}}({\widehat{\beta }}_1)=\frac{1}{200}{\displaystyle {\sum }_{r=1}^{200}{({\widehat{\beta }}_{1r}-{\beta }_1)}^2}$, respectively, in addition to standard error (SE, the square root of the average of the variance), standard deviation (SD, the standard deviation of the MLEs), and coverage probabilities (CP) of 95% confidence intervals. Table 3 suggests that in Setting I, the proposed FJM performs reasonable well with relatively small AMSE values for both coefficient functions and other parameters, SE being close to SD, and the confidence interval coverage probabilities being reasonably close to 95%.

Figure 3 displays the true coefficient functions B^(x)(s) and B^(w)(s) (red solid lines) and their estimated curves (black solid lines), along with the 95% pointwise confidence bands (shaded regions, constructed using Wald-type confidence intervals based on 1,000 bootstrap samples) and the 95% coverage probabilities. All panels suggest that the estimated coefficient functions from the FJM are reasonably close to the true coefficient functions, with 95% pointwise confidence intervals always covering the true functions. The empirical coverage probabilities on all regions over the domain S are close to the nominal level of 95%, except the rightmost tail of the coefficient function B^(w)(s) in the survival submodel. This may be because that B^(w)(s) is not well expanded by the first few principal components calculated from $g_i^{(w)}(s)$ on the rightmost tail. This limitation is further discussed in Section 6.

Figure 3.

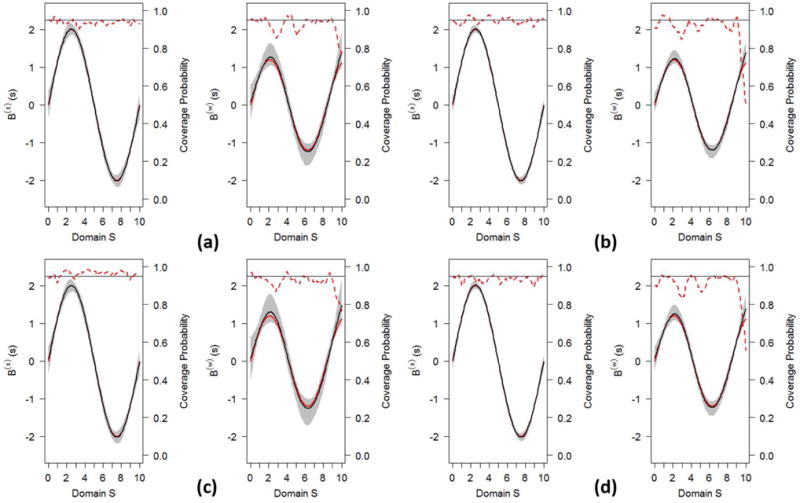
The FJM’s estimates of coefficient functions in Setting I. The true coefficient functions (red solid line) B^(x)(s) (left plot in each panel) and B^(w)(s) (right plot in each panel) and their estimates (black solid line), along with 95% confidence band (shaded region) and converge probability (red dotted line) with a reference line (horizontal line) at 0.95. Panel (a): I=200, CR=0.3; Panel (b): I=500, CR=0.3; Panel (c): I=200, CR=0.5; Panel (d): I=500, CR=0.5.

In Setting II, we keep the same parameters as in Setting I, but simulate a functional predictor which is mapped to a 3D bean surface to resemble the hippocampal surfaces. We evaluate the performance of our FJM when the 3D functional predictor is converted to a 1D vector, as described in the Web Supplement. To do this conversion, we first construct the triangular surface meshes of the bean surface, and then conformally map the triangular surface meshes to a rectangle plane. We align the points on the rectangle plane to form a 1D vector, but still retain the one-to-one correspondence with points on the original bean surface.

To generate the 1D functional predictor, we use the first 25 orthonormal eigenfunctions ϕ(s) = [ϕ₁(s), …, ϕ₂₅(s)]^⊤ and corresponding eigenvalues λ = [λ₁, …, λ₂₅]^⊤ that derived from the hippocampal radial distance in Section 4. The functional predictor for the ith subject g_i(s) is simulated by $g_i(s)={\displaystyle {\sum }_{l=1}^{25}{\xi }_{il}{\varphi }_l(s)}$, for i = 1, …, 400, where ξ_il is the subject-specific principle component score generated from a Normal distribution as ξ_il ~ N(0, λ_l), where l = 1, …, 25. Thus, the simulated functional predictor g_i(s) retains many features of the hippocampal radial distance. Next, we construct a two-dimensional (2D) coefficient function (coefficient image) on the rectangle plane to match the size of the bean surface using the densities of bivariate Normal distributions. Let

$$P_1~N\left[\begin{array}{cc}\left(\begin{array}{c}0.5\\ 0.3\end{array}\right),& \left(\begin{array}{cc}0.025& 0\\ 0& 0.015\end{array}\right)\end{array}\right]\text{and }{P}_2~N\left[\begin{array}{cc}\left(\begin{array}{c}0.7\\ 0.8\end{array}\right),& \left(\begin{array}{cc}0.03& -0.01\\ -0.01& 0.03\end{array}\right)\end{array}\right],$$

be density functions denoted by f_P1 and f_P2, respectively. The coefficient image is given by 0.8f_P1 − 1.0f_P2, and its 1D representation B(s) can be achieved by aligning points in the same order described above. After both functional predictor and its coefficient are transformed to 1D domain, the longitudinal and survival data are generated via the same method as in Setting I. We select an approximate censoring rate of 30% and generate 200 simulated datasets. Our objective is to estimate the coefficient image via estimating its 1D representation B(s) and mapping back to the 3D surfaces. Figure 4 displays the true and estimated coefficient functions mapped back to the bean surface. The close similarity of two figures indicates that the estimated coefficient function captures the main feature of the true coefficient function, suggesting the feasibility of our approach to transforming the high dimensional surface image to the 1D domain.

Figure 4.

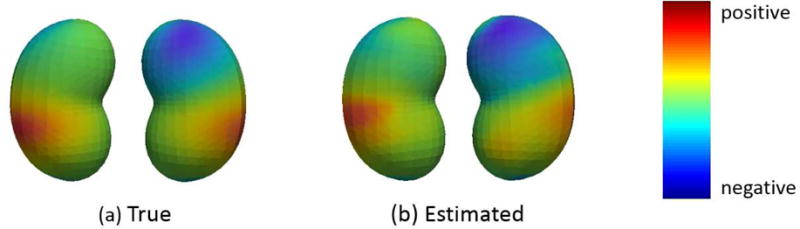
The true coefficient function (Panel (a)) and estimated coefficient function (Panel (b), the mean of 200 estimated B(s)) on a 3D bean surface.

6 Discussion

Functional data are increasingly collected in public health and medical studies to better understand important public health issues and complex diseases. Both theoretical and computational complexity in functional data analysis (FDA) often makes health care practitioners to reduce the rich functional data into several scalar measures, e.g., volumes of a few brain regions. This enormous data reduction may distort the true underlying relationship between population’s health condition and the functional data. Moreover, some nontraditional functional data, such as genetic variant profiles defined along chromosomes or genomic regions, may not be able to reduce to scalar measures. To this end, FDA methods are increasingly used.

In this article, we develop a functional joint model (FJM) to account for functional predictors in both longitudinal and survival submodels within the framework of joint modeling. We use the functional principal component analysis (FPCA) to approximate the functional predictor, and expand its corresponding coefficient function using the empirical orthonormal eigenfunctions obtained from FPCA. FPC scores can be readily included as scalar covariates in a standard joint model consisting of a linear mixed model for the longitudinal scalar response variable and a Cox model for the survival outcome. The parameters of the FJM are estimated in a maximum likelihood framework via EM algorithm. The proposed FJM provides a flexible framework to incorporate many features both in joint modeling of longitudinal and survival data and in functional data analysis. We demonstrate through a simulation study that the FJM performs well in estimating the coefficient functions and other parameters.

Several studies have documented diminishing hippocampal thickness at baseline is associated with an increased likelihood of progressing to clinical dementia [42]. However, these studies only assess changes to hippocampal volume rather than its surface morphology. Enormous information loss may result when aggregating the high dimensional image data into a scalar volumetric value [43]. In comparison, our FJM framework accounts for the functional predictor (hippocampal radial distance, HRD) and other scalar covariates and efficiently estimate the association between the trajectory of cognitive functions measured by the ADAS-Cog 11 score and time to AD diagnosis. The inclusion of functional predictor HRD into the longitudinal submodel improves model fitting. We have identified that the regional radial atrophy in the CA1 subfield and the subiculum subfield is a good predictor of AD progression among patients with mild cognitive impairment. The identification of these subfields may facilitate case selection in clinical trials for evaluating therapeutic efficacy in slowing or modifying AD-related pathophysiology. Moreover, the proposed FJM can readily include multiple brain regions, and even genotype profiles, as functional predictors to assess whether they are associated with Alzheimer’s disease progression.

There are some advantages of using FPC expansion, besides the convenience of FPC implementation. FPC expansion allows borrowing strength across subjects in estimating basis functions, and it can capture complex correlations within the functions, as in the ADNI study [44]. Moreover, FPC can easily handle observation with missing values in functions, or functions measured with errors [11]. However, we retain the first K eigenfunctions to approximate the functional predictor. Although the selected number of K eigenfunctions can explain the majority of the variability in the functional predictor, they may not adequately represent the coefficient function. Therefore, the features on the tail region of the coefficient function are not well captured as demonstrated in our simulation study. Furthermore, it is possible that some retained FPCs are not significantly associated with the outcome. On the other hand, in the functional predictor regression, there are various choices of basis functions, e.g., splines, Fourier, wavelet, and their combinations, and regularization approaches. Splines are well suited to modeling simple and smooth functions, and usually work better when the dimension of the grid is not too high [45]. However, no single basis function is superior in all settings. In the future work, we will investigate the performance of other basis functions and new methods for selecting among various candidate basis functions and regularization approaches.

There are some limitations we will address in the future. First of all, we exclude from analysis the subjects with missing data in baseline covariates of interest. A majority of these subjects either do not have baseline image data measured or do not have image data in the archive due to the technical difficulty in image data collection and storage. We have assumed the baseline covariates are missing completely at random. We would like to investigate the validity of this assumption in the future. Moreover, there is some longitudinal MRI measurements available for some ADNI participants. About 30% these participants have at least one missed MRI measurement, creating the missing data issue in longitudinal functional data. The complex within-subject correlation among functional data should be carefully modeled when handling missing data. In addition, we use a time-invariant functional predictor in this article. It would be of scientific interest to extend the proposed FJM to accommodate longitudinal functional data. We can treat the longitudinal functional variable as a functional predictor which can be decomposed by longitudinal FPCA (LFPCA) [46] to account for it longitudinal data structure. Alternatively, the longitudinal functional variable can be treated as a functional response variable in the longitudinal submodel (function-on-scalar regression problem) and it can be incorporated in the survival submodel as a time-dependent functional predictor. This model can investigate how the longitudinal functional variable directly impacts the time to event of interest. Furthermore, in model (2), different formulations can be used to postulate how the hazard of a survival event depends on the longitudinal trajectory. For example, both the unobserved true value of m_i(t_ij) as in model (1) and its time-dependent slope $m_i^{\prime }(t_{ij})$ can be included in model (2). A good summary of these various formulations in the joint modeling framework can be found in Rizopoulos et al. [47] and Yang et al. [48]. Finally, we would like to develop an user-friendly R package which addresses the aforementioned issues and incorporate some useful features, e.g., nonparametric smoothing and missing data.