Abstract
Subgroup identification (clustering) is an important problem in biomedical research. Gene expression profiles are commonly utilized to define subgroups. Longitudinal gene expression profiles might provide additional information on disease progression than what is captured by baseline profiles alone. Therefore, subgroup identification could be more accurate and effective with the aid of longitudinal gene expression data. However, existing statistical methods are unable to fully utilize these data for patient clustering. In this article, we introduce a novel clustering method in the Bayesian setting based on longitudinal gene expression profiles. This method, called BClustLonG, adopts a linear mixed-effects framework to model the trajectory of genes over time while clustering is jointly conducted based on the regression coefficients obtained from all genes. In order to account for the correlations among genes and alleviate the high dimensionality challenges, we adopt a factor analysis model for the regression coefficients. The Dirichlet process prior distribution is utilized for the means of the regression coefficients to induce clustering. Through extensive simulation studies, we show that BClustLonG has improved performance over other clustering methods. When applied to a dataset of severely injured (burn or trauma) patients, our model is able to identify interesting subgroups.
Keywords: Bayesian factor analysis, Bayesian nonparametrics, Clustering, Longitudinal gene expression study
1. Introduction
Subgroup identification is an important problem in disease studies, especially in complex diseases such as cancers, which are highly heterogeneous among individuals [1, 2]. Accurate identification of subgroups could be beneficial in disease diagnosis, treatment, and prognosis as well as understanding the underlying biological mechanisms. Gene expression data are commonly used to define subgroups [3, 4, 5, 6], and subgroups thus identified are usually significantly associated with clinical features, providing valuable clinical insights into diseases [5, 6].
Longitudinal monitoring of molecular profiles can be predictive of the onset of diseases [7], which suggests that the dynamic trend of gene expression profiles might provide extra information on disease progression in addition to baseline gene expression profiles. Moreover, longitudinal gene expression data allow us to account for intra-individual variability of gene expression when grouping patients. Therefore, subgroup identification could be improved with the aid of longitudinal gene expression data.
As our motivating study, a large-scale collaborative research program, Inflammation and the Host Response to Injury, aims to improve understanding of the host responses to severe injury in a systematic way through genomics, which might help develop improved treatments for severe trauma or burn injured patients. In this study, a cohort of critically injured patients (burn injury or blunt trauma) were longitudinally followed immediately after the injury occurred [8]. At each visit, the whole genome gene expression profile in the whole blood leukocytes was measured for the patient. Despite considerably different clinical presentations of burn injury and blunt trauma, the changes in the gene expression profiles were rather similar in the sense that similar genetic pathways are invoked in response to injury. However, the magnitudes and durations in the changes of the gene expression profiles were different for different types of injury, which might be related to the development of complications often observed in the severely injured patients.
Our first goal is to use the longitudinal gene expression profiles to cluster the patients based on the cause of injury, which might reveal differences in the molecular responses to different types of injury and hence lead to an improved understanding of these injuries at the molecular level. The longitudinal gene expression profiles of patients with the same injury type may also vary significantly due to patient heterogeneity. Thus, our second goal is to cluster the patients with the same type of injury in order to identify clinically distinctive subgroups, which might be related to the development of complications and hence help design early interventions.
In the statistical literature, a number of methods have been developed that can be used for clustering patients with longitudinal trajectories. Most methods adopt a functional approximation of the curves using some standard basis systems and then perform clustering based on the coefficients. For example, James et al. [9] used B-splines while Serban et al. [10] used the Fourier transformation to approximate the trajectories and then both studies adopted the K-means algorithm for clustering based on the coefficients. Model-based clustering of the coefficients has also been employed after functional approximation [11, 12]. Each of these methods is designed for the cases where each subject has only a single trajectory. Recently, Rodriguez et al. [13] developed a Bayesian method for clustering subjects with multiple trajectories measuring the same variable. However, none of these methods are applicable in our setting, where each subject has multiple trajectories measuring different genes over time. Although some clustering methods based on multivariate longitudinal data have been developed [14, 15], they do not scale up well for high-dimensional variables, such as the gene expression profiles.
There are many clustering methods developed for time course gene expression data [16, 17, 18, and references therein]. However, the time course and longitudinal gene expression data are inherently different in that multiple gene expression profiles over time are taken from different patients/subjects. Because of this, most of the existing methods, if not all, focus on grouping similar genes into clusters instead of patients/subjects. Moreover, the repeated measurements on a single patient in the longitudinal gene expression data allow us to cluster patients, which requires different statistical models from those methods developed for time course gene expression data.
In this article, we propose a nonparametric Bayesian method, called BClustLonG (Bayesian Clustering method for Longitudinal Gene expression data), for subgroup identification based on longitudinal gene expression profiles. In BClustLonG, we use a linear model to approximate the trajectories of genes while clustering is carried out based on the regression coefficients obtained from all genes. In order to properly account for high correlations often observed among some of the genes when modeling multiple genes simultaneously, we adopt the factor analysis model for the regression coefficients. Factor analysis is commonly used in genomics studies [19, 20] to alleviate the high dimensionality challenges. To induce clustering, the Dirichlet process (DP) prior [21, 22] is specified for the means of the regression coefficients of each subject.
The remainder of the article is organized as follows. Section 2 details our statistical model and clustering inference. Section 3 gives the prior specification and computational details. Section 4 displays the performance of BClustLonG in simulation studies and comparisons to other clustering methods. Section 5 shows results of BClustLonG applied to the data of critically injured patients. We conclude the paper in Section 6.
2. Methods
2.1. Statistical Model
Let Yig(xit) be the expression value of gene g for subject i at time xit, for i = 1, …, N, g = 1, …, G, t = 1, …, Ti and fig(·) be the true underlying trajectory of gene g for subject i. We assume
| (1) |
where is the gene specific variance. Based on the observed trajectories in our data (see Figure 1) and the relatively small number of time points for each patient, we adopt a linear regression model to approximate the trajectories such that
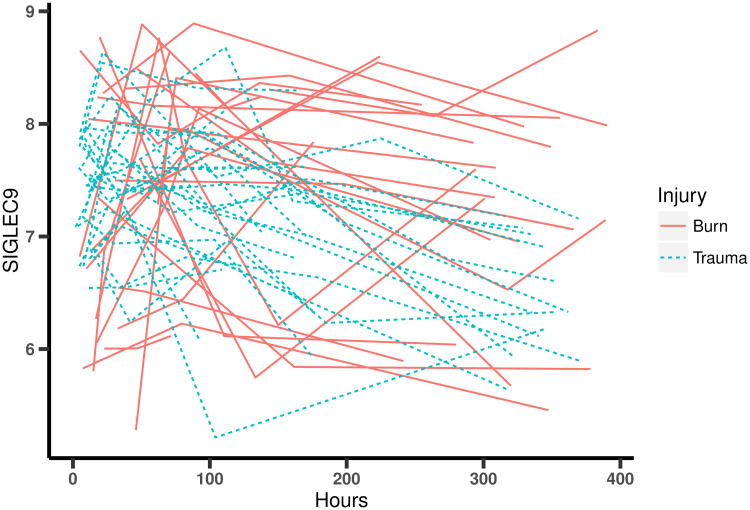
Figure 1.
Expression trajectories of gene SIGLEC9 over time for 26 burn patients and 26 randomly selected trauma patients.
| (2) |
where (aig, big)T is the vector of gene-specific regression parameters for subject i.
Then, conditional on the regression and variance parameters, the data generating model can be written as
| (3) |
where Yi(xit) = {Yi1(xit), …, YiG(xit)}T denotes the expression values of the G genes at time xit for subject i, ai = (ai1, …, aiG)T, bi = (bi1, …, biG)T, , and Σ is a diagonal covariance matrix with .
For each patient, we introduce 2G parameters in our model, i.e. . More specifically, these parameters control the baseline expression values of the G genes and the trend of the longitudinal trajectories (increasing, decreasing, or unchanged over time). Depending on the clinical outcome of interest, intercept coefficients ai, slope coefficients bi, or both could be informative for clustering. In the following, we assume both sets of coefficients are informative when describing our proposed method. The model can be easily extended to clustering only on ai or bi if appropriate.
To induce clustering, we specify DP mixture models for the vectors of subject-specific regression parameters such that
| (4) |
| (5) |
where . More specifically, if a distribution P on parameters μi follows a DP with parameters c, G0, then P can be written as , μ*∼G0, where wj = uj∏s<j(1 − us), , δμ* is the point mass on μ*, and G0 is the base distribution on μ*. This is the well known stick-breaking representation of the DP [22]. Then, we say that μi|c, . In our case, we use the following base distribution, which results in semi-conjugacy in the model,
| (6) |
where aμ0 and bμ0 are the grand mean vectors for the intercepts and slopes, and describe the variability of the mean parameters aμi and bμi, and IG is the identity matrix with dimension G. Let ei be the cluster membership for the ith subject. Due to the discrete nature of the DP distribution, the subject-specific means of the regression parameters could take exactly the same values for different subjects, that is for some subjects i and j or, equivalently, ei = ej, which induces clustering. The number of unique values for , that is the number of clusters, depends on the similarities among the subjects. Therefore, the DP mixture model provides a data-driven method of determining the number of clusters, which avoids the need to pre-specify the number of clusters.
We choose to account for potentially high correlations among genes through the modeling of Σaa and Σbb in Equations (4) and (5). An obvious starting point would be to assume that Σaa and Σbb are unstructured covariance matrices. However, when G is large, this specification will be computationally difficult to work with due to the large dimension of each matrix. To strike a balance between efficiency and high dimensionality, we adopt a factor analysis model for ai and bi. Specifically, we introduce a model for the covariance matrices in Equations (4) and (5) such that
| (7) |
| (8) |
where [Λa]G×Ma and [Λb]G×Mb are the loading matrices for intercepts and slopes, respectively (Ma and Mb are numbers of factors), [ηai]Ma×1 and [ηbi]Mb×1 are factor scores for subject i, and [Σa]G×G and [Σb]G×G are the diagonal covariance matrices with and . In this way, we use low-rank matrices to approximate the large covariance matrices for intercept and slope parameters that take into account the major correlations among genes while avoiding estimation of a large covariance matrix, since Ma and Mb are usually small.
This model can be easily extended to clustering only on intercepts or slopes. For example, let us assume that only the intercepts are informative for the clinical outcome of interest and therefore we only want to base clustering on these parameters. Then, we only need to change the prior distribution for bi in Equation (8) to bi|b0, and the base distribution in Equation (6) accordingly. Here, we could again use a factor analysis model to approximate the large covariance matrix Σb. While this could improve the model fit, the increased model complexity might not result in improved clustering for intercepts. Alternatively, we can assume that the Σb is diagonal and allow the correlations among genes to be accounted for by the intercepts. Similarly, if we only want to cluster on slopes, the model could be adjusted accordingly.
2.2. Clustering Inference
The cluster structure can be derived as follows for BClustLonG. First, we calculate the posterior similarity matrix, where the (i, j)th entry of the matrix represents the posterior probability that the ith subject and jth subject are in the same cluster. This can be easily calculated based on the S posterior samples as , where δ(·) is the indicator function and and is the cluster membership for the ith and jth subjects in the sth iteration, respectively. The posterior similarity matrix is commonly used to derive the cluster structure based on the posterior samples, since it is robust to the label switching issue in Bayesian mixture models.
Based on the posterior similarity matrix, there are two categories of methods that could be used to determine the clustering structure. For the first category, the number of clusters does not need to be pre-specified. These approaches, including Binder [23], Dahl's criterion [24], and MPEAR [25], can be used to determine the optimal number of clusters and the corresponding cluster structure based on the posterior similarity matrix. In simulation studies, where the true number of clusters is known, we adopt these approaches so that we can study their performance in terms of determining both the number of clusters and the clustering structures. Specifically, we choose the MPEAR method among the others for our analyses, since it has the positive feature of maximizing the expectation of the adjusted Rand index between the estimated and true clustering. The adjusted Rand index represents the degree of agreement between two clustering partitions with higher value indicating better agreement (it typically ranges from 0 to 1 and sometimes it could be negative) and is a commonly used measure of clustering performance [26, 27, 28].
For the second category, the number of clusters has to be pre-specified. Specifically, the classical agglomerative hierarchical clustering method (HCLUST), as introduced in [29], can be used to infer the clusters. We choose HCLUST in our analysis because it is one commonly used clustering method that works on a pairwise distance matrix, which is the output of our algorithm. Most existing clustering methods are not applicable in this setting. In this approach, the posterior similarity matrix is used to generate the pairwise distance of all subjects and then the pairwise distance is given as input to HCLUST with average linkage to infer the clustering structure for a given number of clusters. This approach is useful when the number of clusters is known a priori or can be determined based on clinical relevance for better interpretation. Since the adjusted Rand index could be affected by the number of clusters, which is usually unknown in real data, we compare different clustering methods by fixing a reasonable number of clusters and hence we use this approach in the real data analysis.
3. Computations
3.1. Prior Specification
To complete the model specification, we select prior distributions for all unknown model parameters. Most of the prior distributions are selected to be conjugate for computational convenience while still being weakly informative to reflect our lack of prior information regarding the true parameter values. The concentration parameter c in the DP prior controls the prior expectation of number of clusters in the data. We specify a Uniform(0, 10) prior distribution for c where c = 10 results in the prior expected number of clusters to be 15.42 based on Theorem 1 in [13]. This upper bound should be large enough for our dataset which includes at most 159 patients. For datasets with more subjects, a larger value might be needed for the upper bound of the uniform distribution.
We select conjugate priors for the mean and variance parameters in the base distribution of the DP prior. For the mean parameters aμ0 and bμ0, we use independent multivariate normal distributions, that is aμ0 ∼ MVN(0G, hIG) and bμ0 ∼ MVN(0G, hIG), where 0G is a vector of length G with all elements being zeros. We set h = 100 in our analysis, resulting in weakly informative prior distributions. For the variance parameters and , we select weakly informative Inverse Gamma(0.1, 0.1) prior distributions. When considering the model that only clusters on the intercepts, we set b0 ∼ MVN(0G, hIG). Similar adaptation is done when we use the model that only clusters on slopes. We specify independent and weakly informative conjugate prior distributions for all variance parameters involved in the diagonal matrices (Σ, Σa, Σb) through use of the Inverse Gamma(0.1,0.1) prior distribution.
Next, we specify prior distributions for the unknown parameters in the factor analysis model. Since the factor models for the intercepts and slopes are symmetric, we only describe the prior specification for Λa and ηai noting that the same prior distributions are selected for Λb and ηbi. In order to ensure identifiability of the factor loading matrix and hence the factor scores, constraints have to be placed on the loading matrix, as done in [30] and [31]. However, the factor model is used to account for the correlation among genes in our case and hence only the covariance matrix is involved in the posterior sampling. Therefore, the identifiability issue of the factor loading matrix and factor scores is not a problem in our case, as long as the covariance matrix is well identified. As a result, we adopt the multiplicative gamma process shrinkage prior for the factor loadings proposed in [32]. To be specific, the priors for the entries of Λa are as follows:
| (9) |
| (10) |
where [Λa]gm is the (g, m)th entry of Λa and [ϕa]gm and [τa]m control the shrinkage of these factor loadings in an element-wise and column-wise manner, respectively. The multiplicative gamma process shrinkage prior on the factor loadings allows the introduction of infinitely many factors and hence avoids the need for specification of the number of factors, a notoriously difficult problem in past work [33]. It also introduces sparsity on the factor loading by shrinking them towards to zero as the number of factors increases through use of [τa]m, since [τa]m is stochastically increasing if αa2 > 1. Moreover, it was shown in [32] that the multiplicative gamma process shrinkage prior ensures the weak consistency of the posterior distribution and provides a large support for the positive definite covariance matrix. The efficient adaptive Gibbs sampler, proposed in [32], is used to sample Λa, which can handle the infinite number of factors. The prior distributions for αa1 and αa2 are taken to be Gamma(2, 1) as in [32]. As in a standard Bayesian factor analysis model, the prior distribution for ηai is taken to be MVN(0, IMa).
3.2. Computational Details
The selected prior distributions lead to semi-conjugacy for the majority of introduced model parameters. Therefore, Gibbs sampling is a straightforward approach to performing Markov chain Monte Carlo (MCMC) posterior sampling. Use of the DP prior distribution results in an infinite number of mixture components, which can be computationally difficult to handle in practice. Numerous algorithms have been proposed for sampling in DP mixture models [34, 35, 36, 37, 38]. Here, we use the method proposed in [34] and [35], where the parameters in the mixture components follow a generalized Polya urn scheme obtained by integrating out the distribution of these parameters over the prior distributions. The detailed sampling algorithm is provided in Section 3 of the Supplementary Materials.
In simulation studies, 20,000 MCMC samples are generated and the first 5,000 samples are discarded as burn-ins. All subjects are randomly assigned to ten different clusters to start with. The initial values for the A, B, aμ0, bμ0, Σ, Σa, and Σb parameters are set based on the intercept and slope coefficients estimates from the linear mixed-effect model with random intercepts and random slopes fitted for each gene separately, where [A]n×G = (a1, …, an)T and [B]n×G = (b1, …, bn)T. The initial values for σa0 and σb0 are both set to be 1. The initial values for the other parameters are chosen according to the assigned prior distributions.
For our analyses of real data, 60,000 samples are collected after a burn-in period of 15,000 iterations from three separate chains for a total of 180,000 posterior samples available for making posterior inference. Starting values for each chain are selected to be overdispersed with respect to the target marginal posterior distributions based on preliminary runs of the model. This allows us to calculate the potential scale reduction factor convergence diagnostic [39]. Convergence monitoring is conducted on all parameters based on the visual inspection of Gelman-Rubin plots and trace plots, and the Gelman-Rubin diagnostic statistics.
4. Simulation Studies
In this section, we apply BClustLonG to simulated data and evaluate its performance in comparison to four competing methods. The first three methods for comparison are two-step empirical procedures. In the first step, a linear mixed-effects model with random intercepts and slopes is fitted for each gene separately and estimates of the intercepts and slopes are obtained for each individual. Then, a clustering method is applied to the standardized parameter estimates from step one to obtain the optimal number of clusters and underlying cluster structure. For the second step, we adopt two model-based clustering methods, MCLUST [40] and EPGMM [41], and one distance-based clustering method, K-means. EPGMM also uses a factor analysis model to approximate the covariance matrices while MCLUST employs eigen-decomposed covariance matrices, both of which can deal with high-dimensional data. For brevity, we denote these two-step procedures as MCLUST, EPGMM, and K-means, respectively. Another method for comparison is similar to our proposed model except that the factor analysis component is removed. Instead, diagonal covariance matrices are assumed for both vectors of intercepts and slopes in Equations (4) and (5). This method, referred to as BCluseLonG0 from here on, allows us to assess the necessity of the factor analysis structure in our proposed method. Note that the correlations among genes are ignored in BCluseLonG0. In contrast, the correlations among genes are ignored when estimating intercepts and slopes in MCLUST and EPGMM, but the covariance matrices for the intercept and slope vectors are estimated during clustering. Another major difference between our framework and the two-step procedures is that BCluseLonG is a DP mixture model while MCLUST and EPGMM are finite mixture models, for which the number of mixture components is determined based on Bayesian Information Criterion. To run MCLUST, EPGMM, and K-means, we adopt the Mclust function in R package “mclust”, pgmmEM function in R package “pgmm”, and kmeansruns function in R package “fpc”, respectively. For EPGMM, the algorithm is run with CCC and CCU models and the numbers of factors under consideration are from one to six (See [41] for details on the CCC and CCU models). The possible numbers of clusters under consideration range from one to five for each method and we use default values for all other parameters.
Specifically, we compare the performance of the five methods (BClustLonG, BClustLonG0, MCLUST, EPGMM, and K-means) in four different data generating scenarios. In order to preserve the properties of our observed data and create realistic simulation scenarios of interest, many features of the simulated data are taken directly from the injury data. The total number of patients is 100 (N = 100 patients), the number of genes is the same as that for the observed study (G = 40 genes), the sampled time points of each subject are taken directly from the 100 randomly selected patients in the observed data, and the true number of underlying clusters is two with each cluster including 50 patients.
The intercepts and slopes for patients in each cluster are drawn from multivariate normal distributions as follows. For all scenarios, the means of intercepts and slopes are 1G for patients in cluster one and are 0G for patients in cluster two, where νG is a length G vector with all elements being ν (ν = 0,1). The covariance matrices of the intercepts and slopes for patients in both clusters are taken to be (R, R), (IG, R), (R, IG), and (IG, IG) for the four scenarios, respectively, where IG denotes identity covariance matrix and R is the correlation matrix estimated from the baseline measurements in the injury data. Each scenario is named based on the covariance matrix specifications for the intercepts and slopes (for example, scenario RR indicates that R is specified for both intercepts and slopes). Finally, the data are simulated based on the data generating model given in Equation (3), where the matrix of gene specific variances Σ is taken to be IG in all simulation settings.
We simulate 20 datasets from each scenario as described in the previous paragraph. From the results in Table 1, we can see that BClustLonG outperforms the other four methods in all four scenarios as indicated by the larger values of the adjusted Rand Index. Comparing the performance of BClustLonG and BClustLonG0, we can see that BClustLonG performs well for different specifications of covariance matrices while BClustLonG0 only has reasonably good performance when the corresponding covariance matrices are independent (II scenario). This suggests that the adoption of the sparse factor analysis model to approximate the covariance matrix allows the model to adapt to different scenarios (even when the true covariance matrices have an independent structure) and that the misspecification of covariance matrix could lead to misleading clustering results. K-means has similar performance to BClustLonG in scenario II while performing worse than BClustLonG in other scenarios. This makes sense as K-means ignores the correlation structure and hence it is not efficient when the genes are correlated.
Table 1.
Comparisons of BClustLonG, BClustLonG0, MCLUST, EPGMM, and K-means in simulation settings. The numbers in each cell indicate the average adjusted Rand index (Avg.Rand) and the average number of clusters (Avg.Clust) estimated by each method under each scenario with standard deviations in parentheses.
| Scenarios | BClustLonG | BClustLonG0 | MCLUST | EPGMM | K-means | |
|---|---|---|---|---|---|---|
| RR | Avg.Rand | 0.972 (0.054) | 0.303 (0.065) | 0.407 (0.114) | 0.050 (0.224) | 0.566 (0.123) |
| Avg.Clust | 2.2 (0.4) | 7.9 (1.7) | 3.5 (0.8) | 1.1 (0.2) | 2.0 (0.0) | |
|
| ||||||
| RI | Avg.Rand | 0.990 (0.017) | 0.447 (0.073) | 0.627 (0.121) | 0.840 (0.362) | 0.756 (0.096) |
| Avg.Clust | 2.1 (0.3) | 5.5 (1.4) | 3.0 (0.6) | 1.8 (0.3) | 2.0 (0.0) | |
|
| ||||||
| IR | Avg.Rand | 1.000 (0.000) | 0.474 (0.066) | 0.695 (0.127) | 1.000 (0.000) | 0.860 (0.086) |
| Avg.Clust | 2.0 (0.0) | 5.6 (1.2) | 3.1 (0.9) | 2.0 (0.0) | 2.0 (0.0) | |
|
| ||||||
| II | Avg.Rand | 0.998 (0.009) | 0.998 (0.009) | 0.000 (0.000) | 0.000 (0.000) | 0.998 (0.009) |
| Avg.Clust | 2.0 (0.0) | 2.0 (0.0) | 1.0 (0.0) | 1.0 (0.0) | 2.0 (0.0) | |
Also, we can see that BClustLonG outperforms MCLUST and EPGMM in all data generation scenarios, which suggests that accounting for the uncertainties in estimating the intercepts and slopes could help improve the clustering results. It is worth noting that MCLUST and EPGMM perform poorly in the RR and II scenarios. For the RR scenario, where the covariance matrix is complex, EPGMM would favor a large number of factors in order to approximate the covariance matrix well and estimation of a large number of parameters could increase the uncertainties in the model and hence leads to unstable clustering results. Similar explanation also applies to MCLUST. And, the sparsity assumption in BClustLonG could be beneficial in this case. When the true covariance matrices have an independent structure, the sparsity assumption also helps, as shown by the results in II scenario.
In addition, comparing the estimated number of clusters, we can see that BClustLonG can accurately estimate the number of clusters while BClustLonG0 tends to overestimate when covariance matrices are misspecified. For MCLUST and EPGMM, the estimated number of clusters is generally unstable and can vary substantially across different data generating scenarios. It seems K-means consistently estimates the number of clusters well in all scenarios. In fact, K-means is rather conservative in estimating the number of clusters. In the additional simulations as shown in Section 1 of the Supplementary Materials, K-means estimates the number of clusters to be two in most settings while the true number of clusters is four (See Table S1 in the Supplementary Materials).
To show the robustness of BClustLonG, we conduct additional simulations. From the results shown in Table S1 in the Supplementary Materials, we can see that BClustLonG is robust to the varying number of genes and clusters, different covariance matrices, and model specifications, and has improved performance over competing methods in all scenarios.
5. Injury Data Analysis
Next, we apply BClustLonG to the injury data briefly described in Section 1. In the injury data, there are a total of 244 severe burn patients (having burns covering more than 20% of the total body surface area) and 167 severe blunt trauma patients. For the burn patients, the blood samples were drawn irregularly from within several hours of the injury and up to one year after the injury while, for the trauma patients, the blood samples were taken more regularly within 12 hours of the injury and 1, 4, 7, 14, 21, and 28 days after the injury. The whole-genome gene expression profile was measured for each blood sample.
In our analyses, we focus on the measurements taken within 400 hours (about two weeks) after the injury, during which the patients experience rapid changes in the gene expression profiles in response to the injury [8], since we are more interested in the magnitudes and the rates of changes. We only include patients having at least three measurements within 400 hours after the injury in order to have relatively reliable slope estimates, resulting in 26 burn patients and 159 trauma patients with each patient having three to five measurements. It is challenging to select informative genes out of the tens of thousands of genes available for clustering given that we have no information on the true underlying clusters [42]. As commonly done, the genes with the largest variances are selected for clustering, since they explain a large proportion of the variance in the data, which is likely related to the underlying clustering structure in the data [43]. Here, we select 40 genes with large variances both in intercepts and slopes estimated by a linear mixed-effect model using the 185 patients from our study.
In this dataset, two major clusters exist, that is burn and trauma patients. However, the “true” number of clusters is unknown, as there might be subgroups within burn and/or trauma patients, due to the different clinical features such as the severity of the injury. Also, the adjusted Rand index could be affected by the inferred number of clusters. Thus, in order to make a fair comparison among all methods, we pre-specify the number of clusters to be 2 for all methods (i.e. the HCLUST method is used for BClustLonG to determine the clustering structure, as mentioned in Section 2.2). As a result, the adjusted Rand indices are 0.94, 0.02, 0.18, 0.07, and 0.24 for BClustLonG, BClustLonG0, MCLUST, EPGMM, and K-means, respectively, suggesting that BClustLonG performs better in separating burn and trauma patients into two clusters than other methods.
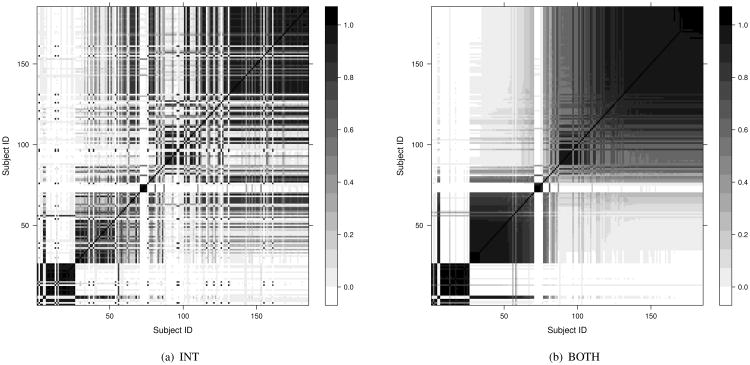
Then, we compare the performance of two versions of our model in order to establish the need for incorporating the longitudinal data into the modeling framework. The first version (INT) represents a modification of the full BClustLonG model where only the intercepts are allowed to inform about potential clusters in the data. The second version (BOTH) is the previously described BClustLonG method where both intercepts and slopes are allowed to inform about clustering. We are interested in determining which model can better separate burn patients and trauma patients based on their gene expression profiles and to determine if the longitudinal nature of the data is informative for clustering (i.e. slopes). The adjusted Rand indices are 0.94 and 0.82 for the BOTH model and INT model, respectively. As shown by the posterior similarity matrices in Figure 2, the burn patients (Subject IDs 1 to 26) are more tightly clustered when using the BOTH model compared to the INT model. A similar result is observed for the trauma patients. These findings suggest that the rates of changes (slopes) in certain genes are different for burn patients and trauma patients in addition to the differences in the magnitudes of initial changes (intercepts), as also suggested in Figure 1.
Figure 2.
The posterior similarity matrices from the two versions of our model in the injury data application. INT: only include intercepts for clustering; BOTH: include both intercepts and slopes for clustering.
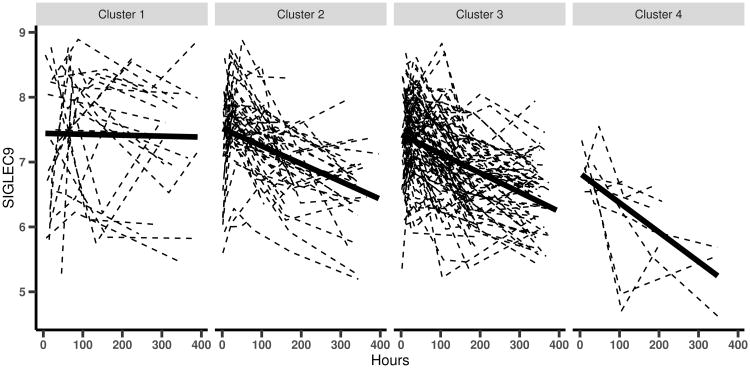
Next, we take a closer look at the clustering results from the full BClustLonG model (BOTH). Based on the posterior similarity matrix (Figure 2(b)), we can see that the magnitudes and the rates of changes in these 40 genes not only separate trauma patients from burn patients, but also identify several subgroups within trauma patients. In fact, there are four identified clusters in the injury data (including the burn patients) based on the MPEAR criterion. To see the differences in the trajectories for the these four clusters, we select one of the 40 genes, SIGLEC9, and plot its trajectory for each patient in each cluster with a fitted line for each cluster. From Figure 3, we can see that the trajectories of SIGLEC9 show differences in both intercepts and slopes for the four clusters. In particular, the patients in cluster 1 (all of them are burn pateints) have relatively stable expression of SIGLEC9 over time while the expression values of SIGLEC9 are decreasing for patients in all other clusters (the majority is trauma patients), although the baseline values are similar across all clusters. Comparing patients in clusters 2, 3, and 4, we can see that, in addition to the differences in the baseline values, the expression values of SIGLEC9 are decreasing faster for patients in cluster 4, although the trajectories from all three clusters display decreasing trends. This suggests that different trauma patients respond to the injury in different ways and hence respond differently during the recovery process as well. Although there is no obvious difference between clusters 2 and 3 for this particular gene, clusters 2 and 3 do differ in other genes. Detailed investigation of the trajectories of these genes for patients in different clusters together with their clinical outcomes (e.g. if complications developed during the process) might provide insights into the molecular mechanisms of the host response to the trauma injury.
Figure 3.
The trajectories of gene SIGLEC9 for the four clusters in the injury data.
The means of the Gelman-Rubin diagnostic statistics for all parameters across all chains are 1.018 with standard deviation 0.07 and 1.001 with standard deviation 0.003 for the BOTH and INT models, respectively. These results, along with visual inspection of the trace plots, suggest there is no significant evidence of convergence issues. In Section 2 of the Supplementary Materials, we also conduct a sensitivity analysis regarding the prior distributions for αa1 and αa2, which are taken to be Gamma(2,1) in each of our analyses. As shown in Figure S1 of the Supplementary Materials, the clustering structures obtained from BClustLonG using different hyperparameters in the prior distributions for αa1 and αa2 are similar, suggesting that BClustLonG is generally robust to the choice of prior distributions for αa1 and αa2.
6. Discussion
In this paper, we developed a new Bayesian method, called BClustLonG, for clustering based on longitudinal gene expression profiles. By taking into account the mixture structure and the correlations among genes when estimating the model parameters, our model was able to improve the clustering performance over other methods. Through both simulation studies and real data application, BClustLonG is shown to be a useful tool for analyzing longitudinal gene expression profiles. In addition, the adoption of the DP mixture model and the infinite sparse factor analysis model makes the inference of the number of clusters and factors an inherent feature of our proposed method, which can be very useful in practice.
In our method, the longitudinal trajectories of all genes are approximated by linear regression models, which is reasonable for our settings where each subject only has a few time points, thereby making more complex non-linear modeling extremely difficult. Also, including only the intercepts and slopes for clustering improves interpretation of the findings, as both intercepts and slopes are clinically meaningful. However, our model framework is quite general and can be extended to deal with non-linear trajectories. For example, we can add polynomial terms of time in Equation (2). However, the number of parameters that need to be estimated will increase as the number of terms increases, as the covariance matrix for each of the added terms has to be estimated. Some further assumptions might be needed to reduce the number of parameters in those situations to achieve good bias-variance balance.
It has been widely recognized that most genes in a gene expression dataset are redundant and selecting informative genes before clustering can improve the results [43]. Based on our experience, BClustLonG can deal with the cases where the number of informative genes is on the scale of tens or hundreds. However, if the number of informative genes increases drastically, slow mixing issues might present in the DP mixture model, in which case more advanced algorithms such as the split merge algorithm might be used to improve the mixing. In our analysis, we pre-selected the genes based on the variances before clustering. A possible extension of our current model is to incorporate the variable selection feature into the model, that is to perform variable selection and clustering simultaneously, which avoids the need to pre-select genes. However, resulting computational complexities may be difficult to overcome.
Supplementary Material
Acknowledgments
Jiehuan Sun and Hongyu Zhao are supported in part by the National Institutes of Health grants R01 GM59507 and P01 CA154295. Jose D. Herazo-Maya is supported by the Harold Amos Faculty development program of the Robert Wood Johnson Foundation and the Pulmonary Fibrosis Foundation. Naftali Kaminski is supported in part by the National Institutes of Health grants U01 HL108642 and R01 HL127349. Joshua L. Warren is supported in part by the National Institutes of Health grants UL1 TR001863 and KL2 TR001862. The contents are solely the responsibility of the authors and do not necessarily represent the official view of NIH.
References
- 1.Meacham CE, Morrison SJ. Tumour heterogeneity and cancer cell plasticity. Nature. 2013;501(7467):328–337. doi: 10.1038/nature12624. URL http://dx.doi.org/10.1038/nature12624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jeste SS, Geschwind DH. Disentangling the heterogeneity of autism spectrum disorder through genetic findings. Nature Reviews Neurology. 2014;10(2):74–81. doi: 10.1038/nrneurol.2013.278. URL http://dx.doi.org/10.1038/nrneurol.2013.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, Rosenwald A, Boldrick JC, Sabet H, Tran T, Yu X, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403(6769):503–511. doi: 10.1038/35000501. URL http://dx.doi.org/10.1038/35000501. [DOI] [PubMed] [Google Scholar]
- 4.Garber ME, Troyanskaya OG, Schluens K, Petersen S, Thaesler Z, Pacyna-Gengelbach M, van de Rijn M, Rosen GD, Perou CM, Whyte RI, et al. Diversity of gene expression in adenocarcinoma of the lung. Proceedings of the National Academy of Sciences. 2001;98(24):13 784–13 789. doi: 10.1073/pnas.241500798. URL http://dx.doi.org/10.1073/pnas.241500798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sorlie T, Perou CM, Tibshirani R, Aas T, Geisler S, Johnsen H, Hastie T, Eisen M, Van de Rijn M, Jeffrey S, et al. Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proceedings of the National Academy of Sciences. 2001;98(19):10 869–74. doi: 10.1073/pnas.191367098. URL http://dx.doi.org/10.1073/pnas.191367098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wigle DA, Jurisica I, Radulovich N, Pintilie M, Rossant J, Liu N, Lu C, Woodgett J, Seiden I, Johnston M, et al. Molecular profiling of non-small cell lung cancer and correlation with disease-free survival. Cancer Research. 2002;62(11):3005–3008. [PubMed] [Google Scholar]
- 7.Chen R, Mias GI, Li-Pook-Than J, Jiang L, Lam HY, Chen R, Miriami E, Karczewski KJ, Hariharan M, Dewey FE, et al. Personal omics profiling reveals dynamic molecular and medical phenotypes. Cell. 2012;148(6):1293–1307. doi: 10.1016/j.cell.2012.02.009. URL http://doi.org/10.1016/j.cell.2012.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xiao W, Mindrinos MN, Seok J, Cuschieri J, Cuenca AG, Gao H, Hayden DL, Hennessy L, Moore EE, Minei JP, et al. A genomic storm in critically injured humans. The Journal of Experimental Medicine. 2011;208(13):2581–2590. doi: 10.1084/jem.20111354. URL https://doi.org/10.1084/jem.20111354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.James GM, Sugar CA. Clustering for sparsely sampled functional data. Journal of the American Statistical Association. 2003;98(462):397–408. doi: 10.1198/016214503000189. URL http://dx.doi.org/10.1198/016214503000189. [DOI] [Google Scholar]
- 10.Serban N, Wasserman L. CATS: clustering after transformation and smoothing. Journal of the American Statistical Association. 2005;100(471):990–999. doi: 10.1198/016214504000001574. URL http://dx.doi.org/10.1198/016214504000001574. [DOI] [Google Scholar]
- 11.Heard NA, Holmes CC, Stephens DA. A quantitative study of gene regulation involved in the immune response of anopheline mosquitoes: An application of Bayesian hierarchical clustering of curves. Journal of the American Statistical Association. 2006;101(473):18–29. doi: 10.1198/016214505000000187. URL http://dx.doi.org/10.1198/016214505000000187. [DOI] [Google Scholar]
- 12.Ray S, Mallick B. Functional clustering by Bayesian wavelet methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2006;68(2):305–332. doi: 10.1111/j.1467-9868.2006.00545.x. URL http://dx.doi.org/10.1111/j.1467-9868.2006.00545.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rodriguez A, Dunson DB. Functional clustering in nested designs: Modeling variability in reproductive epidemiology studies. The Annals of Applied Statistics. 2014;8(3):1416–1442. doi: 10.1214/14-AOAS751. URL http://dx.doi.org/10.1214/14-AOAS751. [DOI] [Google Scholar]
- 14.Villarroel L, Marshall G, Barón AE. Cluster analysis using multivariate mixed effects models. Statistics in Medicine. 2009;28(20):2552–2565. doi: 10.1002/sim.3632. URL http://dx.doi.org/10.1002/sim.3632. [DOI] [PubMed] [Google Scholar]
- 15.Komárek A, Komárková L, et al. Clustering for multivariate continuous and discrete longitudinal data. The Annals of Applied Statistics. 2013;7(1):177–200. doi: 10.1214/12-AOAS580. URL http://dx.doi.org/10.1214/12-AOAS580. [DOI] [Google Scholar]
- 16.Ma P, Castillo-Davis CI, Zhong W, Liu JS. A data-driven clustering method for time course gene expression data. Nucleic Acids Research. 2006;34(4):1261–1269. doi: 10.1093/nar/gkl013. URL https://doi.org/10.1093/nar/gkl013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Booth JG, Casella G, Hobert JP. Clustering using objective functions and stochastic search. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2008;70(1):119–139. doi: 10.1111/j.1467-9868.2007.00629.x. URL https://doi.org/10.1111/j.1467-9868.2007.00629.x. [DOI] [Google Scholar]
- 18.Sun W, Wei Z. Multiple testing for pattern identification with applications to microarray time-course experiments. Journal of the American Statistical Association. 2011;106(493):73–88. doi: 10.1198/jasa.2011.ap09587. URL http://dx.doi.org/10.1198/jasa.2011.ap09587. [DOI] [Google Scholar]
- 19.West M. Bayesian factor regression models in the “large p, small n” paradigm. In: Bernardo J, Bayarri M, Dawid A, Heckerman D, Smith A, West M, editors. Bayesian Statistics. Vol. 7. Oxford University Press; 2003. pp. 723–732. [Google Scholar]
- 20.Carvalho CM, Chang J, Lucas JE, Nevins JR, Wang Q, West M, et al. High-dimensional sparse factor modeling: Applications in gene expression genomics. Journal of the American Statistical Association. 2008;103(484):1438–1456. doi: 10.1198/016214508000000869. URL http://dx.doi.org/10.1198/016214508000000869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ferguson TS. A Bayesian analysis of some nonparametric problems. Annals of Statistics. 1973;1(2):209–230. [Google Scholar]
- 22.Sethuraman J. A constructive definition of Dirichlet priors. Statistica Sinica. 1994;4:639–650. [Google Scholar]
- 23.Binder DA. Bayesian cluster analysis. Biometrika. 1978;65(1):31–38. doi: 10.1093/biomet/65.1.31. URL https://doi.org/10.1093/biomet/65.1.31. [DOI] [Google Scholar]
- 24.Dahl DB. Bayesian Inference for Gene Expression and Proteomics. Cambridge University Press; 2006. Model-based clustering for expression data via a Dirichlet process mixture model; pp. 201–218. [Google Scholar]
- 25.Fritsch A, Ickstadt K, et al. Improved criteria for clustering based on the posterior similarity matrix. Bayesian Analysis. 2009;4(2):367–391. doi: 10.1214/09-BA414. URL https://doi.org/10.1214/09-BA414. [DOI] [Google Scholar]
- 26.Hubert L, Arabie P. Comparing partitions. Journal of Classification. 1985;2(1):193–218. [Google Scholar]
- 27.Yeung KY, Ruzzo WL. Principal component analysis for clustering gene expression data. Bioinformatics. 2001;17(9):763–774. doi: 10.1093/bioinformatics/17.9.763. URL https://doi.org/10.1093/bioinformatics/17.9.763. [DOI] [PubMed] [Google Scholar]
- 28.Lock EF, Dunson DB. Bayesian consensus clustering. Bioinformatics. 2013;29(20):2610–2616. doi: 10.1093/bioinformatics/btt425. URL https://doi.org/10.1093/bioinformatics/btt425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Medvedovic M, Yeung KY, Bumgarner RE. Bayesian mixture model based clustering of replicated microarray data. Bioinformatics. 2004;20(8):1222–1232. doi: 10.1093/bioinformatics/bth068. URL https://doi.org/10.1093/bioinformatics/bth068. [DOI] [PubMed] [Google Scholar]
- 30.Geweke J, Zhou G. Measuring the pricing error of the arbitrage pricing theory. Review of Financial Studies. 1996;9(2):557–587. [Google Scholar]
- 31.Wang F, Wall MM. Generalized common spatial factor model. Biostatistics. 2003;4(4):569–582. doi: 10.1093/biostatistics/4.4.569. URL https://doi.org/10.1093/biostatistics/4.4.569. [DOI] [PubMed] [Google Scholar]
- 32.Bhattacharya A, Dunson DB. Sparse bayesian infinite factor models. Biometrika. 2011;98(2):291–306. doi: 10.1093/biomet/asr013. URL https://doi.org/10.1093/biomet/asr013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hoyle RH, Duvall JL. Determining the number of factors in exploratory and confirmatory factor analysis. In: Kaplan D, editor. Handbook of Quantitative Methodology for the Social Sciences. chap 16. Sage; Thousand Oaks, CA: 2004. pp. 301–315. [Google Scholar]
- 34.Neal RM. Bayesian mixture modeling Maximum Entropy and Bayesian Methods. Springer; 1992. pp. 197–211. [Google Scholar]
- 35.MacEachern SN. Estimating normal means with a conjugate style Dirichlet process prior. Communications in Statistics - Simulation and Computation. 1994;23(3):727–741. doi: 10.1080/03610919408813196. URL http://dx.doi.org/10.1080/03610919408813196. [DOI] [Google Scholar]
- 36.Walker SG. Sampling the Dirichlet mixture model with slices. Communications in Statistics - Simulation and Computation. 2007;36(1-3):45–54. doi: 10.1080/03610910601096262. URL http://dx.doi.org/10.1080/03610910601096262. [DOI] [Google Scholar]
- 37.Papaspiliopoulos O, Roberts GO. Retrospective Markov chain Monte Carlo methods for Dirichlet process hierarchical models. Biometrika. 2008;95(1):169–186. doi: 10.1093/biomet/asm086. URL http://dx.doi.org/10.1093/biomet/asm086. [DOI] [Google Scholar]
- 38.Kalli M, Griffin JE, Walker SG. Slice sampling mixture models. Statistics and Computing. 2011;21(1):93–105. doi: 10.1007/s11222-009-9150-y. URL http://dx.doi.org/10.1007/s11222-009-9150-y. [DOI] [Google Scholar]
- 39.Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science. 1992;7(4):457–472. [Google Scholar]
- 40.Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. Journal of the American Statistical Association. 2002;97(458):611–631. doi: 10.1007/BF01908075. URL https://doi.org/10.1007/BF01908075. [DOI] [Google Scholar]
- 41.McNicholas PD, Murphy TB. Model-based clustering of microarray expression data via latent Gaussian mixture models. Bioinformatics. 2010;26(21):2705–2712. doi: 10.1093/bioinformatics/btq498. URL https://doi.org/10.1093/bioinformatics/btq498. [DOI] [PubMed] [Google Scholar]
- 42.Maugis C, Celeux G, Martin-Magniette ML. Variable selection for clustering with gaussian mixture models. Biometrics. 2009;65(3):701–709. doi: 10.1111/j.1541-0420.2008.01160.x. URL https://doi.org/10.1111/j.1541-0420.2008.01160.x. [DOI] [PubMed] [Google Scholar]
- 43.Hastie T, Tibshirani R, Eisen MB, Alizadeh A, Levy R, Staudt L, Chan WC, Botstein D, Brown P. ‘gene shaving’ as a method for identifying distinct sets of genes with similar expression patterns. Genome biology. 2000;1(2) doi: 10.1186/gb-2000-1-2-research0003. research0003–1. URL http://dx.doi.org/10.1186/gb-2000-1-2-research0003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.