A Statistical Framework to Evaluate Extreme Weather Definitions from A Health Perspective

Abstract

A statistical framework for evaluating definitions of extreme weather phenomena can help weather agencies and health departments identify the definition(s) most applicable for alerts nd other preparedness operations related to extreme weather episodes.

An extreme heat event (EHE) is defined as a sustained period of abnormally and uncomfortably hot, and usually humid, weather (Meehl and Tebaldi 2004). EHEs can negatively impact vital aspects of society, including agriculture, power production and consumption, and human health (National Research Council 2010; IPCC 2007). In the United States, fatalities related to naturally occurring ambient temperature extremes (hypothermia or hyperthermia) account for far more deaths in most years than those resulting from the combined effects of natural disasters such as storms and floods (Berko et al. 2014). The relationship between extreme temperature and mortality has been well described (Barnett et al. 2012; Barnett et al. 2010; Curriero et al. 2002; Medina-Ramon and Schwartz 2007), and studies have reported an added effect of heat waves independent of the effects of individual daily temperature extremes (Anderson and Bell 2011; Gasparrini and Armstrong 2011; Hajat et al. 2010; Hertel et al. 2009). Previous studies have also explored the sensitivity of the temperature–mortality relationship to different measures of temperature, as well as the duration and threshold type/intensity, used to define EHEs (Barnett et al. 2012; Barnett et al. 2010). Adverse health outcomes associated with EHEs are often preventable (Fowler et al. 2013; Choudhary and Vaidyanathan 2014); however, it is imperative to identify such events in advance and take measures to reduce the public health risk.

Many EHE definitions are available from the literature (Anderson and Bell 2011; Basagaña et al. 2015; CDC 2013; Easterling et al. 2000; Hajat et al. 2006; Hajat et al. 2010; Huth et al. 2000; Kent et al. 2014; Kovats and Hajat 2008; Meehl and Tebaldi 2004; Nairn and Fawcett 2014; Pascal et al. 2006; Pascal et al. 2013; Peng et al. 2011; Robinson 2001; Smith et al. 2013). Typical EHE definitions can be decomposed into the following core variables:

1. daily heat metric—heat metrics, such as daily maximum and mean temperature, and diurnal temperature difference are typically employed in EHE definitions;

2. duration—the number of consecutive days of extreme heat needed to constitute an EHE; the minimum duration for most definitions varies from 2 to 4 days;

3. threshold type—absolute, which is based on a daily heat metric threshold that does not change, or relative, which is based on an exceedance above a set percentile, which varies according to the underlying daily heat metric distribution for a given location; and

4. threshold intensity, which indicates the extremity of deviation considered to represent exposure to extreme heat. Most definitions refer to exceedances above absolute thresholds such as 90°, 95°, 100°, or 105°F or exceedances above relative thresholds such as 95th, 97th, 98th, or 99th percentiles.

Extreme heat exposures (distinct from EHEs) have been defined using thermal indices, which are derived based on human energy balance and incorporate physiological attributes as well as the effects of the thermal environment on human health (Cheng et al. 2012; Höppe 1999; Matzarakis et al. 1999; Nastos and Matzarakis 2012; Parsons 2014; Vanos et al. 2012). Additionally, EHEs have been defined using biometeorological indices that utilize ambient temperature and other relevant weather parameters; widely used examples of such indices are wet-bulb globe temperature (Budd 2008), apparent temperature (heat index) (Rothfusz 1990), humidex (Vaneckova et al. 2011), the Thom discomfort index (Thom 1959), and the spatial synoptic classification (SSC) (Sheridan et al. 2009). Of note is that the SSC is an airmass-based categorical classification system that is customized to a geographic area using retrospective health data and has been adopted by some local weather forecast offices in the United States (Hondula et al. 2014).

Within the context of the outline above, EHEs are defined using several daily heat metrics but are primarily based on meteorological variable deviations (e.g., temperature) from the historical norm, and a majority of studies have applied one definition to all climate regions. Studies that have evaluated EHEs are limited to a few geographic areas (Gasparrini and Armstrong 2011; Hajat et al. 2010; Ishigami et al. 2008) and extending definitions from such studies to the entire United States could result in the misidentification of EHEs in terms of human health effects. Some studies that have been published evaluated EHE definitions using health data (Anderson and Bell 2009; Hajat et al. 2010; Kent et al. 2014; Pascal et al. 2006; Zhang et al. 2012) but almost all of the studies conducted nationally failed to evaluate EHE definitions using data on health outcomes having a clear causal link to extreme heat. On the whole, there is a lack of consensus in the scientific literature on definitions and procedures to accurately identify periods of extreme heat having the potential for adverse health impacts.

Issuance of alerts and health advisories, prior to or during extreme weather events, can be critical to averting adverse health outcomes and is a service currently supported by weather and public health agencies involved in preparedness, response, and recovery operations. Alerts and health advisories are presumably most effective when based on weather event definitions that best reflect related health concerns. In this paper, we use episodes of extreme heat as an example to illustrate the application of a statistical framework within which to evaluate a candidate set of definitions in the context of heat mortality.

The evaluation is conducted by climate regions, recognizing that populations living under different prevailing climate conditions might adapt differently to weather-related exposures, including episodes of extreme heat (Davis et al. 2003), which in turn allows for the possibility that the most appropriate definitions might vary with climate region. Although we demonstrate the application of this framework to identify appropriate EHE definitions using county-level heat mortality data, the basic framework might also be applied to data describing other extreme weather events with well-established links to adverse health outcomes and, potentially, at other levels of geography.

Methods

Meteorological data

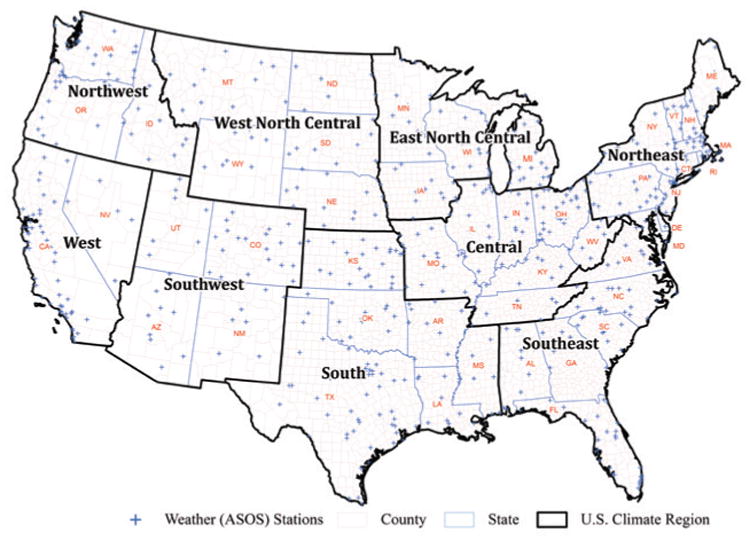
We used station-based meteorological data for the years 1999–2009, and any county in the contiguous United States (lower 48 states) that had an automated surface observing system (ASOS) unit (NOAA/NWS 1999) was considered for the present demonstration. We obtained these data from the National Oceanic and Atmospheric Administration's National Centers for Environmental Information (NCEI; www.ncei.noaa.gov/). The spatial coverage of the ASOS stations is shown in Fig. 1. For each station we adopted a completeness criterion requiring nonmissing values for at least 75% of the hourly weather observations in a given day (at least 18 of 24 hourly measurements) for purposes of calculating daily heat metric summaries. For each county and day, a county-level estimate was calculated as the average of all available station-level heat metric summaries. Counties with estimates for at least 95% of the days covered by the summer months (1 May– 30 September) of each individual year (1999–2009) were included in the demonstration dataset.

Fig. 1. Spatial coverage of ASOS weather stations with climate regions.

EHE definitions and core variables

For this study, we considered a number of EHE definitions that have been used in public health research and/or widely cited in the literature. Table 1 summarizes the different combinations of core variables used to define an EHE in this analysis. We used daily maximum temperature (T_max), daily maximum heat index (HI_max), daily average temperature (T_avg), and a combination of T_max and daily minimum temperature (T_min) as daily heat metrics; all heat metrics were represented in degrees Fahrenheit and we used the formula cited in Robinson (2001) to compute HI_max. We considered EHE definitions with both absolute and relative thresholds. Absolute thresholds were set at various intensity values, including 90°, 95°, 100°, and 105°F. Relative thresholds were calculated using two different approaches. We calculated percentile-based relative thresholds representing different intensities, including the 80th, 85th, 90th, 95th, 98th, and 99th percentile values and, for one definition, that of Huth et al. (2000),¹ we used the 81st and 97.5th percentile values. We computed these percentiles using heat metric data for the summer months for the years 1999–2009. We obtained station-level climate normal information from the NCEI, that is, the mean and standard deviation of the daily heat metrics computed based on data from 1981 to 2010 (Arguez et al. 2012); climate normals were unavailable for the heat index. We operationalized EHE definitions with minimum duration, that is, the number of consecutive days needed to constitute an EHE, variously ranging from 2 to 4 days. Varying minimum durations coupled with the various thresholds for each daily heat metric resulted in a total of 92 variants (Table 1). Table ES1 (in the online supplemental material; http://dx.doi.org/10.1175/BAMS-D-15-00181.2) provides precise details for each of these variants. We operationalized each EHE definition/variant using a binary [yes (1) or no (0)] variable, classifying each day in each county during the summer months as either an “EHE day” or a “non-EHE day.”² Days for which daily county-level data were not available could in some instances have interrupted a data sequence that might otherwise have qualified the surrounding days as EHE days. However, because of the high data completeness threshold employed, we believe any such effects to be minimal.

Table I. Core variables used in EHE definitions. Capital X's indicate definitions used in this analysis; boldface X's with asterisks indicate definitions published in the literature.

Daily heat metric	Duration (days)	Intensity
		Relative threshold							Climate-normal-based threshold		Absolute threshold
		P80	P85	P90	P95	P81/P97.5	P98	P99	Mean + one std dev	Mean + two std dev	90°F	95°F	100°F	105°F
Daily max temp (Tmax)	≥2			X*	X*		X*	X*	X	X	X	X*	X*	X*
	≥3		X*	X	X		X*	X*	X*	X*	X	X	X	X
	≥4		X	X	X		X*	X*	X	X	X	X	X	X
Daily avg temp (Tav)	≥2			X*	X*		X*	X	X	X	X	X*	X	X
	≥3		X	X	X		X	X	X*	X*	X	X	X	X
	≥4		X	X	X		X	X	X	X	X	X	X	X
Daily max heat index (HImax)	≥2			X*	X*		X*	X*			X*	X*	X*	X*
	≥3		X*	X	X		X*	X			X*	X*	X	X
	≥4		X*	X	X		X	X			X	X	X	X
Daily max and min temp (Tmax and Tmin.)	≥3	X*
Hutha	≥3					X*

^aPer Huth's definition, a heat wave is defined as the longest period of consecutive days satisfying the following three conditions: 1) the daily maximum temperature is above Tl (97. 5th percentile) for at least three consecutive days; 2) the daily maximum temperature is above T2 (81 th percentile) during the entire period; and 3) the average of daily maximum temperature over the entire period is greater than Tl.

Mortality data

We obtained mortality data from the National Center for Health Statistics (NCHS) National Vital Statistics System for the years 1999–2009 and identified records representing heat deaths based on International Classification of Diseases, 10th revision (ICD-10; www.who.int/classifications/icd/icdonlineversions/en/), external cause codes. Specifically, we selected death records for which exposure to excessive natural heat (ICD-10 code X30) was listed as the underlying cause of death; the underlying cause of death is defined as the disease or injury that initiated the chain of events leading to death (Hanzlick et al. 2006). We summarized the extracted death records for the summer months to obtain counts of heat deaths by county of residence and day. (County of residence was used as opposed to county where death occurred to facilitate calculation of population-based rates.) We then assigned the data for each county to one of the nine U.S. climate regions, which are aggregations of states based on homogeneous long-term climatology (Fig. 1); a description of these regions is available from the NCEI (www.ncdc.noaa.gov/monitoring-references/maps/us-climate-regions.php). Additionally, as a result of small death counts in the West North Central and Northwest regions, we combined these two regions into the “North West Central.” We excluded counties that did not have meteorological data (or that did not meet the completeness criterion for such data) and made adjustments to account for county boundary changes that occurred between 1999 and 2009 (www.census.gov/geo/reference/county-changes.html).

Population and other ancillary data

For incidence rate denominators we used county-level bridged-race population estimates developed by NCHS and the U.S. Census Bureau (www.cdc.gov/nchs/nvss/bridged_race.htm). In addition to the meteorological data described in the meteorological data section above, we note the availability of a number of county-level measures of health, behavior, and economic conditions that could influence heat-related health outcomes. Percentages of residents of all ages living in poverty and percentages of residents aged 0–64 years without health insurance are available from the U.S. Census Bureau; prevalence estimates of current adult smokers are available from the Centers for Disease Control and Prevention (CDC) Behavioral and Risk Factor Surveillance System; data on diabetes prevalence, adults that reported no leisure-time physical activity, and obesity prevalence (body mass index ≥ 30) are available from the CDC National Center for Chronic Disease Prevention and Health Promotion, Division of Diabetes Translation, while residential air conditioning prevalence data are available from a private vendor (efficiency 2.0). For the present demonstration, however, we felt that these data could not be meaningfully summarized across entire climate regions, as would be necessary for their inclusion in the modeling process described subsequently (see the section on rate regression modeling below). While EHEs tend to occur over broad geographic scales (and can thus be plausibly summarized across regions), measures such as those identified above might be expected to vary at more localized scales.

Evaluating EHE definitions using heat mortality data

Separately evaluating 92 different EHE definitions/variants and compiling results could become unmanageable from an operational standpoint; hence, we used cluster analysis as a preliminary data reduction technique to group EHE definitions into homogeneous sets. We differentiated any two EHE definitions based on county-day disagreements between the binary variables representing the operationalized definitions. For a given county and year, the total count of daily disagreements between two definitions is provided by the sum of the off-diagonal frequencies, as shown in Table ES2 in the online supplemental material to this article. (This sum represents the squared Euclidean distance between two vectors of binary variables.) Because the main research focus is on human health effects, these counts were weighted by the yearly county population estimates in order to ensure proportional representation. The population-weighted disagreement counts were then summed across counties (nationwide) and years to obtain an overall measure of disagreement (or distance) between the two EHE definitions. A distance matrix containing the overall disagreement measures for all pairs of EHE definitions (4,186 pairs) was used as input into the clustering procedure.

We applied a hierarchical clustering technique and employed an average distance metric to determine distances between clusters that might be merged in each step of the clustering process (Kalkstein et al. 1987; Zhang et al. 1996). Average distance is calculated using the formula

$$\sum _{i=1}^{n_a}\sum _{j=1}^{n_b}\frac{d(C{a}_i,C{b}_j)}{n_a\times n_b},$$ (1)

where Ca and Cb are two disjoint clusters; n_a and n_b are the number of members within clusters Ca and Cb, respectively; and d is the squared Euclidean distance between two members of the two disjoint clusters.

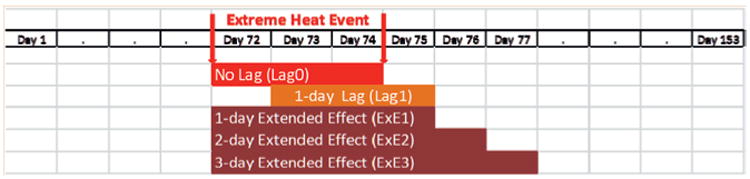
We divided the final hierarchical cluster (one large cluster encompassing all definitions) into smaller clusters, taking into consideration various diagnostics including the R-squared, pseudo-F, and pseudo-t-squared indices. Based on these diagnostics, we identified relatively distinct high-level clusters. One representative EHE definition was then selected from each high-level cluster. Representative definitions were selected according to the following criteria: 1) EHE definitions/variants that are well recognized in the literature, 2) application in studies conducted in the United States, and 3) application in nationally representative studies (i.e., those studies that covered the various climate regions of the United States). Recognizing the possibility of delayed or extended health effects associated with EHEs, each representative EHE definition was combined with the following exposure offsets: no lag (i.e., no offset), a 1-day lag, and 1-, 2-, and 3-day extended (post-EHE) effects (Fig. 2).

Fig. 2. Exposure offsets.

Rate regression modeling

We applied rate regression models to evaluate the relationship between operationalized EHE definitions and heat deaths. The following model was used to estimate the death rate per person day for each EHE definition/variant and exposure offset combination:

$$log(E[D]P)=\alpha +{\beta }_{\text{region}}+{\beta }_{\text{EHE}}\times \text{EHE}+{\beta }_{\text{EHE}.\text{Region}}\times \text{EHE}\times \text{Region},$$ (2)

with model terms defined as follows: D is the count of deaths for each combination of region, year, and EHE status;³ E[D] is the expected count of deaths; P is the number of person-days of exposure for which D is measured; α is the intercept; β_region is the inter cept offset for the climate region; β_EHE is the effect parameter for the binary variable representing the operationalized EHE definition/variant and exposure offset combination; EHE is the binary variable representing the operationalized EHE definition/ variant and exposure offset combination; β_EHE.Region is the effect parameter for the interaction between the region and EHE; and Region is the classification (indicator) variable for the region.

To compensate for overdispersion, we specified a negative binomial link. Using this modeling approach, we estimated region-specific baseline rates of the heat death (in the absence of an EHE) and region-specific EHE rates of heat death (in the presence of an EHE). We termed the estimated increases in rates due to EHEs as “EHE effects.”

We used the estimated EHE effects to identify the “best” EHE definition/variant and exposure offset combinations for each region. One might hypothesize that there is some “gold standard” EHE definition that best explains heat mortality; the various EHE definitions considered in this evaluation represent approximations to this hypothetical gold standard. The extent to which each operationalized EHE definition deviates from the hypothetical gold standard can be expected to materialize in the form of attenuation bias (i.e., weaker estimated EHE effects than might be ideally attained). By this reasoning, the strongest estimates, presumably corresponding to those with the least attenuation bias, are assumed to best represent the gold standard. We tested this reasoning by simulating various “ideal” datasets, each with health outcomes following a probability distribution conforming to a different (and arbitrary) gold standard EHE definition, and then observing the influence of deviations from the gold standard. The steps in our simulation exercise are described in Fig. 3.

Fig. 3. Simulation exercise to test the attenuation bias concept.

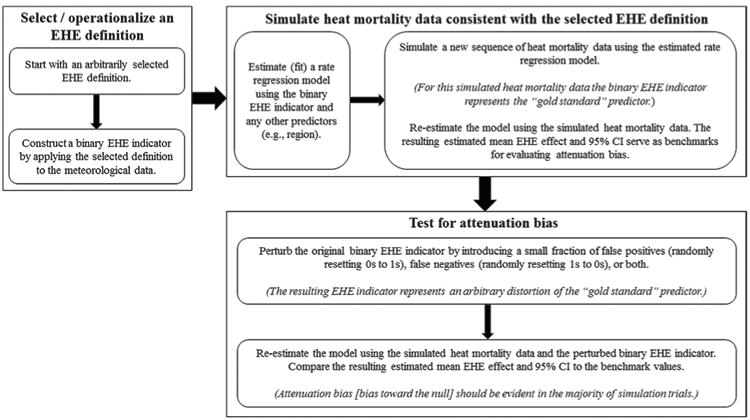
After the simulation exercise indicated that the attenuation bias concept is applicable to our situation, we employed model (2) to identify the EHE definition/ variant and exposure offset combinations having the strongest effect estimates. We evaluated each of the EHE definitions/variants selected as high-level cluster representatives crossed with the five exposure offsets and ranked the results in descending order based on the lower confidence limit associated with each EHE effect estimate, for each climate region. Further, to characterize the region-specific differences in population-level susceptibility to extreme heat, we conducted a random effects meta-analysis, by region, based on the 10 “best” region-specific EHE definition/variant and exposure offset combinations, to estimate the mean baseline rate, the mean EHE effect, and associated confidence intervals (CIs) for each region. We carried out our data analyses using the Statistical Analysis System (SAS version 9.3), Environmental Systems Research Institute's GIS software (ESRI, ArcGIS version 9.3), and comprehensive meta-analysis software (CMA version 2.0).

Results

Table 2 summarizes the number of heat deaths and counties with meteorological data, by climate region. A total of 3,829 heat deaths were identified for the contiguous United States during the summer months of 1999–2009, and 2,218 (58%) of these deaths were among residents of counties with meteorological data meeting the stated completeness criterion (complete data). For the latter group the state of residence and the state where death occurred were the same in 94% of cases; the county of residence and the county where death occurred were the same in 83% of cases and in another 6% of cases the counties were geographically adjacent. The average fraction of the U.S. population living in counties with complete meteorological data was 57% over the 11-yr period considered here. The South region had the largest number of counties with complete meteorological data (n = 91) and also the largest number of heat deaths (n = 481) among residents of those counties. The West region had the smallest number of counties (n = 38) with complete meteorological data, although counties in this region are notably among the most geographically expansive. The North West Central region, which was formed by combining the Northwest and West North Central regions, had the smallest number of heat deaths (n = 72) among residents of counties with complete meteorological data.

Table 2. Heat deaths (U.S. residents) and counties with meteorological data, by climate region, 1999–2009.

U.S. climate region	No. of heat deaths	No. of counties with complete meteorological data	No. of heat deaths in counties with complete meteorological data	Percentage of regional population living in counties with complete meteorological data
Central	640	78	314	49
East North Central	150	54	93	49
Northeast	474	70	212	47
Northwest	70	40	51	73
South	890	91	481	60
Southeast	541	71	224	49
Southwest	508	43	367	64
West	508	38	455	92
West North Central	48	48	21	42
Total contiguous United States	3,829	533	2,218	57

Figure 4 shows a dendrogram (or cluster tree), which depicts the sequential clustering of the EHE definitions/variants in a hierarchical manner. We delineated the final high-level clusters, taking into consideration the R-squared, pseudo-F, and pseudo-t-squared indices (data not shown). The break points were also influenced by subjective assessments of the homogeneity of members within clusters and the heterogeneity across clusters. We ultimately settled on five high-level clusters. We labeled each high-level cluster to reflect the underlying feature(s) common to the definitions/variants comprising it. Cluster 1 was the first cluster delineated and it contains only definitions/variants that are based on absolute thresholds for several of the daily heat metrics. Cluster 2 contains definitions/variants based on thresholds that are predominantly moderate in intensity. Cluster 3 contains definitions/variants based on thresholds that are slightly more severe than those for cluster 2. Cluster 4 contains definitions/variants based on thresholds that are predominantly extreme in nature. Cluster 5 consists of definitions/variants that rely on relative thresholds constructed from long-term climate-normal data, with thresholds that are predominantly low. Table ES3 in the online supplemental material lists the EHE definition/ variant that was selected as the representative from each high-level cluster. The five representative EHE definitions/variants crossed with the five exposure offsets resulted in 25 different combinations to be evaluated using the rate regression modeling framework.

Fig. 4. Dendrogram of hierarchical clusters.

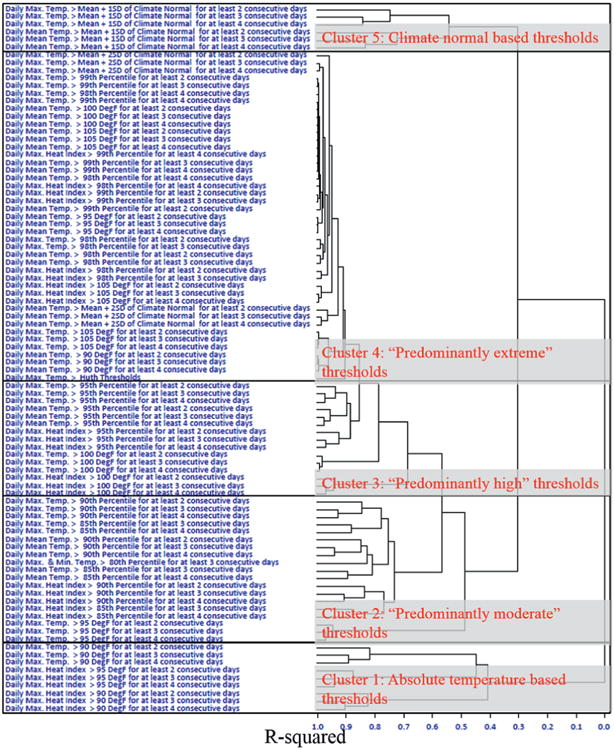
Table 3 ranks the EHE definition/variant and exposure offset combinations by climate region. The representative definition/variant from cluster 3, daily maximum temperature greater than the 95th percentile for at least two consecutive days, is most strongly associated with heat mortality for six of the eight climate regions. The combinations of this definition/ variant with exposure offsets representing a 1-day lag (Lag1) or no lag (Lag0) show the strongest estimated EHE effects for all regions except the Southwest and South. The representative definition/variant from cluster 1, daily maximum heat index greater than 90°F for three consecutive days, combined with each of the different exposure offsets, shows the strongest estimated EHE effects for the Southwest. The representative definition/variant from cluster 4, the Huth definition, was the best definition for the South but generally shows the weakest estimated EHE effects for other regions. The representative definition/variant from cluster 2, daily maximum and minimum temperature greater than the 80th percentile for at least three consecutive days, ranked fairly high (depending on the exposure offset) for the Central, Northeast, and Southeast regions; Lag1 and Lag0 represent the best exposure offsets. The representative definition/variant from cluster 5, daily mean temperature greater than the mean plus one standard deviation of the long-term climate normal for at least three consecutive days, shows the weakest estimated EHE effects overall. For most regions, no one definition/variant is distinctly superior to all others. We also provide a table in the online supplement (see Table ES4) that describes other metrics such as the percentage of days classified as EHE days and percentage of heat deaths covered by EHE days for each representative EHE definition/variant and exposure offset combination.

Table 3. Rankings of representative EHE definition and exposure offset combinations derived using the statistical framework, by U.S. climate region. The table values highlighted in bold are the top 5 EHE definition and exposure offset combinations for that region.

EHE definition	Exposure offset type	Ranking and EHE effect by climate regions
		Central		East North Central		North West Central		Northeast		South		Southeast		Southwest		West
		Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)	Rank	EHE effect (95% CI)
Daily max heat index greater than 90°F for at least 3 consecutive days	ExE1	10	13.1 (8.4, 20.4)	7	19.0 (10.7, 33.8)	6	21.7 (13.6, 34.7)	10	10.9 (5.9, 20.3)	14	5.3 (3.3, 8.6)	14	4.4 (2.6, 7.3)	4	10.4 (6.4, 16.9)	7	7.1 (4.7, 10.7)
	ExE2	13	12.6 (8.1, 19.7)	6	19.5 (10.9, 34.7)	5	22.0 (13.7, 35.3)	11	9.9 (5.3, 18.3)	11	5.7 (3.5, 9.5)	12	4.9 (2.8, 8.3)	2	11.6 (7.1, 19.0)	8	7.0 (4.6, 10.6)
	ExE3	14	12.1 (7.7, 19.1)	9	17.4 (9.7, 31.2)	8	20.1 (12.4, 32.5)	14	8.7 (4.7, 16.1)	12	5.8 (3.5, 9.8)	4	6.4 (3.5, 11.5)	1	11.7 (7.1, 19.4)	9	6.6 (4.4, 10.1)
	Lag0	15	11.3 (7.3, 17.4)	10	15.6 (8.8, 27.7)	10	17.3 (10.9, 27.5)	5	12.6 (6.8, 23.5)	20	4.6 (2.9, 7.2)	16	4.3 (2.6, 7.0)	5	9.5 (5.9, 15.1)	4	7.4 (4.9, 11.1)
	Lagl	5	14.8 (9.5, 23.0)	3	22.6 (12.7, 40.1)	2	22.3 (14.0, 35.5)	6	11.8 (6.3, 22.1)	15	5.2 (3.3, 8.3)	13	4.4 (2.7, 7.3)	3	10.9 (6.8, 17.6)	5	7.4 (4.9, 11.1)
Daily max and min temp greater than the 80th percentile for at least 3 consecutive days	ExEl	6	14.8 (9.3, 23.5)	12	13.9 (7.7, 24.8)	11	16.8 (10.3, 27.2)	9	11.0 (5.9, 20.6)	19	4.7 (3.0, 7.4)	9	5.6 (3.3, 9.5)	7	7.0 (4.5, 11.0)	13	5.4 (3.5, 8.3)
	ExE2	7	14.5 (9.2, 23.0)	13	13.7 (7.7, 24.4)	12	16.7 (10.3, 27.0)	13	9.3 (5.0, 17.2)	16	4.8 (3.1, 7.4)	7	5.6 (3.4, 9.3)	8	6.8 (4.4, 10.6)	14	5.0 (3.3, 7.8)
	ExE3	9	13.8 (8.7, 21.8)	15	12.2 (6.9, 21.8)	15	14.6 (9.0, 23.7)	15	8.0 (4.3, 14.9)	18	4.7 (3.0, 7.2)	6	5.6 (3.4, 9.2)	12	6.3 (4.0, 9.7)	15	4.9 (3.2, 7.5)
	Lag0	4	15.2 (9.6, 24.0)	14	12.5 (7.0, 22.4)	14	15.1 (9.4, 24.4)	3	13.0 (7.0, 24.2)	13	5.1 (3.3, 8.0)	5	6.0 (3.5, 10.1)	9	6.6 (4.2, 10.3)	12	5.6 (3.6, 8.6)
	Lagl	2	17.0 (10.7, 27.0)	11	15.3 (8.5, 27.4)	9	19.4 (12.0, 31.6)	8	11.5 (6.1, 21.7)	17	4.8 (3.1, 7.6)	10	5.5 (3.2, 9.4)	6	7.9 (5.0, 12.5)	11	5.8 (3.7, 9.0)
Daily max temp greater than the 95th percentile for at least 2 consecutive days	ExEl	3	16.1 (10.1, 25.7)	2	23.5 (13.0, 42.4)	4	22.8 (13.8, 37.7)	2	14.0 (7.4, 26.6)	4	7.1 (4.5, 11.3)	2	6.2 (3.7, 10.4)	11	6.6 (4.1, 10.7)	3	8.0 (5.1, 12.4)
	ExE2	8	14.4 (9.1, 22.9)	4	21.7 (12.1, 39.1)	3	22.8 (13.9, 37.6)	7	11.6 (6.2, 21.8)	6	6.4 (4.1, 10.2)	8	5.6 (3.4, 9.4)	15	6.0 (3.7, 9.6)	6	7.4 (4.8, 11.5)
	ExE3	12	13.1 (8.3, 20.7)	5	20.2 (11.2, 36.3)	7	20.7 (12.6, 34.1)	12	9.5 (5.1, 17.8)	7	6.3 (4.0, 9.9)	11	4.8 (2.9, 8.0)	13	6.0 (3.8, 9.6)	10	6.7 (4.3, 10.3)
	Lag0	11	13.7 (8.4, 22.5)	8	18.2 (9.8, 33.6)	13	15.9 (9.4, 27.0)	1	14.9 (7.6, 29.0)	3	7.5 (4.6, 12.2)	1	7.2 (4.2, 12.5)	14	6.3 (3.8, 10.5)	2	8.3 (5.2, 13.2)
	Lagl	1	18.8 (11.6, 30.6)	1	31.0 (16.9, 56.7)	1	24.8 (14.8, 41.7)	4	13.7 (7.0, 26.9)	2	7.6 (4.6, 12.4)	3	6.2 (3.5, 10.8)	10	6.8 (4.1, 11.3)	1	9.5 (5.9, 15.1)
Huth definition	ExEl	22	5.5 (3.0, 10.1)	20	11.0 (5.6, 21.6)	22	7.7 (4.0, 14.7)	23	4.6 (1.5, 14.0)	5	7.3 (4.2, 12.7)	25	3.6 (1.7, 7.7)	22	3.0 (1.5, 6.1)	23	5.1 (2.4, 10.9)
	ExE2	24	5.3 (2.9, 9.6)	21	10.6 (5.5, 20.5)	23	7.4 (3.9, 13.9)	24	3.8 (1.2, 11.8)	8	6.8 (3.9, 11.8)	23	3.7 (1.8, 7.7)	23	2.9 (1.5, 5.8)	19	5.4 (2.6, 11.2)
	ExE3	25	4.7 (2.6, 8.5)	25	9.3 (4.8, 18.0)	24	6.6 (3.5, 12.4)	25	3.3 (1.1, 10.2)	10	6.4 (3.7, 11.2)	24	3.6 (1.8, 7.3)	24	2.7 (1.4, 5.3)	22	4.9 (2.4, 10.1)
	Lag0	23	5.5 (3.0, 10.3)	23	10.5 (5.2, 20.9)	25	5.9 (2.9, 11.9)	21	5.6 (1.8, 17.2)	9	6.6 (3.8, 11.7)	22	3.9 (1.8, 8.5)	25	2.3 (1.1, 5.2)	24	4.9 (2.2, 10.9)
	Lagl	21	5.9 (3.2, 10.8)	16	13.2 (6.7, 25.8)	21	8.6 (4.5, 16.7)	22	5.6 (1.8, 17.3)	1	8.3 (4.8, 14.4)	21	4.3 (2.0, 9.1)	21	3.6 (1.8, 7.4)	25	4.9 (2.2, 10.9)
Daily mean temp greater than mean + one std dev of climate normal for at least 3 consecutive days	ExEl	17	7.7 (4.8, 12.4)	19	10.4 (5.7, 18.9)	17	10.8 (6.5, 17.9)	17	5.6 (3.0, 10.5)	24	3.2 (2.0, 5.1)	18	4.2 (2.5, 6.9)	17	3.7 (2.3, 5.9)	17	4.2 (2.7, 6.7)
	ExE2	19	7.4 (4.6, 11.9)	18	10.6 (5.8, 19.3)	18	10.2 (6.2, 16.9)	19	4.6 (2.5, 8.6)	22	3.2 (2.0, 5.1)	19	3.8 (2.3, 6.3)	19	3.7 (2.3, 5.8)	20	4.1 (2.6, 6.4)
	ExE3	20	6.9 (4.3, 11.0)	22	9.8 (5.4, 18.0)	20	9.0 (5.4, 14.9)	20	3.9 (2.1, 7.4)	25	3.0 (1.9, 4.7)	20	3.7 (2.2, 6.0)	18	3.7 (2.3, 5.8)	21	4.0 (2.5, 6.2)
	Lag0	18	7.6 (4.7, 12.3)	24	9.0 (5.0, 16.4)	19	10.1 (6.1, 16.6)	16	6.0 (3.2, 11.4)	23	3.2 (2.0, 5.1)	17	4.2 (2.5, 7.0)	20	3.5 (2.2, 5.5)	18	4.2 (2.6, 6.6)
	Lagl	16	8.7 (5.4, 14.0)	17	12.0 (6.6, 21.6)	16	11.2 (6.8, 18.5)	18	5.0 (2.6, 9.5)	21	3.4 (2.1, 5.4)	15	4.3 (2.6, 7.1)	16	3.8 (2.4, 6.0)	16	4.5 (2.9, 7.2)

Table 4 provides the results of the random effects meta-analyses of the estimated baseline rates and EHE effects, based on the 10 best EHE definition/variant and exposure offset combinations, for each climate region. The North West Central region shows the lowest mean (95% CI) baseline rate, 1.8 (1.5–2.2) deaths per one billion person-days of risk, and the highest mean (95% CI) EHE effect of 22.0 (17.7–27.3). The South region shows the highest mean (95% CI) baseline rate of 10.0 (8.8–12.0) deaths per one billion person-days of risk. The lowest mean EHE effect of 6.2 (4.9–7.9) was observed in the Southeast. In general, colder regions of the United States show a relatively low baseline rate and a relatively high EHE effect, while the warmer regions of the United States show a relatively high baseline rate and a relatively low EHE effect.

Table 4. Meta-analyzed baseline rate and EHE effect by U.S. climate region.

U.S. climate region	Mean (95% CI) baseline heat mortality rate (deaths per person day) × 10–9	Mean (95% CI) EHE effect
Central	4.1 (3.5–4.8)	15.0 (12.2–18.4)
East North Central	2.3 (1.9–2.8)	20.7 (15.9–26.9)
North West Central	1.8 (1.5–2.2)	22.0 (17.7–27.3)
Northeast	2.9 (2.4–3.5)	13.1 (9.9–17.4)
South	10.0 (8.8–12.0)	7.1 (5.7–8.8)
Southeast	3.8 (3.2–4.5)	6.2 (4.9–7.9)
Southwest	5.0 (4.1–6.0)	10.1 (8.1–12.5)
West	4.7 (4.0–5.5)	7.6 (6.2–9.2)

Summary and Perspectives

EHE definitions used for issuing alerts in most heat warning systems are calibrated to the extreme end of the daily heat metric spectrum. As noted by Hajat et al. (2010), our findings similarly suggest that using a definition that only identifies extremely hot days may have a greater tendency to introduce false negatives and thereby underestimate the risks associated with extreme heat, whereas using a less stringent threshold for EHE definitions may have a greater tendency to introduce false positives and thereby overestimate the risks. Additionally, prior approaches to evaluating EHE definitions that relied on mortality data mostly considered deaths due to all causes (Gasparrini and Armstrong 2011; Hajat et al. 2010; Zhang et al. 2012). The relationship between all-cause mortality and extreme heat is confounded by other factors, including long-term trends in mortality and various sociodemographic factors (Anderson and Bell 2009; Reid et al. 2009; Semenza et al. 1996). While this may also be true of the relationship between heat-related health outcomes and extreme heat, the extent of confounding might be expected to be less pronounced because of the presumably stronger causal link between the exposure and such outcomes.

To the best of our knowledge, the framework described here represents the first nationally consistent scheme for evaluating definitions of extreme weather events, within the context of adverse health outcomes with clear causal links to exposures characterized by such definitions. The framework, applied here to the evaluation of EHE definitions, employs cluster analysis to identify homogeneous groupings of event definitions followed by rate regression modeling to estimate the effects for representatives from these groupings. It provides a cohesive approach to identifying those definitions (and their variants) most closely associated with the adverse health outcome(s) of interest. Moreover, the approach can also shed light on definitions that are most weakly associated with adverse health outcomes. For example, in our demonstration, EHE definitions with thresholds that are either too extreme or too moderate tend to be among those most weakly associated with heat mortality for most climate regions.

Extending the basic framework to include a random effects meta-analysis proved useful in summarizing baseline health risks and event-specific effects for different climate regions. As exemplified in this demonstration, the warmer regions of the United States appear to have relatively modest EHE effects coinciding with relatively high baseline rates, whereas colder areas of the United States have relatively strong EHE effects coinciding with low baseline rates. This may indicate that in warmer regions, some summer days that are not classified as EHE days are nonetheless warm enough to put susceptible populations at an elevated risk for adverse heat-related health outcomes. To the extent that this might elevate estimated baseline rates, it would simultaneously offset estimated EHE effects. Prior knowledge of such geographic differences in health risks over an event timeline (preevent, event, and postevent) could potentially assist public health practitioners and emergency planners with advance preparations for extreme weather events.

While our demonstration relied on heat mortality data to evaluate EHE definitions, the general framework might be applied to other adverse health outcomes with well-established links to extreme weather events. Further, considering a fuller range of outcome severity, including nonfatal hospitalizations and emergency department visits, might allow application of the framework at finer levels of geography such as cities and/or greater metropolitan areas. Applying the framework at finer geographic scales could facilitate the integration of measures reflecting local population attributes into the modeling process, as potential con-founders or modifiers of the relationship between extreme weather and related health outcomes. For example, air conditioning (a material adaptation) is a significant protective factor for heat-related health outcomes (Reid et al. 2009). Studies have also shown differing degrees of susceptibility to extreme heat among different ethnic groups (Klinenberg 2002; Klinenberg 2003). Incorporating such factors into the evaluation scheme might also provide information useful for community-specific response plans.

There are some limitations to the present demonstration. Because we used station-based measurements as the source of the ambient heat data, approximately 40% of heat deaths nationwide were excluded. While sparseness in the region-wide numbers of heat deaths did not lead to convergence or statistical power issues in the modeling process, it prevented us from conducting an evaluation at a finer geographic scale. However, our ultimate goal was not to evaluate different EHE definitions but rather to present a general statistical framework for ranking EHE definitions, independent of geographic resolution to the extent possible. Relying on ambient weather data may also misrepresent true individual-level exposures, particularly in regions where summertime indoor climate control is widely employed (Davis et al. 2003) and in places where weather stations are not in close proximity to population centers. Further, this study did not consider daily heat metrics that are calculated using sophisticated algorithms and/or involve several synoptic weather parameters to identify EHEs; however, in this regard at least one other study noted a high degree of agreement among different temperature metrics used to characterize EHEs (Barnett et al. 2010). Finally, the mortality data used to test our framework are based on death certificates, which in some instances could lead to misclassification of deaths resulting from extreme heat exposure (Combs et al. 1999).

Conclusions

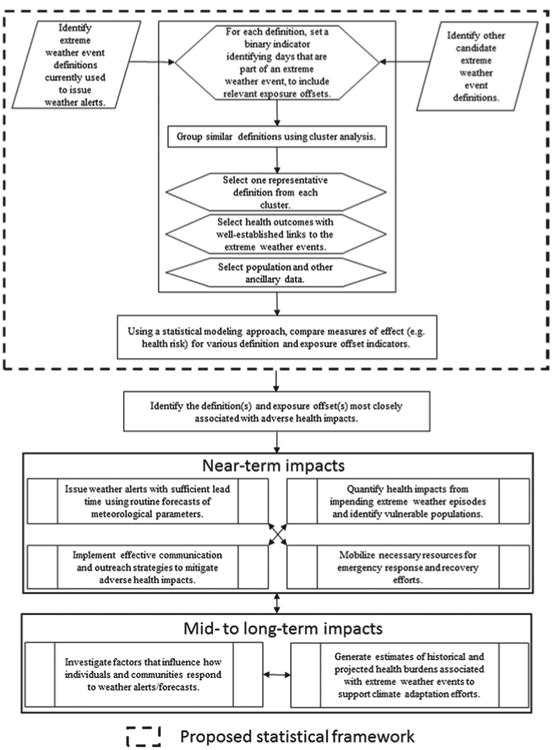
Increasingly, collaborations between public health and weather agencies are growing into a community of practice with an interest in examining the impacts of a wide range of extreme weather events on human health and the accompanying economic burdens. The evaluation framework proposed here, based on systematic but flexible statistical components, could be adopted by this community of practice to validate existing (or newly proposed) definitions of extreme weather events used to issue alerts and mitigate adverse health impacts. The schematic presented in Fig. 5 illustrates how the proposed framework might be adopted by agencies involved in emergency preparedness and response operations and identifies potential end-user benefits resulting from identifying definitions that are most appropriate from a health perspective. For example, once the definitions for extreme heat most directly associated with heat-related health outcomes have been identified, statistical modeling approaches could be extended to quantify all excess deaths and illnesses associated with EHEs over historical (decadal) time scales, provided the necessary meteorological and health data are available. Noting that climate change is projected to increase the frequency and/or magnitude of EHEs (Morss et al. 2011), estimates of the historical (and projected) health burden associated with EHEs might help identify vulnerable populations and also inform adaptation efforts.

Fig. 5. Potential uses of the statistical framework.