Principles of Experimental Design for Big Data Analysis

Abstract

Big Datasets are endemic, but are often notoriously difficult to analyse because of their size, heterogeneity and quality. The purpose of this paper is to open a discourse on the potential for modern decision theoretic optimal experimental design methods, which by their very nature have traditionally been applied prospectively, to improve the analysis of Big Data through retrospective designed sampling in order to answer particular questions of interest. By appealing to a range of examples, it is suggested that this perspective on Big Data modelling and analysis has the potential for wide generality and advantageous inferential and computational properties. We highlight current hurdles and open research questions surrounding efficient computational optimisation in using retrospective designs, and in part this paper is a call to the optimisation and experimental design communities to work together in the field of Big Data analysis.

1. Introduction

In this ‘Big Data’ age, massive volumes of data are collected from a variety of sources at an accelerating pace. Traditional measurements and observations are now complemented by a wide range of digital data obtained from images, audio recordings and other sensors, and electronic data that are often available as real-time data streams. These are further informed by domain-specific data sources such as multi-source time series in finance, spatio-temporal monitors in the neurosciences and geosciences, internet and social media in marketing and human systems, and ‘omic’ information in biological studies.

Many of these data sets have the potential to provide solutions to important problems in health, science, sociology, engineering, business, information technology, and government. However, the size, complexity and quality of these data sets often makes them difficult to process and analyse using standard statistical methods or equipment. It is computationally prohibitive to store and manipulate these large data sets on a single desktop computer and one may instead require parallel or distributed computing techniques that involve the use of hundreds or thousands of processors. Similarly, the analysis of these data often exceeds the capacity of standard computational and statistical software platforms, demanding new technological or methodological solutions. This motivates the development of tailored statistical methods that not only address the inferential question of interest, but also account for the inherent characteristics of the data, address potential biases and data gaps, and appropriately adjust for the methods used to deal with the storage and analysis of the data.

A number of break-through approaches have emerged to address these challenges in managing, modelling and analysing Big Data. With respect to data management, the most popular current approaches employ a form of ‘divide-and-conquer’ or ‘divide-and-recombine’ (e.g., Xi et al. (2010); Guhaa et al. (2012)) in which subsets of the data are analysed in parallel by different processors and the results are then combined. Similar approaches have also been promoted, such as ‘consensus Monte Carlo’ (Scott, Blocker and Bonassi, 2013) and ‘bag of little bootstraps’ (Kleiner et al., 2014), while others have studied the properties of Markov chain Monte Carlo (MCMC) subsampling algorithms (Bardenet, Doucet and Holmes, 2014, 2015).

With respect to modelling, the focus has turned from traditional statistical models to more scalable techniques that can more successfully accommodate the large sample sizes and high dimensionality. Some popular classes of scalable methods are based on dimension reduction such as principal components analysis (PCA) and its variants (Kettaneha, Berglund and Wold, 2005; Elgamal and Hefeeda, 2015), clustering (Bouveyrona and Brunet-Saumard, 2014), variable selection via independence screening (Fan and Lv, 2008; Fan, Feng and Rui Song, 2011) and least angle regression (Efron et al., 2004). Other methods have been developed for specific types of data, such as sequential updating for streaming data (Schifano et al., 2015) or sketching (Liberty, 2013). Many popular statistical software packages such as R are also starting to include libraries of models for Big Data (Wang et al., 2015). The development of these methods represents an active point of intersection in both the statistical and machine learning communities (Leskovec, Rajaraman and Ullman, 2014) under the umbrella of Data Science.

Finally, the library of computational algorithms for the analysis of Big Data has also been multi-focused. Because of the size of the data, traditional estimation methods have been overshadowed by optimisation algorithms such as gradient descent and stochastic approximations (Liang et al., 2013; Toulis, Airoldi and Renni, 2014) and a wide variety of extensions and alternatives (Fan, Han and Liu, 2014; Cichosz, 2015; Suykens, Signoretto and Argyriou, 2015). Many algorithms also exploit sparsity in high-dimensional data to improve speed, efficiency and scalability of algorithms; see, for example, Hastie, Tibshirani and Friedman (2009).

Summaries of these technological, methodological and computational approaches can be found in a number of excellent reviews (e.g., Fan, Han and Liu (2014); Wang et al. (2015)). Reviews of discipline-specific methods for analysing Big Data are also emerging (e.g., Yoo, Ramirez and Juan Liuzzi (2014); Gandomi and Haider (2015); Oswald and Putka (2015)). Despite the highlighted advantages, almost all of these authors concur that substantial challenges still remain. For example, Fan, Han and Liu (2014) identify three ongoing challenges: dealing adequately with accumulation of errors (noise) and spurious patterns in high-dimensional data; continuing to improve computational and algorithmic efficiency and stability; and accommodating heterogeneity, experimental variations and statistical biases associated with combining data from different sources using different technologies. Indeed, given the acceleration of size and diversity of data, it could be argued that these will remain as stumbling blocks for the foreseeable future.

In this paper, we explore an alternative approach that has the potential to circumvent or overcome many of these issues. Our approach is targeted toward applications of regression models with large N number of observations and small to moderate p predictors, so called ‘tall data’ situations (see also Bardenet, Doucet and Holmes (2015) and Xi et al. (2010)). We suggest that, depending on the aim of the analysis, one could adopt an optimal experimental design perspective whereby instead of (or as well as) analysing all of the data, a retrospective sample set is drawn in accordance with a sampling plan or experimental design, based on an identified statistical question and corresponding utility function. The analyses and inferences are then based on this designed sample. This allows the analyst to consider an ideal experiment or sample to answer the question of interest and then ‘lay’ that experiment over the data. Thus the Big Data management challenge becomes one of being able to extract the required design points; the modelling problem reduces to a designed analysis with reduced noise and less potential for spurious correlations and patterns relative to a randomly selected sub-sample of the same size.

There are several Big Data inferential goals for which this approach might be applicable. Goals for which design principles and corresponding utility functions are well established include estimation and testing of parameters and distributions, prediction, identification of relationships between variables, and variable selection. Other aims include identification of subgroups and their characteristics, dimension reduction and model testing.

The suggested approach can also be considered as a targeted way of undertaking sampling in divide-and-conquer algorithms or for “sequential learning” in which a given design is applied to incoming data or new data sets until the question of interest is answered with sufficient precision or a pre-determined criterion is reached. It can also be used for evaluating the quality of the data, including potential biases and data gaps, since these will become apparent if the required optimal or near-optimal design points cannot be extracted from the data.

Finally, it is worth emphasising that this approach is a first exploration into the potential for retrospective experimental design for improved Big Data analysis. Many open research questions and challenges exist, not least of which the is need for new computational optimisation methods coupled to design criteria that can deliver a targeted sample set in a time compatible with that of a randomised sampling strategy.

2. Brief Overview of Experimental Design

In this section we provide a brief introduction to the principles of optimal experimental design that are relevant to our approach, referring the interested reader to Appendix A for a more extensive background overview.

The design of experiments is an example of decision analysis where the decision is to select the optimal experimental settings, d, under the control of the investigator in some design space of options, d ∈ D. This is to maximise the expected return as quantified through a known utility function, U (d, θ, y), that depends on some, possibly unknown, state of the world θ ∈ Θ and on a potential future dataset y ∈ Y that may be observed when design d is applied. For example, in a regression analysis with continuous response Y , measurement covariates X, and where the study objective is to learn about the parameters θ of a mean regression function, E[Y] = f(X; θ); then the design space might be points in X with, d ∈ D ⊆ X, and the utility function might be based on the variance of an unbiased estimator $\widehat{\mathit{\theta }}=S(Y,X)$ that targets the true unknown θ.

Following the Savage axioms (Savage, 1972) the coherent way to proceed is to select the design that maximises the expected utility,

$$\begin{array}{l}{\mathit{d}}^{\mathbf{*}}=\text{arg}\underset{d\in \text{D}}{\text{max}}{E}_{\text{Y},\Theta }\left\{U\left(\mathit{d},\mathit{\theta },\mathit{y}\right)\right\}\\ =\text{arg}\underset{d\in \text{D}}{\text{max}}{\displaystyle {\int }_{\text{Y}}{\displaystyle {\int }_{\Theta }U\left(\mathit{d},\mathit{\theta },\mathit{y}\right)p\left(\mathit{y}|\mathit{\theta }\right)}}p\left(\mathit{\theta }\right)d\mathit{\theta }d\mathit{y}\mathbf{.}\end{array}$$ (1)

In classical experimental design, the utility is often a scalar function of the Fisher information matrix, which already considers the expectation with respect to the future data y, and in this case we can write the utility as U (d, θ) and the integral over y is no longer required. Further, if the model parameter θ is assumed known then the problem reduces to an optimization task over the design space. When θ is unknown the expected utility can be considered with respect to the distribution of θ, p(θ), which is a probability measure that quantifies the decision maker’s current state of uncertainty on the unknown value of θ. This is often referred to as a pseudo-Bayesian design, as the prior information p(θ) is discarded upon the collection of the actual data.

In a fully Bayesian experimental design, the utility function is often some functional of the posterior distribution, p(θ|y, d). For example, a common parameter estimation utility is U (d, y, θ) = log p(θ|y, d) − log p(θ), which is the Shannon information gain. Integrating with respect to θ produces the Kullback-Leibler divergence between the prior and the posterior, U (d, y) = KLD(p(θ)||p(θ|y, d)). If the KLD can be computed/approximated directly, the integral over θ is not required. In this case the expected utility is formed by integrating over the prior predictive distribution, p(y|d). Integrals are typically approximated by Monte Carlo methods (see, for example, Drovandi and Tran (2016)).

Of relevance to what follows, in some experimental design situations one may not be able to sample at specific design points or regions, so that D is restricted, in which case “design windows” or “sampling windows” may be required. These consist of a range of near optimal designs and represent regions of planned sub-optimality. Examples of the use of sampling windows include the design of population pharmacokinetic studies (e.g., Ogungbenro and Aarons (2007); Duffull et al. (2012)), which consisted of specific sampling time intervals.

3. Experimental Design in the Context of Big Data

As motivation we consider a general regression set up where the response data Y ∈ Y^N consists of N observations and the ith response Y_i ∈ Y ⊆ ℝ^m is the realisation of an m dimensional random variable. Covariate or predictor information is provided in the matrix X ∈ X^N where the ith row is X_i ∈ X ⊆ ℝ^p where p is the number of predictors. We assume that N is very large and that p is small relative to N. Our objective is to avoid the analysis of the Big Data of size N by selecting a subset of the data of size n_d using the principles of optimal experimental design where the goal of the analysis is pre-defined. Below we outline a sequential design approach that can achieve this in a sub-optimal but computationally feasible manner and then point to some possible extensions.

3.1. The Algorithm

At a high level, the experimental design principles described in Section 2 can be applied directly to a Big Dataset in order to obtain a sub-sample. Here we consider a generic procedure inspired by sequential experimental design in order to obtain a close-to-optimal sub-sample of the data with respect to a pre-defined goal of the analysis. This is shown in Algorithm 1. There are two main motivations for our sequential approach: (1) iteratively gain information so that in subsequent iterations more informative data can be extracted, and (2) an optimal design problem only needs to be solved for a single observation at each iteration. In the algorithm d ∈ D ⊆ X represents some or all values of the covariates for a hypothetical single observation. We denote as x ∈ X values for the covariates for a single observation that is actually present in the dataset. Let x_s ∈ D be the covariate values for a single observation in the dataset that correspond to the same covariates in d. We denote the observed response corresponding to x as y, re-defining the notation y used in Section 2. We now denote the potential future observation collected at design d as y_d.

Algorithm 1 Proposed algorithm to subset Big Data using experimental design methodology.

• 1:Use a training sample of size n_t to obtain $\widehat{\mathit{\theta }}$ or to form a prior distribution p(θ). Set n_c = n_t.
• 2:while n_c ≤ n_d (where n_c is the current sample size, and n_d is the desired sample size) or when the goal of the analysis is not met do
• 3:   Solve the optimisation problem d* = arg max_d∈D E{U (d, θ, y_d)}. Note that U (d, θ, y_d) may not depend on θ and/or y_d depending on the utility function selected.
• 4:   Find x in the remaining dataset that has not already been sampled such that ||x_s − d*|| is minimised. Take the corresponding observation y. This step may be performed multiple times to subsample a batch of data of size m, ${\{{\mathit{x}}_i,{\mathit{y}}_i\}}_{i=1}^m$. Increase the size of the subsample, n_c = n_c + m.
• 5:   Add ${\{{\mathit{x}}_i,{\mathit{y}}_i\}}_{i=1}^m$ into the data subset and re-estimate $\widehat{\mathit{\theta }}$ or update the prior p(θ) using all available data in the subset. Remove the data ${\{{\mathit{x}}_i,{\mathit{y}}_i\}}_{i=1}^m$ from the original dataset.
• 6:end while

The objective is to first solve a design optimisation problem with the utility function incorporating the goal of the analysis (e.g. parameter estimation), which produces an optimal d*. It is important to note that this design optimisation problem is informed by the data currently in the subsample in the form of a point estimate $\widehat{\mathit{\theta }}$ or a ‘prior’ distribution p(θ), which is a posterior conditional on the data sampled thus far. Given that d* is unlikely to be exactly present in the data, as a pragmatic approach we propose to find the x in the remaining dataset that has not been sampled that minimises the distance ||x_s − d*|| between the relevant covariate values of each observation and the optimal design d*. Finally, take the corresponding y and update the information we have about the parameter θ.

It is interesting to note that when selecting a sub-sample of size n_d from the Big Data of size N, the optimal search would involve a comparison across all of the ${(}_{n_d}^N)$ potential designs, which is computationally prohibitive. Hence we propose to solve an approximate, but computable design problem, by first searching over all designs d in D, and then subsequently searching in the Big Dataset for the best matching collection of samples x minimising the distance to the approximating design solution d*. If at each step of our sequential design process the utility function U (d, θ, y) and model p(θ, y, x) are “smooth” in the design space d, meaning that for a small change in the design we can expect a small change in the expected utility, then for Big Data we can expect to lose little information from using this computable approximation.

3.2. Algorithm Discussion

For classical analysis problems, the training sample is an important component of the algorithm, since it affects the reliability of the parameter estimates. The training sample size n_t is likely to depend on the quality of the data available and the complexity of the data analysis that is to be performed. In the context of a Bayesian analysis, the training sample is used to form a prior distribution. The more data used in the training sample, the more precisely parameter estimates (classical) or parameters (Bayesian) can be determined, which helps to facilitate more optimal choices of data to take from the original dataset during subsequent iterations. However, the training sample is not optimally extracted from the data and therefore one may want to limit its size. We suggest that the training data can be selected on the basis of a design with generally “good” properties, e.g. balance, orthogonality etc.

Line 3 of Algorithm 1 is the most challenging. If the number of design variables (covariates) is small enough then a simple discrete grid search might suffice to obtain a near-optimal design. For more complex design spaces, it may be necessary to perform some numerical optimisation procedure. Some approaches that been used in the design literature are the exchange algorithm (e.g., Fedorov (1972)), numerical quadrature (e.g., Long et al. (2013)), MCMC simulation (e.g., Müller (1999)), or sequential Monte Carlo methods (e.g., Kück, de Freitas and Doucet (2006); Amzal et al. (2006)). This step of the algorithm may be computationally intensive and is currently the largest stumbling block for the general applicability of our approach. However, we demonstrate in several case studies in Section 5 that our approach is applicable in a number of non-trivial settings. Nonetheless, there is interest in developing new approaches to accelerate this step, which is an on-going research direction in the experimental design literature.

To reduce the number of design optimisations that need to be performed we may extract from the Big Data a cluster of m data points where the x_s is closest to d* (Line 4 in Algorithm 1). The optimal value of m trading off problem specific computational cost versus information loss, although we do not explore this further. In other applications using standard design criteria, such as D-optimality, means that the optimal design may be simple to determine (e.g., Pukelsheim (1993); Tan and Berger (1999); Ryan, Drovandi and Pettitt (2015)).

In the examples we consider later, we find that the Euclidean distance for the norm ||x_s − d*|| on standardised covariates works reasonably well. It should be noted that the user is free to choose an appropriate norm for their data.

To reduce the computational burden to implement Line 4 in Algorithm 1, the data set may need to be split up amongst multiple CPUs using a framework such as Hadoop. The minimisation problem (Line 4) can be performed on each of the CPUs, and then a minimisation can be performed over the results of all of the CPUs. This is similar to the “split-and-conquer” approach (e.g., Xi et al. (2010)). Rather than finding an optimal design that consists of fixed points, as in Line 3 of Algorithm 1, we could instead find sampling windows, since the optimal design points d* may not be present in the data set, and so we may require regions of near optimal designs. Moreover, in Line 2, one could instead run the algorithm until the utility function reached a certain pre-specified value (e.g. a certain level of precision).

A similar design algorithm is considered in follow-up studies, where only a small proportion of subjects are measured on the second occasion to reduce costs (Karvanen, Kulathinal and Gasbarra, 2009; Reinikainen, Karvanen and Tolonen, 2014). In these studies, the objective is to determine the best n out of N individuals to consider for the next follow-up. This difficult computational problem is solved by Karvanen, Kulathinal and Gasbarra (2009) and Reinikainen, Karvanen and Tolonen (2014) in a greedy manner by sequentially adding participants for the next follow-up that lead to the largest improvement in expected information gain until n subjects are selected. Our approach is different to this. Firstly, it is not feasible in our context to scan through the entire Big Data to find the next observation that leads to the largest improvement in expected or observed utility. Instead we solve an optimal design problem first, and then we simply need to find the design in the Big Data that is close to this optimal design. Secondly, our design approach uses the information from each selected data point to make better decisions about which design (and observation) to include next. In contrast, the applications of Karvanen, Kulathinal and Gasbarra (2009) and Reinikainen, Karvanen and Tolonen (2014) are static design problems (parameter values are not updated) that are solved in an approximate sequential manner. Thirdly, our approach allows for the detection of potential holes in the data. Finally, our framework is more general as it is inclusive of both classical and Bayesian frameworks, whereas Karvanen, Kulathinal and Gasbarra (2009) and Reinikainen, Karvanen and Tolonen (2014) only consider classical designs.

3.3. Computational Overheads

The key challenge in the practical application of our approach is being able to implement algorithms, such as Algorithm 1, in a computational time such that the extra effort of obtaining design points does not outweigh the information benefits. That is, if n_d is the maximum sample size available through the designed approach given the constraints in compute infrastructure and runtime, and n_s is the corresponding sample size from using random subset selection. For our approach to be worthwhile we require that the expected utility of the designed approach learned from n_d samples is higher than the expected utility using n_s random samples, where typically n_s > n_d. Clearly this will be study dependent but, given the potential benefits shown below, it also motivates the need for new computational optimisation strategies targeted to general design criteria for Big Data analysis.

4. Simulation Study

Here we apply our methods to data that is simulated from a logistic regression model that contains two covariates, x₁ and x₂. The following logistic model is used to describe the binary response variable Y_i ∼ Binary(π_i) where logit(π_i) = θ₀ + θ₁x_1,i + θ₂x_2,i. We assume that the true parameter values are (θ₀, θ₁, θ₂) = (−1, 0.3, 0.1) and that the sample size for the full data set is N = 10000. Although N is small for Big Data it will serve to illustrate and motivate the essential features of our approach. We simulate the covariate values of x₁ and x₂ for each observation from a multivariate normal distribution with a mean vector of zeros and three different options for the covariance matrix:

1. $\left[\begin{array}{ll}3\hfill & \hfill 0\hfill \\ 0\hfill & 3\hfill \end{array}\right]$, no dependence between covariates;

2. $\left[\begin{array}{cc}3& 1.5\\ 1.5& 3\end{array}\right]$, positive correlation between covariates;

3. $\left[\begin{array}{cc}3& -1.5\\ -1.5& 3\end{array}\right]$, negative correlation between covariates.

Here we are interested in finding the ‘best’ n_d = 1000 observations from the full data set to most precisely estimate the model parameters (θ₀, θ₁, θ₂). We demonstrate the use of both classical and Bayesian sequential design methods to subset the data.

The design variable for line 3 of Algorithm 1 is given by potential values for the two covariates for a single observation, d = (x₁, x₂).

4.1. Classical Approach

For line 1 of Algorithm 1 we select n_t = 20 training samples randomly from the full data and determine the MLE of the parameter, $\widehat{\mathit{\theta }}$. We denote the data present in the subset currently as $𝒟$_s, which consists of response and covariate values. The utility function we use for line 3 is given by

$$U(\mathit{\text{d}})=\left|\mathcal{O}({\mathcal{D}}_s,\widehat{\mathit{\theta }})+\mathcal{I}(\mathit{\text{d}},\widehat{\mathit{\theta }})\right|,$$

where $\mathcal{O}({\mathcal{D}}_s,\widehat{\mathit{\theta }})$ is the observed information matrix based on data collected so far and $\mathcal{I}(\mathit{d},\widehat{\mathit{\theta }})$ is the expected information matrix if we apply the design d for the next observation. For the optimal design procedure in line 3 of Algorithm 1 we use a grid search over the design region [−5, 5] × [−5, 5]. The grid consists of evenly-spaced points that are separated by an increment of 0.1.

Once the optimal design d* is estimated from line 3 we use the Euclidean distance in line 4 to determine the next observation to take from the remaining Big Data. Following this, the parameter estimate $\widehat{\mathit{\theta }}$ is updated using maximum likelihood in line 5. Then the process is repeated. Conditional on the training sample, the overall subsetting procedure is deterministic so we only perform the procedure once and obtain a single subset of size 1000. We denote the subsetted data generated from our design procedure as ${\mathcal{D}}_s^d$.

For comparison purposes we generated 10000 subsets of size 1000 randomly, with each subset denoted by ${\mathcal{D}}_s^{r_i}$ for r = 1, …, 10000. The final estimates for (θ₀, θ₁, θ₂) based on ${\mathcal{D}}_s^d$ are given in Table 1. Table 1 also displays $\left|\mathcal{O}({\mathcal{D}}_s^d,\widehat{\mathit{\theta }})\right|$ where for notational simplicity the MLE $\widehat{\mathit{\theta }}$ is always based on the dataset present as the first argument of the observed information matrix. The largest observed information obtained out of the 10000 randomly sampled data subsets is displayed in the final column of Table 1. Each row of Table 1 corresponds to the different correlation structures that were investigated for the simulated covariate data. Table 2 contains the estimates for (θ₀, θ₁, θ₂) (and their associated variance-covariance matrix) based on the full data under each of the covariance structures for the covariate data.

Table 1.

Estimated θ values (where θ = (θ₀, θ₁, θ₂)) and the observed information value for the subsample of size n_d = 1000 obtained using the principled design approach $(|\mathcal{O}({\mathcal{D}}_s^d,\widehat{\mathit{\theta }})|)$. The last two columns contain the median (IQR) and maximum utility function values that were obtained from 10000 randomly drawn subsamples of data, each of size n_d = 1000

Covariance Structure	$\widehat{\mathit{\theta }}\hspace{0.17em}\text{based}\hspace{0.17em}\text{on}\hspace{0.17em}{𝒟}_s^d$	$|𝒪(D_s^d,\widehat{\mathit{\theta }})|$	median$(|𝒪({𝒟}_s^{r_i},\widehat{\mathit{\theta }}){|}_{i=1}^{10000})$ (IQR)	max$(|𝒪({𝒟}_s^{r_i},\widehat{\mathit{\theta }}){|}_{i=1}^{10000})$
No correlation	(−1.03, 0.34, 0.11)	2.8 × 108	5.3(4.9, 5.8) × 107	9.0 × 107
Positive correlation	(−1.01, 0.32, 0.08)	1.4 × 108	3.9(3.6, 4.2) × 107	6.0 × 107
Negative correlation	(−0.94, 0.41, 0.17)	8.0 × 107	4.1(3.8, 4.5) × 107	6.6 × 107

Table 2.

Estimated θ values (where θ = (θ₀, θ₁, θ₂)) and their covariance using the full data sets that were simulated under different covariance structures of X.

Covariance Structure of X	$\widehat{\mathit{\theta }}$	Estimated covariance of $\widehat{\mathit{\theta }}$
No correlation	(−0.98, 0.28, 0.08)	$\left[\begin{array}{ccc}5.4\times {10}^{-4}& -6.5\times {10}^{-5}& -2.1\times {10}^{-5}\\ -6.5\times {10}^{-5}& 1.9\times {10}^{-4}& 8.5\times {10}^{-6}\\ -2.1\times {10}^{-5}& 8.5\times {10}^{-6}& 1.8\times {10}^{-4}\end{array}\right]$
Positive correlation	(−1.02, 0.30, 0.08)	$\left[\begin{array}{ccc}5.6\times {10}^{-4}& -7.3\times {10}^{-5}& -1.9\times {10}^{-5}\\ -7.3\times {10}^{-5}& 2.6\times {10}^{-4}& -1.2\times {10}^{-4}\\ -1.9\times {10}^{-5}& -1.2\times {10}^{-4}& 2.4\times {10}^{-4}\end{array}\right]$
Negative correlation	(−1.00, 0.29, 0.08)	$\left[\begin{array}{ccc}5.4\times {10}^{-4}& -6.4\times {10}^{-5}& -1.9\times {10}^{-5}\\ -6.4\times {10}^{-5}& 2.4\times {10}^{-4}& 1.1\times {10}^{-4}\\ -1.9\times {10}^{-5}& 1.1\times {10}^{-4}& 2.3\times {10}^{-4}\end{array}\right]$

From Table 1 it can be seen that the estimates of (θ₀, θ₁, θ₂) that were based on the subsets of data that were obtained via the principled design approach are quite close to the true parameter values, as well as the values that were obtained using the full data set (displayed in Table 2). Only a small amount of precision for the parameter estimates was lost by using the subset of data rather than the full dataset (Tables 1 and 2). This indicates that our method is fairly accurate in this example for subsetting the data so that our model parameters can be estimated precisely. One run of the optimal design process had a similar computational time to running 10000 random subsets (approximately 40 seconds). However, the determinants of the observed information from the subsets of data that were obtained via our design approach were higher than the determinant of the observed information obtained from 10000 randomly selected data subsets of the same sample size (Table 1). This highlights the potential of our designed approach.

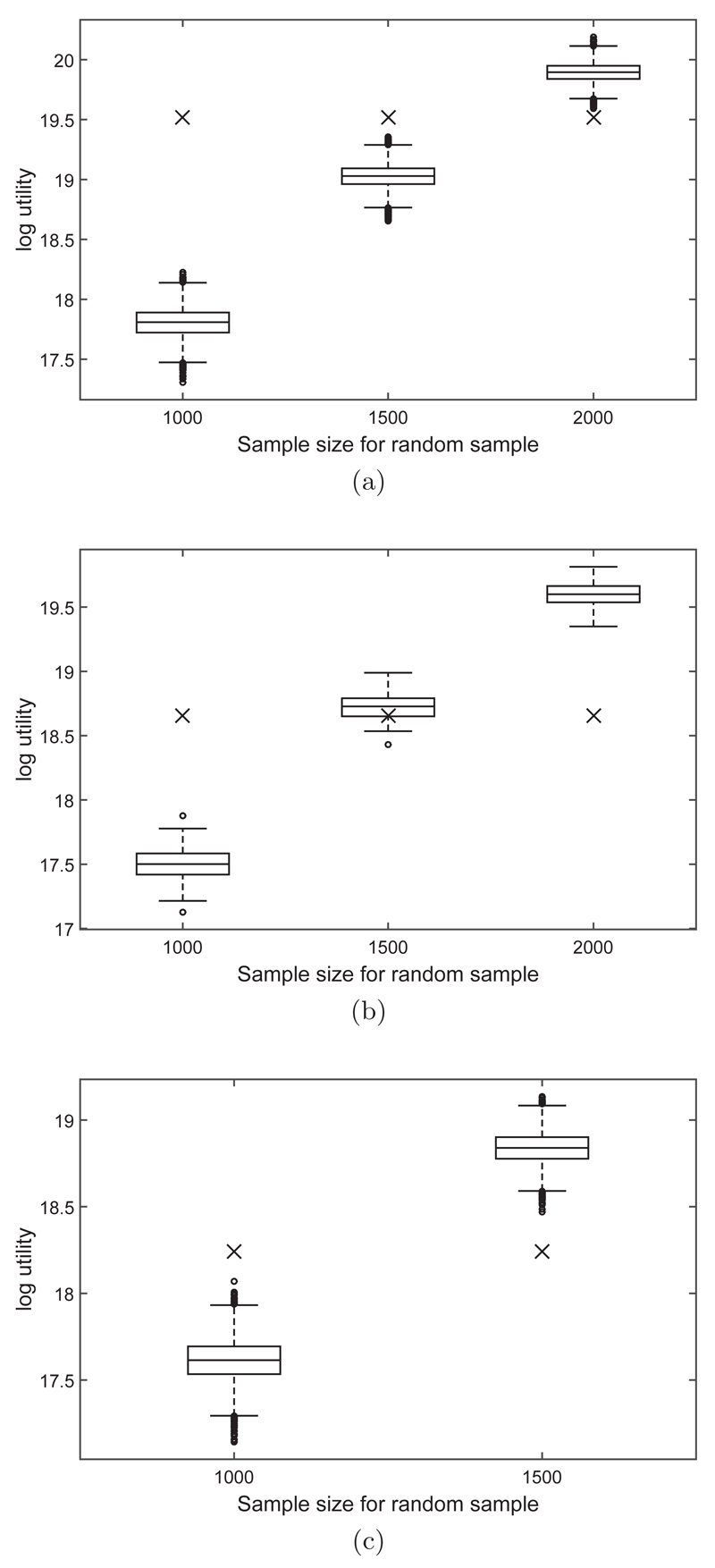
However, the extra time used to determine the designed subset could be used to analyse a larger random sample. We investigated different sample sizes for the subsets that were selected randomly from the full data set and ran 10000 replicates for each sample size. The results are displayed in Figure 1. For the simulation studies where the data were generated using a covariate structure with no correlation, or with positive correlation, the randomly selected data subset size had to be roughly doubled to obtain a higher utility (overall) than for the designed approach. For the simulation study where the data were generated using negative correlation between the covariates, the subset size of 1500 showed higher utility than the designed approach. We provide more discussion on the negative correlation case later.

Fig 1.

Boxplots of the log utility (determinant of the observed information matrix) for 10000 randomly drawn data subsets of various sample sizes (x-axis) to compare against the utility function value of the designed approach (for a data subset size of 1000; displayed as a cross in each boxplot), for each of the correlation structures of the covariates: (a) no correlation between x₁ and x₂, (b) positive correlation between x₁ and x₂, (c) negative correlation between x₁ and x₂.

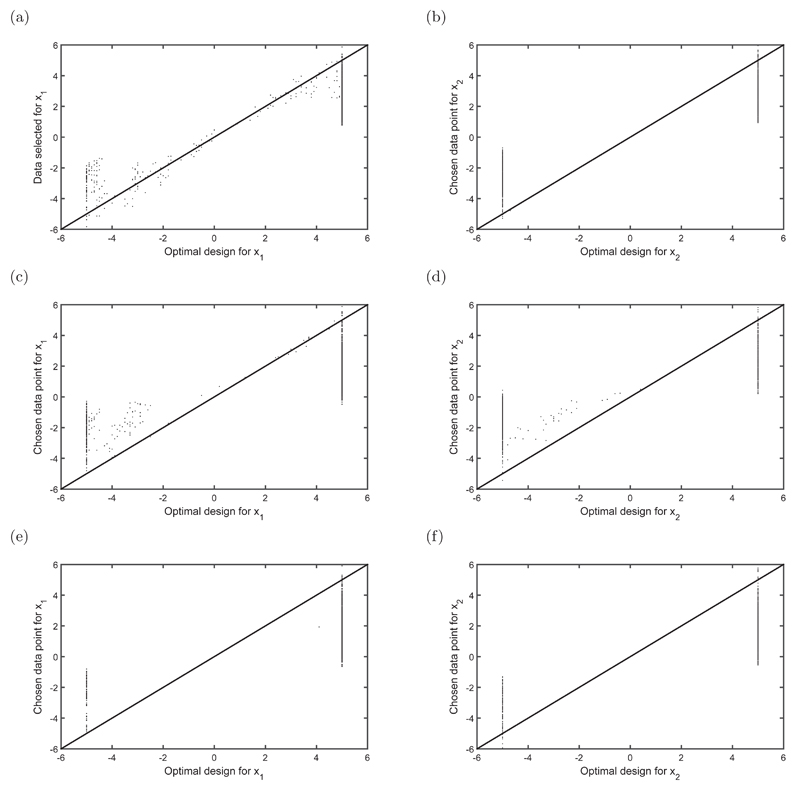
Figure 2 shows the x values that minimise the Euclidean distance to the optimal designs at each iteration/time point based on the observed information thus far (and were thus extracted into the subset) against the optimal designs at that iteration. Ideally, these points should be equal and would lie along the 45 degree line in Figure 2. From Figure 2, it appears that there are two support points for both x₁ and x₂, one at either end of the design region. Since the covariates were drawn from a normal distribution, there are not many design values in the data that occur on the boundaries of the design region, and so less than optimal values will have to be chosen for the data subset and the data will be less informative than if the full dataset contained more values on the boundaries of the design region. When the covariates are correlated with one another, there are even less design values on the “corners” or boundaries of the design region and so the full dataset will be generally less informative. We discuss this further in the Bayesian section below.

Fig 2.

Chosen designs for x₁ and x₂ vs optimal designs for x₁ and x₂ where the correlation structures for the covariates are: (a) and (b) no correlation between x₁ and x₂; (c) and (d) positive correlation between x₁ and x₂; (e) and (f) negative correlation between x₁ and x₂. The 45 degree line indicates where the selected data points for the subset are equal to the optimal design.

4.2. Bayesian Approach

For the Bayesian approach we use an SMC algorithm, similar to that used by Drovandi, McGree and Pettitt (2013), to sequentially generate samples from the posterior as more data are added into the subsample. We place independent normal priors on the parameters each with a mean of 0 and a standard deviation of 5; we do not use any training data in line 1 of Algorithm 1. For the utility function required in line 3 we use:

$$U\left(\mathit{d},y\right)=-\text{log}\text{det}\left(\text{cov}\left(\mathit{\theta }|\mathit{d},{𝒟}_s,y\right)\right),$$

where $𝒟$;_s represents the data currently in the subset and y ∈ {0, 1} is a possible outcome for the next observation. The expected utility is given by

$$U\left(\mathit{d}\right)={\displaystyle \sum _{y\in \left\{0,1\right\}}U\left(\mathit{d},y\right)p\left(y|\mathit{d},{𝒟}_s\right).}$$

The quantities inside the summation are estimated using the posterior samples maintained through SMC and additional importance sampling to accommodate the possible outcomes for the next observation (see Drovandi, McGree and Pettitt (2013) for more details). The optimisation procedure used in line 3 is the same as that used for the classical approach above. For line 4 we again use the Euclidean distance to obtain the next observation to add to the subset in line 5. This process is repeated until 1000 observations are obtained. The final posterior mean estimates from one run of our sequential design approach for (θ₀, θ₁, θ₂) are given in Table 3, along with the estimates based on the full data set.

Table 3.

Posterior estimates of θ (where θ = (θ₀, θ₁, θ₂)) and the observed utility using the data subset obtained via the designed approach and using the full data sets that were simulated under different covariance structures of X.

Full or subset data	Covariance Structure of X	$\widehat{\mathit{\theta }}$	observed utility
Subset	No correlation	(−1.11, 0.33, 0.11)	18.9
Full	No correlation	(−1.02, 0.31, 0.10)	24.7
Subset	Positive correlation	(−0.91, 0.27, 0.13)	19.3
Full	Positive correlation	(−1.00, 0.31, 0.10)	24.4
Subset	Negative correlation	(−1.04, 0.31, 0.15)	17.3
Full	Negative correlation	(−1.03, 0.32, 0.12)	24.6

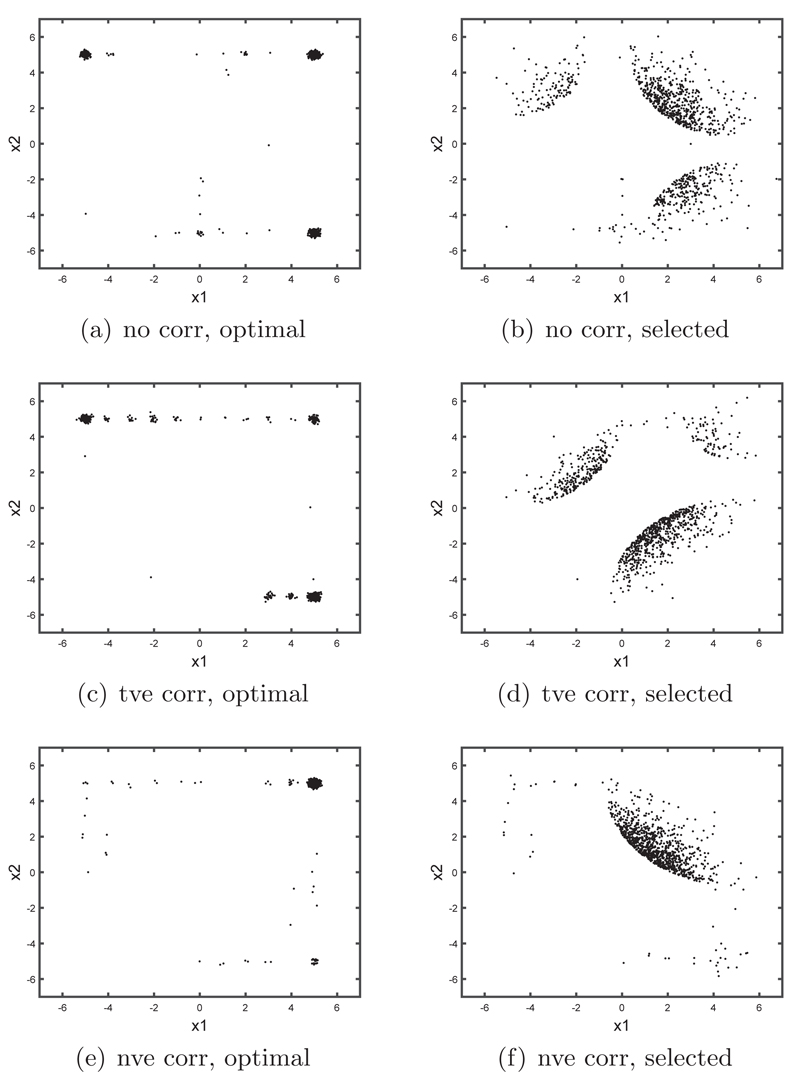
For one run of our algorithm, the optimal designs and the corresponding covariate values actually extracted from the data are shown in Figure 3 for the three different correlation structures. Most of the optimal design values appear in the ‘corners’ of the design search space. When there is no correlation between the predictors, it is easier to find covariate values that are close to the optimal design values (top row of Figure 3). When there is correlation (middle and bottom rows of Figure 3), the corners of the design space are not as well covered by the data. We found that this was a particular issue when there was negative correlation. It can be seen from the bottom row of Figure 3 that the optimal design requested by the algorithm was often in the top right corner but there was no data there to satisfy this request. Thus there is a chance that the actual data selected may not have a relatively high utility value. In this respect, below we demonstrate that the optimal design approach can perform worse than a simple random sample. We plan to develop methods to address this issue in future research. In the least, plots as in Figure 3 can be used as an exploratory tool to determine how close the data subsample is to the ideal design for the chosen research objectives.

Fig 3.

Left hand column shows the optimal designs (with slight jittering) selected for one run of Algorithm 1 for the Bayesian logistic regression example. The right hand column shows the corresponding covariate values that were actually selected from the data. Results are shown for different covariance structures of X in the original (full) data: (top row) no correlation, (middle row) positive correlation, and (bottom row) negative correlation.

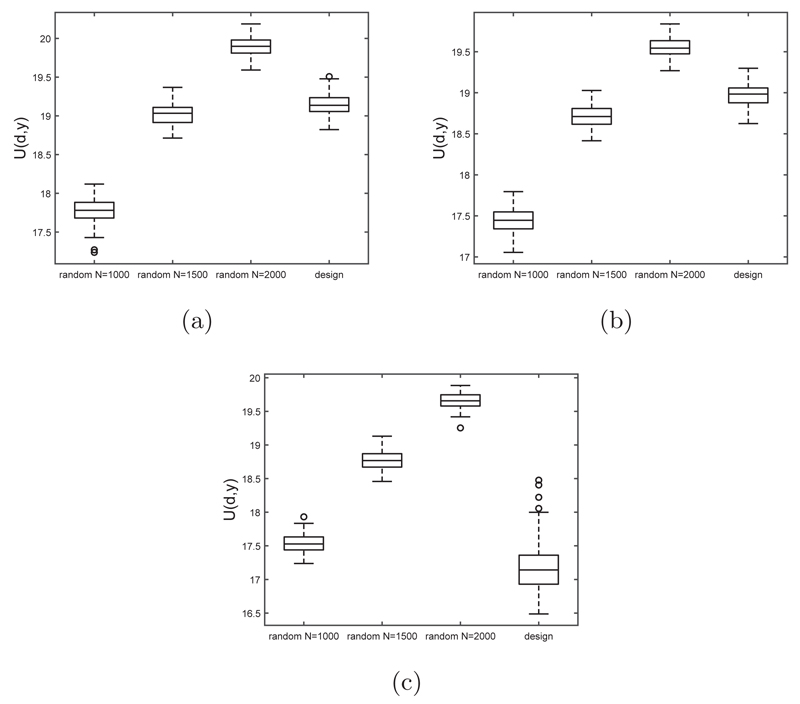
The subset obtained from our method is affected by the Monte Carlo variability of the SMC approximation to the posteriors and also the Monte Carlo variability from the importance sampling procedure to determine the optimal designs. Thus we repeated our process 1000 times independently. To determine how well our data subsets perform, we compared it to randomly selected datasets of size 1000 from the original dataset. We obtained 1000 such datasets. For each of these randomly chosen datasets we estimated the posterior distribution via SMC, which was then used to estimate the utility function. The distribution of the utility values obtained from our subsets is compared with that of the random datasets in Figure 4. It can be seen that our data subset outperforms the randomly selected designs as it generally produces a higher utility value then the randomly chosen datasets, except for the negative correlation structure (see earlier discussion). One run of the optimal design process took approximately 22 seconds, whereas investigating 1000 random subsets took approximately 25 minutes. Therefore we were generally able to obtain a data subset of a particular size that produced higher observed utility in a shorter amount of time.

Fig 4.

Boxplots of the observed utility values obtained for 1000 runs of a random design and the optimal sequential design for the Bayesian logistic regression example for the different covariance structures of X in the original (full) data.

To determine the sample size savings for the designed approach (compared to random subsets of data), we varied the size of the subsets that were selected randomly from the full data set and repeated this process 100 times. The results are displayed in Figure 5. It was found that the random sample data subset would have to be increased to a size of 1500-2000 to obtain an overall higher utility than for the designed approach, except for the negative correlation structure.

Fig 5.

Boxplots of the observed utility values obtained for 100 runs of randomly drawn data subsets of various size (x-axis) and the optimal sequential design for the simulation study for the different covariance structures of X in the original (full) data: (a) no correlation, (b) positive correlation, and (c) negative correlation.

Overall, in this simulation study, analysing a larger random subset would be more efficient than analysing the smaller designed subset. However, this example still demonstrates the potential of the designed approach.

5. Case Studies

The two case studies described here showcase our principled design approach applied to real data. Algorithm 1 is used together with a number of computational algorithms. For the purposes of cohesion and comparison, the first study employs a logistic regression model to predict risk of mortgage default, whereas the second study employs a more challenging mixed effects model. The cases differ with respect to the study aims; variable selection and precise regression parameter estimation. Comparisons are also made with results obtained from analysing the full (Big) data.

To further illustrate our design approach to subsetting Big Data, two additional case studies are provided in Appendices B and C, respectively. The case study in Appendix B is similar in spirit to case study 1 and involves the estimation of regression coefficients of covariates that might influence on-time flight arrivals. The case study in Appendix C highlights that experimental design principles may be useful in some applications for subsetting Big Data without needing to resort to optimal design methods such as those presented in Algorithm 1. This case study involves applying static experimental design principles for performing an ANOVA on a dataset of colorectal cancer patients in Queensland, Australia.

5.1. Case Study 1 - Mortgage default

In this case study, we consider the simulated mortgage defaults data set found here: http://packages.revolutionanalytics.com/datasets/. The scenario is that data have been collected every year for 10 years on mortgage holders, and contains the following variables:

• default: a 0/1 binary variable indicating whether or not the mortgage holder defaulted on the loan (response variable);

• creditScore: a credit rating (x₁);

• yearsEmploy: the number of years the mortgage holder has been employed at their current job (x₂);

• ccDebt: the amount of credit card debt (x₃);

• houseAge: the age (in years) of the house (x₄); and

• year: the year the data were collected.

The proposed model for the binary outcome is the logistic regression model, with the above covariates as main effects (credit rating, years employed, credit card debt and house age) potentially significantly influencing the probability of defaulting. To determine which covariates are useful for prediction, we focus on the default data for the year 2000 which contains 1,000,000 records. We initially allowed all covariates to appear in the model, and obtained prior information about the parameters by extracting a random selection of n_t = 5, 000 data/design points from the full dataset in an initial learning phase.

From this initial learning phase, it is useful to develop prior distributions about the model(s) appropriate for data analysis and the corresponding parameter values based on the extracted data. The primary motivation for this is the avoidance of the computational burden associated with continually considering a potentially large dataset within a (full) Bayesian analysis. To facilitate this, maximum likelihood estimates (MLEs) of parameters (and standard errors) were found for all potential models. Prior information about the parameters was then constructed by assuming all parameters follow a normal distribution with the mean being the MLE and the standard deviation being the standard error of the MLE.

The next step was to ‘value add’ to the information gained from the initial learning phase through our sequential design process. To do this, we implemented the SMC algorithm of Drovandi, McGree and Pettitt (2013) to approximate the sequence of target distributions which will be observed as data are extracted from the full data set (see Section 4.2). For line 3 of Algorithm 1 we used a similar estimation utility to the simulation study in Section 4.2 to select designs which should yield precise estimates of the model parameters, and this utility was approximated via importance sampling. The optimisation procedure we apply in line 3 is again a simple grid search by considering potential design points based on all combinations of the following covariate levels (formed by inspecting the full data set):

Covariate	Scaled levels
creditscore	−4,−3,−2,−1, 0, 1, 2, 3, 4
yearsemploy	−2,−1, 0, 1, 2, 3, 4
ccDebt	−2,−1, 0, 1, 2, 3, 4
houseAge	−2,−1, 0, 1, 2

This results in the consideration of 2,205 potential design points at each iteration of the sequential design process. For line 4 we find the data point in the remaining Big Data with a design closest to the optimal design in terms of Euclidean distance.

As we are interested in determining which variables are useful for prediction, each time the prior information was updated to reflect the information gained from a new data point, a 95% credible interval was formed for all regression coefficients in the model. If any credible interval was contained within (–tol, tol), then this parameter/variable was dropped from the model. The reduced model was then re-fit using SMC based on the appropriate prior information on the parameters (from the initial learning phase) and all sequentially extracted data. This process iterated until 1,000 data points had been extracted in this sequential design process. To investigate this methodology, we considered four different values for tol (0.25, 0.5, 0.75 and 1).

Table 4 shows the covariates that remained in the model after an additional 1,000 data points had been observed for tol = 0.25, 0.50, 0.75 and 1.00. The results suggest that if we are only interested in large effect sizes (> 1.0), then credit card debit appears to be the only useful covariate. In contrast, if effects larger than 0.25 are deemed important then all variables remain in the model. Most notably, these results agree with the results from fitting the full main effects model based on the full data set, see Table 5. This model was fitted with a prior distribution based on 5,000 randomly drawn data points (as in the above described initial learning phase), and sequentially updating these priors using a single data point at a time until all data had been included. The covariate information found here should be useful to lenders, as it seems to indicate that individual information is more informative than property characteristics for determining if someone will default on their mortgage.

Table 4.

The covariates in the mortgage case study which were deemed useful for prediction based on tol = 0.25, 0.50, 0.75 and 1.00.

tol	Remaining covariates
0.25	x1, x2, x3, x4
0.50	x2, x3
0.75	x3
1.00	x3

Table 5.

Summary of the posterior distribution of the parameters for the full main effects model based on all mortgage default data for the year 2000.

Parameter	Mean	SD	2.5th	Median	97.5th
β0	-11.40	0.13	-11.67	-11.40	-11.16
β1	-0.42	0.03	-0.48	-0.42	-0.36
β2	-0.63	0.03	-0.68	-0.63	-0.56
β3	3.03	0.05	2.94	3.03	3.13
β4	0.20	0.03	0.12	0.20	0.26

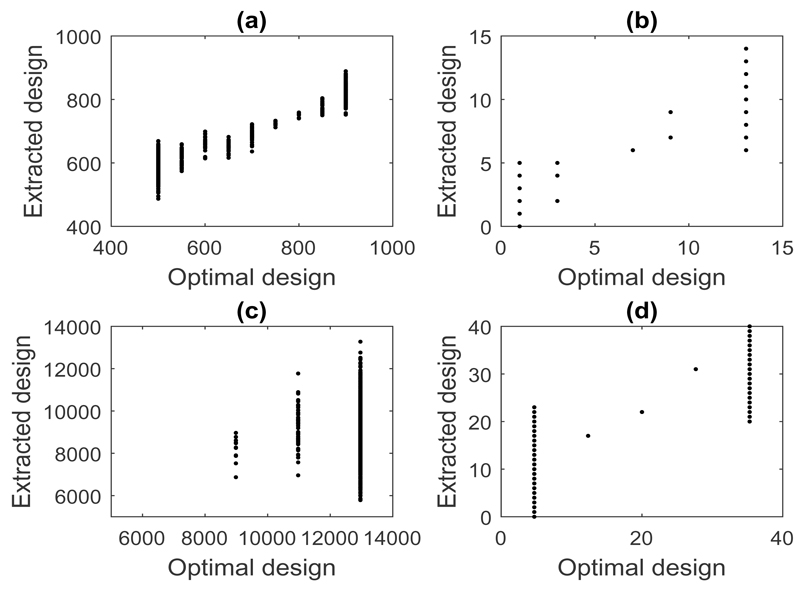
At each iteration of the sequential design process, the Bayesian optimal design and the corresponding extracted design was recorded. A comparison of the two is shown in Figure 6, by covariate (for tol = 0.25). Ideally, one would like to observe a one-to-one relationship between the two designs. Unfortunately, this was not observed in this study. For example, from Figure 6(c) which corresponds to credit card debt, values of around $11,000 and $13,000 were found as optimal, but the values extracted from the Big Data set varied between $5,000 and $13,000. This suggests that there is potentially a lack of mortgage default data on those with large credit card debts. Intuitively, this might make sense as such individuals may generally not have their loan approved.

Fig 6.

Extracted versus optimal design points for the mortgage default case study for tol = 0.25 for (a) credit score, (b) years employed, (c) credit card debit and (d) house age.

For each of the four different values of tol, it took approximately 40 minutes to run the learning phase and sequential design process. To explore the computational gains/losses involved in implementing this designed approach, a comparison with randomly selected subsets of the same size was undertaken. The comparison was conducted such that priors from the initial learning phase were formed in the same manner as the designed approach but, for the sequential design process, instead of searching for an optimal design, a design was randomly selected from the data set. The analysis of such subsetted data in general took approximately 2 minutes, which means that around 20 randomly selected data sets could be analysed in the time it took to implement a designed approach. When these 20 random designs were run, only x₁ was removed from any model (across all values of tol). Indeed, this only occurred when tol = 0.75 or 1. In these cases, x₁ was removed from the model 1/20 and 20/20 times, respectively. Such results show that no random design provided more information about the parameter values as that of the designed approach. Thus, despite the designed approach having relatively high computational requirements, the benefits are seen in analysing highly informative data, and thus efficiently addressing analysis aims.

In summary, in this mortgage case study, through analysing a small fraction of the full data set, we were able to determine, with confidence, which covariates appear important for prediction, and also identify potential ‘holes’ in the full data set in regards to our analysis aim.

5.2. Case Study 2

To illustrate the method with a more complex statistical model, we consider an analysis performed on accelerometer data (see, for example, Trost et al. (2011)). Here 212 participants performed a series of 12 different activities at four different time points, approximately one year apart. The age range of the data was 5 to 18 years old. The purpose of the analysis was to assess the performance of 4 different so-called ‘cut-points’, which are used to predict the type of activity performed based on the output of the accelerometer. The response variable is whether or not the cut-point correctly classifies the activity. Each individual at each time point performed all 12 activities and all 4 cut-points are applied (observations with missing classification responses were discarded). There are roughly 35000 observations in the dataset. Although this sample size is not as large as in the previous case study, we show that it is sufficient to demonstrate our proposed approach.

A logistic regression mixed effects model was fitted to the data that included age as a continuous covariate (linear in the logit of the probability of correct classification), and the type of activity (12 levels) and the cut-point (4 levels) as factor variables. The model also included all two-way interactions, which resulted in a total of 63 fixed effects parameters. A normal random intercept was included for each participant. For completeness, we assume that the observed classification for the ith observation for subject t is Y_ti ~ Binary(π_ti) with

$$\begin{array}{l}\text{logit}\left({\pi }_{ti}\right)={\beta }_0+b_t+{\beta }_{\text{age}}{\text{age}}_{ti}+{\displaystyle \sum _{j=1}^3{\beta }_{\text{cut}}^j{\text{cut}}_{ti}^j+{\displaystyle \sum _{j=1}^{11}{\beta }_{\text{trial}}^j{\text{trial}}_{ti}^j+}}\\ {\displaystyle \sum _{j=1}^{33}{\beta }_{\text{cut},\text{trial}}^j{\text{cut}}_{ti}^j\times {\text{trial}}_{ti}^j+{\displaystyle \sum _{j=1}^3{\beta }_{\text{age},\text{cut}}^j{\text{age}}_{ti}^j\times {\text{cut}}_{ti}^j+}}\\ {\displaystyle \sum _{j=1}^{11}{\beta }_{\text{age},\text{trial}}^j{\text{age}}_{ti}^j\times {\text{trial}}_{ti}^j,}\end{array}$$

where $b_t\stackrel{iid}{\sim }𝒩\left(0,\varphi \right)\text{for}t=1,\mathrm{\dots },212$ (with ϕ being the between subject variance), i = 1, …, s_t where s_t is the number of observations taken on subject t, age_ti is the age in years, ${\text{cut}}_{ti}^j$ is a dummy variable defining which cut-point is applied, ${\text{trial}}_{ti}^j$ is a dummy variable defining which trial is applied and the β parameters are the fixed effects. The intercept parameter β₀ relates to an age of 0 years, cut-point 1 and trial 1.

Here we assume that interest is in estimating the age effect on correct classification (both main and interaction effects, consisting of 15 fixed effects parameters). Thus for our utility in line 3 of Algorithm 1 we considered the negative log of the determinant of the posterior covariance matrix for these 15 parameters, and aimed to maximise this utility. For line 1 we took a pilot dataset consisting of n_t ≈ 500 observations where a full replicate was taken from different individuals at ages 6 to 18 years with an increment of two years. Then we performed our sequential design strategy to continually accrue data until at least 3000 observations were obtained. Thus we attempted to obtain a close-to-optimal sub-sample of size n_d ≈ 3000 to precisely estimate the age related parameters. The optimisation procedure for line 3 is a simple grid search over the age covariate (between 6 and 18 with 2 year increments) to guide the next selection of data. For line 4 we took all the data from the individual with the closest age (in terms of Euclidean distance) to the optimal design selected (48 observations when a full replicate is available). Note that we did not force data to be collected from different individuals than what has already been collected in the sub-sample. The optimal design was near the boundaries of the age range, so that naturally the sub-sampled data were usually taken from different individuals. However, a different design strategy could be adopted where data is taken from an individual who is not already present in the sub-sample with the closest age to the optimal design. Ryan, Drovandi and Pettitt (2015) considered Bayesian design for mixed effects models and found that it is not obvious whether to sample a few individuals heavily or sample many individuals sparsely, highlighting the importance of optimal Bayesian design in the context of mixed effects models. Furthermore, the amount of computation required to analyse the extracted data may depend not only on the size of the subset but on how many distinct individuals are sampled. We have not factored this in to our subsetting procedure, but it may be possible to do so.

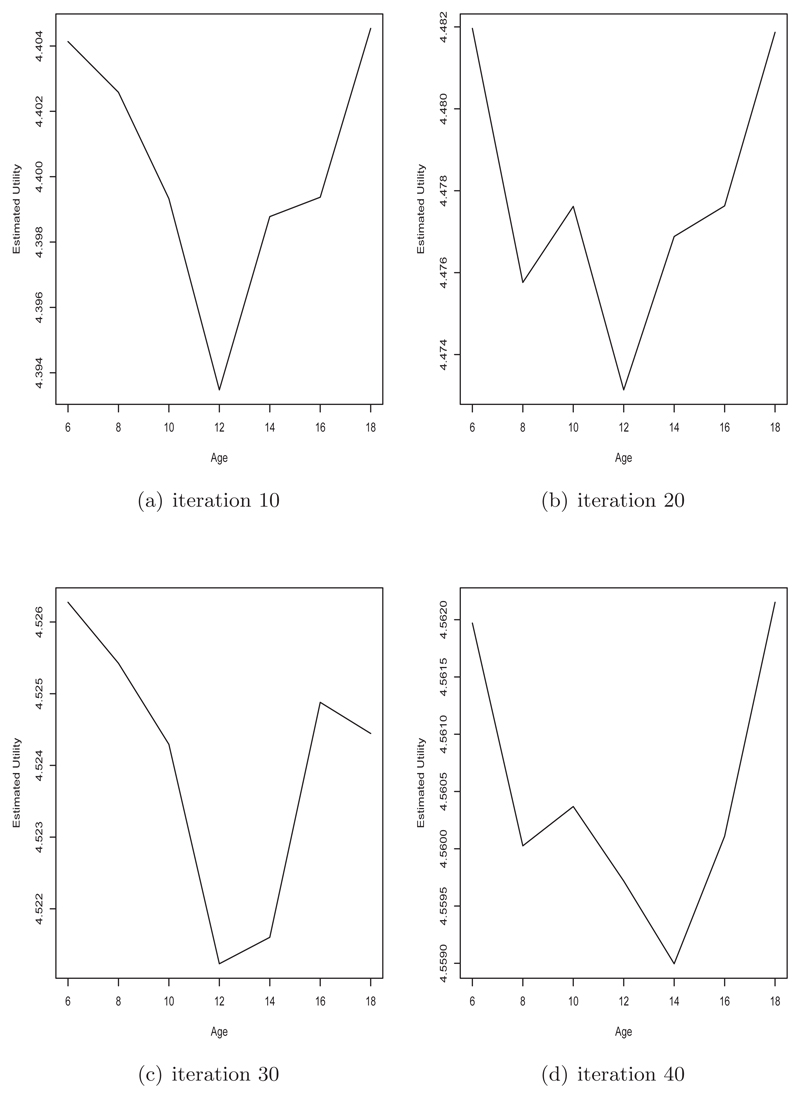
We required a fast method to approximate the posterior distribution and hence the utility function. Here we used the integrated nested Laplace approximation (INLA, Rue, Martino and Chopin (2009)) with the default priors in the R-INLA package (www.r-inla.org). Note that high accuracy of the posterior distribution is not required, it is only necessary that the method produces the appropriate ranking of potential designs. To estimate the expected utility at some proposed age, we took only a single sample from the current INLA posterior distribution and simulated a full replicate for a new individual at that age and estimated the new posterior distribution based on all the data in the sub-sample so far and the simulated data. This is performed for each proposed age, and the age that produced the highest utility was selected. We found that it was sufficient to use a single simulation to obtain a close-to-optimal design. A more precise determination of the optimal design could be obtained by considering more posterior predictions. The only stochastic part of the algorithm is the fact that we only draw a single posterior simulation. To investigate the variability in the observed utility of the subsetted data determined from the optimal design, we repeated our process 20 times.

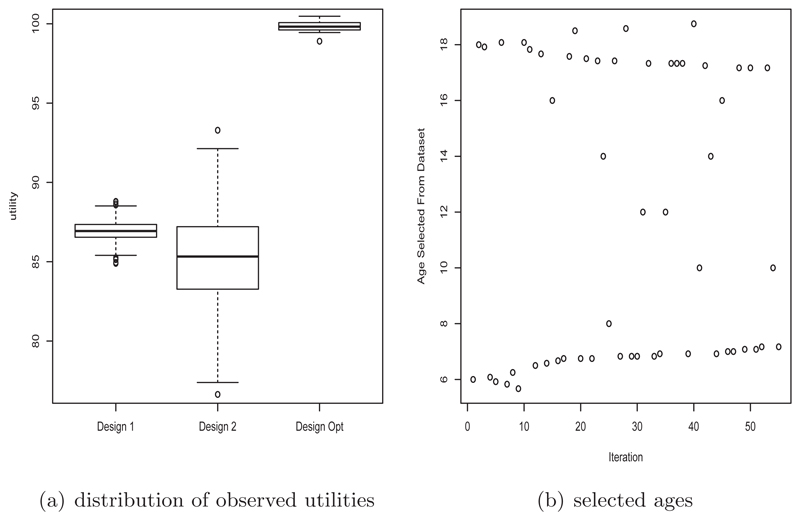
Figure 7 shows the estimated utility for each proposed age at different stages of the algorithm for 1 of the 20 runs. It is evident that it is not difficult to estimate the optimal age to select, even with a single posterior simulation. We compared our sub-sample with two other more standard designs. The first (design 1) takes a completely random sample without replacement of the data with the same size as our optimally designed sub-sample. The second design (design 2) randomly samples without replacement from the unique combinations of individuals and age (with all the data taken at that combination) until a sample size not less than the size of the optimally designed sub-sample is taken. Designs 1 and 2 are repeated 1000 times. The boxplots of the estimated utilities for these two design schemes together with that obtained from the optimal design procedure are shown in Figure 8(a). It is evident that the optimally designed sub-sample approach leads to a much higher utility than those taken from designs 1 and 2. One run of the optimal design process took roughly 1 hour while investigating 1000 random subsets took roughly 3 hours. Thus we were able to obtain a data subset with higher observed utility in a much shorter amount of time.

Fig 7.

Estimated (log) utility values for each proposed design (age) at iteration 10 (a), 20 (b), 30 (c) and 40 (d) of the optimal design sub-sampling algorithm for the cut-point dataset.

Fig 8.

Results from the sub-sampling optimal design process for the cut-point dataset. (a) Comparison of observed utilities of sub-samples obtained from designs 1 and 2 with the observed utilities of the sub-samples obtained from the optimal design process. (b) Ages selected from the dataset during the optimal design sub-sampling process.

The actual ages selected by the algorithm over the iterations for one of the runs is shown in Figure 8(b). It is evident that the optimal ages to sample are generally at the age boundaries.

6. Discussion

This paper has explored the concept of a designed approach to analysing Big Data in order to answer specific aims. The proposed approach exploits established ideas in statistical decision theory and experimental design. The decision-theoretic framework facilitates formal articulation of the purpose of the analysis, desired decisions and associated utility functions. This forms the basis for designing an optimal or near-optimal sample of data that can be extracted from the Big Dataset in order to make the required decisions. Under this regime, there may be no need to analyse all of the Big Data. This has potential benefits with respect to data manipulation, modelling and computation. The extracted sample of data can be analysed according to the design, avoiding the need to accommodate complex features of the Big Data such as variable data quality, aggregated datasets with different collection methods and so on. The model can be extended in a more deliberate and structured manner to accommodate remaining biases such as non-representativeness or measurement error, and the design can be replicated to facilitate critical evaluation of issues such as model robustness and “concept drift”.

Consideration of the issue of model fit serves to illustrate the potential versatility of the designed approach to Big Data analysis. A natural by-product of the analysis of Big Data is very little statistical uncertainty for many models. However, this rarely reflects reality: in practice, we know that the model can be wrong in many ways. Through the designed approach, the aim of assessing model robustness can be incorporated into the design, in particular into the utility function, and a corresponding optimal sample can be extracted that will facilitate this investigation. For example, the experimental design can incorporate the intention to apply posterior predictive checks, or include a designed hold-out sample set drawn from the Big Data to evaluate goodness-of-fit via a posterior predictive check. Indeed, the utility function can be used as a vehicle to express a very wide range of statistical ambitions. There are implications for robustness in that the initial design of the training data set is predicated on the statistical model, and all models are wrong. Our suggestion here is to proceed in the spirit of Box (1980) in that the analysis should take place as an iterative process of criticism and estimation. The design subsetting procedure takes place as if the model were true, but following this model criticism should be used to help identify artefacts and systematic discrepancies of model fit with the aim to improve the robustness of inference. Such model criticism may of course lead to the consideration of more complex models in the design step. Unfortunately, optimal design has typically been restricted to low to moderate dimensional problems for linear models (Myers, Montgomery and Anderson-Cook, 2009), GLMs (Woods et al., 2006) and nonlinear mixed effects models (Mentré, Mallet and Baccar, 1997). Thus, in order for optimal design to adequately facilitate a wide range of analyses across Big Data sets which are invariably complicated, messy, heterogeneous, heteroscedastic with a large number of different types of variables and fraught with missing data, it seems there is a need for further developments in this area.

This designed approach may also be used not as a substitute for the Big Data analysis but as a complementary evaluation. Thus the question of interest can be investigated in multiple ways and although the same data are being used for both analyses, the insights and inferences drawn from the two approaches can potentially provide a deeper understanding of the problem; see Appendix D for further discussion.

We have presented throughout the paper various advantages to the designed approach for subset selection that are not computational. An additional advantage is that the design generated could be re-used or harnessed for future/other datasets collected under similar conditions.

There are many ways in which the approach described above can be extended. In addition to expansions to accommodate more complex experimental aims, the designs and models can be extended to accommodate features of the obtained data. We discuss three examples: adjustment for inadequacies in the dataset from which the samples are extracted, extensions to allow for aggregation of information from different sources, and the inclusion of replication.

The mismatch between the Big Data and the target population is widely acknowledged as a concern in many disciplines (Wang et al., 2015). Other widely acknowledged inadequacies include measurement error in variables of interest and missing data. If characteristics of these attributes are known in advance, they can be included in the design. There is a large classical literature on adjusting for non-coverage and selection bias in sampling design, for example through the use of sampling weights (Kish and Hess, 1950; Lessler and Kalsbeek, 1992; Levy and Lemeshow, 1999), design-adjusted regression and its variants (Chambers, 1988) and propensity scores (Dagostino, 1998; Austin, 2011). Analogous weighting methods have been developed to account for missing data and measurement error (Brick and Montaquila, 2009). A growing literature is also available for Bayesian approaches to weighting (Si, Pillai and Gelman, 2015; Gelman, 2007; Oleson et al., 2007). Further, although the experimental design approach described here mitigates the endemic problem of data quality to some extent by extracting only those observations corresponding (at least approximately) to the design points and ignoring the remaining (possibly poorer quality) data, issues such as bias, nonrepresentativeness, missingness and so on may persist. In this case, a variety of methods can be adopted for adjusting the data (Chen et al., 2011), the likelihood (Wolpert and Mengersen, 2014), the model (Espiro-Hernandez, Gustafson and Burstyn, 2011), the prior (Lehmann and Goodman, 2000) or the utility (Fouskakis, Ntzoufras and Draper, 2009), and the experimental design can be modified accordingly.

An alternative to adjusting the design is to augment the corresponding statistical model used to analyse the extracted data. In a Bayesian framework, this can be implemented through specification of informative priors in a Bayesian hierarchical or joint model (Wolpert and Mengersen, 2004; Richardson and Gilks, 1993; Mason et al., 2012; Muff et al., 2015).

In a Big Data context, aggregation of data from different sources can be cumbersome due to the different characteristics of the datasets and the very large precisions of the obtained parameter estimates. A designed approach can provide at least partial solutions to these issues. For example, the experimental design can be augmented to sample efficiently from each data source, taking into account the characteristics associated with the source and the overall aim of the analysis. The corresponding statistical model can then be extended hierarchically to allow for the aggregation (McCarron et al., 2011). One could also conceive this problem as a meta-analysis, in which each data source is sampled and analysed according to an independently derived design and the results are combined via a random effects model or similar (Pitchforth and Mengersen, 2012; Schmid and Mengersen, 2013).

The designed approach can also be augmented to allow for potential deficiencies in the statistical model. For example, if the data are ‘big enough’, then replicate samples can be extracted from the data using the same design strategy. The methodology for replication can be adapted in a straightforward manner from classical design principles (Nawarathna and Choudhary, 2015). These replicates can be employed for a variety of purposes, such as more accurate estimation and analysis of sources of variation or heterogeneity in the data, identification of potential unmodelled covariates or confounders, assessment of random effects, or evaluation of the robustness of the model itself. They can also be extracted according to a hyper-design to allow for evaluation of issues such as concept drift, whereby the response variable changes over time (or space) in ways that are not accounted for in the statistical model; see Gama et al. (2014) for a recent survey of this issue.

Finally, we stress once more that the benefits of the designed approach must be weighed up against the computational overheads and potentially reduced sample size in comparison to say a random subsampling strategy. We see this as motivation for the study of new computational optimisation methods that can exploit modern computer architectures to deliver designed samples for Big Data analysis.