Abstract
Förster resonance energy transfer (FRET) measurements from a donor, D, to an acceptor, A, fluorophore are frequently used in vitro and in live cells to reveal information on the structure and dynamics of DA labeled macromolecules. Accurate descriptions of FRET measurements by molecular models are complicated because the fluorophores are usually coupled to the macromolecule via flexible long linkers allowing for diffusional exchange between multiple states with different fluorescence properties caused by distinct environmental quenching, dye mobilities, and variable DA distances. It is often assumed for the analysis of fluorescence intensity decays that DA distances and D quenching are uncorrelated (homogeneous quenching by FRET) and that the exchange between distinct fluorophore states is slow (quasistatic). This allows us to introduce the FRET-induced donor decay, εD(t), a function solely depending on the species fraction distribution of the rate constants of energy transfer by FRET, for a convenient joint analysis of fluorescence decays of FRET and reference samples by integrated graphical and analytical procedures. Additionally, we developed a simulation toolkit to model dye diffusion, fluorescence quenching by the protein surface, and FRET. A benchmark study with simulated fluorescence decays of 500 protein structures demonstrates that the quasistatic homogeneous model works very well and recovers for single conformations the average DA distances with an accuracy of < 2%. For more complex cases, where proteins adopt multiple conformations with significantly different dye environments (heterogeneous case), we introduce a general analysis framework and evaluate its power in resolving heterogeneities in DA distances. The developed fast simulation methods, relying on Brownian dynamics of a coarse-grained dye in its sterically accessible volume, allow us to incorporate structural information in the decay analysis for heterogeneous cases by relating dye states with protein conformations to pave the way for fluorescence and FRET-based dynamic structural biology. Finally, we present theories and simulations to assess the accuracy and precision of steady-state and time-resolved FRET measurements in resolving DA distances on the single-molecule and ensemble level and provide a rigorous framework for estimating approximation, systematic, and statistical errors.
1. Introduction
Förster resonance energy transfer (FRET) experiments monitor the energy migration from a donor, D, to an acceptor fluorophore, A. The rate constant of a FRET process depends directly on the DA distance and the dye’s orientation1 so that the measurements of FRET are often used as a spectroscopic ruler.2 FRET experiments are most sensitive in a distance range 20 to 150 Å qualifying them as a molecular ruler for macromolecules,2 that has frequently been used to determine DA distance distributions,3−9 structural models,2,10−17 and dynamic features18,19 of biomolecules. In the case of flexible tethered dyes, the position of the labels is variable so that the fluorescence is additionally influenced by the dye’s diffusion and collisional quenching by their local environment.20
Depending on the complexity of the sample, FRET experiments can be applied for single-molecule, subensemble (selectively averaged single-molecule events), and ensemble studies in a cuvette or in living cells. Intensity-based ensemble FRET measurements are popular because they are easy to perform as outlined below. However, if the molecular system is heterogeneous (e.g., due to different conformations and complex structures, respectively), one has to be aware that these experiments yield only average observables due to ensemble averaging over the mixture. Additionally, it is crucial for accurate results that the sample is carefully characterized with respect to its purity, its degree of labeling, its homogeneity, and the fluorescence quantum yields of fluorophores.21 One possibility to overcome ensemble averaging are single-molecule FRET studies that are widely used nowadays.22−24 They have the key advantage in that they allow one to resolve distributions of FRET observables and to obtain kinetic information at the same time. In this way, static (multiple distinguishable static states) and dynamic (interconverting states) heterogeneities can be directly identified. The achievable time resolution of single-molecule fluorescence spectroscopy can be limited by instrumental factors25,26 and/or by the photon flux of individual fluorophores.27,28 Thus, it is advantageous to employ additional complementary fluorescence methods such as time-resolved fluorescence spectroscopy that can exploit further information on the system heterogeneity contained in the time dependence of the fluorescence intensities. The temporal resolution of these experiments reaches the ultimate limit set by the fluorescence lifetime of the donor fluorophore which is sensitive to its environment.
In the following sections, we compare the key concepts and limitations of intensity-based and time-resolved FRET experiments so as to become aware of the common principles and to take advantage of the specific strengths of each approach.
1.1. Intensity-Based FRET Measurements
The fundamental characteristic of FRET processes is the rate constant of dipolar coupling between the involved donor and acceptor dye. Experimentally, steady-state fluorescence intensities contain information on this rate constant. However, they depend additionally on sample concentrations and dye-specific fluorescence properties. To eliminate such unwanted dependencies, fluorescence properties of the dyes are characterized and considered by reference samples, and fluorescence intensities are combined to relative quantities. Usually, FRET processes are described by their average yield, referred to as FRET efficiency, E. It is defined by the fraction of donor dyes which transferred energy due to FRET to acceptor dyes with respect to all excited donor dyes. There are five main methods to derive FRET efficiencies from experimental observables. FRET efficiencies can be determined from: (1) the fraction of FRET-sensitized acceptor fluorescence to the total donor and acceptor fluorescence (classical method), (2) the enhancement of acceptor fluorescence ((ratio)A method21), (3) the decrease of the donor fluorescence quantum yield by FRET ((ratio)D method21), (4) the reduction of the donor’s fluorescence lifetime, or (5) changes in the anisotropy of the donor and acceptor, respectively, as an alternative observable for changes of the fluorescence lifetime.
The most popular approach to determine E is method
1, which monitors the donor fluorescence intensity,  , and the FRET-sensitized acceptor fluorescence
intensity,
, and the FRET-sensitized acceptor fluorescence
intensity, 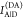 . With these fluorescence intensities, the
yield of the FRET process can be determined by
. With these fluorescence intensities, the
yield of the FRET process can be determined by
| 1 |
The subscript D|D symbolizes
donor detection (D|D)
given donor excitation (D|D), and A|D corresponds to
acceptor detection given donor excitation. The superscripts refer
to the sample: DA represents an FRET sample, containing a donor and
an acceptor; D0 and A0 are samples solely containing a donor and acceptor
fluorophore, respectively; F stands for fluorescence
intensities corrected for the quantum yield, ΦF,
of the dyes.24 The Abbreviations section (Table 2)
provides a comprehensive list of symbols with descriptions used throughout
this paper. The donor, 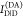 , and acceptor,
, and acceptor, 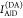 , fluorescence intensities
must be distinguished
from the measured signals. For the determination of
, fluorescence intensities
must be distinguished
from the measured signals. For the determination of 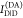 and
and 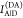 , numerous corrections
and calibrated instruments
are needed.21 Full expressions relating
measured signal intensities to absolute FRET efficiencies are given
in Section 3.1.
, numerous corrections
and calibrated instruments
are needed.21 Full expressions relating
measured signal intensities to absolute FRET efficiencies are given
in Section 3.1.
Table 2. Used Symbols and Their Definitions.
The alternative ratiometric approaches (eqs 2 and 3) monitor the
fluorescence of a direct excited and FRET-sensitized acceptor and
the fluorescence of a donor in the absence and the presence of FRET,
respectively. These approaches have the advantage to eliminate dependencies
on spectral sensitivities of the measurement instrument and the fluorescence
quantum yield of the dyes.21 For example,
measuring the donor fluorescence intensity in the presence, 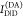 , and in the absence,
, and in the absence, 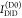 , of an acceptor, the FRET efficiency is
given by a relative difference:
, of an acceptor, the FRET efficiency is
given by a relative difference:
| 2 |
A disadvantage of this donor-based method is the need for a separate reference sample, i.e., a sample, (D0), singly labeled with a donor dye in addition to the doubly labeled FRET sample, (DA).
1.2. Time-Resolved FRET Measurements
Time-resolved
measurements are an attractive alternative to intensity-based in vitro FRET measurements for several reasons.3−8,18 (1) Without instrumental calibrations,
the FRET efficiency can be accurately determined from the slope of
the fluorescence decay characterized by the excited state lifetime
τ of the donor. The slope is a relative observable so that the
difficult determination of calibration factors for the spectrally
dependent instrumental sensitivity become expandable (eq 1, and Section 3.1). (2) The curvature of the decay curve
also provides information on the heterogeneity of a FRET ensemble
by detecting multiple decay components (j) with the
species fractions 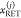 and specific rate constants for FRET,
and specific rate constants for FRET, 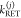 . In this way, a donor–acceptor distance
distribution can be directly resolved without an intermediate calculation
of FRET efficiencies, provided that the distinct species live longer
than the donor lifetime (usually a few nanoseconds for most small
organic fluorophores). Moreover, the analysis of a fluorescence decay
also yields an important average parameter: the species fraction weighted
average fluorescence lifetime, ⟨τ⟩x, which is proportional to the fluorescence intensity
of the sample.29 Hence, two observables,
the average lifetime of a donor in the absence,
. In this way, a donor–acceptor distance
distribution can be directly resolved without an intermediate calculation
of FRET efficiencies, provided that the distinct species live longer
than the donor lifetime (usually a few nanoseconds for most small
organic fluorophores). Moreover, the analysis of a fluorescence decay
also yields an important average parameter: the species fraction weighted
average fluorescence lifetime, ⟨τ⟩x, which is proportional to the fluorescence intensity
of the sample.29 Hence, two observables,
the average lifetime of a donor in the absence, 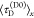 , and in the presence of FRET,
, and in the presence of FRET, 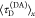 , allow for computation of the
average steady-state
FRET efficiency analogous to eq 2:
, allow for computation of the
average steady-state
FRET efficiency analogous to eq 2:
| 3 |
(3) Fluorescent probes that are flexibly tethered to biomolecules can be affected by their brightness and mobility so that distinct dye species often exist as shown below. Thus, time-resolved FRET measurements are mandatory for an accurate FRET analysis so that species averaging is avoided and the distinct dye species are treated separately. (4) Time-resolved fluorescence measurements are essentially independent of the sample concentration. Therefore, a precise control of DA concentrations, which is essential in intensity-based approaches, is unnecessary. However, varying the ratio of the donor to acceptor labeled molecules in intermolecular FRET studies of biomolecular complexes also allows analysis of the complex stoichiometry.30 (5) Finally, we want to stress the synergy of simultaneous intensity-based and time-resolved FRET analyses in single-molecule studies,31,32 so that the lack of correlation of both methods within an analysis time window readily detects the presence of dynamic averaging of FRET observables without the need of a complex kinetic analysis by FCS, (26,33) dynamic photon distribution analysis (dynPDA),31 and recoloring of photon trajectories by a maximum likelihood function,34,35 respectively. (6) Time-resolved measurements are additionally attractive as a robust method to study molecular ensembles in living cells by FRET36 using fluorescence lifetime microscopy (FLIM)37,38 or multiparameter fluorescence image spectroscopy (MFIS).39−45 In multiparameter fluorescence detection (MFD), a whole set of parameters, such as the time-resolved anisotropy and fluorescence lifetimes, can be simultaneously determined by efficient estimators even if the numbers of detected photons are small.46−49 The knowledge of all fluorescence parameters allows one to optimize the precision and accuracy of FRET studies.
1.3. Resolving Heterogeneities
FRET efficiencies report on average sample properties. Therefore, homogeneous samples are mandatory in ensemble measurements to correctly relate FRET efficiencies to molecular structural models.2,12,13,17 Single-molecule (sm) techniques overcome these limitations and may be applied to heterogeneous samples.10,11,50−53 However, heterogeneity of highly dynamic molecules may be overlooked, if the integration time, limited by count rate of the experiment, is longer than the time scale of dynamics.54 This limitation is circumvented by analysis of the fluctuation in sm-experiments,26,55 and by time-resolved fluorescence measurements of molecular ensembles or subensembles.
Time-resolved fluorescence measurements resolve an ensemble of molecules by recording cumulative fluorescence intensity decay curves as opposed to average fluorescence intensities. These decay curves contain fluorescence lifetime characteristics of all ensemble members.29 Thus, a careful analysis of these decays by appropriate models and references reveals heterogeneities of FRET parameters, such as FRET rate constants, kRET, and corresponding species fractions. Mainly, fluorescence decays of donors in the presence of FRET are jointly (also referred to as globally) analyzed with fluorescence decays of donors in the absence of FRET.3−8 However, contrary to steady-state experiments, which typically represent experimental data intuitively by FRET efficiencies, no established intensity-independent quantifier for time-resolved FRET experiments exists. Hence, a set of fluorescence decay curves is used to communicate experimental results3−8,18 so that the effects of FRET are hard to recognize and the concept of the joint analysis of the decay curves is not captured visually.
1.4. Sample-Dependent Fluorescence Properties
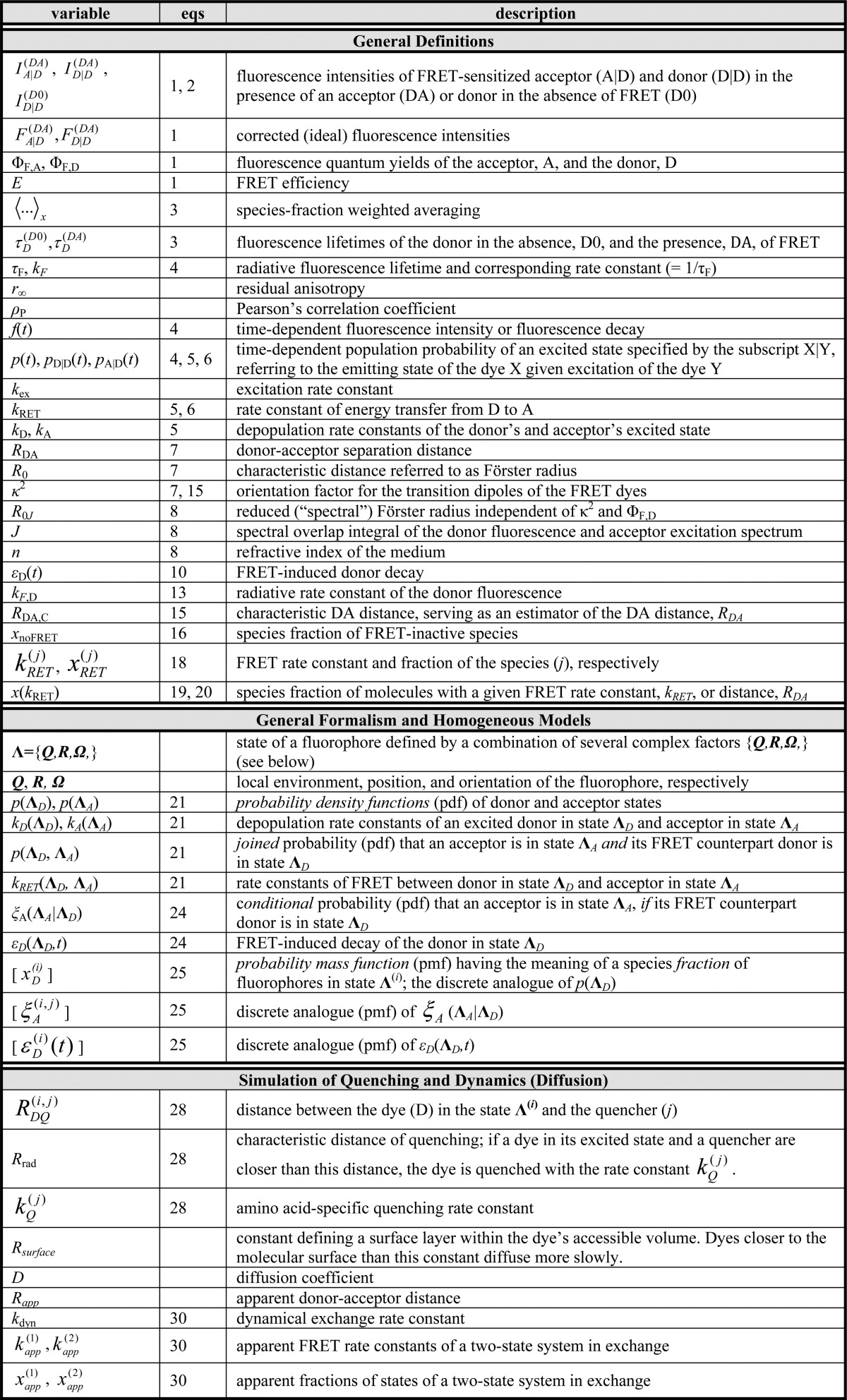
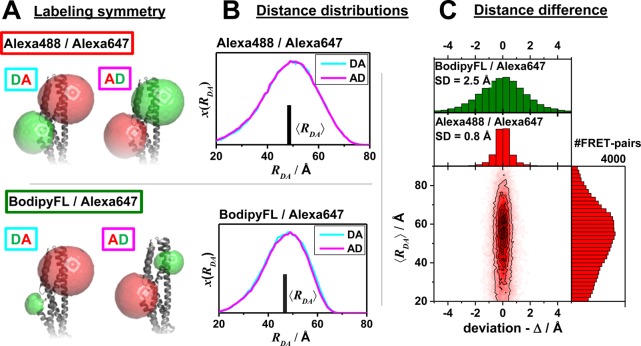
In addition to an efficient global analysis of multiple curves, which will be introduced in Section 2.1, complex (nonexponential) fluorescence decays of donor reference samples, usually stemming from heterogeneities of the tethered dye’s local environment, must be considered. It is generally known, but often unconsidered in the analysis of fluorescence decays, that the properties of the dyes used to measure FRET are dependent on the dye’s local environment. This results in a sample-to-sample variation of the dye’s fluorescence characteristics. Such variations are shown in Figure 1A for the two frequently used dyes Alexa488 and Alexa647 attached to several proteins measured in our laboratory. For both dyes, we often found complex fluorescence decays, which we formally describe by multiexponential decays (see Tables S1 and S2). As the fluorescence quantum yield, ΦF, of the bright species is proportional to the species average of the lifetimes, ⟨τ⟩x, we can approximate ΦF by the ratio of the average fluorescence lifetime to the radiative lifetime, ⟨τ⟩x/τF. In this way, the experimental ΦF can be compared with the theoretically predicted value obtained by Brownian dynamics simulations of a coarse-grained dye (see Section 2.2.2). For the cyanine dye Alexa647 we found ⟨τ⟩x ranging from 1.0 to 1.8 ns (see Figure 1A). For the xanthene dye Alexa488 we found ⟨τ⟩x values between 2.6 and 4.2 ns (see Figure 1A). We attribute these variations to the dye’s local environment, which is determined by the surface of the proteins. Xanthene dyes are known to be quenched by the side chains of electron rich amino acids on the protein surface by photoinduced electron transfer (PET).58−61 For tethered Alexa488, the quenched fraction ranges approximately between 5% and 30% which correlates with an increase of the residual anisotropy. The fluorescence intensity decays of the Alexa488 samples were formally resolved into two components τ1 and τ2 with the respective fractions x1 and x2 = 1−x1 to highlight the quenched dye species (Figure 1B).
Figure 1.
Fluorescence properties of the dyes Alexa488 and Alexa647 tethered to proteins are sample-dependent due to variations of the local dye environment. Average fluorescence lifetimes, ⟨τ⟩x, and residual anisotropies, r∞, of the fluorophores Alexa647 and Alexa488 attached via maleimide or hydroxylamine click chemistry to different amino acids of various proteins (human guanylate binding protein 1, T4 lysozyme, postsynaptic density protein 95, lipase foldase of Pseudomonas aeruginosa and the cyclin-dependent kinase inhibitor 1B). (A) For each sample, the species weighted averaged lifetime ⟨τ⟩x and r∞ are shown as dots overlaid by a Gaussian kernel density estimation.56 The fluorescence parameters are compiled in Table S1 for Alexa647 and in Table S2 for Alexa488 together with individual fluorescence lifetimes from a detailed decay analysis. Using radiative lifetimes of τF = 3.1 ns and τF = 4.5 ns for Alexa64757 and Alexa488, respectively, the relative brightnesses, ⟨τ⟩x/τF, were calculated. The average values of all Alexa647 and Alexa488 samples are ⟨τ⟩x/τF = 0.43 ± 0.07 and ⟨τ⟩x/τF = 0.76 ± 0.11, respectively. The average residual anisotropies of Alexa647 and Alexa488 for all samples are ⟨r∞⟩ = 0.25 ± 0.07 and ⟨r∞⟩ = 0.18 ± 0.05, respectively. (B) The fluorescence intensity decays of the Alexa488 samples were formally resolved into two components τ1 and τ2 with the respective fractions x1 and x2 = 1 – x1. For each sample the lifetimes and fractions are shown as open circles overlaid with a Gaussian-kernel density estimation (green). The average lifetimes of the populations are τ1 = 3.9 ± 0.2 ns and τ2 = 1.0 ± 0.5 ns with species fractions of x1 = 0.8 ± 0.1 and x2 = 0.2 ± 0.1, respectively. The presented data are summarized in Table S2.
Cyanines are more sensitive to solvent effects and steric constraints.62−68 Obviously, a relation between steric constraints and the brightness of Alexa647 results in a positive correlation (Pearson’s ρP = 0.8) of the residual anisotropy, r∞, with ⟨τ⟩x (see Figure 1A), which confirms similar observations of immobile and bright Cy5 subpopulations in single-molecule confocal MFD experiments.69 This sensitivity can be utilized to sense interactions of proteins and nucleic acids by single fluorophores70−72 and causes a broadening of FRET efficiency histograms beyond the shot noise in single-molecule measurements.69
1.5. Sample-Specific References
According to eqs 1–3, the consideration of sample-dependent fluorescence properties of the dyes is mandatory for accurate FRET measurements. Thus, a suitable pair of samples for DA and D0 must be studied. While averaged fluorescence quantum yields calibrate intensity-based measurements for absolute average FRET efficiencies (eq 1), decay shapes of the dyes in the absence of FRET must be considered in the analysis of fluorescence decays. Donor fluorescence decays are often multiexponential, even in the absence of FRET (see Figure 1B and Table S2). Usually, the physical causes for complex fluorescence decays, i.e., the effects of the dye’s environments, are not explicitly considered in the analysis.3−8 Currently, there are extensive studies for developing appropriate dye models for accurate FRET-based structural modeling.8,11,73−77 The data in Figure 1 indicate that a model with a primarily mobile dye is more consistent with the experiments than a model with a static (fixed position) dye. To the best of our knowledge, the resulting uncertainties of such approximations, with respect to the precision and accuracy of FRET-derived distances, were not quantified so far.
1.6. Overview
For the accurate analysis of fluorescence decays, we introduce a general framework (Section 2). We perform a detailed error analysis of recovered donor–acceptor distances and apply this framework to simulated fluorescence decays of protein structures. This answers the question regarding how precise distances are recovered by time-resolved FRET measurements (Section 3).
In detail, we present the fundamental principles of time-resolved FRET measurements (Sections 2.1.1 and 2.1.2) at first and introduce a graphical representation for time-resolved FRET measurements which captures the essence of joint/global analysis of reference and FRET samples (Section 2.1.3). Using this representation, we demonstrate how to interpret fluorescence decays to obtain DA distances visually (Section 2.1.4). Next, we extend our analysis method to consider partially quenched donors (Section 2.1.5). We describe these cases by heterogeneous models, meaning that donor species with differing fluorescence properties are quenched by distinct FRET rate constants. Such cases may be important when a macromolecule adopts conformations with significantly different fluorescence properties of the dyes. We show that homogeneous models, used in numerous experimental studies,3,5−7 are a special case of more general heterogeneous models (Section 2.1.5). To relate our analysis framework to physical models, we introduce fast numerical methods for the simulation of fluorescence and FRET of dynamically quenched dyes flexibly attached to proteins (Section 2.2). Using these simulation methods, we discuss the influence of diffusion (Section 2.2.3) and dynamic quenching (Section 2.2.3) on FRET. Finally, we study the precision and accuracy of DA distances recovered from time-resolved fluorescence measurements (Section 3). Previous studies focused on statistical limits in resolving fluorescence lifetimes.46,47 Our analysis considers the accuracy and precision for intensity and time-resolved FRET measurements of single DA distances (Section 3.1), approximation errors of the homogeneous model for flexibly tethered dynamically quenched dyes (Section 3.2), and resolution limits of DA distances set by the shot noise of the experiment (Section 3.3). Overall, our uncertainty estimates set clear limits of DA distances studied by time-resolved fluorescence measurements, and our approximation analysis of the homogeneous model demonstrates that average DA distances for single protein conformations can be recovered with an accuracy better than 2.0% (Section 3.2.1).
The presented methods are generally applicable to fluorescence decays recorded by time-correlated single photon counting (TCSPC) on the ensemble3,5−7 and subensemble11 level using regular spectrometers or confocal microscopes.37−45,78
Finally, we want to mention that this paper is restricted to singlet–singlet energy transfer between a donor and a spectrally red-shifted acceptor (hetero-FRET). Nevertheless, the general concepts for data analysis and molecular interpretation presented here can also be applied to FRET between equals79−81 (homo-FRET). In this case, however, this process must be monitored via the fluorescence anisotropy of the labels, because in an ideal case their fluorescence intensities are not changed by homo-FRET unless “similar” fluorophores with distinct fluorescence lifetimes are used.82
2. Concepts and Results
2.1. Time-Resolved Fluorescence
2.1.1. Basic Definitions
Time-resolved fluorescence measurements record fluorescence signals relative to an excitation pulse with picosecond resolution. Ideally, the time-dependent fluorescence intensity at the time t since excitation f(t) is proportional to the radiative rate constant of fluorescence kF and the time-dependent population of the fluorescent excited electronic state p(t):
| 4 |
In practice, recorded signal intensities depend on the intensity of excitation, the fluorescence quantum yield of the state, detection efficiencies of the experimental setup, and spectral cross-talks. However, as usual mainly decay shapes are analyzed, proportionality factors relating p(t) to f(t) are often omitted. Below is briefly outlined how to obtain p(t) for the simplest possible system.
A system composed of a single donor, D, and acceptor, A, with single ground (D, A) and excited states (D*, A*) each, can be described by four distinct states: DA, D*A, DA*, D*A*.78 The time-dependent population of these states is determined by the excitation rate constant of the donor, kex, the rate constant of energy transfer from D to A, kRET, and the depopulation rate constants kD and kA of the donor and the acceptor, respectively. If kex ≪ kRET, the D*A*-state can be neglected, and a rate scheme as depicted in Figure 2 applies. Next, if a pulsed excitation is used and the repetition rate of the excitation pulses is low enough, the ground state DA can also be ignored, and only the excited states D*A and DA* have to be considered. Under these conditions, the change of the population probabilities of the state D*A, pD|D(t), and the state DA*, pA|D(t), following an excitation of the donor (designated by the right side of the subscript: |D) is described by
| 5 |
Figure 2.
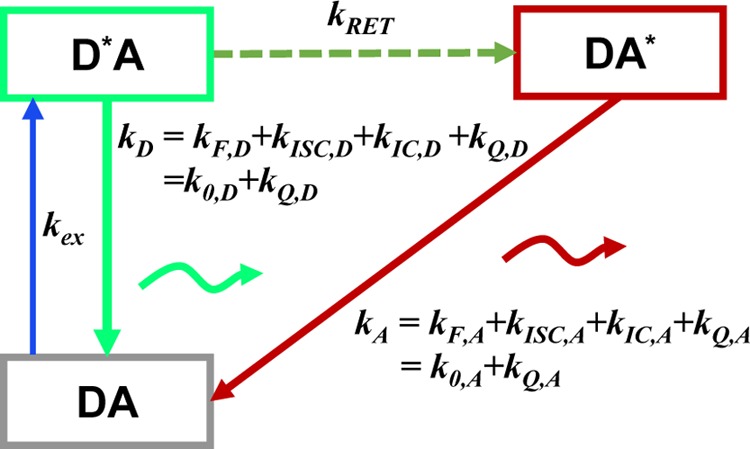
Set of rate constants for the excitation of the dyes, their de-excitation, and FRET that defines the time-dependent fluorescence decays. Definition of states and rate constants of a system composed of a single donor, D, and acceptor, A, excited by a single photon. The asterisk (*) indicates an excited fluorophore: D*A (excited donor, ground state acceptor), DA* (excited acceptor, ground state donor), and DA (ground state donor, ground state acceptor). kex is the rate constant of excitation; kD and kA are the rate constants of deactivation of the excited donor and acceptor state, and kRET is the rate constant of energy transfer from D to A. kD and kA are the sums of the respective radiative rate constant of fluorescence kF, internal conversion kIC, intersystem crossing kISC, and the quenching rate constant kQ. kQ depends on the local environments of the dyes. kF, kISC, and kIC are dye-specific and joined in the constants k0.
The solution of these equations for the initial condition pD|D(0) = 1 and pA|D(0) = 0 is given by
| 6 |
By combining eq 6 with eq 4 the expected time-resolved fluorescence intensities of the donor and acceptor are obtained.
2.1.2. Distance Dependence
The Förster equation describes the distance and orientation dependence of the rate constant of energy transfer, kRET, due to dipolar coupling between D and A.1 It depends on the sixth power of the distance between donor and acceptor, RDA:
| 7 |
Herein, R0 is a characteristic distance, referred to as Förster radius. This classical definition of the rate constant of energy transfer has two disadvantages: (1) the effect of the mutual fluorophore orientation, accounted by the orientation factor κ2 is implicit; (2) both R0 and kD depend on the fluorescence quantum yield, ΦF,D, while kRET actually depends only on the radiative rate constant of fluorescence, kF,D, and is independent of donor quenching.36,83−85 This causes uncertainties, as R0 is often not reported together with the corresponding ΦF,D. To avoid such complications, we define a reduced “spectral” Förster radius, R0J, a function of the refractive index of the medium, n, and the spectral overlap integral, J, of the donor fluorescence and the acceptor absorption spectrum (wavelength λ in nm; extinction coefficient in mol–1 dm3 cm–1):
| 8 |
Such a Förster radius is independent of orientation effects (i.e., κ2) and the sample-specific quenching of the donor dye (i.e., ΦF,D). Furthermore, the corresponding Förster equation emphasizes the physical dependence of kRET on κ2:
| 9 |
Additional advantages include the clearly separated orientation effects and the reduced ambiguity with respect to ΦF,D.
As D and A may rotate after excitation of the donor, the expected κ2 is generally characterized by a time-dependent distribution, p(κ2, t). In this paper, we focus on flexible coupled organic dyes which rotate quickly compared to the FRET rate constant. Thus, we approximate p(κ2, t) by the dynamic isotropic average ⟨κ2⟩ =2/3 and use for convenience the classical definition of a Förster radius, R0, which assumes isotropically oriented dipoles (κ2 = 2/3), and a reduced Förster radius, R0,r (R06 = R0r6·ΦF,D = R0J6·ΦF,D·2/3). For accurate interpretations of time-resolved FRET measurements in live-cell measurements,45 with slowly rotating fluorophores, e.g., fluorescent proteins with a rotational correlation time of ∼16 ns,86,87 the static orientation factor distribution as proposed by Haas and Steinberg and Hochstrasser et al. can be considered.3,88
2.1.3. Definition of the FRET-Induced Donor Decay
Time-resolved measurements require references, similarly to steady-state measurements, which utilize either internal (eq 1) or external (eq 2) references for absolute FRET efficiencies. In time-resolved measurements, decay curves serve as references. Unfortunately, no widespread time-resolved absolute measure for FRET exists. Such a time-resolved measure should: (1) be independent of absolute fluorescence intensities, (2) be derivable from experimental observables, (3) recover steady-state FRET efficiencies by fluorescence weighted integration, and (4) behave analogously to the time-resolved anisotropy, r(t), to take advantage of existing global analysis approaches.
The FRET process can be described from the perspective of the donor
or acceptor, which can be considered as an educt or product, respectively.
The FRET efficiency describes the FRET process as a yield defined
by the fraction of excited donors that transferred energy to an acceptor.
Van der Meer et al. used this concept to describe
FRET from the perspective of the product, by introducing the “time-resolved
FRET efficiency”, TRE, obtained by replacing the steady-state
fluorescence intensities, F, in eq 2 by time-resolved fluorescence intensities, f(t).89 Note
that the TRE is not an efficiency in the sense of
a yield of a process (see Supporting Information, Note S2). Conceptually and experimentally, it is simpler to
quantitate FRET from the viewpoint of the donor, as by time-resolved
fluorescence intensities the quenching of the donor by FRET is directly monitored. The measure of FRET can be defined as
the ratio of the donor fluorescence decays in presence, 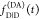 , and in the absence,
, and in the absence, 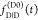 , of FRET:
, of FRET:
| 10 |
We refer to this
ratio as the FRET-induced donor decay as it quantifies
the quenching of the donor by FRET. The TRE and εD(t) are analogous (TRE = 1 – εD(t)). However, εD(t) relates 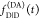 directly to
directly to 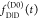 :
:
| 11 |
This factorization was originally introduced by Förster90 and is often implicitly used.3−8,91 Nevertheless, experimental data are rarely represented by such a ratio, and are only occasionally used in theoretical papers.85 In a theoretical paper, van der Meer and Gratton displayed time-resolved data by such a ratio,92 without stressing its fundamental relevance.
Analogies between εD(t) and Time-Resolved Anisotropies
Using εD(t), the FRET efficiency is obtained by a weighted fluorescence integration:
| 12 |
In this sense, εD(t) behaves exactly as the time-resolved anisotropy, r(t). An additional analogy to r(t) is that two observables are used to
derive an intensity-independent, time-resolved quantity: r(t) is given by the difference of the parallel and
perpendicular fluorescence decays, normalized by the total fluorescence
decay; εD(t) is given by the donor
fluorescence intensity in the presence of FRET normalized by its intensity
in the absence of FRET. The anisotropy decay, r(t), describes the time scale and degree of depolarization,
while εD(t) describes the time scale
of FRET and the fraction of chromophores undergoing FRET. Table 1 summarizes further
analogies, which make the rich knowledge developed for the analysis
of fluorescence anisotropies93 available
for FRET. An experimental difference from fluorescence anisotropies
is that 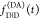 and
and 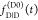 are recorded
using separate samples. Thus,
their relative amplitude is usually undefined and has to be determined
by analysis of the decay curves. This is particularly problematic
for samples with high FRET efficiencies and instruments with broad
instrumental response functions, because experimental nuisances, i.e.,
scattered light and time-shifts of the detector, may be mistaken for
high FRET and vice versa. To overcome such problems,
steady-state measurements of FRET efficiencies on calibrated instruments
may be combined with time-resolved experiments via eq 12 to determine a relative amplitude
of
are recorded
using separate samples. Thus,
their relative amplitude is usually undefined and has to be determined
by analysis of the decay curves. This is particularly problematic
for samples with high FRET efficiencies and instruments with broad
instrumental response functions, because experimental nuisances, i.e.,
scattered light and time-shifts of the detector, may be mistaken for
high FRET and vice versa. To overcome such problems,
steady-state measurements of FRET efficiencies on calibrated instruments
may be combined with time-resolved experiments via eq 12 to determine a relative amplitude
of 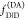 and
and 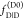 .
.
Table 1. Formal Analogy of the Description of FRET and Anisotropy for Homogeneous Quenching/Rotation in the Absence of Conformational Dynamicsa.
| observables | FRET | anisotropy |
|---|---|---|
| specific fluorescence intensity decays | fD|D(DA)(t) | 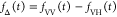 |
| fD|D(D0)(t) | 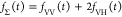 |
|
| intensity-independent quantifier | 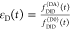 |
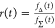 |
| species fraction of no FRET molecules/residual anisotropy | xnoFRET | r∞ |
| direct interpretation of intensity-independent quantifier | εD(t) = xnoFRET+∑ixRET(i)e–kRET(i)t | 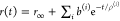 |
| steady-state quantifier by time-resolved measurements | 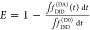 |
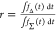 |
| derived steady-state values for single exponential decays | 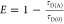 |
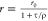 |
E is the FRET efficiency eq 1; kRET is the rate constant of the FRET process eq 9. τD(0) = 1/kD is the lifetime of the donor in the absence of an acceptor, and τD(A) = 1/(kD + kRET) is the lifetime of the donor in the presence of an acceptor. εD(t) is the FRET-induced donor decay. The letters V (vertical) and H (horizontal) represent the polarization of the excitation (first letter) and detection (second letter), respectively. Ideally, the time-resolved anisotropy decay r(t) is obtained by the difference fΔ and the sum f∑ of the experimental measurable intensity decays fVV and fVH. r is the steady-state anisotropy. ρ is the rotational correlation time.
It does not follow from its definition by eq 10 that εD(t) solely depends on FRET. Nevertheless, it is a common approximation, which implies that FRET and donor quenching are uncorrelated. This means that in a mixture of distinct donors all donors are quenched by the same FRET rate constants. For this reason, we refer to such a case as “homogeneous”. Notably, an equivalent approximation is frequently used for the analysis of time-resolved anisotropy decays.94 Even though such homogenous models are frequently used, their limits of are rarely pointed out. Below in Section 2.1.4, we demonstrate that homogeneous models applied to heterogeneous data may result in significant errors if minorly populated states are studied. Still, the ratio εD(t), defined by eq 10, expresses the joint analysis of the donor reference and the FRET sample in an elegant fashion. Hence, we suggest using εD(t) as a time-dependent quantifier for FRET similarly as the time-resolved anisotropy, r(t), is used to illustrate anisotropy data.
2.1.4. Visual Interpretation of FRET-Induced Donor Decays
To interpret a time-resolved FRET experiment, at least
two fluorescence decay curves must be analyzed: the fluorescence decay
of the donor in the presence, 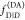 , and the absence,
, and the absence, 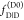 , of FRET. An advantage of εD(t) is that a time-resolved FRET experiment
can be displayed by a single curve. Additionally,
for systems where the donor is quenched homogeneously by FRET, εD(t) directly relates to the distribution
of FRET rate constants (compare Table 1). In this section, we exemplify how εD(t) facilitates the analysis of fluorescence decays
and demonstrate how distributions of FRET rate constants can be visually
recovered from graphs of εD(t).
, of FRET. An advantage of εD(t) is that a time-resolved FRET experiment
can be displayed by a single curve. Additionally,
for systems where the donor is quenched homogeneously by FRET, εD(t) directly relates to the distribution
of FRET rate constants (compare Table 1). In this section, we exemplify how εD(t) facilitates the analysis of fluorescence decays
and demonstrate how distributions of FRET rate constants can be visually
recovered from graphs of εD(t).
Single FRET Species
The fluorescence intensity decays of a single exponential donor in the absence and in the presence of an acceptor, quenching the donor by a single FRET rate constant, are
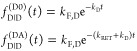 |
13 |
Here, kF,D is the radiative rate constant
of fluorescence of the donor. As 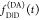 informs only on the sum of the rate constants kRET and kD, the
FRET rate constant, kRET, can only be
determined if
informs only on the sum of the rate constants kRET and kD, the
FRET rate constant, kRET, can only be
determined if 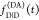 and
and 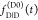 are known. Given
both decays, εD(t) provides the
FRET rate constant:
are known. Given
both decays, εD(t) provides the
FRET rate constant:
| 14 |
Thus, a plot of εD(t) directly
visualizes the FRET rate constant, kRET, and facilitates the interpretation of time-resolved FRET measurements.
Furthermore, εD(t) rationalizes
the joint/global analysis of two fluorescence decays sharing a common
donor fluorescence lifetime in the absence of FRET. This is illustrated
in Figure 3A for a
“short” (RDA(1)/R0 = 0.8) and a “long”
(RDA(1)/R0 = 1.3) DA distance, respectively, assuming kD–1 = 4.0 ns. These distances correspond
to kRET–1 = 0.95 ns
and kRET–1 = 0.05 ns
as characteristic times of the FRET process, respectively. In a semilogarithmic
plot of εD(t) (Figure 3, middle panels), kRET is obtained as the slope of the decay curve. Alternatively,
the inverse FRET rate constant, 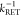 , is obtained at the
time point at which
εD(t) decayed to a value of 1/e,
best seen in a plot of εD(t) with
a logarithmic time axis (Figure 3, lower panels).
, is obtained at the
time point at which
εD(t) decayed to a value of 1/e,
best seen in a plot of εD(t) with
a logarithmic time axis (Figure 3, lower panels).
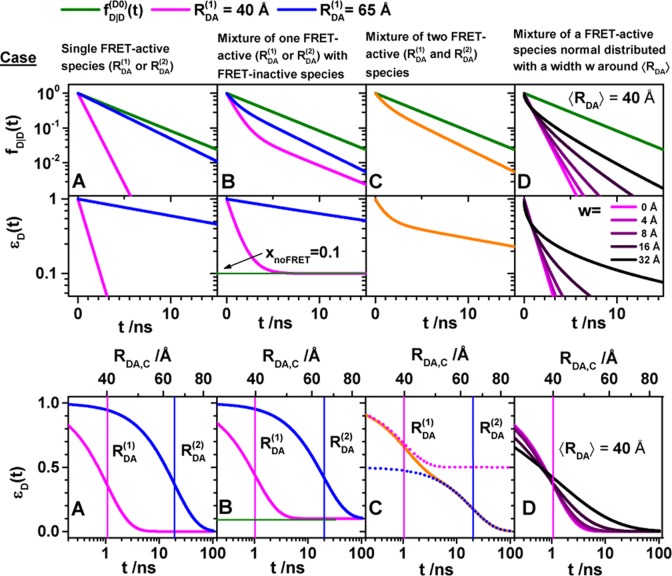
Figure 3.
FRET-induced donor decay directly visualizes FRET rate constants and donor–acceptor distances. Fluorescence intensity decays of a donor fD|D(t) (top row) in the absence (green) and in the presence (blue, magenta, and orange) of FRET. The corresponding FRET-induced donor decays, εD(t)’s, are shown in the lower two rows. The fluorescence decays were calculated by eq 13 (single FRET-active species), eq 16 (mixture of FRET-active and FRET-inactive species), and eq 18 (mixture of FRET species and distribution of FRET species) (R0 = 50 Å and kD–1 = 4.0 ns). Information on FRET is obtained by comparing the fluorescence decay of the donor in the presence of an acceptor (blue or magenta) to its reference given by the fluorescence decay in the absence of FRET (green). εD(t) contains the reference implicitly. In the middle row, εD(t) is shown in linear scale. In the lower row, εD(t) is shown with a logarithmic time axis, and the time t between excitation and detection of fluorescence was converted into a critical donor–acceptor distance axis RDA,C by eq 15. This allows for the determination of the characteristic times of FRET kRET–1 and distances graphically at the point where εD(t) decayed to the value 1/e (shown as vertical lines). The time t corresponds to the DA distance of the FRET process. (A) Single distance of RDA = 40 Å (magenta) and RDA = 65 Å (blue), respectively. (B) Mixture of a FRET-active RDA = 40 Å (magenta) and RDA = 65 Å (blue) and a FRET-inactive species (fraction, xnoFRET = 0.1). (C) Mixture of two FRET-active species RDA(1) = 40 Å (50%) and RDA(2) = 65 Å (50%) (orange). The position and the height of the “steps” in the lowest plot relate to the FRET rate constant and the species fractions of the individual species. For comparison, the components (dotted blue and magenta lines) of the individual species are overlaid. (D) Normal distributed distance with a mean of ⟨RDA⟩ = 40 Å and a distribution width varying from 0 to 32 Å (black to magenta).
The interpretation of the FRET-induced donor decay is further facilitated by rewriting the Förster relationship (eq 9) to express the time between excitation and detection of fluorescence as a characteristic DA distance, RDA,C, which serves as an estimator for the DA distance, RDA:
| 15 |
Here, ⟨κ2(t)⟩ is the average orientation factor of the fluorophore pair at time t. Dynamic effects of freely rotating dyes could be considered given the time-dependent orientation factor distributions, p(κ2, t).95 However, we assume that rotation is fast compared to the FRET process. Hence, the Förster radius R0 is time-independent. In plots of the FRET-induced donor decay (Figure 3, lower panel), this transformation directly visualizes DA distances and minimizes ambiguities, as the Förster radius, R0, the mean orientation factor, and the fluorescence properties of the donor are implicitly accounted for.
Mixtures of FRET-Active and FRET-Inactive Species
The FRET-induced donor decay visualizes species mixtures. This helps to separate FRET-active from FRET-inactive species. The total fluorescence intensity of a species mixture is given by a species fraction weighted sum. Hence, the fluorescence decay of a mixture of FRET-active and FRET-inactive species, with respective species fractions of 1 – xnoFRET and xnoFRET, is given by
| 16 |
The top row of Figure 3B illustrates fluorescence decays for “low-FRET” and “high-FRET” species and a fraction of 10% FRET-inactive molecules, xnoFRET = of 10%. In the FRET-induced donor decay, xnoFRET is a constant offset:
| 17 |
For high-FRET species, where εD(t) decays fast (Figure 3, magenta), this offset is easily determined. For low-FRET species (Figure 3, blue) FRET-inactive molecules may be difficult to distinguish from FRET-active molecules. This issue is discussed rigorously in Section 3.3.
Mixtures of FRET Species
The FRET-induced donor decay, εD(t), of a mixture of N otherwise static FRET species sharing common donor fluorescence properties, is given by a species fraction weighted sum:
| 18 |
Here, 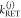 and
and 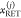 are the FRET rate constant and the species
fraction of the species (j), respectively. Decays
of a mixture of a high-FRET and a low-FRET species (N = 2) are shown in Figure 3C.
are the FRET rate constant and the species
fraction of the species (j), respectively. Decays
of a mixture of a high-FRET and a low-FRET species (N = 2) are shown in Figure 3C.
For a large ensemble of molecules, such discrete distribution of species can be approximated by a continuous distribution of FRET rate constants x(kRET). The corresponding εD(t) is given by
| 19 |
Here, x(kRET) is the species population distribution (or species fraction distribution) of molecules with a given FRET rate constant. With the transformation of the time axis to a critical distance axis using eq 15, the FRET-induced donor decay is given
| 20 |
This is illustrated in Figure 3D for normal distributed distances centered at the mean distance ⟨RDA⟩= 40 Å (R0 = 50 Å) with a width w that varied from 0 to 32 Å.
To visualize species mixtures, it is most informative to use a logarithmic time axis to illustrate FRET-induced donor decays (Figure 3C, bottom panel). In this representation, the characteristic times (the inverses of the FRET rate constants) and DA distances are obtained from the positions of “steps”. The corresponding fractions are given by the height of these steps. Distance distributions, due to multiple FRET states, are identified by deviations from the exponential decays (Figure 3D).
Application to Experimental Data
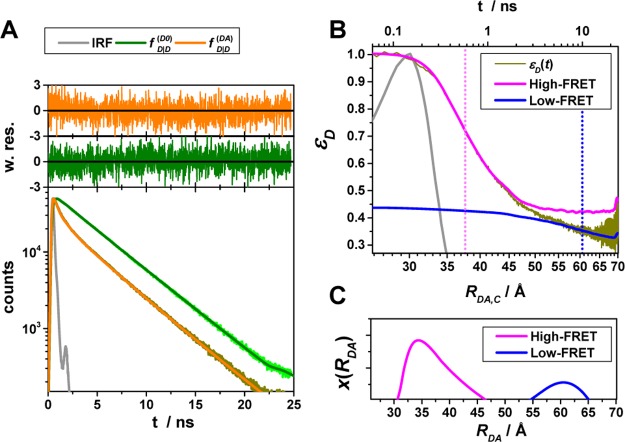
Similar to the time-resolved anisotropy experiments, experimental fluorescence decays inform on FRET when visualized by the FRET-induced donor decay. This is highlighted by Figure 4, which shows the experimental intermolecular time-resolved FRET measurements of a human guanylate binding protein 1 (hGBP1) dimer,7,96 singly labeled at amino acid Q577C using Alexa 488 and Alexa 647 as donor and acceptor, respectively. The fluorescence decays of the FRET sample (the donor in the presence of an acceptor) and the donor reference sample (the donor in the absence of an acceptor) are clearly distinguishable. However, neither DA distances nor species fractions are easily recovered visually from the fluorescence decays (Figure 4A).
Figure 4.
Experimental data can be visualized by the FRET-induced donor decay to reveal donor–acceptor distance distributions. Experimental fluorescence decays, FRET-induced donor decay, and maximum entropy analysis (MEM) of ensemble measurements of the human guanylate binding protein 1 dimer (hGBP1) singly labeled at amino acid Q577C by the donor, D (Alexa 488), and the acceptor, A (Alexa 647), respectively. The dimerization was induced by 500 μM GTPγS. (A) Donor fluorescence decays in the absence (τD(1) = 4.2, xD(1) = 0.94, τD(2) = 1.7 ns, xD(2) = 0.06) (green) and in the presence (orange) of an acceptor; the instrument response function (IRF) is shown as a gray line. The time axis measures the time between excitation and detection of donor photons. (B) Corresponding FRET-induced donor decay εD(t). The distance axis RDA,C(t) is given by the Förster relationship RDA,C = R0(ΦF,Dtk0,D)1/6 (k0,D–1 = 4.1 ns, R0 = 52 Å). The fluorescence decay was analyzed by a two component (N = 2) model (Supporting Information eq S1 in Note S1) using a width of w = 12 Å). The individual components with average distances of 38 and 58 Å are visualized by solid magenta and blue lines, respectively. (C) The DA distance distribution obtained by analyzing the fluorescence decays by the maximum entropy method (magenta high FRET, blue low FRET, dark-yellow experimental FRET-induced donor decay, orange fit).
In a semilogarithmic plot of the corresponding εD(t), two “steps” and a constant offset are visible (Figure 4B). The offset reveals that ∼20% of the donor molecules are FRET-inactive. The position of the steps reveals distances of FRET species, while the associated step-heights recover the respective species fractions. The first step is located at a critical DA distance, RDA,C, of ∼30–40 Å. A second step is positioned at ∼60 Å. The height of the first step demonstrates that the corresponding high-FRET state is more populated compared to the second low-FRET state.
For comparison, we displayed a model-free analysis of the fluorescence decays (Figure 4C) by the maximum entropy method (MEM).97,98 This analysis explicitly considers the instrument response function (IRF) and nuisance parameters as the background signal.7 The agreement between both methods highlights that, provided the IRF is sufficiently narrow, DA distances can be recovered visually by εD(t).
2.1.5. Treating Systems with Heterogeneous Fluorescence Properties
The properties of fluorescent dyes depend critically on their local environment. For a dye flexibly coupled to a macromolecule, multiple conformational states with distinct fluorescence properties are possible, even for macromolecules with single conformational states. Suppose that a donor, D, exhibits, due to quenching by its environment, two lifetimes. In the presence of FRET, both D-species may be quenched by the same or different FRET rate constants. Such ambiguities complicate the analysis of εD(t). Therefore, εD(t) can generally not be interpreted as described above. Fortunately, the frequently used donor Alexa488 is relatively insensitive toward changes of its local environment, and its fluorescence lifetime distribution in the absence of FRET is approximately a single exponential. Therefore, we anticipate small errors for major populated states analyzed by homogeneous models. To improve the accuracy for minorly populated states, we provide a framework for donors and acceptors in heterogeneous environments.
To describe the donor and acceptor fluorescence of a static ensemble, we define the state Λ of a fluorophore on a structural level by a combination of several factors. First, the absolute position and the orientation of the fluorophore in space needs to be considered by the vectors R and Ω, respectively. Additionally, the local environment Q determines the state Λ = {Q, R, Ω} of the fluorophores. Different states can have the same rate constants. Therefore, rate constants cannot replace sets of independent variables Λ. The states of the donor, D, and acceptor, A, are distributed with probability density functions (pdfs) p(ΛD) and p(ΛA). These pdfs define the population of the rate constants kD(ΛD) and kA(ΛA). In general, all factors which define D- and A-states define states of FRET pairs. A joined pdf, p(ΛD, ΛA), with corresponding FRET rate constants, kRET(ΛD, ΛA), characterize the distribution of FRET pairs. The probabilities of finding a donor and an acceptor in an excited state in the presence or absence of FRET are given by
where
| 21 |
The corresponding time-dependent expected fluorescence decays are proportional to the integral of these probabilities over all relevant states. For the donor fluorescence, this gives
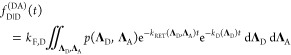 |
22 |
To factorize 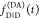 equivalently to eq 11, the factors depending on ΛD and ΛA must be separated.
Here, for simplicity, the orientation effects on FRET are neglected.
The position of A is defined by the position of the donor and the
DA separation vector (RA = RD + RDA). Thus, ΛA can be characterized by the separation vector RDA. The Jacobian determinant of the change of
variables ΛA = {QA, RA} → Λ′A = {QA, RDA} equals unity. Therefore, the last integral in eq 22 takes the following form:
equivalently to eq 11, the factors depending on ΛD and ΛA must be separated.
Here, for simplicity, the orientation effects on FRET are neglected.
The position of A is defined by the position of the donor and the
DA separation vector (RA = RD + RDA). Thus, ΛA can be characterized by the separation vector RDA. The Jacobian determinant of the change of
variables ΛA = {QA, RA} → Λ′A = {QA, RDA} equals unity. Therefore, the last integral in eq 22 takes the following form:
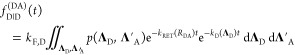 |
23 |
Next, the joint pdf p(ΛD, Λ′A) can be rewritten as the product of the marginal probability p(DA)(ΛD) and the conditional probability ξA(Λ′A|ΛD). The marginal probability, p(DA)(ΛD), is the probability that the donor of a FRET pair is in state ΛD; the conditional probability ξA(Λ′A|ΛD) is the probability that an acceptor is in state Λ′A, given that its FRET counterpart donor is in state ΛD. Under the condition that the probability of ΛD is unaffected by the presence of an acceptor, the marginal probability p(DA)(ΛD) equals p(ΛD), and the expression for the donor decay in eq 21 can be rewritten as
with
| 24 |
Here, εD(ΛD, t) is the FRET-induced decay of the donor in the state ΛD.
Experimentally recovered FRET rate constants are insensitive to a discretization of the donor fluorescence relaxation.99 Therefore, in practice, the distributions of states can be discretized, and the expressions for the donor fluorescence decays can be rewritten by sums:
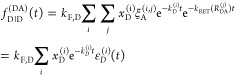 |
where
| 25 |
Here, [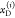 ] is a probability
mass function having
the meaning of a species fraction of fluorophores
in the state Λ(i).
In eq 25, the indices i and j run over all possible combination
of factors ΛD = {QD, RD} and ΛA = {QA, RDA}, correspondingly. This general expression is illustrated in Figure 5A. Similar expressions
have been derived for the analysis of time-resolved anisotropies,94 to relate quenching and dye mobilities. In this
sense, the interpretation εD(t)
is a challenge similar to that of the interpretation of time-resolved
anisotropy measurements, in terms of precise rotational spectra.94,100
] is a probability
mass function having
the meaning of a species fraction of fluorophores
in the state Λ(i).
In eq 25, the indices i and j run over all possible combination
of factors ΛD = {QD, RD} and ΛA = {QA, RDA}, correspondingly. This general expression is illustrated in Figure 5A. Similar expressions
have been derived for the analysis of time-resolved anisotropies,94 to relate quenching and dye mobilities. In this
sense, the interpretation εD(t)
is a challenge similar to that of the interpretation of time-resolved
anisotropy measurements, in terms of precise rotational spectra.94,100
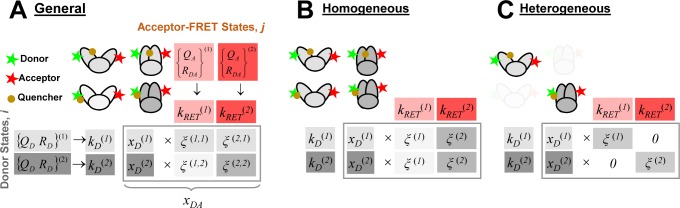
Figure 5.
In a general framework for the analysis of time-resolved FRET experiments, a conditional probability matrix relates the acceptor to the donor states. Schematics illustrating the meaning and relation of the parameters in the eq 23. The donor states, indicated by green shades, are characterized by sets of variables {QD, RD}(i), defining corresponding rate constants kD(i), and their fractions xD(i). The acceptor FRET states are characterized by sets of variables {QA, RDA}(j), defining corresponding FRET rate constants kRET(i), and are indicated by red shades. The gray frame outlines the fraction matrix [xDA(i,j)] of FRET pairs where the donor is in state i and the acceptor in state j. This matrix is presented implicitly by the row product of the donor fraction vector xD and conditional probability matrix [ξ(i,j)] (shades of gray). The gray shades of the protein picture shown in the top left edges illustrate different correlation between donor and acceptor-FRET parameters and indicate corresponding values of the [xDA(i,j)] matrix (the darker shades correspond to the higher fractions). Note that the structure of matrix [xDA(i,j)] and [ξ(i,j)] is not the same. (A) The general case. (B) The homogeneous case. In this case the donor fluorescence decay can be factorized in form of eq 11 and the matrix [ξ(i,j)] has special, uniform-row shape. (C) Case of the full correlation between donor and acceptor states. In this case the number of FRET states is reduced to the number of donor or acceptor states, and the conditional probability matrix turns into an identity matrix.
It can be seen that donor fluorescence decays can only be factorized in the form of eq 11, if εD(t) depends exclusively on FRET rate constants and their fractions ξA(i,j), meaning that the donor and acceptor states are uncorrelated. This is equivalent to the statement that the conditional probability ξA(Λ′A|ΛD) in eq 24 is independent of ΛD, or that elements of the conditional probability matrix [ξA(i,j)] in eq 25 are independent of the index i:
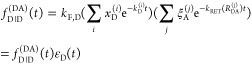 |
26 |
In this case the matrix [ξA(i,j)] consists of homogeneous rows [ξA(j)]. Therefore, we call this approximation “homogeneous”. If we are interested only in donor fluorescence, this approximation is equivalent to the assumption that all ΛD are quenched by rate constants with the same distribution. In this case, we can identify the rows [ξA(j)] as the distribution of FRET states, ξA(j) = xRET(j), and the expressions in eq 26 take the form
| 27 |
These equations are often used for
the joint (or global) analysis
of 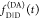 and
and 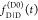 .3−8 While this description of fluorescence decays is common in the literature,
it obfuscates the possibility of factorization in the form of eq 11.
.3−8 While this description of fluorescence decays is common in the literature,
it obfuscates the possibility of factorization in the form of eq 11.
The meaning of
the general, the homogeneous, and the correlated
(heterogeneous) case is illustrated in Figure 5 for a hypothetical protein with two conformations:
(1) an “open” (low-FRET) configuration and (2) a “closed”
(high-FRET) configuration. In this example, the donor is either weakly
or strongly quenched by its local environment. The protein conformations
define two distinct acceptor states: {QA, RDA}(1) and {QA, RDA}(2). The presence or absence
of the quencher defines two donor states: {QD, RD}(1) and {QD, RD}(2). Thus, overall,
four conditional probabilities, ξΑ(i,j), have to be considered. The aim is to determine
the probability of each state along with the associated FRET rate
constants. This is shown in Figure 5A in the form of a table which summarizes all relevant
parameters. A priori the FRET rate constants and
the probabilities of the states are unknown. Hence, overall, 8 parameters
(three conditional probabilities ξΑ(i,j), two donor depopulation rate constants 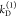 ,
, 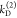 with the fractions
with the fractions 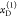 , and two FRET rate constants
, and two FRET rate constants 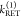 ,
, 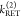 ) have to be determined by the analysis
of two fluorescence decays. With the imposition of a restriction on
the shape of the probability matrix [ξΑ(i,j)], the number of free parameters can
be reduced; in the example presented in Figure 5B, the homogeneous approximation reduces
the number of free parameters from seven to six.
) have to be determined by the analysis
of two fluorescence decays. With the imposition of a restriction on
the shape of the probability matrix [ξΑ(i,j)], the number of free parameters can
be reduced; in the example presented in Figure 5B, the homogeneous approximation reduces
the number of free parameters from seven to six.
The donor fluorescence
lifetime is shortened by quenching by the
donor’s local environment and by FRET. A challenge, when analyzing
fluorescence decays, is to distinguish both. In fact, if only the
donor fluorescence in the absence and presence of an acceptor is monitored,
FRET and quenching by the local environment are hardly distinguishable.
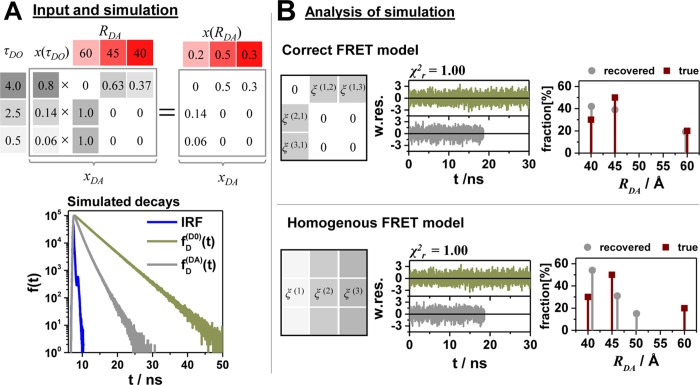
This is exemplified in Figure 6 where the fluorescence intensity decays 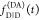 and
and 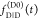 of a heterogeneous case were simulated
and analyzed by the correct heterogeneous model and a homogeneous
model. We chose a heterogeneous case with three donor states and three
FRET states with single FRET rate constants (Figure 6A). Next, we simulate a typical FRET experiment
in terms of photon statistics and the instrument response function
(IRF) and analyze the simulated data by the correct heterogeneous
and the homogeneous model. Overall, 12 × 106 registered
photons were simulated for the FRET sample and 30 × 106 photons for the donor sample. The analysis results with respect
to the recovered DA distances and fractions depend strongly on the
model used. Unfortunately, the homogeneous and the correct models
are indistinguishable as judged by the quality of the fits (Figure 6B). While the minorly
populated FRET state (RDA(1) = 60 Å) is strongly influenced by the choice of the model and
the recovered distance differs considerably by approximately 10 Å
among the models, the two major populated FRET states (RDA(2) = 45 Å, RDA(3) = 40 Å) are less affected by the choice of the
model and differ only by 1 Å from the correct value (Figure 6B). Notably, the
error of the amplitudes is bigger than the error of the distances,
and the amplitudes differ at most by 22% from the correct value. When
the correct model is applied, both distances and amplitudes are correctly
recovered (Figure 6B).
of a heterogeneous case were simulated
and analyzed by the correct heterogeneous model and a homogeneous
model. We chose a heterogeneous case with three donor states and three
FRET states with single FRET rate constants (Figure 6A). Next, we simulate a typical FRET experiment
in terms of photon statistics and the instrument response function
(IRF) and analyze the simulated data by the correct heterogeneous
and the homogeneous model. Overall, 12 × 106 registered
photons were simulated for the FRET sample and 30 × 106 photons for the donor sample. The analysis results with respect
to the recovered DA distances and fractions depend strongly on the
model used. Unfortunately, the homogeneous and the correct models
are indistinguishable as judged by the quality of the fits (Figure 6B). While the minorly
populated FRET state (RDA(1) = 60 Å) is strongly influenced by the choice of the model and
the recovered distance differs considerably by approximately 10 Å
among the models, the two major populated FRET states (RDA(2) = 45 Å, RDA(3) = 40 Å) are less affected by the choice of the
model and differ only by 1 Å from the correct value (Figure 6B). Notably, the
error of the amplitudes is bigger than the error of the distances,
and the amplitudes differ at most by 22% from the correct value. When
the correct model is applied, both distances and amplitudes are correctly
recovered (Figure 6B).
Figure 6.
Uncertainties of the condition probability matrix may propagate to errors of the donor–acceptor distances in particular for minorly populated states. Limitations of the homogeneous approximation illustrated by simulations of a typical time-resolved experiment with three discrete FRET states. (A) Simulated time-resolved fluorescence decay histograms with 100 000 photons in peak (bin width 14.1 ps) using an experimental recorded IRF with a fwhm of 250 ps of a system with three discrete donor states 4 ns (80%), 2.5 ns (14%), and 0.5 ns (6%), and three discrete FRET states 40 Å (30%), 45 Å (50%), and 60 Å (20%) (R0 = 50 Å, k0–1 = 4 ns). The 40 and 45 Å state are associated with the donor lifetime of 4 ns; the 60 Å state is associated with the donor lifetimes 2.5 and 0.5 ns. The conditional probability matrix [ξ(i,j)] and the corresponding values of the [xDA(i,j)] matrix are shown as numbers in the tables. (B) The analysis result using the correct model and the inappropriate homogeneous model are shown on the top and bottom, respectively. The weighted residuals (w.res.) of both models are indistinguishable. To the right the recovered distances and fractions are plotted in a bar diagram.
This demonstrates that the interpretation of the donor fluorescence decay is ambiguous if no knowledge on the connectivity of the donor and FRET states is available. This connectivity is usually unknown a priori. Thus, homogeneous models are often used for dyes dynamically quenched by their local environment. Below we will show that the homogeneous approximation correctly recovers average DA distances for flexibly coupled dyes dynamically quenched within their sterically accessible volume (AV). Furthermore, we introduce fast simulations that predict quenching on the basis of structural models. Thus, predicting quenching by FRET and quenching by PET using structural models may in future reduce ambiguities of interpreting fluorescence decays.
2.2. Mobile Dyes and FRET
2.2.1. Fundamental Principles
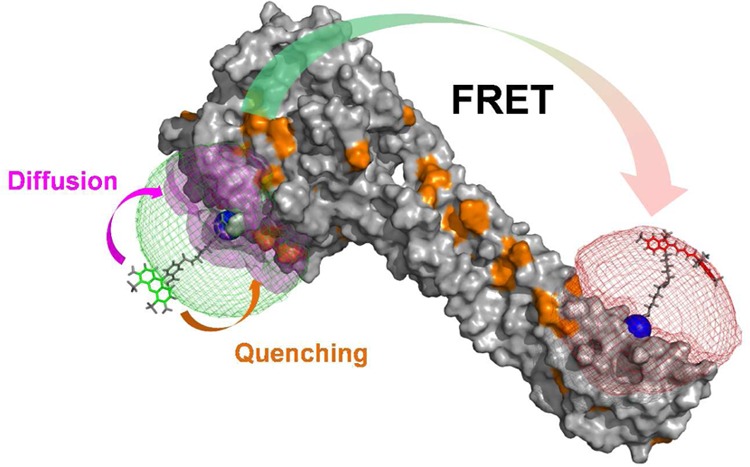
With the goal of generating and validating structural models, fluorophores coupled by flexible linkers to the molecule of interest impose a challenge.11 The linkers have typically a length of ∼20 Å. Consequently, the fluorophores explore a large conformational space which needs to be quantified either by molecular dynamics (MD)74,101,102 or by fast coarse-grained accessible volume (AV) simulations.51,75 The dyes may explore multiple distinct local environments and diffuse among them during their fluorescence lifetime resulting in dynamic quenching. Thus, the spatial and dynamic properties of the donor and acceptor fluorophores have to be considered for an accurate FRET analysis.74 To the best of our knowledge, the effect of dye diffusion, dynamic quenching, and FRET on the outcome of a time-resolved FRET experiment has not been quantified yet in molecular detail. Therefore, we established a toolkit for fast simulations using coarse-grained models to study the effects of diffusion and dynamic quenching on time-resolved FRET measurements.
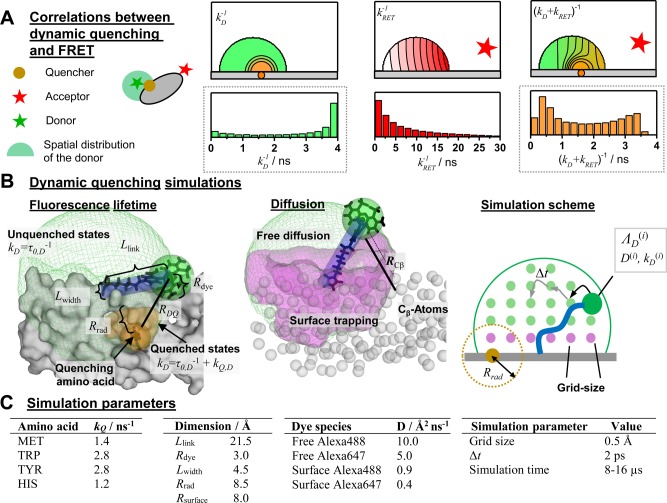
In FRET experiments, changes of the donor and acceptor fluorescence properties might be correlated with changes of their coupling constant kRET. This is illustrated in Figure 7A where a cross-section through a spatial population density of a donor tethered to a flat protein surface in the proximity of a quencher is shown. Due to quenchers, both the fluorescence lifetimes in the absence of FRET and the FRET rate constants are position-dependent. Consequently, changes of FRET rate constants and fluorescence lifetimes in the absence of FRET may be correlated. Experimentally, such correlations are usually inaccessible, as only fluorescence intensities and derived parameters, e.g., fluorescence lifetime distributions, are measurable. As discussed above (see Figure 6), this may result in ambiguous interpretations of the fluorescence intensity decays and raises the question regarding what accuracy of the recovered DA distances can be achieved for flexibly coupled dyes, if the FRET-induced donor decay, εD(t), is directly analyzed and potential correlations between kRET and kD–1 are neglected (analysis by eq 18). Additionally, it is well-known that only apparent FRET rate constants and distances are recovered if conformational dynamics is not explicitly accounted for.103 These effects are important for the accurate analysis of FRET in the presence of dye diffusion and dynamic quenching.
Figure 7.
Coarse-grained BD simulations describe the dye’s spatial distribution, dynamics, and the quenching by amino acids. (A) Effect of a quencher (orange) on the fluorescence lifetime distribution of a donor (green) in the absence (left) and presence (right) of FRET. The donor is located within its sterically accessible volume (AV) shown as a half-circle. The lines in the half-circles are isolines for the donor fluorescence lifetimes in the absence of FRET kD–1 (left), the characteristic times of FRET kRET–1 (middle), and the donor fluorescence lifetimes in the presence of FRET (kD + kRET)−1 (right), respectively. Histograms of the corresponding lifetimes are shown below. Experimentally, the lifetime distributions in the absence (left) and presence (right) of FRET are accessible (highlighted by gray dotted boxes). (B) Illustration of relevant simulation parameters of the coarse-grained Brownian dynamics (BD) simulations. The donor dye Alexa488 (shown in black) is approximated by a sphere (green) with a radius Rdye and is connected to the protein by a flexible linker (blue) of the length Llink and diameter Lwidth. The green mesh outlines the AV of the dye and limits all possible conformational states ΛD. The quenching amino acids Q are approximated by spheres of radius RQ located at their respective centers of mass. On the basis of the distance RDQ between the dye and Q and the radiation boundary Rrad, the fluorescence lifetimes of ΛD are calculated by eq 28 considering all quenching amino acids. This assigns fluorescence lifetimes kD–1 to all ΛD which are either unquenched kD = τ0–1 or quenched τ0–1 + kQ. Quenched states are highlighted in orange. To each state a diffusion coefficient D is assigned on the basis of its distance to the molecular surface. Dyes close to the molecular surface within the accessible contact volume ACV (magenta) diffuse more slowly. The ACV is determined by a critical distance Rsurface and the distances RCβ to all Cβ-atoms. For fast simulations, the conformational space Λ of the dye is discretized, and ΛD(i), a diffusion coefficient D(i), and 1/kD(i) are associated to each state. In each iteration of the BD simulations with time steps Δt the location of the dye is randomly changed to generate a trajectory of states Λ(t) and fluorescence lifetimes 1/kD(t). (C) The used simulation parameters are summarized in the shown tables.
2.2.2. Simulation of Dynamic Donor Quenching
In our simulations, we focus on the donor dye Alexa488, which can be quenched via photo-induced electron transfer (PET) by electron rich amino acids.104 In PET, the rate constant decreases exponentially with the distance between the electron donor and acceptor.105 The characteristic length of electron transfer is on the order of a few angströms.106,107 Therefore, out of all conformations (or states Λ) a dye flexibly coupled to a macromolecule via a long linker may adopt, only a subset is quenched by PET. This is illustrated in Figure 7 for a donor and a single quenching amino acid. In this example, the strong dependence of the quenching rate constant on the distance between the quencher and the dye, RDQ, results in an uneven distribution of fluorescence lifetimes, kD–1, among potential dye conformations and in a distribution of fluorescence lifetimes (Figure 7A, left). In FRET experiments we are interested in the rate constants of energy transfer from a donor to an acceptor, kRET–1 (eq 7). As flexibly coupled dyes may adopt multiple conformations, a distribution of FRET rate constants is anticipated even for a fixed acceptor (Figure 7A, middle). The donor fluorescence decay monitors a combined effect of quenching by the dye’s local environment and FRET (Figure 7A, right).
The heterogeneous models presented in eqs 20 and 21 may disentangle such complicated situations, if the spatial population density of the dye and the quenchers are known, and the exchange between distinct donor ΛD and acceptor states ΛA is slow (quasistatic) compared to the time scale of fluorescence. However, usually neither the spatial population density of the dye nor the distribution of quenchers are a priori known. Therefore, in practice, static homogeneous models are applied to approximate complex situations as shown in Figure 7A. Static homogeneous models have the advantage that they require no prior knowledge, as quenching by the local environment is assumed to be decoupled (uncorrelated) from quenching by FRET. This allows researchers to conveniently interpret εD(t) by a distribution of FRET rate constants (eq 26). However, such a direct interpretation neglects dye dynamics due to diffusion and correlations between FRET and quenching.
The effects of dye diffusion and correlations between FRET and PET could be assessed by means of calibrated all-atom molecular dynamic (MD) simulations.101 However, for quantitative statements, sufficient sampling, i.e., microseconds-long simulations, is mandatory, and for general statements, a large number of distinct structures have to be studied currently making conventional MD simulations unfeasible. To nevertheless determine expected errors of the homogeneous approximations for single protein conformations, we combine coarse-grained AV with Brownian dynamics (BD) simulations in a computationally fast model to simulate microsecond-long trajectories within seconds on a conventional desktop computer. This allows us to study transient effects of FRET and quenching for many distinct structures.
Simulation Procedure
As a first step to simulate fluorescence
decays and FRET, we determine all sterically allowed conformational
states of the donor, ΛD, and the acceptor, ΛA, by accessible volume (AV) simulations.
To find accessible dye positions, the AV simulations approximate dyes
by spheres attached to the protein by a flexible cylindrical linker
and use a geometrical search algorithm on a rectilinear grid.74 The green mesh in Figure 7B surrounds an accessible volume. As a second
step, we define the fluorescence properties of the states Λ by their distances to all quenching amino acids. We determine the
fluorescence lifetimes of the dyes in a particular state kD–1(ΛD) by the radiation boundary condition.108−110 We assume that, if the distance 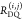 between the dye D in a state Λ(i) and the quencher (j) is smaller than a characteristic distance Rrad, the dye is quenched with an amino-acid-specific rate constant kQ(j). The total
quenching rate constant in the presence of multiple quenchers was
obtained by summation over all quenching amino acids:
between the dye D in a state Λ(i) and the quencher (j) is smaller than a characteristic distance Rrad, the dye is quenched with an amino-acid-specific rate constant kQ(j). The total
quenching rate constant in the presence of multiple quenchers was
obtained by summation over all quenching amino acids:
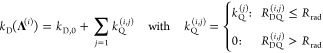 |
28 |
The result
of such a procedure is demonstrated
in Figure 7B, where
the orange region highlights parts of the AV which are quenched. As
a third step, we assign diffusion coefficients to the donor and acceptor
states ΛD and ΛA, respectively. In line with previous molecular dynamics simulations
and experiments,111,112 dyes in the vicinity of a molecular
surface diffuse slower. We identify such species by the dye’s
distance to the Cβ-atoms. If a dye is closer to a
Cβ-atom than a threshold Rsurface, its diffusion is slowed down. In Figure 7B such dye states are shown as magenta volume.
Previously, such surface layers were utilized to measure the stacking
probability of cyanines on nucleic acids.112 Finally, we perform BD simulations of the dye within its AV. After
each iteration of the BD simulation, a fluorescence lifetime is calculated
by eq 28 to yield a
trajectory kD–1(t) of fluorescence lifetimes. By combining trajectories
of a donor and acceptor dyes, we calculate by eq 7 trajectories of rate constants, kRET(t). We assume that the rotational
diffusion is fast compared to the time scale of FRET and approximate
the time-dependent orientation factor κ2(t) by the isotropic average. Using kD(t) and kRET(t), we calculate fluorescence intensity
decays of the donor in the absence 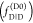 and presence
and presence 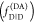 of an
acceptor at time t0 by
of an
acceptor at time t0 by
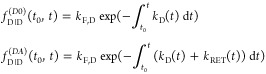 |
29 |
Finally, we average the fluorescence decays over the initial time t0 to generate representative average fluorescence decays. As an alternative to this approach, we use kD(t) and kRET(t) to simulate the Poisson process of photon emission, to obtain counting statistics comparable to experiments.
Parametrization of the Model
The unimolecular quenching rate constant kQ of the dye close to its quencher (RQD < Rrad) and the diffusion coefficients of the tethered dyes are essential parameters to simulate kD(t) and kRET(t). It is well-known that the amino acids Met, Trp, Tyr, and His quench Alexa488 dynamically by PET.104 For these amino acids, we estimated a quenching rate constant of kQ = 2.0 ns–1 by comparing simulated and experimental fluorescence decays. We refined this estimate to the constants presented in Figure 7 using the relative differences of experimental diffusion limited rate constants.104 Free xanthene dyes are known to have diffusion coefficients in the range 40–45 Å2/ns.113,114 The tethered dyes diffuse more slowly as their motion is hindered by the linker. MD simulations of Alexa488 and Alexa647 attached to nucleic acids which served as a model system for an initial parametrization. These simulations showed a bimodal distribution of the diffusion coefficients for both dyes. The fraction of the dyes located close to the molecular surface diffused approximately a factor of 10 slower. Compared to Alexa488, Alexa647 diffused a factor of 2 slower.
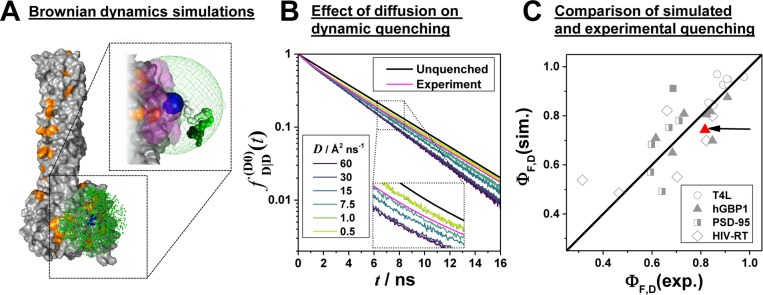
With these parameters everything was in place for simulating dyes tethered to proteins. The simulation results are presented and compared to experimental data in Figure 8. A short excerpt of a BD simulation of the dye Alexa488 attached to a structure of hGBP1 is shown as an example in Figure 8A. To fine-tune the initial estimate of the diffusion coefficients for proteins, we compared the simulated fluorescence decays to experimental curves by performing a series of BD simulations with distinct diffusion coefficients (see Figure 8B). The simulations and the experiments best coincide if Alexa488 diffuses with a diffusion coefficient of ∼10 Å2/ns.
Figure 8.
Coarse-grained model captures the diffusion and dynamic quenching of Alexa488 and correlates with experimental data. Simulation of donor fluorescence decays by Brownian dynamics (BD) simulations: (A) BD simulation of the donor, D, Alexa488-C5-maleimide attached to the human guanylate binding protein 1 (PDB-ID: 1F5N). The attachment atom (on amino acid Q18C) is shown as a blue sphere, and quenching amino acids (His, Tyr, Met, and Trp) are highlighted in orange. D states close to the surface are shown in magenta. The green dots represent a subset of potential fluorophore positions of an 8 μs BD simulation. In the upper-right corner a contiguous part of a trajectory is displayed (colored from white to dark green). (B) Comparison of simulated donor fluorescence decays for various diffusion coefficients D. The analysis result of the corresponding experimental fluorescence decay, formally analyzed by a biexponential relaxation model (x1 = 0.82, τ1 = 4.15, x2 = 0.18, τ2 = 1.35), is shown in magenta. The decay of the unquenched dye with a fluorescence lifetime of 4.1 ns is shown in black. (C) Simulated fluorescence quantum yields of fluorescent species ΦF,D(sim) for a diffusion coefficient D = 15 Å/ns vs experimentally determined quantum yields ΦF,D(exp) for a set of variants of the proteins T4L, hGBP1, PSD-95, and HIV-RT. The black line shows a 1:1 relationship. ΦF,D(exp) was determined by ensemble TCSPC (hGBP1, T4L, PSD-95) or single-molecule measurements (HIV-RT). The data point highlighted by the red arrow corresponds to the experiment shown in panel B. The crystal structures used to simulate the donor fluorescence decays are listed in Table S3.
Cross-Validation of the Parameters
These estimates were cross-validated by various reference measurements of Alexa488 tethered to proteins with known local environment of the dyes: crystal structures of the open115 and closed116 conformations of T4 lysozyme (T4L), the human guanylate binding protein 1 (hGBP1),117 a PDZ1-PDZ2 tandem of the postsynaptic density protein 95 (PSD-95),118 and the reverse transcriptase of HIV-1 (HIV-RT).119 The experimental fluorescence lifetimes, anisotropies, and the PDB-IDs of the used crystal structures used for BD simulation are compiled in Tables S2 and S3, respectively. For best comparison of the BD simulations with the experiments, we simulated a Poisson process and generated fluorescence decay histograms. These histograms were analyzed analogously to the experimental decays by fitting a multiexponential relaxation model. The analysis results were averaged to yield species averaged fluorescence lifetimes ⟨τ⟩x and quantum yields ΦF,D = ⟨τ⟩x/τF of the fluorescent species (see Figure 8C). Experimental fluorescence quantum yields of the fluorescent species were estimated by ensemble TCSPC (PSD-95, T4L), by single-molecule MFD-measurements and by subensemble TCSPC (hGBP1), or by their molecular brightness (HIV-RT) estimated by filtered FCS26 using rhodamine 110 as a reference.
As highlighted by the comparison of the simulated and the experimental data in Figure 8C, our model predicts dynamic quenching for Alexa488. Deviations are possibly due to the simplifications of the model or sample heterogeneities. In the model, neither strong binding of the dye to the protein nor steric aspects of PET were considered. Such a model describes experiments on dyes in sterically undemanding environments,10,74,75,101 which are slowly diffusing compared to the fast (∼100 ps) side chain rotation.
The experimentally measured fluorescence decays are species fraction weighted averages representative for all conformational states a protein may adopt. The proteins PSD-95, T4L, and HIV-RT are known for their conformational dynamics while little is known about hGBP1. PSD-95 is a protein with an unstructured flexible linker that connects two supposable rigid PDZ-domains and thus undergoes significant conformational dynamics.120 In HIV-RT and T4L conformational dynamics is tightly related to their catalytic function.121,122 Therefore, we anticipated large-scale changes in the global superteriary structures and were surprised that the local microenvironment of the dyes within the folded domains of the studied proteins seems to be rather independent of the conformational state of the proteins.
2.2.3. Impact of Dye Diffusion on FRET (Dyes in Confined Geometry)
It is well-known that conformational dynamics
affects fluorescence decays92,103 and may result in
effects, such as diffusion enhanced FRET.123 Our experiments and simulations suggest that Alexa488 tethered to
a protein diffuses with a diffusion coefficient of ∼10 Å2/ns (see Figure 8B). Hence, a considerable displacement (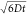 ∼ 10 Å for t = 2 ns) of the dyes is anticipated while being in an excited
fluorescent
state. However, as the linker restricts the dye’s movement,
the effective displacement will be smaller. Commonly used static models,
i.e., eq 20, do not
consider diffusion of dyes in their excited state. They implicitly
assume that the displacement of the dye while being in its excited
state is negligible. If such a static model is applied to fast diffusing
dyes, only apparent distances, Rapp, and
fractions, xapp, will be obtained from
a trajectory. Surprisingly, the error of approximating a DA distance
distribution, x(RDA),
by an apparent DA distance distribution, x(Rapp), for tethered dyes is to our knowledge
unknown.
∼ 10 Å for t = 2 ns) of the dyes is anticipated while being in an excited
fluorescent
state. However, as the linker restricts the dye’s movement,
the effective displacement will be smaller. Commonly used static models,
i.e., eq 20, do not
consider diffusion of dyes in their excited state. They implicitly
assume that the displacement of the dye while being in its excited
state is negligible. If such a static model is applied to fast diffusing
dyes, only apparent distances, Rapp, and
fractions, xapp, will be obtained from
a trajectory. Surprisingly, the error of approximating a DA distance
distribution, x(RDA),
by an apparent DA distance distribution, x(Rapp), for tethered dyes is to our knowledge
unknown.
Here, we use BD simulations to study the effect of translational diffusion on apparent DA distance distributions. Fluorescence decays and the corresponding FRET-induced donor decays, εD(t), were calculated by eqs 29 and 10, respectively. Next, eq 20 was solved to yield apparent distance distributions, x(Rapp). In Figure 9A the outcome of such a procedure is presented for different donor and acceptor diffusion coefficients, DD and DA, respectively. For small diffusion coefficients x(Rapp) is broad. It narrows with increasing diffusion coefficients. Additionally, a shift toward shorter distances and a shoulder at small Rapp is observed. For a dye interacting with the macromolecular surface, such transient effects are less pronounced as the diffusion of the dye is slowed down (Figure 9A, right).
Figure 9.
Fast translational diffusion of the donor and acceptor dyes affects the recovered apparent donor–acceptor distribution due to averaging during their fluorescence lifetime. Effects of dye diffusion on apparent DA distance distributions, x(Rapp). (A) Apparent DA distance distributions, x(Rapp) recovered from a fluorescence decay of a donor with a lifetime of 4 ns attached to amino acid F379C and an acceptor attached to amino acid D467C of the hGBP1 protein structure (PDB-ID: 1F5N) in dependence of the diffusion coefficients of the donor DD and the acceptor DA = 1/2DD without interaction of the dyes (left) and with interaction of the dyes (right) with the protein surface. Interacting dyes close to the protein surface diffused 10 times slower. (B) Apparent distances of a two-state system in dynamic exchange. The equally populated discrete states RDA(1) = 40 Å and RDA(2) = 60 Å (R0 = 52 Å) are in dynamic exchange with a rate constant kdyn. The resulting biexponential FRET-induced donor decay was converted to yield two apparent distances (orange lines). Using these apparent distances, the average distance (black) was calculated. The gray line is the static average of the two distances.
The effects of a constrained dye diffusion can be rationalized by approximating the complex DA distance distribution by a two-state system with a low-FRET (LF) and a high-FRET (HF) state in exchange. If the DA pair is in a LF-state, the donor fluorescence lifetime is long. Hence, within the donor fluorescence lifetime, the DA pair is likely to change to a HF-state. Thus, with increasing exchange rate constant, kdyn, the apparent fraction of the LF-state decreases first. For such systems, an analytical solution of the fluorescence decays is known.103 The corresponding FRET-induced donor decay is
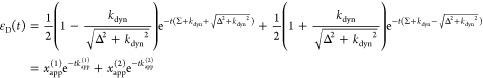 |
with
| 30 |
Herein, 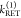 and
and 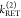 are the FRET rate constants defining the
states in dynamic exchange with an exchange rate constant kdyn as an approximate for the dye diffusion
effects.
are the FRET rate constants defining the
states in dynamic exchange with an exchange rate constant kdyn as an approximate for the dye diffusion
effects. 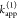 and
and 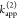 are apparent FRET rate constants with apparent
fractions
are apparent FRET rate constants with apparent
fractions 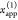 and
and 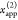 , respectively. Figure 9B visualizes this equation and presents the
apparent distances (Rapp = R0(kappτD,0)−1/6) in dependence of the exchange rate constant kdyn. With increasing kdyn the apparent distance of the LF-state shifts first toward
shorter distances. This is followed by a pronounced shift of the apparent
HF-state toward shorter distances. The fraction of the apparent HF-state,
the prefactor of the first summand in eq 30, decreases with kdyn. For large kdyn the FRET-induced donor
decay is given by exp(−tΣ), and a single
apparent distance Rapp = R0(Σ/kD)1/6 will be recovered. This simple model describes qualitatively the
observed effects in the BD simulations.
, respectively. Figure 9B visualizes this equation and presents the
apparent distances (Rapp = R0(kappτD,0)−1/6) in dependence of the exchange rate constant kdyn. With increasing kdyn the apparent distance of the LF-state shifts first toward
shorter distances. This is followed by a pronounced shift of the apparent
HF-state toward shorter distances. The fraction of the apparent HF-state,
the prefactor of the first summand in eq 30, decreases with kdyn. For large kdyn the FRET-induced donor
decay is given by exp(−tΣ), and a single
apparent distance Rapp = R0(Σ/kD)1/6 will be recovered. This simple model describes qualitatively the
observed effects in the BD simulations.
2.2.4. Impact of Dye Diffusion and Quenching on FRET
Quenching by the local environment and quenching by FRET might be correlated. This may introduce systematic deviations if a homogeneous model is applied. We use BD simulations of DA pairs attached to a crystal structure of the human guanylate binding protein 1 (PDB-ID: 1F5N) to illustrate this effect. First, no amino acid was treated as a quencher. Next, we introduce a single quencher into the local environment in proximity of a donor. Overall, 23 simulations with quenchers located at different positions were performed. For each simulation, the equilibrium distance distribution, x(RDA), and donor fluorescence decays in the absence and presence of FRET were calculated (see Note S1). Next, εD(t) and x(Rapp) were calculated as described above, and the average apparent distance ⟨Rapp⟩ was compared to the average distance ⟨RDA⟩. To visualize the effect of a quencher, the relative difference of these averages was mapped color-coded to the Cβ-atom of the respective quenching amino acid (see Figure 10).
Figure 10.
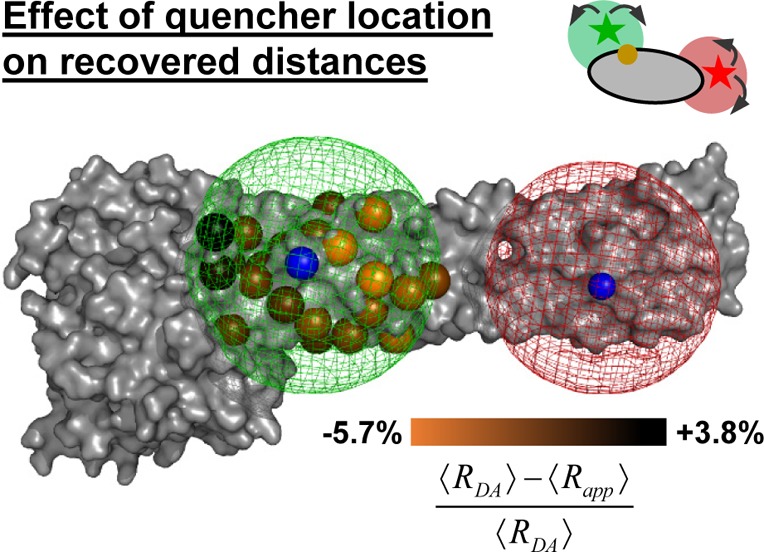
Average donor–acceptor distance and the recovered average distance systematically deviate on a small scale. The effect of the quencher location on the mean apparent distance between the donor, D, and acceptor, A , ⟨Rapp⟩ is illustrated using a crystal structure (PDB-ID: 1F5N) of the human guanylate binding protein 1. A set of 23 simulations (quencher located at amino acid number: 156, 158, 299, 313, 317, 321, 325, 326, 329, 336, 329, 336, 374, 378, 382, 387, 390, 393, 524, 532, 538, 539, 542) was performed. The simulations consider dye diffusion and D quenching. The relative distance difference between the average distance ⟨RDA⟩ (52 Å) and the average apparent distance ⟨Rapp⟩ was mapped on the Cβ-atom of the respective quencher. The D and A accessible volume are shown as green and red mesh, respectively. The blue spheres mark the attachment points of D (F379C) and A (D467C).
Obviously, quenchers introduce small systematic differences between ⟨Rapp⟩ and ⟨RDA⟩. If a quencher is located in the high-FRET region of the donor AV, the average distance is overestimated by 5.7% (55 Å instead of 52 Å). Otherwise, the mean distance is underestimated by 3.8% (50 Å instead of 52 Å). This effect can be rationalized as follows: If the dye is in the proximity of a quencher, less fluorescence light is emitted. So, the quencher depletes fractions of the corresponding FRET species. Hence, if a quencher is in a high-FRET region, which corresponds to shorter distances, the mean value is increased and vice versa.
3. Error Estimation
Considering the DA distance, RDA, three main factors determine the uncertainty, ΔRDA: (1) the precision (noise) of the measurement, Δnoise; (2) the uncertainty of the calibration, Δcal; and (3) the approximation error, Δmodel, introduced by the model chosen to analyze the experimental data. The total uncertainty of the distance, ΔRDA, is estimated by combining these error sources. With the assumption that the contributions follow a normal distribution, ΔRDA is given by
| 31 |
The noise introduces a random error, Δnoise, and limits the degree of resemblance (precision) among different measurements. In fluorescence measurements with single photon counting, the noise of the measured signal (shot noise) is precisely known and follows Poissonian statistics. The degree to which a measured distance, RDA, represents the true distance, i.e., the accuracy of the estimated distance, is limited by the uncertainty of the calibration, Δcal, and the error introduced by the model, Δmodel, used to analyze the data.
The sources for the uncertainties of the calibration in time-resolved and steady-state FRET measurements differ. In steady-state measurements, the detection efficiencies, the background correction, and the excitation and the emission cross-talks are the most relevant calibration parameters. In time-resolved measurements, the fluorescence decays of the dyes in the absence of FRET provided by a reference sample calibrate the measurements. The shot noise of the experiment, Δnoise, contributes to the precision of both measurement types. The error introduced by the model, Δmodel, stems from the fact that reduced models are used to interpret the experimental data (approximation error); e.g., when structural models are derived by a set of FRET constraints, the spatial population densities of the dyes are modeled using their accessible volume that can introduce a systematic error.77
Overall, we discuss all sources of uncertainties for time-resolved FRET experiments in this Feature Article. In Section 3.1, we compare the uncertainties of time-resolved and intensity-based measurements introduced by the noise, Δnoise, and the calibration, Δcal. In Section 3.2, we focus on the approximation error, Δmodel. In Section 3.2.1, we use simulations to study the approximation error when the static-homogeneous FRET models are applied to flexibly coupled dynamically quenched dyes. In Section 3.2.2, the expected error of the FRET analysis is estimated for the case where proteins are randomly labeled at two sites which are equally reactive for the donor and acceptor dye. Finally, we discuss the resolution of time-resolved methods limited by the shot noise of the measurement in Section 3.3. Altogether, we provide estimates for the uncertainties of all three error sources (Δnoise, Δcal, Δmodel). These estimated uncertainties combined with the expected resolution limits of time-resolved fluorescence experiments may help for the planning and design of experiments.
3.1. Accuracy and Precision
3.1.1. Intensity-Based Single-Molecule FRET Studies
In intensity-based single-molecule FRET (smFRET) measurements we define the experiment as follows: a donor, D, is excited by a “green” light source, G, and the fluorescence emissions of the donor, D, and the corresponding acceptor, A, are detected in “green”, G, and “red”, R, detection channels, respectively. Using the measured signal intensities of the “green” and “red” detectors, the distance, RDA, between D and A is determined. Often, the acceptor is also directly excited by a “red” light-source, R, so that the brightness of the acceptor can be monitored as a control in the red-detection channel. Direct excitation of A allows for determination of correction factors for absolute FRET efficiencies.124 This is realized either by an alternating continuous wave laser excitation (ALEX with a pulse length of a microsecond or longer)125 or by pulsed interleaved excitation (PIE) for time-resolved detection with picosecond resolution.126 Here, we follow the notion as presented in the introduction: the subscripts describe the excitation and emission, while the superscripts describe the sample. The subscripts are read from right to left, e.g., R|G denotes red detected signal (R|G) given green excitation (R|G).
The detected red, SR|G, and green, SG|G, signal intensities have to be distinguished from the ideal (fully corrected) donor, FD|D, and acceptor, FA|D, fluorescence intensities (eq 1). First, the detected signals, S, are sums of the fluorescence intensities, I, and a nonfluorescent background, B: S = I + B. Second, the fluorescence intensities of the dyes depend on their excitation cross-section, σ, and the excitation intensity, L. Here, dependences of the excitation on the wavelength are not considered, since usually lasers are used in smFRET to excite the sample at a fixed wavelength. In experiments with two-color excitation by a green, G, and red, R, light source, we must consider two distinct cross-sections for D and A, e.g., σD|G is the cross-section of the donor for the green light source. Third, not all the molecules in the excited state emit fluorescence. This is considered by the fluorescence quantum yield of the donor, ΦF,D, and acceptor, ΦF,A. Finally, not all emitted photons are detected by the measurement device. The nonideal detection is accounted for by correction factors for dye and detection channel specific detection efficiencies, g. As D and A have distinct fluorescence spectra, and the detection efficiency is wavelength-dependent, the green and the red detector have different detection efficiencies for both dyes. For instance, gG|D is the detection efficiency for the donor (G|D) in the green channel (G|D). Note that the detected signals can also be mixtures of the D and A fluorescence.
Overall, the signal intensity of a DA molecule detected in the channel Y (green (G) or red (R) detection) excited by the light source X (green (G) or red (R) excitation) is given by
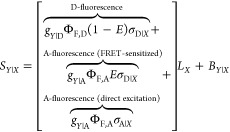 |
32 |
The equation above is valid in the absence of acceptor saturation, i.e., for those cases where the rate constant of acceptor excitation, σA|XLX + kRET ≪ kA, is smaller than the S1 depopulation rate constant kA. Additionally, saturation effects due to dark states of the acceptor are not considered. For cyanine dyes, such dark states are important, as two states (a cis- and a trans-state) coexist and only the molecules in the trans-state are fluorescent.64 Such dark states must be corrected experimentally by scaling the fluorescence quantum yield, ΦF,A, by the fraction of molecules, a, in the bright trans-state83 to obtain an apparent fluorescence quantum yield (a·ΦF,A). Following eq 32, the detected signal intensities of D and A, respectively, can be written for excitation by two light sources, G and R, in matrix form:
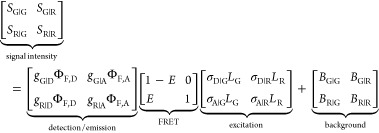 |
33 |
These matrices highlight the effect of the background, excitation, FRET, and detection on the signal intensities. The columns of the matrices correspond to different excitation wavelengths and rows to different detection channels in one-color excitation FRET experiments or different time frames in PIE experiments.
For the case where the donor excitation by the red light source, σD|RLR, and the emission cross-talk of the acceptor into the green-detection channel, gG|AΦF,A, are negligible, the observed signal SG|R becomes negligible too. Under these conditions, we can introduce four correction parameters, α, β, γ, and η, which are sufficient to determine the FRET efficiency, E, by the green and red signal.
| 34 |
The parameter α is a correction factor for the spectral fluorescence cross-talk of the donor (leakage) into the red “acceptor” detection channel. β normalizes the direct acceptor excitation rates in the FRET experiment to that in the PIE experiment, defined by the acceptor excitation cross-sections, σA|G and σA|R, at the green (G) and at the red (R) excitation wavelength, respectively, and the corresponding excitation irradiances [photons/cm2], LG and LR. γ is a correction factor for the fluorescence quantum yields, ΦF,D and ΦF,A, and the detection efficiencies of the green- and the red-detection channel, gG|D and gR|A, for the donor and acceptor dyes, respectively. η normalizes the donor excitation rate of the FRET studies to the direct acceptor excitation rate of the PIE experiment defined by the excitation cross-sections for D, σD|G, and A, σA|R, respectively, and the direct excitation irradiances [photons/cm2] LG and LR for the donor and acceptor at the wavelengths G and R.
Using these parameters, we can convert an experimentally observed intensity I (with I = S – B) to a fluorescence intensity, F, for computing the FRET efficiency, E:124
| 35 |
The FRET efficiency, E, of isotropically oriented dyes with a Förster radius, R0, separated by a distance, RDA, is given by
| 36 |
The distance, RDA, can be expressed as a function of experimentally observable fluorescence intensities and correction parameters:
| 37 |
Note that the uncertainty of RDA depends on the correction parameters and the shot noise of the experiment.
In the following, the error contributions of the parameters α, β, and γ are presented as relative errors of the distance δRDA = ΔRDA/RDA. Additionally, the shot noise, determined by the number of detected photons, is propagated to an error of the distance, considering the signal intensities and the background signals. These contributions were estimated by standard error propagation, where the total relative error of a DA distance, δRDA, is given by
| 38 |
The contribution of the parameter γ to the error of RDA, δγ = ΔRDA(Δγ)/RDA, is given by
| 39 |
It is important to note that δγ is independent of the donor fluorescence quantum yield, ΦF,D, as the rate constant of energy transfer from D to A is independent of ΦF,D. Above, Δγ′ and ΔΦF,A are absolute errors of γ′ and ΦF,A, respectively.
Contrary to δγ, the error contributions of the donor emission cross-talk, δα, and the red detector excitation cross-talk, δβ, depend on RDA:
| 40 |
Above, Δα and Δβ are the absolute errors of α and β, respectively.
The number of detected
photons follows Poissonian statistics. Hence,
to determine the error contribution of the measured signals (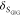 and
and 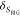 ) and the nonfluorescent
background (
) and the nonfluorescent
background (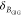 and
and 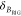 ), the corrected number of fluorescence
photons has to be calculated for a given number of detected photons, N. For signal intensities and the integration time, Tmeas, of the experiment the total number of
detected photons is
), the corrected number of fluorescence
photons has to be calculated for a given number of detected photons, N. For signal intensities and the integration time, Tmeas, of the experiment the total number of
detected photons is
| 41 |
A certain number, NB, of the detected photons is attributed to the nonfluorescent background. Thus, the corrected number of fluorescence photons, NF, is smaller than the number of detected photons, N.
| 42 |
Here, ζ is a distance-dependent function which determines the total number of fluorescence photons:
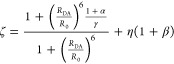 |
43 |
As the photons are distributed among the “green” and “red” detector, the total number of detected fluorescence photons is distance-dependent. For “large” RDA, more photons will be detected in the “green” detector, and for “short” RDA more photons will be detected in the “red” detector. The total corrected number of fluorescence photons originating from “green” excitation channel, NF|G, is given by
| 44 |
Then, the relative error contributions of the green, δBG, and red background, δBR, are given by
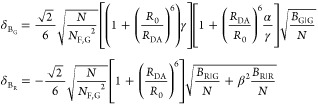 |
45 |
Similarly, the error contributions of the green signal, δSG, and the red signal, δSR, are
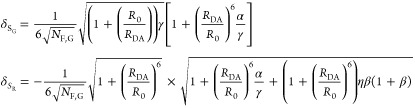 |
46 |
Note that both the error of the background (δBG and δBR) and the error of the signal (δSG and δSR) depend on RDA.
3.1.2. Time-Resolved FRET Studies
In fluorescence decay measurements, the DA distance, RDA, is estimated via the FRET rate constant, kRET (compare eq 9). For a given reduced Förster radius, R0,r, the DA distance, RDA, is obtained via
| 47 |
In eq 47, kF,D is the radiative rate constant of the donor fluorescence. The FRET rate constant, kRET, is estimated experimentally by the fluorescence lifetime of the donor in the presence of FRET, τD(A) = kDA–1, and the fluorescence lifetime of the donor in the absence of FRET, τD = kD–1:
| 48 |
The fluorescence lifetime of the donor in the absence of FRET is determined by a separate reference sample. Hence, the error of the rate constant of energy transfer, ΔkRET, and thus the uncertainty of the DA distance, ΔRDA, depends on the uncertainty of donor fluorescence rate constant in the absence, ΔkD, and presence, ΔkDA, of FRET:
| 49 |
Following common rules of error propagation, the relative error of RDA is given by
| 50 |
In single-photon counting, the variance of kDA for NF detected fluorescence photons is estimated by:47
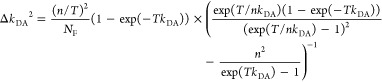 |
51 |
Above, n is the number of detection time channels in TCSPC, and T is the time-window of the fluorescence decay histogram used to estimate kDA.
3.1.3. Distance-Dependent Uncertainty
Using eqs 35–46 for intensity and eqs 47–51 for time-resolved
DA distance measurements (TCSPC), we estimate relative errors 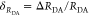 . For time-resolved measurements, we use
the experimental sample-to-sample variation of the donor fluorescence
lifetimes in the absence of FRET (compare Figure 1C) to define an uncertainty, ΔkD–1, of the reference donor
fluorescence lifetime in the absence of FRET. Furthermore, we assume
that the width of a “typical” instrumental response
function is 0.3 ns, defines the smallest “reasonable”
bin width of a fluorescence decay histogram and sets a lower limit
of a measurable RDA via eq 51. For intensity-based single-molecule
distance measurements by multiparameter fluorescence detection with
one-color excitation (MFD-OCE) and MFD with pulsed interleaved excitation
(MFD-PIE), we estimate δRDA using a typical green/red-detection
efficiency ratio, fluorescence quantum yields for the donor Alexa488
and the acceptor Alexa647, nonfluorescent background, and cross-talks
α and β. We compare the estimated relative errors, δRDA, of FRET measurements by TCSPC,
MFD-OCE, and MFD-PIE in Figure 11. The minima of δRDA (RDA), located at RDA/R0 < 1.0,
emphasize that TCSPC, MFD-OCE, and MFD-PIE have optimal working ranges.
For the chosen noise level, calibration/correction parameters, and
uncertainties, DA distances are best measured at RDA/R0 ≈ 0.80 (MFD-OCE,
MFD-PIE) and RDA/R0 ≈ 0.65 (TCSPC).
. For time-resolved measurements, we use
the experimental sample-to-sample variation of the donor fluorescence
lifetimes in the absence of FRET (compare Figure 1C) to define an uncertainty, ΔkD–1, of the reference donor
fluorescence lifetime in the absence of FRET. Furthermore, we assume
that the width of a “typical” instrumental response
function is 0.3 ns, defines the smallest “reasonable”
bin width of a fluorescence decay histogram and sets a lower limit
of a measurable RDA via eq 51. For intensity-based single-molecule
distance measurements by multiparameter fluorescence detection with
one-color excitation (MFD-OCE) and MFD with pulsed interleaved excitation
(MFD-PIE), we estimate δRDA using a typical green/red-detection
efficiency ratio, fluorescence quantum yields for the donor Alexa488
and the acceptor Alexa647, nonfluorescent background, and cross-talks
α and β. We compare the estimated relative errors, δRDA, of FRET measurements by TCSPC,
MFD-OCE, and MFD-PIE in Figure 11. The minima of δRDA (RDA), located at RDA/R0 < 1.0,
emphasize that TCSPC, MFD-OCE, and MFD-PIE have optimal working ranges.
For the chosen noise level, calibration/correction parameters, and
uncertainties, DA distances are best measured at RDA/R0 ≈ 0.80 (MFD-OCE,
MFD-PIE) and RDA/R0 ≈ 0.65 (TCSPC).
Figure 11.
Relative error of a normalized donor–acceptor distance, δ(RDA/R0), depends on the normalized donor–acceptor distance, RDA/R0, and a number of experimental parameters. Estimated relative uncertainties δ(RDA/R0) of the DA distance, RDA, for a given number of detected photons, N, with dependence of the distance RDA/R0 for time-correlated single photon counting (TCSPC), intensity-based measurements by multiparameter fluorescence detection (MFD) with one-color excitation (OCE), and pulsed-interleaved excitation (PIE). On the top the contributions of the shot noise and the relevant calibration/correction parameters (colored solid lines) are shown. The resulting total uncertainty is shown as a dotted line. On the bottom, the distance-dependent scaling of the total uncertainty is shown for a different number of photons. The uncertainties for TCSPC were estimated by eqs 46–51 using a radiative rate constant of kF,D = 0.25 ns–1 and a relative error corresponding to the donor fluorescence variation among different protein samples in Figure 1 (τD(0) = 3.9 ± 0.2 ns). The time-window, T = 16 ns, of the fluorescence decay histogram was separated into 53 detection channels resulting in a detection channel width of 0.3 ns (the typical width of an instrument response function in single-molecule (sm) detection). The uncertainties of the MFD-OCE and MFD-PIE measurements were calculated by eqs 35–45. In both cases the fluorescence quantum yield of the donor and acceptor were ΦF,D = 0.8 and ΦF,A = 0.3, respectively. In the MFD-OCE and MFD-PIE plots, α = 0.02 ± 0.005, γ′ = 0.8 ± 0.05, and ΦF,A = 0.3. The relative fractions of the nonfluorescent background were BG|G/IG|G = 0.02 and BR|G/IR|G = 0.01. In MFD-PIE, BR|R/IR|R = 0.02, η = 0.02 ± 0.01, and β = 0.3 ± 0.1. In MFD-OCE, ΔΦF,A = 0.05.
In TCSPC the smallest “reasonable” bin width limits the shortest measurable DA distance. For a bin width of 0.3 ns, corresponding to the typical fwhm of an IRF in sm-detection, only distances RDA/R0 > 0.45 have an uncertainty smaller than δRDA = 0.1. On the other hand, the “longest” possible measurable distance is limited by the uncertainty of the donor reference sample. For the presented example, this upper distance is given by RDA/R0 ≈ 1.5 (Figure 11). As the relative error δRDA scales in sixth-degree with RDA/R0 (eq 50), short distances are very well-resolved.
In intensity-based MFD-OCE measurements, the uncertainty of γ limits δRDA within a range 0.6 < RDA/R0 < 1.2. For “long” distances the shot noise and the uncertainty of the cross-talk from the donor to the red detector, Δα, dominate δRDA. MFD-PIE experiments directly monitor the brightness of the acceptor. Therefore, we assume that the relative error of ΦF,A in MFD-PIE is twice as small compared to MFD-OCE. Hence, the contribution of γ to δRDA in MFD-PIE is smaller. This comes at the cost of an increased shot noise contribution compared to MFD-OCE, because a smaller fraction of donor photons and FRET-sensitized acceptor photons are registered. Nevertheless, the better-defined ΦF,A outweighs the increased error of the shot noise in the range 0.6 < RDA/R0 < 1.2. For the presented set of calibration parameters, β (the factor correcting for the acceptor excitation by the green “donor” light source) is only of minor importance.
This comparison demonstrates that TCSPC is particularly strong in resolving “short” distances while intensity-based MFD-OCE and MFD-PIE measurements are better for resolving longer distances. This is particularly true if the spectral cross-talk from the donor to the acceptor is well-controlled. Short distances are very accurately measured by TCSPC as they are nearly independent of the donor reference (compare eq 50). In intensity-based techniques the error is nearly constant over a large distance range and is mainly limited by the calibration of the instrument and the sample (acceptor fluorescence quantum yield). At the cost of a higher shot noise, such calibration uncertainties may be reduced by MFD-PIE measurements. Alternatively, instruments may be calibrated by “short” distance samples using a combination of TCSPC and MFD-OCE.
3.2. Approximation Error of Homogeneous Models
3.2.1. Effect of Dye Diffusion
Due to their convenience, homogeneous models are used even though quenchers near the dye may introduce systematic deviations. We demonstrated for a single exemplary structure (Figure 10) that a single quencher could introduce position-dependent relative deviations of the average distance in the range −6% to 4%. To test whether these results are generally valid, we present in this section the simulations of 2133 FRET experiments using 500 distinct protein structures and labeling positions. Following the BD simulations, we compare the recovered average apparent distances ⟨Rapp⟩ to the average DA distances ⟨RDA⟩ and account for (1) spatial population density of the dyes due to flexible coupling, (2) transient effects on FRET due to dye diffusion, and (3) dynamic quenching of the donor by aromatic amino acids.
We used the
coarse-grained BD simulations as presented in Figure 7B and the experimentally calibrated parameters
of Alexa488 and Alexa 647 (see Figure 8C) to simulate overall 2133 FRET experiments using
500 of the currently best-resolved protein crystal structures (the
Top500).127 For each structure, six labeling
positions were chosen at random, and surface inaccessible sites were
discriminated, if the volume of an AV of a DA pair was smaller than
3.0% of a typical AV volume of the dye. For each simulation, fluorescence
decays of the donor in the absence, 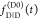 , and the presence,
, and the presence, 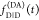 , of an acceptor,
and the corresponding
FRET-induced donor decay, εD(t),
were calculated by eqs 29 and 10, respectively. With solutions to eq 20, apparent distance distributions
were obtained and compared to the actual DA distance distributions,
by their respective means ⟨Rapp⟩ and ⟨RDA⟩. In
addition to these averages, the simulated fluorescence quantum yields
of the donor in the absence of FRET, were calculated to study its
influence on deviations between ⟨Rapp⟩ and ⟨RDA⟩.
, of an acceptor,
and the corresponding
FRET-induced donor decay, εD(t),
were calculated by eqs 29 and 10, respectively. With solutions to eq 20, apparent distance distributions
were obtained and compared to the actual DA distance distributions,
by their respective means ⟨Rapp⟩ and ⟨RDA⟩. In
addition to these averages, the simulated fluorescence quantum yields
of the donor in the absence of FRET, were calculated to study its
influence on deviations between ⟨Rapp⟩ and ⟨RDA⟩.
As shown in Figure 12A, the recovered average distance ⟨Rapp⟩ and the correct average donor–acceptor distance ⟨RDA⟩ follow nearly a 1:1 relationship. As highlighted by Figure 12, ⟨Rapp⟩ overestimates ⟨RDA⟩ in the case of “short” distances (⟨RDA⟩/R0 < 0.9) and underestimates ⟨RDA⟩ for “long” distances (⟨RDA⟩/R0 > 0.9). We quantify the differences between ⟨Rapp⟩ and ⟨RDA⟩ by the absolute deviation Δ and the relative deviation δ:
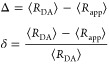 |
52 |
Figure 12.
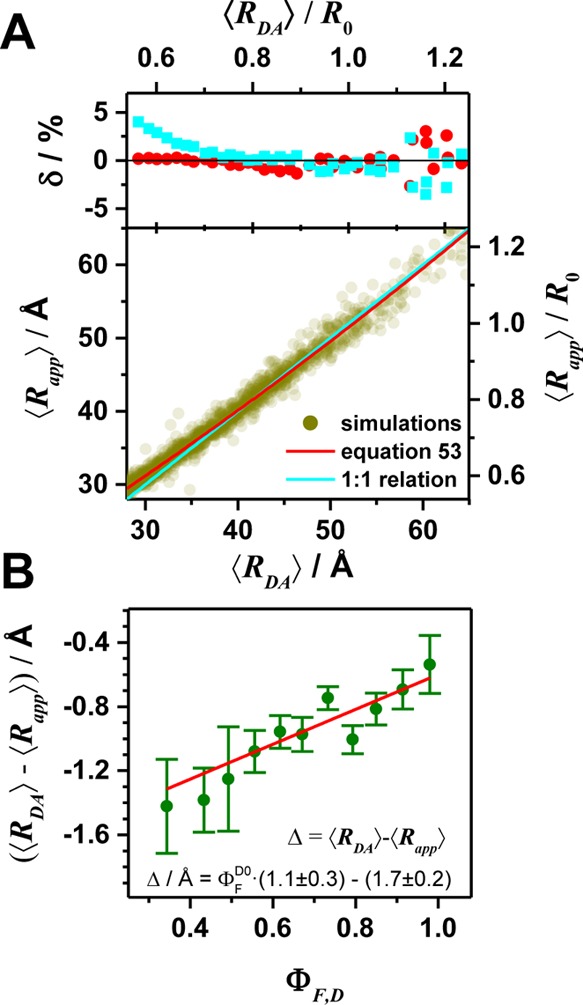
Expected relative error, δ, of the recovered average donor–acceptor distance, ⟨Rapp⟩, which was estimated from simulated FRET experiments of diffusing dyes tethered to proteins. This validates the homogeneous FRET model for the analysis of fluorescence decays of flexibly coupled quenched dyes. Fluorescence decays for the currently best-resolved protein structures were simulated using coarse-grained BD simulations and parameters of the donor–acceptor (DA) pair Alexa488/Alexa647 (see Figure 7). FRET rate constants were calculated using a donor fluorescence lifetime of τD = 4.0 ns and a Förster radius of R0 = 52 Å assuming an orientation factor κ2=2/3. The average apparent DA distances ⟨Rapp⟩ were determined by the FRET-induced donor decay εD(t) by solving eq 20. (A) The obtained ⟨RDA⟩ values are compared to the recovered ⟨Rapp⟩ values. The cyan line corresponds to a 1:1 relationship. The red line describes the empirical relation ⟨Rapp⟩ and ⟨RDA⟩ given by eq 53. On the top, the relative deviation δ = (⟨RDA⟩ – ⟨Rapp⟩)/⟨RDA⟩ is shown. For better comparison, binned deviations are shown. (B) The dependence of the absolute difference Δ = ⟨RDA⟩ – ⟨Rapp⟩ on the simulated fluorescence quantum yield of the donor ΦF,D is shown. This dependence was characterized by a linear model shown in the inset of the figure. To reduce the noise, the data were binned. The circles and error bars correspond to the average and the standard deviation of each bin, respectively.
In the simulations, short distances (< 40 Å) are over-represented, and the distance range relevant for FRET (30–80 Å) is not uniformly sampled. Therefore, we binned the ⟨Rapp⟩ in the range from 30 to 65 Å, and compare the mean ⟨Rapp⟩ to the mean ⟨RDA⟩. The relative deviation δ between these averages is shown in Figure 12B. Overall, δ does not exceed 4%. However, as already evident by Figure 12A and highlighted by Figure 12B, the deviation between ⟨RDA⟩ and ⟨Rapp⟩ is systematic. We quantified these deviations by fitting them with a second-order polynomial. This allowed us to directly relate ⟨RDA⟩ to ⟨Rapp⟩ and vice versa:
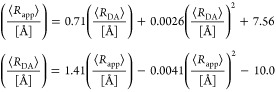 |
53 |
This conversion function minimizes systematic deviations (see Figure 15B) and reduces the anticipated relative error from ∼2.0% (uncorrected) to ∼1.5% for the presented case.
Figure 15.
Distances estimated
by time-resolved fluorescence measurements
for the simplest bimodal model of two discrete distances are highly
correlated. (A) Correlation coefficients 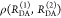 . (B, left) The 2D probability distribution
function (counterfeit normal) of observed estimates of parameters
. (B, left) The 2D probability distribution
function (counterfeit normal) of observed estimates of parameters 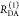 ,
, 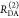 for expectations
for expectations 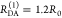 ,
, 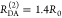 . (B, right) The marginal (1D projections)
probability distribution functions of estimations of
. (B, right) The marginal (1D projections)
probability distribution functions of estimations of 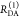 (blue),
(blue), 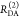 (green),
and the probability distribution
functions of ΔRDA estimation (red,
shifted for comparison) for 4 sets of expected parameters marked by
circles in Figure 14A,B and here in panel A. Indices (i, ii, iii) correspond to the regions
defined in Figure 14B.
(green),
and the probability distribution
functions of ΔRDA estimation (red,
shifted for comparison) for 4 sets of expected parameters marked by
circles in Figure 14A,B and here in panel A. Indices (i, ii, iii) correspond to the regions
defined in Figure 14B.
To reveal potential correlations
between Δ = ⟨RDA⟩
– ⟨Rapp⟩ and ΦF,D, the same procedure
was applied. ΦF,D was binned in the range 0.34–1.0.
For each ΦF,D bin, Δ and the standard deviation
of Δ was calculated. The outcome of this procedure reveals a
clear (nearly linear) dependence of Δ on ΦF,D (Figure 12B). This
dependency demonstrates that ⟨Rapp⟩ overestimates ⟨RDA⟩
for strongly quenched dyes (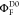 = 0.34) by less than 2 Å.
= 0.34) by less than 2 Å.
To sum up, a static homogeneous model applied to flexibly coupled mobile dyes recovers average DA distances with surprisingly high accuracy (δ < 0.025 for 0.7 < ⟨RDA⟩/R0 < 1.1). Furthermore, dynamic quenching only plays a minor role; i.e., even for strongly quenched donor dyes (ΦF,D = 0.4) only deviations of Δ = −1.6 Å are anticipated.
3.2.2. Effect of Labeling Symmetry
In FRET measurements between a single donor, D, and acceptor, A, the distribution of D and A between the two possible labeling sites of a protein is often unknown, as both dyes are attached by the same labeling chemistry. Consequently, two cases for a FRET sample must be distinguished. The first case refers to the sample DA, where D is attached to the first labeling position, and the second case refers to the sample (AD) where D is attached to the second position. In each labeling site, the dyes may be specifically quenched by the protein and may sample positions within distinct sterically accessible volumes. Therefore, the DA and AD labeled species could have distinct fluorescence properties and FRET rate constant distributions introducing additional uncertainties. The fluorescence decay of a mixture of DA and AD species, {AD}, is given by
| 54 |
Here,
the species fraction x(DA) determines
the fraction of the DA species.
Ideally, 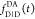 is analyzed by two independent FRET-induced
donor decays
is analyzed by two independent FRET-induced
donor decays 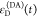 and
and 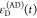 for the DA and AD species,
and the initially
unknown fraction x(DA) is determined.
However, by considering two distinct molecular species, the number
of unknown parameters significantly increases. Therefore, in practice
for the DA and AD species,
and the initially
unknown fraction x(DA) is determined.
However, by considering two distinct molecular species, the number
of unknown parameters significantly increases. Therefore, in practice 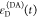 and
and 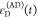 are often approximated by a single average
decay function, εD(t):
are often approximated by a single average
decay function, εD(t):
| 55 |
For the three dyes Alexa Fluor 647 C2 maleimide (Alexa647), Alexa Fluor 488 C5 maleimide (Alexa488), and BodipyFL C1 maleimide (BodipyFL) and the dye pairs Alexa488/Alexa647 and BodipyFL/Alexa647, we assess the error of this approximation by comparing simulated distance distributions of DA and AD species.
The dye pairs Alexa488 and Alexa647 have
linkers of comparable
length (∼20 Å) whereas the linker of BodipyFL is significantly
shorter (∼10 Å). Therefore, the sterically allowed spaces
of Alexa488 and Alexa647 are very similar, and the sterically allowed
space of BodipyFL is considerably smaller. This is visualized for
a pair of labeling sites in Figure 13A. Distance distributions x(RDA) for both species are calculated (Figure 13B). In a direct
comparison, the distance distributions of the DA and the AD species
are merely indistinguishable. This suggests that 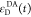 and
and 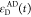 can be approximated by
a joint decay εD(t).
can be approximated by
a joint decay εD(t).
Figure 13.
Deviation of the distance distribution between a donor, D, and an acceptor, A, for the two possible combinations DA and AD was studied to assess the error of a random labeling. The effect of labeling symmetry on the expected distance distributions evaluated by the accessible volume (AV) simulations (see Supporting Information, Note S3). (A) AVs of Alexa488/Alexa647- and BodipyFL/Alexa647-dye pairs attached to the amino acids Q344C/A496C of a hGBP1 protein structure (PDB-ID: 1DG3). (B) The resulting distance distributions x(RDA) and mean distances ⟨RDA⟩. (C) Comparison of both possible average distances for a set of large protein structures (with more than 360 amino acids). The average distances ⟨RDA⟩ = 1/2(⟨RDA(DA)⟩ + ⟨RDA⟩) are plotted vs their deviation Δ = ⟨RDA(DA)⟩ + ⟨RDA⟩ in a two-dimensional histogram for a random set of fluorophore pairs for Alexa488/Alexa647 (red). The histograms to the side and the top are the projections of the respective axes. For the dye pair BodipyFL/Alexa647 only a histogram of Δ is shown (green).
To assess this approximation in more depth, we simulated AVs using a large a set of distinct protein structures (5592) with at least 360 amino acids in the chain and a minimum resolution of 1.8 Å (see Supporting Information, Note S3). These protein structures were selected from the Protein Data Bank using the software PDBselect.128 For each structure, at least 180 random FRET pairs were chosen, and all possible AVs were calculated. Inaccessible and poorly accessible labeling positions were excluded, by a threshold criterion based on the size of the accessible volume (AV) as described above (Section 3.2.1).
This procedure resulted in overall
∼50 000 FRET pairs
for both dye pairs. For all FRET pairs the distance distribution of
the DA and AD species and their average distances 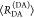 and
and 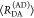 were calculated. These averages
are compared
in Figure 13C by the
average
were calculated. These averages
are compared
in Figure 13C by the
average 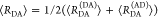 and the deviation
and the deviation 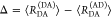 . This expected deviation Δ between
. This expected deviation Δ between 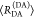 and
and 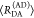 species is especially
small (∼0.8
Å) for the fluorophore pair Alexa488/Alexa647 with similar linker
lengths. Bigger deviations (∼2.5 Å) were found for the
fluorophore pair BodipyFL/Alexa647 with linker lengths differing by
50%. These results suggest that the labeling symmetry is generally
only of minor importance for freely diffusing dyes that weakly interact
with their host molecule.
species is especially
small (∼0.8
Å) for the fluorophore pair Alexa488/Alexa647 with similar linker
lengths. Bigger deviations (∼2.5 Å) were found for the
fluorophore pair BodipyFL/Alexa647 with linker lengths differing by
50%. These results suggest that the labeling symmetry is generally
only of minor importance for freely diffusing dyes that weakly interact
with their host molecule.
3.3. Statistical Resolution of Time-Resolved Measurements
3.3.1. Model and Statistical Uncertainty Estimates
The effects discussed above are only of practical relevance if the quality of the experiment is sufficiently high, meaning that the error, given in TCSPC by the photon shot noise, is sufficiently low. The errors of derived parameters can be determined by exhaustive sampling the model parameter space.7,129 However, to stress fundamental limitations, we estimate the statistical errors for a simple distance distribution with a given noise level of the experiment, and ask under which conditions the underlying parameters are still resolvable that define this distribution.
In this section we
consider the simplest possible model with two fluorescent species
with equal fractions sharing a common fluorescence lifetime, 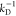 , of the donor in the
absence of FRET and
characterized by two distinct DA distances, RDA. The corresponding distance distribution is given by two
δ-peaks located at the expectation values
, of the donor in the
absence of FRET and
characterized by two distinct DA distances, RDA. The corresponding distance distribution is given by two
δ-peaks located at the expectation values 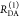 and
and 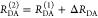 . The corresponding
expected donor fluorescence
decay of such a system is given by
. The corresponding
expected donor fluorescence
decay of such a system is given by
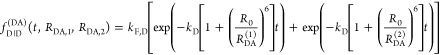 |
56 |
Using this model, we address
the following questions: (1) How many
photons have to be measured to determine 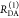 and
and 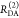 (or ΔRDA) with a given confidence? (2) Beyond which
upper limit of
(or ΔRDA) with a given confidence? (2) Beyond which
upper limit of 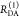 is no other second longer distance
is no other second longer distance 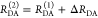 able to be resolved?
able to be resolved?
To answer these questions, we estimate the statistical variances for this model using the Cramér–Rao inequality which states that the standard deviation cannot be smaller than a well-defined limit given by the inverse of the Fisher information matrix (FIM):
| 57 |
Here, 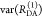 ,
, 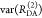 , and
, and 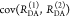 are the variance
and the covariance of
are the variance
and the covariance of 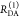 and
and 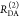 , respectively.
, respectively. 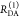 and
and 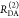 are independent
of the number of counted
fluorescence photons, NF. Therefore, their
variances and covariances scale with 1/NF, and their expected variances can be estimated a priori. Note that we report the variances of
are independent
of the number of counted
fluorescence photons, NF. Therefore, their
variances and covariances scale with 1/NF, and their expected variances can be estimated a priori. Note that we report the variances of 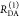 ,
, 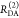 by their
respective relative standard errors (
by their
respective relative standard errors (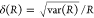 ).
).
To discuss this model for practically relevant cases, we
determined
the variances and covariances of the model parameters estimates 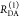 and
and 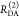 in eq 56 numerically (see Supporting Information, Note S4, discussion of the estimation of statistical errors).
In addition, we computed the variance of the difference
in eq 56 numerically (see Supporting Information, Note S4, discussion of the estimation of statistical errors).
In addition, we computed the variance of the difference 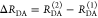 to quantify their
separability, S = δ(ΔRDA)−1. We considered fluorescence decays
with NF = 106 counted photons
in a time-window T = 50 ns for the fluorescence decay
histogram assuming
a dye pair with a Förster radius of R0 = 50 Å and a donor fluorescence lifetime of kD–1 = 4 ns.
to quantify their
separability, S = δ(ΔRDA)−1. We considered fluorescence decays
with NF = 106 counted photons
in a time-window T = 50 ns for the fluorescence decay
histogram assuming
a dye pair with a Förster radius of R0 = 50 Å and a donor fluorescence lifetime of kD–1 = 4 ns.
The dependence
of the relative errors of the parameter estimates 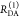 ,
, 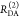 and
and 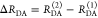 on the first distance
on the first distance 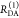 (in relative
fractions of R0) is displayed by isolines
in Figure 14A. We
define a parameter estimate as “reliable”,
if its relative standard error δ is smaller than 0.5. This criterion
corresponds to a confidence level of 68%. Isolines for this criterion
(Figure 14A, white
lines) are overlaid for comparison as colored lines in a joint plot
(Figure 14B). These
isolines partition the parameter space into four regions: In region
i, all three parameters (
(in relative
fractions of R0) is displayed by isolines
in Figure 14A. We
define a parameter estimate as “reliable”,
if its relative standard error δ is smaller than 0.5. This criterion
corresponds to a confidence level of 68%. Isolines for this criterion
(Figure 14A, white
lines) are overlaid for comparison as colored lines in a joint plot
(Figure 14B). These
isolines partition the parameter space into four regions: In region
i, all three parameters (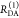 ,
, 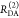 , and
, and 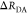 ) are resolved. In region ii, only the distances
) are resolved. In region ii, only the distances 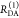 ,
, 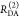 are reliably
estimated. In region iii,
only the shorter distance
are reliably
estimated. In region iii,
only the shorter distance 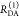 is reliably
determined, meaning that the
distance distribution is only partially resolved, and low-FRET species
cannot be distinguished from non-FRET species. Finally, in region
iv, no parameter is resolved. The isolines of
is reliably
determined, meaning that the
distance distribution is only partially resolved, and low-FRET species
cannot be distinguished from non-FRET species. Finally, in region
iv, no parameter is resolved. The isolines of 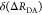 and
and 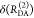 do not exceed certain values of
do not exceed certain values of 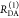 and thus
define limiting distances (Figure 14B, vertical lines).
We refer to these limits as
and thus
define limiting distances (Figure 14B, vertical lines).
We refer to these limits as  and
and 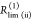 . If
. If 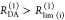 , the difference ΔRDA is uncertain. If
, the difference ΔRDA is uncertain. If 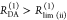 , neither ΔRDAnor
, neither ΔRDAnor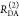 is resolved. The dependencies of these
limiting distances on the number of detected photons are presented
in Figure 14C.
is resolved. The dependencies of these
limiting distances on the number of detected photons are presented
in Figure 14C.
Figure 14.
Considering
the simplest bimodal model with two discrete distances,
the distance resolution of time-resolved fluorescence measurements
is limited by the shot noise of the experiment. Statistical error
estimates of a two-distance model described by eq 56 with distances 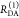 and
and 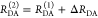 , fluorescence
lifetime τD(0) = 4 ns, and a time-window of 12.5τD(0). (A) Relative
standard error δ per 106 photons of the distances
, fluorescence
lifetime τD(0) = 4 ns, and a time-window of 12.5τD(0). (A) Relative
standard error δ per 106 photons of the distances 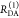 (blue, left),
(blue, left), 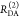 (green, middle),
and their difference ΔRDA (red,
right). White lines are isolines
δ = 0.5 (also shown at panel D). (B) Isolines of δ(
(green, middle),
and their difference ΔRDA (red,
right). White lines are isolines
δ = 0.5 (also shown at panel D). (B) Isolines of δ(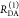 )) = 0.5 (blue line), δ(
)) = 0.5 (blue line), δ(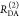 ) = 0.5 (green
line), and δ(ΔRDA)=0.5 (red
line) for 106 counted photons (the same as white lines
at panel A). The isolines
partition the parameter space in four regions: (i) All three parameters
are resolved. (ii) The distances
) = 0.5 (green
line), and δ(ΔRDA)=0.5 (red
line) for 106 counted photons (the same as white lines
at panel A). The isolines
partition the parameter space in four regions: (i) All three parameters
are resolved. (ii) The distances 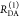 ,
, 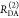 can be reliably
determined while the relative
standard error of their difference δ(ΔRDA) increases above value 0.5. (iii) Only the shorter
distance
can be reliably
determined while the relative
standard error of their difference δ(ΔRDA) increases above value 0.5. (iii) Only the shorter
distance 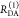 is reliably estimated. The distance distribution
is only partially resolved, and the species with small FRET rate constant
cannot be distinguished from non-FRET species. (iv) None of the parameters
is resolved. The vertical lines indicate limiting distances
is reliably estimated. The distance distribution
is only partially resolved, and the species with small FRET rate constant
cannot be distinguished from non-FRET species. (iv) None of the parameters
is resolved. The vertical lines indicate limiting distances 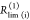 of the region
i (red) and
of the region
i (red) and 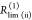 of the region
ii (green). (C) Dependence
of the limiting distances
of the region
ii (green). (C) Dependence
of the limiting distances 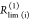 and
and 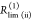 on the number of detected photons.
on the number of detected photons.
3.3.2. Correlations between Estimated Distances
To understand the significant
difference between the two limiting
distances and why in region ii 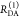 and
and 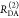 are resolved
while ΔRDA is unresolved, the correlation
between the parameter
estimates should be considered. According to error propagation rules,
the standard error of ΔRDA may vary
between
are resolved
while ΔRDA is unresolved, the correlation
between the parameter
estimates should be considered. According to error propagation rules,
the standard error of ΔRDA may vary
between 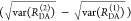 , if the
estimates of
, if the
estimates of 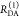 and
and  are fully correlated, and
are fully correlated, and 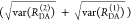 , if the estimates of
, if the estimates of 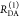 and
and 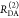 are anticorrelated.
We found that, for
the most experimentally interesting combinations of the parameters
are anticorrelated.
We found that, for
the most experimentally interesting combinations of the parameters  and
and 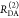 , the estimates
are highly anticorrelated,
i.e., the corresponding Pearson’s correlation coefficient,
, the estimates
are highly anticorrelated,
i.e., the corresponding Pearson’s correlation coefficient,  , tends to −1)
(see Figure 15A). Consequently, the second limit applies
that predicts large errors
of ΔRDA. This correlation means
that the estimates of
, tends to −1)
(see Figure 15A). Consequently, the second limit applies
that predicts large errors
of ΔRDA. This correlation means
that the estimates of 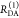 and
and 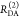 are dependent
on each other; i.e., if
are dependent
on each other; i.e., if 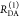 is underestimated,
is underestimated, 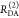 will be most
probably be overestimated
and vice versa. The effect of such an anticorrelation
is illustrated in Figure 15B for a Gaussian approximation of a two-dimensional probability
distribution
will be most
probably be overestimated
and vice versa. The effect of such an anticorrelation
is illustrated in Figure 15B for a Gaussian approximation of a two-dimensional probability
distribution 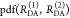 . The standard
deviations of
. The standard
deviations of 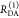 and
and 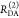 are the widths of the marginal distributions
obtained by a projection of 2D distribution
are the widths of the marginal distributions
obtained by a projection of 2D distribution 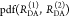 to the corresponding axes.
to the corresponding axes.
3.3.3. Using the Correlation between Model Parameters
If the fluorescence
decays are analyzed in a traditional manner
by using a mathematical model, the influence of increasing 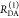 on the resolution
of distance pairs (cases
i–iii) can be directly visualized by plotting the corresponding
marginal error distributions (Figure 15B, right). However, due to anticorrelation, these marginal
distributions do not allow us to analyze the joint distribution
on the resolution
of distance pairs (cases
i–iii) can be directly visualized by plotting the corresponding
marginal error distributions (Figure 15B, right). However, due to anticorrelation, these marginal
distributions do not allow us to analyze the joint distribution 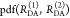 . This limitation can be overcome by directly
exploiting the correlation between the model parameters via a joint
pdf as displayed for two distances in Figure 15B, left. Furthermore, if either structural
considerations, i.e., prior structural knowledge or global analysis
of multiple fluorescence decays, reduce the parameter space of either
. This limitation can be overcome by directly
exploiting the correlation between the model parameters via a joint
pdf as displayed for two distances in Figure 15B, left. Furthermore, if either structural
considerations, i.e., prior structural knowledge or global analysis
of multiple fluorescence decays, reduce the parameter space of either  or
or 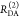 , the remaining
parameter is better resolved.
This stresses the importance of considering the nonzero covariance
for precise analysis of fluorescence decays and clarifies why global
analysis of multiple fluorescence decays harbors potential to improve
the overall resolution.
, the remaining
parameter is better resolved.
This stresses the importance of considering the nonzero covariance
for precise analysis of fluorescence decays and clarifies why global
analysis of multiple fluorescence decays harbors potential to improve
the overall resolution.
3.3.4. Planning FRET Experiments
Statistical
uncertainties and correlations between model parameters can be estimated
by Figures 14Α
and 15A for given expectation values. Hence,
the presented graphs can be used to plan experiments. For example,
given expectation values of 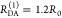 , ΔRDA= 0.2R0, the relative
standard errors for 106 counted photons are
, ΔRDA= 0.2R0, the relative
standard errors for 106 counted photons are 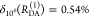 ,
, 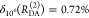 ,
, 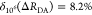 , and correlation coefficient
, and correlation coefficient 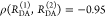 . The errors for any other number of counted
photons, NF, can be obtained by dividing
the reported values by the factor
. The errors for any other number of counted
photons, NF, can be obtained by dividing
the reported values by the factor 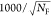 . Using the presented
dependence of the
two limits
. Using the presented
dependence of the
two limits 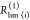 and
and 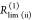 on the number of counted photons in Figure 14C, the limiting
resolvable distances can be estimated. First, this plot reveals that
the limiting resolvable distances scale only weakly (nearly logarithmically)
with the number of photons. Second, the resolution of the width of
distance distribution (given by
on the number of counted photons in Figure 14C, the limiting
resolvable distances can be estimated. First, this plot reveals that
the limiting resolvable distances scale only weakly (nearly logarithmically)
with the number of photons. Second, the resolution of the width of
distance distribution (given by 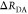 for our simple bimodal model) requires
1–2 orders of magnitude more counted photons. Considering larger
distances with
for our simple bimodal model) requires
1–2 orders of magnitude more counted photons. Considering larger
distances with 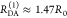 , at
least 106 photons have to
be detected to be able to estimate all parameters of our model system,
whereas for smaller distances with
, at
least 106 photons have to
be detected to be able to estimate all parameters of our model system,
whereas for smaller distances with 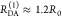 this is already achieved with
104 detected photons, i.e., within 0.1 s at a detection
count rate of
100 kHz of a typical confocal single-molecule experiment. This confirms
the observations for the TSCP experiments in Section 3.1 (Figure 11, left panel), that precision of time-resolved measurements
decreases strongly for interdye distances >1.2R0. Considering case i (all three parameters (
this is already achieved with
104 detected photons, i.e., within 0.1 s at a detection
count rate of
100 kHz of a typical confocal single-molecule experiment. This confirms
the observations for the TSCP experiments in Section 3.1 (Figure 11, left panel), that precision of time-resolved measurements
decreases strongly for interdye distances >1.2R0. Considering case i (all three parameters (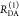 ,
, 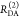 and ΔRDA are resolved), practical limits for the measurements
of large interdye
distances are recognized. For example, for case ii (only the distances
and ΔRDA are resolved), practical limits for the measurements
of large interdye
distances are recognized. For example, for case ii (only the distances 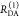 ,
, 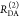 are resolved)
two orders of magnitude more
photons have to be detected to resolve
are resolved)
two orders of magnitude more
photons have to be detected to resolve 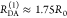 compared to
compared to 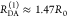 .
.
Finally, let us note that the presented values are lower bounds of the real error. In practice, the errors will be bigger if the fractions of components need to be determined and further experimental nuisances are considered.
4. Summary and Outlook
We presented an analysis method for time-resolved FRET measurements which rationalizes the global analysis of the donor fluorescence decays and the use of reference measurements. We introduced the concept of the FRET-induced donor decay (Figure 3) that allows us to directly resolve heterogeneities and visualize donor–acceptor distance distributions (Figure 4). This significantly facilitates the communication of experimental results to nonexperts. We quantified the effect of systematic errors due to inappropriate reference samples, statistical uncertainties due to shot noise, and the influence of dynamic donor quenching on recovered donor–acceptor distances. We found that potential systematic errors and statistical errors are the main error source. Therefore, a precise characterization of the reference sample is mandatory.
To account for potential correlations between FRET rate constants and the reference donor lifetimes in the absence of FRET, we presented a framework for a more accurate analysis (Figure 5) using refined dye models.77 In practice, such correlations are often unknown. This introduces ambiguities to the interpretation of the fluorescence decays. A fast coarse-grained BD simulation approach (Figure 7) which describes dye diffusion and PET in the nanosecond regime potentially solves such ambiguities by relating structural models with fluorescence observables. Using such introduced fast simulations, we demonstrated that such correlations are negligible for the flexibly coupled dyes attached to proteins in a single conformation.
In future, integrative modeling combining fast numerical simulations of fluorescence observables may allow for high precision quantitative structural models of proteins based on FRET and PET. Alternatively, as the simple relations between the average recovered distance and the average distance (see eq 52) suggest, dye diffusion could be explicitly accounted in the analysis using a transfer-matrix which converts apparent distance distributions x(Rapp) into donor–acceptor distance distributions x(RDA). All equations presented apply for cases of low excitation in the absence of acceptor saturation. Given strong excitation, the acceptor saturation has to be considered.78 However, recent measurements indicate that for dye pairs such as Alexa488/Alexa594 excited-state annihilation is considerable so that the power dependence is reduced.130,131 Therefore, the presented methods may also apply to single-molecule measurements recorded at high excitation power.
Similar to NMR spectroscopy where a deep understanding of the underlying physics is key to distilling observables reporting on molecular properties of interest from the measured signal, a better molecular understanding of the physical dyes’ properties combined with simulations of molecular detail and microscopic techniques will harness the rich information provided by fluorescence measurements at a higher level of detail. A number of parameters and processes exist for both spectroscopies, which have a similar information type, if the different distance dependencies around the probe (nucleus or dye label) are taken into account. Illustrative examples for NMR–fluorescence analogies are (1) dipolar coupling (nuclear Overhauser effect (NOE)–FRET), (2) conformational dynamics in the millisecond time scale (relaxation dispersion experiments132–dynamic photon distribution analysis (dynPDA,31)), and (3) unique information on the local probe environment (chemical shift–fluorescence quenching). Such developments will render fluorescence spectroscopy an indispensable tool for integrative structural modeling because dynamic information with subnanosecond time resolution on biomolecules can be obtained in vitro and in live cells. Since fluorescence information is sparse, a combination with molecular simulations, often referred to as “computational microscopy”,133 and high-resolution structural data is particularly fruitful.
Moreover, these spectroscopic methods can be combined with super-resolution microscopy, in particular stimulated emission depletion (STED) microscopy,134,135 and with high-resolution structural data (e.g., cryoEM and crystallography) to realize molecular fluorescence microscopy that allows localizing biomolecular systems in live cells and describing biomolecular dynamics by structural models. These recent methodological and technical advances in fluorescence spectroscopy and microscopy as well as in multiscale modeling of complex biochemical systems set the stage to tackle cross-fertilizing challenges in biophysics, biochemistry, and cell biology.
Abbreviations
Methods and Processes
FRET, Förster resonance energy transfer; PET, photoinduced electron transfer; TCSPC, time-correlated single photon counting; IRF, instrument response function; pdf, probability density function; MD, molecular dynamics; AV, accessible volume simulation; BD, Brownian dynamics simulations
Theory and Analysis
Acknowledgments
Prof. Dr. Walter Frank encouraged one of the authors (CAMS) to perform interdisciplinary research at the Heinrich Heine University Düsseldorf. Therefore this paper is dedicated my colleague Prof. Dr. Walter Frank on the occasion of his 60th birthday. We thank C. Hengstenberg and C. Herrmann for providing hGBP1-samples triggering this work, J. J. McCann and M. E. Bowen for PSD-95 samples, M. Tsytlonok, R. Kriwacki, and P. Tompa for providing p27 samples, and J. Kubiak (J.K.), P. Dollinger, K .E. Jäger, and F. Kovacic for LiF samples. We thank the following members of the Seidel group for contributing data on the fluorescence properties of donor and acceptor dyes in different proteins compiled in Figure 1 and Table S1: J.K. for PSD-95 data, Suren Felekyan, H. Sanabria (H.S.), K. Hemmen (K.H.) for p27 data; H.S., K.H., and D. Rodnin for T4L samples and data. C.A.M.S. acknowledges financial support from the German Research Foundation (DFG, SE 1195/17-1) and the European Research Council ERC (Advanced Grant hybrid-FRET, 671208). T.-O.P. thanks the International Helmholtz Research School of Biophysics and Soft Matter (IHRS BioSoft). Additionally, we thank Mykola Dimura, Christian Hanke, Aiswaria Prakash, Jan-Hendrik Budde for proofreading the paper, Hugo Sanabria for creative discussions on the design of the cover, and Attila Szabo, Thorsten Hugel and Björn Hellenkamp for fruitful scientific discussions.
Biographies

Thomas-Otavio Peulen (to the right) completed his Ph.D. as a fellow of the International Helmholtz Research School of Biophysics and Soft Matter (BioSoft) in Claus Seidel’s group. His interest is in relating biomolecular structure and dynamics in vitro and live cells by fluorescence spectroscopy. During his M.Sc. he studied nanoparticles in biofilms by fluorescence spectroscopy and microscopy at the University of Montreal and received his M.Sc. in Water-Science from the University Duisburg-Essen, Germany.
Oleg Opanasyuk (to the left) is a PostDoc in Claus Seidel’s group. He is interested in the development of models and computer simulations for the analysis of fluorescence data. He received his Ph.D. from the Department of Chemistry, Umea University, in Sweden for research in the group of Prof. Lennart B.-A. Johansson. Before that, he received his M.Sc. in physics from Kazan State University (Russian Federation), where he was involved in studies of molecular mobility in porous media and plants using NMR spectroscopy.
Claus A. M. Seidel is Full-Professor (in the middle) in physical chemistry at the University Düsseldorf, Germany. His primary research interests are multimodal fluorescence spectroscopy and imaging and molecular biophysical chemistry. He studied chemistry at the Universities of Stuttgart and Heidelberg. He received his Ph.D. in physical chemistry at the Heidelberg University in the group of Prof. Dr. Jürgen Wolfrum. Next, he was a PostDoc at a Sandoz research institute in Vienna. Before becoming Professor in Düsseldorf, he was the head of a junior research team focused on single-molecule fluorescence spectroscopy at the Max Planck Institute for Biophysical Chemistry in Güttingen, Germany.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.7b03441.
Tables of fluorescence lifetime components of Alexa647 (Table S1) and Alexa488 (Table S2) which are shown graphically in Figure 1, a table of PDB-IDs of structural models used for the BD simulations (Table S3), details on the decay analysis by normally distributed distances (Note S1), a brief discussion of a time-dependent yield of the FRET process (Note S2), and details of accessible volume simulations (Note S3) and statistical error estimations by the Cramér–Rao inequality (Note S4) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Förster T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 437, 55–75. 10.1002/andp.19484370105. [DOI] [Google Scholar]
- Stryer L.; Haugland R. P. Energy transfer: A spectroscopic ruler. Proc. Natl. Acad. Sci. U. S. A. 1967, 58, 719–726. 10.1073/pnas.58.2.719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochstrasser R. A.; Chen S. M.; Millar D. P. Distance distribution in a dye-linked oligonucleotide determined by time-resolved fluorescence energy transfer. Biophys. Chem. 1992, 45, 133–141. 10.1016/0301-4622(92)87005-4. [DOI] [PubMed] [Google Scholar]
- Klostermeier D.; Millar D. P. Time-resolved fluorescence resonance energy transfer: A versatile tool for the analysis of nucleic acids. Biopolymers 2002, 61, 159–179. 10.1002/bip.10146. [DOI] [PubMed] [Google Scholar]
- Muretta J. M.; Jun Y.; Gross S. P.; Major J.; Thomas D. D.; Rosenfeld S. S. The structural kinetics of switch-1 and the neck linker explain the functions of kinesin-1 and Eg5. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, E6606–E6613. 10.1073/pnas.1512305112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesmelov Y. E.; Agafonov R. V.; Negrashov I. V.; Blakely S. E.; Titus M. A.; Thomas D. D. Structural kinetics of myosin by transient time-resolved FRET. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 1891–1896. 10.1073/pnas.1012320108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vöpel T.; Hengstenberg C. S.; Peulen T.-O.; Ajaj Y.; Seidel C. A. M.; Herrmann C.; Klare J. P. Triphosphate induced dimerization of human guanylate binding protein 1 involves association of the C-terminal helices: A joint double electron-electron resonance and FRET study. Biochemistry 2014, 53, 4590–4600. 10.1021/bi500524u. [DOI] [PubMed] [Google Scholar]
- Hofig H.; Gabba M.; Poblete S.; Kempe D.; Fitter J. Inter-dye distance distributions studied by a combination of single-molecule FRET-filtered lifetime measurements and a weighted accessible volume (wAV) algorithm. Molecules 2014, 19, 19269–19291. 10.3390/molecules191219269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gryczynski I.; Wiczk W.; Johnson M. L.; Cheung H. C.; Wang C. K.; Lakowicz J. R. Resolution of end-to-end distance distributions of flexible molecules using quenching-induced variations of the Förster distance for fluorescence energy transfer. Biophys. J. 1988, 54, 577–586. 10.1016/S0006-3495(88)82992-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brünger A. T.; Strop P.; Vrljic M.; Chu S.; Weninger K. R. Three-dimensional molecular modeling with single molecule FRET. J. Struct. Biol. 2011, 173, 497–505. 10.1016/j.jsb.2010.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalinin S.; Peulen T.; Sindbert S.; Rothwell P. J.; Berger S.; Restle T.; Goody R. S.; Gohlke H.; Seidel C. A. M. A toolkit and benchmark study for FRET-restrained high-precision structural modeling. Nat. Methods 2012, 9, 1218–1225. 10.1038/nmeth.2222. [DOI] [PubMed] [Google Scholar]
- Clegg R. M.; Murchie A. I.; Lilley D. M. The solution structure of the four-way DNA junction at low-salt conditions: A fluorescence resonance energy transfer analysis. Biophys. J. 1994, 66, 99–109. 10.1016/S0006-3495(94)80765-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clegg R. M.; Murchie A. I. H.; Zechel A.; Carlberg C.; Diekmann S.; Lilley D. M. J. Fluorescence resonance energy transfer analysis of the structure of the four-way DNA junction. Biochemistry 1992, 31, 4846–4856. 10.1021/bi00135a016. [DOI] [PubMed] [Google Scholar]
- Boura E.; Rozycki B.; Herrick D. Z.; Chung H. S.; Vecer J.; Eaton W. A.; Cafiso D. S.; Hummer G.; Hurley J. H. Solution structure of the ESCRT-I complex by small-angle X-ray scattering, EPR, and FRET spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 9437–9442. 10.1073/pnas.1101763108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murchie A. I. H.; Clegg R. M.; von Kitzing E.; Duckett D. R.; Diekmann S.; Lilley D. M. J. Fluorescence energy transfer shows that the four-way DNA junction is a right-handed cross of antiparallel molecules. Nature 1989, 341, 763–766. 10.1038/341763a0. [DOI] [PubMed] [Google Scholar]
- Tuschl T.; Gohlke C.; Jovin T. M.; Westhof E.; Eckstein F. A three-dimensional model for the hammerhead ribozyme based on fluorescence measurements. Science 1994, 266, 785–789. 10.1126/science.7973630. [DOI] [PubMed] [Google Scholar]
- Mekler V.; Kortkhonjia E.; Mukhopadhyay J.; Knight J.; Revyakin A.; Kapanidis A. N.; Niu W.; Ebright Y. W.; Levy R.; Ebright R. H. Structural organization of bacterial RNA polymerase holoenzyme and the RNA polymerase-promoter open complex. Cell 2002, 108, 599–614. 10.1016/S0092-8674(02)00667-0. [DOI] [PubMed] [Google Scholar]
- Möglich A.; Joder K.; Kiefhaber T. End-to-end distance distributions and intrachain diffusion constants in unfolded polypeptide chains indicate intramolecular hydrogen bond formation. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 12394–12399. 10.1073/pnas.0604748103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeRocco V. C.; Anderson T.; Piehler J.; Erie D. A.; Weninger K. Four-color single-molecule fluorescence with noncovalent dye labeling to monitor dynamic multimolecular complexes. BioTechniques 2010, 49, 807–816. 10.2144/000113551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice S. A.Diffusion-Limited Reactions; Elsevier: Amsterdam, 1985; Vol. 25. [Google Scholar]
- Clegg R. M. Fluorescence resonance energy transfer and nucleic acids. Methods Enzymol. 1992, 211, 353–388. 10.1016/0076-6879(92)11020-J. [DOI] [PubMed] [Google Scholar]
- Ha T.; Enderle T.; Ogletree D. F.; Chemla D. S.; Selvin P. R.; Weiss S. Probing the interaction between two single molecules: Fluorescence resonance energy transfer between a single donor and a single acceptor. Proc. Natl. Acad. Sci. U. S. A. 1996, 93, 6264–6268. 10.1073/pnas.93.13.6264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss S. Fluorescence spectroscopy of single biomolecules. Science 1999, 283, 1676–1683. 10.1126/science.283.5408.1676. [DOI] [PubMed] [Google Scholar]
- Sisamakis E.; Valeri A.; Kalinin S.; Rothwell P. J.; Seidel C. A. M. Accurate single-molecule FRET studies using multiparameter fluorescence detection. Methods Enzymol. 2010, 475, 455–514. 10.1016/S0076-6879(10)75018-7. [DOI] [PubMed] [Google Scholar]
- Farooq S.; Hohlbein J. Camera-based single-molecule FRET detection with improved time resolution. Phys. Chem. Chem. Phys. 2015, 17, 27862–27872. 10.1039/C5CP04137F. [DOI] [PubMed] [Google Scholar]
- Felekyan S.; Sanabria H.; Kalinin S.; Kühnemuth R.; Seidel C. A. M. Analyzing Förster resonance energy transfer with fluctuation algorithms. Methods Enzymol. 2013, 519, 39–85. 10.1016/B978-0-12-405539-1.00002-6. [DOI] [PubMed] [Google Scholar]
- Eggeling C.; Widengren J.; Rigler R.; Seidel C. A. M. Photobleaching of fluorescent dyes under conditions used for single-molecule-detection: Evidence of two-step photolysis. Anal. Chem. 1998, 70, 2651–2659. 10.1021/ac980027p. [DOI] [PubMed] [Google Scholar]
- Chung H. S.; McHale K.; Louis J. M.; Eaton W. A. Single-molecule fluorescence experiments determine protein folding transition path times. Science 2012, 335, 981–984. 10.1126/science.1215768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakowicz J. R.Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, 2006. [Google Scholar]
- Greife A.; Felekyan S.; Ma Q.; Gertzen C. G. W.; Spomer L.; Dimura M.; Peulen T.-O.; Wöhler C.; Häussinger D.; Gohlke H.; et al. Structural assemblies of the di- and oligomeric G-protein coupled receptor TGR5 in live cells: an MFIS-FRET and integrative modelling study. Sci. Rep. 2016, 6, 36792. 10.1038/srep36792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalinin S.; Valeri A.; Antonik M.; Felekyan S.; Seidel C. A. M. Detection of structural dynamics by FRET: A photon distribution and fluorescence lifetime analysis of systems with multiple states. J. Phys. Chem. B 2010, 114, 7983–7995. 10.1021/jp102156t. [DOI] [PubMed] [Google Scholar]
- Gopich I. V.; Szabo A. Theory of the energy transfer efficiency and fluorescence lifetime distribution in single-molecule FRET. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 7747–7752. 10.1073/pnas.1205120109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurunathan K.; Levitus M. FRET fluctuation spectroscopy of diffusing biopolymers: Contributions of conformational dynamics and translational diffusion. J. Phys. Chem. B 2010, 114, 980–986. 10.1021/jp907390n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopich I. V.; Szabo A. Decoding the pattern of photon colors in single-molecule FRET. J. Phys. Chem. B 2009, 113, 10965–10973. 10.1021/jp903671p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopich I. V.; Szabo A. FRET efficiency distributions of multistate single molecules. J. Phys. Chem. B 2010, 114, 15221–15226. 10.1021/jp105359z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jares-Erijman E. A.; Jovin T. M. FRET imaging. Nat. Biotechnol. 2003, 21, 1387–1395. 10.1038/nbt896. [DOI] [PubMed] [Google Scholar]
- Becker W.; Benndorf K.; Bergmann A.; Biskup C.; König K.; Tirlapur U.; Zimmer T. FRET measurements by TCSPC laser scanning microscopy. Proc. SPIE 2001, 4431, 94–98. 10.1117/12.447406. [DOI] [Google Scholar]
- Becker W.; Bergmann A.; Hink M. A.; König K.; Benndorf K.; Biskup C. Fluorescence lifetime imaging by time-correlated single-photon counting. Microsc. Res. Tech. 2004, 63, 58–66. 10.1002/jemt.10421. [DOI] [PubMed] [Google Scholar]
- Biskup C.; Zimmer T.; Kelbauskas L.; Hoffmann B.; Klöcker N.; Becker W.; Bergmann A.; Benndorf K. Multi-dimensional fluorescence lifetime and FRET measurements. Microsc. Res. Tech. 2007, 70, 442–451. 10.1002/jemt.20431. [DOI] [PubMed] [Google Scholar]
- Biskup C.; Kusch J.; Schulz E.; Nache V.; Schwede F.; Lehmann F.; Hagen V.; Benndorf K. Relating ligand binding to activation gating in CNGA2 channels. Nature 2007, 446, 440–443. 10.1038/nature05596. [DOI] [PubMed] [Google Scholar]
- Weidtkamp-Peters S.; Felekyan S.; Bleckmann A.; Simon R.; Becker W.; Kühnemuth R.; Seidel C. A. M. Multiparameter fluorescence image spectroscopy to study molecular interactions. Photochem. Photobiol. Sci. 2009, 8, 470–480. 10.1039/b903245m. [DOI] [PubMed] [Google Scholar]
- Sustarsic M.; Kapanidis A. N. Taking the ruler to the jungle: Single-molecule FRET for understanding biomolecular structure and dynamics in live cells. Curr. Opin. Struct. Biol. 2015, 34, 52–59. 10.1016/j.sbi.2015.07.001. [DOI] [PubMed] [Google Scholar]
- Stahl Y.; Grabowski S.; Bleckmann A.; Kühnemuth R.; Weidtkamp-Peters S.; Pinto K. G.; Kirschner G. K.; Schmid J. B.; Wink R. H.; Hülsewede A.; et al. Moderation of Arabidopsis root stemness by CLAVATA1 and ARABIDOPSIS CRINKLY4 receptor kinase complexes. Curr. Biol. 2013, 23, 362–371. 10.1016/j.cub.2013.01.045. [DOI] [PubMed] [Google Scholar]
- Somssich M.; Ma Q.; Weidtkamp-Peters S.; Stahl Y.; Felekyan S.; Bleckmann A.; Seidel C. A. M.; Simon R. Real-time dynamics of peptide ligand-dependent receptor complex formation in planta. Sci. Signaling 2015, 8, ra76. 10.1126/scisignal.aab0598. [DOI] [PubMed] [Google Scholar]
- Kravets E.; Degrandi D.; Ma Q.; Peulen T.-O.; Klümpers V.; Felekyan S.; Kühnemuth R.; Weidtkamp-Peters S.; Seidel C. A. M.; Pfeffer K. Guanylate binding proteins directly attack Toxoplasma gondii via supramolecular complexes. eLife 2016, 5, e11479 10.7554/eLife.11479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall P.; Selinger B. Better estimates of exponential decay parameters. J. Phys. Chem. 1981, 85, 2941–2946. 10.1021/j150620a019. [DOI] [Google Scholar]
- Köllner M.; Wolfrum J. How many photons are necessary for fluorescence lifetime measurements. Chem. Phys. Lett. 1992, 200, 199–204. 10.1016/0009-2614(92)87068-Z. [DOI] [Google Scholar]
- Schaffer J.; Volkmer A.; Eggeling C.; Subramaniam V.; Striker G.; Seidel C. A. M. Identification of single molecules in aqueous solution by time-resolved fluorescence anisotropy. J. Phys. Chem. A 1999, 103, 331–336. 10.1021/jp9833597. [DOI] [Google Scholar]
- Maus M.; Cotlet M.; Hofkens J.; Gensch T.; De Schryver F. C.; Schaffer J.; Seidel C. A. M. An experimental comparison of the maximum likelihood estimation and nonlinear least squares fluorescence lifetime analysis of single molecules. Anal. Chem. 2001, 73, 2078–2086. 10.1021/ac000877g. [DOI] [PubMed] [Google Scholar]
- Wozniak A. K.; Schröder G. F.; Grubmüller H.; Seidel C. A. M.; Oesterhelt F. Single-molecule FRET measures bends and kinks in DNA.. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 18337–18342. 10.1073/pnas.0800977105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrecka J.; Treutlein B.; Arcusa M. A. I.; Muschielok A.; Lewis R.; Cheung A. C. M.; Cramer P.; Michaelis J. Nano positioning system reveals the course of upstream and nontemplate DNA within the RNA polymerase II elongation complex. Nucleic Acids Res. 2009, 37, 5803–5809. 10.1093/nar/gkp601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margittai M.; Widengren J.; Schweinberger E.; Schröder G. F.; Felekyan S.; Haustein E.; König M.; Fasshauer D.; Grubmüller H.; Jahn R.; et al. Single-molecule fluorescence resonance energy transfer reveals a dynamic equilibrium between closed and open conformations of syntaxin 1. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 15516–15521. 10.1073/pnas.2331232100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theissen B.; Karow A. R.; Köhler J.; Gubaev A.; Klostermeier D. Cooperative binding of ATP and RNA induces a closed conformation in a DEAD box RNA helicase. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 548–553. 10.1073/pnas.0705488105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopich I. V.; Szabo A. Single-macromolecule fluorescence resonance energy transfer and free-energy profiles. J. Phys. Chem. B 2003, 107, 5058–5063. 10.1021/jp027481o. [DOI] [Google Scholar]
- Haustein E.; Schwille P. Fluorescence correlation spectroscopy: Novel variations of an established technique. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 151–169. 10.1146/annurev.biophys.36.040306.132612. [DOI] [PubMed] [Google Scholar]
- Sheather S. J.; Jones M. C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. 1991, 53, 683–690. [Google Scholar]
- Klehs K.; Spahn C.; Endesfelder U.; Lee S. F.; Fürstenberg A.; Heilemann M. Increasing the brightness of cyanine fluorophores for single-molecule and superresolution imaging. ChemPhysChem 2014, 15, 637–641. 10.1002/cphc.201300874. [DOI] [PubMed] [Google Scholar]
- Neubauer H.; Gaiko N.; Berger S.; Schaffer J.; Eggeling C.; Tuma J.; Verdier L.; Seidel C. A. M.; Griesinger C.; Volkmer A. Orientational and dynamical heterogeneity of rhodamine 6G terminally attached to a DNA helix revealed by NMR and single-molecule fluorescence spectroscopy. J. Am. Chem. Soc. 2007, 129, 12746–12755. 10.1021/ja0722574. [DOI] [PubMed] [Google Scholar]
- Seidel C. A. M.; Schulz A.; Sauer M. H. M. Nucleobase-specific quenching of fluorescent dyes. 1. Nucleobase one-electron redox potentials and their correlation with static and dynamic quenching efficiencies. J. Phys. Chem. 1996, 100, 5541–5553. 10.1021/jp951507c. [DOI] [Google Scholar]
- Eggeling C.; Fries J. R.; Brand L.; Günther R.; Seidel C. A. M. Monitoring conformational dynamics of a single molecule by selective fluorescence spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 1998, 95, 1556–1561. 10.1073/pnas.95.4.1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doose S.; Neuweiler H.; Sauer M. Fluorescence quenching by photoinduced electron transfer: A reporter for conformational dynamics of macromolecules. ChemPhysChem 2009, 10, 1389–1398. 10.1002/cphc.200900238. [DOI] [PubMed] [Google Scholar]
- Sauerwein B.; Murphy S.; Schuster G. B. Dynamics of solute motion: photoisomerization shows linear-dependence on solvent mass. J. Am. Chem. Soc. 1992, 114, 7920–7922. 10.1021/ja00046a053. [DOI] [Google Scholar]
- Buschmann V.; Weston K. D.; Sauer M. Spectroscopic study and evaluation of red-absorbing fluorescent dyes. Bioconjugate Chem. 2003, 14, 195–204. 10.1021/bc025600x. [DOI] [PubMed] [Google Scholar]
- Widengren J.; Schwille P. Characterization of photoinduced isomerization and back-isomerization of the cyanine dye Cy5 by fluorescence correlation spectroscopy. J. Phys. Chem. A 2000, 104, 6416–6428. 10.1021/jp000059s. [DOI] [Google Scholar]
- Levitus M.; Ranjit S. Cyanine dyes in biophysical research: The photophysics of polymethine fluorescent dyes in biomolecular environments. Q. Rev. Biophys. 2011, 44, 123–151. 10.1017/S0033583510000247. [DOI] [PubMed] [Google Scholar]
- Chibisov A. K.; Zakharova G. V.; Görner H.; Sogulyaev Y. A.; Mushkalo I. L.; Tolmachev A. I. Photorelaxation processes in covalently-linked indocarbocyanine and thiacarbocyanine dyes. J. Phys. Chem. 1995, 99, 886–893. 10.1021/j100003a009. [DOI] [Google Scholar]
- Widengren J.; Schweinberger E.; Berger S.; Seidel C. A. M. Two new concepts to measure fluorescence resonance energy transfer via fluorescence correlation spectroscopy: Theory and experimental realizations. J. Phys. Chem. A 2001, 105, 6851–6866. 10.1021/jp010301a. [DOI] [Google Scholar]
- Stennett E. M. S.; Ciuba M. A.; Lin S.; Levitus M. Demystifying PIFE: The photophysics behind the protein-induced fluorescence enhancement phenomenon in Cy3. J. Phys. Chem. Lett. 2015, 6, 1819–1823. 10.1021/acs.jpclett.5b00613. [DOI] [PubMed] [Google Scholar]
- Kalinin S.; Sisamakis E.; Magennis S. W.; Felekyan S.; Seidel C. A. M. On the origin of broadening of single-molecule FRET efficiency distributions beyond shot noise limits. J. Phys. Chem. B 2010, 114, 6197–6206. 10.1021/jp100025v. [DOI] [PubMed] [Google Scholar]
- Kalinin S.; Felekyan S.; Valeri A.; Seidel C. A. M. Characterizing multiple molecular states in single-molecule multiparameter fluorescence detection by probability distribution analysis. J. Phys. Chem. B 2008, 112, 8361–8374. 10.1021/jp711942q. [DOI] [PubMed] [Google Scholar]
- Lerner E.; Ploetz E.; Hohlbein J.; Cordes T.; Weiss S. A quantitative theoretical framework for Protein-Induced Fluorescence Enhancement-Förster-type Resonance Energy Transfer (PIFE-FRET). J. Phys. Chem. B 2016, 120, 6401–6410. 10.1021/acs.jpcb.6b03692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristóvão M.; Sisamakis E.; Hingorani M. M.; Marx A. D.; Jung C. P.; Rothwell P. J.; Seidel C. A. M.; Friedhoff P. Single-molecule multiparameter fluorescence spectroscopy reveals directional MutS binding to mismatched bases in DNA. Nucleic Acids Res. 2012, 40, 5448–5464. 10.1093/nar/gks138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muschielok A.; Andrecka J.; Jawhari A.; Brückner F.; Cramer P.; Michaelis J. A nano-positioning system for macromolecular structural analysis. Nat. Methods 2008, 5, 965–971. 10.1038/nmeth.1259. [DOI] [PubMed] [Google Scholar]
- Sindbert S.; Kalinin S.; Nguyen H.; Kienzler A.; Clima L.; Bannwarth W.; Appel B.; Müller S.; Seidel C. A. M. Accurate distance determination of nucleic acids via Förster resonance energy transfer: Implications of dye linker length and rigidity. J. Am. Chem. Soc. 2011, 133, 2463–2480. 10.1021/ja105725e. [DOI] [PubMed] [Google Scholar]
- Walczewska-Szewc K.; Corry B. Accounting for dye diffusion and orientation when relating FRET measurements to distances: Three simple computational methods. Phys. Chem. Chem. Phys. 2014, 16, 12317–12326. 10.1039/C4CP01222D. [DOI] [PubMed] [Google Scholar]
- Beckers M.; Drechsler F.; Eilert T.; Nagy J.; Michaelis J. Quantitative structural information from single-molecule FRET. Faraday Discuss. 2015, 184, 117–129. 10.1039/C5FD00110B. [DOI] [PubMed] [Google Scholar]
- Dimura M.; Peulen T. O.; Hanke C. A.; Prakash A.; Gohlke H.; Seidel C. A. M. Quantitative FRET studies and integrative modeling unravel the structure and dynamics of biomolecular systems. Curr. Opin. Struct. Biol. 2016, 40, 163–185. 10.1016/j.sbi.2016.11.012. [DOI] [PubMed] [Google Scholar]
- Beutler M.; Makrogianneli K.; Vermeij R. J.; Keppler M.; Ng T.; Jovin T. M.; Heintzmann R. satFRET: estimation of Förster resonance energy transfer by acceptor saturation. Eur. Biophys. J. 2008, 38, 69–82. 10.1007/s00249-008-0361-5. [DOI] [PubMed] [Google Scholar]
- Edman P.; Westlund P. O.; Johansson L. B. A. On determining intramolecular distances from donor-donor energy migration (DDEM) within bifluorophoric macromolecules. Phys. Chem. Chem. Phys. 2000, 2, 1789–1794. 10.1039/a909701e. [DOI] [Google Scholar]
- Clayton A. H. A.; Hanley Q. S.; Arndt-Jovin D. J.; Subramaniam V.; Jovin T. M. Dynamic fluorescence anisotropy imaging microscopy in the frequency domain (rFLIM). Biophys. J. 2002, 83, 1631–1649. 10.1016/S0006-3495(02)73932-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opanasyuk O.; Johansson L. B. A. On the analyses of fluorescence depolarisation data in the presence of electronic energy migration. Part I: Theory and general description. Phys. Chem. Chem. Phys. 2012, 14, 1907–1916. 10.1039/C1CP22483B. [DOI] [PubMed] [Google Scholar]
- Kalinin S.; Molotkovsky J. G.; Johansson L. B. A. Distance measurements using partial donor-donor energy migration within pairs of fluorescent groups in lipid bilayers. J. Phys. Chem. B 2003, 107, 3318–3324. 10.1021/jp022672c. [DOI] [Google Scholar]
- Rothwell P. J.; Berger S.; Kensch O.; Felekyan S.; Antonik M.; Wöhrl B. M.; Restle T.; Goody R. S.; Seidel C. A. M. Multi-parameter single-molecule fluorescence spectroscopy reveals heterogeneity of HIV-1 reverse transcriptase:primer/template complexes. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 1655–1660. 10.1073/pnas.0434003100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czuper A.; Gryczynski I.; Kusba J. Förster energy transfer from nonexponentially decaying donors. J. Photochem. Photobiol., B 2007, 87, 200–208. 10.1016/j.jphotobiol.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Toptygin D.; Chin A. F.; Hilser V. J. Effect of diffusion on resonance energy transfer rate distributions: Implications for distance measurements. J. Phys. Chem. B 2015, 119, 12603–12622. 10.1021/acs.jpcb.5b06567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Striker G.; Subramaniam V.; Seidel C. A. M.; Volkmer A. Photochromicity and fluorescence lifetimes of green fluorescent protein. J. Phys. Chem. B 1999, 103, 8612–8617. 10.1021/jp991425e. [DOI] [Google Scholar]
- Volkmer A.; Subramaniam V.; Birch D. J. S.; Jovin T. M. One- and two-photon excited fluorescence lifetimes and anisotropy decays of green fluorescent proteins. Biophys. J. 2000, 78, 1589–1598. 10.1016/S0006-3495(00)76711-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas E.; Katchalski-Katzir E.; Steinberg I. Z. Effect of the orientation of donor and acceptor on the probability of energy transfer involving electronic transitions of mixed polarization. Biochemistry 1978, 17, 5064–5070. 10.1021/bi00616a032. [DOI] [PubMed] [Google Scholar]
- van der Meer W. B.; van der Meer D. M.; Vogel S. S.. Optimizing the orientation factor kappa-squared for more accurate FRET measurements. In FRET—Förster Resonance Energy Transfer: From Theory to Applications; Medintz I., Hildebrandt N., Eds.; Wiley-VCH Verlag: Weinheim, Germany, 2014. [Google Scholar]
- Förster T. Experimentelle und theoretische Untersuchung des zwischenmolekularen Übergangs von Elektronenanregungsenergie. Z. Naturforsch. 1949, 4, 321–327. [Google Scholar]
- Olofsson M.; Kalinin S.; Zdunek J.; Oliveberg M.; Johansson L. B. A. Tryptophan-BODIPY: A versatile donor-acceptor pair for probing generic changes of intraprotein distances. Phys. Chem. Chem. Phys. 2006, 8, 3130–3140. 10.1039/B601313A. [DOI] [PubMed] [Google Scholar]
- van der Meer B. W.; Raymer M. A.; Wagoner S. L.; Hackney R. L.; Beechem J. M.; Gratton E. Designing matrix models for fluorescence energy transfer between moving donors and acceptors. Biophys. J. 1993, 64, 1243–1263. 10.1016/S0006-3495(93)81490-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beechem J. M.; Gratton E.; Ameloot M.; Knutson J. R.; Brand L.. The global analysis of fluorescence intensity and anisotropy decay data: Second-generation theory and programs. In Topics in Fluorescence Spectroscopy; Springer, 2002; Vol. 2, pp 241–305. [Google Scholar]
- Bialik C. N.; Wolf B.; Rachofsky E. L.; Ross J. B. A.; Laws W. R. Dynamics of biomolecules: Assignment of local motions by fluorescence anisotropy decay. Biophys. J. 1998, 75, 2564–2573. 10.1016/S0006-3495(98)77701-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hummer G.; Szabo A. Dynamics of the orientational factor in fluorescence resonance energy transfer. J. Phys. Chem. B 2017, 121, 3331–3339. 10.1021/acs.jpcb.6b08345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwemmle M.; Staeheli P. The interferon-induced 67-kDa guanylate-binding protein (hGBP1) is a GTPase that converts GTP to GMP. J. Biol. Chem. 1994, 269, 11299–11305. [PubMed] [Google Scholar]
- Livesey A. K.; Skilling J. Maximum entropy theory. Acta Crystallogr., Sect. A: Found. Crystallogr. 1985, 41, 113–122. 10.1107/S0108767385000241. [DOI] [Google Scholar]
- Brochon J. C. Maximum entropy method of data-analysis in time-resolved spectroscopy. Methods Enzymol. 1994, 240, 262–311. 10.1016/S0076-6879(94)40052-0. [DOI] [PubMed] [Google Scholar]
- Kalinin S.; Johansson L. B. A. Energy migration and transfer rates are invariant to modeling the fluorescence relaxation by discrete and continuous distributions of lifetimes. J. Phys. Chem. B 2004, 108, 3092–3097. 10.1021/jp031096x. [DOI] [Google Scholar]
- Rachofsky E. L.; Laws W. R. Kinetic models and data analysis methods for fluorescence anisotropy decay. Methods Enzymol. 2000, 321, 216–238. 10.1016/S0076-6879(00)21196-8. [DOI] [PubMed] [Google Scholar]
- Best R. B.; Hofmann H.; Nettels D.; Schuler B. Quantitative interpretation of FRET experiments via molecular simulation: Force field and validation. Biophys. J. 2015, 108, 2721–2731. 10.1016/j.bpj.2015.04.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoefling M.; Grubmüller H. In silico FRET from simulated dye dynamics. Comput. Phys. Commun. 2013, 184, 841–852. 10.1016/j.cpc.2012.10.018. [DOI] [Google Scholar]
- Westlund P. O.; Wennerstrom H. Electronic energy transfer in liquids. The effect of molecular dynamics. J. Chem. Phys. 1993, 99, 6583–6589. 10.1063/1.465850. [DOI] [Google Scholar]
- Chen H.; Ahsan S. S.; Santiago-Berrios M. B.; Abruna H. D.; Webb W. W. Mechanisms of quenching of Alexa fluorophores by natural amino acids. J. Am. Chem. Soc. 2010, 132, 7244–7245. 10.1021/ja100500k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus R. A.; Sutin N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta, Rev. Bioenerg. 1985, 811, 265–322. 10.1016/0304-4173(85)90014-X. [DOI] [Google Scholar]
- Moser C. C.; Keske J. M.; Warncke K.; Farid R. S.; Dutton P. L. Nature of biological electron transfer. Nature 1992, 355, 796–802. 10.1038/355796a0. [DOI] [PubMed] [Google Scholar]
- Gray H. B.; Winkler J. R. Electron transfer in proteins. Annu. Rev. Biochem. 1996, 65, 537–61. 10.1146/annurev.bi.65.070196.002541. [DOI] [PubMed] [Google Scholar]
- Joshi N.; Johnson M. L.; Gryczynski I.; Lakowicz J. R. Radiation boundary-conditions in collisional quenching of fluorescence; Determination by frequency-domain fluorometry. Chem. Phys. Lett. 1987, 135, 200–207. 10.1016/0009-2614(87)85142-4. [DOI] [Google Scholar]
- Nemzek T. L.; Ware W. R. Kinetics of diffusion-controlled reactions: Transient effects in fluorescence quenching. J. Chem. Phys. 1975, 62, 477–489. 10.1063/1.430501. [DOI] [Google Scholar]
- Kusba J.; Lakowicz J. R. Diffusion-modulated energy-transfer and quenching - Analysis by numerical-integration of diffusion equation in Laplace space. Methods Enzymol. 1994, 240, 216–262. 10.1016/S0076-6879(94)40051-2. [DOI] [PubMed] [Google Scholar]
- Hoefling M.; Lima N.; Haenni D.; Seidel C. A. M.; Schuler B.; Grubmüller H. Structural heterogeneity and quantitative FRET efficiency distributions of polyprolines through a hybrid atomistic simulation and Monte Carlo approach. PLoS One 2011, 6, e19791. 10.1371/journal.pone.0019791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steffen F. D.; Sigel R. K. O.; Börner R. An atomistic view on carbocyanine photophysics in the realm of RNA. Phys. Chem. Chem. Phys. 2016, 18, 29045–29055. 10.1039/C6CP04277E. [DOI] [PubMed] [Google Scholar]
- Gendron P. O.; Avaltroni F.; Wilkinson K. J. Diffusion coefficients of several rhodamine derivatives as determined by pulsed field gradient-nuclear magnetic resonance and fluorescence correlation spectroscopy. J. Fluoresc. 2008, 18, 1093–1101. 10.1007/s10895-008-0357-7. [DOI] [PubMed] [Google Scholar]
- Müller C. B.; Loman A.; Pacheco V.; Koberling F.; Willbold D.; Richtering W.; Enderlein J. Precise measurement of diffusion by multi-color dual-focus fluorescence correlation spectroscopy. EPL 2008, 83, 46001. 10.1209/0295-5075/83/46001. [DOI] [Google Scholar]
- Zhang X. J.; Wozniak J. A.; Matthews B. W. Protein flexibility and adaptability seen in 25 crystal forms of T4 lysozyme. J. Mol. Biol. 1995, 250, 527–552. 10.1006/jmbi.1995.0396. [DOI] [PubMed] [Google Scholar]
- Kuroki R.; Weaver L. H.; Matthews B. W. A covalent enzyme-substrate intermediate with saccharide distortion in a mutant T4 lysozyme. Science 1993, 262, 2030–2033. 10.1126/science.8266098. [DOI] [PubMed] [Google Scholar]
- Prakash B.; Praefcke G. J. K.; Renault L.; Wittinghofer A.; Herrmann C. Structure of human guanylate-binding protein 1 representing a unique class of GTP-binding proteins. Nature 2000, 403, 567–571. 10.1038/35000617. [DOI] [PubMed] [Google Scholar]
- Bach A.; Clausen B. H.; Moller M.; Vestergaard B.; Chi C. N.; Round A.; Sorensen P. L.; Nissen K. B.; Kastrup J. S.; Gajhede M.; et al. A high-affinity, dimeric inhibitor of PSD-95 bivalently interacts with PDZ1–2 and protects against ischemic brain damage. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 3317–3322. 10.1073/pnas.1113761109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H.; Chopra R.; Verdine G. L.; Harrison S. C. Structure of a covalently trapped catalytic complex of HIV-I reverse transcriptase: Implications for drug resistance. Science 1998, 282, 1669–1675. 10.1126/science.282.5394.1669. [DOI] [PubMed] [Google Scholar]
- McCann J. J.; Zheng L. Q.; Rohrbeck D.; Felekyan S.; Kühnemuth R.; Sutton R. B.; Seidel C. A. M.; Bowen M. E. Supertertiary structure of the synaptic MAGuK scaffold proteins is conserved. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 15775–15780. 10.1073/pnas.1200254109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothwell P. J.; Allen W. J.; Sisamakis E.; Kalinin S.; Felekyan S.; Widengren J.; Waksman G.; Seidel C. A. M. dNTP-dependent conformational transitions in the fingers subdomain of Klentaq1 DNA polymerase: Insights into the role of the ″nucleotide-binding″ state. J. Biol. Chem. 2013, 288, 13575–13591. 10.1074/jbc.M112.432690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yirdaw R. B.; Mchaourab H. S. Direct observation of T4 lysozyme hinge-bending motion by fluorescence correlation spectroscopy. Biophys. J. 2012, 103, 1525–1536. 10.1016/j.bpj.2012.07.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob M. H.; Dsouza R. N.; Ghosh I.; Norouzy A.; Schwarzlose T.; Nau W. M. Diffusion-enhanced Förster resonance energy transfer and the effects of external quenchers and the donor quantum yield. J. Phys. Chem. B 2013, 117, 185–198. 10.1021/jp310381f. [DOI] [PubMed] [Google Scholar]
- Lee N. K.; Kapanidis A. N.; Wang Y.; Michalet X.; Mukhopadhyay J.; Ebright R. H.; Weiss S. Accurate FRET measurements within single diffusing biomolecules using alternating-laser excitation. Biophys. J. 2005, 88, 2939–2953. 10.1529/biophysj.104.054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapanidis A. N.; Laurence T. A.; Lee N. K.; Margeat E.; Kong X.; Weiss S. Alternating-laser excitation of single molecules. Acc. Chem. Res. 2005, 38, 523–533. 10.1021/ar0401348. [DOI] [PubMed] [Google Scholar]
- Müller B. K.; Zaychikov E.; Bräuchle C.; Lamb D. C. Pulsed interleaved excitation. Biophys. J. 2005, 89, 3508–3522. 10.1529/biophysj.105.064766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovell S. C.; Davis I. W.; Arendall W. B. 3rd; de Bakker P. I.; Word J. M.; Prisant M. G.; Richardson J. S.; Richardson D. C. Structure validation by Calpha geometry: phi,psi and Cbeta deviation. Proteins: Struct., Funct., Genet. 2003, 50, 437–450. 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- Griep S.; Hobohm U. PDBselect 1992–2009 and PDBfilter-select. Nucleic Acids Res. 2010, 38, D318–D319. 10.1093/nar/gkp786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straume M.; Frasier-Cadoret S. G.; Johnson M. L.. Least-squares analysis of fluorescence data. In Topics in Fluorescence Spectroscopy, Vol. 2: Principles; Lakowicz J. R., Ed.; Plenum Press: New York, 1991; pp 177–240. [Google Scholar]
- Nettels D.; Haenni D.; Maillot S.; Gueye M.; Barth A.; Hirschfeld V.; Hübner C. G.; Leonard J.; Schuler B. Excited-state annihilation reduces power dependence of single-molecule FRET experiments. Phys. Chem. Chem. Phys. 2015, 17, 32304–32315. 10.1039/C5CP05321H. [DOI] [PubMed] [Google Scholar]
- Hofkens J.; Cotlet M.; Vosch T.; Tinnefeld P.; Weston K. D.; Ego C.; Grimsdale A.; Müllen K.; Beljonne D.; Bredas J. L.; et al. Revealing competitive Förster-type resonance energy transfer pathways in single bichromophoric molecules. Proc. Natl. Acad. Sci. U. S. A. 2003, 100, 13146–13151. 10.1073/pnas.2235805100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henzler-Wildman K.; Kern D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- Shaw D. E.; Maragakis P.; Lindorff-Larsen K.; Piana S.; Dror R. O.; Eastwood M. P.; Bank J. A.; Jumper J. M.; Salmon J. K.; Shan Y. B.; et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- Hell S. W.; Wichmann J. Breaking the diffraction resolution limit by stimulated-emission: Stimulated-Emission-Depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. 10.1364/OL.19.000780. [DOI] [PubMed] [Google Scholar]
- Hell S. W. Far-field optical nanoscopy. Science 2007, 316, 1153–1158. 10.1126/science.1137395. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.