Mechanisms of synaptic depression at the hair cell ribbon synapse that support auditory nerve function

Significance

Sensory systems use adaptation as a mechanism to enhance the range of responses to incoming stimuli. In the auditory system, the synapses between inner hair cells and dendrites of auditory nerve neurons have been pointed as the adaptation site. This synapse is responsible for converting graded acoustic signals into trains of action potentials. We present evidence showing that depletion of rapidly releasing vesicles produces an early depression of the synaptic response. Also, we observed that desensitization of postsynaptic receptors plays a fundamental role in synaptic decay. Stronger stimuli produce larger and longer lasting responses that are more profoundly affected by desensitization. Both pre- and postsynaptic mechanisms contribute to depression at this synapse, imparting multiple features to auditory nerve function.

Abstract

Inner hair cells (IHCs) in the cochlea are the mammalian phono-receptors, transducing sound energy into graded changes in membrane potentials, the so called “receptor potentials.” Ribbon synapses between IHCs and auditory nerve neurons are responsible for converting receptor potentials into spike rates. The characteristics of auditory nerve responses to sound have been described extensively. For instance, persistent acoustic stimulation produces sensory adaptation, which is revealed as a reduction in neuronal spike rate with time constants in the range of milliseconds to seconds. Since the amplitude of IHC receptor potentials is invariant during this period, the classic hypothesis pointed to vesicle depletion at the IHC as responsible for auditory adaptation. In this study, we observed that fast synaptic depression occurred in responses to stimuli of varying intensities. Nevertheless, release continued after this initial depression, via synaptic vesicles with slower exocytotic kinetics. Heterogeneity in kinetic elements, therefore, favored synaptic responses with an early peak and a sustained phase. The application of cyclothiazide (CTZ) revealed that desensitization of postsynaptic receptors contributed to synaptic depression, which was more pronounced during stronger stimulation. Thus, desensitization had a twofold effect: It abbreviated signaling between IHC and the auditory nerve and also balanced differences in decay kinetics between responses to different stimulation strengths. We therefore propose that both pre- and postsynaptic mechanisms at the IHC ribbon synapse contribute to synaptic depression at the IHC ribbon synapse and spike rate adaptation in the auditory nerve.

In multiple sensory modalities, persistent stimuli generate adaptations of the system’s response that can be observed as a reduction in gain (1, 2). Adaptive processes prevent saturation and allow for a rescale of the response range, to match the input domain. Different strategies have been described in sensory systems to account for these phenomena, including changes in synaptic strength (3). In the auditory system, adaptation is critical for coding of temporal and spectral features of sound. For instance, adaptation shortens the time window in which the onset component is encoded and thus increases its temporal precision (4).

Neurons in the auditory nerve carry information from the environment to the brain and undergo adaptation in its firing rate upon constant tonal stimulation (5–8). Electrical activity in each neuron is controlled synaptically (9), via a single synaptic contact with an inner hair cell (IHC) from the cochlea (10). IHCs are also responsible for mechano-sensory transduction, producing graded changes in membrane potential, the so-called “receptor potential” (11, 12). As the amplitude of the receptor potential remains constant when stimuli are continuous in time, it was classically proposed that adaptation originated in IHC–auditory neuron synapses. Specifically, depletion of synaptic vesicles was identified as the primary cause of adaptation in experiments with capacitance measurements or in vivo auditory nerve recordings (8, 13–15).

However, detailed investigations have questioned this hypothesis. For instance, if a pedestal increase in sound intensity is applied on a background stimulus, auditory nerve neurons present a fixed rise in firing rate, regardless of how much adaptation was produced by the background tone (16). The rise in firing rate is only determined by the difference in sound intensities between background and pedestal tones, not by the time delay between them. Moreover, decay kinetics does not vary with sound intensity, which seems incompatible with a simple vesicle depletion scheme (17–19). If high-intensity stimuli produce vesicle depletion, why would a moderate one, releasing fewer vesicles, also bring about synaptic depression? Even more so, why do responses decay with constant kinetics?

In this study, we investigated synaptic depression by performing simultaneous recordings from IHC and a contacting bouton of the auditory nerve fiber. We used stimulation paradigms with pedestal changes in IHC membrane potential and investigated changes in synaptic efficacy with maximal and submaximal stimuli. These manipulations, together with the block of AMPA receptor desensitization, allowed us to conclude that both pre- and postsynaptic mechanisms contribute to synaptic depression at the IHC ribbon synapse.

Results

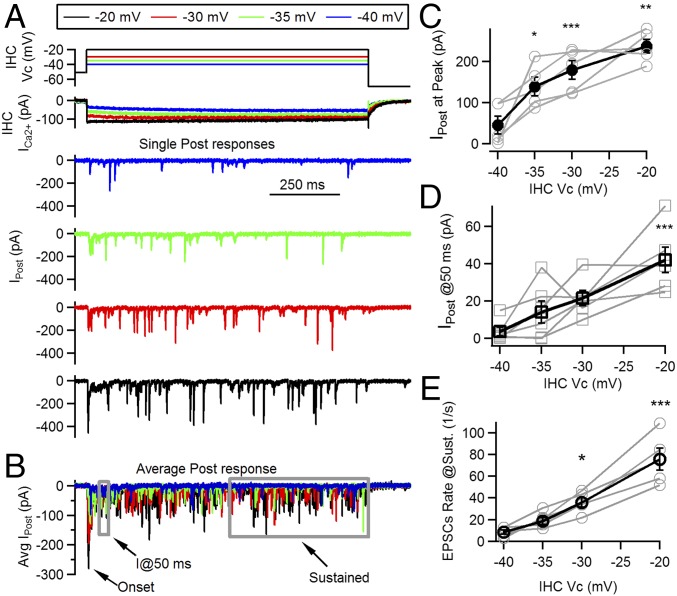
Fig. 1A shows typical synaptic responses to prolonged (1 s) depolarizations at various IHC potentials, covering the range at which IHCs operate physiologically (11, 12). Multiple EPSCs with variable amplitudes were activated in postsynaptic neurons throughout the 1-s stimuli. The timing of each EPSC within the 1-s pulse was stochastic, although at the onset of the presynaptic depolarization, a higher release probability was consistently obtained. This phenomenon was evident in average traces of ensemble responses to maximal depolarization (−20 mV) but also with submaximal stimuli (Figs. 1B and 2A) and was always followed by a decay in activity.

Fig. 1.

Multiple release phases evoked at different IHC potentials. (A) Schematics of IHC voltage protocol (Top), Ca²⁺ current (Middle), and representative single postsynaptic responses at four different presynaptic potentials (−40, −35, −30, and −20 mV). (B) Average traces for responses at the four selected IHC potentials. Different phases of the ensemble response are indicated: the peak at the onset, the response at 50 ms after stimulus onset, and the sustained phases. (C) Amplitude at the peak of the average postsynaptic responses as a function of IHC potential (black symbols/lines). Individual values for each recording are included in gray. (D) Response amplitude at 50 ms after stimulus onset (average of current response between t = 45 and 50 ms). (E) Rate of EPSCs activated per second as a function of IHC potential, measured at the sustained phase of the response (in the last 0.5 s of the 1-s pulse). *P < 0.05; **P < 0.01; ***P < 0.001.

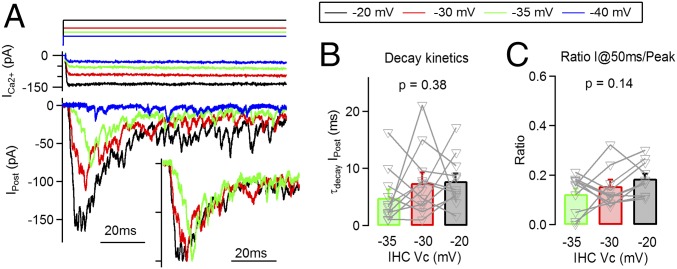
Fig. 2.

Time course of average synaptic responses is constant across stimulus intensities. (A) Detail of the onset phase of postsynaptic responses obtained at four different IHC Vcs, −40, −35, −30, and −20 mV (average traces, Bottom), together with IHC Ca²⁺ current (Middle), and voltage command (Top). (Inset) Normalized traces illustrating a similarity in response time courses (responses to −40 mV steps were excluded due to a lack of onset phase). (B) Time constant of decay of the postsynaptic response at each presynaptic membrane potential. (C) Ratio of postsynaptic responses between peak and at 50 ms, for different IHC potentials.

In accordance with previous results (20, 21), the amplitude of the peak was determined by the magnitude of the Ca²⁺ influx to the IHC, which in turn is highly dependent on the IHC membrane potential. Fig. 1C shows the peak of the onset component for pulses to −20 mV, with an average value of 237 ± 16 pA (n = 6 cell pairs, four to six repetitions each). The average amplitude decreased with submaximal pulses: 179 ± 23 pA at −30 mV, 139 ± 22 pA at −35 mV, and 46 ± 22 pA at −40 mV (n = 6 cell pairs, four to six repetitions each, ANOVA, P < 0.0001). This onset peak would represent the ensemble activation of multiple synaptic events, and its timing also varied with IHC membrane pulses: At −20 mV, the peak occurred at 10.5 ± 1.5 ms after the pulse onset, with −30 mV at 9.3 ± 1.4 ms, −35 mV at 16.6 ± 1.7 ms, and −40 mV at 37.8 ± 6.0 ms (n = 6 cell pairs, ANOVA, P < 0.0001) (due to the sparse activity obtained in −40 mV depolarizations, to estimate peak amplitude and its timing, we used the first 50-ms interval). We further quantified the response amplitude after this initial peak, by measuring the current at 50 ms (I@50 ms) (relative to the onset of IHC pulse). The obtained values were as follows: 42 ± 7 pA at −20 mV pulses, 22 ± 4 pA at −30 mV, 14 ± 6 pA at −35 mV, and 4 ± 2 pA at −40 mV (n = 6 cell pairs, ANOVA, P < 0.001) (Fig. 1D). Finally, release was also estimated at a later time point, by counting EPSC occurrence at the last half of the pulse. We obtained maximal rate values of 78 ± 9 EPSCs per second, with pulses at −20 mV, whereas lower rates were obtained with submaximal pulses: 37 ± 4 for −30 mV, 18 ± 3 for −35 mV, and 7 ± 2 at −40 mV (P < 0.0001, ANOVA) (Fig. 1E). Ca²⁺ currents at the IHC varied accordingly, with peak values of 201 ± 31 pA with pulses at −20 mV, 139 ± 25 pA at −30 mV, 102 ± 25 pA at −35 mV, and 72 ± 20 pA at −40 mV steps.

Thus, results shown in Fig. 1 indicated that synaptic responses present different phases when activated within the −40 to −20 mV range of IHC potentials. The presence of a transient onset component indicates that all responses underwent synaptic depression during the first few milliseconds.

Kinetics of Synaptic Depression.

Fig. 2A shows in detail the onset of the average ensemble responses to IHC depolarizations at different membrane potentials. The similarity between response time courses can be clearly observed in scaled traces (Fig. 2A, Inset). By fitting the decay of average responses with an exponential function, within the first 50 ms from the peak, we obtained the following time constants (Fig. 2B): 7.8 ± 1.3 ms for −20 mV pulses, 7.5 ± 1.8 ms for −30 mV, and 4.9 ± 1.4 ms for −35 mV (n = 11 recordings). These values did not differ statistically (ANOVA, P = 0.38), indicating that fast decay kinetics of postsynaptic responses did not vary with the stimulation level. Responses to −40 mV did not show a consistent peak at the onset in all recordings, and thus, fitting could not be performed.

We further calculated a ratio between the response after depression relative to the maximum (Fig. 2C). This ratio (I@50 ms per peak) represented an estimation for depression level, alternative to fitting the decay phase. It is important to indicate that a larger ratio would represent a more sustained release. No significant difference was observed at different IHC depolarization levels (Vcs): 0.19 ± 0.02 for the −20 mV pulses, 0.16 ± 0.03 for −30 mV, and 0.12 ± 0.02 at −35 mV steps (P = 0.14, ANOVA) (as indicated before, −40 mV pulses were excluded from the analysis).

This result is intriguing given that if we assumed that vesicles were depleted at maximal stimulation (−20 mV), then a more sustained release should be expected with submaximal pulses (producing smaller responses). In other words, it is reasonable to think that responses to −30 or −35 mV should present reduced depression as less vesicles were released at the onset phase. However, no variations in decay kinetics were found. Taken together, results shown in Fig. 2 question the original hypothesis of a mere vesicle depletion to explain adaptation.

Presynaptic Determinants of Synaptic Depression.

Previous studies have shown that Ca²⁺ currents present a strong Ca²⁺-dependent inactivation that could affect release decay (22, 23). We evaluated this possibility and first measured the current at 50 ms (the time point used to calculate the ratio of Fig. 2C; see SI Methods) and calculated a percentage change with respect to the current maximum reported before. At −20 mV pulses, we observed a 7.9 ± 2.1% reduction from the peak; at −30 mV, only a 1.3 ± 2.0% decrease; and at −35 mV, 2.2 ± 2.5% decrease (n = 6 recordings). These results suggest that changes in Ca²⁺ influx during step depolarizations of the IHC had a limited contribution to the synaptic depression shown in Figs. 1 and 2, especially at −30 and −35 mV pulses.

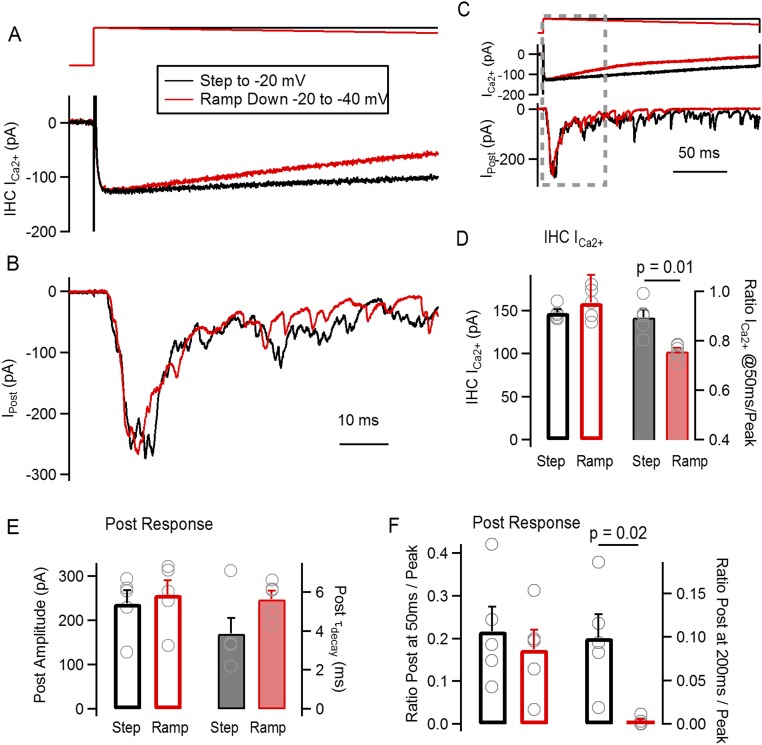
To further evaluate how much the reduction in Ca²⁺ influx could affect depression in the −20 mV pulses, we decided to use a modified voltage protocol that emphasized Ca²⁺ current inactivation. The voltage protocol consisted of an immediate step to −20 mV, followed by a voltage ramp from −20 mV down to −40 mV, within a 200-ms time window (Fig. S1). This protocol produced a sudden activation of the Ca²⁺ current, followed by a steady decrease in amplitude, similarly to a strongly inactivating current (22, 23). With the ramp, we obtained a peak Ca²⁺ current amplitude not different from the square pulses (ramp: 159 ± 8 pA, n = 5 recordings, P = 0.11, t test) but a faster decay (−24 ± 1% at 50 ms, P = 0.01, t test) (Fig. S1D). However, this rapid reduction did not have an effect on the fast decay of the postsynaptic response: No differences were found between decay time constants, with τ = 3.9 ± 0.8 ms for pulses and 5.6 ± 0.4 ms for ramps (n = 5 recordings, P = 0.08, t test) (Fig. S1E). It is also important to note that the peak amplitude of postsynaptic responses did not differ (Fig. S1E). Considering the full extension of the 200-ms stimuli in Fig. S1, we observed differences in the postsynaptic responses at the end of the ramp, indicating that the ramp protocol had an effect when there was a further reduction in Ca²⁺ influx (Fig. S1F). Overall, these results suggest that the fast decay of the postsynaptic response would not be significantly affected by an early reduction in Ca²⁺ current size.

Fig. S1.

We decided to investigate the role of Ca²⁺ current inactivation on release decay. A voltage protocol was designed to mimic and emphasize the effect that inactivation of IHC Ca²⁺ current could have on the kinetic of neurotransmitter release on the ribbon synapse. (A) Schematics of the voltage protocol applied on the IHC (Top), consisting of either a square voltage step to −20 mV (black traces) or a step to −20 mV followed by a negative ramp changing the holding potential from −20 mV to −40 mV in a 200-ms time frame. Representative Ca²⁺ currents obtained with both protocols are included in Bottom. (B) Representative average postsynaptic responses to both voltage schemes. Both A and B show a zoom-in of the first 70 ms of the complete protocol. (C) Scheme of the complete voltage protocol and synaptic responses. (D) Average IHC Ca²⁺ current peak amplitude (left axis) and the ratio of the current at 50 ms over the peak (right axis). (E) Average amplitude of the peak postsynaptic responses for both square steps and ramps (left axis). Time constant of response decay for both protocols (right axis). (F) Ratio of postsynaptic response amplitude at 50 ms over peak (left axis) and at 200 ms over peak (right axis). The voltage protocol consisted of an immediate step to –20 mV followed by a voltage ramp from –20 mV down to –40 mV, in 200 ms. This protocol produced a sudden activation of the Ca²⁺ current followed by a steady decrease in amplitude, similarly to an inactivating current [Marcotti et al. (23), Grant and Fuchs (22)]. We proceeded to compare the result of such ramp protocol to a square step depolarization to –20 mV (see A). Firstly, the peak of the Ca²⁺ current was measured in both cases, obtaining similar average values (step: 147 ± 4 pA; ramp: 159 ± 8 pA; n = 5 recordings each, P = 0.11, t test) (D, left axis). This similarity contrasts with the current decay that was significantly faster with the ramp protocol. We measured the Ca²⁺ current at 50 ms after the step onset and calculated a ratio to the peak, as shown in D (right axis), obtaining values of 0.90 ± 0.30 for the square pulse and 0.76 ± 0.10 for the ramp (n = 5 recordings, P = 0.01, t test). We chose to analyze the first 50 ms of the IHC Ca²⁺ current because this was the time frame in which the decay of the postsynaptic response was analyzed (see below, and Figs. 1 and 2). This result indicates that the ramp protocol was successful in producing a faster decay in Ca²⁺ current and could be used to analyze the effect of this decay on transmitter release kinetics. In E and F, we analyzed the postsynaptic responses to such protocols. First, we measured the average amplitude of the postsynaptic responses and obtained a value of 239 ± 29 pA for the step to –20 mV and 258 ± 32 pA for the ramp from –20 mV down to –40 mV (n = 5 recordings, P = 0.46, t test). Similar to what was described in Fig. 2, an exponential decay fitting was applied from the peak of the average postsynaptic response, within the first 50 ms. An average τ of decay of 3.9 ± 0.8 ms was obtained in response to square pulses to –20 mV, whereas τ = 5.6 ± 0.4 ms with the ramp (n = 5 recordings, P = 0.08, t test). Also, a comparison was drawn from the ratio between the response at 50 ms and the peak, as shown in F (see also Fig. 2). The average ratio for the pulse was 0.22 ± 0.06 and 0.17 ± 0.05 for the ramp (P = 0.25, t test). However, if a ratio was calculated at the end of the stimulus (at 200 ms), a strong reduction was observed with the ramp protocol. The ratio between the response at 200 ms and the peak for the square pulse to –20 mV was 0.10 ± 0.03, and 0.01 ± 0.01 for the ramp (n = 5, P = 0.029, t test) (F). These results suggest that a steady decay in Ca²⁺ current amplitude has limited effect on the kinetics of the postsynaptic response depression, specifically on the fast phase of decay. With further reduction in the Ca²⁺ influx toward the end of the stimulus, release shows a stronger decay and significantly lower responses to square pulses.

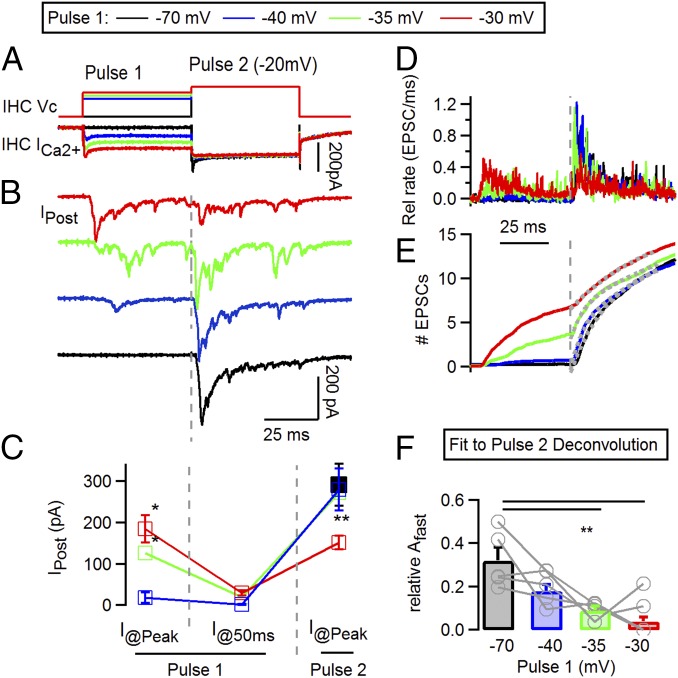
Vesicle depletion of presynaptic IHC has been pointed out as a main mechanism for the decay in auditory nerve activity (8, 13–15). To evaluate the availability of vesicles after depression occurred, a voltage protocol was designed in which a combination of two depolarizing steps was used, 50 ms each, one with variable amplitude (pulse 1) and a second one at a −20 mV fixed potential (pulse 2) (Fig. 3A). The potential of pulse 1 was set at four different values: −70 mV, −40 mV, −35 mV, and −30 mV. The first one (−70 mV) was used as a control of responses from a resting condition. During the first half of the protocol, shown in Fig. 3B, responses showed a similar pattern to recordings in Fig. 2: Increasing the potential of pulse 1 produced larger responses, followed by a subsequent decay in all cases. For instance, when pulse 1 was set at −35 mV, the peak response was 126 ± 23 pA and decayed to 20 ± 4 pA within the first 50 ms (Fig. 3C, n = 5 cell pairs, four to seven repetitions each). As indicated, previous studies suggested that this decay was due to vesicle depletion at the IHC (8, 13–15). However, Fig. 3 B and C shows that pulse 2 (to −20 mV) produced an increase in the postsynaptic current from the aforementioned depressed value, up to 273 ± 41 pA. This result indicates that vesicles were still available at the end of pulse 1 and ready to be released when pulse 2 was delivered. Similar results were obtained when pulse 1 was at −30 mV with peak values of 184 ± 33 pA, reaching a depressed state of 30 ± 6 pA and bouncing back to 151 ± 17 pA at pulse 2 (n = 5, four to six repetitions each) (Fig. 3 B and C). This latter protocol elicited the larger responses at pulse 1 (ANOVA, P = 0.001) but also the smaller responses left at pulse 2 (ANOVA, P = 0.002) (Fig. 3C). When pulse 1 was set to −40 mV, a very small response was obtained (17 ± 12 pA), and in three out of five recordings, no EPSCs were elicited at all. Thus, these results indicate that complete vesicle exhaustion cannot account for the observed synaptic depression.

Fig. 3.

A protocol with pedestal changes in stimulation intensity reveals that vesicles remain after synaptic depression in submaximal stimuli. (A) Voltage protocol applied on IHC (Top) consisting of a 50-ms first depolarization (pulse 1) at various potentials, followed by a second one at −20 mV (pulse 2, 50 ms). Bottom traces show IHC Ca²⁺ currents. (B) Average postsynaptic responses to the voltage protocol applied on the IHC and shown in A. Note that submaximal pulses (−35, −30 mV) also produce synaptic depression. (C) Postsynaptic current amplitudes at different time points during stimulation protocol. Three values are indicated for each variation of the voltage protocol: the peak of the response to pulse 1 (I@Peak), current value at the end of pulse 1 (I@50 ms, showing depressed response), and maximal responses to pulse 2 (I@Peak). (D) Representative traces of deconvolution of postsynaptic responses, as shown in A. (E) Integral of deconvolution traces. Gray dashed line indicates onset of pulse 2. Gray dotted lines represent fitting functions. (F) Fit of integrated deconvolution with double exponentials. The amplitude (A_fast) of the fast component in the fit is shown. *P < 0.05; **P < 0.01.

Multiple vesicle pools have been implicated in transmitter release at the hair cell’s ribbon synapse with different kinetic signatures (15, 24–26). We next sought to determine which vesicle pools underlie the responses shown in Fig. 3. To this end, we further quantified the responses to pulse 2 by deconvolving the postsynaptic traces (Fig. 3D) and integrating the result of the deconvolution to obtain a cumulative release plot (SI Methods) (Fig. 3E). Fitting these latter traces provides an estimate of how fast vesicles are released at pulse 2 and allows for comparison in how previous activity at pulse 1 affects these kinetics (27). Responses to pulse 2 were fitted with double exponential equations (with fast and slow components). Fast and slow time constants did not differ compared with the control: τ_fast = 4.1 ± 0.7 ms and τ_slow = 85.6 ± 16.5 ms for protocols with pulse 1 = −40 mV, 5.6 ± 1.2 ms and 116.8 ± 53.9 ms with −35 mV pulses, and 2.4 ± 0.25 and 76.8 ± 16.9 ms with −30 mV (ANOVA, P = 0.14 and P = 0.22 respectively). However, the relative amplitude of the fast component decreased as pulse 1 was more depolarized: 0.32 ± 0.06 at −70 mV (control), 0.18 ± 0.03 at −40 mV, 0.09 ± 0.02 at −35 mV, and 0.04 ± 0.02 at −30 mV (ANOVA, P = 0.0013). It is important to mention that in three out of five recordings with pulse 1 at −30 mV, A_fast was zero.

Taken together, the data presented so far indicate that synaptic depression at submaximal pulses (−40, −35, and −30 mV) produced mainly depletion of fast releasing vesicles but not complete exhaustion of the synapse. In other words, vesicles that remained after the initial peak were released at a slower pace, indicating that a heterogeneity in release kinetics can contribute to shape the transient response.

Synaptic Depression with CTZ.

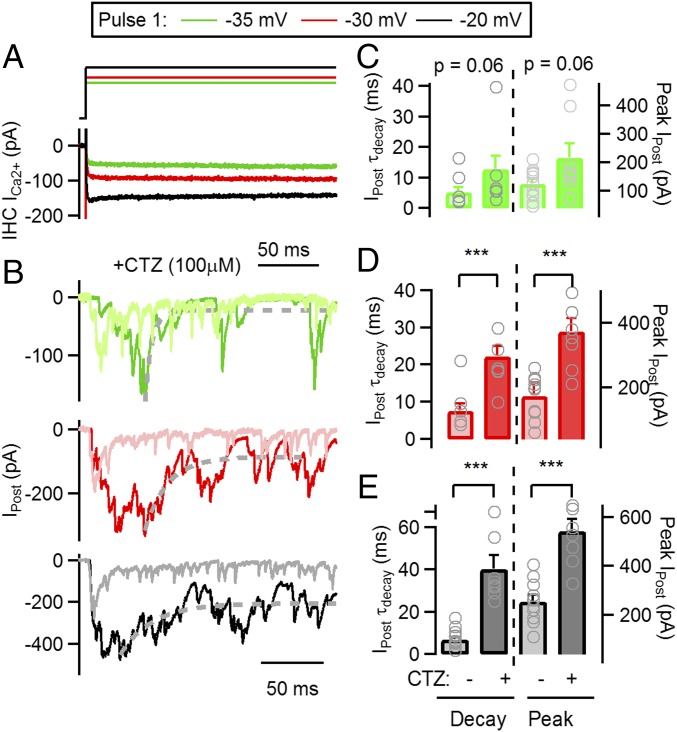
AMPA receptors, present in postsynaptic terminals of auditory nerve neurons, desensitize shortly after being activated (28). To investigate how desensitization affected the decay in synaptic activity and contributed to adaptation, we used IHC depolarizations of maximal (−20 mV) and submaximal (−30, −35 mV) intensity and investigated the effect of the desensitization inhibitor CTZ. Fig. 4 shows synaptic responses at −35, −30, and −20 mV pulses in 100 μM CTZ together with recordings obtained in a control situation (superimposed in paled colors). A robust increase in the peak of ensemble responses and decay time was obtained at −20 mV maximal stimulation, as shown in Fig. 4E, with maximum values of 543 ± 48 pA (n = 8 recordings, n = 3–9 repetitions each, 2.1-fold increase compared with control, t test, P < 0.001) and τ_decay = 40.5 ± 5.1 ms (5.2-fold change and P < 0.001, respectively). CTZ had a similar effect in pulses to −30 mV, with an average peak of 374 ± 39 pA (Fig. 4D) (2.1-fold increase from control, t test, P < 0.001) and a τ_decay = 22.3 ± 2.7 ms (2.9-fold change, P = 0.001). However, the effect observed at −35 mV was weaker (Fig. 4C) (peak: 218 ± 49 pA; decay: 12.8 ± 4.2 ms; t test, P = 0.06 and P = 0.06, respectively). These results suggest that desensitization plays a very important role in shortening responses to high-intensity stimuli and less so to weaker ones.

Fig. 4.

Application of CTZ during synaptic transmission produces a slowing of decay kinetics. (A) Voltage protocol applied on IHC (Top) consisting of a sustained depolarization at −35 (green), −30 (red), and −20 mV (black). Bottom traces show IHC Ca²⁺ currents. (B) Average postsynaptic responses to the voltage protocol applied on the IHC and shown in A, following the same color code. Control recordings (obtained in the absence of CTZ) are also included (−35 mV responses in pale green, −30 mv in pale red, and −20 mV in gray). Dashed gray line represents exponential fitting function. (C) Average τ_decay (left axis) for responses at −35 mV in control and CTZ (Left), and average peak amplitude (right axis) in the same experimental conditions. Gray symbols represent values for individual cell pairs. (D) Same as in C, but for −30 mV responses. (E) Same as in C, but for −20 mV responses. ***P < 0.001.

We further analyzed the role of desensitization of postsynaptic receptors by comparing decay kinetics in responses to −20, −30, and −35 mV pulses in the presence of CTZ. In contrast to the kinetic invariance observed in control conditions (Fig. 2), a significantly slower τ_decay was obtained with pulses to −20 mV in CTZ compared with submaximal pulses (Fig. 4, ANOVA, P = 0.002). The ratios between the depressed state of the response (I@200 ms in CTZ experiments) and the peak at different pulses also showed statistical differences: 0.41 ± 0.04 for −20 mV, 0.26 ± 0.06 at −30 mV, and 0.26 ± 0.04 at −35 mV (ANOVA, P = 0.01).

Taken together, these results indicate that desensitization plays a very important role in sharpening synaptic responses and compensating for intrinsic differences in decay kinetics of responses to strong and weak stimuli. It is important to note that even in CTZ, postsynaptic responses show a strong depression of ∼60–75% within a 200-ms range (Fig. 4) and up to ∼90% in 1 s (21).

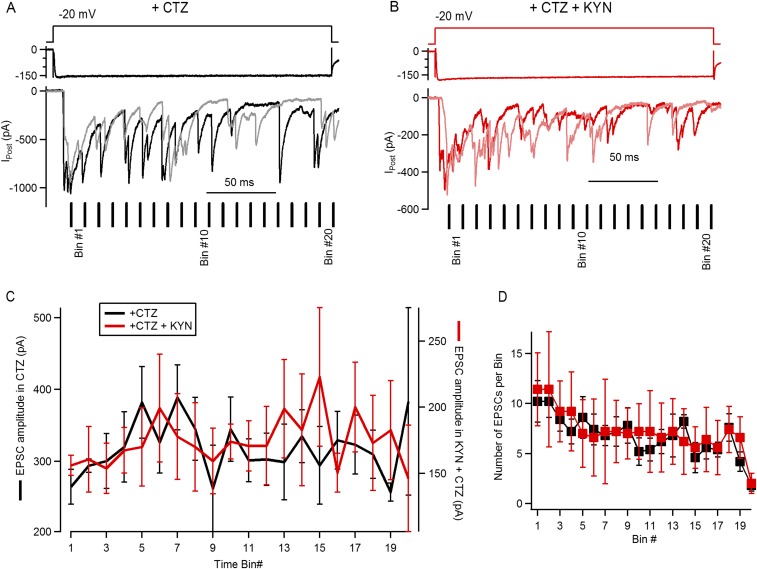
Previous evidence indicates that in certain circumstances CTZ also produces an increase in the affinity of AMPA receptors for agonists (29), raising the possibility that at the peak of maximal synaptic responses (to −20 mV pulses) glutamate could saturate AMPA receptors. If this happened, CTZ would produce an artificial effect on some of the parameters characterizing depression (Fig. 4). To address this point, we proceeded to use the low-affinity AMPA receptor antagonist kynurenic acid (KYN) (1 mM), producing a partial block of the receptors and alleviating a potential saturation. As shown before, prolonged stimulation of the IHC produced postsynaptic responses composed of an initial superposition of multiple EPSCs (determining the peak) and subsequent activation of EPSCs occurring randomly throughout the duration of the stimulus, at a lower rate (see refs. 20, 21, and 30 and Fig. 1). We reasoned that if the postsynaptic response was saturated at the initial peak, EPSCs occurring shortly after this should present a smaller average amplitude compared with later ones. In Fig. S2, we analyzed this possibility, by evoking synaptic responses with IHC pulses to −20 mV in the presence of CTZ or CTZ and KYN. As EPSCs occurred randomly during a steady depolarization (see also Fig. 1), the amplitude of individual events was averaged in 10-ms time bins, considering t = 0 when the peak occurred. We observed a small reduction in EPSC size in the first few time bins, both in CTZ and CTZ + KYN (264 ± 24 pA and 156 ± 17 pA at bin 1, respectively) and a consequent increase in the following five to six bins (Fig. S2C). However, none of these differences were statistically significant (ANOVA, P = 0.08 and P = 0.95, respectively). These results suggest that even in the presence of CTZ, maximal stimulation of the IHC would not produce saturation of postsynaptic receptors and that the decay kinetics should be mostly attributed to the desensitization removal.

Fig. S2.

Determining saturation of postsynaptic receptors during maximal stimulation of the IHC ribbon synapse. (A) Representative synaptic responses to step depolarizations in the presence of CTZ: schematics of the voltage pulse (Top), IHC Ca²⁺ current (Middle), and two individual postsynaptic currents (Bottom). The 10-ms time bins, used to analyze amplitudes (C), are indicated for this specific example. (B) Same as A, but for two recordings obtained with CTZ and KYN, 1 mM (KYN). (C) Average amplitude of EPSCs occurring within each time bin for events obtained during superfusion of CTZ (left axis) or both CTZ and KYN (right axis). (D) Number of EPSCs obtained per time bin, per recording. These results suggest that a steady decay in Ca²⁺ current amplitude has limited effect on the kinetics of the postsynaptic response depression, specifically on the fast phase of decay. With further reduction in the Ca²⁺ influx toward the end of the stimulus, release shows a stronger decay and significantly lower responses to square pulses. Some evidence indicates that CTZ not only reduces desensitization of AMPA receptors but could also produce a left shift in the agonist dose–response curve [Patneau et al. (29)]. This observation raises the possibility that at the onset of the postsynaptic response, when maximal release occurs, CTZ could produce an artificial saturation of the receptors, and this in turn alters the decay parameters established in Fig. 4. We decided to evaluate saturation of postsynaptic receptors during the superfusion of CTZ, using the competitive antagonist KYN that partially blocks AMPA responses and potentially relieves saturation. Step depolarizations to –20 mV were applied on the IHC in the presence of CTZ (100 μM), similarly to Fig. 4A. We reasoned that if the postsynaptic response was saturated at the initial peak, EPSCs occurring shortly after this should present a smaller average amplitude compared with later ones. We took advantage of the release mode at this ribbon synapse, in which steady stimulation produces the activation of multiple EPSCs [Keen and Hudspeth (20); Goutman and Glowatzki (21)]. The amplitude of individual EPSCs was measured and then averaged in 10-ms time bins, considering t = 0 when the peak occurred (i.e., EPSCs occurring at the peak were excluded of the analysis) (see A). In CTZ, EPSCs that occurred at bin 1 (first 10 ms after the peak) presented an average amplitude of 264 ± 24 pA (n = 5 recordings, six to nine repetitions each, 4–17 EPSCs each) (C). Considering that the peak response obtained in this set of experiments in CTZ was 774 ± 61 pA (n = 5 recordings), the average EPSC size represented ∼34% of the maximal response. The amplitude in the following bins increased up to bin 5, with an average of 382 ± 50 pA, ∼49% of the peak (n = 5 recordings, six to nine repetitions, 2 to 14 EPSCs). We also calculated the average amplitude of the last 10 time bins, obtaining a value of 313 ± 10 pA (n = 5). None of these differences were statistically significant (ANOVA, P = 0.08). As shown in B, the same stimulation protocol was repeated with the addition of 1mMKYN (+CTZ). As expected, the maximal response was reduced to 403 ± 63 pA, representing a 49 ± 5% reduction compared with responses obtained in CTZ (n = 5 recordings, P < 0.001, t test). We also measured EPSC amplitudes and averaged them in 10-ms time bins. Interestingly, having partially blocked postsynaptic receptors, a similar profile was observed in EPSC sizes, with an average amplitude of 156 ± 17 pA in bin 1 (n = 5 recordings, six to nine repetitions each, 6–16 EPSCs), rising to 199 + 91 pA at bin 6 (3–11 EPSCs), and with an average amplitude of 180 ± 7 pA for the last 10 bins (ANOVA, P = 0.95). The amplitude of the first bin represented ∼39% of the corresponding peak response in CTZ + KYN, whereas bin 6 was ∼49%. The average number of EPSCs obtained in each time bin (over repetitions in each recording) is compared in D. The number of EPSCs decreased on later time bins, but no differences were found between drug treatments (two-way ANOVA, P < 0.001 for bin number and P = 0.72 for drugs). Results indicate that saturation of AMPA receptors during the peak of the postsynaptic response would be very limited and that the effect of CTZ on the decay kinetics should be mostly attributed to the desensitization removal.

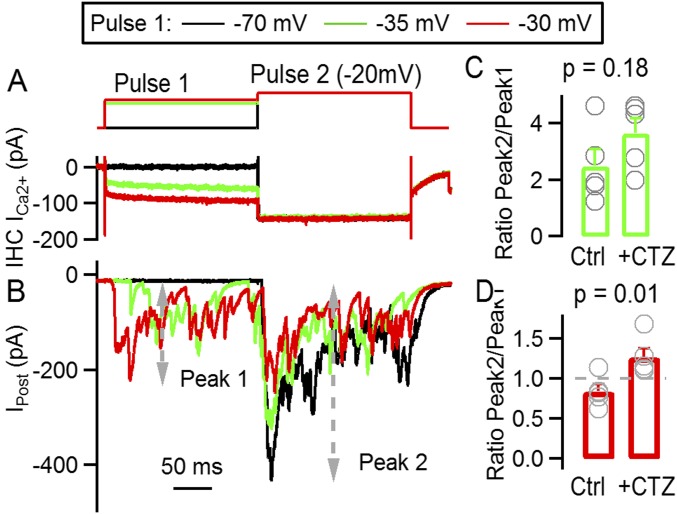
Finally, we also analyzed how much synaptic responsiveness was affected by desensitization of postsynaptic receptors. A consecutive two-step protocol was used, similar to that in Fig. 3 but adapting the duration of each step to the slower kinetics due to the presence of CTZ (200 ms each) (Fig. S3). The capacity of the synapse to further respond to pulse 2, after adaptation to pulse 1, was estimated with a ratio between the peak responses obtained in each depolarization (response to pulse 2/response to pulse 1). When pulse 1 was set to −35 mV, the ratio in the presence of CTZ was 3.65 ± 0.53 and did not significantly differ from the control ratio, 2.49 ± 0.06 (Fig. S3C) (t test, P = 0.18). But when pulse 1 was set at −30 mV, responses to pulse 2 were proportionally larger in the presence of CTZ (ratio, 1.27 ± 0.11, vs. control, 0.84 ± 0.08; P = 0.01), suggesting that the removal of desensitization uncovers a larger capacity of IHC for neurotransmitter release (Fig. S3D).

Fig. S3.

CTZ application uncovers a reduction in synaptic responsiveness due to desensitization of postsynaptic receptors. (A) Voltage protocol applied on IHC (Top) consisting of a 200-ms first depolarization (pulse 1) at various potentials, followed by a second one at −20 mV (pulse 2, 200 ms). Bottom traces show IHC Ca²⁺ currents. (B) Average postsynaptic responses to the voltage protocol applied on the IHC and, shown in A, following the same color code. The amplitude of peak 1 and peak 2 are indicated with gray dashed lines. (C) Ratio of peak 2/peak 1 responses with pulse 1 at −35 mV, in control and CTZ. Gray symbols represent values for individual experiments. (D) Same as C, but for responses with pulse 1 at −30 mV. Desensitization of postsynaptic receptors typically decreases the chance of the system to respond to newly coming stimuli. We evaluated how much synaptic responsiveness was affected by desensitization of postsynaptic receptors at the IHC ribbon synapse. Similar to Fig. 3, a two-step protocol was used, with variable amplitude in pulse 1 (–70, –35, and –30 mV) and fixed –20 mV at pulse 2 (A). The duration of each step was increased due to the slower kinetics of synaptic responses in the presence of CTZ (200 ms each). The capacity of the synapse to further respond to pulse 2, after adaptation to pulse 1, was estimated with a ratio between the peak responses obtained in each depolarization (response to pulse 2/response to pulse 1). When pulse 1 was set to –35 mV, the ratio in the presence of CTZ was 3.65 ± 0.53 and did not significantly differ from the control ratio, 2.49 ± 0.06 (C) (t test, P = 0.18). But when pulse 1 was set at –30 mV, responses to pulse 2 were proportionally larger in the presence of CTZ (ratio, 1.27 ± 0.11, vs. control, 0.84 ± 0.08, P = 0.01), suggesting that the removal of desensitization uncovers a larger capacity of IHC for neurotransmitter release (D). Similar to what was observed in the absence of CTZ (Fig. 3), the average amplitude of responses to pulse 2 was different depending on the intensity of pulse 1. When setting pulse 1 to –70 mV (control), the amplitude of responses elicited by pulse 2 was 483 ± 53 pA; when pulse 1 was applied at –40 mV, the amplitude was 485 ± 70 pA; and 501 ± 81 pA was obtained when pulse 1 was used at –35 mV and 399 ± 70 pA at –30 mV (ANOVA, P = 0.0083). Integrating these traces, we also found that during pulse 2 the total charge varied with the previous activity elicited by pulse 1. When this latter pulse was set to –70 mV (control), the charge due to pulse 2 was 49 ± 16 pC, at –40 mV was 51 ± 20 pC, at –35 mV was 48 ± 19 pC, and finally at –30 mV was 39 ± 15 pC (n = 5 cell pairs, ANOVA, P < 0.001). Taken together, results indicate that in CTZ an additional burst of activity is uncovered at pulse 2, suggesting that desensitization limits the capacity of the synapse to respond to newly coming stimuli.

These results indicate that desensitization produces an acceleration of synaptic decay, reducing kinetic differences produced by stimuli of different strengths, but it also has the detrimental effect of reducing the synaptic capacity to respond to newly coming stimuli.

SI Methods

Recordings of IHCs and Afferent Postsynaptic Boutons.

Excised apical turns of 9–11-d-old rat cochleae (Sprague-Dawley, either sex) were placed into a chamber under an upright microscope (BX51WI; Olympus) and superfused with saline at 2–3 mL/min. IHCs and contacting postsynaptic terminals were visualized on a monitor via a water immersion objective (60×), difference interference contrast optics, and a CCD camera (Rolera XR, QImaging, or Andor iXon). For simultaneous, paired whole-cell patch-clamp recordings, the postsynaptic recording was established first and the IHC recording second.

The pipette solution for isolating IHC Ca²⁺ currents was as follows (in mM): CsMeSO₃ 135, TEA Cl 13, Hepes 5, MgCl₂ 3.5, CaCl₂ 0.1, Na₂ATP 5, Na Phosphocreatine 5, Na GTP 0.3, EGTA 1, pH 7.2 (CsOH), and liquid junction potential (LJP) 9 mV. The postsynaptic pipette solution was as follows (in mM): KCl 135, MgCl₂ 3.5, CaCl₂ 0.1, EGTA 5, Hepes 5, Na₂ATP 2.5, pH 7.2 (KOH), LJP = 4 mV. The extracellular solution contained (in mM) KCl 5.8, NaCl 144, MgCl₂ 0.9, CaCl₂ 1.3, NaH₂PO4 0.7, d-glucose 5.6, Hepes 10, pH 7.4 (NaOH). All chemicals were purchased from Sigma.

Recording pipettes were fabricated from 1 mm borosilicate glass (WPI), Sylgard-coated, and fire-polished with tip resistances of 9–10 (postsynaptic) and 7–8 (IHC) MΩ. Series resistance errors, 10–20 MΩ for IHC recordings, were compensated up to 70%. Holding potentials were not corrected for LJPs. Experiments were done at 22–24 °C. Recordings were performed with two 200B Axopatch amplifiers or a MultiClamp 700B amplifier and Digidata 1440 board (Axon Instruments) or a National Instruments board filtered at 10 kHz and digitized at 50 kHz. Electrophysiological signals were acquired with pClamp 10 (Axon Instruments) or WinWCP (Strathclyde Electrophysiological Software). Data collection started 3–5 min after the IHC whole-cell recording. A “run-up” of Ca²⁺ currents was typically observed during the first few minutes of recording. After ∼30 min of recording, rundown of synaptic activity was observed, and therefore, only data recorded within this time window were analyzed.

Data Analysis.

Data were analyzed offline using MiniAnalysis (Synaptosoft) and custom routines implemented in Igor Pro (WaveMetrics). For leak subtraction of IHC currents, IHC membrane resistance was calculated from voltage steps between −80 and −60 mV. Postsynaptic peak amplitude was calculated on the average traces in each recording, whereas the response amplitudes at 50 ms (I@50 ms) were obtained from the average traces by calculating a mean of the traces between t = 45 ms and t = 50 ms (same for I@200 ms, using t = 180 ms and t = 200 ms). Deconvolution was performed using an average EPSC trace as template, scaling the amplitude with the average value obtained in each recording. The deconvolution traces were taken through a binomial smoothing before integrating and fitting.

For statistical comparison, t test or one-way ANOVA (repetitive measures) was used. Tukey’s was used as a post hoc test when one-way ANOVA analyses were significant. Mean values are presented as ±SE.

Discussion

In this study, we uncover some of the cellular mechanisms underlying auditory adaptation. This phenomenon was described decades ago at the auditory nerve level (5–8) and is a fundamental process that has been proposed to influence the operating range of each auditory nerve fiber’s response and to play a key role in sound encoding (4). We show that adaptation is brought about by a combination of pre- and postsynaptic mechanisms at the IHC ribbon synapse with auditory nerve neurons.

Synaptic Depression as a Determinant of Adaptation in the Auditory Nerve.

It is well documented that the IHC ribbon synapse function drives auditory nerve activity, both in the absence and in the presence of sound (9, 31). Fatigue in IHC exocytosis could be responsible for adaptation in auditory nerve activity. Thus, it has been proposed that vesicle pool depletion is a chief determinant underlying adaptation (8, 13–15). However, detailed investigation of adaptation mechanisms has questioned the validity of this hypothesis. In this regard, the analysis of the interaction between adaptation and stimulus intensity has shown that the decay time constant of the firing rate in auditory nerve neurons (within the milliseconds range) remained constant across stimulation levels (18, 19). Coincident evidence was found in seminal studies by Furukawa and Matsuura (8) at the goldfish saccullar afferent synapse. How can the decay in synaptic activity be the same at different stimulus intensities? If a high-intensity stimulus depletes a vesicle pool, why does a moderate one, which releases less vesicles, produce similar synaptic depression?

In Figs. 1 and 2, we present evidence for synaptic depression at (at least) three different depolarizing potentials that mostly span the operating range for this synapse. It is interesting to see not only that submaximal pulses (e.g., to −30 or −35 mV) produce depression but also that responses are identical when scaled up and that decay kinetics do not differ (Fig. 2). Fig. 3 also shows that an increase in stimulus intensity, over a background level, can evoke a second burst of activity. These results contribute to the idea that auditory nerve adaptation in firing rate can be attributed in great extent to the function of ribbon synapses in IHC. It is interesting to note that other features in auditory nerve function, such as rate-level functions (15, 20, 21), variability in dynamic ranges (32), and phase locking to low-frequency stimuli (33, 34), were also proven to be synaptic in origin. These studies were carried out in ex vivo preparations of the inner ear and in some cases in prehearing animals (such as this current study), and thus, conclusions should not be extended directly to the in vivo mature situation. Moreover, spike generation refractoriness at the auditory nerve are important for phasic signaling of acoustic inputs and could also contribute to the decay in firing rate (35). This should also be considered in a comprehensive model for adaptation.

Synaptic Vesicle Pools and Depression.

Using deconvolution of postsynaptic responses, we identified two kinetic components that support the hypothesis of two (or multiple) different vesicle populations. These results confirm previous observations obtained with capacitance measurements (15, 24–26) and Ca²⁺ uncaging (36) and also match our previous analysis (21). Experiments in Fig. 3 help reveal the nature of synaptic depression at the IHC ribbon synapse and the role of different vesicle pools. It becomes clear that synaptic depression at submaximal pulses (−30, −35, and −40 mV) leaves remnant vesicles that can be released with a stronger pulse (pulse 2), indicating noncomplete pool depletion. The proportion of “fast” and “slow” vesicles at each pulse 2 is variable, as indicated in Fig. 3F, and depends on how many are released at pulse 1, according to stimulus intensity. We therefore propose that in an unstimulated synapse, a given pulse produces first a transient response consisting predominantly of fast vesicles. As these vesicles are exhausted, the ensemble response decays, and release continues at a slower pace supported by slow vesicles. The existence of additional kinetic components, not detected in our experiments, should not be dismissed.

Previous studies at bipolar-AII amacrine cell synapses have shown that applying stimulation protocols with pedestal increments in intensity (as in Fig. 3) could also elicit secondary bursts of activity (37, 38). A different interpretation was drawn from those experiments, proposing that a single pool of vesicles could mediate these responses (38). In this latter study, Oesch and Diamond focused on a time scale of seconds in their synaptic responses, whereas our study investigates synaptic depression within the first tens to hundreds of milliseconds. It would be interesting to simulate our current data using a single pool model as in ref. 38. In a previous unrelated study, we simulated synaptic activity with a single pool model, obtaining faster decay times with stronger stimuli, although it should be mentioned that the stimulation paradigm differs from that used here (see figure 8A in ref. 33).

The identity of fast and slow vesicles remains to be investigated. In central synapses, some studies propose a positional difference, as fast vesicles would sit closer to Ca²⁺ channels and slow ones farther apart (39), whereas others implicate intrinsic differences in vesicular affinity for Ca²⁺ (40). If differences were positional, it is possible that multiple types of vesicles (not only fast and slow) could coexist depending on the distance to the Ca²⁺ channels. At ribbon synapses, there is evidence indicating that in the absence of the ribbon the enhanced activity at the onset (due to fast vesicles) is missing but not the sustained response (represented by slow vesicles) (41, 42). These results point to positional heterogeneity of vesicles (ribbon-associated vesicles and extra ribbon vesicles).

There is evidence indicating that IHC ribbon synapses operate under a “nanodomain” model, with vesicles sitting in close proximity of single Ca²⁺ channels (43, 44). The opening of this single channel highly determines the probability of release of that one vesicle. It remains possible that heterogeneity in these nanodomains could produce high release probabilities, underlying the first synaptic responses in Fig. 3, and low release probabilities, determining the second phase.

Desensitization Abbreviates Synaptic Responses.

A presynaptic mechanism with multiple vesicle pools could greatly contribute to shape a combined transient and sustained synaptic response. But results in Fig. 4 imply that desensitization also had a fundamental role. The application of CTZ produced the expected slowing in kinetics (29) (Fig. 4). Interestingly, the extent of this effect varied with presynaptic depolarization level. A maximal difference in decay kinetics (but also amplitude) was observed at −20 mV pulses, where release reaches a peak. This indicates that desensitization abbreviates signaling between IHC and auditory nerve neurons and accelerates the otherwise slower depression. But most importantly, by generating a stronger effect on more sustained (and also larger) responses, desensitization helps leveling off differences in decay kinetics. This effect comes at a price: Synapses remain less responsive, and the post onset activity is reduced (Fig. S3).

It is also surprising that pulses to −20 mV produced not only the larger peaks but also the more sustained responses (Fig. 4). In other words, stronger stimuli did not produce faster decaying responses as we proposed from modeling results (33), but actually the opposite.

It has been reported that CTZ has presynaptic effects through K⁺ and Ca²⁺ channels but, most importantly, on the release machinery in central synapses (45). In a previous work, we have addressed this issue by comparing the rate of EPSC activation in long pulses in control vs. CTZ conditions and found no significant differences (21). In this current study, we also evaluated saturation of postsynaptic receptors, on the grounds that a secondary effect of CTZ on glutamate affinity (29) could have an artificial consequence on the kinetics of the response relaxation. Results obtained in Fig. S2 indicate that even during the maximal release scenario, saturation would not affect synaptic responses. Therefore, the differential effect of CTZ on responses shown in Fig. 4 and Fig. S3 can be attributed to the removal of postsynaptic desensitization. Another implication of the Fig. S2 results is that multivesicular EPSCs occurred even shortly after the onset peak, confirming that this mechanism of release is resistant to manipulation (28).

Physiological Implications of Adaptation Kinetics Invariance.

The importance of adaptation in sound encoding has been discussed (4). It is still intriguing why this peculiar pattern of adaptation, with invariant decay kinetics, evolved. One emerging possibility is that since adaptation could be beneficial for establishing spatiotemporal contrast in auditory signaling (4), constant decay kinetics would enable similar contrast patterns regardless of the intensity of the sound. In addition, adaptation might serve to directional hearing. As sounds produce larger responses on the ipsilateral ear, invariant decay kinetics would ensure that responses of the ipsilateral auditory nerve would never fall below the firing rate of a contralateral neuron. If on the contrary larger stimuli produced faster adaptation, the time courses of responses from the two ears would eventually cross over, producing higher firing rates on the contralateral auditory nerve. This would implicate contradictory sound source localization information. Therefore, invariance in adaptation kinetics might be a mechanism to maintain differences in amplitude of adapting auditory nerve responses from the two ears.

Methods

Simultaneous recordings from IHC and boutons of auditory nerve neurons were obtained from P9–P11 rat cochleas in the whole-cell configuration. Drugs were introduced through the bath perfusion system. For a full description of methods, see SI Methods.