Abstract
Gene Set Enrichment Analysis (GSEA) aims at identifying essential pathways, or more generally, sets of biologically related genes that are involved in complex human diseases. In the past, many studies have shown that GSEA is a very useful bioinformatics tool, which plays critical roles in the innovation of disease prevention and intervention strategies. Despite its tremendous success, it is striking that conclusions of GSEA drawn from isolated studies are often sparse, and different studies may lead to inconsistent and sometimes contradictory results. Further, in the wake of next generation sequencing technologies, it has been made possible to measure genome-wide isoform-specific expression levels, calling for innovations that can utilize the unprecedented resolution. Currently, enormous amounts of data have been created from various RNA-seq experiments. All these give rise to a pressing need for developing integrative methods that allow for explicit utilization of isoform-specific expression, to combine multiple enrichment studies, in order to enhance the power, reproducibility and interpretability of the analysis. We develop and evaluate integrative GSEA methods, based on two-stage procedures, which, for the first time, allow statistically efficient use of isoform-specific expression from multiple RNA-seq experiments. Through simulation and real data analysis, we show that our methods can greatly improve the performance in identifying essential gene sets compared to existing methods that can only use gene-level expression.
Keywords: GLM, fixed effect, integrative GSEA, pathway analysis, random effects, RNA-seq, score statistic
1 INTRODUCTION
To understand molecular mechanisms underlying complex human diseases, one important task in transcriptome studies is to identify groups of related genes that are combinatorially involved in such biological processes, mainly through Gene Set Enrichment Analysis (GSEA), where gene sets are pre-defined according to a variety of criteria (e.g., genes/proteins participating in common pathways, sharing similar or closely related annotated functions and so on). Given a gene set, the goal of GSEA is typically to infer whether it is enriched by “essential” genes (i.e., genes associated with a phenotype of interest), where the set is defined to be enriched if it contains more essential genes than would be expected by chance. In the past, various statistical approaches have been developed for GSEA (see Song and Black 2008, Ackermann and Strimmer 2009 and Hung et al. 2012 for detailed review); and many biomedical studies have achieved spectacular successes with the aid of GSEA in the innovation of disease prevention and intervention strategies (e.g., Downward 2006; Wang 2011; Ullah et al. 2012; Farkas et al. 2011).
In the dawn of a big data era, however, there is an increasingly urgent need to perform integrative GSEA (iGSEA), i.e., integrating multiple relevant GSEA studies, to avoid indecisive or potentially conflicting conclusions from individual data and to leverage “wisdom of crowds” for more effective and reliable scientific discoveries. Typically, the integrative process is operated by meta-analysis, which uses a statistical approach to synthesize results from multiple studies. To our best knowledge, there are only two publications (Shen and Tseng, 2010; Chen et al., 2013) that develop meta-analysis methods for iGSEA. Shen and Tseng (2010) proposed three methods for Meta-Analysis of Pathway Enrichment (MAPE), based on the widely used GSEA algorithm proposed by Subramanian et al. (2005): the first method conducts meta-analysis by combining results from multiple studies at the gene level (MAPE_G), the second at the pathway level (MAPE_P), while the third further integrates end results from the first two methods (MAPE_I). All these methods rely on gross summary statistics such as the maximum, minimum or sum of the P-values from individual studies, which might cause substantial information loss and lead to poor performance. Chen et al. (2013) proposed a powerful Bayesian method to integrate multiple GSEA studies, which has been shown to work well with binary phenotypes. However, it cannot be used with other discrete or any continuous phenotypes. Also, it is computationally intensive and requires great effort in selecting starting points and detecting convergence if users do not choose the default setting.
The above existing methods were originally developed for microarray data analysis, requiring gene-level expression even when data are from Next Generation Sequencing (NGS) experiments. Advances in RNA-seq technologies have provided unprecedented resolution that enables researchers to identify novel transcripts and extract genome-wide isoform-specific expression. In the human genome, almost all multi-exon genes have more than one mRNA isoform produced by alternative transcription initiation, splicing and termination (Pan et al., 2008; Wang et al., 2008). Transcript variants from a gene can generate protein isoforms with different structures, which have diverse and sometimes opposite functions (Pal et al., 2011, 2012). In addition, differentially expressed isoforms are widely observed in different tissue types and disease status. Recent studies have shown that (i) there exist many genes for which differential expression of transcript isoforms occurs in opposite directions, with some of the transcripts being up-regulated while others being down-regulated, resulting in insignificant expression differences at the gene level (Liu et al., 2013; Zhang et al., 2013); (ii) aberrant expression of alternative gene isoforms is associated with various cancer formation and progression (Akgul et al., 2004; Rajan et al., 2009); (iii) isoform-level expression can provide better cancer signatures than gene-level expression (Zhang et al., 2013; Liu et al., 2013). Thus, explicitly utilizing isoform-level expression in GSEA may add new findings besides those from the common practice of examining gene-level expression only.
So far, no existing approach has addressed the problem of iGSEA based on isoform expression data. In this article, we develop and evaluate iGSEA methods based on two-stage procedures, which allow statistically efficient use of isoform-specific expression from multiple RNA-seq experiments. In the first stage, we adapt meta-analysis approaches based on fixed-effect (FE) (Hu et al., 2013b) and random-effects (RE) models (Tang and Lin, 2014), newly developed for metaanalysis of genome-wide association studies (GWAS), into iGSEA, for association testing using isoform-specific expression based on generalized linear models (GLMs). In the second stage, set enrichment analysis is conducted using size-adjusted Kolmogorov–Smirnov statistics based on the ordering of P-values from the first stage. Through simulation and a data example, we illustrate the advantages of our new procedures over existing iGSEA methods.
2 METHODS
Suppose we wish to combine K independent RNA-seq studies, and there are Sk samples in study k, k = 1, …, K. Suppose gene g has Ig ≥ 1 isoforms for g = 1, …, G, where G is the total number of genes involved in these K studies. Each gene does not need to be present in all the K studies so we define an indicator variable: Tkg = 1 if gene g is present in study k; Tkg = 0, otherwise. Given Tkg = 1, let Xksgi denote the expression level of isoform i of gene g for sample s in study k. Let Y ks be the phenotype of interest for sample s in study k, which is assumed to follow an exponential family distribution so that it can be either discrete or continuous. A pathway database matrix {Zgp} (1 ≤ g ≤ G, 1 ≤ p ≤ P) represents the gene membership information of P pathways, where Zgp = 1 when gene g belongs to pathway p and Zgp = 0 otherwise. For a list of important notation used in this paper, see Section S1 in Supplementary Material.
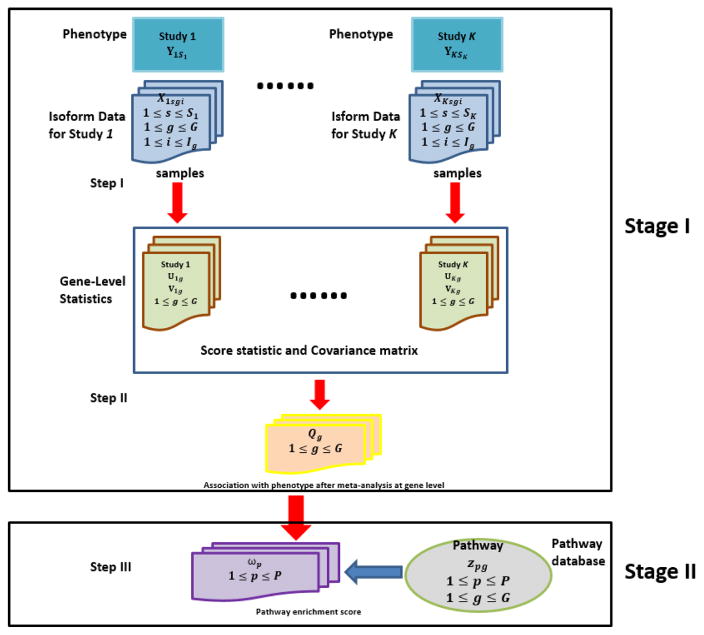
Figure 1 presents the framework of iGSEA methods that utilize isoform-level expression from multiple RNA-seq studies. There are three key steps in our two-stage procedures, where the first two steps belong to the first stage. Step I is to conduct gene-wise analysis of isoform expression in each study k and calculate gene-level statistics, a score statistic Ukg and its covariance matrix Vkg, for each gene g. In Step II, meta-analysis is performed to combine the results of component studies, using gene-level statistics from Step I. Step III is to conduct set enrichment analysis. For a gene set (or more specifically, a pathway) of interest, based on the P-values of combined gene-level statistics Qgs, we calculate the enrichment score (ES), and estimate its statistical significance. Given a database of pathways, we further adjust the P-value of each ES for multiple testing, and report pathways achieving a fixed level of significance as enriched.
Figure 1.
A flow chart of proposed iGSEA procedures that utilize isoform-specific expression
2.1 Stage I: meta-analysis of isoform expression analysis
In step I, for each gene g that appears in study k, we build a GLM to model the relationship between isoform-specific expression levels of gene g and the phenotype Y, calculate the corresponding score statistic Ukg, and estimate its covariance matrix Vkg. Given Tkg = 1, the isoform expression vector of gene g for sample s in study k is represented by Xksg = (Xksg1, …, XksgIg). We relate Yks to Xksg through a GLM by specifying the following relationship:
| (1) |
where h(·) is a link function, αkg is the intercept, and βkg = (βkg1, …, βkgIg)T is a vector of the regression parameters; that is, βkgi stands for the effect of the ith isoform of gene g on Y. Further, we express the density function of Yks given Xksg and Tkg = 1 by
where a(·), b(·), and c(·) are specific functions that jointly determine the distribution type of Yks; and θksg is the unknown canonical parameter satisfying θksg = b′−1 ·h−1(αkg +Xksgβkg) under (1), and ϕkg is the dispersion parameter.
To test gene g’s association with the phenotype Y in study k, the null hypothesis is H0: βkg = 0, and rejecting the null hypothesis concludes that the gene is isoform-active; that is, at least one of βkgis are not equal to 0, meaning that the expression from at least one isoform of gene g is associated with the phenotype Y in study k. Under the commonly used canonical link h = b′−1(·), for each gene g with Tkg = 1, the score statistic Ukg under the null hypothesis of study k is given by where α̂kg and ϕ̂kg are the restricted maximum likelihood estimators (MLEs) of αkg and ϕkg under H0. The asymptotic null distribution of Ukg is Ig-variate normal with mean 0 and covariance matrix estimated by .
In step II of Figure 1, meta-analysis is performed to combine the results of the K independent RNA-seq studies, and a quadratic statistic Qg (1 ≤ g ≤ G) is produced at the gene level based on either an FE or RE model.
An FE model assumes that the effects of gene g’s isoforms on the phenotype are common among different studies, namely βkg = μg, where μg = (μg1, …, μgIg) represents the overall isoform effects of gene g across studies. In meta-analysis, testing whether gene g is isoform-active or not becomes testing H0: μg = 0 under the FE model. The quadratic statistic for testing H0: μg = 0 can be defined as (Lin and Zeng, 2010; Hu et al., 2013a)
| (2) |
where . Under H0, Ug is asymptotically Ig-variate normal with mean 0 and estimated covariance matrix Vg; and Qg has an asymptotic chi-square distribution with Ig degrees of freedom. Lin and Zeng (2010) showed that when effect sizes are constant across studies, the meta-analysis approach based on the FE model has the best statistical efficiency in testing H0: μg = 0; and it can reach the same efficiency as mega-analysis (i.e., joint analysis of raw individual-level data from multiple studies) without information loss.
In some practical situations, the assumption that the isoform effects are the same/similar in all component studies is restrictive. To accommodate between-study heterogeneity, a standard analytical strategy is to specify βkg as a vector of random effects with mean μg, and then test H0: μg = 0. The corresponding RE model can be given by
| (3) |
where ξkg = (ξkg1, …, ξkgIg) is a set of random terms representing the study-specific deviations from the overall effect μg, and ξkg is assumed to follow a multivariate normal distribution with mean 0 and covariance matrix Σg. Surprisingly, researchers in GWAS (Han and Eskin, 2011; Thompson et al., 2011) have found that, when both FE and RE methods are applied to the same data, RE tends to give substantially less significant P-values, and so cannot find anything new from those already identified by FE. Recently, the reasons for this paradox were revealed by Han and Eskin (2011) and an innovative RE approach, namely, testing H0: μg = 0 and Σg = 0, was proposed to achieve higher efficiency than the FE model when the heterogeneity is large in meta-analysis of GWAS (Han and Eskin, 2011; Tang and Lin, 2014).
Under the RE model in (3), we adapt the above null hypothesis H0: μg = 0 and Σg = 0 into our iGSEA, which represents that gene g is isoform-active in none of the K studies. Following Tang and Lin (2014), to avoid estimating a large number of unknown parameters in the covariance matrix, we express Σg = σgBg, where σg is an unknown constant, and Bg is a Ig×Ig pre-specified matrix with a commonly used structure (e.g., independent, autoregressive, compound symmetry). Because σg = 0 is equivalent to Σg = 0, the null hypothesis becomes H0: μg = 0 and σg = 0. Then the test statistic under the RE model can be defined as
| (4) |
where , and tr stands for the trace. Approximately, the limiting null distribution of Qg is chi-square with Ig + 1 degrees of freedom, if ignoring the correlation of the two additive components in (4). Our empirical evidence shows that this approximation seems to be adequate (see Section S2 in the Supplementary Material).
Using either (2) or (4) to combine multiple studies requires that Ukgs (and Vkgs) have the same dimensionality in all K studies. Thus, we should only include the isoforms that are present in all the studies in our analysis; or we can set Tkg = 0 if gene g’s isoform information is not complete in study k but complete in other studies. However, this would not be a general issue as quantifying isoform-specific expression requires raw sequencing data in FASTQ or BAM format. When raw data from all individual studies are available, we are then able to align raw reads to the human reference genome using the same isoform and gene annotation files across different studies. Thus, the set of isoforms for any specific gene is the same in every component study. This is the case in our data example.
2.2 Stage II: set enrichment analysis
In Step III, the pathway enrichment score ωp is calculated for each pathway p in the pathway database, 1 ≤ p ≤ P. Let Cp and Dp denote the P-values of random genes within and out of pathway p based on the gene-level statistics Qgs, respectively. Let cp and dp denote the numbers of genes within and out of pathway p, respectively, satisfying dp = G − cp. Let F̂Cp (x) and F̂Dp (x) denote the corresponding empirical distribution functions of Cp and Dp. The enrichment score, defined as the one-sided Kolmogorov–Smirnov (OKS) statistic for testing Cp ≼st Dp (Shen and Tseng, 2010) (i.e., pathway p is enriched with genes with small P-value), is the maximum deviation from F̂Dp (x) to F̂Cp (x), i.e. . Then the P-value that reflects the statistical significance of ωp, denoted by p(ωp), is computed through permuting gene labels in and out the pathway.
The distribution of the OKS statistic ωp is obviously affected by the corresponding pathway size. Previous work (e.g. Subramanian et al. 2005, Shen and Tseng 2010) did not consider the effect of varying set sizes when testing multiple gene sets from a pathway database. Here, we use a corrected version of ωp, , which is based on the asymptotic result in Gail and Green (1976): when cp and dp are sufficiently large, for z > 0. From simulation, we find that when min(cp, dp) > 30, the above asymptotic distribution works very well so that the distribution of becomes virtually independent of the set sizes. Note that for a single pathway, the proposed correction does not affect its statistical significance; that is, .
When testing multiple pathways, we estimate the adjusted P-value based on , the so-called Q-value, denoted by , for each pathway p, p = 1, … P. Usually, to control the false discovery rate within a pre-specified threshold δ, all pathways with a Q-value< δ are reported as enriched.
3 ALGORITHMS
We have two algorithms outlined below, and the difference lies in how to estimate the P-value p(Qg). In Algorithm 1, we use the (approximate) asymptotic reference distribution of Qg under the FE or RE model for association testing, which requires regularity conditions of the central limit theory. In Algorithm 2, we calculate p(Qg) via permutation, which is usually more robust than asymptotic testing in practical situations. But Algorithm 1 is noticeably faster.
We mention that an adaptive permutation procedure can be used to improve the computational efficiency of Algorithm 2, where the number of permutations can vary from gene to gene. Since we are mainly interested in identifying isoform-active genes, we may use less permutations for genes with relatively large P-values. We first estimate P-values based on a small number of permutations (say N0 = 200) only. Given gene g, if the estimated p(Qg) is smaller than a threshold C0 (say 0.1–0.2, to be conservative), we perform an additional large number of permutations (say N+ = 2, 000) and update accordingly. This adaptive procedure is much more efficient in computing when the number of isoform-active genes is small compared to the total number of genes G.
Algorithm 1.
Procedure with P-values of gene-level statistics computed via asymptotic testing
|
Algorithm 2.
Procedure with P-values of gene-level statistics computed via permutation
|
4 SIMULATION
We evaluate the performance of the proposed methods (iGSEAi-FE and iGSEAi-RE for the approaches based on the FE and RE models, respectively, where the “i” after iGSEA stands for “isoform”) and compare them with the existing MAPE methods in Shen and Tseng 2010 (i.e., MAPE_G, MAPE_P, MAPE_I). Currently, none of the existing methods can handle isoform-specific expression. So we supply the three MAPE methods with gene-level expression mapped from simulated isoform-level expression. We conduct two sets of simulation studies, one for discrete phenotypes and the other for continuous phenotypes. For each set of simulation, we compare the type I error and power under a single-pathway simulation model; and we further evaluate the FDR and compare the sensitivity and specificity using Receiver Operating Characteristic (ROC) curves under a multiple-pathway simulation model.
All numerical results reported in this paper are based on Algorithm 1; and for iGSEAi-RE, we simply set Bg as an identity matrix. This is because we find via preliminary simulation that (1) there was not much difference in the overall performance between Algorithms 1 and 2, but Algorithm 1 is much faster, as mentioned before; and (2) other common choices of Bg did not provide better performance but slowed down the RE procedure and made it less numerically stable. We note that the similar performance between Algorithms 1 and 2 in identifying enriched pathways is mainly due to the following reasons (i) the chi-square approximation to the null distribution of Qg is adequate, as shown in simulation; and (ii) although Algorithm 2 is better than Algorithm 1 in estimating P-values based on Qgs (see Section S3 of Supplementary Material for detail), the subsequent enrichment analysis only relies on the orderings of these P-values, and so whether the permutation or asymptotic approach is used in the first stage would not matter much.
4.1 Discrete Case
Simulation I-1: comparing power
Here, we consider a binary Y as a typical example of the discrete case. Each simulated data set includes K = 6 independent studies, and in each study, there are 40 samples, where the first 20 are controls (i.e., Yks = 0), and the other 20 are cases (i.e., Yks = 1).
Suppose there are 600 genes in the genome. In the single-pathway model, the first 150 genes are assigned to the pathway of interest, among which 150 × α genes are isoform-active. In the next 450 genes, there are 450×α0 isoform-active genes. Thus, if α > α0, the pathway is enriched. We fix α0 = 0.20, and set α ∈ {0.25, 0.30, 0.35} for a weak, median and strong enrichment signal, respectively. Recall that we use a binary variable Tkg to indicate whether the data for gene g are available in study k. We define the gene sampling rate by λ ≡ Pr(Tkg = 1), and use Bernoulli(λ) to generate a random number of genes present in study k, where we set λ ∈ {0.7, 0.8, 0.9, 1.0}. We set Ig ∈ {1, 2, 3, 4} and among the 600 genes, we set the number of genes with one isoform or four isoforms to be 100 each, and with two or three isoforms to be 200 each. Further, to compare the two proposed methods, we generate data based on the FE and RE models, respectively. For all non-active isoforms, we assume βkgi ≡ 0 in both FE and RE models. For active isoforms, under the FE model, we allow βkgis to vary across genes randomly, but stay constant for any specific gene across studies; and we assume |βkgi| = |β.g.| ~ abs(N(v, 1)); under the RE model, we allow βkgis to vary among both genes and studies randomly; and we assume |βkgi| = |βkg.| ~ abs(N(v, 1)). We further set v ∈ {0.5, 0.75, 1} for varying strength of mean isoform effects.
Recent genome-wide studies suggest that more than half of human genes produce multiple protein isoforms through alternative splicing and alternative usage of transcription initiation and/or termination, and for the majority of human genes, the inclusion or exclusion of exonic sequences enhances the generation of transcript variants and/or protein isoforms with varying structures, which have diverse and sometimes opposite functions (Pal et al., 2011, 2012), as mentioned in the introduction. For this reason, for 50% of the isoform-active genes, we set the number of positive isoforms (i.e., isoforms with βkgi > 0) and the number of negative isoforms (i.e., isoforms with βkgi < 0) approximately equal in the following way: we first use , which is generated from binomial(Ig, 0.5) (if , discard it and regenerate a value until ), to decide the number of active isoforms within gene g; and then we generate positive isoforms and negative isoforms if is odd; and the numbers of positive and negative isoforms are both if is even. For the rest 50%, we generate one active isoform (either positive or negative) first; and the sign of the other isoforms are randomly generated and can be positive, negative or non-active.
We simulate isoform expression levels xksgis of gene g from a multivariate normal distribution N(μkg, Σx.kg), where μkg = (ukg1, …, ukgIg) and Σx.kg is set to an identity matrix for simplicity. For all isoforms in the control samples, we set ukgi = 0. For the case samples, the mean expression levels of active isoforms are set to satisfy ukgi = βkgi. After generating isoform-level data for all studies, the gene-level expression is obtained by summing up gene g’s corresponding isoform-level data.
In Section S4 of Supplementary Material, we evaluate the type I error of each method at the significance level 0.05 under the null hypothesis of no enrichment in the gene set. We find from Table SI that our iGSEA methods seem to be a bit conservative and so tend to reject the null less than expected; MAPE-P and MAPE-I seem to be a bit aggressive and so tend to reject the null more than expected while MAPE-G tends to be less biased than the others. Thus, for a fair comparison of power, we simulate 1000 datasets for each setting, fix the test significance level at 0.05 and control the actual type I error to be 0.05 for all the methods compared. That is, for each of the methods and each setting, we compute the critical value from the empirical distribution of the corresponding statistic using 1000 datasets generated for the null case by resetting α = α0 (i.e., the pathway is not enriched); then the power of each method is estimated by the proportion of the 1000 datasets in which the pathway is found to be enriched.
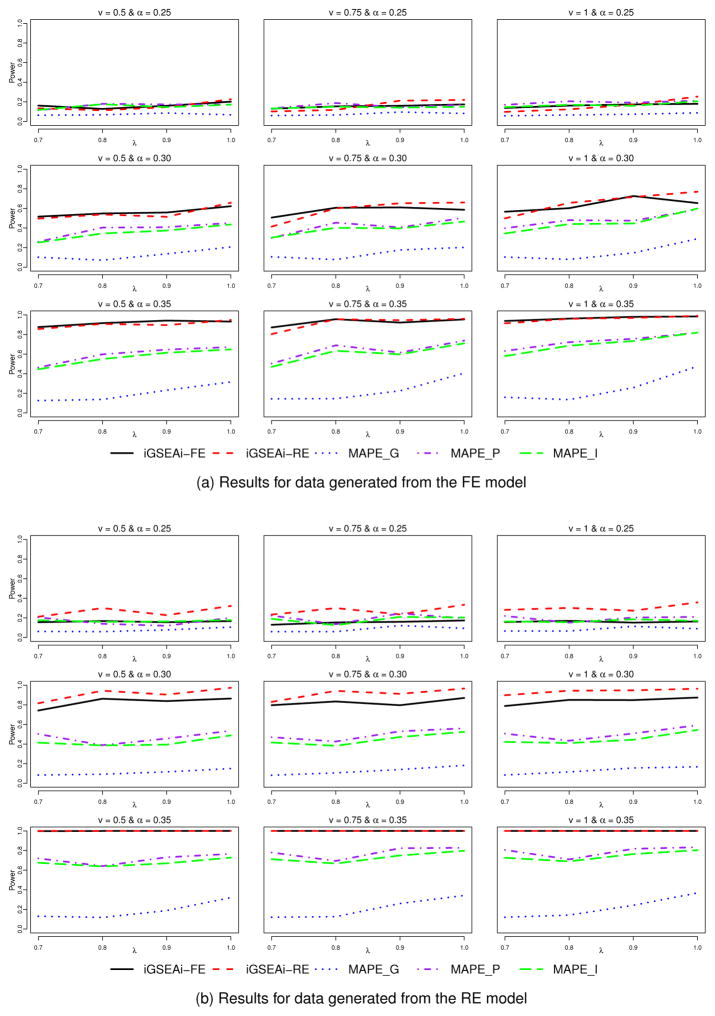
Figure 2(a) shows results of power comparison for data generated from the FE model. We can see that the performance of iGSEAi-FE is comparable to that of iGSEAi-RE. In the cases with weak enrichment signal, the power of the proposed methods is pretty close to that of MAPE_P and MAPE_I. In all the other cases, both the proposed methods have higher power than the MAPEs and in some cases, the power is even doubled. Among the three MAPE methods, MAPE_G is the worst; and MAPE_P is slightly better than or comparable to MAPE_I. The power of all the methods tends to increase as the sampling rate λ or the mean isoform effect size ν or the enrichment signal α increases, as one may expect. But the power seems to be much more sensitive to the change of α than the change of λ or ν. As the enrichment signal gets stronger, the difference in power between the iGSEA and MAPE methods becomes larger; and for the strong signal, the proposed iGSEA methods have power close to 1. Figure 2(b) displays the results for data generated from the RE model. Conclusions are similar to those in Figure 2(a) except that the power of iGSEAi-RE is clearly better than that of the other methods for weak and median enrichment signals. For the strong signal, the power of the proposed methods is both close to 1.
Figure 2.
Simulation I-1 – power comparison for the discrete case.
Simulation I-2: comparing sensitivity and specificity
Here, we assume 1200 genes in the genome, where the first 240 genes are isoform-active, and the remaining genes are not. To compare the sensitivity and specificity, a total of 500 pathways are generated from the genome, where the first 100 are enriched with isoform-active genes, and the last 400 are not. We use the median enrichment signal α = 0.30 in this simulation; that is, each of the first 100 enriched pathways includes 30% isoform-active genes, while the others include 20% as in the whole genome. We use Np, simulated from N (150, 20) left truncated at 0, to decide the size of pathway p, and in each pathway, genes are randomly selected from the genome according to the percentage of isoform-active genes. We also fix υ = 0.75 and λ = 1.0. Other simulation setups not mentioned above are similar to those in Simulation I-1.
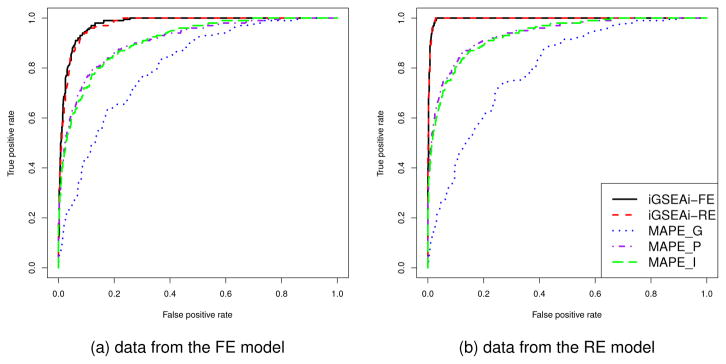
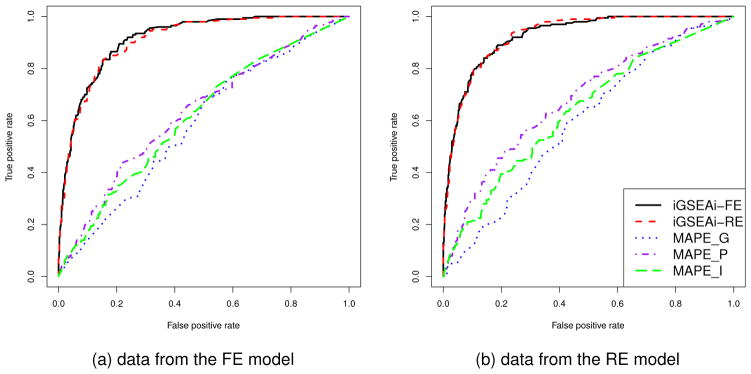
The results of ROC comparison for data generated from the FE model are shown in Figure 3(a), where each curve represents the median function over 50 replicate datasets. Both the proposed methods perform consistently better than the MAPEs and their ROC curves dominate those of MAPEs. The performance of iGSEAi-FE is slightly better than that of iGSEAi-RE. Figure 3(b) displays the results for data generated from the RE model. The curves of iGSEAi-FE and iGSEAi-RE are virtually overlapping, which, again, dominate the curves of MAPEs uniformly.
Figure 3.
Simulation I-2 – ROC comparison for the discrete case
4.2 Continuous Case
Simulation II-1: comparing power
We use a normal response Y as a typical example of the continuous case, and assume Xksg and Yks are from a multivariate normal distribution with mean μx.kg = (μkg1, μkg2, …, μkgIg) and μy.k, and covariance matrix . Here, we first simulate the responses Yks’s from a normal distribution with μy.k ≡ 0 and . Then we simulate xksg using the conditional distribution , where and . Note that βkg is the vector of parameters for regressing Y on X, as defined in (1). For simplicity, we assume that Σx.kg is an identity matrix so that βkg = Σxy.kg. We also suppose all μkgi ≡ 0 for i = 1, 2, …, Ig. For each non-active isoform, we set the corresponding regression coefficient βkgi = 0 and generate xksgi from directly. For active isoforms in the FE model, we set |βkgi| = |β.g.| ~ abs(N (υ, 0.25)), but right truncated at 1.5; for active isoforms in the RE model, we set |βkgi| = |β.g. + εkg.|, where β.g. is the same as the FE model, and εkg. ~ N (0, 1) but |εkg.| is right truncated at 1. We still set υ ∈ {0.5, 0.75, 1} for varying strength of mean isoform effects. Again, we set K = 6 and the sample size of each study at 40.
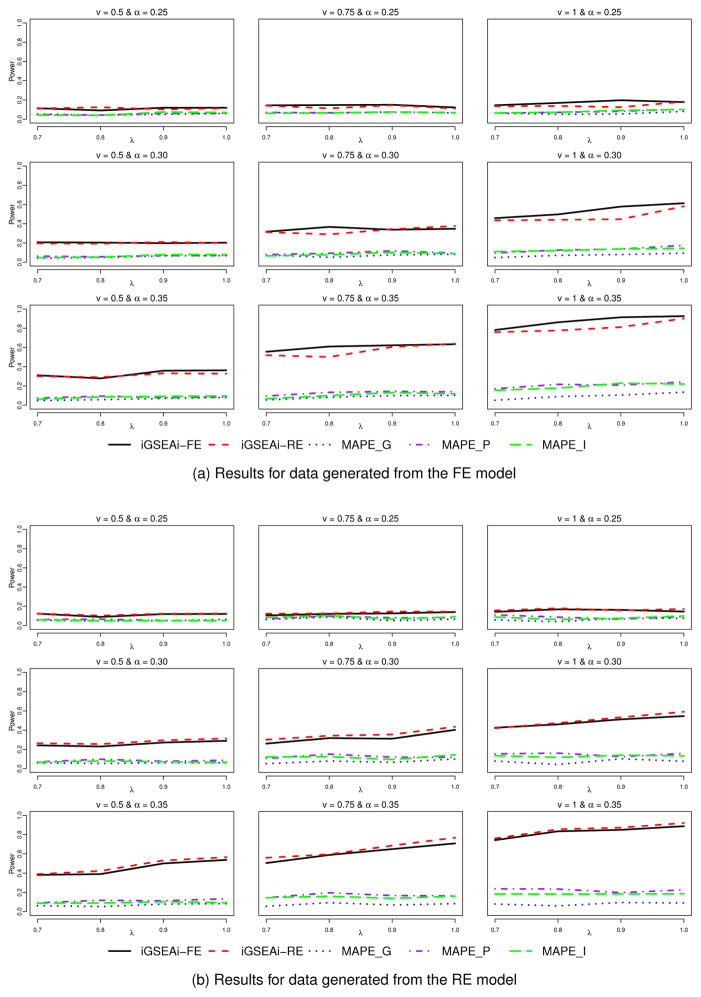
Results for the type I error can be found in Table SI of Supplementary Material. The patterns observed are similar to those in the binary case, except that MAPE-P and MAPE-I tend to be slightly conservative in rejecting the null instead of being aggressive. Figure 4 reports the results of power comparison for the continuous case. Here, the proposed iGSEA methods are consistently better than the three MAPE methods and substantial gain in power can be obtained in many of the settings, no matter whether the data are from the FE or RE model. For data from the FE model, iGSEAi-FE seems to outperform iGSEAi-RE a bit; and for data from the RE model, the opposite occurs, but the difference is typically smaller. Recall that for the discrete case, the difference between the two iGSEA methods for data from the FE model is not as noticeable but the difference for data from the RE model is more noticeable.
Figure 4.
Simulation II-1 – power comparison for the continuous case
Simulation II-2: comparing sensitivity and specificity
We generate 500 pathways and set α = 0.30, υ = 0.75 and λ = 1.0, as in the binary case. The results of ROC comparison based on 50 replicate datasets are reported in Figure 5. Here, iGSEAi-FE/RE is slightly better than iGSEAi-RE/FE when data are generated from the FE/RE model; and both are substantially better than the MAPEs.
Figure 5.
Simulation II-2 – ROC comparison for the continuous case
Finally, we mention that our iGSEA methods seem to outperform MAPEs in controlling the false discovery rate for both discrete and continuous cases, as shown in Section S5 of Supplementary Material; and our additional simulation for analysis of gene-level expression only, reported in Section S6, suggests that utilizing isoform-level expression may improve the power of the iGSEA methods.
5 DATA EXAMPLE
Breast cancer is one of the most common types of cancer, with more than 249,000 new cases expected in the United States in 2016. Identifying essential genes and pathways involved breast cancer tumorigenesis, progression and prognosis is the key to improve patient care in breast cancer. GSEA provides a powerful way to identify new therapeutic targets and predict signatures for personalize treatment of breast cancer. One example is the identification of phosphatidylinosi-tol 3-kinase (PI3K) as a therapeutic target through pathway analysis (Baselga, 2011; Mukohara, 2015). In this study, we applied our proposed methods to identify the pathways that are associated with breast cancer to improve our understanding of the underlying molecular mechanisms of the disease. In order to increase the accuracy and reliability of resulting pathways, we combine multiple mRNA expression datasets measured by the RNA-seq platform and conduct iGSEA. The five RNA-seq datasets used in this study are summarized in Table I.
Table I.
Data example: summary of breast cancer datasets used
| Data Set Name | Case, Control Number |
|---|---|
| GSE45419 (Kalari et al., 2013) | 24,8 |
| GSE47462 (Brunner et al., 2014) | 47,25 |
| GSE52194 (Eswaran et al., 2012) | 16,3 |
| GSE58135 (Varley et al., 2014) | 122,3 |
| GSE69240 (Abba et al., 2015) | 25,10 |
We first map all raw sequencing data in FASTQ files to the genome to get BAM files. Based on these BAM files, the software Cufflinks (Trapnell et al., 2010, 2012), one of the most popular packages for preprocessing RNA-seq data, is used to assemble transcriptomes and quantify both gene-level and isoform-level expression. We also apply log(x + 1) transformation, and median normalization to the isoform expression data so that all the isoforms have the same median zero across different samples and studies. Among 19838 protein-coding genes, those with ≤ 20 isoforms are included in our analysis because genes with too many isoforms are considered as non-informational. In total, the five datasets contain 283 patients in which the expression levels of 18860 protein-coding genes were measured. The pathway database used is KEGG (Kanehisa et al., 2012) which belongs to the C2 collections of MSigDB (Liberzon, 2014) and contain 186 pathways. We only consider pathways that have > 15 but < 500 genes, and so we test 175 pathways in total. Five methods are applied to combine these datasets, including the three MAPE methods and the two proposed iGSEA methods. In addition, we simply pool all the five datasets into one super dataset and perform GSEA, and we label this method by “Pooling”. In order to objectively assess the performance of each method, we generate 50 positive control and 50 negative control pathways. For each positive control pathway, 70% of the member genes are randomly selected from a list of genes which are known to be highly related to breast cancer, and the remaining 30% are from the genes neither in any KEGG pathway nor in the list, while for each negative control pathway, only 10% of the member genes are selected from the list. The performance of six different methods is summarized using ROC curves in Figure 6, and compared using AUC.
Figure 6.
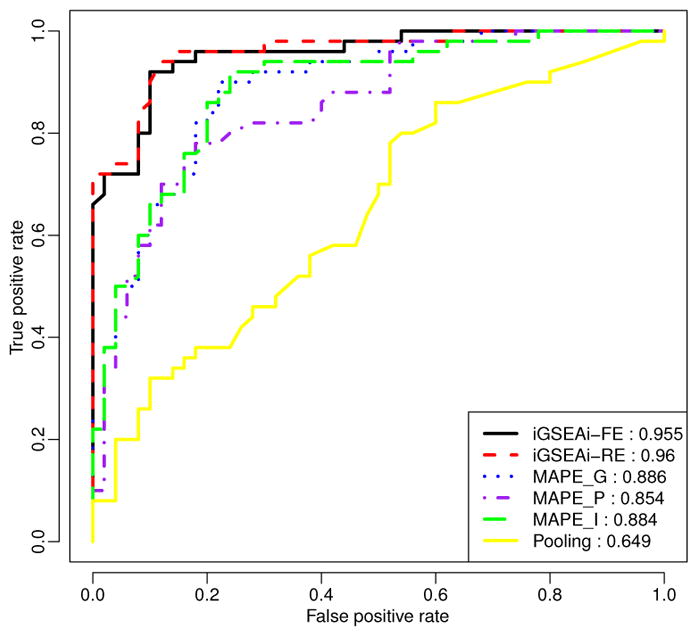
Data example: ROC comparison of positive and negative control pathways.
Figure 6 shows that iGSEAi-RE performs best (AUC = 0.960) in this application, but the performance of iGSEAi-FE is very close (AUC = 0.955). Both iGSEA methods perform significantly better than the MAPE methods, with AUC equal to 0.886, 0.884, and 0.854 for MAPE_G, MAPE_I and MAPE_P, respectively. Also, the ROC curves of the proposed methods are always higher than those of MAPEs; especially for the false positive rate smaller than 0.3, the gain is quite sizable. Among all, the pooling method is the worst, and its AUC is 0.649, much lower than the others, con-firming the known advantages of meta-analysis over direct combination (e.g., Bravata and Olkin 2001; Cohn and Becker 2003.)
Table SIII in Section S7 of Supplementary Material summarizes the top pathways identified based on the Q-values determined by iGSEAi-RE, while iGSEAi-FE gives very similar results in this example. In this table, among the 28 top pathways, some are clearly cancer related (labelled by “X” in Table SIII), including PATHWAYS_IN_CANCER, CELL_CYCLE, COLORECTAL_CANCER, PANCREATIC_CANCER, CLIOMA, POSTATE_CANCER, CHRONIC_MYELOID_LEUKEMIA, ACUTE_MY ELOID_LEUKEMIA, and SMALL_CELL_LUNG_CANCER. In addition, some reported pathways are likely to be related to breast cancer (labelled by “+” in the table). For example, translational machineries are usually more active in cancer because of the increasing demand for biomass accumulation, RNA turnover and splicing, therefore RIBOSOME, RNA_DEGRADATION and SPLICEO-SOME are very likely to be altered in breast cancer. The ENDOCYTOSIS pathway is related to the process of internalizing cell surface proteins and sorting them to be degraded or recycled. Dys-regulated endocytosis could mediate growth signaling and cell motility and invasion (Mosesson et al., 2008). Furthermore, both FOCAL_ADHESION and ADHERENS_JUNCTION are related to the cell adhesion function. Loss of cell adhesion often occurs in tumor invasion and metastasis. The APOPTOSIS pathway is related to program cell death, which is a machinery that cancer cells need to escape from. In summary, many of the pathways identified by the proposed iGSEA methods are consistent with our current knowledge of breast cancer, but they are overlooked by the MAPE methods.
6 CONCLUSIONS AND DISCUSSIONS
We have proposed integrative GSEA methods, namely, iGSEAi-FE and iGSEAi-RE, for meta-analysis of gene set enrichment studies utilizing isoform-specific expression analysis. Through simulation and a data example, we have shown that, compared with the MAPE methods that only use gene-level expression, our iGSEAi-FE and iGSEAi-RE can significantly improve the power of detecting enriched gene sets for most conditions considered for both discrete and continuous phenotypes. As to the choice between iGSEAi-FE and iGSEAi-RE, we prefer to using iGSEAi-RE for binary phenotypes since its power can be much better than that of iGSEAi-FE when data are generated from the RE model but is almost as good as iGSEAi-FE when data are generated from the FE model. For continuous phenotypes, it is not surprising that each iGSEA method works the best under its own model. Thus, it would be reasonable to test the between-study heterogeneity of the isoform effects, to help determine which method to apply. In the worst situation when the test suggests the wrong model, there is typically not much to lose in power if either iGSEA method is used over MAPEs based on our numerical experience.
Due to the transcriptome complexity and limitations of previous experimental approaches, the current gene isoform annotation is still incomplete (Jiang and Wong, 2009), leading to possible loss of analysis power. For example, if the test concludes that gene g’s transcript expression is not significantly associated with the trait, potentially existing isoforms, if “active”, may reverse this conclusion. Nonetheless, even with the incomplete annotation, using isoform-specific expression improve the power over using gene-level expression. We anticipate that more RNA-seq data will be available in the near future for various tissues and cell types, coupled with novel detection methods (Guttman et al., 2010; Trapnell et al., 2010; Schulz et al., 2012; Hiller and Wong, 2013; Behr et al., 2013), making it feasible to discover most of the expressed isoforms.
The sequencing depth/coverage often varies from experiment to experiment, affecting the abundance estimation of isoforms. For example, in one study, an isoform can have zero or low read counts in some samples, and so its signal may not be separated from the background noise (especially when the sample size is small), while it can have a higher signal-to-noise ratio in another study with deeper sequencing or a larger sample size. To account for heterogeneity caused by varying depth of the coverage, sample sizes, platforms, etc., our iGSEA methods are built on FE and RE approaches, which can naturally down-weight studies with low signal-to-noise ratios by estimating the variances of the corresponding effect sizes to be large. This is an advantage over existing MAPE methods that use gross summary statistics to combine results besides utilization of isoform-specific expression.
The availability of raw data from individual RNA-seq studies (either in FASTQ or BAM format) would ensure that all the data are processed using the same rigid quality-control criteria and estimating the same quantities. If raw data in some studies are not available, our methods are applicable if the same gene and isoform annotation files are used in component studies; or we can simply skip the isoform level and apply our methods to gene-level expression (given the same gene annotation file is used), a reduced case in which we pretend that each gene only has one isoform. For the same reason, our methods are applicable to combine multiple microarray GSEA studies, where only gene-level expression data are typically available.
Finally, we mention that when both microarray and RNA-seq studies are involved in iGSEA, there exists a mix of isoform-level and gene-level expression data; and score statistics are not directly combinable using either the FE or RE approach discussed in Section 2.1, due to different dimensionality involved. This is because for microarray studies Ukgs and Vkgs are all scalars while for RNA-seq studies, Ukgs are vectors and Vkg are matrices for genes with more than one iso-form. Obviously, even for the same gene, (Ukg, Vkg) typically has different null distributions across studies from the different technologies, depending on the cardinality of Ukgs so that combining (Ukg, Vkg)s through the FE or RE model-based approaches would require major modifications. Further, analysis of microarray data tends to generate more extreme values of score statistics and P -values even for less important differences or associations due to much larger sample sizes (compared to RNA-seq studies). Thus, to integrate a mix of microarray and RNA-seq expression data, we recommend to develop rank-based meta-analysis approaches as a promising research direction in iGSEA.
Supplementary Material
Acknowledgments
This work was supported by the NIH grants R15GM113157 (PI: Xinlei Wang) and R01CA172211 (PI: Guanghua Xiao).
Contributor Information
Lie Li, Ph.D. Student, Department of Statistical Science, Southern Methodist University, 3225 Daniel Avenue, P O Box 750332, Dallas, Texas 75275.
Xinlei Wang, Professor, Department of Statistical Science, Southern Methodist University, 3225 Daniel Avenue, P O Box 750332, Dallas, Texas 75275.
Guanghua Xiao, Associate Professor, Quantitative Biomedical Research Center, Department of Clinical Sciences, The University of Texas Southwestern Medical Center, Dallas, TX 75390.
Adi Gazdar, W. Ray Wallace Distinguished Chair Professor in Molecular Oncology Research, Department of Pathology, University of Texas Southwestern Medical Center, 6000 Harry Hines Blvd., Dallas, TX 75235-8593.
References
- Abba MC, Gong T, Lu Y, Lee J, Zhong Y, Lacunza E, Butti M, Takata Y, Gaddis S, Shen J, et al. A molecular portrait of high-grade ductal carcinoma in situ. Cancer Research. 2015;75(18):3980–3990. doi: 10.1158/0008-5472.CAN-15-0506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackermann M, Strimmer K. A general modular framework for gene set enrichment analysis. BMC Bioin-formatics. 2009;10:47. doi: 10.1186/1471-2105-10-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akgul C, Moulding DA, Edwards SW. Alternative splicing of bcl-2-related genes: functional consequences and potential therapeutic applications. Cell Mol Life Sci. 2004;61(17):2189–2199. doi: 10.1007/s00018-004-4001-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baselga J. Targeting the phosphoinositide-3 (pi3) kinase pathway in breast cancer. The oncologist. 2011;16(Supplement 1):12–19. doi: 10.1634/theoncologist.2011-S1-12. [DOI] [PubMed] [Google Scholar]
- Behr J, Kahles A, Zhong Y, Sreedharan VT, Drewe P, Rätsch G. Mitie: Simultaneous rna-seq-based transcript identification and quantification in multiple samples. Bioinformatics. 2013;29(20):2529–2538. doi: 10.1093/bioinformatics/btt442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bravata DM, Olkin I. Simple pooling versus combining in meta-analysis. Evaluation & the Health Professions. 2001;24(2):218–230. doi: 10.1177/01632780122034885. [DOI] [PubMed] [Google Scholar]
- Brunner AL, Li J, Guo X, Sweeney RT, Varma S, Zhu SX, Li R, Tibshirani R, West RB. A shared transcriptional program in early breast neoplasias despite genetic and clinical distinctions. Genome Biol. 2014;15(5):R71. doi: 10.1186/gb-2014-15-5-r71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M, Zang M, Wang X, Xiao G. A powerful bayesian meta-analysis method to integrate multiple gene set enrichment studies. Bioinformatics. 2013;29(7):862–869. doi: 10.1093/bioinformatics/btt068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohn LD, Becker BJ. How meta-analysis increases statistical power. Psychological methods. 2003;8(3):243. doi: 10.1037/1082-989X.8.3.243. [DOI] [PubMed] [Google Scholar]
- Dabney A, Storey J, Warnes G. r package version 1.26. 0. 2011. qvalue: Q-value estimation for false discovery rate control. [Google Scholar]
- Downward J. Cancer biology: signatures guide drug choice. Nature. 2006;439(7074):274–275. doi: 10.1038/439274a. [DOI] [PubMed] [Google Scholar]
- Eswaran J, Cyanam D, Mudvari P, Reddy SDN, Pakala SB, Nair SS, Florea L, Fuqua SA, Godbole S, Kumar R. Transcriptomic landscape of breast cancers through mrna sequencing. Scientific reports. 2012:2. doi: 10.1038/srep00264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farkas IJ, Korcsmáros T, Kovács IA, Mihalik A, Palotai R, Simkó GI, Szalay KZ, Szalay-Beko M, Vellai T, Wang S, Csermely P. Network-based tools for the identification of novel drug targets. Sci Signal. 2011;4(173):pt3. doi: 10.1126/scisignal.2001950. [DOI] [PubMed] [Google Scholar]
- Gail MH, Green SB. A generalization of the one-sided two-sample kolmogorov-smirnov statistic for evaluating diagnostic tests. Biometrics. 1976:561–570. [PubMed] [Google Scholar]
- Guttman M, Garber M, Levin JZ, Donaghey J, Robinson J, Adiconis X, Fan L, Koziol MJ, Gnirke A, Nus-baum C, Rinn JL, Lander ES, Regev A. Ab initio reconstruction of cell type-specific transcriptomes in mouse reveals the conserved multi-exonic structure of lincrnas. Nat Biotechnol. 2010;28(5):503–510. doi: 10.1038/nbt.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han B, Eskin E. Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am J Hum Genet. 2011;88(5):586–598. doi: 10.1016/j.ajhg.2011.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiller D, Wong WH. Simultaneous isoform discovery and quantification from rna-seq. Stat Biosci. 2013;5(1):100–118. doi: 10.1007/s12561-012-9069-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu YJ, Berndt SI, Gustafsson S, Ganna A, Hirschhorn J, North KE, Ingelsson E, Lin DY Consortium GIANT. Meta-analysis of gene-level associations for rare variants based on single-variant statistics. Am J Hum Genet. 2013a;93(2):236–248. doi: 10.1016/j.ajhg.2013.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu YJ, Berndt SI, Gustafsson S, Ganna A, Hirschhorn J, North KE, Ingelsson E, Lin DY, et al. of ANthropometric Traits (GIANT) Consortium GI. Meta-analysis of gene-level associations for rare variants based on single-variant statistics. The American Journal of Human Genetics. 2013b;93(2):236–248. doi: 10.1016/j.ajhg.2013.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hung JH, Yang TH, Hu Z, Weng Z, DeLisi C. Gene set enrichment analysis: performance evaluation and usage guidelines. Brief Bioinform. 2012;13(3):281–291. doi: 10.1093/bib/bbr049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang H, Wong WH. Statistical inferences for isoform expression in rna-seq. Bioinformatics. 2009;25(8):1026–1032. doi: 10.1093/bioinformatics/btp113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalari KR, Necela BM, Tang X, Thompson KJ, Lau M, Eckel-Passow JE, Kachergus JM, Anderson SK, Sun Z, Baheti S, et al. An integrated model of the transcriptome of her2-positive breast cancer. PloS one. 2013;8(11):e79298. doi: 10.1371/journal.pone.0079298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, Goto S, Sato Y, Furumichi M, Tanabe M. Kegg for integration and interpretation of large-scale molecular data sets. Nucleic Acids Research. 2012;40(D1):D109–D114. doi: 10.1093/nar/gkr988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberzon A. A description of the molecular signatures database (msigdb) web site. Stem Cell Transcriptional Networks: Methods and Protocols. 2014:153–160. doi: 10.1007/978-1-4939-0512-6_9. [DOI] [PubMed] [Google Scholar]
- Lin DY, Zeng D. On the relative efficiency of using summary statistics versus individual-level data in meta-analysis. Biometrika. 2010;97(2):321–332. doi: 10.1093/biomet/asq006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q, Zhao S, Su PF, Yu S. Gene and isoform expression signatures associated with tumor stage in kidney renal clear cell carcinoma. BMC Systems Biology. 2013;7(Suppl 5):S7. doi: 10.1186/1752-0509-7-S5-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosesson Y, Mills GB, Yarden Y. Derailed endocytosis: an emerging feature of cancer. Nature Reviews Cancer. 2008;8(11):835–850. doi: 10.1038/nrc2521. [DOI] [PubMed] [Google Scholar]
- Mukohara T. Pi3k mutations in breast cancer: prognostic and therapeutic implications. Breast Cancer: Targets and Therapy. 2015;7:111. doi: 10.2147/BCTT.S60696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pal S, Gupta R, Davuluri RV. Alternative transcription and alternative splicing in cancer. Pharmacol Ther. 2012;136(3):283–294. doi: 10.1016/j.pharmthera.2012.08.005. [DOI] [PubMed] [Google Scholar]
- Pal S, Gupta R, Kim H, Wickramasinghe P, Baubet V, Showe LC, Dahmane N, Davuluri RV. Alternative transcription exceeds alternative splicing in generating the transcriptome diversity of cerebellar development. Genome Res. 2011;21(8):1260–1272. doi: 10.1101/gr.120535.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan Q, Shai O, Lee LJ, Frey BJ, Blencowe BJ. Deep surveying of alternative splicing complexity in the human transcriptome by high-throughput sequencing. Nat Genet. 2008;40(12):1413–1415. doi: 10.1038/ng.259. [DOI] [PubMed] [Google Scholar]
- Rajan P, Elliott DJ, Robson CN, Leung HY. Alternative splicing and biological heterogeneity in prostate cancer. Nat Rev Urol. 2009;6(8):454–460. doi: 10.1038/nrurol.2009.125. [DOI] [PubMed] [Google Scholar]
- Schulz MH, Zerbino DR, Vingron M, Birney E. Oases: robust de novo rna-seq assembly across the dynamic range of expression levels. Bioinformatics. 2012;28(8):1086–1092. doi: 10.1093/bioinformatics/bts094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen K, Tseng GC. Meta-analysis for pathway enrichment analysis when combining multiple genomic studies. Bioinformatics. 2010;26(10):1316–1323. doi: 10.1093/bioinformatics/btq148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Black MA. Microarray-based gene set analysis: a comparison of current methods. BMC Bioinformatics. 2008;9:502. doi: 10.1186/1471-2105-9-502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proceedings of the National Academy of Sciences. 2003;100(16):9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, Paulovich A, Pomeroy SL, Golub TR, Lander ES, Mesirov JP. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci U S A. 2005;102(43):15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang ZZ, Lin DY. Meta-analysis of sequencing studies with heterogeneous genetic associations. Genetic epidemiology. 2014;38(5):389–401. doi: 10.1002/gepi.21798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JR, Attia J, Minelli C. The meta-analysis of genome-wide association studies. Brief Bioinform. 2011;12(3):259–269. doi: 10.1093/bib/bbr020. [DOI] [PubMed] [Google Scholar]
- Trapnell C, Roberts A, Goff L, Pertea G, Kim D, Kelley DR, Pimentel H, Salzberg SL, Rinn JL, Pachter L. Differential gene and transcript expression analysis of rna-seq experiments with tophat and cufflinks. Nature protocols. 2012;7(3):562–578. doi: 10.1038/nprot.2012.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapnell C, Williams BA, Pertea G, Mortazavi A, Kwan G, van Baren MJ, Salzberg SL, Wold BJ, Pachter L. Transcript assembly and quantification by rna-seq reveals unannotated transcripts and isoform switching during cell differentiation. Nat Biotechnol. 2010;28(5):511–515. doi: 10.1038/nbt.1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullah U, Tripathi P, Lahesmaa R, Rao KVS. Gene set enrichment analysis identifies lif as a negative regulator of human th2 cell differentiation. Sci Rep. 2012;2:464. doi: 10.1038/srep00464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varley KE, Gertz J, Roberts BS, Davis NS, Bowling KM, Kirby MK, Nesmith AS, Oliver PG, Grizzle WE, Forero A, et al. Recurrent read-through fusion transcripts in breast cancer. Breast cancer research and treatment. 2014;146(2):287–297. doi: 10.1007/s10549-014-3019-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang ET, Sandberg R, Luo S, Khrebtukova I, Zhang L, Mayr C, Kingsmore SF, Schroth GP, Burge CB. Alternative isoform regulation in human tissue transcriptomes. Nature. 2008;456(7221):470–476. doi: 10.1038/nature07509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X. Identification of common tumor signatures based on gene set enrichment analysis. In Silico Biol. 2011;11(1–2):1–10. doi: 10.3233/ISB-2012-0440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Pal S, Bi Y, Tchou J, Davuluri R. Isoform level expression profiles provide better cancer signatures than gene level expression profiles. Genome Medicine. 2013;5(4):33. doi: 10.1186/gm437. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.