Electric Fields and Enzyme Catalysis

Abstract

What happens inside an enzyme’s active site to allow slow and difficult chemical reactions to occur so rapidly? This question has occupied biochemists’ attention for a long time. Computer models of increasing sophistication have predicted an important role for electrostatic interactions in enzymatic reactions, yet this hypothesis has proved vexingly difficult to test experimentally. Recent experiments utilizing the vibrational Stark effect make it possible to measure the electric field a substrate molecule experiences when bound inside its enzyme’s active site. These experiments have provided compelling evidence supporting a major electrostatic contribution to enzymatic catalysis. Here, we review these results and develop a simple model for electrostatic catalysis that enables us to incorporate disparate concepts introduced by many investigators to describe how enzymes work into a more unified framework stressing the importance of electric fields at the active site.

1. HISTORICAL INTRODUCTION

1.1. A Brief History of Stark Effects

In 1913, German physicist Johannes Stark (1) and Italian physicist Anthony Lo Surdo (2) simultaneously discovered the splitting of the spectral lines of the hydrogen atom in the presence of an external electric field. The significance of the findings could scarcely be understated. Many early experiments in atomic physics could be made consistent with classical physics as well as early versions of quantum theory propounded by Bohr and Sommerfeld. The Stark–Lo Surdo effect (typically, though unfortunately, abbreviated to the Stark effect), however, was incongruent with models that described the motion of hydrogen’s electron classically (which predicted a miniscule shift), providing clear evidence in favor of quantum theory (3). The following decade, Stark’s data proved decisive again, by conforming to new predictions from Schrödinger’s wave mechanics (4). In this way, the careful observation of spectral perturbations accompanying electric fields helped usher in not one but two paradigm shifts in our understanding of the electronic structure of atoms.

When applied to molecules, Stark experiments provide a means to measure the difference in dipole moment, Δμ⃗, accompanying a transition from one state to another, typically from the ground to an electronically excited state. Early measurements focused on comparisons between experiment and theory for simple aromatic molecules, sometimes in fluid solution, where the response is greatly complicated by molecular reorientation in the applied field (5), and sometimes in crystals (6) or films (7), where these effects can be avoided. An important early biological example came from the work of Mathies & Stryer (8) on the electronic absorption of retinal in rhodopsin where a very large |Δμ⃗| was observed and interpreted as triggering a conformational change. Early work from our laboratory focused on measuring the magnitude and direction of Δμ⃗ for the primary electron donor in photosynthetic reaction centers (9).

A particularly surprising result was the observation of a very large |Δμ⃗| for the carotenoid spheroidene in the light-harvesting complex LH11 (B800-850) from Rhodobacter sphaeroides (10). Because spheroidene has a small |Δμ⃗| outside of the antenna complex, we suggested that the electric field from the protein surrounding the highly polarizable carotenoid induces this large |Δμ⃗| (a similar effect may also be responsible for what was observed for rhodopsin). Turning this around, the spectroscopic consequences of the electric fields created in organized protein environments could provide a quantitative readout on those electric fields.

If we broaden the concept to include effects of electric fields that are always present (and changing) in the condensed phase, there are many familiar examples. These include transistors and other field-modulated properties of electronic materials, the transmembrane potential in primary metabolism, and voltage gating that lies at the heart of neural signaling. The role of electrostatics in biological systems is widely appreciated, though often used qualitatively. As discussed below, quantitative investigation of protein electrostatics is possible with the assistance of spectroscopic tools and physical models to interpret the data.

1.2. A Brief History of the Enzyme Question

The physical basis for enzymes’ catalysis has been a central and recurring question in biochemistry since as early as 1930 when J. B. S. Haldane (11) published his seminal book on the topic. However, unlike the other classical questions of early molecular biology, the nature of enzyme catalysis was not settled by X-ray structures and, indeed, continues to be widely discussed and disputed to this day in spite of the great abundance of structural data available on enzymes. The work by Wolfenden and coworkers (12–14), which made evident the astronomical proportions of enzymes’ catalytic proficiency, and the promise of human-designed de novo enzymes (15) have only increased our appreciation of these marvelous molecules over time.

Many reviews have been published addressing this core question: How do enzymes work?—several have had that question as the title (16–18)—and there are, unsurprisingly, many opinions. The following is by no means meant to be comprehensive but to provide a broad overview of some commonly encountered theories to place the role of electric fields in perspective.

Linus Pauling (19) and other early enzymologists (11) suggested that enzymes deform (strain) their substrates along reactive coordinates toward their transition states. This idea, which would now be labeled ground state destabilization (GSD), received early support from David Phillips and coworkers’ (20) 2-Å-resolution structure of lysozyme because the active site was found to possess a cleft shaped in such a way as to accept substrate, but the mode of substrate binding could favor distortion. The hypothesis proved problematic because enzymes still have to bind their substrates from solution with a net reduction in free energy and are usually not stable enough (i.e., too soft) to appreciably distort covalent bonds (21). The GSD concept became more nuanced and regained thermodynamic plausibility when Jencks (22) proposed the Circe effect: The enzyme could selectively destabilize the substrate’s reactive region while still exercising favorable binding interactions to distal regions of the substrate that do not participate in chemistry. This hypothesis is consistent with the broadly attested phenomenon that truncated substrates are generally much less reactive than the corresponding full substrates (23–26).

Pauling (19) also insinuated that enzymes stabilize their reactions’ transition states, and the idea was formalized with the familiar thermodynamic relation, $k_{\text{cat}}/k_{\text{uncat}}=K_D^S/K_D^{\text{TS}}$, introduced by Kurz (27). Transition state stabilization (TSS) is now so accepted as a facet of enzyme catalysis that it is nearly considered tautological (28). More controversy arises when one tries to identify the specific interactions that are responsible for TSS, bearing in mind that transition states differ but slightly in structure from their progenitor ground states. Short, strong hydrogen bonds (H-bonds) (29, 30), geometrical discrimination (31, 32), electrostatic interactions (33), and packing interactions (34) have been put forth as capable of providing the basis for TSS. Nevertheless, the overall failure of catalytic antibodies to serve as proficient catalysts on the scale of enzymes, despite boasting impressive affinities to transition state analogs (35), could suggest that TSS provides an incomplete picture for understanding enzyme catalysis. Moreover, a description that can unify these seemingly disparate sources of TSS would be advantageous.

Another key consideration is entropy. A common misconception is that enzymes work simply by placing reacting groups of substrate(s) close together. Statistical mechanics suggests that such an effect would maximally raise ΔS^‡ by 15–18 cal K⁻¹ mol⁻¹, or a rate enhancement of 10⁴–10⁵ (36), which we know to be small relative to the rate enhancements many enzymes achieve (14). Page & Jencks (37) expanded the case for entropy by arguing that enzymes can also reduce the substrate’s entropy associated with rotations and internal degrees of freedom; that is, it can select rotamers that are closer to the transition state’s pose. This idea gained support from classic experiments by Bruice & Pandit (38), who demonstrated that dramatic increases in rates of intramolecular reactions in solution as a backbone forced the reacting groups into positions more akin to the presumed reactive geometry. Bruice and coworkers (39, 40) later recast this idea in molecular terms by asserting that enzymes promote near-attack conformations among their substrates. Although attractive ideas in principle, the observed temperature dependence of most enzyme-catalyzed (and noncatalyzed) reactions indicates that the majority of enzyme-derived rate enhancements are, in fact, enthalpic in origin (41), with the primary (intriguing) exception being the ribosome (42).

It is important to emphasize that any study that seeks to methodically identify the physical basis of enzyme catalysis must start with a process whose chemical mechanism (i.e., the set of intermediates traversed en route from substrates to products) is known, and comparisons must be made between such a reaction and a chemically filtered reference reaction (43, 44) that proceeds through the same mechanism without the enzyme. This definition is admittedly stringent and tends to limit the range of application of this analysis to a small cohort of extensively studied enzymes. In many cases, especially with metalloenzymes, heroic exertions are needed to determine the mechanism and the reaction cannot be mimicked in solution. Enormous catalytic effects can be realized by breaking down a process with a single large barrier into several steps with smaller barriers through judicious application of cofactors and metals. Nevertheless, it is a mistake to assume that determining an enzyme’s mechanism of action is tantamount to understanding its catalytic power. Bacterial ketosteroid isomerase (KSI) serves as an intriguing counterexample as the mechanism it utilizes to isomerize 5-androstene is identical to the path taken in solution, and yet the same process is approximately 1 trillion times more rapid (45). In summary, although understanding an enzyme’s mechanism of action is a critical first step to understanding the source of its catalytic power, it does not provide a full energetic accounting (46).

2. ELECTROSTATIC CATALYSIS

2.1. A Primer on Electrostatics of Solutions

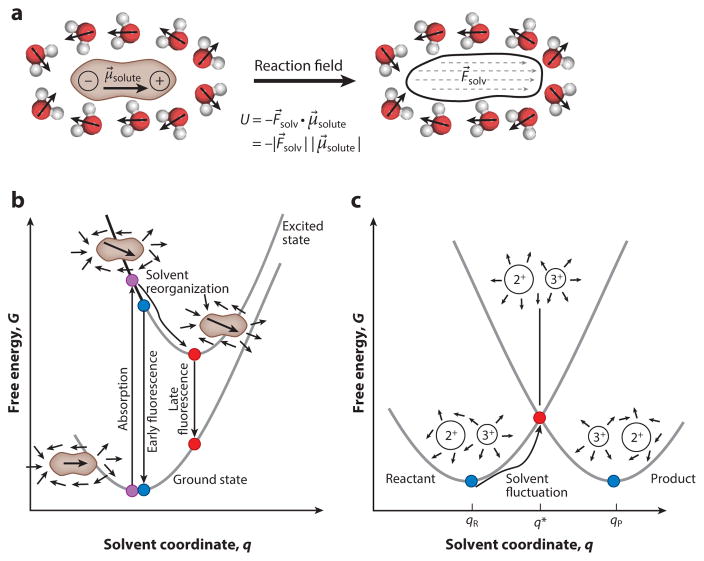
When a molecule with a permanent dipole is placed into fluid solution, it forces the dipoles of the solvent molecules to reorient to the same general direction as the solute’s dipole, thereby minimizing the system’s potential energy (Figure 1a). Because the solvent molecules in that vicinity are no longer randomly oriented (within the solute’s internal frame of reference), the electric fields created by their own permanent dipoles no longer cancel out, and so they exert a net electric field back onto the solute, termed the reaction field (47, 48). This reaction field will point in the same direction as the solute’s dipole, and its magnitude will depend on the size of the solute’s dipole and the polarity of the solvent. The reaction field interacts with the solute dipole that created it, resulting in a solvation energy (5). For solutes with more complicated charge configurations (i.e., multiple polar groups), solvent molecules adjacent to different regions of the solute will reorganize in response to the local dipoles in that region of the solute.

Figure 1.

Properties of reactants and reactions in polar solvents. (a) A solute with a permanent dipole, μ⃗_solute, organizes polar solvent molecules (shown as H₂O) around it such that they exert a net solvent reaction field, F⃗_solv, on the dipole oriented in the same direction as μ⃗_solute. (b) The dipole of a molecule changes when it is electronically excited. This causes solvent molecules to reorganize to optimize their electrostatic interactions with the solute’s new charge configuration. This process can be monitored indirectly by observing the solute’s fluorescence (the dynamic Stokes shift). (c) In the Fe⁺²-Fe⁺³ self-exchange reaction (ΔG°_rxn = 0), solvent dipoles need to fluctuate away from their equilibrium conformation, q_R, to a particular high-energy conformation, q^*, to satisfy the conditions for a Franck–Condon electron transfer.

Electronic excited states of molecules typically possess dipoles of different magnitudes and orientations relative to their ground states (Figure 1b), implying that the solvent will interact differently with a molecule following photoexcitation. Consider the instant the molecule has become electronically excited: The solvent molecules will still be oriented (collectively termed the solvent coordinate, q) in a way that is optimally aligned to the ground state’s dipole moment (more generally, its charge configuration if the solute possesses charges or numerous polar groups). Over several picoseconds, the solvent molecules will reorganize to adopt a conformation that optimally interacts with the excited state’s dipole. The reorganization explains why the earliest emitted photons from a fluorophore are always at higher energies than the later ones, an effect called the dynamic Stokes shift (49, 50). In the case of photoexcitation, a fluorophore’s dipole reorientation is fast and decisive; the solvent has no choice but to follow along in tow. During chemical reactions, molecules’ charge configurations also undergo large changes, but here the process is more intimately coupled to the solvent reorganization because reactions are thermally activated processes. This discussion raises two questions (that will be addressed below): What language should be used to describe the collective motion that occurs in solvation dynamics, and how do these concepts transfer to the more heterogeneous “solvent” of an enzyme active site?

2.2. Solvent Reorganization During Chemical Reactions

Marcus and coworkers (51) considered the simplest possible chemical reaction between two identical metal ions in solution, in which the first transfers an electron to the second. In practice, such reactions’ rates vary enormously depending on the metal ions in question (51), despite the fact that no bonds need to break and ΔG°_rxn = 0. The reactant state and product state have quite different charge configurations, so the solvent coordinate with which either is in equilibrium (q_R and q_P, respectively) will be very different (Figure 1c). Marcus reasoned that the solvent must first come to adopt a perturbed configuration, q^*, in which the total energies of the reactant electronic state (Fe²⁺ + Fe³⁺) and the product electronic state (Fe³⁺ + Fe²⁺) are equal before an electron can be transferred (52). The q^* configuration solvates the reactant state much more poorly than the typical equilibrium solvent configuration, q_R, so this state is fleetingly sampled as a rare fluctuation. As solvent reorganization is in fact the rate-determining step of the electron self-exchange reaction, Marcus’s model could predict the absolute rates of these types of reactions.

A solvent coordinate is a way of packaging all the solvent atoms’ positional information into one number that captures the net interaction energy between the solvent and the solute. If the solute’s charge configuration can be described as a dipole, then the solvent coordinate is the electric field that it exerts onto the solute, due to the relationship U = −F⃗_env · μ⃗_solute (where U is the interaction energy, μ⃗_solute is the solute’s dipole moment, and F⃗_env is the electric field the solvent exerts onto the solute). Solvent reaction fields are oriented along the solute’s dipole (at equilibrium) which further simplifies the equation to U = −|F⃗_solvent||μ⃗_solute| for this case (Figure 1a). The electric field effectively sums over all the dipole-dipole interactions, dipole-induced dipole interactions, and hydrogen-bonding interactions that the solvent atoms furnish, and for conventional solvents typically spans a range between 0 and approximately 80 MV/cm [N.B.: 1 MV/cm equals 10⁸ V/m (the SI unit), 1.944 × 10⁻⁴ atomic units, or 0.0480 kcal mol⁻¹ Debye⁻¹]. The electric field description is powerful because it acts as a unifier across noncovalent interactions, enabling us to compare and combine the effects of long-range, nonspecific interactions with short-range, spe-cific ones (such as H-bonds) all with a common set of units (53). Importantly, our research has demonstrated that H-bonds, often emphasized as playing critical roles in enzyme catalysis, are amenable to this electric field description at a reasonable level of approximation (54, 55).

Most chemical reactions require rearranging a molecule’s atoms to form a transition state. In polar reactions, a reactant’s dipole is expected to change substantially upon activation, implying that the transition state would be stabilized by a rather different solvent coordinate, harkening back to Marcus’s model for electron transfers. Such reactions could be catalyzed by an environment that stabilizes the transition state’s dipole more than the reactant’s dipole. Expressed mathematically, electric field catalysis is given by

$$\mathrm{\Delta }\mathrm{\Delta }{G}^{‡}=-\left(\left({\overrightarrow{F}}_{\text{env},\text{TS}}·{\overrightarrow{\mu }}_{\text{TS}}\right)-\left({\overrightarrow{F}}_{\text{env},\mathrm{R}}·{\overrightarrow{\mu }}_{\mathrm{R}}\right)\right)$$ 1

where μ⃗_R is the reactant’s dipole moment, μ⃗_TS is the transition state’s dipole moment, F⃗_env,R is the electric field the environment exerts on the reactant dipole, and F⃗_env,TS is the electric field the environment exerts on the transition state dipole.

In general, reactions may involve complicated changes in charge configuration that are not amenable to a point dipole description, in which case Equation 1 would have to be expanded to include every region of the molecule that undergoes a charge rearrangement and the respective electric field at each of those sites. We refer to this more general situation with the term electrostatic catalysis, though in this context we do not mean to exclude polarization, which certainly contributes (though normally is not the primary contributor) to local electric fields. Nevertheless, we focus here on substrates where charge rearrangement occurs primarily at a single site (typically a carbonyl), and denote the local electric field at a carbonyl bond with ${\overrightarrow{F}}_{\text{env}}^{\mathrm{C}=\mathrm{O}}$.

2.3. Two Limiting Cases of Electric Field Catalysis

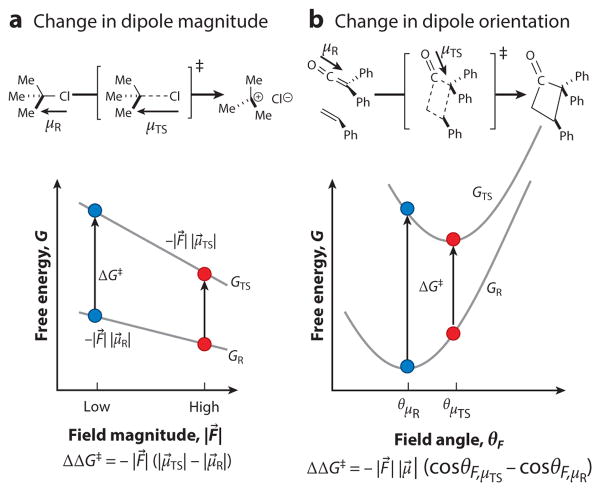
We suggest dividing electric field catalysis into two categories (Figure 2). In the first, we consider a molecule whose dipole moment increases (or less typically, decreases) in magnitude during a chemical reaction but does not reorient, for which the rate-determining carbocation formation of the S_N1 reaction is an excellent example (Figure 2a). In such a reaction, the rate is accelerated by an environment that furnishes an electric field with greater (smaller) magnitude, an effect encountered in normal (inverse) solvent-rate correlations (56). In the reactant form, the molecule’s dipole gives rise to a reaction field (which is oriented in the same direction as the dipole); however, the transition state will be even more stabilized by the same electric field because its dipole is identically oriented but of greater magnitude. Equation 1 simplifies to

Figure 2.

Two limiting cases of electric field catalysis. Electric field catalysis lowers a reaction’s activation barrier by ΔΔG^‡ = −((F⃗_TS · μ⃗_TS) − (F⃗_R · μ⃗_R)). This expression simplifies in two limiting scenarios, where blue dots represent a reference case and red dots represent catalysis. (a) If the transition state’s (TS) and reactant’s (R) dipole moments are oriented in the same direction but the transition state’s dipole is greater (such as in the rate-determining heterolysis step of an S_N1 reaction), larger electric fields (such as provided by a polar solvent) will catalyze the reaction. (b) If the transition state’s and reactant’s dipole moments have the same magnitude but have different orientations (such as is approximately true in the cycloaddition of a ketene), the magnitude of the electric field will not have a catalytic effect. Electric field catalysis can be achieved only by “correctly” orienting the field, that is, aligning it with the transition state’s dipole orientation instead of the reactant’s dipole orientation.

$$\mathrm{\Delta }\mathrm{\Delta }{G}^{‡}=-\left|{\overrightarrow{F}}_{\text{env}}\right|(\mid {\overrightarrow{\mu }}_{\text{TS}}\mid -\mid {\overrightarrow{\mu }}_{\mathrm{R}}\mid ),$$ 2

and the reduction in the free energy barrier will be larger for transition states of greater dipole, and for solvents of greater polarity (which generate larger reaction fields). For example, the S_N1 reaction of tert-butylchloride is accelerated in solvents of higher polarity, proceeding 10¹¹ times faster in water relative to benzene (57). Treating the solvents in terms of the difference in their reaction fields (60 MV/cm), Equation 2 implies a value of 5.2 D for (|μ⃗_TS| − |μ⃗_R|), close to its calculated value of 5.52 D.

As a second case, consider a reaction in which a reactant’s dipole reorients but does not change in magnitude upon forming a transition state, of which the [2 + 2] cycloaddition of a ketene is a decent example (Figure 2b). The polar carbonyl group is kept intact by the reaction, but as the carbon to which it is attached goes from sp-hybridization to sp²-hybridization, the carbonyl dipole is reoriented substantially over the reaction course. The rate of this reaction is insensitive to solvent, because however much a solvent reaction field could stabilize the transition state, it would always stabilize the reactant by more (given that the solvent reaction field’s orientation is set by the dipole of the ground state). Indeed, most polar organic reactions exhibit solvent rate effects that are significantly more modest than that for the S_N1 reaction, because typically molecules’ dipoles reorient at the same time that they change magnitude (56). A reaction in which dipoles reorient but do not change magnitude could be catalyzed by an environment that, in effect, anticipates the orientation of the transition state’s dipole and provides an electric field oriented in such a direction (θ_μTS) (Figure 2b) even before the transition state is formed.

To summarize, an environment associated with a large electric field can catalyze reactions with changes in dipole magnitude (Figure 2a), and an environment with a “correctly” oriented electric field can catalyze reactions with changes in dipole orientation (Figure 2b). The first strategy is sometimes referred to as transition state stabilization and the second as reduction of the reorganization energy, though it results in transition state stabilization as well.

These concepts in electrostatic catalysis are not new ideas at all; many of them were originally articulated in the late 1970s by Warshel and Levitt (58, 59), who developed approaches to simulate proteins (now commonly employed by computational biochemists) explicitly to “understand the molecular origins of enzyme catalysis” (60, p. 3,167). Warshel and coworkers (33) went on to apply these methods to a wide panel of enzymes, and their computational evidence has supported the hypothesis that active sites are electrostatically preorganized to specifically stabilize their transition states. In several cases, the catalytic effect arising from these electrostatic considerations has been estimated to account for a preponderance of the measured rate acceleration exhibited by the enzyme (33, 61, 62).

Despite these successes, these computational studies have not been fully accepted, primarily because electrostatic catalysis proved exceedingly difficult to quantify (or even identify) experimentally; this was not helped by repeated assertions that these effects can only be understood through computation (33). In contrast, we argue here that measurements of electric fields inside enzymes provide a path to understand and quantify electrostatic effects in catalysis.

2.4. Approaches to Measuring Protein Electrostatics

How does one measure an electric field (or potential) inside a protein? The first class of such approaches is based on systematic measurements of free energies of chemical processes whose energetics are (believed to be) strongly influenced by electrostatics. Consider, for instance, the acid dissociation constant (expressed as pK_a) of a titratable moiety, such as lysine. The pK_a is influenced by the electric potential at the site of the protonatable amine, as a more negative potential would stabilize the cationic form over the neutral form; therefore, pK_a shifts report on local electric potential. This premise was applied to calibrate Poisson–Boltzmann models for proteins (63) and to probe electrostatics in enzymes (64–68). Shifts in redox potentials (69, 70) or in dissociation constants of charged ligands (71) have also been considered as reporters of local electrostatics at the site of the redox-active moiety/ligand binding site. These free energy–based probes of electrostatics suffer from several limitations, the primary one being that the introduction of a new charge into a protein will reorganize the environment to compensate (solvate) it, introducing new interactions that were not present in the original state. An equilibrium constant gives information only about a process, never about an individual state.

The second class of approaches centers on spectroscopic reporters of the local electric field. This concept has been variously applied to shifts in fluorescence (72, 73), ¹⁹F chemical shifts (74, 75), and ¹³C chemical shifts (76). Spectroscopic probes remedy some of the problems associated with measurements of free energy: On one hand, the measurement is associated with a state (rather than a process), and it need not alter the system (e.g., inserting or removing an extra charge). On the other hand, these probes raise new concerns, the primary one being that factors other than electrostatics can influence spectral shifts. For instance, although electric fields certainly do perturb NMR chemical shifts (77), so also do ring currents and local valence geometry (78). In this context, vibrational probes have recently emerged a more ideal experimental probe of electrostatics (79, 80), as frequency shifts of certain vibrations have been shown to correlate exceptionally well with the local electric field experienced by the vibration (the projection of the local electric field onto the vibrational bond axis). Moreover, vibrational probes can be as small as two atoms, and their sensitivity to electric fields is directional (81). Another feature of vibrational probes is that their frequency’s sensitivity to electric fields can be independently calibrated using vibrational Stark spectroscopy (82, 83).

3. STARK SPECTROSCOPY AND ELECTRIC FIELD MEASUREMENTS

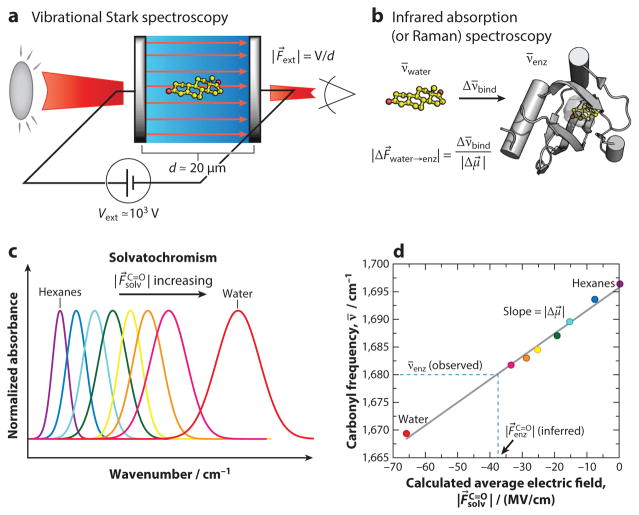
In a typical Stark spectroscopy experiment (Figure 3a), a uniform, homogeneous, external electric field of order approximately 1 MV/cm is applied onto an immobilized molecule of interest, and the resultant effect on the optical (infrared) spectrum is recorded. The molecule of interest can range in size from a small molecule to a large multiprotein complex and can be immobilized by either vit-rification or embedding into a polymer film; the electric field is created by applying a large voltage (1–2 kV) against two slightly displaced (10–20 μm) transparent conductors containing the sample. Experimental details of Stark spectroscopy have been reviewed previously (84, 85). As mentioned above, when electronically (or vibrationally) excited, the dipole moments of molecules change. For optical transitions, the difference dipole, Δμ⃗ = μ⃗_es − μ⃗_gs, is often of the same magnitude as the ground state dipole (84, 86), whereas for vibrational transitions, Δμ⃗ = μ⃗_v=1 − μ⃗_v=0 is typically two orders of magnitude smaller (between 0.03 and 0.12 D) (82, 83 85). Because these two states have different dipoles, they will be (de)stabilized differently by an external field, F⃗_ext. By perturbing the energy levels, an applied field will shift the transition frequency (ν̄, units of cm⁻¹) in a manner that is linear with the difference in the dipole moments of the two states: Δν̄ = −Δμ⃗ · F⃗_ext (53). Detailed analyses of Stark spectra can also tease out the difference polarizability, Δα, of a molecule, as well as the relative orientation between the difference dipole and the transition moment. For vibrational (but typically not electronic) transitions, Δα is typically very small (82, 87, 88).

Figure 3.

Calibrating vibrational frequency (shifts) to (changes in) electric field. (a) In vibrational Stark spectroscopy, an external electric field is applied to a frozen isotropic sample, and the perturbation to the infrared spectrum is recorded. For many carbonyls, the response is linear and the experiment yields the linear Stark tuning rate, |Δμ⃗| (units given in cm⁻¹/(MV/cm); 1 cm⁻¹/(MV/cm) = 0.0595 D). (b) The frequency shift, Δν̄, caused by changing the environment surrounding a carbonyl (e.g., by binding but also by mutation, folding, pH change, etc.) can be translated into differences in the electric field projection along the C=O bond, using the Stark tuning rate as the conversion factor. (c) The size of the electric field a solvent projects onto a carbonyl bond, $\mid {\overrightarrow{F}}_{\text{solv}}^{\mathrm{C}=\mathrm{O}}\mid$, increases for solvents of increasing polarity and is observed as vibrational solvatochromism. (d) As solvent electric fields can be reliably calculated, solvent-induced shifts provide reference data that calibrate vibrational frequency to electric field projected on the vibration, $\mid {\overrightarrow{F}}_{\text{env}}^{\mathrm{C}=\mathrm{O}}\mid$. This allows one to map the vibrational frequency in an enzyme active site to an absolute electric field. Figure adapted with permission from Reference 53, © 2015, American Chemical Society.

In addition to describing the charge configuration of the excited state of a molecule, the difference dipole can also be used to calibrate frequency shifts of a molecule to unknown electric fields, via an “inverted” Stark experiment (Figure 3a,b) (81, 87–89). First, we perform Stark spectroscopy, applying a known external electric field onto a molecule and recording the frequency shift. This calibrates the transition’s sensitivity to electric field (i.e., it measures |Δμ⃗|). Then in a separate experiment, we place that same molecule (now acting as a probe) into a new environment (such as an enzyme) that we seek to characterize and measure the frequency shift caused by that environment. In combination with the difference dipole, this shift measures the change in electric field the molecular probe experiences upon moving from one environment to another (Figure 3b). By further calibrating a vibrational probe with solvent-induced frequency shifts (solvatochromism) (Figure 3c) and using molecular dynamics simulations to calculate the electric fields those solvents project onto the vibrational probe (Figure 3d), vibrational frequencies can be mapped to absolute electric fields (54, 90). As a key validation of this approach, the slopes of these field-frequency plots (Figure 3d) have been close to difference dipoles measured in Stark spectroscopy.

Though conceptually straightforward, the main development that made the “inverted” Stark experiment useful in practice was the transition from employing optical probes to vibrational probes, which was made for four reasons. First, vibrational difference dipoles are miniscule, so vibrational excitation with infrared light minimally perturbs the system. In other words, the recorded frequency shifts report on the electrostatic environment experienced by the ground state (as the excited state will not cause the environment to reorganize in any appreciable way). Second, |Δμ⃗| tends to be insensitive to the probe’s environment (another consequence of small Δα) (54, 91). Third, vibrations can be confined to as few as two atoms (to a good level of approximation), so the experiment provides a more local, higher-resolution description of electric fields (88, 92). Fourth, because Δμ⃗ for many high-frequency vibrational transitions (e.g., C≡N and C =O) is approximately parallel to the internuclear bond axis (82, 83), the direction of a probe’s Δμ⃗ can be determined from the X-ray structure of the probe-bearing protein.

A substantial body of work has focused on the nitrile group (C≡N) because it is a local vibration with a frequency that is easy to distinguish from the complex background of vibrations in proteins, and it has a fairly strong sensitivity to electric fields [|Δμ⃗| = 0.2–0.3 cm⁻¹/(MV/cm)] (92–95). Several approaches have been devised to incorporate nitriles into proteins, either through chemical modification of cysteines (81, 94), solid-phase peptide synthesis (92), amber suppression (96), or exploiting drugs that bear nitrile moieties (88, 97). The nitrile-centered approach proved instrumental to several studies in protein biophysics and has recently been used to directly measure phospholipid membrane dipole fields (98) and probe the physical basis for a tyrosine kinase inhibitor’s selectivity profile (97).

Nitrile probes were shown to behave less predictably in hydrogen-bonding solvents (98)—an effect that can be exploited in some cases (97, 99), though it mandates the implementation of more ad hoc models (100, 101) to interpret their frequency shifts in H-bonding environments in terms of electric fields. As predicted by Choi & Cho (102), carbonyl vibrational probes maintain a simple and linear dependence on electric field even when H-bonded (54), which opened up the types of environments that could reliably be probed with vibrational Stark probes. Naturally, carbonyl groups are often relevant in enzyme mechanisms and their vibrational spectra in enzyme active sites have been reported previously (103–107). In those works, vibrational frequency red-shifts were interpreted to imply that the bond probed is destabilized from strain (mechanically or electrostatically) imposed onto it by the enzyme. In contrast, data from our laboratory accrued over the past few years have supported the view that most vibrational frequency variation (in carbonyls, at least) can be explained through a static electric field–difference dipole effect (53, 91), not by bond weakening or strain (i.e., changes in the force constant) (103, 104). This represents a departure from how vibrational measurements (both infrared and Raman) have traditionally been interpreted in enzymology (105–107), and efforts are ongoing to reinterpret this corpus of biochemical data within this physical framework (108, 109).

4. ELECTRIC FIELDS IN THE KETOSTEROID ISOMERASE ACTIVE SITE

4.1. Ketosteroid Isomerase Is a Model Enzyme for Biophysical Studies of Catalysis

Catalysis by KSI (EC 5.3.3.1) has been the subject of extensive studies since its discovery in 1955 by Talalay & Wang (110), and has also been a focal point for many of our studies on electrostatics. In eukaryotes, KSI is involved in steroid biosynthesis and degradation pathways that transform sterols (such as cholesterol) to the hormonally active class of Δ⁵-3-ketosteroids. KSI activity was originally discovered from an organotrophic strain of the soil bacterium genus Pseudomonas that can utilize steroids as its primary source of carbon (111). The consensus mechanism for KSI, presented in Figure 4a for the substrate 5-androstene-3,17-dione, is a textbook example of enzymatic enolization chemistry, in which a 4β-proton is abstracted by a weak general base (Asp40) to form an enzyme-stabilized dienolate intermediate and then reinserted onto C6, two carbons away (45). This mechanism has been broadly supported by structural, mutational, kinetic, and spectroscopic studies (112–114).

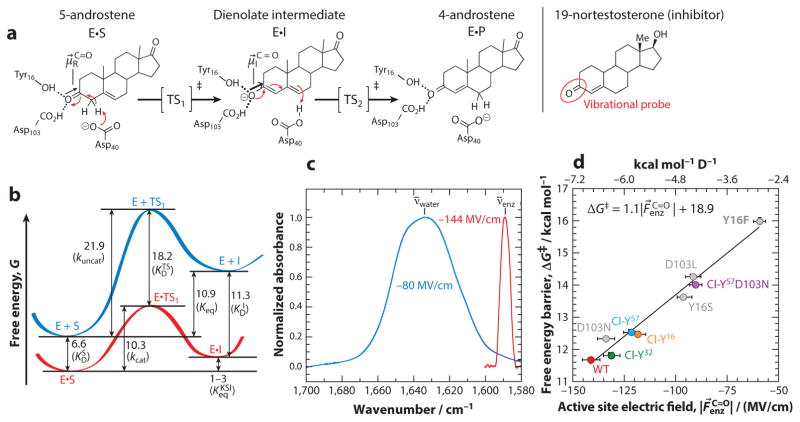
Figure 4.

Mechanism, energetics, and electric field catalysis of ketosteroid isomerase (KSI). (a) The steroid substrate 5-androstene-3,17-dione is converted to the conjugated isomer 4-androstene-3,17-dione via the enolization (first step) and reketonization (second step) of the carbonyl. (b) Reaction coordinate diagram for the enolization of androstene (S) to the dienolate intermediate (I), either in KSI (red) or in solution (blue). Numbers correspond to free energy differences in kcal mol⁻¹ (45, 113, 115). The solution reaction proceeds through a mechanism identical to that of the enzymatic reaction. (c) KSI exerts a very large and homogeneous electric field on 19-nortestosterone’s carbonyl bond relative to water’s reaction field, based on the significant redshift and band narrowing detected in the infrared spectrum (53). (d) Linear correlation between KSI’s catalytic power (expressed as ΔG^‡) and the electric field its active site projects onto the carbonyl of the inhibitor 19-nortestosterone. Represented are mutations of the oxyanion hole residues to other canonical amino acids (gray points) (118) and subtle mutations to noncanonical amino acids (colored points) (119). Abbreviations: TS, transition state; WT, wild type. Figure adapted with permission from References 53 and 119, © 2015, 2016, American Chemical Society.

The challenge KSI surmounts of deprotonating a very weak, carbon-based acid with a rather weak base is widely encountered in biochemistry, for example, in other well-known enzymes like enolase (which deprotonates 2-phosphoglycerate), fumarase (deprotonates malate), and triose phosphate isomerase (deprotonates glyceraldehyde 3-phosphate). On the basis of its unimolecular rate constant, KSI is one of the fastest enzymes known (k_cat ≃ 10⁴–10⁵ s⁻¹), at least for its optimal substrates. Moreover, the isomerization of 5-androstene-3,17-dione can occur in solution through the same mechanism utilized by KSI (115), albeit much more slowly (k_uncat = 6 × 10⁻⁴ M⁻¹ s⁻¹). Hence, KSI meets the prerequisites we laid out in Section 1.2 for a detailed analysis of catalysis. With precise measurements of KSI’s microscopic rate constants, Pollack and coworkers (45) were able to quantify the exact energetics of the reaction, and the magnitude of the KSI’s catalytic effect (Figure 4b). A concentrated effort from several biochemists has focused on moving beyond mechanism to understand the interactions and strategies utilized by the active site to stabilize the dienolate transition state by approximately 18 kcal mol⁻¹ (Figure 4b).

Numerous experiments have highlighted the importance of the general base, Asp40, and its precise positioning with respect to the steroid substrate, which constitutes an important element in KSI catalysis (116, 117). In addition, the active site provides an environment, sometimes called the oxyanion hole, that stabilizes the dienolate-like transition state via H-bonds (46) (Figure 4a). Building on the discussion about electrostatic catalysis in Section 2, we hypothesized that the oxyanion hole, in collaboration with the charges and dipoles on distal residues, works by producing an electric field that stabilizes the dipole that builds on the C =O bond toward the transition state.

4.2. The Carbonyl Vibration as an Intrinsic Stark Probe

By employing the carbonyl bond of the inhibitor 19-nortestosterone as a vibrational probe, we could measure the electric field at a locus of substantial charge rearrangement during KSI’s first (and rate-determining) chemical step (see mechanism in Figure 4a), making it directly relevant for electric field catalysis. We found that wild-type KSI exerts an extremely large average electric field on this carbonyl bond, with a magnitude of 144 ± 6 MV/cm (118) (Figure 4c). It is important to point out that this is an equilibrium measurement, such that this electric field reflects a typical enzyme-substrate conformation, not a rarely sampled substate. In fact, the C =O vibrational band in the enzyme is significantly narrower in the enzyme than in solution (Figure 4c), implying less heterogeneity (variability) in the electric field experienced at this locus, though definitive statements about dynamics will require nonlinear infrared experiments. Returning to the discussion about electrostatic catalysis in Section 2, a large electric field would be expected to have a catalytic effect if the dipole along this C =O bond increases in magnitude upon passage to the transition state. Chemical intuition would suggest as much, which can be quantified from ab initio electronic structure methods (which estimate $\mid {\overrightarrow{\mu }}_{\text{TS}}^{\mathrm{C}=\mathrm{O}}\mid -\mid {\overrightarrow{\mu }}_{\mathrm{R}}^{\mathrm{C}=\mathrm{O}}\mid$ to be 0.7 D).

As one might expect, mutations in residues of KSI’s oxyanion hole (Tyr16, Asp103) that impair catalysis decrease the magnitude of the electric field exerted onto the C =O bond of 19-nortestosterone (118). More importantly, the precise amount of increase to the activation barrier for each mutant formed a strong linear correlation with the extent of electric field decrease for each mutant (Figure 4d). Although linear free energy relationships of this kind are not infrequently obtained using various parameters or empirical solvent scales, it is important to emphasize that the x-axis in Figure 4d has a meaningful physical interpretation and the observed trend is what we would predict from Equation 2, as explained in Figure 2a. Therefore, we can assign an experimental value of 1.1 D to $\mid {\overrightarrow{\mu }}_{\text{TS}}^{\mathrm{C}=\mathrm{O}}\mid -\mid {\overrightarrow{\mu }}_{\mathrm{R}}^{\mathrm{C}=\mathrm{O}}\mid$ and provide support to the hypothesis that the function of the oxyanion hole is to produce a large electric field that stabilizes the increased dipole of the transition state. Using this value, and the experimental value of $\mid {\overrightarrow{F}}_{\text{enz}}^{\mathrm{C}=\mathrm{O}}\mid$ for wild-type KSI, the model in Figure 2a estimates a contribution to ΔΔG^‡ from electric field catalysis of 7.6 kcal mol⁻¹, which is 72% of the total rate acceleration (k_cat/k_uncat = 4 × 10⁷, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{obs}}^{‡}=10.5\text{kcal}{\text{mol}}^{-1}$).

This model predicts that the size of $\mid {\overrightarrow{\mu }}_{\text{TS}}^{\mathrm{C}=\mathrm{O}}\mid -\mid {\overrightarrow{\mu }}_{\mathrm{R}}^{\mathrm{C}=\mathrm{O}}\mid$, which we dubbed the reaction difference dipole, is a measure of a reaction’s sensitivity to electric field catalysis, or in other words, the catalyzability of a given reaction by an enzyme.

4.3. Effect of Subtle Mutations on Electric Fields

In the context of KSI’s precisely constructed active site, the mutations we made to Tyr16 (to Phe and Ser) and Asp103 (to Leu) were fairly large (118), begging the question of whether the electric field decreases perhaps resulted from populating a less catalytically competent binding mode or subtly distorting the active site. Amber suppression and protein semisynthesis enables the installation of more minute mutations than afforded by the 20 canonical proteinogenic amino acids. Studies by Wu & Boxer (119) and Natarajan et al. (120) explored the effect of replacing the critical Tyr16 residue with chlorosubstituted and fluorosubstituted tyrosines, respectively. These mutants perturbed KSI’s rate by up to 1.1-fold (for F) and 3.8-fold (for Cl), showing that KSI has no special need to match its substrate’s pK_a to act as a proficient catalyst. On one hand, these observations are inconsistent with theories that KSI’s catalysis relies on a low-barrier H-bond or concerted proton transfer to lower the energy of the intermediate. On the other hand, they are consistent with the electric field catalysis model in that Tyr16’s O–H dipole contributes substantively to the electric field experienced by the substrate’s C =O as they are in such close proximity, and electron-withdrawing groups subtly lower the size of the O–H dipole (order of dipole magnitude: 3-Cl-Tyr < 3-F-Tyr < 2-F-Tyr < Tyr), thereby reducing the electric field exerted by the oxyanion hole without introducing structural alterations (119). It was found that the trend between electric field and catalytic proficiency, initially detected for conventional mutations, also held for the subtle Cl-Tyr variations (Figure 4d), implying that the electric field magnitude reductions that accompany oxyanion hole mutation derive from reducing the electrostatic strength of critical interactions rather than from structural rearrangements or alterations to substrate-binding mode (119).

5. UNIFYING CONSEQUENCES OF THE ELECTRIC FIELD CATALYSIS MODEL

5.1. Orientational Electric Field Catalysis

In Section 2.3, we introduced two limiting cases of electric field catalysis that were dependent on whether a substrate’s dipole, upon activation, changed in magnitude (Figure 2a) or orientation (Figure 2b). KSI is a paragon of the first category: In the enzyme active site, the substrate’s carbonyl reorients very little upon activation. This explains why the simple model for electric field catalysis that ignored orientation (Equation 2) fit the experimental data (Figure 4d) so well, and why KSI uses an electric field of high magnitude to provide differential stabilization of the transition state.

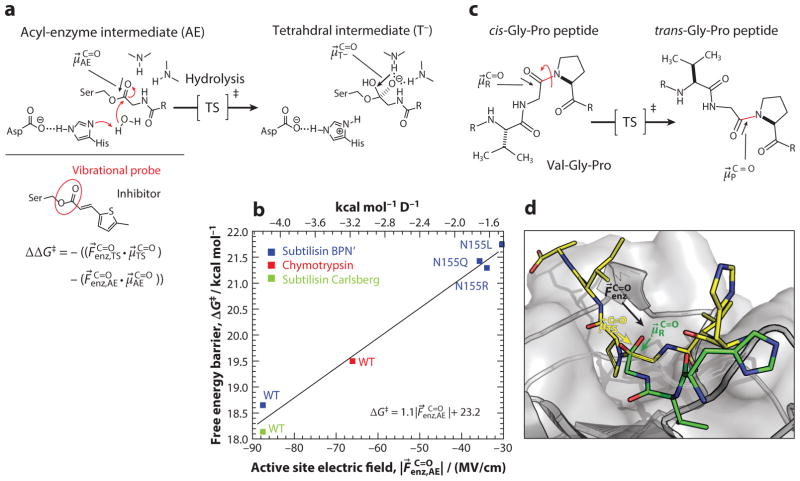
For the serine proteases, the rate-limiting formation of an anionic tetrahedral intermediate involves changes in both dipole magnitude and orientation at C =O (121) (Figure 5a); however, the inhibitor utilized only reports on the enzyme active site field projected on the carbonyl of the ground state (i.e., the acyl-enzyme intermediate). The field-barrier plot (Figure 5b) analogous to that drawn up for KSI (Figure 4d) will therefore not capture the full catalytic effect implied by the more general Equation 1 (108). Hence, experiments are needed that measure the projection of the active site electric field on both the transition state ( $\mid {\overrightarrow{F}}_{\text{enz},\text{TS}}^{\mathrm{C}=\mathrm{O}}\mid$) and ground state ( $\mid {\overrightarrow{F}}_{\text{enz},\text{AE}}^{\mathrm{C}=\mathrm{O}}\mid$) geometries to assign values to both terms in the equation.

Figure 5.

Orientational electric field catalysis in serine proteases and cyclophilin A. (a) The rate-limiting step of serine proteases, in which a water molecule attacks the acyl-enzyme intermediate (AE) to form an anionic tetrahedral intermediate (T⁻). Electric field catalysis depends both on the electric field the active site projects onto the carbonyl in the ground state (AE) and the transition state (TS) geometries, of which the inhibitor captures only the former. (b) Linear correlation between serine proteases’ catalytic power (expressed as ΔG^‡) and the electric fields their active sites project onto the carbonyl of an inhibitor (108). (c) Cyclophilin A rotates the N-terminal portion of the Gly-Pro peptide bond (red). (d) In the transition state, the carbonyl is nearly perpendicular to its orientation in the ground state and the active site electric field is more closely aligned to ${\overrightarrow{\mu }}_{\text{TS}}^{\mathrm{C}=\mathrm{O}}$ than to ${\overrightarrow{\mu }}_{\mathrm{R}}^{\mathrm{C}=\mathrm{O}}$. Abbreviation: WT, wild type. Figure adapted with permission from Reference 108, © 2016, American Chemical Society.

Cyclophilin A, a peptidyl-prolyl isomerase (122), provides an instructive example of orientational electric field catalysis. This enzyme catalyzes the cis–trans isomerization of the proline imide peptide bond in a single chemical step (Figure 5c) through a transition state that brings the carbonyl perpendicular to the peptide plane, thereby reorienting this dipole by nearly 90° (123) (Figure 5d). The enzyme preferentially stabilizes the transition state by exerting an electric field with the appropriate direction; that is, the projection of ${\overrightarrow{F}}_{\text{enz}}^{\mathrm{C}=\mathrm{O}}$ is large on ${\overrightarrow{\mu }}_{\text{TS}}^{\mathrm{C}=\mathrm{O}}$ but small on ${\overrightarrow{\mu }}_{\mathrm{R}}^{\mathrm{C}=\mathrm{O}}$ (124) (Figure 2b). Using a typical value (3.5 D) for a peptide carbonyl dipole and a calculated estimate for the electric field magnitude along ${\overrightarrow{\mu }}_{\text{TS}}^{\mathrm{C}=\mathrm{O}}$ of 50 MV/cm (124), the model in Figure 2b estimates a contribution to ΔΔG^‡ from electric field catalysis of 8.4 kcal mol⁻¹, or 92% of the total rate acceleration (k_cat/k_uncat = 5 × 10⁶; $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{obs}}^{‡}=9.1\text{kcal}{\text{mol}}^{-1}$).

5.2. Electric Field Catalysis in Other Enzymes

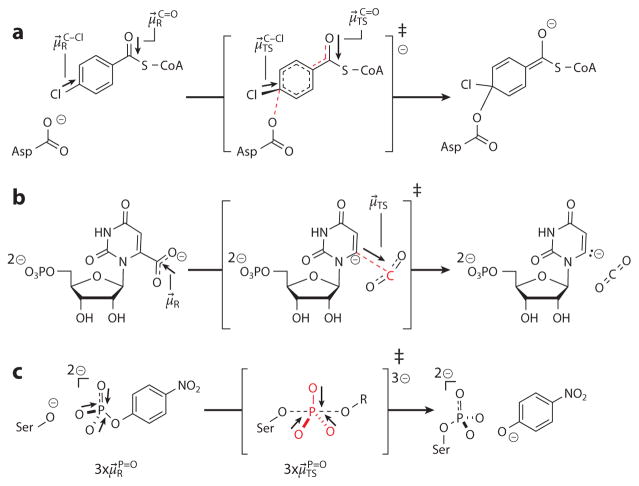
As of this writing, the analysis described for KSI has been extended to 4-chlorobenzoyl-CoA dehalogenase and a serine protease (108). 4-Chlorobenzoyl-CoA dehalogenase activates its substrate through a nucleophilic attack on the C4 position of the benzoyl ring (Figure 6a), forming a Meisenheimer intermediate in the presumed rate-limiting step (125, 126). It is instructive that, qualitatively, a larger charge displacement occurs in its rate-determining step than in KSI’s, and consequently the slope of ΔG^‡ versus $\mid {\overrightarrow{F}}_{\text{enz}}^{\mathrm{C}=\mathrm{O}}\mid$ (2.1 D) is greater (108). This supports the idea that the slopes of these linear free energy relationships report on the substrate’s change in dipole that accompanies activation to the transition state. As with KSI, the dehalogenase’s rate-determining step produces a charged carbonyl, supported by an oxyanion hole, which contributes to a large overall active site electric field. However, for dehalogenase, the primary H-bond donors come from backbone amides rather than acidic side chains (as in KSI). This observation demonstrates that large electric fields need only enzyme dipoles to be precisely oriented and closely positioned with respect to the substrate; their chemical identity is less important, and in fact, they can even be ordered water molecules (118). Hence, electric field catalysis is diverse at the chemical level, but its sine qua non is precise positioning and organization. Via computational studies, Glu232(B) has also been attributed to play an important role via electrostatic catalysis, but this residue is quite far away from the substrate’s carbonyl (127). Here, it is important to point out that the electrostatic changes that accompany activation (Figure 6a) are not limited to the carbonyl moiety but also include the reorienting of the C–Cl bond and the charge attenuation of the nucleophile. All of these sites may be viewed as handles for electrostatic catalysis in which the enzyme’s environment provides a field more stabilizing for the transition state’s charge configuration than for the ground state’s.

Figure 6.

Mechanisms of rate-limiting steps of (a) 4-chlorobenzoyl-CoA dehalogenase catalysis, (b) orotidine monophosphate decarboxylase catalysis, and (c) alkaline phosphatase catalysis. In each mechanism, bonds broken/formed in the transition state are highlighted (red), as are sites whose dipole moments change in the transition state (arrows).

Catalysis of the serine proteases has been discussed extensively (121), typically with the greatest weight given to the catalytic triad (Asp, His, Ser) (128, 129), which helps prepare the nucleophilic serine for attack, and a secondary effect from oxyanion hole stabilization (32, 130). Although the data in Figure 5b show that oxyanion hole catalysis is well described by an electric field effect, the physical nature of the catalytic triad has been explained in various ways. The conserved juxtaposition of an aspartic acid and histidine relative to the serine nucleophile (Figure 5a) has been described as activating the serine nucleophile by (a) concerted proton transfer (129), (b) low-barrier H-bonds (29), or (c) alteration of its effective pK_a (121). Calculations carried out by Warshel and coworkers (33, 131) showed that the first two explanations are not energetically plausible and the third is consistent with an electric field effect. Because serine’s O–H bond is not as convenient a vibrational probe as a carbonyl is, this claim would be more difficult to assess experimentally. Nevertheless, it is important to note that an enzyme’s nucleophile can serve as a handle for electrostatic catalysis equally as well as the substrate itself.

5.3. Proficiency or Catalyzability?

Earlier we introduced the concept of catalyzability to express the idea that reactions that involve large alterations in the electrostatic character of their substrates are in some sense easier reactions for enzymes to catalyze. The charge rearrangement in KSI’s rate-determining step is quite small (between 0.7 and 1.1 D) and involves little reorientation, which may well explain why its active site utilizes such a large electric field to differentially stabilize its reaction’s transition state. Enzymes famous for their astronomical rate accelerations, such as alkylsulfatases (12), phosphatases (13), and decarboxylases (14), have been previously deemed extremely proficient enzymes. Alternatively, it is possible that these particular chemical reactions are more catalyzable than other reactions because they involve larger charge rearrangements.

The mechanism of orotidine monophosphate decarboxylase features a step in which a full charge on a carboxylate group is translocated across 2.4 Å to form a carbanion on the C6 of the pyrimidine ring (132) (Figure 6b). This nominally corresponds to a dipole change of 11 D, which is significantly larger than the charge perturbation that accompanies KSI’s chemical transformation.

As a second case, the structure of the transition state of alkaline phosphatase (AP) is a pentavalent phosphoryl species with three nonbridging oxygen atoms (133) (Figure 6c). Along each P–O bond, bond lengths and charge separations increase somewhat upon passage from the ground state to the transition state (134). This gives AP three “sites” at which to perform electric field catalysis. If each P–O bond had a reaction difference dipole of 1 D and experienced an electric field in the AP active site similar to that of KSI, the predicted contribution of electric field catalysis would be 22.8 kcal mol⁻¹ (N.B.: $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{elec},\text{KSI}}^{‡}=7.6\text{kcal}{\text{mol}}^{-1}$), which is quite close to the observed catalytic power of AP (k_cat/k_uncat = 1 × 10¹⁹; $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{obs}}^{‡}=25.9\text{kcal}{\text{mol}}^{-1}$).

5.4. The Chemical Space of Enzymology

The central importance of electrostatic catalysis in enzymology could explain biases in the chemical reaction space utilized by nature. For instance, the dearth of Diels–Alderases in biology has perplexed many chemists who wonder how such a synthetically useful reaction could get passed over (135–137). This concerted pericyclic reaction, however, has little charge rearrangement in the transition state because bonds are broken and formed almost simultaneously and as such is a poorer candidate for electrostatic catalysis (56). If electrostatic catalysis is an essential strategy for many enzymes, it would explain this conspicuous absence, and why the catalytic power of an artificial Diels–Alderase evolved to perform the reaction is so modest and best explained by a simple proximity effect (138).

In the Mechanism, Annotation, and Classification in Enzymes (MACiE) database, the majority of bond-breaking events compiled are heterolytic, and the functional role most commonly assigned to a catalytic residue is electrostatic stabilization (139, 140). Although redox-active metals like Fe^2+/3+/4+, Co^2+/3+, and Cu^+/2+ play central roles in the mechanistically rich world of oxidoreductases, for the majority of enzymes in the Metal-MACiE database, the metals utilized are non-redox-active cations (Zn²⁺, Mg²⁺, Mn²⁺) that act to make functional groups more elec-trophilic or more acidic or otherwise stabilize charged intermediates/transition states (141). In other words, a major role of metals in biochemistry is probably the exertion of electric fields onto substrates at specific sites rather than electron transfer or covalent catalysis, though those roles are certainly important in many enzymes.

5.5. Electrostatic Catalysis and Catalytic Promiscuity

A further implication of the electrostatic catalysis model is a rationale for the pervasiveness of promiscuous activities by enzymes (142, 143). The realization that enzymes can catalyze multiple reactions has become increasingly accepted, but this begs the question, what’s the underlying physical framework? To begin with, it is not overtly consistent with the paradigmatic view that enzymes specifically stabilize a reaction’s transition state, because different reactions’ transition states will have different structures. One explanation commonly offered is that promiscuous enzymes are more dynamic, and different conformations are responsible for different activities (143). However, the electrostatic catalysis model provides an alternative solution without invoking extra conformations: If a primary consideration is the transition state’s dipole moment, we might hypothesize that an enzyme could catalyze the subset of reactions whose transition states possess similarly oriented dipoles (and, of course, are accommodated sterically by the active site).

One of the best case studies for enzyme promiscuity is AP, which in addition to its primary function of hydrolyzing phosphate monoesters, possesses sulfatase activity (134, 144). The structure and charge pattern of the transition states for these two reactions are nearly identical (Figure 6c), but the magnitude of the charge on each of the three nonbridging oxygen atoms is approximately half that of an analogous phosphate. Assuming that this twofold reduction in dipole along the S–O bonds is also true for the transition state, the simple model ΔΔG^‡ = −|F⃗_enz|(|μ⃗_TS| − |μ⃗_R|) predicts that the electrostatic rate enhancement AP provides to sulfate monoester hydrolysis would be half that for phosphate monoester hydrolysis. This prediction is strikingly consistent with experiment ( $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{obs}}^{‡}=11.6\text{kcal}{\text{mol}}^{-1}$).

5.6. How Do Enzymes Create Large, Oriented Electric Fields?

This question is critical to address, or else we risk passing the buck on the mystery of how enzymes work to a new mystery of how active sites generate the appropriate electric field to catalyze a reaction! We offer two answers.

5.6.1. Electrostatic preorganization

Enzymes have evolved protein structures that organize the dipoles and charges into an idiosyncratic pattern that can maximize or specifically orient the electric field they exert onto particular regions of their bound substrates (33, 58–60). This effect is called electrostatic preorganization.

Whereas a solvent’s electric field is set by the solute’s charge configuration and invariably stabilizes the solute’s ground state, a preorganized enzyme active site can create an electric field with a particular orientation with respect to its substrate because the enzyme’s field is controlled by the protein’s folded structure, not by the dipole(s) of its substrate (as in a solvent reaction field). This highlights the difference between a field created by preorganization versus reorganization.

Moreover, a solvent cannot maximize the electric field it exerts onto a specific region of a solute, because thermodynamics requires that the total energy of the system be minimized. Invariably, this compromise requires some solvent molecules to adopt configurations that favor solvent-solvent interactions or interactions with distal regions of the solute. To exert a large electric field onto a specific region of a substrate, a preorganized active site can organize its dipoles and charges in such a way that optimizes a particular electrostatic interaction but not the total electrostatic energy, because this energy deficit can be offset by other interactions that stabilize the protein (e.g., hydrophobic assembly) (60). In other words, the energy stored in the active site electric field is necessarily an energy cost that must be balanced by a network of interactions that stabilize the protein structure.

These considerations could explain the type of observations, initially made by Shoichet and coworkers (145) on lysozyme, that mutations that dramatically stabilize lysozyme also lower its catalytic efficacy (146). We hypothesize that these activity-stability trade-offs would lower the active site electric field, an effect that is testable with the methods described here. Furthermore, the need for the active site electric field’s energetic cost to be compensated to meet the stability requirements for a protein could explain why enzymes tend to be rather large proteins, much exceeding the dimensions of the active site region itself (33, 147), and why it has proved so difficult to create small-molecule catalysts with proficiencies approaching those of enzymes.

5.6.2. Distal binding interactions

Electrostatic preorganization enables enzymes to generate a specific electric field in their active site, but how do substrates get correctly positioned within that field? This is achieved by binding substrates in a specific way. To take KSI as an example, the electric field has a strong local component arising from two residues in the oxyanion hole (148). These critical electrostatic interactions have been accentuated by proximity; that is, the substrate’s carbonyl group approaches the O–H dipoles of Tyr16 and Asp103 with O ··· O distances as short as 2.4–2.6 Å (149). Such small distances can greatly increase the electric field experienced by the substrate carbonyl due to the 1/r³-dependence for the field due to a dipole. Close packing of essential catalytic groups to reactive parts of the substrate is commonly observed in X-ray structures of enzyme-substrate complexes, suggesting that proximity is a commonly used strategy enzymes may use to exert a large field onto a specific region of a substrate [though other enzymes may achieve the same end by combining many distal electrostatic interactions (148)].

From an energetic perspective, these close O ··· O distances seldom occur in solution, because they reflect a regime in which van der Waals repulsion exceeds electrostatic attraction. As such, it is not immediately obvious how this catalytically competent state is stabilized, allowing KSI to form it and maintain it for significant periods of time. One possible explanation comes from considering distal binding interactions: The binding interactions between the enzyme and nonre-active regions of the substrate compensate for the van der Waals penalty at the reactive carbonyl accompanying the formation of the catalytically competent state. This hypothesis is consistent with the widespread observation that truncated substrates are often much poorer substrates for enzymes (23–25), including for KSI itself (26).

Cyclophilin A orients its active site electric field to have a large projection along its substrate’s transition state dipole (124); hence, this field will necessarily stabilize the C =O dipole in the ground state form less than water’s reaction field does (Figures 2b and 5c). This would introduce a destabilizing term during binding that would have to be offset by other favorable binding interactions involving the nonreactive portions of the substrate.

Our discussion here amounts to an alternative formulation of the Circe effect (22), whereby distal binding interactions (e.g., to anchoring groups or substrate handles) are not utilized to destabilize a substrate as such but rather to facilitate its positioning into an electric field, either large or oriented, in the active site. In the case of KSI, this positioning requires a few repulsive van der Waals interactions, and in the case of cyclophilin A, it requires the reactive carbonyl in the ground state to experience a lower electric field than it does in solution.

Typically, these aspects of enzyme catalysis have gone under the headings of GSD, desolvation, or distortion, which have been used to describe the mode of action of several different enzymes (121–123, 127, 132). In our view, electric field catalysis provides a context for why enzymes sometimes need to destabilize certain portions of their substrate relative to solution: The electric field at a particular site that is optimal for transition state stabilization may not be optimal for substrate stabilization, especially if the reaction proceeds with a large geometric change at that site. If the attendant loss in stabilization is great enough to render the binding energy of the substrate less than the substrate’s solvation energy, distal binding interactions are necessary to compensate for and enable proper binding of the substrate.

6. CONNECTING ELECTRIC FIELD CATALYSIS TO OTHER PROPOSALS

6.1. Catalysis by Positioning

Differentiating between electrostatic catalysis and catalysis by positioning can be conceptually subtle, as the electric field inside an active site is nothing but the superposition of the electric field contributions arising from all the charges from the atoms in the enzyme, positioned (preorganized) in a specific way due to the structure of the protein. In this most general sense, electrostatic catalysis is catalysis by positioning. Nevertheless, electric field effects can be separated from the rate enhancement that derives from positioning reactive sites on the substrate(s) adjacent to the groups on the enzyme (or other substrates) that must react with it, which we refer to as chemical positioning (118). For KSI, this corresponds to the amenable location of Asp40 to approach and abstract the steroid’s 4β-proton. To effect this separation, one delineates the molecular regions that undergo changes in covalent bonds during a chemical reaction as a group; chemical positioning effects derive from the arrangement of molecules in this subsystem. This “chemically active” system then interacts with the electric field created by all the other atoms.

It is noteworthy that Lamba et al. (116) used chemical rescue experiments to estimate the rate acceleration derived from the positioning of Asp40 (10²- to 10³-fold), which we had qualitatively predicted (150), because in combination with the contribution we assign to electric field catalysis (10⁵-fold) (118), the two now account for the totality of KSI’s rate enhancement (k_cat/k_uncat = 10^7.5). These weights assigned to chemical positioning and electric field catalysis are also consistent with mutational studies that monitored the loss in catalysis following mutations that misposition the base or remove the oxyanion hole (117, 151, 161). The rate acceleration associated with K_M (80 μM, or 10⁴-fold using a 1 M reference concentration) is best explained in terms of substrate binding and the attendant reduction in translational entropy.

Because cyclophilin A catalyzes a unimolecular reaction, there is no opportunity for catalysis by chemical positioning (Figure 5c). Hence, electric field catalysis accounts for nearly the entire catalytic effect of this enzyme.

Revisiting Marcus’s treatment of the Fe²⁺/Fe³⁺ self-exchange reaction (Figure 1c), the two iron atoms are assumed to be close together, a necessary condition regardless of solvent organization. The two requirements for the reaction—proximity and solvent reorganization—are separable because they correspond to two orthogonal coordinates of the system, the Fe–Fe distance and q. The catalytic strategies of chemical positioning and electrostatic catalysis increase the probability each requirement is met, and in tandem, drastically increase the joint probability that both requirements are met.

6.2. Catalysis by Geometric Discrimination

Geometric discrimination is the notion that the structures of active site pockets are spatially organized to optimize transition state interactions over substrate interactions (31, 32, 152, 153). An enzyme achieves this, for example, by constraining the substrate’s position with respect to H-bond donors, such that those H-bonds are only efficiently accepted when the substrate is perturbed to a transition state geometry (e.g., Figure 5a). This type of catalysis can be understood as electric field catalysis once orientation has been taken into account. In the scenario just mentioned, the electric field generated by the H-bond donors is oriented in such a way to have a greater projection on the H-bond acceptor’s dipole moment when it is in the transition state. The clear advantage of the electric field formalism in describing this effect is that it combines the contributions from distal sites more remote from the active site, not just the first shell H-bond donors, which may also contribute to the angular preference. The vectorial nature of electric fields (as well as their steep distance dependence at close range) provides the means to differentially stabilize a transition state by exploiting geometric changes that accompany its formation.

6.3. Enzyme Dynamics in Light of the Electric Field Model

A large body of research has come together in the previous decade on conformation dynamics in enzymes, and their possible importance for catalysis, and these topics have been widely discussed and reviewed (e.g., 154–157). Although electrostatic and dynamic hypotheses have been pitted against each other as competing theories (156, 157), we see room for cohesion between the two. Electric field catalysis works best, prima facie, in a static environment in which enzyme residues hold still in their proper places to exert a large and correctly oriented electric field. This seems to be an appropriate description of KSI, suggested by the simplest interpretation of the narrow linewidth observed for 19-nortestosterone (118) (Figure 4c) and ultrafast spectroscopy (158), and probably contributes to its catalytic power because barrier crossing takes a finite amount of time and could be prematurely aborted if the environment’s field fluctuates away too quickly (154), an effect that undoubtedly contributes to water’s ineffectiveness in electrostatic catalysis.

In this regard, however, KSI should be considered as a limiting case as the nature of its binding mode requires practically no internal movements within the protein, and the chemical mechanism requires no internal movements other than swiveling of Asp40 to reinsert the C4 proton onto C6. In other words, KSI catalysis involves very little protein dynamics because it does not need to. In KSI, evolution found a structure that is simultaneously proficient at binding steroids, isomerizing them via two chemical steps, and then letting them go.

Because the structural requirements for a large electric field are stringent, it should not surprise us that few enzymes are capable of performing these disparate tasks with one structural form, and that they have been selected for the ability to toggle between multiple states that perform various functions in a catalytic cycle. This model seems to be a satisfactory description for dihydrofolate reductase (DHFR), which is known to undergo fairly large conformational changes (159); such changes are necessary to cycle through various substrates and position them appropriately, but these conformational changes are decoupled from hydride transfer, which occurs in a conformation with a moderately large electric field oriented favorably along the hydride donor-acceptor vector (94, 160). In DHFR, evolution found a protein sequence that is proficient at toggling through these several conformations to perform substrate binding, hydride transfer, and product release. However, this multifaceted solution comes at the price of much more time spent undergoing conformational changes than occupying catalytically competent substates (154), resulting in an overall rate more modest than KSI’s.

7. CONCLUDING REMARKS

By correctly understanding vibrational frequency shifts in terms of Stark effects, a powerful tool is available that can measure the electrostatic interactions in enzyme active sites critical for catalysis. The past few years have seen early examples of vibrational Stark effects applied in this manner, supporting the notion that electrostatic catalysis is a key strategy enzymes use. Appreciating the centrality of electrostatic catalysis has enabled us to incorporate disparate concepts, such as geometric discrimination and distal binding interactions, into a unified framework that we hope will be both instructive to mechanistic enzymologists and useful to researchers tackling current challenges such as enzyme design.

SUMMARY POINTS.

1. Noncovalent interactions between a given molecule and its environment (including H-bonds) can be expressed and quantified in terms of the electric field the environment exerts on the molecule.

2. The electric field created by an environment can be experimentally measured through the vibrational Stark effect, which maps the frequencies of vibrational probes to the electric field experienced by that vibration.

3. A chemical reaction can be catalyzed by an electric field if the reactant’s charge configu-ration (dipole moment) changes upon passing to a transition state. If the dipole moment increases (decreases) in magnitude, an electric field of greater (smaller) magnitude will accelerate the reaction; if the dipole reorients, an electric field aligned with the transition state’s dipole orientation will accelerate the reaction.

4. Electrostatic catalysis is pervasive in enzymology because most chemical reactions in biology involve charge rearrangements.

FUTURE ISSUES.

1. Electric field catalysis has been characterized for a few model enzymes but needs to be examined for enzymes with richer, more complex mechanisms and chemistries and those with multisite charge rearrangements.

2. The many simplifying assumptions that go into formulating our model of electric field catalysis need to be tested with further simulation and experiment.

3. Whether the application of the electric field catalysis model can be applied to forward rational design of artificial enzymes remains to be seen.

4. The hypothesis that electric field catalysis has biased the course of biochemical evolution (to favor reactions with larger charge rearrangements) would be interesting to test through a more extensive bio- and chemoinformatic analysis.

Glossary

Electric field

total interaction energy a test dipole experiences at a given point in space due to charges, dipoles, and induced dipoles of all other atoms in the system

Electrostatics

a description of interactions between molecules due to their permanent charges and dipoles; can specifically exclude polarization (induced dipoles)

Electric field catalysis

a catalytic strategy that involves placing a reacting molecule in an environment that stabilizes the transition state’s dipole moment by more than the ground state’s through electric fields

Electric potential

total interaction energy a test charge experiences at a given point in space due to the charges, dipoles, and induced dipoles of all other atoms in the system

Electrostatic preorganization

the placement and orienting of charges and dipoles in a specific pattern; the main way enzymes can create large, correctly oriented electric fields

Chemical positioning

a catalytic strategy that involves placing reactive groups in close proximity and correct orientations