Modeling gold nanoparticle-eluting spacer degradation during brachytherapy application with in situ dose painting

Abstract

Objective:

To investigate the dosimetric impact of slow vs burst release of gold nanoparticles (GNPs) from biodegradable brachytherapy spacers loaded with GNPs, which has been proposed to increase therapeutic efficacy during brachytherapy application with in situ dose painting.

Methods:

Mathematical models were developed based on experimental data to study the release of GNPs from a spacer designed with poly(lactic-co-glycolic acid) polymer. The models addressed diffusion controlled-release process and poly(lactic-co-glycolic acid) degradation kinetics that were used to determine GNP concentration profiles in tumour and the corresponding dose enhancement.

Results:

The results show a significant delay of GNP diffusion in the tumour in comparison to burst release assumed in previous studies. The model for diffusion controlled-release process and the model for combined processes of both diffusion and polymer degradation indicated that it may take about 25 and 45 days, respectively, for all GNPs to release from the spacer. Based on tumour concentration profiles, a significant dose enhancement factor (>2) could be attained at a tumour distance of 5 mm from a spacer loaded with 2-, 5- and 10-nm GNP sizes.

Conclusion:

The results highlight the need to account for the slow release of GNPs from spacers and polymer biodegradation in research development of the GNP-eluting spacers. The findings suggest the use of radioisotopes with longer half-lives, such as iodine-125, in comparison with others with shorter half-lives such as Pd-103 and Cs-131.

Advances in knowledge:

The study provides a scientific platform and basis for research development of GNP-eluting spacers that can be used during brachytherapy to boost dose to tumour subvolumes, towards enhancing therapeutic efficacy. It concludes that the use of iodine-125 would be more feasible.

INTRODUCTION

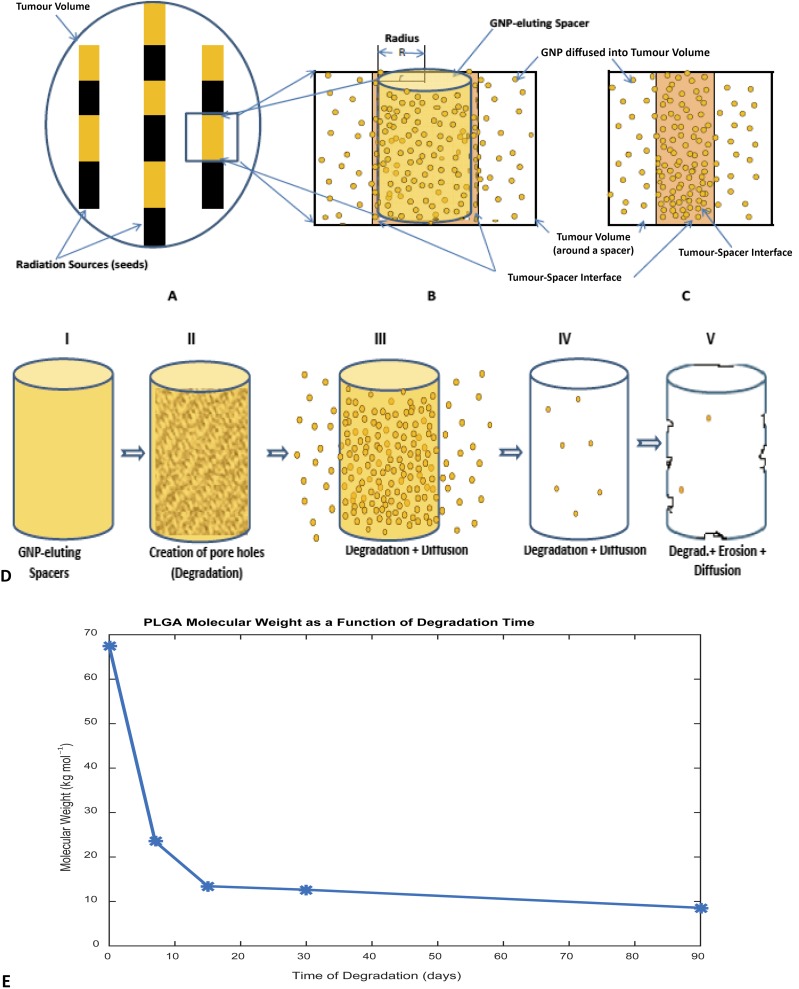
Brachytherapy is one of the therapeutic modalities for localized prostate cancers, among others, using radioisotopes (brachytherapy seeds).^1–5 The treatment of cancers (e.g. early-stage prostate cancers) with brachytherapy seeds such as with caesium-131 (Cs-131) of half-life 9.7 days, with iodine-125 (I-125) of half-life of 59.4 days or with palladium-103 (Pd-103) of half-life 17.0 days as a monotherapy have merits such as cost-effectiveness, patient convenience and low morbidity.^1–3 However, there is a probability of cancer recurrence which may be due to suboptimal dose from the implanted seeds or the quality of the implant.^1,4–6 To address the cancer recurrence and to enhance therapeutic efficacy, researchers have proposed the use of drug-eluting brachytherapy spacers eluting anticancer agents [such as gold nanoparticles (GNPs) or other tumour radiosensitizers] for in-situ dose painting (Figure 1).^3,7–9 Such eluting spacers are meant to replace the traditional inert spacers that have no additional function besides geometric accuracy.^3,7–11 The recent work by Ngwa et al^12,13 and others have broadened the potential of such an approach to incorporate other anti-cancer payloads such as GNPs, immunoadjuvants, silica nanoparticles and radioprotectants such as cerium oxide.^3,11 One approach considered is to incorporate the payload (e.g. GNPs) in poly(lactic-co-glycolic acid) (PLGA) polymer, then coating the traditional spacers with the mixture.^3,7,8 Another approach is to fabricate the whole spacer from the polymer–preload mixture.¹¹ Such next generation (smart) spacers can then be programmed to elute/deliver their payload directly into the tumour subvolume post implantation as the polymer degrades.

Figure 1.

Schematic diagram for the tumour volume (prostate) showing the location of brachytherapy sources (radiation sources) and gold nanoparticles (GNP)-eluting spacers, as well as poly(lactic-co-glycolic acid) (PLGA) polymer degradation process: (a) tumour volume; (b) a single GNP-eluting spacer, releasing GNP into spacer–tumour interface before transporting/diffusing into the tumour cells/region; (c) assumed burst release into spacer–tumour interface (Sinha et al³ assumption); (d) PLGA degradation and GNP diffusion process (I—Spacer, II—creation of pore hole after fluid/water enters, III—diffusion via pore holes, IV—degradation and diffusion continue, and V—degradation resulting in erosion while GNP diffuses); and (e) a graph showing decreasing molecular weight during the degradation process for 90 days.

The capability of these smart spacers to provide the needed radiosensitizing may depend on the amount of agent loaded into the spacer or coated with, the type of polymer used, the number of spacers used and the tumour microenvironmental condition of the implant.^3,9,13 Polymers such as PLGA have been used in many applications in drug delivery systems due to their biodegradability and compatibility.^14–16 One of the advantages of the PLGA is the absorption of the degraded byproducts by the body, eliminating the need for post-implantation surgery for removal of leftovers.⁶

However, the current mathematical models for these smart spacers only account for diffusion of the released radiosensitizers into tumour cells, assuming a burst release from the spacers after implantation at the tumour site, without accounting for the release mechanisms from the spacers from the time of implantation until the release of the preload from the spacer.^3,8 Nevertheless, researchers have shown that release of preload from polymer matrix such as smart spacers may take a significant amount of time before the initial burst may occur or all the agents are released.^7,17–20 For instance, Nagesha et al⁷ demonstrated that a release of radiosensitizers from polymer-coated fiducials occurred for over 4 weeks. Engineer et al²¹ reported 60–70% burst release of paclitaxel from stent within the first week (7 days) after incubation and release of residual drug within 90 days, whereas Alexis et al²² recorded initial burst release about 10–20% with 17 days in a similar study. Steele et al²³ also reported a drug release of 10–60% within 14 days and 10–90% drug release in 20 days, respectively, from PLGA 53/47 thin films subject to different PLGA/PLGA preparation and the acidic terminal functional groups concentration. These studies imply that there may be no payload (drug/GNP) present at the spacer–tumour interface immediately after implantation. Also there is a significant time (days or weeks) interval before all the payload may be released from the spacer into the spacer–tumour interface while diffusing the released GNPs into tumour cells concurrently. Therefore, the assumptions made by previous studies^3,8 may overestimate the payload diffusion into tumour volume leading to less radiosensitization of tumour cells and resulting in suboptimal therapeutic efficacy. It may also lead to incorporating less payload content in the spacers during fabrication, which may undermine the manufacturing of these smart spacers as well as clinical applications.

Besides, the previous studies also did not account for factors such as polymer degradation or erosion phenomenon.^3,8 A study reported by Alexis et al²² shows that drug release from polymeric matrix is governed by a combined process of diffusion and polymer degradation, whereas Chiu et al²⁴ and Lao et al²⁵ reported independently that drug release was a combination of both diffusion- and degradation-controlled mechanisms, proving the fact that diffusion of drug depends on polymer degradation.²¹ Polymer degradation refers to bond cleavage (enzymatic or hydrolytic cleavage leading to scission of the polymer backbone) and is a chemical process resulting in pores/holes in the matrix (Figure 1d), resulting in a decrease in molecular weight (Figure 1e), whereas polymer erosion (surface or bulk erosion) refers to depletion of the polymeric matrix, which is a physical processes, depending on other processes including morphological changes, degradation, dissolution and diffusion of oligomers and monomers, and swelling of the polymer matrix.^18,26–30

To advance the research development and application of the proposed eluting spacers, it is therefore imperative to take into account the polymer–GNP spacer degradation, the slow and initial burst release of GNPs embedded in the smart spacers in relation to the decaying process of the brachytherapy seed implants. Herein, we developed mathematical models for smart spacers to investigate the dosimetric impact of slow vs burst release of GNPs from biodegradable smart spacers eluting GNPs during brachytherapy application with in situ dose painting. The models addressed diffusion controlled-release process and PLGA degradation kinetics that were used to determine GNP concentration profiles in tumours and the corresponding dose enhancement.

The results obtained were compared with those of Sinha et al,³ which assumed a burst release of 7 mg g⁻¹ concentration of 10-nm GNPs from a spacer into the spacer–tumour interface (Figure 1c), diffused into the tumour for cells sensitization, based on experimental determined diffusion coefficient for 10-nm nanoparticles obtained by Wong et al.³¹ In the study, a dose enhancement factor (DEF) for each tumour voxel was analytically calculated using the dose-painting-by-numbers approach over time (for brachytherapy sources: I-125, Pd-103 and Cs-131) and for other GNP sizes apart from 10 nm. However, in this work, DEF for only I-125 would be considered because of the prolonged release time of the GNPs from the spacers, but Pd-103 and Cs-131 were not examined due to their short half-lives, which has been emphasized by Sinha et al.³

METHODS AND MATERIALS

Mathematical models for the GNPs released from spacer were developed based on diffusion controlled-release mechanism and degradation kinetics of the PLGA polymers taking into account the experimental data reported by Engineer et al,²¹ in which 50/50 PLGA was combined with paclitaxel drug and the mixture was spray-coated on cardiovascular stents. The PLGA molecular weight reportedly decreased from 67,416 to 23,470 g mol⁻¹ in 7 days, to 13,426 g mol⁻¹ in 15 days, to 12,632 g mol⁻¹ in 30 days and to 8562 g mol⁻¹ in 90 days, respectively.²¹ An in vivo pre-determined tumour diffusion coefficient (D_T = 2.2 × 10⁻⁸ cm² s⁻¹) for 10-nm nanoparticles of concentration 7 mg g⁻¹ was used based on Wong et al³¹ and Sinha et al,³ respectively. Diffusion coefficients for other nanoparticles were estimated using the Stoke–Einstein equation; and a MATLAB^® (MathWorks^®, Natick, MA) R2015a (Student use) was used for calculations. Figure 1 illustrates brachytherapy seeds and GNP-eluting spacer in a tumour volume (prostate).

Model of a gold nanoparticle-eluting spacer based on diffusion controlled-release process

A radial diffusion equation for a cylinder was assumed for a spacer (PLGA-GNP matrix) of radius R (R = 0.5 mm, from Cormack et al⁸) and height H = 5 mm with the surface concentration C equal to zero (C = 0). Radial diffusion was assumed since the ends of the spacers were practically placed between two seeds. The average concentration of the GNPs remaining in the spacer at any time t, with the boundary conditions: C = 0 at r = R, for all times t; and C = C_i for R < r < 0 at t = 0 is given by:³²

$$C_{\text{Avg}}\left(t\right)=\frac{4C_i}{R^2}\ast {\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\alpha }_n^2}\ast \exp \left(-{\alpha }_n^{2}Dt\right)}$$ (1)

where C_Avg is the average concentration of the GNPs in the spacer at time t, r is the radial distance (0 ≤ r ≤ R), C_i = C (t = 0) is the initial GNP concentration which is distributed uniformly in the spacer (matrix), α_n are roots of the Bessel function of the first kind of order zero [roots of J₀(x) = 0], R is the radius of the cylindrical spacer and D is the diffusion coefficient of the GNPs inside the spacer.³² Therefore, the average concentration of GNPs, C_ST(t), released/transported from the spacer to the spacer–tumour interface (ST) via the diffusion process at time t, is given by:

$$C_{\text{ST}}\left(t\right)=C_i\left[1-\frac{4}{R^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\alpha }_n^2}}\exp \left(-{\alpha }_n^{2}Dt\right)\right]$$ (2)

However, the diffusion coefficient D, of the GNPs in the spacer (polymer–GNP matrix), was determined from the Stoke–Einstein equation and is given by:^33–35

$$D=\frac{K_{\text{B}}T}{6\pi \eta a}$$ (3)

where T is the body temperature in kelvin, K_B is the Boltzmann constant, η is the viscosity of the polymer, a is the radius of the GNPs and N_A is the Avogadro's number (6.023 × 10²³ mol⁻¹).^33–35

Model for gold nanoparticle release from spacer due to polymer degradation kinetics

The model based on the polymer degradation process was assumed to be characterized by the decrease in polymer molecular weight (Figure 1d,e) governed by the first-order degradation kinetic equation, which is usually fitted to the experimental results.^15,29 The first-order (pseudo) equation was given by:^36–42

$$M_{\text{w}}\left(t\right)=M_{\text{w}}\left(0\right)\exp \left(-k_{\text{d}}t\right)$$ (4)

where M_w(t) and M_w(0) are the polymer molecular weight at times t and t = 0 (before placing into the release medium), respectively; k_d is the degradation rate constant of the PLGA polymer.^{17,37–39,42} Hence, from Equation (4), the degradation rate constant, k_d, is given by:^21,42

$$k_{\text{d}}=\frac{\text{In}\left[\frac{M_n\left(t\right)}{M_n\left(0\right)}\right]}{t}$$ (5)

According to Engineer et al,²¹ the burst release of paclitaxel drug from the PLGA matrix (stent) was found to occur in two phases/stages: Phase I (initial burst release) and Phase II (the second burst release) which determine the degradation constants. These stages occur depending on factors such as the drug–polymer matrix, matrix geometry and the fabrication technique.^16,30,43 Then, from Batycky,¹⁸ the concentration of GNPs released from the spacer into the spacer–tumour interface via spacer (PLGA–GNP mixture) degradation kinetics for the initial burst release (Phase I) and second burst release (Phase II) may be expressed as:

$$C_{\text{d}}\left(t\right)=C_i\left[1-\exp \left(-k_{\text{d}}t\right)\right]$$ (6)

where C_d(t) is the concentration of GNPs released from the spacer due to polymer degradation (Phases I and II), C_i = C (t = 0) is the initial GNP concentration in the spacer and k_d is the degradation constant for the initial burst release (Phase I) and second or late burst release (Phase II).²¹ Since initial surface concentration of the GNPs on a spacer was assumed to be zero, there were no GNPs released due to the desorption process but only initial burst release of the GNPs from inside the spacer as a result of degradation.

Gold nanoparticles released due to combination of diffusion and degradation processes

The total concentration of GNPs in a spacer or at the spacer–tumour interface may be described as a combined process of both diffusion and degradation. Therefore, the total concentration released into the spacer–tumour interface from a spacer at time t may be expressed similar to that expressed by Lao et al³⁷ as:

$$C_{\text{T}}\left(t\right)=C_i\ast \left\{\begin{array}{l}{F}_{\text{I}}\ast \left[1-\exp \left(-k_{\text{d}1}\left(t\right)\right)\right]+\\ F_{\text{II}}\ast \left[\exp \left(-k_{\text{d}2}\left(t-t_{\text{d}1}\right)\right)-1\right]+F_D\ast \left[1-\frac{4}{R^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\alpha }_n^2}}\exp \left(-{\alpha }_n^{2}Dt\right)\right]\end{array}\right\}$$ (7)

where k_d1 is the first degradation constant for the initial burst release (Phase I) and k_d2 is the first degradation constant for the second burst release (Phase II); t_d1 is the time in days for the initial burst release (Phase I), where F_I + F_II + F_D = 1 and F_I is the fraction of GNPs released due to the initial burst (Phase I), F_II is the fraction due to the final burst release (Phase II) and F_D is the fraction due to the diffusion process, respectively.

However, since the initial burst released (Phase I) resulted in a high percentage of the GNPs released (more than half), Equation (7) proposed above was modified to account for only the Phase I degradation constant and diffusion process, leading to elimination of Phase II degradation kinetics as given by:

$$C_{\text{BD}}\left(t\right)=C_i\ast \left\{F_{\text{I}}\ast \left[1-\exp \left(-k_{\text{d}1}\left(t\right)\right)\right]+F_{\text{D}}\ast \left[1-\frac{4}{R^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\alpha }_n^2}}\exp \left(-{\alpha }_n^{2}Dt\right)\right]\right\}$$ (8)

where C_BD(t) is the total concentration of GNPs released from the spacer into the spacer–tumour interface, F_I + F_D = 1, where F_I is the fraction of GNPs released due to the initial burst (Phase I) and F_D is the fraction of drug release due to diffusion process.

Model for gold nanoparticle at the spacer–tumour interface diffused into tumour volume

In this case, we assumed that at the spacer–tumour interface, the GNPs released from the spacers are diffused into the tumour volume via the diffusion process, assuming that diffusion in a semi-infinite system in one dimension as discussed by Sinha et al³ and is given by:^31,44

$$\frac{C\left(x,t\right)-C_0}{C_S-C_0}=1-\text{erf}\left(\frac{x}{2\sqrt{D_{\text{T}}t}}\right)$$ (9)

where D_T is the diffusion coefficient of the GNPs in the tumour, C(x,t) is the concentration of GNP in the tumour cells at any time t, which is a solution of Fick's second diffusion equation with initial boundary condition for the concentration of GNPs in the tumour cells assumed to be zero (C₀ = 0, at all-time) prior to the initial burst release from the spacer, but concentration of GNP at the spacer–tumour cells C_S (C_S = 0 at time t = 0) at any time t during the GNP release, as a dependence on diffusion controlled-release mechanism expressed in Equation (2) [i.e. C_S = C_ST(t)]; or on the polymer degradation and diffusion processes expressed in Equation (7) or Equation (8) above [i.e. C_S = C_T(t) or C_S = C_BD(t)], respectively. Whereas Sinha et al assumed that C_S = 7 mg g⁻¹.⁴³ Therefore, Equation (9) was expressed as in Equations (10) or (11), respectively, for diffusion controlled-release mechanism/process is given by:

$$C\left(x,t\right)=C_{\text{ST}}\left(t\right)\ast \left[1-\text{erf}\left(\frac{x}{2\sqrt{D_{\text{T}}t}}\right)\right]$$ (10)

or the corresponding equation for a combined process PLGA degradation and diffusion is given by:

$$C\left(x,t\right)=C_{\text{BD}}\left(t\right)\ast \left[1-\text{erf}\left(\frac{x}{2\sqrt{D_{\text{T}}t}}\right)\right]$$ (11)

where C_ST(t) and C_BD(t) are the total concentrations of GNPs released from the spacer into the spacer–tumour interface via diffusion controlled process [Equation (2)] and a combined process of polymer degradation and diffusion controlled processes [Equation (8)], respectively.

RESULTS

Figure 2 illustrates the release profiles for the 10-nm GNPs released from the spacer at a given time in days via diffusion controlled-release process and a combination of diffusion and polymer degradation processes based on 1.14 × 10⁻⁹ cm² s⁻¹ diffusion coefficient of the 10-nm GNPs in the spacer determined from the PLGA viscosity (400 cP; 1 cP = 0.01g cm⁻¹ s) for simplicity,^45,46 whereas Alexis et al²² reported a diffusion coefficient of 5.7 × 10⁻⁹ cm² s⁻¹ of paclitaxel from a PLGA-coated stent. Figure 2a shows that it will take about 25 days for all 7mg g⁻¹ concentration²² of 10-nm GNPs to be released from the spacer into the spacer–tumour interface based on the diffusion controlled-release process described by Equation (2), which confirms that it takes more than a day for all the GNPs in the spacer to release from the spacer. On the other hand, Figure 2b shows a combined model for diffusion and PLGA degradation processes as described by Equations (7) and (8), respectively, which shows that it may take about 45 days for all the GNPs to be released from the spacer. From Equation (7), the fraction of GNPs released due to the initial burst (Phase I), F_I, was determined to be 0.445; the fraction due to the final burst release (Phase II), F_II, was 0.077; and the fraction due to diffusion process F_D was 0.478, respectively. From Equation (8), the fraction of GNPs released due to the initial burst (Phase I), F_I, determined was 0.482 and the fraction of drug release due to diffusion process, F_D, was 0.518. From Figure 2b, on the basis of the experimental results obtained by Engineer et al,²¹ about 70% of the GNPs may be released on Day 7 (1 week) after implantation.

Figure 2.

Concentration profile for 10-nm gold nanoparticles (GNP) released from a spacer via: (a) diffusion controlled-release process [using Equation (2)], (b) poly(lactic-co-glycolic acid) (PLGA) polymer degradation and diffusion processes [using Equations (7) and (8)].

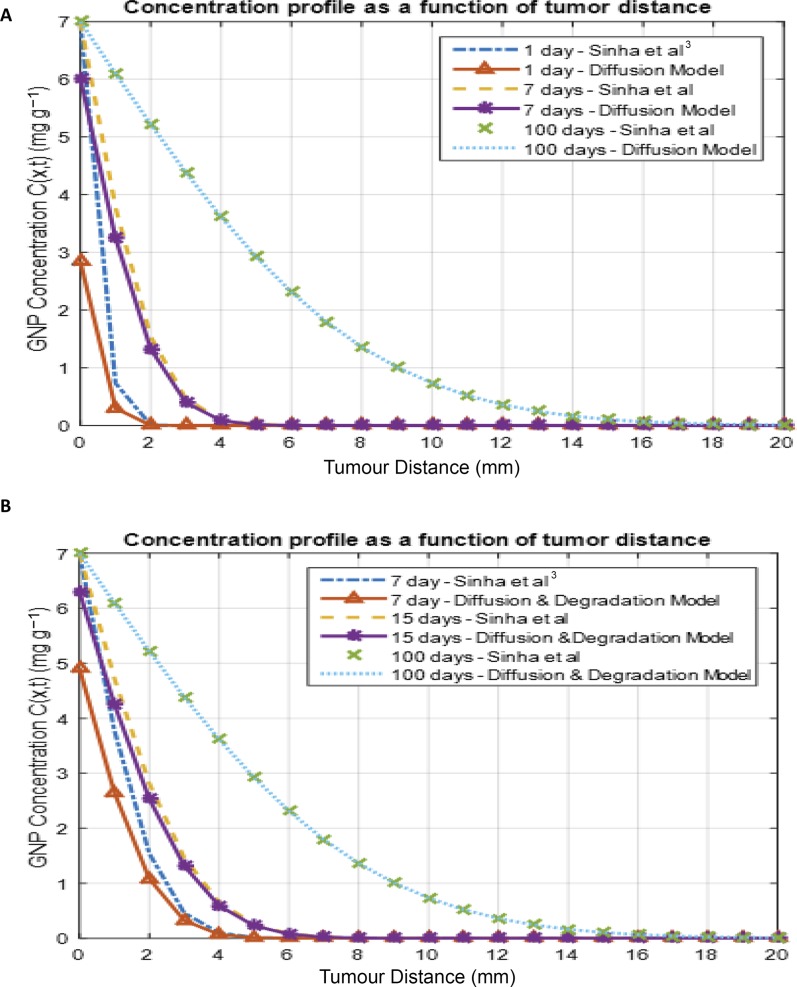
However, in Figure 3, we compared concentration profile as a function of tumour distance obtained by Sinha et al³ [based on Equation (9)] to a similar profile if the release of the GNPs from the spacer was on the basis of the diffusion controlled-release model [Equation (10)] or a combination of both diffusion process and polymer degradation process [Equation (11)]. Figure 3a shows how GNPs diffused into the tumour cell after the GNPs released from the spacer into the spacer–tumour interface in comparison to the assumption made by Sinha et al. Figure 3b shows similar comparison between assumption of burst release and GNP release via polymer degradation kinetics and diffusion process, as the released GNPs diffused into the tumour. It could be noted that at a longer time, our models agree with the assumption made by Sinha et al.

Figure 3.

Concentration as a function of tumour distance (mm) for 10-nm gold nanoparticles (GNP) at different times after release from a spacer into the tumour cells in comparison with Sinha et al:³ (a) GNP release from spacer via diffusion controlled-release process; and (b) GNP release from spacer via a combined process of both polymer degradation and diffusion processes.

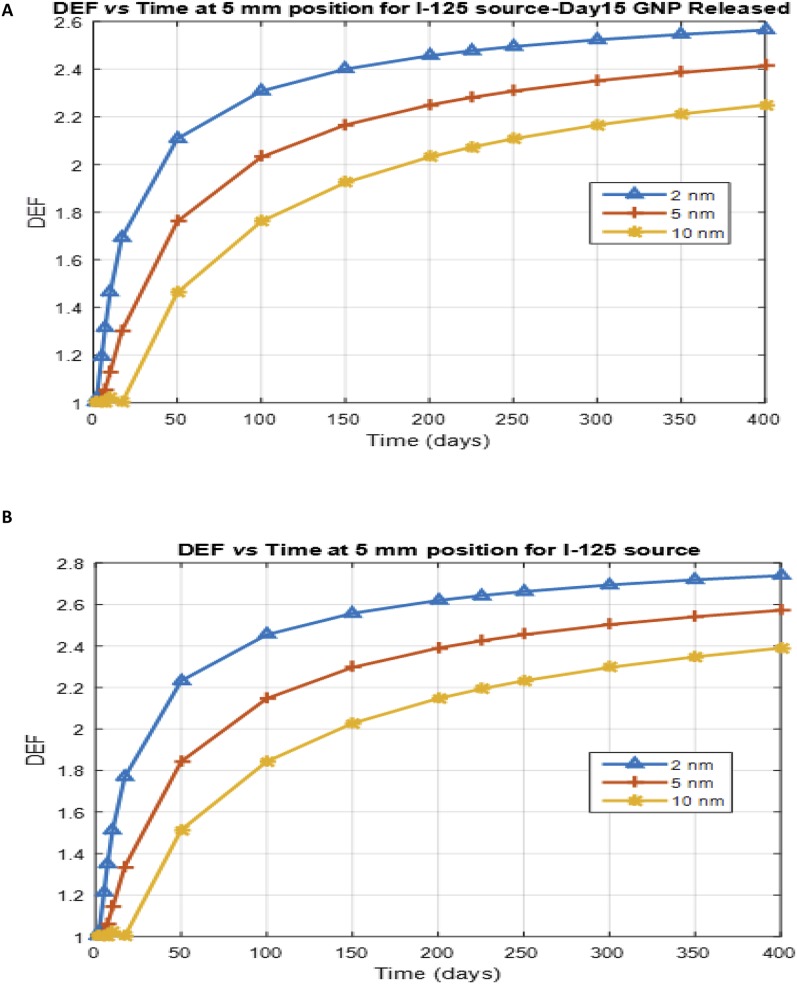
Furthermore, Figure 4 shows the DEF as a function of time at a distance of 5 mm from a spacer for different GNP sizes (2, 5 and 10 nm), with diffusion coefficients of 11 × 10⁻⁸, 4.4 × 10⁻⁸ and 2.2 × 10⁻⁸ cm² s⁻¹, respectively (Sinha et al³) for the I-125 source. The DEF profile shows that smaller GNP sizes have higher DEF over time at a specified tumour distance, as the released GNPs diffuse in the tumour. A significant DEF (of >2) may be attained at a distance of 5 mm from a spacer loaded with GNP sizes (2, 5 and 10 nm) when the I-125 source is used during treatment,³ as indicated in Figure 4.

Figure 4.

Dose enhancement factor (DEF) as a function of time for nanoparticles of different sizes at a distance of 5 mm for iodine-125 (I-125) source at different gold nanoparticles (GNP) concentration released from a spacer: (a) for Day 15 GNP released and (b) for Day 45 GNP released from the spacer.

DISCUSSION

From the results obtained, it was noted that there were no GNPs present at the tumour site just after implantation. However, it can be inferred from Figure 2 that in the case of diffusion controlled-release process (without polymer degradation kinetics), it took about 25 days for all GNPs to release from the spacer after implantation (as indicated in Figure 2a), whereas it took approximately 45 days when a combination of polymer degradation and diffusion process was considered (Figure 2b). Polymer degradation constants were found to be 0.1076 1/day and 0.0061 1/day for Phase I and II, respectively, on the basis of Equation (4), although Engineer et al²¹ reported the degradation constant of Phase I to be 0.1064 1/day.²⁶ About 70% (70.13%) of the GNPs released on Day 7 (1 week), similar to the result obtained by Engineer et al²¹ on the basis of Equation (8), accounting for the omission of Phase II degradation constant. The inclusion or exclusion may depend on the amount of GNPs incorporated in the spacer(s) and the release pattern observed experimentally. Likewise, the PLGA relaxation time was not accounted for since it was not reported by Engineer et al.²¹ Nevertheless, Engineer et al²¹ reported 60–70% release of paclitaxel for burst release within the first week (7 days) after incubation, equivalent to what our model predicted for Day 7 (70.13%). A similar study (in vitro study of stents coated with polymer and paclitaxel drug) by Drachman⁴⁷ recorded 36% burst release in 1 day, of which the first-order kinetics happened in 2 months with 90% paclitaxel drug release.

Although, the PLGA-paclitaxel drug-coated stents differ from PLGA-GNP-coated spacer or customized drug-eluting spacer, the results from Engineer et al²¹ provide good PLGA degradation information for our studies. Again, viscosity chosen may not present a typical PLGA-GNP matrix since polymer viscosity is related to polymer type and molecular weight.^40,45,48 Therefore, polymer complexities should be examined when tailoring GNP-eluting spacers to suite brachytherapy procedure for therapeutic efficacy. When polymer degradation is taken into consideration, the spacer/matrix preparation method used should be such that the initial burst release can occur as early as possible (in hours) to obtain a maximum GNP concentration at the spacer–tumour interface to enable enough GNPs to be diffused into the tumour for prompt tumour cells sensitization for optimum therapeutic efficacy due to the decay characteristics of the brachytherapy seeds as discussed by Ngwa et al^12,13 and Sinha et al.³

The permeation and distribution of GNPs in tumour depend on the microenvironment of the tumour and the amount of GNP concentration present at the spacer–tumour interface as indicated in Figure 3 [expressed in Equations (10) and (11) above].⁴⁹ Generally, deep penetration and distribution of nanoparticles into tumours are hindered by factors such as the properties of the nanoparticles (particle size, surface area, surface chemistry, circulation time etc.) and tumour pathological characteristics (e.g. cell density, elevated interstitial fluid pressure, rigid collagen network, cell proliferation, tumour cells, tumour extracellular matrix etc.).⁴⁹ The same diffusion coefficient of 2.2 × 10⁻⁸ cm² s⁻¹ of the nanoparticles with 7 mg g⁻¹ concentration determined experimentally by Wong et al³¹ was used for simplicity as it was used in Sinha et al.³ However, the diffusion coefficient of 10-nm GNPs in polymer–GNP matrix may differ from the diffusion coefficient in tumour cells and in the collagen gel.³¹

This study was based on GNP release from only one drug-eluting spacer, with an assumption of 7 mg g⁻¹ concentration; however, more spacers can be loaded with the GNPs and a higher GNP concentration (customized) used to achieve the desired results.³ Since more than one spacers are used in practice, depending on the tumour volume and the number of brachytherapy seeds used,⁹ it would be beneficial for replacing the conventional inert spacers with additional spacers loaded with GNPs without increasing the number of injectable spacers required for the procedure. Also, since drug distribution is not isotropic such as the radioisotope seeds, rather the permeation and distribution depend on the tumour pathological characteristics and particles properties, the GNP-eluting spacers could be loaded with a higher GNP concentration and placed in position(s) such that the tumour volume may have the minimum concentration needed (to sensitize tumour cells) to enhance the dose significantly for therapeutic efficacy. Increasing the GNP concentration in the PLGA spacer should be performed to ensure that the integrity of the eluting spacer is not compromised. Customizable spacers loaded with higher GNP concentration could be fabricated by modifying the dimensions of the current spacers, such as increasing the length or diameter of the spacers depending on the tumour/application. For instance, increasing the diameter from 1 mm, as used in this model, to about 2.0 mm, as reported by Shirato et al, was found to be feasible in prostate, liver and lung tumours with appropriate techniques.⁵⁰

The results suggest that either the GNP release mechanisms from the spacer was based on diffusion controlled-release process only or a combination of both diffusion or polymer degradation processes; the spacer–tumour interface and the tumour region initially have no GNPs immediately after the implantation.⁴⁹ However, this study supports the work of Sinha et al,³ emphasizing the potency of GNP-enhancing therapeutic efficacy. The authors noted that brachytherapy seeds with shorter half-lives (e.g. Cs-131) may be limited for dose enhancement applications due to the time it takes for the GNP release from the spacer.³ Therefore, seeds with long half-life such as I-125 may be more appropriate candidates for this application.³ For emphasis, significant DEF (of >2) may be attained at a tumour distance of 5 mm from a spacer loaded with different GNP sizes (2, 5 and 10 nm as shown in Figure 4) when the I-125 source is used during treatment. Also small-size GNPs (e.g. 2 nm) may enhance GNP release mechanism from the spacer in vivo, thereby enhancing GNP concentration distribution/diffusion in the tumour cells resulting in greater DEF.^3,51,52 Moreover, this study and that of Sinha et al³ provide a useful reference for future studies, including experimental studies that will be helpful to unfold different polymer degradations and initial burst release patterns of GNPs from spacers. The ideas outlined in this study also may be helpful for immunoadjuvant drugs incorporated in the polymer matrix in various applications.

On the basis of the results, we suggest that to achieve maximum efficiency, the spacers could be loaded with PEGylated GNPs with surface properties optimized, such as coating the surface with multifunctional poly(ethylene glycol) with carboxyl, amine and methoxy functional groups, to make the GNPs flexible for conjugating with moieties (e.g. peptides, chemotherapy drugs, fluorophores or radiolabels).⁵³ The GNP sizes could also be optimized for higher tumour uptake, prolong tumour retention/circulation or modulated tumour clearance resulting in higher radiation dose enhancement.⁵³ Since the GNP uptake depends on the physiochemical properties, the surface ligands and charge of the GNPs are vital in tumour uptake, transport and tumour distribution.⁵⁴

However, the study does not suggest modification of the radioactive seeds, rather suggests that to achieve high loading efficiency, and uniform or customizable design of eluting spacers, the spacers should be fabricated using polymer film loaded with GNPs instead of coating conventional spacers, which results in non-uniform shapes, as reported by Nagesha et al.⁷ Again, we suggest that polymers with lower molecular weights could be used to fabricate eluting spacers since they exhibit slightly higher initial release rates than those with higher molecular weights.⁵⁵ Thus, polymers with higher molecular weight generally exhibited lower degradation rates due to longer polymer chains, which require more time to degrade than the small polymer chains.^15,56

CONCLUSION

This study for the first time considered release of GNPs from spacers without assuming burst release. The study shows that there is a significant delay of many days before the GNP diffusion profile in the tumour is similar to that when burst release is assumed. However, the results support the main conclusions from Sinha et al³ that I-125 may be the more appropriate radioisotope for brachytherapy application with in situ dose painting. Furthermore, our results suggest that PLGA/polymers with a higher initial burst release (80–90%) in few days should be used for fabricating eluting spacer for radiotherapy applications. In this scenario, radioisotopes with shorter half-lives such as Pd-103 and Cs-131 might be applicable. Our proposed models provide a theoretical and scientific platform for research development of the next generation of eluting spacers appropriate for radiotherapy applications and for other GNP/drug delivery disciplines, reducing experimental time and cost.