Design optimization of PVDF-based piezoelectric energy harvesters

Abstract

Energy harvesting is a promising technology that powers the electronic devices via scavenging the ambient energy. Piezoelectric energy harvesters have attracted considerable interest for their high conversion efficiency and easy fabrication in minimized sensors and transducers. To improve the output capability of energy harvesters, properties of piezoelectric materials is an influential factor, but the potential of the material is less likely to be fully exploited without an optimized configuration. In this paper, an optimization strategy for PVDF-based cantilever-type energy harvesters is proposed to achieve the highest output power density with the given frequency and acceleration of the vibration source. It is shown that the maximum power output density only depends on the maximum allowable stress of the beam and the working frequency of the device, and these two factors can be obtained by adjusting the geometry of piezoelectric layers. The strategy is validated by coupled finite-element-circuit simulation and a practical device. The fabricated device within a volume of 13.1 mm³ shows an output power of 112.8 μW which is comparable to that of the best-performing piezoceramic-based energy harvesters within the similar volume reported so far.

1. Introduction

There are many unutilized energy sources in the environment, e.g. thermal energy, electromagnetic waves, and mechanical vibration [1]. The conversion of these ambient energies into electric energy has motivated the development of the energy harvesting devices (EHDs). Meanwhile, the ongoing rapid reduction in the power consumption of electronic devices and micro-electro-mechanical systems (MEMS) make the application of EHDs increasingly promising [2, 3]. Mechanical vibration exists broadly in the environment and human body movement, thus EHDs for mechanical vibration show great potential for wide applications, for example, in wireless sensor networks where the battery replacement is a crucial issue [4, 5]. EHDs which scavenge energy from human walk can play an important role as a backup power for artificial heart pacemakers in which the power cutoff is fatal [6, 7].

Among various routes to collect vibration energy, piezoelectric energy harvesting (PEH) has the advantage of simple device structure, high power density and no need for extra power supply, thus has attracted extensive investigations [8, 9]. Most of the previous studies on the PEH devices have chosen piezoceramics as the key material for the mechanical-electrical energy conversion [10, 11, 12, 13, 14, 15, 16]. Piezoceramics such as lead zirconate titanate (Pb[Zr_xTi_1-x]O₃, or PZT) possess high electromechanical coupling coefficient, high mechanical quality factor and large elastic stiffness, which makes them good candidates for the energy-conversion element in PEH devices. However, there has been severe concern on the environmental impact due to the heavy content of Pb in the high-end piezoceramics in recent years [17]. In addition, as piezoceramics are fragile and unable to bear large deformation, a nonpiezoelectric substrate layer is usually necessary in the construction of piezoceramics-based PEH which however degrades the electromechanical coupling coefficient of the whole device. Compared to piezoceramics, piezoelectric polymers such as polyvinylidene fluoride (PVDF) show good environmental compatibility and their flexibility makes it feasible to adopt a full piezoelectric beam without any substrate layers. In addition, the device based on piezoelectric polymers is more resistant to mechanical shock.

The off-resonance figure of merit (d_ijg_ij) of PVDF for energy scavenging is as good as that of PZT ceramics [18]. There have been experimental attempts to use PVDF on off-resonance mode for energy harvesting. For instance, Kymissis et al. [19] installed an insole stave made of PVDF film-stacks in shoes to collect the energy due to bending of soles during human walking and obtained an average power output of ∼1 mW. Vatansever et al [20] used PVDF films to collect energy from wind and rain drops and showed that piezoelectric polymer materials can generate power more efficiently than piezoceramics.

In 2003, Roundy et al [21] calculated the power output of cantilever-type PEH devices working on resonant mode with a seismic mass placed on the free end by means of coupled modal analysis. The derived maximum power output for a PVDF-based PEH device fabricated within 1 cm³ reached over 200 μW at 120 Hz, under an input vibration with an acceleration magnitude of 0.25g (g = 9.8 m/s²), comparable to PZT-based PEH devices. However, the experimental result on the performance of PVDF-based PEH devices was far inferior to what Roundy et al estimated. Jiang et al [22] obtained only around 16 μW at 17 Hz resonant frequency under 1.2g sinusoidal vibration and Cao et al [23] reported a power output of 3.0 μW in air and 10.6 μW in vacuum, under 1.0g vibration input at ∼100 Hz. The output power density (output power per beam volume) is ∼176 μW/cm³ [22] and ∼1943 μW/cm³ [23] in the two experimental studies while it reaches as large as 30000 μW/cm³ [21] in the calculation of Roundy et al.

It should be noted that as far as we know, none of the experimental attempts have fabricated the PVDF-based PEH devices through configuration optimization process. It is hence worthy to develop a facile and reliable optimization approach for PVDF-based PEH devices based on analytical models. In this paper, an uncoupled model is introduced to study how the configuration of PVDF-based PEH devices affects their output power density that is used as a criterion for high-performance PEH devices. Strategies for the configuration optimization have been formulated according to the analytical results and an example of optimized device has been given. A coupled finite-element-circuit simulation (CFECS) approach is conducted to justify the approximations used in the analytical model as well as to prove the structure-performance relation that is deduced from the analytical model. We also fabricated a real device according to the optimized configuration and experimentally characterized its performance under the given vibration condition. Both the finite element simulation and experimental data demonstrate the high output power density of the optimized device, proving the reliability and efficiency of our optimization approach.

2. Theory/Calculation

2.1. Device configuration

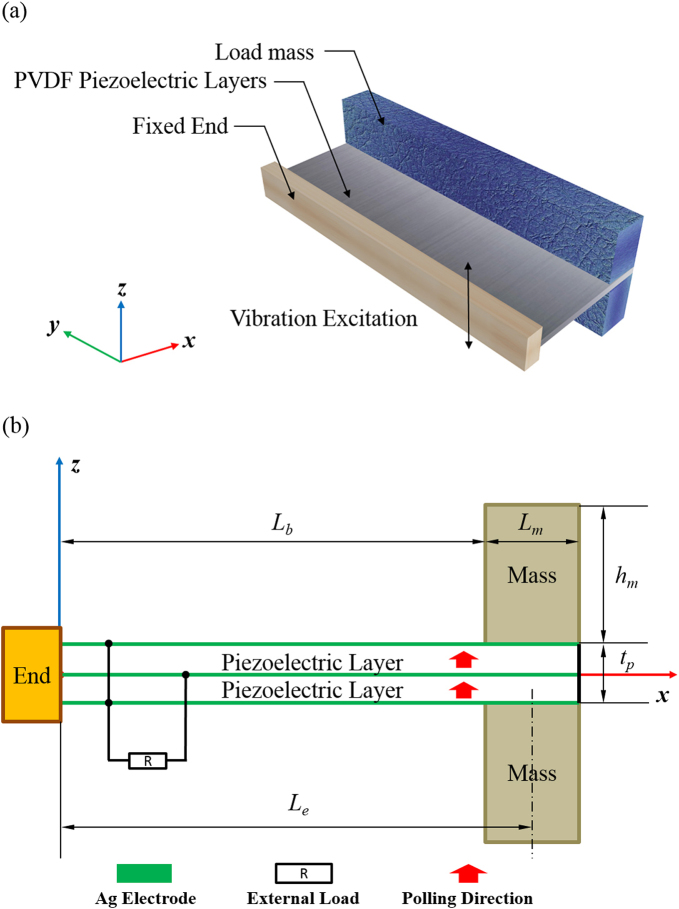
Fig. 1 illustrates the basic structure of the PVDF-based PEH device. The bimorph cantilever beam fully made of PVDF, with the steel load mass adhered to the free end of the beam, is clamped by the fixed end. The PVDF films are 50-μm-thick each with thin Ag electrode on the surface, and bonded in the same polling and stretching directions. The adhesive layers between the PVDF films and two pieces of load mass are attached to the end of the PVDF beam with epoxy whose thickness can be ignored. The two layers of the PVDF are connected in parallel in the circuit with a resistance as an output load.

Fig. 1.

(a) Overall structure and, (b) configuration of the PVDF-based PEH device.

2.2. Analytical model

Owing to the low electromechanical coupling coefficients of PVDF (k₃₁ < <1), two approximations are made in the following analysis:

(1) The optimum working frequency of the device is equal to the natural frequency of the beam.

(2) In the mechanical equation of motion, the reverse piezoelectric effect is neglected.

The optimum working frequency of the device with external load lies between the open-circuit frequency (f_open) and short-circuit frequency (f_short). It is known that the natural frequencies of a piezoelectric beam under open-circuit condition and short-circuit condition are correlated as Eq. (1) [24]:

$$f_{short}=f_{open}\sqrt{1-k_{31}^2}$$ (1)

As k₃₁ of PVDF is only about 0.12 [2, 22], the difference between f_open and f_short, is commonly within 1%. The device’s electromechanical coupling coefficient is even lower than that of the material. Therefore, unlike the case of PZT-based PEH devices of which resonant frequency shows a remarkable shift upon the connection to the external electric load [25], the resonant frequency shift in PVDF PEH devices can be neglected, thus justifying approximation (1). Secondly, ${\text{k}}_{31}^2$ represents the distribution between the electrical energy and the elastic energy in the piezoelectric beam, accordingly, with ${\text{k}}_{31}^2$ << 1, the impact of the reverse piezoelectric effect on the vibration amplitude can be neglected.

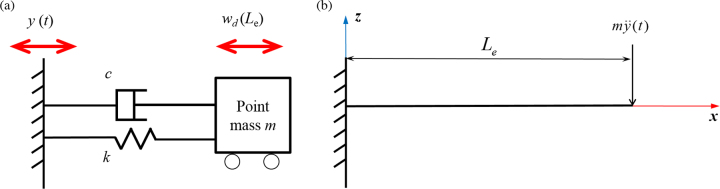
Typically, when the cantilever is under vibration excitation, it can be approximately treated as a spring with damping and a point mass as illustrated in Fig. 2a. When L_b >> L_m and m_m >> m_b (m_m and m_b represent the weight of the end mass and the cantilever beam respectively), an effective length of the cantilever L_e which is equivalent to ${\text{L}}_{\text{b}}+\frac{{\text{L}}_{\text{m}}}{2}$ and an effective mass m which is approximate to m_m can be used to depict the system as an cantilever with a point end-mass. The equivalent stiffness of the beam is then as Eq. (2):

$$\text{k}=\frac{3EI}{L_e^3}$$ (2)

Fig. 2.

Approximated analytical model of the cantilever beam. (a) The damping model, where m stands for the effective mass, c stands for the system damping, k stands for the stiffness of the beam and y(t) stands for the excitation vibration. (b) The excitation model in which a point force $\text{m}{\displaystyle \ddot{\text{y}}}(\text{t})$ is applied at the free end of the beam to determine w_d at any point along x direction.

where E is the elastic modulus of the beam material and I the moment of inertia of the cross sectional area of the beam. Accordingly ω_n can be derived as Eq. (3):

$${\omega }_n^2=\frac{E{W}_b{t}_p^3}{4m{L}_e^3}$$ (3)

Then, the movement of the point mass in which the reverse piezoelectric effect is not involved can be expressed as Eq. (4):

$$\text{m}\frac{d^2{w}_d(L_e)}{d{t}^2}+c\frac{d{w}_d(L_e)}{dt}+k{w}_d(L_e)=-m\frac{d^{2}y}{d{t}^2}$$ (4)

where c = 2ξmωn, ξ represents damping factor; the motion of the vibration source is y(t) = Acos(ωt) where ω stands for the angular frequency; w_d(L_e) represents the displacement of the mass. For a sinusoidal vibration source, w_d(L_e) can be expressed as w_d(L_e) = W₀cos(ωt+θ). Putting the expression of w_d(L_e) into Eq. (4), W₀ can be solved at ω = ω_n as shown by Eq. (5):

$${\text{W}}_0=\frac{m{\omega }_n^{2}A}{2k\xi }$$ (5)

In order to determine the displacement of the neutral plane of the beam at any point w_d(x) along its length, the excitation acting on cantilever beam through the fixed end can be equivalent to a point force $\text{m}{\displaystyle \ddot{\text{y}}}(\text{t})$ applying at its free end, which is illustrated in Fig. 2b. Then w_d(x) can be expressed as $w_d\left(x\right)=W_0\varphi \left(x\right)\text{cos}\left(\omega t+\theta \right)$, where $\varphi \left(x\right)$ is the normalized shape function representing the amplitude ratio of the points at x and L_e, with the expression in Eq. (6):

$$\varphi \left(x\right)=\frac{{\left(L_e-x\right)}^3}{2L_e^3}-\frac{3\left(L_e-x\right)}{2L_e}+1$$ (6)

In a linear elastic beam, the stress in the x direction in PVDF beam can be expressed as Eq. (7):

$${\sigma }_x\left(x,z\right)=Ez\frac{d^2{w}_d\left(x\right)}{d{x}^2}$$ (7)

where z represents the distance to the neutral layer of the beam. With Eq. (5) and Eq. (6) for the expression of w_d(x), the maximum stress can be solved at ${\sigma }_{max}=\sigma \left(0,\frac{1}{2}{t}_p\right)$. A relation between ω_res and σ_max can be obtained as Eq. (8) with the vibration source’s acceleration ACC = Aω_n²:

$${\sigma }_{max}·{\omega }_n^2=\frac{3E}{4\xi }·\frac{t_p}{L_e^2}·ACC$$ (8)

The piezoelectricity of PVDF dictates that the relation of electric displacement D₃, electric field E₃ and stress σ_x can be expressed as Eq. (9):

$${\text{D}}_3=d_{31}·{\sigma }_x+{\epsilon }_p^{\sigma }·E_3$$ (9)

where d₃₁ is the piezoelectric constant in 31 mode, ${\epsilon }_p^{\sigma }$ the permittivity of the piezoelectric layers under the condition of constant stress. D₃ is uniform within each layer of PVDF as there is no free charges within PVDF. Integrating Eq. (9) in z direction from the neutral layer to the top surface of the beam, E₃ can be replaced by the output I_R as Eq. (10):

$$D_3=\frac{{{\displaystyle \int }}_0^{\frac{1}{2}{t}_p}{D}_{3}dz}{\frac{1}{2}{t}_p}=\frac{d_{31}E\frac{d^2{w}_d\left(x\right)}{d{x}^2}·{{\displaystyle \int }}_0^{\frac{1}{2}{t}_p}zdz+{\epsilon }_p^{\sigma }·{{\displaystyle \int }}_0^{\frac{1}{2}{t}_p}{E}_{3}dz}{\frac{1}{2}{t}_p}=d_{31}E·\frac{t_p}{4}·\frac{d^2{w}_d\left(x\right)}{d{x}^2}-\frac{2{\epsilon }_p^{\sigma }}{t_p}·I_R·R$$ (10)

where R represents the resistive load in the circuit. Integrating Eq. (10) with total beam surface, the generated charge Q₀ is expressed as Eq. (11):

$$Q_0={\displaystyle \underset{S}{\overset{\mathrm{}}{{\displaystyle \iint }}}}{D}_{3}dxdy=\frac{3E{W}_b{d}_{31}{t}_p{W}_0}{4L_e}\cos \left(\omega t+{\theta }_1\right)-C_{equ}·I_R·R$$ (11)

where C_equ represents the capacitance of one PVDF layer. Since $I_R=\frac{d{Q}_0}{dt}$, differentiating both sides in Eq. (11) and putting $I_R=I_0\text{cos}\left(\omega t+{\theta }_2\right)$ leads to an equation of I₀. Then the average output power P can be deduced as Eq. (12):

$$\text{P}=\frac{I_0^2·R}{2}=\frac{9E^2·W_b^2·d_{31}^2·t_p^2·W_0^2}{64·L_e^2}·\frac{R}{1+{\left(\omega C_{equ}·R\right)}^2}\le \frac{9E^2·W_b^2·d_{31}^2·t_p^2·W_0^2}{64·L_e^2}·\frac{1}{2\omega C_{equ}}$$ (12)

When and only when $\text{R}=\frac{1}{\omega ·C_{equ}}$, P gets the maximum value. We call this R the optimum resistance, and the maximum power at resonant frequency can be expressed as Eq. (13):

$${\text{P}}_{max}=\frac{9E^2·d_{31}^2·A^2·m^2·{\omega }_n^5·t_p^3·W_b}{1024k^2·L_e^3·{\xi }^2·{\epsilon }_p^{\sigma }}=\frac{d_{31}^2}{64·{\epsilon }_p^{\sigma }}·{\omega }_n·{\sigma }_{max}^2\left(W_b{L}_e{t}_p\right)$$ (13)

Adding the expression for σ_max as shown in Eq. (8) into Eq. (13), the output power density is as Eq. (14):

$${\left(\frac{P}{V}\right)}_{max}=\frac{{\text{P}}_{max}}{W_b{L}_e{t}_p}=\frac{d_{31}^2}{64·{\epsilon }_p^{\sigma }}·{\omega }_n·{\sigma }_{max}^2\le \frac{d_{31}^2}{64·{\epsilon }_p^{\sigma }}·{\omega }_n·{\sigma }_{yield}^2$$ (14)

where V stands for the effective volume of the cantilever.

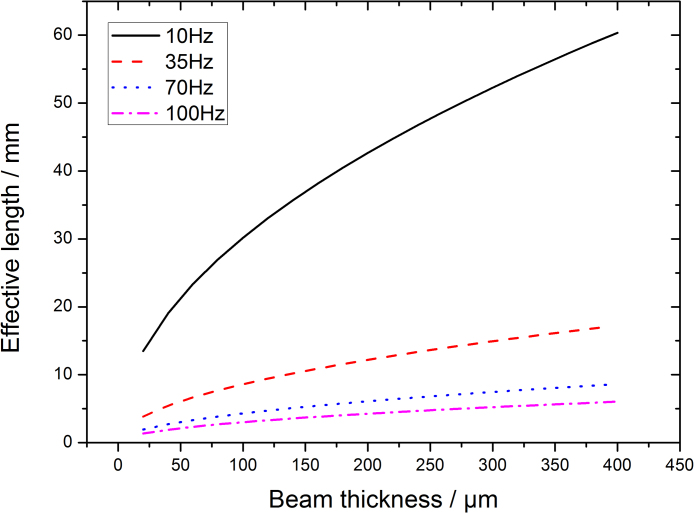
It is interesting that the output power density is determined solely by σ_max and ω_n. For given vibration environment, there exists maximum power density which is determined by the maximum stress allowed in the cantilever. Thus, the maximum output power density of a PVDF PEH device is achieved when setting σ_max reaches σ_yield (or σ_yield divided by a safety factor for practical use) via adjusting $\frac{t_p}{L_e^2}$ as shown in Eq. (8). In other words, for each given ω_n, there is an optimal $\frac{t_p}{L_e^2}$ to maximize output power density, and $\frac{m}{W_b}$ is determined by Eq. (3) accordingly, thus leading to optimized device configurations. Fig. 3 presents the dependence of the optimal L_e and t_p on f_res for given ACC = 10 m/s² and the given commercially available PVDF film (from Jinzhou Ke-xin electronic materials Co. Ltd, with properties listed in Table 1), with σ_max=30 MPa. Notably, the maximum output power density does not depend on the vibration acceleration amplitude ACC although the optimum L_e does.

Fig. 3.

The dependence of optimal L_e and t_p at different resonant frequency, for given ACC = 10 m/s² and σ_max = 30 MPa.

Table 1.

Material parameters of the configuration.

Piezoelectric material: PVDF (Jinzhou Ke-xin electronic materials Co. Ltd)
Piezoelectric constants (pC/N)	d31	23.9	Coupling coefficients	k31	0.14
	d33	-32.5		k33	0.19
Young’s modulus (GPa)	E	4.18	Density (kg/m3)	ρb	1700
Elastic constants (10−11Pa−1)	s11	23.9	Relative dielectric constant	εr	13
	s12	-7.18	Mechanical quality factor	Qm	17.2
	s13	-7.18	Damping factor in air	ξ	0.0291
	s44	62.2	Thickness (μm)	tb	50
	s66	62.2	Yield strength (MPa)	σyield	50
Seismic mass material: 45# steel (Yong-teng-da machinery Co. Ltd)
Young’s modulus (GPa)	E	200	Poisson’s ratio	υ	0.29
			Density (kg/m3)	ρm	7800

2.3. Example of an optimized configuration

In this section, we illustrate the determination of an optimized PVDF-based PEH device excited by a vibration source working at 35 Hz (a frequency easily found in surrounding environment) and with ACC of 0.5g, whose performance will be verified with finite-element simulation and experimental test as discussed in the next sections. To assure the PEH device can work sustainably in a long run, σ_max should be sufficiently lower than σ_yield (∼42 MPa [26]), thus we set σ_max = 30 MPa in the optimization of our device. The commercially available PVDF sheets to be used for device fabrication are 50 μm in thickness, giving the total thickness of the beam 100 μm. Using the property data of PVDF in Table 1, the optimum $\frac{t_p}{L_e^2}$ can be worked out from Eq. (8) and accordingly L_e is known. The weight of the end mass m and the width of the beam W_b can be determined from Eq. (3) plus a limit (preference) of the area of device with known ω_n, t_p and L_e. Noting that L_e is determined by a combination of L_b and L_m, we can set them with a certain freedom as long as L_b >> L_m is satisfied. In this demonstration, we set L_m to 2 mm for convenience, and L_b and h_m can be worked out accordingly. R_opt, which is needed for test of the device, can be calculated from${\text{R}}_{opt}=\frac{1}{\omega ·C_{equ}}$. Once the shape of the device is determined. The final configuration parameters of the designed device are listed in Table 2. The expected output power density can reach 15.4 mW/cm³ according to Eq. (14), which is on the same level of best-performing piezoceramic-based PEH devices [27, 28, 29, 30, 31].

Table 2.

Calculated parameters of the configuration.

Dimension of the PVDF film (mm, two layers)	Le × Wb × tp	6.3 × 20 × 0.1
Dimension of the seismic mass (mm, one block)	Lm × Wm × hm	2 × 20 × 3
Equivalent capacitance (pF)	Cequ	672
Optimum resistance (MΩ)	Ropt	6.76
Maximum power density (mW/cm3)	(P/V)max	15.4

3. Results and discussion

3.1. CFECS approach

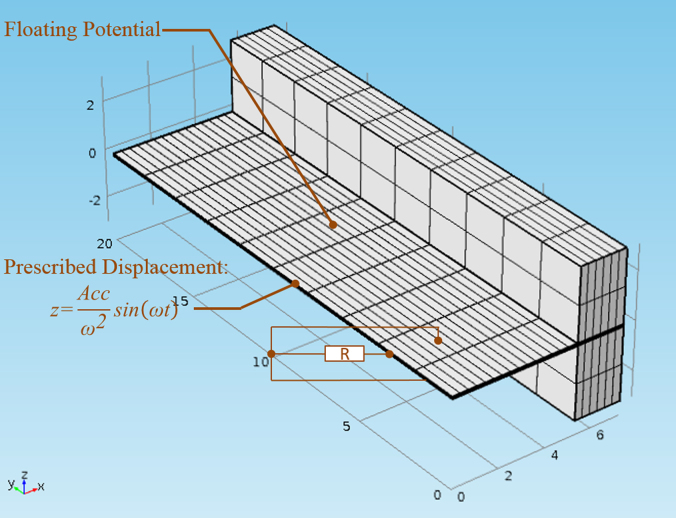
Recently, the CFECS approach [31] has been proposed to simulate the performance of PZT-based PEH devices connected to external electric loads and shows good reliability. We thus conducted CFECS for PVDF-based PEH devices on the commercial software COMSOL Multiphysics 4.2 to check the two assumptions made in the derivation of the analytical results as well as to simulate the performance of the exemplar device proposed in the previous section. The mesh distribution of the model are shown in Fig. 4 with the boundary condition “prescribed displacement” as excitation and “floating potential” as the surface electrode which connected external resistance.

Fig. 4.

CFECS model in COMSOL.

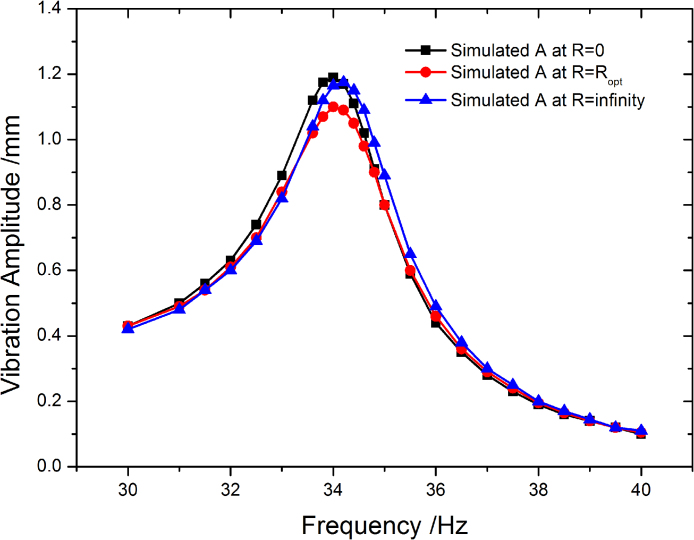
Fig. 5 shows the simulation of the frequency-dependent vibration amplitude (A) of the proposed optimized device under different circuit conditions, with the vibration acceleration maintained at 0.5g upon varying the frequency. It is seen that the resonant frequency changes only by less than 0.3 Hz (<1%) with external resistance spanning zero, optimum resistive load and infinity, confirming that the load-induced frequency shift can be safely neglected. The vibration amplitude also has a weak dependence on the connected external resistance. It decreases a bit (by <10%) with optimum resistance load compared to that under the open-circuit and short-circuit condition, as the converse piezoelectric effect counter plays with the mechanical excitation. This indicates that slight overestimate of output power might occur in the uncoupled model.

Fig. 5.

Simulation result of the frequency response to vibration amplitude in different circuit states under constant 0.5g vibration acceleration.

3.2. Experimental results and discussions

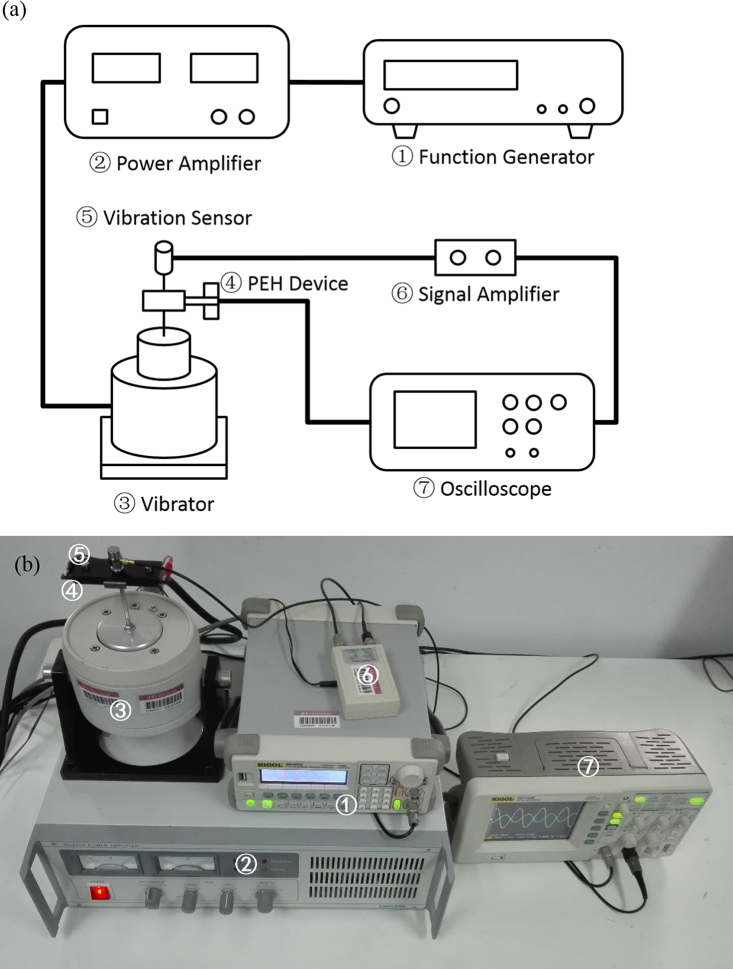
The experimental setup for the device test is shown in Fig. 6a and Fig. 6b. A function generator (RIGOL DG1022U) is used to generate a sinusoidal signal. Amplified by the power amplifier (SINOCERA YE5872A), the signal is sent to the vibrator (SINOCERA JZK-5). A vibration sensor (SINOCERA CA-YD-1181) is attached on the vibrator, noting that the accelerometer is placed as close as possible to the attached beam end. The accelerometer processes a sensitivity of 100 mV/g and a signal amplifier (SINOCERA YE3822A) is used to magnify the output signal. Both the sensor signal and the PVDF-based PEH voltage output are measured by a digital oscilloscope (RIGOL DS1102E). Note that the optimum external resistive load is rather high, a 100MΩ 1.7pF oscilloprobe (RIGOL RP1300H) is used to diminish current shunt effect.

Fig. 6.

(a) Instruments used for device measurement and (b) their assembling sketch.

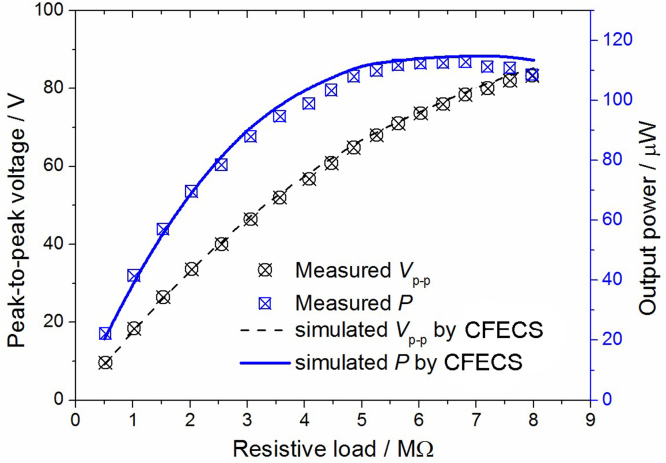
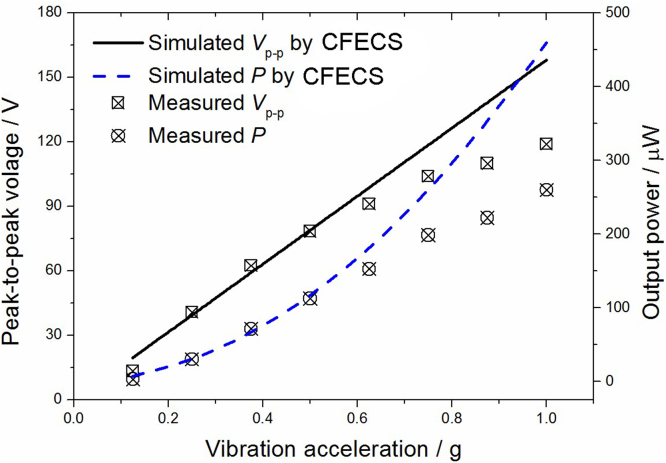
The resonant frequency of the fabricated device is measured to be 34.4 Hz from the frequency sweep of the output voltage under open-circuit condition. The performance of the device as a function of external load was then measured at 34.4 Hz under 0.5g excitation acceleration. The output power value is obtained according to $\text{P}=\frac{V_{p-p}^2}{8R}$ where V_p-p is peak-to-peak voltage measured with the oscilloscope. The measured output voltage and output power are presented in Fig. 7. A peak power value of 112.8 μW appears at 6.5–7.0 MΩ, in good agreement with the optimum resistive load R_opt of 6.81 MΩ calculated from the overall actual capacitance of the device. The output power density of the fabricated device is 8.61 mW/cm³, which is the highest among the reported PVDF-based PEH devices and even comparable to high-performance PZT-based PEH devices (as listed in Table 3).

Fig. 7.

The effects of external loads on V_p-p and P at 0.5g excitation and resonant frequency.

Table 3.

Comparison of the cantilever PEH devices in our work and reported literature.

Piezoelectric layers	ACC	fres (Hz)	Pmax (μW)	(P/V)max (mW/cm3)	Ref.
PVDF	0.5g	34.4	112.8	8.61	This work
PZT	0.25g	109.5	335.2	0.296	[11]
PZT	0.6g	42	0.114	1.48	[13]
PVDF	1.2g	17	16	0.176	[22]
PVDF	1g	103.8	10.6	1.94	[23]
PZT	1g	29.6	15300	13.5	[29]
PMN-PT	0.23g	174	586	0.753	[30]

It should be noticed that the measured value 8.61 mW/cm³ is clearly lower than the expected 15.4 mW/cm³ from the analytical model. Two factors account for the difference between the analytically predicted output power density P_ana/V and that measured in the practical device P_pra/V. The first is the impact of the additional capacitance. The PVDF part clamped in the fixed end as well as between the two pieces of stiff mass do not deform to generate the potential. Wiring/electroding of these parts leads to a decrease in the output power compared to the case with only the deformed PVDF part electrode, with a relationship of P_pra/P_ana = C_deform/C_total where C_deform is the capacitance of the deformed part of the PVDF beam while C_total is the capacitance of the overall beam. The overall capacitance of the fabricated device is measured to be 720 pF, while the capacitance of the deformed part is estimated to be 488 pF, leading to P_pra/P_ana = 0.68. Secondly, as pointed out previously, the overestimation of vibration amplitude of the beam and the corresponding overestimation of the strain, which also leads to overestimation of output power, following a law of P_pra/P_ana = (A_prac/A_ana)². As shown in Fig. 5, A_prac/A_ana ≈ 0.91, leading to P_pra/P_ana = 0.83. Summarizing the impact of the two factors, P_pra/P_ana ≈ 0.53, well explaining the origin of the difference between measured output power density of 8.61 mW/cm³ and the predicted value of 15.4 mW/cm³ in the uncoupled model. The above argument was also confirmed by the CFECS results, which include the effect of both the additional capacitance and the converse piezoelectric in the modeling. As shown by blue curve in Fig. 7, the simulated output voltage and power as a function of external resistive load are in good agreement with the measured data.

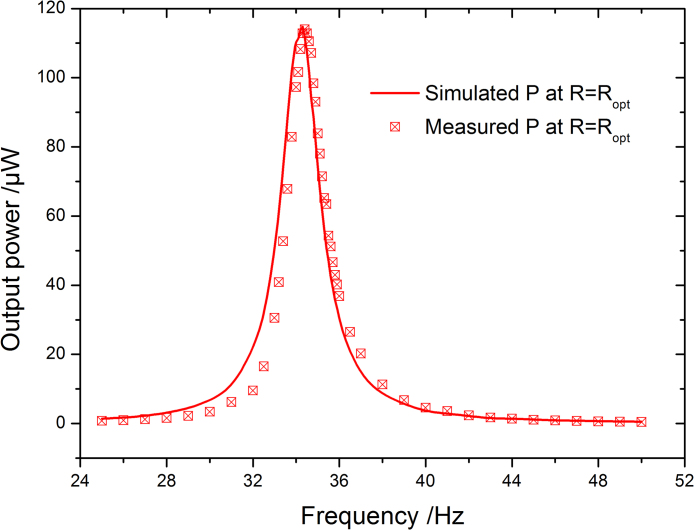
The frequency-dependent output power was then measured at R = R_opt under 0.5g acceleration, and the result is shown in Fig. 8. It is seen that the optimum working resonant frequency is 34.4 Hz, closely matching the designed frequency of 35 Hz. The full width at half maximum (FWHM) is about 3.5 Hz.

Fig. 8.

Simulation and measurement result of the frequency response to output power with optimum working resistance.

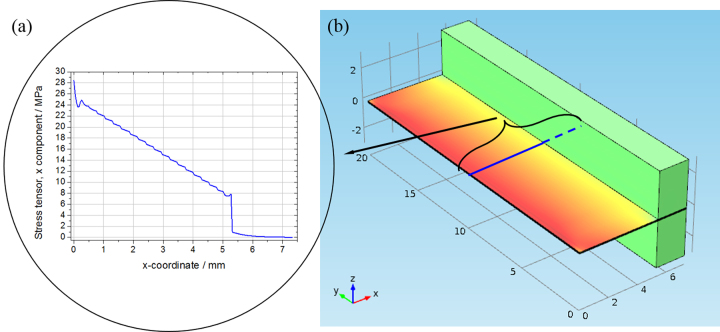
The output performance under different vibration accelerations (ACC) were measured at the optimum working frequency with optimum external load, and the result is shown in Fig. 9. According to Eq. (8) and Eq. (14), the output power density increases quadratically with the vibration acceleration ACC. The CFECS also indicates that P∝ACC² and V_p-p∝ACC, as shown with the blue dash line and black solid line in Fig. 9. It is seen that the device behaves as predicted when ACC ≤ 0.5g while fails in following the expected output power for ACC ≥ 0.625g. The maximum stress in the PVDF beam occurs at the top or bottom surface of the fixed end of the beam and it reaches 28.5 MPa (close to the analytical result) under 0.5g vibration excitation as simulated by CFECS (Fig. 10). As the stress approaches σ_yield, the output power is lower than that simulated from the linear stress-strain relationship, because PVDF begins to yield and some non-linear effects start to be prominent. Therefore, the power under 0.5g vibration excitation has been proved to be the maximum one under the allowable stress and the proposed device configuration is well-optimized.

Fig. 9.

Influence of vibration acceleration on V_p-p and P of the device which is excited at resonant frequency and connected to optimum resistance load.

Fig. 10.

The distribution of stress in the x-direction simulated with COMSOL, showing that the maximum stress reaches 28.5 MPa. (a) The distribution of stress in x direction. (b) The distribution of stress on the whole surface.

4. Conclusion

An optimization strategy based on an uncoupled point-mass-model analysis on PVDF-based PEH devices has been presented in this paper. It is shown that with given vibration environment, the power density of the PVDF-based PEH is related to the maximum stress in the PVDF beam that is limited by the yield strength of the material. By properly selecting $\frac{t_p}{L_e^2}$, the maximum allowed stress in the PVDF beam can be achieved, thus enabling maximum power density output. The resonant frequency also affects proportionally the output power density, but it is subject to the vibration source which generally has low frequency.

An example of optimized device has been proposed according to the strategy. The optimal output power density of the device under the maximum allowable stress can be obtained as high as 15.4 mW/cm³. A finite element simulation method was adopted and a practical device was fabricated to verify the analytical model. In accordance with the exact design calculated from the model, simulation results and experimental measure fit well in terms of the resonant frequency (34.4 Hz) and the maximum stress (28.5 MPa). The power output and power density were 112.8 μW and 8.61 mW/cm³ respectively, which was lower than the analytical result, because the influence of the external resistance and the additional capacitance are ignored in the analytical model. Nevertheless, the measured power density is still the highest as far as we have seen in the literature of PVDF-based PEH devices, which proves the efficiency of our optimization approach. It is noted that the impact of additional capacitance can be further diminished by selective patterning of the electrode on the beam and thus a higher output power density can be expected.

Declarations

Author contribution statement

Jundong Song: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Guanxing Zhao: Conceived and Designed the experiments; Performed the experiments; Analyzed and interpreted the data.

Bo Li: Analyzed and interpreted the data; Wrote the paper.

Jin Wang: Conceived and Designed the experiments; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This work was supported by Guangdong Natural Science Fund for Distinguished Young Scholars (Grant No. 2016A030306020), Guangdong Youth Talent Plan (Grant No. 2015TQ01C536), Shenzhen Special Fund for the Development of Emerging Industries (Grant No. JCYJ20140417115840233) and Shenzhen Peacock Plan (Grant No. KQCX20140521161756228).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.