IMPROVING EFFICIENCY IN BIOMARKER INCREMENTAL VALUE EVALUATION UNDER TWO-PHASE DESIGNS

Abstract

Cost-effective yet efficient designs are critical to the success of biomarker evaluation research. Two-phase sampling designs, under which expensive markers are only measured on a subsample of cases and non-cases within a prospective cohort, are useful in novel biomarker studies for preserving study samples and minimizing cost of biomarker assaying. Statistical methods for quantifying the predictiveness of biomarkers under two-phase studies have been proposed (Cai and Zheng, 2012; Liu, Cai and Zheng, 2012). These methods are based on a class of inverse probability weighted (IPW) estimators where weights are ‘true’ sampling weights that simply reflect the sampling strategy of the study. While simple to implement, existing IPW estimators are limited by lack of practicality and efficiency. In this manuscript, we investigate a variety of two-phase design options and provide statistical approaches aimed at improving the efficiency of simple IPW estimators by incorporating auxiliary information available for the entire cohort. We consider accuracy summary estimators that accommodate auxiliary information in the context of evaluating the incremental values of novel biomarkers over existing prediction tools. In addition, we evaluate the relative efficiency of a variety of sampling and estimation options under two-phase studies, shedding light on issues pertaining to both the design and analysis of biomarker validation studies. We apply our methods to the evaluation of a novel biomarker for liver cancer risk conducted with a two-phase nested case control design (Lok et al., 2010).

1. Introduction

Novel biomarkers have the potential to improve risk prediction for diseases such as cancer. Due to the cost associated with biomarker measurement, the improvement in the predictive performance of a model enriched with novel biomarkers over a model with only clinical risk factors, throughout referred to as the incremental value (IncV) of the novel biomarkers, needs to be rigorously assessed before incorporating the enriched risk model into routine clinical practice. A major barrier to validating prediction models is that measuring novel markers from a large prospective cohort study may be too expensive, especially if the event rate is low. Two subcohort sampling designs, the case cohort (CCH) (Prentice, 1986) and nested case control (NCC) (Thomas, 1977), are often employed as cost-effective alternatives to the standard full-cohort design, and have been recently adopted for risk marker evaluation studies (Lok et al., 2010; Wang et al., 2011).

These designs, while cost effective, can be challenging due to the outcome-dependent missingness on the marker information. Statistical methods have been developed to incorporate such missingness in estimating relative and absolute risk parameters (Self et al., 1988; Borgan, Goldstein and Langholz, 1995; Langholz and Borgan, 1997). However, evaluation of the clinical utility of risk markers adds another level of complexity, requiring additional estimation of distribution of risks in the population and its summary indices. Appropriate statistical methods for risk model evaluation under two-phase studies and guidance to efficiently conduct the design are still lacking. Novel statistical tools that can be used for estimating the predictive performance of a single biomarker have also been developed for both CCH and NCC studies (Cai and Zheng, 2012; Liu, Cai and Zheng, 2012). In these approaches, simple inverse probability-weighted (IPW) estimators were considered, with weights as the reciprocals of true selection probabilities calculated based on the observed data and study design.

While such IPW estimators are simple to implement, limitations exist. First, in many practical situations, two-phase sampling plans can be quite complicated, due to practical considerations such as the need to reuse samples previously assayed for other studies or missing measurements due to inadequate samples. Retrieving ‘true’ sampling weights can therefore be considerably difficult in practice. In addition, these simple IPW estimators tend to be quite inefficient because they discard information from individuals without biomarker information. When auxiliary variables related to both outcome and incomplete marker measurement are available from the entire cohort, incorporating such information in estimation may lead to improvement in efficiency (Breslow et al., 2009a,b; Saegusa and Wellner, 2013). In this manuscript we propose novel estimators of prediction performance measures for two-phase studies, aiming to improve efficiency and practicality over existing estimators. Our estimators are based on the idea of augmentation, previously considered for estimating relative risk parameters under case-cohort studies. The augmented estimators adopt the IPW principal but use nonparametrically estimated weights based on auxiliary information.

Our second goal is to address study design issues, particularly regarding the impact of matching on estimation efficiency when the goal is to evaluate the IncV of novel biomarkers. In settings where routine markers or other auxiliary information exist, matching controls to cases on baseline predictors is usually considered. Matching is frequently adopted as a way to improve efficiency, particularly for the estimation of relative risk parameters (Breslow et al., 1980). However, little is known regarding whether matching improves efficiency for the estimation of prediction performance and IncV measures. In addition, it has been previously noted that using augmented weights can lead to the efficiency gain of hazard ratio parameters for the fully observed covariates in a Cox regression model, but not so much for the partially observed biomarkers (Qi, Wang and Prentice, 2005). The extent of efficiency gain due to augmentation for the estimation of prediction performance or IncV parameters has not yet been studied. In this paper, we perform extensive numerical studies to provide insight on the connection between the augmented estimators under minimally matched sampling designs and the simple IPW estimators under matched/stratified designs. We evaluate the relative efficiency of a variety of sampling and estimation options to identify strategies that are both efficient and practical.

2. Model Specification and General Estimation under Two-phase Studies

2.1. Notation

Suppose the full cohort has N individuals from the targeted population followed prospectively. Due to censoring, the underlying full cohort data consist of N i.i.d copies of the vector, $\mathcal{D}=\left\{{\mathbf{D}}_i={\left(X_i,{\delta }_i,{\mathbf{Y}}_i^{\top },{\mathbf{Z}}_i^{\top }\right)}^{\top },i=1,\cdots ,N\right\}$, where X_i = min(T_i, C_i), δ_i = I(T_i ≤ C_i), T_i and C_i denote failure time and censoring time respectively, and subscript i indexes the subjects in the cohort. Here, ${\mathbf{Y}}_i=\left({\mathbf{Y}}_{\text{old}i}^{\top },{\mathbf{Y}}_{\text{new}i}^{\top }\right)$ is the vector of all potential risk predictors, Y_oldi includes a set of routine markers available for all, Y_newi represents novel risk markers only ascertained at the second phase for a selected subset of individuals, and Z_i represents auxiliary variables including matching and stratification variables available for the entire cohort. While ${\mathbf{W}}_i={({\mathbf{Z}}_i^{\top },{\mathbf{Y}}_{\text{old}i})}^{\top }$ is available for the entire cohort, Y_newi is only available if V_i = 1, where V_i is a binary variable indicating whether subject i is selected to the phase II subcohort. The two-phase sampling only depends on X_i, δ_i and Z_i, with the true sampling probability ${\stackrel{\sim }{\pi }}_i=P\left(V_i=1|\mathcal{D}\right)=P\left(V_i=1|X_i,{\delta }_i,{\mathbf{Z}}_i\right)$ known by design. We also assume that the risk ${ℛ}_t\left(\mathbf{Y}\right)=P\left(T_i\le t|{\mathbf{Y}}_i=\mathbf{Y}\right)$ follows a semi-parametric transformation model (Cheng, Wei and Ying, 1995, 1997; Zeng and Lin, 2006)

$$1-{ℛ}_t\left(\mathbf{Y}\right)={\mathcal{T}}_0\left[\text{log}\left\{H\left(t\right)\right\}+{\beta }_{\text{new}}^{\top }{\mathbf{Y}}_{\text{new}}+{\beta }_{\text{old}}^{\top }{\mathbf{Y}}_{\text{old}}\right]={\mathcal{T}}_0\left[\text{log}\left\{H\left(t\right)\right\}+{\beta }^{\top }\mathbf{Y}\right],$$ (2.1)

where H(t) is an increasing function and ${\mathcal{T}}_0$ is a cumulative distributional function. When ${\mathcal{T}}_0\left(x\right)=\text{exp}\{-\text{exp}(x\left)\right\}$, the model corresponds to the proportional hazards model (Cox, 1972).

2.2. A General Inverse Probability Weighted Framework for Two-phase Studies

To incorporate outcome dependent missingness in Y_new, estimation of IPW procedures is based on subjects with V_i = 1 and reweight the ith observation by ω_i = V_i/π_i. Consider a generic IPW statistic $\widehat{\mathrm{ℝ}}=N^{-\frac{1}{2}}{\displaystyle {\sum }_{i=1}^N{\omega }_i{\mathbf{R}}_i}$, where E(R_i) = 0. An obvious choice for π_i is the true sampling probability ${\stackrel{\sim }{\pi }}_i=P\left(V_i=1|\mathcal{D}\right)$, which leads to a class of True Weights based IPW (TIPW) statistics ${\widehat{\mathrm{ℝ}}}^{\text{TIPW}}=N^{-\frac{1}{2}}{\displaystyle {\sum }_{i=1}^N{\stackrel{\sim }{\omega }}_i{\mathbf{R}}_i}$. The form of ${\stackrel{\sim }{\pi }}_i$ can be obtained explicitly for both stratified CCH (sCCH) (Gray, 2009; Liu, Cai and Zheng, 2012) and NCC (Samuelsen, 1997; Cai and Zheng, 2012) designs. See Appendix A of the supplementary article (Zheng et al., 2017) for details.

When ${\stackrel{\sim }{\pi }}_i$ is not directly available from the study and/or to improve efficiency over the simple TIPW estimators, we focus on AIPW estimators that leverage information on auxiliary variables W by non-parametrically estimating π_i given W_i. The AIPW approach replaces ${\stackrel{\sim }{\omega }}_i$ with an augmented weight ${\widehat{\omega }}_i=V_i/{\widehat{\pi }}_i$, where ${\widehat{\pi }}_i=\widehat{\pi }\left({\mathbf{W}}_i\right)$ is an estimate of ${\stackrel{\sim }{\pi }}_i$ using W_i. The key to the efficiency gain from the AIPW approach is to choose W and the estimator $\widehat{\pi }(·)$ such that $E\left({\widehat{\omega }}_i|{\mathbf{W}}_i\right)\approx 1$ and W is highly correlated with R_i. For example, one may consider ${\mathbf{W}}_i^{\text{NCC}}={\left({\delta }_i,X_i,{\mathbf{Z}}_i^{\top },{\mathbf{Y}}_{\text{old}i}^{\top }\right)}^{\top }$ for mNCC design, and ${\mathbf{W}}_i^{\text{CCH}}={\left({\delta }_i,{\mathbf{Z}}_i^{\top },{\mathbf{Y}}_{\text{old}i}^{\top }\right)}^{\top }$ for sCCH to enable both consistent estimation of the sampling weights and efficiency improvement by leveraging full cohort information on Y_oldi.

When W_i is discrete, a natural choice for $\widehat{\pi }(·)$ is the empirical proportion based on the observed data: $\widehat{\pi }\left(\mathbf{w}\right)=\frac{{\displaystyle {\sum }_{i=1}^N{V}_{i}I\left({\mathbf{W}}_i=\mathrm{w}\right)}}{{\displaystyle {\sum }_{i=1}^{N}I\left({\mathbf{W}}_i=\mathrm{w}\right)}}$However, W_i often involves continuous variables. For example, for NCC designs, the sampling is dependent on X; thus, W needs to include X to ensure the consistency of the AIPW estimators. To incorporate continuous W, one may consider the Nadaraya-Watson estimator,

$$\widehat{\pi }\left(\mathbf{w}\right)=\frac{{\displaystyle {\sum }_{i=1}^N{V}_i{K}_h\left(\mathbf{w}-{\mathbf{W}}_i\right)}}{{\displaystyle {\sum }_{i=1}^N{K}_h\left(\mathbf{w}-{\mathbf{W}}_i\right)}}$$ (2.2)

where K_h(·) = K(·/h)/h, K is a symmetric kernel density function, and h > 0 is the bandwidth. Selection of appropriate h can follow the recommendations in Wang and Wang (2001) and Qi, Wang and Prentice (2005). Since the IPW estimators could be biased if ${\widehat{\pi }}_i$ does not consistently estimate $P\left(V_i=1|\mathcal{D}\right)$, such a widely applicable nonparametric estimator, applicable to a wide range of practical situations, is appealing.

Asymptotic Behavior of AIPW Estimators

Making inference under a two-phase design with weight is generally difficult because the sampling scheme leads to weak correlation between the V_i’s, which is not ignorable even in large samples. Derivations for the asymptotic properties of the AIPW estimators accounting for such correlations are given in the Appendix B of the supplementary article (Zheng et al., 2017). For ease of presentation, we focus on a setting where all cases are selected and controls are sampled according to the CCH or NCC design without additional matching. We also show in the Appendix B that the variance reduction, ${\mathrm{\Delta }}_{\mathbf{R}}=\text{Var}({\widehat{\mathrm{ℝ}}}^{\text{TIPW}})-\text{Var}({\widehat{\mathrm{ℝ}}}^{\text{AIPW}})$ is always great than or equal to 0, and thereby justifies the efficiency gain by AIPW estimators over the TIPW estimators.

3. Accuracy and Incremental Value Evaluation

3.1. Parameters of Interest

For any subvector of Y, Y_*, and the associated risk model for ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)\equiv P\left(D_t=1|{\mathbf{Y}}_{\ast }\right)$, Y_* affects D_t only through the risk score ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$. Thus, we quantify the predictiveness of Y_* based on the predictiveness of ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$. One main goal here is to quantify the prediction performance of a risk score ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$ for predicting D_t = I(T ≤ t), for various choices of ${ℛ}_t^{\ast }$. An array of measures can be considered for such evaluations. Key summary indices for characterizing the accuracy of ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$ in classifying D_t include

$${\text{TPR}}_t^{\ast }\left(p\right)=P\left[{ℛ}_t^{\ast }\left(\mathbf{Y}\right)\ge p|T\le t\right]{\text{and}\text{FPR}}_t^{\ast }\left(p\right)=P\left[{ℛ}_t^{\ast }\left(\mathbf{Y}\right)\ge p|T>t\right],$$

$${\text{PPV}}_t^{\ast }\left(p\right)=P\left[T\le t|{ℛ}_t^{\ast }\left(\mathbf{Y}\right)\ge p\right]{\text{and}\text{NPV}}_t^{\ast }\left(p\right)=P\left[T>t|{ℛ}_t^{\ast }\left(\mathbf{Y}\right)<p\right],$$

where p is a risk threshold that can potentially be used to form different clinical decisions.

The pair of summaries ${\text{TPR}}_t^{\ast }\left(p\right)$ and ${\text{FPR}}_t^{\ast }\left(p\right)$ specifies the cumulative distribution of risks among t-year cases with D_t = 1 and non-cases with D_t = 0, respectively, and is a building block for other measures. For example, taking D_t as a binary outcome for a fixed t, the proportion of t-year cases followed (Pfeiffer and Gail, 2011) can be expressed as ${\text{PCF}}_t^{\ast }\left(v\right)={\text{TPR}}_t^{\ast }\left\{{\mathcal{V}}^{\ast -1}\left(1-v\right)\right\}$, where ${\mathcal{V}}^{\ast }\left(p\right)\equiv \mathrm{P}\left\{{ℛ}_t^{\ast }\left(\mathbf{Y}\right)\le p\right\}$. Its inverse function ${\text{PNF}}_t^{\ast }\left(p\right)={\text{PCF}}_t^{\ast -1}\left(p\right)$ is the fraction of the general population at the highest risk that needs to be followed to ensure that a fraction p of the t-year cases will be captured.

When no specific risk thresholds are of key interest, one may consider summary measures to complement the display of case and control risk distributions. For example,

$${\text{AUC}}_t^{\ast }={\displaystyle \int {\text{TPR}}_t^{\ast }\left\{{\text{FPR}}_t^{\ast -1}\left(u\right)\right\}du=P\left\{{ℛ}_t^{\ast }\left({\mathbf{Y}}_i\right)>{ℛ}_t^{\ast }\left({\mathbf{Y}}_j\right)|T_i\le t,T_j>t\right\}}$$

is a time-dependent version of the area under the ROC curve (AUC), which provides a measure of separation between the distributions of ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$ among t-year cases and non-cases. Another frequently used prediction performance measure is the difference in mean risks (DMR) between cases and non-cases at time t, which is related to the Integrated Discrimination Improvement (IDI) statistic for comparing risk models (Pencina et al., 2008), ${\text{DMR}}_t^{\ast }=E\left\{{ℛ}_t^{\ast }\left(\mathbf{Y}\right)|T\le t\right\}-E\left\{{ℛ}_t^{\ast }\left(\mathbf{Y}\right)|T>t\right\}$.

To quantify the IncV in risk prediction based on a generic prediction summary index denoted by ${\mathcal{A}}_t$, one may consider ${\text{IncV}}_{{\mathcal{A}}_t}={\mathcal{A}}_t^{\text{upd}}-{\mathcal{A}}_t^{\text{old}}$, where ${\mathcal{A}}_t^{\text{upd}}$ is evaluated for the updated model ${ℛ}_t\left(\mathbf{Y}\right)$ constructed with $\mathbf{Y}={\left({\mathbf{Y}}_{\text{new}}^{\top }{\mathbf{Y}}_{\text{old}}^{\top }\right)}^{\top }$ as predictors, and ${\mathcal{A}}_t^{\text{old}}$ is the corresponding value for the risk model ${ℛ}_t^{\text{old}}\left(\mathbf{Y}\right)=P\left(D_t=1|{\mathbf{Y}}_{\text{old}}\right)$ developed using only Y_old.

3.2. Estimation and Inference of Accuracy Summaries and IncV

We now investigate the AIPW estimation procedures for the evaluation of IncV under the semi-parametric transformation model as specified in (2·1). Specifically following the approaches taken in Murphy, Rossini and Van der Vaart (1997) and Zeng and Lin (2006), the model parameters $\mathit{\beta }={\left({\mathit{\beta }}_{\text{old}}^{\top },{\mathit{\beta }}_{\text{new}}^{\top }\right)}^{\top }$ can be obtained by maximizing a weighted semiparametric likelihood:

$$\widehat{\ell }\left(H,\mathit{\beta }\right)={\displaystyle \sum _{i=1}^N{\widehat{w}}_i\left({\delta }_i\left[\text{log}{\lambda }_1\left\{e^{{\beta }^{\top }{\mathbf{Y}}_{\mathbf{i}}}H\left(X_i\right)\right\}+\text{log}\mathrm{\Delta }H\left(X_i\right)+{\mathit{\beta }}^{\top }{\mathbf{Y}}_{\mathbf{i}}\right]-{\mathrm{\Lambda }}_1\left\{e^{{\mathit{\beta }}^{\top }{\mathbf{Y}}_{\mathbf{i}}}H\left(X_i\right)\right\}\right),}$$

where ${\mathrm{\Lambda }}_1\left(x\right)=-\text{log}{\mathcal{T}}_1\left(x\right),{\mathcal{T}}_1\left(x\right)={\mathcal{T}}_0\left\{\mathit{log}\right(x\left)\right\}$ and λ₁(x) = dΛ₁(x)/dx, ΔH(x) = H(x) − H(x−). With $\widehat{\mathit{\beta }}$ as estimators for ß, we can calculate ${\widehat{ℛ}}_t\left(\mathbf{Y}\right)=1-{\mathcal{T}}_0\left[\text{log}\left\{\widehat{H}\left(t\right)\right\}+{\widehat{\beta }}^{\top }\mathbf{Y}\right]$, where $\widehat{H}\left(t\right)=\widehat{H}\left(t;\widehat{\beta }\right)$.

To estimate the pair of key predictive performance summaries, ${\text{TPR}}_t^{\ast }\left(p\right)$ and ${\text{FPR}}_t^{\ast }\left(p\right)$, for a generic risk function ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$, we first note that under model (2.1),

$${\text{TPR}}_t^{\ast }\left(p\right)=\frac{E\left\{I\left({ℛ}_t^{\ast }\left(\mathbf{Y}\right)\ge p\right){ℛ}_t\left(\mathbf{Y}\right)\right\}}{E\left\{{ℛ}_t\left(\mathbf{Y}\right)\right\}}{\text{ and FPR}}_t^{\ast }\left(p\right)=\frac{E\left[I\left({ℛ}_t^{\ast }\left(\mathbf{Y}\right)\ge p\right)\left\{1-{ℛ}_t\left(\mathbf{Y}\right)\right\}\right]}{E\left\{1-{ℛ}_t\left(\mathbf{Y}\right)\right\}}.$$

We assume that (2.1) holds but allow the risk function ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)$ to be derived from a potentially mis-specified submodel. This along with the AIPW principle motivates us to estimate ${\text{TPR}}_t^{\ast }\left(p\right)$ and ${\text{FPR}}_t^{\ast }\left(p\right)$ respectively as

$${\widehat{\text{TPR}}}_t^{\ast }\left(p\right)=\frac{{\displaystyle {\sum }_{i=1}^N{\widehat{\omega }}_i\widehat{{ℛ}_t}\left({\mathbf{Y}}_i\right)I\left\{{\widehat{ℛ}}_t^{\ast }\left({\mathbf{Y}}_i\right)\ge p\right\}}}{{\displaystyle {\sum }_{i=1}^N{\widehat{\omega }}_i\widehat{{ℛ}_t}\left({\mathbf{Y}}_i\right)}},$$ (3.3)

$${\widehat{\text{FPR}}}_t^{\ast }\left(p\right)=\frac{{\displaystyle {\sum }_{i=1}^N{\widehat{\omega }}_i\left\{1-\widehat{{ℛ}_t}\left({\mathbf{Y}}_i\right)\right\}I\left\{{\widehat{ℛ}}_t^{\ast }\left({\mathbf{Y}}_i\right)\ge p\right\}}}{{\displaystyle {\sum }_{i=1}^N{\widehat{\omega }}_i\left\{1-\widehat{{ℛ}_t}\left({\mathbf{Y}}_i\right)\right\}}},$$ (3.4)

where ${\widehat{ℛ}}_t^{\ast }\left(\mathbf{Y}\right)$ is the estimated risk function derived under the submodel for ${ℛ}_t^{\ast }\left(\mathbf{Y}\right)=P\left(D_t=1|{\mathbf{Y}}_{\ast }\right)$. Subsequently, we may construct augmented estimators for other risk parameters. For example, we estimate ${\text{PCF}}_t^{\ast }\left(v\right)$ as ${\widehat{\text{PCF}}}_t^{\ast }\left(v\right)={\widehat{\text{TPR}}}_t^{\ast }\left\{\widehat{{\mathcal{V}}^{\ast -1}}\left(1-v\right)\right\}$, and ${\text{PNF}}_t^{\ast }\left(q\right)$ as ${\widehat{\text{PNF}}}_t^{\ast }\left(q\right)={\widehat{\text{PCF}}}_t^{\ast -1}(q)$, where ${\widehat{\mathcal{V}}}^{\ast }\left(p\right)=N^{-1}{\displaystyle {\sum }_{i=1}^N{\widehat{w}}_{i}I\left\{{\widehat{ℛ}}_t^{\ast }\left({\mathbf{Y}}_i\right)\le p\right\}}$. An estimator for ${\text{DMR}}_t^{\ast }$ is ${\widehat{\text{DMR}}}_t^{\ast }={\widehat{\text{ITP}}}_t^{\ast }-{\widehat{\text{IFP}}}_t^{\ast }$, with ${\widehat{\text{ITP}}}_t^{\ast }={\int }_p{\widehat{\text{TPR}}}_t^{\ast }\left(p\right)dp$ and ${\widehat{\text{IFP}}}_t^{\ast }={\int }_p{\widehat{\text{FPR}}}_t^{\ast }\left(p\right)dp$, and an estimator for ${\text{AUC}}_t^{\ast }$ is ${\widehat{\text{AUC}}}_t^{\ast }={\int }_u{\widehat{\text{TPR}}}_t^{\ast }\left(u\right){\widehat{\text{FPR}}}_t^{\ast -1}\left(du\right)$.

For IncV evaluations, we compare the prediction performance of the ${ℛ}_t\left(\mathbf{Y}\right)$ to that of ${ℛ}_t^{\text{old}}\left(\mathbf{Y}\right)$ obtained by fitting (2.1) with Y_old only. When the full cohort data are available for Y_old, the estimation of model parameters associated with P(D_t = 1 | Y_old) can be obtained using the standard procedures as in Zeng and Lin (2006) without weighting.

For a generic prediction accuracy parameter ${\mathcal{A}}_t$ representing either TPR_t(p), FPR_t(p), PCF_t(v), PNF_t(p), AUC_t or DMR_t, let ${\mathcal{A}}_t^{\text{upd}}$, ${\mathcal{A}}_t^{\text{old}}$, ${\widehat{\mathcal{A}}}_t^{\text{upd}}$ and ${\widehat{\mathcal{A}}}_t^{\text{old}}$ denote the true and estimated accuracy for ${ℛ}_t\left(\mathbf{Y}\right)$ and ${ℛ}_t^{\text{old}}\left(\mathbf{Y}\right)$, respectively. The IncV with respect to ${\mathcal{A}}_t$, ${\mathrm{IncV}}_{\mathcal{A}t}={\mathcal{A}}_t^{\text{upd}}-{\mathcal{A}}_t^{\text{old}}$, can be calculated as ${\widehat{\mathrm{IncV}}}_{{\mathcal{A}}_t}={\widehat{\mathcal{A}}}_t^{\text{upd}}-{\widehat{\mathcal{A}}}_t^{\text{old}}$.

To construct confidence intervals for the accuracy and IncV parameters, in the supplementary article Appendix C (Zheng et al., 2017), we provide the asymptotic variances of ${\widehat{\mathrm{ℝ}}}_{{\mathcal{A}}_t}^{\text{IncV}}$ for the CCH and NCC design based on the asymptotic linear expansion of ${\widehat{\mathrm{ℝ}}}_{{\mathcal{A}}_t}^{\text{upd}}$ and ${\widehat{\mathrm{ℝ}}}_{{\mathcal{A}}_t}^{\text{IncV}}$.

4. Simulations

We conducted simulations to examine the finite sample performances of our proposed procedures under both two-phase designs and the impact of different sampling and analysis strategies on efficiency. With a cohort of size N = 5000, we first generated Y_old and Y_new from a zero-mean bivariate normal distribution with unit variances and correlation 0.8. The event time T was generated by conditioning on Y_old and $P(T\le t|\mathbf{Y})={\mathcal{T}}_0\{\text{log}\left({\alpha }_{0}t\right)+{\beta }_1{Y}_{\text{old}}+{\beta }_2{Y}_{\text{new}}\}$, with ${\mathcal{T}}_0\left(x\right)=1-\text{exp}\{-\text{exp}(x\left)\right\}$, where β₁ = log(3), β₂ = log(2) and α₀ was chosen to be (i) 0.1 for studying CCH designs, representing a moderate event rate scenario; and (ii) 0.01 for NCC designs, representing a rare case scenario. The censoring time C was taken to be the minimum of 2 and W, where W followed a gamma distribution, with a shape parameter of 2.5 and a rate parameter of 2. The event rate was about 20% under the setting for studying CCH designs, and 4% under the setting for studying NCC designs. These two full cohort data generating mechanisms were used for all simulation settings, and a variety of sampling strategies were implemented to assemble the phase II data. For each sampling design and parameter of interest, we obtained two IPW estimators: one with true sampling weights, and one with the weights estimated by nonparametrically estimating P(V_i = 1 | W) as in Equation (2.2).

4.1. Finite Sample Performance of the Proposed Estimators

We first assessed the validity of our proposed inference procedures in finite samples. For simplicity, no additional matching variables were used for sampling. For the CCH design, we randomly sampled n₁ = 105 cases from {i : δ_i = 1} and n₀ = 3n₁ controls from {i : δ_i = 0}. For the NCC design, we included all individuals with δ = 1 as cases, and for each case, we randomly selected 3 controls from the risk set of the case. To estimate the sampling weights for augmentation, we let W = (δ, Y_old)^⊤ for CCH and W = (δ, X, Y_old)^⊤ for NCC.

Based on the results of 5000 simulated datasets as shown in supplementary article Table 1 (Zheng et al., 2017), we found that all point estimates had negligible bias. The asymptotic based standard error estimators approximated the empirical standard errors well with empirical coverage levels of the 95% confidence intervals close to the nominal level for all parameters except NPV under the NCC design. This was not surprising because, in this case, the true NPV levels were extremely close to 1, which made finite sample standard error and interval estimation generally difficult as in any binomial proportion estimation setting (Brown, Cai and Dasgupta, 2002). We also varied the values of bandwidth in the nonparametric kernels to evaluate the robustness of the proposed estimators. Varying bandwidths had little impact on estimates of accuracy summaries in the simulated settings as shown in supplementary article Table 2 (Zheng et al., 2017). Reducing cohort size to 1000 for CCH and 2000 for NCC showed efficiency improvement of AIPW estimators over TIPW estimators, with slightly increasing in bias. See supplementary article (Zheng et al., 2017) Table 3(a) and (b) for details.

4.2. Relative Efficiency of Different Sampling and Analytical Options

We conducted simulation studies to examine the effect of matching or stratification by a discrete variable Z on the efficiency of estimating various accuracy summaries. We let $Z={\displaystyle {\sum }_{l=1}^{2}I\left(Y_{\text{old}}\le y_{q_l}\right)}$, where y_q is the 100qth percentile of Y_old and {q₁, q₂} are chosen as (i) {0.5, 0.75} for the CCH design and (ii) {0.33, 0.66} for the NCC design. We compared the efficiency of AIPW and TIPW estimators obtained with data generated from different sampling designs, with and without matching on Z.

CCH Design

Irrespective of sampling strategy, a total of 150 cases with δ = 1 and 450 controls with δ = 0 were included in the phase II subcohort. Three commonly adopted sampling strategies were considered:

• Setting A (random): randomly sampled 150 cases and 450 controls without considering Z.

• Setting B (frequency matched): randomly sampled 150 cases, then sampled controls such that the distribution of Z among the selected controls was the same as that of the cases.

• Setting C (balanced design): sampled 50 cases and 150 controls from each stratum defined by the level of Z, which design led to oversampling categories with lower prevalence.

Under the CCH design, for any given parameter of interest $\mathcal{A}$ that is estimated via the TIPW approach as $\widehat{\mathcal{A}}$, it is possible to calculate the optimal sampling fractions to minimize the variance of $\widehat{\mathcal{A}}$ (Borgan et al., 2000). Suppose $\widehat{\mathcal{A}}-\mathcal{A}=N^{-1}{\displaystyle {\sum }_{i=1}^N{\stackrel{\sim }{\omega }}_i{R}_{\mathcal{A}i}+o_p(N^{-\frac{1}{2}})}$ and the target is to sample n₁ cases and n₀ controls. Then the optimal sampling fractions that minimize the variance of $\widehat{\mathcal{A}}$ are ${\pi }_{l1}^{\ast }$ and ${\pi }_{l0}^{\ast }$ for the cases and controls with Z = l, respectively, where

$${\pi }_{ld}^{\ast }=\frac{n_d}{N_d}\frac{\text{Var}{\left({\mathbf{R}}_{\mathcal{A}}|\delta =d,Z=l\right)}^{1/2}}{{\displaystyle {\sum }_{l^{\prime }=1}^L{v}_{l^{\prime }d}}\text{Var}{\left({\mathbf{R}}_{\mathcal{A}}|\delta =d,Z=j\right)}^{1/2}},$$

$v_{l^{\prime }d}={\displaystyle {\sum }_{i=1}^{N}I\left({\delta }_i=d,Z_i=l^{\prime }\right)/N_d}$ and $N_d={\displaystyle {\sum }_{i=1}^{N}I\left({\delta }_i=d\right)}$. Note that in practice, an estimate of ${\pi }_{ld}^{\ast }$ may only be available to assist in study design if preliminary data are available. In addition, such optimal sampling fractions tend to vary by specific measure – the sampling fractions optimal for one measure may not be optimal for the other. Thus, it is not possible to design a study to achieve optimal efficiency simultaneously for all measures. To mimic the most likely scenario in practice, we calculated optimal fractions for β_new and used them as the basis for sampling. The IPW estimators with true weights obtained under such a design (using sampling fraction optimal for β_new), denoted by TIPW^opt, were then used as the benchmark for comparing the efficiency of various standard designs and gauging the effect of augmentation.

Figure 1(a) shows the efficiencies of the TIPW and AIPW estimators obtained under various sampling strategies, relative to the TIPW^opt estimators. When true weights were used, the frequency matched design had similar efficiency as the optimal design and outperformed the random and balanced designs for a majority of the parameters investigated. However, for the accuracy parameters at various risk threshold levels, the efficiency of the frequency matching was much lower than the optimal design and was comparable to or sometimes worse than the random and balanced designs. On the other hand, the AIPW estimators were substantially more efficient than their corresponding TIPW estimators, except for β₂. Interestingly, the AIPW estimators under random sampling had efficiency comparable to or higher than those obtained from TIPW^opt for all parameters of interest. When comparing the AIPW estimators obtained across the three designs, the balanced design generally performed the worst. Although the frequency matched design achieves a slightly higher efficiency for a few parameters than the random design, the random design appeared to be much more robust with regard to efficiency of AIPW estimators across different parameters. The results here suggested that, in practice, considering a simple random sampling scheme at the design stage and then utilizing auxiliary information in the analysis step has the advantage in both practical simplicity and statistical efficiency.

Fig 1.

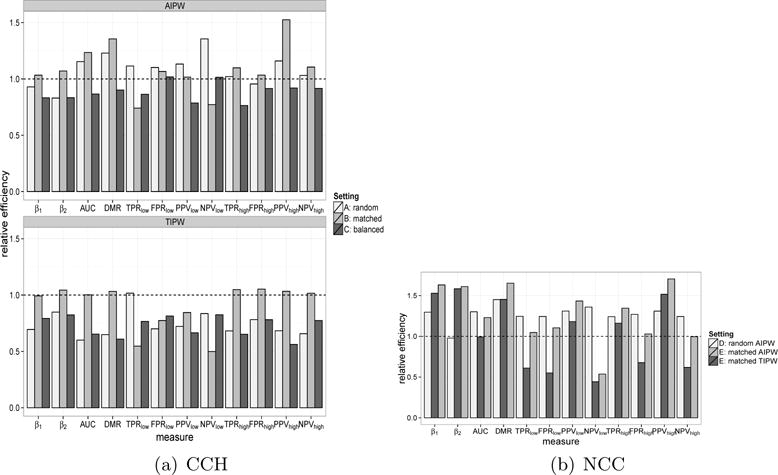
Relative efficiency (RE) of various predictive performance summaries by different designs. Figure (a): results for CCH designs. Setting A: simple random sampling; Setting B: matched design and Setting C: balanced design. TIPW (top panel) and AIPW (bottom pane) estimators for each setting are considered, using TIPW^opt as benchmark for efficiency. Figure (b) results for NCC designs. Setting D: simple random sample; Setting E: matched design. TIPW estimator under setting D is the benchmark for efficiency.

NCC design

For the NCC design, all cases were included and 3 controls were sampled from the risk sets of the cases according to the follow two strategies:

• Setting D (random): randomly sampled from the risk set of the case;

• Setting E (matched): randomly sampled from the case’s risk set and matched on the value of Z of the case.

Since no simple optimal sampling strategies can be implemented for the NCC design, we used the TIPW estimator under random sampling as the benchmark for comparison and present in Figure 1(b) the efficiencies of the TIPW and AIPW estimators obtained under these two designs relative to the benchmark estimator. The matched design led to the most efficient relative risk estimators for β₁ and β₂, however the efficiency gain did not directly translate to the estimation of performance summary parameters, and it may in fact lead to poorer efficiency compared to a simple random sampling design. Indeed, for a majority of summary performance parameters considered, Setting D, using a simple random sampling design with the proposed AIPW estimators, appeared to be the most efficient. The results further suggested the benefit of employing a simple random design followed by the AIPW estimation procedure. Stratifying/matching based on Y_old, while leading to improved efficiency for the regression parameters, could drastically sacrifice the efficiency for various accuracy parameters. On the other hand, the AIPW estimator with random sampling always resulted in efficiency improvement. Numerical results are presented in the supplementary article (Zheng et al., 2017) Table 4(a) and (b).

5. Example

Patients with hepatocellular carcinoma (HCC) often have poor prognosis due to late diagnosis. Since cirrhosis of any cause and chronic infection with hepatitis B virus (HBV) or hepatitis C virus (HCV) are the most common risk factors for HCC, surveillance of high-risk populations may detect tumors at an early stage when curative interventions can be implemented. Alpha fetoprotein (AFP) is the most widely used biomarker for HCC surveillance; however, its sensitivity and specificity in detecting early HCC are low. More reliable biomarkers for HCC surveillance and early detection are sought in order to improve the outcome of the disease.

The Hepatitis C Antiviral Long-Term Treatment against Cirrhosis (HALT-C) Trial included 1050 patients with chronic hepatitis C and bridging fibrosis or cirrhosis who failed to achieve a sustained virologic response (SVR) to combination therapy of pegylated interferon and ribavirin. Patients were randomized to low-dose pegylated interferon or no treatment and examined every 3 months for a total duration of 3.5 years. Blood samples were collected at each visit for subsequent research testing, including assays for HCC biomarkers. Ultrasound examinations were repeated 6 months after enrollment and again every 12 months. Patients with an elevated or rising AFP and those with new lesions detected by ultrasound were evaluated further by CT or MRI.

One goal of the HALT-C Trial was to identify and validate markers for HCC surveillance. As part of the trial, an NCC study was employed to assess and compare the accuracy of AFP and a novel serum biomarker, des-gamma-carboxy prothrombin (DCP), in predicting the risk of HCC. The NCC sub-cohort included all 39 HCC cases diagnosed during the follow-up. For each case, 2 controls without HCC, matched for treatment assignment and presence of cirrhosis on baseline biopsy, were selected from the risk set of the case. This resulted in a total of 77 controls in the NCC subcohort. The biomarkers were evaluated at multiple follow-up visits, and the results on the repeated markers were reported in Lok et al. (2010), where conditional logistic regression models were used to compare characteristics of HCC cases, and matched controls and unconditional logistic regression were used to evaluate the accuracy performance of the biomarkers.

To illustrate our proposed methods, only baseline measurements were considered for risk modeling. Logarithm transformed values were considered for both AFP and DCP, denoted by logAFP and logDCP, respectively. Due to low liver cancer incidence, methods that could improve efficiency would be helpful. For comparison, we obtained parameter estimates using both the TIPW and AIPW approaches, where for the AIPW approach, we let W = (X, δ, log AFP)^⊤ for augmentation. To build a risk model with both logAFP and logDCP, we considered fitting a Cox proportional hazards model. We obtained log hazard ratio (logHR) parameter estimates with the conditional logistic regression, TIPW, and AIPW methods. The conditional logistic regression method yielded a logHR estimate of 0.54 with a standard error (SE) of 0.27 for logAFP and 1.54 with a SE of 0.51 for logDCP, suggesting that DCP may serve as an independent risk factor for HCC beyond AFP. The logHR was estimated as 0.61 (SE: 0.22) for logAFP and 2.04 (SE: 0.33) for logDCP based on TIPW, and 0.82 (SE: 0.18) for logAFP and 1.95 (SE: 0.32) for logDCP based on AIPW. These results indicated that that the AIPW method provided more efficient estimates of the logHR parameters when compared to TIPW and conditional logistic regression methods.

We subsequently evaluated the 2-year predictive performance by combining logDCP and logAFP using the measures described in Section 3.1. The results for evaluating the full model with both logAFP and logDCP included are presented in the first two columns of Table 1. Across the measures we considered, point estimates from the two approaches in general were quite close; however, the AIPW estimators had substantially smaller standard errors than that of the TIPW estimators for most of the parameters. Combing AFP and DCP led to a good predictive model for predicting the 2-year risk of HCC, with AUC estimated as 0.81 (95%CI: [0.68,0.94]) based on TIPW, and 0.82 (95%CI: [0.75, 0.90]) based on AIPW. If the top 20% of the population based on the estimated risks is considered of high risks, then the proportion of individuals who will be diagnosed with HCC within two years, captured by the prediction rule, is 64% (95% CI: [38%, 89%]) based on the TIPW estimate, and 68% (95% CI: [53%, 81%]) based on the AIPW estimate.

Table 1.

Evaluation of biomarkers in predicting 2-year liver cancer incidence in Halt-C study. Shown below are TIPW and AIPW estimates along with their corresponding standard errors shown in parenthesis. The log-hazard ratios and accuracy parameters were estimated for 2-year risks estimated based on both (i) the full model with logAFP + logDCP; and (ii) the reduced model with logAFP alone. Also presented are the TIPW and AIPW estimates for IncV parameters of logDCP above and beyond logAFP.

	logAFP + logDCP		logAFP		IncV of logDCP
Parameters	TIPW (SE)	AIPW (SE)	TIPW (SE)	AIPW (SE)	TIPW (SE)	AIPW (SE)
β1	.614 (.221)	.822 (.177)	.542 (.206)	.771 (.168)	–	–
β2	2.043 (.333)	1.953 (.316)	–	–	–	–
AUC	.809 (.066)	.823 (.040)	.655 (.079)	.694 (.054)	.155 (.129)	.129 (.030)
DMR	.155 (.376)	.173 (.193)	.065 (.148)	.112 (.081)	.090 (.473)	.061 (.267)
ITPR	.168 (.389)	.188 (.199)	.108 (.036)	.142 (.015)	.060 (.353)	.045 (.193)
IFPR	.013 (.013)	.015 (.007)	.043 (.154)	.030 (.087)	−.029 (.126)	−.015 (.082)
TPR(.002)	.979 (.023)	.981 (.024)	.986 (.031)	.989 (.021)	−.007 (.031)	−.008 (.023)
FPR(.002)	.827 (.123)	.824 (.167)	.928 (.060)	.939 (.066)	−.101 (.073)	−.116 (.125)
PPV(.002)	.014 (.004)	.016 (.004)	.016 (.007)	.014(.009)	−.002 (.007)	.002 (.007)
NPV(.002)	.999 (.001)	.999 (.001)	.997 (.005)	.998(.005)	.001 (.006)	.001 (.006)
TPR(.02)	.529 (.287)	.562 (.083)	.201 (.098)	.328 (.050)	.328 (.292)	.234 (.069)
FPR(.02)	.112 (.070)	.114 (.051)	.069 (.328)	.099(.074)	.043 (.249)	.015 (.097)
PPV(.02)	.052 (.015)	.063 (.019)	.042 (.041)	.043 (.041)	.011 (.038)	.021 (.055)
NPV(.02)	.994 (.003)	.993 (.002)	.987 (.018)	.990 (.006)	.007 (.014)	.003 (.005)
PCF(.20)	.636 (.131)	.667 (.071)	.307 (.047)	.453 (.048)	.329 (.117)	.214 (.056)
PNF(.85)	.526 (.119)	.570 (.061)	.400 (.051)	.386 (.037)	.125 (.120)	.183 (.067)

To further evaluate whether adding DCP to the model substantially improves accuracy when compared to the model with AFP alone, we also fit a model with AFP alone and calculated the IncV of DCP with respect to various accuracy parameters as shown in Table 1. The ROC curves and risk distribution for both models are shown Figure 2. As seen in the figures, the enriched model always had higher TPF and higher PCF, but smaller PNF across different risk thresholds p. Formal tests of such observed incremental values for selected p can be based on the results presented in the last two columns in Table 1. For example, ${\text{IncV}}_{{\text{AUC}}_2}$ was estimated as 12.9% with 95% CI (7.0%, 18.7%) based on AIPW, indicating that adding DCP improved in prediction accuracy beyond AFP. In addition, there was also significant improvement with respect to PCF and PNF, with ${\text{IncV}}_{{\text{PCF}}_2\left(0.2\right)}$ estimated as 21.4% (95% CI: [10.4%, 32.3%]) and ${\text{IncV}}_{{\text{PNF}}_2\left(0.2\right)}$ estimated as 18.3% (95% CI: [5.1%, 31.4%]), based on AIPW. The TIPW approach, while generating similar point estimates, did not produce statistically significant IncV estimates for all parameters considered (Table 1). This example demonstrates the advantage of the proposed AIPW method for estimating accuracy summaries and IncV parameters, particularly when there are limited samples with available biomarker measurements.

Fig 2.

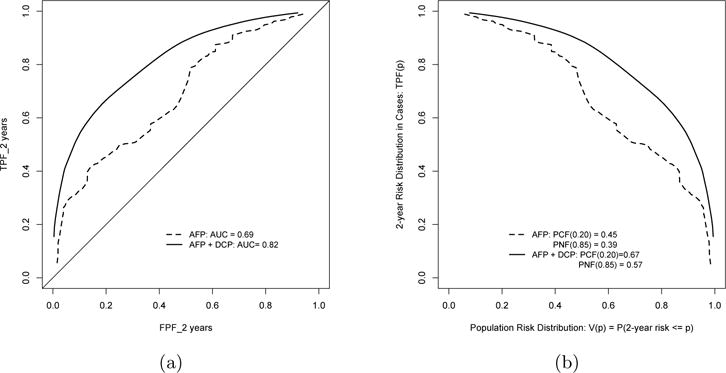
Comparing performance of two prediction models: model with AFP along (solid lines) and model with both AFP and DCP (dashed lines). (a) ROC curves for predicting 2-year risk of HCC with baseline biomarker measurements. (b): risk distribution curves for individuals who diagnosed with HCC in 2 years.

6. Discussion

Large cohort biomarker studies of rare diseases such as cancer require thoughtful planning, from selection of study subjects and measurement of key variables and auxiliary information to analytical strategies. Study design becomes even more demanding in biomarker research, when measurements are based on stored tissue or blood specimens. It is important in this setting to use research resources wisely to achieve optimal efficiency of the study. There is a paucity of appropriate statistical methods for biomarker assessment and guidance on design and analysis strategies to maximize efficiency. Practical and efficient statistical tools can enable clinical investigators to conduct more cost-effective studies and more efficiently allocate research resources.

This manuscript contributes to such an endeavor in two ways. First, we provide a general framework for more efficiently estimating prediction accuracy and IncV parameters via an AIPW approach under two-phase CCH or NCC designs. Our simulation studies and application of Halt-C biomarker validation studies indicate that the use of nonparametric weights to capture design selection is valid and yields significant efficiency gain. Furthermore, the proposed approach also provides a practical solution in study settings where the true design-based sampling probabilities are impractical to ascertain. In addition, previous work on biomarker evaluation with two-phase studies (Cai and Zheng, 2012; Liu, Cai and Zheng, 2012) only considered evaluating the performance of a single marker. We extend the scope of work to the evaluation of multivariate risk models and IncV of novel biomarkers under two-phase designs. Such extensions are non-trivial due to the complex structure induced by both the correlation among different risk markers and the sampling design.

Second, using extensive numerical studies, we demonstrated that stratification sampling for CCH studies or matching for NCC studies can be inefficient in many accuracy summaries when not done optimally. In the absence of preliminary data, it is often unclear what variables for matching, or what sampling fractions should be considered for stratification. A poor choice in matching variables may lead to loss in efficiency and unnecessary complications in analysis. Furthermore, the sampling fractions optimal for one parameter may not be optimal for another, and thus, no sampling strategies would be uniformly optimal across all parameters. Therefore, using a simple sampling scheme at the design stage and then improving estimation efficiency using the proposed augmented estimators in analysis would be a useful alternative to considering matched designs.

We have focused on the estimation of accuracy summaries with a semi-parametric approach to illustrate the AIPW approach. Alternatively, one may consider calculating the accuracy summaries with a nonparametric approach as was previously considered (Cai and Zheng, 2011), without relying on the assumption of Model 2.1. The estimating and inference procedures with AIPW described can be easily adopted to that setting. Our proposed estimators for evaluating the IncV of a new prediction model improves efficiency of the existing IPW-based estimators; however, they do not achieve full efficiency as compared with a full likelihood-based approach (Zeng and Lin, 2014). Future exploration of the additional gain when applying non-parametric likelihood-based procedures is warranted, even at the cost of increased computational burden. Finally, the validity of the class of IPW estimators is based on the assumption that selection is dependent on variables observable from the full cohort. Caution should be taken when the availability of biomarker measurement might be dependent on unmeasured variables.