Incorporating big data into treatment plan evaluation: Development of statistical DVH metrics and visualization dashboards

Abstract

Purpose

To develop statistical dose-volume histogram (DVH)–based metrics and a visualization method to quantify the comparison of treatment plans with historical experience and among different institutions.

Methods and materials

The descriptive statistical summary (ie, median, first and third quartiles, and 95% confidence intervals) of volume-normalized DVH curve sets of past experiences was visualized through the creation of statistical DVH plots. Detailed distribution parameters were calculated and stored in JavaScript Object Notation files to facilitate management, including transfer and potential multi-institutional comparisons. In the treatment plan evaluation, structure DVH curves were scored against computed statistical DVHs and weighted experience scores (WESs). Individual, clinically used, DVH-based metrics were integrated into a generalized evaluation metric (GEM) as a priority-weighted sum of normalized incomplete gamma functions. Historical treatment plans for 351 patients with head and neck cancer, 104 with prostate cancer who were treated with conventional fractionation, and 94 with liver cancer who were treated with stereotactic body radiation therapy were analyzed to demonstrate the usage of statistical DVH, WES, and GEM in a plan evaluation. A shareable dashboard plugin was created to display statistical DVHs and integrate GEM and WES scores into a clinical plan evaluation within the treatment planning system. Benchmarking with normal tissue complication probability scores was carried out to compare the behavior of GEM and WES scores.

Results

DVH curves from historical treatment plans were characterized and presented, with difficult-to-spare structures (ie, frequently compromised organs at risk) identified. Quantitative evaluations by GEM and/or WES compared favorably with the normal tissue complication probability Lyman-Kutcher-Burman model, transforming a set of discrete threshold-priority limits into a continuous model reflecting physician objectives and historical experience.

Conclusions

Statistical DVH offers an easy-to-read, detailed, and comprehensive way to visualize the quantitative comparison with historical experiences and among institutions. WES and GEM metrics offer a flexible means of incorporating discrete threshold-prioritizations and historic context into a set of standardized scoring metrics. Together, they provide a practical approach for incorporating big data into clinical practice for treatment plan evaluations.

Summary.

We demonstrate the utility of dose-volume histogram–based metrics and a visualization method developed in house. The metrics were used to summarize the historical experience for 2 patient groups: patients with head and neck cancer and patients with prostate cancer. This tool allows for simple and intuitive quantification to compare individual treatment plans with historical experiences. As such, this may allow for superior treatment planning, which has the potential to result in improved patient care.

Introduction

Traditional methods of evaluating patient treatment plans do not include a quantitative evaluation of dose-volume histogram (DVH) curves or metrics with respect to historical plans. How a given plan compares with previous experience is typically a qualitative evaluation (eg, “That DVH seems high compared to what I am used to”). Similarly, quantifying practice experiences in meeting DVH constraints for groups of patients to characterize differences over time, between clinics, or among technologies is difficult to summarize with only a few measures. The development of analytics in the form of metrics, visualization methods, and software applications that use historically grouped data to quantify overall practice experience and to score individual treatment plans could improve these comparisons.

These analytics could be used to help treatment planners benchmark individual plans against the range of clinically acceptable plans that are used at their own or other clinics. This would aid efforts to harmonize treatment plan quality within a clinic or facilitate the extension of experience from one clinic to others without requiring the common use of a specific advanced technology. Furthermore, these tools could be used to automate the cross validation of new optimization approaches against historical experiences or be incorporated into clinical trial submissions to quickly prescreen plans.

Methods that use geometric interrelationships that are determined from training subsets for treatment plan evaluation have been described previously as knowledge-based planning.1, 2, 3, 4, 5 The analytics and tools described here take a fundamentally different approach by using statistical characterization of DVH curves and metric value histories, derived from the full set of treated plans, to quantify consistency with objectives and practice norms. This addition increases the scope of knowledge used in plan evaluation.

The emergence of big data systems combined with the use of standardized nomenclatures to systematically aggregate DVH curves and metrics for all patient plans provides an opportunity to develop these analytics. Recently, we created the University of Michigan Radiation Oncology Analytics Resource (M-ROAR) to automate the assembly of a wide range of key data elements for all patients who are treated in the department. In this work, we describe the use of this resource to create and apply these analytics.

Methods and materials

The M-ROAR database (Microsoft SQL Server 2012) details treatments as well as a range of demographic, laboratory, oncologic, and other data elements.⁶ Extraction, transforming, and loading of DVH curves for all treated plans and as-treated plan sums from our current treatment planning system (Eclipse V13.6, Varian Medical Systems) into M-ROAR was carried out using custom programs (Microsoft C#.Net), the Eclipse Scripting Application Programming Interface, and SQL procedure code.

The DVH information stored was described using the DVH nomenclature used by Mayo et al.⁷. For the DVH curves, in addition to the traditional format of volume values stored at equally spaced dose intervals, we created a volume-focused format in M-ROAR. Absolute dose values (in Gy) for a set of 31 variably spaced (0.5%, 1%, and 5% increments) fractional volumes (100%, 99.5%, 99%-96% by 1% step size; 95%-5% by 5% step size; 4%-1% by 1% step size; 0.5%; and 0%) were stored as a set of (Dx%[Gy], x%) dose-volume pairs. Additionally, structure volumes and a standard set of DVH metrics including Max[Gy], Min[Gy], Mean[Gy], Median[Gy], D0.5cc[Gy], and DC0.5cc[Gy] were stored in the same records. The use of a volume-focused DVH format facilitated the construction of a statistical representation of DVH curves and ensures the ability to represent DVH curves independently of Max[Gy] with a small, fixed set of points.

Statistical methods to characterize and display data were developed using R 3.2.3 (https://www.r-project.org). Algorithms were developed to transform the prioritized, multicriterial threshold evaluations into a set of evaluation metrics that reflect both compliance with thresholds and historical experience. Metrics were developed to allow scoring on a per-structure or per-plan (all structure constraints together) basis.

Prototype dashboards, analytics, and display methods were transformed to clinically implementable applications as coded in C#.Net using a Windows Presentation Foundation (WPF Microsoft) with Eclipse Scripting Application Programming Interface to integrate with the treatment planning system. Charting graphics were implemented using the open source libraries of Oxyplot. Statistical methods were implemented using the open source libraries of Accord.Net. Statistical calculations with Accord.Net were benchmarked against corresponding methods in R.

DVH datasets were selected from the M-ROAR database. Because the plans that were stored corresponded to what was actually treated, they intrinsically define the range and time evolution of clinically acceptable plans. Data sets were selected to included intensity modulated radiation therapy/volumetric modulated arc therapy plans for three disease sites: head and neck, prostate, and liver stereotactic body radiation therapy (SBRT).

Statistical dose-volume histogram

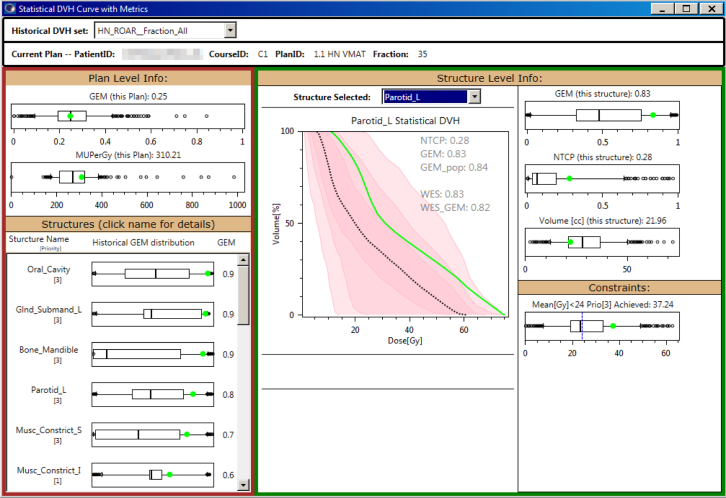
We developed a statistical DVH to quantify the comparison of individual DVH curves with historical experiences. Quantiles were calculated at 1% intervals for the Dx%[Gy] values of the DVH curves and stored in JavaScript Object Notation–formatted files to enable precalculation of historical values and sharing to support multi-institutional comparisons. For the display of individual treatment plans compared with historical experiences, a statistical DVH (Fig 1; plot in the middle of the dashboard) was implemented by overlaying the DVH curve for a user-selected structure (green curve) onto a set of shaded areas that corresponds to the 50%, 70%, and 90% confidence intervals (CIs) of the historical distribution and a dashed line that corresponds to the median.

Figure 1.

Statistical dose-volume histogram (DVH) dashboard quantifies comparison of statistical metrics for the current plan (green) versus historical experience. Statistical DVH (center) compares the DVH curve to historical experience for the median (dashed line), 50% confidence interval (CI; dark pink), 70% CI (intermediate pink), and 90% CI light pink. Box-and-whisker plots compare plan level (left panel) and structure level (right panel) metrics.

Weighted experience score

The weighted experience score (WES) was created to provide a single numerical value to assess the comparison of the present DVH curve within the context of historical experience. WES was calculated by evaluating the weighted cumulative probability (p_i) of historical Dx%[Gy] values being less than or equal to that of the present treatment plan. The magnitude of the components of the first eigenvector from principal component analysis of the Dx%[Gy] set was used to define weighting factor coefficients (wpca_i) to emphasize the Dx%[Gy] values that have the largest impact on minimizing the covariance in data set values. The volume intervals spacing the Dx%[Gy] points defined the weighting values for bin width (wb_i).

$$WES=\frac{{\sum }_{i}w{b}_i\times wpc{a}_i\times p_i}{{\sum }_{i}w{b}_i\times wpc{a}_i}$$ (1)

Generalized evaluation metric

Typically, DVH objectives are expressed as discrete elements with prioritizations (Table 1). A generalized evaluation metric (GEM) was defined to provide a continuous scoring value for a set of discrete threshold-priority constraints.

Table 1.

Head and neck constraints

Selected Structure	Priority	Constraint
Brain	3	Mean[Gy] <60 Gy
Brainstem	1	D0.10cc[Gy] <54 Gy
Brainstem_PRV03	1	D0.10cc[Gy] <54 Gy
OpticChiasm	1	D0.10cc[Gy] <54 Gy
OpticChiasm_PRV3	3	D0.10cc[Gy] <54 Gy
Cochlea_L	1	D0.10cc[Gy] <40 Gy
Cochlea_R	1	D0.10cc[Gy] <40 Gy
Musc_Constric_I	1	Mean[Gy] <20 Gy
Musc_Constric_S	3	Mean[Gy] <50 Gy
SpinalCord	1	D0.10cc[Gy] <45 Gy
SpinalCord_PRV05	1	D0.10cc[Gy] <50 Gy
Esophagus	1	Mean[Gy] <20 Gy
Eye_L	1	D0.10cc[Gy] <40 Gy
Eye_R	1	D0.10cc[Gy] <40 Gy
Glnd_Lacrimal_L	1	Mean[Gy] <30 Gy
Glnd_Lacrimal_R	1	Mean[Gy] <30 Gy
Larynx	1	Mean[Gy] <20 Gy
Lens_L	1	D0.10cc[Gy] <10 Gy
Lens_R	1	D0.10cc[Gy] <10 Gy
Lips	1	V35Gy[%] <5%
Bone_Mandible	3	D0.10cc[Gy] <70 Gy
OpticNrv_L	1	D0.10cc[Gy] <54 Gy
OpticNrv_PRV03_L	3	D0.10cc[Gy] <54 Gy
OpticNrv_R	1	D0.10cc[Gy] <54 Gy
OpticNrv_PRV03_R	3	D0.10cc[Gy] <54 Gy
Oral_Cavity	3	Mean[Gy] <30 Gy
Parotid_L	3	Mean[Gy] <24 Gy
Parotid_R	3	Mean[Gy] <24 Gy
Glnd_Submand_L	3	Mean[Gy] <30 Gy
Glnd_Submand_R	3	Mean[Gy] <30 Gy
Lobe_Temporal_L	3	D0.10cc[Gy] <60 Gy
Lobe_Temporal_R	3	D0.10cc[Gy] <60 Gy

Planning objectives are typically specified by physicians as a set of threshold values and integer values that express prioritization. Agreement is evaluated one by one without benefit of a single numerical scoring system that can rank individual plans in the context of historical experience.

Constraints were arranged so that increasing values are associated with being less desirable (eg, 1-TCP would be used instead of TCP). The functional form of the GEM used a sigmoidal curve with outputs ranging from 0 to 1 to score deviations from constraint values over the allowed range of plan values (≥0). GEM scores of [0, 0.5), 0.5, and (0.5, 1] corresponded to plan values less than, equal to, or exceeding the constraint values. The GEM was calculated as a normalized weighed sum of deviation scores. In keeping with clinical practice, low numerical values for prioritization (eg, 1) conveyed greater weight than higher values (eg, 3).

The normalized incomplete gamma function (P) was used to define the sigmoidal curve. P is the cumulative distribution function for the gamma probability distribution function (p.d.f.), operating over the same range of input values as DVH metrics (≥0). This choice supports future extension to Bayesian modeling because the gamma p.d.f. is a conjugate prior for a wide range of p.d.f. forms (gamma, poisson, exponential) that are used in modeling parameters. Details of the gamma p.d.f. and related functions are presented in Appendix A.

$$\text{GEM}=\frac{{\sum }_{\text{i}}\left[2^{-\left({\text{Priority}}_{\text{i }}-1\right)}\cdot \text{P}\left(k_i,\frac{PlanValu{e}_i}{{\theta }_i}\right)\right]}{{\sum }_{\text{i}}{2}^{-\left({\text{Priority}}_{\text{i}}-1\right)}}$$ (2)

If Upper 90% CI ≥ Constraint Value, the shape parameter k and scale parameter θ were solved numerically for each structure constraint so that $P\left(k_i,\frac{ConstraintValue}{{\theta }_i}\right)=0.5$ and $P\left(k_i,\frac{Upper90\%C{I}_i}{{\theta }_i}\right)=0.95$. If historical values were well below constraint values ($\text{Upper }90{\text{\% CI}}_{\text{i}}<ConstraintValu{e}_i$), k and θ were set to 100 times Constraint Value and 0.01, respectively, to approximate a steep step function.

With this formulation, interpretation of GEM scores is straightforward. A value of 0.5 indicates constraint value thresholds are met. Higher values, approaching the limit of 1, indicate failure to meet the constraint, with the rate of increase tied to the overall historical clinical experience of ability to meet the constraint.

The priorities that were used in calculating GEM were assigned according to the concerns of the prescribing physician (Table 1). They provide relative, qualitative guidance on which constraints to emphasize. In this calculation, we implemented a quantifiable definition of priority (Calculated_Priority) that can be benchmarked against historical experience. This enables deriving integer prioritizations on the basis of the historical record of clinical priorities. These may be useful in guiding the selection of assigned values.

$$Calculated\_Priority=Round\left(1-l{n}_2\left(\frac{Count\left(planvalues\le constraintvalues\right)}{Count\left(planvalues\right)}\right)\right)$$ (3)

In practice, individual treatment plans may rarely exceed the constraint values defined by literature-derived risk factors. In those cases, GEM scores such as NTCP tend to be near 0. An alternative is to use the empirical median of the historical population as the constraint value. We define this as the population-based GEM, or GEM_pop. Using GEM_pop, historical distributions determine the steepness of the penalty for exceeding constraint values and allow measured distributions to quantify as low as reasonably achievable (ALARA) dose limits with respect to historical experience.

Generalized evaluation metric–correlated weighted experience score

Not all points along the DVH curve are equally relevant. Toxicities may be more strongly driven by Max[Gy], Mean[Gy] or Dx%[Gy] values, dependent on the organ at risk structure. To reflect this, an additional weighting factor (wkt_i) was calculated using the Kendall's tau (kt_i) correlation of Dx%[Gy] values with structure GEM scores. The GEM-correlated weighted experience score (WES_GEM) is calculated using the formula

$$WES\_GEM=\frac{{\sum }_{i}w{b}_i\times wpc{a}_i\times wk{t}_i\times p_i}{{\sum }_{i}w{b}_i\times wpc{a}_i\times wk{t}_i}$$ (4)

Weighting factors (wkt) were set equal to 0 for kt <0 so that they only penalize those DVH points that are associated with undesirable outcomes. Kendall tau correlations were also carried out with GEM_pop or NTCP to create WES_GEM_pop or WES_NTCP scores.

Application to clinical plan history

Use of the newly described analytics to construct a common display method characterizing historical experience with DVH constraint metrics was demonstrated. Three cohorts were examined: 1) 351 head and neck cancer patients, dose range from 45 to 76 Gy in 23 to 38 fractions; 2) 104 prostate patients, dose range from 55 to 84 Gy in 22 to 43 fractions; and 3) 94 SBRT liver patients, dose range 40 to 60 Gy in 3 or 5 fractions. Distributions of achieved DVH metrics were compared with threshold values, and clinical prioritization scores were compared with statistically calculated values. The difficulty in meeting each threshold-priority constraint value on the basis of historical experience was quantified with a difficulty ranking score (DRS):

$$DRS=2^{-\left(Priority-1\right)}\cdot GEMUpper50\%CI$$ (5)

In addition, the use of the common display method to facilitate comparison of treatment plan details with reference to historical experience was demonstrated.

Results

Statistical dose-volume histogram dashboard

Figure 1 shows a view from a dashboard application that was created to enable the use of these concepts from within the treatment planning system. Statistical DVH curves and box-and-whisker plots are used to display the current plan in the context of distribution of historical values. The overall plan evaluation metrics are displayed in the left panel, and per-structure metrics are displayed in the right panel. In the left panel, the plan GEM (calculated over all structures) ranks overall ability to meet constraints. The comparison of MU/Gy is a relative indicator of multileaf collimator leaf pattern complexity. The distributions of MU/Gy vary substantially by technique (3-dimensional, intensity modulated radiation therapy, and volumetric modulated arc therapy). Below that, GEM values for individual structures are displayed in order of decreasing GEM with priority listed below the structure to highlight planning challenges. The statistical DVH is displayed in the center panel along with GEM, WES, and NTCP values. In the right panel, distributions of GEM values for the constraints applied to individual structures (left parotid in this example), NTCP, volume, and individual DVH constraints are displayed. Below that, values for individual DVH constraint metrics are displayed, overlaid on a box-and-whisker plot, indicating the historical distribution. A dashed blue line indicates the individual DVH constraint metric value.

For the example plan evaluated in Figure 1, the GEM score was 0.25 with all the constraints in Table 1. The GEM score for the left parotid alone was 0.83. This indicates that the plan overall compared favorably with constraints and historical experience but that the DVH data for this structure (ie, left parotid) were significantly higher than the constraint (GEM = 0.83) and historical experience (WES = 0.83). The first priority 1 structure with GEM >0.5 was the inferior constrictor muscle (Musc_Constrict_I).

Precomputed analytics

The application uses statistics and weighting factors derived from historical values that are precalculated and stored in JavaScript Object Notation (JSON) files. Users select the precalculated historical set to use in the comparison and structure DVH to be evaluated. Precomputed statistics rather than runtime query and analysis from M-ROAR was selected for 4 reasons: 1) minimization of processing time to improve user experience, 2) the ability to define standard clinic comparison groups (eg, patients from 1 year vs 5 years ago), 3) enabling of comparisons with values derived from other clinics without the need for database access, 4) support for the development of machine-learning approaches to combine data from multiple clinics.

Application of analytics to characterize groups and per-patient plans

Use of the metrics provided a basis for numerical rankings to characterize clinical practice experience and individual treatment plans within that historic context. Metrics were valuable for a range of evaluation tasks. Several of these are highlighted in the following.

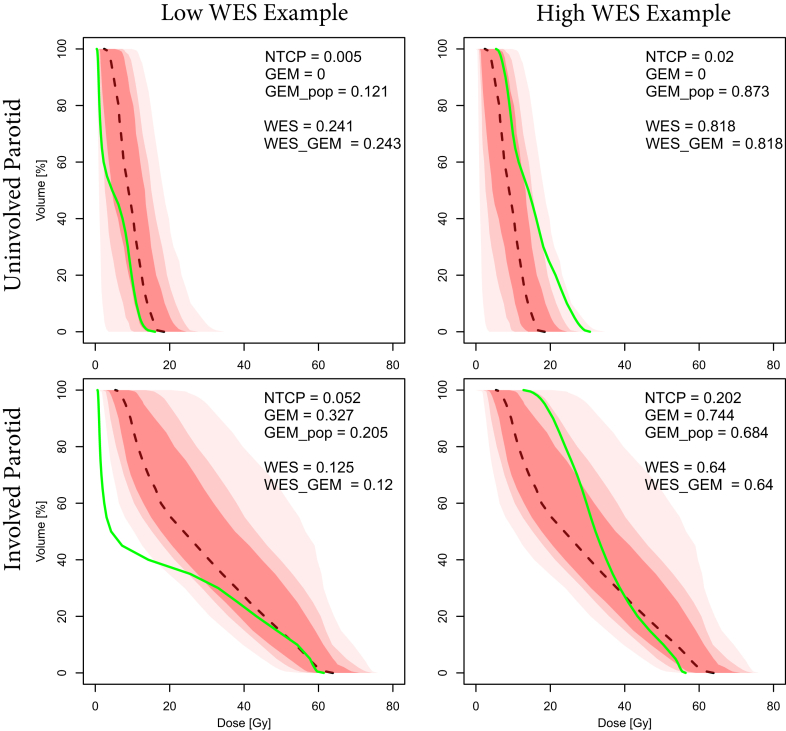
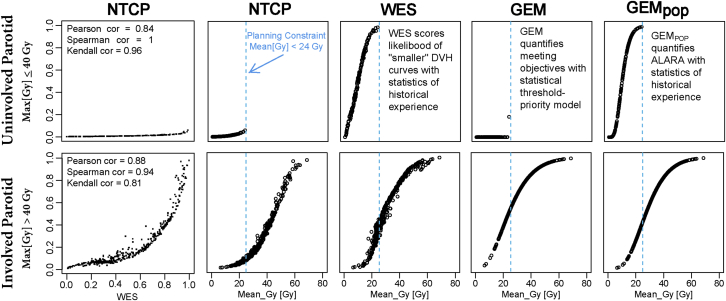
Characterizing involved versus uninvolved parotid dose for head and neck patients

For Head and Neck patients, the distributions of historical values of Max (Gy) for Parotid_L and Parotid_R were found to be bimodal. The midpoint was used to classify parotids as uninvolved (Max[Gy] ≤40Gy) or involved (Max[Gy] >40Gy). Figure 2 illustrates the use of statistical DVH and metrics to compare DVH curves for patients with low and high WES scores for uninvolved versus involved parotid with constraint doses specified for Mean (Gy). Although the odds of toxicity were low (NTCP ≤0.02) and compliance with constraint values was good (GEM ≤0.2), for the uninvolved parotids, the plan with a high WES score (0.818) stood out as having a larger Mean[Gy] dose than was historically normal (GEM_pop = 0.873). WES_GEM and WES_NTCP varied only slightly (<5%) from WES scores, which indicated that WES scores are viable predictors of ability to meet specific constraint values.

Figure 2.

The use of the statistical dose-volume histogram (DVH) and metrics to compare DVH curves for patients with low and high weighted experience scores for uninvolved versus involved parotid.

Summary metrics for practice history

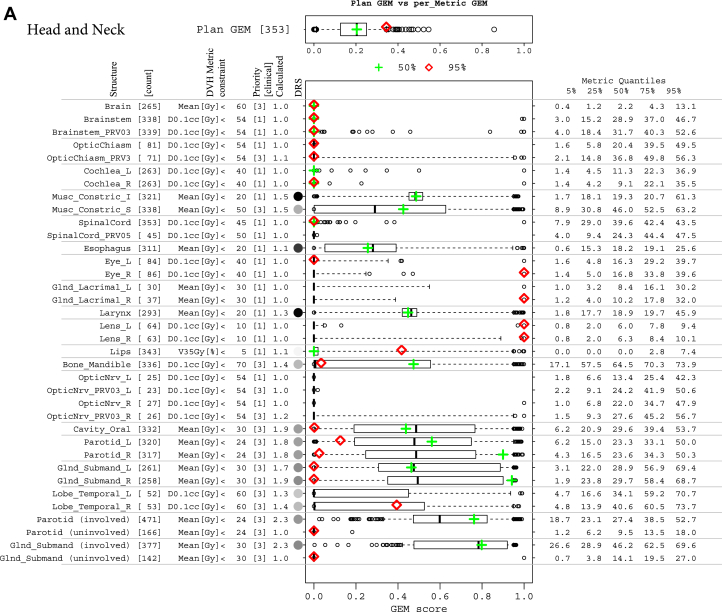
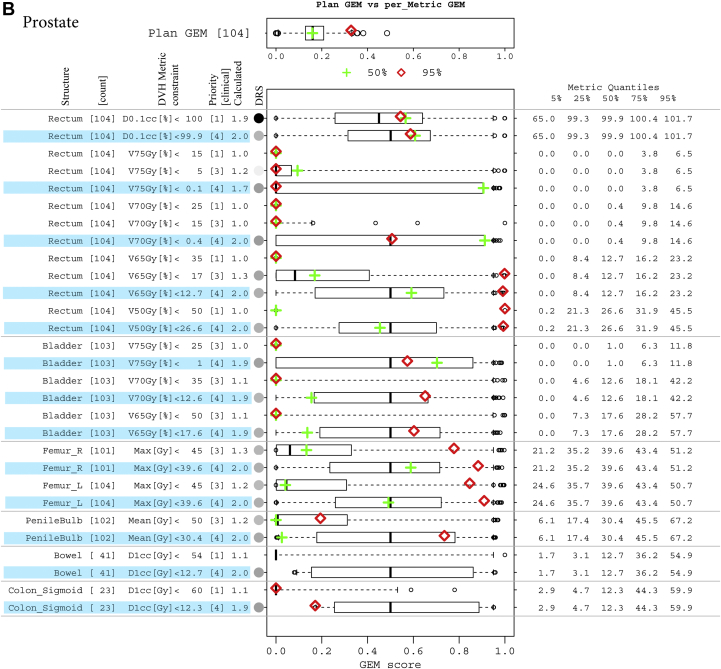
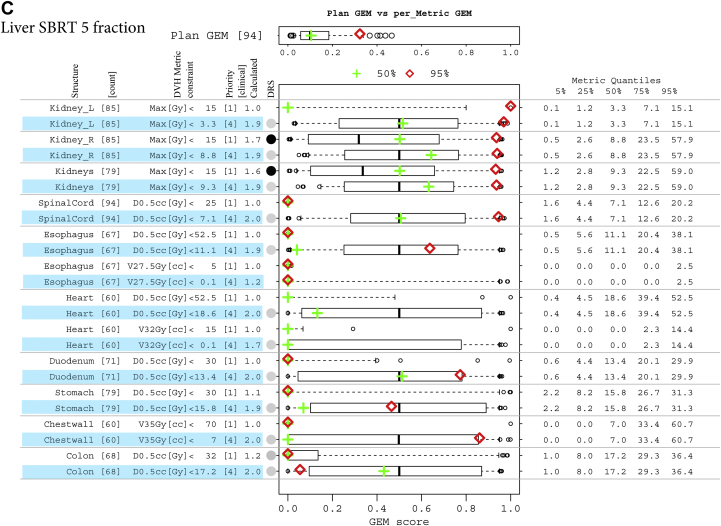
The common range of GEM enabled the expansion of this plan summary metric to detail historic experience with each threshold-priority constraint in a simple metrics display, which was used to detail comparisons of individual treatment plans with respect to historic experience. The approach was generalizable across disease sites. Summaries are illustrated in Figures 3A-C for head and neck, prostate, and 5-fraction SBRT liver sets, respectively. The historic ability to meet the set of constraint values used in the treatment plan evaluation was good for all patient groups. The median and 50% CI GEM values were 0.2 (0.13-0.25), 0.09 (0.05-0.12), 0.13 (0.01-0.19), and 0.09 (0.04-0.15) for head and neck, prostate, and liver SBRT with 3 and 5 fractions, respectively. Box-and-whisker plots that summarize the historic distributions of GEM values for individual structure DVH constraints are plotted alongside the summary statistics for DVH metric values and prioritizations to gauge the suitability of constraints. For example, the constraint values for parotid DVH metrics derived from studies of outcomes in the literature could be augmented with experience-based constraints to define clinically achievable limits for involved versus uninvolved parotids.

Figure 3.

(A) Decomposition and comparison of 2 plans from the head and neck cohort. Two plans of different difficulty levels, overall plan generalized evaluation metrics (GEM) at the median (green plus) and 95% quantile (red diamond), are detailed by GEM scores of each threshold-priority constraint (missing data indicate structure not contoured in that plan). Box-and-whisker plots have their whiskers located at the 5% and 95% quantiles of the GEM scores. Their corresponding metric values are tabled in the right columns of metric quantiles. (B) Decomposition and comparison of 2 plans from the prostate cohort, with as low as reasonably achievable (ALARA) constraints involved. ALARA thresholds (constraint values) are set to be the medians of their corresponding metric values, with an assigned priority of 4 and highlighted in blue. For the Rectum:V75Gy[%] constraint, which has a median of 0 Gy, a small number of 0.1 is used as the threshold. (C) Decomposition and comparison of 2 plans from 5-fraction liver stereotactic body radiation therapy cohort, with ALARA constraints involved. ALARA thresholds (constraint values) are set to be the medians of their corresponding metric values, with an assigned priority of 4 and highlighted in blue.

Evaluating priorities for dose-volume histogram metrics

Structures that were contoured were selected by the physician on the basis of involvement. Superior constrictor muscles (n = 338), brain stem (n = 338), and brain stem planning risk volume (n = 339) were the most frequent, and optic nerve structures (n = 25-27) were the least frequent, which indicates a relative likelihood of involvement. Of the 19 priority 1 structures, only the calculated priority on the inferior constrictor muscle constraint (Mean [Gy] <20) rounded down to a lower integer value of 2, which indicates that this constraint is met only approximately 50% of the time. Possible actions to improve agreement with experience might include modification of the assigned priority to 2 or changing of the constraint value to match the 75% quantile of the achieved metric values (20.7 Gy). Of the 13 priority 3 constraints, the calculated values rounded up to integer 1 (n = 7) or 2 (n = 6). GEM scores for these constraints were near to 0 and 0.5, respectively. If further challenging of plan evaluations were desired, higher priorities could be assigned.

The numerical values of DRS were used to create a grayscale representation of historic difficulty in meeting particular constraints (black = difficult; white = not difficult; gray shading proportional to difficulty). The top 3 difficulty ranking scores were Mean[Gy] <20 for inferior constrictor muscle (0.52), esophagus (0.39), and larynx (0.49). Parotid and submandibular gland DRS was lower (0.19-0.23) due to the assigned priority. Historically, constraints were slightly more difficult to meet for right versus left parotids (0.193 vs 0.188) and submandibular glands (0.225 vs 0.223).

Incorporating quantified ALARA into planning constraints

Clinical judgements for selecting between treatment plans and treatment techniques are not based solely on the binary evaluation of ability to meet specified constraints but also on the ability to keep those values as low as possible. The metrics display can be used to reflect that detail by adding low-priority constraints with thresholds that are set to historic medians (ie, adding ALARA constraints as GEM_pop). Figure 3B illustrates this for the cohort of prostate patients and compares 2 individual patient plans in this historic experience context. A priority of 4 was assigned for the ALARA constraints quantified using GEM_POP. Because the priority was low, the effect on the plan GEM was small (median, 0.14 vs 0.09).

For priority 1 to 3 structures only, Rectum:D0.1cc[%] <100 had a high DRS (0.64) with historic values ≤101.7 for 95% of patients. It had a calculated priority of 1.9 versus the assigned value of 1. All other constraints were readily met (GEM <0.1). For ALARA constraints (priority 4), the distribution of GEM values showed variation in the upper 50% CI (0.7-0.9), reflecting skewing of the upper-end distributions of the DVH metrics (toward/away from the median).

Comparing treatment plans in historical context

The projection of 2 individual plans onto the box-and-whisker plots of the metrics display provided a visual guide to quantifying the primary issues for each plan. Figure 3A illustrates this for 2 head and neck patient plans with GEM scores near the median (green cross) and 95% quantile (red diamond), respectively. In addition to the 32 constraints used in practice, 4 additional constraints for involved and uninvolved parotids and submandibular glands are displayed for reference. The plan with an overall GEM near the median of historic values (green cross) met all but 3 constraint values: left and right parotid-Mean (Gy) <24, priority 3; and right submandibular gland-Mean (Gy) <30, priority 3. The left-sided structures were near historical norms (black line) and constraint values (GEM ≈ 0.5) The plan with GEM in the upper range (red diamond) exceeded 4 priority 1 constraints for eye structures (right eye, right lacrimal gland, and left and right lens) by values much larger than historic norms (GEM >0.95), indicating target involvement of these structures on the right side. This was highly unusual compared with historic norms with DRS <0.005.

Illustrating the use of the figure for prostate patients in Figure 3B, 15 of 16 priority 1 to 3 constraints were met for the first plan with median plan GEM (green). That plan was at the outer range of normal values for Rectum: V75Gy[%] and V70 Gy (%) with GEM scores near the upper 75% quantile of ALARA (blue highlight) values. The second plan (red) irradiated a large volume including nodes and did not meet priority 1 constraints for Rectum-V50Gy[%] or priority 3 constraints for V65Gy[%]. Values for Rectum-V70Gy[%] and V75Gy[%] were near median values for the cohort. Because Rectum:V75Gy[%] has a median of 0, a small number of 0.1 is used as the ALARA constraint value. Priority 3 constraints for both femurs were exceeded with atypically high GEM scores.

Comparison with normal tissue complication probability

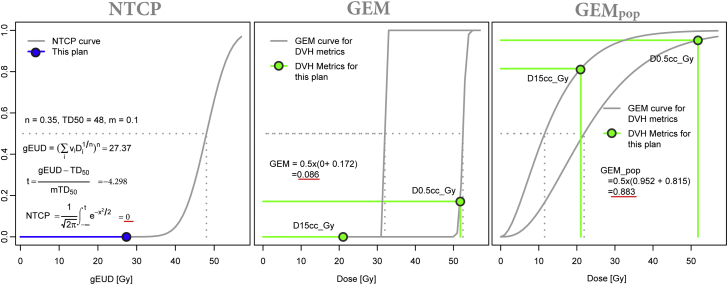
Clinicians select threshold-prioritization values that reflect an implicit intent to minimize NTCPs. GEM and GEM_pop provided a means of transforming a set of discrete threshold-priority limits into a continuous model that reflected physician objectives and historical experience. As a result, GEM and GEM_pop scores were more sensitive to clinically demonstrated, actionable decisions on DVH constraints than NTCP. For example, Figure 4 illustrates a comparison of GEM, GEM_pop, and NTCP (α/β = 2.5, TD50 = 48 Gy, n = 0.35, m = 0.1) calculations on heart dose for a patient with a liver lesion that was treated with SBRT in 5 fractions.

Figure 4.

Comparison of statistical metrics for heart doses in a liver stereotactic body radiation therapy (SBRT) patient treated with 5 fractions. Generalized evaluation metric (GEM) and GEMpop calculations use 2 priority 1 constraint values D15cc (Gy) and D0.5cc (Gy). These increase faster than normal tissue complication probability, consistent with more conservative clinical practice.

On examining distributions of values, GEM, GEM_pop, and WES scores correlated strongly with calculated NTCP while also being more sensitive to clinical decisions that shaped acceptable characteristics of dose distributions. Figure 5 illustrates this comparison for involved and uninvolved parotids of head and neck patients. The increased sensitivity combined with the correlation to clinical objectives make GEM a more direct reflection of preferences in guiding risk reductions than NTCP.

Figure 5.

Comparison of normal tissue complication probability, weighted experience score, generalized evaluation metric (GEM), and GEMpop scores versus mean dose for involved and uninvolved parotids.

Discussion

The analytics (metrics, visualization methods, and software applications) developed provided a practical demonstration of approaches that could be used to incorporate big data into clinical settings. They provide a means to summarize provider-selected objectives into a single score that incorporates historical ability to meet those objectives. Leveraging quantitative statistical measures of experience provides better information than qualitative recollection. Using scripts and precalculated summaries of statistics enables making this information available as part of the treatment planning process.

Recently, Mayo et al demonstrated an electronic prescription and database system that was used for all patients, systematic calculation, and aggregation of achieved DVH objective values and to provide statistical evaluations of practice patterns.⁷ Robertson et al demonstrated a system that was used for head and neck patients to analyze the distributions of DVH metrics for head and neck patients and display sets of DVH curves color-coded according to toxicity.⁸ These efforts demonstrate the value of the adoption of standards and construction of systems to enable aggregating of data that could be mined to reflect practice experience.

The present work demonstrates approaches to standardizing how such data are presented that could improve the ability to carry out treatment plan comparisons. For example, from the nests of DVH curves presented by Robertson et al,⁸ we can observe qualitatively that the distribution of DVH curves for parotids are similar in both shape and dose range, and those for larynx, inferior pharyngeal constrictor, and superior pharyngeal constrictor are shifted to higher values. If either the statistical DVHs or GEM scores calculated with specified threshold-priority constraints had been used, it would have been possible to carry out a more quantitative and accurate comparison.

Plan evaluation requires a comparison of a potentially large set of DVH metric values to constraints and decisions, when needed, for mitigating steps when constraint values are exceeded. The graphic display of the statistical DVH dashboard facilitates rapidly distinguishing structures that are exceeding constraints with scoring including prioritization. By using GEM to harmonize metric evaluations on a common scale and projecting individual plan values onto the distribution of historic values, judgements on whether the deviation is large or small can be based on actual history and quickly factored into decisions. This can help to make plan evaluation better targeted and potentially more efficient.

Recent developments in geometrical (ie, knowledge-based) modeling using training sets and proprietary software have been successfully used in predicting dose distributions and plan quality, mining dose-outcome relationships, and assisting in decision-making.1, 2, 3, 4, 5 However, clinical history is different from geometry. Questions about what characteristics of dose distributions have been found in practice to be clinically acceptable are different from the questions of what characteristics are possible on the basis of the relative geometry of structures in the optimization. Without information on the historical context, the ability to judge the clinical relevance of differences between plans or value added by new technologies is limited. We believe that together geometric and history-based approaches could provide a more comprehensive and responsive approach to treatment plan evaluation and optimization. In addition, the statistically based approach described does not depend on the common implementation of specialized software applications across treatment planning systems to be generalized to multiple clinics.

Incorporating factors into optimization that relate to radiobiological response is desirable.9, 10 Because the formulation of GEM is based only on discrete threshold-prioritization values, it is readily applied as an empirical scoring mechanism without the need for an underlying first-principles model. This may present advantages for forming evaluation models as clinical experience with new factors and constraints evolves. Because clinical practice avoids elevated NTCP values, WES, GEM, and GEM_pop may have advantages in optimization where low NTCP values present very shallow concave penalty functions.11, 12 The functional form of GEM used an incomplete gamma function; however, use of other functional forms (eg, log normal c.d.f., logistic) that produced a unit value sigmoidal curve over the range of allowed input values would also be appropriate.

Additionally, these metrics may have value in future efforts to model outcomes. By enabling development of an analog scoring function on the basis of a discrete set of threshold-priority rules and historic ability to meet these thresholds, the development of phenomenological models as outcomes evidence emerges may be facilitated. In addition, because the approach is independent of data type, models may be developed that incorporate a range of threshold hold-sensitive factors (eg, dose, age, chemotherapy). The unit range and sigmoidal form of the GEM aids its use as a parameter in Bayesian-based machine learning.

Quantified displays such as those presented in this study may be useful in clinical trial settings to facilitate prescreening of submitted cases that are benchmarked against prior submissions as the cohort grows. In that case, distributions of metric values, GEM scores, and calculated priorities would be automatically calculated and the display updated as the number of submissions increases. If the pattern of what is normal changes, then the display method would enable ready identification of plans that are unusual.

In summary, we demonstrated the utility of DVH-based metrics and a visualization method developed in house. Use of the metrics to summarize historical experience for 3 patient groups, head and neck, prostate patients, and liver SBRT patients, was demonstrated. This tool allows for simple and intuitive quantification of the comparison of individual treatment plans against historical experiences. As such, this may allow for superior treatment planning, which has the potential to result in improved patient care.