Groupwise Envelope Models for Imaging Genetic Analysis

Summary

Motivated by searching for associations between genetic variants and brain imaging phenotypes, the aim of this paper is to develop a groupwise envelope model for multivariate linear regression in order to establish the association between both multivariate responses and covariates. The groupwise envelope model allows for both distinct regression coefficients and distinct error structures for different groups. Statistically, the proposed envelope model can dramatically improve efficiency of tests and of estimation. Theoretical properties of the proposed model are established. Numerical experiments as well as the analysis of an imaging genetic data set obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study show the effectiveness of the model in efficient estimation. Data used in preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database.

1. Introduction

To motivate the proposed methodology, we consider an imaging genetic data set from 745 subjects collected by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study (http://www.adni-info.org/) in order to advance the discovery in detection, invention, prevention as well as treatments of the Alzheimer’s disease. Specifically, each subject has brain volumes of 93 regions of interest, single nucleotide polymorphisms (SNPs) on candidate genes of the Alzheimer’s Disease, and other covariates including gender, age, education level, marital status and handedness. Alzheimer’s Disease (AD) is characterized by death of nerve cells and accelerated cerebral atrophy, leading to the shrinkage of various brain volumes, such as hippocampus. Similar to a recent large-scale imaging study for schizophrenia in Franke et al. (2016), we are interested in characterizing the genetic influences of the top 40 AD candidate genes listed on the AlzGene database (www.alzgene.org) as of June 10, 2010 on structural brain phenotypes in ADNI.

A standard model in the imaging genetic literature (Vounou et al., 2010; Thompson et al., 2013; Sun et al., 2015) is the multivariate linear regression given by

$$\mathbf{Y}=\mathit{\mu }+\mathit{\beta }\mathbf{X}+\mathit{\epsilon },$$ (1)

where Y is a r × 1 vector of multiple responses (e.g., brain volumes), X is a p × 1 vector of covariates, and the errors ε follows a distribution with mean 0 and positive definite covariance matrix Σ ∈ ℝ^r×r. Moreover, μ ∈ ℝ^r and β ∈ ℝ^r×p are unknown intercept and regression coefficients. It is common to calculate the ordinary least squares estimator of β by regressing each element in Y on the predictors of interest. This method, however, ignores the relationship among different response components. A novel envelope modeling framework introduced in Cook et al. (2010) explicitly uses such relationship to identify a part of the responses that is immaterial to the estimation of β, while bringing extraneous variation. This immaterial part is then accounted for in the subsequent estimation, making the estimation more efficient. After the original development, advances have been taken place to extend the scope of envelope model (Su and Cook, 2011, 2012, 2013; Cook et al., 2013; Cook and Zhang, 2015; Khare et al., 2017).

However, model (1) is not sufficient for addressing a more specific question of interest. Specifically, it is interesting to investigate how the associations between AD genetic variants and sub-cortical volume measures differ across male and female groups. Suppose that we observe imaging genetic data from subjects in L different groups. For each l = 1,…, L, the l−th group has n_(l) observations and the total sample size is $n={\displaystyle {\sum }_{l=1}^L{n}_{(l)}}$. By incorporating such group information, we can reformulate model (1) as

$${\mathbf{Y}}_{(l)j}={\mathit{\mu }}_{(l)}+{\mathit{\beta }}_{(l)}{\mathbf{X}}_{(l)j}+{\mathit{\epsilon }}_{(l)j}\text{for}l=1,\dots ,L\text{and}j=1,\dots ,n_l,$$ (2)

where Y_(l)j ∈ ℝ^r is the jth observed response vector in the l−th population, μ_(l) ∈ ℝ^r is the mean of the l−th population, X_(l)j ∈ ℝ^p is the jth observed covariate vector in the l−th population, β_(l) ∈ ℝ^r×p contains the regression coefficients for the l−th population, and ε_(l)j follows some distribution with mean 0 and covariance matrix Σ_(l). Throughout this paper, we use subscript (l) to denote the l−th population and subscripts without parenthesis to number the observations. Without loss of generality, we assume that ${\mathbb{X}}_{(l)}={({\mathbf{X}}_{(l)1}^T,\dots ,{\mathbf{X}}_{(l)n_{(l)}}^T)}^T$, l = 1,…,L are centered at 0 in the sample for each group. Model (2) is referred to as the standard model in later discussion.

The aim of this paper is to develop a new groupwise envelope modelling framework for model (2), which allows for distinct regression coefficients and the heteroscedastic error structure across groups. Compared with the existing literature (Su and Cook, 2013; Cook et al., 2010), we make at least three major contributions. First, we develop an efficient estimation method to estimate distinct genetic-volume associations across groups under the heteroscedastic error structure. In contrast, the existing envelope models assume either a homogenous error structure or distinct means across groups without covariate X. Second, we examine the asymptotic properties of the proposed estimates under some mild conditions. Third, our simulation studies and the ADNI data analysis confirm the efficiency gains obtained by using the groupwise envelope model. An alternative way to gain estimation efficiency in model (2) is to fit a separate envelope model to each group. However, as will be shown in Sections 3 and 5, efficiency is lost due to ignoring the common characteristics in response variables across groups.

The article is organized as follows. Section 2 reviews the envelope model and introduces the groupwise envelope model and its estimation procedure. Section 3 systematically investigates the asymptotic properties of all estimators. Simulation studies are conducted in Section 4. A real data analysis of the imaging genetic data set from ADNI is described in Section 5. Conclusion remarks are given in Section 6.

2. Methods

2.1 A Review of Envelope Models

We first introduce some notation. We use P_S to denote the projection matrix onto span(S) or S if S is a matrix or a subspace, and Q_S = I − P_S. With a matrix A ∈ ℝ^m×n, vec(A) ∈ ℝ^mn stacks the columns of A into a vector. The Kronecker product is denoted by ⊗, X ∼ Y means X and Y has the same distribution, and X ⫫ Y means that X and Y are independent.

The original envelope model (Cook et al., 2010) was developed for model (1). Under (1), we partition the response vector Y into a material part and an immaterial part, where the distribution of the material part changes with the predictor X and the distribution of the immaterial part does not. More specifically, let $\mathcal{S}$ be a subspace of ℝ^r, L be an orthogonal basis of $\mathcal{S}$ and L₀ be an orthogonal basis of ${\mathcal{S}}^{\perp }$. The linear combinations of the responses L^TY and ${\mathbf{L}}_0^T\mathbf{Y}$ are called the material part and the immaterial part if the following two conditions are satisfy: (a) ${\mathbf{L}}_0^T\mathbf{Y}|\mathbf{X}~{\mathbf{L}}_0^T\mathbf{Y}$ and (b) $\mathrm{cov}({\mathbf{L}}^T\mathbf{Y},{\mathbf{L}}_0^T\mathbf{Y}|\mathbf{X})=0$. Condition (a) indicates that the distribution of the immaterial part does not depend on X, and condition (b) indicates that given X, the material part and immaterial part are uncorrelated. Let $ℬ=\mathrm{span}(\mathit{\beta })$. Conditions (a) and (b) are also equivalent to: (I) $ℬ\subseteq \mathcal{S}$ and (II) $\sum ={\mathrm{P}}_{\mathcal{S}}\sum {\mathrm{P}}_{\mathcal{S}}+{\mathrm{Q}}_{\mathcal{S}}\sum {\mathrm{Q}}_{\mathcal{S}}$ (Cook et al., 2010). Condition (I) indicates that the immaterial part does not contain information on β and condition (II) indicates that the variation Σ can be decomposed into the variation due to the material part and the variation due to the immaterial part. When Σ has the structure in condition (II), $\mathcal{S}$ is a reducing subspace of Σ (Conway, 1990). Then, the Σ-envelope of $ℬ$, denoted by ${ℰ}_{\sum }(ℬ)$, is defined to be the smallest reducing subspace of Σ containing $ℬ$. Model (1) is called the envelope model when conditions (I) and (II) are imposed.

Let u denote the dimension of ${ℰ}_{\sum }(ℬ)$, Γ ∈ ℝ^r×u be an orthogonal basis of ${ℰ}_{\sum }(ℬ)$, and Γ₀ ∈ ℝ^r×(r−u) be an orthogonal basis of ${ℰ}_{\sum }{(ℬ)}^{\perp }$. The coordinate form of the envelope model is

$$\mathbf{Y}=\mathit{\mu }+\mathbf{\Gamma }\mathit{\eta }\mathbf{X}+\mathit{\epsilon },\sum ={\sum }_1+{\sum }_2=\Gamma \Omega {\Gamma }^T+{\Gamma }_0{\Omega }_0{\Gamma }_0^T,$$

where β = Γη, η ∈ ℝ^u×p carries the coordinates of β with respect to Γ, and Ω = Γ^T ΣΓ and ${\Omega }_0={\Gamma }_0^T\sum {\Gamma }_0$ carry the coordinates of Σ with respect to Γ and Γ₀, respectively. When u = r, ${ℰ}_{\sum }(ℬ)={ℝ}^r$, the envelope model degenerates to the standard multivariate linear regression model. As shown in Cook et al. (2010), the envelope estimator of β is more efficient than or at least as efficient as the standard estimator. The efficiency gains can be substantial when ‖Σ₁‖ ≪ ‖Σ₂‖, where ‖·‖ denotes the spectral norm of a matrix or vector.

2.2 Formulation of Groupwise Envelop Model

Under model (2), let $\mathcal{S}$ be a subspace of ℝ^r, L be an orthogonal basis of $\mathcal{S}$ and L₀ be an orthogonal basis of ${\mathcal{S}}^{\perp }$. Then for each l, the material part L^TY_(l)j and the immaterial part ${\mathbf{L}}_0^T{\mathbf{Y}}_{(l)j}$ should satisfy (A) ${\mathbf{L}}_0^T{\mathbf{Y}}_{(l)j}|{\mathbf{X}}_{(l)}~{\mathbf{L}}_0^T{\mathbf{Y}}_{(l)j}$ and (B) ${\mathbf{L}}^T{\mathbf{Y}}_{(l)j}⫫{\mathbf{L}}_0^T{\mathbf{Y}}_{{(l)}_j}|{\mathbf{X}}_{(l)}$. From conditions (A) and (B), $\mathcal{S}$ is a reducing subspace of all Σ_(l) and $\mathrm{span}({\mathit{\beta }}_{(l)})\subseteq \mathcal{S}$ for l = 1,…,L. Therefore, we define the groupwise envelope to be the intersection of all such $\mathcal{S}$. More specifically, let $ℳ=\{{\sum }_{(1)},\dots ,{\sum }_{(L)}\}$ denote the collection of all covariance matrices, and $ℬ=\mathrm{span}({\mathit{\beta }}_{(1)},\dots ,{\mathit{\beta }}_{(L)})$. Then the $ℳ$-envelope of $ℬ$, denoted by ${ℰ}_{ℳ}(ℬ)$, is the smallest subspace that reduces each matrix in $ℳ$ and contains $ℬ$. When ${ℰ}_{ℳ}(ℬ)$ appears in subscripts, it is shortened to $ℰ$. From the definition of ${ℰ}_{ℳ}(ℬ)$, we have

$$\mathrm{span}({\mathit{\beta }}_{(l)})\subseteq {ℰ}_{ℳ}(ℬ)\text{and}{\sum }_{(l)}={\mathrm{P}}_{ℰ}{\sum }_{(l)}{\mathrm{P}}_{ℰ}+{\mathrm{Q}}_{ℰ}{\sum }_{(l)}{\mathrm{Q}}_{ℰ},\text{for}l=1,\dots ,L.$$ (3)

Model (2) is called the groupwise envelope model if conditions in (3) are imposed.

Let Γ ∈ ℝ^r×u be an orthogonal basis of ${ℰ}_{ℳ}(ℬ)$ and Γ₀ ∈ ℝ^r×(r−u) be its completion. The coordinate form of the groupwise envelope model is given by

$${\mathbf{Y}}_{(l)j}={\mathit{\mu }}_{(l)}+\Gamma {\mathit{\eta }}_{(l)}{\mathbf{X}}_{(l)j}+{\mathit{\epsilon }}_{(l)j},\text{and}{\sum }_{(l)}=\Gamma {\Omega }_{(l)}{\Gamma }^T+{\Gamma }_0{\Omega }_0{\Gamma }_0^T$$ (4)

for each l = 1,…,L, where β_(l) = Γη_(l), η_(l) ∈ ℝ^u×p carries the coordinate of β_(l) with respect to Γ, and Ω_(l) ∈ ℝ^u×u and Ω₀ ∈ ℝ^{(r−u)×(r−u)} are symmetric matrices that carry the coordinates of Σ_(l) with respect to Γ and Γ₀, respectively. The groupwise envelope model degenerates to the envelope model in Cook et al. (2010) if L = 1.

For a fixed dimension u, the number of parameters in the groupwise envelope model (4) is N(u) = Lr + Lup + Lu(u + 1)/2 + (r − u)(r − u + 1)/2 + u(r − u). This is because we need Lr parameters for all μ_(l)s′, Lup parameters for all η_(l)s′, Lu(u + 1)/2 parameters for all Ω_(l)s′, and (r − u)(r − u + 1)/2 parameters for Ω₀. The envelope subspace ${ℰ}_{ℳ}(ℬ)$ is on an r × u Grassmann manifold, which is the set of all u dimensional subspaces in an r dimensional space, so it has u(r − u) free parameters.

2.3 Estimation Procedure

The groupwise envelope model does not require normality, but we will use the normal likelihood function as a pseudo likelihood function to calculate estimators. Technical details are included in Supplemental Section A. Let θ = (μ, η, Ω, Ω₀) be a collection of parameters, where μ = (μ₍₁₎,…,μ_(L)), η = (η₍₁₎,…,η_(L)), and Ω = (Ω₍₁₎,…,Ω_(L)). For a fixed dimension u, u = 0,…,r, the normal log likelihood of the groupwise envelope model is given by

$$\begin{array}{l}\ell (\mathit{\theta })=-\frac{nr}{2}\log (2\pi )-\frac{n}{2}\log |{\Omega }_0|-\frac{1}{2}{\displaystyle \sum _{l=1}^L{n}_{(l)}}\log |{\Omega }_{(l)}|\\ -\frac{1}{2}{\displaystyle \sum _{l=1}^L{\displaystyle \sum _{j=1}^{n_{(l)}}{\{{\Gamma }^T({\mathbf{Y}}_{(l)j}-{\mathit{\mu }}_{(l)}-\Gamma {\mathit{\eta }}_{(l)}{\mathbf{X}}_{(l)j})\}}^T{\Omega }_{(l)}^{-1}\{{\Gamma }^T({\mathbf{Y}}_{(l)j}-{\mathit{\mu }}_{(l)}-\Gamma {\mathit{\eta }}_{(l)}{\mathbf{X}}_{(l)j})\}}}\\ -\frac{1}{2}{\displaystyle \sum _{l=1}^L{\displaystyle \sum _{j=1}^{n_{(l)}}{({\mathbf{Y}}_{(l)j}-{\mathit{\mu }}_{(l)})}^T{\Gamma }_0{\Omega }_0^{-1}{\Gamma }_0^T({\mathbf{Y}}_{(l)j}-{\mathit{\mu }}_{(l)})}}.\end{array}$$ (5)

When Γ is fixed, the estimators of μ_(l), η_(l), Ω_(l), and Ω₀, which maximize ℓ(θ), can be written as explicit expressions of Γ. Let ${\widehat{\sum }}_{\mathrm{res},(l)}=(1/n_{(l)}){\mathbb{Y}}_{(l)c}^T{\mathbf{Q}}_{\mathbb{X}(l)}{\mathbb{Y}}_{(l)c}$, and ${\widehat{\sum }}_{\mathbf{Y}}=(1/n){\displaystyle {\sum }_{l=1}^L{\mathbb{Y}}_{(l)c}^T{\mathbb{Y}}_{(l)c}}$, where ${\mathbb{X}}_{(l)}\in {ℝ}^{n_{(l)}\times p}$ is the centered data matrix for X and ${\mathbb{Y}}_{(l)c}\in {ℝ}^{n_{(l)}\times r}$ is the centered data matrix for Y for group l. Substitute them back to ℓ(θ), we get

$${\widehat{ℰ}}_{ℳ}({ℬ}_{\Gamma })=\underset{\mathrm{span}(\Gamma )\in {ℒ}_{r\times u}}{\mathrm{argmin}}{\displaystyle \sum _{l=1}^L\frac{n_{(l)}}{n}\log |{\Gamma }^T{\widehat{\sum }}_{\mathrm{res},(l)}\Gamma |+\log |{\Gamma }^T{\widehat{\sum }}_{\mathbf{Y}}^{-1}\Gamma |,}$$

where ${ℒ}_{r\times u}$ denotes the r×u Grassmann manifold. To emphasize that Γ is an orthogonal basis of ${ℰ}_{ℳ}(ℬ)$, we put subscript Γ on $ℬ$. After we obtained ${\widehat{ℰ}}_{ℳ}({ℬ}_{\Gamma })$, $\widehat{\Gamma }$ can be any orthogonal basis of ${\widehat{ℰ}}_{ℳ}({ℬ}_{\Gamma })$. For l = 1,…,L, the estimators for all other parameters are given as follows:

• ${\widehat{\mathit{\mu }}}_{\left(l\right)}={\overline{Y}}_{\left(l\right)}$, where ${\overline{Y}}_{\left(l\right)}=(1/n_{\left(l\right)}){\sum }_{j=1}^{n(l)}{\mathbf{Y}}_{\left(l\right)j}$;

• ${\widehat{\mathit{\eta }}}_{\left(l\right)}={\widehat{\Gamma }}^T({\mathbb{Y}}_{\left(l\right)c}^T{\mathbb{X}}_{\left(l\right)}){({\mathbb{X}}_{\left(l\right)}^T{\mathbb{X}}_{\left(l\right)})}^{-1}$;

• ${\widehat{\Omega }}_{\left(l\right)}={\widehat{\Gamma }}^T{\widehat{\sum }}_{\mathrm{res},\left(l\right)}\widehat{\Gamma }$;

• ${\widehat{\Omega }}_0={\widehat{\Gamma }}_0^T{\widehat{\sum }}_{\mathbf{Y}}{\widehat{\Gamma }}_0$, where ${\widehat{\Gamma }}_0$ is the completion of $\widehat{\Gamma }$;

• ${\widehat{\mathit{\beta }}}_{\left(l\right)}=\widehat{\Gamma }{\widehat{\eta }}_{\left(l\right)}={\mathbf{P}}_{\widehat{\Gamma }}{\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{ols}}$, where ${\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{ols}}$ is the ordinary least squares estimator of β_(l);

• ${\widehat{\sum }}_{\left(l\right)}=\widehat{\Gamma }{\widehat{\Omega }}_{\left(l\right)}{\widehat{\mathbf{\Gamma }}}^T+{\widehat{\Gamma }}_0{\widehat{\Omega }}_0{\widehat{\Gamma }}_0^T$.

To estimate the dimension of ${ℰ}_{ℳ}({ℬ}_{\Gamma })$, we apply the Bayesian information criterion (BIC). Let l^∗(u) be the maximized l for a fixed u, and N(u) be the number of parameters discussed in Section 2.2. We choose a value u_opt that minimizes BIC(u) = −2l^∗(u) + log(n)N(u).

3. Theoretical Properties

In this section, we examine the theoretical properties of the groupwise envelope estimators. We present the following theoretical properties, whose proofs are included in Supplemental Section B.

Proposition 1

Under the groupwise envelope model (4), assume that the errors are independent and have finite fourth moments. Then ${\widehat{\mathit{\beta }}}_{\left(l\right)}$ is a $\sqrt{n}$ consistent estimator of β_(l) and ${\widehat{\sum }}_{\left(l\right)}$ is a $\sqrt{n}$ consistent estimator of Σ_(l) for l = 1, …, L.

Proposition 1 establishes the $\sqrt{n}$ consistency of the groupwise envelope estimators. Notice that normality is not required even though the estimators are derived by maximizing the normal likelihood function.

Proposition 2

Suppose that the conditions of Proposition 1 hold and f_(l) = n_(l)/n does not change with n. Then, $\mathrm{vec}({\widehat{\mathit{\beta }}}_{\left(l\right)}-{\mathit{\beta }}_{\left(l\right)})$ converges in distribution to a multivariate normal distribution with mean 0 for each l = 1,…, L. Furthermore, under the normality, we have

$$\sqrt{n}[\mathrm{vec}({\widehat{\mathit{\beta }}}_{\left(l\right)})-\mathrm{vec}({\mathit{\beta }}_{\left(l\right)})]\stackrel{d}{\to }N(0,{\mathbf{V}}_{\left(l\right)}),$$

where $\stackrel{d}{\to }$ denotes convergence in distribution and ${\mathbf{V}}_{\left(l\right)}=f_{\left(l\right)}^{-1}{\displaystyle {\sum }_{{\mathbf{X}}_{\left(l\right)}}^{-1}\otimes \Gamma {\Omega }_{\left(l\right)}{\Gamma }^T+({\mathit{\eta }}_{\left(l\right)}^T\otimes {\Gamma }_0){\mathbf{T}}^{-1}({\mathit{\eta }}_{\left(l\right)}\otimes {\Gamma }_0^T)}$ for l = 1, …, L, in which T is given by

$$\mathbf{T}={\displaystyle \sum _{l=1}^L{f}_{\left(l\right)}({\mathit{\eta }}_{\left(l\right)}{\sum }_{{\mathbf{X}}_{\left(l\right)}}{\mathit{\eta }}_{\left(l\right)}^T\otimes {\Omega }_0^{-1}+{\Omega }_{\left(l\right)}\otimes {\Omega }_0^{-1}+{\Omega }_{\left(l\right)}^{-1}\otimes {\Omega }_0-2{\mathbf{I}}_u\otimes {\mathbf{I}}_{r-u})}.$$

Proposition 2 provides the asymptotic distribution of the groupwise envelope estimator and derives explicit form of the asymptotic variance under the normality. The first term $f_{\left(l\right)}^{-1}{\displaystyle {\sum }_{{\mathbf{X}}_{\left(l\right)}}^{-1}\otimes \Gamma {\Omega }_{\left(l\right)}{\Gamma }^T}$ is the asymptotic variance of ${\widehat{\mathit{\beta }}}_{\left(l\right)}$ for known Γ, and the second term $({\mathit{\eta }}_{\left(l\right)}^T\otimes {\Gamma }_0){\mathbf{T}}^{-1}({\mathit{\eta }}_{\left(l\right)}\otimes {\Gamma }_0^T)$ is the cost of estimating the envelope subspace ${ℰ}_{ℳ}\left(ℬ\right)$.

Suppose that we fit separate envelope model to the data in each group, and we denote their estimators as ${\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{senv}}$ for l = 1, …, L. We have the following results.

Proposition 3

Suppose that the conditions of Proposition 1 hold, then $\mathrm{vec}({\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{snev}})-\mathrm{vec}({\mathit{\beta }}_{\left(l\right)})$ converges in distribution to a multivariate normal distribution with mean 0 for l = 1, …, L. Furthermore, under the normality, we have

$$\sqrt{n}[\mathrm{vec}({\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{senv}})-\mathrm{vec}({\mathit{\beta }}_{\left(l\right)})]\stackrel{d}{\to }N(0,{\mathbf{V}}_{\left(l\right),\mathrm{senv}}),$$

where ${\mathbf{V}}_{\left(l\right),\mathrm{senv}}=f_{\left(l\right)}^{-1}{\displaystyle {\sum }_{{\mathbf{X}}_{\left(l\right)}}^{-1}\otimes }\Gamma {\Omega }_{\left(l\right)}{\Gamma }^T+({\mathit{\eta }}_{\left(l\right)}^T\otimes {\Gamma }_0){\mathbf{T}}_2^{-1}({\mathit{\eta }}_{\left(l\right)}\otimes {\Gamma }_0^T)$ for l = 1, …, L, in which ${\mathbf{T}}_2=f_{\left(l\right)}({\mathit{\eta }}_{\left(l\right)}{\sum }_{{\mathbf{X}}_{\left(l\right)}}{\mathit{\eta }}_{\left(l\right)}^T\otimes {\Omega }_0^{-1}+{\Omega }_{\left(l\right)}\otimes {\Omega }_0^{-1}+{\Omega }_{\left(l\right)}^{-1}\otimes {\Omega }_0-2{\mathbf{I}}_u\otimes {\mathbf{I}}_{r-u})$.

Corollary 4

V_(l),senv ⩾ V_(l) for l = 1, …, L.

Proposition 3 gives the asymptotic distribution of $\mathrm{vec}({\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{senv}})$. Corollary 4 indicates that the groupwise envelope estimator is more efficient. A close examination reveals that V_(l) and V_(l),env differ only in terms of T and T₂. This suggests that if Γ is known, the asymptotic variance for ${\widehat{\mathit{\eta }}}_{\left(l\right)}$ is the same. However, the cost of estimating ${ℰ}_{ℳ}\left(ℬ\right)$ is smaller for the groupwise envelope model. This is because that the groupwise envelope model uses all the data to estimate ${ℰ}_{ℳ}\left(ℬ\right)$, whereas the separate envelope model only uses the data from the l−th group to estimate ${ℰ}_{ℳ}\left(ℬ\right)$. We also notice that with finite sample, the envelope subspace ${ℰ}_{ℳ}\left(ℬ\right)$ calculated by fitting separate envelope model varies across groups.

4. Simulation Study

In this section, we use Monte Carlo simulations to evaluate the finite-sample performance of the groupwise envelope model (4). We generated the data from model (4) with two groups (L = 2), which have 40% and 60% of the observations. We set r = 10, p = 3, and u = 1. The matrix (Γ, Γ₀) was obtained by normalizing an r × r matrix of independent normal variates, μ₍₁₎ was a vector of 3 and μ₍₂₎ was a vector of 10, η₍₁₎ was a vector of independent ${\chi }_{10}^2$ variates and η₍₂₎ was a vector of independent ${\chi }_{20}^2$ variates. Let A ∈ ℝ ^{(r−u)×(r−u)} be a matrix of independent normal (5, 1²) variates, Ω₍₁₎ and Ω₍₂₎ both be ${\chi }_1^2$ variates, and Ω₀ = AA^T. The predictors were independent normal (0, 5²) variates for the first group and independent normal (0, 10²) variates for the second group. We varied the sample size from 100, 300, 1000 and 3000. For each sample size, 200 replications were generated. The standard model (2), the envelope model (Cook et al., 2010), separate envelope model and the groupwise envelope model (4) were fit to the data. Standard deviation of each element in β₍₁₎ and β₍₂₎ was calculated based on the 200 replications for each method at each sample size. We also computed the bootstrap standard deviations of each element in β₍₁₎ and β₍₂₎ based on 200 bootstrap samples. The results for a randomly chosen element in β₍₁₎ and a randomly chosen element in β₍₂₎ are summarized in Figure 1. For clarity, we did not draw the line for the standard deviation of the standard model, but only displayed its asymptotic standard deviation.

Figure 1.

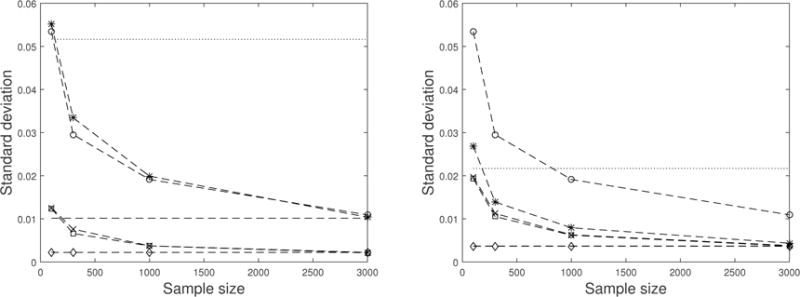
Left panel: Standard deviations for a random picked element in β₍₁₎. Right panel: Standard deviations for a random picked element in β₍₂₎. The –□–, –x– and –◊– lines mark the actual, bootstrap and asymptotic standard deviations of the groupwise envelope model. The –∗– and – – lines mark the actual and asymptotic standard deviation of the separate envelope model. The –o– line marks the standard deviations of the envelope estimator in Cook et al. (2010). The…line marks the asymptotic standard deviations of the standard model.

We have the following observations from Figure 1. The groupwise envelope estimator is consistent and its standard deviation approaches to the asymptotic standard deviation as sample size increases, which agrees with Proposition 1. It is also observed that the groupwise envelope model achieves substantial efficiency gains over the standard model. Take the element in the right panel of Figure 1 for example, the standard deviation of the groupwise envelope estimator is already smaller than the asymptotic standard deviation of the standard estimator with n = 100. This means by using the groupwise envelope model, with 100 samples we have achieved the efficiency of taking infinity number of samples under the standard model. We also notice that the bootstrap standard deviation is a good estimation of the sample standard deviation. The envelope model with constant covariance structure (Cook et al., 2010) has standard deviation about five times as large as the groupwise envelope model, indicating that accommodating the groupwise error structure brings extra efficiency gains. The separate envelope model also has larger standard deviations than the groupwise envelope model, as asserted in Corollary 4. The difference is more pronounced in one group than the other.

We investigated the numerical properties of the groupwise envelope model under non-normal errors in Web Appendix A and Web Appendix B. In Web Appendix A, we considered the estimation standard deviation of the groupwise envelope model under different non-normal error distributions including t distribution with degrees of freedom 6, uniform distribution defined on the unit interval, and chi-squared distribution with degrees of freedom 4. We examined the selection performance of BIC under non-normal errors in Web Appendix B.

5. The Alzheimer’s Disease Neuroimaging Initiative

We applied the groupwise envelope model to the imaging genetic data set obtained from ADNI study as described in Section 1. We used the image processing pipeline and quality control methods described in Zhu et al. (2014) to process the structural Magnetic Resonance Imaging (MRI) data and genetic data downloaded from the ADNI publicly available database (http://adni.loni.usc.edu/). Our problem of interest is to investigate the genetic effects of the SNPs on the top 40 AD candidate genes on the brain volumes of 93 regions of interest (ROI), whose names and abbreviation are given in the supplementary material in Zhu et al. (2014) across male and female groups. The top 40 AD candidate genes are listed on the AlzGene database (www.alzgene.org) as of June 10, 2010 on the brain volumes of 93 ROIs across male and female groups. The selection of the genes is described in Section 4.1 in Zhu et al. (2014). To correct for normal variation in head size, we used the proportion method to calculate ROI tissue-to-intracranial volume ratios and then took logarithm of these ratios. We selected the 1071 SNPs on the 37 top genes and Apolipoprotein E (APOE) ε4. We first performed a principal component analysis on the 1071 SNP predictors. Figure 2 presents the 1071 × 1071 correlation matrix of all 1071 SNPs. We selected 205 principal components (PCs) whose loadings have corresponding eigenvalues greater than 1, and these 205 PCs explain 89.76% of the total variation of all SNP predictors.

Figure 2.

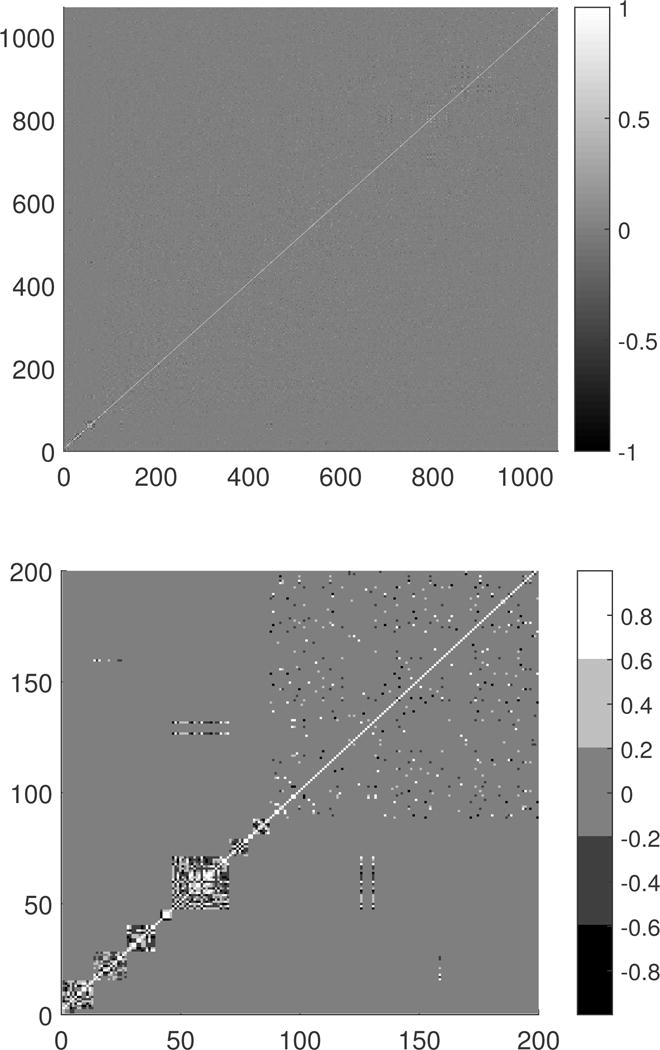
Plot of the correlation matrix. The top panel shows the correlation of 1071 SNPs and the bottom panel is the enlarged version for the first 200 SNPs. This figure appears in color in the electronic version of this article.

We fit a linear regression of the logarithm of the ratios for the brain volumes on five PCs obtained from the entire SNP data accounting for the population stratification. The residuals are used for multivariate responses in the groupwise envelop model (4). We used gender (male versus female) as the group variable and the SNP PCs and all covariates except gender as predictors. Note that the responses are unitless. The covariates include APOE ε4, age (years, from 55 to 91), education level (years, from 6 to 20), marriage status (married, widowed, divorced, other) and handedness (right-handed, other). All variables were standardized. BIC suggests u = 1. For each element in β_(l), we computed the ratio of the bootstrap standard deviation under the standard model versus the bootstrap standard deviation under the groupwise envelope model. As demonstrated in Figure 1, this ratio is a good approximation to the ratio of actual standard deviations. The ratios range from 4.56 to 136.80, with an average of 29.71 for the male group, and from 6.06 to 351.82 with an average of 56.99 for the female group. This indicates that the groupwise envelope model obtains substantial efficiency gains over the standard model (2). A boxplot of the ratios is given in Figure 3. The efficiency gains can be explained by the covariance structure: ${\widehat{\mathrm{\Omega }}}_{(1)}=1.27\times {10}^{-4}$, ${\widehat{\mathrm{\Omega }}}_{(2)}=0.1579$ and $\Vert {\widehat{\mathrm{\Omega }}}_0\Vert =19.29$. This indicates that the variation of the immaterial part is much larger than that of the material part, and by identifying and accounting for the immaterial variation, the groupwise envelope model achieves substantial efficient estimation in this case. The efficiency gains in estimation lead to better prediction performance. The prediction error is estimated by the average of 50 five-fold cross validations with random splits, and the identity inner product is used to bind the responses. The standard model has a prediction error of 21.27, and the groupwise envelope model has a prediction error of 9.65, which is more than a 50% reduction.

Figure 3.

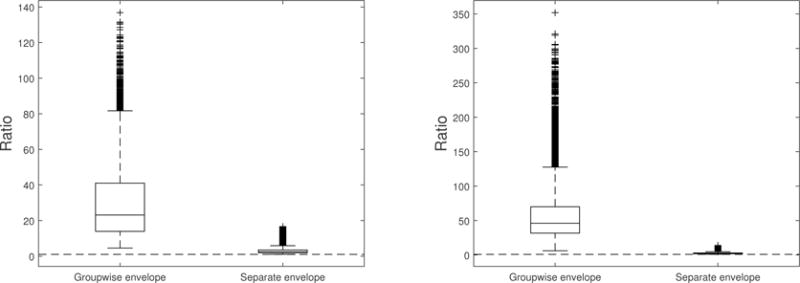
Boxplot of the ratio of the bootstrap standard deviation under the standard model to the bootstrap standard deviation under the groupwise envelope model or separate envelope model. The left panel is boxplot of the ratios for the male group, and the right panel is boxplot of the ratios for the female group. The horizontal line is at 1.

We also fitted the separate envelope model to the data. BIC suggested u = 1 for both male and female groups. The ratios of the bootstrap standard deviation under the standard model to that under the separate envelope model range from 1.05 to 16.63 with an average of 3.16 for the male group, and range from 1.01 to 13.93 with average of 2.68 for the female group. The ratios are also displayed in Figure 3. The boxplot reveals that the groupwise envelope model and the separate envelope model are both more efficient than the standard model. But by using the information from all the groups in the estimation of ${ℰ}_{ℳ}\left(ℬ\right)$, the groupwise envelope model achieves substantially more efficiency gains than the separate envelope model, which confirms the results in Corollary 4.

To investigate the genetic effects of the SNPs on the brain volumes of 93 ROIs through the groupwise envelope model, we looked at a submatrix of $\widehat{\mathit{\beta }}$, say ${\widehat{\mathit{\beta }}}_{\mathrm{sub}}$, which consisted of columns corresponding to the 205 PCs and APOE ε4. And we calculated $c_{j,i}=|{\widehat{\mathit{\beta }}}_{\mathrm{sub},j,i}|/\Vert {\widehat{\mathit{\beta }}}_{\mathrm{sub},j.}\Vert$, where ${\widehat{\mathit{\beta }}}_{\mathrm{sub},j,i}$ denotes the (j, i)th element of ${\widehat{\mathit{\beta }}}_{\mathrm{sub}}$ and ${\widehat{\mathit{\beta }}}_{\mathrm{sub},j}$ denotes the jth row of ${\widehat{\mathit{\beta }}}_{\mathrm{sub}}$, j = 1, …, 93 and i = 1, …, 206. In particular, j = 30 and j = 69 correspond to the right and left part of hippocampal formation region, which are important ROIs. Figure 4 shows c_30,i and c_69,i for the hippocampal formation region. In particular, the 206th element in the horizontal axis corresponds to APOE ε4. We have c_30,206 = c_69,206 = 0.077 for the male group and c_30,206 = c_69,206 = 0.110 for the female group.

Figure 4.

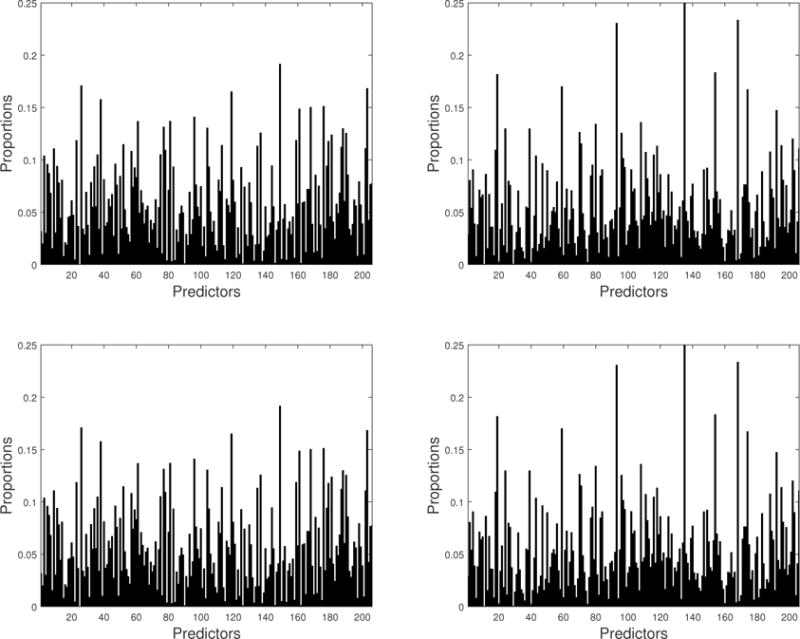
Plot of the proportions of the absolute value of coefficient for SNPs in the Euclidean norm of the coefficient vector corresponding to the region: the last on the horizontal axis denotes APOE ε4 and the remaining is for 205 PCs. The first row is for left hippocampal formation region, and the second row is for the right hippocampal formation region. The left panel is for the male group, and the right panel is for the female group. This figure appears in color in the electronic version of this article.

To consider the relationship between SNPs and ROI volumes in the coefficient matrix, we focused on the PCs with large coefficients based on the 98th quantile of the absolute values of the estimated regression coefficients. After thresholding, 42 PCs were selected for the male group and 49 PCs were selected for the female group. The heatmaps of regression coefficients for each group under the groupwise envelope model and the standard model are displayed in Figure 5. The horizontal axes in Figure 5 include the selected PCs as well as APOE ε4. Under the groupwise envelope model, it is easier to identify the regions with diminishing regression coefficients.

Figure 5.

Heatmaps of the regression coefficients: the last on the horizontal axis denotes APOE ε4 and the remaining is for the selected PCs. The first row is for groupwsie envelope model, and the second row is for the standard model (2). The left panel is for the male group, and the right panel is for the female group. This figure appears in color in the electronic version of this article.

We also tested if a coefficient equals to 0 for all elements in β. An ROI is chosen if at least one of the p-values in the corresponding coefficients is smaller than 0.05. Based on this criterion, all ROIs are selected under the standard model. Under the groupwise envelope model, 41 ROIs are selected for the male group. And eight additional ROIs lat.f-o.gy.R, sup.f.gy.R, hiopp.R, caud.neuc.R, mid.t.gy.L, prec.gy.L, par.lb.WM.R, and ant.caps.R are selected for female group, i.e. 49 ROIs are selected for female group. This indicates that the unselected ROIs are significant under the homogeneous model, but not under the model that considers heteroscedasticity. The selected ROIs are listed in Table 1. Among the selected ROIs, (i) me.f-o.gy.L/R, lat.f-o.gy.R, inf.f.gy.L/R, f.lob.WM.L, sup.f.gy.L/R and me.f.gy.R are related to the function of management (making a decision and carrying out tasks), attention (interest and concentration) and working memory; (ii) tmp.pl.R, sup.gy.R, sup.t.gy.L/R, mid.t.gy.L/R, inf.t.gy.L are related to memory and language; (iii) sup.p.lb.L/R and par.lb.WM.R are related to the sense of the space and size; and (iv) sup.o.gy.L/R, mid.o.gy.R, me.o.gy.L/R are located in the back of the brain playing an important role in vision.

Table 1.

The selected ROIs based on the p-value of β_red. The italic ROIs in groupwise envelope model are regions additionally selected from female group except 41 common selected ROIs.

Groupwise Envelope model		Standard model
me.f-o.gy.R	pstc.gy.R	me.f-o.gy.R	sup.o.gy.R	tmp.pl.L
lat.ve.L	ling.gy.R	mid.f.gy.R	caud.neuc.L	ent.cort.L
insula.R	me.f.gy.R	lat.ve.L	sup.gy.L	inf.o.gy.R
lat.ve.R	amyg.L	insula.R	ant.caps.L	sup.o.gy.L
glob.pal.R	me.o.gy.L	prec.gy.R	oc.lb.WM.R	lat.o.t.gy.R
glob.pal.L	mid.t.gy.R	lat.f-o.gy.R	mid.f.gy.L	ent.cort.R
inf.f.gy.L	corp.col	cing.R	sup.p.lb.L	hiopp.L
ang.gyr.R	sup.t.gy.R	lat.ve.R	caud.neuc.R	thal.L
tmp.pl.R	me.o.gy.R	me.f.gy.L	cun.L	par.lb.WM.R
nuc.acc.R	thal.R	sup.f.gy.R	prec.L	insula.L
f.lob.WM.L	lat.f-o.gy.R	glob.pal.R	par.lb.WM.L	pstc.gy.R
subtha.nuc.L	sup.f.gy.R	glob.pal.L	tmp.lb.WM.R	ling.gy.R
sup.o.gy.R	hiopp.R	putamen.L	sup.gy.R	me.f.gy.R
caud.neuc.L	caud.neuc.R	inf.f.gy.L	sup.t.gy.L	amyg.L
sup.p.lb.L	mid.t.gy.L	putamen.R	unc.L	me.o.gy.L
prec.L	prec.gy.L	f.lob.WM.R	mid.o.gy.R	parah.gy.R
sup.gy.R	par.lb.WM.R	parah.gy.L	mid.t.gy.L	ant.caps.R
sup.t.gy.L	ant.caps.R	ang.gyr.R	ling.gy.L	mid.t.gy.R
unc.L		tmp.pl.R	sup.f.gy.L	occ.pol.R
mid.o.gy.R		subtha.nuc.R	nuc.acc.L	corp.col
ling.gy.L		nuc.acc.R	oc.lb.WM.L	amyg.R
sup.f.gy.L		unc.R	pstc.gy.L	inf.t.gy.R
nuc.acc.L		cing.L	inf.f.gy.R	sup.t.gy.R
inf.f.gy.R		fornix.L	prec.gy.L	mid.o.gy.L
me.f-o.gy.L		f.lob.WM.L	tmp.lb.WM.L	ang.gyr.L
per.cort.R		pec.R	me.f-o.gy.L	me.o.gy.R
sup.p.lb.R		subtha.nuc.L	per.cort.R	cun.R
per.cort.L		post.limb.L	sup.p.lb.R	lat.o.t.gy.L
inf.t.gy.L		post.limb.R	lat.f-o.gy.L	thal.R
ent.cort.L		hiopp.R	per.cort.L	occ.pol.L
ent.cort.R		inf.o.gy.L	inf.t.gy.L	fornix.R

We then use the polygenic score to study the genetic relationship between the SNPs and the brain volumes on 93 ROIs. The genetic effects in our setting are contained in the 205 PCs obtained from the SNPs as well as APOE ε4. Let l be the gender indicator, l = 1 for male and l = 2 for female. Then for group l, Y_l = (Y_l,1,…, Y_l,93)^T is the response vector and Z_l denotes the vector of 205 PCs and all the covariates. For each response Y_l,j, j = 1, …, 93, we fit the linear regression model of Y_l,j on Z_l, and obtained the estimated coefficients ${\widehat{\mathit{\beta }}}_{l,j}$ and the p-values for each element in ${\widehat{\mathit{\beta }}}_{l,j}$. We set the significance level at 0.05. Suppose ${\mathbf{Z}}_{l,j}^{\ast }$ are the significant genetic effects and ${\widehat{\mathit{\beta }}}_l^{\ast }$ are their coefficients, we can construct the polygenic score as ${\widehat{\mathbf{S}}}_{l,j}={\widehat{\mathit{\beta }}}_{l,j}^{\ast }{\mathbf{Z}}_{l,j}^{\ast }$. We then fit the regression of Y_l,j on ${\widehat{\mathbf{S}}}_{l,j}$, and calculated the total sum of squares SST_l,j and regression sum of squares SSR_l,j. We then computed $R_1={\displaystyle {\sum }_{j=1}^{93}{\mathrm{SSR}}_{1,j}}/{\displaystyle {\sum }_{j=1}^{93}{\mathrm{SST}}_{1,j}}$ and $R_2={\displaystyle {\sum }_{j=1}^{93}{\mathrm{SSR}}_{2,j}}/{\displaystyle {\sum }_{j=1}^{93}{\mathrm{SST}}_{2,j}}$. Based on the value of R₁ and R₂, the genetic effects of SNPs explain 9.55% and 9.60% of the variation in the male and female groups, respectively. The association of the polygenic score with the phenotypical variation is tested based on the chi-squared distribution with non-centrality parameter λ_l and degrees of freedom 1, where ${\lambda }_l=(n_{\left(l\right)}{R}_l^2)/(1-R_l^2)$, n₍₁₎ = 441 and n₍₂₎ = 304. Then the power of the two-tailed chi-squared test with significance level α is obtained from

$$1-\mathrm{\Phi }[{\mathrm{\Phi }}^{-1}\left(1-\alpha /2\right)-\sqrt{{\lambda }_l}]+\mathrm{\Phi }[{\mathrm{\Phi }}^{-1}\left(\alpha /2\right)-\sqrt{{\lambda }_l}],l=1,2,$$

where Φ is the cumulative distribution function for the standard normal distribution. We found both groups have power 1 with α = 0.05 in the testing.

6. Conclusion

We have proposed a groupwise envelope model, which is an efficient model for estimating regression coefficients for heterogeneous groups. Since the interest of research in heterogeneity soars, such as the great attention in precision medicine, the development of models dealing with heterogeneity is desired in multivariate response analysis. The groupwise envelope model allows for distinct regression coefficients and heteroscedastic error structure for different groups. Our simulation studies and ADNI data analysis demonstrates the efficiency gains obtained by the groupwise envelope model, compared to both standard model and separate envelope model. The groupwise envelope model leads to a better understanding of the genetic effects of the top 40 AD candidate genes for male and female groups on brain volumes of 93 ROIs in the ADNI dataset.

For future research, a sparse groupwise envelope model that pinpoints the immaterial responses is desired for real applications, as it is more interpretable. If we consider the spatial structure of the brains, we would have a multi-dimensional array (tensor) response. Li and Zhang (2016) developed a tensor response envelope model that achieves efficient estimation in tensor regression. We can expand our methodology to handle heteroscedastic error structure in the tensor envelope model. In addition, a Bayesian version of this model that incorporates prior information from earlier studies is also worth exploration. As longitudinal data and missing data appear in Alzheimer’s study, a groupwise envelope model that can handle these data structures would also be of practical use.

Appendix

A: Estimation of the groupwise envelope model

we first hold Γ fixed and derive the estimators of parameters μ_(l), η_(l), Ω_(l), l = 1,…, L, and Ω₀ as a function of Γ. The derivative of the log likelihood l = l(θ) in (5) with respect to μ_(l) is

$$\frac{\partial l}{\partial {\mathit{\mu }}_{\left(l\right)}}=n_{\left(l\right)}\Gamma {\Omega }_{\left(l\right)}^{-1}({\Gamma }^T{\overline{Y}}_{\left(l\right)}-{\Gamma }^T{\mathit{\mu }}_{\left(l\right)}-{\eta }_{\left(l\right)}{\overline{X}}_{\left(l\right)})+n_{\left(l\right)}{\Gamma }_0{\Omega }_0^{-1}{\Gamma }_0^T({\overline{Y}}_{\left(l\right)}-{\mathit{\mu }}_{\left(l\right)}).$$ (A.1)

Setting the derivative in (A.1) to 0 and using the fact that ${\mathbb{X}}_{\left(l\right)}$ is centered at 0, we have ${\widehat{\mathit{\mu }}}_{\left(l\right)}={\widehat{Y}}_{\left(l\right)}$. Substitute ${\widehat{\mathit{\mu }}}_{\left(l\right)}$ into the likelihood, we now consider the derivative of l in (5) with respect to η_(l):

$$\frac{\partial l}{\partial {\mathit{\eta }}_{\left(l\right)}}={\displaystyle \sum _{j=1}^{n_{\left(l\right)}}{\Omega }_{\left(l\right)}^{-1}({\Gamma }^T{\mathbf{Y}}_{\left(l\right)j}-{\Gamma }^T{\overline{Y}}_{\left(l\right)}-{\mathit{\eta }}_{\left(l\right)}{\mathbf{X}}_{\left(l\right)j})}{\mathbf{X}}_{\left(l\right)j}^T.$$ (A.2)

We set the the derivative in (A.2) to be 0 and obtain

$${\widehat{\mathit{\eta }}}_{\left(l\right)}=\left({\displaystyle \sum _{j=1}^{n_{\left(l\right)}}{\Gamma }^T\left({\mathbf{Y}}_{\left(l\right)j}-{\overline{Y}}_{\left(l\right)}\right){\mathbf{X}}_{\left(l\right)j}^T}\right){\left({\displaystyle \sum _{j=1}^{n_{\left(l\right)}}{\mathbf{X}}_{\left(l\right)j}{\mathbf{X}}_{\left(l\right)j}^T}\right)}^{-1}={\Gamma }^T\left({\mathbb{Y}}_{\left(l\right)c}^T{\mathbb{X}}_{\left(l\right)}\right){\left({\mathbb{X}}_{\left(l\right)}^T{\mathbb{X}}_{\left(l\right)}\right)}^{-1},$$

where ${\mathbb{X}}_{(l)}$ is an n_(l) × p matrix with its ith row being ${\mathbf{X}}_{\left(l\right),i}^T$, ${\mathbb{Y}}_{\left(l\right)c}$ is an n_(l) × r matrix with its ith row being ${\mathbf{Y}}_{\left(l\right),i}^T-{\overline{Y}}_{\left(l\right)}^T$. Substitute ${\widehat{\mathit{\mu }}}_{\left(l\right)}$ and ${\widehat{\mathit{\eta }}}_{\left(l\right)}$ to the log likelihood function, we have

$$\begin{array}{l}l=-\frac{nr}{2}\log \left(2\pi \right)-\frac{n}{2}\log |{\Omega }_0|-\frac{1}{2}{\displaystyle \sum _{l=1}^L{n}_{\left(l\right)}}\log |{\Omega }_{\left(l\right)}|\\ -\frac{1}{2}{\displaystyle \sum _{l=1}^L\mathrm{tr}({\mathbf{Q}}_{{\mathbb{X}}_{\left(l\right)}}{\mathbb{Y}}_{\left(l\right)c}\Gamma {\Omega }_{\left(l\right)}^{-1}{\Gamma }^T{\mathbb{Y}}_{\left(l\right)c}^T{\mathbf{Q}}_{{\mathbb{X}}_{\left(l\right)}})}-\frac{1}{2}{\displaystyle \sum _{l=1}^L\mathrm{tr}({\mathbb{Y}}_{\left(l\right)c}{\Gamma }_0{\Omega }_0^{-1}{\Gamma }_0^T{\mathbb{Y}}_{\left(l\right)c}^T)}.\end{array}$$ (A.3)

We can easily get the estimators of Ω_(l) and Ω₀ by taking the derivatives, and the estimators are

$${\widehat{\Omega }}_{\left(l\right)}=\frac{1}{n_{\left(l\right)}}{\Gamma }^T{\mathbb{Y}}_{\left(l\right)c}^T{\mathbf{Q}}_{{\mathbb{X}}_{\left(l\right)}}{\mathbb{Y}}_{\left(l\right)c}\Gamma ={\Gamma }^T{\widehat{\sum }}_{\mathrm{res},\left(l\right)}\Gamma \text{and}{\widehat{\Omega }}_0=\frac{1}{n}{\displaystyle \sum _{l=1}^L{\Gamma }_0^T{\mathbb{Y}}_{\left(l\right)c}^T}{\mathbb{Y}}_{\left(l\right)c}{\Gamma }_0={\Gamma }_0^T{\widehat{\sum }}_{\mathbf{Y}}{\Gamma }_0.$$ (A.4)

Substitution of (A.4) into (A.3) gives

$$l=\mathrm{constant}-\frac{1}{2}{\displaystyle \sum _{l=1}^L{n}_{\left(l\right)}}\log |{\Gamma }^T{\widehat{\sum }}_{\mathrm{res},\left(l\right)}\Gamma |-\frac{n}{2}\log |{\Gamma }_0{\widehat{\sum }}_{\mathbf{Y}}{\Gamma }_0|.$$ (A.5)

By Lemma 6.2 of Cook et al. (2010), we rewrite the function in (A.5) as

$$l\left(\Gamma \right)=\mathrm{constant}-\frac{n}{2}\log |{\widehat{\sum }}_{\mathbf{Y}}|-\frac{1}{2}{\displaystyle \sum _{l=1}^L{n}_{\left(l\right)}}\log |{\Gamma }^T{\widehat{\sum }}_{\mathrm{res},\left(l\right)}\Gamma |-\frac{n}{2}\log |{\Gamma }^T{\widehat{\sum }}_{\mathbf{Y}}^{-1}\Gamma |.$$

Then the objective function for Γ is

$${\displaystyle \sum _{l=1}^L\frac{n_{\left(l\right)}}{n}\log |{\Gamma }^T{\widehat{\sum }}_{\mathrm{res},\left(l\right)}\Gamma |}+\log |{\Gamma }^T{\widehat{\sum }}_{\mathbf{Y}}^{-1}\Gamma |,$$

and Γ can be obtained by minimizing the preceding objective function.

B: Proofs of theoretical results in Section 3

Proof of Proposition 1 and Proposition 2

For preparation, if A ∈ ℝ^m×m is a symmetric matrix, vech(A) ∈ ℝ^m(m+1)/2 denotes the vector that stacks the lower triangle of A into a vector. The notations ${\mathbf{E}}_m\in {ℝ}^{m^2\times m(m+1)/2}$ and ${\mathbf{C}}_m\in {ℝ}^{m\left(m+1\right)/2\times m^2}$ are expansion and contraction operators that connect vec and vech: vec(A) = E_m vech(A) and vech(A) = C_m vec(A).

We use Proposition 4.1 in Shapiro (1986) to prove Proposition 1. Let h denote the parameters under the standard model, and let ϕ denote the parameters under the groupwise envelope model. Then $\mathbf{h}=\mathrm{vec}[{\{{\mathit{\mu }}_{(1)}^T,\dots ,{\mathit{\mu }}_{(L)}^T,{\mathrm{vec}}^T({\mathit{\beta }}_{(1)}),\dots ,{\mathrm{vec}}^T({\mathit{\beta }}_{(L)}),{\mathrm{vech}}^T({\sum }_{(1)}),\dots ,{\mathrm{vech}}^T({\sum }_{(L)})\}}^T]$, and $\varphi =\mathrm{vec}{\{{\mathit{\mu }}_{(1)}^T,\dots ,{\mathit{\mu }}_{(L)}^T,{\mathrm{vec}}^T({\mathit{\eta }}_{(1)}),\dots ,{\mathrm{vec}}^T({\mathit{\eta }}_{(L)}),{\mathrm{vech}}^T({\Omega }_{(1)}),\dots ,{\mathrm{vech}}^T({\Omega }_{(L)}),{\mathrm{vec}}^T(\Gamma ),{\mathrm{vech}}^T({\Omega }_0)\}}^T$. We use J to denote the Fisher information matrix under the standard model, and G to denote the gradient matrix. Then

$$\mathbf{G}\equiv \frac{\partial \mathbf{h}}{\partial {\varphi }^T}=\left(\begin{array}{lllll}{\mathrm{g}}_1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\mathrm{g}}_2\hfill & 0\hfill & {\mathrm{g}}_3\hfill & 0\hfill \\ 0\hfill & 0\hfill & {\mathrm{g}}_4\hfill & {\mathrm{g}}_5\hfill & {\mathrm{g}}_6\hfill \end{array}\right),$$

where g₁=I_Lr, g₂ is a Lpr × Lpu block diagonal matrix whose all diagonal blocks are I_p ⊗ Γ, g₃ = (η₍₁₎ ⊗ I_r,…,η_(L) ⊗ I_r)^T, g₄ id a Lr(r + 1)/2 × ur block diagonal matrix whose all diagonal blocks are ${\mathbf{C}}_r(\Gamma \otimes \Gamma ){\mathbf{E}}_u,{\mathrm{g}}_5={\{2({\Omega }_{(1)}{\Gamma }^T\otimes {\mathbf{I}}_r–{\Gamma }^T\otimes {\Gamma }_0{\Omega }_0{\Gamma }_0^T){\mathbf{C}}_r^T,\dots ,2({\Omega }_{(L)}{\Gamma }^T\otimes {\mathbf{I}}_r-{\Gamma }^T\otimes {\Gamma }_0{\Omega }_0{\Gamma }_0^T){\mathbf{C}}_r^T\}}^T$ and ${\mathrm{g}}_6={\{{\mathbf{E}}_{r-u}^T({\Gamma }_0^T\otimes {\Gamma }_0^T){\mathbf{C}}_r^T,\dots ,{\mathbf{E}}_{r-u}^T({\Gamma }_0^T\otimes {\Gamma }_0^T){\mathbf{C}}_r^T\}}^T$. Now we match Shapiro’s notations with our notations. Shapiro’s θ is our ϕ; Shapiro’s ξ is our h; Shapiro’s $\widehat{\mathrm{x}}$ is the standard estimator of h; Shapiro’s Δ is our gradient matrix G; Shapiro’s V is our J; and Shapiro’s discrepancy function F is l_max − l, where l is the log likelihood function and l_max is the maximum value of l attained when h is the standard estimator of h. Specifically,

$$\begin{array}{l}{l}_{max}-l=l_{max}+\frac{nr}{2}\log \left(2\pi \right)+\frac{1}{2}{\displaystyle \sum _{l=1}^L[n_{\left(l\right)}\log |{\sum }_{\left(l\right)}|}\\ +\mathrm{tr}\{({\mathbb{Y}}_{\left(l\right)}-1_{n_{\left(l\right)}}{\mathit{\mu }}_{\left(l\right)}^T-{\mathbb{X}}_{\left(l\right)}{\mathit{\beta }}_{\left(l\right)}^T){\sum }_{\left(l\right)}^{-1}{({\mathbb{Y}}_{\left(l\right)}-1_{n_{\left(l\right)}}{\mathit{\mu }}_{\left(l\right)}^T-{\mathbb{X}}_{\left(l\right)}{\mathit{\beta }}_{\left(l\right)}^T)}^T\}]\\ =l_{max}+\frac{nr}{2}\log \left(2\pi \right)+\frac{1}{2}{\displaystyle \sum _{l=1}^L(n_{\left(l\right)}\log |{\sum }_{\left(l\right)}|+\mathrm{tr}[{\sum }_{\left(l\right)}^{-1}\{n{\widehat{\sum }}_{\mathrm{res}\left(l\right)}}\\ +({\mathit{\beta }}_{\left(l\right)}-{\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{ols}}){\mathbb{X}}_{\left(l\right)}^T{\mathbb{X}}_{\left(l\right)}{({\widehat{\mathit{\beta }}}_{\left(l\right)}-{\widehat{\mathit{\beta }}}_{\left(l\right),\mathrm{ols}})}^T+n_{\left(l\right)}({\mathit{\mu }}_{\left(l\right)}-{\overline{Y}}_{\left(l\right)}){({\mathit{\mu }}_{\left(l\right)}-{\overline{Y}}_{\left(l\right)})}^T\}]).\end{array}$$

It is easy to see that l_max − l satisfies the conditions 1 – 4 in Section 3 of Shapiro (1986). Since J is full rank, we have rank (G^T JG) = rank (J). As the standard estimator of h is $\sqrt{n}$ consistent and converges in distribution to a normal distribution with mean 0 and covariance J⁻¹, all the conditions in Proposition 4.1 of Shapiro (1986) are satisfied. Thus, the groupwise envelope estimator $\widehat{h}$ is a $\sqrt{n}$ consistent estimator of h, and $\sqrt{n}(\widehat{h}-\mathbf{h})$ has asymptotically normal distribution with mean 0.

When the errors are normally distributed, then J has a closed form:

$$\mathbf{J}=\left(\begin{array}{ccc}{\mathbf{J}}_1& 0& 0\\ 0& {\mathbf{J}}_2& 0\\ 0& 0& {\mathbf{J}}_3\end{array}\right),$$

where f_(l) = n_(l)/n is the proportion of the l–th population, J₁ is a Lr × Lr block diagonal matrix whose diagonal blocks are $f_{(1)}{\sum }_{(1)}^{-1},\dots ,f_{(L)}{\sum }_{(L)}^{-1}$, J₂ is a Lpr × Lpr block diagonal matrix whose diagonal blocks are $f_{(1)}{\sum }_{{\mathbf{X}}_{(1)}}\otimes {\sum }_{(1)}^{-1},\dots ,f_{(L)}{\sum }_{{\mathbf{X}}_{(L)}}\otimes {\sum }_{(L)}^{-1}$, and J₃ is a {Lr(r + 1)/2} × {Lr(r +1)/2} block diagonal matrix whose diagonal blocks are $(1/2)f_{\left(1\right)}{\mathbf{E}}_r^T({\sum }_{(1)}^{-1}\otimes {\sum }_{(1)}^{-1}){\mathbf{E}}_r,\dots ,(1/2)f_{(L)}{\mathbf{E}}_r^T({\sum }_{(L)}^{-1}\otimes {\sum }_{(L)}^{-1}){\mathbf{E}}_r$. The asymptotic variance of $\widehat{h}$ under the groupwise envelope model then has a closed form V_env = G(G^T JG)^†G^T, where A^† denotes the Moore-Penrose generalized inverse of a matrix A. After some straightforward calculations, the asymptotic variance of vec $({\widehat{\beta }}_{(l)})$ is $(1/f_{(l)}){\sum }_{{\mathbf{X}}_{(l)}}^{-1}\otimes \Gamma {\Omega }_{(l)}{\Gamma }^T+({\mathit{\eta }}_{(l)}^T\otimes {\Gamma }_0){\left\{{\displaystyle {\sum }_{l=1}^L{f}_{(l)}}\left({\mathit{\eta }}_{(l)}{\sum }_{{\mathbf{X}}_{(l)}}{\mathit{\eta }}_{(l)}^T\otimes {\Omega }_0^{-1}+{\Omega }_{(l)}\otimes {\Omega }_0^{-1}+{\Omega }_{(l)}^{-1}\otimes {\Omega }_0-2{\mathbf{I}}_u\otimes {\mathbf{I}}_{r-u}\right)\right\}}^{-1}({\mathit{\eta }}_{(l)}\otimes {\Gamma }_0^T)$ and the asymptotic variance of ${\widehat{\mu }}_{(l)}$ is (1/f_(l))Σ_(l), for l = 1,…,L.

Proof of Proposition 3

Proof of Proposition 3 follows directly from (5.7) in Cook et al. (2010).