Abstract
We investigated the impact of the displacement of sexual activity from adherent recipients of an intervention to others within or outside a trial population on the results from hypothetical trials of different sexual behavior interventions. A short-term model of HIV-prevention interventions that lead to female rejection of male partnership requests showed the impact of displacement expected at the start of a trial. An agent-based model, with sexual mixing and other South African specific demographics, evaluated consequences of displacement for sexual behavior interventions targeting young females in South Africa. This model measured the cumulative incidence among adherent, non-adherent, control and non-enrolled females in a hypothetical trial of HIV prevention. When males made more than one attempt to seek a partnership, interventions reduced short-term HIV infection risk among adherent females, but increased it among non-adherent females as well as controls, non-enrolled (females eligible for the trial but not chosen to participate) and ineligible females (females that did not qualify for the trial due to age). The impact of displacement depends on the intervention and the adherence. In both models, the risk to individuals who are not members of the adherent intervention group will increase with displacement leading to a biased calculation for the effect estimates for the trial. Likewise, intent-to-treat effect estimates become nonlinear functions of the proportion adherent.
Keywords: Displacement, Agent-based modeling, HIV prevention, Trial Design
Introduction
HIV prevention interventions that focus on changing sexual behavior practices among women can have indirect effects, since preventing or changing the risk of infection in one individual may have consequences for the risk of infection in their contacts and, via transmission chains, in other members of the population. With some exceptions (Killeen et al., 2007; Knox, 1985; Kunkel et al., 2015; Lipsitch and Samore, 2002; Miller et al., 2016; Panagiotopoulos et al., 1999), the population-level benefit of interventions specifically designed to control the spread of infectious disease exceeds the sum of individual-level benefits; the paradigm examples are herd immunity from vaccine against communicable diseases (Fine, 1993) and contagion-reducing effects of treatment for infections like tuberculosis, HIV and other sexually transmitted infections, and malaria (Boily et al., 2012; Greenwood, 2010). However, the population-level benefit of interventions that utilize behavioral changes to control for sexually transmitted diseases, can be more complex (Kremer and Morcom, 1998).
The indirect effects of complex behavioral interventions are less well understood, partly because these involve both disease transmission (where reductions in one individual are typically beneficial to others) and population-scale social and economic phenomena (where interactions are more complex). When assessing the impact of an intervention on reducing sexual activity – e.g. an intervention intended to produce a delay of sexual debut, a decrease in the number of partnerships, or encourage abstinence – the sexual acts that are not occurring among those in an intervention group may be displaced to individuals in the control or non-participant groups, increasing their risk. We consider, as a simplifying assumption, that males solicit and females accept or reject sexual acts. Then, reduced sexual activity by an individual female in one of these behavioral intervention groups may lead the males who would have had sex with this female to fail to form a partnership, reducing the total number of acts in the population. Alternatively, the males may seek (and possible have) acts with other females which we refer to as displacement of acts. When a behavior change intervention is implemented population-wide, these displaced acts may be with females who did not receive the intervention, or who received it but who did not avoid sexual activity (non-adherent). In an intervention trial of this kind, those not receiving the intervention would include females ineligible for the trial, those who were eligible but were not enrolled, and those in the control arm of the trial.
A few studies have considered the possibility that certain types of behavioral interventions to control sexually transmitted diseases may have unwanted effects caused by the displacement of sexual acts (Baird et al., 2014a; Baird et al., 2010; Baird et al., 2012; Kremer and Morcom, 1998) that increase the infection risk of some members of the population. Baird et al. discussed this issue while estimating the effects of cash transfer programs on the sexual behavior of young women (Baird et al., 2014a; Baird et al., 2010; Baird et al., 2014b; Baird et al., 2012) and Hallett et al. used a mathematical model to estimate the effects of displaced acts caused by interventions on reducing cross-generational sex in Zimbabwe (Hallett et al., 2007). These displacement effects may occur during a clinical trial of such intervention (Baird et al., 2014a; Baird et al., 2010; Baird et al., 2014b; Baird et al., 2012) and/or during its population-wide implementation (Kremer and Morcom, 1998).
Here we provide a general modeling framework to consider displacement effects in a heterosexual population. We outline the theory behind these displacement effects using an example of an HIV prevention intervention that targets the sexual behavior of young women. Using a static model we calculate the first-order effects of reducing sexual activity in a group of females on the sexual activity and HIV infection risk in other groups while holding constant the HIV risk from each act, as would be expected when a trial starts. However, after such an intervention has been in place for some time, there may be effects on HIV incidence and prevalence in men, which then feedback in more complex ways to effect female trial participants and others in the population. We use a dynamic, individual-based model, the HIV Calibrated Dynamic Model (HIV-CDM) (McCormick et al., 2014), to evaluate the effects as a trial or an intervention proceeds. The HIV-CDM includes a complex pattern of sexual mixing and is well suited to track the evolution of risk over time in various groups under different trial settings.
Materials and Methods
Short-term model
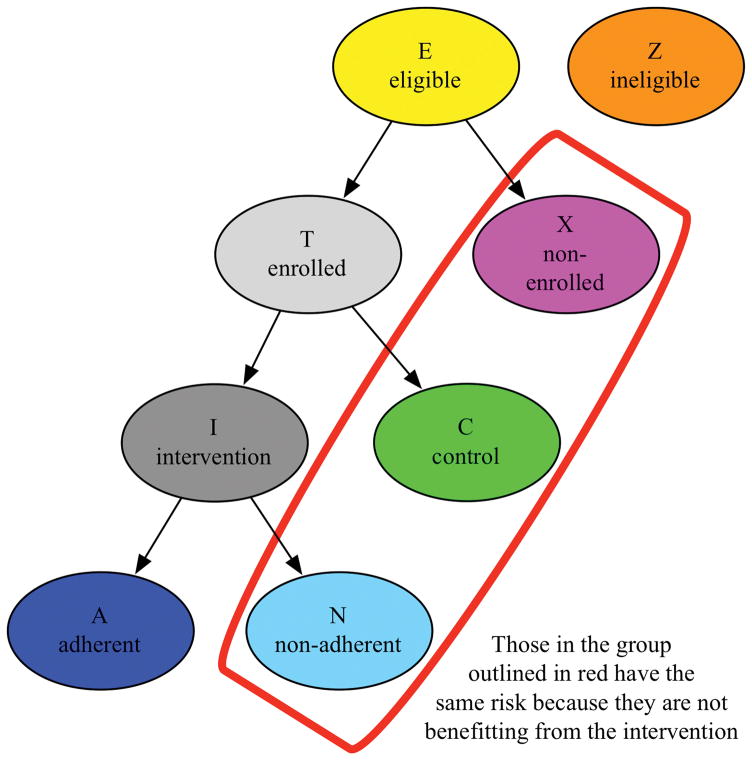
Within a heterosexual population we initially assume that males approach females eligible for a trial (E) with proposals to engage in D sexual acts. Males seek a sexual act with a randomly chosen eligible female. Females reject sexual act requests with a probability p and accept them with probability 1-p. Males seeking an act who do not succeed continue to request acts with other randomly chosen females, up to w requests, at which point they give up and fail to partner. We assume that they are equally likely to seek and be accepted by eligible females who do not receive the intervention – non-adherent, control, or non-enrolled eligible females. Thus we assume there is no Hawthorne effect from the trial and no control intervention that leads to reduced sexual activity; these assumptions could be relaxed at the expense of complicating the algebra. Males rejected in the first round of search by eligible females may also widen their search to consider females who are ineligible for the trial (Z) (Figure 1), We assume that an ineligible female is less desirable than an eligible female by a factor q≤1. For example, ineligible females may be older or geographically more distant. Thus the second (and all subsequent) requests are distributed equally among E+qZ females. This process continues up to w requests.
Figure 1.
The hypothetical population simulated in the models
We define h as the per-act risk of HIV infection from each sexual act; h is the product of the prevalence of HIV among the males requesting acts and the per-act transmission probability from an HIV-positive male. Table S1 shows the short-term model in the absence of intervention, giving the HIV infection risk to eligible females in each round of male requests. We calculate the risk difference for those adherent to the intervention (A), those eligible for the intervention but not receiving or adhering to it (N, C, and X), the intervention group as a whole (A and N), and those ineligible for the intervention (Z). The calculations for this model are shown in the Supplementary Material.
Dynamic model
The changing incidence in various groups of females will affect incidence in males (via changes in transmission), which will in turn affect incidence in females, and so on, over time. An intervention that reduces incidence in the adherent group may reduce overall incidence for other groups of females even if displacement occurs, by reducing transmission to males, and thereby reducing the risk to other females from acts with those males. Thus the second-order effects of the intervention may reduce incidence even in the groups that receive displaced sexual partnerships, depending on the balance between overall reduction in male prevalence and the extent of displacement.
To examine the impact of displacement as an intervention trial proceeds we used the HIV-CDM, an individual-based, stochastic model that includes detailed natural history (based on the CEPAC Model (Freedberg et al., 2001; Walensky et al., 2014)) and heterosexual behavior. The HIV-CDM was calibrated to South African prevalence and behavioral data using modified Bayesian melding (McCormick et al., 2014). In brief, we ran 264,225 simulations of the HIV epidemic in South Africa and found 3,750 parameter sets that both created an epidemic and had behavioral characteristics, such as prevalence of partnerships of various types and of concurrent partnerships, representative of a South African population pre-antiretroviral therapy (ART). We carried out these analyses using ART rollout as reported in South Africa, assuming testing and linkage to care probabilities outlined in Table S3. The interventions used for these analyses were introduced into the model population in 2014. For the present study, we used the single-best-fitting parameter set from these analyses (Table S3); our purpose here is to illustrate how displacement would behave in a dynamic epidemic rather than to make specific predictions about the South African epidemic.
To examine the potential impact of sexual behavior interventions targeting young females on HIV prevalence and incidence, we first divided the eligible females in the HIV-CDM population into the same main groups used for the short-term model (Figure 1). The enrollment period for this hypothetical trial was 2014–2018. All females in the HIV-CDM population who are, or who become, 16 year olds between 2014 and 2018 are eligible for the simulated trial and are randomized to a control, adherent intervention, non-adherent intervention, or non-enrolled group with the proportion of females in each group varied in each analysis. Females in the adherent group alter their sexual behavior while they are between the ages of 16–20 and then at age 20 their behaviors return to the default non-intervention values. Females in the simulated population who are not 16 at any time between 2014 and 2018 are ineligible for the study population.
In the model, annual HIV incidence for the entire eligible HIV-CDM population (2000 females), stratified by the control, adherent, non-adherent, and non-enrolled females, in the period 2014–2029 is observed. This allows the model to consider the post-trial impact on the females in the trial population. We divided the eligible population as follows: 20% non-enrolled; 40% in the control group; 28% in the adherent intervention group; and 12% in the non-adherent intervention group. Therefore, 80% of females 17–24 were enrolled, 50% of whom were in the intervention arm with 70% adherence. Using this population stratification, we ran the HIV-CDM with each intervention implemented independently. An abstinence intervention was modeled in two different ways. First, we considered abstinence as a reduction in size of the sexually active pool of females. Here, individuals who delay their age of sexual debut are not available for partnerships. In the male-driven partner choice algorithm used in HIV-CDM, this delay does not change the total number of partnerships formed, but means that partners can only be formed with females who have become sexually active (Z, X, C, and N are assumed to maintain the baseline age of 17 for sexual debut). The second type of abstinence is defined as a refusal of partnership proposals. In this approach, females who delay sexual debut are considered by males for partnerships, but refuse if asked. If a female refuses, the male may fail to form the partnership, or may attempt to form a partnership with another female (from any female in groups Z, X, C, N or A) with a varying numbers of attempts (w). In this approach, the total number of partnerships formed declines, more strongly as the male threshold w for “giving up” decreases. Also, we also evaluated the impact of 100% condom use for females; adherent females use condoms in 100% of acts. We calculated the cumulative incidence from 2014–2029, under the simple assumption that condom use has no additional behavioral impact; the goal was not to model realistic impacts of condom use but to compare the results for a prevention intervention with no displacement.
In summary, the interventions assessed by the HIV-CDM model were as follows: 100% condom use by adherent females 16–20 years of age (no displacement); Male partner rejection by females until 20 years of age with w=1 (no displacement); Male partner rejection by females until 20 years of age with w=3 (partial displacement); Male partner rejection by females until 20 years of age with w=10 (partial displacement); and Male partner rejection by females until 20 years of age with w=500 (effectively complete displacement).
To examine the impact of adherence on displacement under a population-wide intervention (as opposed to a trial), we ran the HIV-CDM with 100% of eligible females enrolled in the intervention group while varying adherence among females in the range of 0–100%. With this population stratification we ran the HIV-CDM with and without various interventions. The cumulative incidence, , for the adherent, non-adherent, and entire intervention group was calculated using the annual incidence rates (IR) each year (t) up to and including 2029, the final year of the trial for each combination of intervention and proportion adherent.
Results
Short-term Model
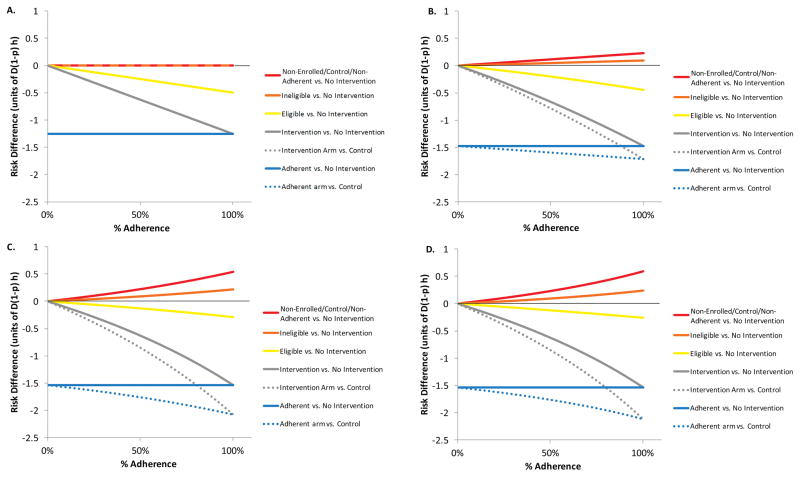
Figure 2 shows the risk difference for females as a function of the extent of displacement (Figure 2 panels A–D) and the proportion of intervention-group females who are adherent to the intervention by rejecting all requests for acts (horizontal axis). Figure S1 shows the same quantities as a function of the proportion of the eligible population enrolled in the trial.
Figure 2.
A–D: Risk difference between groups in the eligible trial population when 80% of the 16 year old female population is eligible and enrolled, 50% is in the intervention group, the relative desirability of ineligible females, q, is 40%, and adherence is varied from 0–100% for values for the maximum number of rejections before a male stops trying to partner, w: 2A. Risk difference without displacement (w=1); 2B. Risk difference with displacement (w=2); 2C. Risk difference with displacement (w=5); and 2D. Risk difference with displacement (w=500). The solid curves show the risk difference for each of several groups relative to the counterfactual scenario of no intervention while the dashed lines show the measured risk differences for the intervention group and the adherent group, relative to controls.
With w=1, there is no displacement (Fig 2A, S1.A), and the risk difference is negative (beneficial) for the adherent members of the intervention group, zero for all other groups, and intermediately negative (beneficial) for the whole intervention group comprising adherent and non-adherent females. As displacement increases, the risk difference becomes positive (harmful) for controls and for ineligible females, more so as w increases (Figure 2B–D and Figure S1B–D), as adherence increases (Figure 2) and as the proportion enrolled increases (Figure S1). Ineligible females face smaller risks because by assumption they are less likely to be sought by males who initially approach eligible females.
The risk reduction for the intervention appears inflated relative to the corresponding counterfactual risk comparison, because controls are at increased risk in the presence of the intervention. In ordinary intervention trials, risk in the control group is intended to represent the counterfactual risk of the intervention group had it not received the intervention. Here, however, the trial itself increases the risk to the control group, thereby inflating the difference between the intervention (or adherent) group and controls. Unlike a typical trial, the risk difference for the intervention group, as a whole, relative to no intervention, is a nonlinear function of adherence. The risk difference in the intervention group is an adherence-weighted average of the risk difference in the adherent and the risk difference in the non-adherent. In typical intervention trials, the risk difference in the non-adherent is zero, and the risk difference in the adherent is independent of the proportion adherent. Thus, the risk difference for the intervention group is ordinarily a linear function of the proportion adherent. Here, however, the risk difference in the non-adherent is positive and an increasing function of the proportion adherent, while the risk difference in the adherent is negative and constant as a function of the proportion adherent. Therefore, the risk difference in the intervention group -as would be measured in an intent-to-treat analysis- is nonlinearly related to adherence (Figures 2 and S1).
In the short-term model, displacement onto the controls, non-adherent, and non-enrolled populations increases with the proportion eligible, proportion enrolled, proportion in the intervention arm, proportion adherent, and the male threshold for giving up (w). It decreases with the desirability (q) of the ineligible females, who divert displaced males away from these groups.
As a trial proceeds, the intervention may change the incidence and thus prevalence of HIV infection in men, thereby changing the risk experienced by each group defined here as time passes. We now proceed to model these changing risks.
Agent-Based Dynamic Model of Displacement
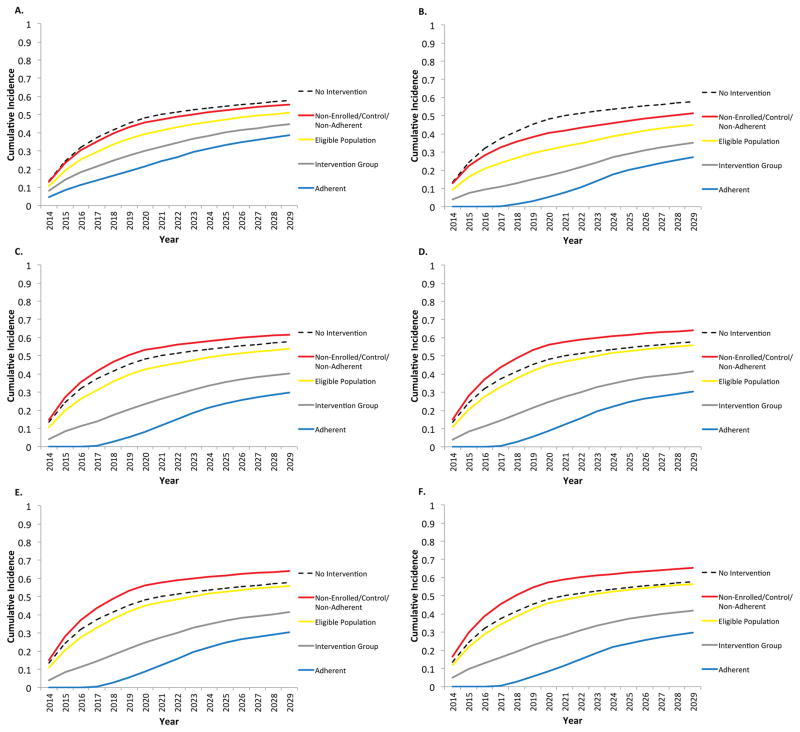
Figure 3 shows the effects of sexual behavior interventions on a hypothetical trial population in which 40% of 16 year-old females are in the intervention group, 40% are controls, and 20% are non-enrolled. Of the females in the intervention group, we assume initially that 70% are adherent and 30% are non-adherent. We consider several different interventions and their effects over time on cumulative incidence for the entire eligible population, as well as the intervention, adherent, and combined non-enrolled, control and non-adherent groups. A condom use intervention is shown in figure 3A –making the assumption that condom use does not affect males’ choice of partner. When 100% condom use is implemented to adherent females 16–20 years of age from 2014–2018, there is no change in the number of partnerships each male has in a month and in turn no displacement of partnerships to others in the population. The adherent females are at a decreased risk of HIV given that they are using condoms 100% of the time until the age of 20 (Figure 3A). Also, a benefit is seen for all other females in the population but to a lesser degree. Each subgroup of the eligible population has a lower cumulative incidence compared to the counterfactual of no intervention.
Figure 3.
A–F. Cumulative incidence using the agent based model where 80% of eligible females are enrolled, 50% in the intervention arm, 70% of the intervention arm are adherent and the intervention is 3A: 100% condom use by adherent females 16–20 years of age (no displacement); 3B: Male partner rejection by females until 20 years of age with w=1 (no displacement); 3C: Male partner rejection by females until 20 years of age with w=3 (partial displacement); 3D: Male partner rejection by females until 20 years of age with w=10 (partial displacement); 3E: Male partner rejection by females until 20 years of age with w=500 (complete displacement); and 3F: Delay of sexual activity by adherent females until 20 years of age (complete displacement).
With abstinence interventions (Figures 3B–E), the extent of displacement increases with the maximum number of attempts, w, males make to seek a partner. When w =1 (Figure 3B), there is no displacement and all individuals in the trial are at a decreased risk of HIV compared to the no-intervention run. As w increases, the effects of displacement become more marked, producing increased incidence in the non-adherent, ineligible and control populations compared to no intervention. Figure 3F shows a slightly different intervention, in which females delay sexual debut until the age of 20. In this case, by assumption, these females are not in the pool of eligible persons to receive an offer for a sexual act or partnership from a male. Under the assumptions of the model, the number of males seeking partners is independent of the number of available females, so all male “demand” is displaced from the females who have not entered the pool to others who have. Here again, the overall cumulative incidence for the eligible population is close to that of a population with no interventions. The adherent females are at less risk for HIV infection and the non-adherent, non-enrolled and control females are at a greater risk (Figure 3F). Importantly, however, the overall eligible population in all scenarios has no higher cumulative incidence with the intervention than without, though in the extreme displacement scenarios the difference is modest. The impact of the intervention with partial displacement is to reduce the number of acts, as the males may attempt to partner with adherent females and be rejected thus decreasing the chance of finding a female to have a sexual act with. These adherent females “absorb” some of the demand from males without having the acts, even though they displace the remainder of the demand.
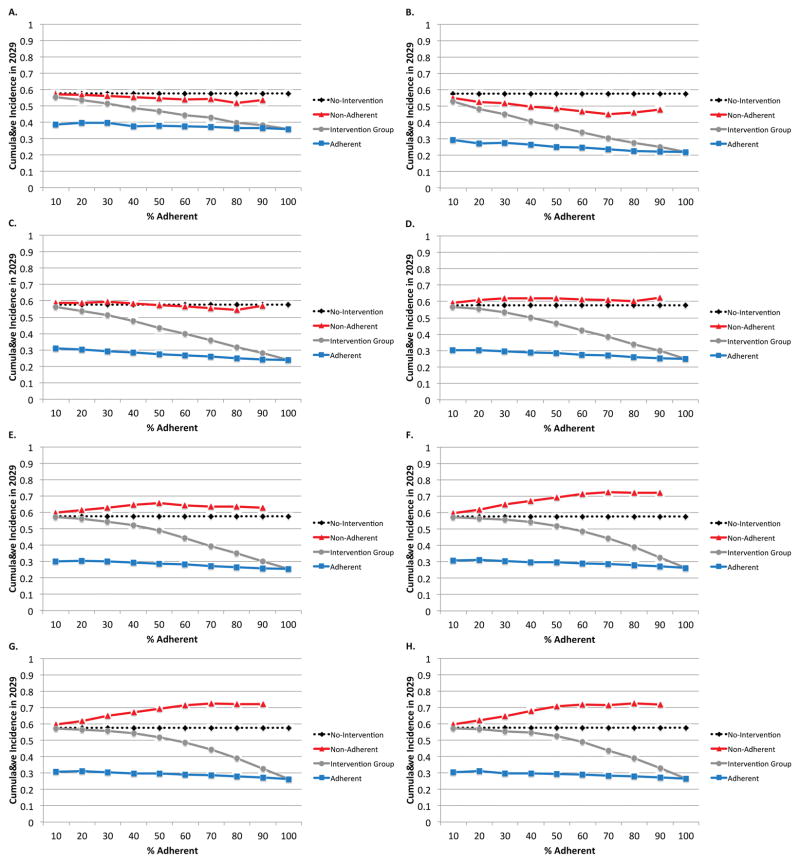
The proportion of adherent females in the population also affects the amount of displacement, as can be seen in Figure 4. The overall patterns of displacement are similar to those seen in Figure 3 with displacement increasing as w increases. Countervailing effects make the shape of the relationship with adherence non-monotonic. As adherence increases, the intervention becomes more effective, leading to fewer partnerships and lower male prevalence. However, as adherence increases so does the amount of displacement to the other females in the population, who become fewer in number and “absorb” a greater share of the displaced partnerships.
Figure 4.
A–H. All eligible 16 year old females are enrolled into the intervention arm with varied adherence from 0–100% for each of the following interventions: 4A: 100% condom use by adherent females 16–20 years of age (no displacement); 4B: Male partner rejection by females until 20 years of age with w=1 (no displacement); 4C: Male partner rejection by females until 20 years of age with w=2 (partial displacement); 4D: Male partner rejection by females until 20 years of age with w=3 (partial displacement); 4E: Male partner rejection by females until 20 years of age with w=4(partial displacement); 4F: Male partner rejection by females until 20 years of age with w=5(partial displacement); 4G: Male partner rejection by females until 20 years of age with w=500 (complete displacement); and 4H: Delay of sexual activity by adherent females until 20 years of age (complete displacement).
When there is 100% condom use among adherent young females (Figure 4A) or when w=1 (Figure 4B), there is no displacement and all cumulative incidences are less than without the intervention. When w=2, marginally increased incidence in the non-adherent (compared to no intervention in the non-adherent) is seen when 40% or fewer females are in the adherent intervention group. When adherence is greater, the benefits of reduced transmission (from the adherent females to the males) outweighs the displacement of their sexual partnerships onto the non-adherent (Figure 4C). When w=3 or greater, net increases in incidence compared to no-intervention are seen in the non-adherent for all levels of adherence, with incidence increasing with w (Figure 4D–G). A delay in the age of sexual debut has approximately the same impact as setting w to 500 (Figure 4H). Overall, cumulative incidence decreases with the intervention and with greater adherence, so a population-level benefit is seen despite increased incidence in the non-adherent.
Discussion
Interventions to decrease the sexual activity of one group may increase that of others in the population, though under all plausible scenarios we have considered, the overall impact on the population of reducing sexual activity by a proportion of females is beneficial. We have shown that if displacement occurs in trials it potentially increases the risk of infection to controls, non-adherent, and non-enrolled individuals. This can in turn affect the interpretation of the trial results by inflating or attenuating effect estimates depending on the proportion of the population adherent to the intervention. Inflation occurs when comparing intervention recipients and controls, because the difference between intervention recipients and controls (who are at increased risk due to the intervention) is larger than the difference between intervention recipients and the counterfactual of their risk had there been no intervention. However, if one made a comparison between intervention recipients and historical controls who were perfect proxies for the counterfactual risk of intervention recipients, the estimate would be attenuated because the overall impact on the intervention population is an adherence-weighted average of decreased risk in the adherent and increased risk in the non-adherent. As the interventions are expanded to the whole population the number of displaced acts diminishes and the benefits of the intervention are increased. In this setting, those who do not adhere to the intervention gain some indirect benefits (from reduced transmission due to the intervention) but also have an increased individual risk because of displaced acts or partnerships that they engage in. For the parameter values we have chosen for illustration, even modest displacement may be enough to outweigh the indirect benefits to those outside the adherent group, and these could be more perverse if the male acts are displaced to commercial sex workers or other higher-risk females. However, in our simulated interventions there was an overall decrease in HIV infection in the population. A deterministic transmission model showed that, unless there is a reduction in the number of sexual contacts, sexual behavior interventions aimed at reducing the cross-generational sex in an intervention group may have a benefit to those in the intervention but not a population-level benefit (Hallett et al., 2007). Models like this and the HIV-CDM can illustrate the potential impact of displacement, which is not easily measured in trials. This can in turn motivate the collection of data to assess the extent of actual displacement in future trials, as well as assess behaviors in the underlying source population from which the trial subjects were recruited.
This effort has begun. In Malawi, Baird and colleagues studied the effect of cash transfers on multiple outcomes, including HIV infection, using a novel “randomized saturation” trial design. In this design, geographic clusters were randomized to varying “saturations” or coverages of the intervention, and then within each village individual females were randomized to receive or not receive the intervention; the probability of receiving intervention was set equal to the “saturation” of their village (Baird et al., 2014a; Baird et al., 2010; Baird et al., 2012). The interventions reduced the prevalence of HIV infection among those receiving the interventions, and the study design made it possible, at least in principle, to assess the extent of displacement of HIV risk; however, results of such analyses have not been published. The study did report that it found no evidence of effects on marriage or pregnancy outcomes to nonrecipients, within clusters including a mix of those randomized to be recipients and nonrecipients of receive cash transfers (9). Future studies using a similar approach, combined with measurements of sexual behavior outcomes in males, could enhance our understanding of this phenomenon and should account for the effects described here. Baird et al. have elaborated a statistical framework in which to do so (Baird et al., 2014a). More recently, a trial in South Africa of conditional cash transfers found no effect of these transfers on school attendance (which was high in both intervention and control groups) or on sexual activity or HIV risk (Pettifor et al., 2016). Because the biases described here occur only when an intervention is effective in changing sexual behavior, there was no opportunity to assess the extent of potential bias in the South African trial.
The possible displacement of risk to trial participants, trial non-participants, and/or ineligible females is an issue that is worthy of consideration from an ethical standpoint, as is the broader issue of how any experimental behavioral intervention may inadvertently affect those within and outside the trial. Such consideration is an area for future work.
The simulations reported here are examples of simulating a complex intervention trial in the field of infectious disease epidemiology. Such simulations can add epidemiologic validity by improving sample-size estimates, comparing competing designs, and assessing potential biases in effect estimates (Boily and Anderson, 1996; Boily et al., 2012; Cooper et al., 2015; Halloran et al., 1996; White et al., 2010). Simulations may also be helpful in understanding the results of completed trials (Boily et al., 2000; Vynnycky et al., 2015). In addition, the process of constructing the simulation itself may lead the researcher to recognize and think more carefully about the timing and nature of the chain of events that occur in the setting of a trial, thereby recognizing complexities that may have been previously overlooked. As previously reported by Bollinger et al. (Bollinger et al., 2004) and Michielsen et al. (Michielsen et al., 2010), there is a need for carefully designed studies that adequately analyze the complex interaction between behavioral interventions, changes in behavior and biological outcomes such as HIV incidence and prevalence. Here, the process of attempting to simulate an intervention trial to delay female sexual activity with an individual-based model required us to specify rules for the behavior of males who encountered (or would have encountered) females in the trial. The process of specifying those rules alerted us to the range of possible behaviors and the rarity of empirical evidence on this topic. In general, the construction and the analysis of simulation (or other) models may be a valuable exercise when considering complex intervention trials.
When considering efforts to create behavioral change in infectious diseases, it should be standard practice to consider, often with a formal model, the downstream consequences of the expected behavioral change on the risk of various groups in the population, particularly the control group within a randomized trial and nonrecipients of the intervention once it is scaled up.
Supplementary Material
Highlights.
Interventions that decrease sexual activity of one group may increase that of others
Adherence to sexual behavior interventions may have unexpected effects
Downstream consequences of behavioral change need to be considered in trial design
Acknowledgments
Funding:
This work was supported by the following grants: National Institutes of Health (RO1-MH-087328, R01-GM-116525, T32-AI-007433, RO1-AI-058736 and U54-GM-088558). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Abbreviations
- AIDS
acquired immune deficiency syndrome
- ART
antiretroviral therapy
- CEPAC-I
Cost Effectiveness of Preventing AIDS Complications
- CSW
Commercial Sex Worker
- HIV
human immunodeficiency virus
- HIV-CDM
HIV Calibrated Dynamic Model
Footnotes
The preliminary results of this manuscript were presented as a poster at the Epidemics 5 Conference in Florida, USA 2015 titled “Displacement of sexual partnerships in trials and implementation of sexual behavior change interventions: A model-based assessment of consequences for evaluation and control”; Abstract #P1.3.56.
There are not conflicts of interest to declare.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Baird S, Bohren A, McIntosh C, Ozler B. Penn Insititue For Economic Research PIER Working Paper 14–006. 2014a. Designing experiments to measure spillover effects. [Google Scholar]
- Baird S, Chirwa E, McIntosh C, Ozler B. The short-term impacts of a schooling conditional cash transfer program on the sexual behavior of young women. Health economics. 2010;19(Suppl):55–68. doi: 10.1002/hec.1569. [DOI] [PubMed] [Google Scholar]
- Baird S, Gong E, McIntosh C, Ozler B. The heterogeneous effects of HIV testing. Journal of health economics. 2014b;37:98–112. doi: 10.1016/j.jhealeco.2014.06.003. [DOI] [PubMed] [Google Scholar]
- Baird SJ, Garfein RS, McIntosh CT, Ozler B. Effect of a cash transfer programme for schooling on prevalence of HIV and herpes simplex type 2 in Malawi: a cluster randomised trial. Lancet. 2012;379:1320–1329. doi: 10.1016/S0140-6736(11)61709-1. [DOI] [PubMed] [Google Scholar]
- Boily MC, Anderson RM. Human immunodeficiency virus transmission and the role of other sexually transmitted diseases. Measures of association and study design. Sex Transm Dis. 1996;23:312–332. doi: 10.1097/00007435-199607000-00012. [DOI] [PubMed] [Google Scholar]
- Boily MC, Lowndes CM, Alary M. Complementary hypothesis concerning the community sexually transmitted disease mass treatment puzzle in Rakai, Uganda. AIDS. 2000;14:2583–2592. doi: 10.1097/00002030-200011100-00022. [DOI] [PubMed] [Google Scholar]
- Boily MC, Masse B, Alsallaq R, Padian NS, Eaton JW, Vesga JF, Hallett TB. HIV treatment as prevention: considerations in the design, conduct, and analysis of cluster randomized controlled trials of combination HIV prevention. PLoS Med. 2012;9:e1001250. doi: 10.1371/journal.pmed.1001250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollinger L, Cooper-Arnold K, Stover J. Where are the gaps? The effects of HIV-prevention interventions on behavioral change. Stud Fam Plan. 2004;35:27–38. doi: 10.1111/j.1728-4465.2004.00003.x. [DOI] [PubMed] [Google Scholar]
- Cooper BS, Boni MF, Pan-ngum W, Day NP, Horby PW, Olliaro P, Lang T, White NJ, White LJ, Whitehead J. Evaluating clinical trial designs for investigational treatments of Ebola virus disease. PLoS Med. 2015;12:e1001815. doi: 10.1371/journal.pmed.1001815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fine PE. Herd immunity: history, theory, practice. Epidemiologic reviews. 1993;15:265–302. doi: 10.1093/oxfordjournals.epirev.a036121. [DOI] [PubMed] [Google Scholar]
- Freedberg KA, Losina E, Weinstein MC, Paltiel AD, Cohen CJ, Seage GR, Craven DE, Zhang H, Kimmel AD, Goldie SJ. The Cost Effectiveness of Combination Antiretroviral Therapy for HIV Disease. N Engl J Med. 2001;344:824–831. doi: 10.1056/NEJM200103153441108. [DOI] [PubMed] [Google Scholar]
- Greenwood B. Anti-malarial drugs and the prevention of malaria in the population of malaria endemic areas. Malaria journal. 2010;9(Suppl 3):S2. doi: 10.1186/1475-2875-9-S3-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallett TB, Gregson S, Lewis JJ, Lopman BA, Garnett GP. Behaviour change in generalised HIV epidemics: impact of reducing cross-generational sex and delaying age at sexual debut. Sex Transm Infect. 2007;83(Suppl 1):i50–54. doi: 10.1136/sti.2006.023606. [DOI] [PubMed] [Google Scholar]
- Halloran ME, Longini IM, Jr, Struchiner CJ. Estimability and interpretation of vaccine efficacy using frailty mixing models. Am J Epidemiol. 1996;144:83–97. doi: 10.1093/oxfordjournals.aje.a008858. [DOI] [PubMed] [Google Scholar]
- Killeen GF, Smith TA, Ferguson HM, Mshinda H, Abdulla S, Lengeler C, Kachur SP. Preventing childhood malaria in Africa by protecting adults from mosquitoes with insecticide-treated nets. PLoS Med. 2007;4:e229. doi: 10.1371/journal.pmed.0040229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knox EG. Theoretical aspects of rubella vaccination strategies. Reviews of infectious diseases. 1985;7(Suppl 1):S194–197. doi: 10.1093/clinids/7.supplement_1.s194. [DOI] [PubMed] [Google Scholar]
- Kremer M, Morcom C. The effect of changing sexual activity on HIV prevalence. Mathematical biosciences. 1998;151:99–122. doi: 10.1016/s0025-5564(98)10010-x. [DOI] [PubMed] [Google Scholar]
- Kunkel A, Colijn C, Lipsitch M, Cohen T. How could preventive therapy affect the prevalence of drug resistance? Causes and consequences. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2015;370:20140306. doi: 10.1098/rstb.2014.0306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipsitch M, Samore MH. Antimicrobial use and antimicrobial resistance: a population perspective. Emerging infectious diseases. 2002;8:347–354. doi: 10.3201/eid0804.010312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick AW, Abuelezam NN, Rhode ER, Hou T, Walensky RP, Pei PP, Becker JE, DiLorenzo MA, Losina E, Freedberg KA, Lipsitch M, Seage GR., 3rd Development, calibration and performance of an HIV transmission model incorporating natural history and behavioral patterns: application in South Africa. PLoS One. 2014;9:e98272. doi: 10.1371/journal.pone.0098272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michielsen K, Chersich MF, Luchters S, De Koker P, Van Rossem R, Temmerman M. Effectiveness of HIV prevention for youth in sub-Saharan Africa: systematic review and meta-analysis of randomized and nonrandomized trials. AIDS. 2010;24:1193–1202. doi: 10.1097/QAD.0b013e3283384791. [DOI] [PubMed] [Google Scholar]
- Miller E, Dushoff J, Huppert A. The risk of incomplete personal protection coverage in vector-borne disease. Journal of the Royal Society, Interface/the Royal Society. 2016:13. doi: 10.1098/rsif.2015.0666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panagiotopoulos T, Antoniadou I, Valassi-Adam E. Increase in congenital rubella occurrence after immunisation in Greece: retrospective survey and systematic review. Bmj. 1999;319:1462–1467. doi: 10.1136/bmj.319.7223.1462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettifor A, MacPhail C, Hughes JP, Selin A, Wang J, Gomez-Olive FX, Eshleman SH, Wagner RG, Mabuza W, Khoza N, Suchindran C, Mokoena I, Twine R, Andrew P, Townley E, Laeyendecker O, Agyei Y, Tollman S, Kahn K. The effect of a conditional cash transfer on HIV incidence in young women in rural South Africa (HPTN 068): a phase 3, randomised controlled trial. Lancet Glob Health. 2016;4:e978–e988. doi: 10.1016/S2214-109X(16)30253-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vynnycky E, Sumner T, Fielding KL, Lewis JJ, Cox AP, Hayes RJ, Corbett EL, Churchyard GJ, Grant AD, White RG. Tuberculosis control in South African gold mines: mathematical modeling of a trial of community-wide isoniazid preventive therapy. Am J Epidemiol. 2015;181:619–632. doi: 10.1093/aje/kwu320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walensky RP, Cohen MS, Freedberg KA. Cost-effectiveness of HIV treatment as prevention in serodiscordant couples. N Engl J Med. 2014;370:581–582. doi: 10.1056/NEJMc1314998. [DOI] [PubMed] [Google Scholar]
- White MT, Griffin JT, Drakeley CJ, Ghani AC. Heterogeneity in malaria exposure and vaccine response: implications for the interpretation of vaccine efficacy trials. Malaria journal. 2010;9:82. doi: 10.1186/1475-2875-9-82. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.