Enhanced Dynamics of Confined Cytoskeletal Filaments Driven by Asymmetric Motors

Abstract

Cytoskeletal filaments and molecular motors facilitate the micron-scale force generation necessary for the distribution of organelles and the restructuring of the cytoskeleton within eukaryotic cells. Although the mesoscopic structure and the dynamics of such filaments have been studied in vitro and in vivo, their connection with filament polarity-dependent motor-mediated force generation is not well understood. Using 2D Brownian dynamics simulations, we study a dense, confined mixture of rigid microtubules (MTs) and active springs that have arms that cross-link neighboring MT pairs and move unidirectionally on the attached MT. We simulate depletion interactions between MTs using an attractive potential. We show that dimeric motors, with a motile arm on only one of the two MTs, produce large polarity-sorted MT clusters, whereas tetrameric motors, with motile arms on both microtubules, produce bundles. Furthermore, dimeric motors induce, on average, higher velocities between antialigned MTs than tetrameric motors. Our results, where MTs move faster near the confining wall, are consistent with experimental observations in Drosophila oocytes where enhanced microtubule activity is found close to the confining plasma membrane.

Introduction

Cytoskeletons of eukaryotic cells contain rigid, polar, filamentous proteins called “microtubules” (MTs). Molecular motors, such as kinesins and dyneins, have arms that cross-link two neighboring MTs, consume energy in the form of ATP, and move toward only one (either plus or minus) end of the attached MT. It has been shown, both in vitro and in vivo, that the motor-arm motion causes the motors to stretch and impart active stresses resulting in MT sliding (1, 2, 3). These biological machines connect chemical reactions to mechanical processes in an environment that is out of equilibrium (4). The consequence of such a mechanism is particularly apparent in the case of cytoplasmic streaming. In this process, MT advection causes the cytoplasm to be circulated (5, 6, 7, 8). In the Drosophila oocyte at midoogenesis, cytosolic molecules, such as the body plan determinant oskar mRNA, are localized inhomogeneously within the cell (9). Moreover, the bulk motion of the cytoplasm, driven by kinesin-1 motors, has been shown to drive important processes, such as cell shape change, organelle transport, and nervous system development in Drosophila (10, 11).

Remarkable examples of these microscopic engines have also been observed in cases of reconstituted systems of MTs and kinesin motors in vitro, e.g., the self-organization of MT–motor protein mixtures into dynamic asters and vortices (12), and the spontaneous motion in an active gel of stabilized MT bundles under the activity of multimotor clusters of kinesins (13, 14). When MTs and motors were constrained to the surface of a giant lipid vesicles, spatiotemporal patterns that gave interacting defect configurations and filopodia-like protrusions were observed (15).

Because all of these systems are active and therefore not in thermodynamic equilibrium, they are inherently elusive to classical statistical mechanics (16). This has necessitated new theoretical and numerical approaches in the study of flows and stresses in bulk cytoskeletal networks (17, 18, 19, 20, 21, 22, 23, 24, 25, 26). One of the biggest challenges faced in this endeavor is the range of length scales in which dynamics takes place. Capturing the dynamics of individual nanoscopic kinesin motors and microscopic MTs within the same simulation is difficult. Therefore, coarse-grained modeling becomes increasingly important to elucidate generic features and emergent behavior (27), such as the collective effect of individual kinesin motor molecules on MT bundles: each motor entity represents kinesins localized in a region of the MT contour, inducing concerted inter-MT sliding.

We consider two different types of motors, both of which have been shown in experiments to cross-link and cause relative sliding between MTs. Dimeric motors, e.g., kinesin-1 and kinesin-14 (2, 10, 28, 29), are composed of a motor domain, motile on one MT, and a secondary, nonmotor, MT-binding site that is anchored and not motile on the other MT. Tetrameric motors (e.g., kinesin-5 (30, 31, 32)) have two motile motor domains at opposite ends, on both cross-linked MTs. When multiple dimeric motors cross-link a MT pair, tangential forces on the MTs arise based on whether the bound motors are correlated (with all anchored arms on one MT and all motile arms on the other MT) or uncorrelated (with anchored arms and motile arms bound on different MTs). Although many simulations have studied the role of tetrameric motors on MTs (19, 21, 23, 26), important aspects in MT-motor-protein mixtures such as different motor-arm speeds (33), and dimeric motors (34, 35), have rarely been considered so far.

Even though cytoskeletal activity inside living cells takes place under the strong effect of confinement of the plasma membrane, only recently have studies addressed its importance in affecting dynamics of active systems (36, 37, 38) and intracellular organization. It has been shown that confinement can decrease critical filament density for the isotropic-nematic phase transition (39) and induce formation of clustering and bundlelike structures (40). Also, it is known that confining the cytoskeleton within cells influences mitotic organization and spindle positioning (41, 42), the deformation and orientation of the nucleus (43), and cellular protrusions produced by actively treadmilling actin filaments called the “lamellipodium” (44). Inhomogeneities in MT distribution within oocytes have also been reported to be key for bulk motion within the cytoplasm, i.e., a layer of stable, immobile MTs at the oocyte cortex, upon which cytoplasmic MTs push against with the aid of kinesins, was observed (5), further highlighting the importance of confinement.

In coarse-graining the molecular details of the cytoskeleton, most simulation studies have largely ignored attractive interactions between MTs, which can occur from the cytoplasm being a crowded environment (45), where macromolecules occupy 20–30% of the total volume (46). MT bundling frees up additional volume for smaller particles, increasing the overall system entropy, resulting in an effective attraction (47). On top of having an effect on the overall structure of a passive MT system without motors, these cohesive interactions bring MTs together, making them amenable for the cross-linking of molecular motors.

This article is organized as follows. In Methods, the model of a 2D active gel, confined within a circular external boundary, is explained. In Results, the results and analysis of the simulations are described. In particular, in Global Structure, macroscopic structures formed by MTs within the entire confinement are discussed. In Local Polar Order, a local polar order parameter is used to distinguish populations of polar-aligned and antialigned MTs. In Motor-Mediated Motion, MT pair orientation is linked to MT velocity, and the difference between cooperative and antagonistic effects of dimeric motors is distinguished. In Dynamics Near Confinement, the large-scale dynamics of MTs and how they move within the confinement is detailed. In Motor Evolution, lifecycles of the different types of motors and the evolution of their lengths after cross-linking are shown. In Discussion, the connection between our work to existing experimental and theoretical studies is discussed.

Methods

To study the collective effects of motors on a network of confined MTs, we reduce molecular level details to a 2D coarse-grained model. MTs are described by their center-of-mass, r_i, and orientation, p_i (Fig. 1). They are modeled as semipenetrable, rigid rods of length L, discretized into nb beads of diameter r_min. We define the bead diameter to be the position of the minimum of the MT-MT interaction potential. In each simulation, we consider a constant number of MTs, N_f, and attached motors, N_m. Motors are modeled as harmonic springs with equilibrium length zero, with two arms, each attached to a point on an MT.

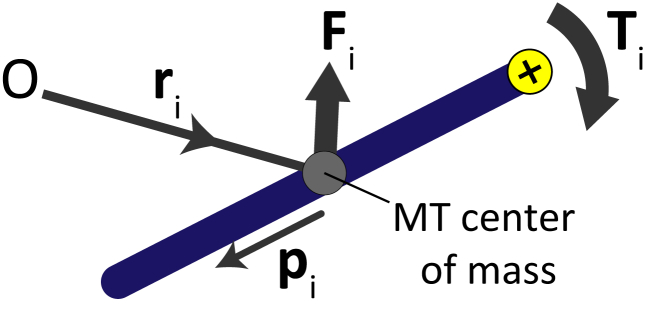
Figure 1.

Force, F_i, and torque, T_i, acting on MT i, with center-of-mass, r_i, with respect to an origin, O, and orientation, p_i, which is in the opposite direction of motor-arm motion. To see this figure in color, go online.

Filaments

Beads of neighboring MTs interact with the separation-shifted Lennard-Jones-like potential (48),

$$U\left(r\right)=\{\begin{array}{ll}\frac{A_R}{{\left(r^2+{\alpha }^2\right)}^8}-\frac{A_A}{{\left(r^2+{\alpha }^2\right)}^4}\hfill & r\le 3r_{\text{min}}\hfill \\ 0\hfill & r>3r_{\text{min}}\hfill \end{array},$$ (1)

where r is the distance between two beads belonging to two neighboring MTs; and A_R, A_A, and α determine the energy of the repulsive peak (E_R), the attractive well (E_A), and the position of the energy minimum (r_min). This relationship is given in the Supporting Material. In units of thermal energy (k_BT), E_R = 20 and E_A is varied between 0.2 and 1.0. The aspect ratio of MTs is given by L/r_min = 5.

The exponents of the potential are chosen such that the superposition of multiple, overlapping beads gives a smooth, attractive MT-MT interaction, with a repulsive core. At the same time, when the MTs encounter large forces and torques, the capped potential will allow for MTs to slide over each other, resembling a crossing in the third dimension (49, 50). The energies associated with the crossing and sliding of MT pairs is discussed in detail in the Supporting Material. To define MT area fraction, we use the length r_eff, which is defined by the first peak of the pair correlation function (Fig. S21).

The beads that make up the MTs interact with an attractive, hard, circular wall of radius R_W/L = 8, via a Lennard-Jones potential given in Eq. S8 in the Supporting Material. A comparison of MT-wall interactions with other interactions involved in the system is given in the Supporting Material.

Motors

The density of motors on cross-linked MTs depends on MT pairs’ overlap lengths, motor speed, and motor concentration in the solution (51). Each motor has two arms that cross-link a MT pair. Dimeric motors have one motile arm and an immobile anchored arm (29). Tetrameric motors have two motile arms that both move toward the positive end of their respective MT, i.e., in the direction −p_i on the MT (Fig. 1).

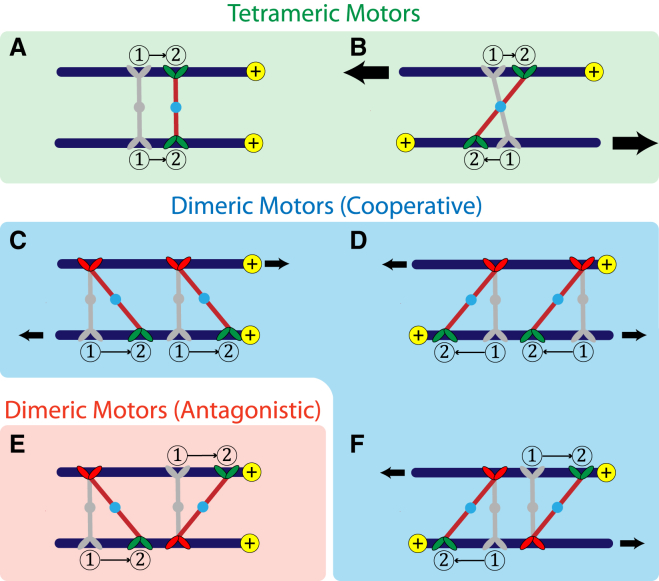
Because tetrameric motors are symmetric upon motor-arm exchange, only the relative alignment of the cross-linked MTs determines the dynamics (Fig. 2, A and B). When polar-aligned MTs are cross-linked by tetrameric motors (Fig. 2 A), the relative velocities of the MTs are small and the force generated by the molecular motors vanishes. Antialigned MTs cross-linked by tetrameric motors (Fig. 2 B), on the other hand, generate the largest tangential velocity between cross-linked MTs because both arms move at the same time.

Figure 2.

Schematic showing the effects of tetrameric and dimeric motors on polar-aligned and antialigned MTs. Motor arms are shown to move from position (1) to position (2), in the direction of MT polarization, represented by the yellow marking at the MT tip. The gray representations show the initial attachment positions of motors. Active motor-arms that move on the MT direction of polarization are colored green, and immobile, anchored motor-arms are colored red. Tetrameric motors have two motile arms on either cross-linking MT. Dimeric motors have an anchored arm and a motile arm. (A) Tetrameric motors cross-linking aligned MTs induce small velocities. (B) Tetrameric motors cross-linking antialigned MTs induce larger velocities. (C) Correlated dimeric motors cross-linking aligned MTs have the same effect as (D) dimeric motors cross-linking antialigned MTs. (E) Uncorrelated dimeric motors cross-linking aligned MTs act antagonistically, (F) whereas uncorrelated dimeric motors cross-linking antialigned MTs act cooperatively. To see this figure in color, go online.

Dimeric motors are not symmetric with respect to motor-arm exchange. Thus, for two dimeric motors cross-linking two MTs, four states corresponding to two relative combinations of motors, and two combinations of MT polarity (Fig. 2, C–F), can be constructed. One possibility is that motors bind to MTs in a spatially correlated manner, such that all motors have their motile arms on one MT and the anchored arms on the other MT (Fig. 2, C and D). In this case, both polar-aligned and antialigned MT orientations cause relative sliding between them. The other possibility is that motors bind in an uncorrelated manner, such that the motile and anchored arms are bound randomly on either MT. Uncorrelated motors cross-linking a polar-aligned MT pair will act antagonistically because the force imparted by a dimeric motor is counteracted by the force imparted by a motor that binds in the conjugate orientation (Fig. 2 E). This leads to relatively small forces between MT pairs. Uncorrelated motors between antialigned MTs, however, act cooperatively, and cause relative sliding between MTs (Fig. 2 F).

In most cases, MT pairs remain in the polar-aligned (antialigned) orientation for the duration that the motor is bound. This allows us to study the properties of tetrameric and dimeric motors cross-linking polar-aligned and antialigned MTs separately, giving four motor categories: dimeric/polar-aligned, dimeric/antialigned, tetrameric/polar-aligned, and tetrameric/antialigned.

At each time step, motors attach at random positions, cross-linking beads of neighboring MTs at distances smaller than the threshold length d_t. A stretched motor of length d with spring stiffness k_m acts as a harmonic bond with energy, V_m = k_md²/2. The motor-arm of each motor moves on its respective MT with a constant velocity v_m until the stall length is reached (d ≥ d_s). If the motor extension is larger than d_t, both motor-arms detach simultaneously. A detailed description of motor attachment, detachment, and motion rules is given in Supporting Material.

Parameters

We introduce dimensionless parameters using MT diameter r_min, thermal energy k_BT, and typical activity timescale τ, which indicates the onset of MT dynamics because of motors, as the basic length, energy, and timescales. Our simulations depend on eight dimensionless parameters: MT area fraction ϕ = N_fr_effL/πR_W², MT aspect ratio L/r_min, confinement radius R_W/L, motor concentration N_m/N_f, maximum motor speed ν_mτ/r_min, maximum motor extension d_t/r_min, motor stall force f_sr_min/k_BT, and motor spring constant k_md_t/fs.

We have studied structure and dynamics of MTs as a function of area fraction, confinement radius, motor spring constant, and motor velocity. In the main text, we have only varied the level of MT attraction, E_A and N_m/N_f, and kept the other parameters constant. We use ϕ = 0.74 and R_W/L = 8 to demonstrate typical structures observed, while simultaneously keeping numerical costs low. The motor spring constant and motor speed used in the main text are motivated by biological values (Table S1). A complete list of simulation parameters and dimensionless groups used in our simulations is given in the Supporting Material. The description of our results for the dynamics of the MT-motor system for other parameter combinations is also deferred to the Supporting Material.

Dynamics

MTs are subject to force, F_i; torque, T_i (Fig. 1); and anisotropic friction, Γ_i. Hydrodynamic interaction of each MT with the background fluid is modeled using resistive-force theory; long-range hydrodynamic interactions between MTs are ignored (52). We use overdamped Brownian dynamics, i.e., the momenta of the MTs lose their memory and relax to thermal equilibrium between consecutive time intervals, δt (53). MTs obey the dynamical equations for translation and rotation,

$${\mathit{r}}_i\left(t+\delta t\right)={\mathit{r}}_i\left(t\right)+{\mathbf{\Xi }}_i^{-1}\left(t\right)\cdot {\mathit{F}}_i\left(t\right)\delta t+\delta {\mathit{r}}_i\left(t\right)$$ (2)

and

$${\mathit{p}}_i\left(t+\delta t\right)={\mathit{p}}_i\left(t\right)+{\gamma }_r^{-1}\left[{\mathit{T}}_i\left(t\right)\times {\mathit{p}}_i\right]\delta t+\delta {\mathit{p}}_i\left(t\right),$$ (3)

respectively. The inverse friction tensor, ${\mathbf{\Xi }}_i^{-1}\left(t\right)$, is orientation dependent and is given by

$${\mathbf{\Xi }}_i^{-1}\left(t\right)={\gamma }_{\parallel }^{-1}{\mathit{p}}_i\left(t\right){\mathit{p}}_i\left(t\right)+{\gamma }_{\perp }^{-1}\left[\mathit{I}-{\mathit{p}}_i\left(t\right){\mathit{p}}_i\left(t\right)\right],$$ (4)

where γ_||, γ_⊥, and γ_r are the parallel, perpendicular, and rotational friction coefficients of the MT, respectively. F_i and T_i are the sums of deterministic forces and torques on MT i, respectively, i.e., the forces and torques due to motors, steric forces from neighboring MTs, and steric repulsion from the confining wall. From hydrodynamics, the following expressions for long hard spherocylinders can be derived: γ_|| = γ₀L, γ_⊥ = 2γ₀L, and γ_r = γ₀L³/6. The friction coefficients are a function of the solution viscosity and the MT’s aspect ratio (54). For the purpose of this simulation, γ₀ is constant for all three friction coefficients, because for the chosen aspect ratios the correction term for γ₀ is approximately equal for all three cases.

The Gaussian-distributed random displacements, δr_i(t), and rotations, δp_i(t), are related to the friction tensors by the fluctuation-dissipation theorem. The anisotropic random displacement and random reorientation vector have the variances

$$\langle \delta {\mathit{r}}_i\left(t\right)\delta {\mathit{r}}_i\left(t\right)\rangle =2k_{\text{B}}T{\mathbf{\Xi }}_i^{-1}\delta t,$$ (5)

and

$$\langle \delta {\mathit{p}}_i\left(t\right)\delta {\mathit{p}}_i\left(t\right)\rangle =2k_{\text{B}}T{\gamma }_r^{-1}\left[\mathit{I}-{\mathit{p}}_i\left(t\right){\mathit{p}}_i\left(t\right)\right]\delta t.$$ (6)

The overall hybrid Brownian dynamics procedure is detailed in the Supporting Material.

Results

Global structure

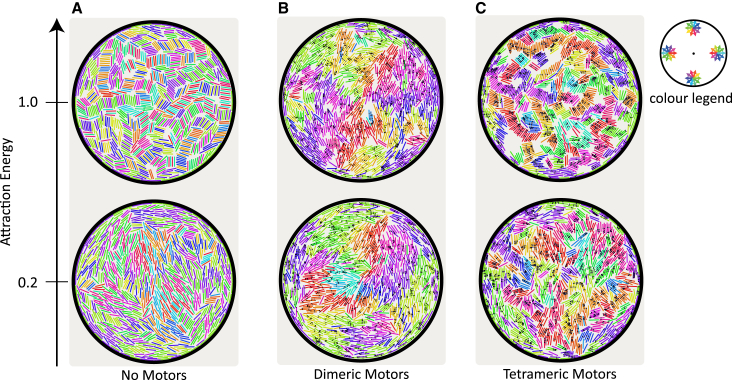
Fig. 3 shows the effect of MT attraction and motor type on the structures formed by confined MTs. The snapshots correspond to the lowest and highest E_A values (0.2 and 1.0 k_BT) probed in our simulations. In Fig. 3 A, stationary configurations reached by simulations without motors are shown. In the case without motors, structures form only because of steric interaction between MTs and geometric frustration induced by the boundary. For weak attractions (E_A = 0.2 k_BT), we observe nematic ordering of MTs at the center of the confinement giving rise to defects at the edge of the confinement (Movie S1). Stronger attraction (E_A = 1.0 k_BT) induces the formation of strong local alignment (but not polar order) that forms a more regular tiling pattern of MT stacks. We call these structures “bundles”.

Figure 3.

Stationary configuration of MTs with (A) no motors, (B) dimeric motors, and (C) tetrameric motors within circular confinement for two attraction energies, E_A = 0.2 k_BT and 1.0 k_BT. Number of motors is equal to the number of MTs for the four cases with motors, i.e., N_m/N_f = 1. Colors of MT represent their orientation with respect to the radial direction from the center. Small black dots represent the position of each motor-arm on MTs. For E_A = 0.2 k_BT; (A), (B), and (C) correspond to Movies S1, S2, and S4, respectively. To see this figure in color, go online.

Dimeric motors (Fig. 3 B) lead to the formation of large polarity-sorted clusters, in which the average polarity changes smoothly (Movies S2 and S3), and bundles are not observed even for the largest MT attraction values. For the higher attraction energy, at stationary state, we observe relative sliding between both polar-aligned and antialigned MTs, meaning that the motor forces are stronger than attraction forces and bundles of MTs are broken up.

Tetrameric motors (Fig. 3 C) bring about a motor-induced polarity sorting mechanism as well (Movie S4). However, as explained in Fig. 2 and the Supporting Material, only motors that cross-link antialigned MT pairs induce large forces that slide MT pairs relative to each other. As a result, antialigned MTs are kinetically disadvantaged and are quickly removed from the system. In contrast to the case of dimeric motors, polar-aligned bundles are preserved because motors do not develop large sliding forces between polar-aligned MTs. Under high MT-MT attraction, multiple large bundles make up the entire system. Besides that, a larger-scale polar order is absent. The density of MT packing is increased due to the combined cohesive effect of the attractive potential and the presence of motors. For low MT-MT attraction, we observe that bundles are not as prevalent as in the case of higher attraction.

With increasing area fraction of MTs, due to higher pairwise MT sliding and steric interactions, polarity sorting becomes more prominent, and polar-aligned structured domains become more pronounced for both types of motors (Fig. S6). The number of these domains increases with R_W/L (Fig. S8). The steady-state global structures are generally preserved for values of k_md_t/f_s (Fig. S12) and ν_mτ/r_min (Fig. S14) close to biologically motivated values.

The timescale for the formation of self-organized structures due to dimeric and tetrameric motors, beginning from an equilibrated, passive configuration, can be estimated from the relaxation of the polar order parameter. The time taken for polarity sorting shortens with increasing motor concentration (Fig. S19). Also, sorting occurs faster in tetrameric motor systems than in dimeric motor systems for all motor concentrations, due to higher motor stresses generated by tetrameric motors for antialigned MT pair configurations.

Local polar order

The dynamics of individual MTs depends on the polar orientation of MTs in their local environment. To capture the notion of the polarity of the local environment around a given MT i, we define a local polar order parameter,

$${\psi }_i=\frac{{\sum }_{j\ne i}^N{\mathit{p}}_i·{\mathit{p}}_j{q}_{ij}}{{\sum }_{j\ne i}^N{q}_{ij}}.$$ (7)

Here, q_ij is the pairwise motor partition function that weights a MT pair consisting of MT i and MT j according to the stretching energy of a uniform distribution of motors cross-linking the two MTs (21). The local polar order parameter ψ_i ranges from −1 (MT i is surrounded by neighbors in the opposite orientation) to 1 (MT i is surrounded by neighbors of same orientation). The precise definition of q_ij and a discussion of the local polar order parameter is given in the Supporting Material.

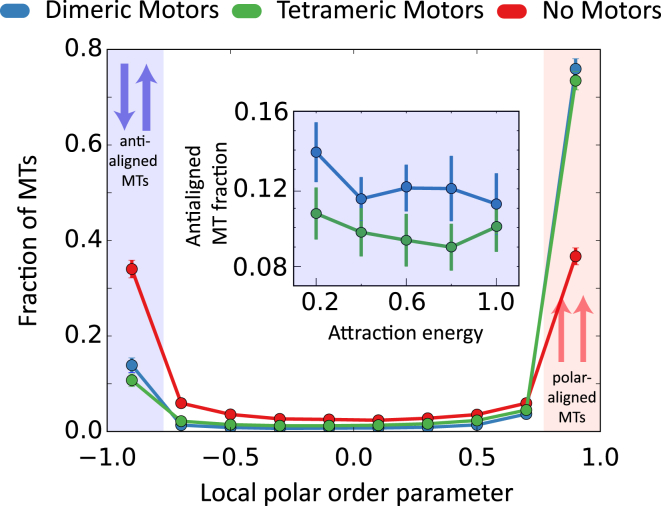
Fig. 4 shows the probability of finding an MT with the local order parameter, ψ. Steric interactions cause MTs to orient parallel to each other, such that most MTs have ψ_i values close to −1 or 1. Passive systems cannot distinguish between polar-aligned and antialigned orientations, implying that either orientations are equally probable. Both types of molecular motors induce an effective polarity sorting, breaking the symmetry between these two orientations. As a consequence, most MTs are in the polar-aligned orientation, and not in the antialigned orientation. For all values of the attraction energy E_A, there is a slightly higher fraction of antialigned MTs in the dimeric motor system than the tetrameric motor system (Fig. 4, inset).

Figure 4.

Fraction of MTs in the system as a function of their local polar order parameter for the E_A = 0.2 k_BT, N_m/N_f = 1 systems. Inset (blue) shows the fraction of antialigned MTs in systems as a function of different E_A values for N_m/N_f = 1. Attraction energy is normalized by k_BT. To see this figure in color, go online.

Motor-mediated motion

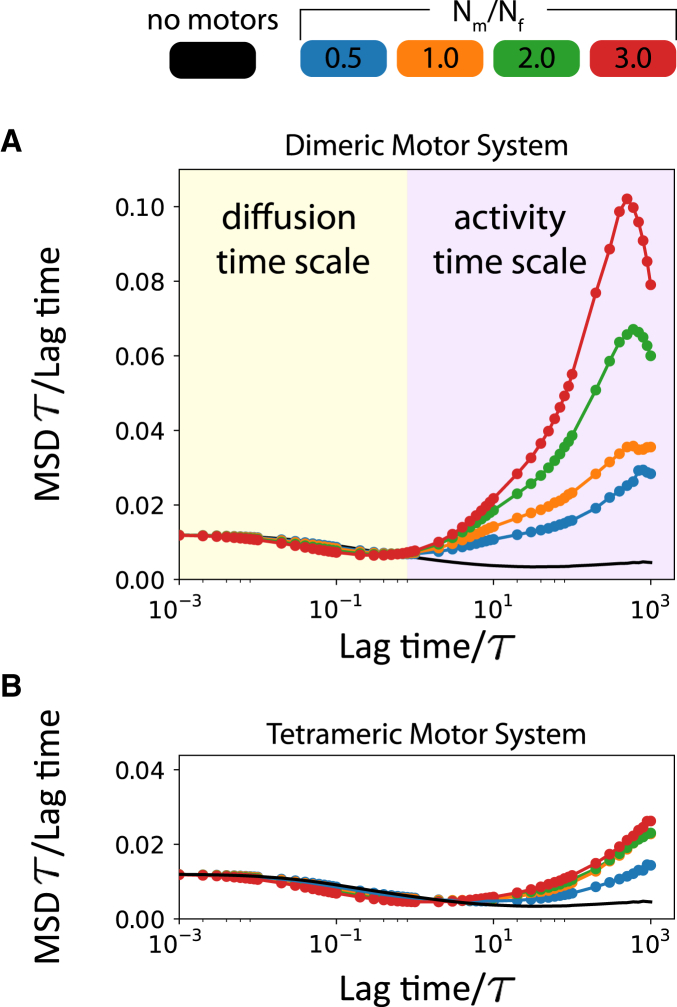
The local polar order parameter gives a structural description of the MT environment. To quantify the influence of local polar order on MT dynamics, we investigate it at two regimes separated by a crossover time τ (Fig. 5). At short timescales, the MT motion is driven by the thermal bath. At large timescales, collective interaction between multiple MTs takes place. At timescales comparable to τ, stresses generated by the motors are dissipated in the thermal bath. We define the mean squared displacement (MSD) of the MTs’ centers of masses using

$$\text{MSD}\left(t^{\prime }\right)\equiv {\langle {\left|{\mathit{r}}_i\left(t\right)-{\mathit{r}}_i\left(t+t^{\prime }\right)\right|}^2\rangle }_{t,i},$$ (8)

where t′ is the lag time. The characteristic lag time, t′ = τ, is chosen such that the MTs’ MSD is just out of the diffusive regime for the dimeric motor system, with N_m/N_f = 2.0 and E_A = 0.2 k_BT. At lag times smaller than τ, Fig. 5 shows that MTs are diffusing, because MSD/(lag time) is constant. At lag times larger than τ, systems with motors cause MTs to displace actively, and activity increases with the concentration of motors. In this time regime, steric interactions with neighboring MTs become dominant, because MSD of MTs without motors shows a decrease in diffusion. The peaks in Fig. 5 A, at large timescales, indicate that MTs are hindered by the confinements and the squared displacements are limited by confinement size. The MSD plateaus approximately at R_W² for lag times larger than 10³ τ, because a significant proportion of MTs have displaced the confinement radius, and are obstructed. This effect results in the curves in Fig. 5 decreasing (to 0) despite the motor-induced activity. A comparison of Fig. 5, A and B, which are both plotted on the same scale, shows that in these timescales, MTs driven by dimeric motors are significantly more dynamic than MTs driven by tetrameric motors for all motor concentrations. However, note that the velocities of MTs depend strongly on k_md_t/f_s (Fig. S13) and ν_mτ/r_min (Fig. S15), and less on MT area fraction and confinement size.

Figure 5.

Translational MSD/lag time of MTs’ center of masses for dimeric motors (A) and tetrameric motors (B) for different motor concentrations, N_m/N_f. The y axis scale for (A) and (B) are the same to show the differences in dynamics between the two systems. MSD is normalized using L² and lag time is normalized using the onset of the activity timescale, τ, i.e., the lag time where motor stresses are manifested in the MT dynamics. E_A = 0.2 k_BT for all simulations. To see this figure in color, go online.

Having defined a characteristic lag time, τ, we now define an effective MT velocity,

$$\mathit{v}\left(t\right)=\frac{\mathit{r}\left(t+\tau /2\right)-\mathit{r}\left(t-\tau /2\right)}{\tau }.$$ (9)

We compute an effective, average MT propulsion velocity due to motor stresses, ν_||, by projecting ν(t) on p(t).

Fig. 5 shows that on average the dimeric motors induce significantly larger displacements than tetrameric motors, despite having only half of the mobility of the tetrameric motors. This is contrary to the case of a single pair of MTs that was intuited in Fig. 2. Doubling the number of motors also induced larger displacements in the dimeric motor system.

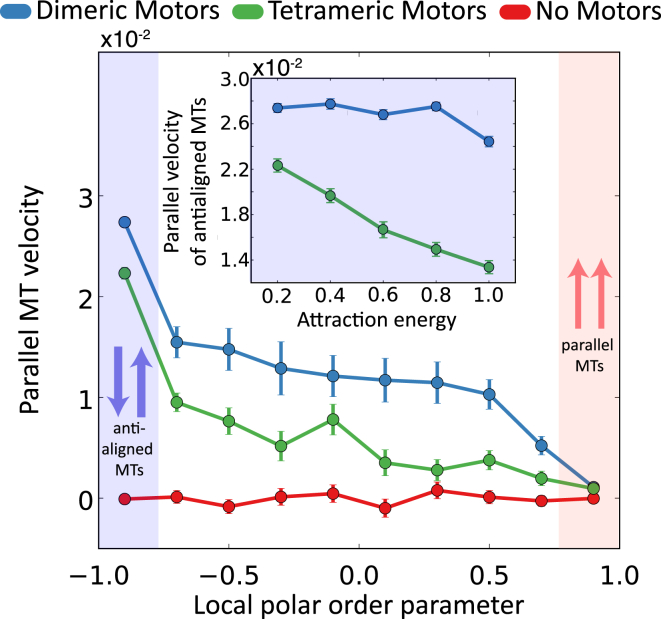
Furthermore, for both dimeric and tetrameric motors, Fig. 6 shows that the MT velocity is strongly correlated with the polarity of its environment, with highest propulsion velocities measured for MTs antialigned with respect to their environments. Velocities generated by the two types of motors depend also on the MTs’ attraction energy E_A (Fig. 6 inset). Namely, tetrameric motors are less able to overcome attractive forces that favor bundle formation (Fig. S3 B), relative to dimeric motors. At E_A = 0.2 k_BT, dimeric motors induce antialigned parallel MT velocity only 1.2 times that induced by tetrameric motors. At E_A = 0.2 k_BT, however, a relative decrease in MT velocities is found in the tetrameric motor system. At this higher level of attraction, mean parallel MT velocity induced by dimeric motors is 1.9 times the velocity induced by the tetrameric motors.

Figure 6.

Parallel velocities as a function of local polar order parameter for E_A = 0.2 k_BT systems and N_m/N_f = 1. Inset (blue) shows the velocity of antialigned MTs in systems with different E_A values for N_m/N_f = 1. Because motor-arms move in the opposite direction of p, by this convention, a propelled MT moves in the opposite direction, giving positive values for ν_||. Velocities are normalized by L/τ. Attraction energy is normalized by k_BT. To see this figure in color, go online.

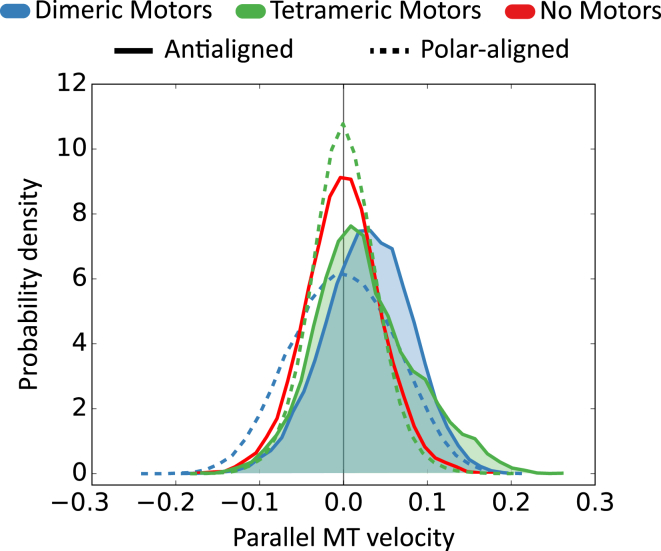
Fig. 7 shows histograms of parallel velocities of MTs for polar-aligned and antialigned MTs (local polar order parameter close to +1 and −1, respectively). The histogram without motors shows the effect of thermal forces at this timescale. Dimeric motors that cross-link polar-aligned MT pairs also cause a parallel MT velocity distribution that is centered around zero, but has a larger width than the passive MTs. Antialigned MTs and polar-aligned MTs cross-linked by dimeric motors have a velocity distribution that corresponds to scenarios posited in Fig. 2, D and F, and Fig. 2, C and E, respectively. Both antialigned MT mechanisms in Fig. 2, D and F, give an effective propulsion in the direction of MT orientation, which results in the skewed velocity distribution, and the peak of the velocity is nonzero (Table 1). Both polar-aligned MT mechanisms in Fig. 2, C and E, are impervious to the MT orientations, and result in motor-induced motion in either direction, depending on the location of the anchored arm(s). This results in a symmetric distribution of velocities shown in Fig. 7, which has a wider distribution of velocities than both polar-aligned tetrameric motor and passive MT systems.

Figure 7.

Histogram of parallel velocities for antialigned and polar-aligned MTs from the antialigned bins (blue) and the polar-aligned bins (red) from Fig. 6 (E_A = 0.2 k_BT and N_m/N_f = 1). Table 1 shows the first three moments of the distribution. The areas under the curve from antialigned MTs in dimeric and tetrameric motor systems are colored blue and green, respectively. The black vertical line represents a parallel MT velocity of zero. Velocities are normalized by L/τ. To see this figure in color, go online.

Table 1.

First Three Moments for the Parallel MT Velocity Distribution from Fig. 7

Motor Type	MT Orientation	Mean	SD	Skew
Dimeric	antialigned	0.029	0.052	−0.154
	polar-aligned	−0.001	0.061	−0.003
Tetrameric	antialigned	0.025	0.060	0.405
	polar-aligned	−0.001	0.040	0.092
No motors	—	0.000	0.045	0.012

Tetrameric motors that cross-link polar-aligned MT pairs lead to bundle formation that results in a narrower velocity distribution. In general, MTs in antialigned environments have a skewed velocity distribution compared to the polar-aligned MTs due to sliding motor stresses. The manner by which this sliding force manifests is different for dimeric and tetrameric motors.

As posited, the relative longitudinal displacement and the resultant maximal force for tetrameric motors is higher than for dimeric motors. However, on average, antialigned MT pairs are propelled more by dimeric motors than by tetrameric motors. Although tetrameric motors between antialigned MTs are able to generate higher velocities, these only make up the tail of the positively skewed distribution (Table 1). Dimeric motors, on the other hand, have the peak of their distribution at a higher velocity than that of tetrameric motors, and the distribution is skewed in the opposite direction.

Dynamics near confinement

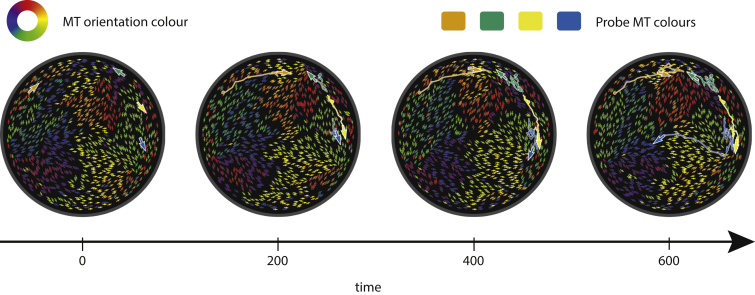
So far, we have compared differences in overall structure and dynamics of confined MT ensembles for dimeric and tetrameric motors. Having established that the dimeric motor system is the more dynamic of the two systems, to understand collective effects of motile MTs, we study how motion is coordinated within the confinement by dimeric motors. Fig. 8 shows trajectories of four especially motile probe MTs (orange, green, yellow, and blue) and the environment upon which they conduct this motion.

Figure 8.

Time-lapse images of MTs in a dimeric motor system, with probe MTs represented with larger arrows and their trajectories plotted in orange, green, yellow, and blue. Smaller arrows represent all the other MTs. All arrows indicate the direction of vector p, i.e., the opposite direction of motor motion, which is generally the direction of MT propulsion. The trail left by the larger arrows corresponds to the path that they have taken. In this case, E_A = 0.2 and N_m/N_f = 1. The time axis is normalized using τ. The images correspond to Movie S5. To see this figure in color, go online.

The MTs travel with higher velocities in an environment of antialigned MTs and show erratic motion in an environment of polar-aligned MTs. If they encounter defects at the boundary (55), such as the blue MT at 500τ in Fig. 8, their trajectory may change direction abruptly.

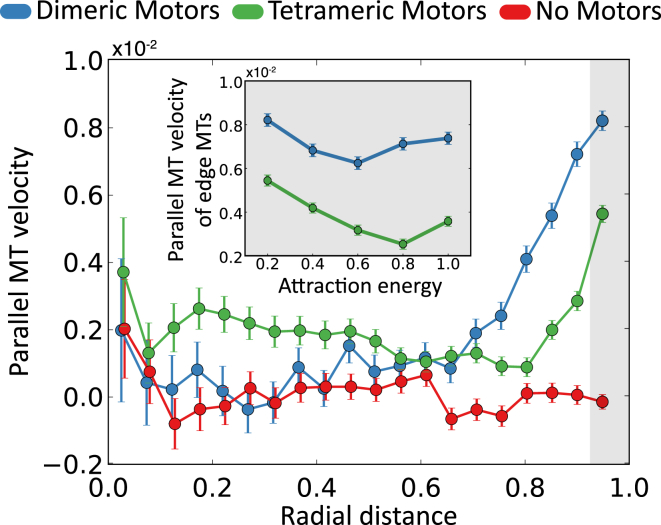
Persistent motion is most prevalent at the edge of the confinement for both dimeric and tetrameric motors (Fig. 9). The parallel MT velocities are higher near the circular boundaries, whereas MTs have small velocities in the center of the confinement for radii below 0.7 R_W. Velocities at the boundary are significantly higher for dimeric motor systems than for tetrameric motor systems (Fig. S22). Parallel MT velocity near the boundary generally decreases with increasing MT attraction. This is due to the lack of MT activity with cohesive interactions that hinder MT-MT sliding (Fig. 9, inset).

Figure 9.

Parallel velocities of MT systems with tetrameric, dimeric, and no-motors as a function of radial distance for E_A = 0.2 k_BT and N_m/N_f = 1. Inset (shaded) shows the mean velocity of the MTs closest to the confinement edge for different E_A values for N_m/N_f = 1. Velocities are normalized by L/τ. Radial distance is normalized by confining wall radius, R_W. Attraction energy is normalized by k_BT. To see this figure in color, go online.

Motor evolution

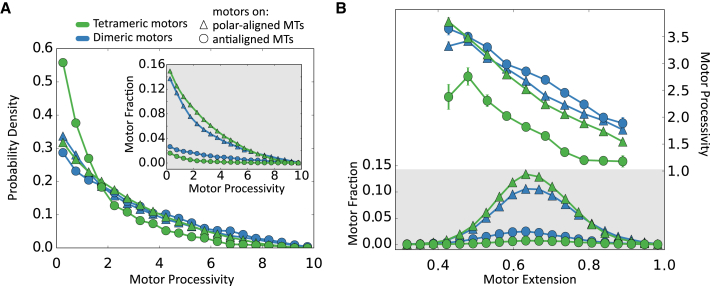
We define motor processivity as the number of consecutive time steps that a motor remains attached without releasing the cross-linked MT pair, i.e., the youngest (oldest) motors with the lowest (highest) processivity are the motors that have been attached for the shortest (longest) period of time. In our simulations, a motor that does not reach stall length will have motor-arms that each cover MT length L in $10\tau$.

Fig. 10 A shows that the youngest motors are the most numerous, and the number of motors decreases exponentially with processivity, i.e., motors detach from MT pairs at a rate proportional to the number of surviving motors. Tetrameric motors that cross-link antialigned MTs have the fastest detachment rate and the shortest mean lifetime (Fig. 10 B; Table 2). The rate of detachment and the mean lifetime in the other three cases are similar. Because the probability of motor attachment is independent of MT alignment and there are fewer antialigned MT pairs than polar-aligned MT pairs, motors between antialigned MTs are fewer than motors between polar-aligned MTs (Fig. 10 A, inset). From Fig. 10 B, we see that the average motor extensions are distributed similarly about a mean of 0.65d_t. It also shows that the contribution of energy from the motors comes mostly from motors cross-linking polar-aligned MTs, especially for the system with tetrameric motors (Table 2), because motors cross-linking antialigned MT pairs are less processive, and fewer in number. We also observe that motor extension decreases linearly with processivity. The relationship between motor extension and motor processivity is similar between all motors, except the tetrameric motors that cross-link antialigned MTs. At N_m/N_f = 1, one-half of the dimeric motors were lone motors connecting MT pairs and of the remaining motors, 70% of the motors were in a correlated orientation, i.e., with their motile (anchored) arms on the same MT.

Figure 10.

(A) Histogram of motor processivity for the four motor categories (dimeric/polar-aligned, dimeric/antialigned, tetrameric/polar-aligned, and tetrameric/antialigned). Inset (shaded) is the histogram before normalization. (B) Histograms (not normalized) of motor extensions, and motor processivity as a function of motor extension. Parameters are E_A = 0.2 and N_m/N_f = 1. Motor processivity is normalized using the timescale, τ. Motor extensions are normalized using motor threshold extension, d_t. To see this figure in color, go online.

Table 2.

Mean Motor Lifetimes are Obtained from Fitting Exponential Curves to Fig. 10A

Motor Type	MT Orientation	Mean Lifetime	Motor Energy Fraction
Dimeric	polar-aligned	2.87	0.789
	antialigned	3.58	0.211
Tetrameric	polar-aligned	3.05	0.936
	antialigned	1.51	0.064

Motor energy fraction is the sum of squared lengths of motors cross-linking polar-aligned (antialigned) MTs relative to all the motors in the system. Mean lifetime is normalized using the timescale, τ.

With increasing motor velocity, particularly in the dimeric motor system, the system becomes more dynamic due to larger sustained active stresses. At high motor velocities (ν_mτ/r_min > 50), tetrameric motors connecting antialigned MTs have significantly lower motor processivity than dimeric motors, which is required to sustain large active stresses (Fig. S20). This is because, at higher motor velocities, motors exceed their threshold length before MTs can respond to the stretched motor.

At low motor velocities (ν_mτ/r_min = 5), MT polarity sorting takes much longer. At a timescale of τ, slow motors behave as passive cross-linkers and hinder diffusion (Fig. S15).

Discussion

Cellular-level processes, such as cytoplasmic streaming, require molecular level characterization and the unification of complex biomolecular systems across length and timescales. Motile systems can be studied either by ignoring microscopic mechanisms and focusing on macroscopic properties, or just measuring the microscopic properties of individual components. We have taken a step toward capturing cellular-scale phenomena by marrying three distinct length scales: 1) molecular motors, the smallest elements; 2) MTs, the major components whose activity is of main interest; and 3) the confining wall, the largest length scale. By subjecting confined MTs to dimeric and tetrameric motors under different levels of MT-MT attraction, we observe a variety of large-scale structures in two dimensions. Although real cells are intrinsically 3D, our simulations should be relevant to experiments that study cytoplasmic streaming within a plane for cells that are attached to a substrate. Moreover, our simulations directly apply to experimental 2D model systems of cytoskeletal filaments (13, 14, 15), and extend previous theoretical and simulation studies of MT-motor systems (19, 21, 23).

The structures observed in the case of passive MTs under low attraction are consistent with calculations based on the generalized Onsager model, where ordered twofold symmetric defect structures are observed between nonattractive filaments within a line boundary at high densities (56). In this model, activity mediated by dimeric motors led to large polar-aligned MT clusters that were nonmotile at short timescales. Tuning MT-MT attraction levels to those prescribed in experiments did not have a significant effect on the structure of this system (47). MTs subject to tetrameric motors formed small polar-aligned bundles, and increasing MT-MT attraction enhanced MT bundling in these systems. Bundling of MTs subject to tetrameric motors were similarly observed in cases of high motor concentration and small motor run lengths in 2D simulations of a minimal physical model of MTs, motors, and static cross-linkers (19). Similar bundles were also reported in simulations of active gels of filaments and motors between two infinite parallel walls, at high motor attachment rates (23).

In computer simulations of a filament-motor system confined to a pressurized cylindrical box, where the confinement radius was slightly larger than the length of a semiflexible filament, rotational motion of filaments and motors during a transient vortex phase was observed (24). This system ultimately collapsed into a semiaster. In contrast, for our circular confinement with a radius eight times the MT length, we find persistent flows close to the confinement wall. Although the large polar-aligned clusters in the case of the dimeric motors do not exhibit significant short-time dynamics (Fig. 9), fluctuations in MT orientations within these clusters close to the confining wall gives antialigned MTs that result in persistent flows and redistribution of MTs throughout the confinement. This activity can be seen in the velocities of MTs in antialigned environments and their trajectories.

With filament lengths comparable to the radius of the confinement, two +1/2 defects were observed at the confinement edge in both active (24) and passive (56) cases. We recovered such defects in passive cases. However, with shorter filaments relative to confinement radius, defects were not distinguishable in the tetrameric motor systems, and multiple +1/2 defects were observed in the dimeric motor system close to the confinement, and conjugate −1/2 defects in the bulk (Fig. S8). We posit that a sufficiently flexible boundary can lead to filopodia-like protrusion, which will be actively extended by the +1/2 defect tip, as observed in experiments where MTs are confined to the surface of a spherical vesicle (15).

We have shown that motor-mediated pairwise interactions give large-scale MT dynamics. The polarity sorting mechanism, where motors induce cohesive interactions between polar-aligned MTs, and larger forces between antialigned MTs, have been previously observed and described in various studies (19, 21, 25). Similarly, we show that MTs move persistently in a direction coupled with their polarity, i.e., in the opposite direction of motor-arm motion. Motors that cross-link aligned and antialigned MTs give symmetric and asymmetric longitudinal displacements of MTs in Fig. 7. Although, in another simulation of MT-motor mixtures, a linear force-velocity dependence for motor velocity is used (21), our simulations give symmetric and asymmetric longitudinal displacement profiles for motors cross-linking aligned and antialigned MTs, respectively.

To disentangle the effect of motors with two active arms, and one active arm and an anchored arm, we keep the active motor arm’s stepping rate constant, unlike in other MT-motor studies (19, 21, 25). In comparison with (21), which observes longer extensions for motors cross-linking antialigned MTs, we observe a similar and symmetric motor extension profile across all types of motors Fig. 10 B. This is because in our model, motors cross-link MTs at a constant rate regardless of their extension (below the motor threshold length). In (21), extension of motors upon attachment is determined by a semigrand canonical ensemble approach. Nevertheless, in our work, motor processivity of motors cross-linking antialigned MTs is smaller for tetrameric motors, as was also found in (21). In general, between the two agents of dipolar force (tetrameric and dimeric motors), we observe that the dimeric motors are more effective at inducing large forces between antialigned MTs.

In our simulations, the attractive wall leads to a layer of less motile, disordered MTs near the wall. This may model a cortical actin cytoskeleton to which motors can cross-link and propel MTs in the bulk. In vivo experiments have shown that a network of stable MTs are anchored to the actin cortex near the cell membrane and that a directed streaming process is carried out by the motors that use these anchored MTs as tracks to propel cytoplasmic MTs (5). These experiments indicate that cytoplasmic MTs travel five times faster than the anchored, cortical MTs; also, cells with kinesin mutants deficient in MT sliding resulted in a 14-fold decrease in cytoplasmic MT velocities under the particular conditions of these experiments. In our simulations, relative to the MTs at the center of the confinement, wall attraction causes a threefold and 1.4-fold increase in parallel MT velocity at the confinement edge for the tetrameric and dimeric motor systems, respectively (Fig. S18). We conclude that the overall dynamics of the system is enhanced by motor asymmetry, and that this is most prominent close to the edge of the confinement (Fig. S22), due to the layer of immobile MTs at the confinement wall.

By comparing dimeric motors with tetrameric motors, we have studied the role of asymmetry of motor-arm velocity in propagating MT motility within confinement. The tetrameric motor model has been considered extensively in computer simulations to describe similar phenomena (19, 21, 23), but the effect of motor asymmetry has been largely ignored, despite its ubiquity in nature to propagate MT-MT sliding. Apart from the role of the dimeric motor, kinesin-1, in streaming systems in nature (5, 9, 10), computer simulations that investigated force generation in 1D bundles of MTs (34) report bundle expansion only in the case of dimeric motors. Tetrameric motors, on the other hand, opposed bundle expansion. In fact, it has been shown that the regulation of axon initiation and growth can only be explained by considering the significant roles of dimeric motors such as kinesin-1 and cytoplasmic dynein (34), on top of MT polymerization. The extensile nature of the aligned 1D filament bundles is reflected by the elongated clusters in our simulations.

Differences in MT motion as a result of motor asymmetry are not immediately obvious. For instance, higher sliding velocities between antialigned MTs cross-linked by tetrameric MTs, due to a higher longitudinal displacement per time step, as depicted in Fig. 2, may be expected. However, we have shown that, on average, antialigned MTs cross-linked by dimeric motors slide faster, and that the higher velocities of the tetrameric motors only make the tail of a skewed parallel MT velocity distribution (Fig. 7; Table 1). The dimeric motors, although incapable of producing as large forces as tetrameric motors, could sustain a larger force for a longer time without detaching, resulting in a more symmetric parallel MT velocity distribution with a larger absolute mean velocity (Fig. 10).

We find that the dynamics of MTs is strongly dependent on the local polar order parameter, i.e., the density of opposite-polarity MTs. This supports simulation results for 1D filament bundles cross-linked by molecular motors, where the drift rate for a given filament has been shown to be a linear function of the density of the opposite-polarity filaments (35). This further consolidates general assumptions made by polarity-dependent continuum models of MTs (57), where interaction between antiparallel filaments phenomenologically leads to filament sorting. Our simulations identify the mechanisms involved (Fig. 2) that contribute to the distribution of parallel MT velocities for dimeric and tetrameric motors.

In reconstituted systems of MTs in vitro (14), biotin-labeled kinesin motors have been conjugated using streptavidin clusters, and applied to a mixture of MTs condensed onto an oil-water interface. Based on MT structures observed in these experiments, we hypothesize that such a system of motors can be modeled using dimeric motors. In vitro motility assays have shown that conventional kinesin motors are processive, i.e., single molecules of kinesin move continuously along a MT for several microns (58, 59). Biochemical experiments have confirmed that kinesin molecules hydrolyze on average 125 molecules of ATP after binding to a MT, consistent with the motor taking 125 8-nm steps (60). When such a processive motor is paired to a motor that is in the rate-limiting nonmotile state (61), the stress generated between MTs will be different from that between MTs connected by a tetrameric motor, which has two fully active arms. From our system, it is clear that the asymmetry in motor-arm motion greatly aids MT activity and the extensile sliding between MTs. Hence, such a model with asymmetric motor-arm motion might be more suited to give a microscopic explanation to the extensile behavior of MT bundles.

In the future, we intend to include semiflexibility of MTs to capture dynamics of MT bundles instead of individual MTs. By simulating larger length scales, we expect to substantiate defect dynamics with accurate microscopic mechanisms for MT bundle extension.

Author Contributions

A.R., G.A.V., G.S., T.A., and G.G. designed the study. A.R. performed the simulations and analyzed the data. All authors discussed and interpreted results. All authors wrote the manuscript.

Editor: Alexander Dunn.

Supporting Citations

References (62, 63, 64, 65, 66) appear in the Supporting Material.

Supporting Material

Movie S1. No-Motor System

Video shows the evolution of the system starting from the random initial condition. The number at the top of the video is time in units of τ. Length units shown in the video are in terms of r_min. E_A = 0.2 k_BT and N_m/N_f = 0.

Movie S2. Dimeric Motor System

Video shows the evolution of the dimeric motor system starting from the random initial condition. The number at the top of the video is time in units of τ. Note the fast moving MTs at the edge of the confinement. Length units shown in the video are in terms of r_min. E_A = 0.2 k_BT and N_m/N_f = 1.

Movie S3. Dimeric Motor System, at Higher Motor Concentration

Video shows the evolution of the dimeric motor system starting from the random initial condition. The number at the top of the video is time in units of τ. Note the fast moving MTs at the edge of the confinement. There are more spaces in-between clusters because a higher concentration of motors binds MTs closer to each other. Length units shown in the video are in terms of r_min. E_A = 0.2 k_BT and N_m/N_f = 2.

Movie S4. Tetramer Motor System

Video shows the evolution of the tetrameric motor system starting from the random initial condition. The number at the top of the video is time in units of τ. The video corresponds to Fig. 8 in the main text. E_A = 0.2 k_BT and N_m/N_f = 1.

Movie S5. Dimeric Motor System with Trajectory of Four Probe MTs

The video corresponds to Fig. 9 in the main text. E_A = 0.2 k_BT and N_m/N_f = 1.