Adaptive Response of Actin Bundles under Mechanical Stress

Abstract

Actin is one of the main components of the architecture of cells. Actin filaments form different polymer networks with versatile mechanical properties that depend on their spatial organization and the presence of cross-linkers. Here, we investigate the mechanical properties of actin bundles in the absence of cross-linkers. Bundles are polymerized from the surface of mDia1-coated latex beads, and deformed by manipulating both ends through attached beads held by optical tweezers, allowing us to record the applied force. Bundle properties are strikingly different from the ones of a homogeneous isotropic beam. Successive compression and extension leads to a decrease in the buckling force that we attribute to the bundle remaining slightly curved after the first deformation. Furthermore, we find that the bundle is solid, and stiff to bending, along the long axis, whereas it has a liquid and viscous behavior in the transverse direction. Interpretation of the force curves using a Maxwell visco-elastic model allows us to extract the bundle mechanical parameters and confirms that the bundle is composed of weakly coupled filaments. At short times, the bundle behaves as an elastic material, whereas at long times, filaments flow in the longitudinal direction, leading to bundle restructuring. Deviations from the model reveal a complex adaptive rheological behavior of bundles. Indeed, when allowed to anneal between phases of compression and extension, the bundle reinforces. Moreover, we find that the characteristic visco-elastic time is inversely proportional to the compression speed. Actin bundles are therefore not simple force transmitters, but instead, complex mechano-transducers that adjust their mechanics to external stimulation. In cells, where actin bundles are mechanical sensors, this property could contribute to their adaptability.

Introduction

The actin cytoskeleton is an essential component of the cell, and plays an important role in many dynamic processes involving cell motility and cell shape changes (1, 2, 3, 4). Indeed, actin assembly into higher-order structures is a prerequisite for force transduction and the regulation of cellular shape (4, 5). Bundling of actin filaments is crucial for the function of cytoskeletal elements such as filopodia, stress fibers, or the contractile ring (6, 7, 8). The main focus of experimental and theoretical investigations has been the mechanical properties of filamentous actin (F-actin) networks (9, 10, 11). In these studies, actin filaments are considered as passive semiflexible polymers that confer mechanical properties onto the network depending on its specific organization. However, it has recently been shown that a single actin filament is not a passive polymer. Instead, F-actin undergoes structural transitions when put under tension, and this phenomenon might explain different affinity of actin filaments with interacting proteins (12, 13). F-actin bundles themselves have been less thoroughly investigated, although bundled F-actin exists in a variety of states in cells. However, F-actin bundles may also undergo changes when under stress, and may not behave like simple beams, but, instead, display distinctive collective properties resulting from their interactions (14). In cells, F-actin bundles are produced by a variety of transiently cross-linking proteins including fascin, fimbrin, and α-actinin. Direct investigation of the mechanical properties of F-actin bundles in vitro, focusing on the important role played by bundling proteins, has been developed by various groups (15, 16, 17). Actin networks cross-linked by α-actinin display strain hardening at high cross-linker concentrations (18, 19). Analysis of thermal fluctuations of rings of cross-linked F-actin bundles allows us to access bundle stiffness as a function of cross-linker types and concentrations (20, 21). Direct manipulation of individual actin bundles reveals elastic and elasto-plastic properties of the bundles at different timescales (22). In cells, specific nucleators of actin polymerization such as formins form parallel bundles (23). In vitro, these bundles can also be reproduced without specific cross-linkers, using methyl-cellulose or PEG as a depletion force agent, or a multivalent cation (MgCl₂) to enhance the electrostatic interaction between the filaments. Such bundles have interesting properties, as they are able to retract after being expanded longitudinally (24), and two actin filaments are able to zipper into a bundle with a force on the order of tenths of piconewtons (25). How weak bonds between the filaments, in the absence of cross-linkers, can impact the mechanical properties of the whole bundle under compression, has not been addressed.

Here, we apply large, cyclic deformations of individual bundles of actin filaments created by unspecific depletion agents like methyl cellulose and divalent cations Mg²⁺. Deformations are applied using an optical tweezers setup to hold the actin bundle at both ends. Our measurements show that the cyclic deformations lead to a decrease in the force necessary to buckle the bundle, which reveals, to our knowledge, a new mechanical behavior of actin bundles. These results can be understood in the framework of a visco-elastic model, demonstrating that the bundle undergoes internal rearrangement under forcing, revealing the magnitude of the adhesion and friction forces between the filaments.

Materials and Methods

Multiplexed optical tweezers setup

Two digital acousto-optical deflectors (DTSXY-400-1064; AA Opto Electronic, Orsay, France) control the x-y position of the laser in a custom-built setup (see Fig. S4). They are used to create two optical traps in time-sharing mode at a switching rate of 20 kHz using a digital controller (DDSPA2X-D423b-34-0dB; AA Optoelectronics). The continuous wave IR-laser beam (YLM-1-1064-LP; IPG Photonics, Oxford, MA) is widened to slightly overfill the back aperture of the focusing objective (UPLSAPO60XW/IR, NA 1.2, 60×, water immersion; Olympus, Melville, NY) and the light is collected by a long distance objective (60×, water immersion, LUMPLFL 60×, NA 0.9; Olympus). A four-quadrant photodiode (QPD; Cat. No. G6849; Hamamatsu, Hamamatsu City, Japan) is connected to an amplifier (Öffner MSR-Technik, Plankstadt, Germany) to detect the position of trapped beads. Two controllers (PCIe-6259 and NI PCIe-6363; National Instruments, Austin, TX) are used for data acquisition and setup control, allowing a sampling rate of 500 kHz per channel of the QPD. The control of the setup and the analysis of the data are realized using the softwares LabVIEW 2010 (National Instruments) and MATLAB 2011b (The MathWorks, Natick, MA).

QPD and trap calibration

The conversion of QPD voltage into spatial position of the trapped bead is done with a calibration procedure that consists of scanning the laser trap over the bead, similarly to a scan over the membrane as done in (26). The bead is first trapped for 40 μs at a reference position, and then the trap is moved to a position along the centerline for 4 μs during which the QPD signal is recorded and averaged. Next, the trap is put back to the reference position for 40 μs before the next scan point is measured. This stepwise scanning is repeated until a complete linescan through the center of the bead is finished. Typically, the scan has a step size of 10 nm and spans the whole diameter of the bead. To avoid systematic errors, subsequent scan points were on opposite sides with respect to the bead. Close to the bead center (±500 nm) the signal at the QPD depends linearly on the distance between the trap and the bead center (Fig. S1). This linear regime allows converting the normalized voltage of the QPD into the spatial distance of bead to trap with subnanometer accuracy, determined from the noise floor. Finally, the trap stiffness is obtained from the power spectral density of the bead fluctuations using an adapted version of the method described by Berg-Sørensen and Flyvbjerg (27) (see Fig. S1 d).

Protein preparation

Globular actin is obtained from powder (Cat. No. AKL99; Cytoskeleton, Denver, CO) resuspended in G-Buffer (5 mM TRIS, 0.2 mM CaCl₂, 0.2 mM ATP) at a concentration of 30 μM. Fluorescent actin (Alexa Fluor 488 Conjugate, Cat. No. A12373; Invitrogen, Carlsbad, CA) is added at a fraction of 12 mol %. The actin solution is stored on ice overnight to allow the remaining F-actin to depolymerize, and is used for up to one week. Formin (Gst-mDia1-FH1-FH2-His, called “mDia1” in the following) is purified following the protocol described in (28, 29). The mDia1 is stored at −80°C and thawed directly before use. Cap-αβ is expressed following the protocol described by Soeno et al. (30) and stored in glycerol at −20°C. Profilin is obtained as described in Lu and Pollard (31) and stored on ice.

Bead functionalization with mDia1-FH1-FH2

The freshly thawed mDia1 is diluted in X-Buffer (10 mM HEPES, 100 mM KCl, 1 mM MgCl₂, 0.1 mM CaCl₂) to a final concentration of 2 μM. A volume of 5 μL of carboxylated latex beads (Cat. No. 17140, 4.5 μm; Polysciences, Warrington, PA) is washed in 100 μL pure water and centrifuged for 2 min at 5000 × g. Sedimented beads are then suspended in the mDia1 solution, and incubated for 30 min on a temperature-controlled shaker (20°C, 750 Rpm). Coated beads are then centrifuged (5000 × g, 2 min, 4°C) and the sediment suspended in 100 μL of X-Buffer with additional 1% of BSA (Cat. No. A7906; Sigma-Aldrich, St. Louis, MO). After 10 min of incubation on ice, the solution is again centrifuged (5000 × g, 2 min, 4°C) and the beads resuspended in 50 μL X-Buffer with additional 0.1% BSA. Prepared beads are stored on ice and used over the next three days.

Sample preparation

The proteins (final concentrations 3.1 mM actin, 9.7 mM profilin, 1 nM Cap-αβ) are prepared in a buffer containing 10 mM HEPES, 85 mM KCl, 13 mM NaCl, 0.3% BSA, 1.3 mM DTT, and1.3 mM DABCO. Just before the transfer to the setup, ATP, methyl cellulose, and MgCl₂ are added to yield a final concentration of 0.5 mM ATP, 0.15% methyl cellulose, and 0.5 mM MgCl₂, respectively. Of this solution, 12 μL are deposited on a large cover slide (Cat. No. 1; 24 × 60 mm; Menzel-Gläser, Thermo Fisher Scientific, Waltham, MA) previously cleaned with ethanol. A smaller, also cleaned, cover slide (Cat. No. 1, 18 × 18 mm; Menzel-Gläser, Thermo Fisher Scientific) is placed on top of it and carefully pressed down to remove bubbles. The chamber is then sealed using a 1:1:1 mixture of Vaseline/lanolin/paraffin. In a typical experiment, one bead is optically trapped and the QPD voltage is calibrated into position as described above. Note that the focused laser beam leads to concentrating actin around the beads, which we exploit to influence the direction of the bundle: we move the trap (or the stage) with a velocity of ∼5 μm/s toward one side of the actin cloud, where actin bundle growth is induced. A second bead is attached to the bundle by utilization of a second optical trap, leading to an individual bundle attached to two independently movable traps (see Fig. 1). Repeated calibration shows that the additional diffraction of actin does not change the behavior of the trap. After the polymerization has stopped (∼30 min), the traps are aligned horizontally or vertically to simplify later analysis. One trap is then used to move the bead and, thereby, to deform the bundle by either compression or elongation, whereas the second, immobile trap is used as the measuring trap.

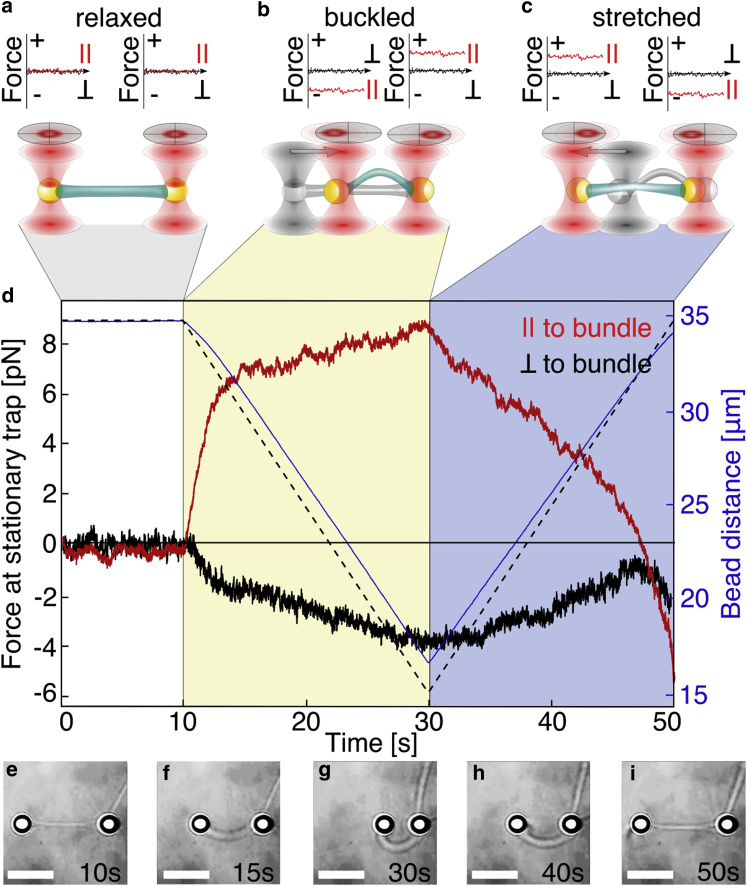
Figure 1.

Deformation of an actin bundle at a velocity of 1 μm/s. (a) The bundle, attached to two beads trapped in optical tweezers, is held at zero force. (b) One trap is then moved closer to the second one (yellow area), consecutively compressing (steep slope after t = 10 s), buckling (shoulder at t = 12 s), and finally bending the actin bundle (slight increase of force). (c) The traps are moved away from each other, reversing the deformation (blue area, negative slope of force) until they reach their initial positions. The sign of the force, positive or negative, indicates directionality, pointing outward or inward, respectively. (a–d) The red and black data curves are the force parallel and perpendicular to the motion, respectively. The nonzero perpendicular force originates from the off-center fixation of the bundle on the bead. The dashed line indicates the distance between the traps, whereas the actual distance between the beads is shown as the blue line. The phase contrast images (e–i) illustrate the aspect of the bundle at different positions in the cycle, indicated by the time in the lower-right corner. The scale bar represents 15 μm.

Results and Discussion

To generate actin bundles, molecular crowding is obtained by using methyl-cellulose as a depletion agent, and electrostatic interaction between actin filaments is obtained by the use of multivalent ions (MgCl₂) (32). Actin filaments are grown from the surface of mDia1-coated latex beads (28, 29), and self-organize into bundles of 20–40-μm length. Beads are optically trapped and provide handles to manipulate the bundle. After 30–90 min of incubation, two mDia1-coated beads are brought close by, and their actin filaments gather into a single bundle. The force on the beads is calibrated before each experiment (Fig. S1 and Materials and Methods), and subsequently measured on both beads simultaneously while manipulating the bundle. Holding the undeformed bundle in place does not show any change in force. Note that whereas single actin filaments generated by mDia detach from the nucleator (28), here, the whole bundle remains attached to the bead, likely through a cooperative phenomenon of a group of filaments being still attached although others detach. We thus perform the following compression/extension protocol (Fig. 1). The entire stationary bundle is first held straight for at least 10 s at zero force, which corresponds to the beads being centered in the traps. One trap is then moved toward the other at a constant absolute speed between 0.25 and 20 μm/s (Fig. 1, yellow area). The force initially increases roughly linearly with time (Fig. 1 d, red curve, after t = 10 s), corresponding to a slight longitudinal compression of the bundle (Fig. 1 d, dashed and blue line, respectively). As the compressive force exceeds a certain threshold of the order of 5 pN, the bundle buckles as observed in video microscopy (Fig. 1 f) and reflected in the shoulder and following plateau in the force curve. As the beads are brought even closer together, the bundle becomes increasingly bent and the force increases slowly, as expected for a rigid beam (Fig. 1 d, t = 15–30 s). The displacement of the beads is stopped when their distance is approximately one-half the initial bundle length, after which we immediately start moving the trap centers apart with the same absolute speed (Fig. 1, blue area). During this expansion phase, the curvature of the bundle relaxes and the force decreases. Traps are moved until they reach their initial position, but the striking observation is that the beads themselves do not return all the way back to their initial positions. Indeed, the distance between the two beads at that time is 670 nm smaller than the initial distance, implying that the bundle is under tension, and pulling is apparent from the negative sign of the force at the end of the expansion phase (Fig. 1). This observation indicates that the compression-extension process alters bundle shape and mechanics.

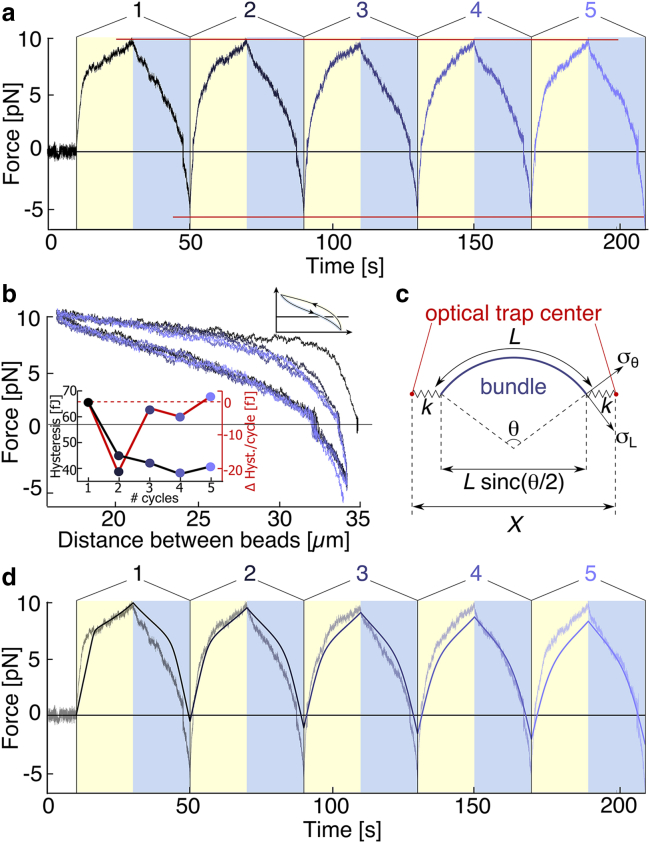
To assess whether further bundle modifications can be induced, we repeat this compression-extension process several times. Strikingly, the subsequent cycles differ from the first one in several respects (Fig. 2). First, the shoulder in the force curve upon buckling becomes less and less pronounced (Fig. 2, a and b, blue curves) compared to the first cycle (Fig. 2, a and b, black curves). The maximal and minimal forces reached at the end of the compression and extension phases only slightly change from cycle to cycle (red lines, Fig. 2 a, ±0.3pN, and nonsystematically (no trend)). The similarity of the curves between the second and the fifth cycles shows that the system rapidly settles into a steady state after the first buckling event. All these observations are a robust feature of the system, as confirmed by experiments at different trap speeds (Fig. S2). Plotting the force as a function of displacement for the compression and extension phases, we find that they do not overlap, indicating irreversible bundle deformation (inset of Fig. 2 b). We measure the hysteresis from the data by numerically calculating the difference between the integral of the compression and the expansion cycle. We find that the energy dissipated over the first hysteresis cycle substantially decreases in subsequent cycles.

Figure 2.

Series of five consecutive deformation cycles at 1 μm/s. (a) Force-time traces of five consecutive deformations as described in Fig. 1; the force shown is the longitudinal component of the force acting on the trap. A negative force corresponds to a situation where the traps are further apart than the beads, i.e., the exerted force is pulling on the bundle. A positive force denotes pushing on the bundle. Individual cycles are shown in different shades of blue, from black (first cycle) to light blue (last cycle). Yellow and blue regions correspond to compression and expansion periods, respectively. (b) Force-distance curves of the bundle deformation during the cycles. In the compression period, shown by the upper curves, the traps move from right to left; in the expansion periods, shown by the lower curves, the traps move from left to right. The inset is a scheme to show the direction of the hysteresis. (c) Schematic of the model used for fitting the data. L denotes the initial length of the bundle, X(t) is the distance between the traps, and k is the trap stiffness. The bundle tension is denoted by σ_L and the bending torque by σ_θ. (d) Comparison between the fit (continuous line) and the original data yield good overall agreement. One set of parameters τ, k_s, and κ is used to fit the whole curve (see Table S1).

To rationalize our observations, we attribute the irreversible bundle deformation and hysteresis to changes in the internal structure of the bundle. We describe these changes using a Maxwell viscoelastic model for extensional and bending deformations of the bundle (Fig. 2 c) with three adjustable parameters: a viscoelastic time τ, a 1D stretching modulus (i.e., the characteristic force required to induce a strain of order one) k_s, and a bending modulus κ. On timescales shorter than τ, the filaments and the bonds between them are strained reversibly, therefore the bundle responds elastically on short timescales as characterized by k_s and κ; on timescales longer than τ, the resulting bond stress relaxes as the bonds are broken and reformed, resulting in relative sliding of the filaments; the bundle flows viscously in the longitudinal direction, implying a change in its resting length and the acquisition of a spontaneous curvature, as filaments slide past each other at its cross section.

We model the actin bundle as a viscoelastic beam and approximate its shape to a circular arc. Introducing the bundle length L and bending angle θ (see Fig. 2 c), the extension and bending dynamics are each described by a Maxwell model, as a function of time t, as follows, in the longitudinal direction:

$$\frac{k_s}{L_0}\frac{\text{d}L}{\text{d}t}=\frac{\text{d}{\sigma }_L}{\text{d}t}+\frac{{\sigma }_L}{\tau },$$ (1a)

and in the transverse direction:

$$\frac{\kappa }{L_0}\frac{\text{d}\theta }{\text{d}t}=\frac{\text{d}{\sigma }_{\theta }}{\text{d}t}+\frac{{\sigma }_{\theta }}{\tau },$$ (1b)

where σ_L is the bundle tension (force conjugate to L), σ_θ is its bending torque (conjugate to θ), and L₀ is its initial length. The bundle is subjected to a longitudinal compressive force f applied by the optical tweezers, and force balance in the longitudinal and angular directions yields

$${\sigma }_L=-f\text{sinc}\theta /2,$$ (2a)

$${\sigma }_{\theta }=\frac{fL}{\theta }\left(\text{sinc}\theta /2-\text{cos}\theta /2\right),$$ (2b)

where the sinc function is defined by sinc(x) = sinc(x)/x. In the experiments, the distance X(t) between the centers of the two optical traps is imposed by the operator. Each bundle end, bound to a bead, is thus confined to the vicinity of the center of one of the traps through a harmonic restoring force with spring constant k = 19 pN/μm equal to the trap stiffness. Using the fact that the distance between bundle ends reads (L sinc θ/2), the longitudinal force plotted in Fig. 2 is given by Hooke’s law as

$$f=\frac{k}{2}\left[X\left(t\right)-L\text{sinc}\theta /2\right],$$ (3)

where the factor 1/2 is due to the presence of two traps in series. In the following, we predict the time dependence of this force for a given protocol X(t) by solving the system of (1a), (1b), (2a), (2b), (3) numerically, as described in the Supporting Materials and Methods.

The model is able to qualitatively capture our observations, as shown by fitting the force curve of Fig. 2 a using τ, k_s, and κ as adjustable parameters (Fig. 2 d) as well as other experimental force curves at different compression velocity, with one set of parameters for each bundle (Fig. S2). As the initial configuration of the bundle is devoid of spontaneous curvature, its response to the first round of compression displays a sharp buckling threshold, reminiscent to that of a straight rod. Once the bundle is curved, its internal reorganization process begins and spontaneous curvature builds up. As in the experiment, the buildup of spontaneous bundle curvature requires the exertion of a negative (pulling) force to stretch it back to its initial length. When the second round of compression begins, the buckling transition is blunted. Over the following rounds of compression-extension, the spontaneous curvature of the bundle builds up, and thus the maximum force required for compression decreases, whereas an increasingly large negative force is required to stretch it back to its initial length. However, the absolute value of this negative force is greater in the experiments than in the model, suggesting some reorganization effects that are not taken into account in the model (see below). After a time on the order of the viscoelastic timescale τ, the bundle settles into a steady state as observed experimentally. Note that this viscoelastic time is found to be inversely proportional to the compression speed (Fig. S6). In fact, the bundle is initially compressed longitudinally (Fig. 1 d and S2) before it buckles. Assuming that the critical strain required for buckling is similar in all experiments presented in Fig. S2, the time to reach it (that we call the “visco-elastic time”) will indeed be inversely proportional to the bundle compression velocity. Moreover, we assume here that the viscoelastic timescale associated with the curvature of the bundle is identical to that associated with its shortening. Although fitting two different viscoelastic times would improve the fit of the model to the experiment, we found that it does not yield any significant additional physical insights here.

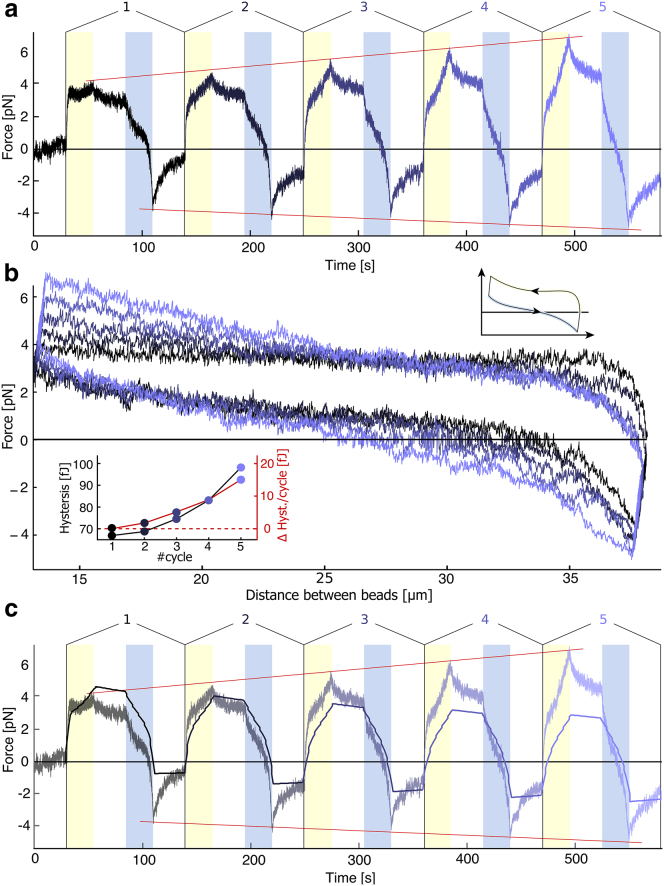
Our proposed picture of viscoelastic bundle relaxation implies that the spontaneous length and curvature of the bundle should relax even in the absence of trap motion. To confirm this, we carried out a second type of measurement that includes two waiting times of typically 30 s, one after the phase of bead approach and one after bead separation. During the waiting phase, traps are fixed at their positions and only the force on the beads is measured. As anticipated, we observe that the force relaxes when the traps are held (Fig. 3). The negative minimal force peak increases much more than in the absence of waiting times over successive cycles (Fig. 3 by +0.7 pN on average), implying that the bundle becomes less and less amenable to stretching and thus that spontaneous curvature builds up over the course of the experiment. In addition, buckling the bundle at the beginning of the compression phase becomes easier in the following cycles, confirming the presence of bundle remodeling, independent of the details of our driving protocol. Note that the model roughly reproduces the trend of the data (Fig. 3 c). Although the detailed understanding of how actin bundles reorganize during the waiting time, pictured by the increase in the hysteresis, may imply more complex deformations of the bundle, these are not taken into account in our current model. One possibility could be that the actin bundle undergoes some plastic rearrangements during this waiting time, and breakage of the filaments may increasingly happen during the waiting time. This effect may explain the greater absolute value of the negative force in experiments compared with the model. Further modeling may include this aspect in the future.

Figure 3.

Series of five cyclic deformations at an absolute speed of 1 μm/s with a relaxation period of 30 s. (a) Shown here are force-time traces of five consecutive deformations, as described in Fig. 1. (b) Shown here are the force-distance curves of the bundle deformation during the cycles. The inset is a scheme to show the direction of the hysteresis. (c) Comparison is given between the fit (continuous line) and the original data.

To elucidate the microscopic underpinning of our observations, we systematically fit our model parameters for all data obtained in the experiment pictured in Fig. 2. This is a global fit, with one set of parameters for each bundle, therefore covering a wide range of driving velocities and deformation amplitudes (n = 15 curves; Table S1). We find a bending rigidity κ = 770 ± 530 pN ⋅ μm², corresponding to an average persistence length of 190 μm, and a bundle stretching rigidity k_s = 120 ± 76 pN. These values support a simple mechanical model where the bundle is constituted of weakly coupled filaments, i.e., its filaments are not constrained to strictly remain in register during an elastic deformation (20, 33). Indeed, measuring bundle thickness from electron micrographs (Fig. S3) leads to an estimate of the number of filaments per bundle N = 20,000 (Supporting Materials and Methods). The weakly coupled model implies a bundle bending rigidity κ = Nκ⁽¹⁾ $\simeq$ 1200 pN ⋅ μm², where κ⁽¹⁾ $\simeq$ 0.06 pN ⋅ μm² is the bending modulus of a single filament (corresponding to a persistence length l_p⁽¹⁾ = 15 μm (34). Similarly, the stretching modulus k_s = Nk_s⁽¹⁾ $\simeq$ 86 pN, where we get the stretching modulus of a single filament of length L₀ = 20 μm as $k_s^{\left(1\right)}=\left(90k_{\text{B}}T{l}_p^2/L_0^3\right)$, as expected from entropic elasticity (35). The estimated values of κ and k_s for weakly coupled filaments are therefore in good agreement with the values obtained from the fit of the experimental data.

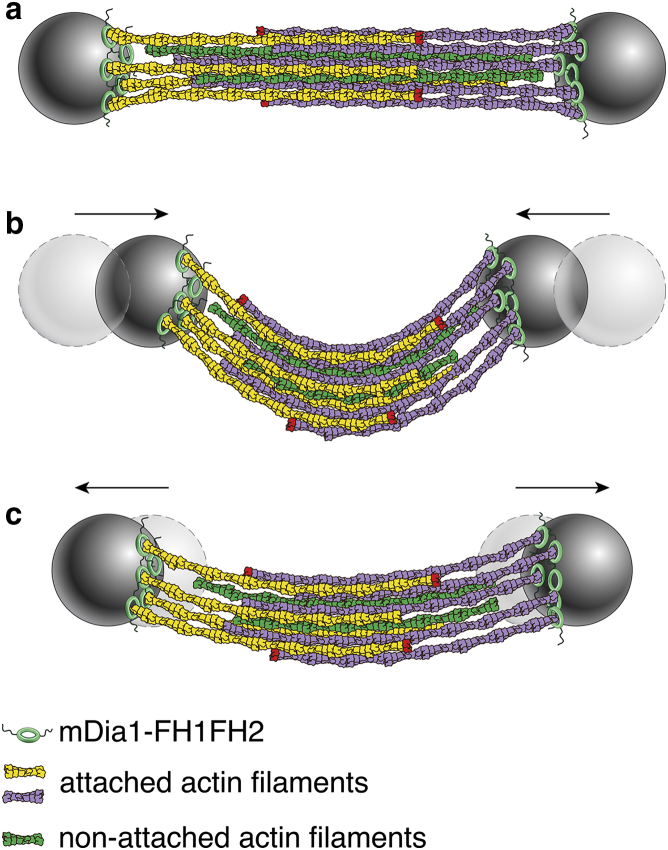
This good understanding of the bundle's short-time elastic response enables us to discuss its long-time viscous relaxation as characterized by the viscoelastic time of τ = 150 ± 200 s (the considerable dispersion-measured τ-values are discussed in the Supporting Materials and Methods). As filaments are nucleated on either bead, any single filament is attached to one bead at most, implying that filaments subjected to sustained forces slide relative to each other (36) (Fig. 4). Such forces arise when the bundle is bent, inducing compression on the inner face of the bundle (that with the largest curvature), and extension on the opposite side (Fig. 4). As filaments slide relative to each other, the outer face of the bundle thus extends and the inner face shortens. This differential extension is equivalent to the acquisition of a spontaneous bundle curvature, as described by Eq. 1 b. From a macroscopic perspective, the viscoelastic time τ can be viewed as the ratio of friction and elasticity in the bundle, reflecting the fact that both small friction and strong elastic restoring forces drive speedy viscoelastic relaxation. Following this idea, a simple model of force relaxation inside the bundle allows us to infer a value for the interfilament friction coefficient ς from our experimental measurement of τ, yielding $\varsigma =\left(8k_s\tau /L_0^2\right)\simeq 117\text{pN}\cdot \text{s}\cdot \mu {\text{m}}^{-2}$. This value is on par with the friction forces measured for two filaments in the absence of bundling (36) (Supporting Materials and Methods and Fig. S5).

Figure 4.

Illustration of the microscopic model leading to adaptive mechanics. At rest (a), the bundle is made of parallel and antiparallel filaments. Filaments are connected to mDia beads on one end and have a free end depicted in red. In compression (b), filaments slide and red ends are further apart at the inside of the buckled bundle and closer at the outside. When the bundle is stretched again, there is a memory of the deformation (c) and the bundle does not go back to its initial position.

The static mechanics of actin bundles have previously been investigated under a wide range of conditions in the presence of cross-linkers. However, their dynamical behavior as well as the role of other physical interactions are still poorly understood. In this study, we reveal that molecular crowding and electrostatic interactions lead to weak elastic coupling between filaments, yet they have strong dynamic friction. As the bundle undergoes cyclic deformation, these interactions lead to changes in its internal structure and mechanical properties, leading it to behave as an adaptive material under mechanical stress. Cells may exploit these properties and the associated diminished bundle buckling force when probing their surroundings using their filopodia, much like snails retracting their antennae when sensing an obstacle. Moreover, the striking mechanical behaviors of actin bundles we uncover here could inspire artificial force probes able to sense force once, transmit information, and conserve the memory of the deformation corresponding to the sensed force.

Author Contributions

C.S. and L.B. designed research and wrote the article. M.L. developed modeling and wrote the article. F.R. carried out and developed experiments and analysis, and wrote the article. R.P.-B. carried out and developed experiments. J.-L.M. contributed to modeling. M.S. contributed to the experimental development. J.M. performed protein purification. T.B. developed the experimental setup and analysis.

Editor: Enrique De La Cruz.