Absolute binding free energies between T4 lysozyme and 141 small molecules: calculations based on multiple rigid receptor configurations

Abstract

We demonstrate the feasibility of estimating protein-ligand binding free energies using multiple rigid receptor configurations. Based on T4 lysozyme snapshots extracted from six alchemical binding free energy calculations with a flexible receptor, binding free energies were estimated for a total of 141 ligands. For 24 ligands, the calculations reproduced flexible-receptor estimates with a correlation coefficient of 0.90 and a root mean square error of 1.59 kcal/mol. The accuracy of calculations based on Poisson-Boltzmann/Surface Area implicit solvent was comparable to previously reported free energy calculations.

1 Introduction

Fast and accurate predictions of noncovalent binding free energies between proteins and small organic ligands would have significant impact on the design of drugs^1–3 and other modulators of biological processes. These potential applications have inspired a vast array of methods for protein-ligand binding free energy prediction, each with a different trade-off between accuracy and computational speed (for a broad review, see Gilson and Zhou⁴).

On one extreme, molecular docking focuses on speed. Docking algorithms are designed to quickly obtain plausible configurations of a protein-ligand complex. Scoring functions are then used to rank one configuration versus another. Docking programs are commonly assessed by their ability to redock ligands into crystallographic structures from which they have been removed. Comparative studies^5,6 and blinded exercises⁷ consistently show that docking methods are adept at generating the native pose but are less competent at giving it the highest rank. Docking scores are also poorly correlated with binding free energies.^5,6,8,9

Alchemical pathway methods, on the other hand, are slower but much more accurate. Built on a rigorous foundation in statistical mechanics,¹⁰ the methods involve sampling from a series of possibly nonphysical thermodynamic states in between end-states where the receptor and ligand are bound and unbound. In the unbound state, the receptor-ligand nonbonded interaction terms may be switched off or the species may be physically separated. Because the timescales involved in conformational changes or interconversions between binding modes are often long compared to simulation times, many published studies may not actually be fully converged¹¹! That is, they sample from only a subset of the Boltzmann distribution and produce biased estimates of the binding free energy for the given force field. To circumvent binding pose sampling issues, most alchemical binding free energy calculations consider systems where there is evidence for a particular pose. Relative binding free energies usually involve small perturbations to a crystallographic reference ligand and assume that the pose does not change. In absolute binding free energy calculations, the fully bound state often includes a confining potential to keep the ligand in a specific pose^12,13. In addition to sampling issues, the accuracy of alchemical pathway calculations can be limited by force field approximations such as the treatment of protonation, tautomerization, and polarizability. Nonetheless, within a domain of applicability where sampling and force field limitations are relatively unimportant, alchemical pathway methods are amassing a growing track record of accurate prediction.^14–19

It may be possible to progressively bridge the gap between the speed of docking and the rigor of alchemical pathway methods by using a recently derived statistical mechanics framework for noncovalent association, implicit ligand theory (ILT).²⁰ Molecular docking scores are typically based on the interaction energy between a ligand and receptor. ILT is based on an exponential average of the receptor-ligand interaction energy (Eq. 2), the binding potential of mean force (BPMF), or the binding free energy between a flexible ligand and a rigid receptor. By computing an exponential average of the BPMF over the apo ensemble, one may obtain the standard binding free energy (Eq. 3). The accuracy of a binding free energy estimate may be incrementally improved by including an increasing number of receptor snapshots to the calculation.

Oostenbrink and van Gunsteren²¹ developed a related but distinct approach to estimate binding free energies based on BPMFs (although they did not use the term). Formally, their method was distinct from ours because they focused on relative rather than absolute binding free energies and their reference state was a holo rather than an apo ensemble. Their approach also differed in that they used a single-step perturbation to estimate BPMFs.

There are reasons to believe that, when the algorithms are better developed and understood, calculations based on BPMFs will be less computationally expensive than alchemical simulations with fully flexible receptors. First, receptor conformations can be sampled once and used with many different ligands. In contrast, conventional alchemical pathway methods require thorough receptor sampling for every receptor-ligand pair. Second, while obtaining binding free energies will require multiple BPMFs, BPMFs are much faster to calculate than binding free energies to a fully flexible receptor. The key reason for this speedup is that a BPMF calculation only requires sampling of the ligand, which usually has significantly fewer degrees of freedom than the complex. Furthermore, nonbonded interactions between a rigid receptor and ligand can be treated by interpolating precomputed three-dimensional grids, a strategy first developed for docking.^22,23 Once the grid is stored, calculation time no longer depends on the size of the receptor. In contrast, conventional alchemical pathway methods require frequent force evaluation between flexible receptor atoms. As the number of pairwise interactions scales as O (N²) with N receptor atoms (neglecting cutoffs), the relative efficiency of BPMF-based methods is more pronounced as receptor size increases.

A key challenge to the successful application of ILT is receptor sampling. The most straightforward way to generate receptor configurations is to run a molecular dynamics simulation of the apo state, the receptor without a ligand. It is not strictly necessary, however, for receptor configurations to be sampled from the apo ensemble as long as they can be reweighted to the apo ensemble. In the first paper on ILT, Minh²⁰ used straightforward molecular dynamics of the apo state to estimate binding free energies for simple host-guest systems. In many complexes, however, receptor configurations that are highly populated when a ligand is bound may be rare when the ligand is not present. If these configurations are not sampled, then then binding free energy will be overestimated (i.e. the affinity would be predicted to be weaker).

Here, we present an alternate strategy for sampling receptor configurations: performing alchemical binding free energy calculations on a small subset of the ligands of interest. These alchemical calculations allow the receptor to assume conformations that accommodate the ligand. Snapshots from the alchemical calculations are then reweighted into the apo state for ILT-based free energy calculations. We apply this strategy to binding free energy calculations between a simple protein binding site, a hydrophobic pocket produced by the L99A mutant of T4 lysozyme, and 141 small molecules that have been experimentally classified as active or inactive. T4 lysozyme is an excellent test case for our receptor sampling strategy because the binding of some, but not all, ligands are known to induce conformational changes: rotation of a side chain in valine 111^24,25 and expansion of the binding site through three discrete conformations of a helix.²⁶

2 Theory and Methods

In this section, we first describe the setup of the system and our protocol for molecular docking and alchemical pathway calculations. We then review ILT and describe our procedure for BPMF and binding free energy estimation based on ILT.

2.1 System setup

A crystallographic structure of T4 lysozyme L99A bound to hexafluorobenzene was downloaded from the Protein Data Bank (PDB ID 3DMZ). Hydrogen atoms were added using pdb2pqr.²⁷ The protein was prepared with AMBER²⁸ ff14 parameters using AmberTools 14.

We prepared a total of 141 ligands whose activity has been measured, primarily by the Shoichet group.^29–35 Of these, 70 are active and 71 inactive. With the exception of iodobenzene, which was determined to be active by isothermal titration calorimetry,³⁶ molecules were considered active if they increase the thermal denaturation temperature of T4 lysozyme. Excluding ligands that appear in multiple references, the library includes 91 ligands from Morton et al.²⁹, 2 from Morton and Matthews³⁰, 6 from Su et al.³¹, 6 from Wei et al.³², 22 from Graves et al.³³, 4 from Mobley et al.³⁴, 9 from Graves et al.³⁵, and 1 from Liu et al.³⁶. For the names and SMILES strings³⁷ of all 141 ligands, see Table S1 in the SI. Ligand protonation states were assigned using OpenEye QUACPAC.³⁸ Three-dimensional models of the ligands were built using BALLOON.³⁹ The models were parameterized with the generalized AMBER force field⁴⁰ from AmberTools 14 using Bondi radii⁴¹ and AM1BCC partial charges^42,43 using antechamber⁴⁴ in UCSF Chimera.⁴⁵

For our binding free energy calculations (both with multiple rigid structures and with a flexible protein) we defined the T4 lysozyme L99A binding site as a sphere that contains the ligand center of mass. The site was measured based on the following crystal structures, given by PDB ID (chain): 188I (A), 187I (A), 186I (A), 185I (A), 184I (A), 183I (A), 182I (A), 3HH6 (A), 3HH5 (A), 3DN6 (A), 3DN3 (A), 3DN2 (A), 3DN1 (A), 3DN0 (A), 2RB2 (X), 2RB1 (X), 2RB0 (X), 2RAZ (X), 2RAY (X), 2OTZ (X), 2OTY (X), 1NHB (A). Prody⁴⁶ was used to align the structures to minimize the α-carbon root mean square deviation between each chain and the reference chain, 3DMZ (A). The center of mass was calculated for each ligand. The site center was defined as the mid-point of the range. The site radius, 5.0 Å, was determined by rounding the maximum distance from the site center to a ligand center of mass up to the nearest Ångstrom.

2.2 Molecular docking calculations

Molecular docking calculations were carried out using the anchor and grow algorithm in UCSF DOCK 6.⁴⁷ First, sphgen was run with default parameters: dotlim = 0.0, radmax = 4.0 Å, and radmin = 1.4 Å. DOCK was run with 5000 maximum orientations, using internal energy with an exponent of 12, a flexible ligand, an a minimum anchor size of 40. Pruning was performed with clustering, 1000 maximum orientations, a clustering cutoff of 1000, and conformer score cutoff of 25.0. A bump filter was used with max_bumps_anchor = 12 and max_bumps_growth = 12. Final conformations were clustered with a root mean square deviation (RMSD) threshold of 2.0 Å.

2.3 Alchemical pathway calculations

Alchemical binding free energy calculations were conducted for 24 ligands (Table S1) using YANK⁴⁸ 0.9.0. Six ligands - methylpyrrole, benzene, p-xylene, phenol, n-hexylbenzene, and (±)-camphor - were chosen to generate snapshots for BPMF calculations (Fig. 1). The first four were simulated in Wang et al.⁴⁸. The last two were chosen due to their relatively large size and potential for opening the binding pocket. The remaining systems for YANK calculations were selected after the AlGDock calculations; they were chosen to assess consistency between YANK and AlGDock for a broad range of binding affinities.

Figure 1.

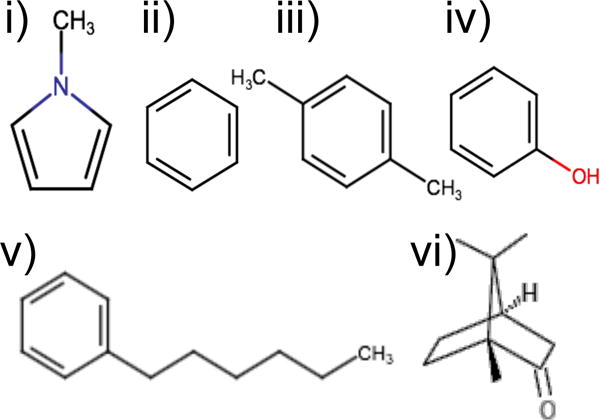
Ligands used in YANK calculations to generate snapshots for BPMF calculations: i) methylpyrrole, ii) benzene, iii) p-xylene, iv) phenol, v) n-hexylbenzene, and vi) (±)-camphor.

Three independent alchemical binding free energy calculations were performed for each complex. The ligand was first docked into the reference structure. The three lowest-scoring poses were used to initialize YANK simulations. The alchemical pathway included 16 thermodynamic states in generalized Born/surface area⁴⁹ implicit solvent (OBC2) at 300 K. In each state, 5,000,000 steps of Langevin dynamics were run with a time step of 2 fs. 8192 Hamiltonian replica exchange moves were attempted every 1 ps. A flat-bottom harmonic restraint was applied to the distance between the β-carbon of valine 111 and a non-hydrogen atom closest to the ligand’s centroid. The restraint force constant and radius were set to 5.92 kcal/mol/Ų and 5 Å, respectively.

Snapshots for BPMF calculations were extracted after 5 and 10 ns, for each of the 16 thermodynamic states, from each of the three independent YANK calculations, and for the six initial systems. The snapshots were chosen from all thermodynamic states, opposed to only the end points, to increase the diversity of conformations. There were a total of 576 snapshots.

2.4 Implicit ligand theory

For the noncovalent association between a receptor R and ligand L to form a complex RL, R + L ⇌ RL, the standard binding free energy is,

$$\mathrm{\Delta }G°=-{\beta }^{-1}\ln \left(\frac{C°C_{RL}}{C_R{C}_L}\right),$$ (1)

where β = (k_BT)⁻¹ is the inverse of Boltzmann’s constant times the temperature, C° is the standard concentration (1 M = 1/1660 ų), and C_X is the equilibrium concentration of species X ∈ {R, L, RL}. Activities have been assumed to be unity, a reasonable approximation in the limit of low concentrations.

Coordinates of the complex, r_RL, are partitioned into receptor (r_R) and ligand internal (r_L) and external (ξ_L) coordinates. Based on this partitioning, the interaction energy is defined as $\mathrm{\Psi }(r_{RL})=\mathcal{U}(r_{RL})-\mathcal{U}(r_R)-\mathcal{U}(r_L)$, where $\mathcal{U}(r)=\mathcal{U}(r)+W(r)$ is an effective potential energy that includes the gas-phase potential energy U(r) and solvation free energy W(r).¹⁰ A BPMF is an exponential average of interaction energies over ligand coordinates in the binding site,²⁰

$$B(r_R)=-{\beta }^{-1}\ln \left(\frac{{\displaystyle \int I_{\xi }{e}^{-\beta \mathrm{\Psi }(r_{RL})}{e}^{-\beta \mathcal{U}(r_L)}d{r}_{L}d{\xi }_L}}{{\displaystyle \int I_{\xi }{e}^{-\beta \mathcal{U}(r_L)}d{r}_{L}d{\xi }_L}}\right),$$ (2)

where I_ξ ≡ I(ξ_L) is an indicator function that takes values between 0 and 1 and specifies whether the receptor and ligand are bound or not.

According to ILT, the standard binding free energy ΔG° is related to an exponential average of BPMFs over Boltzmann-distributed receptor configurations r_R,

$$\mathrm{\Delta }G°=-{\beta }^{-1}\ln \left(\frac{{\displaystyle \int e^{-\beta [B(r_R)+\mathcal{U}(r_R)]}d{r}_R}}{{\displaystyle \int e^{-\beta \mathcal{U}(r_R)}d{r}_R}}\right)-{\beta }^{-1}\ln \left(\frac{\mathrm{\Omega }C°}{8{\pi }^2}\right),$$ (3)

where Ω = ∫I_ξ(ξ_L)dξ_L is the volume of the binding site. Because our site is a sphere and we did not place any restraints on rotation of the ligand, the site volume is the product of the volume of a sphere and an integral over the full range of Euler angles, $\mathrm{\Omega }=\left(\frac{4}{3}\pi r^3\right)\left(8{\pi }^2\right)$

2.5 BPMF estimation

BPMFs were estimated with our program Alchemical Grid Dock (AlGDock),⁵⁰ using the version committed to github on May 3, 2016.⁵¹ In brief, AlGDock uses Hamiltonian replica exchange for two processes: cooling and docking. In both processes, only the ligand molecule is flexible. With cooling, the temperature of the system (which only consists of the ligand) is progressively changed from 600 K to 300 K. With docking, receptor-ligand interactions are modeled by interpolating a pre-computed 3D grid.^22,23 The process consists of reducing the temperature and scaling the strength of the interaction grid from 0 to 1. The version of the program that we used has a few changes from the previous technical report.⁵⁰ Most notably, it now includes a routine to automatically perform hydrogen mass repartitioning^52,53 with a hydrogen mass of 4.0 amu. Another change is that the Lennard-Jones repulsive grid interpolation accuracy is improved by transforming the grid by a power of 1/4, interpolating, and back-transforming the energy by a power of 4; this is variation of a method introduced by Venkatachalam et al.⁵⁴.

Simulation parameters were similar to those previously described.⁵⁰ Due to the relative simplicity of the T4 lysozyme L99A binding site and its ligands, however, they were shorter and used a smaller binding site. Replica exchange was conducted for 20 cooling and 10 docking cycles. Each cycle consists of 150 iterations of Hamiltonian Monte Carlo,⁵⁵ external translation and rotation moves (for docking), and replica exchange. Hamiltonian Monte Carlo moves consist of initializing velocities from the Maxwell-Boltzmann distribution, 50 steps of velocity Verlet using a time step of 3.0 fs, and acceptance or rejection based on the Metropolis criterion.

To calculate solvation free energies, configurations of the ligand at 300 K in vacuum or fully interacting with the receptor were post-processed with two implicit solvent models: Onufreiv-Bashford-Case (OBC2) generalized Born/surface area,⁴⁹ as implemented in OpenMM;⁵⁶ and Poisson-Boltzmann/surface area (PBSA), as implemented in sander from AmberTools.⁵⁷ OBC2 solvent was chosen for direct comparison with YANK, and PBSA was chosen because it is the standard upon which generalized Born solvation models are based. For both implicit solvent models, we used Bondi radii.⁴¹ After the initial review of this manuscript, we became aware that AmberTools 14 only specifies the Bondi radii⁴¹ for hydrogen, carbon, nitrogen, oxygen, fluorine, silicon, phosphorus, and sulfur; other atoms are given a default radius of 1.5 Å. Therefore, we repeated the post-processing with van der Waals radii of 1.75, 1.85, and 1.98 Å, for chlorine, bromine, and iodine, respectively.

AlGDock provides several BPMF estimates, including: the minimum interaction energy, Ψ, which is the usual basis of molecular docking scores; the mean interaction energy, which is the basis of MM/PBSA^58,59 scores; and the multistate Bennett Acceptance Ratio,⁶⁰ the most rigorous estimator. Unless otherwise noted, reported results are based on the latter method.

To verify that these parameters lead to converged BPMF estimates, we conducted 10 independent BPMF calculations for 10 ligands and one random receptor snapshot.

2.6 Free energy calculations based on implicit ligand theory

Standard binding free energies were estimated with a summation over receptor snapshots,

$$\mathrm{\Delta }\widehat{G}°=-{\beta }^{-1}\ln \left[{\displaystyle \sum _{r_R}W(r_R)e^{-\beta B(r_R)}}\right]+{\beta }^{-1}\ln \left(\frac{\mathrm{\Omega }C°}{8{\pi }^2}\right),$$ (4)

where W (rR) is the normalized Boltzmann weight $\left({\displaystyle {\sum }_{r_R}W(r_R)}=1\right)$ associated with each receptor configuration r_R if it were in the apo ensemble.

We used weights based on the multistate Bennett Acceptance Ratio (MBAR),⁶⁰ an estimator for free energies and thermodynamic expectations. Specifically, we calculated the potential energy $\mathcal{U}(r_R)$ of all the receptor snapshots (without a ligand). Potential energies were calculated using either OBC2⁴⁹ in OpenMM⁵⁶ 6.3.1 or the PBSA in sander.⁵⁷ These potential energy values for the apo state were used to augment a weight matrix that includes potential energies for all samples in all thermodynamic states. As described in Eqs. 13 to 15 of Shirts and Chodera⁶⁰, a self-consistent solution to the free energy estimates leads to weights for each snapshot from each YANK calculation.

We tried several ways to convert MBAR weights to W(r_R). There are two issues associated with this conversion. First, the selected receptor snapshots comprise just a small subset of all the snapshots from the YANK simulations. To assign weights to this representative subset, we either (1) used MBAR weights of the selected snapshots, (2) evenly split the cumulative MBAR weight of each thermodynamic state between snapshots that represent the state, (3) assigned the MBAR weight of a snapshot to its most structurally similar (lowest α-carbon RMSD) representative. We will refer to the three approaches as individual, state, and structural weighting, respectively. While individual weighting accounts for the potential energy of the snapshot, state weighting considers the free energy of the thermodynamic state that the snapshot represents, and structural weighting considers the potential energy of structurally similar snapshots. Individual weighting is rigorous, but the other approaches are more numerically stable. The second issue is that MBAR weights are normalized for each YANK simulation, but we combined information from six simulations. We normalized the weights so that (1) each simulation has equal weight or (2) each apo state has equal weight. Hence, we used a total of six different weighting schemes:

1. Each snapshot is assigned its own MBAR weight; each YANK simulation has equal weight.

2. Each snapshot is assigned its own MBAR weight; each apo state has equal weight.

3. Each snapshot is assigned the cumulative MBAR weight of the thermodynamic state it represents; each YANK simulation has equal weight.

4. Each snapshot is assigned the cumulative MBAR weight of the thermodynamic state it represents; each apo state has equal weight.

5. Each snapshot is assigned the MBAR weight of its neighbors; each YANK simulation has equal weight.

6. Each snapshot is assigned the MBAR weight of its neighbors; each apo state has equal weight.

The statistical error of ILT-based binding free energies was estimated based on bootstrapping. That is, the standard deviation was calculated for binding free energies estimated from 100 sets of n BPMFs randomly sampled with replacement from the original n BPMFs.

2.7 Receptor conformational analysis

Principal components analysis was performed for receptor configurations using ProDy.⁴⁶ Histograms for principal components analysis eigenvectors were weighted by

$$w=\{\begin{array}{ll}\frac{e^{-\mathrm{\Delta }{u}_{1,2}(x)}}{{\displaystyle {\sum }_{x\in 1}{e}^{-\mathrm{\Delta }{u}_{1,2}(x)}}}\hfill & \text{if}k=1\hfill \\ \frac{e^{-\mathrm{\Delta }{u}_{k,k+1}(x)}+e^{-\mathrm{\Delta }{u}_{k,k-1}(x)}}{2{\displaystyle {\sum }_{x\in k}{e}^{-\mathrm{\Delta }{u}_{k,k+1}(x)}}+e^{-\mathrm{\Delta }{u}_{k,k-1}(x)}}\hfill & \text{if}1<k<K\hfill \\ \frac{e^{-\mathrm{\Delta }{u}_{K,K-1}(x)}}{{\displaystyle {\sum }_{x\in K}{e}^{-\mathrm{\Delta }{u}_{K,K-1}(x)}}}\hfill & \text{if}k=K\hfill \end{array}$$ (5)

where k is an index for the thermodynamic state, K is the total number of states, and Δu_k,l(x) = u_l(x) − u_k(x) is the potential energy difference for configuration x. This scheme gives high weight to snapshots that are particularly important to estimating the exponential average.

2.8 Correlation and error statistics

Different binding energy calculations and experimental measurements were compared with a variety of statistical measures: the Pearson R, Spearman ρ, Kendall τ⁶¹ correlations, as well as the root mean square error (RMSE) and adjusted RMSE (aRMSE). The Spearman ρ is the Pearson R between two rankings. Unlike the Spearman ρ, the Kendall τ only considers if data have the exact same rank. The RMSE between two series of data points {x₁, x₂, …, x_N} and {y₁, y₂, …, y_N} is,

$$\epsilon =\sqrt{\frac{1}{N}{\displaystyle \sum _{n=1}^N{[x_n-y_n]}^2}.}$$ (6)

The aRMSE is,

$$\epsilon =\sqrt{\frac{1}{N}{\displaystyle \sum _{n=1}^N{[x_n-y_n-(\overline{x}-\overline{y})]}^2},}$$ (7)

where the $\overline{x}$ and $\overline{y}$ are the sample mean of x and y, respectively. The aRMSE accounts for systematic deviation between the series and is useful for assessing whether relative binding free energies are accurate.

Bootstrapping was used to estimate the statistical error of all correlation and error statistics. More specifically, the standard deviation was calculated for metrics estimated from 100 sets of n ligand free energy estimates randomly sampled with replacement from the original n ligand free energy estimates.

3 Results and Discussion

3.1 Ligands can assume multiple poses in the bound state

At high temperature (600 K) and in the absence of interaction with receptor grids, the ligand samples configurations that are uniformly distributed in a sphere (Fig. 2). This behavior is expected from the flat-bottom harmonic potential. As the grid scaling constant α is increased from 0 to 1 and temperature is simultaneously decreased from 600 K to 300 K, the ligand samples a more restricted phase space.

Figure 2.

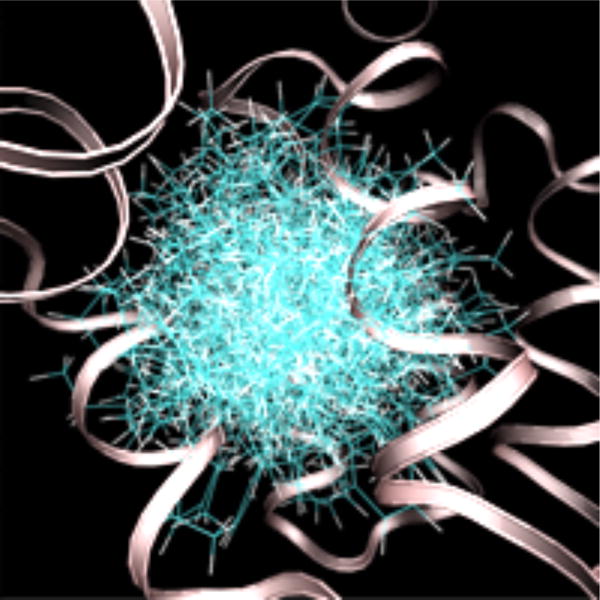
Configurations of n-hexylbenzene sampled at 600 K without a receptor interaction grid. The secondary structure of T4 lysozyme is shown as a ribbon. The protein structure is from an alchemical pathway calculation of DL-camphor binding.

Finally, at the lowest temperature (300 K) and highest grid scaling constant (α = 1), the ligand is confined to a much smaller set of poses (Fig. 3). In most cases the ligand assumes a single pose (e.g. the sampled 1-methylpyrrole and ethanol configurations shown in the figure); the ensemble is well described by fluctuations around a single energetic minima. In some other cases, such as with the thianaphthene and o-xylene configurations shown in the figure, multiple poses are populated.

Figure 3.

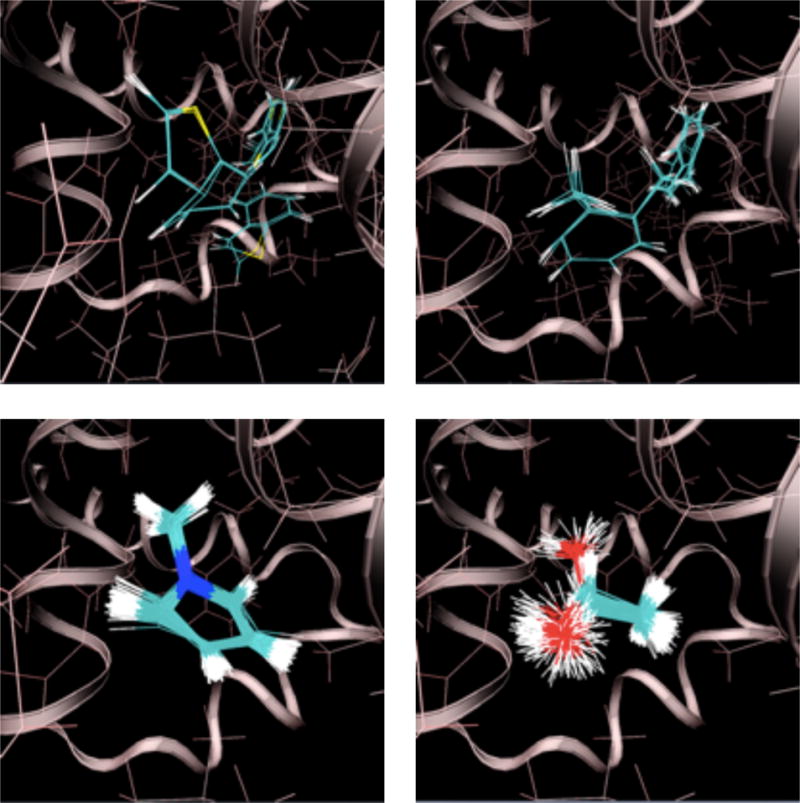
Ligand configurations sampled at 300 K with a full receptor interaction grid. Clockwise from the upper left: thianaphthene, o-xylene, 1-methylpyrrole, and ethanol. The secondary structure of T4 lysozyme is shown as a ribbon. The protein structure is from an alchemical pathway calculation of p-xylene binding.

3.2 BPMF calculations are converged

The chosen AlGDock simulation parameters were sufficient to obtain precise BPMF estimates for our selected complexes. After 20 cycles of replica exchange, the standard deviation of the cooling free energy - the free energy of changing the ligand temperature from 300 K to 600 K - was less than 0.10 kcal/mol (Fig. 4). The free energy of scaling the grid interactions and reducing the temperature to 300 K was estimated within 0.5 kcal/mol. In some cases, the standard deviation appears to level off, suggesting that some simulations are trapped in local minima. However, the standard deviation is not large.

Figure 4. Convergence of AlGDock calculations.

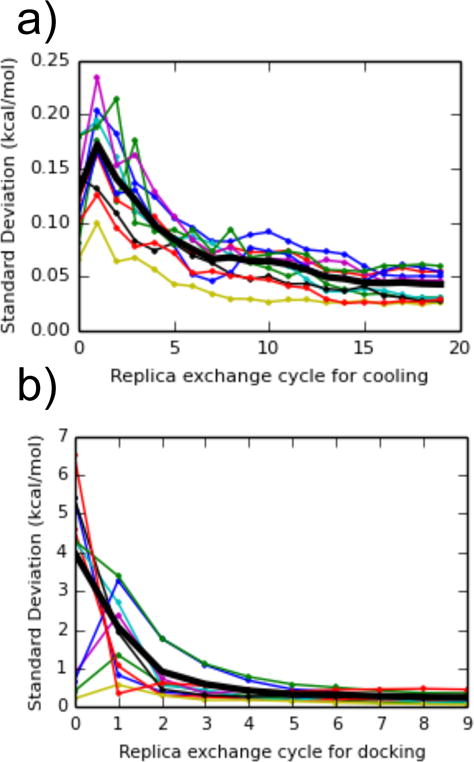
The standard deviation of free energy estimates as a function of the number of replica exchange cycles, for (a) changing the ligand temperature from 300 K to 600 K, and (b) scaling the receptor-ligand interaction grid from 0 to 1 while decreasing the temperature. Values were calculated between dipropyl disulfide, thianaphthene, isobutylbenzene, dibutyl-disulfide, phenylacetylene, cyclohexane, 1-heptanol, 1-propanol, 1,1-diethylurea, p-xylene, and a snapshot of T4 lysozyme from an alchemical pathway calculation with n-hexylbenzene. The thick black line is the average of the standard deviation across the 10 complexes.

BPMF calculations for T4 lysozyme and its ligands are faster than most protein-ligand complexes. Minh⁵⁰ attempted BPMF calculations for 85 protein-ligand complexes in the Astex diverse set, a curated set of publicly available high-quality crystal structures relevant to pharmaceuticals or agrochemistry.⁶² After starting from docked poses and running 18 cycles of replica exchange for grid scaling, only 40% of systems achieved BPMFs within 2 kcal/mol. In contrast, all of the calculations here were converged within 2 kcal/mol within 10 cycles of replica exchange. The relatively fast convergence of the calculations is likely due to the simplicity of the ligands and binding site.

The limiting factor for the convergence of BPMF calculations is likely the sampling of ligand orientations in the binding site. When calculating ligand binding free energies to the same T4 lysozyme mutant, Mobley et al.³⁴ achieved higher accuracy by incorporating multiple binding poses into their calculations. For free energy calculations involving a polar cavity formed by the L99A/M102Q mutant, Boyce et al.¹⁵ found that accurate affinity predictions required near-native starting orientations. One important distinction between these publications and our current work is that we incorporate a Markov chain Monte Carlo move for translation and rotation of the ligand; this move improves sampling of ligand orientations.

3.3 YANK binding free energy estimates are precise

With our simulation protocol, alchemical binding free energy calculations performed with YANK appear to yield precise free energy estimates. In only two out of 24 systems was the standard deviation of the binding free energy estimate larger than 0.5 kcal/mol: benzaldehyde oxime (0.55 kcal/mol) and dimethyl sulfoxide (0.98 kcal/mol). For the mean and standard deviation of YANK binding free energy estimates for all 24 complexes, see Table S2 in the SI.

Low statistical variance, however, does not preclude the possibility that simulations were trapped in local minima and failed to access the global minimum. Indeed, histograms of principal components analysis eigenvectors (Fig. S1 in the SI) show that different independent simulations sometimes access different parts of the receptor configuration space and that the unbound ensemble is not consistent across different YANK simulations. In these cases, the free energy estimates appear to be precise because the different configurations have similar free energies. In spite of the precision of free energy estimates, these calculations are not truly converged because they are not precise for the right reason; they do not draw from all energetic minima in proportion to the Boltzmann distribution.

In the context of other recent results with T4 lysozyme L99A, it is not surprising that our YANK simulations did not all truly converge. Merski et al.²⁶ solved a series of crystal structures with a congeneric series of alkyl benzenes bound to the protein. They found that their structures (and 121 public crystal structures of T4 lysozyme L99A) can be described by three discrete states with different conformations of a helix enclosing the binding site: closed, intermediate, and open. When Lim et al.⁶³ performed replica exchange calculations using a similar protocol to ours, their results were highly dependent on the starting structure. Only by extending their simulations from 5 ns to 55 ns per window were they able to eliminate dependence on initial conditions. Their results suggest that true convergence of our YANK calculations could require an order of magnitude more simulation time. Based on a projection of our 576 representative snapshots onto principal components defined by the crystal structures, it appears that YANK calculations access the three major conformations (Fig. 5). However, interconversions between the conformations are not always sufficiently sampled such that each individual YANK simulation achieves consistent histograms of the apo and holo ensembles (Fig. S1 in the SI).

Figure 5. Comparing representative snapshots with discrete conformations.

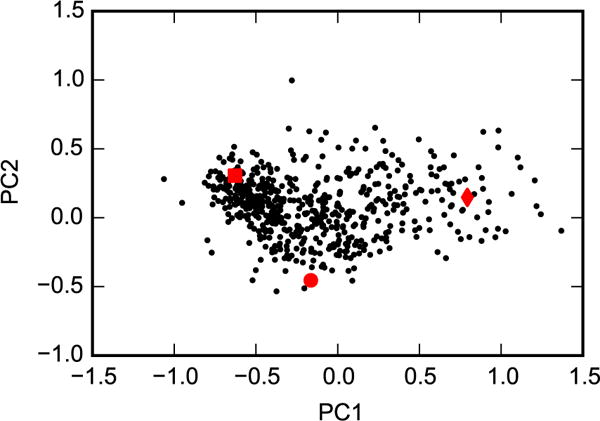
Principal components analysis was performed for the heavy atoms of helix F (residues 107 to 115) based on the crystal structures 2OTZ, 3DN3, and 1QUD, which represent closed (square), intermediate (circle), and open (diamond) conformations, respectively. The 576 representative snapshots (black dots) were then projected onto these eigenvectors.

3.4 AlGDock and YANK binding free energies are consistent

Overall, binding free energies for 24 ligands estimated from 576 AlGDock BPMF calculations with OBC2 implicit solvent and from YANK (which is also based on OBC2 implicit solvent) are consistent with one another (Fig. 6). Consistency between calculations holds for a large range of affinities between −12 and +4 kcal/mol. For all weighting schemes, the Pearson correlation was around 0.90 and root mean square error was around 1.5 kcal/mol (Table 1). Least squares linear regression produced a slope close to 1 and intercept close to 0. The overall consistency between AlGDock and YANK demonstrates that it is feasible to estimate protein-ligand binding free energies using multiple rigid receptor configurations.

Figure 6.

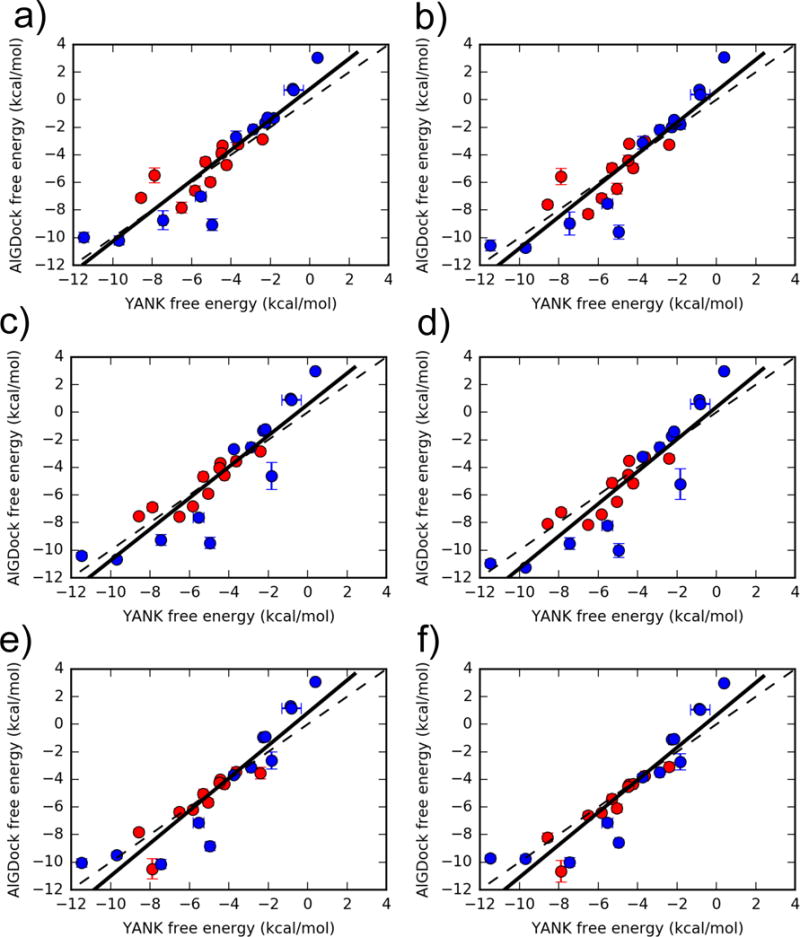
Binding free energies for 24 ligands estimated using YANK (x-axis) and AlGDock (y-axis) based on the OBC2 implicit solvent model. Active molecules are shown as red circles and inactive molecules as blue circles. The labels correspond to different weighting schemes (see text for details). Error bars denote the standard deviation from three independent YANK calculations (x-axis) or from bootstrapping BPMFs (y-axis), with the range of error bars representing a single standard deviation. The function y = x is shown as a dashed line and the linear regression for all ligands as a solid line.

Table 1.

Comparing AlGDock and YANK binding free energy estimates. The AlGDock free energies were calculated using different weighting schemes. RMSE is in units of kcal/mol.

	Full (24)			Active (11)		Inactive (13)
Weighting Scheme	Linear Regression	RMSE	R	RMSE	R	RMSE	R
a	y=1.10x+0.77	1.48(0.23)	0.91(0.02)	1.13(0.20)	0.79(0.04)	1.72(0.33)	0.93(0.03)
b	y=1.14x+0.62	1.57(0.27)	0.91(0.02)	1.23(0.18)	0.75(0.05)	1.81(0.45)	0.93(0.04)
c	y=1.13x+0.56	1.59(0.23)	0.90(0.02)	0.77(0.08)	0.90(0.03)	2.04(0.36)	0.91(0.03)
d	y=1.17x+0.38	1.76(0.27)	0.90(0.02)	0.98(0.16)	0.87(0.04)	2.22(0.44)	0.91(0.03)
e	y=1.18x+0.82	1.53(0.24)	0.92(0.02)	0.93(0.31)	0.90(0.02)	1.90(0.29)	0.92(0.03)
f	y=1.18x+0.66	1.49(0.21)	0.92(0.02)	0.94(0.36)	0.93(0.01)	1.83(0.27)	0.92(0.03)
c1	y=1.09x+0.52	1.75(0.26)	0.87(0.02)	0.89(0.10)	0.87(0.03)	2.23(0.39)	0.87(0.03)

¹Using only snapshots from YANK calculations with active ligands.

The consistency between methods described here is even better than with a previously described host-guest system. Minh²⁰ observed a correlation of 0.71 and root mean square error of 4.5 kcal/mol. While it is surprising that consistency would be worse for a simpler systems, there were some notable differences between the previous and current calculations. The previous BPMF-based calculations were compared to mining minima⁶⁴ rather than alchemical calculations; this introduces some approximation into the reference calculation. Additionally, the previous calculations used fewer receptor snapshots and sampled them based on simple molecular dynamics, which may have limited sampling.

3.4.1 State and structural weighting achieve a balance between accuracy and precision

When considering the effect of weighting schemes, the differences between individual, state, and structural weighting (comparing rows in Fig. 6) are more important than the differences between normalizing each apo state or each YANK simulation. The differences are most evident for a specific ligand, 1-propanol, and for the set of active ligands. For 1-propanol, which has a YANK free energy of around −2 kcal/mol, AlGDock free energy estimates are around −2 kcal/mol based on individual or structural weights, but around −4 kcal/mol based on state weights! The state weighting scheme must endow a snapshot (or several snapshots) that bind tightly to 1-propanol with a larger weight than the other weighting schemes; this is an inaccuracy of the approximation. On a larger scale, however, AlGDock free energy estimates of active ligands using individual weighting (a and b) are not as highly correlated with YANK as those based on state (c and d) or group (e and f) weights (Table 1). This suggests that individual snapshot weights are noisier than the other weighting schemes. For the inactive ligands, on the other hand, individual snapshot weights do not perform worse. This is likely because free energies in the inactive ligand set span a larger range than the active set and the correlation is less sensitive to noise.

Miao et al.⁶⁵ also considered the broader issue - the trade-off between accuracy and precision for importance sampling weights - in the context of accelerated molecular dynamics simulations. They found that the most rigorous approach, exponential average reweighting, only works well if the standard deviation of the boost potential is less than 20 k_BT. Using a first-order cumulant expansion led to precise but inaccurate free energy landscapes. With a second-order expansion, they achieved the best balance between accuracy and precision. For the purposes of reproducing YANK results, it appears that state and structural weighting achieve this balance.

3.4.2 Receptor configuration space overlap is necessary for consistency

In addition to statistical noise of importance sampling weights, another source of inconsistency between AlGDock and YANK is limited receptor configuration space overlap. For the most consistent calculations, the 576 AlGDock snapshots represent regions of configuration space that are most important to YANK calculations (e.g. Fig. 7a). For ligands with the largest differences between AlGDock and YANK results, YANK populates regions of configuration space that are not well-represented by BPMFs (e.g. Fig. 7b). Similar weighted histograms for all 24 YANK calculations are included as Fig. S2 in the SI. In general, it holds that the most consistent calculations have clear receptor configuration space overlap.

Figure 7.

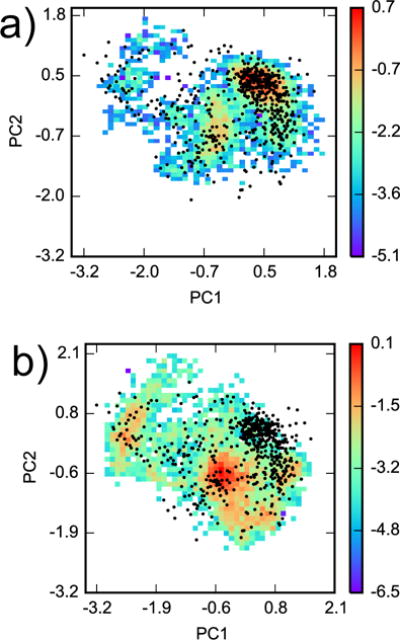
Configuration space comparison between YANK and AlGDock. Principal components analysis was performed on snapshots from all YANK simulations for heavy atoms within 5 Å of Val 111 in PDB ID 3DMZ. Two-dimensional histograms, weighted by Eq. 5, of YANK snapshots from (a) indole and (b) methanol were projected on the first two principal components. The histograms are plotted on a logarithmic scale. The black dots are projections of the 576 snapshots used in AlGDock calculations onto the same eigenvectors.

While it is not ideal that our YANK simulations with six ligands did not access the configuration space necessary for binding 24 ligands, concerns are mitigated by the fact that the worst discrepancies are for inactive molecules. Our YANK calculations essentially force molecules into the binding site and require the receptor to accommodate them. If an inactive molecule is forced into the site, the receptor may adopt conformations that are distinct from the crystal and from those important to binding active ligands. Indeed, we observe that protein configurations observed when binding to active and inactive molecules are distinct (Fig. 8). While the principal components analysis histogram of the former has two distinct peaks, the latter is more diffuse and has three additional high-density peaks. These additional peaks are not supported by experimental evidence, as the three discrete states observed by Merski et al.²⁶ are actually located close to each other within a single peak. Rather, configurations from these additional high-density regions may have an artificially low potential energy due to an artifact of the force field.

Figure 8.

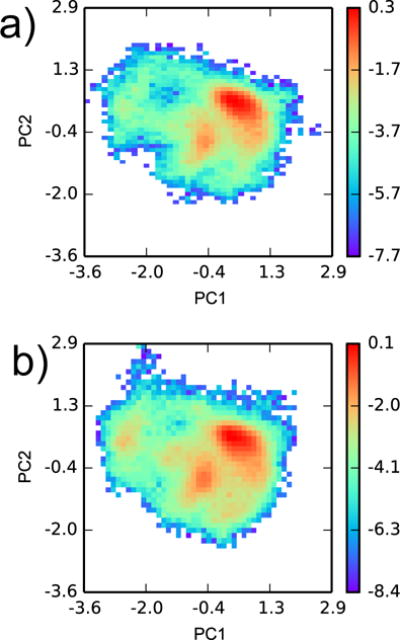
Configuration space comparison between YANK samples from (a) all active and (b) all inactive ligands. Principal components analysis was performed on snapshots from all YANK simulations for heavy atoms within 5 Å of Val 111 in PDB ID 3DMZ. Two-dimensional histograms, weighted by Eq. 5, of YANK snapshots were projected on the first two principal components. The histograms are plotted on a logarithmic scale.

As it is better to estimate a high free energy (weaker binding) for an inactive compound, it may actually be better to not consider these special conformations that preferentially bind inactive molecules. Indeed, we observe that AlGDock systematically estimates a higher free energy for the three weakest binders; these results are less consistent with YANK but more consistent with experiment. Because we are more interested in consistency with experiment than with YANK, our subsequent analysis will focus on calculations with 384 snapshots from YANK simulations with active ligands. We will use weighting scheme (c). The calculations still retain a strong consistency with YANK (Table 1, and Fig. S3 and Table S3 in the SI). Results for all 141 small molecules are reported in Table S4 in the SI.

Table S5 in the SI compares results for halogen-containing molecules with AmberTools radii and with Bondi radii. There are differences in binding free energies up to 2 kcal/mol. For the binding free energy estimated with OBC2 implicit solvent, using Bondi radii has a minimal effect on chlorine, a larger effect on bromine, and the largest effect on iodine, which is consistent with the magnitude of the radius change. Trends with the PBSA implicit solvent energy are less clear.

3.4.3 Snapshots from multiple alchemical calculations improve consistency with YANK

In order to attain configuration space overlap with conformations important to binding a broad range of ligands, it is critical to perform alchemical binding free energy calculations with a variety of different ligands (Table 2 and Fig. S4 in the SI). If binding free energy calculations are only based on snapshots from YANK calculations with the smallest ligands, benzene (ii) and phenol (iv), then the correlation is much weaker and RMSE much larger. In contrast, ΔG° calculations based on snapshots from YANK calculations with p-xylene (iii) and phenol (vi) were nearly as good as with 576 snapshots from simulations with all ligand or 384 snapshots from simulations with active ligands. A simple interpretation of this result is that YANK calculations with larger ligands open up the pocket in ways that accomodate a larger range of molecules. However, BPMF-based calculations based on the large ligand n-hexylbenzene (v) are nearly as bad as those based on benzene or phenol; it opens up the pocket in ways that are not relevant to the binding of most ligands. This counterpoint demonstrates that ligand size is not entirely predictive of receptor sampling. Diverse ligands are helpful for inducing a diversity of receptor conformations.

Table 2.

Correlation coefficients and RMSE of AlGDock free energies with respect to YANK. The AlGDock free energies were calculated using different sets of receptor snapshots, obtained from separate YANK simulations for ligands (i) to (vi) in complex with T4 Lysozyme.

Snapshots used in AlGDock Calculations	Pearson’s R w.r.t. YANK	RMSE w.r.t. YANK (kcal/mol)
all 576 snapshots	0.90 (0.02)	1.59 (0.23)
384 active snapshots	0.88 (0.01)	1.74 (0.22)
i) methylpyrrole	0.77 (0.03)	3.29 (0.35)
ii) benzene	0.72 (0.03)	4.27 (0.45)
iii) xylene	0.86 (0.01)	1.96 (0.32)
iv) phenol	0.19 (0.02)	5.06 (0.77)
v) n-hexylbenzene	0.63 (0.03)	4.75 (0.47)
vi) (±)-camphor	0.91 (0.01)	1.87 (0.15)

3.4.4 Consistency requires only a small subset of snapshots

While a diverse set of receptor conformations is necessary, consistency with YANK may be achieved with significantly fewer snapshots (Fig. 9, a and b). If the snapshots are randomly selected with equal probability, the Pearson correlation rapidly increases for the first 100 snapshots and essentially levels off after about 200 snapshots. The RMSE follows the opposite trend, decreasing instead of increasing with the number of receptor snapshots. If the snapshots are selected in order of increasing dock score or BPMF, however, then significantly fewer snapshots are needed to achieve consistency. The Pearson correlation is high even with a single snapshot. The RMSE diminishes quickly for the first 40 snapshots and then decreases more steadily.

Figure 9. Convergence of free energy estimates.

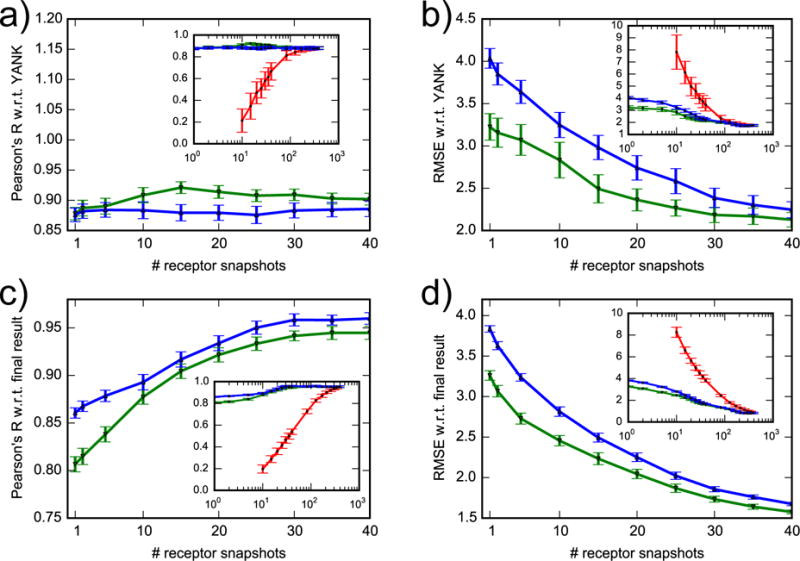
Correlation coefficient and RMSE of AlGDock free energy with respect to YANK (a, b) and to final result (c, d). Snapshots were selected randomly (red line), with lowest docking scores (green line) or with lowest BPMFs (blue line). The x-axis of the inset plots is on a log scale. For clarity, data for randomly selected snapshots are only shown for more than 10.

To analyze receptor-dependent convergence for all 141 ligands, we calculated the Pearson correlation and RMSE compared with using all the receptor snapshots (Fig. 9, c and d). By construction, the Pearson correlation is 1 and the RMSE is 0 kcal/mol for the full 384 snapshots. Consequently, when snapshots are randomly selected, the Pearson correlation continues to steadily increase and the RMSE continues to decrease after 200 snapshots. However, by 200 snapshots, the correlation is already greater than 0.9 and RMSE is already approximately 1.0 kcal/mol; improvements are steady but minor. If the snapshots are selected in order of increasing dock score or BPMF, then the Pearson R increases from approximately 0.8 or 0.85 to 0.95 with around 40 snapshots, increasing more gradually afterwards. The RMSE follows the opposite trend.

These convergence trends suggest that the most efficient way to estimate binding free energies based on ILT is to perform docking with many snapshots and compute BPMFs for a subset with the lowest docking scores. Even if BPMF calculations are significantly optimized, docking calculations are likely to remain faster. Because convergence trends with docking and BPMF-based ranking are similar, docking scores can be used as a reasonable proxy to eliminate receptor snapshots with weak ligand affinities and prioritize BPMF calculations.

3.5 AlGDock free energies are also consistent with experiment

To our knowledge, isothermal titration calorimetry measurements of binding free energies have been reported between T4 lysozyme L99A and 21 active ligands: 16 in Morton et al.²⁹, 3 in Mobley et al.³⁴, and 2 first reported in Liu et al.³⁶. These experimental values and corresponding calculations are shown in Table S6 in the SI. Excluding iodobenzene, an outlier with an anomalously high free energy, AlGDock with PBSA solvent achieves a Pearson correlation coefficient of 0.65 (Fig. 10 and Table 3). If iodobenzene is included, the Pearson correlation coefficient is 0.47 (Fig. S3 in the SI). By all metrics, the MBAR-based estimate is better than estimates based on the minimum interaction energy, mean interaction energy, and docking scores. It also appears, by all metrics except for the absolute RMSE, that PBSA is in better agreement with experiment than OBC2 solvent. The larger RMSE is due to a systematic shift; the aRMSE between PBSA and OBC2 scores is essentially the same (Table 4). We have not determined the cause of this shift. Unless otherwise noted, our subsequent discussion will be based on MBAR-based BPMF estimates using the PBSA solvent model.

Figure 10. Comparing different free energy estimates with experiment.

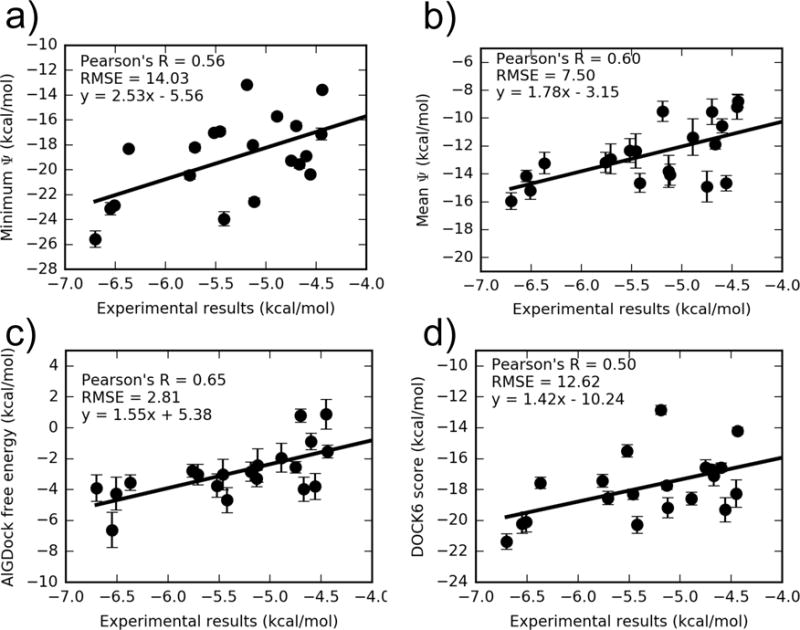
AlGDock free energy estimates in PBSA implicit solvent were based on BPMFs calculated with either the (a) minimum interaction energy, (b) mean interaction energy, or (c) MBAR estimator, using weighting scheme (c). A comparison of the average UCSF DOCK 6 grid score with experiment is shown in (d). Note that the y axes have different limits. The outlier iodobenzene is excluded. For the same plot with iodobenzene, see Fig. S5 in the SI.

Table 3. Comparing different free energy estimates with experiment.

AlGDock calculations were based on 384 snapshots from simulations with active ligands, weighted according to scheme (c). As DOCK 6 does not have an implicit solvent, OBC2 and PBSA describe the receptor potential energies used for snapshot weights. The outlier iodobenzene is excluded from this analysis. For the same table including the outlier, see Table S7 of the SI.

Method	Implicit solvent	Spearman ρ	Kendall τ	Pearson R	RMSE
DOCK 6	OBC2	0.36(0.00)	0.24(0.01)	0.45(0.04)	12.06(0.37)
DOCK 6	PBSA	0.44(0.00)	0.33(0.01)	0.50(0.04)	12.62(0.36)
min Ψ	OBC2	0.39(0.01)	0.27(0.02)	0.55(0.04)	15.46(0.57)
min Ψ	PBSA	0.45(0.01)	0.35(0.01)	0.56(0.03)	14.03(0.59)
mean Ψ	OBC2	0.39(0.01)	0.29(0.01)	0.51(0.04)	9.64(0.47)
mean Ψ	PBSA	0.56(0.00)	0.44(0.01)	0.60(0.05)	7.50(0.38)
MBAR-based	OBC2	0.34(0.01)	0.23(0.02)	0.44(0.06)	1.60(0.17)
MBAR-based	PBSA	0.62(0.01)	0.48(0.01)	0.65(0.05)	2.81(0.32)

Table 4. Comparison of present results and other reported calculations.

Comparing AlGDock and YANK free energy estimates with experiment for different ligand sets. AlGDock calculations were based on 384 snapshots from simulations with active ligands, weighted according to scheme (c). Actual free energies are reported in Table S4 in the SI.

Ligand Set	Statistics	Solvation		Reported
		OBC2	PBSA
All measured except iodobenzene (20 ligands)	Pearson R	0.44 (0.06)	0.65 (0.05)
	Spearman ρ	0.34 (0.01)	0.62 (0.01)
	Kendall τ	0.23 (0.02)	0.48 (0.01)
	RMSE	1.60 (0.17)	2.81 (0.32)
	aRMSE	1.42 (0.18)	1.35 (0.27)
Mobley et al.34 (14 ligands)	Pearson R	0.71 (0.05)	0.71 (0.05)	0.56 (0.06)
	Spearman ρ	0.64 (0.01)	0.69 (0.01)	0.64 (0.01)
	Kendall τ	0.47 (0.02)	0.54 (0.02)	0.45 (0.02)
	RMSE	1.27 (0.14)	2.79 (0.37)	2.00 (0.44)
	aRMSE	1.25 (0.15)	1.26 (0.33)	1.45 (0.32)
Gallicchio et al.68 (4 ligands)	Pearson R	0.93 (0.06)	0.91 (0.05)	0.93 (0.08)
	Spearman ρ	0.80 (0.07)	1.00 (0.00)	0.80 (0.08)
	Kendall τ	0.67 (0.09)	1.00 (0.00)	0.67 (0.09)
	RMSE	1.19 (0.20)	2.37 (0.14)	1.35 (0.09)
	aRMSE	1.05 (0.30)	0.42 (0.10)	0.23 (0.06)
Purisima and Hogues69 (8 ligands)	Pearson R	0.47 (0.11)	0.64 (0.09)	0.91 (0.05)
	Spearman ρ	0.29 (0.07)	0.52 (0.06)	0.98 (0.02)
	Kendall τ	0.14 (0.07)	0.43 (0.07)	0.93 (0.02)
	RMSE	1.37 (0.23)	2.52 (0.21)	1.02 (0.14)
	aRMSE	1.30 (0.21)	0.82 (0.26)	1.02 (0.16)
Ucisik et al.70 (8 ligands)	Pearson R	0.47 (0.11)	0.64 (0.11)	0.82 (0.05)
	Spearman ρ	0.29 (0.05)	0.52 (0.05)	0.69 (0.04)
	Kendall τ	0.14 (0.06)	0.43 (0.06)	0.57 (0.06)
	RMSE	1.37 (0.22)	2.52 (0.24)	10.29 (0.79)
	aRMSE	1.30 (0.23)	0.82 (0.20)	2.42 (0.59)

There are several notable outliers that fall outside the trend line between AlGDock and experimental results. On one hand, AlGDock predicts the affinity of three active ligands, n-methylaniline, iodobenzene, and iodopentafluorobenzene, to be above zero. On the other hand, the AlGDock free energy for four ligands, n-propylbenzene, p-xylene, 2-ethyltoluene, and 4-ethyltoluene, is significantly below the trend line. There are several possible reasons for these outliers. As with the outliers in the comparison between YANK and AlGDock, some outliers are likely artifacts of the state-based weighting scheme. Iodobenzene and iodopentafluorobenzene may be outliers because they contain iodine. There is crystallographic evidence for the formation of a halogen bond between the iodine in iodopentafluorobenzene and the sulfur atom of Met102 in T4 lysozyme L99A.³⁶ Like other fixed-charged force fields with atom-centered partial charges, the GAFF force field that we used cannot model the anisotropic electrostatic potential necessary to create a halogen bond.⁶⁶ Hence, the protein-ligand interaction strength is underestimated. Another potential source of error is the ligand solvation free energy. While iodobenzene does not appear to form a halogen bond with T4 lysozyme L99A,³⁶ AM1BCC charges for the molecule have a large dipole moment that is inconsistent with experiment and cause inaccurate Poisson-Boltzmann solvation energy estimates.⁶⁷ However, the ligand solvation free energy is not the source of the ethyltoluene outliers. The PBSA solvation energies for ethyltoluene with ethyl at the 2, 3, and 4 positions are 2.41, 2,73, 2.70 kcal/mol, respectively (Table S4 in the SI). Since 3-ethyltoluene is consistent with the other isomers, but is not an outlier, ligand solvation is not the reason that 2-ethyltoluene and 4-ethyltoluene are outliers.

3.5.1 AlGDock has comparable accuracy to previous alchemical calculations

Computational binding free energy calculations between small apolar ligands and the artificial cavity in T4 lysozyme L99A have been performed by several groups.^34,68–70

Mobley et al.³⁴ and Gallicchio et al.⁶⁸ used approaches that are similar to YANK. The key methodological difference between their work and our YANK calculations is the solvent model. While Mobley et al.³⁴ calculated binding free energies in explicit solvent, we used PBSA and OBC2 implicit solvent, which are faster but less accurate. Gallicchio et al.⁶⁸ used a different implicit solvent model, AGBNP2.

On the other hand, Purisima and Hogues⁶⁹ and Ucisik et al.⁷⁰ took qualitatively different approaches. Purisima and Hogues⁶⁹ performed exhaustive docking, where they enumerated feasible poses for the ligands and calculated the contribution of each pose to the partition function. Ucisik et al.⁷⁰ performed a Monte Carlo integration of configurational integrals in a rigid binding pocket. They used a number of different force fields (ff99SB, ff94, and PM6DH2) and implicit solvent models (GB, COSMO, and SMD), achieving the best results when combining the semi-empirical PM6DH2 with COSMO.

Each of these studies considered different subsets of the ligands analyzed here (Table S6 in the SI). By the vast majority of metrics, our present results with PBSA are comparable or better than previously reported results (Table 4). Among the Pearson R, Spearman ρ, and Kendall τ correlations, only Purisima and Hogues⁶⁹ outperformed our calculations by achieving nearly perfect Spearman ρ and Kendall τ correlations. For all these sets, our RMSE is relatively large, around 2.5 kcal/mol. However, the aRMSE is comparable to previous calculations for all subsets. With OBC2 implicit solvent, the RMSEs were better, but most correlations were not as good as with PBSA. This is a result of a systematic shift of about 1 kcal/mol in the PBSA calculations.

3.5.2 AlGDock is a better binary classifier than molecular docking

While comparing calculated and experimental binding free energies is the most straightforward assessment of accuracy, the ability to classify molecules as active or inactive is also valuable and nontrivial.

The ability of free energy estimates to discern active from inactive molecules was assessed by the receiver operating characteristic (ROC)⁷¹ curve, the area under the ROC curve (AUC), and the area under the semi-log ROC curve (AUlC)⁷². The ROC illustrates the fraction of true positives versus the fraction of false positives as the threshold separating two categories is changed. An ideal ROC consists of a vertical line from (0,0) to (0,1), and then a horizontal line from (0,1) to (1,1), meaning that all active molecules are more highly ranked than any inactive molecules. The AUC ranges from 0 for completely incorrect to 0.5 for random to 1 for completely correct classification. The intent of the AUlC metric is to emphasize top-ranked molecules, which are more likely to be pursued in subsequent experiments and calculations. For a random classifier, the AUlC is 0.14.

In our hands, the DOCK 6 score for the 141 ligands, which is based on faster sampling and a simpler grid-based scoring function than the AlGDock calculations, is an essentially random binary classifier (Fig. 11 and Table 5). Our poor docking results are consistent with previous comparative studies^5,6 and blinded exercises.⁷

Figure 11.

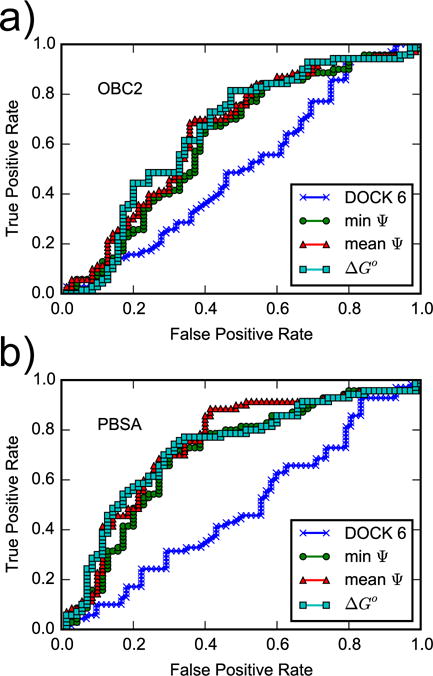
ROC curves for the DOCK 6 score and for AlGDock scores calculated using the (a) OBC2 or (b) PBSA implicit solvent models. Snapshots from YANK simulations with active ligands are weighted according to scheme (c).

Table 5. Area under the ROC curve (AUC) and area under the semi-log ROC curve (AUlC).

ΔG° is estimated from the BPMFs by the minimum (min) or exponential average (exp). BPMFs are estimated by the minimum interaction energy (min Ψ), the mean interaction energy (mean Ψ), or using the MBAR estimator. For comparison, using the minimum BPMF, the AUC and AUlC of DOCK 6 are 0.53 (0.05) and 0.15 (0.03), respectively. Using the exponential average of the BPMF is, they are 0.50 (0.05) and 0.13 (0.03). Errors were estimated by bootstrapping: the standard deviation of the AUC or AUlC based on 100 sets of n free energy estimates randomly sampled with replacement from the original n free energy estimates.

		OBC2		PBSA
Averaging	BPMF	AUC	AUlC	AUC	AUlC
min	min Ψ	0.60 (0.05)	0.17 (0.03)	0.71 (0.04)	0.23 (0.03)
min	mean Ψ	0.63 (0.05)	0.18 (0.03)	0.74 (0.04)	0.25 (0.04)
min	MBAR	0.63 (0.05)	0.18 (0.03)	0.73 (0.04)	0.25 (0.04)
exp	min Ψ	0.61 (0.05)	0.17 (0.03)	0.71 (0.05)	0.23 (0.04)
exp	mean Ψ	0.65 (0.04)	0.19 (0.03)	0.74 (0.04)	0.25 (0.05)
exp	MBAR	0.65 (0.05)	0.18 (0.03)	0.73 (0.04)	0.25 (0.04)

Given a set of sampled ligand configurations from a series of alchemical states, the ability of binding free energy estimates to classify molecules as active or inactive is dependent on the force field used for postprocessing and the statistical estimator. For all estimators, postprocessing with PBSA implicit solvent gives a larger area under the receiver operator characteristic curve than with OBC2 implicit solvent. This result is unsurprising as OBC2 is used as a fast approximation to PBSA. Within the PBSA implicit solvent, the different methods for calculating BPMFs have comparable binary classification performance, with an AUC of and 0.73 and AUlC of 0.25. This suggests that compared to the interaction energy, entropy is not a major factor in the relative binding free energies of small, relatively rigid ligands that bind to the hydrophobic cavity of T4 lysozyme L99A.

The relative performance of OBC2 and PBSA also highlights the importance of the solvent model. This point is further demonstrated by comparision to Mysinger and Shoichet⁷², who used a different solvent model to achieve an AUlC of up to 0.331 for a similar ligand set that included 73 ligands and 64 experimental decoys; this result is better than our best AUlC. Their success suggests that we could improve binding classification with a better treatment of solvation.

One caveat about this comparison is that the computational and experimental definitions of activity are not completely consistent. As our computational approach is based on binding to the active site, it will underestimate the affinity of a ligand that binds to other sites. As the experimental approach is based on a shift in the protein denaturation temperature, it will not account for ligands that bind but do not increase the stability of the protein. It may be worth conducting ITC experiments with some ligands that we predict to bind strongly but have no measurable thermal shift activity.

4 Conclusions and Future Directions

We have demonstrated the feasibility of calculating absolute protein-ligand binding free energies using multiple rigid receptor configurations. Our receptor sampling and weighting strategy based on alchemical free energy calculations for a subset of ligands is capable of reproducing alchemical pathway calculations with a RMSE of about 1.5 kcal/mol. The accuracy of our method compared with experiment is superior to the minimum and mean interaction energies and comparable to previous alchemical pathway calculations. Accuracy is sensitive to the implicit solvent model and is better with PBSA than OBC2 implicit solvent. PBSA implicit solvent, however, is much more computationally expensive than OBC2. In the future, we will explore the accuracy of other molecular mechanics force fields and implicit solvent models. We will also consider the effects of protomers and tautomers.

Because AlGDock and YANK calculations were performed on different computing architectures and we did not undertake significant efforts to optimize them, it is difficult to draw any conclusions about their relative efficiency. For what it’s worth, AlGDock BPMF calculations were performed on single CPUs for less than 10 hours, with the exact wall time depending on the ligand. On the other hand, YANK calculations were performed on single GPUs for about one week. The relative efficiency of the methods is expected to widely vary depending on the size of the system and the extent of conformational changes.

In the long term, a key advantage of the ILT approach is the ability to “tune a knob” between fast but inaccurate and slow but accurate estimates by progressively adding more receptor configurations. Here, we showed that, in line with our expectations, ILT-based free energy estimates became more similar to alchemical results with an increasing number of receptor snapshots. We also found that ranking snapshots based on increasing docking score or BPMF led to much faster convergence than randomly selecting snapshots with equal probability.

The efficiency of ILT-based binding free energy calculations may be improved by future work in methods related to receptor sampling, snapshot selection, and snapshot weighting. Receptor sampling schemes may include biased sampling towards crystallographically-observed structures, Gaussian accelerated molecular dynamics,⁷³ and long molecular dynamics simulations with specialized supercomputers.⁷⁴ Representative snapshots may be selected based on structural features rather than equal simulation time intervals. While there are many ways to improve the calculations, our present results indicate that ILT-based free energy calculations are a promising way to bridge the gap between molecular docking and flexible-receptor alchemical pathway methods.