Dehydration as a Universal Mechanism for Ion Selectivity in Graphene and Other Atomically Thin Pores

Abstract

Ion channels play a key role in regulating cell behavior and in electrical signaling. In these settings, polar and charged functional groups – as well as protein response – compensate for dehydration in an ion-dependent way, giving rise to the ion selective transport critical to the operation of cells. Dehydration, though, yields ion-dependent free-energy barriers and thus is predicted to give rise to selectivity by itself. However, these barriers are typically so large that they will suppress the ion currents to undetectable levels. Here, we establish that graphene displays a measurable dehydration-only mechanism for selectivity of K⁺ over Cl⁻. This fundamental mechanism – one that depends only on the geometry and hydration – is the starting point for selectivity for all channels and pores. Moreover, while we study selectivity of K⁺ over Cl⁻, we find that dehydration-based selectivity functions for all ions, i.e., cation over cation selectivity (e.g., K⁺ over Na⁺). Its likely detection in graphene pores resolves conflicting experimental results, as well as presents a new paradigm for characterizing the operation of ion channels and engineering molecular/ionic selectivity in filtration and other applications.

Ionic transport through protein pores underlies many biological processes. Various factors, such as the presence of charges and dipole moments, structural transitions of the pore, dehydration of ions, make the dynamics of biological pores very complex [1–7]. Solid-state nanopores can delineate these contributions to transport. For instance, a competition of hydrated ion size and pore radius was predicted to result in a drastic drop in ionic conduction [8, 9] – in a way analogous to quantized conductance in electronics – and subsequently observed in graphene laminates [10]. These studies [8, 9], as well as others [11–14], show that, as expected, ions have different free energy barriers due to dehydration, allowing dehydration to yield selectivity on its own. However, the large free-energy barriers typical of ions entering long, narrow pores greatly suppress the current from all ions, making this selectivity difficult to resolve [15, 16].

Due to its atomic thickness, one expects graphene may provide a suitable membrane to detect and exploit dehydration-only selectivity, as we will discuss here. Several recent experiments give tantalizing results in this direction, where, for instance, Refs. 17 and 18 suggest they may have seen dehydration-based selectivity. For instance, Ref. 17 finds that the graphene membrane they use has a small – but measurable – conductance when no pores are present, which they attribute to defect channels. Salts, XCl, with X=Cs⁺, Rb⁺, K⁺, Na⁺ and Li⁺, give conductances that slightly deviate from what their bulk conductivities would predict. However, as their Table 1 and our Table S3 in the Supporting Information (SI) show, the discrepancy is small (less than 50 %). In fact, if the defect channels – the structures of which are not known – are cation selective due to the presence of negative charges, the bulk properties almost perfectly predict the observations. Moreover, the difference in hydration energies is large and not expected a priori to give such a small deviation in conductance (see the SI). These considerations suggest that dehydration is likely not responsible for the small deviation in membrane-only conductance in Ref. 17.

In a similar vein, Ref. 18 finds weak monovalent cation selectivity over divalent cations for sub-2 nm pores. However, the pores had a large variability in conductance over time (see their Fig. 3). Within these uncertainties, the data may be explained by the different mobilities alone, as we show in Table S4 in the SI. Moreover, Ref. 19 recently found highly selective (K⁺ over Cl⁻) graphene pores, where a charged graphene membrane is the likely cause since the selectivity persists for large pore sizes. These membranes also showed a weak monovalent cation selectivity over divalent cations for pores that were 2 nm to 15 nm in diameter. Indeed, for pores in the 2 nm to 6 nm range, the selectivity was of the same magnitude as that observed by Ref. 18, where it is also indicated that their pores are charged. These considerations suggest, as well, that dehydration is not the cause of selectivity in Ref. 18.

The strongest evidence for dehydration-only selectivity in transport comes not from nanopores but from nanochannels in graphene laminates. Ref. 10 shows that channels with a height of ≈ 0.9 nm allow atomic and small molecular ions to permeate but exclude larger molecular ions, and this exclusion is correlated with hydrated radius (as those authors discuss, adsorption may be playing a role in addition to steric hindrance of the water shell). This height, though, is above the scale necessary to mimic and understand biological ion channels.

Another recent study, however, finds selectivity of K⁺ over Cl⁻ in porous graphene [20]. This selectivity drops rapidly when the (mean) pore diameter increases by about 0.1 nm to 0.2 nm. This was attributed to the presence of charges. However, such a sharp feature is indicative of an atomic scale process, of which dehydration is the obvious culprit. Moreover, this is selectivity of a mono-atomic ion over another (with almost identical mobilities), just as in biological systems. We will show that the selectivity they find (≈ 1.3 for a distribution of pore sizes, giving ≈ 1.8 to 2.5 for a pore radius of ≈ 0.2 nm, see our SI) is consistent with the partial dehydration ions experience when going into single atom thick pores with a radius in the sub-nanometer scale. We believe that this is the best evidence of dehydration-only selectivity in nanopore experiments so far.

Results and Discussion

Atomically thin pores – pores that are one to a few atoms thick, such as graphene, MoS₂, or hexagonal boron nitride – display more intricate behavior when the pore radius reaches the scale of the hydration layers compared to long pores and channels. Molecular dynamics (MD) simulations show that the ionic current through graphene pores (see the schematic in Fig. 1) exhibits nonlinear behavior as the pore radius, r_p, is reduced to the sub-nanometer scale. This nonlinear behavior is seen as a rapid drop in the ionic current, Fig. 2(a,b), and an excess noise in the current, see the SI. At these length scales the pore edge begins to deform the hydration layers, increasing the energy barrier for ions to cross the pore.

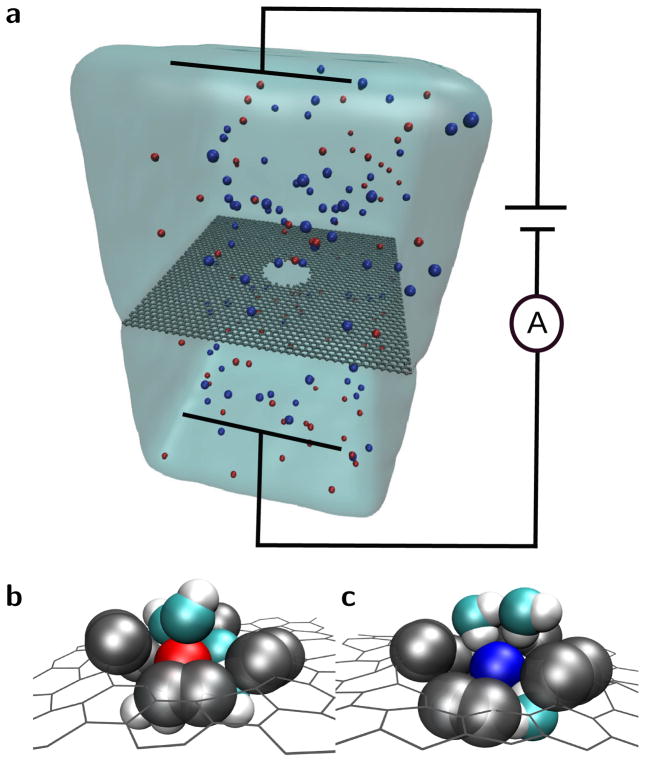
FIG. 1.

Schematic of ion transport through a graphene nanopore. (a) An applied bias across the membrane drives an ionic current so that, when the pore is sufficiently small, the ions have to partially shed their hydration layer in order to translocate through the pore. Red and blue spheres represent K⁺ and Cl⁻ ions, respectively. Water is shown as a continuum even though we use an all-atom model for this work. (b) A potassium ion and (c) a chloride ion crossing the pore maintain significant hydration, unlike in long, narrow pores. Carbon at the edge of the pore, oxygen, and hydrogen are gray, cyan, and white spheres, respectively.

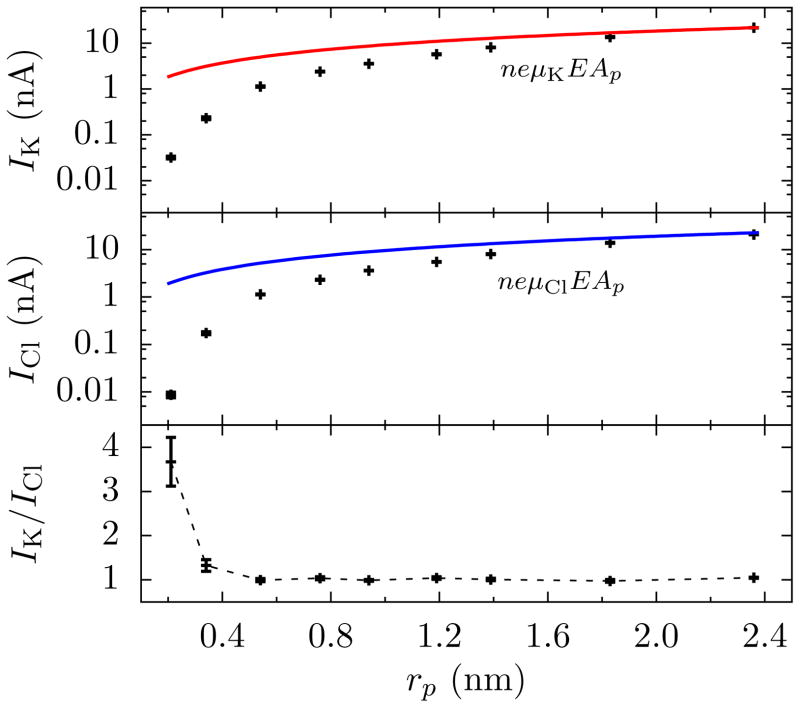
FIG. 2.

Selective behavior of graphene pores as a ratio of cation (I_K) to anion (I_Cl) currents versus the pore radius (as determined by MD simulations). For large pores (r_p ≳ 2 nm), the ionic current is due to bulk flow but limited by the pore’s cross-sectional area, A_p, available for transport. In this situation, the contribution to the current from species ν is proportional to ez_ν n_ν μ_ν (times A_p and the electric field, E, in the vicinity of the pore due to a 1 V applied bias, see Fig. S3), where z is its valency, n its number density, and μ its mobility (shown as red and blue lines for K⁺ and Cl⁻, respectively). Thus, for potassium and chloride, the ratio is I_K/I_Cl = μ_K/μ_Cl ≈ 1, as the relative mobility of K⁺ to Cl⁻ is 1/1.04. When the pore is very small, though, the relative cationic contribution to the total current increases. This is due to a higher dehydration energy of the anion compared to the cation. Connecting lines are shown as a guide to the eye. Error bars are ±1 Block Standard Error (BSE) everywhere unless indicated otherwise (details are discussed in the SI).

In particular, graphene pores with r_p = 0.21 nm and in 1 mol/L KCl display selectivity of K⁺ over Cl⁻ despite containing no charges or dipoles, as shown by the MD simulations in Fig. 2(c). That is, no electrostatic repulsion or specific interaction with the membrane is needed for its appearance. The selectivity and sharp rise in resistance was also seen for lower concentrations of KCl (see the SI), i.e., this behavior is not due to ion-ion interactions or some other many-body effect.

To quantify the energetic differences of K⁺ and Cl⁻, we perform Adaptive Biasing Force (ABF) calculations for the smallest pore size. The ABF results, Fig. 3(a,b), demonstrate that – without an applied voltage – the K⁺ is between 20–40 meV (depending on where we measure the difference) more favored to be in the pore compared to Cl⁻, although both have to pay a substantial energy penalty. These equilibrium energy barriers are determined by the partial dehydration of the ions. When ions are in the atomically thick pore, water molecules can rearrange just outside of the pore to maintain significant hydration of the ion (see Fig. 3c). Ions only have to lose about 1/4 of their inner hydration water molecules in order to be at the pore center. When the pore radius is smaller than the radius of the first hydration layer, a much larger dehydration occurs (about 3/4) in long pores, as water molecules can only be at opposite ends of the ion (see Refs. 8 and 9). This will lead to related, but different, nonlinearities in the current.

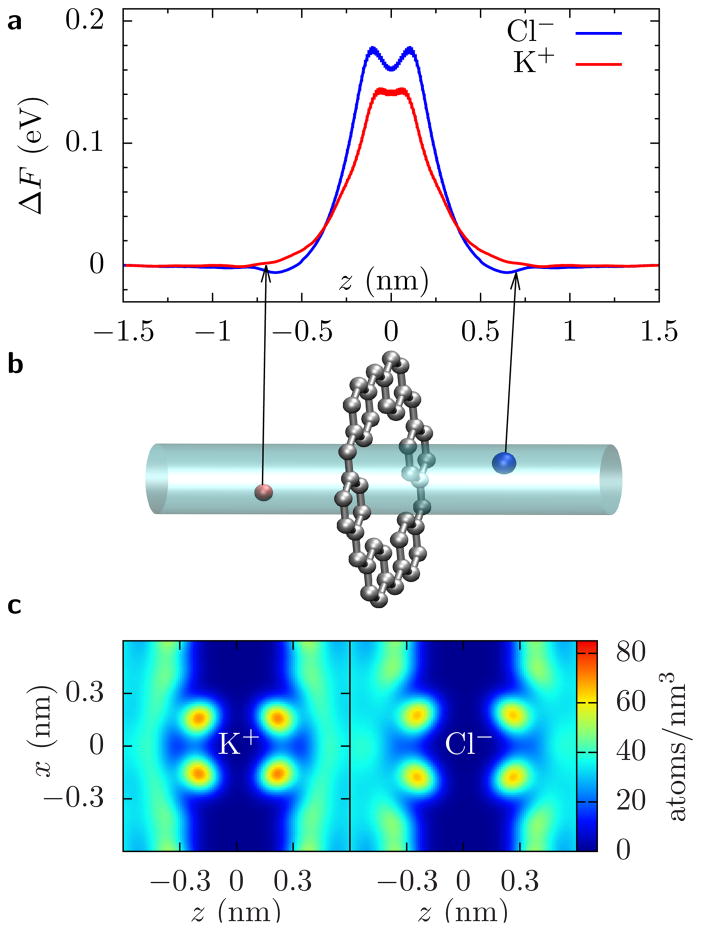
FIG. 3.

Free energy and hydration in graphene pores. (a) The free energy change of an ion to go from bulk into a pore with radius r_p = 0.21 nm versus the ions’ z coordinate. (b) Schematic of the simulation showing the cylindrical region where a K⁺ (red sphere) or a Cl⁻ (blue sphere) ion is con-fined for the ABF calculation. In the smallest pore and at 1 V, the relation I_K/I_Cl = A₀e^{(ΔF_K−ΔF_Cl)/k_BT} ≈ 3.5, where A₀ ≈1, k_B is Boltzmann’s constant, and T is temperature, implies that the free energy change of Cl⁻ should be about 30 meV larger than that for K⁺. This is consistent with the ABF calculation (between 20–40 meV depending on where we measure the difference). (c) Oxygen density from water around a potassium or a chloride ion fixed at the center of the r_p = 0.21 nm pore. Within the first hydration layer, there are 〈n〉 = 5.2 and 〈n〉 = 5.8 waters around K⁺ over Cl⁻, respectively, which is approximately 1/4 less than in bulk in both cases. See the SI for more data regarding ΔF and the density plots. Error bars in (a) are ±1 BSE.

The difference in energy barriers is due to a smaller dehydration energy of K⁺ compared to Cl⁻, which can be estimated from the relation,

$$\mathrm{\Delta }{E}_{\nu }(r_p)=f_{1\nu }(r_p)E_{1\nu },$$ (1)

where f_1ν is the fractional dehydration in the first hydration layer and E_1ν is energy of the first hydration layer [8, 9]. This energy penalty is about 0.27 eV for K⁺ and 0.37 eV for Cl⁻ when using f_1ν ≈ 0.25 (see Fig. 3(c)). Moreover, the fraction f_1ν can be approximated purely on geometric grounds: When an ion is in the center of the smallest pore, water molecules can not enter the pore due van der Waals (vdW) interactions with the carbon and the ion. The area available for water is composed of two spherical caps of radius r_1ν – the radius of the first hydration layer – on either side of the membrane. The fractional area encroached by membrane is d/2r_1ν where d is the thickness of the membrane as seen by the water molecules near the pore edge. This thickness is d ≈ 0.2 nm, slightly smaller than the distance between water and the graphene membrane, as water molecules can move into the corrugated openings at the pore edge. This gives f_1ν ≈ 0.3 for both ions, when using r_1ν = 0.33 nm and 0.31 nm for K⁺ and Cl⁻, respectively [9], in agreement with the full MD calculation.

The free-energy difference from the ABF calculation for each ion is about half of the value estimated using Eq. (1). To show why, we examine the net water dipole in the first layer when the ion is inside and outside the pore. The net dipole is reduced by about 5 % to 10 %. Therefore, when about 25 % of the water is lost, the remaining waters orient more strongly and the energy barrier is not 25 % of the first hydration layer energy, but less than half of that. The energy barrier is thus qualitatively in agreement with what Eq. (1) predicts but reduced due to stronger orientation of the remaining water dipoles (which is possible because interference from water-water interactions decreases). Finally, we note that other effects, such as polarization of graphene and different functional groups and/or pore shape (i.e., different atomic scale structure and graphene edge type), will change the observed barrier. However, when charges or static dipoles are absent, the main contribution to the free energy barrier is due to fractional dehydration – as qualitatively captured by Eq. (1). These barriers will differ from ion to ion, giving rise to weak selectivity (depending on the ion types, this will be cation over anion, anion over cation, cation over cation, etc.). This selectivity will thus appear in other atomically thin pores (pores that have a thickness of one to a few atoms), such as hexagonal boron nitride and MoS₂.

The selectivity also depends on the applied voltage, as seen in Fig. 4 (see also the SI). The increasing selectivity from 0.25 V to 1 V is due to the lower barrier for K⁺ versus Cl⁻. In this region, the current contribution from each ion species ν can be fit with the form

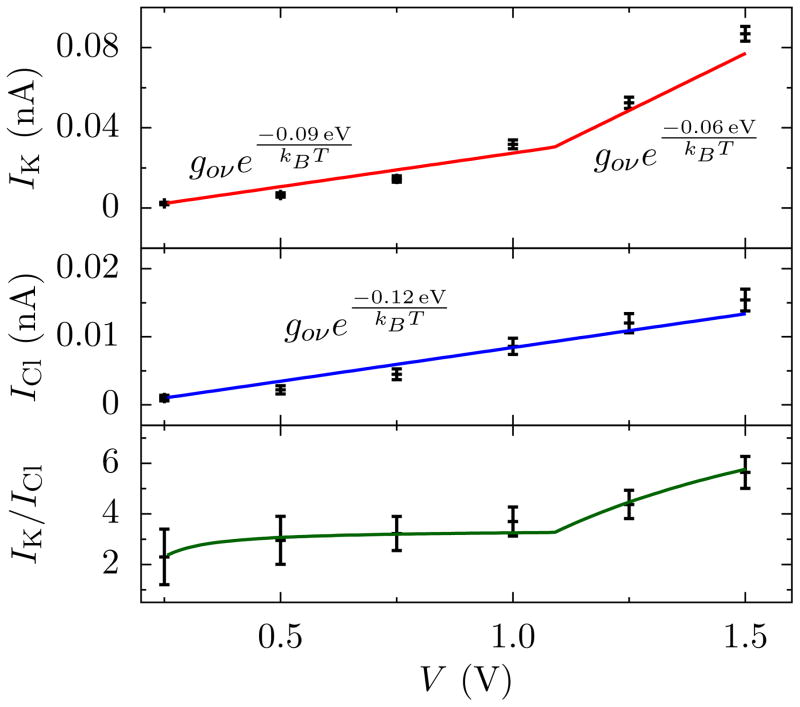
FIG. 4.

Current and selectivity versus voltage. Current-voltage characteristics for K⁺ and Cl⁻ for the pore of radius 0.21 nm at 1 mol/L KCl (top panels). The selectivity of K⁺ over Cl⁻ in the same pore (bottom panel). For small voltages, the ions display roughly linear behavior. Thus, we fit a piece-wise linear model for current taking each region to be linearly related to the differential conductance g_ν = ez_ν n_ν e^{(−ΔF_ν/k_BT)} μ _ν A_p/L = g_0νe^{(−ΔF_ν/k_BT)}. This piece-wise local conductance model (solid lines) can not capture all the features observable in the MD simulations (data points), but it captures the suppression of the current by the free energy barrier and how that barrier changes with voltage. Around (1.1 ± 0.1) V the energy barrier for potassium drops from ≈ (0.09±0.004) eV to ≈ (0.06±0.002) eV, whereas that of chloride remains approximately constant at ≈ (0.12±0.001) eV. This results in sharper rise in the potassium current and, hence, selectivity. Error bars are ±1 BSE.

$$I_{\nu }=g_{\nu }V+c_{\nu },$$ (2)

where

$$g_{\nu }=e{z}_{\nu }{n}_{\nu }{e}^{(-\mathrm{\Delta }{F}_{\nu }/k_{B}T)}{\mu }_{\nu }{A}_p/L$$ (3)

and c_ν is a constant. This form of the current cannot capture all of the intricate behavior, but it does capture the main feature – the suppression of the current by the dehydration free energy barrier. The magnitude of c_ν reflects behavior below 0.25 V, which is a regime that is dificult to reach with all-atom simulations. Given c_ν, the differential conductance, Eq. (3), determines the selectivity as the voltage increases. This conductance depends on the valency, density, mobility, and free-energy barrier of ion ν, as well as the electric field E and pore area A_p. Taking the electric field to be V/L with L = 1 nm (in agreement with the fields found from the MD simulations) and $A_p=\pi r_p^2$, the nonequilibrium free-energy barriers are (0.09±0.004) eV and (0.12±0.001) eV for K⁺ and Cl⁻, respectively. These values are slightly less than the equilibrium free-energy barriers from the ABF calculation in Fig. 3. As we discuss below, this is likely because of water polarization in the pore that helps ions to move through. The value of other parameters, especially A_p and the voltage range, also affect the extracted free-energy barriers both in equilibrium and out of equilibrium (computationally, for instance, sampling a smaller area in Fig. 3(a,b) will lower the barrier, and fitting the I-V curve at lower voltages will increase the barrier extracted). We note, though, that the difference in free-energies between K⁺ and Cl⁻ is the same in equilibrium and at low voltages.

Using the parameters for K⁺ and Cl⁻ in Eq. (2), the selectivity will increase with voltage until it saturates at

$$\frac{I_{\mathrm{K}}}{I_{\text{Cl}}}=\frac{g_{\mathrm{K}}}{g_{\text{Cl}}},$$ (4)

which fits well with the selectivity data from MD, as shown in Fig. 4. However, we see that at ≈ 1 V, the selectivity starts to increase still further. Indeed, the differential conductance of K⁺ increases at ≈ 1 V due to an effective lowering of the barrier to (0.06 ± 0.002) eV. This lower barrier is due to a polarization-induced chaperoning of the ion across the pore. As the local electric field increases with voltage, water becomes increasingly polarized in the vicinity of the pore and also increases its density there. When, for instance, K⁺ sees a pore containing polarized water where the oxygen atoms are pointing towards the ion, it can more easily move to the pore edge and be taken through to the other side. The K⁺ responds to this at lower voltages than Cl⁻ due to – surprisingly – its vdW interaction with carbon, which allows the charging layer of K⁺ to be closer to the membrane than Cl⁻ (see Fig. S-3(a), which shows the voltage drop is mostly on the Cl⁻ side).

There are thus two facets of selectivity: the mechanism and the nonlinear features with voltage. The former depends on the dehydration energy and the pore geometry, and the latter depends on structural changes of water in the pore as the voltage increases (as well as vdW interactions). Since both are dependent only on geometry and ion characteristics in bulk water, these features will be present for other atomically thin pores and channels. This mechanism for nonlinearities and selectivity gives simple predictions that can be tested experimentally by examining multilayer graphene [16], MoS₂ pores, or other pores.

Moreover, selectivity has recently been observed in graphene membranes [19, 20]. In Ref. 20, the selectivity is weak, giving an average ratio of translocation rates of about 1.3 ± 0.1 for potassium to chloride at zero applied bias but in the presence of a concentration gradient across the membrane (see the SI). This experiment has a distribution of pore sizes for each membrane. Assuming the smallest pores make a negligible contribution to the current – and thus do not affect the average selectivity even though they are themselves selective – and the largest pores have no selectivity, the experimental observations yield a selectivity in the range ≈ 1.8 to 2.5 for a r_p = 0.21 nm pore. This is larger than potential variation due to effective mobilities and agrees well with the dehydration-induced selectivity of ≈ 2.3 that we find at low voltages. In addition, using the free energy barriers and areas from MD, we can compute the expected selectivity for the experiment. It comes out to be ≈ 1.5, also in excellent agreement with observations (see the SI). In Ref. 19 the selectivity is much higher (≈ 100), even for large pores (r_p in the 1 nm to 10 nm range, i.e., well above the size of hydration layers). In both experiments, though, the selectivity was attributed to the presence of charges on the graphene.

Our results indicate, however, that weak selectivity is the consequence of different dehydration energies and fractional removal of water (determined by the hydrated ion size and pore geometry) – i.e., not due to local charges or dipoles, which would result in the much higher selectivities observed in Ref. 19 and in biological pores. While charges/dipoles can not be ruled out as an explanation for the results of Ref. 20, they would need to be far from the pore, really small in magnitude, or only present in a minority of pores in order to generate weak selectivity. That is, charge selectivity is much stronger in general and also less sensitive to pore radius. This would leave unexplained why a small increase in pore radius eliminates selectivity. Screening can play a role here, suggesting that changing the molarity of the solution – thereby changing when selectivity disappears as the pore radius increases – is a simple test to determine the presence of local charges/dipoles.

The other effects we predict – nonlinear features in the current-voltage characteristics and enhanced selectivity – can be observable experimentally if the structural and electronic integrity of the membrane can be maintained at higher voltages (e.g., biases in excess of about 250 mV start to degrade some graphene membranes [17]. Polarization-induced chaperoning, though, should be present even in other thin membranes that may keep their integrity to higher voltages). These results elucidate selectivity and dehydration effects in transport when going from the nanoscale [17, 21–24] to sub-nanoscale channels and pores. It should help design and understand the behavior of solid-state pores that serve as hosts for other nanoscale probes, i.e., localizing and interrogating molecules or nanoscale structures, such as DNA sequencing with ionic [25–32] or transverse electronic currents [33–39].

Moreover, selectivity in biological ion channels is complex and due to many competing interactions and processes. Indeed, dehydration is so important in tiny biological ion channels that it is only the presence of charges, dipoles, and protein structure/dynamics that allows ions to pass by counteracting dehydration. Indeed, selectivity occurs because the pore interacts with ions in an ion-dependent manner, e.g., due to the atomic configuration in the protein’s selectivity filter [1]. Although functionalization of, and surface impurities on graphene are currently not completely known and controllable, our results suggest that graphene offers a route to characterize ion transport behavior in confined geometries without the effect of protein structure, surface charges, etc. This will likely lead to the development of experimental model systems to mimic and understand biological channels, e.g., by delineating the dehydration contribution in more complex biological systems.

Finally, one of the core challenges with the use of solid-state membranes for filtration and other applications is to engineer selectivity. Control of surface charges and site-specific chemical functionalization of, e.g., graphene, is currently not possible. Our results suggest that the geometry, which is significantly more controllable, can be designed to give selectivity. Depending on application, dehydration – potentially with other factors – can be exploited to control ion exclusion, selectivity, and flow rates. For instance, layering the graphene (in addition to changing the pore radius) can give measurable dehydration-only selectivities over two orders of magnitude and exclusion over many more[16]. For ion separation, though, one would want to exploit dehydration or charge-based selectivity in combination with functional groups (or charge) to enhance the overall ion flow of the desired ion. Moreover, these results will shed light on the role of the electrostatic environment and functionalization introduced by the fabrication process, as well as other conditions such as pH. Together with a characterization of pore functionalization, solid-state pores will thus allow – for the first time – to experimentally delineate the contributions to transport in more complex biological pores, and for the optimization of porous structures for applications.

Methods

We perform all-atom molecular dynamics using NAMD2 [40] and the CHARMM27 force field, where we first minimize the energy of the system and then heat it to 295 K. A 0.5 ns NPT (constant number of particles, pressure and temperature) equilibration using the Nose-Hoover Langevin piston method followed by 1.5 ns of NVT (constant number of particles, volume and temperature) equilibration generates the initial atomic con-figuration. An electric bias applied perpendicular to the plane of the membrane drives the ionic current through the pore. The production run varies from 100 ns to 1.1 μs depending on convergence of the current and other properties of interest.

We use the adaptive biasing method in the colvar module of NAMD to perform the free energy calculation. In this simulation, an ion is confined within a cylinder of height 1 nm and radius 0.2 nm centered at the origin. The biasing force helps the ion overcome potential barriers and explore the energy landscape. The total simulation consists of about 120 runs of 10 ns each to obtain the free energy difference shown in Fig. 3. We use the block standard error method to compute the error bars for all plots. Additional details are in the Supporting information.